1 Introduction

Natural disasters, especially those related to water -like storms and floods- have increased over the last decades both in number and intensity. According to the Intergovernmental Panel on Climate Change (IPCC) reports, a flood event is defined as the overflowing of the normal confines of a stream or other body of water or the accumulation of water over areas that are not normally submerged (Kundzewicz et al. 2014). This definition includes river floods, flash floods, urban floods, pluvial floods, sewer floods, coastal floods, and glacial lake outburst floods.

One of the most dangerous flooding events is the so-called flash flood, which is related to short rainfalls with high intensity and mainly happens in small basins (less than 1000\(\hbox {km}^2\)) (Marchi et al. 2010). In these areas, the response time to avoid tragedies is often a few hours or even less, which makes alert systems crucial to guarantee human and infrastructure safety (Hofmann and Schuttrump 2019). In Europe, flash food rises up to 40% of the total events in the period 1950-2006 (Barredo 2007), and the level of potential damage is also increasing due to human pressure on ecosystems. Marchi et al. (2010) shows that in the Mediterranean region flash floods are the most common events occuring mainly in autumn.

Under the current Climate Change framework, several reports predict an increase in the intensity and duration of extreme climatic events. In this sense, sea-level rise and the increase of storms are expected to exacerbate the vulnerability of coastal areas to natural hazards (Piggott-McKellar et al. 2021; Hummel et al. 2017). Recent studies show a statistically positive trend in floods during the twentieth century, which is consistent with the climate models’ results and, also, they predict continuity of this tendency (Milly et al. 2002). Besides, this increase is likely to be more evident in short-duration storms. This implies an increase in the magnitude and frequency of flash floods (Westra et al. 2014). However, these results can be partially explained by improvements in reporting, human settlement or urbanization in flood-prone areas, or even a decrease in the awareness about natural risks (Kundzewicz et al. 2014). These same factors can explain the perceived increase in flood risk. In any case, there is evidence that global warming has the potential to increase heavy precipitation patterns but with considerable uncertainty in the magnitude, and huge regional variability (Kundzewicz et al. 2017; Arnell and Gosling 2016). This means that several adaptation plannings are needed (Ramm et al. 2018).

In the last decades, data has become more available. Geographical Information Systems, real-time data sources, the inclusion of expert and stakeholder judgment, together with the integration of socio-ecological frameworks, have increased environmental modelling complexity (Kaikkonen et al. 2021), and hence robust models are necessary (Wang et al. 2022; Ziyi et al. 2022).

In general, methodologies found in the literature are based on objective measurements (precipitation, river basin characteristics or return period), but subjective factors (risk perception, preparedness or awareness) are also considered a crucial aspect (Amundsen and Dannevig 2021; Masuda et al. 2018). For example, Sulong and Romali (2022) review the methods applied in flood damage assessment taking into account measurements like flood depth, or building resistance. The process of translating information about flood risk modeling from scientific discussion to local management or decision making process is often complex and full of misunderstanding and information losses (McDermott and Surminski 2018; Adekola and Lamond 2017). How society estimates or considers the risk of flooding is related with their preparedness, awareness and worry, to reduce negative effects of flood (Huang and Lubell 2022; Sairam et al. 2019). Flood defense structures are also needed to be monitored and controlled (Tarrant et al. 2018). Besides, in order to minimize flooding consequences, emergency response needs to be efficient (Longenecker et al. 2018). All these components merged together have implied a broader development of methodologies and theories, including the inherent uncertainty (Kim et al. 2017). However, the majority of papers are based on specific hydrological models, or a combination between them and others. Other methods applied are regression models, specific equations, or expert knowledge.

Decision support systems (DSS) can be defined as an approach for the management of different natural phenomena, like flood disasters, taking into account several man-made and natural characteristics (Omid et al. 2023). In the literature, it is easy to find several papers about DSS applied to floods based on different methodologies. Omid et al. (2023) develops a DSS for developing sustainable goals and define the proper strategy before, during and after the flood. This model is based on hydrological gathered data, Logistic Regression, Neural Network, and Support Vector Machine as Machine Learning (ML) methods. Scopetani et al. (2022) learns a DSS to provide information enough to define a priority scale of interventions in a river basin of Italy in order to prevent levee breakage. Barbetta et al. (2022) develop a tool named WAter Safety Planning Procedures Decision Support System (WASPP-DSS) for small water utilities. The aim is to assess the impact of floods on water supply systems. Also, Pugliese et al. (2022) present a methodology to increase urban resilience to flooding risk. This tool joins GIS processing with hydraulic simulations, constituting a DSS based on the meta-heuristic optimization algorithm Harmony Search. Finally, Bentivoglio et al. (2022) review a total of 58 papers analyzing the use of deep learning methods in flood mapping and conclude its potential applicability. In the literature, it is easy to find papers that use machine learning techniques to output the assessment of flood risk. Our work moves in this direction and relies on Bayesian networks to develop an alert system in a Mediterranean catchment.

Bayesian Networks (BNs) were initially defined in the 80 s, and applied at length in several fields (Aguilera et al. 2011), including environmental modelling (Das and Chanda 2022; Maldonado et al. 2022). This paper deals with flooding risk analysis, and the literature shows some applications with BNs. Niazi et al. (2021) present a BN model that represents interconnected elements of vegetated hydrodynamic systems to model coastal flooding risk. Paprotny et al. (2021) develop a BN to predict losses derived from a flood in coastal areas. Wu et al. (2020) model flood disaster risk by coupling ontology and BNs models. Finally, Paprotny and Morales-Nápoles (2017) use BNs for estimating mean annual maxima and return periods of discharge in Europe rivers.

The aim of this paper is not to predict if a rainfall event will happen or not; this type of model is extensively developed and applied. The objective is to create a DSS to determine, with a probability value, if the study area will need an alert state or not, i.e., with information about meteorological predictions, if the situation will be considered dangerous or not in the near future. Besides, this decision support system needs to be as simple as possible, so the number of variables and model complexity reduced, but a balance between simplicity and robustness is maintained. Considering that the Mediterranean area suffers from flash floods very often, the model developed in this paper needs to be able to deal with this type of event. Throughout this paper, referring to floods includes both normal and flash floods. The final decision is usually made by a manager or an expert, so this tool helps them to improve the information available. Moreover, the use of BNs as the core model of the decision support system adds interpretability and explainability to the predictions of the model, in contrast to some other black-box models, and develops a trustworthy decision support system. Thus, Sect. 2 shows the methodology of developing an alert system based on BNs. A two-level model was performed, with a first-level composed of an independent model for each catchment, and a second level of a rule system that is developed to join all the previous models into a single meta-model. Section 3 discusses the results, and finally, Sect. 4 draws some conclusions and identifies future works.

2 Methodology

Figure 1 summarizes the methodology followed in this paper. The aim is to develop an alert system based on BNs, able to predict flood alert states in Mediterranean catchments. This model is divided in two levels: i) first-level is composed of a set of individual sub-models (one per each catchment) learnt based on BNs (Sect. 2.3), and ii) a more second-level complex meta-model based on a set of rules to determine the state of alert in the entire system (Sect. 2.4).

Once the entire model was learnt, two scenarios were included (Sect. 2.5), using the data of an extreme storm event (the Filomena storm, January 2021) and a non-extreme storm (October 2020).

Fig. 1
figure 1

Methodological diagram of the model divided into three steps: (i) Data collection, (ii) first-level models learning and (iii) meta-Model learning. White nodes refer to original variables (rainfall and river’s levels), grey nodes refer to artificial discrete (or continuous) target variables. SAIH, Andalusia Hydrological Information System; Naïve Bayes clas., unsupervised classification based on Naïve Bayes; Naïve Bayes reg., regression model based on Naïve Bayes

Full size image

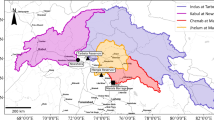
2.1 Study area

Andalusia is the second largest Autonomous Region of Spain and the most densely populated with a cultural heritage from both Europe and Africa. It covers a surface areaFootnote 1 of 87.600 \(\hbox {km}^{2}\), and contains three main catchments (Guadalquivir, Atlántica and Mediterranean). In this paper, we focus on the Mediterranean catchment (Fig. 2), which comprises more than 17000 \(\hbox {km}^2\) and 200 municipalities. Its main characteristic is climatic variability, both in temperature and rainfall patterns, with deep differences between the humid West over 2000 mm annually (Systems I3 and I4) and the dry East, with less than 200 mm annually in some points of Almería province (Systems IV and V). Both physical characteristics and relief make this area quite vulnerable to extreme climatic events, where floods provoke several economic and, often, life costs. This situation is even more intensive in the coastal area, where more than 60% of the population is settled. Scenarios of Climate Change predict for Andalusia a decrease in rainfall patterns, with, at the same time, an intensification of extreme events. This means less amount of water, but in less time and in an intensive, or even, violent, way. For example, last January 2021, the heavy storm event Filomena provoked more than 600 incidences in Andalusia, with 2 people deaths, and more than 200 l in 24 h.

Fig. 2
figure 2

Location of Mediterranean catchments. Map obtained from SAIH website

Full size image

2.2 Data collection and pre-processing

Data were collected from the Andalusian Hydrological Information System (SAIH)Footnote 2 from a set of points shown in Fig. 3. SAIH presents a set of collected points divided into: i) dams, so data are related to meteorological information and dam variables (rainfall, level, volume, among others); ii) river station, with information only about river level (in some cases also includes meteorological variables); and iii) meteorological stations, with variables like rainfall, atmospheric pressure, among others. In all cases, data can be downloaded in different time scales (monthly, weekly, daily or hourly).

Complete hydrological years were used, from October 2011 to September 2021 with data obtained at hourly frequency. Since the aim is to learn our model as simple as possible, variables collected from each point were:

  • Rainfall: total amount of rainfall in one hour expressed in mm.

  • River or Dam level: the water height expressed in m.

Fig. 3
figure 3

Location of collected points. Maps obtained from SAIH website. a System I3, b System I4, c System II, d System III, e System IV and f System V

Full size image

Once data were collected, it was divided into two data sets, one for learning/training (October 2011–September 2020) and one for inference/testing (October 2020–September 2021). All data were continuous, but rainfall variables were discretized using the Equal Frequency method with 3 bins because of the high percentage of zeros, since the Mediterranean area is characterized by large periods of drought. This method makes zeros belong to the first bin, and the rest of the information to the other two bins.

During the data collection step, a block of 5 months of missing data due to a sensor disruption was found in System I3. A data imputation method based on BNs was applied in order to complete the missing values. Due to space limitation, this initial step of missing data imputation was proposed and deeply explained in Ropero et al. (2022). Finally, data were organized by catchment (according to Fig. 2), and a summary of the variables is shown in Appendix A.

For validation purposes, two events of storm were selected from the inference dataset (October 2020–September 2021). First, the extreme event Filomena that begun on 6th January and lasted around 4 days, but the worst days were the 8th and 9th with historical snowfall in the center and East of Spain and high values of rainfall in the rest of the Iberian Peninsula. When this storm ended, an extreme cold spell began and lasted 7 days breaking temperature records. Besides, a non-extreme storm from 20th to 23th October 2020 was selected. It hardly lasts a day in the East, but two days in the West area. However, the highest rain values was achieved on 22th October.

We show in the results how both events can be predicted using the decision support system developed in this paper. Our decision support system was not compared against any other model since we think that the literature did not produce similar models yet. Models for flooding are very common, and also other decision support systems, but they usually include more complexity and a number of variables and inputs. The most similar one is the model developed by the National Agency of Meteorology Footnote 3 and this is not public. However, a comparison between the output of our model and the alert established by the National Agency was done.

2.3 First-level models based on BNs

Bayesian networks (BNs) were proposed in the late 80 s, and deeply developed in the last decades (Aguilera et al. 2011; Jensen and Nielsen 2007; Pearl 1988). They are defined as a directed acyclic graph composed of a set of nodes (variables) and arcs linking them that determine the (in)dependence relationships between variables. These relationships are quantified based on a conditional distribution \(p(x_{i}/pa(x_{i}))\) for each variable \(X_{i},i=1,2,\dots ,n\) given its parents in the graph denoted by \(pa(X_{i})\). Initially, BNs were developed for discrete variables, but nowadays we find a broad and consolidated set of algorithms for hybrid and continuous variables (Cobb et al. 2007; Moral et al. 2001; Lauritzen 1992). In this paper, we follow the so-called Mixture of Truncated Exponential (MTE) model for parameter estimation of the BNs with hybrid data. For detailed information about MTE theory see Cobb et al. (2007); Rumí and Salmerón (2007); Rumí et al. (2006); and Flores et al. (2019); Maldonado et al. (2016) for environmental applications.

According to Aguilera et al. (2011), BNs can cope with different aims depending on the number and nature of the target variable(s). In this work, the specific goal in this first level, is to learn a model that is able to predict the degree of the rainfall event. In this case, the goal is to predict the target variable as precisely as possible, rather than trying to accurately model the joint probability of all the variables. For this reason, the so-called fixed structures are used as they are designed to focus on predicting the goal variable, rather than studying the interdependencies between the variables. There are some fixed structure models developed specifically for classification, but we will work with Naïve Bayes (Minsky 1963). This because, even though it is the simplest one and adds some topology restrictions (the feature variables are assumed to be independent given the class), it gets very competitive results while needing low computation (Flores et al. 2012). This is crucial in this work, since a decision support system like this cannot wait for the results to be handed in. It consists of a BN with a single root node and a set of feature variables having only the root node as a parent. Its name comes from the independence relations derived from the topology of the network; feature variables are independent given the root variable (Fig. 4), the naivety. In the following sections, we explain briefly the main characteristics of each of the submodels.

To this end, the Mediterranean catchment is divided into 6 systems, each of them with different characteristics, and three situations are found, each one of them leading to a different submodel:

  • No information about river level in the coastal area. Systems I3, II, III and V do not present collected points in the coastal area, which means no information about the river level is available. In this case, an unsupervised classification was performed.

  • System IV has no information in the coastal area too. However, it differs in the amount of zeros in the dataset, which makes BNs difficult to be directly used because of the lack of accuracy in the estimations. Thus, this system was modeled using a k-means clustering learned in R software.

  • System I4 has information about river level in the coastal area. A collected point (A38) is found close to the coastal area with continuous data. So, the model for this system aims to accurately predict the river level at A38 point. Since the target variable is continuous, a regression model based on BNs was learnt.

Fig. 4
figure 4

Example of a Naïve Bayes structure where Y is the target variable and \(X_{1}\), ..., \(X_{n}\) are the feature variables

Full size image

2.3.1 Unsupervised classification

As we said before, in this first level, our goal is to predict local alerts for each system. Since we do not have previous information about these alerts and the amount of rain in the past, it is not possible to use supervised methods. So, we need to focus on learning unsupervised models, in which the target variable is defined as a hidden variable and learnt dynamically. In this case, since the target variable is discrete, we will be dealing with an unsupervised classification or soft-clustering problem. For systems I3, II, III and V, unsupervised classification models with a Naïve Bayes structure based on Hybrid Bayesian networks were learnt. The model parameters were estimated based on the probabilistic clustering methodology proposed by Fernández et al. (2014), and implemented in the Elvira software (Elvira-Consortium 2002). Figure 5 shows an outline of this methodology consisting of two steps:

  • Estimating the optimal number of states: Since no prior information about the number of states (or groups) of the target variable is specified, the optimal number needs to be estimated. So, we consider the target variable as a hidden variable H, whose values are missing (Fig. 5i)). Firstly, we consider only two states for variable H, that are uniformly distributed with the same probability value, for each observation, of belonging to both groups, i.e., 50%; see Fig. 5ii). Now, the model is estimated based on the data augmentation method (Tanner and Wong 1987) as follows: a) the values of H are simulated for each data sample according to the probability distribution of H, updated specifically for the corresponding data sample, and b) the parameters of the probability distribution are re-estimated according to the new simulated data. In each iteration, the Bayesian Information Criterion (BIC) score of the model is computed, and the process is repeated until there is no improvement. In this way, the optimal parameters of the probability distribution function of the model with two states and its likelihood value are obtained – Fig. 5iii). The following step consists of a new iterative process in which a new state is included in the variable H by splitting one of the existing states – Fig. 5iv). The model is again re-estimated (by repeating the data augmentation method) and the BIC score is compared with the previous run. The process is repeated until there is no improvement in the BIC score, so achieving the final model containing the optimal number of states – Fig. 5v).

  • Computing the probability of each observation to each state Once we have obtained the optimal number of class variable states, the next step consists of probability propagation, also called the inference process (For more information see Rumí and Salmerón 2007). In this step, all the available information for each observation in the sample is introduced in the model as a new value called evidence, and propagated through the network, updating the probability distribution of the class variable. Finally, from this new distribution, the most probable state of the variable H for each data sample is achieved.

Fig. 5
figure 5

Outline of the unsupervised classification based on hybrid BNs probabilistic clustering. Dotted arrows represent the relations between the variables when parameters have not been estimated yet. B, BIC score. Figure adapted from Ropero et al. (2015)

Full size image

In System IV, k-means clustering was performed in order to explore the potential of BNs to be used together with other statistical methodologies. K-means is an algorithm for unsupervised classification with organized observations into a set of k groups or clusters, which is fixed beforehand. The clusters are then positioned as (groups of) points and all observations, or data points, are assigned to the closest cluster. Using the Elbow Method, k was set at 3 and implementation of the k-means was done with R.

2.3.2 Regression model based on BNs

When the target variable is continuous, we are dealing with a regression problem. Assuming a set of variables \(Y, X_1,\ldots , X_n\) are available, regression analysis aims to find a model g that explains the response variable Y in terms of the feature variables \(X_1,\ldots , X_n\). That is, given a full observation of the features \(x_{1},\ldots , x_{n}\), a prediction about Y can be obtained as \({{\hat{y}}} = g(x_{1},\ldots , x_{n})\), with g being a mean estimator, the sample mean for example.

A BN can serve as a regression model for prediction purposes if it contains a continuous response variable Y and a set of discrete and/or continuous feature variables \(X_1,\ldots ,X_n\). Thus, in order to predict the value for Y from k observed features, with \(k \le n\), the conditional density

$$\begin{aligned} f(y\mid x_1,\ldots ,x_n), \end{aligned}$$
(1)

is computed, and a numerical prediction for Y is given Footnote 4 using the expected value as follows:

$$\begin{aligned} {\hat{y}} = g(x_1,\ldots ,x_n) = {{\mathbb {E}}}[Y\mid x_1,\ldots ,x_n] = \int _{\varOmega _Y} y f(y\mid x_1,\ldots ,x_n)dy, \end{aligned}$$
(2)

where \(\varOmega _Y\) represents the domain of Y.

Note that \(f(y\mid x_1,\ldots ,x_n)\) is proportional to \(f(y)\times f(x_1,\ldots ,x_n\mid y)\), and therefore, solving the regression problem would require a distribution to be specified over the n variables given Y. The associated computational cost can be very high. However, using the factorization determined by the network, the cost is reduced. Although the ideal would be to build a network without restrictions on the structure, usually this is not possible due to the limited data available. Therefore, networks with fixed and simple structures are used.

In any case, regardless of the structure employed, it is necessary that the joint distribution for \(Y,X_1,\ldots ,X_n\) follows a model for which the computation of the density in (1) can be carried out efficiently. As we are interested in models able to simultaneously handle discrete and continuous variables without any restriction in the structure developed, the approach that best meets these requirements is the MTE model. This model allows us to avoid some requirements needed in the traditional multiple linear regression based on the Gaussian distribution, such as distributional assumption or homoscedasticity and can be considered somehow as a non-parametric regression, which leads to more flexible models. Also, lack of independence of the feature variables is solved by the fixed topology of the network (Naïve Bayes). Regarding inference, the posterior MTE distribution, \(f(y \mid x_1,\ldots ,x_n)\), will be computed using the Variable Elimination algorithm.

For learning the model, we follow the approach of Morales et al. (2007) to estimate the corresponding conditional distributions. Let \(X_i\) and Y be two random variables, and consider the conditional density \(f(x_i\mid y)\). The idea is to split the domain of Y by using the equal frequency method with three intervals. Then, the domain of \(X_i\) is also split using the properties of the exponential function, which is concave, and increases over its whole domain (see Rumí et al. 2006). Accordingly, the partition consists of a series of intervals whose limits correspond to the points where the empirical density changes between concavity and convexity or decrease and increase.

At this point, a 5-parameter MTE is fitted for each split of the support of X, which means that in each split there will be 5 parameters to be estimated from data:

$$\begin{aligned} f(x) = a_0+a_1e^{a_2x}+a_3e^{a_4x}, \quad \alpha< x < \beta \,, \end{aligned}$$
(3)

where \(\alpha\) and \(\beta\) define the interval in which the density is estimated.

The reason to use the 5-parameter MTE lies in its ability to fit the most common distributions accurately, while the model complexity and the number of parameters to estimate is low. The estimation procedure is based on least squares (Rumí et al. 2006).

A natural way to obtain the predicted value from the distribution is to compute its expectation. Thus, the expected value of a random variable X with a density defined as in (3) is computed as

$$\begin{aligned} {{\mathbb {E}}}[X]= & {} \int _{-\infty }^{\infty } xf(x)dx = \int _{\alpha }^{\beta } x(a_{0}+a_{1}e^{a_{2}x}+a_{3}e^{a_{4}x}) dx \\= & {} a_{0}\frac{\beta ^{2}-\alpha ^{2}}{2} + \frac{a_{1}}{a_{2}^{2}}((a_{2}\beta -1)e^{a_{2}\beta }-(a_{2}\alpha -1)e^{a_{2}\alpha }) \\{} & {} + \frac{a_{3}}{a_{4}^{2}}((a_{4}\beta -1)e^{a_{4}\beta } -(a_{4}\alpha -1)e^{a_{4}\alpha }). \end{aligned}$$

If the density is defined by different intervals, the expected value would be the sum of the expression above for each part.

In the case of System I4 both the target (A38 river level) and the features (rainfall and river level information) are continuous variables. A Naïve Bayes structure is once again employed to achieve accurate predictions of the target variable. Model learning adhered to the approach outlined by Morales et al. (2007), with a detailed methodology expounded in Ropero et al. (2014), and implemented using the Elvira software (Elvira-Consortium 2002).

2.4 Meta-model

Once the first-level models are learnt, the next step consists in joining them in the second level and learning the final meta-model (Fig. 1). A new virtual data set is created where the feature variables are the results of the previous sub-models (an alert state in each catchment) and the probability of each observation. Then, a rule system was created in order to establish the alert system. This configures the decision support system which gives information about whether an alert state will be necessary or not. To gain interpretability, the different states of the meta-model have been defined by experts (Fig. 6):

  • Normal situation: When all catchments present No Rainfall situation.

  • Drizzle situation: In this case, the study area is divided into West and East areas. To belong to this state, at least one of the systems included has to present a Drizzle situation.

    • West area: including systems I3, I4 and II.

    • East area: including systems III, IV, and V.

  • Local Extreme event: Again, the study area is divided into West and East areas and to belong to this state, at least one of the systems included has to present a Rainfall Event situation.

    • West area: including systems I3, I4 and II.

    • East area: including systems III, IV, and V.

  • Global Extreme event: In this last case, all catchments (i.e., all models), present the Rainfall Event situation.

Note that, with the division into West and East areas, it is possible that, at the same time, two states are activated. For example, it could be possible to activate Drizzle situation in West while the East area presents a Local Event. This allows us to capture real situations with different possible levels of alert.

Fig. 6
figure 6

Diagram of the rules for the meta-model. Note that it is possible that two states coexist (for example, Drizzle at West and Rainfall at East)

Full size image

2.5 Forecasting

Once the meta-model is learnt, new information is included in models as evidence with the aim of predicting changes in the systems through the inference process or probabilistic propagation (Aguilera et al. 2011).

Even when the objective of the decision support system is to predict the behavior of the system in the near future, information about a past storm event is used to validate the model. In order to check the versatility of this model, two scenarios were tested: the extreme event Filomena, and a non-extreme storm during October 2020. In both cases, rainfall values from the storm are included as evidence in the first-level models, specifically, in rainfall variables, and propagated through the network. In both classification and regression models, if we denote the set of evidenced variables as \({{\textbf {E}}}\), and their values as \({{\textbf {e}}}\), then the inference process consists of calculating the posterior distribution \(p(x_i |{{\textbf {e}}})\), for each variable of interest \(X_i \notin {{\textbf {E}}}\):

$$\begin{aligned} p(x_i |{{\textbf {e}}}) = \frac{p(x_{i},{{\textbf {e}}})}{p({{\textbf {e}}})} \propto p(x_{i},{{\textbf {e}}}), \end{aligned}$$
(4)

since \(p({{\textbf {e}}})\) is constant for all \(X_i \notin {{\textbf {E}}}\). This process can be carried out by computing and normalising the marginal probabilities \(p(x_{i},{{\textbf {e}}})\), in the following way:

$$\begin{aligned} p(x_i, {{\textbf {e}}}) = \sum _{{{\textbf {x}}} \notin \{ x_{i},{{\textbf {e}}} \} } p_{e}(x_{1}, \ldots , x_{n}), \end{aligned}$$
(5)

where \(p_{e}(x_{1}, \ldots , x_{n})\) is the probability function obtained from replacing in \(p(x_{1}, \ldots , x_{n})\) the evidenced variables \({{\textbf {E}}}\) by their values \({{\textbf {e}}}\).

In the case of System IV, the information about the storm is also included via the predict function implemented in R, which assigns a cluster to each new observation. So, one of the existing clusters is assigned to each new observation, the closer one according to the Euclidean distance.

The global scheme of usage for prediction is based on the dynamic characteristic of the model. When forecasting, we can include evidence (information) on different variables in different temporal moments. In this way, we can include actual river level measurements together with weather forecasts of rainfall in time +k (\(k>0\)), and obtain the probability of the different flood alerts for time +k+j (\(j>0\)). In this model, these time steps k and j are expressed in hours. As these k and j increase, the accuracy of the flood-alert decreases but they become more relevant as a decision support system, since time is crucial in these type of events.

3 Results and discussion

In this section, we will detail the results of the different parts of the decision support system involved, namely results for the first-level models, for the second-level or integrating meta-model and the forecasting for Filomena and the non-extreme events scenario of the decision support system.

3.1 First-level models results

Table 1 shows a summary of the first-level models. For each system, an individual model was built except for Systems I3 and III which include two main rivers each (Marbella and Guadario, and Adra and Motril, respectively). Thus, for these systems, two models (one per river) were learnt. The number and nature of variables included in each model differ.

Table 1 Summary of the first-level models. Var., Variable; # Number; Unsp.Clas., unsupervised classification based on BNs. The number of variables includes the target variable. Note that System I4 is a regression model and its results are expressed as a continuous variable and no number of states is applied
Full size table

Although each system presents a distinct number of feature variables, both BNs and k-means have estimated in all cases three as the optimal number of states (Table 1). As an example, Figs. 7 and 8 show, respectively, the results that either the hidden target variable or the number of clusters is optimal when 3 is set as the number of states. From the environmental point of view, it implies that the system modeled presents three different situations with the following characteristics:

  • Cluster 0. All observations belonging to this cluster present no rainfall values and the lowest river level. So, it corresponds to the No rainfall situation.

  • Cluster 1. In this state, rainfall variables present lower values and the river level hardly changes with respect to the situation prior to the beginning of the rain. So, we called it a Drizzle situation.

  • Cluster 2. This group includes those observations in which both rain and river level values present higher values. So that corresponds to a Rainfall Event.

Fig. 7
figure 7

Results from k-means based classification model for System IV. Rainfall variables are expressed in mm, Level variables are expressed in meters

Full size image
Fig. 8
figure 8

Results from BNs based classification model for System III, Adra catchment. Rainfall variables are expressed in mm, Level variables are expressed in meters

Full size image

In the case of System I4 model, since the target variable is continuous, results are expressed as estimates of the river level at the A38 collected point, located in the coastal area. The regression model presents an error rate of 0.056, measured as the root mean square error. Figure 9 shows the results of the estimation in black, and the real values in red. In general, the model tends to overestimate the river level increase. In order to include it in the next step, results were discretized according to expert guidelines given by SAIH, which established the threshold of river level that is considered dangerous. Thus, if the river level rises 1.0 m, it is considered as a risk of flooding, and included in the state of Rainfall Event in the virtual dataset created to learn the meta-model. We could have discretized initially, then developed a classification method instead, but we decided to develop the first-level model for continuous variables, and discretized it afterwards, because of the increased accuracy of the first level output for the continuous case, and the interpretability of the corresponding results.

Fig. 9
figure 9

Values estimated vs real values in System I4 (learning data, from October 2011, to September 2020)

Full size image

3.2 Scenario of Filomena

Once the complete meta-model was learnt, we validated it initially with the extreme event Filomena, introduced as evidence in the first-level models. The way evidence was included depends on the type of model:

  • Unsupervised classification models: the evidence items were included in the rainfall variables and propagated through the Naïve Bayes structure to update the class variable. So, we obtain, per hour, the state of the system and its probability.

  • k-means cluster: Finally, the k-means cluster was updated using the predict function, as previously explained.

  • Regression model: for system I4, a regression model was learnt where the target variable is continuous. As in the case of previous classification models, evidence was included in rainfall variables and propagated, but the results are expressed as an estimated value for the continuous target variable.

The Filomena storm started on 7th January afternoon (local Madrid time) and lasted until 10th of January approximately, with intensive rainfall during the first 2 days. This event presents rainfall values hardly achieved in the last decades, so that, not included in the learning dataset. It means that our model is facing with a new situation, not learnt previously, and this validation give us information about how robust is our model against new events, especially, extreme events never seen before.

Figure 10 shows an example of the results from a BNs-based classification (first-level model). Figure 10 a) shows the evolution of the system state and the total rainfall per hour. In this case, it is possible to see the change from No Rainfall state to Event state, and later, when the storm stabilized, the system again changes to Drizzle state. However, hours later, an increase in the rainfall made the system immediately change to Event. This evolution fits with the behaviour of the storm, with a sudden beginning of heavy rainfall, followed by sets of hours of stability but sudden and short rainfalls. The model is able to accurately predict the alert state of the system.

One of the advantages of BNs is the fact that results are expressed in terms of probability, so that, for each observation, we obtain the value of the alert state but also, the probability of that state. These probability values can be used as a measure of the uncertainty in the alert system, and provide information about how probable a situation of alert is. Thus, from an expert point of view, we can determine a threshold to decide if an observation belongs to a cluster (alert situation) or not. In this paper, a 0.9 value of probability was set as threshold, so all observations with a probability over it are considered to belong to this alert state. When the probability is under this threshold, we consider that the system is changing from one state to another and need more time to study the evolution. In this sense, Fig. 10 b) shows the evolution of the system state vs the probability of the state. Here we can see that there is a decrease in the probability of the state when a change is going to happen. See for example the probability values during 6th January, even when the system state is No rainfall, the probability is under 0.9, which gives us the signal that system seems to suffer a change. Close to 7th January, the system state changes to Event, and the probability starts to increase until becoming stable at 1.0 in a couple of hours. Another case is after the first part of the storm, from 9th January rainfall decrease and a set of hours with No rainfall is followed by 3 small rainfall events (Fig. 10 a). In this case, probability moves indicate the change of the system 3-4 h in advance. So, with the inclusion of new information, the model is able to detect, a few hours before, that the system is going to change. Thus, even when the state is No rainfall, its probability tends to decrease and becomes high again when the state change.

This difference is clearly visible against the k-means cluster. While BNs include new data into the previous cluster learned by means of probability propagation, k-means used the Euclidean distance. Thus, a threshold can not be established.

Figure 11 a) shows the results of System IV. In order to compare both methodologies, a classification model was learnt but based on k-means (R software was used). The optimal number of states is not known, so the Elbow rule was carried out, and 3 was set as the optimal number of clusters. In this case, there is no probability value, but again, it is possible to see the evolution of the system state fits with the rainfall evolution. See that at the beginning of the event, the system moves first to Drizzle state, and later to Event. Also, during the worst days of Filomena the system moves through all the states. Finally, just the first rainfall small event (on 10th January) is enough to change the alert state, but not the others. Despite the different methodologies, the results are comparable. However, BNs allow us to measure the uncertainty through the probability values and, in general, predict with more accuracy the system state.

Finally, System I4 is based on a regression model, and results are expressed as an estimation of river level at the coastal area (Fig. 11 b). The root mean square error calculated is 0.31. Due to space limitations, the other systems’ results are not shown.

Fig. 10
figure 10

Results of Adra (System III) under the Filomena storm

Full size image
Fig. 11
figure 11

Results of System IV and System I4 (a regression model based on BNs) under the Filomena storm

Full size image

When all first-level models are updated with the new information, we apply the rule system and obtain, per hour, the alert state of the complete Andalusian Mediterranean catchments during the Filomena storm. According to the rules, Andalusia was divided into West and East areas because of their characteristics. As it was explained in Sect. 2, West Andalusia is more humid than East. This difference is clearly visible in Fig. 12 a) and b). During the Filomena storm, the West area rose more than 150 l per hour, whilst the East hardly achieved 100 l. However, in both areas, the meta-model determines the level of alert, from No rainfall situation to Local Extreme event. As in the first-level models, alert fits with the rainfall evolution. Figure 12 c) shows the alert for all Andalusia, with no difference between West and East. In this case, a new state was defined, Global Extreme event. Results show that, during approximately two days, the situation in all Andalusia was extreme. This agrees with the information collected from the news and Spanish National Meteorological Agency (AEMET) that set the orange and red alert in these areas for these two days.Footnote 5

Fig. 12
figure 12

Temporal evolution of alert both at West (a), East (b) and all (c) Mediterranean Andalusian catchments during the Filomena storm and the total rainfall per hour

Full size image

Note that, even when in this paper we have used data from the past, the idea of the model is to include the wheather forecast in order to predict the behavior of the system in advance. In this way, it could be possible to determine, using probability values, if the weather forecast is going to provoke an alert state or not in Andalusia.

3.3 Scenario of non-extreme storm

A second scenario was also examined. A non-extreme storm was selected from last October 2020. This event last hardly a day in the East, and two days in West area. In total, rainfall values rise more than 50 mm in some areas of Andalusia, far away from the 200 mm during the Filomena storm (a really extreme event). These data were used in order to show that our model does not only give robust results in non common situations, but also in small and not heavy-rain events. Evidences were included in the model in the same way explained previously for the scenario of Filomena (Sect. 3.2). In this case, only results from the meta-model are shown (Fig. 13). As in the previous scenario, rainfall values are printed with the alert state. At the beginning of the storm, just a Drizzle situation is achieved, with rain values lower than 100 mm per hour. But during 22nd October, rain values achieve the highest values with Rainfall state, or even Extreme alert situation. As soon as this storm ends, the situation goes back to normal or no rain.

Fig. 13
figure 13

Temporal evolution of alert in Mediterranean Andalusian catchments during the non-extreme storm and the total rainfall per hour

Full size image

4 Conclusions

This paper aims to develop a decision support system able to predict a flood alert in Andalusian Mediterranean catchments. A set of models based on Bayesian networks was learnt for each catchment, and joined together into a more complex model based on a rule system. BNs are a powerful tool able to be mixed with other mathematical/statistical methodologies and provide proper and accurate results. In this work, the meta-model is created by combining three types of models, two based on BNs (classification and regression) and k-means clusters. Once the model is obtained, it provides an accurate forecast of the flood situation of the greatest catchment areas of Andalusia. The key point is that using simple weather forecasts and live measurements of the river level, we can get a flood-alert several hours before happening.

Results obtained in this paper show that the methodology proposed is at the same time simple enough to be implemented, but robust. Besides, its simple structure allows experts and stakeholders to understand the methodological principles followed. However, some future works have been identified. Firstly, a deeper analysis of the thresholds needs to be done, in order to explore the potentialities of this probabilistic nature. In this paper, the meta-model is based on a rule system to make it easier to interpret and because the threshold of river level to be considered risky is pre-defined by experts. However, as a future work, the meta-model structure could be based on BNs instead of a system of rules.