1 Introduction

In this paper, we build on the opportunities offered to school geometry by dynamic geometry environments (DGEs; Sinclair et al., 2016) while looking for ways to encourage students to reason about geometric shapes and their features and provide teachers with relevant information on the quality of students’ conceptual understanding (Star & Stylianides, 2013). We proceed from Euclidean constructions of quadrilaterals conducted on paper with a straightedge and a compass, transform them into the DGE using the dragging function (Erez & Yerushalmy, 2006), and assign the students tasks that could not be performed on paper due to retroactive changes included in them. We aim to have the DGE tasks as close to the classical geometry as possible so that the construction steps in the dynamic construction comply with the ones in the Euclidean construction and all of them are visible.

Using a data collection instrument consisting of these DGE tasks accompanied by questions directed at the identification and justification of shapes emerging in dynamic constructions, we already conducted a study focusing on reasoning of lower-secondary school students (Vízek et al., 2023). The study confirmed the potential of the instrument for gathering students’ justifications; however, we also experienced some weaknesses in the amount and comprehension of collected data. Therefore, in the present study, we first redesign the instrument to reduce these weaknesses, and then explore what information the instrument provides about the quality of students’ conceptual knowledge. Within this context, we conduct an exploratory qualitative empirical study addressing the following research question:

  • RQ: Having an assessment instrument based on a set of dynamic dragging constructions of quadrilaterals that comply with Euclidean constructions, what information can the instrument provide about the quality of students’ conceptual knowledge?

2 Theoretical background

2.1 Conceptual knowledge in mathematics

In educational research, conceptual knowledge in mathematics can be understood in two ways. Some studies proceed from the widely known characterization by Hiebert and Lefevre (1986) that introduces conceptual knowledge as “knowledge that is rich in relationships,” which “can be thought of as a connected web of knowledge, a network in which the linking relationships are as prominent as the discrete pieces of information” (Hiebert & Lefevre, 1986, p. 3). This view holds conceptual knowledge as knowledge that is known deeply. Other studies (Star & Stylianides, 2013) consider conceptual knowledge as not automatically deep and instead characterize it merely as knowledge of concepts, with the degree of the interconnectedness of the concepts informing about the quality of such knowledge. In both cases, the development (in quality) of conceptual knowledge is achieved by creating new connections between two or more already known concepts, or between a known concept and a newly comprehended one (Hiebert & Lefevre, 1986).

Here we define conceptual knowledge in the latter sense and, similar to Krathwohl (2002) and Nilsson (2020), distinguish among three dimensions of conceptual knowledge: knowledge of classification, knowledge of structures, and knowledge of principles. Knowledge of classification refers to the awareness of a certain mathematical idea that is isolated or loosely connected to other concepts. Such knowledge is typical for novices who, for instance, understand the concept of arithmetic operations of addition and subtraction but may not perceive the inverse relation between them (Schneider & Stern, 2009). Knowledge of structures means the ability to compare and connect concepts that leads to acquisition of the conceptual structure of a mathematical domain. For example, students understand a fraction not only as part of some whole but also as a number that can be compared with integers (Richland et al., 2012). Knowledge of principles refers to generally applicable principles, for instance, to the knowledge that increasing the operands of the addition operation also increases the sum, independent of the particular value of the operands (Prather & Alibali, 2010).

In research studies to date, the measurement of conceptual knowledge is accomplished in two basic ways: by focusing on the implicit understanding manifested while performing a procedure in problem solving, or by targeting the explicit expression of knowledge of concepts (Rittle-Johnson & Schneider, 2015). Measurement instruments aiming at explicit displays of conceptual knowledge are focused on explaining the classification of a mathematical object, describing and justifying its properties, or clarifications of certain general principles (Crooks & Alibali, 2014). The assessment of conceptual knowledge is typically based on non-routine problems that require the use of non-standard or non-algorithmic solving approaches and, so, provide greater manifestations of understanding independent of a certain type of problem (Braithwaite & Sprague, 2021). However, a task that is non-standard for one student may be familiar to another. So, a remaining challenge in the assessment of conceptual knowledge is to design assessments that provide a meaningful system for assessing the levels of conceptual knowledge and are applicable to wider ranges of students (Star & Stylianides, 2013).

2.2 Comprehension of geometric objects

Geometry has a unique visual character that allows us to study the properties of mathematical objects on the basis of their images (Laborde, 2005). Various levels of thinking and various students’ figural concepts correspond to different comprehensions of geometric objects (Fujita, 2012). According to de Villiers (1994), geometric shapes can be grasped through two main approaches: partition classification and hierarchical classification. Partition classification comprehends shapes as separate objects. Specifically, a square, a rectangle, a rhombus, and a parallelogram are understood as different shapes, although they share certain common features. Hierarchical classification represents a structure in which shapes are precisely sorted according to their common features: a rectangle or a rhombus is understood as a specific type of a parallelogram, and a square appears to be the most special of these in terms of hierarchy, having all the common features of the preceding ones.

At primary school, students usually get formally acquainted with planar shapes via initial definitions using lengths of sides and angles. At secondary school, this context is enriched with other attributes of shapes, such as diagonals. The hierarchy of quadrilaterals can be given by properties of sides and angles as well as diagonals (Kabaca, 2017); however, the order of familiarization with individual concepts has an impact on the way students comprehend the shapes and the definitions of the shapes they prefer (Zazkis & Leikin, 2008), and so tasks that are based on properties of diagonals are typically non-routine for secondary school students.

2.3 Classical vs. digital tools and geometry education

In traditional Euclidean geometry education, planar shapes are constructed using a pencil, a straightedge, and a compass on paper and represented by a static composition of points, lines passing the points, and circles. This practice can be supported by DGEs such as Geometer’s Sketchpad, Cabri Geometry, or GeoGebra that allow learners to perform constructions of exactly the same nature as traditional ones and then modify them using a movement called dragging (Leung et al., 2013). Dragging represents a continuous change of a geometric object and, generally, is the essential feature of DGEs (Erez & Yerushalmy, 2006). As a consequence, a geometric object constructed in the DGE does not constitute a single unique object as in the static approach to geometry, but a whole set of dynamic objects—a dragging family of shapes (Forsythe, 2015).

The use of DGEs can change geometrical experience in mathematical classrooms while affecting the way learners comprehend geometrical objects. For instance, Lai and White (2012) reported that working with a dynamic group of objects can support students’ comprehension of hierarchical relationships between shapes. Bokosmaty et al. (2017) focused on triangles implemented in DGEs and found that dynamic manipulations of these objects by students have a bigger effect on their learning outcomes than the traditional static approaches without manipulations. The challenge consists in finding a suitable DGE task design for classroom use (Jones, 2000) and not reducing mathematics to merely an experimental practice (Venturini & Sinclair, 2017).

What also remains to be explored is how to design DGE tasks that would allow teachers to assess students’ knowledge and progress (Sinclair et al., 2016). DGE tasks offer the possibility to explore invariants of construction that are independent of dragging (Leung, 2015) and distinguish students’ dragging schemas that are connected to them (Pittalis & Drijvers, 2023); however, information on conceptual knowledge obtained this way may not be sufficient. For instance, Baccaglini-Frank (2019) found that such tasks encouraged students to come up with conjectures based on phenomena that may not always be considered following from discovered properties of the shape. In this context, Thomsen et al. (2022) and Baccaglini-Frank (2019) call for a more precise consideration of theoretical frameworks when studying the potential of DGEs and for linking phenomenological evidence back to the theoretical embedding of the construction. We address this call by designing DGE constructions as structures of lines and circles. Such structures form a planar shape and allow decomposing it into certain one-dimensional parts that register graphically the properties of the shape and allow the properties to be described when reasoning about them (Duval, 2006).

3 Methodology

3.1 Design of the study

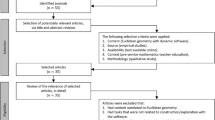
A schematic of the present study is captured in Fig. 1. As already mentioned in the introduction, we returned to the data collection instrument from one of our previous investigations (Vízek et al., 2023), redesigned it to reduce some basic weaknesses in the amount and comprehension of collected data, and then explored its potential for assessing the quality of conceptual understanding.

Fig. 1
figure 1

An overview of the present study (from top to bottom: objectives, data collection instruments, participants, data materials, perspectives of data analysis, and results); elements of the previous study in italics

Full size image

As the present study was exploratory, a qualitative research design (Creswell & Creswell, 2018) was chosen, with substantive coding and theoretical coding (Holton, 2007) as prominent analytical activities. To enable proper triangulation of data and method (Flick, 2018), we analyzed not only data collected from different groups of participants in different settings but also multiple types of data (assignments of tasks and their content background and parameters, written answers to questions focusing on different parts of these tasks, and field notes) from multiple perspectives. To enable proper triangulation of investigators (Flick, 2018), all three authors were involved in data analysis. The first and second authors systematically ran the iterative analytical process: repeatedly, they analyzed data materials first individually, then together, discussed and compared their findings and experience, reported weak points, unclear assignments, and undecided places. The discussion often led to a restructuring of the system of coding categories. Our goal was to end up with the smallest possible number of categories and to have captured and unambiguously assigned all relevant aspects found in data. The intermediate results of this process were continuously shared with the third author, who reflected on them and drew attention to possible rival interpretations or inconsistencies in the structure.

3.2 Participants

Our main theoretical focus concerned conceptual knowledge in relation with the comprehension of geometrical shapes that initially develops at lower-secondary school and then continues developing at upper-secondary school. Therefore, the study participants were lower-secondary and upper-secondary school students. To reach a wide spectrum of conceptual knowledge, we also included future secondary school teachers. We anticipated that we would encounter contrasting data from the different involved groups.

Sorted by data collection dates, the participants were as follows:

  • 20 lower-secondary school students of the age between 13 and 14 years (group A; these students had been participants in the previous study and did not actively participate in the present study);

  • 16 future lower-secondary school teachers, students of the master’s degree program at the university of the second author (group B);

  • 27 future secondary school teachers, students of the bachelor’s degree program at the university of the first author (group C);

  • 25 lower-secondary school students of the age between 14 and 15 years (group D);

  • 28 upper-secondary school students of the age between 16 and 17 years (group E). 

 The two secondary school classes (groups D and E) had been selected specifically because their recent prior geometry lessons covered the topic of planar geometry to the full extent given their level of schooling, but, during these lessons, the students did not work with GeoGebra software individually. Therefore, these participants were familiar with the geometry content but not with software.

The two teacher education classes (groups B and C) served as pilot groups and also as contrast groups during data analysis, as they had a different contextual background: group C had recently completed a geometry content course for future teachers, but had not worked with GeoGebra; group B had completed a geometry content course that included individual GeoGebra work, but three years before the data collection.

3.3 Former data collection instrument and its data

The former version of the data collection instrument had been created by the first author. It comprised a set of six constructions of quadrilaterals placed within an answer sheet in the form of a GeoGebra activity page. The page begins with a text informing that there are various shapes present in the constructions and that these shapes can be achieved by moving green points. Below each construction, a text followed by an answer box asks which shapes are present in the particular construction and why. The English version of the assignment is available online (https://www.geogebra.org/m/gje3p5b2).

Individual constructions in the set have different starting shapes and various numbers of included shapes (see Fig. 2). Most shapes are included in the third and fifth constructions; see Fig. 3 for their overview. Some constructions are based on properties of sides (first and sixth), others on properties of diagonals (second, fourth, and fifth), or on a mix of both (third). The constructions are colored, with two different functions of colors. For circles, the same color means that the circles were constructed with the same radii. For points, the color informs about movability. Green points are movable (the user can drag them); no other points in the construction can be moved directly.

Fig. 2
figure 2

Starting images of the six constructions, each labeled with the list of all included shapes

Full size image
Fig. 3
figure 3

Summary of shapes included in the third and fifth constructions

Full size image

The starting shape of the construction is always the most general one, that is, the quadrilateral that has only the properties arising from the construction. Dragging one or more green points can transform it into a more specific one when a new property of the objects is met. The end shape of the construction is the most specific shape, that is, the shape that meets all the properties that are available to achieve in the construction through dragging.

In the previous study (Vízek et al., 2023), this instrument had been used to collect data on lower-secondary school students’ reasoning about quadrilaterals. During data analysis, we had noticed some weaknesses in the amount and comprehension of collected data (blank responses, missing identifications of shapes, missing justifications, justifications not related to a shape or to its features, etc.). These types of responses could have emerged for various reasons (lack of motivation, lack of knowledge, lack of skills in handling the DGE tasks, etc.) that are not recognizable from data. However, some of them could have been caused by the particular design of the instrument, and a suitable change in the design could reduce them. Therefore, we reanalyzed the data materials with the aim of identifying such changes.

3.4 New design of the answer sheet

The first and second columns of Table 1 specify the weaknesses found in data that could have been caused by the way in which the answers were collected; we attempted to address these weaknesses in the new design of the answer sheet in a way that is explained in detail in the last column of Table 1. The main change consisted of replacing the answer box that was joint for all shapes with a set of structured frames for individual shapes. A sample of a frame for a dynamic construction based on properties of diagonals is shown in Fig. 4.

Table 1 The weaknesses in the amount and comprehensibility of collected data and how we reflected them
Full size table
Fig. 4
figure 4

English translation of the answer frame for a construction based on properties of diagonals

Full size image

3.5 New design of the set of dragging constructions

Given that the weaknesses in the amount and comprehension of data could have also been caused by the dynamic form of the constructions, we proceeded with examining the background and parameters of individual constructions to ascertain which of them could affect the difficulty of the constructions for solvers. Since the former set of constructions had been created independently solely by the first author, the second author could reflect on them from the perspective of a solver; field notes on this topic became an additional source of data for this analysis. As a result of the analysis, we found four particular features that negatively affected the process of finding all shapes in the construction and justifying them properly:

  • a green point that is not a vertex;

  • a green point that cannot be placed precisely to a specific location to establish the desired shape;

  • a combined movement of green points needed to get a shape;

  • more than two shapes included in the construction.

To reflect these findings in the new design of the set, we completely eliminated the first and second features and included the third and fourth only in the latter part of the set to enable scaffolding. To enable precise placements, labeled points were added to the constructions to select from. At the end of the redesign, we reconsidered the role of colors and the kind of information they provided. The coloring of lines and circles had a rather illustrative role and, in some cases, provided additional relational information (e.g., about the diameter of some circles). To remain as close as possible to classical geometry and to reduce phenomenological evidence, the new constructions in the set were created with all lines and circles in black.

The redesigned set of dragging constructions consists of five constructions from different parts of the hierarchical schemes of parallelogram–rhombus/rectangle–square and kite–rhombus–square. Each of these is based on a different Euclidean construction and, to ensure the tasks as non-routine for secondary school students, is based just on properties of diagonals. The English version of the set is available online (https://www.geogebra.org/m/wxxub3ja). The first two constructions are intended for a joint introduction; the other three are for data collection informing the assessment. An overview of the shapes included in the data collection part is presented in Fig. 5, and detail on labeled points is shown in Fig. 6.

Fig. 5
figure 5

An overview of the part of the set used for data collection and assessment purposes

Full size image
Fig. 6
figure 6

Detail on points in the fourth construction

Full size image

3.6 New data collection instrument

For the new data collection instrument, the redesigned set of dragging constructions (Sect. 3.5) was accompanied by a set of answer frames to fill in (Sect. 3.4). For each construction, the number of frames was the same and large enough to fit all the included shapes. As all the constructions in the set were based on properties of diagonals, all the frames were the same as in Fig. 4.

4 The study

4.1 Data collection

At secondary schools (groups D and E), data collection always took place during a regular geometry lesson, with the class teacher present, but the data collection activity itself was carried out completely by the researcher (the first author). At universities (groups B and C), the researcher was the class teacher (the second or first author, respectively).

For data collection, we used the instrument described in Sect. 3.6. The set of GeoGebra constructions was available for individual work on computers or tablets, and the answer sheets with frames were printed on paper. This allowed the participants to maximize the constructions on the screen and, at the same time, comfortably fill in the frames. The researcher discussed the first and second constructions with the entire class and advised how to fill in the frames. Then the participants worked with the other three constructions simultaneously but individually in a time span of 60 min.

4.2 Data analysis

For data analysis, we first considered each answer a data unit, i.e., each shape in each construction was coded separately. With 16 + 27 + 25 + 28 = 96 participants and 2 + 3 + 4 = 9 relevant answer frames for each participant, there were 864 data units. The analysis had a single focus: the quality of conceptual knowledge displayed in the answers. During substantive coding, we studied the completeness and correctness of students’ explanations, as well as different concepts included in the answers and to what extent all the included concepts were interconnected. During theoretical coding, we aimed more precisely and studied whether knowledge of classifications, structures, or principles had been applied in the answers and to what extent.

We started with group B and gradually included other groups. The inclusions of the C and D groups led each to several restructurings of the system of coding categories due to three main reasons: (a) categories to which data could be clearly assigned in one group competed with each other in the other group; (b) meanings and descriptions of individual categories that seemed clear in one group became unclear when confronted with data from the other group; (c) the effort to systematize categories and supplement the system with options that were not present in data but were logically missing led to an exuberant growth in the number of categories.

While the (a) and (b) reasons were usually connected to analyzing the reasoning texts next to the properties to tick, the (c) reason was most prominent when considering not only the texts but also the ticks and the placements. With more included participants, more combinations of correctly or incorrectly given names of shapes, the positions of green points, and the ticked properties of the shape appeared in data. To be able to provide a fitting assessment, we did not want to lose this information; however, we had to process it separately. As data related to the three factors (name, position, properties) can be simply labeled “true” or “false,” we assessed them in this way. Then, for the rest of the analysis, we worked with just the reasoning texts written next to the ticked properties.

During the following analytic process that focused on the reasoning texts only, it turned out that the system of categories can be much more clearly arranged if reasoning to each property is assessed separately.

4.3 Results—two main qualitative categories and their subcategories

For the justification texts in answer boxes next to the ticked properties, the analytical process of substantive coding resulted in two main qualitative categories:

  • Local focus for justifications in which the identified shape is treated as an object separated from the construction, as if there were no circles or lines creating the shape. The focus is local in the sense that selective attention is paid only to the shape and its parts (vertices, sides, angles, diagonals, triangles formed by sides and diagonals, etc.).

  • Global focus for justifications in which the identified shape is perceived as an integral part of the construction. The focus is global in the sense that the texts pay attention not only to the shape and its parts but also to (at least some of) the lines and circles that form the construction

The texts were assessed according to the shape name written above them. When the answer box was empty, no category was assigned. Afterward, the analytical process of theoretical coding resulted in a system of subcategories taking into consideration the three dimensions of conceptual knowledge. The subcategories are introduced below, with illustrative data excerpts presented in respective tables. In these tables, circled numbers below excerpts refer to assigned categories (e.g., ②), complete arguments have the numbers in reverse colors (e.g., ❺), incorrect or incomplete texts are underlined, and explanations are written in brackets in italics.

The category Local focus (see Table 2) has got four subcategories:

  • 1 (defining property) for justifications that are based only on an initial definition of the shape, typically a definition based on the lengths of the sides (e.g., D04/V/rhombus/different) and their perpendicularity (e.g., B15/III/rectangle/different);

  • 2 (property alternative) for justifications that are based just on an alternative definition of the property given next to the answer box (e.g., D04/IV/kite/perpendicular);

  • 3 (property translation) for justifications that are based just on a description of how the given property translates into the particular shape, i.e., where the property occurs in the shape (e.g., D04/IV/kite/bisects, B15/III/bisect, length);

  • 4 (local principle) for justifications that are based on a general principle that holds for the shape or its parts; for instance, C09 applied two different principles in the justifications: triangle congruence that holds for various parts of the shape (C09/III/rectangle/bisect, length, C09/III/square/perpendicular), and hierarchy of quadrilaterals (C09/III/square).

Table 2 Illustrative data excerpts for the category Local focus
Full size table

What the above subcategories do not explicitly reflect are errors or incomplete argumentation. However, complete argumentation can be expected just in subcategory 4 as argumentation in subcategories 1, 2, and 3 is incomplete by definition. Errors appeared, e.g., with C09 who swapped D and B in the description of the second triangle (C09/III/rectangle/length), and also used the sign “∼” instead of “ ≅ ” for congruence (C09/III/rectangle, square).

The category Global focus (see Tab. 3) has got two subcategories:

  • 5 (no principle) for justifications that do not include any application of a general principle (e.g., E14/III/rectangle/bisect, length, E14/III/square/bisect, length, C19/V/parallelogram/bisect);

  • 6 (global principle) for justifications that include an application of a general principle which holds for the construction or its parts, for instance, Thales’s theorem (e.g., E14/III/square/different), or hierarchy of quadrilaterals (e.g., C19/V/square/bisect, length).

Table 3 Illustrative data excerpts for correct and complete argumentation in the category Global focus
Full size table

Unlike the excerpts in Table 3 that all have complete arguments, there appeared also justifications assigned to subcategories 4, 5, and 6 that were not complete (see Table 4). They contained argumentation that was not specific enough (e.g., B02/IV/kite/bisects), or errors such as objects that were misinterpreted (e.g., D14/III/square/perpendicular), incorrectly termed (e.g., E06/III/rectangle/bisect), or swapped (e.g., B02/IV/kite/perpendicular).

Table 4 Illustrative data excerpts for incorrect or incomplete argumentation in the category Global focus
Full size table

Within individual frames, some participants offered justifications of mixed focus in the sense that some of the properties of the identified shape were justified with a local focus and some with a global one. See E12 and D13 in Table 5.

Table 5 Illustrative data excerpts for participants with mixed focus
Full size table

4.4 Results—Boolean variables and the evaluation sheet

To reflect information related to placements and ticks, individual frames were also assessed via an ordered set of four Boolean variables referring to individual shapes:

  • Name (true when the name of the shape is given in the frame; all other data in the frame are considered with respect to this shape);

  • Position (true when the indicated position of green points produces the shape);

  • Properties (true when the combination of ticked properties defines the shape);

  • Different property (true when the given different property defines the shape).

This way, each answer box was assigned an ordered set of Boolean variables and, sometimes, also one or more qualitative categories. We created an evaluation sheet where true values of Boolean variables are indicated by a ✓, all assigned qualitative categories are listed by their circled numbers, instances with complete arguments have the circled numbers in reverse colors, and false values as well as missing qualitative categories are indicated by a blank space. See Fig. 7 for illustrative samples; compare them with data excerpts in Table 5 (D13) and Table 3 (E14).

Fig. 7
figure 7

Two samples of the evaluation sheet for the third construction

Full size image

4.5 Key result—relations between qualitative categories and dimensions of conceptual knowledge

As the analytical process included theoretical coding, the system of qualitative (sub)categories and Boolean variables that constitutes our framework indicates how the three dimensions of conceptual knowledge can be understood in the context of dynamic geometric constructions that comply with Euclidean constructions. To clarify the relations between the framework and the dimensions, we established a system of subdimensions that allows for identifying the conceptual knowledge needed to achieve individual subcategories, see Table 6.

Table 6 The relationship between our framework and the (sub)dimensions of conceptual knowledge; ‘x’ denotes the instances where the particular subdimension of conceptual knowledge is needed to achieve the subcategory
Full size table

The classification dimension has three subdimensions:

  • Knowing the shape in the sense of providing its name.

  • Knowing a property of the shape in the sense of stating that the property is present in the shape. This subdimension applies to properties given in the answer sheet (here the statement is expressed through the tick), and also to other properties of the shape offered by respondents (here the statement is made within the justification text). The classification of another property appeared, for instance, when D04/V (in Table 2) classified one of the shapes as a rhombus because “all sides are the same length.”

  • Knowing a property alternative in the sense of knowing an alternative meaning of the property (an alternative definition of the property, or how the property translates into the particular shape). The alternative definition appeared, for instance, when D04/IV (in Table 2) ticked the property “Diagonals are perpendicular” and justified it with the text “Form an angle 90°.” The particularization appeared when D04/IV (in Table 2) ticked “Only one diagonal bisects the other” and added “Line segment AC bisects line segment BD.” These particularizations are present (implicitly or explicitly) in all justifications where a property is connected to the structure of the shape or to the structure of the construction.

The structure subdimension has got two subdimensions:

  • Knowing the structure of the shape in the sense of recognizing various individual objects in which the shape can be decomposed (vertices, sides, angles, diagonals, triangles formed by sides and diagonals, etc.), their mutual relations, and their relations to the shape. Such argumentation appeared, for instance, when B15 (in Table 2) decomposed diagonals of the rectangle into segments with S as an endpoint to comment on their lengths, but also when C09 (in Table 2) decomposed the rectangle into four triangles to reason about their congruence.

  • Knowing the structure of the construction in the sense of recognizing individual objects in which the construction can be decomposed (lines, circles, quadrilaterals, points, segments, etc.), their mutual relations, and their relations to the construction. Such argumentation appeared, for instance, when E14 (in Table 3) recognized diagonals of the rectangle as diameters of the circle k, but also when E14 (in Table 3) recognized the circle k as the Thales’s circle for any three adjacent vertices of the square.

The principle dimension is not divided into subdimensions as all principles are general in their nature. The fact that principles could be applied globally or locally is reflected in the subdimensions of the structure dimension. For example, C09 (in Table 2) who was assigned the category 4 applied the congruence of triangles only on parts of the shape, so only knowledge of the structure of the shape was needed. E14 (in Table 3) who was assigned the category 6 applied the Thales’s theorem with the circle k, so also knowledge of the structure of the construction was needed.

5 Discussion

The objective of this paper was to address the gap that has appeared in mathematics education research as a consequence of the emergence of DGEs (Sinclair et al., 2016), namely the question of how to elaborate on the general model of conceptual knowledge to make it applicable to dynamic geometric constructions. Specifically, our goal was to enrich research findings on how dynamic geometry can help mathematics teachers understand the nature of conceptual knowledge of their students. Our work addresses the call for designing suitable DGE tasks and assessment tools (Jones, 2000) and for more operational grasping of conceptual knowledge that would be applicable to wider ranges of students (Star & Stylianides, 2013). To achieve it, we propose a design of DGE tasks that includes a dragging family of shapes (Forsythe, 2015) which are interconnected by quadrilateral hierarchy (de Villiers, 1994) and complies with Euclidean constructions of quadrilaterals in the sense that all the construction steps are the same and visible. With our method, we join research on the measurement of conceptual knowledge that aims at explicit displays of knowledge (Crooks & Alibali, 2014). With our results, we complement the findings on individual dimensions of conceptual knowledge that were made in arithmetic (Prather & Alibali, 2010; Richland et al., 2012; Schneider & Stern, 2009).

5.1 Conceptual knowledge perspective

As the answer to the research question “Having an assessment instrument based on a set of dynamic dragging constructions of quadrilaterals that comply with Euclidean constructions, what information can the instrument provide about the quality of students’ conceptual knowledge?,” we provide an example of the assessment instrument (i.e., a set of dynamic constructions, Fig. 5, and a template for the answer sheet, Fig. 4) and propose an assessment framework reflecting a wide range of different levels of conceptual knowledge. The core of the framework consists of a structured set of two qualitative categories and their six subcategories assessing justifications of quadrilateral shapes and their properties (Sect. 4.3). Additionally, we also provide an ordered set of four Boolean variables supplementary monitoring correct identifications of shapes and their properties (Sect. 4.4) and a template for an evaluation sheet (Fig. 7) supporting the use of the framework in practice.

The system of (sub)categories and variables that form our framework allowed us to elaborate on the dimensions of conceptual knowledge (Krathwohl, 2002; Nilsson, 2020) that come into play when reasoning about quadrilateral shapes included in Euclidean constructions. Their specification into subdimensions (Sect. 4.5) is accompanied by a table of relationships between (sub)categories and (sub)dimensions (Table 6) clarifying which quality of conceptual knowledge is needed to achieve a particular (sub)category of the framework. This is how the proposed way of assessing students’ work provides information on the complexity and diversity of the students’ web of concepts (Hiebert & Lefevre, 1986) while distinguishing between different qualities of the connections between individual concepts. In the evaluation sheets (Fig. 7), the ticks and numbers of assigned subcategories inform about the type of concepts that are interconnected in the justifications and about the level on which the connections are attempted to be made, while the coloring of the numbers informs about the actual quality of the connections made.

In Table 6, we also made visible the internal hierarchy of the framework. Due to that, the variables and categories of the framework can be considered a guide for the teacher, as they indicate a potential path of development of conceptual knowledge. The description of individual variables and categories (Sect. 4.3), which is independent of the specific content of the construction, indicates what the differences are between the individual steps of the path, and the “x” symbols in Table 6 show how the difference between the steps translates into subdimensions of conceptual knowledge. In a way similar to Fujita (2012), our framework allows distinguishing between prototypical and hierarchical reasoning, as justifications that could include prototypical reasoning are all gathered in subcategories 1, 2, and 3, and hierarchical justifications are in subcategories 4 and 6.

Although the study participants had already discussed the topic of quadrilaterals during their previous lessons, our results showed that, for some of them (e.g., those in Tables 2 and 4), their knowledge of concepts is still developing. Others (e.g., those in Table 3) provided explanations consisting of connected pieces of information and manifested the ability to organize them in proper schemas (Rittle-Johnson & Schneider, 2015). The two respondents from Fig. 7 represent the findings: D13 is a lower-secondary school student with conceptual knowledge of rather weak quality and unevenly developed, as the assigned subcategories show no knowledge of principles and only occasional knowledge of structures, while all the numbers of assigned categories are in non-reverse color indicating reasoning that is not complete; in contrast, E14 is an upper-secondary school student with deep and evenly developed conceptual knowledge, as the assigned subcategories show knowledge of principles as well as structures (including the structure of the construction), and all the numbers are in reverse color indicating reasoning that is complete.

5.2 Design perspective

We started our study with redesigning a former data collection instrument. The redesigned version addresses the objections voiced by education research toward the use of dynamic geometry in geometry teaching and learning. The two main objections are related to DGE tasks not always respecting or making visible the axiomatic world of Euclidean geometry (Thomsen et al., 2022) and to phenomenological evidence provided by DGEs that may allow us to bypass or neglect the Euclidean grounds (Baccaglini-Frank, 2019) or reduce mathematics to an experimental practice (Venturini & Sinclair, 2017). To deal with these objections, we propose DGE tasks based on Euclidean constructions, using only circles and lines, with all construction steps the same as in Euclidean constructions and visible, and with no relational or measurement information provided by the DGE. The combination of proximity to Euclidean geometry and the lack of additional DGE feedback is not usual among DGE tasks. Some authors hide all construction steps (e.g., Erez & Yerushalmy, 2006) or reduce their amount and visibility by using special buttons, for instance, a button for the center of a segment, the bisector of an angle, a perpendicular line, or a parallel line (Baccaglini-Frank, 2019; Forsythe, 2015; Lai & White, 2012; Leung et al., 2013). Others provide measurement or relational information about the displayed objects, for instance, the size of sides, diagonals, and angles in a quadrilateral (Pittalis & Drijvers, 2023), the size of angles in a triangle and a graphical symbol for the same size of sides (Bokosmaty et al., 2017), or square grid behind the shapes (Fujita, 2012).

When designing our DGE tasks, we also strived to reach the highest possible degree of change compared to paper-and-pencil tasks (Venturini & Sinclair, 2017). To achieve it, we offer tasks that do not exist in paper-and-pencil form, as that form does not allow one shape to be transformed into another. This way, the use of the DGE is necessary for our tasks and, at the same time, the theoretical constructs of classical geometry are accentuated (Laborde, 2005). The transformation included in dynamic constructions brings attention to invariants (Leung, 2015) and encourages users to comprehend them in different ways (Zazkis & Leikin, 2008).

When redesigning the former data collection instrument, we changed the set of dynamic constructions as well as the answer sheet. A visual comparison of the former and redesigned instruments is shown in Fig. 8, and the internal redesign recommendations (visual as well as structural) are summarized in Fig. 9.

Fig. 8
figure 8

Visual comparison of a construction in the former set (3) and in the redesigned set (IV)

Full size image
Fig. 9
figure 9

Internal design recommendations on the composition of the set

Full size image

To ensure an accentuation of student’s conceptual knowledge when solving the tasks (Braithwaite & Sprague, 2021), we included non-routine tasks in the form of constructions based only on diagonal properties (as in Kabaca, 2017). This decision proved to be a key one for the subsequent data analysis, as it enabled us to distinguish displays of prototypical reasoning (e.g., when the respondent referred only to properties of sides and angles) from argumentation based on a decomposition of the shape into one-dimensional constituent parts and on properties registered by them (Duval, 2006).

The redesigned answer sheet (Sect. 3.4) is less open than the former one, as a list of properties to consider is offered within the sheet. In the former sheet, respondents had to come up with the properties themselves. However, the main focus of our analysis is not on the selection of the properties from the list, but on the justifications provided by respondents beside them. The justifications contained most information relevant to (sub)categories and (sub)dimensions of conceptual knowledge, especially knowledge of structures and knowledge of principles. Respondents with weak knowledge could have their work made easier thanks to the list of properties, but the weaknesses then showed up in the justifications. Justifications that described merely the selected property or reasoned prototypically (e.g., D04 in Table 2) were assigned categories corresponding to knowledge of classifications.

6 Conclusions and applications

The combination of substantive and theoretical coding (Holton, 2007) makes the assessment framework applicable in both educational research and practice. We verified the variables and subcategories with four cohorts of participants and not only could they unambiguously be assigned to everyone but also covered all three dimensions of conceptual knowledge (Table 6). The main limitation is the usual with qualitative research: the impossibility of generalizing participant-related results or making group comparisons based on them.

In secondary school education, the framework can serve as a tool for teachers that informs them about conceptual knowledge of their students; the hierarchical nature of variables and subcategories (Table 6) allows long-term developmental focus. With future teachers in our study (group B), we ran the data collection within a didactical course and continued with follow-up activities: the teachers discussed possible classroom implementations of the instrument and the concept of hierarchy of geometric objects, and then posed their own dynamic constructions. In this way, the framework contributed not only to conceptual knowledge as part of content knowledge but also to its pedagogical content knowledge extension.