1 Introduction

Patterning plays a central role in early-years mathematics learning (Wijns et al., 2019b). Patterns and the activity of patterning are perceived to represent the core of mathematical ideas and processes (Steen, 1988), as patterning affords students opportunities to identify, generalise, and communicate the underlying regularities of patterns (Mulligan & Mitchelmore, 2009). Identifying the structure underlying the superficial features of patterns, such as shape and colour, is essential for mathematical development (Nunes et al., 2012). Once students identify the underlying structure, they gain the conceptualisation needed to work with the rules intrinsic to our verbal number system as well (Steen, 1988; Zippert et al., 2020). Low-achieving students have been observed to struggle identifying the underlying structure of patterns’ superficial features and relating the superficial features to their numerical structures (Lüken, 2012; Mulligan, 2011).

Children’s proficiency in repeating patterning from the age of 5–6 years is uniquely associated with and predictive of later mathematical proficiency (Pasnak, 2017; Rittle-Johnson et al., 2017; Wijns et al., 2021b). Previous research has found patterning interventions to increase the mathematical proficiency of students who struggle with mathematics (Hendricks et al., 2006; Kidd et al., 2013, 2014; Pasnak et al., 2015). These findings are likely grounded in a connection between repeating patterning and multiplicative and algebraic thinking, which lays a foundation for (de)composition, partitioning, and the repeating unit (Mulligan et al., 2020; Mulligan & Mitchelmore, 2009; Papic et al., 2011; Tirosh et al., 2019; Warren & Cooper, 2007). Indeed, children’s awareness of mathematical pattern and structure (AMPS), which is generalisable across mathematical concepts, has been found to relate to 4–9-year-olds’ individual differences in mathematics (MacKay & De Smedt, 2019; Mulligan, 2011; Mulligan & Mitchelmore, 2009).

To date, previous research has mostly focused on student success in patterning tasks and not on their patterning strategies. Children start focusing on the repeating unit in a pattern around the age of 6, and few studies have investigated this age group’s attention to repeating patterns and their repeating unit. This study aims to extend our knowledge of similarities and differences in 6-year-old grade 1 students with low and high number sense in terms of their success and the strategies they employ when responding incorrectly to repeating pattern activities.

2 Literature review

2.1 Patterns and number sense

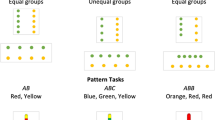
A pattern is any predictable regularity (Mulligan & Mitchelmore, 2009). Repeating patterns comprise elements; these in turn make up a repeating unit that recurs in a cyclic structure (Liljedahl, 2004). To exemplify, ABB is the repeating unit of an ABBABB repeating pattern and □ΔΔ is the repeating unit of a □ΔΔ□ΔΔ□ΔΔ repeating pattern. The complexity of the repeating unit varies (e.g., AB versus ABCBA). Patterns can also be structured by a repeating rule (e.g., like the + 2 rule between each unit of the sequences 1-3-5 and the 2-4-6), referred to as sequencing patterns (MacKay & De Smedt, 2019), or a growing relationship, called growing patterns (Wijns et al., 2021b). Growing patterns increase or decrease systematically, such as in the sequences □ □□□ □□□□□ and □ΔΔ□ΔΔΔ□ΔΔΔΔ, which follow a + 2 and + Δ increasing rule between each unit of the pattern, respectively. Patterns may also vary with respect to their features, such as their colour, shape, texture, and whether the elements are physical or digital (Larkin et al., 2022). Spatial patterns are created by elements to represent a numerical regularity in a specific geometric way that can be visually and tactically experienced, typically to decompose and subitise quantities (Lüken, 2012). In the present study, our focus is on repeating patterns of physical elements with an ABB, AABB, and ABB repeating unit.

Number sense is a student’s ability to flexibly work with numbers and quantities in the preschool and early school years (Andrews & Sayers, 2015; Gersten & Chard, 1999; Griffin, 2004; Jordan et al., 2022; Mcintosh et al., 1992). Number sense is a contested term; however, there is an agreement that number sense proficiency involves flexibly working with regularities of numbers and quantities, e.g., with the successor principle, the base-ten structure, and the alternation between even and odd numbers. Andrews and Sayers (2015) defined number sense as comprising number identification, systematic counting, awareness of the relationship between number and quantity, quantity discrimination, awareness of different representations of numbers, estimation, arithmetic competence, and awareness of number patterns. This might explain the association between patterning and number sense. In a study by Wijns et al. (2021b), a bidirectional association between patterning and numerical abilities from ages 4 to 5 was revealed; however, from ages 5 to 6, patterning predicted numerical abilities but not vice versa and repeating patterning predicted growing patterning but not vice versa. Thereof, they hypothesised children start switching to focus on the (de)composition relations of a pattern and its repeating units and that this is an easier activity in repeating patterns with a visible repeating unit, compared to growing patterns’ invisible unit of systematic change.

2.2 Repeating patterning development

Important milestones in repeating patterning development were indicated in an overview by Sarama and Clements (2009). They found that 3-year-olds recognise simple AB repeating patterns, while 4-year-olds can duplicate AB patterns and other simple patterns, fill in missing elements, and extend AB patterns. Further, 5-year-olds extend simple repeating patterns beyond AB patterns, and many 6-year-olds can identify the repeating unit of a pattern. These findings were supported and expanded by Rittle-Johnson (2019), who observed that children learn patterns with a three- and four-element repeating unit after mastering two-element repeating unit AB patterns. A duplicating activity involves copying a pattern and does not require students to identify the repeating unit. An extending activity entails continuing a pattern (we chose with the repeating unit to explore students’ relational thinking of the repeating part of the whole), while transferring is defined as the use of superficially different materials than the model pattern, still following the same regularity of the model pattern. A unit isolating activity consists of identifying and patterning only the repeating unit in a pattern (Collins & Laski, 2015; Lüken & Sauzet, 2021).

Recent studies have supported that children can often duplicate at the end of preschool (Larkin et al., 2022; Lüken & Sauzet, 2021; Rittle-Johnson et al., 2019; Wijns et al., 2019a) and also add nuance to Sarama and Clements’ (2009) findings by observing that the difficulty level of duplicating can vary depending on the number and repetition of elements of the repeating unit (Lüken & Sauzet, 2021). Overall, recent findings show that children are capable of a range of patterning tasks and that their rate of successful patterning diminishes with the increased number and complexity in arrangement of the elements of the repeating unit (Larkin et al., 2022; Lüken, 2023; Lüken & Sauzet, 2021; Tsamir et al., 2018; Wijns et al., 2019b).

The aforementioned studies focused on students’ success in duplicating patterns. However, the number of elements and their arrangements within a pattern may not be the only source of patterning complexity. There is an ongoing discussion regarding which activities of repeating patterns beyond duplicating require students to identify the repeating unit. To understand this discussion, which relates to strategy use in patterning, we will first define recursive and relational strategies and then go on to describe activities of repeating patterning and strategies.

2.3 Repeating patterning strategies and their relation to number sense development

2.3.1 Defining recursive and relational strategies

Patterning activities that require students to identify the repeating unit likely facilitate relational thinking and the use of relational thinking strategies (Close & Glennon, 1977; Collins & Laski, 2015), which can be described as thinking of “expressions and equations in their entirety rather than as a process to be carried out step by step” (Carpenter et al., 2005, p. 51). Thinking relationally involves considering a pattern as a whole, with its parts made up by elements that relate to each other and to the whole; this includes understanding why procedures are conducted (Carpenter et al., 2005; Kieran, 2004; Skemp, 1976). Relational thinking enables students to use more complex, appropriate, and efficient strategies to represent, abstract, manipulate, generalise, and predict any elements of a pattern (Collins & Laski, 2015; Lüken & Sauzet, 2021; Wijns et al., 2019b). Relational strategies make students attend to the underlying structure of the task by attending to part–whole (de)composing relationships (Kieran et al., 1996), an essential aspect of early mathematical development (Björklund et al., 2021; Kim et al., 2022; Venkat et al., 2019).

In contrast, recursive thinking strategies (also called one-to-one strategies: Collins & Laski, 2015) consist of matching one pattern feature to another or considering the relation between two consecutive elements; in this way, it exclusively enables the student to predict the next element in the pattern (McGarvey, 2012; Wilkie & Clarke, 2016). An ABAB repeating pattern is recursively described as B coming after A if B was previous to A, while, in terms of relational thinking, the pattern is described as a repeating AB unit (McGarvey, 2012; Wilkie & Clarke, 2016). The transition from recursive to relational thinking is a major change that occurs in development and is a sign of conceptual understanding.

2.3.2 Students’ recursive, relational, and different strategies in duplicating, extending, transferring, and unit isolating repeating patterning activities

Unit isolating is the most challenging patterning activity for 5–6-year-olds, as this activity presumably requires the child to identify the pattern’s repeating unit. While most children in this age group can duplicate and many can also extend and transfer, only some can identify the unit in repeating patterns (Collins & Laski, 2015; Papic et al., 2011; Rittle-Johnson et al., 2013, 2015). The repeating patterning activity in which students engage probably requires them to use recursive or relational strategies. Hence, duplicating a pattern with varying complexity of the repeating unit is not the only aspect to consider when assessing students’ patterning proficiency. Table 1 presents an overview over the repeating patterning strategies of 3–5-year-olds observed in different patterning activities. The overview, which is based on findings from five of the studies we mentioned here in the literature review (Collins & Laski, 2015; Garrick, 2000; Lüken & Sauzet, 2021; Papic et al., 2011; Rustigian, 1976), showcases how strategy use develops and provides a rationale for why unit isolation activities are associated with conceptual knowledge and number sense.

Table 1 Repeating patterning strategies in 3–5-year-olds
Full size table

The number of studies investigating students’ strategies when solving different patterning activities is limited. Collins and Laski (2015) found that students could solve patterning activities using one of two strategies: (1) a one-to-one matching strategy focused on superficial features, such as colour or shape, or (2) a relational similarity strategy, elicited by activities involving mental representation and manipulation of the repeating unit that makes students consider the relationships of elements and units of elements. The first strategy is a recursive strategy, while the second is a relational strategy. Some of the strategies Rustigian (1976) and Papic et al. (2011) referred to are the same as those Collins and Laski (2015) suggested as an off-task strategy, which refers to students’ responses that “were unrelated to the task and showed no awareness of patterns” (Collins & Laski, 2015, p. 208). An example of such a typical ‘off-task’ response is described as building towers or sorting cubes based on colour or shape. From their findings, Collins and Laski (2015) hypothesised that transferring and unit isolating patterns elicit relational thinking, while duplicating and extending could be solved using a recursive matching strategy.

Lüken and Sauzet (2021) discovered that the sophistication of students’ strategy use increased with age. In line with Papic et al. (2011), they also found that most 5-year-olds used strategies based on classification and comparison (one-to-one correspondence and matching) and focused on sequence, while in a study of 5-year-old students, only 8% demonstrated strategies reflecting the identification of the repeating unit (Lüken, 2018, 2020; Lüken & Sauzet, 2021). Five-year-olds, therefore, might show an emergent understanding of regularity, order, and succession.

Lüken and Sauzet (2021) observed that children’s strategies employed for more complex patterns were less sophisticated and that transferring was done correctly with either a recursive matching strategy or alternating colours, claiming that transferring patterns is most likely not an abstraction activity requiring students to identify the pattern’s repeating unit. Transferring was previously believed to promote relational thinking by requiring students to decentrate from the pattern and consider the underlying structure; accordingly, it was referred to as “generalising” (Wijns et al., 2019a, b, c) or “abstracting” (Rittle-Johnson et al., 2013). The transferring activity is also named “translating” by some studies (e.g., Lüken & Sauzet, 2021). However, some studies have shown that students succeeded to a greater extent in transferring than extending repeating patterns (Close & Glennon, 1977), while others have observed that students succeeded to a greater extent in extending compared to transferring (Collins & Laski, 2015).

Students’ successful engagement in extending patterns has been found to relate to their number sense (Fyfe et al., 2017; Kidd et al., 2013; Wijns et al., 2021a), leading to the hypothesis that extending might require students to think relationally rather than recursively, as this presumably requires conceptual understanding (Economopoulos, 1998; McGarvey, 2012). However, Wijns et al. (2019c) found that the activities of transferring and unit identification uniquely contributed to understanding number but not the activity of extending repeating patterns.

Lüken and Sauzet (2021) explored the most common strategy use among 5-year-olds solving unit identification activities. The most common strategy children employed was cutting the patterns into single cubes that were then further sorted by colour. Secondly, they cut the pattern into parts of different length with no regularity, followed by cutting the pattern into equal parts, often single cubes, without colour regularity. None of the 5-year-olds focused on the succession of elements, and few separated the pattern into repeating units. The researchers therefore verbally scaffolded the students to compare the units to focus their attention on the repeating unit.

2.3.3 The multimodality of patterning

Björklund and Pramling (2014) found that six-year-olds may not require isolated activities to grasp units of patterns and generalise part–whole relations; instead, they can simultaneously experience a multimodal fusion of different aspects of the parts and the whole. Consequently, they emphasised that children should be given opportunities to differentiate multimodal pattern and structure dimensions to experience that different information from various modalities can constitute the repeating unit. This approach will assist children in generalising and expressing multimodal experiences in both multimodal and non-conventional ways (referred to as “pseudo concepts”). These experiences serve as a pre-stage of conceptual development and the conventional use of words to express an understanding of generalisation (Björklund & Pramling, 2014).

Patterns are experienced and expressed verbally and visually through language and gestures (O’Halloran, 2015). However, only Lüken and Sauzet (2021) have categorised repeating patterning strategies based on children’s multimodal responses.

3 Aim and setting of the present study

Previous studies investigating students’ repeating patterning strategies have mostly explored children up to 5–6 years of age, with findings indicating that it is from this age onwards that students start focusing on the repeating unit. This study aimed to investigate patterning success and strategies among six-year-old grade 1 students with low and high number sense. We used the same patterning activities as Collins and Laski (2015). Specifically, students performed four repeating patterning activities: duplicate, extend, transfer, and unit isolation. We sought to answer the following two research questions:

  • RQI What are the similarities and differences in the success rates of duplicating, extending, transferring, and unit isolating repeating patterning activities among grade 1 students with low and high number sense?

  • RQII What are the similarities and differences in the strategies employed in unsuccessful trials of repeating patterning activities among grade 1 students with low and high number sense?

This study aims to contribute insights regarding six-year-old students’ patterning process and strategy use beyond correct and incorrect responses, considering multimodal expressions.

4 Methods

Employing a multi-method comparative case study design (Bryman, 2016), we explored the repeating patterning response of 75 six-year-old grade 1 students using video analysis of their multimodal responses.

4.1 Grouping students based on number sense

Seventy-five grade 1 students from two primary schools in a Mid-Norway municipality participated in the study with informed parental consent during the 2020/2021 school year; 52 of the 75 students were selected for in-depth analyses based on their number sense.

Number sense was measured using a digital assessment instrument (Saksvik-Raanes, 2024) developed to assess 5–6-year-olds’ number sense based on Andrews and Sayers’ (2015) description of number sense, with the addition of subitising due to its importance to the number sense concept (Sayers et al., 2016). The students completed the assessment with the first author and the developer of the number sense assessment at their respective schools, beginning with a short task instruction. Groups of six to eight students sat together in a classroom and engaged in the digital assessment on individual tablets in a session lasting 20–25 min. The internal consistency of the instrument, as measured by Cronbach’s alpha (α = 0.84), was satisfactory (Saksvik-Raanes, 2024). Due to voluntary participance, not all students conducted the number sense component “representing number.” Consequently, this component was excluded from the study.

Each student was assigned a number sense score in the range of 0–69 points. The 52 students selected were placed into two groups based on their scores: the 26 students with lower scores (16–41) comprised the “students showing low number sense” group and the 26 students with the highest scores (49–62) comprised the “students showing high number sense” group. The within-group number sense score range was larger in the low number sense group.

4.2 Task-based interview

A videotaped, semi-structured task-based interview (TBI) setting inspired by Ginsburg (1981) and Goldin (1997) facilitated observations of the 75 students’ strategies for the repeating patterning tasks. Each student was introduced to three trials for each of the four patterning activities—duplicate, extend, transfer, and unit isolation—totalling 12 activities per student (see Table 2). The verbal instructions of the patterning activities from Collins and Laski’s (2015) study were translated into Norwegian (see Table 2); all patterning trials followed the same order from their study and that of Rittle-Johnson et al. (2013). The order followed for each of the four patterning activities was one ABB pattern, one AAB pattern, and one AABB pattern. The A and B elements differed in both colour and shape in all but the unit isolation activities, for which the elements varied only in colour. Instructions were given visually (pictures of patterns and models of towers, to avoid students seeing the interviewer placing cubes and tiles) and verbally (oral instruction). Students were given more cubes and tiles than needed to solve each task. Previous studies have shown that students’ semantic interpretation of the verbal task instruction is critical to the way they understand number relations, influencing their strategies for solving tasks (Björklund & Kempe, 2022; Corte & Verschaffel, 1987).

Table 2 Patterning tasks including verbal instruction for all activities with repeating patterns
Full size table

The first author collected the data and acted as the interviewer. Students were encouraged to engage in patterning activities in a “four-stage exploration” setting (Goldin, 1997). The student–interviewer interaction was unique for each of the 75 interview settings, and students were scaffolded based on the interviewer’s interpretation of each student’s verbal, spatial, and gestural utterances. All students were presented with a patterning activity followed by a verbal instruction. Then, depending on the interviewer’s interpretation of the student’s response, the interviewer repeated the verbal instructions and expressed the same semantic meaning using different wording to make the pattern structure more accessible. If the student needed more assistance, the interviewer asked a question orally, provided a prompt regarding the pattern structure’s essential features, or asked the student to instruct the interviewer to do the task. Importantly, the analysis for this study was based on each student’s response before being scaffolded to compare the students’ responses with the same information given. The student response examples in the discussion, however, include students’ multimodal responses during the whole session, including scaffolding.

4.2.1 Interpretation of activity response

The data consisted of student responses to the digital number sense assessment and the videotaped task-based interviews.

For each patterning task, the pattern solution the students expressed was dichotomously coded as correct (1) or incorrect (0) according to Collins and Laski (2015). The highest possible total score for the patterning activities was 12. These scores were used for quantitative between-group analysis of patterning success. The videos were then imported into the qualitative data analysis software program NVivo and re-reviewed. The qualitative descriptions of strategy use were based on the interactions beyond the students’ immediate correct/incorrect patterning response. The verbal interaction between each student–interviewer pair was transcribed. Next, the students’ multimodal responses were thematically analysed following Braun and Clarke’s (2006) steps:

  1. 1)

    Initial coding of students’ placement and arrangement of cubes and tiles, intonation of and pauses in speech, and gestures

  2. 2)

    Focused coding to identify codes that emerged frequently from step one and their co-uttered expressions

  3. 3)

    Theoretical coding, in which focused coded responses are interpreted to reflect recursive, relational, or off-task strategies according to Collins and Laski’s (2015) descriptions of one-to-one, relational, and off-task strategies (described in more detail later)

The thematic analysis followed an abductive process (Bryman, 2016). During our deductive analyses, we found that strategies that met Collins and Laski’s (2015) description of an off-task strategy reflected students’ attention to superficial pattern features, such as colour and shape, and therefore were task-related rather than off-task strategies. Next, we applied multimodal analysis to investigate how the verbal task instruction could have promoted or hindered the students’ access and attention to the pattern’s underlying structure. Another purpose of the multimodal analysis was to examine the ways in which students’ verbal and gestural expressions could give insights into the way they perceived a pattern’s structure, supporting or deviating from the understanding they expressed through their patterning response. This was the inductive phase of the thematic analysis, and it resulted in our replacement of Collins and Laski’s (2015) “off-task” strategy with a category we called “different” strategies, as some students attending to colour were found to pay attention to the pattern’s underlying structure (but based on colour) (Table 3).

Table 3 Categories applied in thematic analysis of patterning strategies
Full size table

In a final step, intra- and intercoding were performed. The dichotomous coding of the pattern solutions was intracoded with 100% agreement. Three additional researchers were given the coding scheme for coding the strategies, and video recordings of correct/incorrect responses, and which of the three strategies incorrect responses matched, considering verbal and gestural responses of three students were intercoded, also with perfect agreement.

After coding, we created an Excel database of the students’ number sense and patterning results and imported the data into SPSS for quantitative between-group analysis. A one-way ANOVA with a Scheffe post hoc test in SPSS allowed us to explore the statistical significance of group differences in patterning success at a 0.05 significance level. The Games–Howell test was utilised for comparisons among means of groups with unequal variances. This test was suitable for this purpose because the within-group variation was larger for the low number sense group than for the group of students with high number sense.

Number sense was measured with a 69-item digital assessment, including the following number sense components: number identification, systematic counting, number and quantity, quantity discrimination, estimation, arithmetic competence, number patterns, and subitising (Saksvik-Raanes, 2024). Each student’s total score was imported into the spreadsheet.

5 Results and discussion

The discussion of the findings is structured according to RQI and RQII.

5.1 RQI) What are the similarities and differences in the success rates of duplicating, extending, transferring, and unit isolating repeating patterning activities among grade 1 students with low and high number sense?

For each patterning activity, students solved three tasks, resulting in a maximum of 3 points for each activity. We found a duplicate, transfer, extend, and unit isolation order of success for the 75 students. However, the students with low number sense succeeded in more unit isolation activities than extend activities, while the opposite was observed for the students with high number sense. A statistical investigation of the between-group differences in the success rate for extend activities revealed statistical significance (F[2, 72] = 4.529, p = 0.014); however, this result was not found for the other patterning activities. Table 4 shows the average patterning success for the students with low and high number sense. Each student achieved a total score between 0 and 3 for each patterning activity. The mean values (M) in Table 4 provide all students’ and the low and high number sense student groups’ mean values for each of the repeating patterning activities.

Table 4 Patterning success rate (average number of successful tasks [M] and standard deviation [SD]) for students in the activities duplicate, extend, transfer, and unit isolation
Full size table

As Table 4 shows, almost all the students knew how to duplicate repeating patterns; however, few students mastered extend and unit isolation. Previous studies have shown a duplicate, extend, unit isolation, and transfer order of success (Collins & Laski, 2015) and a duplicate, extend, transfer, and unit isolation trajectory of success (Lüken & Sauzet, 2021). Based on these previous studies, a larger proportion of transfer activities were successfully solved in our study than we could have expected, keeping in mind that the present study uses the tasks described in Collins and Laski (2015). We observed that students in both the low and high number sense groups succeeded in duplicating and transferring by matching one tile at a time from left to right. Some accompanied this patterning with verbal expressions like “This one is that one” or other verbal utterances like “big, small, big, small,” distinguishing the A and B elements with the words “big” and small, respectively, along with a corresponding rhythm and alternating change in vocal pitch, while simultaneously finger-pointing to the respective element. These observations may support Lüken and Sauzet’s (2021) interpretation that transferring patterns allows for recursive matching strategies and does not require relational but rather recursive thinking.

It is puzzling that the 6-year-old students in our study extended (and unit isolated) less successfully than 4- and 5-year-olds in previous studies (e.g., Collins & Laski, 2015; Lüken & Sauzet, 2021; Rittle-Johnson et al., 2013). This may have been due to different operationalisations of the patterning activities. Regarding extend, not all previous studies operationalised the extension of the repeating unit, but rather only asked the students to identify the next element (see, e.g., Garrick, 2000). For an extend response to be coded as successful, we required the students to either pattern only the repeating unit (1 × unit) or duplicate and extend the pattern with its repeating unit (3 × unit). This operationalisation was used in Collins and Laski’s (2015) and Lüken and Sauzet’s (2021) studies. In the present study, students successfully solved unit isolation tasks by isolating the pattern’s repeating unit based on a model pattern that consisted of two repeating units presented to the students. Accordingly, the unit identification requirements for correctly extending and unit isolating indicate these activities are related and may even be inverse processes. Lüken and Sauzet (2021), however, gave a model pattern comprising three repeating units and required students to create a pattern of two repeating units, making it impossible to give a correct response by cutting the pattern in two halves. There is a possibility that the students in our study used such a strategy.

Previous research has concluded unit identification occurs around 5–6 years of age (e.g., Lüken & Sauzet, 2021). Wijns et al. (2021b) hypothesised that students can switch between focusing on parts and the whole of a pattern from 5 to 6 years of age. If this hypothesis is true, the older 6-year-old students in this study could also approach and focus on the (de)composition of the pattern and its parts in extending and unit isolating.

The findings from this study neither support nor reject this hypothesis. The differing results may be due to contextual aspects of the studies, such as how the tasks and instructions are given to the students. Alternatively, the differing results may be related to other factors resulting from differing educational systems. One such factor is the approach to patterning in early education: In the Flemish context in which Wijns et al. (2021b) conducted their study, children are taught in preschool, while in Norway, children start formal schooling the year they turn 6 and preschool is play-based, without an emphasis on teaching. Thus, the 6-year-old participants in the present study, being Norwegian, had not yet been taught to attend to patterns.

5.2 RQII) What are the similarities and differences in the strategies employed in unsuccessful trials of repeating patterning activities among grade 1 students with low and high number sense?

5.2.1 Students’ distribution of strategies in unsuccessful patterning during patterning activities

In the case of unsuccessful patterning, the 75 participating students most often exhibited a recursive matching strategy (81% of unsuccessful trials), which supports Collins and Laski’s (2015) findings. The next most common strategies demonstrated during unsuccessful trials were different approaches (15%) and relational strategies (4%).

The students with low number sense on average failed in 52% of all the patterning activities and the students with high number sense in 40% of all the patterning activities. In 83% of their incorrect responses, the low number sense students’ unsuccessful patterning attempts involved recursive strategies, and in 17%, they involved different strategies. Among the students with high number sense, 81% of the unsuccessful patterning reflected recursive strategies, 6% relational strategies, and 13% different strategies. The strategy categories were therefore distributed similarly between the students with low and high number sense. Notably, only the students with high number sense replaced successful patterning using relational strategies.

At the same time, the distribution of the strategy category on the patterning activities varied. Recursive strategies were used in extend and unit isolation activities by the students with high number sense, while they were additionally used in transfer activities by the students with low number sense. The students with high number sense replaced successful patterning with different strategies, such as focusing on shape, only in transfer activities, while the students with lower number sense additionally used this strategy for duplicate and extend activities.

5.2.2 Low and high number sense students’ variants of recursive strategies

Duplicating was the most observed recursive strategy among all the students and the only recursive strategy observed among the students with high number sense (see Fig. 1).

Fig. 1
figure 1

Most frequent recursive strategy observed: duplicate. Left, the given tower; middle, a correct unit isolate response; right, a duplicate response

Full size image

Students with low number sense were observed to use four recursive strategies: In addition to duplicating, we observed omitting a unit element (e.g., patterning ABB instead of AABB), adding one A or B, constituting an extra element in the pattern unit (e.g., ABBB instead of ABB), which created a non-repeating unit because the omitted or added tile occurred in only one of the units. The fourth recursive strategy was mirroring the pattern (e.g., BBA instead of ABB). The first two variants (omitting or adding a tile) reflected what Collins and Laski (2015) called incomplete one-to-one strategies. Rustigian (1976) also observed students mirroring the pattern in extending activities. These recursive strategies observed in this study resulted in a different order of elements, a different number of (identical) elements (e.g., two As vs. two Bs or a missing/extra A or B), and a non-repeating unit. Mirroring co-occurred with patterning in the opposite direction: from right to left. These three variants beyond duplicating could indicate that the students with low number sense had challenges with the successor principle and ordinality (see, e.g., Zippert et al., 2020).

Previous research has suggested students need extra scaffolding on unit isolation trials, an activity in which the observed duplicating and the other recursive variants occurred, to understand their directive (Collins & Laski, 2015; Lüken & Sauzet, 2021). We will now discuss Agnes’s response (see Table 5), which illustrates this need for scaffolding and the necessity to attend to students’ multimodal ways of expressing their repeating unit understanding.

Table 5 Excerpt of Agnes’s multimodal meaning-making during student–interviewer interaction
Full size table

Instead of giving a correct repeating unit response, one student, Agnes, duplicated the model pattern. Agnes’s duplicate response likely reflected recursive thinking, as she one-to-one matched the number of cubes and the colour of the model pattern to the pattern she created (line 2). We cannot confirm this, but Agnes’s verbal expression (line 4), compared to an alternative explanation like “pattern yellow–yellow–blue twice” makes this a likely interpretation. However, Agnes’s response could result from not understanding what is being asked for, but that she was capable of relational thinking if the questions or the visual model pattern had been posed differently.

The student–interviewer interaction excerpt illustrates the potential of multimodal data for obtaining more comprehensive insights into students’ thinking that are not initially apparent. The interaction scaffolded Agnes to attend to the pattern’s repeating unit. She divided the duplicated tower into two equal units and verbally uttered “hub-hub” (line 8), in sync with the gesture of placing one unit on the given pattern for each “hub.” Agnes’s multimodal way of expressing herself—that is, a simultaneous verbal and gestural patterning response—could indicate she thought relationally in part–whole decomposing terms, at least after some scaffolding. Agnes’s “hub” expression could be referring to the repeating unit, and the “hub-hub” utterance could thus be what Björklund and Pramling (2014) called a pseudo concept of a generalisation. If identifying a pattern’s repeating unit requires students to think relationally about part–whole relations, we argue that extending patterns is an important (de)composing activity for mathematical development (e.g., Mulligan et al., 2020). If so, it is possible that the same applies to unit isolating, as students need to decompose the pattern into its repeating unit before manipulating it.

However, Agnes could have also cut the tower into two equal parts, something many 5-year-olds did in Lüken and Sauzet’s (2021) study. Agnes’s response of decomposing a duplicated tower demonstrates that students can rely on their recursive thinking when decomposing a pattern into halves to create two identical units.

5.2.3 High number sense students’ characteristics of relational strategies

Only the students with high number sense replaced successful strategies with relational strategies. These students added (or omitted) one extra element in both units and created a viable (albeit different from the model) pattern that contained a repeating unit (see Fig. 2). This patterning response likely reflected relational thinking, as these students identified or decomposed the whole pattern (ABBABB) into its repeating unit (ABB) to compose a viable pattern (ABBBABBB) containing a repeating unit (ABBB).

Fig. 2
figure 2

Example of relational strategy ABBBABBB instead of given ABBABB pattern

Full size image

The students with high number sense applied this strategy for all four types of patterning activities, but most often in extending and unit isolating. As will be illustrated in the following subchapter, the verbal instruction provided for unit isolate activities could have led to students’ recursive approach to the activity. Equivalently, in the extend activities, the verbal instruction was [I made a pattern using these tiles. Finish the pattern. How does it continue?]. First, a pattern continues eternally and is never finished, highlighting the weakness of this wording. Second, focusing on single elements, this verbal instruction could have led students toward continuing the step-by-step recursive approach of consecutive motion in a certain direction and elicited recursive thinking strategies (Carpenter et al., 2005; Kieran, 2004; McGarvey, 2012). This could be the reason students with low number sense used recursive strategies in these activities. Interpreting the repeating unit as “next” in the sequence requires interpreting the repeating unit as a unit.

5.2.4 Low and high number sense students’ characteristics of different strategies

For the students with high number sense, the use of different strategies was exclusively shown in the transfer activities. Their peers with low number sense used this strategy in other activities as well. We observed two variants of this strategy, in which students focused on pattern features and not the underlying structure: (1) focus on shape and (2) focus on colour.

The first variant was observed as students tried to create shapes identical to those in the given patterns. Patrick’s response to an ABB repeating pattern (see Fig. 3) may support previous findings that shape is a feature children easily attend to (Rustigian, 1976), especially in low-achieving students (Lüken, 2012; Mulligan, 2011). It also exemplifies the way verbal interaction can help students overcome considering shape an essential feature. Patrick said “I need more triangles” as he combined two triangles to represent the As in the model pattern, giving a diamond-like shape identical to the shape of the A element in the model pattern. Mirroring the shape consequently meant that he ran out of available tiles and could not construct the last A element of the pattern. He attempted to make a square (B element) by rotating three red parallelograms in various ways. The interviewer responded, “Let’s say you do not need to make the same shape.” Patrick immediately made a successful pattern and verbally co-expressed, “Then I just do it like this! Now it’s okay.”

Fig. 3
figure 3

Patrick’s initial patterning response showing attention to shape as essential

Full size image

Similar verbal comments from the interviewer to urge the students to start questioning whether there were other ways of interpreting the task led many students to focus on the underlying pattern structure. These comments pertained to whether the student could see that the pattern tried to convey a rule. In transfer activities, some students likely interpreted the wording “the same” of the verbal instruction (see Table 2) to regard shape.

The other variant of different strategy use was to focus on colour and was only observed among the students with high number sense. However, the following discussion illustrates why we argue this strategy may involve relational thinking. Figure 4 shows the response Petra gave during a unit isolation task, patterning a tower with the same number of cubes as in the given model pattern but in only the dominant colour of the model pattern.

Fig. 4
figure 4

Petra’s different strategy. Left, given unit isolation trial; middle, successful ABB response; right, Petra’s response

Full size image

Her patterning response may reflect a lack of pattern awareness, according to Collins and Laski’s (2015) description of off-task strategies. Her final pattern solution may indicate that she matched cubes one-to-one until the correct number of cubes was reached. However, Petra’s multimodal co-expressions revealed that she point-counted cubes to check the total number of green and pink cubes, accompanied by the verbal expression, “Green comes more times!,” which may disprove that focusing on colour signifies a lack of awareness regarding the pattern’s underlying structure. This response might be a (de)composition strategy through which Petra relationally considered parts of the pattern and their relationship to each other and the whole pattern (Carpenter et al., 2005; Kieran, 2004). She compared the number of green cubes to the number of pink cubes before comparing the number of cubes for both colours to the total number of cubes. The Norwegian word flere [English: more] of the verbal instruction of unit isolation activities (see Table 2) may have guided students’ attention to “more” in terms of quantity instead of the repeating unit, and perhaps led students to focus on colour instead of the pattern’s repeating unit.

6 Limitations and implications

Number sense and patterning are related constructs, and definitions and operationalisations of number sense include awareness of repeating patterns and patterning strategies (e.g., Andrews & Sayers, 2015). As such, the students with higher number sense were expected to have more success in patterning activities compared to their low number sense peers. Nevertheless, we aimed to describe similarities and differences in number sense and patterning associations among students differing in number sense proficiency. Within-group number sense differences were larger for students with low number sense, but we cannot generalise the observations to the whole group.

We did not consider the complexity of the repeating units the students worked with. Different arrangements and complexities of the patterns’ repeating unit could lead to different findings. Wijns et al. (2021a, b) found that repeating patterning predicted growing patterning and number sense from the age of 5–6 years but not vice versa. Based on this finding, they hypothesised that it is easier to identify a visual repeating unit than an invisible, abstract unit of systematic change in growing patterns. Hence, the ability to identify a unit is dependent on its visibility and complexity. Consequently, future studies could further explore the relationships between number sense and repeating and growing patterning with varying complexity of the repeating unit and unit of change. This should include an exploration of pattern features and how they affect students’ access to the underlying structures of patterns.

Our observations indicate patterning strategies were affected by pattern features and language. A limitation of this study is that the students were not asked to verbalise or demonstrate their strategies and thinking. We also believe the verbal instructions affected the students’ patterning by guiding their attention to features of the pattern.

Thus, we emphasise the need to investigate verbal instructions and how students interpret them to expand our knowledge of communication and patterning relations. Observing students’ spontaneous patterning and making them explain their patterning—with more complex patterns as well—is crucial to expand our understanding of students’ thinking and strategy use.

7 Conclusion

This study investigated two research questions: (RQI) What are the similarities and differences in the success rates of duplicating, extending, transferring, and unit isolating repeating patterning activities among grade 1 students with low and high number sense? (RQII) What are the similarities and differences in the strategies employed in unsuccessful trials of repeating patterning activities among grade 1 students with low and high number sense?

In contrast to previous studies (e.g., Lüken & Sauzet, 2021), the current study investigated student strategy use during patterning activities, not merely patterning success. Moreover, some previous studies did not consider students’ multimodal patterning (e.g., Collins & Laski, 2015). In this study, multimodal analysis of students’ strategies to patterning activities revealed novel insights regarding the similarities and differences between high and low number sense students, identifying particular strategies applied for duplicating, extending, transferring, and unit isolating repeating patterning activities.

The findings of this study extend previous research showing that low number sense is correlated with poor AMPS (see Papic et al., 2011; Papic & Mulligan, 2007). The low number sense students in our study were more attentive to patterning structures than what might be expected from previous research. In particular, our interpretation of what Collins and Laski (2015) referred to as an off-task strategy is that it likely reflects pattern and structure sense, although based on other criteria than expected. Previous studies have interpreted attention to colour and shape to reflect a lack of pattern and structure awareness (Garrick, 2000; Lüken & Sauzet, 2021; Papic et al., 2011). In contrast, this study shows that such focus may be a result of relational thinking and strategy use, where quantities are compared based on criteria (e.g., colour) rather than the underlying pattern structure. One reason for this may be, as previous research has shown, that students tend to choose more sophisticated strategies from their repertoire when they perceive patterns as easy (Lüken & Sauzet, 2021). An alternative explanation is that such strategy use stems from a semantic misinterpretation of verbal instructions.

The findings of this study can enhance primary mathematics education by emphasising the use of extending and unit isolating activities of repeating patterns. These activities, through focusing on communicating the decomposition involved in them, can help scaffold the concept of unit identification in young learners. We support Lüken and Sauzet (2021) in recommending scaffolding students in identifying the repeating unit. This study also revealed the importance of exploring students’ understanding behind their strategy choices and use. We argue that both extending the repeating unit (operationalised as requiring unit extension, not only the next element) and unit isolation activities provide students with (de)composition tasks needed to elicit relational thinking (e.g., Kim et al., 2022). Our analysis showed that both student groups could replace successful patterning with recursive and different strategies, while only students with high number sense used relational strategies.