Assessing Multiple Inequalities and Air Pollution Abatement Policies

Abstract

Addressing inequality is recognized a worldwide development objective. The literature has primarily focused on examining economic or social inequality, but rarely on environmental inequality. Centering the discussion on economic or social factors does not provide a holistic view of inequality because it is multidimensional and several facets may overlap imposing a disproportionate burden on vulnerable communities. This study investigates the magnitude of air quality inequality in conjunction with economic and social inequalities in Bogotá (Colombia). It explores where inequalities overlap and assesses alleviation measures by tackling air pollution. We develop a composite index to estimate performance in socioeconomic and air quality characteristics across the city and evaluate inequality with a variety of measures. Using an atmospheric chemical transport model, we simulate the impact of three air pollution abatement policies: paving roads, industry fuel substitution, and diesel-vehicle renewal on fine particle concentrations, and compute their effect on inequality. Results show that allocation of air quality across Bogotá is highly unequal, exceeding economic or social inequality. Evidence also indicates that economic, social and air quality disparities intersect, displaying the southwest as the most vulnerable zone. Paving roads is found to be the most progressive and cost-effective policy, reducing overall inequality between 11 and 46 percent with net benefits exceeding US$1.4 billion.

1 Introduction

Inequality is a worldwide concern. It may impose high costs on society retarding economic growth and human development (Castello and Doménech 2002; Berg et al. 2018). The 2030 Agenda for Sustainable Development has insisted in reducing inequality as one of several strategies for prosperity across the globe (UN 2015). Much of the discussion in relation to inequality has been focused on the study of income and wealth distribution or gender (see Piketty 2015; Hyman 2017). However, the debate around improving the access to goods and services or opportunities by different societal groups has recently recognized the need of studying inequality in an inclusive analytical framework, emphasizing that inequality occurs in multiple and interacting dimensions beyond economic or social scopes (Caillods and Denis 2016). Environmental inequality is one of the suggested dimensions in this holistic view. This paper integrates the environmental dimension into the conventional analysis of inequalities and develops a multidimensional approach.

Our study investigates the magnitude of air quality inequality in conjunction with economic and social inequalities in Bogotá, Colombia. It explores where inequalities overlap and assesses a set of abatement policies that might alleviate them by tackling air pollution. Using information from several sources for more than 100 administrative zones in the city, we develop a composite index that aggregates economic, social, and air quality scores. The composite measure follows the same approach of the Human Development Index (UNDP 2020) and the Sustainable Development Goals Index (Sachs et al. 2021), which are used to monitor the achievement in human development, and country targets and objectives, respectively. We assess inequality between administrative units for each indicator using a variety of measures: Gini coefficient, and Atkinson and Bourguignon indexes.

The analysis of the distribution of environmental indicators has received more attention in the latest decades with an emerging work investigating the distribution of carbon dioxide emissions, solid waste (Duro 2012; Druckman and Jackson 2008), and more recently local air pollution (Zwickl et al 2014; Bouvier 2014; Boyce et al. 2016; Banzhaf et al. 2019; Meya 2020). Air pollution is documented as one of the most important environmental problems for its impacts on human health (Landrigan et al. 2018). Pollution inequality might increase the complexity of understanding and dealing with other forms of inequality. Overall inequality may be worsened when pollution is not homogenously distributed across population and space and is reinforced with economic and social inequalities. Therefore, we examine the spatial distribution of inequalities to assess such possible patterns. Overlapping inequalities increase the cost of policy design and implementation, which suggests that tackling inequality may not only be done through economic and social policies; environmental policy may also play a fundamental role.

In general, several studies that analyze the relationship between air pollution and socioeconomic variables point out the existence of important differences in the distribution of air pollution across communities; a fact that is more evident in the US than in Europe (see Richardson et al. 2013; Hajat et al. 2015; Rosofsky et al. 2018; Boyce et al. 2016; Clark et al. 2014; Bell and Ebisu 2012; Crowder and Downey 2010). For Latin American countries, few studies explore this issue. In Chile, Perez (2015) analyses air pollution in different areas in Santiago, showing that areas with higher poverty levels are more exposed to air pollution. On the contrary, Fernández and Wu (2016) shows that the strength of the correlation between air pollution and wealth depends on the scale at which the analysis is performed, with a negative relationship found in smaller areas. In Bogotá, Blanco-Becerra et al. (2014) finds that socioeconomic status may affect the magnitude of the association between air pollution and mortality from respiratory causes.

We study environmental inequalities in Bogotá, one of the largest cities in Latin America characterized by being exposed to fine particular matter concentrations that exceed by several times the national daily standard (37 μg/m³). This situation is influenced by meteorology and economic activities of the city. Roughly, 5662 tons of particulate matter with diameter less than 2.5 μm (PM_2.5) are emitted every year. Industry contributes with 6%, mobile sources with 30% and resuspended material with 58% of the total PM_2.5 emissions. Local actions to improve air quality in the last years were governed by the Decadal Air Pollution Abatement Plan (PDDAB) 2010–2020 (SDA and Uniandes 2010). Nevertheless, the PDDAB did not achieve the expected results. Some reduction measures were only partially implemented and other abatement actions never occurred. For example, in the industry, the number of establishments that replaced the use of highly polluting fuels by natural gas only increased 24%, and the installation of emission control systems in heavy-duty vehicles, such as Diesel Particulate Filters (DPF), was later eliminated by a local decree (see Bogotá cómo vamos 2020).

Considering that delaying abatement strategies increases the social costs of air pollution and that the unfruitful plan requires to be updated, we investigate the effect on PM_2.5 concentration of three abatement policies for the main pollutant sources under the current conditions: paving unpaved roads, substituting coal by natural gas in industry, and renewing diesel vehicle fleet. With these scenarios, we revisit the coal substitution policy for the industry sector in the PDDAB and include the vehicle renewal program suggested by the new Policy for Air Quality Improvement (PAQI) (DNP 2018). We also introduce the paving road policy that has not been listed as a key strategy of the local authority, but that for us it may treat a large fraction of emissions. Furthermore, East et al. (2021) have found that this policy may achieve significant reduction in PM_2.5 concentrations. We believe that studying the effect of those policies on PM_2.5 and conducting a cost–benefit analysis will shed light on the different actions in which authorities may devote investments. Moreover, the study examines whether those investments might cut air pollution in the most vulnerable zones and reduce overall inequality.

Estimating the effect of emission reductions on pollutant concentration is challenging. One approach is to use the level of emission reduction as a measure of the decrease in pollution exposure (Bouvier 2014). Although it is expected that emissions and air quality correlate, a disadvantage of this procedure is that the health risk is evaluated by pollutant concentrations and not emissions. An alternative to this procedure is to employ conversion factors from other studies to indirectly transform emissions into pollutant concentrations. However, a caveat of this method is that it does not consider the influence of multiple processes that concurrently govern the formation of fine aerosol particles in the atmosphere. Besides primary sources, the formed pollutant may react with other chemical species causing new particles, aerosols or other gases.¹ Wind, sunlight and other meteorological variables mediate those reactions. These dynamics are only captured by another approach called atmospheric chemical transport model. Our study employs a method of this kind, the Weather Research and Forecasting-Chemistry (WRF-Chem) model. This model has been recently used to analyze the contribution of regional biomass burning to aerosols and ozone pollution in Colombian cities (Ballesteros-Gonzales et al. 2020). It allows us to calibrate the current PM_2.5 concentrations and simulate the effect on air quality of the selected policy scenarios.² Simulated concentrations are then used as inputs to compute the potential composite index and inequality. Atmospheric chemical transport models have been primarily applied to investigate the effect of emission reduction plans and quantify ozone and PM_2.5 damage in the United States (US) and Europe (Muller and Mendelsohn 2007; Groosman et al. 2011; Fann et al. 2012; Kerl et al. 2015; Ščasný et al. 2015). Such models have not been widely used in Latin America, and have not, therefore, been employed in the design or evaluation of public policies related to air quality abatement.

The contribution of our study to the existing literature comes in four different streams. First, this research applies a multidimensional analysis of inequality. To the best of our knowledge, it is the first work that employs a composite index based on the Human Development Index (HDI) or the Sustainable Development Goals Index (SDG) to analyze air quality inequality and its aggregation with economic and social dimensions to a city scale. Second, our study is an example of a multidisciplinary approach in which we integrate atmospheric chemical circulation modelling and inequality indexes with especial application to a Latin American country, where the number of studies is scarce. The closest work related to ours is Groosman et al. (2011), which uses an integrated assessment model to analyze the human health benefits of reducing greenhouse emissions in the transport and electric power sectors in the US. Our study differs from Groosman et al. (2011) in the scale of application. While they conduct the analysis for a whole country using the county as the single unit, we run the WRF-Chem model for a city with a smaller spatial grid. Third, we use color bands to detect the most critical zones or sites where inequalities might overlap and to ease interpretation of the composite index by policymakers. Fourth, we conduct a cost–benefit analysis to support the process of policymaking in the construction of the new phase of the abatement plan.

Our results show that air quality inequality in Bogotá is higher than economic or social inequality when society is averse to the presence of disparities. We find evidence of overlapping inequalities. The lowest air quality, economic and social performance occur in the southwest of the city indicating the need for targeting this area as the focal point to address gaps across all dimensions. The three suggested policies not only reduce PM_2.5 concentrations but also overall inequality. Welfare gains range between US $52 million and $13.5 billion depending on the policy, time horizon, discount rate, investment costs and the size of air quality impacts. The findings point out that paving unpaved roads, which is an abatement strategy that treats non-exhaust and non-point source emissions, is the most cost-effective policy that also deals with interacting inequalities in the most critical zones. Our simulations suggest that the current heavy-duty vehicle renewal program has a high cost. Positive net benefits of this policy would only be achieved when assuming a long-time horizon.

The rest of the paper is organized as follows: Section 2 shows the conceptual framework of the study. Section 3 presents the theoretical underpinnings of the composite indicator and inequality measures. Section 4 describes the data and empirical analysis. It includes the socioeconomic and air quality index, the air quality model with policy scenarios, and the cost–benefit analysis. Section 5 presents the results. Section 6 concludes the paper.

2 Conceptual Framework

This study analyses air quality inequality for Bogotá in conjunction with households’ socio-economic characteristics and explores a set of policy actions to reduce air pollution and inequality across the city. Our purpose is not to develop a complete welfare analysis of inequality, we rather suggest a public policy tool that accounts for the multidimensionality of inequality. Fig. 1 presents our conceptual framework.

Fig. 1

Conceptual framework

We study both the current and potential socioeconomic and air quality characteristics of each Urban Planning Zone (UPZ) in the city. UPZ is the administrative unit that comprises neighborhoods with similar urban planning development and predominant activities. This level of aggregation provides a large variation of the city characteristics and corresponds to the spatial unit to which there exists the most detailed information, or where it is possible to estimate several socioeconomic indicators. We use information of 109 out of 112 UPZs.³ Using the methodology of HDI/SDG index (see UNDP 2020; Sachs et al. 2021), we develop the Socioeconomic and Air Quality (SEAQ) index that gathers information from economic, social and air quality variables for each UPZ. We begin estimating inequality between UPZs⁴ for economic, social and air quality sub-indicators and the SEAQ index for the current characteristics of Bogotá. These estimations are measures before policy intervention (henceforth, initial situation).

Subsequently, we investigate potential reduction in air pollution and inequality. Our first stage utilizes air quality modeling to calibrate the current conditions and simulate policy scenarios that consider meteorological and atmospheric chemical processes involved in air pollution dynamics across the city (see Nedbor-Gross et al. 2017; Grell et al. 2005). Three policies that entail pollution reduction from different sources are considered: (1) paving unpaved roads, (2) industry fuel substitution and (3) Heavy- and Light-Duty Vehicles renewal. The use of the air quality model allows us to map changes of pollutant emissions into concentrations for a given location. The second stage employs results from the air quality model to compute the SEAQ index for each UPZ and inequality measures under each policy scenario. After obtaining the current and potential inequality measures and SEAQ indexes, we compare the size of pollution concentration changes and inequality levels among the policy alternatives. Our empirical approach finalizes with a cost–benefit analysis for each policy scenario.

3 Underpinnings of the Composite Indicator and Inequality Measures

Our composite indicator is built on the well-known HDI/SDG index (UNDP 2020; Sachs et al. 2021). Theoretically, the composite indicator, $I_{i}$, summarizes the overall performance for every UPZ i of J aggregated dimensions, where each dimension gathers the achievement of K individual indicators. Let $I_{ij}$ denote the aggregated achievement of UPZ i for dimension j. A flexible function of the composite indicator takes the following form (see Decancq and Lugo 2013):

$$I_{i} = \left\{ {\begin{array}{*{20}l} {\left[ {\mathop \sum \limits_{j = 1}^{J} w_{j} I_{ij}^{\beta } } \right]^{{\frac{1}{\beta }}} } \hfill & {for\; \beta \ne 0} \hfill \\ {\mathop \prod \limits_{j = 1}^{J} I_{ij}^{{w_{j} }} } \hfill & {for \;\beta = 0} \hfill \\ \end{array} } \right.$$

(1)

where $\beta$ and $w_{j}$ are the degree of substitutability between dimensions and the dimension weights, respectively, and $\mathop \sum \nolimits_{j = 1}^{J} w_{j} = 1$ with $w_{j} > 0$. Let $\tilde{x}_{ijk}$ be the achievement of UPZ i for indicator k in dimension j, and $w_{jk}$ be the weight for each individual indicator within a particular dimension such that $\mathop \sum \nolimits_{k = 1}^{K} w_{jk} = 1$, with $w_{jk} > 0$. $I_{ij}$ also takes a similar functional form:

$$I_{ij} = \left\{ {\begin{array}{*{20}l} {\left[ {\mathop \sum \limits_{k = 1}^{K} w_{jk} \tilde{x}_{ijk}^{\beta } } \right]^{{\frac{1}{\beta }}} } \hfill & {for\; \beta \ne 0} \hfill \\ {\mathop \prod \limits_{j = 1}^{J} \tilde{x}_{ijk}^{{w_{jk} }} } \hfill & {for\; \beta = 0} \hfill \\ \end{array} } \right.$$

(2)

For $\beta$ equal to 1, dimensions are perfect substitutes. On the contrary, dimensions behave as perfect complements if $\beta$ goes to $- \infty$. $\beta = 0$ is an intermediate case, representing a Cobb–Douglas specification. The selection of $\beta$ has implications on the composite indicator, within or between dimensions. The HDI and SDG index choose $\beta = 1$ for aggregation within dimension and $\beta = 0$ for aggregation between dimensions. We follow a similar approach. We suggest the SEAQ index entails three dimensions: economic, social, and air quality. When using $\beta = 1$ within a specific dimension, this corresponds to a weighted arithmetic mean of individual indicators. It implies that administrative unit i is indifferent of choosing on which particular individual indicator to make progress within the dimension. Employing a $\beta = 0$ for aggregation between dimensions consists of estimating a geometric mean. Essentially, choosing a Cobb–Douglas form assumes limited substitutability among dimensions. This feature is suitable for the SEAQ index because it considers unequal performance across dimensions. For instance, good economic achievements may not entirely offset poor air quality.

Decancq and Lugo (2012) describes in detail the properties of aggregation functions, as the one we described for the SEAQ index. In general, for aggregation within dimensions, the chosen composite index is a continuous function that satisfies monotonicity, normalization and weak ratio-scale invariance. In the case of aggregation across dimensions, the index satisfies, besides monotonicity and normalization, the strong ratio-scale invariance property. These properties are relevant to maintain a monotonic rank and leave the ordering unaffected under transformations or changes in indicator scores.

Similar to the HDI/SDG index, we do not have a prior preference to provide a higher weight to one dimension than another. Thus, we assume equal weights to aggregate individual indicators and dimensions. Since weighting is one of the factors determining the trade-off between dimensions and may affect the orderings, we also provide estimates using a set of different weights where each $w_{j} = \left( {0.2,{ }0.4,{ }0.6} \right)$. In addition to this, we examine the sensitivity of SEAQ index to changes in the number of indicators per dimension. We use single indicators per dimension or exclude a nearly constant indicator in one dimension. Variations in the results of SEAQ index are assessed by means of the mean of the absolute rank difference $\left( {\overline{R}} \right)$, standard error of $\overline{R}$, and the Spearman's rank correlation coefficient ($\rho$).

Regarding inequality, we estimate inequality measures suggested in the literature to analyze economic and social characteristics such us the Gini coefficient and the Atkinson index, and we apply them to air quality, our environmental indicator. An appealing feature of these measures is that they differ in the weight they assign to different parts of the variable distribution. While the Gini coefficient (Gini) is sensitive to changes at the center of the distribution, the Atkinson index (A) has the flexibility to account for inequality aversion. The degree of aversion is captured by a parameter called $\alpha$. High levels of $\alpha$ imply high aversion to inequality, giving more weight to observations in the lower tail of the distribution. If $\alpha$ is zero no aversion is assumed. This allows us to obtain different inequality values for each indicator according to the judgment of the aversion degree to inequality. Gini has been incorporated in studies analyzing spatial variation of environmental measures (Saha et al. 2018; Soares et al. 2018; Duro 2012). However, despite its widespread application, the use of the Gini has encountered a diverse critique (see Deltas 2003). This has motivated the use of other measures, such as the Atkinson index, which is especially crafted to satisfy axioms grounded on microeconomic theory (Atkinson 1970).⁵

The Gini and Atkinson index have been extended to the context of multiple dimensions. Gajdos and Weymark (2005), and Decancq et al. (2009) develop a family of multidimensional Gini and Atkinson indexes, respectively. These authors discuss index properties in detail. In the literature, two of the main desirable properties are the uniform majorisation principle (UM) and the correlation-increasing majorization (CIM) (Tsui 1999). The first property indicates that if one conducts a uniform mean-preserving average for all dimensions, it leads to a socially preferred situation. The second property implies that if dimensions are highly correlated, for given marginal distributions, inequality increases. In our context CIM is relevant, because inequality would rise if low achievements in air quality correlate with poor economic or social performance for some UPZs. UM is satisfied when $\alpha > 0$ and $\beta < 1$, and CIM requires $\alpha + \beta > 1$ (Decancq et al. 2009).

As an alternative to the previous SEAQ function, for comparison purposes, we also estimate the Bourguignon’s aggregation function, which is strictly monotonic and concave (see Lugo 2007). Bourguignon’s composite indicator is computed as follows:

$$I_{i} = \left[ {\mathop \sum \limits_{j = 1}^{J} w_{j} I_{ij}^{\beta } } \right]^{{\frac{\alpha }{\beta }}} \;{\text{for}}\;{ }\beta \ne 0$$

(3)

$$I_{ij} = \left[ {\mathop \sum \limits_{k = 1}^{K} w_{jk} \tilde{x}_{ijk}^{\beta } } \right]^{{\frac{\alpha }{\beta }}} \; for \;\beta \ne 0$$

(4)

This function is related to the Bourguignon (B) inequality index (Bourguignon 1999). Lugo (2007) shows that this index satisfies UM and CIM when $\beta < 1$, $\alpha > 0$, and $\alpha < \beta$. Lugo (2007) in empirical exercises selected $\beta = 0.5$ and $\alpha = 0.33$. Liotta et al. (2020), a recent study that analyzes the implementation of urban greening policies as a strategy to reduce inequalities in France, also employs those values because they satisfy desirable properties. We guide our work on such $\beta$ and $\alpha$ values when estimating Bourguignon index. For consistency, we calculate the unidimensional and multidimensional Atkinson index using $\alpha = 0.33$, which is equivalent to low degree of inequality aversion. To assess high inequality aversion, we also estimate Atkinson index using $\alpha = 1.5$. Those values of $\alpha$ allow to satisfy CIM property within and between dimensions. All inequality measures are estimated using UPZ population weights.

4 Data and Empirical Analysis

4.1 The Current SEAQ Index

As mentioned earlier, the SEAQ index involves three dimensions: economic, social, and air quality.⁶ The appealing feature of computing an index is that we may estimate both inequality measures for each dimension and the composite score that aggregates the performance across dimensions for certain location. Moreover, the index informs on the score and ranking position of each UPZ according to its performance. This is suitable for policymaking because it displays the spatial distribution of scores and indicates how much the performance of the most vulnerable zones differs from other locations, being a useful tool to analyze policy actions that might induce improvements in the scores or a reduction in inequality.

With the available information, we define a set of variables for each dimension and build the index for year 2018. Data come from multiple sources and calculations are conducted using spatial tools in ArcGis.⁷

4.1.1 Economic Dimension

This includes per capita income, land price, house-building price, and population belonging to the lowest socioeconomic strata. These set of variables provide an indication of the economic conditions of the households and their neighborhoods. Household’s per capita income and socioeconomic strata are obtained from the Bogotá’s Multipurpose Survey 2017 conducted by the National Department of Statistics (DANE). Socioeconomic strata is a classification of households employed by the Colombian government to allocate utility subsidies of water and electricity services. It consists of six discrete groups organized in ascending order based on the quality of external physical characteristics of housing and its surroundings such as house facade and roof materials, the existence of sidewalks, green areas and other factors. From the survey, using household residential location, we calculate for every UPZ the average per capita income and the fraction of population belonging to the lowest socioeconomic strata (classes one and two). Unlike average house-building and land prices, socioeconomic strata provides a measure of heterogeneity in housing and zone characteristics inside each UPZ. Average land and house-building prices per UPZ are computed from the Cadastral Census 2016 of the Secretary of Planning. Monetary values are expressed as constant prices of 2018 using the Consumer Price Index (CPI). We assume that households’ socioeconomic strata remains unaltered between 2017 and 2018.

4.1.2 Social Dimension

This comprises a set of health and education indicators. It involves health center supply, mortality rate, school supply, school dropout, and population with primary school as the highest schooling achievement. Health center supply is proxied by the number of health centers. We use information from the Integral System of Social Protection (SISPRO). We accessed to the detailed list of health care centers (IPS) of Bogotá and selected public and private centers that reported respiratory and cardiovascular diseases cases in 2018, the most prominent diseases related to air pollution exposure. Individual physician outpatient offices were excluded since we want to provide a measure of supply for large institutions. Having the IPS address, we calculate the sum of public and private IPS at the locality level per 100,000 inhabitants. We estimate figures for locality, which is the next level of aggregation to UPZ, because some UPZs do not have presence of health institutions. Thus, the statistics of health centers are assigned to all UPZs inside the same locality. Regarding mortality, rates (for all causes) per 100,000 inhabitants are obtained from the Vital Statistics 2018 of the Secretary of Health. Given that mortality rates are not available for UPZs, we assume a UPZ has the same rate observed for the entire locality.

Our measure of total school supply is the number of schools per 100,000 inhabitants for UPZ. Information is obtained from the School Database 2020 of the Secretary of Education. Using the school address and the UPZ polygons, we compute the sum of private and public schools per zone. In the case of total school dropout, we calculate the average dropout rate for each UPZ and then the average between private and public school rates. Information was accessed combining Private and Public School Dropout Rate Databases from the Secretary of Education for 2019. With respect to schooling level, we estimate the fraction of population with primary school as the highest schooling achievement. The data was also taken from the Multipurpose Survey 2017. Although data from schooling attainment, dropout rate and school supply were not available for 2018, we consider the information obtained for these variables in 2017, 2019 or 2020 is a fair approximation of the figures in 2018.

4.1.3 Air Quality Dimension

This is represented by PM_2.5 concentrations since fine particulate matter is the most critical pollutant. We accessed to the Air Quality-Monitoring Network of Bogotá (RMCAB) database in 2018, which contains information on hourly PM_2.5 concentrations for twelve monitoring stations evenly distributed throughout Bogotá. First, we calculate daily averages, and hence, yearly averages per station. Second, in order to obtain pollutant concentrations for the entire city, we use Inverse Distance Weighting (IDW) approach applying the algorithm of the minimum and maximum number of neighbors that minimize the root mean square error. Third, pollution at UPZ level is calculated as the concentration average of all fishnets of 60 × 60 m laying inside a UPZ polygon. Descriptive statistics for all variables are shown in Table A1 of the Supplementary Material (SM).

The SEAQ index scores are obtained in three steps: definition of the distribution’s extreme values of each indicator (maximum and minimum), normalization of variables, and aggregation of the normalized scores within and across dimensions. We apply the principle of “leave no one behind” to define maximum indicator values for some variables: zero population belonging to the lowest socioeconomic strata, zero school dropout, and zero population with primary school as the highest schooling achievement. For other variables, the upper bound is defined as the average of the ten best performing UPZs, except for the case of mortality, where we choose the lowest rate in the last five years, or for PM_2.5, where we selected the suggested SDG maximum value. Table A2 in SM shows in detail the upper and lower bounds for each variable.

For spatial purposes, Table A2 also displays four-color bands (from green to red) for each indicator. Bands are intended to show which areas of the city may exhibit better or worse SEAQ index scores. We set the color thresholds based on the following procedure. Whether we find some reference values reported in national or international literature, we assign such values for those variables as color thresholds. Per capita income bands use the minimum monthly wage (MW) in Colombia: green for values above four times the MW, yellow for values between two and four MW, orange from one to two MW, and red below one MW. In the case of PM_2.5, green threshold corresponds to the World Health Organization’s (WHO) air quality guideline 2005, yellow and orange to the WHO’s Interim target-3 and -2, respectively, and red to concentrations above the WHO Interim target-2. For mortality, the average city rate is used as the threshold that separates yellow and orange bands. For other monetary variables, we use quartiles as color band thresholds. This is the case of land and house-building prices. For all other variables, we divide the lower or upper bound values in half to define the red or green thresholds, respectively.

To allow comparability each variable is then rescaled in an indicator between 0 and 100 through the formula $\tilde{x}_{ijk} = \left[ {x_{ijk} - \min \left( {x_{jk} } \right)} \right]/\left[ {\max \left( {x_{jk} } \right) - \min \left( {x_{jk} } \right)} \right]$, where $x_{ijk}$ is the variable value, $\tilde{x}_{ijk}$ is the rescaled value, and $\min \left( {x_{jk} } \right)$ and $\max \left( {x_{jk} } \right)$ are the corresponding lower and upper bounds. Aggregation within and between dimensions follows Eqs. (1) and (2), or alternatively Eqs. (3) and (4) for Bourguignon index. Multidimensional inequality is estimated using Gajdos and Weymark (2005) for Gini, Decancq et al. (2009) for Atkinson index, and Lugo (2007) for Bourguignon index.

4.2 Air Quality Modelling

To calibrate particle concentrations in the initial situation and simulate policy scenarios, we use the atmospheric chemical transport model WRF-Chem. The model uses differential equations to represent various complex atmospheric processes that ultimately determine the concentration of particulate matter and other gas-phase species in the atmosphere (Grell et al. 2005). These differential equations are solved over a three-dimensional grid covering the atmospheric domain of interest. As the atmospheric conditions in a given location are affected by processes occurring at different scales, the configuration of the model domain considers a much larger area than Bogotá to allow influences from large-scale atmospheric flows. Three nested domains centered on Colombia and covering the northern half of South America and the Caribbean are created to carry out simulations. The model includes 41 vertical levels and the following horizontal resolutions: 27 × 27 km with 121 × 121 grid cells for domain 1 (D01), 9 × 9 km with 127 × 127 grid cells for domain 2 (D02), and 3 × 3 km with 133 × 133 grid spaces for domain 3 (D03). Available processing power currently prevents us from performing higher resolution analysis. Simulation results of domain 1 serve as input for domain 2. In the same way, results of simulation 2 are used for domain 3, passing data from low to high resolutions. Data from global atmospheric models is used to provide the initial and boundary conditions.

Modeling periods are February and September 2018. These months are chosen as representative of high concentrations and unfavorable meteorological conditions (February), and of lower air pollutant concentrations (September) (Mendez-Espinosa et al. 2019). Besides their large differences in air pollution concentration, these months are believed to be representative of the diverse meteorological conditions encountered throughout the year. Furthermore, the mean PM_2.5 concentration for these months is only slightly higher than the annual mean PM_2.5 concentration.

In the air quality modeling, we included emissions of air pollutants and their chemical precursors from several sources. We consider emissions from agricultural burns and forest fires (Wiedinmyer et al. 2011) as well as emissions of chemical species produced by vegetation (Guenther et al. 2006). Anthropogenic emissions, which are the key component in our analysis, are incorporated from The Emissions Database for Global Atmospheric Research version 4.3.1 (EDGAR V4.3.1) emissions inventory (see Crippa et al. 2016). For Bogotá city limits, we merge EDGAR emissions with the local emission inventory of Bogotá developed by the environmental authority (SDA 2018). Local inventory is disaggregated into commercial, mobile, industrial, and resuspended particulate matter (RPM) sources with a resolution of 1 km × 1 km.⁸ RPM source strength was determined by other studies through direct measurements of the dust loading at many points in the city and an extrapolation of that direct data using information on the number and length of all paved and unpaved roads (Pachón et al. 2018). Total mobile emissions are separated into emissions from diesel and gasoline according to fuel consumption (54% diesel and 46% gasoline).

We calibrate initial situation with the current meteorological, atmospheric and emission conditions in the domains described earlier. Model performance is evaluated by comparing PM_2.5 concentrations observed by the RMCAB versus our modeled data. Performance metrics such as Normalized Mean Bias (NMB), Root Mean Squared Error (RMSE), and Index of Agreement (IOA) are calculated as suggested by Emery et al. (2001, 2017). We define policy scenarios of air pollution reduction for the most influential sources in Bogotá: mobile, industrial, and RPM emissions. For a given scenario, the simulation considers the emission reduction only applies to certain sources, keeping all other emission sources constant. The policy scenarios studied are as follows:

• Scenario 1. Reduction of Resuspended Road Dust Emissions

RPM emissions are caused by constructions, quarries, paved roads, and unpaved roads. PM_2.5 emissions from those sources are 101; 44; 1577; and 1569 Ton/year, respectively. It is salient that unpaved and paved-roads domain RPM emissions, as has been noted in other studies (Pachón et al. 2018; Pérez-Peña et al. 2017). The impact of reducing resuspended road dust emissions from paved and unpaved roads has recently been analyzed by East et al. (2021) using a different chemical transport model. The authors found that PM_2.5 concentration could be considerably reduced (10 µg/m³) by 2030 in some parts of the city through that emission reduction strategy. To our knowledge, no analysis of the impact of such action on environmental inequality has been conducted in the literature. We focus our analysis on reducing all emissions from unpaved roads (see Table 1) because estimation of implementation costs is less complex than for paved roads. Computing the cost of unpaved roads requires information on global dimensions of the roads, while repairing or filling paved roads requires more specific information, i.e., it would imply to know in detail number, size, and current conditions of potholes per road, which is not available. Unpaved roads are present in several areas of the city, but their occurrence tends to be more prevalent in the southwest and northeast. This scenario involves a 48% reduction of total RPM.

• Scenario 2. Reduction of industrial emissions

According to the 2018 emissions inventory, Bogotá has 2030 industrial combustion sources, of which 87% use natural gas, 4% coal, 3% diesel and liquefied petroleum gas, 2% wood and used oil without treatment, and the remaining 1% other fuels such as biogas or other energy sources. Although only 4% of the industrial combustion sources use coal as fuel, they account for 80% of the total industrial particulate matter emissions in Bogotá (SDA 2018). Most emissions from this industrial sector are in the center-west and south of the city. In this scenario, we consider fuel replacement of coal-powered industrial combustion sources by natural gas. Emission factors (EF), activity factors (AF) and the calorific value of carbon and natural gas are considered to calculate fuel conversion.⁹ We disaggregate emissions from industries that use coal into Boiler > 100 boiler horsepower (BHP), Boiler < 100BHP, Brick furnace and Coal furnace (see Table 1). This technological transformation implies a reduction of 99% of PM_2.5 for those industrial plants and 81% for all industrial establishments.

• Scenario 3. Reduction of mobile emissions

Heavy- and Light-Duty Vehicles (trucks and pickups) are the largest emitters of particulate matter from mobile sources in Bogotá. They contribute with 39% of PM_2.5 emissions of more than 2.4 million vehicles registered in the city, but only represent the 4% of all vehicle fleet (SDA 2018). Currently, from all diesel heavy-duty vehicles, 33% of them have Pre-Euro technology and 58% between Euro I and Euro III. Our policy scenario targets the diesel-powered fleet of Heavy- and Light-Duty Vehicles (hereinafter HLDV) and assumes that all new diesel vehicles comply with Euro IV standard. This policy seeks to resemble the expectations of the 2013 Resolution 1111 of the Ministry of Environment, which was enforced since 2015 and attempted by command-and-control to encourage technological upgrade in the entire diesel fleet. We employ EF and AF of HLDV to quantify the emission reduction.¹⁰ Unfortunately, information of emissions from diesel and gasoline vehicles across roads is not disaggregated by vehicle category (cars, bus, trucks, etc.). Hence, we use the spatial distribution of aggregated mobile sources within the city to proportionally assign emission reduction in the HLDV fleet. The greatest HLDV emissions arise in the west and south zones, which is consistent with the fact that the main entry and exit roads of the city are located in those areas. This scenario implies a reduction of 91% in PM_2.5 emissions from HLDV (see Table 1) and 35% from all mobile sources.

Table 1 Baseline and policy scenario emissions

After defining emissions of the initial situation and policy scenarios, we run the WRF-Chem model to obtain the average PM_2.5 concentrations for February and September. Equation (5) quantifies the change in concentrations attributable to the decrease in emissions from each scenario:

$$\Delta PM_{{2.5RS_{m} }} = PM_{2.5BS} - PM_{{2.5RS_{m} }}$$

(5)

where $PM_{2.5BS}$ is the concentration in the initial situation (BS), $PM_{{2.5RS_{m} }}$ is the concentration under the $m$th Reduction Scenario ($RS_{m}$). Therefore, $\Delta PM_{{2.5RS_{m} }}$ represents the expected change in the concentration for a specific policy scenario. The equation is applied temporally and spatially across Bogotá.

4.3 The Potential SEAQ Index

We convert WRF-Chem results in potential inequality measures and SEAQ scores for each policy scenario. Given that WRF-Chem provides outputs of two specific months, February and September, and for pixels of 3 × 3 km, we require harmonizing temporal and spatial resolution of the estimates before computing the scores. To obtain annual estimates of PM_2.5 concentration changes per policy scenario, we compute the mean of WRF-Chem outputs between these two months. As UPZs do not have convex shapes or do not entirely match with pixels of 3 × 3 km, we use fishnets of 60 × 60 m to conduct the spatial joint between UPZs and pixels. Concentration changes of each pixel of 3 × 3 km are assigned to every fishnet laying inside the pixel. The average concentration changes of PM_2.5 for each UPZ under a policy scenario is the average of all fishnets within the UPZ.

Policy scenarios are assumed to affect not only air quality dimension but also social and economic dimensions of the SEAQ index. For social dimension, we explore the impact of air pollution on mortality because it is well established in the literature and its estimation procedures are widely known (see Landrigan et al. 2018; Pope et al. 2011; Burnett and Cohen 2020). Other health and education indicators in social dimension remain unchanged. In the case of economic dimension, we consider that economic dimension is affected by air quality changes through housing markets via land and house-building prices (see Chay and Greenstone 2005; Cariazo and Gomez-Mahecha 2018). Although per capita income may also be affected by air pollution through labor productivity (see Graff-Zivin and Neidell 2012), those changes entail adjustments in labor market, whose estimation is not straightforward. Computing these effects would imply to analyze equilibrium in markets or interactions with other variables, which is out of the scope of this paper. Potential SEAQ index and inequality measures are estimated using the same procedure as the current SEAQ index. Potential scores of air quality, mortality, and land and house-building prices indicators are estimated as follows:

4.3.1 Potential Air Quality Scores

Average concentration change of PM_2.5 in each policy setting is subtracted from current PM_2.5 concentrations. These values represent potential air quality in every UPZ for our three policy scenarios. As in the current air quality, potential concentrations are rescaled in an indicator between 0 and 100.

4.3.2 Potential Mortality Rate Scores

Expected mortality rate under each policy scenario is calculated as the difference between the current total mortality rate and the estimated avoidable mortality rate attributed to the change in air pollutant concentration. Premature deaths attributed to PM_2.5 exposure for each policy setting and initial situation are estimated using Burnett and Cohen (2020). A similar approach is employed by Bonilla (2022). Appendix F in SM describes in detail the estimation procedure. Premature mortality is calculated for population above 25 years of age and five health outcomes as suggested by WB and IHME (2016): ischemic heart disease (IHD), stroke (ST), chronic obstructive pulmonary disease (COPD), lung cancer (LC), and acute lower respiratory infections (LRI). The difference between the attributable burden before and after policy implementation is the avoidable mortality attributed to the change in air pollutant concentration for a particular policy. Values are aggregated at locality level and expressed as rates per 100,000 inhabitants. Subsequently, these new variables are rescaled.

4.3.3 Potential Land and House-Building Price Scores

To calculate the change in those prices we employ hedonic-model estimates of the effect of PM₁₀ concentrations on rental housing values for Bogotá obtained by Carriazo and Gomez-Mahecha (2018). First-stage equation reported by the authors indicates that a decrease of 1 µg/m³ of PM₁₀ would imply an increase of 1.5% in rental prices. As the hedonic model analyzes PM₁₀, we converted changes in PM_2.5 to PM₁₀ concentrations using PM₁₀/PM_2.5 ratios derived by our WRF-Chem model under each policy scenario and UPZ. Then, as rental values are proportional to land and house-building prices, we estimate the change in prices for each policy scenario multiplying the proportional change in rental price by the achieved air quality improvements. These prices are also rescaled.

4.4 Cost–Benefit Analysis

Implementation of the abatement actions assumes that paving unpaved roads, substituting fuel in the industry, and renewing HLDV occur in a given year, named year 0. That is, each policy is fully implemented in year 0 and not in stages or phases.¹¹ Therefore, our study provides a comparative static analysis, without considering transition effects.

Benefits are derived, on the one hand, from avoidable mortality, and on the other, from hedonic prices through the rental housing market.¹² A method that considers the full economic costs of premature mortality is the willingness-to-pay (WTP) approach. WTP provides the marginal value that a person is willing to pay to reduce the risk of dying (WB and IHME 2016). This valuation approach involves many aspects of individual’s life, besides income or consumption, which the person is not willing to lose. WB and IHME (2016) presents the methodology to compute welfare effects from premature mortality using WTP-based approach. The analysis is anchored in the value of statistical life (VSL) that corresponds to the aggregation of several individual’s WTP to reduce the risk of death. As far as we know, there are not available WTP studies for Colombia informing the VSL, hence the VSL for Bogotá is calculated using the benefit-transfer approach suggested by WB and IHME (2016). Appendix G in SM shows the procedure to obtain VSL. Our calculated VSL is equal to US $1.72 million. The product of avoidable deaths times transferred VSL is the estimated benefit from avoidable mortality in a given year.

A flow of benefits from avoidable mortality is scheduled for ten years. The number of avoidable premature deaths is assumed to increase every year according to population growth. Average population growth rate is 0.46%, which is estimated from World Population Prospects Dataset of UN (2019). We also consider VSL increases overtime. GDP and population growth are employed to project VSL values. GDP long-term forecasts are taken from OECD (2021). Average per capita GDP growth is 1.93%. In the absence of the policy (counterfactual), we also assume air quality declines because roads deteriorate and vehicles get older. In the counterfactual, deterioration of roads is around 1.4% per year and emissions from HLDV vehicles grow annually at 7.8% (henceforth, mean deterioration rates). Since historical reports project no increase in coal consumption, in the absence of the policy PM_2.5 emissions from boilers and furnaces remain constant over time.

We estimate benefits of air quality improvements from rental housing market using WTP values reported by Carriazo and Gomez-Mahecha (2018). Hedonic method is supposed to capture benefits in health outcomes, aesthetics and locational amenities due to reduction in air pollution (Portney 1981). However, it may not yield the economic value of any health benefit. Homeowners must be aware of all health impacts of air pollution, including premature mortality, to capitalize total costs or benefits into the housing prices. Given that the local authority launched the air quality-warning program only since 2017, that is, several years after the data collection period (2011) of the survey employed by Carriazo and Gomez-Mahecha (2018) to obtain hedonic values, we believe it is unlikely that households in Bogotá would perceive all health costs of pollution, and particularly mortality risks. Therefore, we assume valuation of benefits estimated from hedonic model is imperfect to account for mortality risks. Portney (1981) indicates that when analyzing environmental policies, we may combine under certain circumstances estimates from health effects and property values to infer the economic value of changes in air pollution. Thus, in our cost–benefit analysis we do not only show benefits obtained from the VSL values for premature mortality and WTP from hedonic prices separately, but also from a combination of these benefits.¹³

Carriazo and Gomez-Mahecha (2018) reported the air-quality demand equations from the second-stage hedonic model for households in low, middle and high socioeconomic strata. We derive total benefits in housing market as the area under the demand curves using data on household distribution per strata from the Multipurpose Survey 2017 of Bogotá and employing PM₁₀/PM_2.5 ratios of the WRF-Chem model to convert PM_2.5 changes to PM₁₀ concentrations. The flow of benefits from hedonic model also adopts mean deterioration rates in the absence of the policy.

Estimation of implementation costs requires different approaches depending on the policy scenario and the available information. Paving roads entails costs of labor, machinery, asphalt concrete pavement and other material costs. An approximation of these costs is the unitary price (per square meter) of infrastructure construction per transport mode, which is accessed from the Urban Development Institute of Bogotá in 2020. To estimate total building costs, we also need a measure of the size of unpaved roads. Using the Road Network Database of the Secretary of Mobility, we calculate the total length of all roads and their average width per UPZ. Length on unpaved roads is proportionally assigned to each UPZ according to PM_2.5 emissions from resuspended material, while width is allocated considering only roads in poor condition. Total building costs of unpaved roads is the multiplication of the unitary construction price of road infrastructure by the size of unpaved roads. In total, this policy entails to pave around 1300 km of unpaved roads with a width that varies from 3.6 to 7.8 m at an average building price of US $93 per square meter of road. We also add a 10% of building costs to account for investments in lighting network and traffic signage.¹⁴

For industry fuel substitution, implementation costs comprise fuel costs and management or adjustment plant costs. Estimations are conducted for boilers and furnaces. Fuel costs are equivalent to the product of unitary fuel prices and consumption. Coal price per ton (US $62) is taken from Resolution 119 of 2019 of the Mining and Energy Planning Unit. Natural gas price per cubic meter is obtained from Vanti S.A. in 2020, the utility service company in Bogotá. Gas prices range between US $0.45 and $0.53 per cubic meter. Consumption of coal and natural gas are accessed from the emissions inventory. We assume that manipulation cost of coal and plant adjustment costs¹⁵ of natural gas are 10% of the total fuel costs. To get the estimate of industry fuel substitution costs, coal expenditures are deducted from total natural gas costs because under this policy scenario boilers and furnaces do not incur fuel and manipulation costs of coal.

In the case of HLDV renewal, we gather information on market prices of new diesel vehicles that accomplish Euro IV emission standard. Information is collected by vehicle type such as pickups and trucks and cylinder capacity (small, medium and large).¹⁶ Prices of these new diesel vehicles in the Colombian market vary between US $24,500 and US $135,500. Data are taken from Motor (2020) and searches in webpages of vehicles dealers. This policy scenario is targeted to 64,102 diesel vehicles: 6691 pickups and 57,411 trucks. We uniformly assigned the number of vehicles inside each vehicle category according to cylinder capacity. The analysis takes into account the current government program to renew load vehicles. The program offers vehicle owners an economic support to purchase a new vehicle once the old vehicle has been scrapped. Values of economic support in 2018 are obtained from the Ministry of Transport. Those values vary from US $9500 to US $18,900 per vehicle. To accelerate renewal, the program also grants an exemption of the value-added tax (VAT) for the new vehicle purchase, which is equivalent to 19% of the price (roughly between US $13,500 and US $25,800 per vehicle). The support is given only to old trucks with a gross vehicle weight above 10.5 tons and varies across vehicle category. The total cost of the HLDV renewal for owners is calculated as the vehicle price, after deducting the program support, times the vehicle fleet size. Monetary values of implementation costs for all policy scenarios are adjusted by inflation and expressed in constant prices of 2018.

In order to conduct a cost–benefit analysis we define a flow of costs for ten years. From year 1 to year 10, annual costs of road maintenance are added to implementation costs of paving roads. Maintenance costs are computed as 10% of building costs. Implementation costs are supposed to be a public investment financed by a credit taken from a multilateral organization using an annual interest rate of 5%. Government pays off the debt with an annual property tax charged to households within the UPZs located in the orange, yellow and green color bands of the land price indicator. That is, investment costs are spatially distributed such that vulnerable households in the red color band are not charged by the tax (almost a quarter of the UPZs). We propose a property tax based on the notion that improvements in air quality would increase housing values.¹⁷ With this funding scheme, implementation costs are not uniformly distributed, therefore, the mechanism to finance the costs preserves the progressive nature of the policy.

In the case of fuel substitution and HLDV renewal, plant and vehicle owners would need to finance the costs of technological change in boilers and furnaces. Note that despite receiving the economic support from the government, vehicle owners have to incur in vehicle costs. We consider that plant and vehicle owners may access a national bank credit for five years with an annual effective interest rate of 13.5%, the current rate in the financial market. This period is, on average, the usual time that banks in Colombia give to consumers to repay their credits. Annual instalments to repay the debt are simulated from year 1 to year 5 using implementation costs in year 0 as the capital borrowed from the bank. Investments costs are shared between the plant or vehicle owners and the government. We consider plant and vehicle owners pay off the principal, while the government is responsible for the loan interests. Households within the non-red color band zones of land price indicator would be charged with an annual property tax to pay off the government investment in each case. Given that the support and VAT exemption of the HLDV renewal policy is an existing program, we assume the government already owns the budget to finance this investment and no additional tax to households is imposed for this purpose. Present values of benefits, costs, net benefits, and benefit/costs ratio are estimated using a discount rate (δ) of 3%.

We also conducted a sensitivity analysis. We provide estimates for low and high discount rates (1% and 5%, respectively) and for a time horizon of fifteen years in each policy scenario. We do not consider a longer period than fifteen years because since 2035 new vehicles must comply Euro VI standard, and thus the renewed vehicles in our simulated policy (Euro IV) would not fulfil the national regulation. In the absence of the policy, we also adopt a high deterioration rate for roads and vehicles that are twice the mean deterioration values reported over time (2.8% and 15.6%, respectively). Coal consumption in the counterfactual is supposed to increase at 2% per year. Finally, investment costs are simulated considering costly interest rates of investments: 10% for credit in paving road policy and 15% for loans in industry fuel substitution and HLDV renewal policy scenarios.

5 Results

5.1 Current SEAQ Index

Table 2 shows inequality measures for each indicator and SEAQ index. For economic dimension, neutral measures such as Gini indicate that house-building price is more unequal than other indicators. On the contrary, Atkinson and Bourguignon measures point out that the highest inequality is exhibited by the fraction of population belonging to the lowest socioeconomic strata. Exploring the spatial distribution of economic indicator scores, color bands reveal that UPZs in the south and west display the poorest performance (maps not shown; available upon request). In those areas, more than 50% of the population belong to the lowest socioeconomic strata. Estimations also suggest that land price is the indicator with the lowest inequality values, irrespective of the measure employed.

Table 2 Inequality measures of current SEAQ index and economic, social, and air quality indicators

Regarding social dimension, all measures indicate that health centers supply exhibits the highest inequality. School dropout shows the lowest inequality according to the Atkinson and Bourguignon indexes. These two variables also provide the highest and lowest inequality values across all individual indicators. It shows progress in school dropout rates because they have reached low values across the city. However, inequality estimates also underline that health centers allocation needs to be improved to offer a fairer access to health service in Bogotá. Such improvement might be focused on the west and south areas that report the lowest number of IPS (maps not shown; available upon request).

We plot Lorenz curves for economic, social, and air quality sub-indicators (see Fig. 2). They illustrate that social dimension is the least unequal dimension and has the most regular performance across population. Results inform that only 10% of population enjoys either 15% of the best air quality or 20% of the best economic scores. Moreover, economic and air quality dimension curves intersect, showing that around 30% of population has the poorest economic or air quality performance. Comparing across measures, Gini and A(0.33) show that economic dimension presents higher inequality than the other dimensions, whereas A(1.5) indicates air quality is the most unequal dimension. This result implies that air quality becomes more relevant when aversion to inequality rises. Interestingly, Bourguignon index, a measure that satisfies both UM and CIM properties, also points out that air quality is more unequal than economic or social dimensions.

Fig. 2

Lorenz curves of economic, social, and air quality dimension and SEAQ index

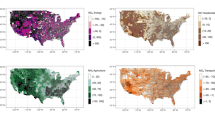
When it comes to our aggregated measure across dimensions, results also show important disparities among UPZs in the SEAQ index. The spatial distribution of economic, social, and air quality dimensions, and SEAQ index scores is presented in Fig. 3. Maps indicate that the lowest economic scores occur in the periphery of the city, mainly in the west and south. The minimum social scores arise essentially in the south or rarely in the southwest. For air quality dimension, there is no evidence of zones with good air quality in the city (green color band), i.e., none UPZ satisfies the WHO’s air quality guideline 2005 of 10 µg/m³. Furthermore, air quality scores are noticeably low in the southwest. Therefore, several UPZs located in the southwest of the city face the worst economic and air quality performance (red shaded area). These findings reveal that economic and air quality disparities overlap for a non-negligible size of the population (11%). Adding social performance to the analysis also highlights this area as the zone with the most critical SEAQ index for the entire city. Using the color bands, our results also show that 22% of the population in Bogotá experience the lowest SEAQ performance (red), 48% the lower-middle (orange), and 28% the upper-middle (yellow), while only 2% enjoys the highest SEAQ performance (green). This distribution reveals the disparities found throughout the city.

Fig. 3

Spatial distribution of economic, social and air quality indicators, and SEAQ index scores

We analyze the sensitivity of our estimates to the selection of weights (see Table D1 in SM). Assessments measures such as the mean of the absolute rank difference and its standard error, and the Spearman's rank correlation coefficient suggest that ordering of the SEAQ index is not largely altered when weights vary across dimensions. UPZs at most, on average, change the rank in five positions with a standard error of 0.4. Spearman’s rank correlation between the original SEAQ index and alternative weighting schemes is above 0.98. A similar result is found when Bourguignon index is compared with an index of the same type varying weights across dimensions. If comparisons are developed between our suggested SEAQ index and Bourguignon index using the same structure of weights, either equal or different weights across dimensions, rank of UPZs varies roughly from 2 to 4 positions. Remarkably, Spearman’s rank correlation for each pair of compared indexes is almost equal to one. This result provides evidence that in the case of Bogotá the standard SEAQ functional form described in Sect. 3 shows approximately equivalent orderings to the Bourguignon index.

We acknowledge that our composite index may be sensitive to the number of indicators. The sensitivity of our estimates to the inclusion and exclusion of indicators is presented in Table D2 in SM. In the first case, we use single indicators per dimension: we include per capita income and health center supply in economic and social dimension, respectively. These two variables have the largest correlation coefficients with the other indicators within the same dimension. In the second case, we exclude a nearly constant indicator in social dimension (school dropout). When it comes to the use of single indicators per dimension, compared to the original specification of the SEAQ index, UPZs move, on average, up to 10 positions in the rank. This variation is much larger than the changes in rank observed when various weights are employed. However, the Spearman’s rank correlation coefficient between original and new scores is very high indicating that somehow part of the orderings is preserved. A similar result is found when we compare the Bourguignon index in its original version with its counterpart using only single indicators. If we exclude school dropout indicator, results of the SEAQ scores are not largely altered. Spearman’s rank correlation coefficient between original and new ranking of scores is almost equal to one. UPZs at most, on average, change two positions in the rank. Equivalent findings are obtained if we carry out a comparison of the same type for Bourguignon index. Thus, excluding a nearly constant indicator, in our specific case, yields almost similar orderings. Moreover, if comparisons are made between our suggested SEAQ index and Bourguignon index, we find that either using single indicators or excluding school dropout indicator the two indexes yield, on average, similar ranks.

5.2 Air Quality Modelling

Fig. B1 in SM shows the simulated monthly-mean spatial distribution of PM_2.5 of the initial situation for domain 1, 2 and 3 in February and September. Results highlight a significant impact of biomass burning emissions for February in southern Colombia, where concentrations may reach 70 µg/m³. As expected, the modeled concentrations for September are much lower than in February. Daily means of modeled and observed concentrations for Bogotá from domain 3 are shown in Fig. B2 in SM. We find that the model accurately simulates PM_2.5 for September. However, there is an underestimation of 22% of concentration level in February.

Wind speed and wind direction are key meteorological variables in air quality modelling. Higher wind speeds cause efficient transport of pollutants, causing concentration to decrease. Wind direction is of paramount importance as well, as it determines the direction of advective transport of air pollutants. For these reasons, it is important to assess the model performance for those fields. In our simulations, wind speed is overestimated in both months (plots not shown; available upon request), causing an underestimation of pollutant concentrations. This, together with the difficulty of accurately representing the medium-range transport of regional-scale biomass burning plumes, might explain why the model in February provides lower PM_2.5 concentrations than observed levels.

At hourly level, modeled concentrations yield NMB values of − 22.54 and 0.6 for February and September respectively, which are considered as satisfactory in this field (see Emery et al. 2001, 2017). We also find a similar spatial pattern between modeled and observed surface concentrations in both months: high concentrations are obtained in stations in the south, intermediate values in the center, and low levels in the north (tables are available upon request). With respect to wind speed and temperature, the best performance is achieved across all monitoring stations when RMSE and IOA metrics are employed. RMSE is less than 2.3 m/s and IOA is above 0.7, respectively; values that lay within the range suggested by Emery et al. (2001, 2017). Therefore, the modeling system represents the general meteorological behavior observed in Bogotá.

5.3 Potential SEAQ

Policy simulations yield across 109 UPZs an average PM_2.5 reduction of 1.64 µg/m³ for paving roads, 0.42 µg/m³ for industry fuel substitution and 0.82 µg/m³ for HLDV renewal. Standard deviations of concentration changes in that order are 1.21, 0.38, and 0.34 µg/m³. Thus, average pollutant concentrations in the city would decline to 15.31, 16.53, and 16.13 µg/m³, respectively. In all scenarios, distribution of the PM_2.5 reduction is positively skewed (see Fig. 4a). Most UPZs experience small changes in concentrations. For example, a reduction of less than 1 µg/m³ due to industry fuel substitution or HLDV renewal occur in around 90% and 75% of UPZs, while less than 10% of the UPZs experience a decline of more than 5 µg/m³. In order to analyze which of the UPZs benefit from the large reductions, air quality scores of the initial situation are ranked in an ordinal variable from 1 to 109, with 1 being the highest score, and then associated with the size of concentration changes (see Fig. 4b). Paving roads is the policy that induces the largest PM_2.5 reduction for UPZs at the bottom of the rank. Industry fuel substitution and HLDV renewal also give relatively higher changes for UPZs in the lower third of the rank, but those changes are less pronounced and regular than for paving roads.

Fig. 4

Changes in annual PM_2.5 concentrations for policy scenarios

As expected, paving roads provides the largest impacts on premature mortality. In total 180 deaths are avoided under this policy. Whether industry fuel substitution or HDLV renewal are implemented, the effect on total mortality is 37 or 79 deaths, respectively. Interestingly, the three policies are progressive because avoidable mortality is greater in UPZs with lower per capita income (see Fig. C1 in SM). Since total mortality in the city is roughly 30,000 deaths (for all causes), mortality rate scores for each UPZ are only slightly affected by the size of avoidable premature deaths of air pollution. This implies that potential social dimension scores are similar to the initial-situation scores. Similarly, economic scores have little variation after policy implementation. We found that both land and house-building prices increase on average 4.6%, 1.4% and 3% due to the air quality improvements obtained from paving roads, industry fuel substitution, and HDLV renewal, respectively. Although some UPZs do not face changes in prices, others increase their housing values up to 13%, particularly with paving roads policy.

Potential air quality and SEAQ index scores obtained for each policy scenario are, on average, greater than the initial-situation scores (see Fig. C2 in SM). Potential scores lay on or above the 45-degree line. For all policies, increases in potential SEAQ index scores are more evident in UPZs with the lowest initial-situation performance. Results also suggest that most arrangements in the SEAQ index happen at the bottom of the initial-situation rank of UPZs, irrespective of the policy. Although some of the UPZ descend in the rank, in absolute terms the aggregated index of economic, social and air quality characteristics improves (see Fig. C2b). In other words, under the policies analyzed, the city would experience better air quality and SEAQ index scores, but those UPZs in the lower third of the rank would remain in the tail of the distribution.

Table E1 in SM presents the inequality measures of potential economic, social and air quality indicators, and SEAQ index. The three policy scenarios studied provide equality gains. For individual indicators A(1.5) offers the highest decline in inequality, while Gini provides the lowest change in inequality. B(0.33) shows intermediate decreases. As paving roads induces the largest decrease in pollutant concentrations, this policy yields the maximum reduction in inequality. Depending on the measure used, paving roads decreases inequality in air quality from 29% to 86%, in mortality from zero to 65%, and for SEAQ index between 11% and 46%. Decline in inequality due to HLDV renewal ranges between 9% and 60% for air quality dimension, from 0.6% to 60% in mortality, and between 3% and 29% for SEAQ index. In the case of industry fuel substitution, inequality decrease is moderately lower than in the HLDV renewal scenario.

The size of improvements in air quality due to policies such as paving roads and HLDV renewal indirectly make economic dimension as the most unequal characteristic when using Gini and Atkinson index. A similar result is found for industry fuel substitution, with the exception for A(1.5) measure where air quality has a slightly higher inequality than economic dimension. In the case of Bourguignon index, irrespective of the policy, it provides higher levels of inequality for air quality than the other dimensions. These results show the relevance of using a battery of inequality measures when analyzing effects of policy interventions. It seems that the assumption of imperfect substitution employed in the Bourguignon index makes more difficult for economic dimension to enhance its relative importance.

Regarding social dimension, changes do not exceed 1%. Variation in economic dimension is slightly larger, reaching a maximum reduction of 5%. When analyzing Lorenz curves, we observe that under the policy scenarios air quality dimension and SEAQ index are closer to the equality line than in the initial situation (see Fig. C3 in SM). For air quality, most changes occur for low scores. Plots also illustrate small movements of the SEAQ index, which might be explained by the fact that Lorenz curves provide more weight to scores in the middle of the distribution. We also found that among inequality measures A(1.5) and B(0.33) show the largest reductions of the composite index. It implies that under the assumption of high inequality aversion or imperfect substitution among dimensions, the three policies would yield sizable reduction of overall inequality.

Spatial distribution of scores in Figs. 5 and 6 shows where simulated policies would induce changes in air quality and the composite index. Paving roads substantially improves air quality in south and west. A large group of UPZs in the southwest would satisfy WHO’s Interim target-2 and areas in the south would comply WHO’s Interim target-3. In other words, air pollution would decrease to less than 25 µg/m³ or less than 15 µg/m³, respectively. With the industry fuel substitution scenario some UPZs of the southwest would also achieve WHO’s Interim target-2, but a large area would still exceed this air quality standard. This policy performs well in the south because several UPZs would satisfy WHO’s Interim target-3. In the case of HLDV renewal, it would not yield noticeable changes in the south, but would improve air quality in more UPZs of the southwest than might be achieved by industry fuel substitution. Maps also show that the three policies increase the SEAQ index in most vulnerable zones. Compared to the initial situation, a better performance is achieved by paving roads policy than for industry fuel substitution and HLDV renewal. However, it is evident that despite these policies reduce air pollution and improve equality, the unequal distribution of economic or social performance across the city persist. It reveals the importance of tackling all dimensions of inequality, particularly to reduce the remarkable disparities in the southwest (see Fig. 6).

Fig. 5

Air quality scores for policy scenarios

Fig. 6

SEAQ index scores for policy scenarios

5.4 Cost–Benefit Analysis

As an example of the benefit and cost stream, Table H1 in SM presents benefits and costs of the policy actions during ten years using a discount rate of 3%. It considers that policy investments are executed at the current interest rates and that air quality decreases in the absence of the policy at the average annual deterioration rate of roads and vehicles. In this exercise, both kind of benefits are presented, from VSL values and hedonic prices. Depending on the policy analyzed, total benefits range between US $1.7 and US $8 billion. Paving roads yields the greatest gains. Regarding implementation costs, we estimate that paving roads would amount to US $1.3 billion. The estimated cost of industry fuel substitution policy reaches US $1.2 million. Furnace owners face the double of the boiler costs. With regard to the HLDV renewal scenario, the owner cost is roughly US $2.8 billion, while the government expenditure associated with the economic support of the program and VAT exemption amounts to US $993 million. Public investments financed by property taxes are around US $0.4 million for industry fuel substitution and US $1.3 billion for HLDV renewal. Among the simulated policies, HLDV renewal becomes the most expensive alternative.¹⁸

Property taxes imposed to finance public investments are, on average, equivalent to two per thousand, one per million, and 3.5 per thousand of the housing values per year for paving roads, industry fuel substitution and HLDV renewal policies, respectively. We analyze how the size of the tax affects land and house-building price inequality. In general, inequality is almost equivalent to the level of inequality when air quality improvements are capitalized into the housing values and the costs are not spatially distributed. In other words, housing prices, on average, are slightly diminished by the tax having a little change in their distribution among UPZs. We acknowledge that we do not provide estimates of the tax effects within UPZs because our approach studies inequality between administrative units.¹⁹

Sensitivity analysis is displayed in Table H2 in SM. When we consider benefits only derived from avoided mortality and a time horizon of ten years, HLDV renewal policy has large negative net benefits, regardless of the discount rate, the level of interest rates for public investments and the degree of deterioration of air quality in the absence of the policy. Hedonic valuation of the benefits alone always yields net gains for each policy whether we employ a time horizon of fifteen years. Combining valuation of avoided mortality by means of VSL, and aesthetic and locational amenities through hedonic model, we show that positive net present benefits can be achieved from any of the policy scenarios. This result is irrespective of the time horizon and other types of sensitivity exercises employed in our study. The lowest net benefits across policies are achieved when we use costly interest rates for public investments, assume an average degree of deterioration of air quality in the absence of the policy, and use a time horizon of ten years. On the contrary, the maximum net benefits are observed for simulations that consider current interest rates for public investments, a high degree of deterioration of air quality in the counterfactual, and a time horizon of fifteen years. Interestingly, across all our simulations paving roads and industry fuel substitution provide net gains. Implementing paving roads yields net benefits that vary from US $1.4 billion to US $13.5 billion, while the net value of adopting industry fuel substitution fluctuates between US $549 million and US $3.5 billion. For HLDV renewal policy, simulations indicate that net benefits range from US $-3.3 billion to US $10.7 billion. The order of magnitude of negative values obtained in some simulations for this scenario is very large compared to the benefits of the other two policies.

The main finding of this analysis is that across all simulations HLDV renewal is a costly policy, whereas investing in paving roads becomes the most cost-effective alternative. The evidence in this study also points out that paving roads would improve the distribution of air quality and SEAQ index scores in the most vulnerable zones where economic, social, and air quality inequalities reinforce. This suggests that, although paving roads has been ignored as an air pollution abatement strategy in the local or national air quality plans, the development of pavement infrastructure would not only reduce premature mortality caused by air pollution or provide aesthetic and locational benefits in the housing market, but also would alleviate overall inequality. Interestingly, industry fuel substitution policy performs relatively well. Its benefit/cost ratio is remarkably larger than the ratio for paving roads. Hence, further efforts of the authorities should be devoted to promote the replacement of coal by natural gas in the industry. The PDDAB and the future PAQI should primarily focus in addressing the barriers that limited adoption in the past. Improving the access to credits that allow smooth management of the financial stream in boilers and furnaces operation would help to circumvent one of the main bottlenecks of adoption. Unlike the other scenarios, implementation costs of diesel vehicle renewal policy require to consider a long-time horizon of the benefit stream to compensate investments. Given the high cost of investments, our results raise the question whether other possible policy scenarios could achieve larger welfare gains than the current renewal program, for instance, a vehicle renewal program with a tighter emission standard (Euro VI technology) or the adoption of emission control systems such as DPF.

6 Concluding Remarks

This paper offers a multidimensional analysis of inequality for Bogotá, Colombia’s capital, in which the environmental dimension is added to the joint study of economic and social inequalities. This research develops a composite index of air quality, economic and social performance of several geographical zones in order to shed light on which dimensions or areas of the city decision-makers might focus their actions to reduce such inequalities. The approach, based on the HDI/SDG index, is simple and straightforward, having the advantage of a broad applicability to other studies.

Our study presents evidence that air quality allocation across the city is highly unequal when high aversion to disparities is assumed. Although the level of aversion to inequality is a judgment made by society that varies in different contexts, the current challenges of sustainability and environmental justice literature suggest that the States pursue a progressive analysis (UN 2015; Banzhaf et al. 2019). This is a relevant element in the perspective of our results because, under the assumption of large aversion to disparities, air quality inequality becomes greater than the economic and social inequalities. Similar results are found when imperfect substitution is included through the Bourguignon index. In other words, this study suggests that air quality inequality should be at least as important as economic or social dimensions. This is in line with Bouvier (2014), who finds more unequal distribution of toxic air emissions compared to income in Maine.

Our results propose to pay attention to the implementation of policies that reduce most critical disparities across zones. The spatial analysis of this study reveals that air quality, economic and social inequalities intersect in the southwest of the city. Hence, improving not only air quality allocation, but also the distribution of economic and social indicators such as socioeconomic strata and health center supply, would benefit vulnerable zones. Policymakers should work to include the southwest zones in their planning priorities. In this article, we present an application of a complex chemical transport model in the assessment of PM_2.5 emission abatement scenarios and use those outcomes to evaluate inequality measures and conduct a cost–benefit analysis. Our paper finds that the three policies studied decrease overall inequality. A salient finding of this work is that paving roads is the most cost-effective and progressive policy among the alternative policies studied. It yields the highest reduction in pollutant exposure and largely decreases premature mortality in the southwest zone where socioeconomic and air quality inequalities overlap.

This research has some limitations. The quality of the modeling results for air pollution is highly sensitive to the completeness and accuracy of the emissions inventory. Not knowing the inventory in detail might bias the results (see Carson and LaRiviere 2018). This fact underlines the significance of periodically updating and improving the accuracy of the emissions inventory of atmospheric pollutants. Aspects such as the chemical speciation of the main emissions sources, as well as the spatial allocation of emissions should be constantly expanded and improved. To address this point, we provide some statistical measures on how the model reproduces the current air quality and atmospheric conditions of Bogotá. With respect to the SEAQ index and other indicators, we obtain them deterministically. As in the HDI/SDG index, scores may be sensitive to the selection of indicators, the procedure of aggregation, weights, the degree of substitution between dimensions, and other factors highlighted in this article. The case of Bogotá is a particular application. In our study some indicators show strong correlation, allowing us to identify hot spots of intersected inequalities. Thus, the application of the SEAQ index to other contexts should consider the particularities in each case. Costs and benefits are computed using prices, interest rates, projections of GDP, population, and coal consumption, and deterioration rates of roads and vehicles that exhibit uncertainty.

Despite these limitations, this work shows how the environmental processes can be incorporated into the decision-making process. Future research may involve further air quality modeling efforts for longer-term simulations. A simulation spanning a full year of meteorological conditions would be ideal to represent the spatial distribution of the potential benefits more accurately. Regarding meteorology, some research suggests that intense extreme weather events influenced by climate change may exacerbate air pollutant concentrations affecting human health (see Hong et al. 2019). Given that our study does not analyze how changes in meteorological conditions affect air quality inequality and policy costs and benefits, additional research could address those questions. Other fronts of research extensions may include exploring the combination of policy scenarios, studying the effect of other abatement policies, or applying a similar exercise to other polluted cities in the world.