Improved user-private information retrieval via finite geometry

Abstract

In a user-private information retrieval (UPIR) scheme, a set of users collaborate to retrieve files from a database without revealing to observers which participant in the scheme requested the file. To achieve privacy, users retrieve files from the database in response to anonymous requests posted to message spaces; assuming that each message space can be accessed by a subset of the participants in the scheme. Privacy with respect to the database is easily achieved, but privacy with respect to coalitions of other users within the scheme is sensitive to the choice of incidence structure determining which users can access each message space. Earlier schemes were based on pairwise balanced designs and symmetric designs, and involved at most one step of message passing to retrieve a file. We propose a new class of UPIR schemes based on generalised quadrangles (GQs), which need up to two steps of message passing in each file retrieval. We introduce a new message passing protocol in which messages are encrypted. Even using this protocol, previously proposed schemes are compromised by finite coalitions of users. We construct a family of GQ-UPIR schemes which maintain privacy with high probability even when $O(n^{1/2-\epsilon })$ users collude, where n is the total number of users in the scheme. We also show that a UPIR scheme based on any family of generalised quadrangles is secure against coalitions of $O(n^{1/4-\epsilon })$ users.

1 Introduction

Private Information Retrieval (PIR) allows a user to retrieve information from a database without revealing which information was requested. A trivial solution is for the user to download all of the information in the database, but when the information is replicated in multiple locations, more efficient schemes are known [1, 3, 5].

A slightly different approach to the problem of private information retrieval attempts to hide the identity of the user downloading a file. One approach to this problem is Onion Routing [11]. An onion is a recursively encrypted data packet, which encodes a path through a network of cooperating users. Each user in the path removes the outermost layer of encryption, and forwards the onion to the next user on the path. The onion carries no identifying features, which would allow an observer to identify it with different outer layers. Anonymity is achieved in this system by choosing sufficiently long paths at random for the onions.

One disadvantage of onion routing is that the number of times a message is passed between users can be large. This results in a low throughput of data when bandwidth in the network is limited. user-private information retrieval (UPIR) is an approach to private information retrieval in which the identities of users are hidden, but the number of times a message is forwarded through the network is tightly controlled. To achieve privacy in a UPIR scheme, it is usual to place strong restrictions on which users can communicate with one another within the scheme.

Definition 1

(cf. Sect. 2, [9]) A UPIR system consists of a bipartite graph $({\mathcal {U}}\cup {\mathcal {M}},E)$, where ${\mathcal {U}}$ is the set of users and ${\mathcal {M}}$ is the set of message spaces. A user $u \in {\mathcal {U}}$ has access to a message space $M \in {\mathcal {M}}$ if (u, M) is in the set of edges E. Furthermore it is assumed that all users have access to a database that evaluates queries.

Example 2

Figure 1 shows a UPIR system with 5 users and 3 message spaces and the incidence matrix of the corresponding bipartite graph.

Fig. 1

A visualisation of a UPIR system

A common requirement in earlier work is that every pair of users share access to a common message space, e.g. [8, p. 1571]. Hence the distance between any two users in the graph is 2 and messages will have to pass through at most 1 message space. In this paper, we require only that the bipartite graph underlying the UPIR scheme is connected; we say that such a UPIR system is connected. If u is incident with M, then user u can both write messages to M and read any messages written to M; if u is not incident with M then u has no access to M. Users communicate within the scheme only by writing messages to one another in the message spaces, and we assume that messages carry an identifier for the intended recipient. Any user may send queries to the database for evaluation. Users preserve their privacy by passing requests via the message spaces to other users to query the database on their behalf. We refer to the user that sends the query to the database as a proxy for the original user that made the request.

In order for users to communicate using a UPIR system, a protocol is required; one example is described explicitly below. We refer to the combination of a UPIR system and a protocol as a UPIR scheme. This distinction is helpful in illustrating the interactions between the combinatorics of the bipartite graph and the privacy properties of the protocol.

Protocol 1

Let $({\mathcal {U}} \cup {\mathcal {M}}, E)$ be a connected UPIR system. Suppose that user u wishes to retrieve the response to the query Q from the database.

• 1. User u chooses a user v uniformly at random from the set of all users.

• 2. If $u = v$, u requests Q directly from the database, receiving response R.

• 3. Otherwise, u chooses uniformly at random a shortest path $(u, M_{1}, u_{1}, \dots , M_{n}, v)$ from u to v in the bipartite graph.

• 4. User u writes a request$[ (u_{1}, M_{2}, \dots , M_{n}, v), Q]$ onto $M_{1}$.

• 5. For $i = 1, 2, \dots , n-1$, user $u_{i}$ observes the request $[(u_{i}, M_{i+1}, \dots , M_{n}, v), Q]$ addressed to him in $M_{i}$. He writes a new request $[(u_{i+1}, M_{i+2}, \dots , M_{n}, v), Q]$ to $M_{i+1}$ and remembers $M_{i}$ and Q.

• 6. When the message [(v), Q] reaches message space $M_{n}$, user v sees it and forwards Q to the database. User v writes the responseR from the database as [Q, R] in $M_{n}$.

• 7. User $u_j$, upon seeing the response [Q, R] in $M_{j+1}$, writes the response [Q, R] to $M_j$.

• 8. User u receives the response R to his query after $u_1$ writes [Q, R] to $M_{1}$.

Remark 3

Many variations of Protocol 1 are possible, including randomising the path, and alterations to save used memory. Such changes do not alter the results in the following sections. Any user with access to a message space $M_{i}$ on the path can observe the request, the identity of the proxy and the response, but gains limited information about the source of the request.

Domingo-Ferrer, Stokes, Bras-Amorós, and co-authors introduced UPIR systems and analysed a protocol where users write queries to message spaces without specifying a proxy [4, 8], while a special case of the above protocol was developed by Swanson and Stinson [9, 10]. Both groups of authors worked on UPIR systems derived from highly structured set systems. In particular, they required that every pair of users share a common message space, in which case Protocol 1 can be implemented so that every path has length at most 2: any user can write requests directly to his chosen proxy.

Stokes and Bras-Amorós [8] considered the problem of constructing a UPIR system under the restrictions that $\deg (M)$ is constant for all message spaces M. This requirement can be interpreted as balancing the load amongst message spaces. They also require that every pair of users share precisely one message space. After rejecting some degenerate solutions in which message spaces have size $1, 2, n-1$ or n; the authors are left with precisely the class of finite projective planes. We recall that a projective plane is a combinatorial structure consisting of points and blocks in which

• 1. every pair of points is contained in a unique block,

• 2. every pair of blocks intersect in a unique point,

• 3. there exist 4 points, no three of which are contained in any one block.

Finite projective planes are a special class of finite geometries which play an important role in combinatorics, geometry and algebra. Inspired by Stokes and Bras-Amorós, Swanson and Stinson analysed attacks on projective plane UPIR systems, and proposed UPIR systems constructed from a broader class of block designs. In particular, they considered balanced incomplete block designs (BIBD) and pairwise balanced designs (PBD). We recall the definition of a PBD.

Definition 4

(Pairwise Balanced Design) Let X be a set of points of cardinality v and $K\subseteq [v]$ be a subset of the natural numbers less than or equal to v. A pair $(X,{\mathcal {B}})$, where ${\mathcal {B}}$ is a family of subsets of X, called blocks, is a $(v, K, \lambda )$-pairwise balanced design if

• (i) $|B| \in K$ for all $B \in {\mathcal {B}}$,

• (ii) every pair of distinct elements of V appears in exactly $\lambda$ different blocks of ${\mathcal {B}}$.

We note that the projective planes defined earlier are examples of $(n^2+n+1, \{n+1\},1)$-PBDs. For more information we refer to the monograph by Beth, Jungnickel and Lenz, as a standard reference for design theory [2].

In the next section, we will show that observers in a UPIR system have an advantage in gathering information about users with whom they share a message space. Motivated by this result, we consider the next obvious class of UPIR systems; those in which users are separated by a path of length at most 2. A natural class of examples is furnished by finite generalised quadrangles. Furthermore we consider a different protocol, based on onion routing, and prove that it aids privacy.

2 Privacy in a UPIR system

It is assumed throughout that the content of any message space is only available to the users who have access to the given message space as in Protocol 1. An external eavesdropper, i.e., someone who is not a user in the system, can observe the requests made to the database, since these are not encrypted, but cannot read messages sent between users. Security in this setting has been studied by Swanson and Stinson; their analysis forms the basis of any UPIR scheme [9].

Definition 5

A UPIR system is private with respect to external observers if, for any request Q forwarded to the database by user v, we have that

$$\begin{aligned} \mathbb {P}(u \text { is the source of } Q \mid v \text { is the proxy}) = \mathbb {P}(u \text { is the source of } Q )\,. \end{aligned}$$

Swanson and Stinson have proved that the obvious strategy in which users select proxies uniformly at random is sufficient for privacy against external observers.

Theorem 6

(Theorems 6.1, 6.2 [9]) A connected UPIR scheme is private against external observers if each user chooses proxies uniformly at random, and the proxies for distinct queries are chosen independently.

Protocol 1 can be implemented on any connected UPIR scheme; and Theorem 6 shows that the scheme is private against external observers.

More recent research on UPIR has aimed at preserving privacy with respect to other users in the UPIR scheme, under the assumption that users are honest but curious, [9, 10]. That is, they act according to Protocol 1, but they may attempt to determine the source of any queries that they observe.

Since the message space into which a request is written already reveals non-trivial information about the source of the request, perfect privacy with respect to other users is, in general, impossible. For example: in a PBD-UPIR scheme, it can be inferred that the source of a request written to the message space M is a user with access to M.

First, we develop a criterion for judging whether a UPIR system is secure in terms of maintaining users’ privacy. We assume that a priori all users have a non-zero probability to be the source of any given query. Our analysis will be based on linked queries, which are a series of queries which are identifiable as coming from a single source. These were first introduced by Swanson and Stinson, who provided the example of a series of requests for information about a fixed, obscure topic [9].

Definition 7

Let ${\mathcal {C}}$ be a coalition of users, collaborating to identify the source of a series of linked queries. Users u and v are pseudonymous with respect to ${\mathcal {C}}$ if for any message space M to which C has access, and for which $\mathbb {P}( v \text { is source} \mid Q \in M) \ne 0$,

$$\begin{aligned} \frac{ \mathbb {P}(u \text { is the source of } Q \mid Q \in M) }{ \mathbb {P}( u \text { is the source of } Q)} = \frac{ \mathbb {P}( v \text { is the source of } Q \mid Q \in M) }{ \mathbb {P}( v \text { is the source of } Q)} \,. \end{aligned}$$

In other words, for any query Q that a coalition might observe the users u and v are equally likely as sources. We allow the possibility that a coalition has non-trivial prior information on the probability that user u wishes to evaluate query Q. In our analysis we focus on the case where this information is limited, and users cannot be identified by their queries alone. The next result follows directly from the definition of pseudonymity, but we record it since we will have use for it in later sections.

Lemma 8

Pseudonymity with respect to the coalition ${\mathcal {C}}$ is an equivalence relation on the users of a UPIR scheme.

Users u and v maintain pseudonymity with respect to C after arbitrarily many requests have been observed if and only if they lie in the same pseudonymity class. The coalition ${\mathcal {C}}$ can identify user u if and only if u belongs to a pseudonymity class of size 1 with respect to ${\mathcal {C}}$. We say that the coalition ${\mathcal {C}}$ is an identifying set if ${\mathcal {C}}$ can identify every other user in the scheme. We propose the following definition for security.

Definition 9

Let $({\mathcal {V}}_i)$ be a family of UPIR schemes indexed by $i \in \mathbb {N}$, where the number of users in ${\mathcal {V}}_{i}$ is $n_{i}$. We say that ${\mathcal {V}}_{i}$ is secure against coalitions of size t if the pseudonymity relation of any coalition of size t contains a giant component, i.e., for any $\epsilon >0$ there exists an $N_\epsilon$ such that for $n_i > N_\epsilon$ the union of all other components has size $O(n_{i}^{1-\epsilon })$. The family $({\mathcal {V}}_i)$ is secure if for every t there exists $N \in \mathbb {N}$ such that ${\mathcal {V}}_{i}$ is secure against coalitions of size t for all $i \ge N$.

Informally, we consider a UPIR scheme to be secure if any coalition of size at most t can observe only a negligible portion of a sufficiently large system. Equivalently, for any fixed coalition ${\mathcal {C}}$ of bounded size a randomly chosen subset of users, of limited size, will be mutually pseudonymous with respect to C with high probability. Our first result is that families of PBD-UPIR schemes are never secure.

Theorem 10

In a PBD-UPIR scheme using Protocol 1, a single eavesdropper can identify any user who makes sufficiently many linked queries. i.e. any coalition of size one is an identifying set.

Proof

Suppose that u makes a series of linked queries. An eavesdropper c will observe a subset of these queries in the unique message space M shared by c and u, and will never observe linked queries in any other message space to which he has access. Since users do not write queries addressed to themselves¹c will be able to identify u as soon as he has observed a linked query addressed to every other possible user in M. Provided that u follows the requirements of Theorem 6, c will observe the required queries with probability 1.$\square$

In fact, a pair of collaborating users $c_{1}$ and $c_{2}$ can identify u far more quickly. If $c_{1}$ observes a query in the message space $M_{1}$ and $c_{2}$ observes a linked query in $M_{2}$, then the collaborators can conclude that the source of the requests is a user in $M_{1} \cap M_{2}$. But in a PBD-UPIR scheme, such a user is unique. This is called an intersection attack in [9]. Theorem 10 can be easily modified to identify all users in any UPIR scheme in which every pair of users share at least one message space. In particular, all of the UPIR schemes proposed by Swanson and Stinson to circumvent the intersection attack are still vulnerable to Theorem 10; although it will take more linked queries to identify the source.

To protect against the attack outlined in Theorem 10 we suggest using a different incidence structure that we will introduce in the following section.

3 Generalised quadrangles

In this section we introduce generalised quadrangles (GQ). For the sake of completeness, we include proofs of some well-known results, for further reading see [7]. Lemma 12 implies that the bipartite incidence graph of a generalised quadrangle has diameter 4. So in a UPIR scheme derived from a GQ using Protocol 1 (GQ-UPIR scheme in short), a pair of users either shares a message space, or there exists a third user sharing message spaces with each of the first two. As a result, when users communicate along a shortest path, a message is written to at most 2 message spaces. In this section, we use the usual language of incidence geometry; in a GQ-UPIR scheme, users are labelled by points and message spaces by blocks.

Definition 11

A generalised quadrangle is an incidence structure containing points and blocks in which

• 1. each point is incident with $1 + t$ blocks ($t \geqslant 1$) and two distinct points are incident with at most one block

• 2. each block is incident with $1 + s$ points ($s \geqslant 1$) and two distinct blocks are incident with at most one point

• 3. given any point x and block L that does not contain x, there is a unique point $x'$ in L that shares a block with x.

The third condition is the GQ-axiom.

Even though we are dealing with an abstract incidence structure, there is a natural representation of this structure as a geometry. It is traditional for the blocks in a generalised quadrangle to be referred to as lines. Indeed, a generalised quadrangle is so-named because there are no triangles (three lines intersecting pairwise in three distinct points) but numerous quadrangles in such a geometry.

Lemma 12

There are no non-degenerate triangles in a generalised quadrangle, but any two non-collinear points are contained in a quadrangle.

Proof

Recall that a triangle is a triple of distinct lines $L_{1}, L_{2}, L_{3}$ with pairwise non-empty intersections, say $x_{ij} \in L_{i} \cap L_{j}$. Note that $x_{12}$ is collinear with both $x_{13}$ and $x_{23}$. By the GQ-axiom, if $x_{12} \notin L_3$, then there exists a unique point on $L_3$ collinear with $x_{12}$: in other words, $x_{13}$ and $x_{23}$ cannot both be collinear with $x_{12}$, and there are no triangles.

On the other hand, consider two non-collinear points x and y, and consider two lines $L_1$ and $L_2$ incident with y. The point x is not incident with either $L_1$ or $L_2$, and, by the GQ-axiom, there is a point w on $L_1$ and a point z on $L_2$ such that x is collinear with both w and z. If the line incident with both x and z is $L_3$ and the line incident with both x and w is $L_4$, then the quadruple of distinct lines $L_1$, $L_2$, $L_3$, $L_4$ is the desired quadrangle. $\square$

If every line of the generalized quadrangle ${\mathcal {Q}}$ has size 2, then ${\mathcal {Q}}$ is a graph. The GQ-axiom and Lemma 12 together force ${\mathcal {Q}}$ to be a complete bipartite graph. Dually, if every point of ${\mathcal {Q}}$ is on precisely two lines, then ${\mathcal {Q}}$ is a grid: points are labelled by two subscripts $x_{i,j}$ where $1 \le i,j \le s+1$; and lines consist of sets of points sharing a common subscript in the same position. A generalised quadrangle is thick if every point lies on more than two lines and every line contains more than two points.

For a point x in a generalised quadrangle ${\mathcal {Q}}$ we write $B_{1}(x)$ for the set of points collinear with x. By convention, $x \notin B_{1}(x)$. Suppose that $y \notin \{x \} \cup B_{1}(x)$, and let L be any line through x. By the GQ-axiom, y is collinear to a unique point on L, so y is at distance 2 from x, which we denote by $y \in B_{2}(x)$. In fact, since the choice of L was arbitrary, we obtain a bijection: every line through x intersects a unique line through y. The standard definition in the literature is to say that a thick finite generalised quadrangle has order (s, t) if there are $s+1$ points incident with a given line and $t+1$ lines incident with a given point. Routine counting arguments can be used to establish the following well-known result.

Lemma 13

The number of points in a finite generalised quadrangle of order (s, t) is $(s+1)(st+1)$. For any point x in the GQ, there are $s(t+1)$ points in $B_1(x)$ and $s^2t$ points in $B_2(x)$.

Proof

There are $t + 1$ lines through x, each containing s points distinct from x. Since a GQ contains no non-trivial triangles, these lines are disjoint (outside of x). So there are $s(t+1)$ points collinear with x, and $|B_1(x)| = s(t+1)$.

Consider now a point y in $B_2(x)$. Since $y \notin B_1(x)$, y is not incident with any line through x; choose such a line L. By the GQ-axiom, y is collinear with a unique point on L. Since there are s points on L other than x, and each of these points is collinear with $s(t+1) - s = st$ points not on L, there are exactly $s\cdot st = s^2t$ points in $B_2(x)$.$\square$

The following result, due to D.G. Higman, shows that the parameters s and t cannot differ by too much in a thick GQ.

Theorem 14

(Higman [6]) In a thick finite generalised quadrangle of order (s, t), we have $s \leqslant t^2$ and $t \leqslant s^2$.

Our analysis of pseudonymity relations in a GQ-UPIR scheme will require the concept of a hyperbolic line in a GQ, which we introduce now. In a finite generalised quadrangle ${\mathcal {Q}}$ of order (s, t), given any two non-collinear points x and y, by the GQ-axiom, there is a collection ${\mathcal {C}}$ of exactly $t+1$ points collinear with both x and y. Thus there are at least two points, x and y, that are collinear with all the points in ${\mathcal {C}}$, but there could be more.

Definition 15

Given a set of pairwise non-collinear points ${\mathcal {X}}$ in a finite generalised quadrangle, we define $B_1(\mathcal {X})$ to be the set of points collinear with each point in ${\mathcal {X}}$, i.e., $B_1({\mathcal {X}}) = \mathop {\bigcap }\limits _{x \in {\mathcal {X}}} B_1(x)$.

We define the span of ${\mathcal {X}}$ to be the set of points collinear with every point of $B_1({\mathcal {X}})$, i.e., $\mathrm{sp}({\mathcal {X}}) = B_1(B_1({\mathcal {X}})) = \mathop {\bigcap }\limits _{z \in \mathop {\bigcap }\limits _{x \in {\mathcal {X}}} B_1(x)} B_1(z).$

When $X = \{x_1, \dots , x_m\}$, we often write $B_1(x_1, \dots , x_m)$ to denote $B_1({\mathcal {X}})$ and $\mathrm{sp}(x_1, \dots , x_m)$ to denote $\mathrm{sp}({\mathcal {X}})$. Note that, for non-collinear points x and y in a generalised quadrangle of order (s, t) we have $\{x,y\} \subseteq \mathrm{sp}(x,y)$ and, by the GQ-axiom, $|B_1(x,y)| = t+1$. The set $\mathrm{sp}(x,y)$ is often referred to as the hyperbolic line defined by x and y. The following results show that hyperbolic lines have incidence properties similar to those of ordinary lines.

Lemma 16

If $a \in \mathrm{sp}(x,y)$, then $\mathrm{sp}(a,x) = \mathrm{sp}(x,y)$.

Proof

Let $a \in \mathrm{sp}(x,y)$. Because $a \in \mathrm{sp}(x,y) = B_1(B_1(x,y))$, a is collinear with each point in $B_1(x,y)$. Since $B_1(x,y) = B_1(a,x,y) \subseteq B_1(a,x)$, we have

$$\begin{aligned} t+1 = |B_1(x,y)| = |B_1(a,x,y)| \leqslant |B_1(a,x)| = t+1. \end{aligned}$$

Hence $B_1(x,y) = B_1(a,x)$, and therefore $\mathrm{sp}(x,y) = B_1(B_1(x,y)) = B_1(B_1(a,x)) = \mathrm{sp}(a,x).$$\square$

Corollary 17

If $|\mathrm{sp}(x,y) \cap \mathrm{sp}(w,z)| > 1$, then $\mathrm{sp}(x,y) = \mathrm{sp}(w,z)$.

Proof

Let $\{a,b\} \subseteq \mathrm{sp}(x,y) \cap \mathrm{sp}(w,z)$. By Lemma 16, $\mathrm{sp}(x,y) = \mathrm{sp}(a,x) = \mathrm{sp}(a,b) = \mathrm{sp}(w,a) = \mathrm{sp}(w,z).$$\square$

Table 1 contains some relevant information about the families of classical generalised quadrangles, see [7]. These families are related to certain classical groups, and are thus highly symmetric. In each case, the size of spans of sets of a given type are constant, regardless of which points within the generalised quadrangle are chosen. In the following table, q is a prime power, and x, y, and z are three mutually noncollinear points.

Table 1 The classical generalised quadrangles

4 Secure GQ-UPIR systems

We begin this section by describing in detail the pseudonymity relation on a GQ-UPIR scheme for a single eavesdropper.

Proposition 18

In a GQ-UPIR scheme using Protocol 1, the pseudonymity classes with respect to a single eavesdropper c are singleton classes for users at distance 1 from c, and are of the form $\mathrm{sp}( c, u) \setminus \{c\}$ for any user u at distance 2 from c.

Proof

Suppose that c observes a series of linked queries coming from a user u; if c shares a message space with u, then the queries always appear in this message space. Otherwise by the GQ-axiom, for every line through c, there is a unique user $u_1$ on that line collinear with u. This implies that c observes linked queries from u distributed uniformly across all message spaces to which c has access. Hence c can decide whether u is at distance 1 or distance 2.

If the distance $d(c,u) = 1$, then an argument exactly analogous to that of Theorem 10 shows that c can identify u. So suppose that $d(c,u) = 2$. For a fixed line M containing c, there is a unique user $u_{1}$ sharing a message space with u. Over sufficiently many linked queries, c will observe intermediate queries addressed to every user in Mexcept for $u_1$. As a result, c learns ${\mathcal {X}} = B_{1}(c) \cap B_{1}(u)$.

Now recalling Definition 15, suppose that $v \in \mathrm{sp}( u, c)$. Then by Lemma 16, $B_{1}(c) \cap B_{1}(v) = {\mathcal {X}}$. It follows that u and v are pseudonymous. Likewise, any other user in $\mathrm{sp}( u, c ) \setminus \{c\}$ falls into the same pseudonymity class. $\square$

As a corollary of Proposition 18 we get that a code contained in ${\mathcal {U}}$ with covering radius 1 is an identifying set, i.e. a set of users that can deanonymize any other user in the scheme. Furthermore, a single user in a GQ-UPIR scheme can identify every other user in the scheme if and only if every hyperbolic line in the GQ has size 2. There are two known families of thick generalised quadrangles with this property: Q(4, q) where q is an odd prime power, and $H(4, q^{2})^{D}$. The data given in Table 1 shows that the pseudonymity relation on a GQ-UPIR scheme will never give a giant component when using Protocol 1. We introduce a new protocol, inspired by onion routing, which will be secure against large coalitions of users.

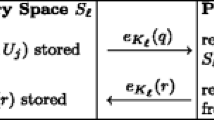
Protocol 2

Let $({\mathcal {U}} \cup {\mathcal {M}}, E)$ be a GQ-UPIR system. Suppose furthermore that a public key infrastructure is in place, and a public key for every user is available. User u wishes to retrieve the response to the query Q from the database.

• 1. u chooses a user v uniformly at random from the set of all users, and generates a secret key $\psi$ for a symmetric cipher.

• 2. If $u = v$, u requests Q directly from the database, receiving response R.

• 3. If $d(u, v) = 1$, then user u encrypts both the query Q and the key $\psi$ using v’s public key $\phi _{v}$, and writes the request $[v, \phi _{v}(Q), \phi _{v}(\psi )]$ to the unique message space that they share.

• 4. Otherwise, $d(u,v) = 2$ and u chooses a shortest path to v, say $[u, M_{1}, u_{1}, M_{2}, v]$. Message passing is as in Protocol 1: u writes the query $[(u_{1}, M_{2}, v), \phi _{v}(Q), \phi _{v}(\psi )]$ to $M_{1}$.

• 5. When v receives the request, he forwards Q to the database, receives response R and writes the response $[(v), \phi _{v}(Q), \psi (R)]$ to the message space in which the query was observed. The response is returned to user u as in Protocol 1.

Remark 19

In Protocol 2, the only user who learns the query Q is the proxy v; this means that users do not observe linked queries addressed to other users. The use of an ephemeral key $\psi$ is necessary since revealing u’s public key to v would compromise u’s privacy.

The next result shows the benefit of encrypting queries with the public-key $\phi _v$ in the GQ-UPIR scheme using Protocol 2.

Proposition 20

In a GQ-UPIR scheme using Protocol 2, all users at distance two from every member of the coalition ${\mathcal {C}}$ are mutually pseudonymous.

Proof

First we consider a single user. As in Proposition 18, a single user $c_{1}$ can identify whether the source u of a series of linked queries is at distance 1 or distance 2. Suppose that u is at distance 2. Then $c_{1}$ observes linked queries in every message space to which he has access with equal probability. Without observing queries addressed to other users he gains no information about members of $B_{1}(u)$, and so no information about the hyperbolic line $\mathrm{sp}( c_{1}, u)$. So the only information that $c_{1}$ learns about u is that $d(c_{1}, u) = 2$. Hence any pair of users at distance 2 from $c_{1}$ are pseudonymous.

By our assumption that coalition members are honest-but-curious, the only information that coalition members gain on other users comes from the message spaces in which they observe linked queries. So if $u_{1}$ and $u_{2}$ are pseudonymous for each member of the coalition ${\mathcal {C}}$ individually, then they are pseudonymous with respect to ${\mathcal {C}}$ collectively. In particular, the users at distance 2 from every member of ${\mathcal {C}}$ form a single pseudonymity class with respect to ${\mathcal {C}}$. $\square$

Theorem 21

A thick GQ-UPIR scheme using Protocol 2 is secure against coalitions of users of size $O(s^{1-\epsilon })$ for any $\epsilon > 0$, where $s+1$ is the number of points on a line in the GQ. Hence any family of thick GQ-UPIR schemes is secure in the sense of Definition 9.

Proof

Let ${\mathcal {C}}$ be a coalition of users of size $O(s^{1-\epsilon })$. By Proposition 20, the set of users at distance 2 from every member of ${\mathcal {C}}$ form a single pseudonymity class. We will show that class forms a giant component in the sense of Definition 9.

By Lemma 13, the number of users at distance 1 from a single user is $s(t+1)$. Taking a union bound, we have that the number of users at distance 1 from at least one member of ${\mathcal {C}}$ is at most

$$\begin{aligned} |{\mathcal {C}}| s(t+1) \le s^{2-\epsilon }(t+1)\,. \end{aligned}$$

(1)

Again by Lemma 13, the total number of users in the scheme is $(s+1)(st+1)$. If ${\mathcal {Q}}$ is a grid, then $t = 1$. So by Eq. (1), the coalition ${\mathcal {C}}$ is at distance one from at most $O(s^{2-\epsilon })$ users, while the total number of users in the scheme is $(s+1)^{2}$. Hence the users at distance 2 from every member of ${\mathcal {C}}$ form a giant component in the pseudonymity relation of ${\mathcal {C}}$ and so the scheme is secure according to Definition 9.

Suppose now that ${\mathcal {Q}}$ is a thick GQ. Then by Lemma 14, we have that $s \ge t^{1/2}$. Hence the number of users not at distance 2 from every member of ${\mathcal {C}}$ is $o(s^{2}t)$, and the scheme is secure. $\square$

Writing n for the total number of users in a GQ-UPIR scheme, a grid GQ-UPIR scheme is secure against coalitions of users of size $O(n^{\frac{1}{2}-\epsilon })$. The grid GQ-UPIR scheme is also notable for having only $\sqrt{n}$ message spaces, while still achieving security; all BIBD-UPIR schemes require at least as many message spaces as users.

Among the families of thick generalised quadrangles $H(3, q^{2})$ is secure against coalitions of users of size $O(n^{\frac{2}{5}-\epsilon })$, while the family $Q^{-}(5, q)$ is secure against coalitions of size $O(n^{\frac{1}{4} - \epsilon })$. These are respectively the families of GQs which are most and least robust against coalitions of eavesdroppers. While grid GQs are secure against proportionally larger coalitions than thick GQs, it should be noted that grid GQ-UPIR schemes may have certain other security concerns. Since there are only two distinct paths between any two users, it is easier to target communications between subsets of users of interest. If the public key encryption used within the system is flawed, any user at distance 1 from user u can observe half of u’s requests.

In fact, applying the Higman bounds of Lemma 14 shows that the families $H(3, q^{2})$ and $Q^{-}(5, q)$ are extremal for a thick GQ, in the sense that rewriting the statement of Theorem 21 as function of the number of users gives a bound of the form $O(n^{t-\epsilon })$ for some $\frac{1}{4} \le t \le \frac{2}{5}$. In the next section, we construct explicit coalitions which show that these bounds are best possible.

5 Small identifying sets in a GQ-UPIR system

In this section we will prove that the result of Theorem 21 is optimal in the sense that the statement is not true when $\epsilon = 0$. We will also show that both the GQ structure and the encryption of Protocol 2 are necessary, since finite identifying sets exist without both of these assumptions.

We have already seen in Theorem 10 that a single user in an unencrypted PBD-UPIR scheme is an identifying set. Protocol 2 offers limited benefits for a PBD-UPIR scheme - since a single eavesdropper learns which message space he shares with another user in a PBD-UPIR scheme, there can be no giant component in the pseudonymity relation even with respect to a single user. It can be shown that a coalition of three users, not all sharing a single message space, suffices to identify any other user in a projective plane UPIR scheme under Protocol 2.

It is easily verified that a single user in a grid GQ-UPIR scheme using Protocol 1 can identify any other user. The next result shows that a coalition of size at most three suffices in any thick GQ using Protocol 1.

Proposition 22

In any GQ-UPIR scheme using Protocol 1 there exists an identifying set of at most three users.

Proof

By Proposition 18, the pseudonymity classes with respect to a single user $c_{1}$ are the hyperbolic lines through $c_{1}$. The intersection of distinct hyperbolic lines has size 0 or 1, since $u_{2} \in \mathrm{sp}( c_{1}, u_{1})$ if and only if $u_{1} \in \mathrm{sp}( c_{1}, u_{2})$. So two coalition members $c_{1}$ and $c_{2}$ fail to identify the user $u_{1}$ if and only if $\mathrm{sp}( c_{1}, u_{1}) = \mathrm{sp}( c_{2}, u_{1})$. In this case, $u_{1}$ can be uniquely identified by any user $c_{3}$ not on the hyperbolic line $\mathrm{sp}( c_{1}, c_{2})$. $\square$

As shown in Theorem 21, the size of an identifying set in an encrypted GQ-UPIR system necessarily grows with the parameter s. In the next result, we show that there exist identifying sets of size O(s). Since any set of $s+1$ users, no pair sharing a message space, is an identifying set of size $s+1$ in a grid GQ, it suffices to construct small identifying sets in thick GQs.

Proposition 23

Let ${\mathcal {Q}}$ be a generalised quadrangle of order (s, t), and consider the encrypted UPIR scheme on ${\mathcal {Q}}$. Then ${\mathcal {Q}}$ contains an identifying set of size $3s+1$.

Proof

We explicitly design a set of users of size $3s+1$ and show that any other user shares at least two different message spaces with users in our set. Let $\ell _1$ and $\ell _2$ be two lines in the GQ that do not intersect. Take any point $x \in \ell _1$, by the GQ-axiom there is a unique point $y \in \ell _2$ such there is a line ${\overline{xy}}$ connecting x and y. Let ${\mathcal {C}}=\ell _1 \cup \ell _2 \cup {\overline{xy}}$, we see that ${\mathcal {C}}$ has size $3s+1$ since every line contains $s+1$ points and we have two intersections.

Any user $u \notin {\mathcal {C}}$ shares a message space $M_1$ with a unique user in $a \in \ell _1$, a message space $M_2$ with a user $b \in \ell _2$, and a message space $M_3$ with a user $c \in {\overline{xy}}$. We claim that at least two of these spaces are different. Assume $M_1 = M_3$, it then follows that $a=c=x$, since it otherwise would imply the existence of a triangle through the points a, x, c. The only line through x that intersects $\ell _2$ is ${\overline{xy}}$, but since $u\in M_1$ it follows that $M_1 \ne {\overline{xy}}$ and hence $M_1$ does not intersect $\ell _2$. Therefore $M_1$ and $M_2$ have to be distinct message spaces.$\square$