On the Hedging of Interest Rate Margins on Bank Demand Deposits

Abstract

In recent years, we have seen a very rapid increase in outstanding bank deposits. This increase has been particularly high since the outbreak of the COVID 19 pandemic, due to the lockdown that has, among other things, drastically reduced household consumption since the beginning of March 2020. This very sharp increase in outstandings increases the risk of banks which offer interest on deposits. In this paper, we deal with the mitigation of the risk contained in interest rate margins of demand deposits. We introduce and analyze hedging strategies of an asset and liability manager who focuses on the bank’s net operating income in a given quarter under standard accounting rules. Demand deposits are assumed to be correlated with market interest rate and to a commercial risk that cannot be fully hedged on the financial markets. We distinguish several types of dynamic hedging strategies based on both quadratic and quantile criteria. We provide explicit formula for all hedging strategies and we discuss their respective robustness. We show in particular that the quantile hedging criterion leads to somewhat riskier strategy since its gain may be nil, due to its knockout feature. We argue that our contribution establishes a stronger basis for the coverage of bank deposits, which is particularly important in the context of the COVID-19 pandemic and its economic consequences.

1 Introduction

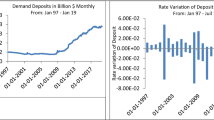
One of the consequences of the COVID-19 pandemic for the banking system is that the bank deposits have dramatically increased. This accumulation of extraordinary savings has been observed from the very first days of lockdown and has continued month after month. For example, in the US zone, the demand deposits have increased from about 1600 billions US dollars to 2700 billions of US dollars during the time period January 2020-October 2020. In the Euro zone, the demand deposits have increased from about 9000 billions of euros to 11000 billions of euros during the same time period. As an illustration, the Bank of France has emphasized that, whereas on average these monthly flows had reached a little over €6 billions before the health crisis, they had jumped to over €22 billions in March, to nearly €27 billions in April, and then remained at around €20 billions until July.¹ The end of the lockdown in mid-May 2020 has therefore not led households to stop saving to consume. On the contrary, the Bank of France statistics indicate that households continue to build up precautionary savings, linked to the uncertainties of the coming months, after having built up forced savings in March, April and May. Households’ financial savings accumulated since March have thus reached a record amount of 85.6 billions of Euros. These huge demand deposits correspond to "forced savings" linked to the fall in consumption and also partly to precautionary savings.

Bank demand deposits are a major component of their liabilities. A worldwide study of the Bank for International Settlements (see English, 2002) shows that risk control of interest rate margins has been a significant concern for banks during the past years. However, European banks suffered negative rates on the excess liquidity they leave in the European Central Bank’s (ECB) safe-deposit boxes on a daily basis. Indeed, as emphasized by Leao and Leao (2007), the current monetary system can be seen as a standard model of the real economic cycle in which the central bank applies a repo interest rate to commercial banks, while the latter ones grant loans and thus create also money. Nevertheless, the economic situation resulting from the Covid-19 pandemic has prompted the ECB to maintain a refinancing rate close to 0%. It should also be noted that commercial banks have to comply with the Basel III capital requirements, which has a very significant impact on their business (see Liu and Moliseb (2019) for an illustration of the impact of rule-based Basel III counter-cyclical capital requirements). Under IFRS – the current international accounting standards – Banks account for demand deposits at amortized cost as opposed to fair value calculations.². The European Commission enacted in November 2007 the IAS 39 Fair Value Option Amendment allowing hedging strategies that lead to a regular income associated with demand deposits (Carved-Out Fair Value Hedge)³. The IASB and the European Banking Federation (EBF) have proposed to replace the previous exceptions by a new kind of hedging strategy, namely the Interest Margin Hedge (IMH).⁴ The purpose of this later strategy is to control the volatility of demand deposits’ interest rate margins instead of the volatility of their fair value. In the United States, the accounting treatment of assets and liabilities in bank books is not as clear. The approach based on interest paid and received remains for the time being. On the regulatory front, the US Securities and Exchange Commission (SEC) requires US banks to disclose in annual (10-K) and quarterly (10-Q) filings indicators of interest rate spreads and their sensitivity to interest rate shocks. As far as demand deposits are concerned, they correspond to the approach developed by Hutchison and Pennacchi (1996), Jarrow and Van Deventer (1998), O’Brien O’Brien (2000). Additionally, as emphasized in Jarrow and van Deventer Jarrow and Van Deventer (1998), demand deposits are not only subject to interest rates but depend on some business risk independent of market risk. The bank’s market structure and its credit risk exposure may impact also the demand deposit amount (see Ho and Saunders, 1981; Wong, 1997; Saunders and Schumacher, 2000; Kalkbrener and Willing, 2004). Note also that banks’ relationships with customers are important as illustrated by Brown et al. (2020).

In this paper, we rely on Ho and Saunders (1981) in accordance with current accounting rules, market practice and standard banking theory. We use main results about option hedging of contingent claims to provide explicit hedging solutions. A first approach to price and hedge an option is to use superhedging strategies, namely trading strategies with terminal value always higher than the option payoff. However, the cost of superhedging may be too high in practice. Another approach is to control the risk by means of the mean-variance criterion, as introduced by Föllmer and Sondermann (1986). It consists in minimizing the expectation of the square of the duplication error. In general, we can provide an explicit and operational formula. However, a disadvantage of this approach is that we equally penalize the situation where the value of the hedge portfolio is lower than the option gain and the situation where the value of the hedge portfolio is higher. Another final approach that we deal with in this paper is the quantile hedging. The problem of hedging is seen by another point of view: what should an investor do if he or she is unwilling to invest all the amount needed for a perfect hedging or a superhedging strategy since such a strategy reduces drastically the potential profit. Quantile hedging strategy has been introduced by Föllmer and Leukert (1999) to control the probability that the value of the hedging portfolio will remain higher than the option payoff. In this paper, we consider both the quadratic and quantile hedging strategies of interest rate margins, in the static and dynamic frameworks.⁵ For the static case, we analyze how the optimal investment can be based on Forward Rate Agreements (FRAs) contracted at initial date. For the dynamic case, hedging strategies can take account of dynamic information about market rates and demand deposits fluctuations. In all cases, we provide explicit formula. We illustrate how such hedging strategies depend on financial parameters and compare their solutions, which provides us with useful informations to best manage demand deposits and their remunerations.

This paper is organized as follows. Section 2 presents the modelling framework and displays the main statistics on market rates and demand deposits in the US and Euro zones. In Section 3, we examine the quadratic and quantile hedging problems and derive the optimal strategies to hedge the interest rate margin for a given quarter⁶. Finally, Section 4 concludes.

2 Modelling framework

2.1 Market rates

The objective of this section of the paper is to study aspects of risk management related to monetary deposits within the framework of Asset Liability Management (ALM). We suppose that market rate follow the BGM model and amount of demand deposit follow the stochastic equation. The empirical illustrations like Average, Standard deviation, Skewness and Kurtosis for the monetary aggregate 1 concern mainly two zones (Euro and the United States). Demand deposits, which are deposits of funds made by an agent (household, business) in a bank account opened with a financial institution, include demand deposits remunerated by interest and unremunerated demand deposits deemed to be stable. We use the linear relation between deposit rate and market rate for parameters estimation the interest rate margin. The monetary data of this article are represented as follows. The data for monetary aggregate 1 for the Euro zone are from January 1980 to October 2020. For the US zone the data are from January 1980 to December 2020. Then we focus for monetary deposits on the period from January 1997 to January 2020. And when we assume a linearity of market rates and deposit rates, the data are represented from January 2003 to January 2020.

In what follows, we deal with quarterly interest rate margin corresponding to some year quarter $\left[ T,T+\frac{1}{4}\right]$. Additionally, the forward market rate at date T for the time period of the interest rate margin – a quarter – is supposed to follow the market model (BGM) defined by Brace et al. (1997):

$$\begin{aligned} dL_{t}=L_{t}\left( \mu _{L}+\sigma _{L}dW_{L,t}\right) , \end{aligned}$$

(1)

where $L_{t}=L\left( t,T,T+\frac{1}{4}\right)$ denotes the market rate and $\left( W_{L,t}\right) _{t}$ is a standard Brownian motion under some historical probability measure $\mathbb {P}$. To simplify the model presentation, we suppose that $\mu _{L}$ and $\sigma _{L}$ are constant.⁷ In this framework, we can take account of higher average returns when investing for instance in long term bonds instead of short-term assets such as the Libor and Euribor rates. (see e.g. Chapter 11 in Campbell et al, 1997).

2.2 Demand deposit amount

We assume that the demand deposit amount satisfies the following stochastic differential equation:

$$\begin{aligned} dK_{t}=K_{t}\left( \mu _{K}+\sigma _{K}dW_{K,t}\right) , \end{aligned}$$

(2)

where $\left( W_{K,t}\right) _{t}$ denotes a standard Brownian motion. To simplify also the model presentation, we suppose that the trend $\mu _{K}$ and the volatility $\sigma _{K}$ are constant, though the results readily extend to the deterministic case, for instance to deal with seasonal effects. Both the trend and volatility parameters depend upon the kind of demand deposits that we investigate. The demand deposits model might involve several different processes $\left( K_{i,t}\right) _{i}$ to better take account of various demand deposit specificities. For the sake of simplicity, we do not go any further in this direction, but the development of optimal hedging strategies in the latter case is very similar to that of a total banking operation. In all cases, the nominal amount remaining at any given time is the result of cash inflows and outflows from existing customers, including account cancellations, as usually evaluated by auditors and accountants as a matter of prudence. Our approach applies to all situations, although the parameters obviously need to be modified. Therefore, the nominal amount $K_{t}$ remaining at any given time may result either from a liquidity risk, arising from concerns about the solvency of the managing bank, or from arbitrage between demand deposits and other asset classes, or also from a commercial risk, e.g. if a given bank loses market share due to mismanagement of deposit accounts. The following figures illustrate the development of the monthly monetary aggregate 1 issued in the the US zone from January 1980 to December 2020 and Euro zone from January 1980 to October 2020.

Fig. 1

Representation of outstanding amounts of Monetary Aggregate 1 in the case of US zone

For the US zone, we observe that the monetary deposits increases slowly during the period 1980-2011; then there is a constant and very significant increase in deposits until the period 2012-2019. But, the amount has increased tremendously from about 5000 billions of US dollars in January 2020 to 6600 billions of US dollars in December 2020. (see Fig. 1).

Fig. 2

Representation of outstanding amounts of Monetary Aggregate 1 in the case of Euro zone

For the Euro zone, demand deposits are increasing steadily during the time period 1980-2011; then the increase of demand deposits is higher during the period 2012-2019 (see Fig. 2). Again, we note that, from the beginning of year 2020, the demand deposits have increased even quicker from about 9000 billions of Euros to 11000 billions of Euros (see Fig. 3).

Fig. 3

Evolution of demand deposits in Euro zone (Oct 2019-Oct 2020)

Tables 1 and 2 provide maximum likelihood estimations of $\mu _{K}$, $\sigma _{K}$ at an aggregate level.

Table 1 Estimation of the Monetary Aggregate 1 parameters for US zone

Looking at Table 1 which provides the main statistics of demand deposits in US Zone, we note that that the average of monthly Log variation is about $0.25\%$ and the standard deviation about $0.43\%$.

Table 2 Estimation of the Monetary Aggregate 1 parameters for Euro zone

For the statistics of Monetary Aggregate 1 in Euro Zone (see Table 2), we note that the monthly mean of Log variation is about $0.28\%$ and the standard deviation about $0.56\%$.

2.3 Deposit amounts and market rates

In what follows, we suppose that the dynamics of the demand deposit amount is correlated to interest rates. Therefore, we assume that both $\left( W_{L,t}\right) _{t}$ and $\left( W_{K,t}\right) _{t}$ are standard correlated Brownian motions under the same filtration $\left( \mathcal {F} t\right) _{t}$. Introduce a Brownian motion $\left( \widetilde{W} _{K,t}\right) _{t}$ independent from $\left( W_{L,t}\right) _{t}$, and consider a constant correlation parameter $\rho$ such that:

$$\begin{aligned} dW_{K,t}=\rho dW_{L,t}+\sqrt{1-\rho ^{2}}d\widetilde{W}_{K,t}. \end{aligned}$$

(3)

Process $\widetilde{W}_{K}$ corresponds to a component independent of interest rates movements that takes account of other sources of risk as emphasized by Fraundorfer and Schurle Frauendorfer and Schurle (2003) and Kalkbrener and Willing Kalkbrener and Willing (2004). Janosi et al. (1999) consider that the correlation between demand deposits and market rates is due to money transfers between demand deposits and other kinds of financial investments. Using bank data coming from the Federal Reserve Bulletin for various types of accounts – namely Negotiable Orders of Withdrawal (NOW), passbooks, statement and demand deposit accounts, they show that the correlation parameter is negative, which means for example that demand deposit amounts decrease when short rates rise. On the contrary, the “liquidity trap” can induce a positive correlation (see Hicks, 1937). Indeed, there is no advantage for clients to invest their money in assets such as bonds or savings accounts if they are not sufficiently remunerative to compensate for commissions and related expenses (see e.g. Krugman, 1998). We estimate the correlation parameter between the deposit amount and the market rate according to the Engle and Granger method (see Ericsson and MacKinnon, 1999). The estimation period for both the US and for the Euro zone lies from 1997 to 2020 (see Table 3).

Table 3 Estimated parameters of deposit rate and market rate in the US and Euro zones (1997-2020)

In the Euro zone, the volatility of deposits is higher than in the US zone, with a lower absolute value of the correlation between interest rates and deposits. The high volatility of the amount of demand deposits ($9.21\%$) seems to be largely due to interest rates fluctuations.

2.4 Deposit rates and market rates

As shown in previous section, the demand deposits are correlated to market rates. In the same manner, the deposit rates exhibit some dependence with respect to market rates. Such feature has been highlighted by Hutchison (1995), Hutchison and Pennacchi (1996) or Jarrow and van Deventer Jarrow and Van Deventer (1998). Hutchison and Pennacchi (1996) assume the deposit rate to be an affine function of the market rate. In this framework, it is possible to provide quite explicit formula for optimal hedging strategies, as shown in Section 3. Therefore, in what follows, we suppose that the deposit rate is a deterministic function g of the market rate. Figure 4 illustrates the deposit rate and market rate in US and Euro zones from January 2003 to October 2020. It confirms the intuition of some linear dependence between the deposit rate and the market rate, at least for some given time periods. Indeed, since we investigate a rather long time period, we can distinguish at least two distinct point clouds corresponding to high rates and low rates.

Fig. 4

The deposit rate and market rate from January 2003 to October 2020 in the Euro and US zones

As from June 2014, the ECB decided to set a negative interest rate on the money market. This situation is perceived as an anomaly since it implies that agents agree to pay for deposits. Figure 4 represents the relationship between the deposit rate and the market interest rate. In the Europe case, we note that interest rate can be negative (from August 2015). In such case, the liability manager must change the benchmark interest rate, for example by using instead a proportion of the reference rate of the loans they grant to other customers. For simplicity, we consider always the Euribor as market rate for the Euro zone. As expected, we note that deposit rates are increasing with respect to market interest rates. As in Hutchison and Pennacchi (1996), we assume the deposit rate to fulfill some affine relation with the market rate, at least on given time periods. Therefore, we perform linear regressions of deposit rates on market rates. Hence, we focus on the following modelling of deposit rates:

$$\begin{aligned} g\left( L_{T}\right) =\alpha +\beta L_{T},\text { (US and Euro Zone cases)}, \end{aligned}$$

(4)

Table 4 displays the corresponding numerical values of $\alpha$ and $\beta$.

Table 4 Estimated relationship between deposit rate and market rate in the US and Euro zones

2.5 Interest rate margins within banking regulation

The IASB and the European Banking Federation (EBF) have proposed to introduce a new kind of hedging strategy, namely the Interest Margin Hedge (IMH), the purpose of which is to control the volatility level of demand deposits’ interest rate margins instead of the volatility of their fair value. Additionally, from the regulation point of view, the US Securities and Exchange Commission (SEC) have required US banks to disclose in annual (10-K) and quarterly (10-Q) filings indicators of interest rate spreads and their sensitivity to interest rate shocks. Therefore, we consider that the interest rate margin (IRM) at date T stands for the cash-flow generated upon the quarter $\left[ T,T+\frac{1}{4}\right]$ by the investment of the amount of demand deposits on the market rate $L_{T}$ minus the interests $g\left( L_{T}\right)$ paid to customers. Thus the interest rate margin is defined as follows:

$$\begin{aligned} IRM\left( K_{T},L_{T}\right) =\frac{1}{4}K_{T}\left( L_{T}-g\left( L_{T}\right) \right) . \end{aligned}$$

(5)

In our numerical illustrations, since we consider rather long periods of time for historical data, we deal as usual with the Libor rate for the US zone and the Euribor for the Euro zone. However, since the manipulation of these market rates during the time period 2005-2009 and the 2008 financial and economic crisis, these rates have proven to be less relevant as they are less used by banks among themselves. The sustainability of these rates as a benchmark has therefore been questioned and the regulators have decided to phase out these rates. The idea is to move from declared rates to actual rates from 2022.⁸ Contrary to the declared rates, each new rate would be calculated a posteriori from a panel, based on a broader scope of transactions, in order to best reflect the actual situation and thus avoid possible manipulation (see Pinter and Boissel, 2016). Thus any contract based on Libor or Euribor with a maturity beyond 2022 will have to be modified. This will impact in particular the computation of the interest rate margin.

3 Hedging of interest rate margin on demand deposits

In this section, we aim at hedging the interest rate margin. For this purpose, In what follows, we investigate the two main hedging strategies used to hedge financial options, namely the hedging strategy based on quadratic criterion introduced by Föllmer and Sondermann (1986) (see also Föllmer and Schweizer, 1991) and the quantile hedging approach introduced by Föllmer and Leukert (1999). We define several sets of payoffs corresponding to hedging on the interest rate margin for the quarter[T,T+((1/4))]. Here we assume that the bank can develop hedging that will impact the interest rate margin at historical cost, from the accounting viewpoint. However the recognition of hedging strategies at historical cost is far from being obvious. Yet, most banking practices tend to design hedging on interest rate securities to alleviate the volatility of the net interest income at historical cost. Thus, from an accounting viewpoint, banks tend to invest on securities recognized as available-for-sale, thus impacting the income statement at historical cost. In the European case, the IFRS-EU Carved-Out Fair Value Hedge allows banks to design swap-based hedging for deposit accounts by date of origination. Thus, each new deposit generation is hedged individually, given the hedging strategy designed for past generations. The hedging of interest rate margins can be performed using interest rate swaps or forward rate agreements. Our main constraint relates to the control of the hedging cost. We consider two frameworks: the first one corresponds to the static hedging case for which we search for the optimal allocation on Forward Rate Agreements (FRAs); the second one allows a dynamic hedging strategy to better take account of market rates flucttuations and of accumulated information about their future values.

3.1 Quadratic hedging for interest rate margins

The approach by quadratic hedging strategy is to measure the risk by the variance criterion, first proposed by Föllmer and Sondermann (1986). It consists in minimizing the expected square of the duplication error between the contingent claim and the terminal portfolio wealth. Usually, we obtain explicit and tractable formula. A similar approach, often equivalent to the variance one is the locally-risk minimizing (see Föllmer and Schweizer, 1991).

In what follows, we consider the static quadratic hedging of interest rate margins. Such hedging strategy can be based on Forward Rate Agreements (FRAs) contracted at initial date. Since the financial market is complete, there exists a risk-neutral probability $\mathbb {Q}$ which allows as usual to price any option. Denote by B(t, T) the value at time $t\le T$ of the zero-coupon bond maturing at time T chosen as numeraire in the GBM framework. We have to solve the following optimization problem:

$$\begin{aligned} Min_{S\in \mathcal {H}_{1}}\text { }Variance\left[ S-IRM\left( K_{T},L_{T}\right) \right] , \end{aligned}$$

(6)

where $\mathcal {H}_{1,m}$ is a subset of linear payoffs with respect to the market rate, defined by:

$$\begin{aligned} \mathcal {H}_{1,m}=\left\{ S\left| S=\theta L_{T}+\widetilde{\theta } \right. with\text { }\mathbb {E}_{\mathbb {Q}}\left[ S\right] \le mB(0,T)\right\} , \end{aligned}$$

where $\theta$ and $\widetilde{\theta }$ are constant parameters to be determined.

Proposition 1

The solution of Problem (6) is given by:

$$\begin{aligned} S^{*}=\theta ^{*}\left( L_{T}+\left( m-L_{0}\right) B(0,T)\right) \text { with }\theta ^{*}=\frac{Covariance\left[ L_{T};K_{T}\left( -\alpha -\left( \beta -1\right) L_{T}\right) \right] }{4Variance\left[ L_{T} \right] }. \end{aligned}$$

(7)

For a zero initial cost ($m=0$) and $B(0,T)=1$, the optimal hedging corresponds to $S^{*}=\theta ^{*}\left( L_{T}-L_{0}\right)$, which corresponds exactly to an investment on Forward Rate Agreements.

Corollary 2

The expectation and the standard deviation of the hedging error are respectively given by:

$$\begin{aligned}&\mathbb {E}_{\mathbb {P}}\left[ IRM\left( K_{T},L_{T}\right) -S^{*}\right] = \\&\mathbb {E}_{\mathbb {P}}\left[ IRM\left( K_{T},L_{T}\right) \right] -\frac{ Covariance\left[ L_{T};K_{T}\left( -\alpha -\left( \beta -1\right) L_{T}\right) \right] }{4Variance\left[ L_{T}\right] }\left( L_{0}e^{\mu _{L}T}-L_{0}\right) +m, \end{aligned}$$

with

$$\begin{aligned} \mathbb {E}_{\mathbb {P}}\left[ IRM\left( K_{T},L_{T}\right) \right] =-1/4\times \end{aligned}$$

$$\begin{aligned}&\left( \alpha K_{0}\exp \left[ \mu _{K}T\right] +\left( \beta -1\right) L_{0}K_{0}\exp \left[ \left( \mu _{L}+\mu _{K}+\sigma _{L}\sigma _{K}\rho \right) T\right] \right) . \\&\sqrt{{\mathbb {V}}ar\left[ IRM\left( K_{T},L_{T}\right) -S^{*}\right] }= \\&\frac{\sqrt{{\mathbb {V}}ar\left[ IRM\left( K_{T},L_{T}\right) \right] {\mathbb {V}}ar\left[ L_{T}\right] -Covariance\left[ L_{T};IRM\left( K_{T},L_{T}\right) \right] ^{2}}}{\sqrt{{\mathbb {V}}ar\left[ L_{T}\right] }}. \end{aligned}$$

Corollary 3

Under assumptions (1) and (2) on both the processes $\left( L_{t}\right) _{t}$ and $\left( K_{t}\right) _{t}$, we get:

$$\begin{aligned}&\theta ^{*}=L_{0}K_{0}\times \nonumber \\&\frac{\left( \begin{array}{c} -\alpha \exp \left[ \left( \mu _{L}+\mu _{K}\right) T\right] \left[ \exp \left[ \sigma _{L}\sigma _{K}\rho t\right] -1\right] \\ -\left( \beta -1\right) L_{0}\exp \left[ \left( 2\mu _{L}+\mu _{K}+\sigma _{L}\sigma _{K}\rho \right) T\right] \left( \exp \left[ \left( \sigma _{L}^{2}+\sigma _{L}\sigma _{K}\rho \right) T\right] -1\right) \end{array} \right) }{4L_{0}^{2}\exp \left[ 2\mu _{L}T\right] \left( \exp \left[ \sigma _{L}^{2}T\right] -1\right) }. \end{aligned}$$

(8)

Corollary 4

We note also that the optimal static hedging strategy $\theta ^{*}$has the following form with respect to the forward rate L:

$$\begin{aligned} \theta ^{*}=\frac{A}{L_{0}}+B, \end{aligned}$$

(9)

with

$$\begin{aligned} A= & {} K_{0}\times \alpha \left( -\frac{\exp \left[ \left( \mu _{L}+\mu _{K}\right) T\right] \left[ \exp \left[ \sigma _{L}\sigma _{K}\rho T\right] -1\right] }{4\exp \left[ 2\mu _{L}T\right] \left( \exp \left[ \sigma _{L}^{2}T\right] -1\right) }\right) , \\ B= & {} K_{0}\times \left( \beta -1\right) \left( -\frac{\exp \left[ \left( 2\mu _{L}+\mu _{K}+\sigma _{L}\sigma _{K}\rho \right) T\right] \left( \exp \left[ \left( \sigma _{L}^{2}+\sigma _{L}\sigma _{K}\rho \right) T\right] -1\right) }{4\exp \left[ 2\mu _{L}T\right] \left( \exp \left[ \sigma _{L}^{2}T\right] -1\right) }\right) . \end{aligned}$$

Consequently, if the correlation $\rho$ is negative, the optimal static quadratic hedging is decreasing with respect to the forward market rate if and only if the intercept $\alpha$ is positive. If the correlation $\rho$ is positive, it is the converse. Finally, note that if process K is constant, we get $\theta ^{*}/K_{0}=B=\left( 1-\beta \right) /4$ implying that, on yearly basis, $\theta _{y}^{*}/K_{0}=\left( 1-\beta \right)$. Then , if there is no deposit rate, we recover immediately that $\theta _{y}^{*}/K_{0}=100\%$ as expected.

In what follows, we illustrate numerically the previous results. For this purpose, we consider the numerical base cases corresponding to our estimates for both Euro and US zones (for Euribor and Libor, we use estimations of $\mu _{L}$ and $\sigma _{L}$ on the time period 1rst January 2009 to 1rst April 2019; for the value of the intercept for the Euro zone, we take $\alpha =0.011$ otherwise we get a negative expectation of the IRM⁹):

- Euro case:

$$\begin{aligned} \mu _{L}= & {} 0.041;\mu _{K}=0.0745;\lambda =0;\sigma _{L}=0.0289;\sigma _{K}=0.0980;\rho =0.1285\overline{;\delta }=0; \\ \alpha= & {} 0.011;\beta =0.633;K_{0}=1;L_{0}=1\%;T=1\text { year}. \end{aligned}$$

- US case:

$$\begin{aligned} \mu _{L}= & {} 0.0295;\mu _{K}=0.0256;\lambda =0;\sigma _{L}=0.0578;\sigma _{K}=0.0249;\rho =-0.1546;\overline{\delta }=0; \\ \alpha= & {} -0.000226;\beta =0.42267;K_{0}=1;L_{0}=1\%;T=1\text { year}. \end{aligned}$$

Fig. 5

Static optimal hedging with respect to trends (on the left) and with respect to volatilities (on the right)(Euro)

Fig. 6

Percentage of expectation of the hedging error with respect to trends (on the left) and with respect to volatilities (on the right)(Euro)

Figure 5 illustrates the hedging strategy as function of both the drifts and both the volatilities of the market rate and the demand deposit amount. Looking at the graphic on the left, we note that the optimal quadratic hedging strategy is increasing w.r.t. the demand deposit trend while slightlty increasing w.r.t. the market rate trend. This is quite intuitive since the higher the demand deposit, the higher the amount to be invested on the market rate. Looking at the graphic on the right, we note that the optimal quadratic hedging strategy is increasing w.r.t. the demand deposit volatility while decreasing w.r.t. the market rate volatility.

Figure 6 displays the percentage of expectation of the hedging error with respect to trend and with respect to volatility. From the graphic on the left, we note that the percentage of expectation of the hedging error is slightlty increasing w.r.t. the demand deposit trend while increasing w.r.t. the trend of rate market. Looking at the graphic on the right, we observe that the percentage of expectation of the hedging error is slightlty decreasing w.r.t. the demand deposit volatility while slightlty increasing w.r.t. the market rate volatility.

Fig. 7

Static optimal hedging with respect to intercept and beta (on the left) and its percentage of hedging error (on the right)(Euro)

Fig. 8

Static optimal hedging with respect to rho and market rate volatility (on the left) and its percentage of hedging error (on the right)(Euro)

Figure 7 represents the static optimal hedging strategy with respect to intercept $\alpha$ and to coefficient $\beta$. Looking at graphic on the left, we note that the static optimal hedging strategy is decreasing w.r.t. intercept $\alpha$ while slightlty decreasing w.r.t. $\beta$. The percentage of expectation of the hedging error is increasing w.r.t. intercept $\alpha$ while slightlty increasing w.r.t. $\beta$. It means that the percentage of expectation of the hedging error is increasing w.r.t. the demand deposit rate.

Figure 8 represents the static optimal hedging with respect to correlation $\rho$ and market rate volatility $\sigma _{L}$ . Looking at graphic on the left, we note that the static optimal hedging strategy is increasing w.r.t. correlation $\rho$ while the sensitivity to market rate volatility depends on the sign of the correlation (increasing when $\rho$ is negative and decreasing when $\rho$ is positive). The percentage of expectation of the hedging error is decreasing w.r.t. correlation $\rho$ while the sensitivity to market rate volatility depends on the sign of the correlation (decreasing when $\rho$ is negative and increasing when $\rho$ is positive).

Fig. 9

Static optimal hedging with respect to trends (on the left) and with respect to volatilities (on the right)(US)

Fig. 10

Percentage of expectation of the hedging error with respect to trends (on the left) and with respect to volatilities (on the right)(US)

Figure 9 illustrates the hedging strategy as function of both the drifts and both the volatilities of the market rate and the demand deposit amount. Looking at the graphic on the left, we note that the optimal quadratic hedging strategy is increasing w.r.t. the demand deposit trend while slightlty increasing w.r.t. the market rate trend. This is quite intuitive since the higher the demand deposit, the higher the amount to be invested on the market rate. Looking at the graphic on the right, we note that the optimal quadratic hedging strategy is increasing w.r.t. the market rate volatility while decreasing w.r.t. demand deposit volatility.

Figure 10 displays the percentage of expectation of the hedging error with respect to trends and with respect to volatilities. From the graphic on the left, we note that the percentage of expectation of the hedging error is slightlty increasing w.r.t. the demand deposit trend while increasing w.r.t. the trend of market rate. Looking at the graphic on the right, we note that the percentage of expectation of the hedging error is slightlty increasing w.r.t. the demand deposit trend while slightlty decreasing w.r.t. the trend of market rate.

Fig. 11

Static optimal hedging with respect to intercept and beta (on the left) and its percentage of hedging error (on the right)(US)

Fig. 12

Static optimal hedging with respect to rho and market rate volatility (on the left) and its percentage of hedging error (on the right)(US)

Figure 11 represents the static optimal hedging strategy with respect to intercept $\alpha$ and to coefficient $\beta$. Looking at graphic on the left, we note that the static optimal hedging strategy is increasing w.r.t. intercept $\alpha$ while decreasing w.r.t. $\beta$. The percentage of expectation of the hedging error is decreasing w.r.t. intercept $\alpha$ and slightlty decreasing w.r.t. $\beta$. It means that the percentage of expectation of the hedging error is decreasing w.r.t. the demand deposit rate. Compared to the Euro case, the sensitivity to intercept $\alpha$ is the converse. Indeed, for the Euro case the correlation $\rho$ is positive while for the US case it is negative. Consequently, the signs of the coefficient $\alpha$ are the opposite (see Relation 8).

Figure 12 represents the static optimal hedging with respect to correlation $\rho$ and market rate volatility $\sigma _{L}$ . Looking at graphic on the left, we note that the static optimal hedging strategy is increasing w.r.t. correlation $\rho$ while the sensitivity to market rate volatility depends on the sign of the correlation (increasing when $\rho$ is negative and decreasing when $\rho$ is positive). The percentage of expectation of the hedging error is decreasing w.r.t. correlation $\rho$ while the sensitivity to market rate volatility depends on the sign of the correlation (decreasing when $\rho$ is negative and increasing when $\rho$ is positive).

We are now looking for the optimal quadratic hedging strategy in a dynamic framework. Indeed, we can extend previous problem by examining a more general form of the quadratic hedging strategy. Unlike the framework of quadratic hedging considered in Adam et al. (2020), we allow the manager to trade on the demand deposit amount itself. For example, he or she may decide not to invest part of this amount at market rates during some time periods. It means that the risk management of interest rate margins is in particular based on the observation of the demand deposit amount.¹⁰. We are facing now the following optimization problem:

$$\begin{aligned} Min_{S}Variance_{\mathbb {P}}\left[ S-IRM\left( K_{T},L_{T}\right) \right] \ under\text { }\mathbb {E}_{\mathbb {Q}}\left[ S\right] =mB(0,T). \end{aligned}$$

Recall that $\mathbb {Q}$ denotes the risk-neutral probability. Consider $\mathcal {H}_{2}$ the set of payoffs S with an integrable square that are perfectly replicated by a self-financing trading strategy $\left( \theta _{t}=\left( \theta _{K,t},\theta _{L,t}\right) \right) _{t}$ adapted to the filtation generated by $\left( W_{K,t},W_{L,t}\right) _{t}$ (i.e. information delivered by the market rate and the demand deposit)¹¹ such that:

$$\begin{aligned} S=\int _{0}^{T}\theta _{K,t}dK_{t}+\int _{0}^{T}\theta _{L,t}dL_{t}. \end{aligned}$$

The set $\mathcal {H}_{2}$ contains the zero cost European options on the market rate.¹²

Introduce the subset $\mathcal {H}_{2,m}$ of $\mathcal {H}_{2}$ taking account of the budget constraint, namely:

$$\begin{aligned} {\mathcal {H}}_{2,m}=\left\{ S=\int _{0}^{T}\theta _{K,t}dK_{t}+\int _{0}^{T}\theta _{L,t}dL_{t}\left| \text { with }{\mathbb {E}}_{\mathbb {Q}}\left[ S^{2}\right] <\infty \text { and }{\mathbb {E}}_{\mathbb {Q}} \left[ S\right] =mB(0,T)\right. \right\} . \end{aligned}$$

We are facing now the following optimization problem:

$$\begin{aligned} Min_{S\in \mathcal {H}_{2,m}}\text { }Variance_{\mathbb {P}}\left[ S-IRM\left( K_{T},L_{T}\right) \right] . \end{aligned}$$

(10)

Let us introduce the Radon-Nikodym derivative $\eta _{T}=$ $\dfrac{d{\mathbb {Q}}}{d{\mathbb {P}}}$ of the risk-neutral probability $\mathbb {Q}$ with respect to the objective probability $\mathbb {P}$. Note that, under model assumptions, $\eta _{T}$ is a function of the market rate at maturity $L_{T}$ and of the path of the demand deposit amount¹³.

Proposition 5

The solution of Problem (10) with the constraint is given by:

$$\begin{aligned} S_{m}^{**}=IRM\left( K_{T},L_{T}\right) +\left( mB(0,T)-\mathbb {E}_{ \mathbb {Q}}\left[ IRM\left( K_{T},L_{T}\right) \right] \right) . \end{aligned}$$

(11)

As can be seen in previous Relation (11), the hedging error $S_{m}^{**}-IRM\left( K_{T},L_{T}\right)$ is simply a constant w.r.t. S. Note that it is increasing w.r.t. m since the higher the initial value, the higher the payoff S. Note also that the variance is nil when we take $m=\mathbb {E}_{\mathbb {Q}}\left[ IRM\left( K_{T},L_{T}\right) /B(0,T)\right]$ which corresponds to the exact replication of the interest rate margin IRM.

3.2 Quantile hedging for interest rate margins

Another final approach that we deal with in this paper is the quantile hedging. The problem of hedging is seen by another point of view: what should an investor do if he or she is unwilling to invest all the amount needed for a perfect hedging or a superhedging strategy? Equivalently, which is the maximal probability of a successful hedge given a smaller initial amount invested? This type of problem seems to be more interesting in practice than the superhedging. Two seminal papers of Föllmer and Leukert (1999, 2000) deal with quantile hedging. We consider the quantile hedging strategies of interest rate margins in both the static and dynamic cases where the amounts of interest rate derivatives are dynamically managed according to the information set related to market rates and to the fluctuations of the deposit amount. This typically leads to replicating interest rate derivatives. In our framework, this allows to derive explicit dynamic strategies to hedge the interest rate margin for a given quarter.

In what follows, we first consider the static quantile hedging of interest rate margins. For this purpose, we have to solve the following optimization problem:

$$\begin{aligned} Max_{S\in \mathcal {H}_{1}(m)}\text { }\mathbb {P}\left[ S\ge IRM\left( K_{T},L_{T}\right) \right] , \end{aligned}$$

(12)

with the same subset $\mathcal {H}_{1,m}$ of linear payoffs with respect to the market rate defined previously, namely:

$$\begin{aligned} \mathcal {H}_{1,m}=\left\{ S\left| S=\theta L_{T}+\widetilde{\theta } \right. with\text { }\mathbb {E}_{\mathbb {Q}}\left[ S\right] =mB(0,T)\right\} , \end{aligned}$$

where $\theta$ is a constant. Recall that the budget constraint corresponds to where Denote by B(t, T) the value of the zero-coupon bond maturing at time T chosen as numeraire in the GBM framework.

We have $\theta L_{0}+\widetilde{\theta }/B(0,T)=m$ which implies that $\widetilde{\theta }=\left( m-\theta L_{0}\right) B(0,T)$. Introduce now the following processes:

$$\begin{aligned} \widetilde{K}_{T}= & {} K_{0}\exp \left[ \left( \mu _{K}-\frac{1}{2}\sigma _{K}^{2}\right) T+\sigma _{K}\sqrt{1-\rho ^{2}}\widetilde{W}_{K,T}\right] , \\ f\left( L_{T}\right)= & {} \left( L_{0}^{-\left( \rho \frac{\sigma _{K}}{\sigma _{L}}\right) }\exp \left[ -\left( \rho \frac{\sigma _{K}}{\sigma _{L}} \right) \left( \mu _{L}-\frac{1}{2}\sigma _{L}^{2}\right) T\right] \right) L_{T}^{\left( \rho \frac{\sigma _{K}}{\sigma _{L}}\right) }\times \frac{ \left( L_{T}-g\left( L_{T}\right) \right) }{4}. \end{aligned}$$

Then the interest rate margin has the form:

$$\begin{aligned} IRM\left( K_{T},L_{T}\right) =K_{T}\left( L_{T}-g\left( L_{T}\right) \right) =\widetilde{K}_{T}f\left( L_{T}\right) . \end{aligned}$$

Therefore, we face the following optimization problem:

$$\begin{aligned} Max_{\theta }\text { }\mathbb {P}\left[ \theta \left[ L_{T}-L_{0}B(0,T)\right] +mB(0,T)\ge \widetilde{K}_{T}f\left( L_{T}\right) \right] . \end{aligned}$$

Proposition 6

With previous notations, Problem (12) is equivalent to the maximization of the following expectation $\mathbb {E}_{\mathbb {P}}\left[ F_{\widetilde{K}_{T}}\left[ \frac{ \theta \left[ L_{T}-L_{0}B(0,T)\right] +mB(0,T)}{f\left( L_{T}\right) } \right] \right]$, where $F_{\widetilde{K}_{T}}$ denotes the cumulative distribution function of random variable $\widetilde{K}_{T}$.

We have to examine the function $\theta \longrightarrow \mathbb {P}\left[ \theta \left[ L_{T}-L_{0}B(0,T)\right] +mB(0,T)\ge \widetilde{K}_{T}f\left( L_{T}\right) \right]$.¹⁴ Figures and illustrate numerically for the two cases, namely the US and the Euro zones (Fig. 13).

If we restrict the search to payoff $S=\theta L_{T}$, we can prove that the probability of superhedging the interest margin is reached at the maximum possible value of parameter $\theta$.

Proposition 7

The solution of Problem (12) with condition $S=\theta L_{T}$ (i.e. $\widetilde{ \theta }=0)$ is given by

$$\begin{aligned} S^{*}=\theta ^{*}L_{T}\text { with }\theta ^{*}=\frac{m}{L_{0}}. \end{aligned}$$

(13)

Corollary 8

The probability of success (i.e. the hedging portfolio $\theta ^{*}L_{T}$ is higher than the interest rate margin on demands deposit) is given by:

$$\begin{aligned} F_{IRM\left( K_{T},L_{T}\right) /L_{T}}\left[ \frac{m}{L_{0}}\right] , \end{aligned}$$

where the ratio $IRM\left( K_{T},L_{T}\right) /L_{T}$ is a linear combination of two Lognormal processes.

In the following, we illustrate numerically the previous results. For this purpose, we consider the numerical base cases corresponding to our estimates for both Euro and US zones (for Euribor and Libor, we use estimations of $\mu _{L}$ and $\sigma _{L}$ on the time period 1rst January 2009 to 1rst April 2019; for the value of the intercept for the Euro zone, we take $\alpha =0.001$ instead $\alpha =0.011$ otherwise we get a negative expectation of the IRM¹⁵):

- Euro case:

$$\begin{aligned} \mu _{L}= & {} 0.041;\mu _{K}=0.0745;\lambda =0;\sigma _{L}=0.0289;\sigma _{K}=0.0980;\rho =0.1285\overline{;\delta }=0; \\ \alpha= & {} 0.011;\beta =0.633;K_{0}=1;L_{0}=1\%;T=1\text { year}. \end{aligned}$$

- US case:

$$\begin{aligned} \mu _{L}= & {} 0.0295;\mu _{K}=0.0256;\lambda =0;\sigma _{L}=0.0578;\sigma _{K}=0.0249;\rho =-0.1546;\overline{\delta }=0; \\ \alpha= & {} -0.00026;\beta =0.42267;K_{0}=1;L_{0}=1\%;T=1\text { year}. \end{aligned}$$

Fig. 13

Probability of super hedging as function of theta

Fig. 14

Probability of super hedging as function of theta and demand deposit trend

Fig. 15

Probability of super hedging as function of theta and demand deposit volatility

Figure 14 shows that the probability of superhedging is decreasing w.r.t. the demand deposit trend for any given theta. This is due to the quantile condition $\mathbb {P}\left[ \theta L_{T}\ge IRM\left( K_{T},L_{T}\right) \right]$ itself since the term on the right does not depend on $K_{T}$ while $IRM\left( K_{T},L_{T}\right) = \frac{1}{4}K_{T}\left( L_{T}-g(K_{T})\right)$ is increasing w.r.t. $K_{T}$.

Figure 15 shows that the probability of superhedging is decreasing w.r.t. the demand deposit volatility for any given theta. This is due to the quantile condition $\mathbb {P}\left[ \theta L_{T}\ge IRM\left( K_{T},L_{T}\right) \right]$ which has the form ${\mathbb {E}}\left[ F\left[ Log(\theta m(L_{T})\right] \right]$ where $F(x)=N(x/\sigma _{K})$ thus decreasing w.r.t. $\sigma _{K}$ (see below decomposition of $K_{T}$ using $\widetilde{K}_{T}$.

Previous result can be extended by searching for a more general payoff S in $\mathcal {H}_{2,m}$.

We are facing now the following optimization problem:

$$\begin{aligned} Max_{S\in \mathcal {H}_{2,m}}\text { }\mathbb {P}\left[ S\ge IRM\left( K_{T},L_{T}\right) \right] . \end{aligned}$$

(14)

Previous hedging strategy is based on static hedging with involves only European options. Therefore, we propose to extend the previous market above to a larger set of dynamic self-financed investment strategies, enabling the manager to adapt his FRA-based hedging strategy to the evolution of the demand deposit amount. We consider now the dynamic quantile strategy problem: The value of the hedging portfolio at time t is given by the process $\int _{0}^{t}\theta _{K,s}dK_{s}+\int _{0}^{t}\theta _{L,s}dL_{s}$. It is right-continuous and with an integrable square. As in Föllmer and Leukert (1999, 2000), let us consider $m\$which is smaller than the initial value of the interest rate margin, namely $\mathbb {E}_{\mathbb {Q}}\left[ IRM\left( K_{T},L_{T}\right) /B(0,T)\right]$. We can now ask for the strategy which maximizes the probability of a successful hedge under the constraint that the initial capital is not larger than m. Thus, we examine the problem:

$$\begin{aligned} Max_{S\in \mathcal {H}_{2,m}}\text { }\mathbb {P}\left[ S=\int _{0}^{T}\theta _{K,t}dK_{t}+\int _{0}^{T}\theta _{L,t}dL_{t}\ge IRM\left( K_{T},L_{T}\right) \right] . \end{aligned}$$

(15)

Using the theory of Neyman-Pearson, consider a randomized test (“success ratio”), i.e, an $\mathcal {F}_{T}$ -measurable function $\varphi$ such that $0\le \varphi \le 1$.

Consider the measure $\widetilde{\mathbb {P}}$ defined by:

$$\begin{aligned} \frac{d\widetilde{\mathbb {P}}}{d\mathbb {Q}}=\frac{IRM\left( K_{T},L_{T}\right) }{\mathbb {E}_{\mathbb {Q}}\left[ IRM\left( K_{T},L_{T}\right) \right] }. \end{aligned}$$

Let $\mathcal {R}$ be the class of all these functions and let us consider the problem of optimization:

$$\begin{aligned} \mathbb {E}_{\mathbb {P}}\left[ \widetilde{\varphi }\right] =\underset{\varphi \in \mathcal {R}}{\max }\mathbb {E}_{\mathbb {P}}\left[ \varphi \right] , \end{aligned}$$

(16)

under the constraint

$$\begin{aligned} \int \varphi d\widetilde{\mathbb {P}}\le \alpha =\dfrac{m}{\mathbb {E}_{ \mathbb {Q}}\left[ IRM\left( K_{T},L_{T}\right) //B(0,T)\right] }. \end{aligned}$$

(17)

Define the level

$$\begin{aligned} \widetilde{a}=\inf \left\{ a:\widetilde{\mathbb {P}}\left[ \dfrac{d\mathbb {P} }{d\mathbb {Q}}>a\text { }IRM\left( K_{T},L_{T}\right) \right] \le \alpha \right\} , \end{aligned}$$

(18)

Then, the Neyman-Pearson lemma gives the solution as being:

$$\begin{aligned} \widetilde{\varphi }=\mathbb {I}_{\left\{ \frac{d\mathbb {P}}{d\widetilde{ \mathbb {P}}}>\widetilde{a}.IRM\left( K_{T},L_{T}\right) \right\} }, \end{aligned}$$

(19)

where $\widetilde{a}$ is given by (18). Therefore, by applying results of Föllmer and Leukert (1999), we get the following result.

Proposition 9

The solution of Problem is a knock-out option defined by:

$$\begin{aligned} V_{T}^{*}=IRM\left( K_{T},L_{T}\right) \mathbb {I}_{\left\{ \frac{d \mathbb {P}}{d\mathbb {Q}}>\widetilde{a}.IRM\left( K_{T},L_{T}\right) \right\} }. \end{aligned}$$

(20)

Remark 10

We note that condition $\frac{d{\mathbb {P}}}{d{\mathbb {Q}}}>\widetilde{a}.IRM\left( K_{T},L_{T}\right)$ is equivalent to condition $\eta _{T}<1/\left( \widetilde{a}.IRM\left( K_{T},L_{T}\right) \right)$. Therefore, as soon as this latter condition is not satisfied, the value of the knock-out option is null, meaning that this kind of strategy can yield actually to no hedge.

4 Concluding remarks and discussion

In recent years, outstanding bank deposits have increased very significantly, in particular since the outbreak of the COVID 19 pandemic. In this paper, we deal with the mitigation of the risk contained in interest rate margins of demand deposits. We assume the demand deposit amount to carry some source of risk called "business risk", independent of market risk. We deal with both the main hedging strategies of the interest margins, namely the quadratic strategy and for the first time the quantile hedging strategy, in particular when the manager wants to control the hedging cost. We examine both the static and dynamic cases for which we provide explicit hedging strategies. For this purpose, we perform linear regressions of deposit rates on market rates. We find that the optimal static quadratic hedging is inversely proportional to the market rate. One of the main features is that the quantile hedging leads to a portfolio which corresponds to a knockout option. Thus, the solution for the quantile hedging criterion is somewhat riskier since its gain may be nil, due to its knockout feature. Further extensions could consider more complex dynamics in particular of the demand deposit rate by introducing stochastic volatility and jumps as well. This will allow us to take account of potential asymmetric effects and fat tails. Other particular hedging strategies such as a risk management strategy based on minimax to take account of a worst case scenario could be also examined as proposed by Howe et al. (1994). New benchmark market interest rates could also be considered since Libor and Euribor rates will be replaced as they are no longer considered as representative of real banking transactions. It should also be noted that the presence of negative rates in Europe has already led banks to rely on other rates for deposit remuneration. However, the war in Ukraine is contributing to a sharp rise in inflation rates, leading central banks to increase their key rates. As a result, short term rates should become positive again. As emphasized by Jawadi and Sousa (2013), we could also take account of nonlinear dynamics associated with the money demand functions and of their elasticities with respect to inflation rate, interest rate, GDP...In any case, we believe that our results have important implications for the hedging of bank deposits, particularly in the context of the global pandemic and the Ukraine crisis.

Appendices

Appendix 1. Quadratic hedging strategies

1.1 Appendix 1.1. Determination of the risk-neutral probability $\mathbb {Q}$

In order to determine the risk-neutral probability $\mathbb {Q}$ (here the forward measure of the market rate for the maturity T), we have to compute its Radon-Nikodym derivative process $\eta$ with respect to the objective probability $\mathbb {P}$ defined by:

$$\begin{aligned} \eta _{t}=\mathbb {E}_{\mathbb {P}}\left[ \dfrac{d\mathbb {Q}}{d\mathbb {P}} \left| \mathcal {F}_{t}\right. \right] . \end{aligned}$$

Recall that the market rate $L_{t}=L\left( t,T,T+\frac{1}{4}\right)$ with duration equal to a quarter is assumed to follow the following dynamics:

$$\begin{aligned} dL_{t}=L_{t}\left( \mu _{L}+\sigma _{L}dW_{L,t}\right) , \end{aligned}$$

(21)

where $\left( W_{L,t}\right) _{t}$ is a standard Brownian motion under the historical probability measure $\mathbb {P}$.

The demand deposit amount is assumed to satisfy:

$$\begin{aligned} dK_{t}=K_{t}\left( \mu _{K}+\sigma _{K}dW_{K,t}\right) , \end{aligned}$$

(22)

where $\left( W_{K,t}\right) _{t}$ is a standard Brownian motion. The dynamics of the demand deposit is correlated with interest rates since we suppose that both $\left( W_{L,t}\right) _{t}$ and $\left( W_{K,t}\right) _{t}$ are standard Brownian motions under the same filtration $\left( \mathcal {F}_{t}\right) _{t}$. and that there exists a Brownian motion $\left( \widetilde{W}_{K,t}\right) _{t}$ independent from $\left( W_{L,t}\right) _{t}$, and a $\rho$ constant correlation parameter such that we have:

$$\begin{aligned} dW_{K,t}=\rho dW_{L,t}+\sqrt{1-\rho ^{2}}d\widetilde{W}_{K,t}. \end{aligned}$$

To compute the Radon-Nikodym $\eta$, we recall that, since it must be equal to an exponential martingale under the filtration $\left( \mathcal {F} _{t}\right) _{t}$ generated by both standard Brownian motions $\left( W_{L,t}\right) _{t}$ and $\left( \widetilde{W}_{K,t}\right) _{t}$, it has the following form:

$$\begin{aligned} \eta _{t}=\exp \left[ -\frac{1}{2}\int _{0}^{t}\left( \beta _{L,s}^{2}+\beta _{K,s}^{2}\right) ds-\int _{0}^{t}\beta _{L,s}dW_{L,s}-\int _{0}^{t}\beta _{K,s}d\widetilde{W}_{K,s}\right] , \end{aligned}$$

where both processes $\left( \beta _{L,t}\right) _{t}$ and $\left( \beta _{K,t}\right) _{t}$ are predictable with integrable squares. They correspond to factor loadings with respect to the sources of risk. To determine these factors, we use the following characterizations: both $\left( \eta _{t}L_{t}\right) _{t}$ and $\left( \eta _{t}K_{t}/B(t,T)\right) _{t}$ are martingales under $\mathbb {P}$, where B(t, T) denotes the value of the zero-coupon bond maturing at time T chosen as numeraire in the GBM framework:

$$\begin{aligned} dB(t,T)=B(t,T)\left( \mu _{B,t}dt+\sigma _{B,t}dW_{L,t}\right) . \end{aligned}$$

Using the fact that both drifts of $\left( \eta _{t}L_{t}\right) _{t}$ and $\left( \eta _{t}K_{t}/B(t,T)\right) _{t}$ must be equal to 0, we get the following system:

$$\begin{aligned} \left\{ \begin{array}{c} \beta _{L}=\frac{\mu _{L}}{\sigma _{L}}, \\ \beta _{K,t}=\frac{\mu _{K}-\mu _{B,t}+\sigma _{B,t}^{2}-\sigma _{K}\rho \left( \frac{\mu _{L}}{\sigma _{L}}+\sigma _{B,t}\right) +\left( \frac{\mu _{L}}{\sigma _{L}}\sigma _{B,t}\right) }{\sigma _{K}\sqrt{1-\rho ^{2}}}. \end{array} \right. \end{aligned}$$

from which we deduce that $\eta _{T}$ is a function of the market rate at maturity $L_{T}$ and of the path of the demand deposit amount given by:

$$\begin{aligned} \eta _{T}=\chi _{T}L_{T}^{-\left( \frac{\mu _{L}}{\sigma _{L^{2}}}\right) }\exp \left[ -\frac{1}{2}\int _{0}^{T}\beta _{K,t}^{2}dt-\int _{0}^{T}\beta _{K,t}d\widetilde{W}_{K,t}\right] ,\text { with }\chi _{T}=\exp \left[ -\frac{ 1}{2}\left[ \mu _{L}-\left( \frac{\mu _{L}}{\sigma _{L}}\right) ^{2}\right] T \right] L_{0}^{\left( \frac{\mu _{L}}{\sigma _{L^{2}}}\right) }. \end{aligned}$$

1.2 Appendix 1.2. Proof of Proposition 1

We have:

$$\begin{aligned}&Variance\left[ IRM\left( K_{T},L_{T}\right) -S\right] = \\&Variance\left[ \theta L_{T}+\widetilde{\theta }-\frac{1}{4}K_{T}\left( L_{T}-\alpha -\beta L_{T}\right) \right] = \\ \theta ^{2}Variance\left[ L_{T}\right] +\frac{1}{16}Variance\left[ K_{T}\left( \alpha +\left( \beta -1\right) L_{T}\right) \right] +\frac{ \theta }{2}Covariance\left[ L_{T};K_{T}\left( \alpha +\left( \beta -1\right) L_{T}\right) \right] . \end{aligned}$$

Previous term is a polynomial function of order 2 with respect to $\theta$ . Its minimum is reached on:

$$\begin{aligned} \theta ^{*}=\frac{Covariance\left[ L_{T};K_{T}\left( -\alpha -\left( \beta -1\right) L_{T}\right) \right] }{4Variance\left[ L_{T}\right] }. \end{aligned}$$

Finally, since $\theta L_{0}+\widetilde{\theta }/B(0,T)=m$, we deduce the result.

1.3 Appendix 1.3. Proof of Proposition 5

We have to solve:

$$\begin{aligned} Min_{S\in \mathcal {H}_{2,m}}\text { }Variance\left[ S-IRM\left( K_{T},L_{T}\right) \right] . \end{aligned}$$

which is equivalent here to:

$$\begin{aligned} Min_{S\in \mathcal {H}_{2}}\text { }Variance\left[ S-\frac{1}{4}K_{T}\left( L_{T}-\alpha -\beta L_{T}\right) \right] , \end{aligned}$$

under

$$\begin{aligned} \mathbb {E}_{\mathbb {Q}}\left[ S/B(0,T)\right] =m. \end{aligned}$$

We introduce the following auxiliary conditions:

$$\begin{aligned} \mathbb {E}_{\mathbb {P}}\left[ IRM\left( K_{T},L_{T}\right) -S\right] =\lambda . \end{aligned}$$

Due to its convexity, we can apply results based on Lagrangian conditions.¹⁶. Let us introduce:

$$\begin{aligned}&{\mathcal {L}}\left( S,\zeta ,\xi \right) = \\&Variance\left[ S-IRM\left( K_{T},L_{T}\right) \right] +2\zeta \left( mB(0,T)- {\mathbb {E}}_{\mathbb {P}}\left[ S\eta _{T}\right] \right) +2\xi \left( {\mathbb {E}}_{\mathbb {P}}\left[ IRM\left( K_{T},L_{T}\right) -S\right] -\lambda \right) , \end{aligned}$$

where $\eta _{T}$ corresponds to the previous Radon-Nikodym derivative $\dfrac{d\mathbb {Q}}{d\mathbb {P}}$ of the risk neutral probability $\mathbb {Q}$ with respect to the objective probability $\mathbb {P}$ and under the filtration generated by $\left( W_{L},W_{K}\right)$.

Then, the optimization problem with the previous additional condition is equivalent to $Min\mathcal {L}\left( S,\zeta ,\xi \right)$. The first order conditions correspond to:

$$\begin{aligned} \frac{\partial }{\partial S}Variance\left[ S-IRM\left( K_{T},L_{T}\right) \right] +2\zeta \left( mB(0,T)-\mathbb {E}_{\mathbb {P}}\left[ S\eta _{T} \right] \right) +2\xi \left( \mathbb {E}_{\mathbb {P}}\left[ IRM\left( K_{T},L_{T}\right) -S\right] -\lambda \right) =0. \end{aligned}$$

We deduce that:

$$\begin{aligned} S_{m,\lambda }^{**}=IRM\left( K_{T},L_{T}\right) +\zeta \eta _{T}+\xi , \end{aligned}$$

with:

$$\begin{aligned} \left\{ \begin{array}{c} -\zeta -\xi =\lambda \\ \zeta \mathbb {E}_{\mathbb {P}}\left[ \eta _{T}^{2}\right] +\xi =mB(0,T)- \mathbb {E}_{\mathbb {Q}}\left[ IRM\left( K_{T},L_{T}\right) \right] \end{array} \right. . \end{aligned}$$

We get:

$$\begin{aligned} \zeta= & {} \frac{\lambda +mB(0,T)-\mathbb {E}_{\mathbb {Q}}\left[ IRM\left( K_{T},L_{T}\right) \right] }{\mathbb {E}_{\mathbb {P}}\left[ \eta _{T}^{2} \right] -1}, \\ \xi= & {} \frac{\mathbb {E}_{\mathbb {Q}}\left[ IRM\left( K_{T},L_{T}\right) \right] -mB(0,T)-\lambda \mathbb {E}_{\mathbb {P}}\left[ \eta _{T}^{2}\right] }{\mathbb {E}_{\mathbb {P}}\left[ \eta _{T}^{2}\right] -1}. \end{aligned}$$

Now we deduce that:

$$\begin{aligned} Variance\left[ S_{m,\lambda }^{**}-IRM\left( K_{T},L_{T}\right) \right]= & {} Variance\left[ \zeta \eta _{T}+\xi \right] \\= & {} \zeta ^{2}Variance\left[ \eta _{T}\right] \\= & {} \zeta ^{2}\left( \mathbb {E}_{\mathbb {P}}\left[ \eta _{T}^{2}\right] -1\right) . \end{aligned}$$

Now, for fixed m, we search the mininimum with respect to $\lambda$. We get:

$$\begin{aligned} \lambda ^{*}\left( m\right) =\mathbb {E}_{\mathbb {Q}}\left[ IRM\left( K_{T},L_{T}\right) \right] -mB(0,T), \\ \zeta ^{*}\left( m\right) =0, \end{aligned}$$

and

$$\begin{aligned} \xi ^{*}\left( m\right) =-\zeta ^{*}\left( m\right) -\lambda ^{*}\left( m\right) =\left( mB(0,T)-\mathbb {E}_{\mathbb {Q}}\left[ IRM\left( K_{T},L_{T}\right) \right] \right) . \end{aligned}$$

The optimal solution is then given by:

$$\begin{aligned} S_{m,\lambda }^{**}=IRM\left( K_{T},L_{T}\right) +\left( mB(0,T)- \mathbb {E}_{\mathbb {Q}}\left[ IRM\left( K_{T},L_{T}\right) \right] \right) . \end{aligned}$$

We note that the variance is obviously minimal for $m^{*}=\mathbb {E}_{ \mathbb {Q}}\left[ IRM\left( K_{T},L_{T}\right) /B(0,T)\right]$.

Appendix 2. Quantile hedging strategies

1.1 Appendix 2.1. Proof of Proposition 6

Note that, using standard calculus, the demand deposit process K can be decomposed as follows:

$$\begin{aligned} K_{T}=\widetilde{K}_{T}\times \left( L_{0}^{-\left( \rho \frac{\sigma _{K}}{ \sigma _{L}}\right) }\exp \left[ -\left( \rho \frac{\sigma _{K}}{\sigma _{L}} \right) \left( \mu _{L}-\frac{1}{2}\sigma _{L}^{2}\right) T\right] \right) L_{T}^{\left( \rho \frac{\sigma _{K}}{\sigma _{L}}\right) }, \end{aligned}$$

with

$$\begin{aligned} \widetilde{K}_{T}=K_{0}\exp \left[ \left( \mu _{K}-\frac{1}{2}\sigma _{K}^{2}\right) T+\sigma _{K}\sqrt{1-\rho ^{2}}\widetilde{W}_{K,T}\right] . \end{aligned}$$

Recall that :

$$\begin{aligned} IRM\left( K_{T},L_{T}\right) =K_{T}\left( L_{T}-g\left( L_{T}\right) \right) . \end{aligned}$$

Therefore, we face the following optimization problem:

$$\begin{aligned} Max_{h}\text { }\mathbb {P}\left[ S\ge \widetilde{K}_{T}f\left( L_{T}\right) \right] \text { under }\mathbb {E}_{\mathbb {P}}\left[ S\eta \left( L_{T}\right) /B(0,T)\right] \le m, \end{aligned}$$

where:

$$\begin{aligned} f\left( L_{T}\right) =\left( L_{0}^{-\left( \rho \frac{\sigma _{K}}{\sigma _{L}}\right) }\exp \left[ -\left( \rho \frac{\sigma _{K}}{\sigma _{L}} \right) \left( \mu _{L}-\frac{1}{2}\sigma _{L}^{2}\right) T\right] \right) L_{T}^{\left( \rho \frac{\sigma _{K}}{\sigma _{L}}\right) }\times \frac{ \left( L_{T}-g\left( L_{T}\right) \right) }{4}>0. \end{aligned}$$

We have:

$$\begin{aligned} \mathbb {P}\left[ S\ge \widetilde{K}_{T}f\left( L_{T}\right) \right] = \mathbb {P}\left[ \frac{\theta \left[ L_{T}-L_{0}B(0,T)\right] +mB(0,T)}{ f\left( L_{T}\right) }\ge \widetilde{K}_{T}\right] \end{aligned}$$

Since the random variables $L_{T}$ and $\widetilde{K}_{T}$ are independent, we deduce:

$$\begin{aligned} \mathbb {P}\left[ \frac{\theta \left[ L_{T}-L_{0}B(0,T)\right] +mB(0,T)}{ f\left( L_{T}\right) }\ge \widetilde{K}_{T}\right] =\mathbb {E}_{\mathbb {P}} \left[ F_{\widetilde{K}_{T}}\left[ \frac{\theta \left[ L_{T}-L_{0}B(0,T) \right] +mB(0,T)}{f\left( L_{T}\right) }\right] \right] , \end{aligned}$$

where $F_{\widetilde{K}_{T}}$ denotes the cumulative distribution function of random variable $\widetilde{K}_{T}$.

Condition for an existence of an inner maximum: The search for an interior maximum yields to the first order condition:

$$\begin{aligned} \frac{\partial }{\partial \theta }\mathbb {E}\left[ F_{\widetilde{K}_{T}} \left[ \frac{\theta \left[ L_{T}-L_{0}B(0,T)\right] +m/B(0,T)}{f\left( L_{T}\right) }\right] \right] =0, \end{aligned}$$

which is equivalent to:

$$\begin{aligned} \mathbb {E}\left[ f_{\widetilde{K}_{T}}\left[ \frac{\theta \left( L_{T}-L_{0}B(0,T)\right) +mB(0,T)}{f\left( L_{T}\right) }\right] \frac{ \left( L_{T}-L_{0}B(0,T)\right) }{f\left( L_{T}\right) }\right] =0, \end{aligned}$$

where $f_{\widetilde{K}_{T}}$ denotes the pdf of process $\widetilde{K}_{T}$.

1.2 Appendix 2.2. Proof of Proposition 7

For $S=\theta L_{T}$, We have to solve:

$$\begin{aligned} Max_{\theta \le m/\mathbb {E}_{\mathbb {Q}}\left[ L_{T}\right] }\mathbb {P} \left[ \theta L_{T}\ge IRM\left( K_{T},L_{T}\right) \right] . \end{aligned}$$

This is equivalent to:

$$\begin{aligned} Max_{\theta \le m/\mathbb {E}_{\mathbb {Q}}\left[ L_{T}\right] }F_{IRM\left( K_{T},L_{T}\right) /L_{T}}\left[ \theta \right] , \end{aligned}$$

where $F_{IRM\left( K_{T},L_{T}\right) /L_{T}}$ is the cumulated distribution function (cdf) of the ratio $IRM\left( K_{T},L_{T}\right) /L_{T}$. Clearly, since any cdf is increasing, the maximum is reached on:

$$\begin{aligned} \theta ^{*}=\frac{m}{\mathbb {E}_{\mathbb {Q}}\left[ L_{T}\right] }. \end{aligned}$$

Finally, since under the risk neutral probability $\mathbb {Q}$, we have $\mathbb {E}_{\mathbb {Q}}\left[ L_{T}\right] =L_{0}$, we deduce the result.

1.3 Appendix 2.3. Proof of Corollary

Under assumptions (1) and (2) on both the processes $\left( L_{t}\right) _{t}$ and $\left( K_{t}\right) _{t}$, we can compute the cdf $F_{IRM\left( K_{T},L_{T}\right) /L_{T}}$. Indeed, we have:

$$\begin{aligned} \frac{IRM\left( K_{T},L_{T}\right) }{L_{T}}=\frac{1}{4}K_{T}(1-\beta )-\frac{ \alpha }{4}\frac{K_{T}}{L_{T}}. \end{aligned}$$

Recall that the processes L and K satisfy:

$$\begin{aligned} dL_{t}=L_{t}\left( \mu _{L}dt+\sigma _{L}dW_{L,t}\right) \end{aligned}$$

where $\left( W_{L,t}\right) _{t}$ is a standard Brownian motion under the historical probability measure $\mathbb {P}$ and where $\mu _{L}$ and $\sigma _{L}$ are assumed to be constant. The demand deposit amount follows:

$$\begin{aligned} dK_{t}=K_{t}\left( \mu _{K}dt+\sigma _{K}dW_{K,t}\right) , \end{aligned}$$

where $\left( W_{K,t}\right) _{t}$ is a standard Brownian motion. The trend $\mu _{K}$ and the volatility $\sigma _{K}$ are assumed to be constant. We have also:

$$\begin{aligned} dW_{K,t}=\rho dW_{L,t}+\sqrt{1-\rho ^{2}}d\widetilde{W}_{K,t}, \end{aligned}$$

where$\left( \widetilde{W}_{K,t}\right) _{t}$ is a Brownian motion independent of $\left( W_{L,t}\right) _{t}$, while $W_{L,t}$ and $W_{K,t}$ have a correlation parameter $\rho t$.

Consequently, we get:

$$\begin{aligned} K_{T}= & {} K_{0}\exp \left[ \left( \mu _{K}-\frac{1}{2}\sigma _{K}^{2}\right) T+\sigma _{K}\rho W_{L,T}+\sigma _{K}\sqrt{1-\rho ^{2}}\widetilde{W}_{K,T} \right] \\ \frac{K_{T}}{L_{T}}= & {} \frac{K_{0}}{L_{0}}\exp \left[ \left( \mu _{K}-\mu _{L}-\frac{1}{2}\sigma _{K}^{2}+\frac{1}{2}\sigma _{L}^{2}\right) T+\left( \sigma _{K}\rho -\sigma _{L}\right) W_{L,T}+\sigma _{K}\sqrt{1-\rho ^{2}} \widetilde{W}_{K,T}\right] \end{aligned}$$

Therefore, the ratio $IRM\left( K_{T},L_{T}\right) /L_{T}$ is a linear combination of two Lognormal processes.

1.4 Appendix 2.4. Quantile hedging strategies: the complete case

This section recalls results about quantile hedging strategies in complete financial markets. We refer to Föllmer and Leukert (1999). In particular, we search for a strategy which maximizes the probability of a successful hedge under the objective probability $\mathbb {P}$, given a constraint on the initial cost. This concept on quantile hedging can be considered as the dynamic version of the “Value-at-Risk” concept. The problem of quantile hedging is formulated in the context of general semimartingale processes. In what follows, to simplify the notations, the riskless rate is supposed to be equal to 0. We assume that the price process of the underlying is a semimartingale $X=(X_{t})_{t\in \left[ 0,T\right] }$ on a probability space $\left( \Omega ,\mathcal {F},\mathbb {P}\right)$ with the filtration $\left( \mathcal {F}_{t}\right) _{t\in \left[ 0,T\right] }.$ For simplicity, we assume that $\mathcal {F}_{0}$ is trivial. Let $\mathcal {Q}$ denote the set of all equivalent martingale measures. We assume absence of arbitrage in the sense that $\mathcal {Q\ne \varnothing }$.

A self-financing strategy is defined by an initial capital $V_{0}\ge 0$ and by a predictable process $\theta$. Such a strategy $\left( V_{0},\theta \right)$ is called admissible if the process defined by

$$\begin{aligned} V_{t}=V_{0}+\int _{0}^{t}\theta _{s}dX_{s},\text { }\forall t\in \left[ 0,T \right] ,\text { }\mathbb {P}-a.s. \end{aligned}$$

(23)

satisfies

$$\begin{aligned} V_{t}\ge 0,\text { }\forall t\in \left[ 0,T\right] ,\text { }\mathbb {P}-a.s. \end{aligned}$$

(24)

In complete markets, there exists an unique equivalent martingale measure $\mathbb {Q}\approx \mathbb {P}.$ Consider a contingent claim given by an $\mathcal {F}_{t}-$measurable, nonnegative random variable H such that $H\in \mathbb {L}^{1}(\mathbb {Q}).$ Completeness implies the existence of a predictable process $\xi ^{H},$ providing a perfect hedge for H

$$\begin{aligned} \mathbb {E}_{\mathbb {Q}}\left[ H/\mathcal {F}_{t}\right] =H_{0}+\int _{0}^{t} \xi _{s}^{H}dL_{s},\text { }\forall t\in \left[ 0,T\right] ,\text { }\mathbb {P} -a.s., \end{aligned}$$

(25)

where ${\mathbb {E}}_{\mathbb {Q}}$ denotes expectation with respect to ${\mathbb {Q}}$. Thus, the claim can be duplicated by the self-financing trading strategy $\left( H_{0},\xi ^{H}\right) .$ This assumes that we allocate the required initial cost

$$\begin{aligned} H_{0}=\mathbb {E}_{\mathbb {Q}}\left[ H/B(0,T)\right] . \end{aligned}$$

(26)

But if the investor is unwilling to invest the initial capital $H_{0},$ he must choose the best strategy that he can achieve with an initial capital $\widetilde{V_{0}}$ $\le H_{0}.$ given our optimality criterion, founded on the maximization of the probability of success, we must look for a strategy $\left( V_{0},\theta \right)$ such that

$$\begin{aligned} \mathbb {P}\left[ V_{0}+\int _{0}^{T}\theta _{s}dL_{s}\ge H\right] =\max , \end{aligned}$$

(27)

under the constraint

$$\begin{aligned} V_{0}\le \widetilde{V_{0}}. \end{aligned}$$

(28)

In a first step, a set of a maximal probability $\widetilde{A}$ is determined under the constraint that the cost of hedging the given claim on that set, i.e, hedging $H\mathbb {I}_{\widetilde{A}},$ satisfies a given bound $\widetilde{V}_{0}$. The set is constructed using the Neyman-Pearson lemma. In a second step, the knockout option $H\mathbb {I}_{\widetilde{A}}$ is replicated (since the market is complete). This strategy maximizes the probability of a successful hedge. More precisely, let us call the set $\left\{ V_{T}\ge H\right\}$ the success set corresponding to the admissible strategy $\left( V_{0},\theta \right)$ where $V_{T}$ is given by (23).

Let $\widetilde{A}\in \mathcal {F}_{T}$ be a solution of the problem.

$$\begin{aligned} \mathbb {P}\left[ A\right] =\max , \end{aligned}$$

(29)

under the constraint

$$\begin{aligned} \mathbb {E}_{\mathbb {Q}}\left[ H/B(0,T)\mathbb {I}_{A}\right] \le \widetilde{V }_{0}, \end{aligned}$$

(30)

where $\mathbb {Q}$ is the unique equivalent martingale measure. Let $\widetilde{\xi }$ denote the perfect hedge for the knockout option $\widetilde{H}=H\mathbb {I}_{\widetilde{A}}\in \mathbb {L}^{1}(\mathbb {Q}),$ i.e.,

$$\begin{aligned} \mathbb {E}_{\mathbb {Q}}\left[ H/B(0,T)I_{\widetilde{A}}/\mathcal {F}_{t} \right] =\mathbb {E}_{\mathbb {Q}}\left[ H/B(0,T)\mathbb {I}_{\widetilde{A}} \right] +\int _{0}^{t}\widetilde{\xi }_{s}dL_{s},\text { }\forall t\in \left[ 0,T\right] ,\text { }\mathbb {P}-a.s. \end{aligned}$$

(31)

Then $\left( \widetilde{V}_{0},\widetilde{\xi }\right)$ solves the optimization problem defined by (27) and (28), and the corresponding success set coincides almost surely with $\widetilde{A}$ .

The problem of constructing a maximal success set is now solved by applying the Neyman-Pearson lemma. To this end, consider the measure $\widetilde{ \mathbb {P}}$ defined by

$$\begin{aligned} \dfrac{d\widetilde{\mathbb {P}}}{d\mathbb {Q}}=\dfrac{H}{\mathbb {E}_{\mathbb {Q} }[H/B(0,T)]}=\dfrac{H}{H_{0}}. \end{aligned}$$

The constraint (30) can be written as:

$$\begin{aligned} \widetilde{\mathbb {P}}[A]\le \alpha \triangleq \dfrac{\widetilde{V}_{0}}{ H_{0}}. \end{aligned}$$

(32)

Define the level

$$\begin{aligned} \widetilde{a}=\inf \left\{ a:\widetilde{\mathbb {P}}[\dfrac{d\mathbb {P}}{d \mathbb {Q}}>a\text { }H]\le \alpha =\dfrac{\widetilde{V}_{0}}{H_{0}}\right\} , \end{aligned}$$

(33)

and the corresponding set

$$\begin{aligned} \widetilde{A}\triangleq \left\{ \dfrac{d\mathbb {P}}{d\mathbb {Q}}>\widetilde{a }\text { }H\right\} . \end{aligned}$$

(34)

Let us assume that the set $\widetilde{A},$ defined by the two preceeding equations, satisfies

$$\begin{aligned} \widetilde{\mathbb {P}}\left[ \widetilde{A}\right] =\alpha . \end{aligned}$$

(35)

Then the optimal strategy solving (27) and (28) is given by $\left( \widetilde{V}_{0},\widetilde{\xi }\right)$ where $\widetilde{\xi }$ is the perfect hedging of the knockout option $H\mathbb {I}_{\widetilde{A}}.$

Therefore, the problem of quantile hedging is reduced to a more simple problem: to hedge a knockout option. As mentioned in Föllmer and Leukert (1999), Condition (35) is satisfied as soon as

$$\begin{aligned} \mathbb {P}[\dfrac{d\mathbb {P}}{d\mathbb {Q}}=c\text { }H]=0. \end{aligned}$$

(36)

Usually, it is not easy to find any set $A\in \mathcal {F}_{T}$ which assumes the constraint in (32) (i.e. is bounded). In this case, the theory of Neyman-Pearson suggests to replace the critical region $A\in \mathcal {F}_{T}$ by a randomized test, i.e. by a $\mathcal {F}_{T}$ -measurable function $\varphi$ such that $0\le \varphi \le 1.$ Let $\mathcal {R}$ be the class of all these functions and let us consider the problem of optimization:

$$\begin{aligned} \mathbb {E}\left[ \widetilde{\varphi }\right] =\underset{\varphi \in \mathcal { R}}{\max }\mathbb {E}\left[ \varphi \right] , \end{aligned}$$

(37)

under the constraint

$$\begin{aligned} \int \varphi d\widetilde{\mathbb {P}}\le \alpha =\dfrac{\widetilde{V}_{0}}{ H_{0}}. \end{aligned}$$

(38)

The Neyman-Pearson lemma gives the solution as being equal to:

$$\begin{aligned} \widetilde{\varphi }=\mathbb {I}_{\left\{ \frac{d\mathbb {P}}{d\mathbb {Q}}> \widetilde{a}.H\right\} }+\gamma \mathbb {I}_{\left\{ \frac{d\mathbb {P}}{d \mathbb {Q}}=\widetilde{a}.H\right\} }, \end{aligned}$$

(39)

where $\widetilde{a}$ is given by (33) and where $\gamma$ is defined by

$$\begin{aligned} \gamma =\dfrac{\alpha -\widetilde{\mathbb {P}}\left[ \frac{d\mathbb {P}}{d \mathbb {Q}}>\widetilde{a}.H\right] }{\widetilde{\mathbb {P}}\left[ \frac{d \mathbb {P}}{d\mathbb {Q}}=\widetilde{a}.H\right] }, \end{aligned}$$

(40)

in the case where the condition (35) is not verified. Note that, in our framework, the contingent claim H corresponds to the interest rate margin $IRM\left( K_{T},L_{T}\right)$. Thus condition $\frac{d\mathbb {P}}{d \mathbb {Q}}=\widetilde{a}.IRM\left( K_{T},L_{T}\right)$ is equivalent to condition $\eta \left( L_{T}\right) ^{-1}=\widetilde{a}.IRM\left( K_{T},L_{T}\right) .\$Applying our previous results, we have:

$$\begin{aligned} \mathbb {P}\left[ \eta \left( L_{T}\right) ^{-1}=\widetilde{a}.IRM\left( K_{T},L_{T}\right) \right] =0. \end{aligned}$$

Therefore, $\gamma =0$. These results lead to the solution given in Proposition 9.