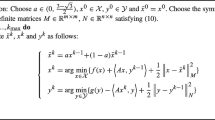Hybrid limited memory gradient projection methods for box-constrained optimization problems

Abstract

Gradient projection methods represent effective tools for solving large-scale constrained optimization problems thanks to their simple implementation and low computational cost per iteration. Despite these good properties, a slow convergence rate can affect gradient projection schemes, especially when high accurate solutions are needed. A strategy to mitigate this drawback consists in properly selecting the values for the steplength along the negative gradient. In this paper, we consider the class of gradient projection methods with line search along the projected arc for box-constrained minimization problems and we analyse different strategies to define the steplength. It is well known in the literature that steplength selection rules able to approximate, at each iteration, the eigenvalues of the inverse of a suitable submatrix of the Hessian of the objective function can improve the performance of gradient projection methods. In this perspective, we propose an automatic hybrid steplength selection technique that employs a proper alternation of standard Barzilai–Borwein rules, when the final active set is not well approximated, and a generalized limited memory strategy based on the Ritz-like values of the Hessian matrix restricted to the inactive constraints, when the final active set is reached. Numerical experiments on quadratic and non-quadratic test problems show the effectiveness of the proposed steplength scheme.

1 Introduction

The subject of this paper is the numerical resolution of the following box-constrained optimization problem

$$\begin{aligned} \begin{aligned}&\min _{x\in {\mathbb {R}}^n} f(x)\\ \text {subject} \,&\text {to} \ \ \ell \le x \le u \end{aligned} \end{aligned}$$

(1)

where $f:{{\mathbb {R}}}^n\longrightarrow {\mathbb {R}}$ is a continuously differentiable function and $\ell , u \in {\mathbb {R}}^n$, with $\ell \le u$. We assume that the feasible set $\Omega = \{x\in {\mathbb {R}}^n \ : \ \ell \le x \le u\}$ is not empty.

Different problems arising from real-life applications, such as signal and image processing, machine learning, compressed sensing, contact problems of elasticity, can be formalized through the optimization model (1), making its study significant (see for instance [1,2,3,4,5,6]).

However, these applications often lead to optimization problems of large or huge size. For this reason, the class of gradient projection (GP) schemes represents a valid tool to face such problems, thanks to their simplicity, computational cheapness and limited storage requirements. In particular, in this paper, we take into account the GP method with a line search along the arc [7] defined by the following iteration

$$\begin{aligned} x^{(k+1)} = P_\Omega \left( x^{(k)} - \alpha _k\nabla f(x^{(k)})\right) , \end{aligned}$$

(2)

where $P_\Omega (\cdot )$ is the projection operator onto the set $\Omega$ and $\alpha _k> 0$ is the steplength parameter chosen in order that the following Armijo-like line search holds [8]:

$$\begin{aligned} \max _{0\le j \le \min \{k,M-1\}} f(x^{(k-j)}) - f(x^{(k+1)})\ge \sigma \nabla f(x^{(k)})^T(x^{(k)}-x^{(k+1)}), \end{aligned}$$

(3)

with $M\ge 1$ and $\sigma \in (0,1)$. We recall that, for $M=1$, the standard Armijo backtracking technique along the curvilinear projected path is considered and a monotone decrease of the objective function is ensured. Otherwise a non-monotone behaviour for the objective function is allowed.

Under different assumptions, the convergence of the sequence of iterates generated by the scheme (2–3) can be proved for both cases $M=1$ [9] and $M\ge 1$ [10, 11].

Moreover, if algorithm (2)-(3) converges to a nondegenerate point of a linearly constrained problem, then the active constraints at the solution are identified in a finite number of iterations [10, 12]. As regards the practical behaviour of GP methods, it is well-known that a proper selection of the steplength values can significantly improve the numerical performance of these algorithms. Indeed, the literature of the last decades provides many attempts of defining good steplength strategies to accelerate the convergence of gradient-like methods in both unconstrained and constrained optimization framework. Papers addressing these issues include but are not limited to [13,14,15,16,17,18,19,20,21,22] for unconstrained problems and [23,24,25,26,27,28,29] in the constrained case.

Most of these proposals share the idea of incorporating second-order information by approximating the reciprocals of the eigenvalues of the Hessian matrix associated to the problem (or a suitable submatrix of the Hessian), at each iteration. In particular, the analysis carried out in [25] for the box-constrained case, highlighted the intrinsic ability of the first Barzilai–Borwein (BB) rule in producing a sequence of steplengths sweeping the spectrum of a submatrix of the Hessian that only depends on the inactive constraints at the current iterate, while a modified version of the second BB rule was proposed, in order to exploit the information prescribed by the first-order optimality conditions. This analysis was extended, in [24], to the case of singly linearly equality constrained minimization problems subject to lower and upper bounds, showing similar results.

The main contribution of this work consists in suggesting a new steplength selection strategy for the GP method (2) equipped with the line search procedure (3) to solve the box-constrained optimization problem (1). To reach this goal we continue the analysis carried out in [25] by taking into account more sophisticated steplength techniques. By deepening the results in [28, 30], we investigate how to employ, in gradient projection methods for box-constrained minimization problems, the so-called limited memory steplength procedures, based on the storage of a prefixed number of past gradients, such as the ones proposed for unconstrained optimization in [18, 21]. In particular, we propose a hybrid steplength selection rule that automatically combines a proper alternation of the modified BB strategies suggested in [25], adopted when the final active set is far to be identified, and the limited memory technique, employed when the sequence generated by the algorithm (2)-(3) provides the same set of active constraints for a suitable number of consecutive iterations. We remark that such hybrid procedure allows to compute steplength values able to approximate the spectrum of the inverse of the Hessian matrix restricted to the indices corresponding to the inactive components of the solution.

In the literature there exist other strategies based on proper switching between different gradient-type methods when the active set of the optimal constraints has been identified: for example, some recent proposals can be found in [31,32,33]. However, our idea is quite different with respect to these approaches since, when the set of active constraints at the solution is well approximated, we do not change the optimization method but only the steplength selection technique.

The paper is organized as follows. In the next section, we recall the BB rules for the selection of the steplength in gradient methods and their recent generalization to GP algorithms for box-constrained problems. We recall also the basic ideas of the limited memory (LM) steplength procedure developed by Fletcher [18] for unconstrained problems. In Sect. 3, we analyse how to extend this procedure to box-constrained minimization problems, highlighting the drawbacks and providing some possible implementations. In Sect. 4, we propose a novel hybrid strategy aimed at employing the LM technique only when the active set has been well approximated. The effectiveness of the approach is evaluated in Sect. 5 for some quadratic test problems and, above all, for non-quadratic test problems. The results of an application concerning the reconstruction of images corrupted by Poisson noise are discussed. Finally, we draw the conclusions in Sect. 6.

Notation. In the following, for a vector x, $\Vert x\Vert$ denotes the Euclidean norm of x; for a matrix A, $\Vert A\Vert$ and $\Vert A\Vert _F$ denote the spectral norm and the Frobenius norm of A, respectively; $\Vert \cdot \Vert _p$, $p\ge 1$ denotes the p-norm of a vector or a matrix; $I_n$ denotes the identity matrix of order n. The simbol $\sharp S$ denotes the cardinality of a set S. Finally, with the notion of spectrum of a matrix, we mean the interval whose bounds are the minimum and the maximum eigenvalues of the matrix itself.

2 Some efficient state-of-the-art steplength rules for gradient-based methods

In this section, we recall some successful steplength selection rules often employed for gradient methods when $\Omega ={\mathbb {R}}^n$, and their recent generalization to gradient projection algorithms.

The pioneering paper on effective steplength selection techniques in gradient algorithms for unconstrained optimization was published in 1988 by Barzilai and Borwein [13]. They suggest to select $\alpha _k$ by forcing quasi-Newton properties on the diagonal matrix $\frac{1}{\alpha _{k+1}}I_n$ to approximate the Hessian matrix $\nabla ^2 f(x^{(k)})$. In more detail, the BB steplength updating rules have to satisfy the following secant conditions

$$\begin{aligned} \begin{aligned} \alpha _{k+1}^{\text {BB1}}&={\mathop {\mathrm{argmin}}\limits _{\alpha \in {\mathbb {R}}}} \Vert \alpha ^{-1} s^{(k)} - y^{(k)}\Vert \\ \alpha _{k+1}^{\text {BB2}}&= {\mathop {\mathrm{argmin}}\limits _{\alpha \in {\mathbb {R}}}} \Vert {s}^{(k)} -\alpha y^{(k)}\Vert , \end{aligned} \end{aligned}$$

(4)

where ${s}^{(k)} = {x}^{(k+1)} - {x}^{(k)}$ and ${y}^{(k)} = \nabla f({x}^{(k+1)})-\nabla f({x}^{(k)})$. The resulting values become

$$\begin{aligned} \alpha _{k+1}^{\text {BB1}} = \frac{{{s}^{(k)}}^T{s}^{(k)}}{{{s}^{(k)}}^T{y}^{(k)}} \qquad ; \qquad \alpha _{k+1}^{\text {BB2}} = \frac{{{s}^{(k)}}^T{y}^{(k)}}{{{y}^{(k)}}^T{y}^{(k)}}. \end{aligned}$$

(5)

When the objective function f in (1) has the form

$$\begin{aligned} f(x)\equiv \frac{1}{2} x^T A x -b^T x+c, \end{aligned}$$

(6)

where $b\in {\mathbb {R}}^n$, $c\in {\mathbb {R}}$ and $A\in {\mathbb {R}}^{n\times n}$ is a symmetric and positive definite matrix, the BB rules (5) provide values belonging to the spectrum of the inverse of A since they satisfy the following inequalities

$$\begin{aligned} \frac{1}{\lambda _{\text {max}}(A)}\le \alpha _{k+1}^{\text {BB2}} \le \alpha _{k+1}^{\text {BB1}} \le \frac{1}{\lambda _{\text {min}}(A)} \end{aligned}$$

(7)

with $\lambda _{\text {min}}(A)$ and $\lambda _{\text {max}}(A)$ denoting the minimum and the maximum eigenvalues of A, respectively. In [34], the author firstly shows how, in the unconstrained quadratic case, the effectiveness of a steplength rule within a gradient method is essentially related to its ability to properly sweep the spectrum of the inverse of the underlying Hessian. Such property has been studied for both quadratic and non-quadratic problems [17, 19, 35, 36] and, based on it, effective steplength rules have been proposed [15, 16, 19, 20, 22]. Most of them exploit suitable adaptive alternation of the two BB schemes to switch from small to large steplengths during the iterations.

In [25] a spectral analysis of the BB steplength rules in GP methods for box-constrained strictly convex quadratic problems has been developed. The authors clarify that, in this setting, the goal is no more the approximation of the eigenvalues of the inverse of the Hessian matrix related to the optimization problem, but the approximation of the spectrum of the inverse of the Hessian submatrix restricted to those indices corresponding to the inactive constraints at the solution. In the following, we refer to this Hessian submatrix as the restricted Hessian matrix at the solution. Since the indices related to the inactive constraints at the solution are not a priori known, in [25] the authors introduce the following sets of indices

$$\begin{aligned} \begin{aligned} {\mathcal {J}}_{k}&=\{i \in {\mathcal {N}}: (x_i^{(k)}=\ell _i \wedge x_i^{(k+1)}=\ell _i) \vee (x_i^{(k)}=u_i \wedge x_i^{(k+1)}=u_i)\}\, ,\\ {\mathcal {I}}_{k}&={\mathcal {N}}\setminus {\mathcal {J}}_{k}, \quad {\mathcal {N}}=\{1,...,n\}, \end{aligned} \end{aligned}$$

(8)

and focus on the estimate of the spectrum of the inverse of $A_{{\mathcal {I}}_{k},{\mathcal {I}}_{k}}$, where $A_{{\mathcal {I}}_{k},{\mathcal {I}}_{k}}$ is the submatrix of the Hessian of the objective function given by the intersection of the rows and the columns with indices in ${\mathcal {I}}_{k}$. Hereafter, we refer to this submatrix as the Hessian matrix restricted to the set ${\mathcal {I}}_{k}$. Assuming nondegeneracy of the solution, the sets ${\mathcal {I}}_{k}$ generated along the iterative process tend to stabilize (see [10, 12]), i.e., after a finite number of iterations their size and their elements do not change, yielding the restricted Hessian matrix at the solution. By denoting with $s_{{\mathcal {I}}_{k}}^{(k)}$ and $y_{{\mathcal {I}}_{k}}^{(k)}$ the subvectors of $s^{(k)}$ and $y^{(k)}$ whose components are indexed in ${\mathcal {I}}_{k}$ and introducing the modified BB2 steplength rule

$$\begin{aligned} \alpha _{k+1}^{\text {BOX-BB2}} = \frac{{s_{{\mathcal {I}}_{k}}^{(k)}}^Ty_{{\mathcal {I}}_{k}}^{(k)}}{\Vert y_{{\mathcal {I}}_{k}}^{(k)}\Vert ^2}, \end{aligned}$$

(9)

the following inequalities are proved [25]:

$$\begin{aligned} \frac{1}{ \lambda _{\text {max}}(A_{{\mathcal {I}}_{k},{\mathcal {I}}_{k}})}\le \alpha _{k+1}^{\text {BOX-BB2}}\le \alpha _{k+1}^{\text {BB1}}\le \frac{1}{\lambda _{\text {min}}(A_{{\mathcal {I}}_{k},{\mathcal {I}}_{k}})}\,. \end{aligned}$$

(10)

Conditions (10) generalize (7) to the case of box-constrained quadratic programming problems.

In this paper we want to make a step further and consider more sophisticated steplength selection strategies which have been proved to be very promising in the unconstrained optimization framework, for both the quadratic and the non-quadratic cases. In particular, we take into account the limited memory (LM) steplength procedure developed by Fletcher in [18] and, in the next sections, we investigate the possibility of generalizing it to box-constrained minimization problems. We briefly recall here the main ideas on which the steplength selection rule suggested in [18] is based. Given a strictly convex unconstrained quadratic optimization problem with Hessian matrix A, the starting point of [18] is to apply m steps of the Lanczos iterative process to A in order to obtain m approximations of its eigenvalues. In more detail, given an integer $m\ge 1$ and a starting vector $q_1 = \nabla f(x^{(k)})/\Vert \nabla f(x^{(k)})\Vert$, the Lanczos process generates orthonormal n-vectors $\{q_1,q_2,\dots ,q_m\}$ such that $Q_k=[q_1,q_2,\dots ,q_m]$ satisfies $Q_k^TQ_k = I_m$ and $T_k=Q_k^TAQ_k$ is a tridiagonal matrix whose eigenvalues, called Ritz values, are approximations of m eigenvalues of A. The inverses of the m eigenvalues of the matrix $T_k$ are employed as steplengths for the successive m iterations. Each group of m iterations is called sweep. The matrix $T_k$ can be computed without involving the matrix A explicitly. To reach this goal, some preliminary considerations are needed. First of all, if $\Omega ={\mathbb {R}}^n$, the iteration defining the GP method (2) for a strictly convex quadratic optimization problem with Hessian matrix A implies that the gradient vectors recur as follows

$$\begin{aligned} \nabla f(x^{(k+1)}) = \nabla f(x^{(k)}) - \alpha _k A \nabla f(x^{(k)}). \end{aligned}$$

(11)

If a limited number m of back values of the gradient vectors

$$\begin{aligned} {G_k} = [\nabla f(x^{(k)}) \ \nabla f(x^{(k+1)}) \ \dots \ \nabla f(x^{(k+m-1)})] \end{aligned}$$

is stored and the $(m+1)\times m$ matrix $J_k$ containing the inverses of the corresponding last m steplengths is considered

$$\begin{aligned} {J_k}= \left( \begin{array}{lll} \frac{1}{\alpha _{k}} &{} &{} \\ -\frac{1}{\alpha _{k}} &{} \ddots &{}\\ &{}\ddots &{} \frac{1}{\alpha _{k+m-1}}\\ &{} &{} - \frac{1}{\alpha _{k+m-1}} \end{array}\right) \, , \end{aligned}$$

then the Eq. (11) can be rewritten in matrix form as

$$\begin{aligned} A {G_k} = [{G_k}, \; \nabla f(x^{(k+m)})] {J_k}. \end{aligned}$$

(12)

Secondly, by taking into account (11), assuming $G_k$ is full-rank and that its columns are in the space generated by the Krylov sequence $\left\{ \nabla f(x^{(k)}),\ A\nabla f(x^{(k)}), \ A^2\nabla f(x^{(k)}),\ \dots ,\ A^{m-1}\nabla f(x^{(k)}) \right\}$, we have $G_k = Q_k R_k$, where $R_k$ is $m\times m$ non-singular upper triangular matrix. Actually, the matrix $R_k$ can be obtained from the Cholesky factorization of $G_k^T G_k$. From both (12) and $G_k^T G_k = R_k^T R_k$, the tridiagonal matrix $T_k$ can be written as

$$\begin{aligned} T_k&= Q_k^T A Q_k = R_k^{-T}G_k^T A G_k R_k^{-1} \nonumber \\&= R_k^{-T}G_k^T [G_k \ \nabla f(x^{(k+m)})] J_k R_k^{-1}\nonumber \\&= [R_k \ r_k] J_k R_k^{-1}, \end{aligned}$$

(13)

where the vector $r_k$ is the solution of the linear system $R_k^{T}r_k = G_k^T\nabla f(x^{(k+m)})$. We remark that, if $m=1$, the matrix $T_k$ reduces to a scalar equal to the inverse of the value $\alpha _{k+1}^{\text {BB1}}$.

Very recently, again for solving unconstrained strictly convex quadratic programming problems by gradient methods, a modified limited memory (MLM) steplength strategy has been proposed in [21]. The authors suggest a way to properly select, at each iteration, a unique steplength among the m values computed through the standard LM procedure previously described, instead of employing all of them as steplengths for the next m iterations. The MLM steplength rule has been proved to outperform the standard LM one in several numerical experiments on unconstrained strictly convex quadratic optimization problems.

In Sect. 3 we analyze how the LM steplength selection procedure can be generalized to the case of GP methods equipped with the non-monotone line search along the arc (3) for box-constrained optimization problems and we discuss the impact of these generalizations. Particularly, we show that the LM scheme becomes effective in approximating the spectrum of the inverse of the restricted Hessian matrix at the solution only if both the active and the inactive components of the iterates are stable for a sufficient number of successive steps of the iterative process. Analogous considerations hold for the generalitazion to the box-constrainted framework of the MLM technique, since its is based on the same ideas which motivate the LM strategy.

3 Generalized limited memory steplength selection rules

Developing suitable steplength selection strategies for algorithm (2)-(3) means to find proper values for the first trial steplength needed to initialize the backtracking procedure (3), in order to eliminate, or at least to reduce, the backtracking steps ensuring the sufficient decrease of the objective function. To reach this goal, we firstly analyse which difficulties arise in the generalization of the standard LM steplength procedure to GP methods along the arc applied to box-constrained optimization problems. In particular, we study if the LM idea can be borrowed in order to generate m approximations of the eigenvalues of the objective function Hessian matrix restricted to those indices corresponding to the inactive components at the solution. A first attempt to achieve this target has been carried out in [28, 30] for GP methods equipped with a line search along the feasible direction. In the following we propose a detailed analysis for the GP method with line search along the projection arc, that deserves an ad hoc study due to its intrinsic differences with respect to the case in which the line search along the feasible direction is used. Moreover, our analysis allows us to understand how to define a new effective steplength selection rule.

Hereafter we indicate by $g^{(k)}$ the gradient of the objective function at $x^{(k)}$, namely $g^{(k)}\equiv \nabla f(x^{(k)})$. Consider the following set of indices

$$\begin{aligned} \begin{aligned} {\mathcal {F}}_{k+1}&=\{ i \ :\ \ell _i< {\underbrace{x_i^{(k)}-\alpha _k g_i^{(k)}}_{=\, x_i^{(k+1)}}< u_i\}}\\ {\mathcal {B}}_{k+1}&={\mathcal {N}}\setminus {{\mathcal {F}}_{k+1}}, \quad \hbox {with} \quad {\mathcal {N}}=\{1,...,n\} \end{aligned} \end{aligned}$$

(14)

in order to distinguish the cases where the projection onto the feasible set is computed from the cases where it has no effect on the components of the current iterate $x^{(k+1)}$. We introduce ${\mathcal {F}}_{k+1}$ to identify the components $x^{(k+1)}_i$ generated by the GP algorithm (2) which are simply updated as

$$\begin{aligned} x^{(k+1)}_i = x^{(k)}_i- \alpha _k g_i^{(k)}. \end{aligned}$$

In detail, the entries of the iterate $x^{(k+1)}$ generated by the GP method (2) are

$$\begin{aligned} x_i^{(k+1)} = \left\{ \begin{array}{lcr} x_i^{(k)} - \alpha _k g_i^{(k)} &{}\qquad \qquad &{} i \in {\mathcal {F}}_{k+1},\\ \gamma _i^{(k+1)} &{}\qquad \qquad &{}i \in {\mathcal {B}}_{k+1}, \end{array} \right. \end{aligned}$$

(15)

where

$$\begin{aligned} \gamma _i^{(k+1)} = \left\{ \begin{array}{lcr} \ell _i &{}\qquad \qquad &{} x_i^{(k)} - \alpha _k g_i^{(k)} \le \ell _i, \\ u_i &{}\qquad \qquad &{} x_i^{(k)} - \alpha _k g_i^{(k)} \ge u_i. \end{array} \right. \end{aligned}$$

Like in [18, 21], our theoretical analysis is carried out for quadratic objective functions, even if the practical implementations of the generalized LM steplength rule suggested in Section 3.3 can be formally employed for general optimization problems.

We now focus on the strictly convex quadratic case (6). In the sequel, we call the submatrices $A_{{\mathcal {F}}_{k+1},{\mathcal {F}}_{k+1}}$, which are obtained by restricting A to the intersection of the rows and the columns with indices in ${\mathcal {F}}_{k+1}$, the Hessian matrices restricted to the set ${\mathcal {F}}_{k+1}$. We remark that, like for the sequence $\{{\mathcal {I}}_{k}\}$ previously mentioned, in presence of a nondegenerate solution, the sets ${\mathcal {F}}_{k+1}$ and the relative submatrices $A_{{\mathcal {F}}_{k+1},{\mathcal {F}}_{k+1}}$ tend to stabilize along the iterative process, i.e., after a suitable numbers of iterations, they do not change anymore, by devising the restricted Hessian matrix at a solution.

3.1 Generalized Barzilai–Borwein rules: the case $m=1$

We firstly provide some considerations useful to understand how, for $m=1$, the limited memory steplength strategy previously discussed can be generalized to the GP method (2)-(3). We recall that, in the unconstrained case, the steplength strategy with $m=1$ produces the value $\frac{1}{\alpha _{k+1}^{\text {BB1}}}$. We introduce the vector $s^{(k)}$ which, by components, is defined as

$$\begin{aligned} s_i^{(k)} = x^{(k+1)}_i - x^{(k)}_i = \left\{ \begin{array}{lcr} -\alpha _{k} g_i^{(k)} &{}\qquad \qquad &{} i \in {\mathcal {F}}_{k+1},\\ \gamma _i^{(k+1)} - x_i^{(k)} &{}\qquad \qquad &{} i \in {\mathcal {B}}_{k+1}. \end{array} \right. \end{aligned}$$

(16)

We now consider the vector $y^{(k)} = g^{(k+1)} - g^{(k)}$. Thanks to (16), any entry $y_i^{(k)}$, $i=1,\dots ,n$ can be written as

$$\begin{aligned} \begin{aligned} y_i^{(k)}&= \sum _{j=1}^n a_{ij}x_j^{(k+1)} - \sum _{j=1}^n a_{ij}x_j^{(k)} \\&=\sum _{j\in {\mathcal {F}}_{k+1}}a_{ij}(-\alpha _kg_j^{(k)}) + \sum _{j\in {\mathcal {B}}_{k+1}}a_{ij}(\gamma _j^{(k+1)} - x_j^{(k)})\\&= \sum _{j\in {\mathcal {F}}_{k+1}}a_{ij}s_j^{(k)} + \sum _{j\in {\mathcal {B}}_{k+1}}a_{ij}s_j^{(k)} \end{aligned} \end{aligned}$$

(17)

Remark 1

If $s^{(k)}_{{\mathcal {B}}_{k+1}} = 0$, equation (17) allows to write the following recurrence formula

$$\begin{aligned} g_{{\mathcal {F}}_{k+1}}^{(k+1)} = g_{{\mathcal {F}}_{k+1}}^{(k)} -\alpha _k A_{{\mathcal {F}}_{k+1},{\mathcal {F}}_{k+1}}g_{{\mathcal {F}}_{k+1}}^{(k)}. \end{aligned}$$

By denoting with $\{\delta _1,\dots ,\delta _{r}\}$ and $\{w_1,\dots ,w_r\}$ the eigenvalues and the associated orthonormal eigenvectors of $A_{{\mathcal {F}}_{k+1},{\mathcal {F}}_{k+1}}$, respectively, where $r=\sharp {\mathcal {F}}_{k+1}$, and by writing $g_{{\mathcal {F}}_{k+1}}^{(k+1)} = \sum _{i=1}^{r}{\bar{\mu }}_i^{(k+1)} w_i$ and $g_{{\mathcal {F}}_{k+1}}^{(k)} = \sum _{i=1}^{r}{\bar{\mu }}_i^{(k)} w_i$, we obtain the following recurrence formula for the eigencomponents:

$$\begin{aligned} {\bar{\mu }}_i^{(k+1)} = {\bar{\mu }}_i^{(k)} (1-\alpha _k\delta _i). \end{aligned}$$

This means that if the selection rule provides a good approximation of $\frac{1}{\delta _i}$, a useful reduction of $|{\bar{\mu }}_i^{(k+1)}|$ can be achieved. As a consequence, in general, efficient steplength selection strategies must aim at approximating the eigenvalues of $A_{{\mathcal {F}}_{k+1},{\mathcal {F}}_{k+1}}^{-1}$.

Theorem 1

If $s^{(k)}_{{\mathcal {B}}_{k+1}} = 0$ then

$$\begin{aligned} \lambda _{\text {min}}(A_{{\mathcal {F}}_{k+1},{\mathcal {F}}_{k+1}}) \le \frac{{s^{(k)}_{{\mathcal {F}}_{k+1}}}^T{y^{(k)}_{{\mathcal {F}}_{k+1}}}}{{s^{(k)}_{{\mathcal {F}}_{k+1}}}^T{s^{(k)}_{{\mathcal {F}}_{k+1}}}}\le \lambda _{\text {max}}(A_{{\mathcal {F}}_{k+1},{\mathcal {F}}_{k+1}}) \end{aligned}$$

where $\lambda _{\text {min}}(A_{{\mathcal {F}}_{k+1},{\mathcal {F}}_{k+1}})$ and $\lambda _{\text {max}}(A_{{\mathcal {F}}_{k+1},{\mathcal {F}}_{k+1}})$ are the minimum and the maximum eigenvalues of $A_{{\mathcal {F}}_{k+1},{\mathcal {F}}_{k+1}}$, respectively.

Proof

Taking into account (16), (17) and the assumption $s^{(k)}_{{\mathcal {B}}_{k+1}} = 0$, we have

$$\begin{aligned} {s^{(k)}_{{\mathcal {F}}_{k+1}}}^T{y^{(k)}_{{\mathcal {F}}_{k+1}}}&= -\alpha _{k} {g^{(k)}_{{\mathcal {F}}_{k+1}}}^T\left( A_{{\mathcal {F}}_{k+1},{\mathcal {F}}_{k+1}}(-\alpha _kg^{(k)}_{{\mathcal {F}}_{k+1}}) + A_{{\mathcal {F}}_{k+1},{\mathcal {B}}_{k+1}}s_{{\mathcal {B}}_{k+1}}^{(k)}\right) \\&= \alpha _k^2{g^{(k)}_{{\mathcal {F}}_{k+1}}}^TA_{{\mathcal {F}}_{k+1},{\mathcal {F}}_{k+1}}g^{(k)}_{{\mathcal {F}}_{k+1}}. \end{aligned}$$

Since

$$\begin{aligned} {s^{(k)}_{{\mathcal {F}}_{k+1}}}^T {s^{(k)}_{{\mathcal {F}}_{k+1}}}= \alpha _{k}^2{g^{(k)}_{{\mathcal {F}}_{k+1}}}^Tg^{(k+1)}_{{\mathcal {F}}_{k+1}} \end{aligned}$$

the thesis easily follows. $\square$

In view of Theorem 1, we define the following generalization of the first Barzilai–Borwein rule:

$$\begin{aligned} \alpha ^{\text {G-BB1}}_{{k+1}} = \frac{{s^{(k)}_{{\mathcal {F}}_{k+1}}}^T{s^{(k)}_{{\mathcal {F}}_{k+1}}}}{{s^{(k)}_{{\mathcal {F}}_{k+1}}}^T{y^{(k)}_{{\mathcal {F}}_{k+1}}}}. \end{aligned}$$

(18)

Furthermore, we observe that, if $s^{(k)}_{{\mathcal {B}}_{k+1}} = 0$, considerations analogous to the ones made in Theorem 1 hold for

$$\begin{aligned} \alpha ^{\text {G-BB2}}_{{k+1}}=\frac{{s^{(k)}_{{\mathcal {F}}_{k+1}}}^T{y^{(k)}_{{\mathcal {F}}_{k+1}}}}{{y^{(k)}_{{\mathcal {F}}_{k+1}}}^T{y^{(k)}_{{\mathcal {F}}_{k+1}}}}. \end{aligned}$$

(19)

In particular, if $s^{(k)}_{{\mathcal {B}}_{k+1}} = 0$, it holds that

$$\begin{aligned} \frac{1}{\lambda _{\text {max}}(A_{{\mathcal {F}}_{k+1},{\mathcal {F}}_{k+1}})} \le \alpha ^{\text {G-BB2}}_{{k+1}} \le \alpha ^{\text {G-BB1}}_{{k+1}} \le \frac{1}{\lambda _{\text {min}}(A_{{\mathcal {F}}_{k+1},{\mathcal {F}}_{k+1}})}. \end{aligned}$$

The approach we follow to obtain (18) and (19) is very similar to the one proposed in [25]. However, in [25] the authors select the different set of indices (8) to which the vectors are restricted. Moreover, it is obvious from the definitions (8) and (14) that ${\mathcal {F}}_{k+1}\subseteq {\mathcal {I}}_{k}$ and, hence, the spectrum of $A_{{\mathcal {F}}_{k+1}, {\mathcal {F}}_{k+1}}$ is contained in the one of $A_{{\mathcal {I}}_k,{\mathcal {I}}_k}$. Nevertheless, we remark that, if $s^{(k)}_{{\mathcal {B}}_{k+1}} = 0$ and ${\mathcal {I}}_k={\mathcal {F}}_{k+1}$, then (18) and (19) correspond to the two generalized Barzilai-Borwein rules developed in [25].

When $s^{(k)}_{{\mathcal {B}}_{k+1}} \ne 0$, from (17) we observe that

$$\begin{aligned} \frac{{s^{(k)}_{{\mathcal {F}}_{k+1}}}^T{y^{(k)}_{{\mathcal {F}}_{k+1}}}}{{s^{(k)}_{{\mathcal {F}}_{k+1}}}^T{s^{(k)}_{{\mathcal {F}}_{k+1}}}}= \frac{{s^{(k)}_{{\mathcal {F}}_{k+1}}}^T A_{{\mathcal {F}}_{k+1},{\mathcal {F}}_{k+1}} {s^{(k)}_{{\mathcal {F}}_{k+1}}}}{{s^{(k)}_{{\mathcal {F}}_{k+1}}}^T{s^{(k)}_{{\mathcal {F}}_{k+1}}}}+ \frac{{s^{(k)}_{{\mathcal {F}}_{k+1}}}^T A_{{\mathcal {F}}_{k+1},{\mathcal {B}}_{k+1}} {s^{(k)}_{{\mathcal {B}}_{k+1}}}}{{s^{(k)}_{{\mathcal {F}}_{k+1}}}^T{s^{(k)}_{{\mathcal {F}}_{k+1}}}}. \end{aligned}$$

(20)

hence, the scalar $\displaystyle \frac{1}{\alpha _{{k+1}}^{\text {G-BB1}}}=\frac{{s^{(k)}_{{\mathcal {F}}_{k+1}}}^T{y^{(k)}_{{\mathcal {F}}_{k+1}}}}{{s^{(k)}_{{\mathcal {F}}_{k+1}}}^T{s^{(k)}_{{\mathcal {F}}_{k+1}}}}$ differs from the Rayleigh quotient of $A_{{\mathcal {F}}_{k+1},{\mathcal {F}}_{k+1}}$ at $s^{(k)}_{{\mathcal {F}}_{k+1}}$ (which falls within the spectrum of the matrix $A_{{\mathcal {F}}_{k+1},{\mathcal {F}}_{k+1}}$) by a quantity equal to $\displaystyle \frac{{s^{(k)}_{{\mathcal {F}}_{k+1}}}^T A_{{\mathcal {F}}_{k+1},{\mathcal {B}}_{k+1}} {s^{(k)}_{{\mathcal {B}}_{k+1}}}}{{s^{(k)}_{{\mathcal {F}}_{k+1}}}^T{s^{(k)}_{{\mathcal {F}}_{k+1}}}}$.

In more detail, from the Cauchy-Schwarz inequality, we can write

$$\begin{aligned} \Bigg |\frac{ {s^{(k)}_{{\mathcal {F}}_{k+1}}}^T y^{(k)}_{{\mathcal {F}}_{k+1}} }{ {s^{(k)}_{{\mathcal {F}}_{k+1}}}^T s^{(k)}_{{\mathcal {F}}_{k+1}} } - \frac{ {s^{(k)}_{{\mathcal {F}}_{k+1}}}^T A_{{\mathcal {F}}_{k+1},{\mathcal {F}}_{k+1}} s^{(k)}_{{\mathcal {F}}_{k+1}} }{ {s^{(k)}_{{\mathcal {F}}_{k+1}}}^T s^{(k)}_{{\mathcal {F}}_{k+1}} } \Bigg |&=\frac{\Big |{s^{(k)}_{{\mathcal {F}}_{k+1}}}^T A_{{\mathcal {F}}_{k+1},{\mathcal {B}}_{k+1}} {s^{(k)}_{{\mathcal {B}}_{k+1}}}\Big |}{\Vert s^{(k)}_{{\mathcal {F}}_{k+1}}\Vert ^2}\nonumber \\&\le \frac{\Vert A_{{\mathcal {F}}_{k+1},{\mathcal {B}}_{k+1}} s^{(k)}_{{\mathcal {B}}_{k+1}}\Vert }{\Vert s^{(k)}_{{\mathcal {F}}_{k+1}} \Vert }\nonumber \\&\le \Vert A_{{\mathcal {F}}_{k+1},{\mathcal {B}}_{k+1}}\Vert \frac{\Vert s^{(k)}_{{\mathcal {B}}_{k+1}}\Vert }{\Vert s^{(k)}_{{\mathcal {F}}_{k+1}} \Vert } \nonumber \\&\le {\sqrt{\Vert A_{{\mathcal {F}}_{k+1},{\mathcal {B}}_{k+1}}\Vert _1 \Vert A_{{\mathcal {F}}_{k+1},{\mathcal {B}}_{k+1}}\Vert _\infty } \frac{\Vert s^{(k)}_{{\mathcal {B}}_{k+1}}\Vert }{\Vert s^{(k)}_{{\mathcal {F}}_{k+1}} \Vert } }\nonumber \\&\le {\Vert A\Vert _1 \frac{\Vert s^{(k)}_{{\mathcal {B}}_{k+1}}\Vert }{\Vert s^{(k)}_{{\mathcal {F}}_{k+1}} \Vert } }. \end{aligned}$$

(21)

To conclude, the generalized rules (18) and (19) do not always ensure that the generated value belongs to the spectrum of the matrix $A_{{\mathcal {F}}_{k+1},{\mathcal {F}}_{k+1}}^{-1}$; however, in view of (21), it is possible to control the distance from the spectrum of $A_{{\mathcal {F}}_{k+1},{\mathcal {F}}_{k+1}}$. Indeed, if an estimate $\delta$ of $\Vert A\Vert _1$ is known, by fixing a value $\epsilon >0$ so that $\delta \epsilon$ is very small, then, when $\frac{\Vert s^{(k)}_{{\mathcal {B}}_{k+1}}\Vert }{\Vert s^{(k)}_{{\mathcal {F}}_{k+1}} \Vert }\le \epsilon$, $\alpha _{k+1}^{\text {G-BB1}}$ can be considered a good trial steplength. Similar considerations hold for $\alpha _{{k+1}}^{\text {G-BB2}}$.

3.2 Generalized LM rule: the case $m>1$

In this section we consider a possible generalization of the LM steplength strategy proposed in [18] to the GP method (2)-(3) for a generic $m>1$. It is useful to give the following definition which will be used for the considerations of this section.

Definition 1

Given the sets ${\mathcal {B}}_j = \{i\in {\mathcal {N}}: \ x_i^{(j)} = \ell _i \ \vee \ x_i^{(j)} = u_i\}$ and ${\mathcal {B}}_h = \{i\in {\mathcal {N}}: \ x_i^{(h)} = \ell _i \ \vee \ x_i^{(h)} = u_i\}$, they are called consistent if ${\mathcal {B}}_j \subseteq {\mathcal {B}}_h$ and $\{i \ : \ x_i^{(j)} = \ell _i\} \subseteq \{i \ : \ x_i^{(h)} = \ell _i\}$ and $\{i \ : \ x_i^{(j)} = u_i\} \subseteq \{i \ : \ x_i^{(h)} = u_i\}$.

Now, we observe that, for any $i = 1, \dots , n$, the new gradient components are given by

$$\begin{aligned} g_i^{(k+1)}&= \sum _{j=1}^n a_{ij}x_j^{(k+1)} - b_i = \sum _{j\in {\mathcal {F}}_{k+1}} a_{ij}(x_j^{(k)} - \alpha _kg_j^{(k)}) + \sum _{j\in {\mathcal {B}}_{k+1}} a_{ij}\gamma _j^{(k+1)} - b_i \nonumber \\&= \sum _{j\in {\mathcal {F}}_{k+1}} a_{ij}(x_j^{(k)} - \alpha _kg_j^{(k)}) + \sum _{j\in {\mathcal {B}}_{k+1}} a_{ij}\gamma _j^{(k+1)} - b_i + \sum _{j\in {\mathcal {B}}_{k+1}}a_{ij}x_j^{(k)} - \sum _{j\in {\mathcal {B}}_{k+1}}a_{ij}x_j^{(k)} \nonumber \\&= g_i^{(k)} - \alpha _k\sum _{j\in {\mathcal {F}}_{k+1}}a_{ij}g_j^{(k)} + \sum _{j\in {\mathcal {B}}_{k+1}}a_{ij}(\gamma _j^{(k+1)} - x_j^{(k)})\nonumber \\&= g_i^{(k)} - \alpha _k\sum _{j\in {\mathcal {F}}_{k+1}}a_{ij}g_j^{(k)} + \sum _{j\in {\mathcal {B}}_{k+1}}a_{ij} s_j^{(k)} \end{aligned}$$

(22)

From equation (22) we can write

$$\begin{aligned} A_{{\mathcal {F}}_{k+1},{\mathcal {F}}_{k+1}} g_{{\mathcal {F}}_{k+1}}^{(k)} = \begin{bmatrix} g_{{\mathcal {F}}_{k+1}}^{(k)},&g_{{\mathcal {F}}_{k+1}}^{(k+1)}\end{bmatrix} \begin{bmatrix} \frac{1}{\alpha _k } \\ - \frac{1}{\alpha _k} \end{bmatrix} + \frac{1}{\alpha _k}A_{{\mathcal {F}}_{k+1},{\mathcal {B}}_{k+1}} s_{{\mathcal {B}}_{k+1}}^{(k)}. \end{aligned}$$

(23)

At the next iteration, using the same argument employed to obtain (23), we get

$$\begin{aligned} A_{{\mathcal {F}}_{k+2},{\mathcal {F}}_{k+2}} g_{{\mathcal {F}}_{k+2}}^{(k+1)}= & {} \begin{bmatrix} g_{{\mathcal {F}}_{k+2}}^{(k+1)},&g_{{\mathcal {F}}_{k+2}}^{(k+2)}\end{bmatrix} \begin{bmatrix} \frac{1}{\alpha _{k+1}} \\ - \frac{1}{\alpha _{k+1}} \end{bmatrix} +\frac{1}{\alpha _{k+1}} A_{{\mathcal {F}}_{k+2},{\mathcal {B}}_{k+2}} s_{{\mathcal {B}}_{k+2}}^{(k+1)} \end{aligned}$$

(24)

with the obvious definitions for ${\mathcal {F}}_{k+2}$ and ${\mathcal {B}}_{k+2}$. At this point, we consider the following subsets of indices by taking into account all the possible cases that may occur

$$\begin{aligned} {\mathcal {F}}_{(k+1,k+2)}&:= {\mathcal {F}}_{k+1} \cap {\mathcal {F}}_{k+2}, \\ {\overline{{\mathcal {F}}}^{k+1}_{(k+1,k+2)}}&:= {\mathcal {F}}_{k+1} \setminus \left( {\mathcal {F}}_{k+1} \cap {\mathcal {F}}_{k+2}\right) ,\\ {\overline{{\mathcal {F}}}^{k+2}_{(k+1,k+2)}}&:= {\mathcal {F}}_{k+2} \setminus \left( {\mathcal {F}}_{k+1} \cap {\mathcal {F}}_{k+2}\right) . \end{aligned}$$

Assuming that ${\mathcal {F}}_{k+1} \cap {\mathcal {F}}_{k+2}\ne \emptyset$, our aim is to understand which conditions have to be satisfied in order to obtain a recurrence formula for the gradient vectors as in (12), but restricted to the set of indices ${\mathcal {F}}_{(k+1,k+2)}$. Indeed this set is the candidate on which the box-constrained generalization of the LM steplength rule can be restricted in the case $m=2$. However, to do so, a generalized recurrence formula for the gradient vectors must hold to guarantee that their components restricted to ${\mathcal {F}}_{(k+1,k+2)}$ belong to the space generated by the Krylov sequence $\{g^{(k)}_{{\mathcal {F}}_{(k+1,k+2)}}, A_{{\mathcal {F}}_{(k+1,k+2)},{\mathcal {F}}_{(k+1,k+2)}}{g^{(k)}_{{\mathcal {F}}_{(k+1,k+2)}}}\}$.

From (23) and (24), we may write

$$\begin{aligned} \begin{aligned}&A_{{\mathcal {F}}_{(k+1,k+2)},{\mathcal {F}}_{(k+1,k+2)}} \begin{bmatrix} g_{{\mathcal {F}}_{(k+1,k+2)}}^{(k) },&g_{{\mathcal {F}}_{(k+1,k+2)}}^{(k+1)}\end{bmatrix} =\\&\quad \ =\begin{bmatrix} g_{{\mathcal {F}}_{(k+1,k+2)}}^{(k) },&g_{{\mathcal {F}}_{(k+1,k+2)}}^{(k+1)},&g_{{\mathcal {F}}_{(k+1,k+2)}}^{(k+2) }\end{bmatrix} \begin{bmatrix} \frac{1}{\alpha _{k}} &{} 0\\ - \frac{1}{\alpha _{k}} &{} \frac{1}{\alpha _{k+1}} \\ 0 &{} -\frac{1}{\alpha _{k+1}} \end{bmatrix} +\\&\qquad \ + \begin{bmatrix} A_{{\mathcal {F}}_{(k+1,k+2)},{\mathcal {B}}_{k+1}} \frac{s_{{\mathcal {B}}_{k+1}}^{(k)}}{\alpha _k},&A_{{\mathcal {F}}_{(k+1,k+2)},{\mathcal {B}}_{k+2}}\frac{s_{{\mathcal {B}}_{k+2}}^{(k+1)}}{\alpha _{k+1}}\end{bmatrix} +\\&\qquad \ - \begin{bmatrix} A_{{\mathcal {F}}_{(k+1,k+2)},{\overline{{\mathcal {F}}}^{k+1}_{(k+1,k+2)}}}\, g_{{\overline{{\mathcal {F}}}^{k+1}_{(k+1,k+2)}}}^{(k)},\ \ A_{{\mathcal {F}}_{(k+1,k+2)},{\overline{{\mathcal {F}}}^{k+2}_{(k+1,k+2)}}}\, g_{{\overline{{\mathcal {F}}}^{k+2}_{(k+1,k+2)}}}^{(k+1)} \end{bmatrix} =\\&\quad \ =\begin{bmatrix} g_{{\mathcal {F}}_{(k+1,k+2)}}^{(k) },&g_{{\mathcal {F}}_{(k+1,k+2)}}^{(k+1)},&g_{{\mathcal {F}}_{(k+1,k+2)}}^{(k+2) }\end{bmatrix} \begin{bmatrix} \frac{1}{\alpha _{k}} &{} 0\\ - \frac{1}{\alpha _{k}} &{} \frac{1}{\alpha _{k+1}} \\ 0 &{} -\frac{1}{\alpha _{k+1}} \end{bmatrix} +\\&\qquad \ + \begin{bmatrix} A_{{\mathcal {F}}_{(k+1,k+2)},{\mathcal {B}}_{k+1}} \frac{s_{{\mathcal {B}}_{k+1}}^{(k)}}{\alpha _k},&A_{{\mathcal {F}}_{(k+1,k+2)},{\mathcal {B}}_{k+2}} \frac{s_{{\mathcal {B}}_{k+2}}^{(k+1)}}{\alpha _{k+1}}\end{bmatrix} + \\&\qquad \ + \begin{bmatrix} A_{{\mathcal {F}}_{(k+1,k+2)},{\overline{{\mathcal {F}}}^{k+1}_{(k+1,k+2)}}}\,\frac{s_{{\overline{{\mathcal {F}}}^{k+1}_{(k+1,k+2)}}}^{(k)}}{\alpha _k},\ \ A_{{\mathcal {F}}_{(k+1,k+2)},{\overline{{\mathcal {F}}}^{k+2}_{(k+1,k+2)}}}\, \frac{s_{{\overline{{\mathcal {F}}}^{k+2}_{(k+1,k+2)}}}^{(k+1)}}{\alpha _{k+1}} \end{bmatrix}. \end{aligned} \end{aligned}$$

(25)

Some comments to (25) are needed.

Remark 2

We observe that:

• (a) if ${\mathcal {F}}_{k+2} = \cap _{s=k+1}^{{{k+2}}} {\mathcal {F}}_{s}$, namely ${\mathcal {F}}_{k+2}\subset {\mathcal {F}}_{k+1}$, then $\overline{{\mathcal {F}}}^{k+2}_{(k+1,k+2)} = \emptyset$, hence $s_{{\overline{{\mathcal {F}}}^{k+2}_{(k+1,k+2)}}}^{(k+1)}$ does not give contribute to (25). Moreover, since ${\mathcal {B}}_{k+1}\subset {\mathcal {B}}_{k+2}$, if they are consistent then the subvector $s^{(k+1)}_{{\mathcal {B}}_{k+1}}$ of $s^{(k+1)}_{{\mathcal {B}}_{k+2}}$ is null;

• (b) if ${\mathcal {F}}_{k+1} = {\mathcal {F}}_{k+2}$ (or, equivalently, ${\mathcal {B}}_{k+1}= {\mathcal {B}}_{k+2}$ ), then $\overline{{\mathcal {F}}}^{k+j}_{(k+1,k+2)} = \emptyset$, $j=1,2$, hence $s_{{\overline{{\mathcal {F}}}^{k+j}_{(k+1,k+2)}}}^{(k+j-1)}$, $j=1,2$, do not give contribute to (25). Moreover, if the sets ${\mathcal {B}}_{k+1}$, ${\mathcal {B}}_{k+2}$ are consistent, then $s_{{\mathcal {B}}_{k+2}}^{(k+1)} = 0$;

• (c) if ${\mathcal {F}}_k = {\mathcal {F}}_{k+1} = {\mathcal {F}}_{k+2}$ (or, equivalently, ${\mathcal {B}}_k = {\mathcal {B}}_{k+1}= {\mathcal {B}}_{k+2}$ ) and the sets ${\mathcal {B}}_k$, ${\mathcal {B}}_{k+1}$, ${\mathcal {B}}_{k+2}$ are consistent, then $s_{{\overline{{\mathcal {F}}}^{k+j}_{(k+1,k+2)}}}^{(k+j-1)}$, $j=1,2$, do not give contribute to (25) and $s_{{\mathcal {B}}_{k+2}}^{(k+1)} = 0$, as in the case (b); furthermore, $s_{{\mathcal {B}}_{k+1}}^{(k)} = 0$.

In other words, in the case (c), both the active and the inactive components of three iterates do not change and we are able to rewrite the original recurrence formula (12) restricted to the set ${\mathcal {F}}_{(k+1,k+2)}$. Actually, in this case, (25) reduces to

$$\begin{aligned} \begin{aligned}&A_{{\mathcal {F}}_{(k+1,k+2)},{\mathcal {F}}_{(k+1,k+2)}} \begin{bmatrix} g_{{\mathcal {F}}_{(k+1,k+2)}}^{(k) },&g_{{\mathcal {F}}_{(k+1,k+2)}}^{(k+1)}\end{bmatrix} =\\&\qquad = \begin{bmatrix} g_{{\mathcal {F}}_{(k+1,k+2)}}^{(k) },&g_{{\mathcal {F}}_{(k+1,k+2)}}^{(k+1)},&g_{{\mathcal {F}}_{(k+1,k+2)}}^{(k+2) }\end{bmatrix} \begin{bmatrix} \frac{1}{\alpha _{k}} &{} 0\\ - \frac{1}{\alpha _{k}} &{} \frac{1}{\alpha _{k+1}} \\ 0 &{} -\frac{1}{\alpha _{k+1}} \end{bmatrix} \end{aligned} \end{aligned}$$

(26)

and this last equation is the basis for a limited memory steplength selection rule with respect to the set ${\mathcal {F}}_{(k+1,k+2)}$. Indeed, it is easy to generate a matrix $T_k$ as in (13) by only considering the indices in ${\mathcal {F}}_{(k+1,k+2)}$. In the case (b), the corresponding recurrence formula differs from (26) for the presence of $\frac{1}{\alpha _k} A_{{\mathcal {F}}_{(k+1,k+2)},{\mathcal {B}}_{k+1}} s_{{\mathcal {B}}_{k+1}}^{(k)}$. By evaluating the contribution of this term, we can control how it influences the approximation of the eigenvalues of $A_{{\mathcal {F}}_{(k+1,k+2)},{\mathcal {F}}_{(k+1,k+2)}}$. In the following (Remark 4) we discuss this scenario.

The arguments so far discussed can be generalized to a sweep of length m starting from the iteration k. By defining ${\mathcal {F}}_{{(k+1,k+m)}}:= \cap _{s=k+1}^{{{k+m}}} {\mathcal {F}}_{s}$ and assuming ${\mathcal {F}}_{{(k+1,k+m)}}\ne \emptyset$, we have

$$\begin{aligned} \begin{aligned}&A_{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {F}}_{{(k+1,k+m)}}} \begin{bmatrix} g^{(k)}_{{\mathcal {F}}_{{(k+1,k+m)}}},&\ldots ,&g^{{(k+m-1)}}_{{\mathcal {F}}_{{(k+1,k+m)}}}\end{bmatrix}=\\&\quad =\begin{bmatrix} g^{(k)}_{{\mathcal {F}}_{{(k+1,k+m)}}},&\ldots ,&g^{{(k+m-1)}}_{{\mathcal {F}}_{{(k+1,k+m)}}}&g^{{(k+m)}}_{{\mathcal {F}}_{{(k+1,k+m)}}} \end{bmatrix} {{J_k}} +\\&\qquad + \begin{bmatrix} A_{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {B}}_{k+1}} \frac{s_{{\mathcal {B}}_{k+1}}^{(k)}}{\alpha _k},&\ldots ,&A_{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {B}}_{k+m}}\frac{s_{{\mathcal {B}}_{k+m}}^{{(k+m-1)}}}{\alpha _{k+m-1}}\end{bmatrix} + \\&\qquad - \begin{bmatrix} A_{{\mathcal {F}}_{{(k+1,k+m)}},{\overline{{\mathcal {F}}}^{k+1}_{(k+1,k+m)}}}\, g_{{\overline{{\mathcal {F}}}^{k+1}_{(k+1,k+m)}}}^{(k)},&\ldots ,&A_{{\mathcal {F}}_{{(k+1,k+m)}},{\overline{{\mathcal {F}}}^{k+m}_{(k+1,k+m)}}}\, g_{{\overline{{\mathcal {F}}}^{k+m}_{(k+1,k+m)}}}^{{(k+m-1)}} \end{bmatrix}=\\&\quad =\begin{bmatrix} g^{(k)}_{{\mathcal {F}}_{{(k+1,k+m)}}},&\ldots ,&g^{{(k+m-1)}}_{{\mathcal {F}}_{{(k+1,k+m)}}},&g^{{(k+m)}}_{{\mathcal {F}}_{{(k+1,k+m)}}} \end{bmatrix} {{J_k}} +\\&\qquad + \begin{bmatrix} A_{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {B}}_{k+1}} \frac{s_{{\mathcal {B}}_{k+1}}^{(k)}}{\alpha _k},&\ldots ,&A_{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {B}}_{k+m}}\frac{s_{{\mathcal {B}}_{k+m}}^{{(k+m-1)}}}{\alpha _{k+m-1}}\end{bmatrix} + \\&\qquad + \begin{bmatrix} A_{{\mathcal {F}}_{{(k+1,k+m)}},{\overline{{\mathcal {F}}}^{k+1}_{(k+1,k+m)}}}\, \frac{s_{{\overline{{\mathcal {F}}}^{k+1}_{(k+1,k+m)}}}^{(k)}}{\alpha _k},&\ldots ,&A_{{\mathcal {F}}_{{(k+1,k+m)}},{\overline{{\mathcal {F}}}^{k+m}_{(k+1,k+m)}}}\, \frac{s_{{\overline{{\mathcal {F}}}^{k+m}_{(k+1,k+m)}}}^{{(k+m-1)}}}{\alpha _{k+m-1}} \end{bmatrix} \end{aligned} \end{aligned}$$

(27)

where $\overline{{\mathcal {F}}}^{k+j}_{(k+1,k+m)} = {\mathcal {F}}_{k+j} \setminus {\mathcal {F}}_{{(k+1,k+m)}}$, $j=1,\dots ,m$. Similar considerations to those of Remark 2 can also be deduced for (27). We report them in Remark 3.

Remark 3

We observe that:

• (a) if ${\mathcal {F}}_{k+m} = \cap _{s=k+1}^{{{k+m}}} {\mathcal {F}}_{s}$, then $\overline{{\mathcal {F}}}^{k+m}_{(k+1,k+m)} = \emptyset$, hence $s_{{\overline{{\mathcal {F}}}^{k+m}_{(k+1,k+m)}}}^{(k+m-1)}$ does not give contribute to (27); moreover, since ${\mathcal {B}}_{k+j}\subset {\mathcal {B}}_{k+m}$, $j=1,...,m-1$, if they are consistent, then the subvectors $s^{(k+m-1)}_{{\mathcal {B}}_{k+j}}$ of $s^{(k+m-1)}_{{\mathcal {B}}_{k+m}}$, $j=1,\dots ,m-1$, are null;

• (b) if ${\mathcal {F}}_{k+1} = \dots = {\mathcal {F}}_{k+m}$ (or, equivalently, ${\mathcal {B}}_{k+1} = \dots = {\mathcal {B}}_{k+m}$ ), then $\overline{{\mathcal {F}}}^{k+j}_{(k+1,k+m)} = \emptyset$, $j=1,\dots ,m$, hence $s_{{\overline{{\mathcal {F}}}^{k+j}_{(k+1,k+m)}}}^{(k+j-1)}$, $j=1,\dots ,m$, do not give contribute to (27). Moreover, by assuming ${\mathcal {B}}_{k+j}$, $j=1,\ldots , m$ consistent, then $s_{{\mathcal {B}}_{k+j}}^{(k+j-1)} = 0$, $j=2,\dots ,m$;

• (c) if ${\mathcal {F}}_k = \dots = {\mathcal {F}}_{k+m}$ (or, equivalently, ${\mathcal {B}}_k =\dots = {\mathcal {B}}_{k+m}$ ) and the sets ${\mathcal {B}}_k, \dots , {\mathcal {B}}_{k+m}$ are consistent, then, as in the case (b), $s_{{\overline{{\mathcal {F}}}^{k+j}_{(k+1,k+m)}}}^{(k+j-1)}$, $j=1,\ldots ,m$, do not give contribute to (27) and $s_{{\mathcal {B}}_{k+j}}^{(k+j-1)} = 0$, $j=1,\dots ,m$.

In other words, as for $m=2$, only in the case (c), we reduce to the original limited memory steplength selection rule with respect to the set ${\mathcal {F}}_{{(k+1,k+m)}}$, namely the following considerations hold true.

• 1. By defining

  $$\begin{aligned} G_{{\mathcal {F}}_{{(k+1,k+m)}}} = \begin{bmatrix} g^{(k)}_{{\mathcal {F}}_{{(k+1,k+m)}}},&\ldots ,&g^{{(k+m-1)}}_{{\mathcal {F}}_{{(k+1,k+m)}}}\end{bmatrix}, \end{aligned}$$

  (28)

  the equation (12) can be rewritten with respect to the indices in ${\mathcal {F}}_{{(k+1,k+m)}}$ as

  $$\begin{aligned} A_{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {F}}_{{(k+1,k+m)}}} G_{{\mathcal {F}}_{{(k+1,k+m)}}} = [G_{{\mathcal {F}}_{{(k+1,k+m)}}}, \ g^{(k+m)}_{{\mathcal {F}}_{{(k+1,k+m)}}}] {{J_k}}. \end{aligned}$$

  (29)

  We assume that $G_{{\mathcal {F}}_{{(k+1,k+m)}}}$ is a full-column rank matrix.

• 2. The columns of $G_{{\mathcal {F}}_{{(k+1,k+m)}}}$ are in the space generated by the Krylov sequence

  $$\begin{aligned} \left\{ g^{(k)}_{{\mathcal {F}}_{{(k+1,k+m)}}},\ A_{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {F}}_{{(k+1,k+m)}}}g^{(k)}_{{\mathcal {F}}_{{(k+1,k+m)}}}, \ \dots ,\ A_{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {F}}_{{(k+1,k+m)}}}^{m-1}g^{(k)}_{{\mathcal {F}}_{{(k+1,k+m)}}} \right\} . \end{aligned}$$

• 3. Given the non-singular upper triangular $m\times m$ matrix $R_{{\mathcal {F}}_{{(k+1,k+m)}}}$ such that $R_{{\mathcal {F}}_{{(k+1,k+m)}}}^TR_{{\mathcal {F}}_{{(k+1,k+m)}}} = G_{{\mathcal {F}}_{{(k+1,k+m)}}}^TG_{{\mathcal {F}}_{{(k+1,k+m)}}}$ and the vector $r_{{\mathcal {F}}_{{(k+1,k+m)}}}$ as the solution of the linear system $R_{{\mathcal {F}}_{{(k+1,k+m)}}}^{T}r_{{\mathcal {F}}_{{(k+1,k+m)}}} = G_{{\mathcal {F}}_{{(k+1,k+m)}}}^Tg_{{\mathcal {F}}_{{(k+1,k+m)}}}^{{(k+m)}}$, the eigenvalues of the tridiagonal matrix

  $$\begin{aligned} \begin{aligned} {{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}&= R_{{\mathcal {F}}_{{(k+1,k+m)}}}^{-T}G_{{\mathcal {F}}_{{(k+1,k+m)}}}^T A_{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {F}}_{{(k+1,k+m)}}} G_{{\mathcal {F}}_{{(k+1,k+m)}}} R_{{\mathcal {F}}_{{(k+1,k+m)}}}^{-1}\\&= R_{{\mathcal {F}}_{{(k+1,k+m)}}}^{-T}G_{{\mathcal {F}}_{{(k+1,k+m)}}}^T [G_{{\mathcal {F}}_{{(k+1,k+m)}}}, \ g^{(k+m)}_{{\mathcal {F}}_{{(k+1,k+m)}}}] {J_k} R_{{\mathcal {F}}_{{(k+1,k+m)}}}^{-1}\\&= [R_{{\mathcal {F}}_{{(k+1,k+m)}}}, \ r_{{\mathcal {F}}_{{(k+1,k+m)}}}]{{J_k}}R_{{\mathcal {F}}_{{(k+1,k+m)}}}^{-1} \end{aligned} \end{aligned}$$

  (30)

  can be considered approximations of m eigenvalues of $A_{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {F}}_{{(k+1,k+m)}}}$.

As for $m=2$, the recurrence formula related to the case (b) differs from (29) for the presence of $A_{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {B}}_{k+1}}s_{{\mathcal {B}}_{k+1}}^{(k)}$. In Remark 4 we discuss how the approximation of the eigenvalues of $A_{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {F}}_{{(k+1,k+m)}}}$ depends on the contribution of this term.

3.2.1 Practical approximation of the eigenvalues of $A_{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {F}}_{{(k+1,k+m)}}}$

In general, we can not ensure that for $m+1$ successive iterations the sets ${\mathcal {F}}_{k+j}$, $j=0, 1,\dots ,m$ are all the same and hence, the matrix ${{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}$, whose eigenvalues are approximations of those of $A_{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {F}}_{{(k+1,k+m)}}}$, can not be simply written as in (30). Indeed, in view of (27), the matrix ${T}_{{\mathcal {F}}_{{(k+1,k+m)}}}$ has the following form

$$\begin{aligned} \begin{aligned} {T}_{{\mathcal {F}}_{{(k+1,k+m)}}}&= {R_{{\mathcal {F}}_{{(k+1,k+m)}}}^{-T}G_{{\mathcal {F}}_{{(k+1,k+m)}}}^T A_{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {F}}_{{(k+1,k+m)}}} G_{{\mathcal {F}}_{{(k+1,k+m)}}} R_{{\mathcal {F}}_{{(k+1,k+m)}}}^{-1}}\\&= \begin{bmatrix} R_{{\mathcal {F}}_{{(k+1,k+m)}}}, \quad r_{{\mathcal {F}}_{{(k+1,k+m)}}}\end{bmatrix} {{J}} R_{{\mathcal {F}}_{{(k+1,k+m)}}}^{-1} + E_{{\mathcal {F}}_{{(k+1,k+m)}}} \end{aligned} \end{aligned}$$

(31)

where

$$\begin{aligned} E_{{\mathcal {F}}_{{(k+1,k+m)}}}= & {} R^{-T}_{{\mathcal {F}}_{{(k+1,k+m)}}} G_{{\mathcal {F}}_{{(k+1,k+m)}}}^T \\&\left( \begin{bmatrix} A_{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {B}}_{k+1}}\frac{s_{{\mathcal {B}}_{k+1}}^{(k)}}{\alpha _k}, \cdots , A_{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {B}}_{k+m}}\frac{s_{{\mathcal {B}}_{k+m}}^{{(k+m-1)}}}{\alpha _{k+m-1}}\end{bmatrix}\right. +\\&\left. + \begin{bmatrix} A_{{\mathcal {F}}_{{(k+1,k+m)}},{\overline{{\mathcal {F}}}^{k+1}_{(k+1,k+m)}}}\, \frac{s_{{\overline{{\mathcal {F}}}^{k+1}_{(k+1,k+m)}}}^{(k)}}{\alpha _k},&\cdots , A_{{\mathcal {F}}_{{(k+1,k+m)}},{\overline{{\mathcal {F}}}^{k+m}_{(k+1,k+m)}}}\, \frac{s_{{\overline{{\mathcal {F}}}^{k+m}_{(k+1,k+m)}}}^{{(k+m-1)}}}{\alpha _{k+m-1}} \end{bmatrix}\right) \\&R_{{\mathcal {F}}_{{(k+1,k+m)}}}^{-1} \end{aligned}$$

In practice, the computation of the matrix $E_{{\mathcal {F}}_{{(k+1,k+m)}}}$ is not affordable and, as a consequence, along the iterative procedure, it is only possible to approximate the eigenvalues of $T_{{\mathcal {F}}_{{(k+1,k+m)}}}$ and we now investigate how to achieve this goal. Two useful results are recalled.

Theorem 2

[37, Theorem 8.1.5] If A and $A+E$ are $n\times n$ symmetric matrices then

$$\begin{aligned} \lambda _i(A)+\lambda _{min}(E) \le \lambda _i(A+E)\le \lambda _i(A)+\lambda _{max}(E) \end{aligned}$$

for $i=1,\dots ,n$.

Corollary 1

[37, Corollay 8.1.6] If A and $A+E$ are $n\times n$ symmetric matrices then

$$\begin{aligned} |\lambda _i(A+E)-\lambda _i(A)|\le \Vert E\Vert \end{aligned}$$

for $i=1,\dots ,n$.

Given the upper Hessenberg matrix

$$\begin{aligned} {{\tilde{T}}}_{{\mathcal {F}}_{{(k+1,k+m)}}} = \begin{bmatrix} R_{{\mathcal {F}}_{{(k+1,k+m)}}}, \quad r_{{\mathcal {F}}_{{(k+1,k+m)}}}\end{bmatrix} {{J_k}} R_{{\mathcal {F}}_{{(k+1,k+m)}}}^{-1}, \end{aligned}$$

(32)

the eigenvalues of $T_{{\mathcal {F}}_{{(k+1,k+m)}}}$ can be approximated by exploiting the following decomposition of ${{\tilde{T}}}_{{\mathcal {F}}_{{(k+1,k+m)}}}$

$$\begin{aligned} {\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}} = D_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}} + L_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}} + U_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}} \end{aligned}$$

where $D_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}}$, $L_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}}$ and $U_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}}$ are the diagonal component, the strictly lower triangular component and the strictly upper triangular component of ${\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}$, respectively. In view of this decomposition, the matrix $T_{{\mathcal {F}}_{{(k+1,k+m)}}}$ can be written as

$$\begin{aligned} T_{{\mathcal {F}}_{{(k+1,k+m)}}}= & {} D_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}} + \, L_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}} +\, U_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}} +\\&+ L_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}}^T -\, L_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}}^T + E_{{\mathcal {F}}_{{(k+1,k+m)}}}. \end{aligned}$$

By setting

$$\begin{aligned} \begin{aligned} {\hat{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}&= D_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}} + L_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}}+ L_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}}^T, \qquad \\ {\hat{E}}_{{\mathcal {F}}_{{(k+1,k+m)}}}&= L_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}}^T - U_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}} - E_{{\mathcal {F}}_{{(k+1,k+m)}}}, \end{aligned} \end{aligned}$$

(33)

we can write

$$\begin{aligned} {\hat{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}} = T_{{\mathcal {F}}_{{(k+1,k+m)}}} + {\hat{E}}_{{\mathcal {F}}_{{(k+1,k+m)}}}. \end{aligned}$$

(34)

Since by definition the matrices $T_{{\mathcal {F}}_{{(k+1,k+m)}}}$ and ${\hat{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}$ are symmetric, ${\hat{E}}_{{\mathcal {F}}_{{(k+1,k+m)}}}$ is also symmetric and we can apply Theorem 2 and Corollary 1 to (34). In particular, we obtain that

$$\begin{aligned} \lambda _i(T_{{\mathcal {F}}_{{(k+1,k+m)}}}) + \lambda _{min}({\hat{E}}_{{\mathcal {F}}_{{(k+1,k+m)}}})\le \lambda _i({\hat{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}) \le \lambda _i(T_{{\mathcal {F}}_{{(k+1,k+m)}}}) + \lambda _{max}({\hat{E}}_{{\mathcal {F}}_{{(k+1,k+m)}}}). \end{aligned}$$

Then the computation of the eigenvalues of ${\hat{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}$ instead of the ones of ${T}_{{\mathcal {F}}_{{(k+1,k+m)}}}$ provides an error bounded as follows

$$\begin{aligned} |\lambda _i({\hat{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}) - \lambda _i({T}_{{\mathcal {F}}_{{(k+1,k+m)}}})|&\le \left\| {\hat{E}}_{{\mathcal {F}}_{{(k+1,k+m)}}}\right\| \end{aligned}.$$

In more detail, the following inequalities hold

$$\begin{aligned}&\left\| {\hat{E}}_{{\mathcal {F}}_{{(k+1,k+m)}}}\right\| \le \left\| L_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}}^T-U_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}}\right\|+ \\&\quad + \left\| R^{-T}_{{\mathcal {F}}_{{(k+1,k+m)}}} G_{{\mathcal {F}}_{{(k+1,k+m)}}}^T\right\| \left\| \begin{bmatrix} A_{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {B}}_{k+1}}\frac{s_{{\mathcal {B}}_{k+1}}^{(k)}}{\alpha _k}, \cdots , A_{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {B}}_{k+m}}\frac{s_{{\mathcal {B}}_{k+m}}^{{(k+m-1)}}}{\alpha _{k+m-1}}\end{bmatrix}\right.+ \\&\quad + \left. \begin{bmatrix} A_{{\mathcal {F}}_{{(k+1,k+m)}},{\overline{{\mathcal {F}}}^{k+1}_{(k+1,k+m)}}}\, \frac{s_{{\overline{{\mathcal {F}}}^{k+1}_{(k+1,k+m)}}}^{(k)}}{\alpha _k}, \cdots , A_{{\mathcal {F}}_{{(k+1,k+m)}},{\overline{{\mathcal {F}}}^{k+m}_{(k+1,k+m)}}}\, \frac{s_{{\overline{{\mathcal {F}}}^{k+m}_{(k+1,k+m)}}}^{{(k+m-1)}}}{\alpha _{k+m-1}} \end{bmatrix}\right\| \cdot \left\| R_{{\mathcal {F}}_{{(k+1,k+m)}}}^{-1}\right\|. \end{aligned}$$

Since $\left\| R^{-T}_{{\mathcal {F}}_{{(k+1,k+m)}}}G_{{\mathcal {F}}_{{(k+1,k+m)}}}^T\right\| =1$, we can rewrite

$$\begin{aligned}&\left\| {\hat{E}}_{{\mathcal {F}}_{{(k+1,k+m)}}}\right\| _2\le \left\| L_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}}^T-U_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}}\right\| _2 +\\&\qquad + \left\| \frac{1}{\alpha _k} A_{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {B}}_{k+1}\cup {\overline{{\mathcal {F}}}^{k+1}_{(k+1,k+m)}}} {s^{(k)}_{{\mathcal {B}}_{k+1}\cup {\overline{{\mathcal {F}}}^{k+1}_{(k+1,k+m)}}}}, \ldots ,\right. \\&\quad \left. \frac{1}{\alpha _{k+m-1}} A_{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {B}}_{k+m} \cup {\overline{{\mathcal {F}}}^{k+m}_{(k+1,k+m)}}} {s^{{(k+m-1)}}_{{\mathcal {B}}_{k+m} \cup \overline{{\mathcal {F}}} ^{k+m}_{(k+1,k+m)}}} \right\| \left\| R_{{\mathcal {F}}_{{(k+1,k+m)}}}^{-1}\right\| \\&\qquad \le \left\| L_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}}^T-U_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}}\right\|+ \\&\qquad +\left\| A_{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {B}}_{k+1}\cup {\overline{{\mathcal {F}}}^{k+1}_{(k+1,k+m)}}},\cdots ,A_{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {B}}_{k+m} \cup {\overline{{\mathcal {F}}}^{k+m}_{(k+1,k+m)}}}\right\| \left\| { \begin{array}{c} \frac{s^{(k)}_{{\mathcal {B}}_{k+1}\cup {\overline{{\mathcal {F}}}^{k+1}_{(k+1,k+m)}}}}{\alpha _k} \\ \vdots \\ \frac{s^{(k+m-1)}_{{\mathcal {B}}_{k+m} \cup {\overline{{\mathcal {F}}}^{k+m}_{(k+1,k+m)}}}}{\alpha _{k+m-1}} \end{array}} \right\|\cdot \\&\quad \cdot \left\| R_{{\mathcal {F}}_{{(k+1,k+m)}}}^{-1}\right\|. \end{aligned}$$

We observe that

$$\begin{aligned} \begin{aligned}&\left\| A_{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {B}}_{k+1}\cup {\overline{{\mathcal {F}}}^{k+1}_{(k+1,k+m)}}},\ldots ,A_{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {B}}_{k+m} \cup {\overline{{\mathcal {F}}}^{k+m}_{(k+1,k+m)}}}\right\| \\&\qquad \le \sqrt{\sharp {\mathcal {F}}_{{(k+1,k+m)}}} \left\| A_{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {B}}_{k+1}\cup {\overline{{\mathcal {F}}}^{k+1}_{(k+1,k+m)}}},\cdots ,A_{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {B}}_{k+m} \cup {\overline{{\mathcal {F}}}^{k+m}_{(k+1,k+m)}}}\right\| _{\infty } \\&\qquad = \sqrt{\sharp {\mathcal {F}}_{{(k+1,k+m)}}} \max _{j=1,...,m}\Vert A_{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {B}}_{k+j} \cup {\overline{{\mathcal {F}}}^{k+m}_{(k+1,k+m)}} }\Vert _{\infty } \le \sqrt{\sharp {\mathcal {F}}_{{(k+1,k+m)}}} \Vert A\Vert _{\infty } \end{aligned} \end{aligned}$$

Then, by recalling that for a generic matrix B we have $\Vert B\Vert \le \Vert B\Vert _F$, we can write

$$\begin{aligned} \begin{aligned}&\left\| {\hat{E}}_{{\mathcal {F}}_{{(k+1,k+m)}}}\right\| \le \left\| L_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}}^T-U_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}}\right\| _F +\\&\qquad + \left\| R_{{\mathcal {F}}_{{(k+1,k+m)}}}^{-1}\right\| \sqrt{\sharp {\mathcal {F}}_{{(k+1,k+m)}}} \Vert A\Vert _{\infty } \left\| {\begin{array}{c} \frac{s^{(k)}_{{\mathcal {B}}_{k+1}\cup {\overline{{\mathcal {F}}}^{k+1}_{(k+1,k+m)}}}}{\alpha _k} \\ \vdots \\ \frac{s^{(k+m-1)}_{{\mathcal {B}}_{k+m} \cup {\overline{{\mathcal {F}}}^{k+m}_{(k+1,k+m)}}}}{\alpha _{k+m-1}} \end{array}} \right\| \\&\quad \le \left\| L_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}}^T-U_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}}\right\| _F +\\&\qquad + \frac{1}{\alpha _{k,k+m-1}}\left\| R_{{\mathcal {F}}_{{(k+1,k+m)}}}^{-1}\right\| \sqrt{\sharp {\mathcal {F}}_{{(k+1,k+m)}}} \Vert A\Vert _{\infty } \left\| w^{(k)}\right\| \end{aligned} \end{aligned}$$

(35)

where $\alpha _{k,k+m-1}=\min _{i=k,...,k+m-1}\alpha _i$ and $w^{(k)}$ is the vector

$$\begin{aligned} \begin{pmatrix} s^{(k)}_{{\mathcal {B}}_{k+1}\cup {\overline{{\mathcal {F}}}^{k+1}_{(k+1,k+m)}}},&\cdots ,&s^{(k+m-1)}_{{\mathcal {B}}_{k+m} \cup {\overline{{\mathcal {F}}}^{k+m}_{(k+1,k+m)}}} \end{pmatrix}^T. \end{aligned}$$

(36)

From the last inequalities, we can conclude that if $\left\| L_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}}^T-U_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}}\right\| _F$ and $\left\| w^{(k)}\right\|$ are small, then the eigenvalues of ${\hat{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}$ can be used as approximations of the eigenvalues of $T_{{\mathcal {F}}_{{(k+1,k+m)}}}$.

Remark 4

We also stress that in the case (c) of Remark 3, ${\hat{E}}_{{\mathcal {F}}_{{(k+1,k+m)}}}=0$. Furthermore, in the case (b) of Remark 3, $s_{\overline{{\mathcal {F}}}^{k+j}_{(k+1,k+m)}}^{(k+j-1)}=0$, $j=1,...,m$, $s_{{\mathcal {B}}_{k+j}}^{(k+j-1)}=0$, $j=2,...,m,$ and only the subvector $s_{{\mathcal {B}}_{k+1}}^{(k)}$ can be different from zero. Then we can control the maximum error performed by computing the eigenvalues of ${\hat{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}$ instead of the eigenvalues of $T_{{\mathcal {F}}_{{(k+1,k+m)}}}$; indeed, given $\epsilon >0$, if $\epsilon > \phi _k\equiv \left\| L_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}}^T-U_{{\tilde{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}}\right\| _F$ and $\delta$ is an estimate of $\Vert A\Vert _{\infty }$, then, this error is at most equal to $\epsilon$ if

$$\begin{aligned} \frac{1}{\alpha _k}\Vert s_{{\mathcal {B}}_{k+1}}^{(k)}\Vert \le \frac{\epsilon -\phi _k}{\delta \sqrt{\sharp {\mathcal {F}}_{{(k+1,k+m)}}} \Vert R_{{\mathcal {F}}_{{(k+1,k+m)}}}^{-1}\Vert }. \end{aligned}$$

To summarize, a generalized LM steplength selection rule for the GP scheme (2)-(3) is fruitful when both the active set and the inactive set related to $m+1$ successive iterates are fixed. As stated in [10, 12], this situation certainly occurs when k is sufficiently large to guarantee that the scheme generates iterates whose active components are all and the only active components at the solution. If this is not the case, the above error estimate can be exploited to decide when the generalized LM steplength rule is convenient within the GP scheme.

3.3 Possible implementations of the generalized LM steplength strategy

This section is devoted to explain how to exploit in practice the considerations drawn in the previous section. Essentially, instead of collecting all the components of the gradient vectors and calculating the eigenvalues of (13) as in the orginal LM scheme for the unconstrained case, our implementation of the LM steplength rule for the constrained case is based on the collection of m past gradient vectors restricted to the set of indices ${\mathcal {F}}_{{(k+1,k+m)}}$, as in (28), and then on the computation of the eigenvalues of the matrix ${\hat{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}$, defined in (33). However, as detailed before, the validity of (29) is not ensured at the beginning of the iterative process; hence the eigenvalues of the matrix ${\hat{T}}_{{\mathcal {F}}_{{(k+1,k+m)}}}$ could not be good estimations of the eigenvalues of the matrix $T_{{\mathcal {F}}_{{(k+1,k+m)}}}$ in (31) which instead approximate those of the matrix $A_{{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {F}}_{{(k+1,k+m)}}}}$. For this reason, we propose to interrupt a sweep and to restart the collection of new restricted gradient vectors when some convenient conditions are not satisfied, by developing a technique which adaptively controls the length ${\tilde{m}}$ of the sweep, up to the given maximum value m. More in detail, we consider two different conditions which allow to arrest a sweep: the second one is stronger than the first one, but it requires a few more computations.

• (i) In the first case, given a sweep starting from the iteration k, if there exists an index j, from $k+1$ to at most $k+m$, such that

  $$\begin{aligned} {\mathcal {F}}_{j}\nsubseteq \cap _{s=1}^{j-k} {\mathcal {F}}_{k+s}, \end{aligned}$$

  (37)

  the sweep is stopped and all the already stored restricted gradient vectors are removed from the stack. The next steplength is selected in according to rule (18), as if ${\tilde{m}}=1$. If instead

  $$\begin{aligned} {\mathcal {F}}_{j}\subseteq \cap _{s=1}^{j-k} {\mathcal {F}}_{k+s}, \qquad j=k+1,\dots ,k+{\tilde{m}} \end{aligned}$$

  (38)

  with ${\tilde{m}}\le m$, i.e., ${\mathcal {F}}_{k+{\tilde{m}}}\subseteq {\mathcal {F}}_{k+{\tilde{m}}-1}\subseteq \cdots \subseteq {\mathcal {F}}_{k+1}$, then we compute the eigenvalues of the matrix ${\hat{T}}_{{\mathcal {F}}_{(k+1,k+{\tilde{m}})}}$ and we employ them as the reciprocals of the steplength values for the next ${\tilde{m}}$ iterations. If conditions (38) are satisfied, then it is true that, at the end of a sweep of ${\tilde{m}}$ steps, ${\mathcal {F}}_{k+{\tilde{m}}}=\cap _{s=k+1}^{k+{\tilde{m}}}{\mathcal {F}}_s$, namely the condition of the case (a) of Remark 3 is guaranteed. Moreover, the requirements in (38) imply that ${\mathcal {B}}_{k+1}\subseteq {\mathcal {B}}_{k+2} \subseteq \cdots \subseteq {\mathcal {B}}_{k+{\tilde{m}}}$. If, in addition, these sets are consistent, then the subvectors $s^{(k+j)}_{{\mathcal {B}}_{k+j}}$ of $s^{(k+j)}_{{\mathcal {B}}_{k+j+1}}$ are null for $j=1,\dots , m-1$.

• (ii) In the second case, given a sweep starting from the iteration k, the sweep is stopped and all the already stored restricted gradient vectors are removed from the stack if there exists an index j, from $k+1$ to at most $k+m$, such that either (37) holds or

  $$\begin{aligned} \sqrt{\sum _{i=1}^{j-k} \left\| \frac{s^{(k+i-1)}_{{\mathcal {B}}_{k+i} \cup \overline{{{\mathcal {F}}}}^{k+i}_{(k+1,k+i)} }}{\alpha _{k+i-1}}\right\| ^2} > {\omega } \sqrt{\sum _{i=1}^{j-k} \left\| \frac{s^{(k+i-1)}}{\alpha _{k+i-1}}\right\| ^2 } \end{aligned}$$

  (39)

  where $\omega$ is a positive prefixed tolerance. In this case, the next steplength is selected in according to rule (18) when $\Vert s_{B_{k+1}}^{(k)}\Vert \le {\omega } \Vert s^{(k)}\Vert$, otherwise by employing the standard BB1 rule. If instead, conditions (38) are fulfilled and, moreover, for any $j=k+1,\dots ,k+{\tilde{m}}$,

  $$\begin{aligned} \sqrt{\sum _{i=1}^{j-k} \left\| \frac{s^{(k+i-1)}_{{\mathcal {B}}_{k+i}\cup \overline{{{\mathcal {F}}}}^{k+i}_{(k+1,k+i)}} }{\alpha _{k+i-1}}\right\| ^2 } \le {\omega } \sqrt{\sum _{i=1}^{j-k} \left\| \frac{s^{(k+i-1)}}{\alpha _{k+i-1}}\right\| ^2}\, \end{aligned}$$

  (40)

  we exploit the inverses of the eigenvalues of the matrix ${\hat{T}}_{{\mathcal {F}}_{(k+1,k+{\tilde{m}})}}$ as steplengths for the next ${\tilde{m}}$ iterations. Inequality (40) controls that the norm of the vector $w^{(k)}$ defined in (36) does not become too large along the sweep.

Both conditions (i) and (ii) try to reduce the error made in computing the eigenvalues of ${\hat{T}}_{{\mathcal {F}}_{(k+1,k+{\tilde{m}})}}$ instead of the ones of $T_{{\mathcal {F}}_{(k+1,k+{\tilde{m}})}}$, i.e., to recover the recurrence formula (29) which ensures the correct generalization of the LM steplength rule restricted to the set of indices ${{\mathcal {F}}_{(k+1,k+{\tilde{m}})}}$. In the following, we refer to LMGP1 and LMGP2 as the GP method along the arc (2)-(3) equipped with the generalized LM steplength rule implemented by means of the criteria (i) and (ii), respectively.

We point out that, even if the analysis reported so far has been developed for quadratic objective function, the procedure described in this section to implement generalized LM steplength strategies can be employed in the non-quadratic case also. In this case, the Hessian matrix of the objective function changes along the iterative process; however, the technique described above to approximate the eigenvalues of $A_{{{\mathcal {F}}_{{(k+1,k+m)}},{\mathcal {F}}_{{(k+1,k+m)}}}}$ can be employed to capture at each iteration the spectrum of the submatrix (whose rows and columns are indexed in ${\mathcal {F}}_{{(k+1,k+m)}}$) of a proper average matrix depending on the Hessian matrix.

4 A novel hybrid steplength selection rule

The previous section highlights that a LM steplength selection rule for the GP methods in the framework of box-constrained optimization can be effective when the active set corresponding to the nondegenerate stationary point has been well approximated or, at least, when the indices corresponding to both the active and the inactive components are fixed for a sufficient number of iterations. Driven by this analysis, in this section we propose a novel hybrid steplength strategy aimed at employing a LM technique only when it is really fruitful. We report in Algorithm 1 the realization of this hybrid rule within the general GP method along the arc for box-constrained optimization problems.

Some observations may be useful to explain the statements of Algorithm 1.

• With Steps 1-3, a new iterate is updated according to the GP scheme along the arc (2)-(3). Moreover, the indices related to the inactive components of $x^{(k+1)}$ are stored in ${\mathcal {F}}_{k+1}$.

• The Step 4 is devoted to check that both the active and the inactive components of two successive iterates correspond. In this case we collect the gradient vector $g^{(k)}$ restricted to the set ${\mathcal {F}}_{k+1}$ and the reciprocal of the steplength $\alpha _k$ employed to update $x^{(k+1)}$. The counter L allows to control if the conditions on the active and inactive components are valid for m successive iterations. If the corresponding inactive sets are not equal or the corresponding active sets are not consistent for a couple of successive iterates, we remove from the stack the already collected restricted gradient vectors and the reciprocals of the steplengths.

• The update of the steplength is made in Step 5. In particular, if the conditions of Step 4 are not verified for m successive iterations, the steplength is computed by means of a proper alternation of the Barzilai-Borwein rules proposed in [25] to account for the box constraints, switching between $\alpha _{k+1}^{\text {BB1}}$ and $\alpha _{k+1}^{\text {BOX-BB2}}$ defined in (5) and (9), respectively, in accordance with the following criterion:

  $$\begin{aligned} \alpha _{k+1}^{\text {BOX-ABB}_{\text {min}}}\! =\! \left\{ \begin{array}{ll} \!\!\! \min \left\{ \alpha _j^{\text {BOX-BB2}} \ \!:\! \ j\!=\!\max \{1,k+1\!-\!m_a\},\dots ,k+1\right\} &{} \hbox {if} \ \frac{\alpha _{k+1}^{\text {BOX-BB2}}}{\alpha _{k+1}^{\text {BB1}}}\!<\!\tau _{k+1},\\ \!\!\!\alpha _{k+1}^{\text {BB1}} &{} \hbox {otherwise,} \end{array} \right. \end{aligned}$$

  (41)

  where $\tau _{k+1}$ is updated as in [38]

  $$\begin{aligned} \tau _{k+1}=\left\{ \begin{array}{ll} \tau _k/\zeta &\quad \hbox {if} \ \frac{\alpha _k^{\text {BOX-BB2}}}{\alpha _k^{\text {BB1}}}<\tau _k,\\ \tau _k\cdot \zeta &\quad \hbox {otherwise,} \end{array} \right. \, \end{aligned}$$

  (42)

  with $\zeta >1$. When this updating rule comes into play after a sequence of LM iterations, the selection for $\alpha _{k+1}^{\text {BOX-ABB}_{\text {min}}}$ is performed between $\alpha _{k+1}^{\text {BB1}}$ and $\alpha _{k+1}^{\text {BOX-BB2}}$, restarting from scratch the alternation.

  If instead, ${\mathcal {F}}_k=\dots ={\mathcal {F}}_{k+m}$ and the corresponding ${\mathcal {B}}_{k}=\dots ={\mathcal {B}}_{k+m}$ are consistent, then a LM steplength selection rule can be employed to select the steplength in the next (at most) m iterations. Indeed in this case the original LM steplength rule proposed in [18] can be recovered with respect to the indices in the set ${\mathcal {F}}_{{(k+1,k+m)}}$ (as explained in Section 3) and the eigenvalues of the matrix $T_{{\mathcal {F}}_{{(k+1,k+m)}}}$ defined in (30) approximate m eigenvalues of the Hessian submatrix restricted to the intersection of rows and columns with indices in ${\mathcal {F}}_{{(k+1,k+m)}}$.

From now on we refer to Algorithm 1 as Hyb-LMGP.

Finally we remark that, instead of considering all the m eigenvalues of $T_{{\mathcal {F}}_{{(k+1,k+m)}}}$ to set the next m steplength as in the standard LM steplength rule, we also take into account the possibility of properly exploiting only one of them as suggested in [21, Algorithm 1] and, as a consequence, of selecting only the value for $\alpha _{k+1}$. These technique, called MLM and developed in [21] for unconstrained optimization problems, is still based on the recurrence formula (12); hence, a possible generalization to the box-constrained framework is really effective if this recurrence formula can be rewritten with respect to the set ${\mathcal {F}}_{{(k+1,k+m)}}$ as in (29). For this reason, in the hybrid scheme, we can apply the MLM approach only when $L=m$. Hereafter, we denote by Hyb-MLMGP the Algorithm 1 in which at the Step 5 (case $L=m$) the MLM steplength strategy is applied instead of the LM one.

In order to clarify the behaviour of Hyb-LMGP, we consider three very small quadratic problems subject to lower bounds. These problems are the corresponding versions for $n=100$ of test problems QP1, QP2 and QP3 examined in Section 5.1; for each problem, the number $n_{act}$ of active constraints at the solution is about 0.8n and the eigenvalue distribution of the positive definite Hessian of the objective function is prefixed. The condition number of A is approximately equal to $10^3$. Figures 1, 2 and 3 show the spectral behaviours of both the Hyb-LMGP method and a GP scheme, for the three problems. In particular, we considered the GP iteration (2)-(3) where the steplength is updated by means of the alternating BB strategy reported at Step 5 of Algorithm 1 with $\tau$ defined as in (42). We refer to this latter approach as ABBGP. Each figure plots, at any iteration k, the inverse of the current steplength, $1/ \alpha _k$, within the distribution of the eigenvalues of the current Hessian sub-matrix $A(x^{(k)})$, given by the intersection of the rows and columns corresponding to the entries of $x^{(k)}$ strictly greater than the lower bounds. For any fixed k, $k\ge 1$, the black dots are the eigenvalues of $A(x^{(k)})$ and the symbol ’$\times$’ is $1/\alpha _k$; the red lines represent the minimum and the maximum eigenvalues of $A(x^{(k)})$ whereas the green lines are at the minimum and the maximum eigenvalues of A. The blue circles at the right of any plot are the eigenvalues of the restricted Hessian at the solution, i.e., $A(x^*)$, and the red circles are the maximum and the minimum bounds for the spectrum of this sub-matrix. In all the cases, we fix $m=3$ in Hyb-LMGP method. Furthermore, the symbol ’$\times$’ in magenta indicates that the current steplength is defined by the generalized Ritz procedure while a blue symbol denotes the use of a BB rule. In Figs. 1 and 3, the Hyb-LMGP method exhibits the same behaviour of ABBGP up to the iteration ${\overline{k}}$ in which the indices of the inactive components are fixed; next, we observe that after the collections of three gradient at iterations ${\overline{k}}, {\overline{k}}+1, {\overline{k}}+2$ ($m=3$), the Ritz procedure can start, enabling to determine values for the steplength which cyclically sweep the spectrum of the submatrix and lead to a faster convergence than that obtained with ABBGP. The switching within the two strategies of the hybrid method arises earlier in QP3 with respect to QP1, due to the faster identification of the active constraints. The behaviour of Hyb-LMGP is different for problem QP2. Indeed, in this case, we observe that the switching between the two strategies occurs several times; after the first iterations, there are several cycles of iterations where the indices of inactive entries of the current iterate are fixed, enabling the Ritz procedure to start; nevertheless, when the scenario changes, i.e., the indices of the inactive entries change, the ABBGP method is restarted from scratch; in the last iterations, the method behaves as for QP1 and QP3.

Fig. 1

Test problem QP1 with $n=100$ and $n_{act}=80$: spectral behaviour of ABBGP and Hyb-LMGP methods (left and right panels respectively); here $m=3$

Fig. 2

Test problem QP2 with $n=100$ and $n_{act}=80$: spectral behaviour of ABBGP and Hyb-LMGP methods (left and right panels respectively); here $m=3$

Fig. 3

Test problem QP3 with $n=100$ and $n_{act}=76$: spectral behaviour of ABBGP and Hyb-LMGP methods (left and right panels respectively); here $m=3$

5 Numerical experiments

This section is devoted to the analysis of the numerical performance of the GP method (2)–(3) equipped with both the generalized LM steplength strategies suggested in Sect. 3.3 and the hybrid techniques proposed in Sect. 4. The resulting algorithms LMGP1, LMGP2, Hyb-LMGP and Hyb-MLMGP will be compared with different state-of-the-art GP methods.In the quadratic case, they will be further compared with the active-set method proposed in [33]. The numerical experiments of Sects. 5.1 and 5.2 were carried out on a workstation equipped with Intel Xeon Quad Core E5620 processor at 2.40 GHz and 18 GB of RAM, in the MATLAB R2019a environment, while those reported in Sect. 5.3 were obtained on an Intel Core i7-10510U processor at 1.80 GHz and 16 GB of RAM, in the MATLAB R2020a environment.

5.1 Quadratic test problems

In this subsection, we study the numerical behaviour of the proposed strategies on randomly generated quadratic test problems subject to lower bounds, in which the solution, the number $n_{act}$ of active constraints at the solution and the eigenvalues distribution of the dense symmetric positive definite Hessian of the objective function is prefixed. For these experiments, we built three test problems of size $n=10000$, having the following features:

• QP1: the eigenvalues of the Hessian matrix are generated by using the Matlab function logspace(1,1e4,n), i.e., they are logarithmically distributed bewtween 1 and $10^4$;

• QP2: the eigenvalues of the restricted Hessian matrix at the solution are logarithmically distributed bewtween 10 and $10^4$ i.e., they are generated using the Matlab function logspace, while $\lambda _{min}(A)\approx 10^{-4}$, $\lambda _{max}(A)\approx 10^9$;

• QP3: the eigenvalues of the Hessian matrix are given by $10^{4\frac{i-1}{n-1}}$, $i=1,\dots ,n$, as in [31].

We compared LMGP1, LMGP2, Hyb-LMGP and Hyb-MLMGP with the GP scheme described in Algorithm 2.1 of [39], here referred to as BB1GP, and with the above mentioned ABBGP method (see the previous section). In order to evaluate the hybrid strategy, we selected quadratic problems in which the ABBGP strategy, while being more efficient than BB1GP, employs a significant number of iterations. All the compared algorithms employed the non-monotone version of Armijo line search with $M=10$, $\beta = 0.4$, $\sigma =10^{-4}$. The initial steplength was set as $s_0 = \frac{{g^{(0)}}^T g^{(0)}}{{g^{(0)}}^T A g^{(0)}}$; furthermore, for LMGP2 we set $\omega =0.1$, and for Hyb-LMGP, Hyb-MLMGP we set $\tau _1 = 0.5$, $m_a = 2$ and $\zeta = 1.1$. The methods were stopped when $\Vert x^{(k+1)} - x^{(k)}\Vert \le 10^{-8}$ or the maximum number of 10000 iterations occurred. Number of iterations (It.), execution time (Time), number of backtracking steps (Backtr.) and absolute error on the objective function $|f(x^{(k)}) - f(x^*)|$ obtained by the considered methods on each test problems are shown in Tables 1, 2 and 3. We observe that for all the schemes, the number of matrix-vector products actually corresponds to the total number of gradient evaluations performed, and it can be deduced from tables by summing iteration numbers and number of backtracking steps. Moreover, in view of the small value of m, the computational cost of matrix-vector products involved in the Ritz procedure is negligible with respect to the matrix-vector products of type Ax. For LMGP1, LMGP2, Hyb-LMGP and Hyb-MLMGP the results for $m=3,5$ are reported. For Hyb-LMGP and Hyb-MLMGP the number of iterations in which the LM strategy was actually employed is reported in brackets. When comparing efficiency, we can observe that LMGP1 and LMGP2 are generally not competitive with ABBGP and the hybrid strategies, while in some cases they outperformed BB1GP. The results of Hyb-LMGP and Hyb-MLMGP are comparable with those obtained by ABBGP, with a slight improvements of the performance achieved by hybrid strategies when the number of active constraints is larger.

Finally, we compared the hybrid strategy Hyb-LMGP with the active-set method MPRGPp proposed in [33]. For a fair comparison both the algorithms were stopped when

$$\begin{aligned} \Vert \varphi (x^{(k)}) \Vert \le 10^{-8}\Vert g(x^{(0)})\Vert , \end{aligned}$$

(43)

where the vector $\varphi (x^{(k)})$ is defined component-wise as follows:

$$\begin{aligned} \varphi ^{(k)}_i = \left\{ \begin{array}{lcl} g^{(k)}_i &\quad \hbox { for } &{} \ell _i< x^{(k)}_i < u_i ,\\ \max \{0,g^{(k)}_i\}&\quad \hbox { for }&{} x^{(k)}_i = u_i ,\\ \min \{0,g^{(k)}_i\}&\quad \hbox { for } &{} x^{(k)}_i = \ell _i . \end{array} \right. \end{aligned}$$

(44)

The maximum number of iterations was set to 10000. The parameter setting of Hyb-LMGP is the same of the previous experiments, while for MPRGPp we considered the parameter assignment reported in ([40], Section 4.1). Table 4 reports the execution time (Time), the number of matrix-vector multiplications ($\left( {\overline{{\mathbf{n}}} } \right)$) and the relative error on the computed solution $\frac{\Vert x^{(k)} - x^*\Vert }{\Vert x^*\Vert }$, obtained by Hyb-LMGP ($m=3,5$) and MPRGPp on the quadratic test problems QP1, QP2, QP3. We can observe that Hyb-LMGP shows, on average, the best time and lower number of matrix-vector products than MPRGPp; however, as still observed in [40] for any GP method, it can achieve solutions of medium accuracy while MRPGPp algorithm can converge to higher accuracy.

Table 1 QP1

Table 2 QP2

Table 3 QP3

Table 4 Hyb-LMGP method versus MPRGPp method on quadratic test problems

5.2 General non-quadratic test problems

The practical efficiency of the considered methods has been assessed also on several box-constrained non-quadratic problems,

generated like in [25] using the technique devised by Facchinei et al. [41]. The resulting optimization problems are of the form

$$\begin{aligned} \min _{\ell \le x\le u } f(x)= g(x) + \sum _{i\in L} h_i(x_i) - \sum _{i\in U}h_i(x_i), \end{aligned}$$

(45)

where $g:{\mathbb {R}}^{n} \rightarrow {\mathbb {R}}$ is a twice continuously differentiable function, L and U denotes, respectively, the subsets of indices related to the components of the solution that are active at the lower bound and at the upper bound, $h_i:{\mathbb {R}}\rightarrow {\mathbb {R}}$, $i\in L\cup U$, are twice continuously differentiable non-decreasing functions whose expressions may change in accordance with the following choices:

• (1) $\beta _i\left( x_i - x^*_i\right)$,

• (2) $\alpha _i\left( x_i - x^*_i\right) ^3$ + $\beta _i\left( x_i - x^*_i\right)$,

• (3) $\alpha _i\left( x_i - x^*_i\right) ^{7/3}$ + $\beta _i\left( x_i - x^*_i\right)$;

here, $\alpha _i$ are random numbers in (0.001, 0.011) and $\beta _i = 10^{-\eta _i ndeg}$, where $\eta _i$ is randomly generated in (0, 1) and $ndeg = 1,4,10$. We remark that problem (45) is built as a corresponding box-constrained version of the unconstrained minimization problem

$$\begin{aligned} \min _{x\in {\mathbb {R}}^n} g(x), \end{aligned}$$

having a known solution point $x^*$ that is still a solution of problem (45). We chose as g(x) the following benchmark functions: Trigonometric function [42], Griewank function from http://www-optima.amp.i.kyoto-u.ac.jp/member/student/hedar/Hedar_files/TestGO_files/Page1905.htm and three test functions available at https://people.sc.fsu.edu/~jburkardt/f_src/test_opt/test_opt.html, namely, Extended Rosenbrock parabolic valley function, Extended Powell function, and Hilbert function. When using the Hilbert function we only considered the non-quadratic instances of formulation (45). For each test problem, the total number $n_{act}$ of active constraints at the solution takes three different values, i.e. $n_{act}\approx 0.1\cdot n,0.5\cdot n,0.9\cdot n$, and was determined in order that the number of lower active constraints was equal to the number of upper active constraints. The resulting dataset is composed of 123 non-convex box-constrained test problems. Problem sizes are set equal to 5000, except for Trigonometric function and Extended Rosenbrock function ($n=1000$). The starting vectors are defined as follows:

• $x^{(0)}= P_{\Omega }(x^*+ 0.3 \, r)$, where $r\in {\mathbb {R}}^n$ has random entries from a uniform distribution in $[-1, 1]$ (Trigonometric test problem);

• $x^{(0)}= P_{\Omega }(x^*+ 0.2 \, r)$, where $r\in {\mathbb {R}}^n$ has random entries from a standard normal distribution of mean 1 (Extended Rosenbrock test problem);

• $x^{(0)}=\frac{\ell +u}{2}$ (Griewank, Extended Powell, and Hilbert test problems).

Parameters setting of the algorithms is the same as previous experiments. We analyse the behaviour of the GP schemes by means of the performance profiles proposed in [43]. In particular, we evaluated the execution time required by each scheme to satisfy the following stopping criterion

$$\begin{aligned} {|f(x^{(k)})-f(x^*)|}\le 10^{-6}, \end{aligned}$$

within the maximum number of 10000 iterations. Runtime performance profiles curves are reported in Figs. 4, 5 and 6. Left panel in Fig. 4 shows the comparison between LMGP1 and LMGP2 with the maximum value m of the length of the sweep set to $m=5$: from this plot we can observe that LMGP1 is faster than LMGP2 on about $72\%$ of problems, whereas the performances of both the limited memory procedures were dominated by Hyb-LMGP on $67\%$ of test problems (right panel). For a fair comparison between Hyb-LMGP versus Hyb-MLMGP, Hyb-LMGP versus ABBGP and Hyb-MLMGP versus ABBGP (Fig. 5), we removed from the performance profiles plots 18 problem instances in which the hybrid strategies did not activate during the procedure. Indeed, if the limited memory strategy is not enabled at Step 5 of Algorithm 1, then the hybrid methods coincide with ABBGP, since they only perform the alternating BB steplength. We may observe that Hyb-MLMGP shows comparable results with respect to ABBGP (Fig. 5, right panel), while it proves to be less efficient than Hyb-LMGP on about $56\%$ of the problems (Fig. 5, left panel). Finally, Hyb-LMGP method looks faster than ABBGP (Fig. 5, middle panel), although its performance can be affected by the number of active constraints at the solution as shown in Fig. 6.

Fig. 4

Runtime performance profiles comparing LMGP1 versus LMGP2 (left panel), LMGP1, LMGP2 and Hyb-LMGP (right panel) on non-quadratic test problems

Fig. 5

Runtime performance profiles comparing Hyb-LMGP versus Hyb-MLMGP (left panel), Hyb-LMGP versus ABBGP (middle panel), ABBGP versus Hyb-MLMGP (right panel) on the 105 problem instances in which the hybrid strategies did not coincide with ABBGP

Fig. 6

Non-quadratic test problems. Runtime performance profiles comparing Hyb-LMGP vs ABBGP on the subsets of test problems generated by setting $n_{act}=0.1\cdot n$ (left panel), $n_{act}=0.5\cdot n$ (middle panel), $n_{act}=0.9\cdot n$ (right panel) in which the hybrid strategies did not coincide with ABBGP

5.3 Imaging problems

Given a corrupted image, Bayesian approaches to the imaging inverse problem suggest to recover the unknown true object by minimizing a functional which can be written as the sum of a discrepancy function and a regularization term. When the noise affecting the data is of Poisson type, the discrepancy function is the generalized Kullback-Leibler (KL) divergence defined as

$$\begin{aligned} \hbox {KL} (x) = \sum _{i=1}^{n} \left\{ b_i \ln \frac{b_i}{(Ax + bg)_i} + (Ax + bg)_i - b_i\right\} \, , \end{aligned}$$

where $A\in {\mathbb {R}}^{n\times n}$ is a linear operator modeling the distortion due to the image acquisition system, $b\in {\mathbb {R}}^n$ represents the data and $bg \in {\mathbb {R}}^n$ is a known positive background radiation constant. The matrix-vector products Ax or $A^Tx$ have been performed by employing the Fast Fourier Transform (FFT) [44]. As for the regularization term, we consider a smooth discrete version of the total variation, also known in the literature as hypersurface potential (HS), that, for a square $m\times m$ image with $m^2=n$, is defined as

$$\begin{aligned} \hbox {HS}(x) = {\sum _{i,j=1}^m} \sqrt{(({\mathcal {D}} {x})_{i,j})_1^2+(({\mathcal {D}} {x})_{i,j})_2^2+\delta ^2}\, , \end{aligned}$$

where ${\mathcal {D}}: {\mathbb {R}}^{m^2}\longrightarrow {\mathbb {R}}^{2m^2}$ is the discrete gradient operator with periodic boundary conditions

$$\begin{aligned} ({\mathcal {D}} {x})_{i,j} = \left( \begin{array}{c} (({\mathcal {D}}{x})_{i,j})_1\\ (({\mathcal {D}}{x})_{i,j})_2 \end{array} \right) = \left( \begin{array}{c} x_{i+1,j}-x_{i,j}\\ x_{i,j+1}-x_{i,j}\\ \end{array} \right) , \ \ \ x_{n+1,j} = x_{1,j}, \ \ \ x_{i,n+1} = x_{i,1}. \end{aligned}$$

We are interested in solving the following minimization problem

$$\begin{aligned} \min _{x\ge 0} \hbox {KL}(x)+\mu \hbox {HS}(x), \end{aligned}$$

(46)

where $\mu$ is a positive regularization parameter controlling the role of the HS functional. It is evident that problem (46) is a non-quadratic problem belongs to the class (1).

We consider two different datasets. The original images are reported in Fig. 7. The value of the regularization parameter has been fixed equal to 0.0045 for the Cameraman test problem and equal to $10^{-5}$ for the Spacecraft one. The value of $\delta$ in the definition of the HS functional has been chosen as 0.1 for both the datasets.

Fig. 7

Original images for the imaging problems

All the compared algorithms employ the non-monotone version of the Armijo line search with $M=10$, $\beta = 0.4$, $\sigma =10^{-4}$. Moreover, for LMGP2 we set $\omega =0.1$ and for Hyb-LMGP, Hyb-MLMGP and ABBGP we set $\tau _1 = 0.5$, $m_a = 2$ and $\zeta = 1.1$. Finally, for LMGP1, LMGP2 Hyb-LMGP and Hyb-MLMGP we report the results for different values of m, specified in brackets in the figures and in the tables reporting the results.

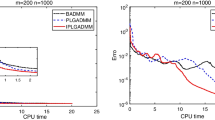
Let $f^*$ be the optimal value of the objective function obtained as the lowest value among those provided by all the methods after a maximum prefixed number of iterations (6000 and 15000 for the Cameraman and Spacecraft datasets, respectively). In Figs. 8 and 9 we report the following relative error on the objective function values

$$\begin{aligned} \frac{|f(x^{(k)}) - f^*|}{|f^*|} \end{aligned}$$

(47)

generated by the considered methods with respect to the iterations and the computational time for the Cameraman and the Spacecraft datasets, respectively. In Tables 5 and 6 we report the number of iterations and the computational time needed by each algorithm to make the relative distance defined in (47) between the objective function values and the optimal value below prefixed thresholds. The corresponding number of matrix-vector multiplications ($\bar{n}$) performed and the corresponding relative reconstruction error (RRE), namely the relative Euclidean errors between the k-th iterate and the true object, are also reported. We remark that, when a regularization term is present in the objective function, the optimization algorithms can be compared only with respect to their efficiency, since the quality of the reconstruction depends on the selected regularization term and the choice of the regularization parameter. However, the information on the RRE is provided for sake of completeness. Where the entries of Table 6 are blank, the relative algorithm does not succeed in making the distance (47) below the prefixed threshold in the prefixed maximum number of iterations.

Fig. 8

Decrease of the relative distance between the objective function values and the optimal value with respect to iterations (left panel) and computational time (right panel) for the Cameraman dataset

Fig. 9

Decrease of the relative distance between the objective function values and the optimal value with respect to iterations (left panel) and computational time (right panel) for the Spacecraft dataset

Table 5 Cameraman dataset: number of iterations and computational time (in seconds) to make the relative distance between the objective function values and the optimal value below given thresholds. The corresponding number of $\bar{n}$ and the RRE are also reported

Table 6 Spacecraft dataset: number of iterations and computational time (in seconds) to make the relative distance between the objective function values and the optimal value below given thresholds. The corresponding number of $\bar{n}$ and the RRE are also reported

From the results presented in Figs. 8 and 9 and Tables 5 and 6, the following comments can be drawn.

• Both the Hyb-LMGP and the Hyb-MLMGP approaches outperform the other algorithms considered in terms of number of iterations and computational time. Particularly, it is quite evident from Figs. 8 and 9 how, until the active components of the solution are not identified, the decrease of the objective function values provided by Hyb-LMGP and Hyb-MLMGP is the same as that achieved by ABBGP. However, from a certain k onwards, the behaviour of Hyb-LMGP and Hyb-MLMGP becomes significantly different from that of ABBGP since the LM or the MLM strategy kicks in and proves to be more efficient than the BB alternating steplength rule.

• For the Spacecraft dataset, whose solution has many more active components than the one of the Cameraman dataset, both Hyb-LMGP and Hyb-MLMGP differ from ABBGP later with respect to that happens for the Cameraman test problem, as evident from the columns related to tol $= 10^{-2}$ in Tables 5 and 6. This is due to the fact that, for the Cameraman dataset, the algorithms need more iterations to well approximate the active set corresponding to the solution.

• In general, the LMGP1 and the LMGP2 methods present the worst performance especially for the Spacecraft test problem whose solution presents many active components.

• The behaviour of the compared methods confirms how a limited memory steplength selection rule can be really effective only if it is employed when both the active and the inactive components of the iterates are stable for a sufficient number of successive iterations.

6 Conclusions

In this paper we consider gradient projection methods for the solution of box-constrained optimization problems. It is well known that the performance of these algorithms strongly depends on an effective strategy to select the steplength parameter. For this reason, we propose a steplength selection technique that automatically alternate standard Barzilai-Borwein like rules and limited memory ones based on a suitable approximation of the optimal active set. Several numerical experiments show the benefits of applying the suggested steplength rule with respect to state-of-the-art GP schemes in terms of number of iterations and computational time, especially in the case of non-quadratic box-constrained problems. Furthermore, in some quadratic experiments, the proposed algorithm showed its advantage with respect to an active set scheme, when medium accuracy solutions are required.