Introduction

Natural polymers and composites generated from renewable resources are receiving widespread consideration (Sharma et al. 2022). These materials are promising as they offer an alternative to synthetic materials and decrease the dependence on fossil sources in various applications (Wertz et al. 2010; Sundarraj and Ranganathan 2018). An important example of these materials is bast fibre-based yarns, which contain about 74% cellulose (Mwaikambo and Ansell 2002). Many efforts have been made to exploit the wide applications of bast fibres like hemp, jute, and flax (Anandjiwala and Blouw 2007). Among these yarns, hemp has an important standing as a natural source of yarns because of its wide availability, low cost, and it is fast-growing. About a quarter of the hemp yarns are utilised in industrial fields including building materials, the automotive industry, and thermal insulation materials (Haverhals et al. 2012b; Fortenbery and Bennett 2004; Tanasă et al. 2020).

The dissolution of cellulose is an area of great interest because cellulose cannot be dissolved in water and most organic solvents, primarily attributed to two factors. Firstly, cellulose chains are assembled into highly crystalline micro-fibrils, creating a crystalline structure (Pinkert et al. 2009). Secondly, due to the existence of intra- and inter-chain hydrogen bonds (Qian 2008), which form between the hydroxyl groups of adjacent chains (Gross and Chu 2010; Chen et al. 2015). The only way to dissolve cellulose is by breaking down the hydrogen bond network (Glasser et al. 2012; Lindman et al. 2010). This process can be achieved either through prior chemical modification of the macromolecule or without it (Sen et al. 2013). Classical solvents such as nitration (Barbosa et al. 2005), and esterification (Ratanakamnuan et al. 2012) have been employed for the first approach. However, the viscose process, historically used in the yarns industry for manufacturing regenerated cellulose, is associated with environmental drawbacks due to the use of hazardous chemicals like carbon disulphide (Lyncke 1908; Mitchell 1949). Consequently, due to these disadvantages, more acceptable solvent systems have been proposed to dissolve cellulose. For example, N-methylmorpholine-N-oxide (NMMO) is used industrially in the Lyocell process (Li et al. 2006). Nevertheless, NMMO still presents certain limitations, including difficult recycling and the requirement of relatively high dissolution temperatures (Cao et al. 2010).

The worries over the environmental impact of conventional organic solvents can potentially be mitigated by replacing them with ionic liquids. Ionic liquids (ILs) have demonstrated great promise as solvents in the last few decades (Bodachivskyi et al. 2020; Abushammala and Mao 2020). ILs are groups of organic salts with a low melting point, below the boiling point of water (100 °C) (Walden 1914; Matandabuzo and Ajibade 2018; Wasserscheid and Keim 2000). These salts have negligible vapour pressure, which means reduced emission of harmful gases, making them safer to handle and recycle (Huber et al. 2012). A large number of ionic liquids can potentially be synthesised through the combination of various anions and cations. Thus, ILs can potentially replace conventional solvents in many applications (Duchemin et al. 2009; Shamsuri et al. 2021). As a result of these properties, ILs have been explored as promising solvents for many science and technology fields, including the dissolution of cellulose to form all-cellulose composites (Abushammala and Mao 2020).

In 2002, ILs were reported to dissolve cellulose to replace conventional toxic solvents by Swatloski et al. This research explored the solubility of cellulose in 1-butyl-3- methylimidazolium chloride-based ionic liquids, where [BMIM] [Cl] was the first use of an ionic liquid in the field of cellulose technology as a suitable solvent. They also found that adding anti-solvents such as water, ethanol, and acetone could readily regenerate the dissolved cellulose (Swatloski et al. 2002; Rogers and Seddon 2003). After that, ILs were employed as an appropriate medium to process cellulosic materials, and several studies confirmed that cellulose, whether regenerated or raw, could be dissolved in ionic liquids (Kilpeläinen et al. 2007; Wu et al. 2004; Gong et al. 2014). [C2mim][OAc] (1-ethyl-3-methylimidazolium acetate) represents an efficient solvent for biopolymers and can dissolve high biomass concentrations (Haverhals et al. 2012a; Marks et al. 2019). [C2mim][OAc] has a low melting point, outstanding thermal stability and low vapour pressure (132.91 mPas) at room temperature (Quijada-Maldonado et al. 2012).

Understanding the behaviour of the dissolution of cellulose fibres in ionic liquids and their interactions with these solutes is extremely important (Ghasemi et al. 2017; Aiello et al. 2022). Especially, for recycling hemp textiles, the dissolution of hemp textiles in ILs is a promising method that involves selective dissolution for fibres while other components such as dyes and finishes remain insoluble. This approach preserves the inherent properties of hemp fibers. However, challenges such as the selection of suitable ionic liquids and the optimization of dissolution and regeneration processes need to be addressed to enhance the efficiency and scalability of the recycling method (Burgada et al. 2021; Lawson et al. 2022).

Lately, cellulose fibres’ dissolution in the ionic liquid [C2mim][OAc] was studied by a number of authors. For example, time-temperature superposition has recently been studied by Chen et al., who found that rising temperature leads to an increase in both the dissolution and swelling phenomena in the ionic liquid [C2mim][OAc]) (Chen et al. 2020a). Several published papers show that the dissolution of cellulose in [C2mim][OAc] follows an Arrhenius behaviour (Liang et al. 2020; Hawkins et al. 2021). This current work investigates the dissolution of hemp yarns in the ionic liquid [C2mim][OAc] upon processing with different temperatures and times. The partially dissolved hemp yarns were coagulated within a water bath as an anti-solvent, forming swollen cellulose by water in the pores, for simplicity, termed hydrogels. Hence, the swelling ratio of different regions of the dissolved cellulose yarns was determined. Optical microscopy (OM) was used to observe the changes in samples’ morphology due to the dissolution process at different temperatures and times. The dissolution process is quantified on both types of samples, hydrogels and dried samples, with different quantifying methods based on the outcomes from OM. This work includes determining the dissolution activation energy \(({E}_{a})\) using time-temperature superposition (TTS). Also, a modelling method for analyzing TTS data was developed to track growth regions within the dissolution system through quantifying the self-diffusion coefficient of [C2mim][OAc] in cellulose. Apart from providing quantitative information on the physics of the cellulose dissolution process, the processing methods and results presented in this study may facilitate future research on the dissolution of cellulose-based materials and the fabrication of hemp-based all-cellulose composites. Also, it may contribute to enhancing recycling methods for cellulose fibres and textiles that require complete dissolution.

Materials and methods

Materials

Hemp-in the form of continuous yarns, with a diameter of approximately 0.4 mm, were purchased from Etsy, Inc., UK. The ionic liquid 1-ethyl-3-methylimidazolium acetate ([C2mim][OAc]) with purity ≥ 98%, and with water content < 0.2% determined using a Karl Fischer titration apparatus (899 Coulometer, Metrohm U.K. Ltd., UK) was purchased from Proionic GmbH, Grambach, Austria). Molecular weight, lignin concentration, and carbohydrate composition of hemicelluloses of hemp yarns are presented in Table 1. Carbohydrate composition was conducted by the acid methanolysis method, as explained in the supplementary information, SI1.

Table 1 Molecular weight, lignin concentration and carbohydrate composition of hemicelluloses of hemp yarns
Full size table

Dried hemp specimens were embedded within Epoxy resin (Epoxicure, Cold Cure Mounting Resin from Buehler, UK) for use with optical microscopy.

Methods

Processing of Hemp samples with [C2mim][OAc]

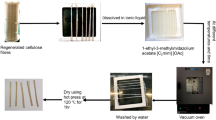
The first step was to wind the hemp yarns around a Teflon picture frame of dimensions 8 cm × 8 cm. Ten individual yarn loops were put onto the Teflon-frames to give a number of samples for repeated optical measurements, all made under the same conditions of time and temperature (see Fig. 1).

Fig. 1
figure 1

The preparation process of partially dissolved hemp samples: a Hemp hydrogel (HH) samples under the optical microscope for the hydrogel method, where the frames were fixed in a water bath to investigate the side view morphology of the samples, b embedded hemp samples in epoxy resins after being dried in a vacuum oven to investigate cross-sections of the dried hemp (DH) samples

Full size image

Teflon dishes filled with about 50 mL of the ionic liquid [C2mim][OAc] were preheated in an oven for 50 min to the desired temperature. Then, the frames were submerged in the dishes containing the preheated [C2mim][OAc] with a solid-to-liquid mass ratio of 1–40, which were placed into a vacuum oven (Shellab 17 L Digital Vacuum Oven SQ-15VAC-16, Sheldon Manufacturing, Inc., USA).

The vacuum was maintained during the dissolution process to prevent the absorption of atmospheric moisture by the IL, since many studies have shown notable interactions between water and [C2mim][OAc] (Hawkins et al. 2021; Lovell et al. 2010; Gschwend et al. 2020). Dissolution occurred for a certain period (0.25, 0.5, 0.75, 1, 2, 4 and 6 h) at the four target temperatures (30 °C, 35 °C, 40 °C, and 50 °C). After taking out the hemp samples from the [C2mim][OAc] solvent with care to avoid any disturbance, a water bath was then utilised for the coagulation process. This step took place under slowly running water for 24 h at room temperature, aiming to remove all the IL from the samples and coagulate any dissolved cellulose.

In the case of the hydrogel method, submerged samples within water were measured using the optical microscope to observe the coagulated section from a longitudinal view of the processed yarns, which were kept on the frames, as shown in Fig. 1a.

To obtain the dried samples, the samples were dried for one hour under a vacuum at 120 °C after being removed from the water. These details of the drying process have been previously reported (Liang et al. 2020). Samples are labelled: hemp hydrogel yarn (HH) and dried hemp yarn capsulation within epoxy resin (DH).

Optical microscopy

Optical Microscopy (OM) is used to obtain morphological images of hemp yarns. It is used both before the processing with [C2mim][OAc] ionic liquid and afterwards. A complementary technique used in a recent cellulose dissolution study was Raman mapping, where this was employed to track the fraction of dissolution with time and temperature (Cosby et al. 2021). However, OM as a simple technique provides substantial insights into the underlying physics of dissolution; it is also considered as a fast method of determining the amount of dissolved yarn due to the noticeable differences between raw and coagulated material when viewed under a microscope. The dissolved and coagulated material is seen to be clear under the microscope as the plant structure (and any small internal voids) are destroyed. Previous studies have verified the efficacy of this measurement technique in quantifying yarns dissolution for flax and cotton materials, which resulted in accurate and reproducible findings (Chen et al. 2020b; Liang et al. 2020; Aslan et al. 2011). An optical microscope (BH2-UMA, Olympus Corporation, Japan) was utilised in reflection and transmission mode to explore the morphology of the processed hemp yarns of the dried samples DH (cross-section) and the hydrogel samples HH (side/longitudinal view), respectively. Hence, the partially dissolved yarns were investigated in two different directions: a dried cross-section encapsulated in an epoxy resin and a longitudinal section within water (hydrogel method) as follows.

In the hydrogel method for partially dissolved hemp yarns within an aqueous medium: immediately after removing the samples from the vacuum oven, the frames were fixed in a water bath to investigate the samples’ morphology using the optical microscope, as shown in Fig. 1a. The lowest magnification (5× magnification) of the objective lens was used to view the samples; the partially dissolved yarns were found to swell when saturated with water.

Two distinct regions are visible in the optical micrographs from this longitudinal view (dark and light areas), as shown in Fig. 2a, where a clear difference between the two sections can be observed. The undissolved inner (dark layer) can be seen to be surrounded by a coagulated outer layer, see Fig. 2a. The outer layer is comprised of cellulose that has undergone the dissolution and coagulation process. Average inner (Wi) and outer (WO) diameters of the (HH) processed yarns were determined using the Image J processing software to find the ring thickness of the swollen dissolved fraction. Four different hydrogel samples (HH), and 20 sampling points along the length of each yarn were measured at each temperature and time to provide more accuracy. Figure 2a illustrates the clear boundaries between core and coagulated material where the ring thickness in water \({(T}_{H})\) was calculated according to Eq. (1).

$${ T}_{H} ={( W}_{o }- { W}_{i } )/2$$
(1)
Fig. 2
figure 2

a Longitudinal section of samples under an optical microscope with a scale bar indicating 200 microns, where (Wi) is the inner diameter and (WO) is the outer diameter of partially dissolved yarn. b Cross-section of partially dissolved yarn, the coagulated fraction (CF) was determined through finding the total area (indicated with the red arrow) of the fibrous cross-section and the area of the central yarn (indicated with the blue arrow). c Determining the ring thickness of coagulated fraction through measuring total outer (indicated with the black arrow) and inner core (indicated with the blue arrow) diameters—the scale bars indicating 200 microns

Full size image

where \({W}_{0 }\) and \({W}_{i }\) represent the total outer diameter of the whole hydrogel sample (HH) and the diameter of the central region of the HH samples, respectively. Later, the calculated inner (Wi) and outer (WO) diameters of the partially dissolved yarns were also used to calculate the swollen coagulated fractions of samples from the hydrogel samples \({(CF}_{H})\) as follows:

$${CF}_{H}=\left[{{\pi ( W}_{o }/2)}^{2}- {{\pi ( W}_{i }/2)}^{2}\right]/\left[{{\pi ( W}_{o }/2)}^{2}\right]$$
(2)

In the case of the dried yarns: the method of measuring the coagulated fraction in these dried partially dissolved yarns has previously been reported by Hawkins et al. on flax fibres (Hawkins et al. 2021). In this work, the same steps were followed to determine the dissolved part of the processed flax yarns. After drying the samples, each set of four DH samples was embedded in an epoxy resin and polished down to the surface in order to allow the micromorphology of a cross-section to be investigated, as shown in Fig. 1b. Upon processing, two different regions are visible in the optical micrographs, see Fig. 2b. The inner fibrous core can be seen to be surrounded by a notably different outer layer. The outer ring of dissolved hemp represents the coagulated cellulosic material.

The ring thickness \(({T}_{E})\) and the fraction of the surrounded coagulated cellulose as measured in the epoxy \({(CF}_{E})\) was determined using the image processing software (Image J). Equations (3) and (4) were used to calculate \(\left({CF}_{E}\right)\) and \(({T}_{E})\) as shown below:

$${CF}_{E}= ( {A}_{0} - {A}_{i}) / {A}_{0}$$
(3)

where \({A}_{0 }\) and \({A}_{i }\) represent the total cross-section area of the whole dried hemp sample (DH) and the cross-section area of the central undissolved fraction of these samples, as shown in Fig. 4c.

Fig. 3
figure 3

a Optical microscope picture of hemp materials before processing with the ionic liquid [C2mim][OAc]. b Hemp material after being processed with [C2mim][OAc], the outer layer (indicated with the blue arrow) is the coagulated section, and the undissolved core (marked with the red arrow)—the scale bars indicating 200 microns

Full size image
$${ T}_{E} ={( D}_{0 }- { D}_{i } )/2$$
(4)

where \({D}_{0 }\) and \({D}_{i }\) represent the total outer diameter of the whole dried hemp sample (DH) and the diameter of the central region of the DH samples, which are represented in Fig. 2c. In both methods, it is assumed that the outer layer is made of cellulose that has undergone the dissolution and coagulation process. The swelling ratio of the outer ring (Rring) and central core (Rcore) was calculated according to the following equations:

$${{R}_{ring}=(W}_{o}-{W}_{i} )/({D}_{o}-{D}_{i} )$$
(5)
$${{R}_{core}=W}_{i} /{D}_{i}$$
(6)

where Wo and Wi represent the outer diameter and the diameter of the inner central core of the submerged HH samples, respectively; while Do and Di measure the diameter of the whole dried DH sample and that of the undissolved/central region of DH respectively, as seen in Fig. 2.

Also, based on time-temperature superposition (TTS) data presented in Fig. 9, a modelling approach is carried out to investigate the behaviour of the growth of the thickness of the outer coagulated region with time. Hence the diffusion behaviour of the ionic liquid [C2mim][OAc] into cellulose was investigated, as detailed in the results section.

Results and discussion

Micromorphology using the hydrogel method

Optical microscopy allowed observation of a longitudinal view of each sample within water. Unprocessed yarns have the appearance of a black region, which consists of yarns compressed tightly together and some internal voids which will scatter light. This tight packing may act to slow the penetration of the solvent deep into the core; so that dissolution proceeds from the outside inwards, as will be seen in later optical micrographs. Images of unprocessed yarns can be seen in Fig. 3a. After the partial dissolution process, two distinct regions were observed in the optical micrographs (dark and light areas). The undissolved inner core (dark layer) can be seen to be surrounded by a notably different outer layer, see Fig. 3b. This outer layer (indicated with the blue arrow) is comprised of cellulose that has undergone the dissolution and coagulation process. The undissolved core is marked with a red arrow. The clear boundaries between the inner (undissolved) section and the outer (coagulated) material can be observed. Immersing in water swells the outer dissolved and coagulated layer and improves the accuracy of following the dissolution with time and temperature by reducing the relative errors in the size/area measurements.

The Image J software was used to trace the boundaries of the inner and outer regions. This was repeated, and average values were calculated from four samples dissolved under identical conditions. Hence, the growth of the ring thickness and the coagulated fraction can be measured as a function of dissolution time and temperature. The swollen ring thickness \({ (T}_{H})\) was calculated using Eq. (1), and then the coagulated fraction \({(CF}_{H})\) was determined through measuring the radii of each sample using Eq. (2). As seen in Fig. 4, the most prominent finding to emerge from observing these optical images is that a notable correlation was found between rising temperature and/or time and the growth of the coagulated fraction. The appearance of the core remains unchanged, and this is taken as evidence that dissolution proceeds inwards with time.

Fig. 4
figure 4

Optical microscope pictures of processing hemp yarns at 40 °C for different times: a 0.5 h, b 1 h, c 2 h, and d 4 h with scale bars indicating 200 microns

Full size image

Epoxy resin method

Optical micrograph of unprocessed hemp yarn, embedded in epoxy resin is seen in Fig. 5a, while Fig. 5b represents a cross-section of the processed DH sample after being partially dissolved with the IL. It can be noted that the unprocessed yarns (before the dissolution process with IL) have rounded edges. Each yarn consists of a loose arrangement of many smaller hemp microfibers, bundles packed tightly together.

Fig. 5
figure 5

a Cross-section of unprocessed hemp material under an optical microscope. b Cross-section of partially dissolved yarn after being processed with [C2mim][OAc]

Full size image

In the case of the partially dissolved yarns, this tight packing prevents the penetration of the IL into the fibrous core, as shown in Fig. 5b. Instead, the clear boundaries between the dissolved and undissolved sections move toward the centre with increasing dissolution time seen in Fig. 6, which represents micrographs of processed yarns at 40 °C for different times 0.5 h, 1 h, 2 h, and 4 h. It is noted that the structure of the undissolved section is visually similar to the structure of the unprocessed yarns, reinforcing this point. This material involved an undissolved central core surrounded by a dissolved and coagulated section.

Fig. 6
figure 6

Optical microscope pictures of processing hemp material embedded in epoxy resin at 40 °C for different times a 0.5 h, b 1 h, c 2 h, and d 4 h with scale bars indicating 200 microns

Full size image

The most striking result is that the yarns display the outer coagulation fraction, where this fraction increases in size with increasing temperature and/or time. This result matches those observed in the earlier described hydrogel method. The coagulated fraction \(\left({CF}_{E}\right)\) of yarns calculated by determining the total area of the fibrous cross-section and the area of the central yarn, was shown above in Fig. 2b. However, the ring thickness \({( T}_{E})\) was determined by measuring the inner diameter and the total diameter of the yarn, as shown in Fig. 2c.

A common finding in both methods (hydrogel and resin epoxy) is that the coagulated fraction notably forms quickly around the inner core, and then growth slows at longer times. This behaviour is thought to be because of the presence of the outer dissolved layer, which works as a barrier between the raw inner part and the ionic liquid.

Time temperature superposition

The ring thickness and the coagulation fraction of the processed yarns at different temperatures and times were measured by optical microscopy via the two methods (hydrogel method and epoxy resin method). The results are presented in the following sections.

Hydrogel method

The swollen thickness \({ (T}_{H})\) and the coagulated fraction \({ (CF}_{H })\) increased with increasing processing time and temperature, as shown in Figs. 7a and 8a, respectively. These results correspond with the previous findings, which were observed via the optical microscope images in Figs. 5 and 6.

Fig. 7
figure 7

a The ring thickness \({ (T}_{H})\) as a function of dissolution time for all dissolution temperatures, the lines are guides to the eye. b \({ (T}_{H})\) as a function of dissolution time for all temperatures expressed in ln time, the line is a polynomial of order two fit to the data. c Master curve showing the influence of both time and temperature on the ring thickness, the line is a polynomial of order two. d Arrhenius plot showing the relation between shift factors ln α and temperature, the line is straight line fit to the data

Full size image

Investigation of the curves in Fig. 7a indicated that: a time-temperature equivalence might be used to obtain a master curve at each temperature, as is routinely used in analysing rheological data and as we have employed in our previous studies on flax, cotton and silk (Hawkins et al. 2021; Liang et al. 2020; Zhang et al. 2021).

The process used to create a master curve at 40 °C was as follows: all data were shifted towards 40 °C, which was selected as the reference temperature (as shown in Figs. 7 and 8a. A scaling factor (αT) was obtained by applying the equation:

$${\text{t}}_{{\text{T}}}^{{\prime }} {\text{ = }}\alpha _{{\text{T}}} {\text{ t}}_{{\text{T}}}$$
(7)

where \(\left( {{\text{t}}_{{\text{T}}}^{{\prime }} } \right)\) is the shifted time, αT scaling factor and, tT time. Written in natural logarithms, this becomes,

$${\text{Ln }} \left( {{\text{t}}_{{\text{T}}}^{{\prime }} } \right){\text{ = ln }}\left( {\alpha _{{\text{T}}} } \right)+{\text{ ln }}\left( {{\text{t}}_{{\text{T}}} } \right)$$
(8)

First, the data is displayed in natural logarithmic time (ln (t)). To provide a visual guide for the shifting, the 40 °C data was fitted with a polynomial function. Each other temperature-dependent data set was horizontally shifted by an amount ln (αT) towards the reference data by eye. After that, a polynomial function was used to fit all the data points. Small adjustments were then made to all the shift factors to maximize the R2 of this polynomial fit. Figure 7b and 8b show data after being shifted to 40 °C as a reference temperature, whilst Figs. 7c and 8c show the time-temperature superposition (TTs) plot after being shifted to 40 °C. It can be noted that the master curve represents evidence of time-temperature superposition (TTs) within the system. The master curves result from Figs. 7c, and 10c, shown in terms of the linear time, indicate that the speed of dissolution is initially relatively fast and then slows down as time progresses. To examine the relationship between the dissolution time and temperature, the shift factors were plotted versus the inverse of their temperatures; see Figs. 7d and 8d. Linear plots resulted from this analysis, which means the dissolution dynamics follow Arrhenius-type behavior. This permits the calculation of the dissolution activation energy for the processed yarns using the Arrhenius equation,

Fig. 8
figure 8

a Coagulated fraction (CF) as a function of dissolution time for all dissolution temperatures, the lines are guides to the eye. b CF as a function of dissolution time for all temperatures expressed in ln time, the line is a polynomial of order two fit to the data. c Master curve showing the influence of both time and temperature on the coagulation fraction. d Arrhenius plot showing the relation between shift factors ln α and temperature, the line is straight line fit to the data.

Full size image
$${ \alpha }_{T} =A {e }^{{- E}_{a} / \text{R}\text{T}}$$
(9)

where \({E}_{a}\) is the dissolution activation energy, \(A\) Arrhenius pre-factor, R the gas constant, T temperature, and αT the scaling factor at temperature (T). The value of the dissolution activation energy \({(E}_{a})\) of hemp yarns in [C2mim][OAc] was determined from the slope of Figs. 7d and 8d. The average value of the dissolution activation energy \({E}_{a}\) resulting from the hydrogel method of hemp yarn in [C2mim][OAc] is 78 ± 2 kJ/mol. The uncertainty here comes from using the LINEST function in Excel.

Epoxy resin method

The second method that has been used to measure the ring thickness and coagulated fraction for hemp yarns was the epoxy resin method. Dried samples were prepared and measured to compare with the results obtained from the hydrogel method. The same analysis, as outlined above, has been followed to determine the value of dissolution activation energy for hemp, see Figs. 9 and 10.

Fig. 9
figure 9

a The ring thickness \((T_E)\) as a function of dissolution time for all dissolution temperatures, the lines are guides to the eye. b \((T_E)\) as a function of dissolution time for all temperatures expressed in ln time, the line is a polynomial of order two fit to the data. c Master curve showing the influence of both time and temperature on the ring thickness; the line is a polynomial of order two. d Arrhenius plot showing the relation between shift factors ln α and temperature, the line is straight line fit to the data

Full size image

The two parameters \(({\text{T}}_{\text{E}})\), and (CFE) were used in analysing data as shown in Figs. 9 and 10 allowed calculating the average value of the dissolution activation energy \({E}_{a}\) resulting from the epoxy resin method of hemp yarn in [C2mim][OAc] is 78 ± 3 kJ/mol.

The rate of rising both ring thickness and coagulation fraction was found to decrease with increasing time, as seen from master curves Figs. 7c, 8c, 9c, and 10c. One hypothesis is that as the time of processing increases, more and more of the outer cellulose is dissolved, which may act as a protective barrier between the inner core and exterior solvent.

Fig. 10
figure 10

a Coagulated fraction (CFE) as a function of dissolution time for all dissolution temperatures, the lines are guides to the eye. b CFE as a function of dissolution time for all temperatures expressed in ln time, the line is a polynomial of order two fit to the data. c Master curve showing the influence of both time and temperature on the coagulation fraction; the line is a polynomial of order two. d Arrhenius plot showing the relation between shift factors ln and temperature, the line is straight line fit to the data

Full size image
Table 2 Measure the ring thickness and coagulated fraction of dissolved yarns to obtain the dissolution activation energy \({(E}_{a})\) for hemp yarns using the hydrogel method of a submerged sample within water, and the epoxy resin method of the dried samples
Full size table

As seen in Table 2, the two methods (Hydrogel and Epoxy resin) and four parameters \({(T}_{H}), \;\)\({(CF}_{H}),{(T}_{E}), \; and \; {(CF}_{E})\) were used to calculate the average dissolution activation energy \({(E}_{a})\) for hemp yarns. Excellent agreement is found between the two methods where the average calculated dissolution activation energy \({(E}_{a})\) is 78 ± 2 kJ/mol. This value compares with many studies that reported values of activation energy of cellulosic yarns in the ionic liquid [C2mim][OAc]. For example, Liang et al. report that a single cotton yarn’s dissolution activation energy is 96 ± 8 kJ/mol, where they showed that the activation energy was independent of the fibre arrangement (e.g. 1, 2 or 3 of the same fibres twisted together) (Liang et al. 2020). In another work, a similar value for the activation energy of flax yarns in [C2mim][OAc] was documented at 100 ± 10 kJ/mol (Hawkins et al. 2021). Other factors could affect the dissolution process such as the source of the material, crystal structure, hemicellulose content and the type and purity of the ionic liquid, see Table S1. This is part of on-going research by this group.

Study swelling ratio in the radial direction of hemp samples

The swelling ratio of different regions of hemp samples was calculated by Eqs. (5) and (6), according to the optical microscope images shown in Figs. 4 and 6.

As shown in Fig. 11a and b, the swelling ratio of both the central core and the outer ring is almost constant within the measurement uncertainties and is consequently independent of the time and temperature of the dissolution process. The average swelling ratios were calculated to be 4.4 ± 0.2 and 1.4 ± 0.1 for the outer ring and central core, respectively. The outer ring swelled by ×3.1 as much as the swelling of the central region. Liang et al. (2022) reported a similar result for the regional swelling ratio of cotton materials. The average swelling ratio of the outer ring was = 5.0 ± 0.1, while it was 1.49 ± 0.05 for the central core, which means the outer ring swelled by ×3.4 times the central one. This suggests that the ionic liquid does not significantly penetrate past the inner boundary of the coagulated region.

Fig. 11
figure 11

Radial swelling ratio as a function of dissolution time for a the outer ring (Rring) and b the central core (Rcore) of hydrogels (HH) samples

Full size image

Modelling growth of Coagulated Region

An interesting further analysis can be done from the data shown in Fig. 9c, which showed the growth of the thickness of the outer coagulated region with time. Based on the analysis of time-temperature superposition (TTS) data it is seen that the rate of growth of this outer region slows with time. Further, Fig. 12 shows that if the layer thickness is plotted against √t, where t is the time of dissolution, then the results fit well to a straight line. This suggests that the growth of the coagulated regions is controlled by diffusion. In one-dimensional diffusion, we have:

$$\text{r}\sim{< {r}^{2}>}^{1/2}={\left(2D\right)}^{1/2}\,{*}\,{\text{t}}^{1/2}$$
(10)

where r is the distance diffused in time t for a molecule with self-diffusion coefficient D, and here r is modelling the thickness of the coagulated region. The gradient of the straight line in Fig. 12 gives the value of D of \(6.74\times {10}^{-13}\) m2/sec at a temperature of 40 °C. In previous work, the diffusion of the ionic liquid ([C2mim][OAc]) in various concentrations of cellulose was measured using nuclear magnetic resonance (NMR). It was found that the diffusion depends on the density of OH-groups and an associated fraction (\(\alpha )\) was quantified (Ries et al. 2014), as shown in the following equation:

$$\alpha =N \times \frac{{M}_{IL}}{{M}_{Cel}}\times \frac{{\varnothing}}{100-{\varnothing}} \left(13\right)$$

Where \(N\) = 3 for cellulose, which is the number of OH-groups per cellulose unit, \({M}_{IL}\) is the molar mass of the ionic liquid (170 g/mol), \({M}_{Cel}\) is the molar mass of a cellulose unit (162 g/mol), and ϕ the weight% of the carbohydrate (Ries et al. 2014). When we substitute \(\alpha\) is 1 (case when IL is saturated by cellulose) in the Eq. 13 this gives \({\varnothing}\) of 23.5 wt%. In the Figure below we plotted the diffusion coefficient versus cellulose concentration at 40 °C from the previous work (Ries et al. 2014) and have extrapolated to 23.5 wt%. This shows that the diffusions coefficient found in the above modelling is consistent with the ions diffusing through a saturated layer of cellulose. As can be seen from Fig. 13 the diffusion coefficient found from this analysis agrees extremely well with the previous published NMR data. The modelling strongly suggests that a saturated cellulose solution developed around the yarn before it coagulated, where the IL diffuses through the system.

Fig. 12
figure 12

Plot of the thickness of the outer layer at 40 °C as a function of \(\sqrt {\mathbf{t}}\)

Full size image
Fig. 13
figure 13

Diffusion coefficient (anion) of the ionic liquid [C2mim][OAc] as a function of cellulose weight percentage. The solid line is quadratic fitting to the experimental data. The red square is the diffusion value found from the analysis of the coagulation thickness against time

Full size image

Conclusion

This article reports the dissolution behaviour of hemp yarns in the ionic liquid [C2mim][OAc]. Yarns were processed with the ionic liquid at different temperatures for a range of dissolution times. Optical microscopy (OM) was used to quantify the amount of dissolution; the ring thickness and the coagulation fraction were calculated from OM pictures of processed yarns. The growth of both the swollen thickness and coagulated fraction was found to follow time-temperature superposition. OM pictures show that hemp yarns were dissolved from the outer layer inwards, with a coagulation layer forming around the undissolved central core. The coagulation layer increased as time and/or temperature increased. An Arrhenius equation was used to calculate dissolution activation energy for hemp yarns. The average dissolution activation energy was determined to be 78 ± 2 kJ/mol. As the hydrogel method was quicker and simpler to perform compared with the epoxy method, this method is highly recommended for applying in the future as the default measurement technique. In addition, the swelling ratio in water of the outer and inner rings of the processed fibres was determined based on the micrographs. It was calculated to be 4.4 ± 0.2 and 1.4 ± 0.1 for the outer ring and central core, respectively. Hence, the outer ring swelled by ×3.1 as much as the swelling of the central region. The growth of the coagulated region with time was modelled by a diffusion-limited process (proportional to the square root of time), giving a diffusion coefficient for the IL of \(6.74\times {10}^{-13}\) m2/s, which compared extremely well with previously published NMR data. The modelling suggests that a saturated cellulose solution developed around the yarn before it coagulated. The processing methods and findings outlined in this study have the potential to significantly advance research in the field of cellulose-based material dissolution. Furthermore, they offer promising prospects for the creation of all cellulose composites using hemp-based materials, which could facilitate the production and recycling of cellulose textiles in the future.