Compression failure in dense non-woven fiber networks

Abstract

Investigating the compression properties of randomly ordered fiber networks experimentally is difficult which has resulted in ongoing disputes as to the mechanisms controlling the compression strength in such materials. In this work, we investigated compression properties of randomly oriented fiber networks with a special emphasis on cellulose products such as paperboard. We numerically reconstructed the conditions of the short span compression test widely used to quantify the compression strength of paperboard. We found that the phenomenological failure mode of such networks is elasto-plastic buckling. The x-shaped failure mode observed in physical experiments appears when test specimen restraints are included in the model. The most significant improvements to sheet strength can be obtained by improving the elastic properties while the strain to failure is increased most by an improvement of the plastic yield and hardening properties of individual fibers. Bond breaks were confirmed to have a smaller influence on the overall response. Fiber level microscopic buckling was investigated in depth, providing quantitative estimates of the fraction of mass likely to buckle at the microscopic level. The analysis indicated that only a low to moderate number of load carrying fibers can be expected to buckle. The inherent strength reserve in non-ordered fiber networks was investigated by introducing hinge mechanisms throughout the network, and the effect was shown to be small for a small to moderate number of hinges.

Introduction

Cellulose based packaging materials are strong candidates to replace fossil-based materials such as plastics in societies that wish to reduce their dependence on non-sustainable resources. Cellulose is abundant, cheap, biodegradable and can be tailored to fit a range of commercial purposes. However, cellulose based materials present challenges due to their micromechanical structure. A sheet is made up of densely packed fibers with a high degree of anisotropy. There is no matrix, and all the load is transferred via points of contact between the fibers. A simple sheet of paper exhibits material non-linearity in the form of plasticity, creep, rate-dependent behavior and inelastic strains induced by moisture and temperature.

Beginning with Cox’ predictions of fiber network elastic modulus, analytic, experimental and numerical methods have been devised to study the tensile network response (Cox 1952). In a series of papers, Page explored the connection between papermaking inputs and product performance, culminating in a theory for the elastic stiffness and tensile strength (Page 1969; Seth and Page 1981).

However, packaging mainly fails in pure compression or failure of the compressed side during bending. The McKee formula predicts the collapse load of boxes and is given in Eq. (1) (McKee et al. 1963). Here, a and b are empirical constants, ECT is the edge crush strength, Z is the perimeter of the box, and $S_{b,MD}$ and $S_{b,CD}$ are the bending stiffness of the paperboard in the machine direction (MD) and cross direction (CD) normalized with respect to the width.

$$\begin{aligned} BCT =a \cdot ECT^{b} (\sqrt{S_{b,MD} S_{b,CD}})^{1-b} Z^{2b-1} \end{aligned}$$

(1)

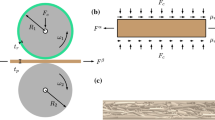
Using the McKee formula with typical fitting parameter values ($b\approx 0.75$) suggests that improvements to the edgewise compression strength is the most effective way to improve performance (McKee et al. 1963), which raises the question of what controls the edgewise compression strength and how it can be increased. A standard way of measuring the ECT is via the Short span Compression Test, illustrated in Fig. 1 and discussed in detail in the "Method" section.

Fig. 1

The Short span Compression Test (SCT). This test is one of the most commonly used to evaluate the edgewise compression strength of paper and board. From a strip of material with dimensions $15 \times 60$ mm$^2$, a short segment (0.7 mm) in the middle is kept free. The rest of the material is clamped with force control. A test consists of moving the clamps using a force-controlled program and recording the force. The program stops once the magnitude of the recorded force at time t is smaller than the force in the previous load step

The strength of paper is lower in compression than in tension, and therefore tensile properties are not directly applicable to explain and improve compression strength. Furthermore, due to the experimental difficulties of accurately capturing the mechanical response of a non-affine and slender structure, different methods of estimating compression strength give dissimilar results (Mark and Borch 2001; Popil 2017). It is not clear from any of the currently adopted compression tests what can be done to delay the initiation of failure, nor what performance gain is possible if a particular failure mode is inhibited. Commonly used methods to predict static strength of even simple geometries such as corrugated boxes have an unaccounted variance in outcome for identical input of 18% (Coffin 2015) and state of the art models are still off by 5–8% (Coffin 2015; Shallhorn et al. 2004; Nordstrand 2003). Given the strong correlation between box strength and material ECT, and the relative ease with which wall thickness can be measured and controlled, much of this variance comes from differences in material strength.

While there are several continuum mechanics models which address the behavior of paper in compression, these models are phenomenological in nature without providing an underlying explanation for the differences between tensile and compression response. Ideally a model to study compression failure should take as input the inputs of the paper-making process: fibers, bond characteristics, and network organization. As outputs, the most relevant measure is that of the macroscopic failure stress or peak force normalized with respect to width, both of which can be compared directly with physical experiments.

Compression failure in paper and paperboard

Edgewise compression strength may refer to many different modes of failure but is understood to apply mainly to failure at slenderness ratios below 30. The slenderness ratio is defined as $\lambda = L/\sqrt{I/A} = \sqrt{12} L/h$ where the cross-section is assumed to be rectangular (hence the factor 12), L refers to the free span length and h to the sheet thickness (Mark and Borch 2001). Although the ECT value is meant to be derived from a corrugated board, it is used for thinner sheets and sheets without fluting as well. The exact sequence of events that lead to compression failure for such specimen remains unclear, but the most widely cited reason is buckling. This explanation comes in many forms: Elastic buckling, plastic buckling, as well as combinations of the two (Mark and Borch 2001; Uesaka and Perkins Jr 1983). It is also employed at all length scales, ranging from boxes (Grangård 1970), to box sides (Ristinmaa et al. 2012; McKee et al. 1963) to sheet laminates (Habeger and Whitsitt 1983) to individual fibers (Cavlin and Fellers 1975; de Ruvo et al. 1978) and even individual microfibrils (Ristinmaa et al. 2012; de Ruvo et al. 1978). Judging from test samples compressed until collapse and the high prevalence of buckled structures after the loss of load-bearing capacity, buckling is either the failure mode or is induced almost instantly after some other change in the microstructure. For higher basis weights, Fellers suggests that shear failure of the fiber wall may be responsible for the failure of the network (Mark and Borch 2001).

At the larger length scales the sheet can be idealized as a set of mutually supporting orthotropic plates, and the compression strength is correlated well with the stiffness components $C_{11}$ and $C_{55}$ of the assembly of plates where the indices indicate the component position in the material stiffness matrix written in Voigt notation (Habeger and Whitsitt 1983). The relation holds even when the results are normalized with respect to density and is amenable to non-destructive monitoring by ultrasonic stiffness determination (Habeger and Whitsitt 1983). It is possible to confirm that an elasto-plastic finite deflection model using only small strain theory successfully predicts the compression strength of paper and board using a commercial finite element solver (Urbanik and Saliklis 2003).

A disadvantage of homogenizing properties is that failure mechanisms stemming from the non-affine nature of the network are hidden. There are indications that some failure characteristics stem directly from meso- and micro-scale variations (Hristopulos and Uesaka 2004). Some authors argue that in the absence of buckling instability, plastic deformation of the fibers will be the dominant damage mechanism and failure initiator (Mark and Borch 2001). The existence of plasticity in pulp fibers is still an open question, with some authors presenting curves which contain some plastic behavior (Page and El-Hosseiny 1983; Dumbleton 1971) while others do not (Mark and Borch 2001). Certainly, single fiber plasticity under compression loading is an under-explored subject in the literature. By varying the bond strength inside networks, it has been shown experimentally and by simulation that the permanent deformation observed at high stresses in sheets made of pulp fibers is due to fiber deformation, not the bonds (Borodulina et al. 2012; Seth and Page 1981).

Sachs and Kuster argue that compression failure of the network is preceded by delamination of the S1 from the S2 layer inside fibers. Such delamination leads to a sudden decrease in effective bonding between fibers inside the network as the S1 layer, which is the outermost layer of the fiber, does not contribute significantly to the mechanical performance of the fiber. As the bonds release, even a small amount of additional load cause fibers to buckle, completing the structural collapse (Sachs and Kuster 1980). The reason buckling takes place directly after delamination may be the increased span length between intact bonds. Sachs performed a second study working with single fibers where the failure sequence was the same – the whole fiber buckled only after several other failure modes had developed (Sachs 1986). Fiber buckling is a somewhat diffuse term, and has been used interchangably with fiber kinking, fiber plastic hinge formation and even fiber bending. A good example of how fiber buckling looks can be found in (Niskanen 2011), p. 86.

In summary, almost every mode of deformation has been suggested. In this work, the previous contributions to the field are expanded upon with the help of a comprehensive modeling framework employing direct simulation of microscale network constituents at sample sizes large enough to be industrially relevant. The principal questions facing the field are

• 1. What is the minimum set of physical mechanisms needed to explain the observed behavior of paper and board in compression? In particular:

  • What is the effect of perturbations to the load bearing capacity of individual fibers?

  • What is the sensitivity of network response to plastic deformation?

  • Is the influence of the number and the strength of fiber-fiber bonds the same as in tension?

• 2. How can compression strength be tailored to the application?

The hypothesis that there are several competing energy release mechanisms acting at the same load level is proposed and investigated.

Method

For thin to moderately thick packaging where there is no fluting, the ECT is typically estimated using the Short span Compression Test, henceforth SCT. The test is constructed by cutting samples with the dimensions 15 $\times$ 60 mm$^2$ (width $\times$ length). The sample is clamped with a predefined force, leaving a 0.7 mm free span over which a displacement-controlled compression test is performed. The width of the sample is chosen to lessen the influence of local variations and edge effects from the unclamped edges. The free span length is kept short to prevent buckling. The test yields a single data point: The maximum load, typically reported as force per unit width or nominal stress. In Fig. 1 the geometry is shown schematically. For the sake of clarity, the sample shown is only 6 mm wide, rather than 15 mm.

The domain in the free span is modeled using its microscopic primitives: For paper sheets these are fibers, bonds, and network affinity. Unlike continuum properties such as sheet shear strength, these primitives correspond directly to the inputs in the papermaking process such as pulp quality, bonding adhesives, the degree of pressing. A typical fiber may have a length to width ratio of 100, and width to wall thickness ratio of 10 (Borodulina et al. 2016). For this reason, simplified kinematic and in turn constitutive relations can be used with little loss of generality. While the fiber has traditionally been reduced to a truss element, the Timoshenko beam-column was used since it is able to capture several deformation modes inaccessible to the truss formulation while at the same time providing a description significantly faster than modeling the fibers using a volumetric approach. Each fiber is represented by three-noded geometrically non-linear Timoshenko beam elements (Ibrahimbegović 1995). The element is geometrically exact and allows both finite rotations and finite strains. The material law used is small strain elasto-plasticity with isotropic hardening, which limits the finite strain effects to scaling of the inertial properties of the cross-section to enforce constant element volume.

Each bond between two fibers is represented by a penalty-based beam-to-beam contact element with cohesive strength. Using a point-to-point contact formulation, it is possible to define the effective mechanical properties of the bond in terms of force-displacement-delamination energy characteristics. Such curves can be found in the literature (Fischer et al. 2012; Magnusson 2016; Magnusson et al. 2013). The point-wise beam-to-beam formulation with rotational constraints described in (Motamedian and Kulachenko 2018) is used. Debonding is modeled using damage based on (Alfano and Crisfield 2001). The contact stiffness is constant up to a specified maximum force on the element, followed by a reduction of the stiffness with a single evolution parameter $D\in [0,1]$. Damage is assumed to be irreversible and unloading after $D>0$ (when damage has begun) is done linearly with a reduced slope such that there is no permanent elongation of the contact element. Upon reloading, the stiffness used during unloading is used. Compression forces along the normal of the contact element are assumed not to cause damage. The tangential forces in the plane spanned by the two elements in contact are combined according to Eq. (2), representing the $L_2$-norm of displacement in the plane formed by the beam tangents at the contact location.

$$\begin{aligned} u_t = \sqrt{u_{t1}^2 + u_{t2}^2} \end{aligned}$$

(2)

Damage begins when the forces acting on the bond exceeds a critical level $F_c$ calculated as shown in Eq. (3) where ${\bar{F}}_n$ is the strength in the normal direction and ${\bar{F}}_t$ is the strength in the tangential plane, respectively, and $F_n$, $F_t$ are the forces in the normal direction and in the tangential plane.

$$\begin{aligned} F_c = \sqrt{\left( \frac{F_n}{{\bar{F}}_n}\right) ^2 + \left( \frac{F_t}{{\bar{F}}_t}\right) ^2} \end{aligned}$$

(3)

The strength can be written in terms of critical displacements ${\bar{u}}_n$ and ${\bar{u}}_t$ as the contact stiffness $k_n$ and $k_t$ in the normal and tangential direction are known prior to damage initiation. A non-dimensional effective distance is defined in Eq. (4) where the critical displacement corresponds to $\beta =1$.

$$\begin{aligned} \beta = \sqrt{\left( \frac{u_n}{{\bar{u}}_n}\right) ^2 + \left( \frac{u_t}{{\bar{u}}_t}\right) ^2} \end{aligned}$$

(4)

The damage parameter D is initialized as 0 and is updated only if $\beta \ge 1$ and the value at the current time step is larger than that in the previous one, $\beta ^{t}>\beta ^{t-1}$ by Eq. (5). The parameter $u_n^c$ in Eq. (5) denotes the distance at which the contact is traction free and completely debonded. The second term in the equation scales D to the range of displacements over which delamination takes place. The normalized normal contact stiffness is shown in Fig. 2, where only the forces that can contribute to the damage (non-compression forces) are included, forming one quarter of an ellipse in the $(u_n,u_t)$-plane due to the definition of $u_t$ in Eq. (2).

$$\begin{aligned} D = \frac{\beta -1}{\beta } \left( \frac{u_n^c}{u_n^c - {\bar{u}}_n}\right) , \quad D\in [0,1] \end{aligned}$$

(5)

The tangential and normal debonding is coupled through the damage parameter D as in Eq. (6).

$$\begin{aligned} \begin{bmatrix} F_n \\ F_t \end{bmatrix} = (1-D) \begin{bmatrix} k_n u_n \\ k_t u_t \end{bmatrix} \end{aligned}$$

(6)

The normal contact stiffness $k_n$ is chosen such that the constraint in Eq. (7) is satisfied, which is necessary to achieve complete debonding in all directions simultaneously.

$$\begin{aligned} \frac{u_n^c}{u_n^c - {\bar{u}}_n} = \frac{u_t^c}{u_t^c - {\bar{u}}_t} \end{aligned}$$

(7)

Fig. 2

Normalized normal contact stiffness as a function of separation distances in the normal and tangential direction. To the left, a schematic illustration of how the damage threshold surface is shaped via the non-dimensional coordinate $\beta$. To the right, a schematic representation of the force-displacement envelope of the contact element (solid line) as well as loading or unloading from a damaged state (dashed line). $u_n^c$,$u_t^c$ and ${\bar{u}}_n$,${\bar{u}}_t$ were taken from Table 2

New contacts do not form during the compression. Although frictional contacts do form during straining of the network, they contribute little to the mechanical properties. Experiments at the microscopic scale of single fiber-fiber bonds show that the frictional contribution to bond strength is small, something which is confirmed by the rapid loss of strength if the network is wetted (dissolving the chemical bonds) or debonding agents are used (Seth and Page 1981; Hirn and Schennach 2015). The non-chemically bonded contacts could potentially improve force transmission when testing in compression. It was assumed that this contribution was small given the small strain at which the sheet fails (<4% for virtually all paper and board grades).

The fiber network is constructed by sampling fiber data extracted via micro-tomography from real sheets and depositing the fibers one by one on a plane surface, resolving any resulting inter-penetrations between the fibers. The solution is obtained with an implicit nonlinear quasi-static solution routine. While the deformations in a paper sheet are typically small before failure, using a nonlinear formulation allows the study of localization phenomena where the strains in small regions may become significantly larger than the macroscopic mean, which is common in many fiber networks (Hagman and Nygårds 2012; Deogekar and Picu 2018). In comparison to recent and similar computational developments (Deogekar and Picu 2018; Zhang et al. 2018; Lavrykov et al. 2012; Berkache et al. 2017; Silberstein et al. 2012), the main differences of the method presented are

• 1. Denser and larger networks are addressed, large enough to be relevant for product design traditional cellulose pulp fibers.

• 2. The network is fully three-dimensional, which is central for the distribution and density of bonds.

• 3. The presented contribution attempts to critically examine claims which have been made repeatedly, but which cannot be easily proved with physical experiments.

Fiber characteristics

The characteristics necessary to model a Timoshenko beam are Young’s modulus, shear modulus, length, width, wall thickness (if the fiber lumen is not collapsed), and height. The Timoshenko beam formulation described in (Ibrahimbegović 1995) is used together with the fiber data in Table 1. The geometric dimensions of the fibers have the mean and standard deviation estimated from the observed data, while the material data is uniformly distributed around the mean value such that e.g. $E_f\sim U(\langle E_f \rangle \cdot 0.5, \langle E_f \rangle \cdot 1.5)$ where $\langle \bullet \rangle$ denotes the mean value of $\bullet$.

The fiber material properties are based on testing in tension. The properties in compression are not known at the level of single fibers because of the difficulties in testing fibers in compression. One method of measuring compression strength of single fibers is the elastica loop (Sinclair 1950). This method has not been used successfully on wood pulp fibers, presumably due to their short length. Although some fibers tested in this way have shown radically lower compression strength [aramid fiber (Greenwood and Rose 1974), polyvinylalcohol and high-performance polyethylene fibers (Peijs et al. 1995)] the most representative model fiber, flax, was shown to have a compression strength equal to about 80% of the tensile strength (Bos et al. 2002).

Table 1 The fiber properties used, obtained through a fiber characterization tool

Bond characteristics

The bond parameters given in Table 2 were used. The data was taken from samples tested in tension and is further described in (Borodulina et al. 2012).

Table 2 The bond properties used

The values are within the ranges expected from experimental works (Fischer et al. 2012; Magnusson 2016; Magnusson et al. 2013), in which the fiber bonds were tested and the load combination acting in the bond area was estimated using inverse procedures using physical models. Although the uniqueness of such estimations cannot be guaranteed, this is probably the only way to quantify the bond strength currently. As we specify the debonding criteria in terms of forces, we were not affected by the inaccuracy in estimating the bonded area. We did not include the moments acting in the point-wise contact in the debonding criteria, which can be an additional enhancement (Deogekar et al. 2019).

Network generation

Many methods of network generation exist, e.g. (Deogekar and Picu 2018; Bronkhorst 2003; Lavrykov et al. 2012). The method used is described in (Motamedian and Kulachenko 2018) in which fibers are deposited on an initially empty surface, incrementally forming a network through random generation and placement of fibers. This method is similar to the physical process of making handsheets. In industrial manufacture, additional effects stemming from the high velocity of deposition must be considered. Due to the stochastic nature of the process, mesoscale clusters of sparser and denser areas appear in the network. The deposition process is two-sided which creates relatively symmetric through-thickness density profiles. The network characteristics used in most of the figures, unless otherwise stated were a grammage of 300 g m$^{-2}$ and a sheet thickness of 0.49 mm. The elastic modulus was probed in tension using larger sections of the same network, and was $2.5 \pm 0.1$ GPa. As this article does not address the effect of changes in fiber orientation, only in-plane isotropic sheets were created.

Enforced boundary conditions

Most of the conditions tested do not explicitly model the clamps. Instead, the following procedure is applied:

• 1. A network with dimensions at 12 $\times$ 12 $\times$ Sheet Thickness mm$^3$ is generated. The network consists of elements connected in series to form fibers.

• 2. The network is centered such that the middle of the network is at the middle of the SCT free span domain.

• 3. The elements which lie outside the free span domain are removed.

• 4. The elements which cross the boundary of the free span domain are edited, by moving the end-node which is outside of the domain to the boundary of the domain. The mid-node coordinate is adjusted such that the mid-node remains in the middle of the element.

Since the SCT has large amounts of material inside the clamps on either side and the free span is shorter than the average fiber length there is a significant number of fibers crossing the free span. Rather than eliminate them, they are truncated at both ends. In the end, the network on which loads are applied contains the free span domain. On the boundary of the free span domain are located 1 node of each element which originally passed through the boundary. The boundary conditions, which are displacement based, are applied on the nodes located on the boundary of the free span domain. The nodes on the boundary of the free span domain are subjected to enforced displacements which are 0 for all degrees of freedom except the degree of freedom along $\times$ (which coincides with the direction of the clamp motion in the real test) on one side of the test. Slippage, which is common in the physical experiment owing to the difficulty of restraining the sample without crushing it, is neglected here. Here, an enforced displacement equal to 5% (for tensile tests) or $-5$% strain (hence $\pm 0.05 \cdot (0.7 \,\mathrm{mm}) = \pm 0.035$ mm is applied. Typically this value is not reached, as the simulation is terminated if softening relative the peak force exceeds 5%. The enforced boundary conditions are shown schematically in Fig. 3, on the left.

Fig. 3

Enforced boundary conditions for models without the clamped material (left) and with the clamped material (right), respectively

When a section of the clamped volume is explicitly included in the model, the same procedure as above is performed except the generated volume is 0.175 mm larger on both sides of the free span domain along the x-axis. The same boundary conditions are applied on the boundary of the domain, now containing both the free span and the modeled section of the clamps. Furthermore, displacement of all nodes inside the clamped domains in the z-direction (out-of-plane) is entirely prohibited as indicated in Fig. 3, on the right.

Pre- and postprocessing

The preparation of results was performed using (MATLAB 2018) and visualized using Gramm (Morel 2018). The pre- and post-processing of models was done using (ANSYS 2015).

Results

A mesh study was performed, and a mean element length of 54 $\upmu$m was chosen as the results did not change upon further refinement. Furthermore, the computational size of the model was minimized by performing a response study where the width of the sample was progressively decreased from the SCT standard of 15 mm to the point where the response began to deviate from the result when using the full width. A width of 6 mm was found to be representative.

The size of the model was 0.7 $\times$ 6 $\times$ Sheet Thickness mm$^3$, which corresponds to 40% of the volume in the free span in the SCT. The material inside the clamps was not modeled unless where explicitly stated (e.g. Fig. 6). When the material inside the clamps was modeled, the volume modeled was 0.175 $\times$ 6 $\times$ Sheet Thickness mm$^3$ on each side, which is 0.2% of the volume inside the clamps in a physical test. However, the reason the clamped volume is so large is to make the test sample easy to handle and allow the clamps to immobilize the test piece with limited damage to the material due to crushing. By assigning numerical boundary conditions slippage at the clamps is entirely prevented, making it unnecessary to explicitly model such a large volume. The main factor investigated when modeling the clamps is whether the geometry-change induced by the force-controlled pressing of the clamps in itself is enough to alter the failure mode as compared to when idealized restraints are used.

Throughout the presentation and discussion of results, compression failure will be taken to mean the point in the force–displacement or engineering stress-engineering strain diagram where the largest negative value of force or stress is recorded. One softening branch per parameter combination is also presented. The accuracy of this softening branch should be considered low. The onset of the post-peak response is shown with a dotted line. The quantitative condition was that the stress should have decreased in magnitude by 5% relative the peak. The post-peak behavior was the most computationally intensive due to deteriorated convergence rate. In some instances, the entire stress–strain curve is shown. Caution should be exercised when comparing the strain values with values obtained using physical experiments, as some slippage is often inevitable in physical testing. Hence, the strain reported here will tend to be less than the strain measured if the correction for slippage is imperfect.

The effect of the short free span on tensile properties

A free span of 0.7 mm is too small to accurately estimate the material properties of a sheet (Kulachenko et al. 2012; Cowan and Cowdrey 1974). Furthermore, at small length scales the structural response is also altered. For example, in a short network segment a significant number of fibers cross the entire domain. As the macroscopic load is applied these fibers carry the load without interacting with the rest of the network. As individual fibers are much stiffer than the sheet, such fibers stiffen the mechanical response.

To establish how big the effect of a small free span length is in tension, tests were performed comparing two networks with the same macroscopic properties but with a free span of 0.7 mm and 0.35 mm, respectively. A sample with significantly longer free span was also included. The results are shown in Fig. 4. Not only are the small networks stiffer, but they also have a higher strain at failure. The failure was defined as the point where the macroscopic response of the network, represented by the tangent to the curve in Fig. 4 turning negative. In tension, paper sheets typically fail due to cascading bond failures across a cross-section. In the smaller samples, bonds are not utilized because a large number of fibers are crossing the entire domain. The softening part of each curve has been removed.

Fig. 4

Tensile force-displacement response of a network with a free span significantly shorter than what is customary in tensile tests. The stiffening influence of fibers crossing the entire model domain and becoming clamped at both edges is clearly visible from the increase in stiffness and strain to failure of the shorter samples. The shaded areas indicate $\pm 1$ standard deviation. Each mean curve and standard deviation is calculated on five samples

In Fig. 5 networks with identical aggregate properties were subjected to a tensile and a compression load. The sample free span length is 0.7 mm, just as in the SCT. The elastic response is independent of load direction, but in compression, the sample begins to deviate from the elastic response at a lower macroscopic strain. Comparing Figs. 4 and 5 compressive strength and strain to failure are 30–50% of tensile strength and strain to failure, as observed experimentally (Fellers et al. 1980; Stockmann 1976; Setterholm and Gertjejansen 1965). The elastic response is the same in tension and compression, in agreement with experimental data (Stockmann 1976; Setterholm and Gertjejansen 1965; Seth et al. 1979).

Fig. 5

Tensile versus compression response for samples with a free span length of 0.7 mm. The tension and compression test were performed from the reference configuration of the network

Both Fellers and Habeger investigated buckling of paper, primarily linerboard, extensively (Fellers 1980; Habeger and Whitsitt 1983). A principal reason for the choice of 0.7 mm free span in the SCT is that it represents the “plateau” in strength observed in experiments (Fellers 1980).

The effect of grammage

The effect of grammage on compression strength is well established (Popil 2017). The model was compared to the experimental data, with an emphasis on correctly capturing the effect of increased grammage. The result is shown in Fig. 6. No fitting was performed as the data reported in the experimental data sets is insufficient to uniquely determine a set of parameters. The response is more similar to the RCT than the SCT, indicating that the chosen parameter combination is somewhat more compliant than the sheets tested experimentally. However, the data is within the bounds of what can be expected. Sheets with a grammage below 80 gm$^{-2}$ are not tested in compression, as there is no commonly accepted test protocol. If the compression strength is normalized with respect to grammage our data and the SCT data would form a horizontal line, independent of the basis weight. Such a constant relationship between compression strength and mass is an indication that what is measured can be regarded as a material property.

Fig. 6

The effect of grammage on the compression strength of the sheet determined by the Ring Crush Test (RCT) and the Short span Compression Test (SCT). The experimental data are taken from (Popil 2017). The model response is not fitted to the experimental data

The effect of clamping the specimen during testing

Due to the orthotropy of many fibrous composites, where the out-of-plane stiffness is much lower than the in-plane elastic properties, even moderate clamping pressure can lead to large out of plane compression strains. Such strains may cause the sample to fail at a lower load and may also promote certain failure modes, such as delamination failure. Typical strains were estimated and imposed by combining the ISO-standard for SCT (Standard 2013) with the out-of-plane strain-stress data from (Stenberg and Fellers 2002). In these tests the clamping causes significant delamination, as shown in Fig. 7. The loss of compression strength is shown in Fig. 8.

Fig. 7

The effect of clamping compression on the failure mode. In the top picture no clamping is introduced, resulting in a uniform deformation consisting mostly of bending. In the bottom picture, $\varepsilon _z = -0.40$ clamping strain in the ZD results in the failure mode shifting, with clearly visible delaminated parts

Fig. 8

The effect of clamping compression on failure stress. The decrease in failure load is mainly due to a change in failure mode, from out-of-plane bending or buckling to delamination as the compression strain is increased

The effect of fiber quality

Using the same networks (meaning that the geometry obtained from the network deposition process was reused, eliminating the sample to sample variance inherent to destructive testing and allowing an exact comparison of response dependent only on the change in constitutive parameters), the effect of changing the material properties of the fibers was examined. This can be seen as a proxy for the fiber structural integrity and pulp type. Four sets of material data were tested and are given in Table 3. The fibers in the reference case, used elsewhere in this article, have mechanical properties representative of chemo-thermomechanical pulp. By screening or using different pulp varieties, it is possible to improve both the average elastic modulus of the fibers and the plastic properties, which correlate with the degree of fiber level damage. Finally, a test where only the bonding properties have been improved is performed by scaling the bond strength by a factor 2. Bond strength is often improved through the use of additives, such as starch, whereas bond stiffness is strongly affected by lumen configuration, and thus may be improved through increased wet pressing.

Table 3 The fiber properties typical of CTMP fibers as well as various modifications that could be made to the pulp

The force-displacement response in Fig. 9 as expected highlights the fiber elastic modulus which has a decisive influence on the mechanical response, mainly through increased stiffness. The failure strain remains almost stationary. There is a moderate effect of bond strength on the results. This may be due to the high degree of bonding already present in the sheet. The response did not show much sensitivity to the plastic parameters specified, indicating that for the chosen parameters, which are representative for paper and board, the plastic parameters have a limited influence in compression. The non-affine character of the sheet appears to have a limited influence (also supported by Fig. 7), which is a by-product of the low porosity of industrially relevant board compared to many other fiber networks.

Fig. 9

The effect of changing material properties. The changes made to each network are described in Table 3. Only the stress–strain curve up to compression failure is shown. Shaded areas indicate ± 1 standard deviation calculated on five samples each

Bond breaks

The ultimate strength of paper in tension is governed by bond strength (Page 1969). In compression, since the ultimate strength is lower, bond strength may be utilized less effectively. In poorly bonded sheets the effect of an increased number of bonds is strongly positive, just as in tension (Watt and Fox 1981). Bond breaks were studied numerically as a function of applied strain for networks subjected to a tensile and a compression load. The networks were identical at the onset of the test. The bond breaks as a function of the applied macroscopic strain were recorded and plotted normalized to the sample width which was always 6 mm in Fig. 10. As the tests were performed on identical samples, all 0.7 mm in length, the bond breaks in the tensile load case are likely underestimated compared to what would be observed if the sample was longer which is typical in tensile testing.

Fig. 10

Bond failures per mm width of the sample in tension and compression, respectively. A compression load causes more bonds to break at a low degree of loading, but due to the development of other deformation mechanisms (mainly bending) as the test progresses, the number of bonds broken at compression failure stress is significantly lower than what is observed in tension

Bonds start breaking at a lower strain in compression than in tension and continue to increase in quantity more rapidly than in the tensile case until failure. In the post-peak response not shown, the number of bond breaks levels off as bending of the sample takes over as the dominant deformation mode. The implications of this result are that while the number of bonds may be important, it is primarily the most stressed bonds that affect the compression strength. No localization of bond breaks was detected in any of the tests performed. Such localization is a central aspect of tensile failure, but seems not to occur in compression.

Fiber buckling

The results presented so far have not explicitly addressed the potential of fiber segments to buckle, although the numerical scheme employed is in principle able to resolve geometric buckling. To include fiber buckling as a deformation mode in the model, it is necessary to make additional assumptions beyond what has been needed up to this point. To fully characterize the mechanical response during and after buckling, a model needs as input

• the load at which buckling occurs (determination of $P_{crit}$),

• the factors that influence the onset of buckling (parametric dependency on e.g. Young’s modulus, second area moment of inertia, free span length), and

• a description of the post-buckled response of the fiber segment.

There are no reported studies which contain such information for pulp fibers. In this article, modeling is substituted in place of experimental data. Buckling is assumed to take place over the free span of the fiber between bonded sites. The buckling onset is modeled by pin-pin column buckling with has the critical load given by Eq. (8) where $E_T$ is the tangent modulus, I is the second area moment of inertia and L is the free span length. We did not track of the stress state of each Gauss point when extracting $E_T$. Once a single Gauss point yielded, the cross-section was regarded as yielded and $E_T$ appropriately lowered. This approach is equivalent to the Shanley elasto-plastic buckling model.

$$\begin{aligned} P_{crit} = \frac{\pi ^2E_TI}{L^2} \end{aligned}$$

(8)

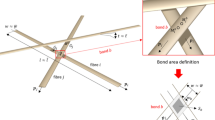
The free spans L in the network at the peak load were calculated, taking into account that some bonds had already delaminated at that point. Any fiber which was bonded in only one place was omitted from the analysis, as it would not transmit mechanical load. The free span can be calculated in two ways, as shown in Fig. 11. The method which accounts for fiber width was used, averaging the free spans $l_1$ and $l_2$.

Fig. 11

Ways of estimating the free span between fiber bonds. One method is to use the distance from centerline to centerline, which results in the distance denoted with L. The alternative method used in this article employs the distance from fiber hull to fiber hull, which results in a strictly smaller free span, but is more physically realistic as the fibers are volumetric entities, as are the bonds

The distribution of free span lengths is given in Fig. 12. Depending on the search radius used in the contact detection algorithm, the median segment length between bond sites was between 10 and 17 $\upmu$m. Given the cross-sectional properties of the fibers (Table 1) the aspect ratio of each segment was below 1. Such a segment could not be used to successfully resolve the geometrical buckling with a Timoshenko beam, but the segment length, cross-section and load can be used to estimate the buckling load. Accounting for fiber width has a large effect and much of the network is in a bonded state. the estimates are shown to be insensitive to the specific distance chosen as demonstrated by varying the distance at which two fibers are considered bonded (denoted search radius in the figure).

Fig. 12

Empirical distribution function of the free spans in the network, with and without taking into account the width of the fibers. The figure shows that a large fraction of the network is bonded

Comparing the predicted buckling load using Eq. (8) with the actual axial load in the fiber at failure, the ratio between the buckling load and the actual load is calculated using Eq. (9).

$$\begin{aligned} \eta = \frac{P_{crit}}{P_{axial}} \end{aligned}$$

(9)

The longest free spans can be expected to both have the lowest buckling load, and to represent a larger proportion of the network mass. To include this effect the results are presented as mass-weighted empirical distribution functions (EDF) using the implementation in (Kovesi 2000). Figure 13 shows the mass-weighted EDF that would buckle for a certain factor $\eta$. As expected, only a fraction of the free spans is able to buckle: Some segments are completely covered by the crossing fiber width, whereas others are in a state of tension.

The results suggest that the majority of fibers are not near the load state $P_{crit}$ that would cause buckling. However, if the network is very brittle, the few fibers that are close to the buckling load could still cause macroscopic failure. Furthermore, the analysis has not taken into account the effect of imperfections and misalignments, which lower the buckling load. Finally, cascading fiber failures are not considered.

Fig. 13

Factor required to induce buckling in the free span. The fraction is calculated by weighting each occurrence by the fraction of mass in the segment. The network used to calculate the figure has a grammage of 300 gm$^{-2}$ and a thickness of 490 $\upmu$m. However, the trend is identical in all of the networks examined

While little of the mass of the system is close to buckling if $\eta =1$, about 10% of the fibers are within a factor 100 of the buckling load. Given the assumptions in the analysis, a factor 100 decrease in buckling load due to defects, fiber curl and load eccentricity is high but not completely unreasonable. Studying the far-right end of the EDF diagrams, the cumulative mass at risk of buckling for any load, given the degree to which the fiber mass is bonded is limited to about 20% in the considered network.

The fiber wall could also buckle, and to investigate that we evaluated Eq. (10) where in addition to previously defined quantities, h is the wall thickness and $\nu$ is the Poisson ratio, assumed to be 0.3. To calculate the estimate of mass able to undergo such instability, we calculated the wall buckling load for all segments where the fiber was not inside a bonded segment and the lumen was open. In Fig. 14 the proportion of mass at risk of buckling in this way is compared to the free span buckling mode. A smaller fraction of the volume is at risk of buckling from wall buckling, mainly because only a fraction of fibers have open cross-sections. Finally, Shanley buckling taking into account the influence of the transverse force in the beam segments is also examined. When taking into account the influence of the transverse force the buckling load no longer tends to infinity for small free spans, although the buckling load remains high if the material is isotropic. If the relation between E and the shear modulus G is very large, the critical load decreases rapidly, as discussed in (Cedolin et al. 2010), chapter 1 according to Eq.  (11) where m is the shear correction factor, set to 1.2 in this work.

$$\begin{aligned} P_{cr}^{wall}= & {} \frac{2\pi E_T h^2}{\sqrt{2(1-\nu ^2)}} \end{aligned}$$

(10)

$$\begin{aligned} P_{cr}^{shear}= & {} \frac{P_{crit}}{1+m\pi ^2 L^{-2} I A^{-1} (E/G)} \end{aligned}$$

(11)

Fig. 14

Factor required to induce either free span buckling or wall buckling. The fraction is calculated by weighting each occurrence by the fraction of mass in the segment

Examining the three proposed buckling modes, the mass at risk of buckling is relatively low, although it may be enough to bring about cascading fiber failures if the network is brittle. As Figs. 13 and 14 show only a single, relatively dense network, we performed a parametric study of several networks for varying density. In Fig. 15 the worst case (free span buckling without neglecting the influence of transverse forces and assuming $E/G=10$) is plotted for a variety of densities, covering the whole range of commercial paperboard densities (400–800 kgm$^{-3}$) and grammages (80 – 400 gm$^{-2}$). The thickness was 280 $\upmu$m for all samples except for the samples discussed in the rest of the article, which had a grammage of 300 gm$^{-2}$ and a thickness of 490 $\upmu$m. The fraction at risk of buckling is moderate to high in the samples with low density. However, while the low density samples are within the limits of what the SCT testing standard allows, it would be practically difficult to generate a sheet with such low density (due to gravity induced draining during sheet forming) and it is unlikely that a sheet with a density below 300 kgm$^{-3}$ would ever be used for the purpose of carrying mechanical compression or bending load. Nonetheless, were such networks used, fiber level buckling is likely to have an influence on the overall sheet compression strength.

Fig. 15

Factor required to induce free span buckling under the assumption that $E/G=10$. The fraction is calculated by weighting each occurrence by the fraction of mass in the segment

Finally, we tabulated some summary statistics on the fiber free span level. Of particular importance is the relation between the fraction in free spans (which could theoretically buckle), the fraction in compression, and the fraction likely to buckle. These quantities are plotted as functions of density in Fig. 16.

Fig. 16

Summary of the fiber state at the peak macroscopic load. Comparing the fraction in compression, the amount of mass at risk of buckling decreases rapidly with increasing density, primarily due to shortening free spans

The presented results give some indication of the likelihood that fiber level buckling can initiate a sheet failure.

A second method of investigating fiber buckling is to study the effect of the presence of weak points in the network. In this setting, the buckled fibers are assumed to be unable to carry any load even at the onset of loading. This is likely a too conservative estimate, but taken together with the buckling analysis above (which is not conservative enough as cascading failures are not accounted for) it can yield an upper bound on the sensitivity to fiber failure. A method is proposed to study the influence of imperfections by making some further assumptions:

• A number of points exist along fibers that buckle instantly.

• The failure results in a local but complete loss of bending stiffness.

• The onset of failure does not depend on any other characteristic of the network.

These extreme conditions will be the topic of the final investigation in this article.

Hinge formation, kinks, and localized damage

In naturally formed materials defects are inevitable. For example, wood fibers often have pits around which stress concentrations form, and paper pulp fibers are damaged during the manufacturing and drying process resulting in kinks, micro-compressions and other types of local defects. Depending on the damage the load-bearing capacity may be adversely affected. This is particularly interesting in compression applications, where various types of kinks and curvature may strongly impact the ultimate load-bearing capacity of the fiber and consequently, the network. The buckling load is strongly influenced by the degree of imperfection along the length of the structural member as well as misalignment.

Some estimates of the number of fiber defect densities are given in Table 4. In this context, an irregularity is some type of visible damage on the fiber, whereas a severe damage is more significant such as a large kink. There are experimental observations indicating that the number of imperfections in the network is not strongly correlated with the compression strength (Panek et al. 2005). In fact, the study found that the correlation between tensile strength and fiber damage was stronger than that between compression strength and fiber damage.

Table 4 Estimations of the number of imperfections per mm length of fiber

These singularities were modeled by introducing discrete hinge elements deposited randomly throughout the network. Each hinge is a relaxation of the compatibility requirement from $C^1$ to $C^0$. Typically, a beam element enforces continuity in both displacements and rotations across elements, but at the hinge locations a frictionless joint is introduced by coupling the beam’s translational degrees of freedom only, that is, allowing one end of the fiber at the place of the hinge to rotate independently of the other. In Fig. 17 it is shown that compression strength is essentially independent of the number of hinges as long as the number is of the same order as the number of singularity-type defects reported in literature. If the number of hinges is increased significantly, the numerical solution method chosen becomes unstable and for that reason no results are shown in the density range of pulp irregularities. It is unlikely that such relatively minor irregularities would be accurately represented by a complete loss of bending stiffness.

Fig. 17

The effect of hinge density on compression strength. While the hinges reduce the compression strength, the reduction is minor for the investigated range, although it may be larger when the number of hinges is increased further. The network has a strength reserve which compensates for the loss of load carrying cappacity of some fibers. The experimental data was taken from (Iribarne 1998)

Conclusions

The compression response of dense non-woven fiber networks was studied. The material parameters and network character was chosen to be similar to paperboard. The model was shown to correctly follow the experimental trend with respect to the grammage of the network. As no experimental data of compression tests performed on single pulp fibers has been published, the material properties in compression were assumed to be equal to those in tension. This is an untested and critical assumption in this work, which should be confirmed with physical experiments. The model behavior and difference between response in tension and compression suggests this is not an unrealistic assumption.

The x-shaped deformation mode often observed in the Short-span Compression Test (SCT) can be an artifact of the clamping pressure necessary to restrain the sample. This is especially true for sheets that are comparatively bulky, with low out-of-plane stiffness, due to the clamping being force controlled. The failure load in samples failing by delamination is not significantly lower than the failure load of the sheet under idealized loading conditions.

The number of bond breaks during the straining or compression of the sample, respectively, were shown to be lower than in the tensile load case, and no localization of bond breaks was observed. The importance of bond strength is therefore less than in the tensile case. However, while the strength of bonds might be less important, the number of bonds may be more important as the number of bonds causes the free spans in the network to decrease rapidly in length.

A detailed analysis of the stress state of individual fibers at the point of macroscopic failure showed that a bifurcation analysis, even when taking into account plastic yielding, predicts that only a small to moderate fraction of fibers will undergo buckling. Since the network is built up by random sampling from distributions obtained using micro-tomography, a large number of observations were drawn upon for analysis. The fact that most of the fiber length is bonded speaks to the unlikeliness of fiber buckling as a failure initiator. Quantitative measures of the total mass at risk of buckling were obtained and could be used for further analysis.

The conclusion that fiber level buckling is unlikely is further supported by the results obtained when introducing hinges explicitly into the model. The introduction of hinge elements randomly deposited throughout the network allows the study of sensitivity to such hinges, which is shown to be small for low to moderate number of hinges.