Orbital dynamics of smart dust with Poynting–Robertson and solar wind drag

Abstract

Smart dust devices are tiny systems-on-a-chip platforms capable of sensing, storing and transmitting data wirelessly as part of a large network with distributed capabilities. Previous works investigated the long-term orbital evolution of smart dust in space by studying the combined effect of gravitational perturbations, solar radiation pressure (SRP) and atmospheric drag. In the current work, the problem of finding long-term orbital equilibria conditions for smart dust is recast and extended to include Poynting–Robertson and Solar Wind (PRSW) drag. By including the PRSW effects and defining new equilibrium conditions on the orbital orientation, some additional partial equilibrium solutions are found. Moreover, it is shown that even though PRSW is not dominant compared to SRP or $J_2$, it still influences the evolution of the relative Sun-orbit orientation. For orbits with higher initial perigee altitudes, where drag and $J_2$ effects subside, it is shown that PRSW influences long-term orbital behavior, and should be considered in the orbit design scheme of smart dust devices.

1 Introduction

The dynamics of dust around the Earth are a fascinating aspect of space science, as tiny particles, ranging from micrometers to millimeters in size, continually orbit our planet. These dust particles can originate from a variety of sources, including meteoroids breaking up upon entering Earth’s atmosphere, remnants from cometary tails and even debris from previous satellite missions. The interaction between these dust particles and the Earth’s gravity, radiation pressure and magnetic fields, as well as their collision and distribution patterns, contribute to the complex dynamics of the dust environment around our planet. Researchers have utilized various techniques, such as space-based instruments like the Cosmic Dust Analyzer on the Cassini spacecraft and ground-based observatories, to study and monitor this dynamic cosmic dust population. Understanding the behavior and characteristics of dust near Earth is essential for space missions, satellite design and space debris mitigation efforts; see Grün et al. (1999), Horányi (1996) and references therein.

In the early 1990s, studies at RAND Corporation gave rise to a concept of tiny, inexpensive systems-on-a-chip platforms capable of sensing, storing and transmitting data wirelessly as part of a large network with distributed capabilities, residing on a physical footprint of a few millimeters. These devices, reminiscent in size and characteristics to the aforementioned dust around the Earth, are commonly referred to as smart dust devices. Defense Advanced Research Projects Agency (DARPA) commissioned a project to study the feasibility of such systems. A team of researchers from University of California, Berkeley subsequently proposed the first such device to DARPA (Kahn et al. 1999). Barker and Barmpoutis (2007) proposed autonomous clusters of smart dust for space exploration, which include distributing large numbers of such sensors, as low-cost and low payload-mass would enable greater redundancy, which could drive the cost of a mission down. In 2016, a team of researchers from Cornell University and Stanford University sent a crowd-sourced satellite on a chip termed ChipSat to a low Earth orbit to study deorbiting characteristics and decay times.¹

Zhao et al. (2018) investigated the long-term orbital evolution of smart dust in space by studying the combined effect of gravitational perturbations, solar radiation pressure (SRP) and atmospheric drag, extending the work done by Colombo and McInnes (2011), who had earlier studied the same problem under the effects of SRP and drag only. Lhotka et al. (2016) studied the effect of Poynting–Robertson and Solar Wind (PRSW) drag on space debris, focusing on the geosynchronous resonance. The seminal work by Burns et al. (1979) has been widely used as reference for understanding the physics behind the Poynting–Robertson effect. Since the area-to-mass ratio (AMR) is high, the orbital dynamics are sensitive to effects such as SRP and PRSW drag.

The evolution of orbits of smart dust over a considerable interval of time, taking into account long-periodic terms, can be calculated by semi-analytical techniques, i.e., numerical integration of a particular set of differential equations obtained through analytical solutions. This process leads to mean elements or mean differentials that can give insight into the long-term dynamics of the problem.

In the last decade, many researchers have extrapolated the idea of smart dust into the field of space exploration (Colombo et al. 2010, 2012; McInnes 2016; Hamilton and Krivov 1996). Smart dust modules can be described as high area-to-mass ratio (HAMR) objects with coupled orbital and attitude dynamics (Früh and Jah 2014). Ever since the discovery of HAMR debris by Schildknecht et al. (2005), the orbital dynamics of HAMR objects have been well studied within the context of planetary, interplanetary or space debris dynamics (Colombo et al. 2012; Hamilton and Krivov 1996; McInnes et al. 2001).

The dynamics usually evolve under the influence of perturbations such as SRP, atmospheric drag, Poynting–Robertson drag and electrostatic forces. Previous studies have usually assumed that smart dust devices have a constant AMR. However, observations suggest otherwise. Früh and Schildknecht (2012) considered the variation of AMR in their study using an enhanced model of CelMech, a custom propagator based on Earth potential models up to order and degree 12, Earth tides and general relativity corrections. In addition, they employed a special model for estimating the direct radiation pressure, as a scaling parameter of which the AMR was determined. Liou and Weaver (2005) used PROP3D, a fast orbit propagator based on the averaging principle that was developed for NASA’s debris evolutionary models, to investigate the HAMR debris problem. PROP3D accounts for the perturbations from Earth gravity up to the fourth zonal harmonic, low-order lunisolar gravitational interactions, and SRP with consideration of the Earth shadow effect. Through comparisons with a high-fidelity orbit integrator based on Encke’s method, it was shown that HAMR objects in GEO are dominated by major perturbations, not those of higher order. They also showed a correlation between AMR and peak eccentricity.

Valk and Lemaître (2008) studied the long-term perturbations of geosynchronous space debris by including Earth’s shadowing effects based on a semi-analytical theory previously developed by the same authors. Their averaged model included short-period effects including radiation pressure, $J_2$, combined third-body effects and the 1:1 resonance long-term effects for geosynchronous objects. In their framework, the nonsingular mean longitude was computed at every shadow entry and shadow exit for every revolution, which is not a common formalism. Pardini and Anselmo (2008) performed numerical investigations of the problem by mapping out dynamics over long timespans (54 years). They propagated the orbit using a model based on all relevant perturbations, such as geopotential harmonics, lunisolar effects and SRP. They found a correlation between AMR and oscillations that dominate eccentricity evolution. Früh and Jah (2014) studied the orbit-attitude coupling effects of HAMR objects. They described a new model of self-shadowing, departing from the traditional cannonball model for radiation pressure. Rosengren and Scheeres (2013) studied the long-term dynamics of HAMR objects in high Earth orbits. Their model included SRP, Earth oblateness and lunisolar perturbations. The study also gave a first-order averaged model in terms of Milankovitch orbital elements, which is faster to numerically integrate than the non-averaged version, while retaining accurate long-term characteristics.

The study presented in this paper investigates the stand-alone dynamics of Poynting–Robertson and Solar Wind drag and its influence on the long-term evolution of the model developed by Zhao et al. (2018). Averaging the effects of PRSW drag in the presence of eclipse leads to interesting and non-trivial equilibria. Such equilibria are studied for different values of initial perigee height and eccentricity. These parameters are then investigated to reveal Sun-Earth geometries in which the perturbations including gravitational perturbations, SRP, drag and PRSW are mitigated, thus enabling to find potentially long-lived orbits, which can be exploited for various mission requirements.

2 Preliminaries

2.1 Frames and transformations

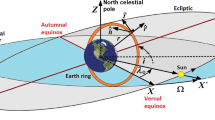
The expression for Poynting–Robertson drag is calculated originally in a Sun rest reference frame. To analyze the perturbations using quantities in a standard spacecraft-fixed radial, along-track, cross-track (RSW) frame (Gurfil and Seidelmann 2016), we must provide a valid coordinate transformation. The base frame is chosen as the Heliocentric Aries Ecliptic (HAE) Fränz and Harper (2002) whose plane lies in the Earth mean ecliptic plane, and the x-axis points toward the first point of Aries as shown in Fig. 1. There are two reasons for selecting this frame: Firstly, this frame shares the same direction reference as the Earth Centered Inertial (ECI) frame; and the velocity of Earth with respect to the Sun is well defined in this frame. The orbital velocity of the Earth is given by

$$\begin{aligned} {\varvec{\textrm{v}}}_{E,HAE}=v_o[\cos (\lambda _{geo}+90^\circ ),\sin (\lambda _{geo}+90^\circ ),0]^{T}, \end{aligned}$$

(1)

where $v_o=29.7859$ km/s is the mean orbital speed of the Earth in the HAE frame, and $\lambda _{geo}$ is the Earth ecliptic longitude calculated as per Fränz and Harper (2002). The transformation to the ECI frame is given by a rotation about the x-axis (Fränz and Harper 2002),

$$\begin{aligned} T(ECI,HAE)=\begin{bmatrix} 1 &{} 0 &{} 0 \\ 0 &{} \cos \epsilon _0 &{} \sin \epsilon _0\\ 0 &{} -\sin \epsilon _0 &{} \cos \epsilon _0 \end{bmatrix}, \end{aligned}$$

(2)

where $\epsilon _0$ is the obliquity angle of the Earth with respect to the ecliptic, and both the HAE and ECI frames are referenced to the Julian date J2000. The final transformation from the ECI to the RSW frame as given by Vallado (2001) is

$$\begin{aligned} T(RSW,ECI)= \begin{bmatrix} \text {c}_ u\text {c}_\varOmega - \text {s}_ u \text {c}_ i \text {s}_\varOmega &{}\text {c}_ u \text {s}_\varOmega +\text {s}_ u \text {c}_ i \text {c}_\varOmega &{} \text {s}_ u \text {s}_ i\\ -\text {s}_ u \text {c}_\varOmega - \text {c}_ u \text {c}_ i \text {s}_\varOmega &{}-\text {s}_ u \text {s}_\varOmega +\text {c}_ u \text {c}_ i \text {c}_\varOmega &{} \text {c}_ u\text {s}_ i\\ \text {s}_ i \text {s}_\varOmega &{} -\text {s}_ i \text {c}_\varOmega &{} \text {c}_ i \end{bmatrix}, \end{aligned}$$

(3)

where $\omega$ is the argument of periapsis, f is the true anomaly, $u=\omega +f$ is the argument of latitude, $\varOmega$ is the right ascension of ascending node, i is the inclination, and the shorthand notation $\text {c}_{(\cdot )}\equiv \cos (\cdot )$ and $\text {s}_{(\cdot )}\equiv \sin (\cdot )$ has been used.

Fig. 1

Frame visualization of Heliocentric and Earth-centered systems

2.2 Variational equations

In this study, as in previous studies (Zhao et al. 2018), we focus on orbits that lie in the ecliptic plane for mathematical simplicity. Hence, only the planar orbital elements are required to propagate the orbit. The variational equations are written using the Lagrange form for conservative specific forces,

$$\begin{aligned} \begin{aligned}&\frac{\text {d}a}{\text {d}t}=\frac{2}{na}\frac{\partial R}{\partial M}\\&\frac{\text {d}e}{\text {d}t}=\frac{1-e^2}{na^2e}\frac{\partial R}{\partial M}-\frac{\sqrt{1-e^2}}{na^2e}\frac{\partial R}{\partial \omega }\\&\frac{\text {d}\omega }{\text {d}t}=\frac{\sqrt{1-e^2}}{na^2e}\frac{\partial R}{\partial e}-\frac{\cot i}{na^2\sqrt{1-e^2}}\frac{\partial R}{\partial i} \end{aligned} \end{aligned}$$

(4)

where a is the semimajor axis, e is the eccentricity, M is the mean anomaly, R is a perturbing potential, and $n=\sqrt{\mu /a^3}$ is the mean motion. For non-conservative specific forces, the Gauss variational equations (GVE) are used. The GVE are written with the true anomaly f as the independent variable in the RSW frame (Fortescue et al. 2011),

$$\begin{aligned} \begin{aligned}&\frac{\text {d}a}{\text {d}f}=\frac{2pr^2}{\mu (1-e^2)}\left( e\sin f \,a_r+\frac{p}{r}a_{s}\right) \\&\frac{\text {d}e}{\text {d}f}=\frac{r^2}{\mu }\left[ \sin f \,a_r+\left( 1+\frac{r}{p}\right) \cos f \,a_s+e\frac{r}{p}a_{s}\right] \\&\frac{\text {d}\omega }{\text {d}f}=\frac{r^2}{\mu e}\left[ -\cos f \,a_r + \left( 1+\frac{r}{p}\right) \sin f \,a_s\right] \end{aligned} \end{aligned}$$

(5)

where p is the semilatus rectum, r is the orbital radius, $\mu$ is the gravitational constant of the Earth, and $a_r,\,a_s$ are the respective radial and along-track components of the specific force.

3 Poynting–Robertson and solar wind drag

In this paper, we extend the model used by Zhao et al. (2018) through the inclusion of PRSW drag in the dynamical model. This section includes the derivation of the semi-analytical model for the PRSW effect. The solar wind component of the PRSW drag is known to potentially have a net acceleration outward of the solar system on particles which experience greater SRP forces than gravity in sizes $<0.1 \mu$m, as noted by Burns et al. (1979).

3.1 Model

Following Burns et al. (1979), Liou et al. (1995) expressed the PRSW drag acceleration in RSW coordinates as

$$\begin{aligned} {\varvec{\textrm{a}}}_{PRSW,RSW}=a_{SRP}\left[ -(1+\alpha )\frac{{\varvec{\textrm{v}}}\cdot {\varvec{\textrm{r}}}_{s}}{c\,r_{Sun}} {\hat{{\varvec{\textrm{r}}}}}_{Sun,RSW}-(1+\alpha )\frac{{\varvec{\textrm{v}}}_{RSW}}{c}\right] , \end{aligned}$$

(6)

where $a_{SRP}$ is the magnitude of the SRP acceleration vector which is inversely proportional to the distance from the Sun, $\alpha$ is the solar wind factor, c is the speed of light, $r_{Sun}$ is the orbital distance to the Sun, ${\varvec{\textrm{v}}} \cdot {\varvec{\textrm{r}}}_s$ is the radial velocity in the Sun rest frame transformed into the RSW frame, and ${\varvec{\textrm{v}}}_{RSW}$ is the velocity in the Sun rest frame transformed into the RSW frame.

The total velocity of the smart dust around any planet’s orbit is the combination of the velocity due to the planet’s revolution around the Sun ${\varvec{\textrm{v}}}_{p}$, and the motion of smart dust around the planet, and can be written in the RSW frame as

$$\begin{aligned} {\varvec{\textrm{v}}}_{RSW}=\Vert {\varvec{\textrm{v}}}_{p}\Vert \begin{bmatrix}A\cos (\omega +f)+B\sin (\omega +f)\\ -A\sin (\omega +f)+B\cos (\omega +f)\\ C \end{bmatrix} +\sqrt{\frac{\mu }{p}} \begin{bmatrix} e\sin f\\ 1+e\cos f\\ 0 \end{bmatrix}, \end{aligned}$$

(7)

where the constants are $A=\cos (\lambda _{geo}+90^{\circ })$, $B=\sin (\lambda _{geo}+90^{\circ })(\cos ^{2} i-\sin ^{2} i)$ and $C=-\sin i\sin (\lambda _{geo}+90^{o})$.

3.2 Averaged equations of motion

Let $\lambda _{sun}$ be the solar ecliptic longitude. We define $\lambda$ as the angle between $\omega$ and $\lambda _{sun}$, i.e., the geocentric angle between the perigee and the sun vector. The averaged elements are studied over a fixed inclination (cf. Eq. 3), which affects the vector ${\varvec{\textrm{v}}}_{RSW}$. To ascertain the long-term effects of PRSW drag, the averaged elements are calculated. Elements of interest are the semimajor axis, eccentricity and argument of perigee. The shorthand notation $\text {c}_{(\cdot )}\equiv \cos (\cdot )$ and $\text {s}_{(\cdot )}\equiv \sin (\cdot )$ has been used. Given the structure of Eq. (6), we average the contributions of the total and radial velocity terms separately, as denoted by the subscripts v and $v \cdot r_s$, respectively, using the averaging procedure

$$\begin{aligned} \bar{{\varvec{\textrm{f}}}}(x)=\frac{1}{T}\int _0^T{\varvec{\textrm{f}}}(x,t)dt \end{aligned}$$

(8)

where T is the period of the vector-valued periodic function ${\varvec{\textrm{f}}}(x,t)$ and $\bar{{\varvec{\textrm{f}}}}$ denotes an averaged value. To facilitate computations, we perform a transformation of the independent variable from true to eccentric anomaly using the relation

$$\begin{aligned} df = \frac{a\sqrt{1-e^2}}{r}dE \end{aligned}$$

(9)

Denoting $v_p \equiv \Vert {\varvec{\textrm{v}}}_p\Vert$, the resulting expressions are

$$\begin{aligned} \varDelta a_{v}&=\frac{2a^{3}\sqrt{1-e^{2}}}{\mu }a_{SRP}{(1+\alpha )}\Biggl \{ \frac{v_{p}}{c}\Biggl [ (A\text {c}_\omega +B\text {s}_\omega )\Biggl ( \frac{2 \text {c}_ E +(\frac{1}{e}-e)\ln (1-e\text {c}_ E)}{\sqrt{(}1-e^{2})}\Biggr )\nonumber \\&\quad +(-A\text {s}_\omega +B\text {c}_\omega ) \Biggl (\frac{\text {s}_ E - eE}{1-e^{2}} - \frac{2 \tan \frac{E}{2}}{1+\tan ^{2}\frac{E}{2}} - \frac{E}{e}\Biggr )\nonumber \\&\quad + \left( 2e-\frac{2}{e}\right) \Biggl (\frac{{{\,\textrm{arctanh}\,}}(\sqrt{\frac{e+1}{e-1}} \tan \frac{E}{2})}{\sqrt{e^{2}-1}}\Biggr ) \Biggr ] + \frac{\sqrt{\mu /p}}{c}(E+e\text {s}_ E) \Biggr \}\Bigg |_{E_{exit}}^{E_{entry}} \end{aligned}$$

(10)

$$\begin{aligned} \varDelta e_{v}&=\frac{a^{2}(1-e^{2})^{3/2}}{\mu }a_{SRP}(1+\alpha )\Biggl \{\frac{v_p}{c}\Biggl [ (A \text {c}_\omega +B \text {s}_\omega ) \frac{1+e}{(1-e^{2})^{3/2}}\nonumber \\&\quad \times \Biggl (-\frac{e}{2}\cos ^{2} E +\left( 1-e+\frac{1}{e}\right) \text {c}_ E +\left( \frac{1}{e^{2}}+ \frac{3}{e}-e-1\right) \ln (1-e\text {c}_ E)\Biggr )\nonumber \\&\quad +(-A\text {s}_\omega +B\text {c}_\omega )\Biggl (\frac{2\tan \frac{E}{2} }{e(1+\tan ^{2}\frac{E}{2})}+\frac{E}{e^2} +\left( \frac{2}{e^{2}}-2\right) \frac{ {{\,\textrm{arctanh}\,}}\left( \sqrt{\frac{e+1}{e-1}} \tan \frac{E}{2}\right) }{e^{2}-1}\Biggr )\Biggr ] \nonumber \\&\quad +\frac{\sqrt{\mu /p}}{c}\Biggl (\frac{2\tan \frac{E}{2} }{e(1+\tan ^{2}\frac{E}{2})}+\frac{E}{e^2}+\left( \frac{2}{e^{2}}-2\right) \frac{ {{\,\textrm{arctanh}\,}}\left( \sqrt{\frac{e+1}{e-1}} \tan \frac{E}{2}\right) }{\sqrt{e^{2}-1}} \Biggr )\Biggr \}\Bigg |_{E_{exit}}^{E_{entry}} \end{aligned}$$

(11)

$$\begin{aligned} \varDelta \omega _{v}&=\frac{a^{2}}{\mu e}\sqrt{1-e^{2}}a_{SRP}(1+\alpha ) \Biggl \{\frac{v_p}{c} \Biggl [ (A \text {c}_\omega +B \text {s}_\omega )\Biggl (-\frac{3E}{2}+\frac{\text {s}_ E \text {c}_ E}{2}+e \text {s}_ E\Biggr )\nonumber \\&\quad +\frac{(-A \text {s}_\omega +B \text {c}_\omega )}{\sqrt{1-e^{2}}} \Biggl (\frac{\sin ^{2} E}{2} + e\text {c}_ E\Biggr ) \Biggr ]\nonumber \\&\quad + \frac{\sqrt{\mu /p}/c}{1-e^{2}}\Biggl (\text {s}_ E\text {c}_ E+(e^{3}-3e)\text {s}_ E+\left( \frac{e^{2}}{2}+2\right) E+\sqrt{1-e^{2}}\left( \frac{\cos ^{2} E}{2}-e \text {c}_ E\right) \Biggr ) \Biggr \}\Bigg |_{E_{exit}}^{E_{entry}} \end{aligned}$$

(12)

$$\begin{aligned} \varDelta a_{v \cdot r_s}&=-\frac{2a^{3}\sqrt{1-e^{2}}}{\mu }a_{SRP}{(1+\alpha )}\frac{{\varvec{\textrm{v}}}_{RSW} \cdot {\varvec{\textrm{r}}}_{Sun}}{c \Vert {\varvec{\textrm{r}}}_{Sun}\Vert }\Biggl \{(\text {c}_ E+\left( \frac{2}{e}-2\right) \ln (1-e \text {c}_ E))\frac{\text {c}_ \lambda }{\sqrt{1-e^{2}}}\nonumber \\&\quad +\Biggl (2\frac{\tan {\frac{E}{2}}}{1+\tan ^{2}\frac{E}{2}}-\frac{4}{e}{{\,\textrm{arctanh}\,}}\left( {\tan \frac{E}{2}}\right) +\left( 4e-\frac{4}{e}\right) \frac{{{\,\textrm{arctanh}\,}}{\sqrt{\frac{e+1}{e-1}}} \tan \frac{E}{2}}{\sqrt{e^{2}-1}}\Biggr )\text {s}_\lambda \Biggr \}\Bigg |_{E_{exit}}^{E_{entry}} \end{aligned}$$

(13)

$$\begin{aligned} \varDelta e_{v\cdot r_s}&=-\frac{2a^{2}(1+e)}{\mu }a_{SRP}{(1+\alpha )}\frac{{\varvec{\textrm{v}}}_{RSW} \cdot {\varvec{\textrm{r}}}_{Sun}}{c \Vert {\varvec{\textrm{r}}}_{Sun}\Vert } \Biggl \{ \Biggl [ \frac{e}{2}\cos ^{2} E+\left( e+\frac{1}{e}-3\right) \text {c}_ E\nonumber \\&\quad + \Biggl (\frac{1}{e^{2}}-\frac{1}{e} +e-1\Biggr ) \ln (1-e \text {c}_ E) \Biggr ] \text {c}_ \lambda +\Biggl [(e^{3}-2e^{2}+e)E+\Biggl (\frac{2}{e}-e-6\Biggr )\frac{\tan ^{3}{\frac{E}{2}}}{(1+\tan ^{2}\frac{E}{2})^{2}}\nonumber \\&\quad +\Biggl (e+\frac{2}{e}-6\Biggr )\frac{\tan {\frac{E}{2}}}{(1+\tan ^{2}\frac{E}{2})^{2}} +\Biggl (7e-2e^{2}-\frac{2}{e}+\frac{2}{e^{2}}\Biggr ){{\,\textrm{arctanh}\,}}({\tan \frac{E}{2}}) \nonumber \\&\quad +\Biggl (\frac{2}{e^{2}}-\frac{2}{e}+6e-2e^{2}-2\Biggr )\frac{{{\,\textrm{arctanh}\,}}{\sqrt{\frac{e+1}{e-1}}} \tan \frac{E}{2}}{\sqrt{e^{2}-1}}\Biggr ] \frac{\text {s}_ \lambda }{\sqrt{1-e^{2}}} \Biggr \}\Bigg |_{E_{exit}}^{E_{entry}} \end{aligned}$$

(14)

$$\begin{aligned} \varDelta \omega _{v \cdot r_s}&=-\frac{a^{2}}{\mu e}a_{SRP}{(1+\alpha )}\frac{{\varvec{\textrm{v}}}_{RSW} \cdot {\varvec{\textrm{r}}}_{Sun}}{c \Vert {\varvec{\textrm{r}}}_{Sun}\Vert }\Biggl \{ \Biggl [\frac{e}{2}\cos ^{2} E+\Biggl (e+\frac{1}{e}-3\Biggr ) \text {c}_ E\nonumber \\ {}&+\Biggl (\frac{1}{e^{2}} - \frac{1}{e}+e-1\Biggr )\ln (1-e\text {c}_ E) \Biggr ](1+e) \text {c}_\lambda \nonumber \\ {}&+ \Biggl [\Biggl ((-2e^{3}+\frac{2}{e}+5e+4\Biggr )\frac{\tan ^{3}{\frac{E}{2}}}{(1+\tan ^{2}\frac{E}{2})^{2}}+\Biggl (-2e^{3}+3e+4-\frac{2}{e}\Biggr )\frac{\tan {\frac{E}{2}}}{(1+\tan ^{2}\frac{E}{2})^{2}}\nonumber \\&\quad +\Biggl (-2e^{2}-5e+2e^{3}-\frac{2}{e^{2}}\Biggr ){{\,\textrm{arctanh}\,}}\left( \tan \frac{E}{2}\right) \nonumber \\&\quad + \Biggl (2e^{4}-6e^{2}+6-\frac{2}{e^{2}}\Biggr )\frac{{{\,\textrm{arctanh}\,}}\left( {\sqrt{\frac{e+1}{e-1}}} \tan \frac{E}{2}\right) }{\sqrt{e^{2}-1}} +2E \Biggr ] \frac{\text {s}_\lambda }{ \sqrt{1-e^{2}} } \Biggr \}\Bigg |_{E_{exit}}^{E_{entry}} \end{aligned}$$

(15)

where E denotes the eccentric anomaly, so that $E_{entry}$ and $E_{exit}$ are the eclipse entry and exit eccentric anomalies (cf. Fig. 8 for the eclipse geometry). Equations (10)–(12) and (13)–(15) form the mean element differentials for the PRSW effect by utilizing the mean angular velocity, $\bar{\dot{f}}$, obtained using the averaging operator as in Eq. (8):

$$\begin{aligned} \varDelta a_{PRSW}= & {} \bar{\dot{f}} \left[ \varDelta {a}_{v } + \varDelta {a}_{v \cdot r_s}\right] \end{aligned}$$

(16)

$$\begin{aligned} \varDelta e_{PRSW}= & {} \bar{\dot{f}} \left[ \varDelta {e}_{v } + \varDelta {e}_{v \cdot r_s}\right] \end{aligned}$$

(17)

$$\begin{aligned} \varDelta \omega _{PRSW}= & {} \bar{\dot{f}} \left[ \varDelta {\omega }_{v } + \varDelta {\omega }_{v \cdot r_s}\right] . \end{aligned}$$

(18)

These equations are not valid for very low eccentricities.

3.3 Standalone effects

Variations of the mean semimajor axis over one orbit, under the influence of Poynting–Robertson and Solar Wind drag only, assuming a constant $\lambda$, for different periods of time, are compared in Fig. 2. The graphs are shown for an AMR of ${A}/{m}=1\, \text {m}^2/\text {kg}$, an initial semimajor axis of $a_0=42167\, \text {km}$ and $i=2^{\circ }$. The PRSW effect depends on $\lambda$; it is positive in the interval $\lambda \in \{3\pi /2,\pi /2\}$ and negative in the remaining interval. At $\lambda =0$ or $\pi$, an orbit under eclipse is symmetric, which is when the maximum effect is observed, while the minimum occurs near $\lambda =\pi /2,3\pi /2$. Consequently, as previous studies indicated (Lhotka et al. 2016), the generally dissipative nature of the PRSW effect exhibits strong dependence on the orbital regime and orbital resonances, and, hence, may become relevant for large area-to-mass ratio object.

Other studies portrayed PRSW to have only a dissipative effect. Our results indicate that this is more nuanced for orbits and depends highly on $\lambda$.

Fig. 2

$\varDelta a$ for quarter, half and full year due to PRSW drag for all $\lambda$ with ${A}/{m}=1\, \text {m}^2/\text {kg}$, $a_0=42167\, \text {km}$ and $i=2^{\circ }$

Variations of the mean eccentricity over one orbit, under the same conditions, are compared in Fig. 3. The eccentricity variation is positive in the interval $\lambda \in \{\pi /2,3\pi /2\}$ and negative in the remaining $\lambda$ values. At $\lambda =0$ or $\pi$, an orbit under eclipse is symmetric, which is when the maximum effect is observed. Variations of the mean argument of perigee over one orbit, under the same conditions, are compared in Fig. 4. Contrary to the semimajor axis and eccentricity, variations in the argument of perigee due to PRSW drag are always positive, with the minima occurring at $\lambda =0,\pi$. It is slightly higher in the first half of the $\lambda$ interval than the second, owing to an unequal eclipse averaging for such Sun-Earth geometries. However, $\lambda$ is not constant and is bound to change. Due to the presence of a finite perigee drift, $\lambda$ constantly evolves. No model in existing literature takes this into account.

Fig. 3

$\varDelta e$ for quarter, half and full year due to PRSW drag for all $\lambda$ with ${A}/{m}=1\, \text {m}^2/\text {kg}$, $a_0=42167\, \text {km}$ and $i=2^{\circ }$

Fig. 4

$\varDelta \omega$ for quarter, half and full year due to PRSW drag for all $\lambda$ with ${A}/{m}=1\, \text {m}^2/\text {kg}$, $a_0=42167\, \text {km}$ and $i=2^{\circ }$

To find the actual change, a new element called $\varDelta \text {\oe }_{true}$ is defined, which represents the actual variation in the element, given a time period, as a function of a drifting $\lambda$. For any given period of time, the cumulative change in an orbital element can, therefore, be calculated by adding the individual differential of the element per orbit, given that its variation as a function of $\lambda$ is known.

Figures 5, 6 and 7 show the above-defined true variation in mean semimajor axis, eccentricity and argument of perigee, respectively, given an initial $\lambda$ for a period of 1 year.

Fig. 5

$\varDelta a_{true}$ per year due to PRSW drag only with ${A}/{m}=1\, \text {m}^2/\text {kg}$, $a_0=42167\, \text {km}$ and $i=2^{\circ }$

Fig. 6

$\varDelta e_{true}$ per year due to PRSW drag only with ${A}/{m}=1\, \text {m}^2/\text {kg}$, $a_0=42167\, \text {km}$ and $i=2^{\circ }$

Fig. 7

$\varDelta \omega _{true}$ per year due to PRSW drag only with ${A}/{m}=1\, \text {m}^2/\text {kg}$, $a_0=42167\, \text {km}$ and $i=2^{\circ }$

4 Modeling orbital dynamics

The standard model for the planeto-orbital dynamics of HAMR objects has mostly been studied in the context of space debris dynamics (Colombo and McInnes 2011). Since smart dust falls in the category of HAMR objects, the dynamics are non-Keplerian, arising from perturbations due to SRP, atmospheric drag and electrostatic forces. The main environmental forces that are most sensitive to the AMR are the likes of SRP and atmospheric drag in low Earth orbits. Zhao et al. (2018) also included the effects of gravitational perturbations into the model. The model used by Zhao et al. (2018) is reviewed in this section, further additions to which are described in subsequent sections.

4.1 Gravitational potential

The perturbing potential can be written in the form (Vallado 2001):

$$\begin{aligned} R= & {} \frac{\mu }{r} \sum _{l=2}^{\infty } \sum _{m=0}^{m}\left( \dfrac{r_e}{r}\right) ^{l} P_{lm}(\sin \varphi ) [C_{lm}\cos (m\ell )+S_{lm}\sin (m\ell )]\nonumber \\{} & {} + \frac{\mu }{r}\displaystyle \sum _{l=2}^{\infty } J_{l} \left( \dfrac{r_e}{r}\right) ^{l} P_{l}(\sin \varphi ), \end{aligned}$$

(19)

where $J_l$ are the zonal potential coefficients, $r_e$ is the average equatorial radius of the Earth, $\varphi$ is the latitude, $\ell$ is the longitude, $C_{lm}$ and $S_{lm}$ represent tesseral and sectorial coefficients, $P_l$ and $P_{lm}(x)$ are the associated Legendre polynomials of degree m and order l. The first term on the right hand side of Eq. (19) refers to the tesseral part, while the second term refers to the zonal part.

Zhao et al. (2018) substituted the secular and long-periodic terms separately to yield averaged differential orbital equations up to $J_4$ as follows:

$$\begin{aligned} \dfrac{\text {d} \bar{a}_{sec}}{\text {d}t}&=0 \nonumber \\ \dfrac{\text {d} \bar{e}_{sec}}{\text {d}t}&=0 \nonumber \\ \dfrac{\text {d} \bar{\omega }_{sec}}{\text {d}t}&=\dfrac{A_2}{p^2}n\left( 2-\frac{5}{2}\sin ^2 i \right) +\dfrac{A_4}{p^4}n\Biggl [\left( \frac{12}{7}+\frac{27}{14}e^2 \right) -\sin ^2 i \left( \frac{93}{14}+\frac{27}{4}e^2 \right) \nonumber \\&+\sin ^4 i \left( \frac{21}{4}+\frac{81}{16}e^2 \right) \Biggr ], \end{aligned}$$

(20)

$$\begin{aligned} \dfrac{\text {d} \bar{a}_{long}}{\text {d}t}&= 0 \nonumber \\ \dfrac{\text {d} \bar{e}_{long}}{\text {d}t}&= 0 \nonumber \\ \dfrac{\text {d} \bar{\omega }_{long}}{\text {d}t}&=-\dfrac{A_3}{p^3}n\frac{1}{e\sin i}\left[ \frac{3}{8}\sin ^2 i(4-5\sin ^2 i)-\frac{3}{8}e^2(4-35\sin ^2 i+35\sin ^4 i)\right] \sin \omega \nonumber \\&+\dfrac{A_4}{p^4}n\left[ \sin ^2 i \left( \frac{9}{14}+\frac{3}{4}\sin ^2 i \right) -e^2 \left( \frac{9}{14}-\frac{15}{4}\sin ^2 i \right) +\frac{21}{4}\sin ^4 i \right] \cos 2\omega \end{aligned}$$

(21)

where p is the semilatus rectum, n is the mean motion, and the remaining coefficients are defined as

$$\begin{aligned} A_2=\frac{3}{2}J_2r_e^2,\quad A_3=-J_3r_e^3,\quad A_4=-\frac{35}{8}J_4r_e^4. \end{aligned}$$

(22)

The tesseral and sectorial harmonics of degree 2 and order 2 have a periodicity of half a day and must be considered. The averaged differential rates due to these harmonics are (Zhao et al. 2018)

$$\begin{aligned} \dfrac{\text {d} \bar{a}_{tess,long}}{\text {d}t}= & {} 0 \nonumber \\ \dfrac{\text {d} \bar{e}_{tess,long}}{\text {d}t}= & {} 0 \nonumber \\ \dfrac{\text {d} \bar{\omega }_{tess,long}}{\text {d}t}= & {} \dfrac{3n^2{r_e}^2J_{22}(1-e^2)^{3/2}}{8\pi p^2 n_e}(3e^2+2-5\sin ^2 i)\nonumber \\{} & {} \times \left[ \sin 2\left( \varOmega -\frac{2n_e\pi }{n}\right) -\sin 2\varOmega \right] , \end{aligned}$$

(23)

where $n_e$ is the Earth rotational rate and $J_{22}$ is the gravitational coefficient of degree 2 and order 2.

4.2 Atmospheric drag

Atmospheric drag is a non-conservative force dominant in low Earth orbits. The perturbing acceleration due to atmospheric drag can be written as

$$\begin{aligned} {\varvec{\textrm{a}}}_{drag}=-\dfrac{1}{2}\dfrac{c_DA_{drag}}{m}\rho |{\varvec{\textrm{v}}}_{rel}|^2 \hat{{\varvec{\textrm{v}}}}_{rel}, \end{aligned}$$

(24)

where $c_D$ is the drag coefficient, $A_{drag}$ is the effective cross-sectional area of the spacecraft, m is the mass, ${\varvec{\textrm{v}}}_{rel}$ is the velocity relative to the rotating atmosphere, and $\hat{{\varvec{\textrm{v}}}}_{rel}$ is the direction of the relative velocity vector.

The greatest challenge in modeling drag is the determination of the correct atmospheric density. The exponential atmospheric model is based on the assumption of an exponentially-varying density with altitude in finite strata for a time-independent spherically-symmetric atmosphere. If h is the altitude at which density is to be determined, then for a given altitude there exists a reference altitude $h_0$ at which density is $\rho _0$ and H represents the scale height within which the density varies according to (Vallado 2001)

$$\begin{aligned} \rho = \rho _0 \exp \left( -\dfrac{h-h_0}{H}\right) . \end{aligned}$$

(25)

Blitzer (1970) provided expressions for $\varDelta a_{drag}$ and $\varDelta e_{drag}$,

$$\begin{aligned} \varDelta a_{drag}= & {} -2\pi \delta \rho _p a^2 \exp (-\gamma ) \Biggl [ I_0 + 2eI_1 + \frac{3e^2}{4}(I_0+I_2) + \frac{e^3}{4}(3I_1+I_3)+ \mathcal {O}(e^4) \Biggr ] \nonumber \\ \varDelta e_{drag}= & {} -2\pi \delta \rho _p a \exp (-\gamma ) \Biggl [ I_1 + \frac{e}{2}(I_0+I_2) - \frac{e^2}{8}(5I_1-I_3)\nonumber \\{} & {} -\frac{e^3}{16}(5I_0+4I_2-I_4)+\mathcal {O}(e^4) \Biggr ], \end{aligned}$$

(26)

where $\rho _p$ is the density at the orbit perigee, computed using Eq. (25), the factor $\gamma =ae/H$, $I_k$ are modified Bessel functions of the first kind of order k and argument $\gamma$ (Abramowitz et al. 1988), and $\delta =Qc_DA_{drag}/{m}$. The drag coefficient $c_D$ is considered to be constant, and the factor Q is equal to 1 for a static atmosphere. These equations are valid only for the eccentricity range $0.01\le e \le 0.8$ (Colombo and McInnes 2011).

4.3 Solar radiation pressure

SRP is one of the most important environmental forces for studying the evolution of smart dust. For an Earth-centric orbit lying in the ecliptic plane, the acceleration due to SRP in the RSW frame can be expressed as

$$\begin{aligned} {\varvec{\textrm{a}}}_{SRP}=\dfrac{p_{SR}\, c_R\, A_s}{m}\begin{bmatrix}\cos (\lambda + f)\\ \sin (\lambda + f) \\ 0 \end{bmatrix}, \end{aligned}$$

(27)

where $p_{SR}=4.56 \times 10^{-6} \,\text {N}/\text {m}^2$ is the solar pressure constant; $c_R$ is the reflectivity coefficient; $A_s$ is the area exposed to the Sun; and the angle $\lambda =\omega -\lambda _{Sun}$ is the relative angle between the perigee and the anti-Sun vector direction (since both $\omega$ and $\lambda _{Sun}$ are measured with respect to a fixed reference direction). Figure 8 shows the eclipse geometry and angle $\lambda$.

Fig. 8

Definition of $\lambda$ and eclipse geometry

Fig. 9

Determination of sun-synchronous conditions at $h_p=700$ km

Fig. 10

Evolution of first equilibrium point of $\varDelta a=0$ for different perigee altitudes

Fig. 11

Evolution of second equilibrium point of $\varDelta a=0$ for different perigee altitudes

Fig. 12

Evolution of first equilibrium point of $\varDelta e=0$ for different perigee altitudes

Fig. 13

Evolution of second equilibrium point of $\varDelta e=0$ for different perigee altitudes

To determine the mean variation of orbital elements, the eclipse geometry must be calculated such that the parallax of the Sun is negligible; $f_{enter}$ and $f_{exit}$ can be determined by solving two independent equations,

$$\begin{aligned} \begin{aligned}&p \sin (\lambda + f_{enter}) = -r_e(1+e \cos f_{enter})\\&p \sin (\lambda + f_{exit}) = -r_e(1+e \cos f_{exit}), \end{aligned} \end{aligned}$$

(28)

Note that for each $\lambda$ there exist distinct solutions for $f_{enter}$ and $f_{exit}$.

Colombo and McInnes (2011) derived the primitive functions, defined formally as

$$\begin{aligned} \text {fun}_x(a,e,\omega -\lambda _{Sun}) = \int \frac{\text {d}x}{\text {d}f}\text {d}f+\text {const.} \end{aligned}$$

(29)

by integrating with respect to true anomaly. Assumptions used in the derivation were that the orbit lies in the ecliptic plane, and that the disturbing acceleration magnitude $a_{SRP}$ is constant while the smart dust is in sunlight. The resulting primitive functions (with the integration constants omitted) are

$$\begin{aligned} \begin{aligned}&\text {fun}_{a}(a,e,\omega -\lambda _{Sun})=-\frac{2a^{3}(1-e^{2})}{\mu }a_{SRP}\left( \frac{\cos (\omega -\lambda _{Sun})+e\sin (\omega -\lambda _{Sun})\sin f}{e(1+e\cos f)}\right) \\&\text {fun}_{e}(a,e,\omega -\lambda _{Sun})=-\frac{a^{2}(1-e^{2})^{2}}{\mu }a_{SRP} \Biggl [\sin (\omega -\lambda _{Sun}) \Biggl (-\frac{3}{2}\frac{E}{(1-e^{2})^{3/2}}\\&+\frac{\sin f(\cos f(-8e^{4}+10e^{2}-2)+6e(1-e^{2}))}{4(1-e^{2})^{2}(1+e\cos f)^{2}} \Biggr )-\frac{\cos (\omega -\lambda _{Sun})}{2e^{2}(1+e\cos f)^{2}}(1+2e\cos f+e^{2}) \Biggr ]\\&\text {fun}_{\omega }(a,e,\omega -\lambda _{Sun})=-\frac{a^{2}(1-e^{2})^{2}}{\mu e}a_{SRP}\Biggl [\cos (\omega -\lambda _{Sun})\Biggl (\frac{3}{2}\frac{E}{(1-e^{2})^{3/2}}\\&-\frac{e\sin f}{(1-e^{2})(1+e\cos f)}-\frac{1}{2}\frac{(e+\cos f)\sin f}{(1-e^{2})(1+e\cos f)^{2}}\Biggr )+\sin (\omega -\lambda _{Sun})\frac{1+2e\cos f}{2e^{2}(1+e\cos f)^{2}}\Biggr ] \end{aligned}\nonumber \\ \end{aligned}$$

(30)

In the current study, the primitive function for eccentricity was replaced by an eccentric-anomaly averaged version, to avoid numerical inconsistencies seen at high-eccentricity cases. The new primitive function developed for eccentricity is obtained by substituting the relations

$$\begin{aligned} \sin f = \frac{\sqrt{1-e^2}\sin E}{1-e\cos E},\;\cos f = \frac{\cos E-e}{1-e\cos E} \end{aligned}$$

(31)

into Eq. (30):

$$\begin{aligned} \begin{aligned} \text {fun}_{e}&=\frac{a^{2}\sqrt{1-e^{2}}}{\mu }\Biggl \{ \sin (\omega -\lambda _{Sun})\Biggl (\frac{3}{2}E+\frac{\cos E\sin E}{2}-2e\sin E\Biggr ) \\&\quad -\cos (\omega -\lambda _{Sun})\sqrt{1-e^{2}}\Biggl (\frac{\sin ^{2}E}{2}\Biggr )\Biggr \} \end{aligned}. \end{aligned}$$

(32)

To calculate the total mean variation of orbital elements over an entire orbit, the functions are evaluated over two arcs: $[0, f_{enter}],\,[f_{exit}, 2\pi ]$. Then, the mean variation in semimajor axis, eccentricity and argument of perigee can be given as

$$\begin{aligned} \begin{aligned} \varDelta a_{SRP}(a,e,\lambda ,f_{exit},f_{enter})=&\bar{\dot{f}} \int _{0}^{f_{enter}}\frac{\text {d}a}{\text {d}t}\text {d}t+\bar{\dot{f}} \int _{f_{exit}}^{2\pi }\frac{\text {d}a}{\text {d}t}\text {d}t\\ \varDelta e_{SRP}(a,e,\lambda ,f_{exit},f_{enter})=&\bar{\dot{f}} \int _{0}^{f_{enter}}\frac{\text {d}e}{\text {d}t}\text {d}t+\bar{\dot{f}} \int _{f_{exit}}^{2\pi }\frac{\text {d}e}{\text {d}t}\text {d}t\\ \varDelta \omega _{SRP}(a,e,\lambda ,f_{exit},f_{enter})=&\bar{\dot{f}} \int _{0}^{f_{enter}}\frac{\text {d}\omega }{\text {d}t}\text {d}t+\bar{\dot{f}} \int _{f_{exit}}^{2\pi }\frac{\text {d}\omega }{\text {d}t}\text {d}t. \end{aligned} \end{aligned}$$

(33)

Fig. 14

Equilibrium plot with both partial equilibria $\varDelta$a = 0 and $\varDelta \omega +\varDelta \varOmega \cos i =\varDelta \lambda _{Sun}$, and a full equilibrium at $e=0.4629$ and $\lambda =180^\circ$ for $h_p=600$ km

Fig. 15

Equilibrium plot with both partial equilibria $\varDelta$a = 0 and $\varDelta \omega +\varDelta \varOmega \cos i =\varDelta \lambda _{Sun}$, and a full equilibrium at $e=0.4629$ and $\lambda =180^\circ$ for $h_p=1200$ km

Fig. 16

Equilibrium plot with both partial equilibria $\varDelta$a = 0 and $\varDelta \omega +\varDelta \varOmega \cos i =\varDelta \lambda _{Sun}$, and a full equilibrium at $e=0.4629$ and $\lambda =180^\circ$ for $h_p=5000$ km

5 Orbital equilibria

5.1 Equilibrium conditions

To investigate the orbital dynamics of smart dust under the influence of Earth’s gravitational potential, SRP, atmospheric drag and PRSW drag, we use the secular and long-periodic variations of semimajor axis, eccentricity and argument of perigee over one orbital period. We also account for eclipse through averaging, in the SRP and PRSW models.

Many missions require a specific orbit orientation relative to the Sun. The original equilibrium criterion by Zhao et al. (2018) was extended herein by including a modified condition on $\varDelta \omega$, leading to the new equilibrium conditions

$$\begin{aligned}{} & {} \varDelta a=0 \end{aligned}$$

(34a)

$$\begin{aligned}{} & {} \varDelta e=0 \end{aligned}$$

(34b)

$$\begin{aligned}{} & {} \varDelta \omega +\varDelta \varOmega \cos i=\varDelta \lambda _{Sun}, \end{aligned}$$

(34c)

where all the orbital elements considered are mean elements averaged per orbit, considering eclipse fractions. Each mean differential element in Eq. (34) is due to the influence of all perturbations combined. These equilibrium equations are searched for by propagating the GVE using the following initial orbital elements: perigee height $h_p$, eccentricity e and argument of perigee $\omega$. For the smart dust, the selected area-to-mass ratio is 32.6087 $\text {m}^2/\text {kg}$, consistent with the value chosen by Zhao et al. (2018).

To determine full equilibrium conditions, the search for Sun-synchronous cases is imperative. Selecting a perigee altitude, $h_p$, one dimension is fixed, while eccentricity and $\lambda$ are varied to reveal eccentricities where Eq. (34c) holds. Each side of the equation represents a surface. The points of intersection of these two surfaces are the solutions for Eq. (34c). Solutions occur in a very narrow corridor of eccentricity for any given orbit. Figure 9 shows such a surface plot for the perigee altitude case of 700 km. For this case, it was found that Sun-synchronous conditions lie in the eccentricity range $e=0.446$ to $e=0.474$. It can be noticed that the condition occurs such that the curve $\varDelta \omega +\varDelta \varOmega \cos i$ intersects $\varDelta \lambda _{Sun}$ at least two $\lambda$ values. In other words, multiple solutions for $\lambda$ might exist even in this small range of eccentricity.

Fig. 17

Phase portrait of $\lambda$ for $a=42167$ km, $i=2^\circ$ and ${A}/{m}=32.6708 \,\text {m}^2/\text {kg}$

Fig. 18

Linearized phase portrait of saddle point about $\lambda =-1.89$ rad

Fig. 19

Linearized phase portrait of saddle point about $\lambda =1.98$ rad

Because the parameter space for the investigation is $\{h_p,e,\lambda \}$, the simulations are executed for the following conditions: (i) initial perigee height $h_p$ from 500 to 5000 km; (ii) the eccentricity e ranges from 0.05 to 0.8; (iii) $\lambda$ from $0^\circ$ to $360^\circ$. A static atmosphere is considered for calculating perturbations due to drag. Perturbed elements in the plane of motion are first considered, while some out-of-plane perturbations that are significant are also discussed later on. The elements are then propagated using semi-analytical methods. $\lambda _{Sun}$ is set for a calendar day of the year that yields the solar ecliptic longitude, and the perigee is varied from $0^\circ$ to $360^\circ$ to yield a variation in $\lambda$.

5.2 Equilibrium solutions

The solutions for the first two parts of Eq. (34) exist for all perigee heights and eccentricity values in the simulation. However, for the third condition, solutions exist only for a certain region in the phase space shown in Fig. 9. A full equilibrium condition can only be found by studying where such solutions occur concurrently. Below, we study equilibrium results owing to each individual condition; all elements described henceforth are mean elements unless mentioned otherwise.

The PRSW drag contribution is quite weak, and would cause the smart dust to spiral inwards for heliocentric orbits. Due to the weak relativistic effects (v/c), the SRP dynamics remain dominant in the ecliptic plane over PR and SW components. However, requiring that the semimajor axis and eccentricity remain fixed entails that the eclipse averaging must be equal on both sides of the perigee, which happens at two points only. This explains the existence of two equilibria for each case.

Before focusing on the equilibrium solutions, we must first clarify that in both models we compare with, namely Colombo and McInnes (2011) and Zhao et al. (2018), only planar elements were propagated. The current paper also takes into account the contribution of nodal precession $\varDelta \varOmega$, because PRSW drag has a finite out-of-plane component that affects apsidal rotation.

The variation of mean semimajor axis due to PRSW drag alone has a maximum effect occurring at $\lambda =0^\circ$ and $\lambda =180^\circ$, which counteracts SRP (cf. Fig. 2). Since it is weaker compared to SRP, the latter remains dominant among all other forces. Drag causes a consistent secular decrease in semimajor axis, while SRP can either increase or decrease the semimajor based on the Sun-relative orientation of the orbit.

When $\lambda =0^\circ ,180^\circ$, the eclipse divides the orbits symmetrically, resulting in null semimajor axis perturbations at such $\lambda$. Figure 10 shows how the first equilibrium point evolves with eccentricity for different perigee altitudes. The variation of the second equilibrium point shown in Fig. 11 only slightly varies with perigee altitude. However, the model is less accurate for lower eccentricities ($e<0.1$). Variations in semimajor axis over one orbit under the influence of SRP and drag are also seen to occur at similar $\lambda$ values as indicated by Colombo and McInnes (2011). When compared to the model without PRSW drag, as in Zhao et al. (2018), the equilibrium solutions lie in two groups: One satisfying $\lambda =0$, and the other for $\lambda =\pi$. This indicates that PRSW drag hardly affects semimajor axis equilibrium solutions.

Variations in eccentricity due to PRSW drag are also opposite to that of SRP, with the minima occurring when $\lambda =\pi /2$ or $3\pi /2$. Conversely, SRP has maxima at the same locations as $\lambda$. This relationship might be explained through the physical concept that whereas SRP pushes the smart dust device away from the Sun, PRSW drag attempts to attract it inwards toward the Sun.

In our study, the solution for $\varDelta e=0$ is given by two points: One near $\lambda =0^\circ$, and one near $\lambda =180^\circ$. Figure 12 shows the variation of the equilibrium point with eccentricity for different perigee altitudes. The variation of the second equilibrium point shown in Fig. 13 only slightly varies with perigee altitude. In Colombo and McInnes (2011), variations of eccentricity due to SRP and drag are in the interval $\pi \le \lambda \le 2\pi$, since drag causes a constant decrease in mean eccentricity. Zhao et al. (2018) considered $J_2$ effects with long-periodic and secular terms, yielding results similar to Colombo and McInnes (2011) (see Eqs. 20, 23). However, for the model in this study, which includes effects of PRSW drag, the zero points are different from Colombo and McInnes (2011).

The orbital element on which PRSW drag has the maximum effect is $\omega$. The fact that Zhao et al. (2018) included long-periodic and secular $J_2$ effects made a significant impact, and, therefore, a marked departure from the results of Colombo and McInnes (2011) for the solution of $\varDelta \omega =\varDelta \lambda _{Sun}$. At lower perigee altitudes, $h_p<2000$ km, both $J_2$ perturbations and SRP are dominant, as shown by Zhao et al. (2018). The current study extends the model by accounting for the nodal component of apsidal rotation, which facilitates finding additional solutions, as described in the Sun-synchronous conditions discussed earlier (cf. Eq. 34c). Figures 14, 15 and 16 show solutions that exist for perigee altitudes $h_p=600,1200,5000$ km at varying eccentricities.

Colombo and McInnes (2011) showed that the condition $\varDelta \omega _{SRP,2\pi }=\varDelta \lambda _{Sun,2\pi }$ can only be obtained in the range $90^\circ \le \lambda \le 270^\circ$. Zhao et al. (2018) conclusively showed that as $J_2$ effects become weaker with increase in perigee altitude, partial equilibrium solutions (as originally defined by Colombo and McInnes (2011)) merge toward $\lambda =180^\circ$. The current study sheds new light on such solutions, obtained by a different method of averaging, which averages over the actual interval for every $\lambda$. At $h_p=600$ km, a full equilibrium solution, i.e., one that satisfies all three constraints of Eq. (34), exists at $\lambda =180^\circ$. At $h_p=1200$ km, the full equilibrium solution still exists at $\lambda =180^\circ$, while solutions satisfying only Sun-synchronous conditions exist in the range $10^\circ \le \lambda \le 340^\circ$. However, at $h_p=5000$ km, we see divergence, such that the full equilibrium solution has now shifted to $\lambda =0^\circ$, and at $\lambda =180^\circ$ the solution is met at $e=0$.

5.3 Stability analysis

Analysis suggests that the variable which is key to understanding the equilibrium of the entire system is $\lambda$. As a dependent variable, $\lambda$ itself changes due to the perturbations in $\omega$ and $\varOmega$. The equilibrium of $\lambda$ can be determined from its phase portrait by determining $\dot{\lambda }$. Using Eq. (34c), these quantities were estimated for a particular semimajor axis, inclination and AMR. Figure 17 is the phase portrait for $\dot{\lambda }$–$\lambda$, which shows four equilibrium points, out of which, two are stable nodes and two are unstable saddle points. To understand the behavior of each equilibrium point, the system is linearized around each type of equilibrium to study behavior around these regions. Figures 18 and 19 show a magnified version of Fig. 17 at regions of interest.

The unstable saddle points occur at $\lambda = -1.89$ rad and $\lambda =1.23$ rad. Figure 18 shows the linearized phase portrait around $\lambda =-1.89$ rad where trajectories that originate on either side of such $\lambda$, move away from the saddle point. The two stable nodes occur at $\lambda = -1.16$ rad and at $\lambda =1.98$ rad. Figure 19 shows the linearized phase portrait about the stable equilibrium at $\lambda =1.98$ rad, around which all trajectories evolve toward the node. This analysis leads to one of the most important observations in this study. It proves that passive control can be exercised over $\lambda$ for targeting specific regions, which over time would evolve to settle at the stable nodes, either collocated or located at opposite stable points, in order to maintain a formation of smart dust modules.

6 Conclusions

The problem of finding long-term equilibria conditions for smart dust was recast by extending previous studies to include Poynting–Robertson and Solar Wind (PRSW) drag. Upgrades made to previous studies include extending the phase space by solving the equilibrium equations for every varying $\lambda$ (the geocentric angle between the perigee and the sun vector), without assuming a constant $\lambda$, which eventually led to studying the phase-space dynamics of $\dot{\lambda }-\lambda$, and studying the averaged variation of PRSW drag over an orbit and corresponding effects on the orbital parameters around a planetocentric orbit for every $\lambda$. Since the phase space was extended to study all possible sun-orbit geometries, it resulted in cognizance of the variation of all parameters with respect to $\lambda$. Given the size and shape of the orbit, this enabled estimating the mean changes in semimajor axis, eccentricity and argument of perigee for each case. The problem of finding long-term equilibrium conditions for smart dust was thus recast by extending previous work to include PRSW drag. By including the effect and defining new equilibrium conditions on the orbital orientation, some additional partial equilibrium solutions, constituting orbits with fixed rate of perigee change with respect to the longitudinal rate of change, were found. Moreover, the study shows that even though PRSW is not dominant as compared to solar radiation pressure or $J_2$, it still influences the evolution of the relative Sun-orbit orientation. For orbits with higher initial perigee altitudes, where drag and $J_2$ effects subside, PRSW definitely influences long-term orbital behavior and should be considered in the orbit design scheme for smart dust devices.