Circular restricted full three-body problem with rigid-body spacecraft dynamics in binary asteroid systems

Abstract

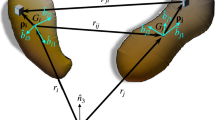
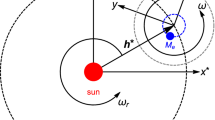
Coupling between the rotational and translational motion of a rigid body can have a profound effect on spacecraft motion in complex dynamical environments. While there is a substantial amount of study of rigid-body coupling in a non-uniform gravitational field, the spacecraft is often considered as a point-mass vehicle. By contrast, the full-N body problem (FNBP) evaluates the mutual gravitational potential of the rigid-body celestial objects and any other body, such as a spacecraft, under their influence and treats all bodies, including the spacecraft, as a rigid body. Furthermore, the perturbing effects of the FNBP become more pronounced as the celestial bodies become smaller and/or more significantly aspherical. Utilizing the comprehensive framework of dynamics and gravitational influences within the FNBP, this research investigates the dynamics of spacecraft modeled as rigid bodies in binary systems characterized by nearly circular mutual orbits. The paper presents an examination of the perturbation effects that arise in this circular restricted full three-body problem (CRF3BP), aiming to assess and validate the extent of these effects on the spacecraft’s overall motion. Numerical results provided for spacecraft motion in the CRF3BP in a binary asteroid system demonstrate non-negligible trajectory divergence when utilizing rigid-body versus point mass spacecraft models. These results also investigate the effects of shape and inertia tensors of the bodies and solar radiation pressure in those models.

Appendix A Inertia tensor models for Moshup and Squannit

Three different inertia tensor models were determined for both Moshup and Squannit. They are presented for each celestial body below based on the either the data from Table 1 or from the shape model developed for this binary system (Ostro and Benner 2018; Ostro et al. 2006; Scheeres et al. 2006).

1.1 A.1 Moshup inertia

For the parameters for Moshup, the spherical, triaxial ellipsoid, and polyhedron-derived models for the inertia tensors are determined. All tensors are given in $\text {kg}\cdot \text {m}^{2}$.

1.1.1 A.1.1 Spherical inertia tensor

Using the spherical inertia tensor described in Eq. (12), the inertia tensor of Moshup is given by

$$\begin{aligned} {}^{\mathcal {B}_{1}}{}{J_{\text {Moshup}}}=4.504837\times 10^{17}~I_{3}~\text {kg}\cdot \text {m}^{2} \end{aligned}$$

1.1.2 A.1.2 Triaxial ellipsoid inertia tensor

Using the triaxial ellipsoid inertia tensor described in Eq. (13), the inertia tensor of Moshup is given by:

$$\begin{aligned} {}^{\mathcal {B}_{1}}{}{J_{\text {Moshup}}}=\begin{bmatrix} 4.733323&{}0&{}0\\ 0&{}4.864237&{}0\\ 0&{}0&{}5.355889 \end{bmatrix}\times 10^{17}~\text {kg}\cdot \text {m}^{2} \end{aligned}$$

1.1.3 A.1.3 Polyhedron-derived inertia tensor

Using the polyhedral inertia determination method, the inertia tensor of Moshup is given by:

$$\begin{aligned} {}^{\mathcal {B}_{1}}{}{J_{\text {Moshup}}}\hspace{-0.06in}=\hspace{-0.06in}\begin{bmatrix} 3.851960e17&{} 9.000294e12&{} -2.787882e13\\ 9.000294e12&{} 4.035425e17&{} 2.923680e13\\ -2.787882e13 &{}2.923680e13&{} 4.575440e17\\ \end{bmatrix}\hspace{-0.05in}\text {kg}\cdot \text {m}^{2} \end{aligned}$$

1.2 A.2 Squannit inertia

For the parameters for Squannit, the spherical, triaxial ellipsoid, and polyhedron-derived models for the inertia tensors are determined. All tensors are given in $\text {kg}\cdot \text {m}^{2}$.

1.2.1 A.2.1 Spherical inertia tensor

Using the spherical inertia tensor described in Eq. (12), the inertia tensor of Squannit is given by

$$\begin{aligned} {}^{\mathcal {B}_{2}}{}{J_{\text {Squannit}}}= 4.672532\times 10^{15}~I_{3}~\text {kg}\cdot \text {m}^{2} \end{aligned}$$

1.2.2 A.2.2 Triaxial ellipsoid inertia tensor

Using the triaxial ellipsoid inertia tensor described in Eq. (13), the inertia tensor of Squannit is given by

$$\begin{aligned} {}^{\mathcal {B}_{2}}{}{J_{\text {Squannit}}}=\begin{bmatrix} 2.256198&{}0&{}0\\ 0&{}3.005683&{}0\\ 0&{}0&{}3.626951 \end{bmatrix}\times 10^{15}~\text {kg}\cdot \text {m}^{2} \end{aligned}$$

1.2.3 A.2.3 Polyhedron-derived inertia tensor

Using the polyhedral inertia tensor determination method, the inertia tensor of Squannit is given by

$$\begin{aligned} {}^{\mathcal {B}_{2}}{}{J_{\text {Squannit}}}\hspace{-0.06in}=\hspace{-0.06in}\begin{bmatrix} 2.157966e15&{}1.617315e12&{}-3.825454e10\\ 1.617315e12&{}3.186037e15&{}1.858829e12\\ -3.825454e10&{}1.858829e12&{}3.756912e15 \end{bmatrix}\hspace{-0.05in}\text {kg}\cdot \text {m}^{2} \end{aligned}$$