The phase space structure of retrograde mean motion resonances with Neptune: the 4/5, 7/9, 5/8 and 8/13 cases

Abstract

We compute planar and three-dimensional retrograde periodic orbits in the vicinity of the restricted three-body problem (RTBP) with the Sun and Neptune as primaries and we concentrate on the dynamics of higher-order exterior mean motion resonances with Neptune. By using the circular planar model as the basic model, families of retrograde symmetric periodic orbits are computed at the 4/5, 7/9, 5/8 and 8/13 resonances. We determine the bifurcation points from the planar circular to the planar elliptic problem and we find all the corresponding families. In order to obtain a global view of the families of periodic orbits, the eccentricity of the primaries takes values in the whole interval $0<e'<1$. Then, we find all the possible vertical critical orbits (v.c.o) of the planar circular problem and we proceed to the three-dimensional circular restricted 3-body problem. In this model, retrograde periodic orbits are generated mainly from the retrograde v.c.o. Also, if we continue families of direct orbits for $i>90^\circ$, then we can obtain families of 3D symmetric retrograde periodic orbits. The linear stability is examined too. Stable periodic orbits are associated with phase space domains of resonant motion where TNOs can be captured. In order to study the phase space structure of the above resonances, we construct dynamical stability maps for the whole inclination interval ($0<i<180^\circ$) by using the well-known “MEGNO Chaos Indicator”. Finally, we discuss about TNOs which are currently located at these resonances.

1 Introduction

The dynamics of exterior mean motion resonances with Neptune has been studied widely in the past and has drawn the attention of many researchers (see Duncan et al. 1995; Morbidelli et al. 1995; Malhotra 1996; Nesvorny and Roig 2000, 2001; Kotoulas and Voyatzis 2004; Celletti et al. 2007; Lykawka and Mukai 2007; Brasil et al. 2014). An atlas of three body mean motion resonances in the Solar System was made by Gallardo (2006), and, especially for the asteroid belt and trans-neptunian region, by Gallardo (2014). Very recently, Malhotra et al. (2018) studied the dynamics of Neptune’s 2/5 resonance using Poincaré sections and then $N-$body simulations including the effects of all four giant planets and a wide range of orbital inclinations of the TNOs. Furthermore, Lan and Malhotra (2019) investigated the phase space structure of a large number of Neptune’s MMRs for $33<a<140$ AU by using the same methods. In a review article, Malhotra (2019) studied the relation between the migration of giant planets and resonant populations of the Kuiper belt. All studies mentioned above refer to direct motion. In the last decade, asteroids in the main or the Kuiper belt have been discovered revolving in retrograde orbits. Li et al. (2019) provided a list of such asteroids which are or may be captured in retrograde resonance with a major planet (Table A.1, pp. 8), e.g. the asteroid (343158) Marsyas is in 3/1 internal resonance with Jupiter, the asteroid 2006 BZ8 is in 2/5 external resonance with Jupiter, the TNO (471325) 2011 KT19, nicknamed ‘”Niku,is currently at the 7/9 resonance with Neptune and so on. So it is important to study the dynamics of retrograde motion, too.

The RTBP model is an efficient model for studying the motion of small bodies in the Solar System under the gravitational perturbation of a giant planet. In this model periodic orbits play an important role in the study of its phase-space structure. Particularly, we consider the system Sun-Neptune-TNO in which periodic orbits are related with MMRs and their stability affects directly the dynamics (Celletti et al. 2007). Two- and three-dimensional prograde symmetric periodic orbits were studied in many cases of resonances (Kotoulas and Hadjidemetriou 2002; Voyatzis and Kotoulas 2005; Voyatzis et al. 2005; Kotoulas and Voyatzis 2005; Kotoulas 2005). Moreover, Voyatzis et al. (2018) computed families of asymmetric periodic orbits for the asymmetric resonances 1/n, $n=2,..,5$, and related their results with asymmetric libration of observed TNOs. We note here that a broad database of symmetric periodic orbits in the planar circular RTBP model is reported by Restrepo and Russell (2018). All these studies refer to prograde orbits.

Families of spatial periodic orbits that extend from planar to the three-dimensional model ($0<i<180^\circ$) were found since many years ago (Jefferys and Standish 1972; Ichtiaroglou et al. 1989) but their stability computation is not included in these works. Greenstreet et al. (2012) performed numerical integrations of NEAs and showed that it is possible, although rare, to have orbit inversions (prograde to retrograde) at the 3/1 mean motion resonance. The dynamics of retrograde resonances was studied by several authors in the previous decade. Morais and Namouni (2013a) obtained a suitable disturbing function to describe retrograde resonance and used it to identify asteroids in these configurations (Morais and Namouni 2013b). Morais and Namouni (2016) studied numerically the coorbital retrograde resonance in the 2D and 3D restricted 3-body problem at Jupiter to Sun mass ratio, and computed the associated families of periodic orbits (Morais and Namouni 2019). This allowed the identification of an asteroid in the retrograde coorbital resonance with Jupiter (Wiegert et al. 2017). Huang et al. (2018) studied the retrograde coorbital resonance using a semi-analytic model based on an averaged disturbing function. Morais and Namouni (2017) identified and studied the dynamics of the first trans-Neptunian object in polar resonance (Namouni and Morais 2017) with Neptune, 471325 (2011 KT19). Li et al. (2019) made an extensive survey of asteroids which are or may be captured in retrograde resonances with planets and confirmed that the near-polar trans-Neptunian objects 471325 (2011 KT19) and 528219 (2008 KV42) have the longest dynamical lifetimes of the discovered minor bodies in retrograde orbits. Analytical or semi-analytical models based on disturbing functions which are valid for arbitrary inclination have been proposed recently for the study of the phase space structure in inclined MMRs by Lei (2019), Gallardo (2020) and Namouni and Morais (2020). The structure and stability of retrograde periodic orbits for $a<a'$ having Sun-Jupiter as primary bodies has been studied in Kotoulas and Voyatzis (2020a) and Kotoulas et al. (2022) and for $a>a'$ considering Sun-Neptune as primary bodies has been studied in Kotoulas and Voyatzis (2020b). Furthermore, retrograde coorbitals in the Earth-Moon system remain stable and may survive the perturbation exherted by the Sun (Oshima 2021).

In the present study, we consider the RTBP model with mass parameter $\mu$=5.15$\times 10^{-5}$. Thus, our results are associated with the planet Neptune. We focus our interest on the study of retrograde orbits of TNOs which are located at mean motion resonances; these orbits are coplanar ($i=180^\circ$) or spatial ($90^\circ< i < 180^\circ$). We study the dynamics of 4/5, 7/9, 5/8 and 8/13 exterior MMRs because trans-Neptunian objects moving near these retrograde resonances have been recently identified. In Sect. 2, we present briefly the basic model and we introduce the basic notions on periodic orbits and their families. In Sect. 3, we compute families of symmetric retrograde periodic orbits at 4/5, 7/9, 5/8 and 8/13 exterior MMRs and we study their stability type. In Sect. 4 we consider the planar elliptic model (nonzero eccentricity of the perturbing planet, $e'$) and we compute families of symmetric periodic orbits for the mass of Neptune but for all possible eccentricity values, $0<e'<1$ in order to obtain a global view of the elliptic model. In Sect. 5, we compute families of three-dimensional periodic orbits. The stability type of these orbits is also examined and the connection between families of prograde and retrograde orbits is presented. We also construct dynamical stability maps by using the MEGNO chaos indicator for different values of the resonant angles and we investigate the phase-space structure of the three-dimensional circular model. Finally, we conclude by summarizing our main results in Sect. 6.

2 Retrograde periodic orbits of the restricted three body problem

We consider the classical RTBP model in the Oxyz rotating frame (see e.g. Szebehely 1967) which can describe efficiently the Sun-Neptune-TNO system. The equations of motion of a massless body are

$$\begin{aligned} \ddot{x}-2{\dot{y}}{\dot{\upsilon }} - y\ddot{\upsilon } -x\dot{\upsilon }^2= & {} -(1-\mu )\frac{{x+\mu }}{{r_{0}^3}}-\mu \frac{{x-1+\mu }}{{r_{1}^3}}, \nonumber \\ \ddot{y}+2{\dot{x}}{\dot{\upsilon }} + x\ddot{\upsilon } -y\dot{\upsilon }^2= & {} -(1-\mu )\frac{{y}}{{r_{0}^3}}-\mu \frac{{y}}{{r_{1}^3}}, \nonumber \\ \ddot{z}= & {} -(1-\mu )\frac{{z}}{{r_{0}^3}}-\mu \frac{{z}}{{r_{1}^3}} \end{aligned}$$

(1)

where $r_{0}=\sqrt{(x+\mu r_{01})^2+y^2+z^2},\quad r_{1}=\sqrt{(x-(1-\mu ) r_{01})^2+y^2+z^2}$, $\upsilon =\upsilon (t)$ is the true anomaly and $r_{01}=r_{01}(t)$ the mutual distance of the primaries along their relative Keplerian orbit.

For $\dot{\upsilon }=1$ and $r_{01}=1$,we obtain the circular problem, either the planar or the spatial. If we set $z=\dot{z}=0$, then we obtain the planar RTBP. For $\mu =0$,we end up to the corresponding degenerate case of the two-body problem in a rotating frame. The circular model has the energy integral defined in our case as

$$\begin{aligned} h=\frac{1}{2} \left( \dot{x}^2+\dot{y}^2+\dot{z}^2 \right) - \frac{1}{2} \left( x^2+y^2 \right) - \displaystyle {\frac{1-\mu }{r_{0}}-\frac{\mu }{r_{1}}} \end{aligned}$$

(2)

We refer also to the osculating orbital elements of the TNO, a (semi-major axis), e (eccentricity), $\omega$ (argument of perihelion), $\varOmega$ (longitude of ascending node), $\varpi$ (longitude of perihelion), M (mean anomaly) and n (mean motion). The same primed symbols refer to the Neptune and, according to the chosen reference system, is $a'=n'=1$, $i'=0$, $\varpi '=0$ or $\pi$ and $M'(t=0)=0$ or $\pi$.

The model obeys the fundamental symmetry

$$\begin{aligned} \varSigma : (t,x,y, z) \rightarrow (-t,x,-y, z) \end{aligned}$$

and, consequently, orbits which show two perpendicular crosses with the section $y=0$ are symmetric periodic orbits (Szebehely 1967). Particularly, for the planar model we consider initial conditions $x(0)=x_0$, $y(0)=0$, $\dot{x}(0)=0$ and $\dot{y}(0)=\dot{y}_0$. The periodic orbits are computed by using differential corrections in order to satisfy the periodicity conditions $y(T/2)=\dot{x}(T/2)=0$,where T the period of orbit, on the surface of section $y=0$ (Broucke 1968, 1969). These orbits are either prograde or retrograde and they exist for open intervals of the energy forming monoparametric families and are characterized by their linear stability (Broucke 1969).

In the three-dimensional model, the periodic orbits also form monoparametric families having as parameter the inclination. They bifurcate from the planar orbits which are vertically critical orbits (v.c.o.) as it has been shown by Hénon (1973).We consider initial conditions $x(0)=x_0$, $y(0)=0$, $z(0)=z_0$, $\dot{x}(0)=0$, $\dot{y}(0)=\dot{y}_0$ and $\dot{z}(0)=0$ (symmetry with respect to the plane xz or type F) which correspond to a periodic orbit of period T. The periodic orbits are computed by using differential corrections in order to satisfy the periodicity conditions $y(T/2)=\dot{x}(T/2)=\dot{z}(T/2)=0$ (Robin and Markellos 1980). Another set of initial conditions is the following: $x(0)=x_0$, $y(0)=0$, $z(0)=0$, $\dot{x}(0)=0$, $\dot{y}(0)=\dot{y}_0$ and $\dot{z}(0)=\dot{z}_0$ (symmetry with respect to the x-axis or type G) which correspond to a periodic orbit of period T, if $y(T/2)=z(T/2)=\dot{x}(T/2)=0$. Also, for $\mu =0$ there could exist families of orbits which start from inclined circular orbits. The orbits of these families are also continued for $\mu >0$ in 3D space (Zagouras and Markellos 1977; Ichtiaroglou and Michalodimitrakis 1980).

3 Families of retrograde orbits in the planar circular model

Fig. 1

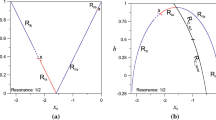
Families of retrograde periodic orbits in the 4/5 MMR presented on the planes $x_{0}-e_{0}$ (left) and $x_{0}-h$ (right). The linear stability is indicated by different colors : solid blue (red) lines stand for horizontal stability (instability) and vertical stability. Vertical instability is indicated by dashed lines. The cross-symbols denote the collision orbits which are computed analytically by using the unperturbed model (see Kotoulas and Voyatzis (2020a)).

In the planar circular problem, for $\mu =0$ there exists the family $R_C$ of retrograde circular orbits which also exists for $\mu \ne 0$ in all cases of resonances. The computations show that the orbits of $R_C$ for $\mu \ll 1$ are nearly circular and stable (Kotoulas and Voyatzis 2020b). We note that the family $R_C$ breaks only at the 1:1 resonance ($a\approx 1$) and is separated into the inner and the outer branch (see also Morais and Namouni 2019, Fig. 2). The continuation of the elliptic families of the unperturbed system is also valid for $\mu \ne 0$ and we obtain two branches, branch $R_{I}$ and branch $R_{II}$ which differ only in phase, $\phi ^\star$=0 and $\phi ^\star$=$\pi$ respectively, where $\phi ^\star$ is defined as

$$\begin{aligned} \phi ^\star =q \lambda - p \lambda ' - (p+q) \varpi ^\star \end{aligned}$$

(3)

where $\varpi ^\star =\omega -\varOmega$ is the longitude of perihelion of a TNO for retrograde motion. Periodic orbits exist for intervals of the energy h or the corresponding eccentricity $e_{0}$. Here, $h=-C_{j}/2$ where $C_{j}$ is the Jacobi constant as defined in Murray and Dermott (1999). So, we can present the characteristic curves of the families on the planes $x_{0}-e_{0}$ and $x_{0}-h$. In Fig. 5 we present a surface of section for $h=0.5$ where many retrograde resonances appear but also chaotic regions are indicated. The centers of islands correspond to stable periodic orbits. Unstable periodic orbits are not clearly distinguished since they are embedded in chaotic regions. At the region close to collision orbits, the characteristic curve of the family breaks, the ratio $n/n'$ varies significantly and takes values far from the nominal values p/q and, also, the orbits become strongly chaotic.

Fig. 2

Characteristic curves of families of retrograde symmetric periodic orbits in the case of 7/9 MMR on the planes $x_0-e_0$ and $x_0-h$ respectively. a, b family $R_{I}$, c, d family $R_{II}$. The presentation of colors is the same as in Fig. 1

In Fig. 1, we present the families of 4/5 resonant periodic orbits. In order to declare the linear stability of the orbits, we use different colours : blue denotes both horizontal and vertical stability, red denotes horizontal instability but vertical stability. The vertical instability is presented with dashed lines. Family $R_{Ia}$ starts from $e_{0}=0$ with horizontally unstable orbits; there is a collision around $e \approx 0.12$ and a gap along this family appears since the computation fails to continue. For higher eccentricities, we obtain the second segment of this family, i.e. $R_{Ib}$, which includes horizontally and vertically stable orbits but another collision exists around $e \approx 0.8$ and a second gap appears along this family. Finally, we obtain the third segment, i.e. $R_{Ic}$, which is all stable too. On the other hand, family $R_{II}$ is full stable except for a collision around $e=0.14$. Another collision appears around $e=0.28$. The segment $R_{IIb}$ consists of horizontally stable orbits. The vertical instability occurs in the part 0.323$<e<0.561$, and, thus, we have two v.c.o.

In Fig. 2, we present the families of 7/9 resonant periodic orbits. Similarly to the $1^{st}$ order resonance 4/5, two families of retrograde orbits $R_{I}$ and $R_{II}$, bifurcate from the corresponding resonant circular orbits of $R_C$. The periodic orbits included in family $R_{II}$ cross vertically the axis Ox (i.e. ${\dot{x}}_0=0$) only for $x<0$, while in family $R_{I}$ such a vertical cross occurs only for $x>0$. Thus, the two families are presented in separated plots $x_0-e_{0}$ or $x_{0}-h$ shown in Fig. 2. Family $R_{Ia}$ starts from $e_{0}=0$ with horizontally unstable orbits; there is a collision area around $e \approx 0.18$ and a gap along this family appears. One v.c.o. exists at $e=0.158$ and it is unstable. For moderate eccentricities, we obtain the second segment of this family, i.e. $R_{Ib}$, which includes horizontally and vertically stable orbits but another collision exists around $e \approx 0.46$ and a second gap appears along this family. At the end, we obtain the third segment, i.e. $R_{Ic}$, which is stable too. On the other hand, family $R_{II}$ is full stable except for a collision around $e=0.16$. Collisions appear also around $e=0.18$, 0.27 and $e=0.795$. The segment $R_{IIc}$ consists of vertically unstable orbits; the vertical instability type occurs in the part 0.340$<e<$0.444, and, thus, we have two v.c.o. These points give rise to the three-dimensional families of symmetric retrograde periodic orbits.

Fig. 3

Families of retrograde periodic orbits in the 5/8 MMR presented on the planes $x_{0}-e_{0}$ (left) and $x_{0}-h$ (right). The presentation of colors is the same as in Fig. 1

In Fig. 3, we present the families of 5/8 resonant symmetric periodic orbits. Family $R_{Ia}$ starts from $e_{0}=0$ with horizontally unstable orbits; there is a collision area around $e \approx 0.27$ and a gap along this family appears. After that the family becomes stable and we obtain the second segment of this family, i.e. $R_{Ib}$ which includes stable orbits. Another collision appears at $e \approx 0.30$ and we obtain the third segment of this family, i.e. $R_{Ic}$. For moderate eccentricities ($e \approx 0.52$) we have another gap and then we get the fourth segment of this family, i.e. $R_{Id}$, which includes horizontally stable and vertically unstable orbits. Thus, we have one v.c.o.at $e=$0.668. Then, the segment becomes vertically stable. On the other hand, family $R_{IIa}$ starts as unstable ($0.0<e<0.09$) and then becomes stable. For $0.09<e<0.999$ we can say that family $R_{II}$ is full stable except for the cases of close encounters. More precisely, close encounters appear around $e=0.28$, 0.38 and $e=0.88$. There is one v.c.o. on the segment $R_{IIa}$ and it is located at $e=$0.274. The segment $R_{IIc}$ consists of vertically stable/unstable orbits; the vertical instability type occurs in the part 0.454$<e<$0.557, and, thus, we have two more v.c.o. These points give rise to the three-dimensional families of symmetric retrograde periodic orbits.

Fig. 4

Families of retrograde periodic orbits in the 8/13 MMR presented on the planes $x_{0}-e_{0}$ (left) and $x_{0}-h$ (right). The presentation of colors is the same as in Fig. 1

In Fig. 4, we present the families of retrograde periodic orbits in the vicinity of 8/13 mean motion resonance with Neptune. Family $R_{Ia}$ starts from $e_{0}=0$ with horizontally unstable orbits; there is a collision around $e \approx 0.28$ and a gap along this family appears. After that the family becomes stable and we obtain the second segment of this family, i.e. $R_{Ib}$ which includes stable orbits. Another collision appears at $e \approx 0.32$ and we obtain the third segment of this family, i.e. $R_{Ic}$. For moderate eccentricities ($e \approx 0.48$) we have another gap and then we get the fourth segment of this family, i.e. $R_{Id}$, which includes horizontally and vertically stable/unstable orbits. There is one v.c.o on the segment $R_{Id}$ and it is located on $e=$0.613. On the other hand, family $R_{II}$ is full stable except for the cases of collision areas. More precisely, collisions appear around $e=0.30$ and $e=0.65$ respectively. The vertical instability type occurs in the part 0.479$<e<$0.505 on the segment $R_{IIb}$.

Fig. 5

The Poincaré surface of section at energy level $h=0.5$. The dominant resonances of first order are indicated

4 The planar elliptic model

In this section we will study the resonant structure of the elliptic restricted three body problem at the 4/5, 7/9, 5/8 and 8/13 mean motion resonances with Neptune. Now, periodic orbits refer not only to the rotating frame but also to the inertial frame. We consider that the planet Neptune moves on an elliptic orbit with a fixed eccentricity $e'$. Families of periodic orbits in the elliptic RTBP bifurcate from the periodic orbits of the circular model with period multiple to the period of the primaries (Broucke 1969). The bifurcation points are presented in Table 1. Two families of retrograde periodic orbits arise from each bifurcation orbit; one with the Neptune at perihelion ($\varpi '=0$) and one at aphelion ($\varpi '=\pi$). Along these families the longitude of perihelion of the TNO ($\varpi$) may change (from 0 to $\pi$ or vice versa) when the family includes a circular orbit ($e=0$). Linear stability is established by computing the Brucke’s indices (Broucke 1969).

Table 1 Bifurcation points from the planar circular to the planar elliptic model

The families of the elliptic model are called as $R_{E,ls}$, where $l=1,2,..$ is an index for indicating different families of orbits in each resonance when there exist more than one bifurcation points and $l=0$ is used when the bifurcation orbit belongs to the $R_{C}$ family. The index s is either p or a and indicates the initial position of the planet (perihelion or aphelion, respectively). Along the families of retrograde periodic orbits the eccentricity of Neptune changes from $e'=0$ to $e'=1$. We present them in Fig. 6 by projecting their characteristic curves on the plane ($e_0 \cos \varpi$, $e' \cos \varpi '$), so the values 0 or $\pi$ of the longitudes of perihelia $\varpi$ and $\varpi '$ are also indicated (Fig. 6).

Fig. 6

Families of retrograde symmetric periodic orbits in the elliptic RTBP presented in the plane ($e_{0} \cos \varpi$, $e' \cos \varpi '$). For each panel the corresponding resonance is indicated. The different line colours indicate the linear stability as in Fig. 1

In the case of 4/5 resonance, family $R_{E, 0p}$ is unstable; on the other hand, the family $R_{E, 0a}$ includes only stable orbits. Family $R_{E, 1p}$ starts with stable orbits and then becomes unstable. On the other hand, the family $R_{E, 1a}$ starts with unstable orbits and then becomes stable. In addition to that, family $R_{E, 2p}$ is also unstable but the family $R_{E, 2a}$ consists of stable orbits. The characteristic curves of these families are smooth and terminate at a collision orbit with Neptune ($e' \approx 0.999$).

For the 7/9 resonance there exist four families. Families $R_{E, 0p}$ and $R_{E, 0a}$ are stable up to $e'=0.4$ and then become unstable. Furthermore, we computed also the other six families which bifurcate from orbits with $e>$0.0 (see Table 1). Families $R_{E, 1p}$ and $R_{E, 2p}$ consist of stable orbits but families $R_{E, 1a}$ and $R_{E, 2a}$ start as unstable and then become stable. Finally, the family $R_{E,3p}$ is unstable up to $e'=0.675$ and then becomes stable; the family $R_{E,3a}$ includes only stable orbits.

In the case of 5/8 resonance, we have four families of retrogarde symmetric periodic orbits in the planar elliptic problem. Families $R_{E, 0p}$ and $R_{E, 1p}$ are both stable; family $R_{E, 0a}$ is all unstable but the family $R_{E, 1a}$ starts as unstable and then becomes stable. Family $R_{E, 2p}$ is unstable but the family $R_{E, 2a}$ is all stable. Family $R_{E, 3p}$ is stable up to $e'=0.235$ and then becomes stable; the family $R_{E, 3a}$ is all unstable.

Finally, studying the 8/13 mean motion resonance with Neptune, we found five families of retrogarde symmetric periodic orbits in the planar elliptic problem. Families $R_{E, 0p}$ and $R_{E, 1p}$ are both stable; family $R_{E, 0a}$ is all unstable but the family $R_{E, 1a}$ starts as unstable and then becomes stable. Family $R_{E, 2p}$ is unstable but the family $R_{E, 2a}$ includes stable orbits and becomes unstable at very high eccentricity values of the planet Neptune ($e' \ge 0.867$). Family $R_{E, 3p}$ starts as stable and terminates to a collision orbit with Sun having stable orbits; there is a big segment with unstable orbits, i.e. $0.196<e'<0.867$. The family $R_{E, 3a}$ is all unstable. Family $R_{E, 4p}$ is all stable and family $R_{E, 4a}$ is all unstable.

5 The 3-D circular model

5.1 Periodic orbits and stability analysis

In a previous paper (Kotoulas and Voyatzis 2020b), the 1/2, 2/3 and 3/4 exterior mean motion resonances with Neptune have been studied focusing mainly on retrograde orbits. We note here that such families of orbits were studied firstly by Robin and Markellos (1980) and later by Kotoulas et al. (2022) for the mass of Jupiter. All the results are referred to the rotating frame of reference Oxyz. We find the families of periodic orbits as smooth curves (characteristic curves) with continuation and we present them on the plane $e_{0}-i_{0}$ while the corresponding semimajor axis is almost constant along the family. In addition to that, we determine the linear stability type of orbits by computing the Broucke’s indices (Broucke 1969). Due to the small mass parameter, the indices are very close to their critical values. So, use ”long double computations” (18 decimal digits) in order to get reliable results on linear stability of periodic orbits.

We regard a MMR, where $n/n'=p/q$ and p, q are mutually primed integers. For 3D prograde motion the resonant angles are defined $\phi _{k}$ (Namouni and Morais 2018)

$$\begin{aligned} \phi _{k}=q \lambda - p \lambda ' - k\varpi + (p-q+k) \varOmega , \end{aligned}$$

(4)

where $\lambda =M+\varpi$ and the longitude of perihelion is defined as $\varpi =\omega +\varOmega$. For $k=(q-p)$ we obtain the general expression of the 2D resonant angle, i.e. $\phi$, for planar prograde orbits.

For 3D retrograde motion the resonant angles are defined (Namouni and Morais 2018)

$$\begin{aligned} \phi _{k}=q \lambda ^{*} - p \lambda ' - k\varpi ^{*} + (q+p-k) \varOmega , \end{aligned}$$

(5)

where $\lambda ^{*}=\lambda -2\varOmega$ and $\varpi ^{*}=\varpi -2\varOmega$ is the mean longitude and the longitude of perihelion, respectively, of the asteroid in retrograde motion . We note that $\lambda '=M'$, since in our reference frame, $\varpi '=0$. For $k=p+q$ we obtain the general expression of the 2D resonant angle for planar retrograde orbits, i.e. $\phi ^\star$ (Eq. 3). We can say that the relation (5) is just another way of writing (4) using retrograde (starred) angles. We also define $\phi _z=\phi _0$ noting that for even (odd) $p-q$ this angle appears in the disturbing function expansion as a first (second) harmonic (Namouni and Morais 2018).

5.2 The MEGNO chaos indicator

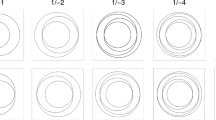
The MEGNO (Mean Exponential Growth factor of Nearby Orbits) chaos indicator (Cincotta and Simó 2000; Goździewski 2003) was obtained by numerical integration of the full equations of motion along with the variational equations, using the Bulirsch and Stoer method with a tolerance 10$^{-14}$ for 2 $\times$ 10$^6$ orbital periods of the perturber. MEGNO converges to 2 for regular orbits and increases at a rate proportional to the Lyapunov exponent for chaotic orbits. The maximum value of MEGNO in the stability maps is set to 8 for chaotic orbits in order to have a high contrast between the regular and chaotic regions. The symbols in the maps indicate:

• x (libration of Kozai angle)

• circle, square, up triangle, down triangle: libration of angles with $k=q-p$ (prograde 2D), $k=q-p+2$, $k=q-p+4$, $k=p+q$ (retrograde 2D)

Moreover, black symbols indicate libration amplitudes smaller than 50 degrees, gray symbols indicate larger amplitudes, while overlap of black symbols indicates a resonant periodic orbit (all resonant angles, $\phi _k$, and argument of pericenter, $\omega$, are fixed). Quasi-periodic motion may occur in: the vicinity of POs; small eccentricity regions such that there is no intersection with Neptune’s orbit; associated with libration of a single resonant angle $\phi _k$; or due to the Kozai resonance.

We set the 2D prograde resonant angle to $\phi =0, \; \pi$ and the argument of pericenter to $\omega =0, \; \frac{{\pi }}{{2}}, \; \pi , \; \frac{{3\pi }}{{2}}$ to construct the dynamical stability maps. In all cases we set $\varOmega =0$. The maps with $\omega =0$ and $\omega =\pi /2$ are in general similar to those with $\omega =\pi$ and $\omega =3\,\pi /2$, respectively. Therefore, we present only 4 maps for each resonance. We produced an additional set of maps corresponding exactly to the initial conditions in Tables 2, 3, 4 and 5, whose features are essentially the same as the maps presented in this article. This confirms that the important dynamical variables are the initial values of $\phi$ and $\omega$. Note that the 2D retrograde and prograde resonant angles are related by $\phi ^\star =\phi -2\,p\,\omega$ hence for a p/q mean motion resonance $\phi ^\star =\phi$ when $\omega =0,\pi$ (p even or odd) or when $\omega =\pi /2,3\,\pi /2$ (p even), and $\phi ^\star =\phi +\pi$ when $\omega =\pi /2,3\,\pi /2$ (p odd).

Table 2 The 11 critical 4/5 resonant orbits and the bifurcating families from the planar circular to the 3D circular model

Fig. 7

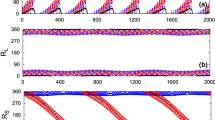
The 4/5 resonance: a Projection of the families of retrograde symmetric periodic orbits in the 3D circular RTBP on the plane ($e_{0}-i_{0}$). Blue (red) colour indicates stability (instability). Time evolution of the resonant angles $\phi (k=9)$ and $\phi _{z}=\phi (k=0)$ for b a stable retrograde periodic orbit belonging to the family $R_{1}$ and c for an unstable retrograde periodic orbit from the family $R_{2}$ at the same energy level $h=0.425069635$. Black (blue) colour indicates the resonant angle $\phi$ ($\phi _z$)

Fig. 8

Resonance: 4/5. Stability maps for a $\phi =\phi ^\star =0, \; \omega =0$, b $\phi =\phi ^\star =\pi , \; \omega =0$, c $\phi =\phi ^\star =0, \; \omega =\frac{{\pi }}{{2}}$ and d $\phi =\phi ^\star =\pi , \; \omega =\frac{{\pi }}{{2}}$. For all cases we set $\varOmega =0$. Blue color stands for stable regions and yellow color stands for unstable regions. The symbols in the maps indicate: x (libration of Kozai angle), circle, square, up triangle, down triangle: libration of angles with $k=q-p$(prograde 2D), $k=q-p+2$, $k=q-p+4$, $k=p+q$ (retrograde 2D). Moreover, black symbols indicate libration amplitudes smaller than 50 degrees, gray symbols indicate larger amplitudes, while overlap of black symbols indicates a resonant periodic orbit (all initial values of resonant angles, $\phi _k$, and argument of pericenter, $\omega$, are fixed)

5.3 The 4/5 MMR

In Table 2 and in Fig. 7 we present the bifurcations to the 3-D model and the characteristic curves of spatial 4/5 resonant families, respectively. As far as the retrograde orbits is concerned, there are three v.c.o. on the planar families from which spatial families bifurcate. The first one is located on the family of circular orbits $R_{C}$ ($e=0.0$) and the other two ones are lying on the family segment $R_{IIc}$. There exist four families of 3-D retrograde periodic orbits. Three families ($R_{0,F}$, $R_{0,G}$, $R_{1}$) are connected with the families of three-dimensional direct periodic orbits forming bridges between retrograde and prograde families of planar orbits. Family $R_{2}$ terminates to a collision orbit with Sun.

In Fig. 8 we present MEGNO stability maps. The regions of quasiperiodic motion surrounding stable branches of the retrograde family $R_1$ and the prograde families $D_1$ and $D_7$ may be seen in Fig. 8d, while the region around the stable branch of the prograde family $D_4$ is seen in Fig. 8c. However, the region of quasiperiodic motion surrounding the stable branch of family $R_{0,G}$ in Fig. 8b is barely visible. There are also regions of quasiperiodic motion associated with libration of the prograde angle $\phi =\phi _1$(identified by circles), the retrograde angle $\phi ^\star =\phi _9$ (identified by down triangles), and large regions in Fig. 8b, c associated with libration of the resonant angle $\phi _3$ (identified by squares). The Kozai resonance occurs at high inclination and/or high eccentricity in panels (a), (b) and (c).

Table 3 The critical 7/9 resonant orbits and the bifurcating families from the planar circular to the 3D circular model

Fig. 9

Resonance: 7/9. Projection of the families of 3D symmetric periodic orbits (direct and retrogarde) on the planes: a $e_{0}-i_{0}$ for nearly circular orbits, b ($e_{0}-i_{0}$) for elliptic orbits which bifurcate from the points $P_{1}$ and $P_{2}$. c ($e_{0}-i_{0}$) for direct and retrograde elliptic orbits. Blue (red) color indicates stability (instability). The magenta color denotes double instability

Fig. 10

Resonance: 7/9. Stability maps for a $\phi =\phi ^\star =0, \; \omega =0$, b $\phi =\phi ^\star =\pi , \; \omega =\pi$, c $\phi =0 \; (\phi ^\star =\pi ), \; \omega =\frac{{\pi }}{{2}}$ and d $\phi =\pi \; (\phi ^\star =0), \; \omega =\frac{{\pi }}{{2}}$. For all cases we set $\varOmega =0$

5.4 The 7/9 MMR

The spatial 7/9 resonant families are presented in Table 3 and in Fig. 9. Assuming planar retrograde periodic motion, the periodic orbits included in family $R_{II}$ cross vertically the axis Ox (i.e. ${\dot{x}}_0=0$) only for $x<0$, while in family $R_{I}$ such a vertical cross occurs only for $x>0$. So, we have two v.c.o. at $e \approx 0.0$ from which families of three-dimensional nearly circular orbits bifuracate; they are called ${\bar{R}}_{01}$ and ${\bar{R}}_{02}$. A similar situation occurs at families of direct periodic orbits where at families $D_{II}$ and $D_{I}$ we have the v.c.o. ${\bar{D}}_{01}$ and ${\bar{D}}_{02}$ (Kotoulas et al. 2022). The families starting from ${\bar{R}}_{0j}$ and ${\bar{D}}_{0j}$ ($j=1,\; 2$) join smoothly, consist of doubly symmetric periodic orbits and can be computed as $F-type$ orbits or $G-$type orbits. Since along these families the eccentricity is almost zero, we present their characteristic curves in the plane $e_0-i_0$ as it is shown in Fig. 9a. At points indicated as ${\bar{P}}_j$ along these families the stability type changes providing bifurcations of new inclined elliptic families. From the points $P_{1}$ and $P_{2}$ two new families of three-dimensional symmetric periodic orbits are generated, i.e. $H_{1,F}$ and $H_{2,G}$. These are connected with families of direct orbits and are presented in Fig. 9b. In Fig. 9c we present the families of three-dimensional symmetric periodic orbits which start from bifurcation points with $e>$0.0. We note here that two families of 3D retrograde symmetric periodic orbits are connected with the families of the corresponding direct periodic orbits and terminate to the bifurcation points of the planar problem.

In Fig. 10 we present MEGNO stability maps. The retrogarde family $H_{2, G}$ can be seen in Fig. 10b. The regions of quasiperiodic motion surrounding stable branches of the retrograde families $R_2$ and $R_3$ may be seen in Fig. 10c while the prograde families $D_{16}$, $D_{59}$ and $D_{8}$ may be seen in Fig. 10b–d respectively and we identify family $D_{10}$ in Fig. 10d. There are also regions of quasiperiodic motion associated with libration of the prograde angle $\phi =\phi _2$(identified by circles), the retrograde angle $\phi ^\star =\phi _{16}$ (identified by down triangles), and regions in Fig. 10b, c associated with libration of the resonant angle $\phi _4$ (identified by squares). The Kozai resonance occurs at high inclination and/or high eccentricity in panels (a) and (b).

Table 4 The critical 5/8 resonant orbits and the bifurcating families from the planar circular to the 3D circular model

5.5 The 5/8 resonance

The three-dimensional families of symmetric periodic orbits, direct or retrograde, in the case of 5/8 resonance are presented in Table 4 and in Fig. 11. We note here that there exist four families of 3D retrograde periodic orbits which are connected with the families of the corresponding direct orbits forming bridges and terminate to the bifurcation points of the planar problem. These are: $R_{0,F}-D_{0,F}, \; R_{0,G}-D_{10}, \; R_{1}-D_{6}, \; R_{2}-D_{5}$. The other two families, $R_{3}$ and $R_{4}$, starting from high eccentricity values terminate to a collision orbit with Sun having stable or unstable orbits respectively.

In Fig. 12 we present MEGNO stability maps. The regions of quasiperiodic motion surrounding stable branches of the retrograde families $R_2$ and $R_3$ may be seen in Fig. 12c. However, the region of quasiperiodic motion surrounding the stable branch of family $R_{0,G}$ in Fig. 12a is very small. The families of three-dimensional direct orbits can be identified in the following figures: $D_{6}$ in Fig. 12a, $D_{38}$ in Fig. 12b, $D_{5}$ in Fig. 12c and finally $D_{7}$ and $D_{9}$ in Fig. 12d. There are also regions of quasiperiodic motion associated with libration of the prograde angle $\phi =\phi _3$(identified by circles), the retrograde angle $\phi ^\star =\phi _{13}$ (identified by up triangles), and large regions in Fig. 12b, c associated with libration of the resonant angle $\phi _5$ (identified by squares). The Kozai resonance occurs at high inclination and/or high eccentricity in panels (a), (b) and (d) and strongly unstable regions cover the biggest parts of the grid of initial conditions ($\phi =\pi , \; \omega =\frac{{\pi }}{{2}}$).

Fig. 11

The 5/8 resonance: projection of the families of retrograde symmetric periodic orbits in the 3D circular RTBP on the plane ($e_{0}-i_{0}$). Blue (red) colour indicates stability (instability)

Fig. 12

The 5/8 resonance: Stability maps for a $\phi =\phi ^\star =0, \; \omega =0$, b $\phi =\phi ^\star =\pi , \; \omega =0$, c $\phi =0 \; (\phi ^\star =\pi ), \; \omega =\frac{{\pi }}{{2}}$ and d $\phi =\pi \; (\phi ^\star =0), \; \omega =\frac{{\pi }}{{2}}$. For all cases we set $\varOmega =0$

Fig. 13

The 8/13 resonance: Projection of the families of retrograde symmetric periodic orbits in the 3D circular RTBP on the plane ($e_{0}-i_{0}$). Blue (red) colour indicates stability (instability)

Table 5 The critical 8/13 resonant orbits and the bifurcating families from the planar circular to the 3D circular model

Fig. 14

The 8/13 resonance: Stability maps for a $\phi =\phi ^\star =0, \; \omega =0$, b $\phi =\phi ^\star =\pi , \; \omega =0$, c $\phi =\phi ^\star =0, \; \omega =\frac{{\pi }}{{2}}$ and d $\phi =\phi ^\star =\pi , \; \omega =\frac{{\pi }}{{2}}$. For all cases we set $\varOmega =0$

5.6 The 8/13 resonance

The three-dimensional families of symmetric periodic orbits, direct or retrograde, in the vicinity of 8/13 resonance are shown in Table 5 and in Fig. 13. We remark here that only two families of 3D retrograde periodic orbits are connected with the families of the 3D direct orbits forming bridges, i.e. $R_{0,F}-D_{0,F}$ and $R_{0,G}-D_{0,G}$. There is another family starting from the point $R_{1}$ and terminates to the point $R_{2}$. The last one, i.e. family $R_{3}$, starts from high eccentricity value and terminates to a collision orbit with Sun including stable orbits.

For the 8/13 mean motion resonance with Neptune, MEGNO stability maps are presented in Fig. 14a–d. The region of quasiperiodic motion surrounding the stable branches of the retrograde families $R_{0,G}$ and $R_3$ may be seen in Fig. 14a, c. The family of retrograde periodic orbits $R_{0, F}$ can also be seen in Fig. 14c. The families $D_{2}$, $D_{0,G}$, $D_{13}$ and $D_{4}$ of three-dimensional direct orbits can be identified in Fig. 14a–d respectively. There are also regions of quasiperiodic motion associated with libration of the prograde angle $\phi =\phi _5$(identified by circles), the retrograde angle $\phi ^\star =\phi _{21}$ (identified by down triangles), and regions associated with libration of the resonant angles $\phi _7$ and $\phi _9$ (identified by squares and up triangles). The Kozai resonance occurs at high inclination and/or eccentricity in panels (a), (b) and (d).

6 Conclusions

In this paper, we computed families of two- and three-dimensional resonant symmetric retrograde periodic orbits of the RTBP by considering $\mu =5.15\times 10^{-5}$ (the normalized mass of Neptune) and studied their stability type at higher order exterior mean motion resonances with Neptune namely 4/5, 7/9, 5/8 and 8/13. Stable periodic orbits are surrounded by invariant tori which correspond to quasiperiodic evolution and long-term stability (Siegel and Moser 1971; Contopoulos 2002). In more realistic models, such regions may not provide dynamical stability for $t \rightarrow \infty$ but long-term capture may occur.

For the circular planar model (Sect. 3), the retrograde circular periodic orbits of the degenerate problem ($\mu =$0) are continued for $\mu \ne 0$ forming the family $R_C$. Contrary to the circular family of direct orbits, along which gaps and instabilities occur, the family $R_C$ has a smooth characteristic curve without gaps and consists of horizontally and vertically stable periodic orbits. The resonant circular orbits of $R_C$ are bifurcation orbits for resonant families of elliptic periodic orbits. All higher-order resonances which were examined here have two families of retrograde elliptic periodic orbits: the family $R_{I}$ and the family $R_{II}$. These families break in two segments at regions where close encounters between asteroid and planet occur. Family $R_{I}$ starts from its bifurcation circular orbit with unstable orbits. Many collison orbits appear along the family $R_{I}$. The segments in higher eccentricities ($R_{Ib},.., R_{Ie}$) include mainly stable orbits (both horizontally and vertically). Bifurcation points from the planar circular to planar elliptic problem and v.c.o. are located on these segments. On the other hand, family $R_{II}$ consists always of stable periodic orbits except for the case of $R_{IIa}^{5/8}$ which includes both unstable and stable periodic orbits. Unstable periodic orbits along the family $R_{II}$ are obtained only at close encounters.

For the elliptic model ($0<e'<1$), we computed families of periodic orbits bifurcating from families of the planar circular model at the critical points where $T=2k\pi$, k is an integer. In the case of 4/5 resonance, there exist three pairs of families of periodic orbits; one starting from the critical orbit of the circular family (family $R_{E, 0p}$ is unstable and family $R_{E, 0a}$, is stable) and the other two pairs bifurcate from points with $e>$0.0. For the 7/9 and 5/8 resonance, we computed eight families of retrograde periodic orbits. Some of them are stable and the rest ones are unstable. In the case of 8/13 resonance we found ten families of retrograde symmetric periodic orbits. The majority of them is unstable.

Fig. 15

Evolution of the orbital elements of the TNO 2017QO33 including the gravitational effect of the four giant planets (time unit is years)

For the three-dimensional circular restricted 3-body problem, we found families of stable three-dimensional retrograde periodic orbits in all cases of the examined MMRs. These families bifurcate from v.c.o. and are connected with the families of direct orbits or terminate to a collision orbit with Sun. For the 4/5 resonance, we found stable three-dimensional retrograde periodic orbits along the family $R_{1}$ instead of the direct ones in the same family, or equivalently in family $D_{3}$, which are unstable. For the 7/9 resonance, we found stable three-dimensional retrograde periodic orbits along the family $R_{2}$ and especially in the interval $140^\circ<i<180^\circ$. The families $R_{1}$ and $R_{3}$ also include segments with stable orbits and the rest ones are unstable. Furthermore, families of stable direct orbits exist but the majority of them are unstable. For the 5/8 resonance, we found stable three-dimensional retrograde periodic orbits along the family $R_{2}$ and especially in the interval $135^\circ<i<180^\circ$. Stable segments of orbits also exist along the families $R_{0}, \; R_{1}$ and $R_{3}$. On the other side, the majority of direct orbits is unstable. For the case of 8/13 resonance, segments of stable orbits exist along all the families of three-dimensional retrograde symmetric periodic orbits; studying the stability type of direct orbits, we found that many of them are unstable. In any case, stable periodic orbits are surrounded by regions of initial conditions which correspond to librations for all resonant angles $\phi _k$.

Furthermore, we computed MEGNO stability maps for different initial values of the argument of pericenter $\omega$ and the prograde (retrograde) resonant angles $\phi$ ($\phi ^\star$) corresponding to the periodic families. The stable branches of the periodic families may be seen in these maps, as well as regions of quasiperiodic motion around these families. There are also stable regions at small ecentricities (below Neptune’s collision line), due to the Kozai resonance or libration of a single resonant angle, $\phi _k$. Therefore, the dynamical stability maps provide information which is complementary to the computation of families of periodic orbits.

Morais and Namouni (2017) showed that TNO (471325) 2011 KT19, nicknamed Niku, is currently in the 7/9 resonance with Neptune. The resonant argument $\phi _4$ librates around 180$^\circ$ and the current orbital elements approximately correspond to the region marked with square symbols in Fig. 10b. Morais and Namouni (2017) also showed that TNO (528219) 2008 KV42, nicknamed Drac, is close to the 8/13 resonance with Neptune. Although there is no libration of the associated resonant arguments for the nominal orbit, a clone with 3-$\sigma$ increase in semi-major axis exhibited libration of the resonant argument $\phi _9$ which corresponds to the region marked with up triangles in Fig. 14b, d. According to the numerical integrations by Li et al. (2019), TNO 2017 QO33 may be captured in the 4/5 resonance with Neptune. We show in Fig. 15 an integration of the nominal orbit for ±100,000 years which includes the timespan investigated in Li et al. (2019). We see that libration in resonance is very short lived (less than 20,000 years) due to frequent close encounters with the other giant planets which cause a random walk in the semi-major axis. Since the argument of pericenter is approximately constant during that time-interval there is apparent libration of all angles $\phi _k$. In our CR3BP model we would expect libration of the retrograde angle $\phi _{21}$ (region marked with down triangles in Fig. 8b), however due to the orbit’s high eccentricity the effect of the other giant planets (close encounters) cannot be neglected in this case.