Tidal locking of habitable exoplanets

Abstract

Potentially habitable planets can orbit close enough to their host star that the differential gravity across their diameters can produce an elongated shape. Frictional forces inside the planet prevent the bulges from aligning perfectly with the host star and result in torques that alter the planet’s rotational angular momentum. Eventually the tidal torques fix the rotation rate at a specific frequency, a process called tidal locking. Tidally locked planets on circular orbits will rotate synchronously, but those on eccentric orbits will either librate or rotate super-synchronously. Although these features of tidal theory are well known, a systematic survey of the rotational evolution of potentially habitable exoplanets using classic equilibrium tide theories has not been undertaken. I calculate how habitable planets evolve under two commonly used models and find, for example, that one model predicts that the Earth’s rotation rate would have synchronized after 4.5 Gyr if its initial rotation period was 3 days, it had no satellites, and it always maintained the modern Earth’s tidal properties. Lower mass stellar hosts will induce stronger tidal effects on potentially habitable planets, and tidal locking is possible for most planets in the habitable zones of GKM dwarf stars. For fast-rotating planets, both models predict eccentricity growth and that circularization can only occur once the rotational frequency is similar to the orbital frequency. The orbits of potentially habitable planets of very late M dwarfs () are very likely to be circularized within 1 Gyr, and hence, those planets will be synchronous rotators. Proxima b is almost assuredly tidally locked, but its orbit may not have circularized yet, so the planet could be rotating super-synchronously today. The evolution of the isolated and potentially habitable Kepler planet candidates is computed and about half could be tidally locked. Finally, projected TESS planets are simulated over a wide range of assumptions, and the vast majority of potentially habitable cases are found to tidally lock within 1 Gyr. These results suggest that the process of tidal locking is a major factor in the evolution of most of the potentially habitable exoplanets to be discovered in the near future.

1 Introduction

The role of planetary rotation on habitability has been considered for well over a century. By the late 1800s, astronomers were keenly interested in the possibility that Venus could support life, but (erroneous) observations of synchronous rotation led to considerable discussion of its impact on planetary habitability (Schiaparelli 1891; Lowell 1897; Slipher 1903; See 1910; Webster 1927). Some researchers asked “[w]ill tidal friction at the last put a stop to the sure and steady clockwork of rotation, and reduce one hemisphere to a desert, jeopardizing or annihilating all existence [of life on Venus]?” (Mumford 1909), while other, more optimistic, scientists suggested “that between the two separate regions of perpetual night and day there must lie a wide zone of subdued rose-flushed twilight, where the climatic conditions may be well suited to the existence of a race of intelligent beings” (Heward 1903). We now know that Venus is covered with thick clouds and that astronomers misinterpreted their results, but their speculations on the habitability of tidally locked worlds are similar to modern discussions.

The possibility that the rotational period of some habitable exoplanets may be modified by tidal interaction with their host stars was first suggested by Stephen Dole in his classic book Habitable Planets for Man over 50 years ago (Dole 1964). At the time, no exoplanets were known, but Dole, motivated by the dawning of the “space age,” was interested in the possibility that humanity could someday travel to distant star systems. Dole (1964) did not compute planetary spin evolution, but instead calculated the heights of tidal bulges in the Solar System to identify a critical height that separates synchronously and freely rotating worlds. Citing the models of Webster (1925), he settled on $\sqrt{2}$ feet (=42 cm) and then calculated the orbital distances from a range of stellar hosts for which Earth’s tide reached that height. Assuming (somewhat arbitrarily) an “ecosphere” of our Solar System to lie between 0.725 and 1.24 AU, he concluded that all potentially habitable planets orbiting stars less than 72% the mass of the Sun would rotate synchronously and that the inner edge of the ecosphere could be affected up to 88%. As Dole believed it was “evident that low rates of rotation are incompatible with human habitability requirements,” a sense of pessimism developed regarding the possibility that planets orbiting M dwarfs could support life.

Kasting et al. (1993) returned to the problem and computed explicitly the orbital radius at which a planet similar to Earth would become a synchronous rotator around main sequence stars. In particular, they used a model in which the phase lag between the passage of the perturber and the tidal bulge is constant and concluded that an Earth-like planet’s rotational frequency would synchronize with the orbital frequency in the habitable zone (HZ; the shell around a star for which runaway atmospheric feedbacks do not preclude surface water) for stellar masses $M_* < 0.42~\mathrm{\,M_\odot }$ within 4.5 Gyr. They called the orbital distance at which this state developed the “tidal lock radius.” They relied on the model of Peale (1977) and used a relatively low energy dissipation rate for Earth, as suggested by models of the evolution of the Earth–Moon system in isolation (MacDonald 1964), see also Sect. 2.4. Furthermore, Kasting et al. (1993) used a sophisticated one-dimensional photochemical-climate model to compute the HZ, which is more realistic than Dole’s ecosphere.

The study of Kasting et al. (1993) differs from Dole (1964) in that the former was interested in planets which could support liquid surface water, whereas the latter imagined where modern humans would feel comfortable. It is important to bear in mind that synchronous rotation represents a state for which the atmospheric modeling approach of Kasting et al. (1993) breaks down—a planet with a permanent dayside and permanent nightside is not well represented by a one-dimensional model in altitude—not a fundamental limit to the stability of surface water on an Earth-like planet. Nonetheless, Kasting et al. (1993) retained Dole’s pessimism and concluded that “all things considered, M stars rank well below G and K stars in their potential for harboring habitable planets.” Clearly, the meaning of “habitable” is important in this discussion and has affected how scientists interpret their results in terms of the search for life-bearing worlds. In this study, a “habitable planet” is one that is mostly rock with liquid water oceans (that may be global) and a relatively thin ( bars) atmosphere.

With the development of 3-dimensional global climate models (GCMs), the surface properties of synchronously rotating planets can be explored more self-consistently. The first models were relatively simple, but found that synchronously rotating planets can support liquid water and hence should be considered potentially habitable (Joshi et al. 1997). More recent investigations have confirmed this result (Wordsworth et al. 2011; Pierrehumbert 2011; Yang et al. 2013; Way et al. 2015; Shields et al. 2016; Kopparapu et al. 2016), and hence, we should no longer view synchronous rotation as a limit to planetary habitability. Moreover, these GCM models suggest the HZ for synchronous rotators may extend significantly closer to the host star than 1-D models predict (Yang et al. 2013). These are precisely the planets likely to be discovered by the upcoming Transiting Exoplanet Survey Satellite (TESS) mission (Ricker et al. 2014; Sullivan et al. 2015) and may also be amenable to transit transmission spectroscopy by the James Webb Space Telescope. Furthermore, low-mass stars are more common than Sun-like stars and so a significant number of exoplanets in the HZ of nearby stars may be in a synchronous state and with a rotational axis nearly parallel with the orbital axis (Heller et al. 2011).

Some recent studies have examined the rotational evolution of planets and satellites (Ferraz-Mello 2015; Makarov 2015), but did not consider their results in relation to the HZ. Motivated by the potential to detect extraterrestrial life, I have performed a systematic study of the tidal evolution of habitable planets to provide more insight into the physical and orbital properties that can lead to significant rotational evolution and in some cases synchronous rotation. This survey focuses solely on the two-body problem and neglects the role of companions and spin–orbit resonances, both of which could significantly affect the tidal evolution, e.g.,  Wu and Goldreich (2002); Mardling and Lin (2002); Rodríguez et al. (2012); Van Laerhoven et al. (2014). In particular, I will use the “equilibrium tide” (ET) model, first proposed by Darwin (1880) and described in more detail in Sect. 2, to simulate the orbital and rotational evolution of rocky planets with masses between 0.1 and 10 $\mathrm{\,M_\oplus }$ orbiting stars with masses between 0.07 and 1.5 $\mathrm{\,M_\odot }$ for up to 15 Gyr.

Kasting et al. (1993) employed an ET model and made many assumptions and approximations, but it was vastly superior to the method of Dole. The Kasting et al.’s model used a $1~\mathrm{\,M_\oplus },~1~\mathrm{\,R_\oplus }$ planet with zero eccentricity, no companions, no obliquity, and an initial rotation period of 13.5 h to compute the orbital radius at which tidal effects cause the planet to become a synchronous rotator. In the ET model of Peale (1977), the rate of tidal evolution scales linearly with the so-called tidal quality factor Q, which essentially links energy dissipation by friction with the torques due to asymmetries in the bodies. Kasting et al. (1993) chose $Q=100$ as suggested by MacDonald (1964) despite the fact that modern measurements based on lunar laser ranging, see Dickey et al. (1994), find that Earth’s value is $12~\pm ~2$ (Williams et al. 1978). Kasting et al. (1993) also ignored the ET models’ predictions that large eccentricities () could result in super-synchronous rotation (Goldreich 1966; Barnes et al. 2008; Ferraz-Mello et al. 2008; Correia et al. 2008). ET models are not well calibrated at large eccentricities, but given the large number of large exoplanets with large eccentricities, it may be that many planets are “tidally locked,” meaning that their rotation rate is fixed by tidal torques, yet they do not rotate synchronously.

The method of calculating HZ boundaries of Kasting et al. (1993) has been improved several times, e.g.,  (Selsis et al. 2007; Kopparapu et al. 2013), and these studies typically include a curve that is similar to that in Kasting et al. (1993) which indicates that rotational synchronization is confined to the M spectral class. Such a sharp boundary in tidal effects is misleading since the initial conditions of the rotational and orbital properties can span orders of magnitude, the tidal dissipation rate is poorly constrained, and the tidal models themselves are poor approximations to the physics of the deformations of planetary surfaces, particularly those with oceans and continents. We should expect a wide range of spin states for planets in the HZ of a given stellar mass, an expectation that is borne out by the simulations presented in Sect. 3.

The ET model ignores many phenomena that may also affect a planet’s rotational evolution such as atmospheric tides (Gold and Soter 1969; Correia and Laskar 2001, 2003; Leconte et al. 2015), the influence of companions (Correia et al. 2013; Greenberg et al. 2013), and rotational braking by stellar winds (Matsumura et al. 2010; Reiners et al. 2014). These effects can be significant, perhaps even dominant, and recently some researchers have improved on ET models by including more realistic assumptions about planetary and stellar interiors, e.g.,  (Henning et al. 2009; Correia 2006; Ferraz-Mello 2013; Zahnle et al. 2015; Driscoll and Barnes 2015). However, tidal dissipation on Earth occurs primarily in the oceans as a result of nonlinear processes and is not well approximated by assumptions of homogeneity. Satellite data reveal that about two-thirds of Earth’s dissipation occurs in straits and shallow seas and about one-third in the open ocean (Egbert and Ray 2000). The former represent bottlenecks in flow as the tidal bulge passes and turbulence leads to energy dissipation. The latter is probably due to seafloor topography in which gravity waves are generated by ocean currents passing over undersea mountain ranges, leading to nonlinear wave interactions that cause energy dissipation. Thus, the tidal braking of an Earth-like planet is most dependent on the the unknown properties of a putative ocean. As no “exo-oceanography” model has been developed, the ET models seem reasonable choices to explore the timescales for tidal braking of habitable exoplanets, but with the caveat that they are not accurate enough to draw robust conclusions in individual cases, rather they should only be used to identify the range of possible behavior. Also note that an implication of Egbert and Ray (2000)’s result is that exoplanets covered completely by liquid water will likely only be a few times less dissipative than one with a dichotomous surface like Earth.

This study focuses on the behavior predicted by the ET model over a wide range of initial conditions using two popular incarnations. Consideration of this broader range of parameter space reveals that nearly any potentially habitable planet could have its rotation period affected by tides. About half of Kepler’s isolated planet candidates are tidally locked if they possess Earth’s tidal properties, and Proxima b is found to have a tidal locking time of less than $10^6$ years for all plausible assumptions. I also calculate the time to tidally lock, $T_\mathrm{lock},$ for the projected yields of NASA’s upcoming TESS mission and find that in almost all cases $T_\mathrm{lock} < 1$ Gyr, suggesting that all potentially habitable worlds it detects will have had their rotations modified significantly by tidal processes. I also examine how eccentricity can grow in some cases in which a habitable planet is rotating super-synchronously, a process that has been briefly discussed for non-habitable worlds (Heller et al. 2010; Cheng et al. 2014). In most cases, eccentricity growth is modest and primarily acts to delay circularization. In Sect. 4, I discuss these results in terms of exoplanet observations in general and the possible impact on planetary habitability.

2 The equilibrium tide model

The ET model assumes the gravitational force of the tide-raiser produces an elongated (prolate) shape of the perturbed body and that its long axis is slightly misaligned with respect to the line that connects the two centers of mass. This misalignment is due to dissipative processes within the deformed body and leads to a secular evolution of the orbit and spin angular momenta. Furthermore, the bodies are assumed to respond to the time-varying tidal potential as though they are damped, driven harmonic oscillators, a well-studied system. As described below, this approach leads to a set of six coupled, nonlinear differential equations, but note that the model is linear in the sense that there is no coupling between the surface waves that sum to the equilibrium shape. A substantial body of research is devoted to tidal theory, (e.g.,  Darwin 1880; Goldreich and Soter 1966; Hut 1981; Ferraz-Mello et al. 2008; Wisdom 2008; Efroimsky and Williams 2009; Leconte et al. 2010), and the reader is referred to these studies for a more complete description of the derivations and nuances of ET theory. For this investigation, I will use the models and nomenclature of Heller et al. (2011), which are presented below.

ET models have the advantage of being semi-analytic and hence can be used to explore parameter space quickly. They effectively reduce the physics of the tidal distortion to two parameters, which is valuable in systems for which very little compositional and structural information is known, e.g., exoplanets. However, they suffer from self-inconsistencies. A rotating, tidally deformed body does not in fact possess multiple rotating tidal waves that create the non-spherical equilibrium shape of a body. The properties of the tidal bulge are due to rigidity, viscosity, structure, and frequencies. ET models are not much more than toy models for tidal evolution—calculations from first principles would require three dimensions and include the rheology of the interior and, for ocean-bearing worlds, a 3-dimensional model of currents, ocean floor topography, and maps of continental margins. For exoplanets, such a complicated model is not available, nor is it necessarily warranted given the dearth of observational constraints.

The ET framework permits fundamentally different assumptions regarding the lag between the passage of the perturber and the passage of the tidal bulge. This ambiguity has produced two well-developed models that have reasonably reproduced observations in our Solar System, but which can diverge significantly when applied to configurations with different properties. One model assumes that the lag is a constant in phase and is independent of frequency. In other words, regardless of orbital and rotational frequencies, the phase between the perturber and the tidal bulge remains constant. Following Greenberg (2009), I will refer to this version as the “constant-phase-lag” or CPL model. At first glance, this model may seem to be the best choice, given the body is expected to behave like a harmonic oscillator: In order for the tidal waves to be linearly summed, the damping parameters must be independent of frequency. However, for eccentric orbits, it may not be possible for the phase lag to remain constant as the instantaneous orbital angular frequency changes in accordance with Kepler’s second law (Touma and Wisdom 1994; Efroimsky and Makarov 2013). This paradox has led numerous researchers to reject the CPL model, despite its relative success at reproducing features in the Solar System, e.g.,  (MacDonald 1964; Hut 1981; Goldreich and Soter 1966; Peale et al. 1979), as well as the tidal circularization of close-in exoplanets (Jackson et al. 2008).

The second possibility for the lag is that the time interval between the perturber’s passage and the tidal bulge is constant. In this case, as frequencies change, the angle between the bulge and the perturber changes. I will call this version the “constant-time-lag,” or CTL, model (Mignard 1979; Hut 1981; Greenberg 2009). The CPL and CTL models, while qualitatively different, reduce to the same set of governing equations if a linear dependence between phase lags and tidal frequencies is assumed.

In terms of planetary rotation rate, many of the timescales are set by masses, radii, and semimajor axes. For typical main sequence stars, and Mars- to Neptune-sized planets in the classic HZ of Kasting et al. (1993), the timescales range from millions to trillions of years, with the shortest timescales occurring for the largest planets orbiting closest to the smallest stars. The CPL and CTL models predict qualitatively similar behavior for the orbital evolution of close-in exoplanets when rotational effects are ignored, e.g.,  (Jackson et al. 2009; Levrard et al. 2009; Barnes et al. 2013; Barnes 2015).

The two tidal models are effectively indistinguishable in our Solar System. Most tidally interacting pairs of worlds are now evolving so slowly that changes due to tidal evolution are rarely measurable. The Earth–Moon system is by far the best measured, but interpretations are hampered by the complexity of the binary’s orbital history and the dissipation of energy due to Earth’s ever-changing continental configuration (Green et al. 2017). Nonetheless, the present state of the Earth–Moon system provides crucial insight into the rotational evolution of habitable exoplanets.

When the ET framework is limited to two bodies, it consists of six independent parameters: the semimajor axis a, the eccentricity e, the two rotation rates $\varOmega _i$, and two obliquities $\psi _i$, where i (=1, 2) corresponds to one of the bodies. If the gravitational gradient across a freely rotating body induces sufficient strain on that body’s interior to force movement, then frictional heating is inevitable. The energy for this heating comes at the expense of the orbit and/or rotation, and hence, tidal friction decreases the semimajor axis and rotation period. The friction will also prevent the longest axis of the body to align exactly with the perturber. With an asymmetry introduced, torques arise and open pathways for angular momentum exchange. There are three reservoirs of angular momentum: the orbit and the two rotations. ET models assume orbit-averaged torques, which is a good approximation for the long-term evolution of the system. The redistribution of angular momentum depends on the amount of energy dissipated, and the heights and positions of the tidal bulge relative to the line connecting the two centers of mass. The ET model can therefore be seen as a mathematical construction that couples energy transformation to conservation of angular momentum.

The tidal power and bulge properties depend on the composition and microphysics of planetary and stellar interiors, which are very difficult to measure in our Solar System, let alone in an external planetary system. In ET theory, the coupling between energy dissipation and the tidal bulge is therefore a central feature and is scaled by two parameters, the Love number of degree 2, $k_2$, and a parameter that represents the lag between the line connecting the two centers of mass and the direction of the tidal bulge. In the CPL model, this parameter is the “tidal quality factor” Q, and in CTL it is the tidal time lag $\tau$. $k_2$ is the same in both models.

Although energy dissipation results in semimajor axis decay, angular momentum exchange can lead to semimajor axis growth. This growth can occur if enough rotational angular momentum can be transferred to the semimajor axis to overcome its decay due to tidal heating. Earth and the Moon are in this configuration now.

A tidally evolving system has three possible final configurations (Counselman 1973): Both bodies rotate synchronously with spin axes parallel to the orbital axis, and they revolve around each other on a circular orbit; the two bodies merge; or the orbit expands forever. The first case is called “double synchronous rotation” and is the only stable solution. In the latter case, encounters with other massive bodies will likely to prevent the unimpeded expansion of the orbit. As the rotation rates decay, the less massive body will probably be the first to reach the synchronous state, and this is the case for habitable exoplanets of main sequence stars.

2.1 The constant-phase-lag model

In the second-order CPL model of tidal evolution, the angle between the line connecting the centers of mass and the tidal bulge is constant. This approach is commonly utilized in Solar System studies (e.g.,  Goldreich and Soter 1966; Greenberg 2009), and the evolution is described by the following equations:

$$\begin{aligned} \frac{{\mathrm {d}}e}{{\mathrm {d}}t}= & {} - \frac{ae}{8 G M_1 M_2} \sum \limits _{i = 1}^2Z'_i \Bigg (2\varepsilon _{0,i} - \frac{49}{2}\varepsilon _{1,i} + \frac{1}{2}\varepsilon _{2,i} + 3\varepsilon _{5,i}\Bigg ), \end{aligned}$$

(1)

$$\begin{aligned} \frac{{\mathrm {d}}a}{{\mathrm {d}}t}= & {} \frac{a^2}{4 G M_1 M_2} \sum \limits _{i = 1}^2 Z'_i \ {\Bigg (} 4\varepsilon _{0,i} + e^2{\Big [} -20\varepsilon _{0,i} + \frac{1 47}{2}\varepsilon _{1,i} + \frac{1}{2}\varepsilon _{2,i} - 3\varepsilon _{5,i} {\Big ]} \nonumber \\&-\,4\sin ^2\left( \psi _i\right) {\Big [}\varepsilon _{0,i}-\varepsilon _{8,i}{\Big ]}{\Bigg )}, \end{aligned}$$

(2)

$$\begin{aligned} \frac{{\mathrm {d}}\varOmega _i}{{\mathrm {d}}t}= & {} - \frac{Z'_i}{8 M_i r_{\mathrm {g},i} ^2 R_i^2 n} {\Bigg (}4\varepsilon _{0,i} + e^2{\Big [} -20\varepsilon _{0,i} + 49\varepsilon _{1,i} + \varepsilon _{2,i} {\Big ]}\nonumber \\&+ \ 2\sin ^2\left( \psi _i\right) {\Big [} - 2\varepsilon _{0,i} + \varepsilon _{8,i} + \varepsilon _{9,i} {\Big ]} {\Bigg )}, \end{aligned}$$

(3)

and

$$\begin{aligned} \frac{{\mathrm {d}}\psi _i}{{\mathrm {d}}t} \ = \ \frac{Z'_i \sin (\psi _i)}{4 M_i r_{\mathrm {g},i}^2 R_i^2 n \varOmega _i} {\Bigg (} {\Big [} 1-\xi _i {\Big ]}\varepsilon _{0,i} + {\Big [} 1+\xi _i {\Big ]}{\Big \{}\varepsilon _{8,i}-\varepsilon _{9,i}{\Big \}} {\Bigg )} \ , \end{aligned}$$

(4)

where t is time, G is Newton’s gravitational constant, $M_i$ are the two masses, $R_i$ are the two radii, and n is the mean motion. The above equations are mean variations of the orbital elements, averaged over the orbital period, and are only valid to second order in e and $\psi$. The quantity $Z'_i$ is

$$\begin{aligned} Z'_i \equiv 3 G^2 k_{2,i} M_j^2 \left( M_i+M_j\right) \frac{R_i^5}{a^9} \ \frac{1}{n Q_i} \ , \end{aligned}$$

(5)

where $k_{2,i}$ are the Love numbers of order 2, and $Q_i$ are the “tidal quality factors.” The parameter $\xi _i$ is

$$\begin{aligned} \xi _i \equiv \frac{r_{\mathrm {g},i}^2 R_i^2 \varOmega _i a n }{ G M_j}, \end{aligned}$$

(6)

where i and j refer to the two bodies, and $r_g$ is the “radius of gyration,” i.e., the moment of inertia is $M(r_gR)^2$. The signs of the phase lags are

$$\begin{aligned} \begin{array}{l} \varepsilon _{0,i} = \varSigma \left( 2 \varOmega _i - 2 n\right) \\ \varepsilon _{1,i} = \varSigma \left( 2 \varOmega _i - 3 n\right) \\ \varepsilon _{2,i} = \varSigma \left( 2 \varOmega _i - n\right) \\ \varepsilon _{5,i} = \varSigma (n)\\ \varepsilon _{8,i} = \varSigma \left( \varOmega _i - 2 n\right) \\ \varepsilon _{9,i} = \varSigma \left( \varOmega _i\right) \ ,\\ \end{array} \end{aligned}$$

(7)

with $\varSigma (x)$ the sign of any physical quantity x, i.e., $\varSigma (x)~=~+1, -1$ or 0.

The CPL model described above only permits four “tidal waves” and hence does not allow a continuum of rotation rates, only spin to orbit frequency ratios of 3:2 and 1:1. Essentially, for eccentricities below $\sqrt{1/19}$, the torque on the rotation by the tidal waves is insufficient to change the rotation rate, but above it, the torque is only strong enough to increase the rotation rate to 1.5n. In other words, these rotation rates are the only two resolved by the truncated infinite series used in the CPL framework, and the equilibrium rotation period is

$$\begin{aligned} P^\mathrm{CPL}_\mathrm{eq} = {\left\{ \begin{array}{ll} P, &{} e < \sqrt{1/19}\\ \frac{2P}{3}, &{} e~\le ~\sqrt{1/19}, \end{array}\right. } \end{aligned}$$

(8)

where P is the orbital period. Goldreich (1966) suggested that the equilibrium rotation period, i.e., the rotation period of a “tidally locked” body, is

$$\begin{aligned} P_\mathrm{eq}^{G66} = \frac{P}{1 + 9.5e^2}. \end{aligned}$$

(9)

Murray and Dermott (1999) presented a derivation of this expression, which assumes $\sin (\psi ) = 0$, and predicts the rotation rate may take a continuum of values.

Barnes et al. (2013) suggested the CPL model should be implemented differently depending on the problem. When modeling the evolution of a system, one should use the discrete spin values for self-consistency, i.e., as an initial condition, or if forcing the spin to remain tide-locked. However, if calculating the equilibrium spin period separately, the continuous value of Eq. (8) should be used. I refer to these rotational states as “discrete” and “continuous” and will use the former throughout this study.

Note in Eq. (1) that e can grow if

$$\begin{aligned} {} \sum \limits _{i = 1}^2Z_i\Bigg (2\varepsilon _{0,i} - \frac{49}{2}\varepsilon _{1,i} + \frac{1}{2}\varepsilon _{2,i} + 3\varepsilon _{5,i}\Bigg ) < 0, \end{aligned}$$

(10)

which depends on the orbital and rotational frequencies, as well as the physical properties of the two bodies. Eccentricity growth by tidal effects has been considered for brown dwarfs (Heller et al. 2010), but has not been examined for potentially habitable exoplanets. If e grows, then by Eq. (8), we expect a planet’s equilibrium rotational period to decrease, i.e., it will never be synchronized. Thus, synchronization is not necessarily the end state of the tidal evolution of a planet’s spin, if the equilibrium tide models are approximately valid at high eccentricity.

2.2 The constant-time-lag model

The CTL model assumes that the time interval between the passage of the perturber and the tidal bulge is constant. This assumption allows the tidal response to be continuous over a wide range of frequencies, unlike the CPL model. But, if the phase lag is a function of the forcing frequency, then the system is no longer analogous to a damped driven harmonic oscillator. Therefore, this model should only be used over a narrow range of frequencies, see Greenberg (2009). However, this model’s use is widespread, especially at high e, so I use it to evaluate tidal effects as well.

Here I use the model derived by Leconte et al. (2010), with the nomenclature of Heller et al. (2011). The evolution is described by the following equations:

$$\begin{aligned}&\frac{{\mathrm {d}}e}{{\mathrm {d}}t} \ = \ \frac{11 ae}{2 G M_1 M_2} \sum \limits _{i = 1}^2Z_i \Bigg (\cos \left( \psi _i\right) \frac{f_4(e)}{\beta ^{10}(e)} \frac{\varOmega _i}{n} -\frac{18}{11} \frac{f_3(e)}{\beta ^{13}(e)}\Bigg ), \end{aligned}$$

(11)

$$\begin{aligned}&\frac{{\mathrm {d}}a}{{\mathrm {d}}t} \ = \ \frac{2 a^2}{G M_1 M_2} \sum \limits _{i = 1}^2 Z_i \Bigg (\cos \left( \psi _i\right) \frac{f_2(e)}{\beta ^{12}(e)} \frac{\varOmega _i}{n} - \frac{f_1(e)}{\beta ^{15}(e)}\Bigg ), \end{aligned}$$

(12)

$$\begin{aligned}&\frac{{\mathrm {d}}\varOmega _i}{{\mathrm {d}}t} \ = \ \frac{Z_i}{2 M_i r_{\mathrm {g},i}^2 R_i^2 n} \Bigg ( 2 \cos \left( \psi _i\right) \frac{f_2(e)}{\beta ^{12}(e)} - \left[ 1+\cos ^2(\psi ) \right] \frac{f_5(e)}{\beta ^9(e)} \frac{\varOmega _i}{n} \Bigg ), \end{aligned}$$

(13)

and

$$\begin{aligned} \frac{{\mathrm {d}}\psi _i}{{\mathrm {d}}t} \ = \ \frac{Z_i \sin \left( \psi _i\right) }{2 M_i r_{\mathrm {g},i}^2 R_i^2 n \varOmega _i}\left( \left[ \cos \left( \psi _i\right) - \frac{\xi _i}{ \beta } \right] \frac{f_5(e)}{\beta ^9(e)} \frac{\varOmega _i}{n} - 2 \frac{f_2(e)}{\beta ^{12}(e)} \right) , \end{aligned}$$

(14)

where

$$\begin{aligned} Z_i \equiv 3 G^2 k_{2,i} M_j^2 \left( M_i+M_j\right) \frac{R_i^5}{a^9} \ \tau _i \ , \end{aligned}$$

(15)

and

$$\begin{aligned} \begin{array}{l} \beta (e) = \sqrt{1-e^2},\\ f_1(e) = 1 + \frac{31}{2} e^2 + \frac{255}{8} e^4 + \frac{185}{16} e^6 + \frac{25}{ 64} e^8,\\ f_2(e) = 1 + \frac{15}{2} e^2 + \frac{45}{8} e^4 \ \ + \frac{5}{16} e^6,\\ f_3(e) = 1 + \frac{15}{4} e^2 + \frac{15}{8} e^4 \ \ + \frac{5}{64} e^6,\\ f_4(e) = 1 + \frac{3}{2} e^2 \ \ + \frac{1}{8} e^4,\\ f_5(e) = 1 + 3 e^2 \ \ \ + \frac{3}{8} e^4. \end{array} \end{aligned}$$

(16)

It can also be shown that the equilibrium rotation period is

$$\begin{aligned} P_\mathrm{eq}^\mathrm{CTL}(e,\psi ) = P\frac{\beta ^3f_5(e)\left( 1 + \cos ^2\psi \right) }{2f_2(e)\cos \psi }, \end{aligned}$$

(17)

which for low e and $\psi = 0$ reduces to

$$\begin{aligned} P_\mathrm{eq}^\mathrm{CTL} = \frac{P}{1 + 6e^2}. \end{aligned}$$

(18)

Figure 1 shows the predicted ratio of the equilibrium rotational frequency $\varOmega _\mathrm{eq}$ to n as a function of e for the CPL model (solid curve), Goldreich (1966)’s model (dotted), and the CTL model (dashed). All models predict that as e increases, the rotational frequency of a tidally locked planet will grow, and hence, planets found on eccentric orbits may rotate super-synchronously.

Fig. 1

Equilibrium spin frequency of a tidally locked exoplanet as a function of eccentricity for the CPL model (solid curve), the CTL model (dashed), and Goldreich (1966)’s model (dotted)

As in the CPL model, the CTL model also predicts configurations that lead to eccentricity growth, which could prevent rotational synchronization. If (19) holds, then the orbital eccentricity will grow:

$$\begin{aligned} \sum \limits _{i = 1}^2Z_i \Bigg (\cos \left( \psi _i\right) \frac{f_4(e)}{\beta ^{10}(e)} \frac{\varOmega _i}{n} -\frac{18}{11} \frac{f_3(e)}{\beta ^{13}(e)}\Bigg ) > 0. \end{aligned}$$

(19)

2.3 Numerical methods (EQTIDE)

To survey the range of rotational evolution of habitable exoplanets, I performed thousands of numerical simulations of individual star–planet pairs and tracked their orbital and rotational states. To compute the models described in the previous two subsections, I used the software package EQTIDE.¹ This code, written in C, is fast, user-friendly, and has a simple switch between the CTL and CPL models. The governing equations are calculated with a fourth-order Runge–Kutta integrator (although Euler’s method works surprisingly well), with an adaptive timestep determined by the most rapidly evolving parameter. This software package and its variants have been used on a wide range of binary systems, including exoplanets (Barnes et al. 2013; Barnes 2015), binary stars (Gomez Maqueo Chew et al. 2012, 2014), brown dwarfs (Fleming et al. 2012; Ma et al. 2013), and exomoons (Heller and Barnes 2013).

For the simulations presented below, I used the Runge–Kutta method with a timestep that was 1% of the shortest dynamical time ($x/(\mathrm{d}x/\mathrm{d}t)$, where x is one of the six independent variables) and assumed a planet became tidally locked if its rotation period reached 1% of the equilibrium rotation period. If a planet becomes tidally locked, its rotation period is forced to equal the equilibrium period (Eqs. 8, 17) for the remainder of the integration. Note that the obliquity, eccentricity and mean motion can continue to evolve and so the spin period can also.

2.4 What is the tidal response?

The ET models described above have two free parameters: $k_2$ and either Q or $\tau$. The former can only have values between 0 and 1.5, but the latter can span orders of magnitude. As is well known, the current estimates for Q and $\tau$ of Earth, 12 and 640 s, respectively, predict that the Moon has only been in orbit for 1–2 Gyr (MacDonald 1964; Touma and Wisdom 1994), far less than its actual age of 4.5 Gyr. This contradiction has led many researchers to assume that the historical averages of Earth’s tidal Q and $\tau$ have been about 10 times different. Indeed, Kasting et al. (1993) assumed $Q=100$ when they calculated their tidal lock radius. Previous researchers have argued that such discrepancies are justified because tidal dissipation in the oceans is a complex function of continental positions and in the past different arrangements could have allowed for weaker dissipation. A recent study of ocean dissipation over the past 250 Myr found that the modern Earth is about twice as dissipative as compared to the historical average (Green et al. 2017). Another possibility is that the continents grow with time (Dhuime et al. 2012), resulting in a larger fraction of the surface consisting of highly dissipative straits and shallow seas. Whether these suppositions are true remains to be seen, but clearly the ET models fail when using modern values of the tidal dissipation. On the other hand, if Q ($\tau$) has been shrinking (growing), then we might expect it to continue to do so, and planets older than Earth may be more dissipative.

However, one also needs to bear in mind the complexities of the Earth–Moon system’s presence in the Solar System. Ćuk (2007) showed that the Moon’s orbit and obliquity have been perturbed by passages through secular resonances with Venus and Jupiter as the Moon’s orbit expanded. During these perturbations, the eccentricity of the Moon could have reached 0.2, and hence, the simple picture invoked by classic studies of the two-body Earth–Moon system may be invalid (and that there may have been epochs in Earth history during which the Moon rotated super-synchronously). Moreover, the early evolution of the Earth–Moon system may have been affected by an evection resonance involving the Earth’s orbit about the Sun and by energy dissipation inside the solid Earth (Ćuk and Stewart 2012; Zahnle et al. 2015). Given these complications, it is unclear that the modern dissipation of Earth is not representative of its historical average, nor is it obvious that other ocean-bearing exoplanets should tend to have less dissipation than Earth.

In Fig. 2, the semimajor axis and eccentricity history of the Earth–Moon system are shown for the two ET models with different choices for the tidal response and different approximations. For the simple case of a circular orbit and no obliquities, I recover the classic results. However, dissipation rates that are 10 times less than the current rate, as advocated by Kasting et al. (1993), do not accurately calibrate the models either. Instead I find rates that are 3–5 times weaker place the Moon at Earth’s surface 4.5 Gyr ago ($Q=34.5$ and $\tau =125$ s). When the assumption that $e~=~\sin \psi ~=~0$ is relaxed and the modern values are used, the CTL model predicts slightly different behavior, but the CPL model is qualitatively different and actually predicts large values of a and e in the past. This history is strongly influenced by the current values of e and $\psi$, which were modified by the secular resonance crossings (Ćuk 2007).

Fig. 2

Tidal evolution of the semimajor axis (top) and eccentricity (bottom) of the Earth–Moon system for different assumptions. Solid curves correspond to the CPL model, dotted to CTL. The black curves assume the modern value of Earth’s tidal response, but the eccentricity and 2 obliquities have been set to 0. These curves reproduce the classic result that the Moon was at Earth’s surface 1–2 Gyr ago. The blue curves show the history if the Q and $\tau$ values are chosen so that the Moon’s orbit began expanding 4.5 Gyr ago. The green curves use the modern tidal response and the current values of e and $\psi$. Cyan curves are similar, but use the calibrated values of Q and $\tau$

In summary, the ET models predict reasonable histories for the Earth–Moon system, but the history is sufficiently complicated that we cannot unequivocally state that the modern Earth’s Q and $\tau$ values should be discarded when considering habitable exoplanets. It is also currently impossible to know how different continents and seafloor topography affect the tidal response of habitable exoplanets. In light of these uncertainties, I will use the modern Earth’s values of Q and $\tau$ in the simulations of the tidal evolution of habitable exoplanets. In general, the timescales scale linearly with these parameters, so if one prefers different choices, it is relatively straightforward to estimate the evolution based on the plots provided below, or to directly calculate it with EQTIDE.

2.5 Initial conditions

Every trial run requires specific physical and orbital properties, some of which can be constrained by models, but others cannot. A star’s mass is roughly constant over its main sequence lifetime, but its radius and luminosity can change significantly over time. I fit the 5-Gyr mass–radius–luminosity relation from Baraffe et al. (2015) to a third-order polynomial using Levenberg–Marquardt minimization (Press et al. 1992) and found

$$\begin{aligned} \frac{R_*}{R_\odot } = 0.003269 + 1.304\frac{M_*}{M_\odot } - 1.312\frac{M_*}{M_\odot }^2 + 1.055\frac{M_*}{M_\odot }^3, \end{aligned}$$

(20)

and

$$\begin{aligned} \log \left( \frac{L_*}{L_\odot }\right) = -0.0494 + 6.65X + 8.73X^2 + 5.208X^3, \end{aligned}$$

(21)

where $X = \log (M_*/M_\odot )$. The star’s $k_2$, Q, and $\tau$ values are set to 0.5, $10^6$, and 0.01 s for all cases, similar to previous studies (Rasio et al. 1996; Jackson et al. 2008; Matsumura et al. 2010; Barnes 2015). For the CPL model, the initial values of the phase lags are determined by the initial rotational and orbital frequencies as described in Eq. (7).

For the planet, I used the mass–radius relationship of Sotin et al. (2007) for planets with Earth-like composition:

$$\begin{aligned} \frac{R_p}{\mathrm{\,R_\oplus }} = \left\{ \begin{array}{rl} \Big (\frac{M_p}{\mathrm{\,M_\oplus }}\Big )^{0.306}, &{}10^{-2}~\mathrm{\,M_\oplus }< M_p< \mathrm{\,M_\oplus }\\ \Big (\frac{M_p}{\mathrm{\,M_\oplus }}\Big )^{0.274}, &{}\mathrm{\,M_\oplus }< M_p < 10~\mathrm{\,M_\oplus }. \end{array} \right. \end{aligned}$$

(22)

The planet’s $k_2$, Q, and $\tau$ values are set to 0.3, 12, and 640 s (Lambeck 1977; Williams et al. 1978; Yoder 1995).

Fixing each of the physical parameters as described does not represent a comprehensive study of the problem, as planets and stars of a given mass can have a wide range of radii and tidal response. However, as shown in the next section, using these standard parameters and allowing the initial rotation period to vary admits a wide enough range of possibilities that there is no need to explore the other parameters at this time.

I also calculate the predicted tidal evolution of planets found by Kepler, and projected for TESS. For these simulations, I used both the CPL and CTL models, and three sets of initial conditions: ($P_0, \psi _0, Q, \tau$) = (10 d, 0, 12, 640 s), (1 d, 23.5$^\circ$, 34, 125 s), and (8 h, 60$^\circ$, 100, 64 s), where $P_0$ is the initial rotation period. I will refer to these options as “short,” “Earth-like,” and “long” timescales for $T_\mathrm{lock}$, respectively.

3 Results

This section considers the tidal evolution of ocean-bearing exoplanets orbiting various stars and with different, but reasonable, initial and physical conditions with the goal of mapping out regions of parameter space that lead to synchronous rotation on Gyr timescales. First, I consider the tidal evolution of Kepler-22 b, a $2.3~\mathrm{\,R_\oplus }$ planet orbiting a G5V star near the inner edge of its HZ with no known companions (Borucki et al. 2012). This planet is probably too large to be terrestrial (Rogers 2015), but is similar to others worlds that may be (Dumusque et al. 2014; Espinoza et al. 2016), and so is potentially habitable (Barnes et al. 2015). Next, I examine the tidal evolution of the recently discovered planet Proxima Centauri b (Anglada-Escudé et al. 2016). Then, I consider the potentially habitable planets discovered by the Kepler spacecraft that do not have planetary companions. Then, I survey a broad range of parameter space and show that habitable exoplanets of G dwarf stars with an initially slow rotation period and low obliquity can become tidally locked within 1 Gyr. Next, I explore the coupled orbital/rotational evolution of planets orbiting very small stars () and find that they are likely to be synchronous rotators. Finally, I compute the rotational evolution of the projected exoplanet yield from TESS (Sullivan et al. 2015) and find that nearly every potentially habitable planet the mission will discover will be tidally locked.

3.1 Kepler-22 b

Figure 3 shows plausible spin period evolutions of Kepler-22 b assuming a mass of $23~\mathrm{\,M_\oplus }$, an initial spin period of 1 day, and an initial obliquity of 23.5$^\circ$. The mass of the host star is 0.97 $\mathrm{\,M_\odot }$, and the initial semimajor axis is 0.849 AU. The solid curves show results from the CPL model, dashed CTL. The different line colors represent different initial eccentricity, which is not well constrained at this time. The age of the system is not known, but could be 10 Gyr (Borucki et al. 2012). For such an age, the CPL model predicts that the planet will have spun down into a synchronous state for and into a 3:2 spin–orbit frequency ratio for larger values. On the other hand, the CTL model predicts significantly less evolution. This system demonstrates that the CPL model predicts that tidal braking can be important in the HZs of G and K dwarfs, not just M dwarfs as is usually assumed.

Fig. 3

Evolution of the rotation period of Kepler-22 b with different orbital eccentricities as shown in the legend. Solid lines assume the CPL model, dashed CTL. The evolution of semimajor axis and eccentricity is negligible

3.2 Proxima Centauri b

Recently, Anglada-Escudé et al. (2016) announced the discovery of a planet orbiting in the HZ of Proxima Centauri with a period of 11.2 days and an inferred semimajor axis of 0.0485 AU. The orbital eccentricity could only be constrained to be less than 0.35, and since the discovery was made via radial velocity data, the radius and actual mass are not known. Barnes et al. (2016) considered its tidal evolution in the CPL framework and found that the rotational frequency is synchronized in less than $10^6$ years and that the orbital eccentricity is damped with a characteristic timescale of 1 Gyr. In this subsection, I expand on those results and also consider evolution in the CTL model.

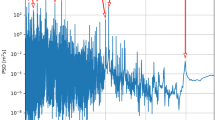
In Fig. 4, the evolution of rotation period, e and a are shown for a planet with Proxima b’s minimum mass, a radius of $1.07~\mathrm{\,R_\oplus }$, an initial rotation period of 1 day, an initial obliquity of 23.5$^\circ$, and an initial semimajor axis of 0.05 AU. The different linestyles correspond to different initial eccentricities and different tidal models.

The CPL model predicts the rotational frequency becomes locked in less than $10^4$ years and that for $e>0.23$ planet b settles into a 3:2 spin–orbit frequency ratio that leads to semimajor axis growth. As a increases, so does the rotation period until $e~\approx ~0.23$ at which point the discrete nature of the CPL solution instantaneously forces the synchronous state. At this point, the torques are reversed and a begins to decrease, ultimately settling into orbits that are significantly larger than the initial orbits.

The CTL model predicts the tidal locking time to be less than $10^5$ years and that for $e~>~0$ the planet will reach non-synchronous “pseudo-equilibrium” periods that are a function of e. The CTL model does not suffer from discontinuities and predicts longer times for e to damp. Thus, if Proxima b ever reached a high eccentricity state, the two ET models predict qualitatively different types of evolution.

Fig. 4

Evolution of Proxima Centauri b due to tides. Solid lines assume the CPL model, dashed CTL. Top: rotation period. Middle: eccentricity. Bottom: semimajor axis

3.3 The Kepler sample

The previous examples are illustrative of the tidal evolution process for potentially habitable planets, but are not comprehensive. In this subsection, the analysis is expanded to the Kepler candidate planets for which no other planets are known in the system. Figure 5 shows the time for Kepler candidates (Batalha et al. 2013) to tidally lock, assuming that they formed with 1-day rotation periods and obliquities of $23.5^\circ$. Also shown is each candidate’s “habitability index for transiting exoplanets” (HITE) (Barnes et al. 2015), which is an estimate of the likelihood that the energy received at the top of the planet’s atmosphere could permit liquid surface water and is inversely proportional to the planet’s radius, as larger planets are more likely to be gaseous and uninhabitable. For each planet candidate in Batalha et al. (2013), I calculated the tidal evolution for six assumptions.

The column of planets at 15 Gyr is those candidates that did not tidally lock within 15 Gyr. About half of the isolated and potentially habitable planets discovered by Kepler could be tidally locked. Table 1 (available in Online Supplement) lists the properties of the planet candidates shown in Fig. 5. The previously undefined symbols are: $P_\mathrm{orb}$ = orbital period; $T_\mathrm{CPL}^\mathrm{short}$ = CPL model, “short” assumptions (see Sect. 2.5); $T_\mathrm{CPL}^{\oplus }$ = CPL model, Earth-like assumptions; $T_\mathrm{CPL}^\mathrm{long}$ = CPL model, “long” assumptions; $T_\mathrm{CTL}^\mathrm{short}$ = CTL model, short assumptions; $T_\mathrm{CTL}^{\oplus }$ = CTL model, Earth-like assumptions; $T_\mathrm{CTL}^\mathrm{long}$ = CTL model, long assumptions.

Fig. 5

Comparison of the time to tidally lock and the habitability index for transiting exoplanets. The dot size is proportional to planet mass, which is part of the habitability index, and the color corresponds to the equilibrium tide model. Planet candidates that did not tidally lock are placed at 15 Gyr

Fig. 6

Timescale for planets on circular orbits to rotate synchronously. The left panels assume the CPL model; right CTL. The top row assumes an initial rotation period of 8 h and an obliquity of $60^\circ$. The bottom row assumes an initial rotation period of 10 days and an obliquity of 0. The HZ is shown by the gray shading, with the darker gray corresponding to the conservative HZ, and lighter gray to the optimistic HZ (Kopparapu et al. 2013). Note the different scale on the bottom left plot

3.4 Parameter space survey

Next, I consider a broader range of parameter space to explore the limits of the timescale to synchronize habitable exoplanets on circular orbits. Figure 6 shows the results of four-parameter sweeps. The left column is the CPL framework, right is CTL. The top row is the more stable case, a planet with an initial spin period of 8 h and an initial obliquity of $60^\circ$. The bottom row shows the more unstable case, a planet with an initial spin period of 10 days, and an initial obliquity of 0. The former has higher initial rotational angular momentum, and its direction is misaligned with the orbital angular momentum, and hence it takes longer to equilibrate into the synchronous state. The latter is a plausible initial condition from simulations of terrestrial planet formation (Kokubo and Ida 2007; Miguel and Brunini 2010). The HZ of Kopparapu et al. (2013) is shown as shading with the lighter gray representing empirical or optimistic limits, and the darker gray representing theoretical or conservative limits.

This figure demonstrates that for early M through G dwarfs, the possibility of rotational synchronization of habitable exoplanets on circular orbits depends on the initial conditions and the tidal response. Slower spin periods with aligned rotational and orbital axes are more likely to lead to tidal synchronization within 1 Gyr. Earth–mass planets in the HZ of the entire G spectral class can be synchronized if the CPL model is correct, but if CTL is, then planets orbiting G dwarfs will not be synchronized, unless they form with a very large rotational period, which is possible (Miguel and Brunini 2010). This difference is due to the different frequency dependencies between the two models. The ratio of Eqs. (5)–(15) is $1/(2nQ\tau |n - \varOmega |)$, and for an Earth with an initial rotation period of 10 days, the ratio is 9, i.e., the CPL model initially de-spins the planet 9 times faster than the CTL model. The dependence on $\varOmega$ forces the ratio to increase with time as $\varOmega ~\rightarrow ~n$, and, indeed, for this case the difference in the time to tidally lock is a factor of 50. If Earth formed with no Moon, an initial rotation period of 3 days, and maintained a constant Q value of 12, then the CPL model predicts it would become synchronously rotating within 5 Gyr. The reader is cautioned that extrapolating from the Earth–Moon frequency to the Earth–Sun frequency could introduce significant error in the tidal modeling. The CTL’s frequency dependence maintains more similar responses over a wider frequency range than CPL, and hence, the CTL model does not predict such short tidal locking times for Earth-like planets in the HZ of G dwarfs.

Fig. 7

$\mathrm{d}e/\mathrm{d}t$ for an Earth-like planet orbiting a $0.1~\mathrm{\,M_\odot }$ star as a function of the angular frequencies, with $\varOmega _2$ being the rotational frequency of the planet. The semimajor axis of the orbit is 0.05 AU, and the eccentricity is 0.2. Both models predict that for fast rotators, $\mathrm{d}e/\mathrm{d}t$ is positive

Fig. 8

Rotational and orbital evolution of an Earth-like planet orbiting a $0.1~\mathrm{\,M_\odot }$ star at 0.05 AU. The CPL model is represented by the solid curve and the CTL by the dashed. Note that after 680 Myr the CPL model predicts the planet will merge with the host star. Top Left: eccentricity. Top Right: the ratio of the planet’s rotational frequency to mean motion. Bottom Left: the time derivative of the eccentricity. The CPL predicts several discontinuities as the rotational frequency evolves. Bottom Right: the planet’s rotational period. The CPL model predicts a will decay rapidly after about 100 Myr, and since the planet is rotationally locked its period drops. The CTL model predicts later eccentricity damping without much evolution in a, and hence, the rotational period rises

Fig. 9

Time in Gyr for an Earth-like planet with an initial eccentricity of 0.3 to circularize. The format is the same as Fig. 6. The left panel is the CPL model, right is CTL

If the assumption of a circular orbit is relaxed, then the evolution can be significantly more complicated. As demonstrated in Fig. 3, planets on higher eccentricity orbits can rotate super-synchronously. This aspect of tidal theory is well known (Goldreich 1966; Murray and Dermott 1999; Barnes et al. 2008), but the details depend on the planet. ET models predict that super-synchronous rotation will occur for any $e>0$, but it is far more likely that planets will be locked into spin–orbit resonance such as 1:1, 3:2, or 2:1 (Rodríguez et al. 2012). However, the tidal braking process results in transfer of rotational angular momentum to orbital angular momentum and can lead to a change in e. The sign of the change depends on the ratio of the rotational and orbital frequencies of both bodies. Previous results that predict eccentricities always decrease, such as Rasio et al. (1996) and Jackson et al. (2008), have assumed the planets had already synchronized.

The coupled evolution of the rotational frequency and the orbital eccentricity is a complex function of the dissipation rates and the distribution of the angular momentum among the spins and orbit. As given in Eqs. (1) and (11), the change in eccentricity can be positive or negative depending on the ratios of several parameters. In general, e will decay for rotational periods longer than or similar to the orbital period. This behavior can be understood in terms of forces. A body rotating faster than it is revolving at pericenter will have a bulge that leads the perturber. This bulge has a gravitational force that accelerates the perturber in the direction of the motion. This acceleration increases the tangential velocity at pericenter, and hence, the eccentricity must grow. Because the pericenter distance must remain constant, the semimajor axis must also grow. Thus, the equilibrium rotation period can grow or shrink depending on the rates of change of a and e. As an example, the value of $\mathrm{d}e/\mathrm{d}t$ as a function of $\varOmega /n$ for an Earth-like planet orbiting $0.1~\mathrm{\,M_\odot }$ star with $a=0.05$ AU and $e=0.2$ is shown in Fig. 7. In the CPL model, planets that rotate faster than 1.5n will experience eccentricity growth, while slower rates lead to eccentricity decay. In the CTL model, the critical frequency ratio depends on eccentricity. The difference between the two models is due to the different assumptions of the frequency dependence.

Fig. 10

Maximum timescale for tidal locking, HITE values and apparent J band magnitudes of potentially habitable planets predicted for TESS from Sullivan et al. (2015). The tidal locking time assumes a tidal Q of 100, and initial rotation periods and obliquities of 8 h and $60^\circ$, respectively. The circles correspond to planets for which only one planet is detected, x’s correspond to planets in multiplanet systems. Dot and x sizes are proportional to the HITE value

Figure 8 shows the orbital and rotational evolution of an Earth-like planet orbiting at 0.05 AU. The eccentricity grows slightly until $n~\approx ~1.5\,\Omega$ at which point it begins to decay. For many cases, this process can act to delay the circularization process. The eccentricity distribution of radial-velocity-detected exoplanets with orbits that are unaffected by tidal interaction, i.e., those with $a>0.2$ AU, has a mean² of $\sim$0.3. While the vast majority of these exoplanets is expected to be gaseous, we should nonetheless expect many terrestrial exoplanets to possess large eccentricities and those that are tidally locked will rotate super-synchronously. However e will likely also tidally evolve, and hence, the equilibrium period will change with time, too. As rotational evolution tends to be more rapid than orbital evolution, tidal locking generally occurs prior to orbital circularization. If $\mathrm{d}e/\mathrm{d}t > 0$, then the planet can be tidally locked and evolving to ever shorter rotation periods. In most cases, e decays with time and hence the rotational period slows, possibly in a series of sudden transitions between spin and orbit resonances, a fascinating scenario for the biospheres of inhabited exoplanets.

Figure 9 shows the time required for the eccentricity of an Earth twin planet to drop from 0.3 to 0.01, the circularization timescale $T_\mathrm{circ}$, for a range of stellar masses. The initial period is 1 day, and the initial obliquity is $23.5^\circ$ in these calculations. The contour lines denote $T_\mathrm{circ}$ in Gyr. For both models, Earth-like planets orbiting stars less massive than $0.1~\mathrm{\,M_\odot }$ will likely be on circular orbits and in synchronous rotation. Planets with initially fast rotation rates, or strong perturbations from other planets might not be synchronous rotators around stars of any mass.

3.5 TESS projections

The results of the previous section provide a foundation to interpret future discoveries from transit (Berta-Thompson et al. 2015; Gillon et al. 2016), radial velocity (Anglada-Escudé et al. 2016), and astrometric data (Malbet et al. 2016). In the immediate future, the Transiting Exoplanet Survey Satellite (TESS) will likely discover dozens to hundreds of potentially habitable worlds, a handful of which could be amenable to atmospheric characterization by JWST (Sullivan et al. 2015; Barnes et al. 2015). In this section, I calculate the tidal evolution of the predicted sample provided by Sullivan et al. (2015), which convolved realistic models for the detector, stellar models and variability, planet occurrence rates from Kepler, etc., to produce a hypothetical catalog of detected exoplanets and their properties. I find that nearly every potentially habitable planet it will discover will be tidally locked.

Figure 10 shows the results of these simulations for the “long” cases, i.e., these represent a maximum timescale for these planets to tidally lock, assuming that they are terrestrial. Nearly every planet tidally locks within 1 Gyr for both models. Table 1 lists the planets that are predicted to be single (at least in terms of those that can be discovered), and Table 3 (available in Online Supplement) lists those planets that would be known to be in multiple planet systems. In principle, any of these predicted planets could be in a high eccentricity state, but those that are known to be in multiple systems may be more likely to have eccentricities that are sufficiently perturbed by companions to force the rotation rate into a spin–orbit resonance.

Table 1 Orbital and physical parameters for projected isolated exoplanets from TESS

4 Discussion and conclusions

Previous studies of the tidal evolution of habitable exoplanets identified those orbiting M dwarfs as the most likely, or perhaps only, candidates for synchronous rotation, but this study has shown that the CPL model predicts that planets orbiting in the HZ of solar–mass stars may also be synchronously rotating. Figure 11 compares the results of Kasting et al. (1993) to the extreme contours of Fig. 6 and shows that the Kasting et al. (1993) prediction is close to the innermost “tidal lock radius” found in this study. As recent simulations of planet formation have found that initial rotation periods between 10 h and 40 days are approximately equally likely (Miguel and Brunini 2010), the tidal lock radius of Kasting et al. (1993) is now seen to be based on a very short initial rotation period. The above calculations only considered initial rotation periods up to 10 days, and so those results are still conservative—tidal locking may be even more likely than presented here, let alone than in Kasting et al. (1993).

As astronomers develop technologies to directly image potentially habitable planets orbiting FGK dwarfs (e.g., Dalcanton et al. 2015), they must be prepared for the possibility that planets orbiting any of them may be tidally locked. Such a rotation state can change planetary climate, and by extension the reflected spectra. 3D models of synchronously rotating habitable planets should be applied to planets orbiting K and G dwarfs in addition to Ms. While not explicitly considered here, habitable worlds orbiting brown dwarfs and white dwarfs are even more likely to be synchronous rotators, but their potential habitability is further complicated by the luminosity evolution of the central body (Barnes and Heller 2013).

Current technology favors the detection of habitable planets that orbit close to their host star, and hence, the planets are more likely to be tidally locked than Earth. This expectation is borne out by the simulations presented in Sect. 3. Proxima b will be a prime target for future observations, and it is almost assuredly tidally locked, and it is highly likely that all potentially habitable TESS planets will be tidally locked. The JWST telescope may be able to spectroscopically characterize the atmosphere of a few TESS planets, and so any biosignature search should consider the role of tidal locking.

Fig. 11

A comparison of the HZ and the extreme limits for tidal locking obtained in this study and Kasting et al. (1993). The gray regions are the HZ as shown in previous figures. The dashed red curve is the tidal lock radius for the model used by Kasting et al. (1993) (Earth–mass, 13.5-day period, 4.5 Gyr age). The dotted black line is for the CTL model and a 1 Earth-mass planet with an initial spin period of 8 h, an initial obliquity of $60^\circ$, and an age of 1 Gyr. The solid black line is for the CPL model and a 1 Earth-mass planet with an initial spin period of 10 days, an obliquity of 0, and an age of 10 Gyr

Both the CPL and CTL models predict that fast rotation can cause eccentricity growth, but in most cases such growth is modest, acting primarily to delay circularization. This delay can be significant, and thus, studies that use current orbits to estimate tidal parameters (Jackson et al. 2008; Matsumura et al. 2010) may incorrectly constrain the dissipation rates because they did not take into account the role of rotation. The initial rotation rate is unknown in the vast majority of cases, and so constraining the orbital history of a planet that is currently on a circular orbit and synchronously rotating is very challenging.

For , the exoplanet is likely to be trapped in a 1:1 spin–orbit resonance (Rodríguez et al. 2012), as is the case for Earth’s Moon with $e=0.05$. However, the position of the host body will not be fixed in the sky, but will librate due to the changing orbital angular velocity and the torques that try to drive the tidally locked body into a super-synchronous state (Makarov et al. 2016). Given the propensity of M dwarf planets to be multiple (Ballard and Johnson 2016), planets in their HZs will likely have nonzero eccentricities due to mutual gravitational perturbations. Thus, the climates of librating planets should be modeled to determine how libration affects the limits of habitability.

The role of rotation is critical for planetary habitability and could also be used to discriminate between tidal models. The results presented here show that a more thorough examination of the differences between the CPL and CTL model admits possibilities that could significantly impact our search for life in the universe. As astronomers have focused on discovering habitable exoplanets, a natural synergy will emerge between measuring rotation rates and constraining tidal evolution. When numerous planetary rotation rates of habitable exoplanets have been measured, the nature of tidal evolution may also be revealed.