Turbulence Characteristics Across a Range of Idealized Urban Canopy Geometries

Abstract

Good representation of turbulence in urban canopy models is necessary for accurate prediction of momentum and scalar distribution in and above urban canopies. To develop and improve turbulence closure schemes for one-dimensional multi-layer urban canopy models, turbulence characteristics are investigated here by analyzing existing large-eddy simulation and direct numerical simulation data. A range of geometries and flow regimes are analyzed that span packing densities of 0.0625 to 0.44, different building array configurations (cubes and cuboids, aligned and staggered arrays, and variable building height), and different incident wind directions ($0^\circ$ and $45^\circ$ with regards to the building face). Momentum mixing-length profiles share similar characteristics across the range of geometries, making a first-order momentum mixing-length turbulence closure a promising approach. In vegetation canopies turbulence is dominated by mixing-layer eddies of a scale determined by the canopy-top shear length scale. No relationship was found between the depth-averaged momentum mixing length within the canopy and the canopy-top shear length scale in the present study. By careful specification of the intrinsic averaging operator in the canopy, an often-overlooked term that accounts for changes in plan area density with height is included in a first-order momentum mixing-length turbulence closure model. For an array of variable-height buildings, its omission leads to velocity overestimation of up to $17\%$. Additionally, we observe that the von Kármán coefficient varies between 0.20 and 0.51 across simulations, which is the first time such a range of values has been documented. When driving flow is oblique to the building faces, the ratio of dispersive to turbulent momentum flux is larger than unity in the lower half of the canopy, and wake production becomes significant compared to shear production of turbulent momentum flux. It is probable that dispersive momentum fluxes are more significant than previously thought in real urban settings, where the wind direction is almost always oblique.

1 Introduction

Urban canopies are highly heterogeneous with unsteady three-dimensional flow. To represent such heterogeneity, particularly in larger-scale simulations that cannot explicitly resolve microscale flow characteristics, parametrizations of turbulence, drag, and surface energy exchange are required (e.g., Masson 2006; Salamanca et al. 2010; Grimmond et al. 2011; Krayenhoff et al. 2014, 2020). These parameterizations of urban canopy processes are critical in air quality models (AQMs) and numerical weather prediction (NWP) models, both to reliably predict pollution concentration, temperature, and wind speed in urban areas, and to provide a lower boundary condition to the larger-scale flow. Modelled urban-flow characteristics are also required to inform effective urban planning aimed at mitigating pollution and heat exposure, providing crucial foundations in epidemiological studies.

The simplest approaches to incorporating the influence of the urban canopy on turbulent exchange are based on using bulk morphological surface characteristics or micrometeorological methods to determine aerodynamic roughness length $z_0$ and displacement height d, which in turn are used in Monin–Obukhov similarity theory (MOST) (Grimmond and Oke 1999). Most mesoscale NWP models now employ single-layer urban canopy models where the exchange between the air and the urban facets is calculated according to MOST, and the contributions from the facets are combined using aerodynamical resistance networks and coupled at the first atmospheric level above the canopy (Masson 2000; Kusaka et al. 2001; Porson et al. 2010).

Multi-layer urban canopy models have several layers within the canopy and form part of the NWP boundary-layer scheme, rather than the surface-layer scheme, with coupling between the two at every layer (Martilli et al. 2002; Kondo et al. 2005; Schoetter et al. 2020). This avoids the use of simple relations such as exponential velocity profiles to extrapolate down from the bottom atmospheric level and predict values within the canopy. The time- and horizontally space-averaged (double-averaged) equations of motion are solved with terms explicitly representing turbulence and form drag, enabling a more physically based parametrization. Multiple levels within the canopy also in theory enable multiple sources (for example, of anthropogenic emissions) and two-way exchanges with the built environment at multiple heights.

The multi-layer approach becomes increasingly appealing as NWP and climate models move to sub-kilometre horizontal grid lengths (Barlow et al. 2017; Lean et al. 2019), where neighbourhood scale surface characteristics start to become resolved. The building geometry and flow becomes more statistically homogeneous within each model grid cell (unless there are wakes from isolated tall buildings), consistent with solving double-averaged equations. NWP systems that are coupled to multi-layer urban canopy models have been shown to give improved wind-speed and temperature prediction in the canopy in comparison with simple MOST surface representations (Gutiérrez et al. 2015), and also compared to single-layer urban canopy models in the case of temperature (Salamanca et al. 2011).

Much of the inspiration for urban canopy turbulence and drag parametrization development has come from the vegetation canopy literature. The vegetation canopy-top shear layer is viewed as a plane mixing layer (Raupach et al. 1996), where the drag of the canopy elements reduces the flow velocity below the canopy-top and causes an inflection in the double-averaged velocity profile, which in turn generates Kelvin–Helmholtz waves. The latter themselves undergo secondary instabilities that lead to the formation of large three-dimensional eddies. Vegetation canopy elements are usually either very close together (for example in wheat crops) or form a porous mesh (for example the foliage in a rainforest crown), so the mixing-layer eddies generated at canopy top are much larger than the separation of canopy elements (Raupach et al. 1996). These eddies are not local to the canopy elements and are the dominant turbulent motions in the canopy, a point that supports the use of a constant turbulent length scale in vegetation canopy models (Finnigan 2000; Harman and Finnigan 2007; Finnigan et al. 2015).

There are distinct differences between urban and vegetation canopies. The shear generated at the top of urban canopies is more local to the canopy elements than in vegetation canopies (Coceal et al. 2007a). Also, flow separation occurs at the edges of buildings causing vortex shedding and sometimes also turbulent flapping motions at canopy top (Coceal et al. 2007b; Perret and Savory 2013). In current urban canopy models that solve the double-averaged equations, a constant turbulent length scale is often used throughout the entire depth of the canopy (Santiago and Martilli 2010; Schoetter et al. 2020), and the mixing-layer analogy is sometimes used as justification (Hamdi and Masson 2008). To evaluate this assumption, the extent to which canopy top mixing-layer-type turbulence contributes to momentum transport within different urban canopy geometries requires investigation.

Additionally, the solid fraction in urban canopies is typically much larger than in vegetation canopies. The flow has to deviate more around the obstacles, and time-averaged flow patterns exhibit appreciable dispersive transport of momentum, which is distinct from turbulent transport. A recent study of a realistic urban canopy geometry conducted by Giometto et al. (2016) found that the dispersive momentum flux (DMF) can be as significant as the turbulent momentum flux (TMF), which is greater than previously thought. Also, Schmid et al. (2019) argue that, due to the non-negligible solid fraction of the urban canopy, more attention needs to be paid to the formal definition of the spatial average operator. When the intrinsic spatial average (an average only within the fluid volume) is applied to vertical derivatives of flow quantities, a generally overlooked term appears that accounts for changing solid fraction with height (see Sect. 3.2). The importance of including this term in urban canopy turbulence closures for velocity prediction needs to be investigated.

Despite its well-known limitations, a first-order momentum mixing-length turbulence closure approach has been successfully applied in vegetation canopies (Poggi et al. 2004; Harman and Finnigan 2007), and is simple and flexible, requiring no extra prognostic equations. We take inspiration from this pragmatic approach and in Sect. 3.4 formulate a momentum mixing-length closure suitable for urban canopies, which, following Schmid et al. (2019), accounts for the non-negligible urban solid fraction.

There have been various investigations of turbulent and dispersive momentum transport in urban canopies (e.g., Roth 2000; Belcher 2005; Coceal et al. 2007a; Takimoto et al. 2011; Nazarian et al. 2020), but this study is unprecedented in the range of large-eddy simulation (LES) and direct numerical simulation (DNS) datasets available. We take advantage of this rich source of data to: (1) characterize the momentum mixing-length behaviour in the urban surface layer and propose a general momentum mixing-length profile suitable for a wide range of urban flows (Sects. 4.1–4.5), (2) determine the impact on predicted velocity when the term accounting for solid fraction height variation is included within the turbulence closure (Sect. 4.6), (3) test the mixing-layer analogy for turbulence within urban canopies (Sect. 4.7), and (4) explain the differences in DMF characteristics across geometries to motivate future DMF parametrizations (Sect. 4.8).

2 Computational Fluid Dynamics Datasets

2.1 Large-Eddy Simulations

The analysis draws primarily on LES datasets described in Nazarian et al. (2020). A suite of simulations were carried out for idealized urban-like staggered and aligned arrays of cubes of uniform height. The flow was oriented perpendicular to the array, and the stratification was neutral. The cases we study have packing densities (planar area fraction occupied by obstacles) $\lambda _p=$ 0.0625, 0.11, 0.16, 0.25, 0.35, 0.44 for staggered cubes, and $\lambda _p=$ 0.0625, 0.44 for aligned cubes. A summary of the LES datasets is given in Table 1. Schematics in Fig. 1a, b are illustrative of the aligned and staggered geometries respectively. The simulations were performed using the Parallelized Large-Eddy Simulation Model (PALM) which solves the non-hydrostatic incompressible Boussinesq equations (Raasch and Schröter 2001; Letzel et al. 2008; Maronga et al. 2015). The subgrid turbulence parametrization is based on a 1.5-order closure (Deardorff 1980) that involves solving the subgrid scale (SGS) turbulence kinetic energy (TKE) equation.

The flow is driven by a constant pressure gradient force $F_p=\rho u_{\tau }^2/H$, where $\rho$ is the density of dry air (taken to be 1 kg m$^{-3}$), $u_\tau \approx 0.21$ m s$^{-1}$ is the wall friction velocity, $H=7.4h$ is the domain height, and h is the mean average height of the obstacles. The grid length in the x, y, and z directions, ${\Delta }_{xyz}$, is equal to h/32, except above $z=4h$ where ${\Delta }_{z}$ slowly increases.

The Reynolds number of the flow is $Re = U h / \nu \approx 10^6$, which is in the fully rough regime. Here U is the velocity at the top of the domain and $\nu$ is the molecular viscosity of air. It has been demonstrated using LES that flow through cube arrays only has a weak dependency on Re between $5\times 10^3$ and $5\times 10^6$ (Xie and Castro 2006). For momentum the boundary conditions are no-slip at the ground and building surfaces, free-slip at the domain top, and periodic in the horizontal. Spin-up time is $125 h/u_\tau$, and data are output every 20 timesteps, which corresponds to a time interval of 40 s or $0.46 h/u_\tau$. The time-averaging interval is $250 h/u_\tau$. The time-averaged data are also ensemble averaged over repeating units to effectively increase the averaging time.

Table 1 LES and DNS datasets: prefixes N, B, and C represent data from Nazarian et al. (2020), Branford et al. (2011), and Castro et al. (2017) respectively. Under “Case” numbers correspond to $\lambda _p$, S and A denote staggered and aligned respectively, and cb and cd denote cubes and cuboids respectively

Fig. 1

Plan view of selected geometries—(a) the $\lambda _p=0.25$ aligned and (b) staggered cube geometries, and (c) $\lambda _p=0.33$ aligned cuboid geometry. The large black arrows denote the $0^\circ$ and $45^\circ$ driving-flow directions. Note that only a subsection of the domains is shown here

2.2 Direct Numerical Simulations

Several DNS datasets are included in the analysis as summarized in Table 1. Unlike in the LES approach, there is no subgrid parametrization in DNS and turbulent scales are resolved through the majority of the dissipation spectrum. As seen in Table 1, a compromise is made by reducing Re due to computational demands.

Branford et al. (2011) conducted simulations of flow through an aligned array of $\lambda _p=0.25$ cubes (see Fig. 1a for a schematic). Castro et al. (2017) documented simulations for an aligned array of $\lambda _p=0.33$ cuboids, with cuboid length-to-width ratio of 1/2 and height-to-length ratio of 1, where the long faces were orientated perpendicular to the flow (see Fig. 1c for a schematic). Both studies had neutral stratification, and forcing flow directions of $0^\circ$ and $45^\circ$ to the normal of the building faces. Throughout the entirety of each domain ${\Delta }_{xyz}=h/32$. All time-averaged data are also ensemble-averaged over repeating units.

3 Double-Averaging Theory

In this section the double-averaged momentum equation and first-order momentum mixing-length closure parametrization of the TMF term are given. The definitions of the spatial average operator and spatial averaging theorem are first presented, since they are necessary in deriving budget equations and parametrizations. The intrinsic first-order momentum mixing-length closure is used in later sections to investigate its use as an urban canopy turbulence closure model and to explore the turbulence behaviour across different canopy geometries. Equations are given using the intrinsic average and comprehensive average (where the spatial average is done over the fluid and solid volume). Following Schmid et al. (2019), the importance of representing $\lambda _p$ height variation in the turbulence closure for predicted values of velocity is investigated in the context of both horizontal averaging approaches (see Sect. 4.6).

3.1 Intrinsic and Comprehensive Averaging

In NWP models flow through canopies is often modelled at grid lengths much larger than the typical turbulent eddies and obstacle wakes. An increasingly common approach in such circumstances is to apply to the instantaneous equations temporal averaging over a longer interval than the time scale of the slowest eddies and spatial averaging over a length scale greater than the largest spatial deviations in the flow (Raupach and Shaw 1982; Nikora et al. 2007; Martilli and Santiago 2007). A one-dimensional representation is taken, assuming quasi-horizontal homogeneity of the flow and canopy geometry within vertically thin horizontal-averaging slabs. Terms arise representing the effects of turbulence, form drag, and persistent flow structures on vertical transport of momentum and scalars, and can subsequently be parametrized.

In vegetation canopies the obstacles are considered to occupy a negligible fraction of the canopy, and the comprehensive average (also known as the superficial or extrinsic average) and intrinsic average are equivalent (Finnigan 2000). In porous media hydrodynamics, as in urban canopies, the volume fraction occupied by obstacles can be more significant. At any given height it is proportional to $\lambda _p$ and it is well known that vertical changes in $\lambda _p$ should be treated when applying the spatial average operator (Nikora et al. 2007).

The use of the operators $\langle \phi \rangle$, ${\overline{\phi }}$, ${\tilde{\phi }}$, and $\phi '$, on a variable $\phi$ defined only within the fluid region, denote its horizontal spatial average, time average, dispersive fluctuations (${\tilde{\phi }}={\overline{\phi }}-\langle {\overline{\phi }}\rangle$), and turbulent fluctuations ($\phi '=\phi - \langle {\overline{\phi }}\rangle$), respectively. The intrinsic and comprehensive spatial operators are defined by Whitaker (1999) as

$$\begin{aligned} \langle \phi \rangle _I(t,z) = \frac{1}{V_f}\int _{x,y,z\in V_f} \phi (t,x,y,z) \,dV, \end{aligned}$$

(1)

and

$$\begin{aligned} \langle \phi \rangle _C(t,z) = \frac{1}{V}\int _{x,y,z\in V_f} \phi (t,x,y,z) \,dV, \end{aligned}$$

(2)

respectively. Here x, y, and z are spatial coordinates with z in the vertical, and t is time: $\epsilon (z)=1-\lambda _p(z)$ is the fluid fraction: the ratio of fluid volume within a thin horizontal-averaging slab, $V_f$, to the total volume of the slab including the solid volume, V. The relationship between the comprehensive (subscript C) and intrinsic (subscript I) average of a quantity $\phi$ is given by $\langle \phi \rangle _C = \epsilon \langle \phi \rangle _I$.

The application of the comprehensive operator twice results in $\langle \langle \phi \rangle _C\rangle _C=\epsilon \langle \phi \rangle _C$, whereas for the intrinsic operator $\langle \langle \phi \rangle _I\rangle _I=\langle \phi \rangle _I$. This means factors of $\epsilon$ appear in parametrizations of comprehensive spatially-averaged quantities when they are functions of spatially-averaged parameters.

The comprehensive averaging approach has a disadvantage when used to compute dispersive fluctuations (${\tilde{\phi }}$) of a variable $\phi$, since interpretation of quantities involving dispersive fluctuations can become more difficult (Schmid et al. 2019). When $\langle {{\overline{\phi }}}\rangle _C$ is non-zero, ${\tilde{\phi }}$ is non-zero in the building region. The dispersive flux due to the correlation of two such variables can then also be non-zero in the building region, which is physically unintuitive. In the context of parametrizing vertical dispersive momentum (and scalar) fluxes the issue is not important. They involve ${\tilde{w}}$, and $\langle {{\overline{w}}}\rangle _C=0$ due to mass continuity, so they are zero in the building region. However, some terms in higher-order turbulence parametrization schemes (e.g., wake production of TKE) involve dispersive fluctuations, and in the comprehensive averaging framework would be non-zero in the building region, thus complicating their parametrization.

There has been some debate in the recent literature on whether the intrinsic or comprehensive spatial average should be used in urban canopy modelling (Xie and Fuka 2018; Schmid et al. 2019; Sützl et al. 2021). The double-averaged momentum equation (and budget equations in general) derived using either method are equally valid if obtained correctly. Equivalently to solving the intrinsic double-averaged momentum equation, one could solve the comprehensive double-averaged momentum equation using parameters that have also been derived using the comprehensive average, and then convert the predicted comprehensive velocity to the intrinsic velocity via division by $\epsilon (z)$. Intrinsic average values are used here since they are more directly representative of the fluid and hence easier to interpret physically. However, neither spatial averaging approach is being advocated in a parametrization context.

3.2 Spatial Averaging Theorem

The relation between averages of spatial derivatives and spatial derivatives of averages is given by the spatial averaging theorem (Whitaker 1999). For intrinsic averages

$$\begin{aligned} \left\langle \frac{\partial \phi }{\partial x_i} \right\rangle _I = \frac{\partial \langle \phi \rangle _I}{\partial x_i} + \frac{\langle \phi \rangle _I}{\epsilon } \frac{\partial \epsilon }{\partial x_i} + \frac{1}{V_f} \iint _{S_{\mathrm{int}}} \phi n_i \,dS, \end{aligned}$$

(3)

and for comprehensive averages

$$\begin{aligned} \left\langle \frac{\partial \phi }{\partial x_i}\right\rangle _C = \frac{\partial \langle \phi \rangle _C}{\partial x_i} + \frac{1}{V} \iint _{S_{\mathrm{int}}} \phi n_i \,dS, \end{aligned}$$

(4)

where $x_i$ ($x_1=x$, $x_2=y$, $x_3=z$) is spatial location, $S_\mathrm{int}$ is the interface between the fluid and solid regions, and $n_i$ is the unit vector normal to the interface directed from fluid to solid.

The first term on the right-hand side (r.h.s.) of Eq. 3 is the spatial derivative of the intrinsic average $\phi$. The second and third terms account for variations in $\epsilon$ (i.e., changes in averaging volume) and discontinuities in flow properties over the surface of obstacles respectively. The second term does not appear in Eq. 4 since the comprehensive averaging region does not change with height. The first and second terms in the comprehensive spatial averaging theorem have equivalent interpretations to the first and third terms in the intrinsic spatial averaging theorem.

For horizontal derivatives ($i=1,2$), the second term on the r.h.s. of Eq. 3 is zero, since the canopy is assumed horizontally homogeneous within the averaging region, so that $\epsilon$ is only a function of z. The third term also vanishes for horizontal derivatives if $\phi$ is constant at the fluid–solid interface, as is the case for velocity due to the no-slip boundary condition. However, for example, pressure is variable at the interface, tending to be larger at the windward than leeward obstacle faces. It is the discontinuity in the pressure field over obstacles that gives rise to form drag.

For vertical derivatives ($i=3$), the second term on the r.h.s. of Eq. 3 is non-zero everywhere that $\epsilon (z)$ varies and $\langle \phi \rangle _I \ne 0$. The third term on the r.h.s. is only zero for vertical derivatives of quantities like velocity, where $\phi =0$ at the vertical facing interfaces. Unlike when calculating horizontal derivatives for the $x{-}z$ and $y{-}z$ plane interfaces, when calculating vertical derivatives for the $x{-}y$ plane interfaces there are no adjacent fluid–solid interfaces. Therefore, the third term on the r.h.s. cannot have cancellation of adjacent interfaces, and is non-zero so long as $\phi >0$.

3.3 Double-Averaged Momentum Equation

The approach of solving the double-averaged momentum equations in canopies was first developed by Wilson and Shaw (1977) and Raupach and Shaw (1982). The influence of changing solid fraction was treated as negligible in the context of vegetation canopies, where comprehensive and intrinsic averaged values are approximately equal.

The double-averaged momentum equation can be obtained by first applying the time-averaging operator to the instantaneous momentum equation to obtain the time-averaged momentum equation, then applying the spatial averaging operator, taking particular care with use of the spatial averaging theorem. The intrinsic and comprehensive double-averaged momentum equations for a statistically stationary, horizontally homogeneous flow at height z in the canopy are given by (Schmid et al. 2019)

$$\begin{aligned} \frac{\partial \langle \overline{u'_iw'}\rangle _I + \langle {\tilde{u}}_i{\tilde{w}}\rangle _I}{\partial {z}} + \frac{1}{\epsilon }\left( \langle \overline{u'_iw'}\rangle _I + \langle {\tilde{u}}_i{\tilde{w}}\rangle _I\right) \frac{\partial \epsilon }{\partial z} = \langle F_p \rangle _I -\frac{1}{\rho } \left\langle \frac{\partial {\tilde{p}}}{\partial x_i}\right\rangle _I, \end{aligned}$$

(5)

and

$$\begin{aligned} \frac{\partial \langle \overline{u'_iw'}\rangle _C + \langle {\tilde{u}}_i{\tilde{w}}\rangle _C}{\partial {z}} = \langle F_p \rangle _C -\frac{1}{\rho } \left\langle \frac{\partial {\tilde{p}}}{\partial x_i}\right\rangle _C, \end{aligned}$$

(6)

respectively. Here $\rho$ is the density of dry air, p is pressure, $F_p$ is a volumetric body force driving the flow and $u_i$ are velocity components ($u_1=u$, $u_2=v$, $u_3=w$). It has been assumed that atmospheric stability is neutral, that the Coriolis force and molecular transport are negligible, and that the viscous drag can be neglected since it is usually only a few percent of the total drag, as discussed in Leonardi and Castro (2010).

The first and second terms on the left-hand sides (l.h.s.) of Eqs. 5 and 6 are the gradients of the TMF and DMF respectively. They are generally negative within the canopy, while above the canopy the TMF gradient is positive and the DMF gradient can be positive or negative but becomes negligible in the inertial sublayer.

The third and fourth terms on the left-hand side of Eq. 5, which are not usually included in urban canopy literature, appear due to the second term on the r.h.s. of Eq. 3. When $\epsilon (z)$ increases with height, vertical momentum transport occurs through a larger cross-sectional area, and consequently the intrinsic averaged TMF and DMF decrease. The extra terms act to increase the contribution of the intrinsic averaged vertical TMF and DMF gradients to the double-average momentum equation, when momentum transport occurs through increasing cross-sectional area with height.

The first term on the r.h.s. of Eqs. 5 and 6 is a body force applied uniformly throughout the fluid and drives the flow in the computational fluid dynamics (CFD) simulations. It is noted here that a mean streamwise pressure gradient is not actually present within the fluid in the CFD simulations, so $\langle F_p \rangle$ does not arise from spatial averaging of the time-averaged pressure gradient term, $-(1/\rho ) \partial {\overline{p}} / \partial x_i$, and should be included as a separate term in the instantaneous momentum equation when deriving Eq. 5. The second term on the r.h.s. of Eqs. 5 and 6 is the form drag exerted by the obstacles and is the sink of momentum in the canopy. It appears after spatial averaging of the time-averaged pressure gradient term.

3.4 Parametrization of Momentum Fluxes

K-theory is often used to parametrize the TMF term in Eqs. 5 and 6. The momentum eddy-diffusivity $K_{m,i}$ can be represented using a first-order momentum mixing-length-closure approach, where $l_{m,i}$ is the momentum mixing length. It is well known that Prandtl-mixing-length-type turbulence closures break down when applied to the local flow in urban canopies, for example, due to counter-gradient momentum transport in building wakes. The momentum mixing-length closure is therefore formulated in terms of horizontally-averaged properties of the flow, so that for intrinsic averages

$$\begin{aligned} \begin{aligned} \langle \overline{u_i'w'}\rangle _I = -\langle K_{m,i} \rangle _I \left\langle \frac{\partial {\overline{u}}_i}{\partial z} \right\rangle _I&= -\langle l_{m,i} \rangle _I^2 \left| \left\langle \frac{\partial {\overline{u}}_i}{\partial z} \right\rangle _I\right| \left\langle \frac{\partial {\overline{u}}_i}{\partial z} \right\rangle _I \\&= -\langle l_{m,i} \rangle _I^2 \left| \frac{\partial \langle {\overline{u}}_i\rangle _I}{\partial z} + \frac{\langle {\overline{u}}_i\rangle _I}{\epsilon }\frac{\partial \epsilon }{\partial z} \right| \left( \frac{\partial \langle {\overline{u}}_i\rangle _I}{\partial z} + \frac{\langle {\overline{u}}_i\rangle _I}{\epsilon }\frac{\partial \epsilon }{\partial z} \right) , \end{aligned} \end{aligned}$$

(7)

and for comprehensive averages

$$\begin{aligned} \begin{aligned} \langle \overline{u_i'w'}\rangle _C = -\frac{1}{\epsilon } \langle K_{m,i} \rangle _C \langle \frac{\partial {\overline{u}}_i}{\partial z} \rangle _C = -\frac{1}{\epsilon ^3} \langle l_{m,i} \rangle _C^2 \left| \frac{\partial \langle {\overline{u}}_i\rangle _C}{\partial z} \right| \frac{\partial \langle {\overline{u}}_i\rangle _C}{\partial z}. \end{aligned} \end{aligned}$$

(8)

$\langle K_{m,i} \rangle$ and $\langle l_{m,i} \rangle$ are parameters representing the global properties of the flow at height z. The modulus operators ensure $\langle K_{m,i} \rangle$ is positive and that turbulent diffusion is only down-gradient. The $\epsilon$ terms in Eq. 7 occur due to the second term on the r.h.s. of the intrinsic spatial averaging theorem; $\epsilon ^{-3}$ occurs in Eq. 8 to balance the number of comprehensive spatial averaging operator applications on the l.h.s. and r.h.s., accounting for the zeros introduced into the horizontal average by the building volume.

Schmid et al. (2019) derived the same intrinsic and comprehensive mixing-length closures (although without the modulus operator). However, they started from application of the horizontal averaging operator to parameters representing the local flow. Following use of their Eqs. 10 and 11, the derivation involved neglecting correlations between spatial fluctuations of $l_{m}$ (${\tilde{l}}_{m}$), and between ${\tilde{l}}_{m}$ and spatial fluctuations of $\partial \langle {\overline{u}}\rangle / \partial z$. This implies that our approach of starting from global properties of the flow assumes spatial fluctuations are small or terms involving them largely cancel.

3.5 Application to Urban Canopy Geometry

The $i=1$ and $i=2$ components of double-averaged flow properties (e.g., $\langle {\overline{u}} \rangle$ and $\langle \overline{u'w'} \rangle$, and $\langle {\overline{v}} \rangle$ and $\langle \overline{v'w'} \rangle$) in general take different values, except in the special case when the canopy has lateral symmetry and the driving flow has equal components in the x and y axes. As an approximation one could use the same turbulent parameters in both axes, and derive them with the x axis aligned with the driving flow direction. However, given urban morphology information such as the frontal area variation with driving flow angle, it is conceivable that parametrizations might be developed that account for flow direction relative to the two axes. We therefore analyze separately the $i=1$ and $i=2$ TMF components.

In real-world urban canopies the double-averaged flow properties are never exactly the same along the two axes, but the $0^\circ$ driving flow and B-25-A-$45^\circ$ simulations are special cases for which subscript i can be dropped from $\langle l_m \rangle$ and $\langle K_m \rangle$. In the $0^\circ$ driving-flow simulations turbulence is not the same in the two axes but $\langle \overline{v'w'}\rangle \approx 0$ so the $i=2$ component of the turbulent momentum flux need not be represented. For B-25-A-$45^\circ$ the canopy is symmetric about the driving-flow direction and the driving flow has equal components in the x and y axes, so that $\langle l_{m,1} \rangle =\langle l_{m,2} \rangle$ and $\langle K_{m,1} \rangle =\langle K_{m,2} \rangle$. In this study the $i=1$ and $i=2$ components only need to be retained for C-33-A-$45^\circ$ where the geometry is asymmetric about the streamwise axis.

A pragmatic approach to parametrizing the DMF is to include it with the TMF on the l.h.s. of Eq. 7 (Simón-Moral et al. 2017; Nazarian et al. 2020). Horizontally-averaged DMF can be negative or positive at different heights within the canopy, but when summed with the horizontally-averaged TMF the total tends to be negative. The DMF can thereby be parametrized using K-theory but avoiding the unphysical scenario where $\langle K_m \rangle$ becomes negative, which would occur if the DMF was parametrized separately.

K-theory assumes that turbulent fluctuations are related to local gradients. Although it seems plausible that downward transport of momentum from higher in the canopy leads to increased velocity lower in the canopy, it has not been demonstrated that there is a strong relation between DMF and local velocity gradients in urban canopies. Time-averaged motions might largely be determined by non-local forcings. For example recirculations within building wakes often span the entire depth of the canopy, and are likely largely driven by strong shear at roof level behind the buildings, rather than local velocity gradients within the wake. An analogy can be drawn from two-dimensional street canyon literature where it is well known that recirculation within the canyon can be modelled as solid body rotation (Caton et al. 2003). Recirculation is driven by the flow above the canyon and occurs due to the requirements that tangential stresses be continuous at cavity top, and mass within the cavity be conserved. Flows in urban canopies consisting of cuboidal buildings are more three-dimensional in nature, and streamlines can diverge in the spanwise direction within building wakes, but it seems reasonable to assume that canopy recirculations share some properties with two-dimensional street canyons.

Since the aim is for the first-order turbulence parametrization presented here to be applicable to multi-layer urban canopy models in general and to analyze the turbulent flow properties using $\langle l_m \rangle$, it is chosen not to include the DMF in the turbulence closure; $\langle l_m \rangle$ can be interpreted as a length scale that describes only the turbulence. The horizontal-average and three-dimensional characteristics of the DMF are investigated across geometries in Sect. 4.8, as a first step towards developing separate parametrizations of DMF.

4 Results and Discussion

4.1 Mixing Length Within the Canopy

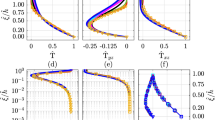
It is investigated whether $\langle l_m \rangle _I$ (calculated using Eq. 7) shares similar characteristics within the canopy across different idealized urban geometries and driving-flow directions. Figures 2 and 3 correspond to the $0^\circ$ and $45^\circ$ driving flow datasets, respectively. In both figures, plots a–e correspond to intrinsic average profiles of velocity, TMF, DMF, the ratio of DMF to TMF and momentum mixing length, respectively. Figure 2f shows $\langle l_m \rangle _I$ normalized by the maximum mixing length $\langle l_{m} \rangle _I^{{\max }}$ within the canopy. The DMF profiles are discussed later in Sect. 4.8.

4.1.1 $0^\circ$ Driving Flow Mixing Length Characteristics

There is some collapse in the $0^\circ$ simulation $\langle l_m \rangle _I$ profiles from Fig. 2e when normalized by $\langle l_{m} \rangle _I^{{\max }}$ in Fig. 2f. The shear is largest near the surface and at canopy top so that $\langle l_m \rangle _I$ is smaller there. $\langle l_{m} \rangle _I^{{\max }}$ occurs at $z/h\approx 0.6$, since the minimum gradient of double-averaged velocity tends to occur near the middle of the canopy (Fig. 2a), but the magnitude of TMF increases with height within the canopy (Fig. 2b). This description of $\langle l_m \rangle _I$ is consistent with Coceal et al. (2006) for a $\lambda _p=0.25$ staggered cube dataset and is qualitatively similar to the turbulent length scales presented in Fig. 9a of Nazarian et al. (2020).

Fig. 2

Intrinsic double-averaged profiles of the $0^{\circ }$ driving flows. (a) x-component of velocity, (b) TMF, (c) DMF, (d) ratio of DMF to TMF, (e) $\langle l_m\rangle _I/h$, and (f) $\langle l_m\rangle _I/\langle l_{m} \rangle _I^{{\max }}$

From Fig. 2e it can be seen that $\langle l_{m} \rangle _I^{{\max }}$ does not vary monotonically with $\lambda _p$ for either the aligned or staggered geometries. This has also been observed for staggered geometries when turbulent length scales are calculated with the sum of DMF and TMF, as presented by Nazarian et al. (2020); $\langle l_{m} \rangle _I^{{\max }} \approx 0.3$ across the $0^\circ$ simulations apart from the N-11-S and N-16-S simulations which have $\langle l_{m} \rangle _I^{{\max }} \approx 0.43$.

The $\langle l_m \rangle _I$ peaks are broader for N-44-A, B-25-A-$0^\circ$ and C-33-A-$0^\circ$ than the other geometries since the double-averaged velocity profiles are approximately linear between $z/h=0.15{-}0.85$, so that the gradient of double-averaged velocity varies little in the middle of the canopy. The $0^\circ$ aligned simulations tend to have $\langle l_{m} \rangle _I^{{\max }}$ higher within the canopy than the $0^\circ$ staggered simulations, since the double-averaged velocity gradient (or shear) within the canopy does not increase significantly until very close to canopy top in the $0^\circ$ aligned simulations. For the same $\lambda _p$, the aligned geometries have larger double-averaged velocity and TMF than staggered geometries. The aligned geometries have unobstructed channelling regions (see Fig. 1a) where flow is fast and there is large shear, which promotes shear production of TMF.

The magnitude of TMF generally decreases with increasing $\lambda _p$ throughout the canopy as seen in Fig. 2b, particularly for the staggered geometries. A possible explanation is that increasing $\lambda _p$ results in less mean kinetic energy penetrating into the canopy, particularly for the staggered arrays where there is more flow obstruction, and therefore less conversion into TKE. TMF and TKE have broadly similar dependence on $\lambda _p$ and aligned versus staggered canopy geometry as seen from Fig. 6 of Nazarian et al. (2020).

Between $z/h=0.34-0.44$ the N-44-S simulation TMF just becomes positive so that flow is counter-gradient, and $\langle l_m \rangle _I$ cannot be computed. A first-order momentum mixing-length-closure approach is less suitable for very high-density idealized staggered arrays. Future investigations are required to explore whether this is the case in more realistic staggered type urban geometries, where there is more horizontal randomness in positioning of buildings.

The N-25-S, N-35-S and N-44-S simulations have negative double-averaged velocity near the surface as seen in Fig. 2a. Inspection of individual velocity profiles (not shown) indicates that regions of recirculation, both upstream of the windward and downstream of the leeward faces of the cubes, tend to have negative velocity near the surface. The N-25-S, N-35-S and N-44-S simulations have recirculation regions in a large portion of the flow. In these denser staggered configurations the contribution of negative near-surface flow in the recirculations dominates the spatial average. The aligned simulations have channelling regions where there is no obstruction of the flow, and there is large positive velocity near the surface. The contribution from such regions to the spatial average results in positive overall double-averaged velocity near the surface. The gradient of double-averaged velocity between the surface and the first grid point above the surface is negative in the N-25-S, N-35-S and N-44-S simulations, and along with TMF being positive above the surface (Fig. 2b), means that $\langle l_m \rangle _I$ at the first grid point above the surface cannot be computed, since transport is counter-gradient.

4.1.2 Impact of Flow Incidence Angle on Mixing-Length Characteristics

The $45^\circ$ driving-flow simulations in Fig. 3e have larger $\langle l_m \rangle _I$ in the canopy than their corresponding $0^\circ$ driving-flow simulations in Fig. 2e. Figure 3e shows that $\langle l_{m} \rangle _I^{{\max }}$ is largest for B-25-A-$45^\circ$, and is equal to 2.2h at $z/h=0.25$ (off the axis). This is unphysical considering that eddies cannot be so large due to the limiting effect of the ground, and the largest eddies are not expected to exceed h in any case. $\langle l_{m} \rangle _I^{{\max }}$ occurs at $z/h=0.31$ and $z/h=0.75$ for $\langle l_{m,1} \rangle _I$ and $\langle l_{m,2} \rangle _I$ respectively in the C-33-A-$45^\circ$ simulation. Since $\langle l_{m,1} \rangle _I$ and $\langle l_{m,2} \rangle _I$ are parameters describing the turbulence in the x and y directions, it is evident that turbulence characteristics can be significantly different in the two axes, when the geometry of the urban canopy is not diagonally symmetric.

Fig. 3

Intrinsic double-averaged profiles of the $45^{\circ }$ driving flows. (a–e) are the same as in Fig. 2 except that both $i=1$ and $i=2$ components are given for C-33-A-$45^\circ$. B-25-A-$45^\circ$ has only one curve because the canopy is symmetric about the flow direction, and the average of the $i=1$ and $i=2$ components is plotted

The $45^\circ$ driving flow $\langle l_m \rangle _I$ are large because the double-averaged velocity profiles (Fig. 3a) have small gradients (except near the ground and canopy top), but significant TMF (Fig. 3b). There are two possible explanations for significant TMF despite small shear (i) there is large transport of TMF down into the canopy (see Finnigan (2000), Eq. 2.11 for a definition) and (ii) there is large wake production of TMF. Either way, this indicates that a first-order momentum mixing-length-closure approach may be less appropriate for oblique flows, since the approach assumes TMF is related to (i) the local flow (implying TMF has not been transported) and (ii) vertical velocity gradients (but wake production involves vertical and horizontal gradients of spatial velocity fluctuations).

Shear production of TMF is given by

$$\begin{aligned} P_{s,ik} = -\langle \overline{u'_ju_k'}\rangle \frac{\partial \langle {\overline{u}}_i\rangle }{\partial x_j} -\langle \overline{u'_iu'_j}\rangle \frac{\partial \langle {\overline{u}}_k\rangle }{\partial x_j} -\frac{\langle \overline{u'_ju_k'}\rangle \langle {\overline{u}}_i\rangle + \langle \overline{u_i'u'_j}\rangle \langle {\overline{u}}_k\rangle }{\epsilon }\frac{\partial \epsilon }{\partial x_j}. \end{aligned}$$

(9)

The third term on the r.h.s. is a new term that does not appear in Eq. 2.11 of Finnigan (2000), and arises from accounting for changes in $\lambda _p$ with height, when applying the intrinsic spatial averaging operator to the time-averaged TMF budget equation. For uniform-height canopies it is only non-zero at canopy top. Wake production of TMF is due to correlations between spatial deviations in turbulent stresses and gradients of spatial deviations in velocity, typically caused by building wakes and deviation of the flow around buildings, and is given by

$$\begin{aligned} P_{w,ik} = -\langle \widetilde{u_j'u'_k}\frac{\partial {{\tilde{u}}_i}}{{\partial x_j}}\rangle - \langle \widetilde{u'_iu'_j}\frac{\partial {{\tilde{u}}_k}}{{\partial x_j}}\rangle . \end{aligned}$$

(10)

Plotted in Fig. 4a, b are the shear and wake production of TMF respectively, and Fig. 4c shows their ratio ($P_w/P_s$). The production of $\langle \overline{u'w'} \rangle _I$ is plotted for the $0^\circ$ driving flows, the production of $\langle \overline{u'w'} \rangle _I$ and $\langle \overline{v'w'} \rangle _I$ for C-33-A-$45^\circ$, and the average of the two components for B-25-A-$45^\circ$. All geometries have a large $P_s$ peak at canopy top, as expected due to the canopy-top shear layer. The staggered geometries and N-0625-A have a small $P_s$ peak near the surface because the double-averaged velocity gradient is large there, and is associated with flow reversal in the denser staggered cases. Between $z/h = 0.2 - 0.8$ the aligned geometries tend to have larger $P_s$ than the staggered geometries, particularly the denser ones. In general $P_w$ is positive near the ground (i.e., acts as a TMF sink), becomes negative and increases in magnitude with height within the canopy, then changes sign and has a positive peak at canopy top, before becoming negligible in the inertial sublayer. The largest outlier is N-44-S, which has positive $P_w$ in the middle of the canopy.

In vegetation canopies it is generally assumed that $P_s$ dominates $P_w$ (Raupach et al. 1986). However, from Fig. 4c it can be seen that this is not always the case for urban canopies, particularly for the $45^\circ$ driving flows, and away from the canopy top and ground where $P_s$ is smaller. The $45^\circ$ driving flows tend to have large DMF (as discussed in Sect. 4.8.2). It is unlikely that $P_w$ and DMF are both large by chance, since they are both associated with spatial fluctuations in the flow. Also, a key assumption in the arguments presented by Raupach and Shaw (1982) and Raupach et al. (1986) for $P_s$ dominating $P_w$, is that terms involving spatial deviations in the time-mean flow are negligible. This is often not true for urban canopies (as demonstrated for the case of DMF in Sect. 4.8.2).

In addition to the $45^\circ$ driving-flow simulations, N-44-S and C-33-A-$0^\circ$ have comparable magnitude $P_w$ and $P_s$ near the middle of the canopy. Like the $45^\circ$ driving-flow simulations (Fig. 3d), N-44-S has significant DMF compared to TMF (Fig. 2d) at heights where $P_w/P_s$ is largest. C-33-A-$0^\circ$ is the outlier in that it has small DMF (Fig. 2d) compared to TMF despite having large $P_w$. This shows that large $P_w$ is not always related to large DMF. As demonstrated in Sect. 4.8.1, urban canopies often have large local dispersive velocity correlations, whose sign may partially cancel upon horizontal averaging.

It has been demonstrated that wake production can have a large contribution to TMF, particularly when the flow is oblique to the building faces. Investigation of TMF transport is out of scope here.

Fig. 4

(a) Shear production of TMF, (b) wake production of TMF and (c) their ratio. The $i,k=1,3$ component is plotted for the $0^\circ$ driving flows, the $i,k=1,3$ and $i,k=2,3$ components are plotted for C-33-A-$45^\circ$, and the average of the two components is plotted for B-25-A-$45^\circ$

4.2 Mixing Length at Canopy Top

The behaviour of $\langle l_m \rangle _I$ at $z/h=1$ can be most easily understood in terms of comprehensively averaged variables. Rearranging Eq. 8 for $\langle l_{m,i} \rangle _C^2$, and substituting into $\langle l_{m,i} \rangle _I^2 = \langle l_{m,i} \rangle _C^2/\epsilon ^2$ gives

$$\begin{aligned} \begin{aligned} \langle l_{m,i} \rangle _I^2 = -\langle \overline{u_i'w'}\rangle _C \epsilon \bigg / \left( \left| \frac{\partial \langle {\overline{u}}_i\rangle _C}{\partial z} \right| \frac{\partial \langle {\overline{u}}_i\rangle _C}{\partial z}\right) . \end{aligned} \end{aligned}$$

(11)

At $z/h=1$ for a uniform-height canopy with perfectly flat roofs $\langle {\overline{u}}_i\rangle _C$ and $\langle \overline{u_i'w'}\rangle _C$ are continuous, and $\epsilon$ and $\partial \langle {\overline{u}}_i\rangle _C / \partial z$ are finite but discontinuous. $\partial \langle {\overline{u}}_i\rangle _C / \partial z$ increases at $z/h=1$ due to the sudden contribution of shear along the roofs, as opposed to beneath the roofs where there is no shear since ${\overline{u}}_i$ is not defined within the buildings. The discontinuities in $\epsilon$ and $\partial \langle {\overline{u}}_i\rangle _C / \partial z$ do not cancel, so that $\langle l_{m,i} \rangle _I$ is also discontinuous at $z/h=1$. Parametrizing $\langle l_m (h) \rangle _I$ for situations with flat-roofed buildings would be challenging. Rather than analyze $\langle l_m \rangle _I$ at h, we instead choose to focus on values just above and below. In practice roofs are not perfectly flat and there is a variety of building heights, so that $\langle l_m (h) \rangle _I$ might reasonably be approximated as a continuous function.

Fig. 5

(a) and (b) correspond to $\langle l_m \rangle _I$ at heights 1.03h and 0.97h respectively, plotted against $\lambda _p$

Plotted in Fig. 5a and b is $\langle l_m \rangle _I$ on the grid levels just above and below canopy top respectively; $\langle l_m \rangle _I$ is small near canopy top since there are large velocity gradients. $\langle l_m(1.03h) \rangle _I$ and $\langle l_m(0.97h) \rangle _I$ are between 2 and 10 times smaller than $\langle l_{m} \rangle _I^{{\max }}$. Also, $\langle l_m(1.03h) \rangle _I$ is approximately a factor of 2 smaller than $\langle l_m(0.97h) \rangle _I$, because $\langle l_m(1.03h) \rangle _I$ has velocity gradient contributions from just above the roofs where there is large shear.

Values of $\langle l_m(1.03h) \rangle _I$ and $\langle l_m(0.97h) \rangle _I$ tend to increase faster than linearly with decreasing $\lambda _p$. It is expected that $\langle l_m \rangle$ increases near canopy top with decreasing $\lambda _p$ since there are fewer buildings generating canopy-top shear. In the limit of an infinitely sparse canopy, flow should resemble that over a smooth wall, so that $\langle l_m \rangle \approx \kappa h$, where $\kappa$ is the von Kármán coefficient. In the limit of a very dense canopy, flow should also resemble that over a smooth wall, except displaced by h so that $\langle l_m \rangle \approx \kappa (z-h)$, and $\langle l_m(h) \rangle \approx 0$. Although neither limit is reached in the geometries examined here, it provides some explanation for the $\langle l_m \rangle$ behaviour near canopy top.

4.3 Mixing Length Above Canopy Top

The dispersive momentum flux occurs due to spatial deviations in the mean flow, and where it falls to zero can be used as a definition of the roughness sublayer height (Coceal et al. 2007c). As seen in Figs. 2d and 3d, by $z/h=1.5$ DMF is generally negligible (apart from N-44-A and C-33-A-$0^\circ$ which is likely due to insufficient averaging time); $\langle l_m \rangle _I$ tends towards an approximately linear increase by $z/h=1.5$, which is typical of inertial sublayer flow where $\langle l_m \rangle _I \approx \kappa (z-d)$. By inspecting $\langle l_m \rangle _I$, a linear portion was found to exist for $z/h=1.5{-}2.3$ across simulations (not shown), and was identified as the inertial sublayer. Linear regression of $\langle l_m \rangle _I$ against z was performed in the inertial sublayer, where the gradient corresponds to $\kappa$. The $\kappa$ results are plotted in Fig. 6. The N-44-A and C-33-A-$0^\circ$ simulations are excluded since they were not linear by $z/h=1.5$, due to large DMF.

Parameter $\kappa$ varies between 0.20 and 0.51, showing no clear relationship with canopy geometry, and has many values far from the classical value of 0.41. Alternative inertial sublayer height definitions were tested to investigate the sensitivity of $\kappa$. For $1.5{-}3.0h$ where the top height was extended and 1.1–2.3h where the bottom height was extended, the $\kappa$ ranges were 0.18 to 0.41 and 0.22 to 0.51, respectively. Extending the top height resulted in the $l_{m,1}$ component of C-33-A-$45^\circ$ no longer being linear in the fitting portion, and its linear regression gave reduced $\kappa$ compared to its original height range value, reducing the upper range of the $\kappa$ values. Extending the bottom height had little effect on the range of $\kappa$ values.

Fig. 6

$\kappa$ calculated as the gradient of the linear regression between (a) $\langle l_m \rangle _I$ and z, and (b) $u_{\tau ,i}\sqrt{1-d/H}/(\partial \langle \overline{u_i}\rangle _I/\partial z)$ and z, for $z/h=1.5$–2.3, plotted against $\lambda _p$

There are several studies which suggest that $\kappa$ is not a universal constant in rough wall flows, as discussed by Leonardi and Castro (2010). For example, Frenzen and Vogel (1995) argue that roughness influences $\kappa$ through the ratio of TKE production and dissipation in the inertial sublayer. For DNS of flow over packed beds (Breugem et al. 2006) and LES of a staggered array of cubes (Claus et al. 2012), values as low as 0.23 and $\approx 0.3$ have been observed, respectively, by logarithmic fitting to simulated velocity in the inertial sublayer. However, to the authors’ knowledge this is the first set of results to demonstrate such a range of $\kappa$ values across a range of geometries in the urban canopy literature.

4.3.1 Scale Separation

Jiménez (2004) suggests that two conditions must be satisfied so that a region exists where the only relevant turbulent length scale is the distance from the wall and the velocity profile is truly logarithmic. First $\delta /h>40$–80, where $\delta$ is the boundary-layer depth, so that the flow is far enough from the surface that inner-layer turbulence associated with roughness elements does not interact with it. Second $z/\delta <0.15$, so that the flow is close enough to the wall to not interact with the outer-layer turbulence of scale $\delta$. The first condition may not be met in urban areas under near-neutral atmospheric stability since the atmospheric boundary layer over deeper urban canopies may not grow to $\delta /h>40$–80. This might explain some of the large variability in relations for $z_0$ and d which are often found using experimental datasets (e.g., Kent et al. 2017).

In CFD half-channel flow investigations domain height H places a limit on $\delta$. The first condition is not met in the majority of the simulations presented here where $H/h=8$. The second condition becomes $z/H<0.15$, which is also not met since the region defined earlier as the inertial sublayer ($z/h=1.5$–2.3) corresponds to $z/H=0.19$–0.29 for $H/h=8$. However, N-35-S and C-33-A-$45^\circ$ have $H/h=12$, so that the region defined earlier as the inertial sublayer corresponds to $z/H=0.125$–0.19. Roughly the lower half of the region is then close enough to the wall for the outer-scale turbulence to not interact with the flow according to Jiménez (2004). It is therefore interesting that N-35-S, the C-33-A-$45^\circ$ x-component and the C-33-A-$45^\circ$ y-component have $\kappa$ values of 0.38, 0.39 and 0.5 respectively, which are generally larger than the other values, and, with the exception of the C-33-A-$45^\circ$ y-component, $\kappa \approx 0.4$. This provides tentative evidence that H used in urban canopy modelling can place limitations on $\delta$, and lead to inadequate separation of the inner- and outer-scales in the inertial sublayer resulting in modification of the turbulence.

That H might influence flow in the inertial sublayer does not affect the validity of results presented within the canopy. Turbulence statistics within the canopy have been demonstrated to converge with H in the DNS studies of Coceal et al. (2006) and Coceal et al. (2007a) for H/h values of up to 6 and 8 respectively. Also, large-eddy simulations with $H/h \approx 8$ have been shown to agree well with experiments (Xie and Castro 2006, 2009; Nazarian and Kleissl 2016).

4.3.2 Influence of Vertical Turbulent Momentum Flux Variation

Replacing $\langle l_m \rangle _I$ with $\kappa (z-d)$ in Eq. 7 and assuming that momentum transport is down-gradient, after rearranging one can obtain

$$\begin{aligned} \begin{aligned} \frac{\partial \langle {\overline{u}}_i\rangle _I}{\partial z} = \frac{\tau _i^{1/2}}{\kappa (z-d)}, \end{aligned} \end{aligned}$$

(12)

where $\tau _i=-\langle \overline{u_i'w'}\rangle _I$. In the $\kappa$ analysis presented in the previous section, the exact value of $\tau _i$ derived from the CFD simulations was used in Eq. 12, following Coceal et al. (2006). If instead $\tau _i$ is taken to be constant then Eq. 12 has the form of the MOST flux–gradient relationship under neutral conditions. Its integral from $z_0 + d$ to z results in the standard logarithmic law (Garratt 1994), where $z_0$ is the roughness length.

When $\tau _i$ is taken to be constant it is not obvious what value it should take. In the CFD simulations there is a body force applied uniformly throughout the fluid, which results in $\tau _i$ decreasing linearly with height above the roughness sublayer. A linear fit would equal $u_{\tau ,i}^2$ if extrapolated to the surface, where $u_{\tau ,i}=u_\tau \cos \theta$ and $\theta$ is the angle between the x axis and the driving-flow direction. Therefore, above the roughness sublayer $\tau _i^{1/2}=u_{\tau ,i}\sqrt{1-z/H}$. The effective ground experienced by the flow in the inertial sublayer is d. Assuming that the TMF is constant in the surface layer (as is done in derivation of the logarithmic law), one might then take $\tau _i^{1/2}=u_{\tau ,i}\sqrt{1-d/H}$ in the inertial sublayer (Leonardi and Castro 2010).

Taking this approach $\kappa$ was estimated from the gradient of the linear regression between $u_{\tau ,i}\sqrt{1-d/H}/(\partial \langle \overline{u_i}\rangle _I/\partial z)$ and z. The fits were similarly good in the region $z/h=1.5$–2.3 across simulations when compared to the linear regressions in the previous analysis. The $\kappa$ values are plotted in Fig. 6b and vary widely between $0.27-0.50$. When performing fitting analysis to obtain d and $z_0$ in the inertial sublayer, neither the approach of taking the exact value of $\tau _i$ or constant $\tau _i$ is advocated here as being correct. We instead note that in both approaches a large range of $\kappa$ are found, and taking a fixed value in any fitting analysis would have a large influence on the values of d and $z_0$ obtained. If the domain height used in CFD simulations is increased this could have the twin benefits of improving scale separation and reducing $\tau _i$ variation in the inertial sublayer.

4.4 General Characteristics of Mixing Length in Urban Canopies

The general features of the $\langle l_m \rangle _I$ profiles for uniform-height, flat-roofed geometries are summarized in a schematic in Fig. 7 and consist of: an increase from zero at the surface to a maximum around the middle of the canopy, a decrease until canopy top (where there is a discontinuity), and a rapid increase above $z/h=1$ before transitioning to a linear increase by approximately $z/h=1.5$. The vertical extent of the arrow reflects the fact that the aligned simulations have $\langle l_{m} \rangle _I^{{\max }}$ nearer canopy top with increasing $\lambda _p$, and that $\langle l_{m} \rangle _I^{{\max }}$ can be below the middle of the canopy for $45^\circ$ driving-flow simulations; $\langle l_{m} \rangle _I^{{\max }} /h \approx 0.3$ is a reasonable approximation apart from the $45^\circ$ simulations which have much larger values.

Fig. 7

Schematic showing the main features of $\langle l_m \rangle _I$ across the various uniform-height geometries. The double ended arrow indicates the range of heights over which $\langle l_{m} \rangle _I^{{\max }}$ occurs for the different geometries

4.5 Mixing-Length Characteristics of a Variable Height Building Array

Xie et al. (2008) conducted an LES of flow through $\lambda _p=0.25$ staggered cuboids with equal length and width, and varying heights. The horizontal layout was the same as that in Fig. 1b. Within each repeating unit there were 16 cuboids ($1\times 0.27h$, $3\times 0.63h$, $7\times 0.98h$, $4\times 1.33h$ and $1\times 1.68h$). The dataset offers more realistic variability in $\epsilon (z)$ than uniform-height roofs. The influence of variable building height on the flow and the general applicability of the $\langle l_m \rangle _I$ schematic in Fig. 7 to urban canopies is investigated.

Plotted in Fig. 8a, b are the $\epsilon (z)$ and $\langle l_m \rangle _I$ profiles, respectively. Below h the momentum mixing-length profile for the variable height array is similar to the schematic for the uniform-building-height arrays (Fig. 7); $\langle l_{m} \rangle _I^{{\max }}$ occurs at $z/h = 0.49$, which is almost identical to $z/h = 0.50$, the height at which $\langle l_{m} \rangle _I^{{\max }}$ occurs for N-25-S, a case with identical layout but with uniform-height buildings; $\langle l_{m} \rangle _I^{{\max }}/h$ equals 0.41 which is 0.1 larger than the N-25-S value. This could be due to contributions from larger-scale turbulence associated with buildings taller than the mean height.

The variable height array $\langle l_m(h) \rangle _I/h$ was equal to 0.14, and can be compared with the N-25-S simulation at grid points just below and above $z/h=1$, where $\langle l_m \rangle _I/h=0.09$ and 0.05, respectively. Smaller values occur for N-25-S because there is a larger proportion of roofs at h. Flow interacts with the roofs producing large double-averaged velocity gradients (i.e., shear) and small $\langle l_m(h) \rangle _I/h$.

There are two less pronounced $\langle l_m \rangle _I$ minima above $z/h=1$ compared to the minima at $z/h=1$ in Fig. 8, and are a result of shear generated at the tops of the 1.33h and 1.68h buildings. The peaks are less pronounced because there is a smaller number of height 1.33h and 1.68h buildings than height h buildings.

$\langle l_m \rangle _I$ minima do not occur at the tops of the 0.27h and 0.63h buildings, despite them occurring in similar proportion to the 1.33h and 1.68h buildings respectively. This is likely because the buildings shorter than h are sheltered from the flow above, due to shear layers shed from the taller buildings (Coceal et al. 2006). This would result in little time-mean flow penetrating to their heights, reducing the shear production of turbulence associated with the shorter building roofs. The turbulence would then become dominated by turbulence originating from the taller buildings. The taller building eddies are likely larger scale than the eddies generated by the roofs of the shorter buildings. This is because eddies generated at roof level are small in scale (as demonstrated in Sect. 4.7), and the shorter buildings are in the wakes of the taller buildings, and eddies in building wakes scale with building dimensions.

Fig. 8

Panels (a) and (b) show the $\epsilon (z)$ and $\langle l_m \rangle _I$ profiles respectively, for the Xie et al. (2008) LES of $\lambda _p=0.25$ staggered cuboids with variable-height buildings. The black dotted line in (b) is obtained from a linear fit to the solid black line between $z/h=3.0$–4.0

This explanation is consistent with Giometto et al. (2016) who conducted an LES of flow through a portion of Basel’s urban canopy. They identified three modes in the building-height probability distribution function (PDF)—two above h and one below h (see their Fig. 2). The buildings with heights at the mode below h had little influence on the flow, and (upon inspection of their Fig. 4) a double-averaged velocity gradient maximum cannot obviously be identified at the mode below h.

Yoshida and Takemi (2018) conducted LES of variable-height, flat-roofed buildings, with $\lambda _p=0.25$ between the ground and the height of the short buildings, and $\lambda _p=0.0625$ between the height of the short buildings and tall buildings. The ratio of the taller to the shorter building heights was 2.7 in one simulation and 7.25 in another. The number of $\langle l_m \rangle$ local maxima and minima within the canopy corresponded to the number of building heights (i.e., 2). Therefore, unlike in the Xie et al. (2008) and Giometto et al. (2016) variable-building-height simulations, a $\langle l_m \rangle$ minimum occurred below h at the height of the shortest buildings. One possible explanation is that the tall buildings in the Yoshida and Takemi (2018) simulations are sparse, so do not block flow from reaching the shorter buildings.

In contrast with the uniform-height, Xie et al. (2008) and Giometto et al. (2016) simulations, the Yoshida and Takemi (2018) simulations had two rather than one double-averaged velocity inflections. Again this is likely due to flow being able to penetrate to the heights of the shorter buildings in the Yoshida and Takemi (2018) simulations, and a clear separation of shear layers owing to the large difference in building heights.

As seen in Fig. 8, the transition to a linear $\langle l_m \rangle _I$ profile above $z/h=1$ is much slower compared to the uniform-height buildings. The inertial sublayer was taken to be $z/h=3.0-4.0$ since $\langle l_m \rangle _I$ was linear there, and a straight line was fitted in the region (see Fig. 8). Compared to the inertial sublayer fit there was generally a small decrease in $\langle l_m \rangle _I$ between $z/h=1$–3. This is likely due to shear layers shed from the tops of the taller buildings.

Based on the results presented here it is proposed that the characteristic $\langle l_m \rangle _I$ shape in Fig. 7 can be applied generally to canopy geometries with uni-modal building height PDFs. A single $\langle l_m \rangle _I$ minimum can then be expected at the mode canopy height, where maximum shear is associated with the building roofs. The $\langle l_m \rangle _I$ minimum is smaller with increasing proportion of building roofs at the mode height. The transition to a linear $\langle l_m \rangle _I$ profile above the canopy is likely to occur for all canopy geometries, so long as the tallest buildings are significantly smaller than the boundary-layer depth, thus giving adequate scale separation of inner- and outer-layer turbulence for an inertial sublayer to develop. For urban canopies with multi-modal building height PDFs the schematic would require extension. Whether $\langle l_m \rangle _I$ minima exist at each mode depends on several factors such as whether there is a large proportion of buildings at the mode, if the mode occurs below h, whether the taller buildings are densely packed, and the height separation between modes.

4.6 Importance of Accounting for Solid Fraction Variation in Mixing-Length Turbulence Closures

The importance of accounting for $\epsilon (z)$ in the first-order momentum mixing-length closure and the consequent effect on predicted $\langle {\overline{u}} \rangle$ was investigated. The variable-building-height LES of Xie et al. (2008) was used since of the datasets available, its $\epsilon (z)$ is most representative of that in a real urban neighbourhood. The detailed analysis is in the Appendix.

It was found that if the solid fraction is not accounted for in the intrinsic mixing-length closure, then errors in the predicted double-averaged velocity of up to $17\%$ occur. If the solid fraction is not accounted for in the comprehensive mixing-length closure, then errors in the predicted double-averaged velocity do not occur, so long as $\epsilon$ is not included in Eq. 8 when deriving $\langle l_{m,i} \rangle _C$ and solving the momentum equation.

4.7 Relationship Between Canopy-Top Shear Length Scale and Mixing Length

Based on similarity arguments Finnigan et al. (2015) argued that when most of the momentum is absorbed as drag by the canopy elements rather than by the ground, then there is only one relevant length scale in the canopy $(S(z)C_d(z))^{-1}$, which can be interpreted as a drag length scale $L_c$ (Belcher et al. 2003; Coceal and Belcher 2004). Here S(z) is the sectional obstacle area density (obstacle area facing the wind divided by canopy air volume) and $C_d(z)$ is the sectional drag coefficient. In dense vegetation canopies the approximation that S(z) and $C_d(z)$ are constant with height is also often made. This is consistent with the mixing-layer analogy, which suggests that there is one dominant turbulent length scale in the canopy, determined by the shear length scale $L_s(h)$ associated with the canopy-top mixing-layer.

With decreasing vegetation canopy density there is increasing flow penetration into the canopy, and there are length scales other than $L_s(h)$ that become important. For example those associated with eddies originating from shear near the surface (Watanabe and Kondo 1990), and penetration of inner layer eddies into the canopy and von Kármán street vortices (Poggi et al. 2004).

It is investigated here to what extent turbulence in urban canopies is dominated by mixing-layer eddies. If mixing-layer eddies are generated with length scale $L_s(h)$ due to the inflection in the double-average velocity profile at canopy top, and are dominant within urban canopies so that only they control turbulent mixing, it would be expected that $L_s(h) = \alpha \langle l_m \rangle ^{av}$ across canopy geometries. $\alpha$ is a constant and $\langle l_m \rangle ^{av}$ is the depth averaged value of $\langle l_m \rangle$ within the canopy.

The shear length scale is defined here as

$$\begin{aligned} L_{s,i}(z)=\langle {\overline{u}}_i\rangle _I \left( \frac{\partial \langle {\overline{u}}_i\rangle _I}{\partial z} + \frac{\langle {\overline{u}}_i\rangle _I}{\epsilon }\frac{\partial \epsilon }{\partial z} \right) ^{-1}. \end{aligned}$$

(13)

This is the same as the definition given by Raupach et al. (1996) but with the addition of the second term in the brackets, which is included to account for the influence of solid fraction on the intrinsic spatial average of the velocity gradient. The component label i has been retained to allow the possibility of the shear being different in the x and y axes, while the shear of vertical velocity is zero since $\langle {\overline{w}} \rangle _I=0$.

Fig. 9

$L_s(h)/\langle l_m \rangle _I^{av}$ plotted against $\lambda _p$

Figure 9 shows $L_s(h) / \langle l_m \rangle _I^{av}$ plotted against $\lambda _p$. For the $0^\circ$ aligned and staggered cube geometries it can be seen that with decreasing $\lambda _p$ the ratio $L_s(h) / \langle l_m \rangle _I^{av}$ increases faster than linearly. $\alpha$ is not constant suggesting that mixing-layer eddies are not always the dominant turbulence within urban canopies. Similar $L_s / \langle l_m \rangle _I^{av}$ versus $\lambda _p$ relationships occurred when $L_s$ was evaluated at $z/h=0.94$ and $z/h=1.06$ (not shown), but $L_s$ tended to be $\sim 50\%$ larger because maximum shear generally occurs at $z/h=1$. The only outliers to the $L_s / \langle l_m \rangle _I^{av}$ versus $\lambda _p$ trend were the N-33-S and N-44-S datasets at $z/h=1.06$. For them $L_s / \langle l_m \rangle _I^{av}$ was $10\%$ and $40\%$ larger respectively than N-25-S, so increased with increasing $\lambda _p$.

Inspection of individual velocity profiles reveals that inflections in the velocity profile occur at canopy top behind each roof, consistent with Letzel et al. (2008). The inflections are much weaker $\sim \!h$ downstream and extend little in the cross-stream. As suggested by Coceal et al. (2007a), the urban canopy top shear layer is highly heterogeneous and velocity profile inflections are local to individual buildings. As the canopy becomes sparser, fewer mixing-layer eddies are produced, and more flow penetrates into the canopy, making turbulence increasingly likely to be associated with other turbulence production mechanisms.

Ghisalberti (2009) argues that in ‘obstructed shear flows’, where part of a flow is obstructed via a permeable medium, the mixing-layer eddies generated at the interface between the permeable medium and unobstructed flow, cause environmental flows of this type to be dynamically similar. Ghisalberti (2009) observed that across canopy types (e.g., sediment beds, aquatic and terrestrial vegetation canopies, and coral reefs) the depth turbulence penetrates into the canopy is proportional to $L_c$. However, urban canopies were found to be an outlier with smaller penetration depth. In moderately dense and dense vegetation canopies $L_s/h \approx 0.1-0.5$ (Raupach et al. 1996). For moderately dense and dense urban canopies ($\lambda _p \ge 0.25$) presented here, $L_s/h$ ranged between 0.06 and 0.16 (not shown). The mixing-layer eddies are generally smaller and more localized to the obstacles than in vegetation canopies, which explains why Ghisalberti (2009) found urban canopy turbulence to penetrate less deep into the canopy than in the other canopy types.

It can be seen from Fig. 9 that for the denser ($\lambda _p\ge 0.25$) $0^\circ$ staggered cube geometries that $L_s(h) / \langle l_m \rangle _I^{av}$ varies less with $\lambda _p$. This suggests that mixing-layer eddies likely make a large contribution to turbulent mixing in those geometries. As seen in Fig. 2a, b the velocity and TMF respectively are small within the canopy for the dense staggered geometries, since they have no unobstructed portions of the canopy. It is probable that most of the conversion of time-mean flow into turbulence occurs at canopy top, and is transported into the canopy.

The $45^\circ$ simulations have lower $L_s(h) / \langle l_m \rangle _I^{av}$ values compared to the $0^\circ$ simulations with the same $\lambda _p$ (see Fig. 9). The $0^\circ$ and $45^\circ$ simulations with the same $\lambda _p$ have similar $L_s(h)/h$ (not shown), but the $45^\circ$ simulations have larger $\langle l_m \rangle _I^{av}$. Mixing-layer eddies generated by shear at the canopy top are therefore unlikely to be the cause of the differences in turbulence characteristics within the canopy between the $0^\circ$ and $45^\circ$ simulations.

In summary, the relation $L_s(h) = \alpha \langle l_m \rangle _I^{av}$ does not hold across geometries, and turbulence is not dominated by mixing-layer eddies within the canopy, apart perhaps for the dense ($\lambda _p\ge 0.25$) $0^\circ$ staggered geometries.

4.8 Dispersive Momentum-Flux Characteristics

As a preliminary step towards developing DMF parametrizations, the behaviour of the three-dimensional DMF fields and horizontally-averaged profiles are investigated across geometries.

From Figs. 2c and 3c, it is seen that generally the horizontally-averaged DMF magnitude increases with height in the canopy until $z/h=0.7$–0.95. The maximum magnitude of DMF tends to occur lower in the canopy for the sparser geometries. For the $0^\circ$ driving flows, DMF is typically negative in the middle and just below the top of the canopy, and positive near the surface (Fig. 2c). For the $45^\circ$ driving flows, DMF is negative throughout the canopy, with increasing magnitude from the surface until approximately $z/h=0.8$ (Fig. 3c). These trends are understood in terms of the three-dimensional DMF field in the following sections.

4.8.1 ${ 0}^\circ$ Driving Flows

Horizontal cross-sections of DMF through canopy geometry repeating units at $z/h=0.75$ are shown in Fig. 10. Dispersive velocities are calculated using intrinsic averages to simplify interpretation as explained in Sect. 3.1. Inspecting the 0$^\circ$ simulations in Fig. 10a, c, d, e reveals that DMF is generally negative along the leeward face of the buildings (${\tilde{u}}<0$, ${\tilde{w}}>0$) and positive along the windward face (${\tilde{u}}<0$, ${\tilde{w}}<0$), in agreement with Coceal et al. (2007c) and Yoshida and Takemi (2018). For $\lambda _p < 0.44$ the negative fluxes on the leeward side have significantly larger streamwise extent than the positive fluxes on the windward side (Fig. 10a, d), and therefore dominate the spatial average flux. This flow pattern exists in the middle and top portions of the canopy for these cases, and it explains why the horizontal average DMF is generally negative there in Fig. 2c.

For $\lambda _p=0.44$ (Fig. 10c, e) the streamwise extent of the negative fluxes on the leeward side is much reduced, since recirculations in wakes are very limited by the downstream building separation. In Fig. 10c it can be seen that for N-44-A the extent of negative fluxes from the leeward wall is still slightly larger than the positive fluxes at the windward wall. However, the magnitude of the positive fluxes is larger, and positive fluxes dominate the spatial average (as seen in Fig. 2c). From Fig. 10e it can be seen that for N-44-S the positive and negative fluxes occupy similar fractions of the canopy, with comparable magnitude, so that the horizontal average DMF is small (as seen in Fig. 2c).

Fig. 10

Panels (a), (c), (d) and (e) show DMF ${\tilde{u}}{\tilde{w}}/u_{\tau }^2$ cross-sections at $z/h=0.75$ for B-25-A-0$^\circ$, N-44-A, N-25-S and N-44-S respectively. Panel (b) shows a $({\tilde{u}}{\tilde{w}}+{\tilde{v}}{\tilde{w}})/u_{\tau }^2$ cross-section at $z/h=0.75$ for B-25-A-45$^\circ$

Figure 2d shows the ratio of DMF to TMF for the $0^\circ$ simulations. The $\lambda _p=0.0625$–0.35 geometries have ratio between 0.2–0.6 for $z/h=0.4$–0.9. These values are consistent with other studies (Kanda et al. 2004; Xie et al. 2008; Castro 2017). DMF for $\lambda _p \le 0.25$ tends to be convex within the canopy but TMF across all $\lambda _p$ tends to be concave. The ratio is generally largest at $z/h\approx 0.5$. Near the surface the ratio is negative because DMF is positive there. The regions of negative flux in Fig. 10a, d at $z/h=0.75$ are smaller near the surface, and the large positive fluxes confined close to the windward wall dominate the spatial average.

The ratio has different behaviour when $\lambda _p = 0.44$. The N-44-A ratio is negative below $z/h=0.85$, with a minimum value of $-0.72$ at $z/h=0.3$. The N-44-S ratio is complicated, being generally negative below $z/h=0.55$ but with both very large positive and negative values in the region due to small values of TMF.

That the ratio of DMF to TMF is far from constant across the range of geometries presented here is further evidence that they are not governed by the same processes. DMF is related to the correlation of ${\overline{u}}$ and ${\overline{w}}$ (since $\langle {\overline{u}}\,{\overline{w}} \rangle$ = $\langle {\tilde{u}}{\tilde{w}} \rangle$), and so requires knowledge of the three-dimensional time-averaged flow field.

4.8.2 ${ 45}^\circ$ Driving Flows

Compared to the 0$^\circ$ simulation DMF cross-sections in Fig. 10, B-25-A-45$^\circ$ in Fig. 10b has distinctly different characteristics, with negative fluxes dominating the cross-section. There are strong negative fluxes in the wakes of the buildings as in the 0$^\circ$ driving flows, but at the windward walls ($x/h=2$, $y/h=0-1$ and $x/h=0-1$, $y/h=2$) there are no strong positive fluxes. There are two separate streams either side of each building where flow is diverted around them as also noted by Claus et al. (2012). At the windward walls they have downward motion (${\tilde{w}}<0$), like the flow at the windward walls in the 0$^\circ$ driving flows. The flow streams have large positive horizontal velocity at the windward walls (${\tilde{u}},{\tilde{v}}>0$) so correlation with ${\tilde{w}}<0$ gives negative fluxes, unlike the 0$^\circ$ driving flows where ${\tilde{u}}<0$ at the windward wall so that there are positive fluxes. This flow pattern extends throughout the canopy and explains why the B-25-A-45$^\circ$ horizontally-averaged DMF is positive within the canopy in Fig. 3c.

The $45^\circ$ datasets have particularly large ratios in the lower canopy with values larger than 1 for $0.05<z/h<0.5$ (Fig. 3d). Unlike in the $0^\circ$ driving flows where DMF tends to be negative near the surface, in the $45^\circ$ driving flows it is positive. The ratio is maximum at $z/h\approx 0.15$, and has values 2.9, 129.1 and 2.3 for B-25-A-45$^\circ$, C-33-A-45$^\circ$ x-component and C-33-A-45$^\circ$ y-component respectively. The ratio of 129.1 is off the axis limit and the particularly large value is due to very small TMF. It has already been shown by Castro et al. (2017) using the C-33-A-45$^\circ$ dataset that DMF is a significant and at times dominant fraction of the total momentum flux. It is demonstrated for the first time here in the B-25-A-45$^\circ$ case, suggesting that this might be a general result for $45^\circ$ driving flows.

Using LES, Giometto et al. (2016) found for a portion of Basel’s urban canopy ($\lambda _p=0.5$ near the surface), with two prevailing wind directions, that TMF and DMF are approximately equal up to h. This is consistent with our finding that DMF can be much larger when flow is oblique to building faces. They found the DMF to increase approximately linearly with height up to h, above which it starts to decrease, whereas the TMF peaks above h. The TMF profiles were slightly convex and reasonably similar in shape to the DMF profiles.

It may be expected that the magnitude of DMF increases with height (if $\lambda _p(z)$ is approximately constant) since $|{\overline{u}}|$ tends to increase with height. It is less obvious that DMF might increase approximately linearly with height for realistic urban canopy geometries. It is possible at high $\lambda _p$ in realistic geometries where buildings have varying orientations to the flow, that there is a mixture of convex and concave shaped DMF in different regions of the canopy. It was found here that when $\lambda _p \ge 0.25$, the 0$^\circ$ and 45$^\circ$ driving flows produce concave and convex profiles, respectively. Upon spatial averaging this could give rise to approximately linearly increasing spatially-averaged DMF with height. More CFD and experimental evidence of realistic urban geometries is required to see if this is the case.

5 Conclusions

5.1 Summary

The influence of different surface morphologies on urban canopy turbulence characteristics was investigated for numerous urban canopy LES and DNS datasets covering a range of idealized geometries ($\lambda _p=0.0625$ to 0.44, cubes and cuboids, uniform and variable building heights, driving flows at $0^\circ$ and $45^\circ$ to the building faces, and aligned and staggered arrays). A first-order momentum mixing-length turbulence closure was formulated and momentum mixing-length profiles examined across geometries, with a view towards developing a new urban-canopy turbulence model. The dispersive momentum-flux profiles were calculated and interpreted in terms of the three-dimensional flow field.

The intrinsic average of vertical gradients in velocity gives rise to a term that accounts for changes in $\lambda _p$ with height. Without it there are large discontinuities in the gradient whenever there are step changes in $\lambda _p$, which cause spikes in the momentum mixing length. For a variable-height building geometry it was shown that excluding the extra term in the momentum mixing-length closure results in overestimation of predicted velocity by up to $17\%$ near the top of the canopy. For denser urban canopies ($\lambda _p>0.25$) the error is expected to be larger. The intrinsic averaging approach is used commonly in urban canopy models (Martilli and Santiago 2007), and when K-theory turbulence closures do not account for the extra term large errors can be expected, since they involve horizontal averaging of velocity gradients.

It was found that the shear length scale at the canopy top does not vary with depth-averaged momentum mixing length within the canopy in a systematic way. This suggests that the mixing-layer analogy (Raupach et al. 1996) does not apply to turbulence in urban canopies, unlike in vegetation canopies, since it is not dominated by one length scale associated with mixing-layer eddies generated at canopy top. Shear-generated eddies at the top of urban canopies are local to the buildings (Coceal et al. 2007a), and do not penetrate as far down into the canopy as in vegetation canopies. Flow velocity can be considerable near the surface in unobstructed regions of urban canopies so that significant shear can be generated there. The momentum mixing length might be better interpreted as a combination of two length scales—the distance from the ground and from canopy top, both of which act to block eddies (Coceal et al. 2006).

The momentum mixing length demonstrated common characteristics across urban canopy geometries. For uniform-height, flat-roofed obstacles it increases from zero at the surface to a maximum roughly in the middle of the canopy, decreases until canopy top and increases rapidly above $z/h=1$, before transitioning to a linear increase by approximately $z/h=1.5$. The $0^\circ$ driving flows typically have a maximum momentum mixing length in the canopy of $\approx 0.3 h$.

There were some outliers to the trend, specifically the $\lambda _p=0.44$ staggered geometry and the $45^\circ$ driving flows as discussed in Sect. 4.1. Within the canopy these tended to have similar order magnitude wake production compared to shear production of turbulent momentum flux (away from the ground and canopy top), and larger magnitude ratios of dipersive to turbulent momentum flux than the other simulations. Wake production and dispersive momentum flux are both associated with building-scale spatial fluctuations in the flow, and are not directly related to the vertical gradient of the double-averaged velocity, as assumed by the mixing-length parametrization.

Using a variable-building-height dataset, it was demonstrated that the momentum mixing-length profile shape and magnitude below mean building height is similar to that with uniform-height geometries. Above mean building height, mixing length increases approximately linearly with height, but is slightly reduced from what would be expected in a logarithmic region, due to multiple shear layers associated with the tops of the buildings. A minimum in the mixing-length profile occurs at the mean building height but is larger compared to uniform-height geometries.

Von Kármán’s parameter (constant) $\kappa$ was calculated from the gradient of linear regressions fitted to momentum mixing-length profiles in the inertial sublayer. It was found that $\kappa$ varies between 0.20 and 0.51, and there is no clear relationship between canopy geometry and $\kappa$. The simulations with larger domain heights tended to have larger $\kappa$. Whether the ratio of roughness height to boundary-layer depth is insufficient for adequate scale separation in the logarithmic region, as suggested by Jiménez (2004), requires further investigation.

Dispersive momentum-flux profiles for the $0^\circ$ driving flow datasets were in line with those in the literature (Kanda et al. 2004; Xie et al. 2008; Castro 2017), with dispersive to turbulent momentum-flux ratios of 0.2–0.6 for $z/h=0.4$–0.9 in the $\lambda _p=0.0625$–0.35 simulations. The $45^\circ$ datasets have larger dispersive momentum flux, and ratios to turbulent momentum flux that exceed 1 for $0.05<z/h<0.5$. As ratios of approximately unity have also been found for realistic geometries (Giometto et al. 2016), dispersive momentum flux in oblique flows may be more important than previously thought.

5.2 Implications for Parametrization

Many urban canopy models assume turbulent length scales that are constant up to mean canopy height and linearly increasing above (Hamdi and Masson 2008; Santiago and Martilli 2010; Nazarian et al. 2020). In NWP the main role of the urban canopy model is to provide a boundary condition for the flow above. The use of a constant turbulent length scale is not necessarily a poor approximation, if its value is determined so that the correct fluxes are provided to the levels above the canopy. However, if vertical profiles of velocity and scalars are of interest within the canopy, then using a turbulent length scale that varies with height in the correct way is important. TMF is proportional to $\langle l_m \rangle ^2$ in first-order momentum mixing-length closures and proportional to the turbulent length scale in commonly used $k-l$ TKE closures (Martilli et al. 2002; Schoetter et al. 2020), so the turbulent length scale (of which momentum mixing length is an example) is an important parameter.

Models that use a constant turbulent length scale often do not enforce the no-slip condition at the surface, so velocity gradients at the surface are very small. Canopy dispersion parametrizations based on the double-averaging approach involve velocity gradients, so it is necessary to correctly predict velocity for use in determining the vertical scalar distribution. This is especially the case near the surface where there are strong velocity gradients collocated with various scalar sources (e.g., pollution emissions, and anthropogenic and sensible heat).

Based on sensitivity tests (not shown), changing the turbulent length scale alone in urban canopy models does not always improve the predicted velocity profile, if the drag term is not treated properly. It is well known that the $C_d(z)$ tends to be larger near the surface than close to the tops of buildings (Macdonald 2000; Cheng and Castro 2002; Coceal et al. 2006; Santiago et al. 2008; Leonardi and Castro 2010), so it follows that the drag length scale $L_c$ is variable in urban canopies. Future multi-layer canopy models will likely need to account for both turbulent length scales and drag length scales that vary with height in the canopy.

It was found that the $45^\circ$ driving flow simulations have large turbulent momentum flux despite having small double-average velocity gradient. Turbulent transport was proposed as a possible explanation. When turbulent transport of turbulent momentum flux is important then first-order closures are insufficient. A possible pragmatic approach to a higher-order closure is to add an extra term to the first-order momentum mixing-length closure, so that $\langle \overline{u'w'}\rangle = -\langle l_m \rangle ^2 \left| \langle \partial {\overline{u}}/\partial z \rangle \right| \langle \partial {\overline{u}}/\partial z\rangle +N_l$, where $N_l$ represents turbulent transport (i.e., the non-local turbulence). Such an extension to the first-order momentum mixing-length approach has already been formulated by Wang (2014). This approach could also offer a method of parametrizing buoyancy effects which drive non-local momentum transport, in a way analogous to some convective-boundary-layer schemes (e.g., Lock et al. 2000), whilst maintaining first-order momentum mixing-length closure of mechanical turbulence.

It was argued in Sect. 4.8 that dispersive and turbulent transport are not governed by the same processes. Rather than representing dispersive momentum flux as part of the turbulence closure it could be treated separately. For example, if it is found more generally that dispersive momentum flux is an approximately linearly increasing function across different realistic geometries, then it could be taken as a function that is scaled with velocity and building morphology parameters such as $\lambda _p$. Recirculations in building wakes cause the majority of dispersive momentum flux since they are where large magnitude ${\tilde{u}}$ and ${\tilde{w}}$ occur. Recirculations are likely predominantly driven by the flow at canopy top as in street canyons, so that $\langle {\overline{u}}(h) \rangle$ is the relevant velocity scale.

Appendices

Appendix: Importance of Accounting for Solid Fraction Variation in Mixing-Length Turbulence Closures

The importance of accounting for $\epsilon (z)$ in the first-order momentum mixing-length closure and the consequent effect on predicted $\langle {\overline{u}} \rangle$ is investigated. The variable-building-height LES of Xie et al. (2008) is used.

Impact of Accounting for Solid Fraction Variation on Mixing Length

Plotted in solid black and dashed blue in Fig. 11a are $\langle l_m \rangle _I$ calculated with and without the $\epsilon$ terms in Eq. 7 respectively. If the $\epsilon$ terms are excluded spikes occur at grid levels where there is a discontinuity in $\epsilon (z)$ [see Fig. 8a for the $\epsilon (z)$ profile], due to $\partial \langle {\overline{u}}\rangle _I/\partial z$ discontinuities. At $\epsilon (z)$ discontinuities, $\langle {\overline{u}} \rangle _I$ has discontinuities of size

$$\begin{aligned} \begin{aligned} \langle {\overline{u}}(z+\Delta _z) \rangle _I-\langle {\overline{u}}(z-\Delta _z) \rangle _I&= \frac{\langle {\overline{u}}(z+\Delta _z) \rangle _C}{\epsilon (z+\Delta _z)}-\frac{\langle {\overline{u}}(z-\Delta _z) \rangle _C}{\epsilon (z-\Delta _z)} \\&\approx \langle {\overline{u}}(z)\rangle _C \left( \frac{\epsilon (z-\Delta _z)-\epsilon (z+\Delta _z)}{\epsilon (z+\Delta _z)\epsilon (z-\Delta _z)}\right) , \end{aligned} \end{aligned}$$

(14)

where the approximation is in the limit of $\Delta _z \rightarrow 0$, and uses the fact that $\langle {\overline{u}} \rangle _C$ is a continuous function. When discretized, $\partial \langle {\overline{u}}\rangle _I/\partial z$ at $\epsilon (z)$ discontinuities tends to be reduced compared to values above and below $\epsilon (z)$ discontinuities, as seen from inspecting the intrinsic average velocity profile (solid black line in Fig. 11c), most notably at $z/h=1$ where $\epsilon (z)$ changes most. $\partial \langle {\overline{u}}\rangle _I/\partial z$ is reduced at $\epsilon (z)$ increases, because $\langle {\overline{u}}\rangle _I$ is small at the grid level above, due to low velocity contributions from flow influenced by the no-slip condition along the roofs. At $z/h=1$ where there is largest change in $\epsilon (z)$, the velocity gradient is reduced to the point it turns negative, such that $\langle l_m \rangle _I$ is not well defined if the $\epsilon$ term is not included in its calculation (as seen from the absence of the dashed blue curve at $z/h=1$ in Fig. 11a).

If taking the approach of not accounting for $\epsilon (z)$ variation, it would not be possible to incorporate the spikes into a general $\langle l_m \rangle _I$ parametrization. The best one could do is to ignore the spikes and represent the smooth part of the $\langle l_m \rangle _I$ behaviour. Such an approach might be achieved by linearly interpolating between the points either side of the spikes and this is shown as a dotted red curve in Fig. 11a.

Plotted in solid and dashed grey in Fig. 11b are $\langle l_m \rangle _C$ calculated with and without accounting for $\epsilon (z)$ variation in Eq. 8 respectively. The two profiles are identical up to a factor of $\epsilon (z)^{3/2}$. Neither profile exhibits large spikes since $\langle {\overline{u}} \rangle _C$ is a continuous function and has small $\langle \partial {\overline{u}}/\partial z \rangle _C$ discontinuities. It is noted that $\langle l_m \rangle _C=\epsilon (z)\langle l_m \rangle _I$ (according to $\langle \phi \rangle _C = \epsilon \langle \phi \rangle _I$ as explained in Sect. 3.1). This is consistent with inspection of the $\langle l_m \rangle _I$ and $\langle l_m \rangle _C$ curves plotted in Fig. 11a, b when $\epsilon (z)$ variation is accounted for in both their calculations.

Fig. 11

(a) Profiles of $\langle l_m \rangle _I$ calculated according to Eq. 7: including the $\epsilon$ term (black), excluding the $\epsilon$ term (dashed blue), and excluding the $\epsilon$ term followed by removing the spikes and interpolating (dotted red). (b) $\langle l_m \rangle _C$ calculated according to Eq. 8: including (solid) and excluding (dashed) the $\epsilon ^3$ factor. (c) Solution to Eq. 15 using the full $\langle l_m \rangle _I$ from (a) (solid black), using the interpolated $\langle l_m \rangle _I$ from (a) and excluding the $\epsilon$ term (red dotted), alongside the solution to Eq. 16 excluding the $\epsilon ^3$ factor and using the dashed grey $\langle l_m \rangle _C$ from (b) (dotted grey). The solution to Eq. 16 including the $\epsilon ^3$ factor and using the solid grey $\langle l_m \rangle _C$ from (b) is plotted in (c) and is identical to the dotted grey curve. (d) The ratio of the dotted red and solid black profiles from (c)

Impact of Accounting for Solid Fraction Variation on Predicted Velocity

Here we investigate the impact on predicted velocity by accounting for solid fraction variation in the momentum mixing-length closure formulation. To do so, TMF and $\langle l_m \rangle$ are taken to be known from the LES, and the corresponding double-averaged velocity is solved by discretising the momentum mixing-length closure.

A simple discretization of the intrinsic averaged closure (Eq. 7) is given by

$$\begin{aligned} u_{j+1} = u_j + \Delta _z \left( \frac{\pm (u' w')_{j+1/2}}{l_{m,j+1/2}}\right) ^{1/2} - \frac{u_j(\epsilon _{j+1}-\epsilon _j)}{\epsilon _{j+1/2}}, \end{aligned}$$

(15)

where time and spatial averaging symbols, and spatial indices i have been dropped for brevity. j labels the LES grid levels and $+1/2$ indicates their midpoints, with linear interpolation of values at the adjacent levels where necessary. The ± is to be taken as negative (positive) when the value within the modulus in Eq. 7 is positive (negative). Discretization of the comprehensive averaged closure (Eq. 8) is given by

$$\begin{aligned} u_{j+1} = u_j + \Delta _z \left( \frac{\pm (u'w')_{j+1/2}\epsilon _{j+1/2}^3}{l_{m,j+1/2}}\right) ^{1/2}, \end{aligned}$$

(16)

where ± is negative (positive) when the value within the modulus in Eq. 8 is positive (negative).

The solution to Eq. 15 using $\langle l_m \rangle _I$ calculated including the $\epsilon$ term is plotted as solid black in Fig. 11c. As a simple matter of consistency, this solution reproduces the true $\langle {\overline{u}} \rangle _I$, since this was used along with $\langle \overline{u'w'} \rangle _I$ to derive $\langle l_m \rangle _I$. Plotted as dotted red in Fig. 11c is the solution using $\langle l_m \rangle _I$ calculated when the $\epsilon (z)$ term is excluded and spikes are interpolated. The second term on the r.h.s. of Eq. 15 was dropped in the calculation for consistency with that approach. Inspecting the ratio of $\langle {\overline{u}} \rangle _I$ values when the $\epsilon (z)$ term is excluded and included (Fig. 11d), reveals that excluding the $\epsilon (z)$ term results in velocity overestimation of up to $17\%$ just above h. Each time there is an $\epsilon (z)$ discontinuity the percentage error increases, and between discontinuities the percentage error decreases, since the magnitude of the error remains constant with increasing height, but the magnitude of the two velocities increases.

So long as the $\epsilon (z)^3$ factor is dropped in Eq. 16 as well as in the $\langle l_m \rangle _C$ calculation, then the factor cancels, and the solution is the same as when the $\epsilon (z)^3$ factor is included. Multi-layer canopy model turbulence closures based on comprehensive averaging therefore do not encounter errors in predicted velocity due to incorrect application of the comprehensive spatial-averaging theorem to velocity gradients. The two solutions are plotted as one dotted grey curve in Fig. 11c.