On Milstein approximations with varying coefficients: the case of super-linear diffusion coefficients

Abstract

A new class of explicit Milstein schemes, which approximate stochastic differential equations (SDEs) with superlinearly growing drift and diffusion coefficients, is proposed in this article. It is shown, under very mild conditions, that these explicit schemes converge in $\mathscr {L}^p$ to the solution of the corresponding SDEs with optimal rate.

1 Introduction

Following the approach of Kumar and Sabanis [7], Sabanis [10], we extend the techniques of constructing explicit approximations to the solutions of SDEs with super-linear coefficients in order to develop Milstein-type schemes with optimal rate of (strong) convergence.

Recent advances in the area of numerical approximations of such non-linear SDEs have produced new Euler-type schemes, e.g. see [3, 5, 6, 9,10,11], which are explicit in nature and hence achieve reduced computational time when compared with the corresponding implicit schemes. Note that we do not claim that the superiority of the newly developed explicit schemes over the implicit schemes is absolute. For example, implicit schemes may exhibit better stability properties under different scenarios, typically when large step sizes are used or initial conditions are introduced with large numerical values. Nevertheless, we primarily focus on strong convergence of explicit schemes mainly due to their importance in Multi-level (and/or Markov chain) Monte Carlo, see for example Giles [4] and Brosse et al. [2]. High-order schemes have also been developed in this direction. In particular, Milstein-type (order 1.0) schemes for SDEs with super-linear drift coefficients have been studied in Wang and Gan [12] and in Kumar and Sabanis [7] with the latter article extending the result to include Lévy noise, i.e. discontinuous paths. Furthermore, both drift and diffusion coefficients are allowed to grow super-linearly in Zhang [13] and in Beyn et al. [1]. The latter reference has significantly relaxed the assumptions on the regularity of SDE coefficients by using the notions of C-stability and B-consistency. More precisely, the authors in Beyn et al. [1] produced optimal rate of convergence results in the case where the drift and diffusion coefficients are only (once) continuously differentiable functions (see the assumptions A-1 and A-5 precisely stated below). Our results, which were developed at around the same time as the latter reference by using different methodologies, are obtained under the same relaxed assumptions with regards to the regularity that is required of the SDE coefficients. Crucially, we relax further the moments bound requirement which is essential for practical applications.

We illustrate the above statement by considering an example which appears in Beyn et al. [1], namely the one-dimensional SDE given by

$$\begin{aligned} dx_t=x_t(1-x_t^2)dt+\sigma (1-x_t^2)dw_t, \qquad \forall \, t \in [0,\,T], \end{aligned}$$

with initial value $x_0$ and a positive constant $\sigma$. Theorem 2.1 below yields that for $p_0=14$ (note that $\rho =2$) one obtains optimal rate of convergence in $\mathscr {L}^2$ (when $\sigma ^2 \le \frac{2}{13}$ and $p_1>2$ such that $\sigma ^2(p_1-1)\le 1$) whereas the corresponding result in Beyn et al. [1], Table 1 in Section 8, requires $p_0=18$ for their explicit (projective) scheme. The same requirement, i.e. $p_0=14$, as in this article is only achieved by the implicit schemes considered in Beyn et al. [1].

Finally, we note that Theorem 2.1 establishes optimal rate of convergence results in $\mathscr {L}^p$ for $p>2$ under the relaxed assumption of once continuously differentiable coefficients, which is, to the best of the authors’ knowledge, the first such results in the case of SDEs with super-linear coefficients. As an immediate consequence of this, and for high values of p, one can prove an almost sure convergence result of the proposed approximation scheme (2.6) to the solution of SDE (2.1). The interested reader may consult Corollary 1 from Sabanis [10].

We conclude this section by introducing some notations which are used in this article. The Euclidean norm of a d-dimensional vector b and the Hilbert-Schmidt norm of a $d\times m$ matrix $\sigma$ are denoted by |b| and $|\sigma |$ respectively. The transpose of a matrix $\sigma$ is denoted by $\sigma ^*$. The ith element of b is denoted by $b^i$, whereas $\sigma ^{(i,j)}$ and $\sigma ^{(j)}$ stand for (i, j)-th element and j-th column of $\sigma$ respectively for every $i=1,\ldots ,d$ and $j=1,\ldots ,m$. Further, xy denotes the inner product of two d-dimensional vectors x and y. The notation $\lfloor a \rfloor$ stands for the integer part of a positive real number a. Let D denote an operator such that for a function $f: \mathbb {R}^d \rightarrow \mathbb {R}^d$, Df(.) gives a $d \times d$ matrix whose (i, j)-th entry is $\frac{\partial f^i(.)}{\partial x^j}$ for every $i,j=1,\ldots ,d$. For every $j=1,\ldots ,m$, let $\varLambda ^j$ be an operator such that for a function $g: \mathbb {R}^d \rightarrow \mathbb {R}^{d \times m}$, $\varLambda ^j g(.)$ gives a matrix of order $d \times m$ whose (i, k)-th entry is given by

$$\begin{aligned}{}[\varLambda ^j g(.)]_{(i,k)} := \sum _{u=1}^d g^{(u,j)}(.) \frac{\partial g^{(i,k)}(.)}{\partial x^u} \end{aligned}$$

for every $i=1,\ldots , d$, $k=1,\ldots ,m$.

2 Main results

Suppose $(\varOmega , \{\mathscr {F}_t\}_{t \ge 0}, \mathscr {F}, P)$ is a complete filtered probability space satisfying the usual conditions, i.e. the filtration is right continuous and $\mathscr {F}_0$ contains all P-null sets. Let $T>0$ be a fixed constant and $(w_t)_{t \in [0, T]}$ denotes an ${\mathbb {R}}^m$-valued standard Wiener process. Further, suppose that $b(\cdot )$ and $\sigma (\cdot )$ are $\mathscr {B}(\mathbb R^d)$-measurable functions with values in ${\mathbb {R}}^d$ and ${\mathbb {R}}^{d\times m}$ respectively. Moreover, $b(\cdot )$ and $\sigma (\cdot )$ are continuously differentiable in $x\in \mathbb {R}^d$. For the purpose of this article, the following d-dimensional SDE is considered,

$$\begin{aligned} x_t&= \xi + \int _{0}^t b(x_s)ds+\int _{0}^t \sigma (x_s)dw_s, \end{aligned}$$

(2.1)

almost surely for any $t \in [0,T]$, where $\xi$ is an $\mathscr {F}_{0}$-measurable random variable in $\mathbb {R}^d$.

Let $p_0, p_1 \ge 2$ and $\rho \ge 1$ (or $\rho =0$) are fixed constants. The following assumptions are made.

A- 1

$E|\xi |^{p_0} < \infty$.

A- 2

There exists a constant $L>0$ such that

$$\begin{aligned} 2xb(x)+ (p_0-1)|\sigma (x)|^2 \le L(1+|x|^2) \end{aligned}$$

for any $x\in \mathbb {R}^d$.

A- 3

There exists a constant $L>0$ such that

$$\begin{aligned} 2(x-\bar{x})(b(x)-b(\bar{x}))+ (p_1-1)|\sigma (x)-\sigma (\bar{ x})|^2 \le L|x-\bar{x}|^2 \end{aligned}$$

for any $x, \bar{x} \in \mathbb {R}^d$.

A- 4

There exists a constant $L>0$ such that

$$\begin{aligned} |D b(x)-D b(\bar{x})|&\le L (1+|x|+|\bar{x}|)^{\rho -1}|x-\bar{x}| \end{aligned}$$

for any $x, \bar{x} \in \mathbb {R}^d$.

A- 5

There exists a constant $L>0$ such that, for every $j=1,\ldots , m$,

$$\begin{aligned} |D\sigma ^{(j)}(x)-D\sigma ^{(j)}(\bar{x})|&\le L (1+|x|+|\bar{x}|)^{\frac{\rho -2}{2}}|x-\bar{x}| \end{aligned}$$

for any $x,\bar{x} \in \mathbb {R}^d$.

Remark 2.1

Assumption A-4 means that there is a constant $L>0$ such that

$$\begin{aligned} \Big |\frac{\partial b^i(x)}{\partial x^j}\Big |&\le L(1+|x|)^{\rho } \end{aligned}$$

for any $x \in \mathbb {R}^d$ and for every $i,j=1,\ldots ,d$. As a consequence, one also obtains that there exists a constant $L>0$ such that

$$\begin{aligned} |b(x)-b(\bar{x})|&\le L (1+|x|+|\bar{x}|)^{\rho }|x-\bar{x}| \end{aligned}$$

for any $x , \bar{x} \in \mathbb {R}^d$. Moreover, this implies that b(x) satisfies,

$$\begin{aligned} |b(x)|&\le L(1+|x|)^{\rho +1} \end{aligned}$$

for any $x \in \mathbb {R}^d$. Furthermore, due to Assumption A-5, there exists a constant $L>0$ such that

$$\begin{aligned} \Big |\frac{\partial \sigma ^{(i,j)}(x)}{\partial x^k}\Big |&\le L(1+|x|)^{\frac{\rho }{2}} \end{aligned}$$

for any $x \in \mathbb {R}^d$ and for every $i,k=1,\ldots ,d$, $j=1,\ldots ,m$. Also, Assumption A-3 along with the estimate $|b(x)-b(\bar{x})| \le L (1+|x|+|\bar{x}|)^{\rho }|x-\bar{x}|$ obtained above, implies

$$\begin{aligned} |\sigma (x)-\sigma (\bar{x})|&\le L (1+|x|+|\bar{x}|)^\frac{\rho }{2} |x-\bar{x}| \end{aligned}$$

for any $x, \bar{x} \in \mathbb {R}^d$. Moreover, this means $\sigma (x)$ satisfies,

$$\begin{aligned} |\sigma (x)|&\le L(1+|x|)^{\frac{\rho +2}{2}} \end{aligned}$$

for any $x \in \mathbb {R}^d$. In addition, one notices that

$$\begin{aligned} |\varLambda ^j \sigma (x)|&\le L(1+|x|)^{\rho +1} \end{aligned}$$

for any $x \in \mathbb {R}^d$ and for every $j=1,\ldots ,m$.

For every $n \in \mathbb {N}$ and $x \in \mathbb {R}^d$, we define the following functions,

$$\begin{aligned} b^n(x)&:=\frac{b(x)}{1+n^{-\theta }|x|^{2\rho \theta }},\\ \sigma ^n(x)&:= \frac{\sigma (x)}{1+n^{-\theta }|x|^{2\rho \theta }}, \end{aligned}$$

where $\theta \ge \frac{1}{2}$ and, similarly, for the purposes of establishing a new, explicit Milstein-type scheme, for every $j=1,\ldots ,m$, we define

$$\begin{aligned} \varLambda ^{n,j}\sigma (x)&:= \frac{ \varLambda ^j \sigma (x)}{1+n^{-\theta }|x|^{2\rho \theta }}. \end{aligned}$$

Throughout this article, $\theta$ is taken to be 1, which corresponds to an order 1.0 Milstein scheme.

Remark 2.2

The case $\theta =1/2$ is studied in Sabanis [10], without the use of $\varLambda ^{n,j}\sigma (x)$, as the aim is the formulation of a new explicit Euler-type scheme. By taking different values of $\theta =1.5,2,2.5, \ldots$ and by appropriately controlling higher order terms, one can obtain analogous (to the value of $\theta$) rate of convergence results for higher order schemes by adopting the approach developed in Sabanis [10], Kumar and Sabanis [7] and in this article. One notes, of course, that further smoothness assumptions are also required in such cases.

Let us define $\kappa (n,t):=\lfloor nt \rfloor / n$ for any $t \in [0,T]$. Moreover, let us also define

$$\begin{aligned} \sigma _1^n(t, x)&:=\sum _{j=1}^{m}\int _{\kappa (n,t)}^t \varLambda ^{n,j}\sigma (x) dw_r^j =\sum _{j=1}^{m} \varLambda ^{n,j}\sigma (x) (w_t^j-w_{\kappa (n,t)}^j) \end{aligned}$$

and hence set

$$\begin{aligned} \tilde{\sigma }^n(t,x):= \sigma ^n(x) + \sigma _1^n(t,x) \end{aligned}$$

almost surely for any $x \in \mathbb {R}^d$, $n \in \mathbb {N}$ and $t \in [0,T]$. The above equality holds true when x is replaced by an $\mathscr {F}_{\kappa (n,t)}$-measurable random variables, which is the case always throughout this article.

Remark 2.3

In the following, $K>0$ denotes a generic constant that varies from place to place, but is always independent of $n \in \mathbb {N}$ and $x\in \mathbb {R}^d$.

Lemma 2.1

Let Assumptions A-3 to A-5 hold, then

$$\begin{aligned} |b^n(x)|&\le \min ( K n^{\frac{1}{2}}(1+|x|),|b(x)|)\\ |\sigma ^n(x)|^2&\le \min ( K n^{\frac{1}{2}}(1+|x|^2),|\sigma (x)|^2)\\ |\varLambda ^{n,j}\sigma (x)|&\le \min ( K n^{\frac{1}{2}}(1+|x|),|\varLambda (x)|) \end{aligned}$$

for every $n \in \mathbb {N}, x \in \mathbb {R}^d$ and $j=1,\ldots ,m$ where the positive constant K does not depend on n.

Proof

Clearly, Assumptions A-3 to A-5 give Remark 2.1 which are used throughout the proof of this lemma. Recall the definition of $b^n(x)$,

$$\begin{aligned} b^n(x):=\frac{b(x)}{1+n^{-\theta }|x|^{2\rho \theta }} \end{aligned}$$

for every $n\in \mathbb {N}$, $x\in \mathbb {R}^d$ and $\theta \ge 1/2$. For any $\theta \ge 1/2$, by noticing that the denominator of $b^n(x)$ is greater than 1, one can write

$$\begin{aligned} |b^n(x)|^{2\theta }=\frac{|b(x)|^{2\theta }}{(1+n^{-\theta }|x|^{2\rho \theta })^{2\theta }} \le \frac{|b(x)|^{2\theta }}{1+n^{-\theta }|x|^{2\rho \theta }} \end{aligned}$$

for any $n\in \mathbb {N}$ and $x\in \mathbb {R}^d$. Also, notice from Remark 2.1 that $|b(x)| \le L(1+|x|)^{\rho +1}$ for any $x\in \mathbb {R}^d$ which further gives,

$$\begin{aligned} |b^n(x)|^{2\theta }&\le L \frac{(1+|x|)^{2\theta (\rho +1)}}{1+n^{-\theta }|x|^{2\rho \theta }} = L n^\theta \frac{(1+|x|)^{2\theta \rho }}{n^{\theta }+|x|^{2\rho \theta }} (1+|x|)^{2\theta } \\&\le L 2^{2\theta \rho -1} n^\theta \frac{1+|x|^{2\theta \rho }}{n^{\theta }+|x|^{2\rho \theta }} (1+|x|)^{2\theta } \le L2^{2\theta \rho -1} n^{\theta } (1+|x|)^{2\theta } \end{aligned}$$

for every $n \in \mathbb {N}$ and $x\in \mathbb {R}^d$. By raising the power $1/(2\theta )$ on both the sides, one obtains

$$\begin{aligned} |b^n(x)| \le K n^{1/2}(1+|x|) \end{aligned}$$

(2.2)

where $K:=(L2^{2\theta \rho -1})^{1/(2\theta )}$, for every $n \in \mathbb {N}$ and $x\in \mathbb {R}^d$. Also, since in the definition of $b^n(x)$ above, the denominator is always greater than one, hence,

$$\begin{aligned} |b^n(x)| \le |b(x)| \end{aligned}$$

(2.3)

for every $n \in \mathbb {N}$ and $x\in \mathbb {R}^d$. On combining the estimates in (2.2) and (2.3), one obtains,

$$\begin{aligned} |b^n(x)| \le \min (K n^{\frac{1}{2}}(1+|x|), |b(x)|) \end{aligned}$$

for every $n \in \mathbb {N}$ and $x\in \mathbb {R}^d$.

The same proof will work for $\varLambda ^{n,j}\sigma (x)$ because $\varLambda ^{j}\sigma (x)$ has same polynomial growth as b(x) (see Remark 2.1). Also, similar proofs can be constructed for $\sigma ^n(x)$ by raising the power to $4\theta$ instead of $2\theta$. Again, recall definition of $\sigma ^n(x)$,

$$\begin{aligned} \sigma ^n(x):=\frac{\sigma (x)}{1+n^{-\theta }|x|^{2\rho \theta }} \end{aligned}$$

for every $n\in \mathbb {N}$, $x\in \mathbb {R}^d$ and $\theta \ge 1/2$. For any $\theta \ge 1/2$, by noticing that the denominator of $\sigma ^n(x)$ is greater than 1, one can write

$$\begin{aligned} |\sigma ^n(x)|^{4\theta }=\frac{|\sigma (x)|^{4\theta }}{(1+n^{-\theta }|x|^{2\rho \theta })^{4\theta }} \le \frac{|\sigma (x)|^{4\theta }}{1+n^{-\theta }|x|^{2\rho \theta }} \end{aligned}$$

for any $n\in \mathbb {N}$ and $x\in \mathbb {R}^d$. Also, notice that due to Remark 2.1, $|\sigma ^n(x)| \le L(1+|x|)^{\frac{\rho }{2}+1}$ which gives

$$\begin{aligned} |\sigma ^n(x)|^{4\theta }&\le L n^\theta \frac{(1+|x|)^{2\theta \rho }}{n^{\theta }+|x|^{2\rho \theta }} (1+|x|)^{4\theta } \le L 2^{2\theta \rho -1} n^\theta \frac{1+|x|^{2\theta \rho }}{n^{\theta }+|x|^{2\rho \theta }} (1+|x|)^{4\theta } \\&\le L2^{2\theta \rho -1} n^{\theta } (1+|x|)^{4\theta } \end{aligned}$$

for every $n \in \mathbb {N}$ and $x\in \mathbb {R}^d$. By raising the power $1/(4\theta )$ on both the sides, one obtains

$$\begin{aligned} |\sigma ^n(x)| \le K n^{1/4}(1+|x|) \end{aligned}$$

(2.4)

where $K:=(L2^{2\theta \rho -1})^{1/(4\theta )}$, for every $n \in \mathbb {N}$ and $x\in \mathbb {R}^d$. Also, since in the definition of $\sigma ^n(x)$ above, the denominator is always greater than one, hence,

$$\begin{aligned} |\sigma ^n(x)| \le |\sigma (x)| \end{aligned}$$

(2.5)

for every $n \in \mathbb {N}$ and $x\in \mathbb {R}^d$. On combining the estimates in (2.4) and (2.5), one obtains,

$$\begin{aligned} |\sigma ^n(x)| \le \min (K n^{\frac{1}{4}}(1+|x|), |\sigma (x)|) \end{aligned}$$

for every $n \in \mathbb {N}$ and $x\in \mathbb {R}^d$. This completes the proof.

We propose below a new variant of the Milstein scheme with coefficients which vary according to the choice of the time step. The aim is to approximate solutions of non-linear SDEs such as Eq. (2.1). The new explicit scheme is given below

$$\begin{aligned} x_t^n&= \xi + \int _{0}^t b^n(x_{\kappa (n,s)}^n)ds+\int _{0}^t \tilde{\sigma }^n(s, x_{\kappa (n,s)}^n)dw_s \end{aligned}$$

(2.6)

almost surely for any $t \in [0,T]$.

The main result of this article is stated in the following theorem.

Theorem 2.1

Let Assumptions A-1 to A-5 be satisfied with $p_0\ge 2(3\rho +1)$ and $p_1>2$. Then, the explicit Milstein-type scheme (2.6) converges in $\mathscr {L}^p$ to the true solution of SDE (2.1) with a rate of convergence equal to 1.0, i.e. for every $n \in \mathbb {N}$

$$\begin{aligned} \sup _{0 \le t \le T}E|x_t-x_t^n|^p \le K n^{-p}, \end{aligned}$$

(2.7)

when $p=2$. Moreover, if $p_0\ge 4(3\rho +1)$, then (2.7) is true for any $p \le \frac{p_0}{3\rho +1}$ provided that $p<p_1$.

Remark 2.4

One observes immediately that for the case $\rho =0$, one recovers, due to Assumptions A-1 to A-5 and Theorem 2.1, the classical Milstein framework and results (with some improvement perhaps as the coefficients of (2.1) are required only to be once continuously differentiable in this article).

Remark 2.5

In order to ease notation, it is chosen not to explicitly present the calculations for, and thus it is left as an exercise to the reader, the case where the drift and/or the diffusion coefficients contain parts which are Lipschitz continuous and grow at most linearly (in x). In such a case, the analysis for these parts follows closely the classical approach and the main theorem/results of this article remain true. Furthermore, note that such a statement applies also in the case of non-autonomous coefficients in which typical assumptions for the smoothness of coefficients in t are considered (as, for example, in [1]).

The details of the proof of the main result, i.e. Theorem 2.1, and of the required lemmas are given in the next two sections.

3 Moment bounds

It is a well-known fact that due to Assumptions A-1 to A-3, the $p_0$-th moment of the true solution of (2.1) is bounded uniformly in time.

Lemma 3.1

Let Assumptions A-1 to A-3 be satisfied. Then, there exists a unique solution $(x_t)_{t \in [0,T]}$ of SDE (2.1) and the following holds,

$$\begin{aligned} \sup _{0 \le t \le T }E|x_t|^{p_0} \le K. \end{aligned}$$

The proof of the above lemma can be found in many textbooks, e.g. see Mao [8]. The following lemmas are required in order to allow one to obtain moment bounds for the new explicit scheme (2.6).

Remark 3.1

Another useful observation is that for every fixed $n \in \mathbb {N}$ and due to Remark 2.1, the $p_0$-th moment of the new Milstein-type scheme (2.6) is bounded uniformly in time (as in the case of the classical Milstein scheme/framework with SDE coefficients which grow at most linearly). Clearly, one cannot claim at this point that such a bound is independent of n. However, the use of stopping times in the derivation of moment bounds henceforth can be avoided.

Lemma 3.2

Let Assumption A-5 be satisfied. Then,

$$\begin{aligned} E|\sigma _1^n(t, x_{\kappa (n,t)}^n)|^{p_0} \le K (1+ E|x_{\kappa (n,t)}^n|^{p_0}) \le K E(1+ |x_{\kappa (n,t)}^n|^2)^{p_0/2} \end{aligned}$$

for any $t \in [0,T]$ and $n \in \mathbb {N}$.

Proof

On using an elementary inequality of stochastic integrals and Hölder’s inequality, one obtains

$$\begin{aligned} E|\sigma _1^{n}(t, x_{\kappa (n,t)}^n)|^{p_0}&= K E\Big |\sum _{j=1}^{m}\int _{\kappa (n,t)}^t \varLambda ^{n,j} \sigma (x_{\kappa (n,s)}^n)dw_s^j\Big |^{p_0}\\&\le K n^{-\frac{p_0}{2}+1} E \int _{\kappa (n,t)}^t |\varLambda ^{n,j} \sigma (x_{\kappa (n,s)}^n)|^{p_0} ds \end{aligned}$$

which due to Remark 2.1 gives

$$\begin{aligned} E|\sigma _1^{n}(t, x_{\kappa (n,t)}^n)|^{p_0}&\le K n^{-\frac{p_0}{2}+1} E \int _{\kappa (n,t)}^t n^{\frac{p_0}{2}}(1+|x_{\kappa (n,s)}^n|^{p_0}) ds \end{aligned}$$

and hence the proof completes.

The following corollary is an immediate consequence of Lemma 3.2 and Remark 2.1.

Corollary 3.1

Let Assumption A-5 be satisfied. Then

$$\begin{aligned} E|\tilde{\sigma }^n(t, x_{\kappa (n,t)}^n)|^{p_0} \le K n^{\frac{p_0}{4}}(1+E|x_{\kappa (n,t)}^n|^{p_0})\le Kn^\frac{p_0}{4}E(1+|x_{\kappa (n,t)}^n|^2)^\frac{p_0}{2} \end{aligned}$$

for any $n \in \mathbb {N}$ and $t \in [0,T]$.

Lemma 3.3

Let Assumptions A-1 to A-5 be satisfied. Then, the explicit Milstein-type scheme (2.6) satisfies the following,

$$\begin{aligned} \sup _{n \in \mathbb {N}} \sup _{0 \le t \le T}E|x_t^n|^{p_0} \le K. \end{aligned}$$

Proof

By Itô’s formula on the functional $(1+|x|^2)^{p/2}$ for $x\in \mathbb {R}^d$, one obtains

$$\begin{aligned} (1+|x_t^n|^2)^{p_0/2}&=(1+|\xi |^2)^{p_0/2} + p_0 \int _0^t (1+|x_s^n|^2)^{p_0/2-1} x_s^n b^n(x_{\kappa (n,s)}^n)ds\\&\quad +p_0 \int _0^t (1+|x_s^n|^2)^{p_0/2-1} x_s^n \tilde{\sigma }^n(s, x_{\kappa (n,s)}^n) dw_s\\&\quad +\frac{p_0(p_0-2)}{2} \int _0^t (1+|x_s^n|^2)^{p_0/2-2} |\tilde{\sigma }^{n*}(s, x_{\kappa (n,s)}^n)x_s^n|^2 ds\\&\quad + \frac{p_0}{2} \int _0^t (1+|x_s^n|^2)^{p_0/2-1} |\tilde{\sigma }^{n}(s, x_{\kappa (n,s)}^n)|^2 ds, \end{aligned}$$

and then on taking expectation along with Schwarz inequality,

$$\begin{aligned} E(1+|x_t^n|^2)^{p_0/2}&\le E(1+|\xi |^2)^{p_0/2} +p_0 E\int _0^t (1+|x_s^n|^2)^{p_0/2-1} (x_s^n-x_{\kappa (n,s)}^n) b^n(x_{\kappa (n,s)}^n)ds\\&\quad +p_0 E\int _0^t (1+|x_s^n|^2)^{p_0/2-1} x_{\kappa (n,s)}^n b^n(x_{\kappa (n,s)}^n)ds\\&\quad +\frac{p_0(p_0-1)}{2} E \int _0^t (1+|x_s^n|^2)^{p_0/2-1} |\tilde{\sigma }^{n}(s, x_{\kappa (n,s)}^n)|^2 ds \end{aligned}$$

for any $t \in [0,T]$ and $n\in \mathbb {N}$. Then, one uses $|z_1+z_2|^2 = |z_1|^2+2\sum _{i=1}^{d}\sum _{j=1}^{m}z_1^{(i,j)}z_2^{(i,j)}+|z_2|^2$ for $z_1,z_2 \in \mathbb {R}^{d\times m}$ to obtain the following estimates,

$$\begin{aligned} E(1+|x_t^n|^2)^{p_0/2}&\le E(1+|\xi |^2)^{p_0/2} +p_0 E\int _0^t (1+|x_s^n|^2)^{p_0/2-1} (x_s^n-x_{\kappa (n,s)}^n) b^n(x_{\kappa (n,s)}^n)ds \nonumber \\&\quad +\frac{p_0}{2} E\int _0^t (1+|x_s^n|^2)^{p_0/2-1} \{2x_{\kappa (n,s)}^n b^n(x_{\kappa (n,s)}^n)+(p_0-1)|\sigma ^{n}(x_{\kappa (n,s)}^n)|^2\}ds \nonumber \\&\quad +\frac{p_0(p_0-1)}{2} E \int _0^t (1+|x_s^n|^2)^{p_0/2-1} |\sigma ^{n}_1(s, x_{\kappa (n,s)}^n)|^2 ds \nonumber \\&\quad +p_0(p_0-1) E \int _0^t (1+|x_s^n|^2)^{p_0/2-1} \sum _{i=1}^{d}\sum _{j=1}^{m}\sigma ^{n,(i,j)}(x_{\kappa (n,s)}^n) \sigma ^{n,(i,j)}_1(s, x_{\kappa (n,s)}^n) ds \nonumber \\&=: C_1+C_2+C_3+C_4+C_5. \end{aligned}$$

(3.1)

Here, $C_1:=E(1+|\xi |^2)^{p_0/2}$. For $C_2$, one notices that it can be written as

$$\begin{aligned} C_2&:= p_0 E\int _0^t (1+|x_s^n|^2)^{p_0/2-1} (x_s^n-x_{\kappa (n,s)}^n) b^n(x_{\kappa (n,s)}^n)ds\\&= p_0 E\int _0^t (1+|x_s^n|^2)^{p_0/2-1} \int ^s_{\kappa (n,s)} b^n(x_{\kappa (n,r)}^n)dr b^n(x_{\kappa (n,s)}^n)ds\\&\quad +\, p_0 E\int _0^t (1+|x_s^n|^2)^{p_0/2-1} \int ^s_{\kappa (n,s)} \tilde{\sigma }^n(r, x_{\kappa (n,r)}^n)dw_r b^n(x_{\kappa (n,s)}^n)ds \end{aligned}$$

which on the application of Remark  2.1 and Young’s inequality gives,

$$\begin{aligned} C_2 \le&K \int _0^t E (1+|x_s^n|^2)^{p_0/2} ds + K \int _0^t E (1+|x_{\kappa (n,s)}^n|^2)^{p_0/2} ds\\&+ p_0 E\int _0^t (1+|x_{\kappa (n,s)}^n|^2)^{p_0/2-1} \int ^s_{\kappa (n,s)} \tilde{\sigma }^n(r, x_{\kappa (n,r)}^n)dw_r b^n(x_{\kappa (n,s)}^n)ds\\&+ p_0 E\int _0^t ((1+|x_s^n|^2)^{p_0/2-1}-(1+|x_{\kappa (n,s)}^n|^2)^{p_0/2-1}) \nonumber \\&\times \int ^s_{\kappa (n,s)} \tilde{\sigma }^n(r, x_{\kappa (n,r)}^n)dw_r b^n(x_{\kappa (n,s)}^n)ds \end{aligned}$$

for any $t \in [0,T]$ and $n\in \mathbb {N}$. Further, one observes that the second term of the above equation is zero and the third term can be estimated by the application of Itô’s formula as below,

$$\begin{aligned} C_2 \le&\, K \int _0^t \sup _{0 \le r \le s}E(1{+}|x_r^n|^2)^{p_0/2} ds {+} K E\int _0^t \int _{\kappa (n,s)}^s (1{+}|x_r^n|^2)^{p_0/2-2} x_r^n b^n(x_{\kappa (n,r)}^n)dr\\&\times \int ^s_{\kappa (n,s)} \tilde{\sigma }^n(r, x_{\kappa (n,r)}^n)dw_r b^n(x_{\kappa (n,s)}^n)ds\\&+ K E\int _0^t \int _{\kappa (n,s)}^s (1+|x_r^n|^2)^{p_0/2-2} x_r^n \tilde{\sigma }^n(r, x_{\kappa (n,r)}^n) dw_r\\&\times \int ^s_{\kappa (n,s)} \tilde{\sigma }^n(r, x_{\kappa (n,r)}^n)dw_r b^n(x_{\kappa (n,s)}^n)ds\\&+ K E\int _0^t \int _{\kappa (n,s)}^s (1+|x_r^n|^2)^{p_0/2-2} |\tilde{\sigma }^{n}(r, x_{\kappa (n,r)}^n)|^2 dr\\&\times \mid \int ^s_{\kappa (n,s)} \tilde{\sigma }^n(r, x_{\kappa (n,r)}^n)dw_r \mid \mid b^n(x_{\kappa (n,s)}^n)\mid ds \end{aligned}$$

for any $t \in [0,T]$ and $n\in \mathbb {N}$. Due to Remark 2.1 along with an elementary inequality of stochastic integrals, the following estimates can be obtained,

$$\begin{aligned} C_2&\le K \int _0^t \sup _{0 \le r \le s}E(1+|x_r^n|^2)^{p_0/2} ds\\&\quad + K n E\int _0^t \int _{\kappa (n,s)}^s (1+|x_{\kappa (n,s)}^n|^2)(1+|x_r^n|^2)^{(p_0-3)/2} dr\\&\qquad \Big |\int ^s_{\kappa (n,s)} \tilde{\sigma }^n(r, x_{\kappa (n,r)}^n)dw_r \Big | ds\\&\quad + K n^{\frac{1}{2}}E\int _0^t \int _{\kappa (n,s)}^s (1+|x_{\kappa (n,s)}^n|)(1+|x_r^n|^2)^{(p_0-3)/2} |\tilde{\sigma }^n(r, x_{\kappa (n,r)}^n)|^2 dr ds\\&\quad + K n^\frac{1}{2} E\int _0^t \int _{\kappa (n,s)}^s (1+|x_{\kappa (n,s)}^n|) (1+|x_r^n|^2)^{(p_0-4)/2} |\tilde{\sigma }^{n}(r,x_{\kappa (n,r)}^n)|^2 dr\\&\quad \times \Big |\int ^s_{\kappa (n,s)} \tilde{\sigma }^n(r, x_{\kappa (n,r)}^n)dw_r \Big |ds \end{aligned}$$

for any $t\in [0,T]$ and $n\in \mathbb {N}$. Noticing that when $p_0\le 3$, $(1+|x_r^n|^2)^{(p_0-3)/2}\le 1$, one can obtain the following estimate,

$$\begin{aligned} C_2&\le K \int _0^t \sup _{0 \le r \le s} E(1+|x_r^n|^2)^{p_0/2} ds\\&\quad + K E\int _0^t n^\frac{3}{4} \int _{\kappa (n,s)}^s (1+|x_{\kappa (n,s)}^n|^2+|x_r^n|^2)^{(p_0-1)/2} dr n^\frac{1}{4}\Big |\int ^s_{\kappa (n,s)} \tilde{\sigma }^n(r, x_{\kappa (n,r)}^n)dw_r \Big | ds\\&\quad + K E\int _0^t \int _{\kappa (n,s)}^s n^{1-\frac{2}{p_0}}(1+|x_{\kappa (n,s)}^n|^2+|x_r^n|^2)^{(p_0-2)/2} n^{-\frac{1}{2}+\frac{2}{p_0}}|\tilde{\sigma }^n(r, x_{\kappa (n,r)}^n)|^2 dr ds\\&\quad + K E\int _0^t n^\frac{1}{4} \int _{\kappa (n,s)}^s (1+|x_{\kappa (n,s)}^n|^2+|x_r^n|^2)^{(p_0-2)/2} \frac{ |\tilde{\sigma }^{n}(r, x_{\kappa (n,r)}^n)|^2}{1+|x_{\kappa (n,r)}^n|} dr\\&\quad \times n^{\frac{1}{4}} \Big |\int ^s_{\kappa (n,s)} \tilde{\sigma }^n(r, x_{\kappa (n,r)}^n)dw_r \Big |ds \end{aligned}$$

and then one uses Young’s inequality to obtain the following estimates,

$$\begin{aligned} C_2&\le K \int _0^t \sup _{0 \le r \le s}E(1+|x_r^n|^2)^{p_0/2} ds\\&\quad + K n^\frac{3p_0}{4(p_0-1)} E\int _0^t \Big (\int _{\kappa (n,s)}^s (1+|x_{\kappa (n,s)}^n|^2+|x_r^n|^2)^{(p_0-1)/2} dr\Big )^\frac{p_0}{p_0-1} ds\\&\quad + K n E\int _0^t \int _{\kappa (n,s)}^s (1+|x_{\kappa (n,s)}^n|^2+|x_r^n|^2)^{p_0/2} dr ds\\&\quad {+} K n^\frac{p_0}{4(p_0-1)} E\int _0^t \Big (\int _{\kappa (n,s)}^s (1{+}|x_{\kappa (n,s)}^n|^2+|x_r^n|^2)^{(p_0-2)/2} \frac{\mid \tilde{\sigma }^n(r,x_{\kappa (n,r)}^n) \mid ^2}{1+|x_{\kappa (n,s)}^n|} dr\Big )^\frac{p_0}{p_0-1}ds\\&\quad + K n^{\frac{p_0}{4}} E\int _0^t \Big |\int ^s_{\kappa (n,s)} \tilde{\sigma }^n(r,x_{\kappa (n,r)}^n)dw_r \Big |^{p_0} ds\\&\quad + K n^{-\frac{p_0}{4}+1} E\int _0^t \int ^s_{\kappa (n,s)} |\tilde{\sigma }^n(r, x_{\kappa (n,r)}^n)|^{p_0}dr ds \end{aligned}$$

for any $t \in [0,T]$ and $n\in \mathbb {N}$. Further, by the application of Hölder’s inequality and an elementary inequality of stochastic integrals, one obtains the following estimates,

$$\begin{aligned} C_2&\le K \int _0^t \sup _{0 \le r \le s}E(1+|x_r^n|^2)^{p_0/2} ds\\&+ K n^{\frac{3p_0}{4(p_0-1)}-\frac{p_0}{p_0-1}+1} E\int _0^t \int _{\kappa (n,s)}^s (1+|x_{\kappa (n,s)}^n|^2+|x_r^n|^2)^{\frac{p_0}{2}} dr ds\\&+ K E\int _0^t n \int _{\kappa (n,s)}^s (1+|x_{\kappa (n,s)}^n|^2+|x_r^n|^2)^{\frac{p_0(p_0-2)}{2(p_0-1)}}\\&\times n^{-\frac{3p_0}{4(p_0-1)}} \Big ( \frac{\mid \tilde{\sigma }^n(r,x_{\kappa (n,r)}^n)\mid ^2}{1+|x^n_{\kappa (n,r)}|}\Big )^\frac{p_0}{p_0-1} drds\\&+ K n^{-\frac{p_0}{4}+1} E\int _0^t \int ^s_{\kappa (n,s)} |\tilde{\sigma }^n(r, x_{\kappa (n,r)}^n)|^{p_0}dr ds \end{aligned}$$

which due to Corollary 3.1 and Young’s inequality yields

$$\begin{aligned} C_2&\le K \int _0^t \sup _{0 \le r \le s}E(1+|x_r^n|^2)^{p_0/2} ds\\&+ K E\int _0^t n \int _{\kappa (n,s)}^s (1+|x_{\kappa (n,s)}^n|^2+|x_r^n|^2)^{\frac{p_0}{2}} dr\\&+ K E\int _0^t n \int _{\kappa (n,s)}^s n^{-\frac{3p_0}{4}} \Big ( \frac{\mid \tilde{\sigma }^n(r,x_{\kappa (n,r)}^n)\mid ^2}{1+|x^n_{\kappa (n,r)}|}\Big )^{p_0} drds \end{aligned}$$

for any $t\in [0,T]$ and $n\in \mathbb {N}$. Now, one only requires the estimates of the last term of $C_2$ which can be done as follows. Due to Remark 2.1, one has

$$\begin{aligned} E\Big ( \frac{\mid \tilde{\sigma }^n(r,x_{\kappa (n,r)}^n)\mid ^2}{1+|x^n_{\kappa (n,r)}|}\Big )^{p_0}&\le K E \frac{\mid \sigma ^n(x_{\kappa (n,r)}^n)\mid ^{2p_0}}{(1+|x^n_{\kappa (n,r)}|)^{p_0}} + K E \frac{\mid \sigma ^n_1(r, x_{\kappa (n,r)}^n)\mid ^{2p_0}}{(1+|x^n_{\kappa (n,r)}|)^{p_0}}\\&\le K n^\frac{p_0}{2} E \frac{(1+\mid x_{\kappa (n,r)}^n\mid )^{2p_0}}{(1+|x^n_{\kappa (n,r)}|)^{p_0}}\\&+ K E \frac{\mid \sum _{j=1}^m\int _{\kappa (n,r)}^r \varLambda ^{n,j}\sigma (x_{\kappa (n,u)}^n)dw_u^j\mid ^{2p_0}}{(1+|x^n_{\kappa (n,r)}|)^{p_0}} \end{aligned}$$

and then the application of and an elementary inequality of stochastic integrals,

$$\begin{aligned} E\Big ( \frac{\mid \tilde{\sigma }^n(r,x_{\kappa (n,r)}^n)\mid ^2}{1+|x^n_{\kappa (n,r)}|}\Big )^{p_0}&\le K n^\frac{p_0}{2} E (1+\mid x_{\kappa (n,r)}^n\mid )^{p_0}\\&+ K E \Big ( \sum _{j=1}^m\int _{\kappa (n,r)}^r \frac{|\varLambda ^{n,j}\sigma (x_{\kappa (n,u)}^n)|^2}{1+|x^n_{\kappa (n,u)}|} du \Big )^{p_0} \end{aligned}$$

which again due to Remark 2.1 gives,

$$\begin{aligned} E\Big (\frac{\mid \tilde{\sigma }^n(r,x_{\kappa (n,r)}^n)\mid ^2}{1+|x_{\kappa (n,r)}|}\Big )^{p_0}&\le K n^\frac{p_0}{2} E (1+\mid x_{\kappa (n,r)}^n\mid ^2)^{p_0/2}\nonumber \\&\quad + K E \Big (\int _{\kappa (n,r)}^r \frac{n(1+|x_{\kappa (n,u)}^n|)^2}{1+|x^n_{\kappa (n,u)}|} du \Big )^{p_0}\nonumber \\&\le K n^\frac{p_0}{2} E (1+\mid x_{\kappa (n,r)}^n\mid ^2)^{p_0/2} \end{aligned}$$

(3.2)

for any $t\in [0,T]$ and $n\in \mathbb {N}$. By substituting the estimates from (3.2) in $C_2$ above, one obtains the following,

$$\begin{aligned} C_2&\le K \int _0^t \sup _{0 \le r \le s}E(1+|x_r^n|^2)^{p_0/2} ds \end{aligned}$$

(3.3)

for any $t\in [0,T]$ and $n\in \mathbb {N}$. For $C_3$, one uses Assumption A-2 to obtain the following,

$$\begin{aligned} C_3&:=\frac{p_0}{2} E\int _0^t (1+|x_s^n|^2)^{p_0/2-1} \{2x_{\kappa (n,s)}^n b^n(x_{\kappa (n,s)}^n)+(p_0-1)|\sigma ^{n}(x_{\kappa (n,s)}^n)|^2\}ds\\&= \frac{p_0}{2} E\int _0^t (1+|x_s^n|^2)^{p_0/2-1} \frac{2x_{\kappa (n,s)}^n b(x_{\kappa (n,s)}^n)+(p_0-1)|\sigma (x_{\kappa (n,s)}^n)|^2}{1+n^{-1}|x_{\kappa (n,s)}^n|^{2\rho +4}} ds \\&\le K E\int _0^t (1+|x_s^n|^2)^{p_0/2-1} \frac{1+|x_{\kappa (n,s)}^n|^2}{1+n^{-1}|x_{\kappa (n,s)}^n|^{2\rho +4}} ds \end{aligned}$$

which due to Young’s inequality gives,

$$\begin{aligned} C_3\le K \int _0^t \sup _{0 \le r \le s}E(1+|x_r^n|^2)^{p_0/2} ds \end{aligned}$$

(3.4)

for any $t \in [0,T]$ and $n\in \mathbb {N}$. Furthermore, by using Young’s inequality, $C_4$ in (3.1) is estimated as,

$$\begin{aligned} C_4&:=\frac{p_0(p_0-1)}{2} E \int _0^t (1+|x_s^n|^2)^{p_0/2-1} |\sigma ^{n}_1(s, x_{\kappa (n,s)}^n)|^2 ds\\&\le K E \int _0^t (1+|x_s^n|^2)^{p_0/2} ds + K E \int _0^t |\sigma ^{n}_1(s, x_{\kappa (n,s)}^n)|^{p_0} ds \end{aligned}$$

and then on the application of Lemma 3.2, one obtains

$$\begin{aligned} C_4 \le K \int _0^t \sup _{0 \le r \le s}E(1+|x_r^n|^2)^{p_0/2} ds \end{aligned}$$

(3.5)

for any $t \in [0,T]$ and $n\in \mathbb {N}$. Now, for estimating $C_5$, one writes

$$\begin{aligned} C_5&:=p_0(p_0{-}1) E \int _0^t (1+|x_s^n|^2)^{p_0/2-1} \sum _{i=1}^{d}\sum _{j=1}^{m}\sigma ^{n,(i,j)}(x_{\kappa (n,s)}^n) \sigma ^{n,(i,j)}_1(s, x_{\kappa (n,s)}^n) ds\\&\le K E \int _0^t (1+|x_{\kappa (n,s)}^n|^2)^{p_0/2-1} \sum _{i=1}^{d}\sum _{j=1}^{m}\sigma ^{n,(i,j)}(x_{\kappa (n,s)}^n)\\&\qquad \times \sum _{k=1}^{m} \int _{\kappa (n,s)}^{s} \varLambda ^{n,k} \sigma ^{n,(i,j)}(x_{\kappa (n,r)}^n)dw_r^k ds\\&\qquad +K E \int _0^t ((1+|x_s^n|^2)^{p_0/2-1}-(1+|x_{\kappa (n,s)}^n|^2)^{p_0/2-1}) \\&\qquad \times \sum _{i=1}^{d}\sum _{j=1}^{m}\sigma ^{n,(i,j)}(x_{\kappa (n,s)}^n)\sigma ^{n,(i,j)}_1(s, x_{\kappa (n,s)}^n) ds \end{aligned}$$

for any $t \in [0,T]$ and $n\in \mathbb {N}$. Clearly, the first term is zero and one uses Itô’s formula for the second term to obtain the following,

$$\begin{aligned} C_5&\le K E \int _0^t \int _{\kappa (n,s)}^{s} (1+|x_r^n|^2)^{p_0/2-2}x_r^nb^n(x_{\kappa (n,r)}^n)dr\\&\qquad \quad \times \sum _{i=1}^{d}\sum _{j=1}^{m}\sigma ^{n,(i,j)}(x_{\kappa (n,s)}^n)\sigma ^{n,(i,j)}_1(s, x_{\kappa (n,s)}^n) ds\\&\qquad \quad +K E \int _0^t \int _{\kappa (n,s)}^{s} (1+|x_r^n|^2)^{p_0/2-2}x_r^n \tilde{\sigma }^n(r,x_{\kappa (n,r)}^n)dw_r\\&\qquad \times \sum _{i=1}^{d}\sum _{j=1}^{m}\sigma ^{n,(i,j)}(x_{\kappa (n,s)}^n)\sum _{k=1}^{m} \int _{\kappa (n,s)}^{s} \varLambda ^{n,k} \sigma ^{n,(i,j)}(x_{\kappa (n,r)}^n)dw_r^k ds\\&\qquad +K E \int _0^t \int _{\kappa (n,s)}^{s} (1+|x_r^n|^2)^{p_0/2-2} |\tilde{\sigma }^n(r,x_{\kappa (n,r)}^n)|^2dr\\&\qquad \times \left| \sum _{i=1}^{d}\sum _{j=1}^{m}\sigma ^{n,(i,j)}(x_{\kappa (n,s)}^n)\sigma ^{n,(i,j)}_1(s, x_{\kappa (n,s)}^n)\right| ds \end{aligned}$$

which on using Schwarz inequality and Remark 2.1 along with an elementary inequality of stochastic integrals yields,

$$\begin{aligned} C_5&\le K n^{\frac{3}{4}} E \int _0^t (1+|x_{\kappa (n,s)}^n|)^2\int _{\kappa (n,s)}^{s} (1+|x_r^n|^2)^{(p_0-3)/2}dr |\sigma ^{n}_1(s,x_{\kappa (n,s)}^n)| ds\\&\quad +K n^{\frac{3}{4}} E \int _0^t (1+|x_{\kappa (n,s)}^n|)^2 \int _{\kappa (n,s)}^{s} (1+|x_r^n|^2)^{(p_0-3)/2} |\tilde{\sigma }^n(r,x_{\kappa (n,r)}^n)|dr ds\\&\quad +K n^{\frac{1}{4}}E \int _0^t (1+|x_{\kappa (n,s)}^n|) \int _{\kappa (n,s)}^{s} (1+|x_r^n|^2)^{(p_0-4)/2} |\tilde{\sigma }^n(r,x_{\kappa (n,r)}^n)|^2\\&\quad dr|\sigma ^{n}_1(s,x_{\kappa (n,s)}^n)| ds \end{aligned}$$

and this can further be estimated as,

$$\begin{aligned} C_5&\le K E \int _0^t n^{\frac{3}{4}} \int _{\kappa (n,s)}^{s} (1+|x_{\kappa (n,s)}^n|^2+|x_r^n|^2)^{(p_0-1)/2}dr \times |\sigma ^{n}_1(s,x_{\kappa (n,s)}^n)| ds\\&\quad +K E \int _0^t \int _{\kappa (n,s)}^{s} n^\frac{p_0-1}{p_0}(1+|x_{\kappa (n,s)}^n|^2+|x_r^n|^2)^{(p_0-1)/2}\\&\quad \times n^{\frac{3}{4}-\frac{p_0-1}{p_0}}|\tilde{\sigma }^n(r,x_{\kappa (n,r)}^n)|dr ds\\&\quad +K E \int _0^t n^{\frac{1}{4}}\int _{\kappa (n,s)}^{s} (1+|x_{\kappa (n,s)}^n|^2+|x_r^n|^2)^{(p_0-2)/2} \frac{|\tilde{\sigma }^n(r,x_{\kappa (n,r)}^n)|^2}{1+|x_{\kappa (n,r)}^n|}\\&\qquad dr |\sigma ^{n}_1(s,x_{\kappa (n,s)}^n)| ds \end{aligned}$$

for any $t \in [0,T]$ and $n\in \mathbb {N}$. Further, one uses Young’s inequality to obtain the following estimates,

$$\begin{aligned} C_5&\le K E \int _0^t \Big (n^{\frac{3}{4}} \int _{\kappa (n,s)}^{s} (1+|x_{\kappa (n,s)}^n|^2+|x_r^n|^2)^{(p_0-1)/2}dr \Big )^{\frac{p_0}{p_0-1}}ds\\&\quad +K E \int _0^t \int _{\kappa (n,s)}^{s} n (1+|x_{\kappa (n,s)}^n|^2+|x_r^n|^2)^{p_0/2} dr ds\\&\quad + K E \int _0^t \int _{\kappa (n,s)}^{s} n^{\frac{3p_0}{4}-p_0+1}|\tilde{\sigma }^n(r,x_{\kappa (n,r)}^n)|dr ds\\&\quad {+}K E \int _0^t\Big (n^{\frac{1}{4}} \int _{\kappa (n,s)}^{s} (1+|x_{\kappa (n,s)}^n|^2+|x_r^n|^2)^{(p_0-2)/2} \frac{|\tilde{\sigma }^n(r,x_{\kappa (n,r)}^n)|^2}{1+|x_{\kappa (n,r)}^n|} dr \Big )^\frac{p_0}{p_0-1} ds\\&\quad + K E \int _0^t |\sigma ^{n}_1(s,x_{\kappa (n,s)}^n)|^{p_0} ds \end{aligned}$$

which on using Hölder’s inequality, Lemma 3.2 and Corollary 3.1 gives,

$$\begin{aligned} C_5&\le K \int _0^t \sup _{0 \le r \le s}E(1+|x_r^n|^2)^{p_0/2} ds\\&\quad + K E \int _0^t n^{\frac{3p_0}{4(p_0-1)}-\frac{p_0}{p_0-1}+1} \int _{\kappa (n,s)}^{s} (1+|x_{\kappa (n,s)}^n|^2+|x_r^n|^2)^{p_0/2}dr\\&\quad +K E \int _0^t \int _{\kappa (n,s)}^{s} n^{\frac{p_0-2}{p_0-1}} (1+|x_{\kappa (n,s)}^n|^2+|x_r^n|^2)^\frac{p_0(p_0-2)}{2(p_0-1)} n^{-\frac{3p_0}{4(p_0-1)} -\frac{p_0-2}{p_0-1}+1}\\&\quad \times \Big (\frac{|\tilde{\sigma }^n(r,x_{\kappa (n,r)}^n)|^2}{1+|x_{\kappa (n,r)}^n|} \Big )^\frac{p_0}{p_0-1}dr ds \end{aligned}$$

and then one again uses Young’s inequality to obtain,

$$\begin{aligned} C_5&\le K \int _0^t \sup _{0 \le r \le s}E(1+|x_r^n|^2)^{p_0/2} ds\\&\quad +K E \int _0^t n \int _{\kappa (n,s)}^{s} (1+|x_{\kappa (n,s)}^n|^2+|x_r^n|^2)^{p_0/2} dr ds\\&\quad +K E \int _0^t n^{-\frac{3p_0}{4}+1} \int _{\kappa (n,s)}^{s} \Big (\frac{|\tilde{\sigma }^n(r,x_{\kappa (n,r)}^n)|^2}{1+|x_{\kappa (n,r)}^n|} \Big )^{p_0} dr ds \end{aligned}$$

for any $t\in [0,T]$ and $n\in \mathbb {N}$. Thus by the estimates obtained in (3.2), one has

$$\begin{aligned} C_5&\le K \int _0^t \sup _{0 \le r \le s}E(1+|x_r^n|^2)^{p_0/2} ds \end{aligned}$$

(3.6)

for any $t \in [0,T]$ and $n\in \mathbb {N}$. By substituting estimates from (3.3), (3.4), (3.5) and (3.6) in (3.1), the following estimates are obtained,

$$\begin{aligned} \sup _{0 \le s \le t} E(1+|x_s^n|^2)^{p_0/2} \le K+ K \int _0^t \sup _{0 \le r \le s}E(1+|x_r^n|^2)^{p_0/2} ds<\infty \end{aligned}$$

for any $t \in [0,T]$ and $n\in \mathbb {N}$. The proof is completed by the Gronwall’s lemma.

4 Proof of main result

A simple application of the mean value theorem, which appears in the Lemma below, allows us to simplify substantially the proof of Theorem 2.1. Furthermore, throughout this section, it is assumed that $p_0\ge 2(3\rho +1)$ and $p_1>2$.

Lemma 4.1

Let $f:\mathbb {R}^d \rightarrow \mathbb {R}$ be a continuously differentiable function which satisfies the following,

$$\begin{aligned} |Df(x)-Df(\bar{x})| \le L(1+|x|+|\bar{x}|)^{\gamma }|x-\bar{x}| \end{aligned}$$

(4.1)

for all $x ,\bar{x}\in \mathbb {R}^d$ and for a fixed $\gamma \in \mathbb {R}$. Then, there exists a constant L such that

$$\begin{aligned} |f(x)-f(\bar{x})-\sum _{i=1}^d\frac{\partial f(\bar{x})}{\partial y^i}(x^i-\bar{x}^i)| \le L(1+|x|+|\bar{x}|)^{\gamma }|x-\bar{x}|^2 \end{aligned}$$

for any $x,\bar{x} \in \mathbb {R}^d$.

Proof

By mean value theorem,

$$\begin{aligned} f(x)-f(\bar{x})=\sum _{i=1}^{d}\frac{f(qx+(1-q)\bar{x})}{\partial y^i}(x^i-\bar{x}^i) \end{aligned}$$

for some $q\in (0,1)$. Hence, for a fixed $q \in (0,1)$,

$$\begin{aligned} |f(x)&-f(\bar{x})-\sum _{i=1}^{d}\frac{\partial f(\bar{x})}{\partial y^i}(x^i-\bar{x}^i)|\\&= \Big |\sum _{i=1}^{d}\frac{\partial f(qx+(1-q)\bar{x})}{\partial y^i}(x^i-\bar{x}^i)-\sum _{i=1}^{d}\frac{\partial f(x)}{\partial y^i}(x^i-\bar{x}^i)|\\&\le \sum _{i=1}^{d}\Big | \frac{\partial f(qx+(1-q)\bar{x})}{\partial y^i}-\frac{\partial f(x)}{\partial y^i}\Big ||x^i-\bar{x}^i| \end{aligned}$$

which on using equation (4.1) completes the proof.

Lemma 4.2

Let Assumptions A-1 to A-5 be satisfied. Then, for every $n\in \mathbb {N}$

$$\begin{aligned} \sup _{0 \le t \le T }E|\sigma _1^n(t, x_{\kappa (n,t)}^n)|^{p} \le K n^{-\frac{p}{2}} \end{aligned}$$

for any $p \le \frac{p_0}{\rho +1}$.

Proof

By the application of an elementary inequality of stochastic integrals, Hölder’s inequality, Lemma 2.1 and Remark 2.1, one obtains

$$\begin{aligned} E|\sigma _1^n(t, x_{\kappa (n,t)}^n)|^{p}&\le K \sum _{j=1}^{m}E\Big |\int _{\kappa (n,t)}^t \varLambda ^{n,j}\sigma (x_{\kappa (n,s)}^n)dw_s^j\Big |^{p}\\&\le K n^{-\frac{p}{2}+1} E \int _{\kappa (n,t)}^t |\varLambda ^{j}\sigma (x_{\kappa (n,s)}^n)|^{p} ds\\&\le K n^{-\frac{p}{2}+1} E \int _{\kappa (n,t)}^t (1+|x_{\kappa (n,s)}^n|)^{(\rho + 1)p} ds \end{aligned}$$

which due to Lemma 3.3 completes the proof.

As a consequence of the above lemma, one obtains the following corollary.

Corollary 4.1

Let Assumptions A-1 to A-5 be satisfied. Then, for every $n \in \mathbb {N}$,

$$\begin{aligned} \sup _{0 \le t \le T }E|\tilde{\sigma }^n(t, x_{\kappa (n,t)}^n)|^{p} \le K \end{aligned}$$

for any $p \le \frac{p_0}{\rho +1}$.

Lemma 4.3

Let Assumptions A-1 to A-5 be satisfied. Then, for every $n \in \mathbb {N}$,

$$\begin{aligned} \sup _{0 \le t \le T}E|x_t^n-x_{\kappa (n,t)}^n|^{p} \le K n^{-\frac{p}{2}} \end{aligned}$$

for any $p \le \frac{p_0}{\rho +1}$.

Proof

Due to the scheme (2.6),

$$\begin{aligned} E|x_t^n-x_{\kappa (n,t)}^n|^{p} \le&K E\Big |\int _{\kappa (n,t)}^t b^n(x_{\kappa (n,s)}^n)ds \Big |^{p} + K E\Big |\int _{\kappa (n,t)}^t \tilde{\sigma }^n(s, x_{\kappa (n,s)}^n) dw_s\Big |^{p} \end{aligned}$$

and then the application of Hölder’s inequality along with an elementary inequality of stochastic integrals gives

$$\begin{aligned} E|x_t^n-x_{\kappa (n,t)}^n|^{p} \le&K n^{-p+1}E\int _{\kappa (n,t)}^t |b^n(x_{\kappa (n,s)}^n)|^{p} ds\\&+ K n^{-\frac{p}{2}+1} E\int _{\kappa (n,t)}^t|\tilde{\sigma }^n(s,x_{\kappa (n,s)}^n)|^{p} ds \end{aligned}$$

which on using Lemma  2.1 and Remark 2.1 yields the following estimates,

$$\begin{aligned} E|x_t^n-x_{\kappa (n,t)}^n|^{p}&\le K n^{-p+1}E\int _{\kappa (n,t)}^t (1+|x_{\kappa (n,s)}^n|)^{(\rho +1)p} ds\\&\quad + K n^{-\frac{p}{2}+1} E\int _{\kappa (n,t)}^t|\tilde{\sigma }^n(s,x_{\kappa (n,s)}^n)|^{p} ds \end{aligned}$$

for any $t \in [0,T]$. Thus, one uses Lemma 3.3 and Corollary 4.1 to complete the proof.

Lemma 4.4

Let Assumptions A-1 to A-5 be satisfied. Then, for every $n \in \mathbb {N}$,

$$\begin{aligned} \sup _{0 \le t \le T}E|b(x_{\kappa (n,t)}^n)-b^n(x_{\kappa (n,t)}^n)|^p \le Kn^{-p} \end{aligned}$$

for any $p \le \frac{p_0}{3 \rho +1}$.

Proof

One observes that

$$\begin{aligned} |b(x_{\kappa (n,t)}^n)-b^n(x_{\kappa (n,t)}^n)|&=n^{-1}\frac{|b(x_{\kappa (n,t)}^n)||x_{\kappa (n,t)}^n|^{2\rho }}{1+n^{-1}|x_{\kappa (n,t)}^n|^{2\rho }} \le Kn^{-1}(1+|x_{\kappa (n,t)}^n|)^{3\rho +1} \end{aligned}$$

and hence Lemma 3.3 completes the proof.

Lemma 4.5

Let Assumptions A-1 to A-5 be satisfied. Then, for for every $n \in \mathbb {N}$,

$$\begin{aligned} \sup _{0 \le t \le T}E|\sigma (x_{\kappa (n,t)}^n)-\sigma ^n(x_{\kappa (n,t)}^n)|^p \le Kn^{-p} \end{aligned}$$

for any $p \le \frac{p_0}{2.5 \rho +1}$.

Proof

The proof follows using same arguments as used in Lemma 4.4.

Lemma 4.6

Let Assumptions A-1 to A-5 be satisfied. Then, for every $n \in \mathbb {N}$,

$$\begin{aligned} \sup _{0 \le t \le T}E|\sigma (x_t^n)-\sigma (x_{\kappa (n,t)}^n)-\sigma _1^n(t, x_{\kappa (n,t)}^n)|^p \le K n^{-p} \end{aligned}$$

for any $p \le \frac{p_0}{3\rho +1}$.

Proof

First, one observes that

$$\begin{aligned} \sum _{u=1}^{d}\frac{\partial \sigma ^{(k,v)}(x_{\kappa (n,t)}^n)}{\partial x^u}(x_t^{n,u}-x_{\kappa (n,t)}^{n,u})&=\sum _{u=1}^{d}\frac{\partial \sigma ^{(k,v)}(x_{\kappa (n,t)}^n)}{\partial x^u} \bigg ( \int _{\kappa (n,t)}^{t} b^{n,u}(x_{\kappa (n,s)}^n)ds \nonumber \\&\quad +\int _{\kappa (n,t)}^{t}\sum _{j=1}^{m}\sigma ^{n,(u,j)}(x_{\kappa (n,s)}^n)dw_s^j\nonumber \\&\quad +\int _{\kappa (n,t)}^{t}\sum _{j=1}^{m}\sigma _1^{n,(u,j)}(s,x_{\kappa (n,s)}^n)dw_s^j \bigg ) \nonumber \\&=\sum _{u=1}^{d}\frac{\partial \sigma ^{(k,v)}(x_{\kappa (n,t)}^n)}{\partial x^u} \int _{\kappa (n,t)}^{t}b^{n,u}(x_{\kappa (n,s)}^n)ds\nonumber \\&\quad +\,\sigma _1^{n,(k,v)}(t,x_{\kappa (n,t)}^n) +\,\sum _{u=1}^{d}\frac{\partial \sigma ^{(k,v)}(x_{\kappa (n,t)}^n)}{\partial x^u}\nonumber \\&\quad \int _{\kappa (n,t)}^{t}\sum _{j=1}^{m}\sigma _1^{n,(u,j)}(s,x_{\kappa (n,s)}^n)dw_s^j \end{aligned}$$

(4.2)

for any $t \in [0,T]$. Also, one can write the following,

$$\begin{aligned} \sigma ^{(k,v)}&(x_t^n)-\sigma ^{(k,v)}(x_{\kappa (n,t)}^n)-\sigma _1^{n,(k,v)}(t, x_{\kappa (n,t)}^n)\\&=\sigma ^{(k,v)}(x_t^n)-\sigma ^{(k,v)}(x_{\kappa (n,t)}^n)-\sum _{u=1}^{d}\frac{\partial \sigma ^{(k,v)}(x_{\kappa (n,t)}^n)}{\partial x^u}(x_t^{n,u}-x_{\kappa (n,t)}^{n,u})\\&\quad +\sum _{u=1}^{d}\frac{\partial \sigma ^{(k,v)}(x_{\kappa (n,t)}^n)}{\partial x^u}(x_t^{n,u}-x_{\kappa (n,t)}^{n,u})- \sigma _1^{n,(k,v)}(t, x_{\kappa (n,t)}^n) \end{aligned}$$

and hence due to equation (4.2), Remark 2.1 and Lemma 4.1 (with $\gamma =(\rho -2)/2$), one obtains

$$\begin{aligned} |\sigma ^{(k,v)}&(x_t^n)-\sigma ^{(k,v)}(x_{\kappa (n,t)}^n)-\sigma _1^{n,(k,v)}(t, x_{\kappa (n,t)}^n)|\\&\le L(1+|x_t^n|+|x_{\kappa (n,t)}^n|)^{\frac{\rho -2}{2}}|x_t^{n}-x_{\kappa (n,t)}^{n}|^2\\&\quad +\Big |\sum _{u=1}^{d}\frac{\partial \sigma ^{(k,v)}(x_{\kappa (n,t)}^n)}{\partial x^u}\int _{\kappa (n,t)}^t b_s^{n,u} (x_{\kappa (n,s)}^n)ds \Big |\\&\quad +\Big |\sum _{u=1}^{d}\frac{\partial \sigma ^{(k,v)}(x_{\kappa (n,t)}^n)}{\partial x^u} \int _{\kappa (n,t)}^{t}\sum _{j=1}^{m}\sigma _1^{n,(u,j)}(s,x_{\kappa (n,s)}^n)dw_s^j\Big | \end{aligned}$$

for any $t \in [0,T]$. Thus, on the application of Hölder’s inequality and an elementary inequality of stochastic integrals along with Lemma 2.1 and Remarks 2.1, the following estimates are obtained,

$$\begin{aligned} E&|\sigma ^{(k,v)}(x_t^n)-\sigma ^{(k,v)}(x_{\kappa (n,t)}^n)-\sigma _1^{n,(k,v)}(t, x_{\kappa (n,t)}^n)|^p\\&\le KE(1+|x_t^n|+|x_{\kappa (n,t)}^n|)^{\frac{\rho p}{2}}|x_t^{n}-x_{\kappa (n,t)}^{n}|^{2p}+Kn^{-p}E(1+|x_{\kappa (n,t)}^n|)^{\frac{\rho p}{2}+(\rho +1)p}\\&+Kn^{-\frac{p}{2}+1} \int _{\kappa (n,t)}^{t}E(1+|x_{\kappa (n,t)}^n|)^\frac{\rho p}{2}|\sigma _1^{n}(s,x_{\kappa (n,s)}^n)|^pds \end{aligned}$$

for any $t\in [0,T]$. One again uses Hölder’s inequality and obtains,

$$\begin{aligned} E&|\sigma ^{(k,v)}(x_t^n)-\sigma ^{(k,v)}(x_{\kappa (n,t)}^n)-\sigma _1^{n,(k,v)}(t, x_{\kappa (n,t)}^n)|^p\\&\le K\{E(1+|x_t^n|+|x_{\kappa (n,t)}^n|)^\frac{p_0}{2}\}^{\frac{\rho p}{p_0}}\{E|x_t^{n}-x_{\kappa (n,t)}^{n}|^\frac{2pp_0}{p_0-\rho p}\}^\frac{p_0-\rho p}{p_0}+ Kn^{-p}\\&\quad +Kn^{-\frac{p}{2}+1} \int _{\kappa (n,t)}^{t}\{E(1+|x_{\kappa (n,t)}^n|)^{p_0}\}^\frac{\rho p}{2p_0}\{E|\sigma _1^{n}(s,x_{\kappa (n,s)}^n)|^\frac{2pp_0}{2p_0-\rho p}\}^\frac{2p_0-\rho p}{2p_0}ds \end{aligned}$$

for any $t \in [0,T]$. The proof is completed by Lemmas [3.3, 4.3, 4.2].

Let us at this point introduce $e_t^n:=x_t-x_{t}^n$ for any $t \in [0,T]$.

Lemma 4.7

Let Assumptions A-1 to A-5 be satisfied. Then, for every $n \in \mathbb {N}$ and $t \in [0,T]$,

$$\begin{aligned} E\int _{0}^{t} |e_s^n|^{p-2}e_s^n(b(x_s^n)-b(x_{\kappa (n,s)}^n))ds\le K \int _{0}^t \sup _{0 \le r \le s}E|e_r^n|^p ds + K n^{-p} \end{aligned}$$

(4.3)

for $p=2$. Furthermore, if $p_0 \ge 4(3\rho +1)$, then (4.3) holds for any $p \le \frac{p_0}{3\rho +1}$.

Proof

First, one writes the following,

$$\begin{aligned}&E\int _{0}^t |e_s^n|^{p-2} e_s^n(b(x_s^n)-b(x_{\kappa (n,s)}^n))ds \nonumber \\&\quad = \sum _{k=1}^d E\int _{0}^t |e_s^n|^{p-2} e_s^{n,k}(b^k(x_s^n)-b^k(x_{\kappa (n,s)}^n))ds \nonumber \\&\quad = \sum _{k=1}^d E\int _{0}^t |e_s^n|^{p-2} e_s^{n,k}(b^k(x_s^n)-b^k(x_{\kappa (n,s)}^n)-\sum _{i=1}^{d}\frac{\partial b^k(x_{\kappa (n,s)}^n)}{\partial x^i}(x_s^{n,i}-x_{\kappa (n,s)}^{n,i}))ds \nonumber \\&\qquad +\sum _{k=1}^d E\int _{0}^t |e_s^n|^{p-2} e_s^{n,k} \sum _{i=1}^{d}\frac{\partial b^k(x_{\kappa (n,s)}^n)}{\partial x^i}(x_s^{n,i}-x_{\kappa (n,s)}^{n,i}) \nonumber \\&\quad \le \sum _{k=1}^d E\int _{0}^t |e_s^n|^{p-1} |b^k(x_s^n)-b^k(x_{\kappa (n,s)}^n)-\sum _{i=1}^{d}\frac{\partial b^k(x_{\kappa (n,s)}^n)}{\partial x^i}(x_s^{n,i}-x_{\kappa (n,s)}^{n,i})|ds \nonumber \\&\qquad +\sum _{k=1}^d E\int _{0}^t |e_s^n|^{p-2} e_s^{n,k} \sum _{i=1}^{d}\frac{\partial b^k(x_{\kappa (n,s)}^n)}{\partial x^i}\int _{\kappa (n,s)}^{s} b^{n,i}(x_{\kappa (n,r)}^n)dr \nonumber \\&\qquad +\sum _{k=1}^d E\int _{0}^t |e_s^n|^{p-2} e_s^{n,k} \sum _{i=1}^{d}\frac{\partial b^k(x_{\kappa (n,s)}^n)}{\partial x^i}\int _{\kappa (n,s)}^{s} \sum _{l=1}^{m}\bar{\sigma }^{n,(i,l)}(x_{\kappa (n,r)}^n)dw_r^l \nonumber \\&\quad =: T_1+T_2+T_3 \end{aligned}$$

(4.4)

for any $t \in [0,T]$.

Notice that when $p=2$, $|e_s^n|^{p-2}$ does not appear in $T_2$ and $T_3$ of the above equation. One keeps this in mind in the following calculations because their estimations require less computational efforts as compared to the case of $p \ge 4$.

Now, $T_1$ can be estimated by using Lemma 4.1 (with $\gamma =\rho -1$) as below,

$$\begin{aligned} T_1&:=\sum _{k=1}^d E\int _{0}^t |e_s^n|^{p-1} |b^k(x_s^n)-b^k(x_{\kappa (n,s)}^n)-\sum _{i=1}^{d}\frac{\partial b^k(x_{\kappa (n,s)}^n)}{\partial x^i}(x_s^{n,i}-x_{\kappa (n,s)}^{n,i})|ds\\&\le E\int _{0}^t |e_s^n|^{p-1} (1+|x_s^n|+|x_{\kappa (n,s)}^n|)^{\rho -1}|x_s^{n}-x_{\kappa (n,s)}^{n}|^2 ds \end{aligned}$$

which on the application of Young’s inequality and Hölder’s inequality gives

$$\begin{aligned} T_1&\le \int _{0}^t E|e_s^n|^{p} ds + \int _{0}^t E(1+|x_s^n|+|x_{\kappa (n,s)}^n|)^{(\rho -1)p}|x_s^{n}-x_{\kappa (n,s)}^{n}|^{2p} ds \\&\le \int _{0}^t E|e_s^n|^{p} ds + \int _{0}^t \{E(1+|x_s^n|+|x_{\kappa (n,s)}^n|)^{p_0}\}^\frac{(\rho -1)p}{p_0}\\&\quad \times \{E|x_s^{n}-x_{\kappa (n,s)}^{n}|^\frac{2pp_0}{p_0-(\rho -1)p}\}^\frac{p_0-(\rho -1)p}{p_0} ds \end{aligned}$$

and then by using Lemmas [3.3, 4.3], one obtains

$$\begin{aligned} T_1 \le Kn^{-p}+\int _{0}^t \sup _{0 \le r \le s}E|e_r^n|^{p} ds \end{aligned}$$

(4.5)

for any $t \in [0,T]$.

For $T_2$, one uses Schwarz, Young’s and Hölder’s inequalities and obtains the following estimates,

$$\begin{aligned} T_2&:= \sum _{k=1}^d E \int _{0}^t |e_s^n|^{p-2}e_s^{n,k} \sum _{i=1}^d\frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \int _{\kappa (n,s)}^s b^{n,i}(x_{\kappa (n,r)}^n)dr ds \\&\le K E \int _{0}^t |e_s^{n}|^p ds +K n^{-p+1}\sum _{k,i=1}^d E \int _{0}^t \int _{\kappa (n,s)}^s |\frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i}|^p \\&\quad \times |b^{n,i}(x_{\kappa (n,r)}^n)|^p dr ds \end{aligned}$$

which on the application of Lemma 2.1 and Remark 2.1 yields

$$\begin{aligned} T_2 \le K \int _{0}^t E|e_s^{n}|^p ds +K n^{-p+1} E \int _{0}^t \int _{\kappa (n,s)}^s (1+|x_{\kappa (n,r)}^n|)^{(2\rho +1)p} dr ds \end{aligned}$$

for any $t \in [0,T]$. Furthermore, due to Lemma 3.3, the following estimates are obtained,

$$\begin{aligned} T_2&\le K n^{-p} + \int _{0}^t \sup _{0 \le r \le s}E |e_r^{n}|^p ds \end{aligned}$$

(4.6)

for any $t \in [0,T]$. One can now proceed to the estimation of $T_3$. For this, one uses Itô’s formula and obtains the following estimates,

$$\begin{aligned} |e_s^n|^{p-2} e_s^{n,k}=&\,|e_{\kappa (n,s)}^n|^{p-2} e_{\kappa (n,s)}^{n,k} + \int _{\kappa (n,s)}^s |e_r^n|^{p-2}(b^k(x_r)-b^{n,k}(x_{\kappa (n,r)}^n) ) dr \\&+ \int _{\kappa (n,s)}^s |e_r^n|^{p-2} \sum _{j=1}^m\big (\sigma ^{(k,j)}(x_r)-\tilde{\sigma }^{n,(k,j)}(r, x_{\kappa (n,r)}^n)\big )dw_r^j \\&+ (p-2) \int _{\kappa (n,s)}^s e_r^{n,k} |e_r^n|^{p-4} e_r^n (b(x_r)-b^n(x_{\kappa (n,r)}^n)) dr \\&+ (p-2) \int _{\kappa (n,s)}^s e_r^{n,k} |e_r^n|^{p-4} e_r^n (\sigma (x_r)-\tilde{\sigma }^n(r, x_{\kappa (n,r)}^n)) dw_r \\&+ \frac{(p-2)(p-4)}{2} \int _{\kappa (n,s)}^s e_r^{n,k} |e_r^n|^{p-6}| (\sigma (x_r)-\tilde{\sigma }^n(r, x_{\kappa (n,r)}^n))^{*}e_r^n|^2 dr \\&+ \frac{p-2}{2} \int _{\kappa (n,s)}^s e_r^{n,k}|e_r^n|^{p-4}|\sigma (x_r)-\tilde{\sigma }^n(r, x_{\kappa (n,r)}^n)|^2 dr \\&+ (p-2) \int _{\kappa (n,s)}^s \sum _{j=1}^m (\sigma ^{(k,j)}(x_r)-\tilde{\sigma }^{n,(k,j)}(r, x_{\kappa (n,r)}^n))|e_r^n|^{p-4} \\&\times \sum _{u=1}^d e_r^{n,u} (\sigma ^{(u,j)}(x_r)-\tilde{\sigma }^{n,(u,j)}(r, x_{\kappa (n,r)}^n)) dr \end{aligned}$$

for any $s \in [0,T]$.

In the above equation, notice that when $p=2$, the last five terms are zero, $|e_{\kappa (n,s)}^n|^{p-2}$ is absent from the first term and $|e_r^n|^{p-2}$ does not appear in the second and third terms. Hence, this on substituting in $T_3$ and then using Schwarz inequality gives the following estimates,

$$\begin{aligned} T_3&\le \sum _{k=1}^d E\int _{0}^t |e_{\kappa (n,s)}^n|^{p-2} e_{\kappa (n,s)}^{n,k} \int _{\kappa (n,s)}^s \sum _{l=1}^m \sum _{i=1}^d \frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l ds \nonumber \\&\quad +\sum _{k=1}^d E\int _{0}^t \int _{\kappa (n,s)}^s |e_r^n|^{p-2}|b(x_r)- b^{n}(x_{\kappa (n,r)}^n) | dr \nonumber \\&\quad \times \Big |\int _{\kappa (n,s)}^s \sum _{l=1}^m \sum _{i=1}^d \frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l \Big |ds \nonumber \\&\quad + \sum _{k=1}^d E\int _{0}^t \int _{\kappa (n,s)}^s |e_r^n|^{p-2} \sum _{j=1}^m\big (\sigma ^{(k,j)}(x_r)-\tilde{\sigma }^{n,(k,j)}(r, x_{\kappa (n,r)}^n)\big )dw_r^j \nonumber \\&\quad \times \int _{\kappa (n,s)}^s \sum _{l=1}^m \sum _{i=1}^d\frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l ds \nonumber \\&\quad + K \sum _{k=1}^d E\int _{0}^t \int _{\kappa (n,s)}^s e_r^{n,k} |e_r^n|^{p-4} e_r^n (\sigma (x_r)-\tilde{\sigma }^n(r, x_{\kappa (n,r)}^n)) dw_r \nonumber \\&\quad \times \int _{\kappa (n,s)}^s \sum _{l=1}^m \sum _{i=1}^d \frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l ds \nonumber \\&\quad + K \sum _{k=1}^d E\int _{0}^t \int _{\kappa (n,s)}^s |e_r^n|^{p-3}|\sigma (x_r)-\tilde{\sigma }^n(r, x_{\kappa (n,r)}^n)|^2 dr \nonumber \\&\quad \times \Big |\int _{\kappa (n,s)}^s \sum _{l=1}^m \sum _{i=1}^d \frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l \Big | ds \nonumber \\&=:T_{31}+T_{32}+T_{33}+T_{34}+T_{35} \end{aligned}$$

(4.7)

for any $t \in [0,T]$. In order to estimate $T_{31}$, one writes,

$$\begin{aligned} T_{31}&:=K\sum _{k=1}^d E \int _{0}^t |e_{\kappa (n,s)}^n|^{p-2} e_{\kappa (n,s)}^{n,k}\\&\quad \times \int _{\kappa (n,s)}^s\sum _{l=1}^{m} \sum _{i=1}^d\frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l ds \\&=K\sum _{k=1}^d E \int _{0}^t |e_{\kappa (n,s)}^n|^{p-2} e_{\kappa (n,s)}^{n,k}\\&\quad \times \int _{\kappa (n,s)}^s\sum _{l=1}^{m} \sum _{i=1}^d\frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \sigma ^{n,(i,l)}(x_{\kappa (n,r)}^n)dw_r^l ds\\&\quad +K\sum _{k=1}^d E \int _{0}^t |e_{\kappa (n,s)}^n|^{p-2} e_{\kappa (n,s)}^{n,k}\\&\quad \times \int _{\kappa (n,s)}^s \sum _{l=1}^{m} \sum _{i=1}^d\frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \sigma _1^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l ds \end{aligned}$$

for any $t \in [0,T]$. In the above, notice that first term is zero. Then, on using the Young’s inequality, Hölder’s inequality and an elementary inequality of stochastic integrals, one obtains,

$$\begin{aligned} T_{31}&\le K \int _{0}^t \sup _{0 \le r \le s}E|e_r^n|^p ds\\&\quad +K\sum _{k=1}^d E \int _{0}^t \Big |\int _{\kappa (n,s)}^s\sum _{l=1}^{m} \sum _{i=1}^d \frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \sigma _1^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l\Big |^p ds\\&\le K \int _{0}^t \sup _{0 \le r \le s}E|e_r^n|^p ds +Kn^{-\frac{p}{2}+1} E \int _{0}^t \int _{\kappa (n,s)}^s(1+|x_{\kappa (n,r)}^n|)^{\rho p} \\&\quad \times |\sigma _1^n(r, x_{\kappa (n,r)}^n)|^p dr ds\\&\le K \int _{0}^t \sup _{0 \le r \le s}E|e_r^n|^p ds +Kn^{-\frac{p}{2}+1} \int _{0}^t \int _{\kappa (n,s)}^s \{E(1+|x_{\kappa (n,r)}^n|)^{p_0}\}^\frac{\rho p}{p_0} \\&\quad \times \{E|\sigma _1(x_{\kappa (n,r)}^n)|^{\frac{p p_0}{p_0-\rho p}}\}^\frac{p_0-\rho p}{p_0} dr ds \end{aligned}$$

and then by using Lemmas [3.3, 4.2], one obtains

$$\begin{aligned} T_{31}&\le Kn^{-p}+K \int _{0}^t \sup _{0 \le r \le s}E|e_r^n|^p ds \end{aligned}$$

(4.8)

for any $t \in [0,T]$. Moreover, for estimating $T_{32}$, one uses the following splitting,

$$\begin{aligned} b(x_r)-\tilde{b}^{n}(x_{\kappa (n,r)}^n)&= (b(x_r)-b(x_r^n))+(b(x_r^n)-b(x_{\kappa (n,r)}^n)) \nonumber \\&+(b(x_{\kappa (n,r)}^n) -b^{n}(x_{\kappa (n,r)}^n)) \end{aligned}$$

(4.9)

and hence $T_{32}$ can be estimated by

$$\begin{aligned} T_{32}&:=\sum _{k=1}^d E\int _{0}^t \int _{\kappa (n,s)}^s |e_r^n|^{p-2}|b(x_r)-\tilde{b}^{n}(x_{\kappa (n,r)}^n) | dr\\&\quad \times \Big |\int _{\kappa (n,s)}^s \sum _{l=1}^m \sum _{i=1}^d \frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l \Big |ds\\&\le K \sum _{k=1}^d E\int _{0}^t \int _{\kappa (n,s)}^s \big (n^\frac{1}{p}|e_r^n|\big )^{p-1}(1+|x_r|+|x_r^n|)^{\rho } dr\\&\quad \times n^{-\frac{p-1}{p}} \Big |\int _{\kappa (n,s)}^s \sum _{l=1}^m \sum _{i=1}^d\frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l \Big |ds\\&\quad + K \sum _{k=1}^d E\int _{0}^t \int _{\kappa (n,s)}^s \big (n^\frac{1}{p}|e_r^n|\big )^{p-2}(1+|x_r^n|+|x_{\kappa (n,r)}^n|)^{\rho }|x_r^n-x_{\kappa (n,r)}^n| dr\\&\quad \times n^{-\frac{p-2}{p}} \Big |\int _{\kappa (n,s)}^s\sum _{l=1}^m \sum _{i=1}^d\frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l \Big |ds\\&\quad + K \sum _{k=1}^d E\int _{0}^t \int _{\kappa (n,s)}^s \big (n^\frac{1}{p}|e_r^n|\big )^{p-2}|b(x_{\kappa (n,r)}^n)-b^{n}(x_{\kappa (n,r)}^n) | dr\\&\quad \times n^{-\frac{p-2}{p}} \Big |\int _{\kappa (n,s)}^s \sum _{l=1}^m \sum _{i=1}^d \frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l \Big |ds \end{aligned}$$

which on the application of Young’s inequality gives

$$\begin{aligned} T_{32}&\le K E \int _{0}^t n \int _{\kappa (n,s)}^s |e_r^n|^{p} dr ds + K n^{-p+1} \sum _{k=1}^d E \int _{0}^t \int _{\kappa (n,s)}^s (1+|x_r|+|x_r^n|)^{\rho p} dr\\&\quad \times \Big |\int _{\kappa (n,s)}^s \sum _{l=1}^m \sum _{i=1}^d \frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l \Big |^p ds\\&\quad + K n^{-\frac{p-2}{2}} \sum _{k=1}^d E \int _{0}^t \int _{\kappa (n,s)}^s (1+|x_r^n|+|x_{\kappa (n,r)}^n|)^\frac{\rho p}{2} |x_r^n-x_{\kappa (n,r)}^n|^\frac{p}{2} dr\\&\quad \times \Big |\int _{\kappa (n,s)}^s \sum _{l=1}^m \sum _{i=1}^d \frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l \Big |^\frac{p}{2} ds\\&\quad + K n^{-\frac{p-2}{2}} \sum _{k=1}^d E \int _{0}^t \int _{\kappa (n,s)}^s |b(x_{\kappa (n,r)}^n)-b^{n}(x_{\kappa (n,r)}^n) |^\frac{p}{2} dr\\&\quad \times \Big |\int _{\kappa (n,s)}^s \sum _{l=1}^m \sum _{i=1}^d \frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l \Big |^\frac{p}{2} ds \end{aligned}$$

for any $t \in [0,T]$. Due to Hölder’s inequality and an elementary inequality of stochastic integrals, one obtains

$$\begin{aligned} T_{32}&{\le } K \int _{0}^t \sup _{0 \le r \le s} E|e_r^n|^{p} ds {+} K n^{-p+1} \sum _{k=1}^d \int _{0}^t \Big [ E \Big (\int _{\kappa (n,s)}^s (1{+}|x_r|+|x_r^n|)^{\rho p} dr \Big )^{\frac{p_0}{\rho p}}\Big ]^\frac{\rho p}{p_0}\\&\quad \times \Big [E\Big |\int _{\kappa (n,s)}^s \sum _{l=1}^m \sum _{i=1}^d \frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l \Big |^\frac{pp_0}{p_0-\rho p} \Big ]^\frac{p_0-\rho p}{p_0} ds\\&\quad + K n^{-\frac{p-2}{2}} \sum _{k=1}^d \int _{0}^t \Big [E \Big (\int _{\kappa (n,s)}^s (1+|x_r^n|+|x_{\kappa (n,r)}^n|)^\frac{\rho p}{2} |x_r^n-x_{\kappa (n,r)}^n|^\frac{p}{2} dr \Big )^2\Big ]^\frac{1}{2}\\&\quad \times \Big [E\Big |\int _{\kappa (n,s)}^s \sum _{l=1}^m \sum _{i=1}^d \frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l \Big |^p\Big ]^\frac{1}{2} ds\\&\quad + K n^{-\frac{p-2}{2}} \sum _{k=1}^d \int _{0}^t \Big [E \Big (\int _{\kappa (n,s)}^s |b(x_{\kappa (n,r)}^n)-b^{n}(x_{\kappa (n,r)}^n) |^\frac{p}{2} dr \Big )^2\Big ]^\frac{1}{2}\\&\quad \times \Big [E\Big |\int _{\kappa (n,s)}^s \sum _{l=1}^m \sum _{i=1}^d \frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l \Big |^p\Big ]^\frac{1}{2} ds \end{aligned}$$

and this further implies due to Hölder’s inequality,

$$\begin{aligned} T_{32} {\le }&\, K \int _{0}^t \sup _{0 \le r \le s} E|e_r^n|^{p} ds {+} K n^{-p+1} \int _{0}^t \Big [ n^{-\frac{p_0}{\rho p}+1}E \int _{\kappa (n,s)}^s (1+|x_r|+|x_r^n|)^{p_0} dr \Big ]^\frac{\rho p}{p_0}\\&\times \Big [n^{-\frac{p p_0}{2 p_0-2\rho p}+1}E\int _{\kappa (n,s)}^s (1+|x_{\kappa (n,r)}^n|)^{\frac{p \rho p_0}{ p_0- \rho p}} | \tilde{\sigma }^n(r,x_{\kappa (n,r)}^n)|^{\frac{pp_0}{ p_0-\rho p}} dr \Big ]^{\frac{ p_0- \rho p}{p_0}} ds\\&+ K n^{-\frac{p-2}{2}} \int _{0}^t \Big [n^{-1}E \int _{\kappa (n,s)}^s (1+|x_r^n|+|x_{\kappa (n,r)}^n|)^{\rho p} |x_r^n-x_{\kappa (n,r)}^n|^p dr \Big ]^\frac{1}{2}\\&\times \Big [ n^{-\frac{p}{2}+1} E\int _{\kappa (n,s)}^s (1+|x_{\kappa (n,r)}^n|)^{\rho p} |\tilde{\sigma }^n(r, x_{\kappa (n,r)}^n)|^p dr \Big ]^\frac{1}{2} ds\\&+ K n^{-\frac{p-2}{2}} \int _{0}^t \Big [n^{-1}E\int _{\kappa (n,s)}^s |b(x_{\kappa (n,r)}^n)-b^{n}(x_{\kappa (n,r)}^n) |^p dr \Big ]^\frac{1}{2}\\&\times \Big [n^{-\frac{p}{2}+1}E\int _{\kappa (n,s)}^s (1+|x_{\kappa (n,r)}^n|)^{\rho p} |\tilde{\sigma }^n(r, x_{\kappa (n,r)}^n)|^p dr \Big ]^\frac{1}{2} ds \end{aligned}$$

for any $t \in [0,T]$. Again, by using the Hölder’s inequality along with Lemmas [3.1, 3.3, 4.4], one obtains the following estimates,

$$\begin{aligned} T_{32} {\le }&\, K \int _{0}^t \sup _{0 \le r \le s} E|e_r^n|^{p} ds {+} K n^{-p} \int _{0}^t \Big [n^{-\frac{pp_0}{2p_0-2 \rho p}+1}\int _{\kappa (n,s)}^s \{E(1+|x_{\kappa (n,r)}^n|)^{p_0}\}^\frac{\rho p}{p_0-\rho p}\\&\times \{E|\tilde{\sigma }^n(r, x_{\kappa (n,r)}^n)|^\frac{pp_0}{p_0-2\rho p}\}^{\frac{p_0-2\rho p}{p_0-\rho p}} dr \Big ]^\frac{p_0-\rho p}{p_0} ds\\&+ K n^{-\frac{p-2}{2}} \int _{0}^t \Big [n^{-1} \int _{\kappa (n,s)}^s \{E(1+|x_r^n|+|x_{\kappa (n,r)}^n|)^{p_0}\}^\frac{\rho p}{p_0}\\&\times \{E |x_r^n-x_{\kappa (n,r)}^n|^{\frac{pp_0}{p_0-\rho p}}\}^\frac{p_0-\rho p}{p_0} dr \Big ]^\frac{1}{2}\\&\quad \times \Big [ n^{-\frac{p}{2}+1} \int _{\kappa (n,s)}^s \{E(1+|x_{\kappa (n,r)}^n|)^{p_0}\}^\frac{\rho p}{p_0}\\&\times \{E|\tilde{\sigma }^n(r, x_{\kappa (n,r)}^n)|^{\frac{pp_0}{p_0-\rho p}}\}^\frac{p_0-\rho p}{ p_0} dr \Big ]^\frac{1}{2} ds\\&+ K n^{-p} \int _{0}^t \Big [n^{-\frac{p}{2}+1}\int _{\kappa (n,s)}^s \{E(1+|x_{\kappa (n,r)}^n|)^{p_0}\}^\frac{\rho p}{p_0}\\&\times \{E|\tilde{\sigma }^n(r, x_{\kappa (n,r)}^n)|^{\frac{p_0p}{p_0-\rho p}}\}^\frac{p_0-\rho p}{p_0} dr \Big ]^\frac{1}{2} ds \end{aligned}$$

for any $t \in [0,T]$. Hence, on using Lemmas [3.3, 4.3] and Corollary 4.1, one obtains,

$$\begin{aligned} T_{32}&\le K n^{-p}+K \int _{0}^t \sup _{0 \le r \le s}E|e_r^n|^p ds \end{aligned}$$

(4.10)

for any $t\in [0,T]$. Further, one observes that the estimation of $T_{33}$ and $T_{34}$ can be done together as described below. First, one observes that $T_{33}$ can be expressed as

$$\begin{aligned} T_{33}&:=\sum _{k=1}^d E\int _{0}^t \int _{\kappa (n,s)}^s |e_r^n|^{p-2} \sum _{j=1}^m \big (\sigma ^{(k,j)}(x_r)-\tilde{\sigma }^{n,(k,j)}(r,x_{\kappa (n,r)}^n)\big )dw_r^j\\&\times \int _{\kappa (n,s)}^s \sum _{l=1}^m \sum _{i=1}^d\frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l ds\\&= \sum _{k=1}^d E\int _{0}^t \int _{\kappa (n,s)}^s |e_r^n|^{p-2} \sum _{j=1}^m \big (\sigma ^{(k,j)}(x_r)-\tilde{\sigma }^{n,(k,j)}(r, x_{\kappa (n,r)}^n)\big )\\&\quad \times \sum _{i=1}^d\frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,j)}(r, x_{\kappa (n,r)}^n)dr ds \end{aligned}$$

which due to Schwartz inequality and Remark 2.1 yields

$$\begin{aligned} T_{33}&\le K E\int _{0}^t \int _{\kappa (n,s)}^s |e_r^n|^{p-2} |\sigma (x_r)-\tilde{\sigma }^{n}(r, x_{\kappa (n,r)}^n)| (1+|x_{\kappa (n,r)}^n|)^{\rho } |\tilde{\sigma }^{n}(r, x_{\kappa (n,r)}^n)|dr ds \end{aligned}$$

for any $t \in [0,T]$. Similarly, $T_{34}$ can be estimated as

$$\begin{aligned} T_{34}&:= K \sum _{k=1}^d E\int _{0}^t \int _{\kappa (n,s)}^s e_r^{n,k} |e_r^n|^{p-4} e_r^n (\sigma (x_r)-\tilde{\sigma }^n(r, x_{\kappa (n,r)}^n)) dw_r \\&\quad \times \int _{\kappa (n,s)}^s \sum _{l=1}^m \sum _{i=1}^d\frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l ds \nonumber \\&=K \sum _{k=1}^d E\int _{0}^t \int _{\kappa (n,s)}^s \sum _{j=1}^m \sum _{u=1}^d e_r^{n,k} |e_r^n|^{p-4} e_r^{n,u} (\sigma ^{(u,j)}(x_r){-}\tilde{\sigma }^{n,(u,j)}(r, x_{\kappa (n,r)}^n)) dw_r^j\\&\quad \times \int _{\kappa (n,s)}^s \sum _{l=1}^m\sum _{i=1}^d \frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l ds \\&=K \sum _{k=1}^d E\int _{0}^t \int _{\kappa (n,s)}^s \sum _{j=1}^m \sum _{u=1}^d e_r^{n,k} |e_r^n|^{p-4} e_r^{n,u} (\sigma ^{(u,j)}(x_r)-\tilde{\sigma }^{n,(u,j)}(r, x_{\kappa (n,r)}^n))\\&\quad \times \sum _{i=1}^d \frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,j)}(r, x_{\kappa (n,r)}^n)dr ds \end{aligned}$$

which on using Remark 2.1 gives

$$\begin{aligned} T_{34}&\le K E\int _{0}^t \int _{\kappa (n,s)}^s |e_r^n|^{p-2} |\sigma (x_r)\\&\quad -\tilde{\sigma }^{n}(r, x_{\kappa (n,r)}^n)| (1+|x_{\kappa (n,r)}^n|)^{\rho }|\tilde{\sigma }^{n}(r, x_{\kappa (n,r)}^n)|dr ds \end{aligned}$$

for any $t \in [0,T]$. For estimating $T_{33}+T_{34}$, one uses the following splitting,

$$\begin{aligned} \sigma (x_r) -\tilde{\sigma }^{n}(r,x_{\kappa (n,r)}^n)&=\sigma (x_r) -\sigma ^{n}(x_{\kappa (n,r)}^n)- \sigma ^{n}_1(r, x_{\kappa (n,r)}^n) \nonumber \\&=(\sigma (x_r)-\sigma (x_r^n)) +(\sigma (x_r^n)-\sigma (x_{\kappa (n,r)}^n)\nonumber \\&\qquad -\sigma _1^{n}(r,x_{\kappa (n,r)}^n))+ (\sigma ( x_{\kappa (n,r)}^n)- \sigma ^{n}(x_{\kappa (n,r)}^n)) \end{aligned}$$

(4.11)

and hence obtains the following estimates,

$$\begin{aligned} T_{33}{+}T_{34} {\le }&\, K E\int _{0}^t \int _{\kappa (n,s)}^s |e_r^n|^{p-2} |\sigma (x_r)-\sigma (x_r^n)| (1+|x_{\kappa (n,r)}^n|)^{\rho } |\tilde{\sigma }^{n}(r, x_{\kappa (n,r)}^n)|dr ds\\&+K E\int _{0}^t \int _{\kappa (n,s)}^s |e_r^n|^{p-2} |\sigma (x_r^n)-\sigma (x_{\kappa (n,r)}^n) - \sigma _1^{n}(r, x_{\kappa (n,r)}^n)|\\&\times (1+|x_{\kappa (n,r)}^n|)^{\rho }|\tilde{\sigma }^{n}(r, x_{\kappa (n,r)}^n)|dr ds\\&+ K E\int _{0}^t \int _{\kappa (n,s)}^s |e_r^n|^{p-2} |\sigma (x_{\kappa (n,r)}^n)-\sigma ^{n}(x_{\kappa (n,r)}^n)|\\&\times (1+|x_{\kappa (n,r)}^n|)^{\rho } |\tilde{\sigma }^{n}(r, x_{\kappa (n,r)}^n)|dr ds \end{aligned}$$

which also gives the following expressions,

$$\begin{aligned} T_{33} +T_{34} \le&\, K E\int _{0}^t \int _{\kappa (n,s)}^s (n^\frac{1}{p}|e_r^n|)^{p-1} n^{-\frac{p-1}{p}} (1+ |x_r|+|x_r^n|)^\frac{\rho }{2}\\&\times (1+|x_{\kappa (n,r)}^n|)^{\rho } |\tilde{\sigma }^{n}(r, x_{\kappa (n,r)}^n)|dr ds\\&+K E\int _{0}^t \int _{\kappa (n,s)}^s (n^\frac{1}{p}|e_r^n|)^{p-2} n^{{-}\frac{p-2}{p}}|\sigma (x_r^n){-}\sigma (x_{\kappa (n,r)}^n) - \sigma _1^{n}(r, x_{\kappa (n,r)}^n)|\\&\times (1+|x_{\kappa (n,r)}^n|)^{\rho }|\tilde{\sigma }^{n}(r, x_{\kappa (n,r)}^n)|dr ds\\&+K E\int _{0}^t \int _{\kappa (n,s)}^s (n^\frac{1}{p}|e_r^n|)^{p-2} n^{-\frac{p-2}{p}}|\sigma (x_{\kappa (n,r)}^n)-\sigma ^{n}(x_{\kappa (n,r)}^n)|\\&\qquad \times (1+|x_{\kappa (n,r)}^n|)^{\rho } |\tilde{\sigma }^{n}(r, x_{\kappa (n,r)}^n)|dr ds \end{aligned}$$

for any $t \in [0,T]$. Also, on the application of Young’s inequality, one obtains

$$\begin{aligned} T_{33} +&T_{34} \le \, K E\int _{0}^t n\int _{\kappa (n,s)}^s |e_r^n|^p ds\\&+ K n^{-p+1} E\int _{0}^t \int _{\kappa (n,s)}^s (1{+} |x_r|{+}|x_r^n|)^\frac{\rho p}{2} (1{+}|x_{\kappa (n,r)}^n|)^{\rho p}|\tilde{\sigma }^{n}(r, x_{\kappa (n,r)}^n)|^p dr ds\\&+K n^{-\frac{p-2}{2}} E\int _{0}^t \int _{\kappa (n,s)}^s |\sigma (x_r^n)-\sigma (x_{\kappa (n,r)}^n) - \sigma _1^{n}(r, x_{\kappa (n,r)}^n)|^\frac{p}{2}\\&\times (1+|x_{\kappa (n,r)}^n|)^\frac{\rho p}{2}|\tilde{\sigma }^{n}(r, x_{\kappa (n,r)}^n)|^\frac{p}{2} dr ds \\&+K n^{-\frac{p-2}{2}} E\int _{0}^t \int _{\kappa (n,s)}^s |\sigma (r, x_{\kappa (n,r)}^n)-\sigma ^{n}(x_{\kappa (n,r)}^n)|^\frac{p}{2}\\&\quad \times (1+|x_{\kappa (n,r)}^n|)^\frac{\rho p}{2} |\tilde{\sigma }^{n}(r,x_{\kappa (n,r)}^n)|^\frac{p}{2} dr ds \end{aligned}$$

for any $t \in [0,T]$. Moreover, one uses Hölder’s inequality to get the following estimates,

$$\begin{aligned} T_{33} +T_{34} \le&\, K E\int _{0}^t \sup _{0 \le r \le s} E|e_r^n|^p ds\\&+ Kn^{-p+1} \int _{0}^t \int _{\kappa (n,s)}^s \{E(1{+} |x_r|{+}|x_r^n|)^{p_0}\}^\frac{p \rho }{2p_0}\{\{E(1+|x_{\kappa (n,r)}^n|)^{p_0}\}^\frac{2\rho p}{2p_0-\rho p}\\&\times \{E|\tilde{\sigma }^n(x_{\kappa (n,r)}^n)|^\frac{2pp_0}{2p_0-3\rho p}\}^\frac{2p_0-3\rho p}{2p_0-\rho p}\}^\frac{2p_0-\rho p}{2p_0} dr ds\\&+K n^{-\frac{p-2}{2}} \int _{0}^t \int _{\kappa (n,s)}^s \Big \{E|\sigma (x_r^n)-\sigma (x_{\kappa (n,r)}^n) - \sigma _1^{n}(r, x_{\kappa (n,r)}^n)|^{p}\Big \}^\frac{1}{2}\\&\times \Big \{E(1+|x_{\kappa (n,r)}^n|)^{p_0}\}^\frac{\rho p}{p_0} \{E|\tilde{\sigma }^{n}(r, x_{\kappa (n,r)}^n)|^{\frac{pp_0}{p_0-\rho p}}\}^\frac{p_0-\rho p}{p_0}\Big \}^\frac{1}{2} dr ds\\&+K n^{-\frac{p-2}{2}} \int _{0}^t \int _{\kappa (n,s)}^s \Big \{E|\sigma (x_{\kappa (n,r)}^n)-\sigma ^{n}(r, x_{\kappa (n,r)}^n)|^p\Big \}^\frac{1}{2}\\&\times \Big \{ \{E(1+|x_{\kappa (n,r)}^n|)^{p_0}\}^\frac{\rho p}{p_0} \{E|\tilde{\sigma }^{n}(r, x_{\kappa (n,r)}^n)|^{\frac{pp_0}{p_0-\rho p}}\}^\frac{p_0-\rho p}{p_0}\Big \}^\frac{1}{2} dr ds \end{aligned}$$

and then Lemmas [3.3,  4.5, 4.6] and Corollary 4.1 yield

$$\begin{aligned} T_{33}&+T_{34} \le K n^{-p}+ K \int _{0}^t \sup _{0 \le r \le s} E |e_r^n|^p ds \end{aligned}$$

(4.12)

for any $t \in [0,T]$. For $T_{35}$, due to (4.11),

$$\begin{aligned} T_{35} :=&\,K \sum _{k=1}^d E\int _{0}^t \int _{\kappa (n,s)}^s |e_r^n|^{p-3}|\sigma (x_r)-\tilde{\sigma }^n(r,x_{\kappa (n,r)}^n)|^2 dr\\&\times \Big |\int _{\kappa (n,s)}^s \sum _{i=1}^d \sum _{l=1}^m \frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r,x_{\kappa (n,r)}^n)dw_r^l \Big |ds\\&\le K \sum _{k=1}^d E\int _{0}^t \int _{\kappa (n,s)}^s (n^\frac{1}{p}|e_r^n|)^{p-1}(1+|x_r|+|x_r^n|)^{\rho } dr\\&\times n^{-\frac{p-1}{p}}\Big |\int _{\kappa (n,s)}^s \sum _{l=1}^m \sum _{i=1}^d \frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l \Big |ds \\&+ K \sum _{k=1}^d E\int _{0}^t \int _{\kappa (n,s)}^s (n^\frac{1}{p}|e_r^n|)^{p-3}|\sigma (x_r^n)-\sigma (x_{\kappa (n,r)}^n)- \sigma ^n_1(r,x_{\kappa (n,r)}^n)|^2 dr\\&\times n^{-\frac{p-3}{p}}\Big |\int _{\kappa (n,s)}^s \sum _{l=1}^m \sum _{i=1}^d \frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l \Big |ds \\&+ K \sum _{k=1}^d E\int _{0}^t \int _{\kappa (n,s)}^s (n^\frac{1}{p}|e_r^n|)^{p-3}|\sigma (x_{\kappa (n,r)}^n)- \sigma ^n(x_{\kappa (n,r)}^n)|^2 dr\\&\times n^{-\frac{p-3}{p}}\Big |\int _{\kappa (n,s)}^s \sum _{l=1}^m \sum _{i=1}^d \frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l \Big |ds \end{aligned}$$

which on using Young’s inequality yields,

$$\begin{aligned} T_{35}&\le K E\int _{0}^t n \int _{\kappa (n,s)}^s |e_r^n|^{p} ds + K n^{-p+1}\sum _{k=1}^d E\int _{0}^t \int _{\kappa (n,s)}^s (1+|x_r|+|x_r^n|)^{\rho p} dr\\&\quad \times \Big |\int _{\kappa (n,s)}^s \sum _{l=1}^m \sum _{i=1}^d \frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l \Big |^p ds\\&\quad + K n^{-\frac{p-3}{3}} \sum _{k=1}^d E\int _{0}^t \int _{\kappa (n,s)}^s |\sigma (x_r^n)-\sigma (x_{\kappa (n,r)}^n)- \sigma ^n_1(r, x_{\kappa (n,r)}^n)|^\frac{2p}{3} dr\\&\quad \times \Big |\int _{\kappa (n,s)}^s \sum _{l=1}^m \sum _{i=1}^d \frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l \Big |^\frac{p}{3} ds \\&\quad + K n^{-\frac{p-3}{3}} \sum _{k=1}^d E\int _{0}^t \int _{\kappa (n,s)}^s |\sigma (x_{\kappa (n,r)}^n)- \sigma ^n(x_{\kappa (n,r)}^n)|^{\frac{2p}{3}} dr\\&\quad \times \Big |\int _{\kappa (n,s)}^s \sum _{l=1}^m \sum _{i=1}^d \frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r,x_{\kappa (n,r)}^n)dw_r^l \Big |^\frac{p}{3} ds \end{aligned}$$

and then on applying Hölder’s inequality, one obtains

$$\begin{aligned} T_{35} \le&\, K \int _{0}^t \sup _{0 \le r \le s} E|e_r^n|^{p} ds\\&+ K n^{-p+1} \sum _{k=1}^d \int _{0}^t \Big \{ n^{-\frac{p_0}{\rho p}+1}E\int _{\kappa (n,s)}^s (1+|x_r|+|x_r^n|)^{p_0} dr \Big \}^\frac{\rho p}{p_0}\\&\times \Big \{E\Big |\int _{\kappa (n,s)}^s \sum _{l=1}^m \sum _{i=1}^d \frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l \Big |^{\frac{pp_0}{p_0-\rho p}}\Big \}^\frac{p_0-\rho p}{p_0} ds\\&+ K n^{-\frac{p-3}{3}} \sum _{k=1}^d \int _{0}^t \Big \{E\Big (\int _{\kappa (n,s)}^s |\sigma (x_r^n)-\sigma (x_{\kappa (n,r)}^n)- \sigma ^n_1(r, x_{\kappa (n,r)}^n)|^\frac{2p}{3} dr \Big )^\frac{3}{2}\Big \}^\frac{2}{3}\\&\times \Big \{E\Big |\int _{\kappa (n,s)}^s \sum _{l=1}^m \sum _{i=1}^d \frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l \Big |^{p}\Big \}^\frac{1}{3} ds \\&+ K n^{-\frac{p-3}{3}} \sum _{k=1}^d \int _{0}^t \Big \{ E\Big (\int _{\kappa (n,s)}^s |\sigma (x_{\kappa (n,r)}^n)- \sigma ^n(x_{\kappa (n,r)}^n)|^{\frac{2p}{3}} dr \Big )^\frac{3}{2}\Big \}^\frac{2}{3}\\&\times \Big \{E\Big |\int _{\kappa (n,s)}^s \sum _{l=1}^m \sum _{i=1}^d \frac{\partial b^k(x_{\kappa (n,r)}^n)}{\partial x^i} \tilde{\sigma }^{n,(i,l)}(r, x_{\kappa (n,r)}^n)dw_r^l \Big |^p\Big \}^\frac{1}{3} ds \end{aligned}$$

for any $t \in [0,T]$. Further, one uses Remark 2.1, an elementary inequality of stochastic integrals and Hölder’s inequality to obtain the following estimates,

$$\begin{aligned} T_{35} \le&\, K \int _{0}^t \sup _{0 \le r \le s} E|e_r^n|^{p} ds + K n^{-p} \int _{0}^t \Big \{n^{-\frac{pp_0}{2p_0-2\rho p}+1}\\&\times E\int _{\kappa (n,s)}^s (1+|x_{\kappa (n,r)}^n|)^{\frac{p \rho p_0}{p_0-\rho p}} |\tilde{\sigma }^{n}(r,x_{\kappa (n,r)}^n)|^{\frac{pp_0}{p_0-\rho p}} dr \Big \}^\frac{p_0-\rho p}{p_0} ds \\&+ K n^{-\frac{p-3}{3}} \int _{0}^t \Big \{n^{-\frac{1}{2}}E \int _{\kappa (n,s)}^s |\sigma (x_r^n)-\sigma (x_{\kappa (n,r)}^n)- \sigma ^n_1(r,x_{\kappa (n,r)}^n)|^p dr \Big \}^\frac{2}{3}\\&\quad \times \Big \{n^{-\frac{p}{2}+1}E\int _{\kappa (n,s)}^s (1+|x_{\kappa (n,r)}^n|)^{\rho p} |\tilde{\sigma }^{n}(r,x_{\kappa (n,r)}^n)|^p dr \Big \}^\frac{1}{3} ds\\&+ K n^{-\frac{p-3}{3}} \int _{0}^t \Big \{ n^{-\frac{1}{2}}E\int _{\kappa (n,s)}^s |\sigma (x_{\kappa (n,r)}^n)- \sigma ^n(x_{\kappa (n,r)}^n)|^{p} dr \Big \}^\frac{2}{3}\\&\times \Big \{n^{-\frac{p}{2}+1}E\int _{\kappa (n,s)}^s (1+|x_{\kappa (n,r)}^n|)^{\rho p} |\tilde{\sigma }^{n}(r, x_{\kappa (n,r)}^n)|^p dr \Big \}^\frac{1}{3} ds \nonumber \end{aligned}$$

which due to further application of Young’s inequality gives,

$$\begin{aligned} T_{35} \le&\, K \int _{0}^t \sup _{0 \le r \le s} E|e_r^n|^{p} ds+ K n^{-p} \int _{0}^t \Big \{n^{-\frac{pp_0}{2p_0-2\rho p}+1} \\&\times \int _{\kappa (n,s)}^s \{E(1+|x_{\kappa (n,r)}^n|)^{p_0}\}^{\frac{\rho p}{p_0-\rho p}} \{E|\tilde{\sigma }^{n}(r,x_{\kappa (n,r)}^n)|^{\frac{pp_0}{p_0-2\rho p}}\}^\frac{p_0-2\rho p}{p_0-\rho p} dr \Big \}^\frac{p_0-\rho p}{p_0} ds \\&+ K n^{-\frac{p-3}{3}} \int _{0}^t \Big \{n^{-\frac{1}{2}}E \int _{\kappa (n,s)}^s |\sigma (x_r^n)-\sigma (x_{\kappa (n,r)}^n)- \sigma ^n_1(r,x_{\kappa (n,r)}^n)|^p dr \Big \}^\frac{2}{3}\\&\times \Big \{n^{-\frac{p}{2}+1}\int _{\kappa (n,s)}^s \{E(1+|x_{\kappa (n,r)}^n|)^{p_0}\}^\frac{\rho p}{p_0} \{E|\tilde{\sigma }^{n}(r,x_{\kappa (n,r)}^n)|^{\frac{p_0p}{p_0-\rho p}}\}^\frac{p_0-\rho p}{p_0} dr \Big \}^\frac{1}{3} ds \\&+ K n^{-\frac{p-3}{3}} \int _{0}^t \Big \{ n^{-\frac{1}{2}}E\int _{\kappa (n,s)}^s |\sigma (x_{\kappa (n,r)}^n)- \sigma ^n(x_{\kappa (n,r)}^n)|^{p} dr \Big \}^\frac{2}{3}\\&\times \Big \{n^{-\frac{p}{2}+1}E\int _{\kappa (n,s)}^s \{E(1{+}|x_{\kappa (n,r)}^n|)^{p_0}\}^\frac{\rho p}{p_0} \{E|\tilde{\sigma }^{n}(r,x_{\kappa (n,r)}^n)|^{\frac{p_0p}{p_0-\rho p}}\}^\frac{p_0-\rho p}{p_0} dr \Big \}^\frac{1}{3} ds \nonumber \end{aligned}$$

and finally on the application of Lemmas [3.3, 4.5, 4.6] and Corollary 4.1, one obtains

$$\begin{aligned} T_{35} \le K n^{-p} + K\int _{0}^t \sup _{0 \le r \le s}E|e_r^n|^p ds \end{aligned}$$

(4.13)

for any $t \in [0,T]$. Hence, on substituting estimates from (4.8), (4.10), (4.12) and (4.13) in (4.7), one obtains

$$\begin{aligned} T_{3} \le K n^{-p}+K\int _{0}^t \sup _{0 \le r \le s}E|e_r^n|^p ds \end{aligned}$$

(4.14)

for any $t \in [0,T]$. Thus, the proof is completed by combining estimates from (4.5), (4.6) and (4.14) in (4.4).

Proof of Theorem 2.1

Let $\bar{b}^n(s):=b(x_s)-b^n(x_{\kappa (n,s)}^n)$ and $\bar{\sigma }^n(s):=\sigma (x_s)-\tilde{\sigma }^n(x_{\kappa (n,s)}^n)$ and then one writes

$$\begin{aligned} e_t^n:=x_t-x_t^n= \int _0^t \bar{b}^n(s) ds + \int _0^t \bar{\sigma }^n(s)dw_s \end{aligned}$$

for any $t \in [0,T]$. By the application of Itô’s formula,

$$\begin{aligned} |e_t^n|^p&=p \int _0^t |e_s^n|^{p-2} e_s^n \bar{b}^n(s)ds+p \int _0^t |e_s^n|^{p-2} e_s^n \bar{\sigma }^n(s)dw_s\\&\quad +\frac{p(p-2)}{2} \int _0^t |e_s^n|^{p-4} |\bar{\sigma }^{n*}(s)e_s^n|^2 ds + \frac{p}{2} \int _0^t |e_s^n|^{p-2} |\bar{\sigma }^{n}(s)|^2 ds \end{aligned}$$

for any $t \in [0,T]$. As before, when $p=2$ the third term does appear on the right hand side of the above equation and $|e_s^n|^{p-2}$ is absent from the rest of the terms. Due to Cauchy–Bunyakovsky–Schwartz inequality, one obtains

$$\begin{aligned} E|e_t^n|^p&\le p E\int _0^t |e_s^n|^{p-2} e_s^n \bar{b}^n(s)ds +\frac{p(p-1)}{2} E \int _0^t |e_s^n|^{p-2} |\bar{\sigma }^{n}(s)|^2 ds \end{aligned}$$

for any $t \in [0,T]$. Furthermore, one observes that for $z_1,z_2 \in \mathbb {R}^{d \times m}$, $|z_1+z_2|^2 = |z_1|^2+2\sum _{i=1}^{d}\sum _{j=1}^{m} z_1^{(i,j)} z_2^{(i,j)}+|z_2|^2$, which on using Young’s inequality further implies $|z_1+z_2|^2 \le (1+\epsilon )|z_1|^2+(1+1/\epsilon )|z_2|^2$ for every $\epsilon >0$. Let us now fix $\epsilon >0$. Hence, one can use this arguments for estimating $|\sigma (x_s)-\sigma (x_s^n)|^2$ when using the splitting given in equation (4.11). This along with the splitting of equation (4.9) gives

$$\begin{aligned} E|e_t^n|^p \le&\, p E\int _0^t |e_s^n|^{p-2} e_s^n\{b(x_s)-b(x_s^n)\}ds\\&+ p E\int _0^t |e_s^n|^{p-2} e_s^n \{b(x_s^n)-b(x_{\kappa (n,s)}^n)\} ds\\&+ p E\int _0^t |e_s^n|^{p-2} e_s^n \{b(x_{\kappa (n,s)}^n)-b^n(x_{\kappa (n,s)}^n)\} ds\\&+\frac{\epsilon +1}{2}p(p-1) E\int _0^t |e_s^n|^{p-2} |\sigma (x_s)-\sigma (x_s^n)|^2 ds\\&+ K E\int _0^t |e_s^n|^{p-2} |\sigma (x_s^n)-\sigma (x_{\kappa (n,s)}^n)-\sigma ^{n}_1(x_{\kappa (n,s)}^n)|^2 ds\\&+ K E\int _0^t |e_s^n|^{p-2} |\sigma (x_{\kappa (n,s)}^n)-\sigma ^n(x_{\kappa (n,s)}^n)|^2 ds \end{aligned}$$

for any $t \in [0,T]$. Notice that the constant $K>0$ (a large constant) in the last two terms of the above inequality depends on $\epsilon$. Also, one obtains the following estimates,

$$\begin{aligned} E|e_t^n|^p \le&\, \frac{p}{2} E\int _0^t |e_s^n|^{p-2} \Big [e_s^n\{b(x_s)-b(x_s^n)\}+ (1+\epsilon )(p-1) |\sigma (x_s)-\sigma (x_s^n)|^2 \Big ] ds \\&+ p E\int _0^t |e_s^n|^{p-2} e_s^n \{b(x_s^n)-b(x_{\kappa (n,s)}^n)\} ds \\&+ p E\int _0^t |e_s^n|^{p-2} e_s^n \{b(x_{\kappa (n,s)}^n)-b^n(x_{\kappa (n,s)}^n)\} ds\\&+ K E\int _0^t |e_s^n|^{p-2} |\sigma (x_s^n)-\sigma (x_{\kappa (n,s)}^n)-\sigma ^{n}_1(x_{\kappa (n,s)}^n)|^2 ds \\&+ K E\int _0^t |e_s^n|^{p-2} |\sigma (x_{\kappa (n,s)}^n)-\sigma ^n(x_{\kappa (n,s)}^n)|^2 ds. \end{aligned}$$

for any $t \in [0,T]$. Since $p < p_1$, thus on using Assumption A-3, Lemmas [4.6, 4.7] and Young’s inequality, one obtains

$$\begin{aligned} E|e_t^n|^p&\le K E\int _0^t |e_s^n|^{p} ds + Kn^{-p} + K E\int _0^t |b(x_{\kappa (n,s)}^n)-b^n(x_{\kappa (n,s)}^n)|^p ds\\&\quad + K E\int _0^t |\sigma (x_{\kappa (n,s)}^n)-\sigma ^n(x_{\kappa (n,s)}^n)|^p ds \end{aligned}$$

and hence Lemmas [4.4, 4.5] give

$$\begin{aligned} \sup _{0 \le s \le t}E|e_s^n|^p&\le K \int _0^t \sup _{0 \le r \le s}E|e_r^n|^{p} ds + Kn^{-p} <\infty \end{aligned}$$

(4.15)

for any $t \in [0,T]$. Finally, the use of Gronwall’s lemma completes the proof.

5 Numerical example

In this section, numerical experiments are implemented by using the proposed Milstein type scheme and it is demonstrated that their findings support our theoretical results.

5.1 First example

Consider a one-dimensional SDE which is given by

$$\begin{aligned} dx_t=x_t(1-x_t^2)dt +\sigma (1-x_t^2)dw_t, \end{aligned}$$

(5.1)

for any $t \in [0,1],$ with initial value $x_0=2.0$ and $\sigma =0.3$. Our Milstein type scheme of SDE (5.1) at the $(l+1)h$-th gridpoint is given by, for any $l=0, 1, \ldots , 2^{n}-1$,

$$\begin{aligned} x_{(l+1)h}^{n}&=x_{lh}^{n}+\frac{x_{lh}^{n}(1-(x_{lh}^{n})^2)}{1+h|x_{lh}^{n}|^4}h +\sigma \frac{1-(x_{lh}^{n})^2}{1+h|x_{lh}^{n}|^4} \varDelta w_{lh} \nonumber \\&\qquad +\sigma ^2\frac{(x_{lh}^{n})^3-x_{lh}^{n}}{1+h|x_{lh}^{n}|^4}((\varDelta w_{lh})^2-h) \end{aligned}$$

(5.2)

with $h=2^{-n}$ where $\varDelta w_{lh}:=w_{(l+1)h}-w_{lh}$. Our aim is to calculate

$$\begin{aligned} (E(|x_1^{\text {exact}}-x_1^n|^p))^{1/p}, \quad p=2,3, \end{aligned}$$

(5.3)

where $x_1^{\text {exact}}$ is the exact solution of the SDE (5.1) and $x_1^n$ is the value of the scheme at $(l+1)h=1$ and for step length h. Since the exact solution of the SDE is not known, the scheme (5.2) with $h^*=2^{-21}$ and $n^*=21$ is taken to be the true solution of SDE (5.1). Letting

$$\begin{aligned} \varDelta w_{lh^*}^i=w_{(l+1)h^*}^i-w_{lh^*}^i, \quad l=0, \ldots , 2^{n^*}-1 \end{aligned}$$

(5.4)

to denote one particular (i.e. the i-th) realization of the driving Wiener process with $h^*=2^{-21}$, the corresponding sequences of Wiener increments with step size $h=2^{-n}$ and for the same realisation, where $n=6,\ldots , 20$, are given according to

$$\begin{aligned} \varDelta w_{kh}^i=w_{(k+1)h}^i-w_{kh}^i=\sum \limits _{l=kN^*/N}^{(k+1)N^*/N-1}\varDelta w_{lh^*}^i , \quad k=0, \ldots , 2^{n}-1, \end{aligned}$$

(5.5)

where

$$\begin{aligned} \dfrac{N^*}{N}=\dfrac{1/h^*}{1/h}=2^{21-n}. \end{aligned}$$

(5.6)

Hence,

$$\begin{aligned} h^2=Var(\varDelta w_{kh}^i)=Var\left( \sum \limits _{l=kN^*/N}^{(k+1)N^*/N-1}\varDelta w_{lh^*}^i\right) =\dfrac{N^*}{N}(h^*)^2. \end{aligned}$$

(5.7)

Let $Y_i:=|x_1^{\text {exact},i}-x_1^{n,i}|^p$ for the i-th path and let $M_n$ denote the Monte Carlo estimate of $E(|x_1^{\text {exact}}-x_1^n|^p)$. Then, one defines

$$\begin{aligned} V_n:=\dfrac{1}{N-1}\left( \sum \limits _{i=1}^N Y_i^2-NM_n^2 \right) \end{aligned}$$

(5.8)

to denote the corresponding sample variance. Thus, the $100\alpha$% confidence interval is given by

$$\begin{aligned}&L_{\alpha ,n}^V=M_n-\sqrt{\dfrac{V_n}{(1-\alpha )N}}, \nonumber \\&R_{\alpha ,n}^V=M_n+\sqrt{\dfrac{V_n}{(1-\alpha )N}}, \end{aligned}$$

(5.9)

meaning that

$$\begin{aligned} \liminf \limits _{n \rightarrow \infty } P\left( \omega \in \varOmega : L_{\alpha ,n}^V \le E(|x_1^{\text {exact}}-x_1^n|^p) \le R_{\alpha ,n}^V\right) \ge \alpha . \end{aligned}$$

(5.10)

Hence, the confidence interval for $(E(|x_1^{\text {exact}}-x_1^n|^p))^{1/p}$ is given by

$$\begin{aligned} \liminf \limits _{n \rightarrow \infty } P\left( \omega \in \varOmega : (L_{\alpha ,n}^V)^{1/p} \le (E(|x_1^{\text {exact}}-x_1^n|^p))^{1/p} \le (R_{\alpha ,n}^V)^{1/p}\right) \ge \alpha . \end{aligned}$$

(5.11)

The numerical values for the MC estimate of $(E(|x_1^{\text {exact}}-x_1^n|^p))^{1/p}$, $p=2,3$ with 60,000 paths and the corresponding 95% confidence intervals (with $\alpha =0.95$) are given in the Tables 1 and 2 below.

Table 1 $\mathscr {L}^2$-error estimates of scheme (5.2) of SDE (5.1) along with confidence intervals; 60,000 paths

Table 2 $\mathscr {L}^3$-error estimates of scheme (5.2) for SDE (5.1) along with confidence intervals; 60,000 paths

Fig. 1

$\mathscr {L}^2$- and $\mathscr {L}^3$-rate of convergence of scheme (5.2) of SDE (5.1) along with confidence intervals; 60,000 paths

Fig. 2

$\mathscr {L}^p$-rate of convergence for scheme (5.13) of SDE (5.12) when initial value $x_0$ follows Pareto distribution ($\xi$)

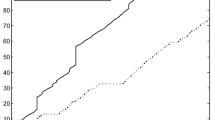
Figure 1 indicates that the rate of $\mathscr {L}^2$- and $\mathscr {L}^3$-convergence of the scheme (5.2) is 1.0.

5.2 Second example

Consider the following one-dimensional SDE,

$$\begin{aligned} dx_t=-x_t|x_t|^\frac{5}{2} dt + x_t|x_t|dw_t, \end{aligned}$$

(5.12)

for any $t \in [0,1],$ where the initial value $x_0$ follows a Pareto distribution with density function $f(x)=(1+\xi x)^{-(1+1/\xi )}$ for $x >0$ and $\xi \ge 0$. Notice that $E|x_0|^p<\infty$ iff $p<1/\xi$. Take $\xi =1/18$ so that $E|x_0|^p<\infty$ for all $p<18$ which implies that Theorem 2.1 holds for $p=2$. Our Milstein-type scheme of SDE (5.12) at the $(l+1)h$-th gridpoint is given by, for any $l=0, 1, \ldots , 2^{n}-1$,

$$\begin{aligned} x_{(l+1)h}^{n}&=x_{lh}^{n}+\frac{-x_{lh}^{n}|x_{lh}^{n}|^\frac{5}{2}}{1+h|x_{lh}^{n}|^5}h+\frac{x_{lh}^{n}|x_{lh}^{n}|}{1+h|x_{lh}^{n}|^5} \varDelta w_{lh} +\frac{x_{lh}^{n}|x_{lh}^{n}|^2}{1+h|x_{lh}^{n}|^5}((\varDelta w_{lh})^2-h) \end{aligned}$$

(5.13)

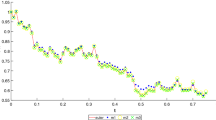
with $h=2^{-n}$ where $\varDelta w_{lh}:=w_{(l+1)h}-w_{lh}$. Figure 2a and Table 3a indicate that the rate of $\mathscr {L}^2$-convergence of the scheme (5.13) is 1.0. The scheme (5.2) with $h=2^{-21}$ is taken to be the true solution of SDE (5.12). The number of paths is 60, 000.

Let us now take $\xi =1/35$ so that $E|x_0|^{p_0}< \infty$ for all $p_0<35$ which implies that Theorem 2.1 holds for $p=2,3,4$. Figure 2b and Table 3b show that the theoretical rate of convergence is realised in these three cases.

Table 3 $\mathscr {L}^p$-error estimates for scheme (5.2) of SDE (5.1) when initial value $x_0$ follows Pareto distribution ($\xi$)