1 Introduction

Historic masonry structures constitute a significant portion of the world’s cultural heritage and, thus, present a multitude of challenges in analysis, diagnosis, conservation and rehabilitation (ICOMOS 2003). Due to their uniqueness and construction complexity, these constructions require careful consideration and specialised expertise to preserve and maintain their inestimable cultural, social and economic value. Historic masonry structures were built based on the knowledge and experience of builders, who over time developed best practices referred to as “rules of art” (Giuffrè 1993, 1996). However, this traditional approach often resulted in randomly textured masonries, combined use of different materials and subsequent alterations to the original structure. The geometric complexity of these masonry structures, usually built to resist only gravitational loads, further contributes to their seismic vulnerability (Chieffo et al. 2023). In addition, their structural behaviour is affected by the decay of materials and the damaged state. Due to the difficulty of considering all the variables involved and the limited knowledge of construction and evolutionary characteristics, predicting the structural behaviour of historic masonry structures is challenging, especially under seismic actions.

Historic masonry structures encompass a vast majority of archaeological ruins, which are spread around the world and serve as tangible evidence of past human civilisations (Aguilar et al. 2015). Conserving these sites extends beyond safeguarding the structures themselves; it involves preserving their immense cultural and historical value (Lagomarsino and Podestà 2010). These remains are limited, unique, and non-renewable resources, making their conservation even more critical (De la Torre and Mac Lean 1997). Many of these structures have deteriorated over the years, losing structural integrity and suffering deterioration, leading to partial or total collapse (Albuerne and Williams 2017; Autiero et al. 2021; Ruggieri et al. 2018). As a result, ruins often exhibit isolated structural elements, such as arches, individual walls, columns etc., which are highly vulnerable. Archaeological sites face a variety of potential risks that compromise their preservation. Oftentimes, these sites remain buried for many centuries after their construction, and when unearthed, they become exposed to natural and human hazards, respectively. Natural events such as earthquakes, floods, landslides, fires, and others represent direct and acute risks whereas slowly developing issues such as water infiltration, soil settlement, and anomalous stresses in the structure gradually compromise the site's long-term stability (Marino 2019). However, vulnerability also depends on non-structural phenomena, which may involve the archaeological site as a whole (landscapes, decorations, etc.). Tourism growth and the subsequent development of facilities lead to increased pressure on the fragile historical remains. For instance, willingness to attract tourists often results in the reconstruction of architectural elements and structures, which can compromise the authenticity of the site. In addition, insufficient human and financial resources further hamper proper preservation efforts, especially when dealing with the heritage of a cultural minority (De la Torre and Mac Lean 1997). Thus, all these sources of damage make the vulnerability assessment of the archaeological ruins a complex problem, requiring analytical (cognitive and diagnostic) and design activities (Formisano et al. 2018; Di Lorenzo et al. 2019) within a systematic and long-term plan of maintenance (Cecchi and Gasparoli 2010; De la Torre and Mac Lean 1997).

In particular, with a special focus on structural behaviour, seismic hazard poses a significant threat to archaeological sites, as even low-intensity events can cause extensive damage. This is mainly due to the high seismic vulnerability of archaeological remains, i.e. their susceptibility to damage or collapse during an earthquake. The latter mainly occur due to the absence of global structural integrity and the absence of connections between structural elements, which generally lead to shear cracking and disintegration (Roca et al. 2019) and out-of-plane failure. Vulnerability is a critical parameter when determining the seismic risk of a site, along with exposure, i.e. its intrinsic value, and seismic hazard. Given the challenging nature of controlling seismic hazards and exposure, it is important to investigate a site's vulnerability for potential mitigation measures. The Italian Directive P.C.M (2007) proposes simplified models for conducting territorial-scale analyses of cultural heritage. However, these models are primarily intended for assessing the seismic vulnerability of archaeological assets that still exhibit global structural behaviour. Conversely, when dealing with masonry fragments lacking structural integrity, Podestà has introduced a more suitable methodology for defining limit domains. Once the hazard is known, this methodology specifies the geometric characteristics that macro-elements must possess to be considered safe (Podestà 2010). To date, several methodologies have also been proposed for seismic vulnerability assessment, commonly developed for buildings. In general, three main categories are identified: (i) empirical or statistical methods, (ii) analytical methods and (iii) hybrid methods, resulting from a combination of the other two (Shabani et al. 2021). Empirical methods rely on statistical data from observed damage in past earthquakes or expert judgement. They are commonly used for rapid assessments performed on an urban scale since geometric surveys and on-site inspections are sufficient to provide the necessary (Ferreira et al. 2017; Basaglia et al. 2018; Chieffo et al. 2022, 2019; Chieffo and Formisano 2019). Screening (ATC 1989), Vulnerability Index methods (Benedetti and Petrini 1984; GNDT 1993; Vicente 2008; Formisano et al. 2010), and Damage Probability Matrices (Whitman and Reed 1973) fall into this category. These approaches can be also combined with the Macroseismic method, developed by Lagomarsino and Giovinazzi (2006), to evaluate the expected damage scenarios (Maio et al. 2015; Biglari and Formisano 2020). In contrast, analytical methods provide a more precise seismic assessment, as they use vulnerability curves derived from numerical analyses based on detailed or simplified models. Specifically, detailed analytical methods consist of nonlinear analyses that require sophisticated numerical simulations. Simplified analytical analyses, on the other hand, include collapse mechanism-based, capacity spectrum-based methods and fully displacement-based methods (Shabani et al. 2021). Besides a few attempts on the global-aggregate scale through automated procedures (Leggieri et al. 2022, 2023), analytical methods, both detailed and simplified, are commonly adopted for seismic assessment on a local scale. This is because of the computational effort required, a large number of variables and the uncertainties involved. Although limited, there have been a few attempts at using analytical methods for the seismic assessment of archaeological sites. In Aguilar et al. (2015), Ruggieri et al. (2018) and Lorenzoni et al. (2019), Finite Element (FE) models were used for both global non-linear static (push-over) analysis and local kinematic limit analysis. Lourenço et al. (2012) also employed an FE model to conduct push-over and time history analyses, while Chácara et al. (2014) conducted a global linear static analysis and a local pushover analysis. Complementarily, Galassi et al. (2020a, b) and Sassu et al. (2013) used rigid-block models. It is important to note that numerical models require an accurate calibration of the actual conditions of the structure, which can be achieved through on-site non-destructive testing. For instance, Marques et al. (2014) utilised ambient vibration tests to calibrate FEM models, and their outcomes were subsequently validated through kinematic limit analysis. Furthermore, understanding the structural performance of archaeological sites is particularly challenging due to difficulties in defining the geometry, materials, and level of damage. To address this, Di Miceli et al. (2017) proposed determining unknown parameters in probabilistic terms. Nevertheless, the presence of numerous uncertainties still implies that developing reliable models may be problematic. Furthermore, several authors (Ruggieri et al. 2018; Galassi et al. 2020a, b) have recommended validating these models by different numerical methods (Galassi et al. 2022; Seçkin and Sayin 2022). Due to the time and effort required, this approach may not always be feasible, particularly for extensive sites. Recognizing the inherent lack of structural continuity in most archaeological sites, it becomes evident that conducting local analyses is imperative to ascertain necessary preventive interventions (Podestà 2010). Nonetheless, in line with the Italian Directive P.C.M (2007), a large-scale seismic assessment is an essential preliminary measure aimed at identifying the most vulnerable parts warranting further local studies (Lagomarsino and Podestà 2010). Empirical methods, such as Vulnerability Index methods, may be suited to this purpose, however, their effectiveness for seismic evaluation of archaeological sites has not yet been studied in the literature.

Based on the above considerations, the present work proposes a simplified approach for assessing the seismic vulnerability of archaeological sites. The suggested evaluation approach seeks to be a straightforward and quick tool, relying exclusively on data gathered through the geometry survey and on-site examination. While the methods utilised are well-established in the literature and have been widely applied to buildings, the contribution of this study lies in proposing a structured framework that integrates different assessment methods at different levels of analysis to evaluate archaeological contexts. To this end, the use of index-based procedures is herein explored for the first time by comparing and adapting them to the unique characteristics of archaeological sites. The methodology suggested was applied at the Wupatki Pueblo archaeological site, in Arizona (US), as part of the Integrated Site Conservation and Management Plan and Training for Wupatki National Monument, Arizona project, supported by the J. Paul Getty Trust.

This paper contextualises the case study and provides an overview of its main architectural and historical features. This is followed by a detailed description of the methodological approach, divided into three levels of analysis: (i) application of the Masonry Quality Index to selected walls, (ii) seismic vulnerability assessment and expected damage estimation of the site, and (iii) analysis of individual wall structural response. Accordingly, the outcomes of the case study application are presented and discussed. Finally, the main conclusions of the work are drawn and potential areas for future research and development are outlined.

2 The case study

Wupatki Pueblo is one of the largest and most impressive prehistoric ruins in the American Southwest. It was occupied by Ancestral Puebloans, also known as the Sinagua people, between 1100 and 1250 AD. The site is located within the Wupatki National Monument (WUPA), which covers over 140 km2 of diverse landscapes and more than 2500 cultural sites. Located approximately 56 km northeast of Flagstaff (Coconino County, Arizona), Wupatki Pueblo is an open-air archaeological site that sits at an altitude of about 1480 m in the Wupatki Basin. The basin extends for about 130 km2 along the East side of the East Kaibab Monocline and is bound to the southwest by the northeast edge of the San Francisco Volcanic Field. To the northeast, the basin descends to the Little Colorado River, which flows across the WUPA and demarcates its eastern boundary (Fig. 1).

Fig. 1
figure 1

Location of the Wupatki Pueblo

Full size image

Hundreds of earthquakes were recorded in the Coconino County area between 1830 and 2011, most of them of magnitude, Mw, less than or equal to 3.0. A few earthquakes were of medium magnitude (3.0 ≤ Mw ≤ 5.0), and only three had a magnitude of 6.0 or higher (Anderson et al. 2021). While these earthquakes were typically not felt by residents and rarely caused damage, it is important to keep in consideration the potential seismic hazard of the area to ensure the structural integrity of the site. Still, considering historical seismicity, the probability of a catastrophic earthquake in the area is low as described in the study proposed by Anderson et al. (2021). Specifically, according to the Unified Hazard Tool provided by USGS (Unified Hazard Tool 2023), the site area is characterised by a Peak Ground Acceleration (PGA) of 0.16 g and 0.05 g with a probability of exceeding 2% and 10%, respectively, in 50 years.

2.1 Description of the site

Wupatki Pueblo was built on a narrow sandstone ridge that extends in a north–south direction. It comprises two main compact room blocks, known as the South and North Pueblos or Units, which are together referred to as the Main Pueblo. The site also includes a Ballcourt in the vicinity of the Main Pueblo, and a Community Room, also known as the Amphitheatre, located at the east of the North Unit (Fig. 2). While the room units are now two separate entities, they were most likely connected in the past (Brennan and Downum 2001). Both blocks are characterised by intersecting rock formations that cut through many of the rooms, some of which were built partially or entirely on boulders. Since the site is in ruins, this study focuses on the areas with relevant parts of the structure remaining. Specifically, the upper part of the South Pueblo has been considered as a structural aggregate (SA) consisting of 12 structural units (SUs), while the SA of the North Pueblo consists of 4 relevant SUs, as shown in Fig. 3.

Fig. 2
figure 2

Overview of the Wupatki Pueblo archaeological site, view to the west

Full size image
Fig. 3
figure 3

Satellite view of the Wupatki Pueblo indicating the area evaluated and the location of sonic tests

Full size image

The complex was originally constructed with irregularly shaped Moenkopi sandstone blocks and earth-based mortar joints (Fig. 4a). However, cement mortar was used during the reconstruction period, and over time the joints have been repointed with stabilised earth-based mortars. Although precise information on the cross-sections of the walls is lacking, observations of collapsed sections indicate that they consist of a double leaf with a few stones passing through the entire thickness (Fig. 4b). Generally, there is no evidence of corner connecting elements, such as quoins, between orthogonal walls. The walls were built directly on the soil or boulders without a visible foundation (Fig. 4c). Horizontal elements at floors and roofs are no longer present, but evidence of past timber beams remains, including a pair of beams and sockets in the walls where beams were hosted.

Fig. 4
figure 4

Material and building techniques: a Moenkopi sandstone blocks and earth-based mortar joints; b wall cross-section; c orthogonal walls and boulder intersection

Full size image

The Wupatki Pueblo, mostly unearthed after centuries, is now alarmingly exposed to weathering, as it experiences hot, wet summers and approximately 100 days of below-zero temperatures during winter. Issues like water drainage, water and snow accumulation, freeze–thaw cycles due to temperature fluctuations and salt crystallisation cause deterioration in both the masonry walls and boulders, weakening the mechanical properties of the materials and damaging the structural integrity of the walls. Furthermore, recent extreme weather events, like heavy rainfalls, and the expected climate change further compound challenges in preserving the site.

2.2 Historical background

The Sinagua people were drawn to the area due to its natural resources. The surrounding landscape indeed provided the Ancestral Puebloans with water, fertile land for agriculture, and a variety of natural resources such as wood, clay, and stone. During its heyday between AD 1150 and 1250, the complex served as the largest and most influential pueblo in the WUPA region, acting as a hub for trade and exchange between neighbouring communities. The site supposedly consisted of over 100 rooms and housed about 100 people.

Today, Wupatki Pueblo is part of the Wupatki National Monument, which was established in 1924 by the National Park Service (NPS) to preserve the site and other cultural and natural resources in the area. However, early excavations in the 1930s and subsequent ones in the 1940s to 1960s were conducted arbitrarily and without proper documentation. Moreover, conservation efforts involved demolishing and reconstructing parts of the site to attempt to restore its original appearance (Brennan and Downum 2001).

In recent decades, the NPS has taken a more cautious approach to conservation efforts, to preserve the original features of the site. However, the lack of detailed reports makes it challenging to distinguish between original features and more recent interventions. Still, the most obvious reconstructions and invasive interventions have been removed.

2.3 In-situ non-destructive testing

As part of the project, several investigations and diagnostic activities were carried out to better understand the structural performance of the site. Non-destructive testing (NDT) was an important component, given the unique nature of the masonry and the wide range of materials used in its construction. Specifically, sonic tests were performed on six selected walls, as indicated in Fig. 3. The sample size was constrained by the time available for the inspection and site accessibility. Nevertheless, the number of tests conducted was deemed adequate to estimate the mechanical properties of the masonry that, despite its peculiarity, apparently exhibited consistent characteristics across the entire archaeological site. The sonic pulse velocity test is a non-destructive method that employs elastic waves in the sonic range (20–20000 Hz) to evaluate the properties of a structural element (Miranda et al. 2013). Indeed, the analysis of the wave velocities enables qualitative characterization of the element, encompassing its consistency, homogeneity and deterioration. Additionally, the velocities of propagating waves can be correlated with the mechanical properties of the material (ASTM 2000). To make a quantitative assessment, the medium is assumed as elastic, isotropic, homogeneous and non-dispersive. Under this assumption, the mechanical P-wave velocity \({V}_{P}\) can be related to the material's dynamic elastic modulus \(E\), Poisson’s ratio ν and density ρ through:

$$V_{P} = \sqrt {\frac{E}{\rho } \cdot \frac{(1 - \nu )}{{(1 + \nu )(1 - 2\nu )}}}$$
(1)

Then, the dynamic elastic modulus \(E\) of the masonry can be obtained from the wave velocity \(V_{P}\), assuming a density of 2000 kg/m3 and a Poisson’s ratio ν of 0.2. Six walls were investigated using both direct and indirect sonic pulse velocity tests, depending on the accessibility of the walls’ sides. Tests were conducted using an instrumented impact hammer (PCB Model 086D05) and an accelerometer (PCB model 352B) with a measurement range of ± 5 g and 1000 mV/g sensitivity. The adopted Data Acquisition System (NI model USB-4431) allows for a high sampling rate of up to 100 kHz, which is necessary for such tests. All tests were exclusively conducted on the stones within an approximately one-square-meter area by striking them. However, due to the irregularity of the masonry, it was not possible to define a regular grid with a constant distance between the points. Consequently, for each acquisition point, measurements were repeated to achieve at least five records that were then averaged. The results are summarised in Table 1, with an average dynamic \(E\) of 1538 MPa. It is noteworthy that significant variations in velocity results were observed between direct and indirect tests. Indeed, direct tests produced higher values, sometimes comparable to the velocity in the stones, probably due to the presence of larger blocks and fewer mortar joints across the wall thickness. Additionally, the masonry’s compressive strength \({f}_{m}\) was estimated by dividing the dynamic elastic modulus \(E\) by a value equal to 550, as derived for the masonry from NTC (2018), with an average of 2.8 MPa. This indicates a reasonable quality of the masonry.

Table 1 Sonic test results
Full size table

3 Multi-level methodological approach

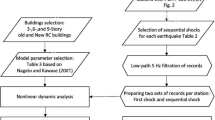
The purpose of this section is to provide a detailed description of the methodology herein developed for a rapid seismic vulnerability assessment of archaeological sites. The methodological approach comprises an easy-to-use structured framework that combines well-established building-assessment methods adapted to evaluate archaeological sites. The workflow, depicted in Fig. 5, is structured into three main tasks as follows:

  1. (1)

    Masonry characterisation using the Masonry Quality Index (MQI) method—The method is applied to selected walls to estimate the shear strength τ0 and minimise uncertainties in determining the Conventional strength parameter within vulnerability index forms. It is important to analyse an adequate number of walls to ensure the findings accurately represent the actual masonry properties. As the method can be applied to any type of masonry walls without any modification or adaptation to the specific characteristics of the site, the authors believe there is no need to compare results with similar methods. Nevertheless, it is advisable to validate MQI results by comparing them with NDT findings, whenever available. If MQI and NDT results align, the reliability of the MQI is confirmed and the shear strength derived from the index can be used. Conversely, it is left to the operator’s discretion to determine which method they consider more reliable. Factors such as the number and techniques of the on-site tests should be carefully considered in this evaluation. It is worth noting that the methodological approach can be applied effectively regardless of the availability of such experimental data. In such cases, a comparison can still be made between the shear strength derived from the MQI and values found in the literature.

  2. (2)

    Seismic vulnerability assessment—Four different Vulnerability Index methods, namely GNDT, Formisano, Vicente and Ferreira methods, are applied to the site under investigation. Each method is to be accomplished in three steps: (i) selection of the form parameters that can be evaluated for the specific archaeological site; (ii) estimation of the conventional strength parameter using the simplified formulation herein proposed; (iii) calculation of the vulnerability index. Finally, these methods are compared to critically analyse the reliability of vulnerability estimations. If there are disparities in the vulnerability indices, it is essential to identify the parameters responsible for such discrepancies and assess whether their incidence in the overall index calculation reflects the site’s actual characteristics. In the last phase, the expected damage is also estimated through damage vulnerability curves based on the calculated vulnerability indices.

  3. (3)

    Local analyses—The response of individual walls is evaluated using strength domain, capacity curves and fragility curves. It is recommended that walls in the most sensitive areas, according to the vulnerability distribution, are analysed.

Fig. 5
figure 5

Structured framework of the methodological approach

Full size image

In the subsequent sections, each task is described more in detail, outlining its implementation for the specific case study.

3.1 Masonry quality index

The quality of a masonry wall depends on both its constituents and the execution. The “rules of art” are a set of construction rules that ensure the wall’s compactness and monolithic behaviour. The mechanical properties and the structural response of walls are strongly influenced by the masonry’s quality. Indeed, irregular and low-quality masonries that lack monolithic behaviour (Vintzileou et al. 2015) exhibit a higher seismic vulnerability, as the collapse mechanism during seismic events often occurs due to disaggregation and leaf separation (Borri et al. 2020). This type of failure anticipates local and global mechanisms (Borri et al. 2015) and typically occurs at lower seismic intensities (De Felice et al. 2022). The Masonry Quality Index (MQI) method uses a visual survey and analysis of seven parameters related to structural behaviour to define a numerical index of masonry quality (Borri et al. 2015). The parameters are the following: mechanical characteristics and quality of masonry units (SM), dimensions of the masonry units (SD), the shape of the masonry units (SS), level of connection between adjacent wall leaves (WC), horizontal of mortar bed joints (HJ), staggering of vertical mortar joints (VJ), and quality of the mortar/interaction between masonry units (MM). Based on engineering judgement, each parameter is classified into three possible outcomes, i.e. fulfilled (F), partially fulfilled (PF) and not fulfilled (NF), and is associated with a numerical value according to the degree of fulfilment. The MQI is therefore calculated as the sum of these seven values according to Eq. (2):

$$MQI = SM \cdot \left( {SD + SS + WC + HJ + VJ + MM} \right)$$
(2)

The index ranges from 0 to 10, where a lower index value corresponds to a lower masonry quality. Additionally, the method accounts for different structural responses according to loading conditions, i.e. vertical, horizontal in-plane and horizontal out-of-plane loads. These conditions are reflected in three different indices, e.g. MQIV, MQII and MQIO, respectively. Based on the index value, the masonry category can be therefore defined as A, good behaviour, B, average quality behaviour, and C, inadequate behaviour for each of the loading conditions (Borri et al. 2015).

The above-introduced method was applied to six walls of the case study, which had been investigated by sonic testing. It is important to note that the WC parameter was established using a qualitative approach as access to the cross-section of the examined walls was feasible, whereas the VJ parameter was determined quantitatively. Furthermore, the MM parameter was defined based on the results of non-destructive testing, including penetrometer, Schmidt hammer and pendulum hammer tests, performed on the earth-based mortars to estimate the mechanical properties. The results show that none of the walls falls into category A, i.e., good behaviour, under any loading condition. Specifically, five masonry panels exhibit average quality behaviour under vertical load, while under horizontal in-plane loading, only four walls still fall into the same category. All the examined walls are classified as inadequate under horizontal out-of-plane loading.

Applying the equations proposed by Borri et al. (2020) to relate the masonry quality index to the masonry mechanical properties, a range of values was calculated for compressive strength fm, Young’s modulus E and shear strength τ, as reported in Table 2. To further check whether the MQI method is appropriate for the present study, a comparison is proposed between the average Young’s modulus E and compressive strength fm values obtained from the MQI method and sonic tests. It is important to acknowledge that there is a difference between the static (Est) and dynamic (Edy) modulus of elasticity of stones (Vasconcelos 2005). The dynamic Young’s moduli from the sonic tests were therefore corrected into static values using the equation proposed by Makoond et al. (2020):

$$E_{st} = 0.87 \cdot E_{dy}$$
(3)
Table 2 MQI results
Full size table

For comparison purposes, accordingly the masonry’s compressive strength \({f}_{m}\) was derived from the static modulus Est by dividing it by 550 (NTC 2018).

Figure 6 shows the comparison of Young’s modulus and compressive strength values derived from both the index and the experimental data. For the majority of the walls analysed, fair consistency was found between the two sets of properties, with a similar average Young’s modulus and a difference in compressive strength of about 20%. Nevertheless, a notable difference was noted in walls 1, 2 and 6, which is likely attributed to the irregularity of the masonry. Also, it is important to consider that although the masonry construction technique appears to be consistent across the site, there is a lack of information concerning the majority of the cross-sections. Consequently, this could have a significant impact on the results of the sonic tests, especially in cases where walls were improperly restored or rebuilt. As stated in De Santis (2022), the comparison provides further confirmation of the index’s reliability in evaluating the in-plane and out-of-plane behaviour of the walls in the specific case study. Moreover, the validation of the MQI method legitimises the use of the shear strength τ, equal to 52 KN/m2, estimated according to the index and averaged across all the wall panels analysed, in the calculation of the conventional strength parameter of the Vulnerability Index methods, as described in the following sections. It is worth noting that the shear strength τ estimated via the MQI method is higher than the value recommended for this type of masonry in the Italian NTC 18 Code (2018), which is equal to 36 KN/m2 (the second knowledge level and a confidence factor of 1.2 are considered). Nevertheless, the authors contend that this variation is acceptable, given that the MQI method accounts for a more comprehensive set of parameters in its estimation.

Fig. 6
figure 6

Comparison between MQI and sonic test results: a Young’s modulus E [MPa]; b compressive strength fm [MPa]

Full size image

3.2 Seismic vulnerability assessment

Seismic vulnerability analyses aim to assess the level of damage that a generic structure may suffer under a seismic event of a certain intensity measure. It is therefore a fundamental and preliminary phase in conservation processes to evaluate the need for strengthening interventions.

As mentioned, simplified models for assessing the seismic vulnerability of archaeological sites on a territorial scale have been proposed in the Italian Directive P.C.M (2007) and by Podestà (2010). Nevertheless, this study examines the applicability and reliability of empirical methods, proposed in the literature for buildings, when applied to archaeological sites. Among empirical methodologies, the Vulnerability Index methods have been widely used for assessing the expected vulnerability of structural units, SUs, and structural aggregates, Sas, in historical centres (Chieffo et al. 2023). These methods consist of determining a vulnerability indicator through the evaluation of typological, structural and material parameters, both qualitative and quantitative, which characterise the seismic structural response of the unit. Each parameter is assessed individually according to four classes of increasing vulnerability (from A-lowest to D-highest), to which class scores \({S}_{i}\) are assigned. The influence of each parameter is then determined by multiplying \({S}_{i}\) by a weight factor \({W}_{i}\), which depends on the relative importance of the parameter in the calculation of the global vulnerability. Thus, the vulnerability index Iv is expressed as the weighted sum of the parameters:

$$I_{v} = \sum\limits_{i = 1}^{n} {S_{i} \cdot W_{i} }$$
(4)

The methodology was first proposed by Benedetti and Petrini (1984) and consisted of a ten-parameter survey form for the estimation of the vulnerability of masonry buildings in isolated conditions, i.e. not interacting with adjacent units. The approach involved expert judgments to assign weights and scores based on damage survey data. The Gruppo Nazionale per la Difesa dai Terremoti (GNDT) then developed and calibrated the original approach, proposing new survey forms based on eleven evaluation parameters (GNDT 1993). Later on, the original formulation (Benedetti and Petrini 1984) was extended to masonry building blocks in Vicente (2008) and Formisano et al. (2010), introducing 4 and 5 parameters, respectively, to account for mutual interaction among SUs in the same aggregate. These approaches provided important progress in the vulnerability assessment of buildings within aggregates, as the interaction effects with adjacent buildings significantly affect the seismic behaviour of the unit analysed. Furthermore, the calibration of class scores and weights was improved by Formisano et al. (2014) through the use of parametric analyses based on numerical models. While the aforementioned methods consider the single SU either isolated or within a SA, the Vulnerability Index method proposed by Ferreira et al. (2012) assesses the SA as a whole. The vulnerability assessment is therefore conducted at an urban scale through five evaluation parameters referred to the aggregate, dealing with geometrical irregularities, typology differences and interaction issues among buildings (Ferreira et al. 2012).

In general, the vulnerability assessment method should be set by the purpose of the analysis as well as the typological and structural characteristics of the units or aggregates being evaluated (Ferreira et al. 2013). As already stated, the application to archaeological sites is rather limited in the literature, so it seems appropriate to propose a comparative analysis between the mentioned methods. The comparison aims at determining the most reliable above-introduced methods to assess the vulnerability of the ruins, as well as to better address the uncertainties involved. The characteristics of archaeological sites differ from those of buildings in historic centres on which the Vulnerability Index methods have been developed. A first attempt to adapt these methods to archaeological sites is herein presented.

The form of each method was therefore revised by discarding the parameters that do not apply to the specific case study. For instance, the parameter accounting for the quality of floors could not be assessed since floors no longer exist. The selection of the evaluation parameters for each applied method is listed in Tables 3, 4, 5, and 6. For details on both the selected and discarded parameters, please consult the original forms in GNDT (1993), Vicente (2008), Formisano et al. (2010) and Ferreira et al. (2012). As a result, new maximum vulnerability values were determined by summing the individual parameters, which were deemed applicable to the specific case study. Furthermore, assuming that the walls of each SU behave as independent panels due to poor connections, a simplified method for estimating the conventional strength parameter is proposed, as detailed in the following paragraph.

Table 3 Parameters applicable to the case study archaeological site: GNDT form
Full size table
Table 4 Parameters applicable to the case study archaeological site: Formisano form
Full size table
Table 5 Parameters applicable to the case study archaeological site: Vicente form
Full size table
Table 6 Parameters applicable to the case study archaeological site: Ferreira form
Full size table

3.2.1 The conventional strength parameter

The conventional strength parameter, also referred to as the distribution of plan resisting elements, accounts for the strength of the masonry SU against horizontal actions. The vulnerability class is determined based on the factor \(\alpha =C/\overline{C }\), where \(C\) is intended as the ratio between the ultimate shear strength \({T}_{k}\) at the base of the SU, derived from Turnšek and Cacovic’s formulation, and the unit’s weight P; while \(\overline{C }\) is assumed equal to 0.4 as proposed in the literature (GNDT 1993). Denoting as \({A}_{t}\) the total in-plan area of the walls, \(A\) and \(B\) represents the minimum and maximum values between \({A}_{x}\) and \({A}_{y}\) (i.e. the areas of resisting elements in the orthogonal directions). Moreover \({a}_{0}\) and \(\gamma\) parameter indicates the surface ratios \(A/{A}_{t}\) and \(B/A\), respectively. However, according to Benedetti and Petrini (1984), the following equation was adopted for the estimation of the above-introduced C parameter:

$$C = \frac{{a_{0} \tau_{k} }}{qN}\left[ {1 + \frac{qN}{{1.5a_{0} \tau_{k} (1 + \gamma )}}} \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}$$
(5)

where \({\tau }_{k}\) is the characteristic shear strength of the wall, \(N\) is the number of floors and \(q\) is the average weight per unit of the total area of the floor. The parameter \(q\) is calculated as a function of the average specific weight of the masonry \({p}_{m}\), the average floor height \(h\) and the average weight per unit area of the floor \({p}_{s}\), as shown in Eq. (6):

$$q = \frac{(A + B)h}{{A_{t} }}p_{m} + p_{s}$$
(6)

The reliability of Benedetti’s formulation is limited to the assumption of global box-like behaviour. Archaeological sites are usually characterised by primitive construction and ruinous systems that do not guarantee a box-like behaviour. Adjacent walls are often poorly or not connected, and there are no headers between wall leaves. Furthermore, due to the conservation state of ruins, the walls are often totally or partially collapsed, thus with varying heights, and floors no longer exist. Therefore, a new formulation for the estimation of parameter C is proposed to assess the strength of masonry SUs under horizontal actions in archaeological sites. This formulation assumes that the unit’s walls behave as independent panels. Given the definition of C, assumed as the ratio between the ultimate shear strength \({T}_{k}\) concerning the verification level and the weight above \(P\), \({T}_{k}\) can be estimated through Turnšek and Cacovic’s formula:

$$T_{k} = A_{T(sec)} \cdot \tau_{k} \cdot \sqrt {1 + \frac{{\sigma_{0} }}{{1.5\tau_{k} }}}$$
(7)

where \({A}_{T(\text{sec})}\) is the total cross-section area of the resisting elements, given by the sum of \({A}_{x}\) and \({A}_{y}\) (Fig. 7); \({\tau }_{k}\) is the characteristic tangential strength that can be deduced either from the prescriptions in Table C8.5.1 of the NTC 18 Code (2018) or, as stated in Sect. 3.1, as a function of the MQI according to the equations proposed in Borri et al. (2020); and finally, \({\sigma }_{0}\) is the mean compressive stress among the corresponding compressive stress values achieved in the orthogonal directions, \({\sigma }_{0x}\) and \({\sigma }_{0y}\). The compressive normal stress in the i-th direction \({\sigma }_{0i}\) is then evaluated as the ratio between the axial stress \({N}_{i}\) and the resistant area, \({A}_{i}\), of the masonry wall section, given by:

$$\sigma_{0i} = \frac{{N_{i} }}{{A_{i} }}$$
(8)
Fig. 7
figure 7

Schematisation of a typical structural unit

Full size image

In the absence of floors, \({N}_{i}\) is only equal to the dead loads of the masonry \({P}_{i}\) in the i-th direction, calculated as:

$$P_{i} = p_{m} \cdot \sum\limits_{k = 1}^{n} {h_{av \cdot k,i} \cdot L_{k,i} \cdot t_{k,i} }$$
(9)

where \({p}_{m}\) is the specific weight of the masonry; \({h}_{av. k,i}\) is the height of the k-th wall in the considered direction, taken as the mean value in the case of irregular walls; \({L}_{k,i}\) and \({t}_{k,i}\) are the length and thickness of the walls, respectively (Fig. 7). The dead load \(P\) of the SU is then given by the sum of the dead loads of the walls in both orthogonal directions:

$$P = \sum\limits_{i} {P_{i} }$$
(10)

Therefore, it is proposed to estimate the C-factor according to Eq. (11), in which the factor \({a}_{0}=A/{A}_{t}\) is introduced to consider the percentage of resisting walls:

$$C = \frac{{T_{k} }}{P} \cdot a_{0}$$
(11)

The above-introduced formulation was applied to evaluate the conventional strength parameter in the GNDT, Formisano and Vicente forms for the seismic vulnerability assessment of the Wupatki Pueblo. The results were compared with those obtained from the formulation found in the literature (Benedetti and Petrini 1984). As shown in Fig. 8, due to higher values of \(\alpha =C/\overline{C }\), the latter significantly underestimates the vulnerability of the SU, all of which fall into class A. Instead, in an archaeological site such as the Wupatki Pueblo, the proposed formulation performs better in estimating the parameter, demonstrating a fair distribution of results and vulnerability classes that are more consistent with the observed reality.

Fig. 8
figure 8

Comparison between conventional strength parameter results from the literature formulation and the simplified one proposed by the authors

Full size image

In addition, the C-factor was calculated considering two different values of the characteristic shear strength \({\tau }_{k}\), derived from Table C8.5.I in the NTC 18 Code (2018) and the MQI method. The first evaluated value is equal to 36 kN/m2, obtained by dividing the average value of the \({\tau }_{k}\) range provided for the class “masonry with rough-hewn blocks, with leaves of uneven thickness” by a confidence factor, CF, equal to 1.2 assuming a knowledge level, KL, set to 2. On the other hand, the MQI method provided a characteristic shear strength \({\tau }_{k}\) equal to 52 kN/m2, suggesting a better masonry performance. However, despite the higher values of \({\tau }_{k}\), the vulnerability class of most SUs remains unvaried, as shown in Fig. 8.

Finally, correlation curves are proposed in Fig. 9 to graphically determine the C-factor as a function of \({\alpha }_{0}=A/{A}_{t}\), given the characteristic shear strength \({\tau }_{k}\) of the masonry. The aim is to simplify the estimation of the conventional strength parameter, which is one of the most time-consuming parameters of the vulnerability forms, and to extend the assessment to all archaeological sites close to the case study. It is important to mention that the curves developed are applicable for “masonry with rough-hewn blocks, with leaves of uneven thickness”, namely with an average specific weight of 20 kN/m3. Table 7 presents the angular coefficients of the correlation curves for varying \({\tau }_{k}\), along with the standard deviation \(\sigma\) that should be taken into account within the range of variation.

Fig. 9
figure 9

The evaluation of the C-factor: a correlation curves assuming τk in KN m−2; b variation range with a standard deviation \(\sigma\) of ± 0.03

Full size image
Table 7 The determination of the C-factor: Angular coefficients of the correlation curves and standard deviation for the variation range
Full size table

3.2.2 Vulnerability index calculation

The archaeological site of Wupatki Pueblo was first assessed by assigning a vulnerability index \({I}_{v}\) to each SU according to Eq. (4). GNDT, Formisano and Vicente methods were also implemented and three different indices were calculated for each SU. For comparison purposes, the values of the vulnerability index \({I}_{v}\) were normalised in the interval [0 ÷ 1], taking the notation \({V}_{i}\). Specifically, \({I}_{v}\) values obtained from GNDT and Formisano methods were normalised according to Chieffo et al. (2023):

$$V_{i} = \frac{{I_{v} - \left( {\sum\nolimits_{i}^{n} {S_{i\;min} \cdot W_{i} } } \right)}}{{\left( {\sum\nolimits_{i}^{n} {S_{i\;max} \cdot W_{i} } } \right) - \left( {\sum\nolimits_{i}^{n} {S_{i\;min} \cdot W_{i} } } \right)}}$$
(12)

while the vulnerability indices \({I}_{v}\) determined through Vicente’s form were first normalised in the interval [0 ÷ 100], adopting the notation \({{I}_{v}}^{*}\), and then in the interval [0 ÷ 1] according to Vicente (2008):

$$V_{i} = 0.592 + 0.0057 \cdot I_{v}^{*}$$
(13)

As shown in Fig. 10, the three methods adopted resulted in quite different vulnerability indices. Indeed, average \({V}_{i}\) values of 0.60, 0.50 and 0.85 were obtained for the GNDT, Formisano and Vicente methods, respectively. Specifically, the GNDT results show that about 80% of the SUs analysed have a vulnerability index within the range [0.5 ÷ 0.8], i.e. medium–high, about 13% in the range [0.3 ÷ 0.5], i.e. medium, and a lesser percentage of 7% between [0.8 ÷ 1.0], i.e. high vulnerability. According to the Formisano method, about 63% of the SUs fall into the medium–high range [0.5 ÷ 0.8], while about 37% show a medium vulnerability [0.3 ÷ 0.5]. On the other hand, Vicente’s form classifies about 80% of the SUs as a high vulnerability, with indices between [0.8 ÷ 1.0], and the remaining part as a medium–high vulnerability.

Fig. 10
figure 10

Comparison between \({V}_{i}\) results from GNDT, Formisano and Vicente’s methods

Full size image

The results are also depicted in the vulnerability maps in Fig. 11. Both the GNDT and Formisano methods classify most SUs as medium–high vulnerabilities. However, the overall distribution of results shows lower indices in the Formisano method, resulting in a higher number of SUs in the medium vulnerability. This is mainly influenced by the parameter that considers the position of the SU within the aggregate. Most of the SUs are in fact in an intermediate position, i.e. surrounded on three or more sides, and hence have a lower vulnerability class, which is assigned a negative class score. The overall index is thus significantly diminished by the negative class score multiplied by a high parameter weight of 1.5. However, the incidence of the parameter is not consistent with the reduced interaction between adjacent SUs due to poor wall connections. On the other hand, the indices from Vicente’s method are likely overestimated and not representative of the real vulnerability of the site. From the comparison, it can be therefore deduced that the GNDT method provided the most reliable vulnerability values. Based on the above considerations, it is reasonable to assume that in archaeological sites where the walls behave as independent panels due to the absence of connection or floors, or where the site configuration cannot be considered an aggregate, the GNDT method performs better in assessing its vulnerability. This is because the parameters of this method are designed and weighted based on isolated buildings, aligning well with such scenarios. Conversely, evaluating parameters that account for the structural unit within the aggregate, such as in the Formisano and Vicente methods, could potentially distort results by considering a structural behaviour that does not correspond to reality. For further discussion on the comparison between Vulnerability Index methods, please refer to appendix A.

Fig. 11
figure 11

Distribution of the estimated vulnerability index according to GNDT, Formisano and Vicente methods

Full size image

Finally, the vulnerability index for the entire South unit aggregate was determined using Ferreira’s method. Through Eq. (12), the vulnerability index was normalised in the interval [0;1], resulting in a value of 0.55. It is worth noting that Ferreira’s overall index \({V}_{i}\) falls between the average values of \({V}_{i}\) (0.61 and 0.48) calculated among the SUs of the aggregate using the GNDT and Formisano forms. Although the result seems reliable, it is important to acknowledge that Ferreira's method only employs three parameters, which may not be sufficient for accurately assessing the vulnerability of an archaeological site.

3.2.3 Damage vulnerability curves

To estimate the expected damage to the archaeological site following a seismic event, vulnerability curves were drawn using a macroseismic approach. The curves provide an estimate of the expected damage, defined according to the EMS-98 scale (Grünthal 1998), as a function of the macroseismic intensity. This correlation is expressed through an analytical function derived from the parameterisation of the Damage Probability Matrices (DPMs) introduced by Whitman and Reed (1973). The function, proposed by Lagomarsino and Giovinazzi (2006), is reported as follows:

$$\mu_{D} = 2.5 \cdot \left[ {1 + \tanh \left( {\frac{{I_{EMS - 98} + 6.25 \cdot V_{i} - 13.1}}{Q}} \right)} \right]$$
(14)

where \({V}_{i}\) is the vulnerability index normalised in the interval [0 ÷ 1], \({I}_{EMS-98}\) is the macroseismic intensity from V to XII and \(Q\) is the ductility factor ranging from 1 to 4. The mean damage grade \({\mu }_{D}\) is therefore the mean value of the probability histogram of the damage thresholds \({D}_{k}\), from 0 (no damage) to 5 (collapse), defined in the EMS-98 Scale according to the observed damage.

The damage vulnerability curves, shown in Fig. 12, were derived according to the vulnerability indices \({V}_{i}\) reported in Sect. 3.2.2 (see Eq. (13)). Considering the low mechanical strength and precariousness of the structures at the archaeological site, and in the absence of specific values for archaeological sites, a ductility factor \(Q\) equal to 2 is deemed adequate based on the study proposed by Despotaki et al. (2018). Specifically, the curves were drawn for each Vulnerability Index method considering the average value of the \({V}_{i}\) indices calculated for the SUs analysed. The lower and upper boundary curves were also defined based on the minimum and maximum values of the achieved \({V}_{i}\) indices, which were considered thresholds of the expected vulnerability domain. There is an increase in damage as the intensity of a potential earthquake increases. Furthermore, the greater the vulnerability considered, the greater the damage that would occur at lower seismic intensities. The curve obtained from the GNDT method (\({V}_{i(mean)}\hspace{0.17em}\)= 0.60), considered as the most reliable for the evaluation of archaeological sites, shows maximum damage slightly higher than1 (D1—slight, non-structural) within the intensity range V < \({I}_{EMS-98}\hspace{0.17em}\)< VIII. The damage progressively increases at higher intensities until the collapse, D5, (\({\mu }_{D}\)=5) is reached at an intensity of approximately XI.

Fig. 12
figure 12

Damage vulnerability curves in terms of IEMS-98

Full size image

A further representation of the vulnerability curves was derived by relating the expected damage to the PGA. This has the advantage of simulating damage scenarios in terms of a measurable intensity parameter rather than macroseismic intensity (Bernardini et al. 2007). The PGA thresholds that can be withstood are thus easily determined. Several correlations between macroseismic intensity and PGA have been reported in the literature. Since these correlations have been developed based on different contexts and seismic events, the uncertainties to be considered are significant (Chieffo et al. 2023). The PGA values, denoted by \({a}_{g}\)[g], were herein derived according to the correlation proposed in Lagomarsino and Giovinazzi (2006):

$$a_{g} = c_{1} \cdot c_{2}^{{\left( {I_{EMS - 98} - 5} \right)}}$$
(15)

where \({c}_{1}\) and \({c}_{2}\) are empirical coefficients, assumed equal to 0.04 and 1.65 respectively (Margottini et al. 1992). Figure 13 shows the vulnerability curves obtained for each Vulnerability Index method in terms of PGA. In particular, when considering the mean \({V}_{i}\) value equal to 0.60, derived from the GNDT method, the resulting curve indicates that moderate damage (D2) is expected for a PGA value of around 0.25 g, whereas significant structural damage (D3) is expected for a PGA of approximately 0.35 g. By considering the maximum expected PGA, equal to 0.16 g (Unified Hazard Tool 2023), the damage level is therefore expected lower than D1.

Fig. 13
figure 13

Damage vulnerability curves in terms of PGA

Full size image

However, when analysing the curves obtained by applying Vicente’s approach, which generally results in higher vulnerability indices, a PGA of approximately 0.25 g corresponds to an estimated D4 damage level. This suggests that the structure is approaching a state of near collapse. In this case, the expected damage corresponding to a PGA of 0.16 g is D3, which means that the site would experience structural damage. It is worth noting that the expected damage level varies significantly depending on the index-based method used. Nevertheless, since the GNDT method was considered the most reliable approach, the expected damage is minimal even in the worst-case scenario.

3.3 Response of individual walls

To conduct a thorough assessment of archaeological sites, it is recommended to carry out local analyses by considering individual walls. This is due to the construction characteristics and the current state of conservation of the sites, which often involve the absence of floors or the presence of deformable ones and inadequate wall connections. These factors mean that global box behaviour cannot be guaranteed, highlighting the importance of analysing the local response of individual walls. Strength domains, characteristics and fragility curves are developed herein under static conditions. While the authors acknowledge the importance of assessing the out-of-plane stability of freestanding walls in seismic areas, this study is confined to analysing in-plane behaviour.

3.3.1 Strength domains

The failure mechanisms of masonry walls depend on the structural configuration and loading conditions. For walls with slender panels, compression-flexural stresses are the primary cause of failure, while for walls with stocky panels, shear mechanisms are more likely to cause failure (Augenti and Parisi 2019). Specifically, the main failure mechanisms are (i) flexural cracking, which occurs when bending stresses cause masonry blocks to crack along the tensile side of the wall; (ii) diagonal cracking, due to the shear stresses that cause masonry blocks to crack diagonally; (iii) sliding shear, which occurs when the wall slides along the horizontal plane at the base due to a combination of shear and vertical loads. The occurrence of damage depends on the mechanism that is triggered first, which corresponds to the minimum shear value \(V\), as given in EN 1998–3—Eurocode 8 (2004).

To evaluate the behaviour of masonry wall panels in archaeological sites, a local analysis has been conducted using strength domains developed for in-plane actions. This approach is considered suitable, as suggested in Augenti and Parisi (2019), for analysing the expected performance of walls based on the mentioned failure mechanisms. By analysing the strength domains, it is indeed possible to assess how well the masonry panels can tolerate flexural and shear forces and to establish a failure hierarchy. In practice, strength domains analyse the relationship between the shear strength \(V\) and the axial force \(N\) of a masonry wall panel. This is because the typical verification criteria for masonry walls depend on the precompression stress \({\sigma }_{0}\), which is a function of the axial force \(N\).

The capacity of the wall panel to withstand shear forces is thus expressed by its axial force. Operatively, as suggested in Augenti and Parisi (2019), the failure boundary of the domain has been normalised by the maximum axial capacity \({N}_{u}\) (\({N}_{u}=0.85\cdot {f}_{d}\cdot L\cdot H\), where \({f}_{d}\) is the design compressive strength, and \(L\) and \(H\) are the length and height of the panel, respectively), taking the notation \(\overline{V }\) and \(\overline{N }\). Based on the normalised axial force value \(\overline{N }\), the domain boundaries are then intersected and the shear stress \(V\) corresponding to each mechanism is derived as \(\overline{V}\cdot {N }_{u}\). As an example, though the methodology can be extended to the entire site, two wall panels, labelled as A and B walls and identified in Fig. 14, were analysed within the case study. These panels were selected for analysis as they represented the highest walls on the site. Panel A has geometry (\(L\) × \(H\) × \(t\)) equal to 3.98 × 1.78 × 0.42 m, while panel B measures 4.08 × 3.76 × 0.51 m. Figures 15 and 16 show the strength domains derived for the chosen masonry panels. Specifically, the curves denoted as cracking, elastic and plastic correspond to the linear elastic (fully resisting section), elastic (partialized section) and ultimate limit states associated with the flexural failure mechanism. In addition, it is worth noting that, in the present case, the axial force is only provided by the panel’s weight due to the absence of floors.

Fig. 14
figure 14

Identification of wall panels

Full size image
Fig. 15
figure 15

Strength domain for panel A

Full size image
Fig. 16
figure 16

Strength domain for panel B

Full size image

Table 8 presents a summary of the local behaviour results obtained from the selected wall panels. For panels A and B, an axial force \(N\) of 0.01\({N}_{u}\) and 0.02\({N}_{u}\), was estimated. The analysis revealed that in both panels, the initial response involves the activation of the flexural mechanism at the cracking limit state (elastic limit state). At this stage, shear forces of 37.4 kN and 69.9 kN were observed for panels A and B, respectively. Then, panels A and B exhibited a shear sliding mechanism at the shear thresholds \(V\) equal to 85.3 kN and 164.2 kN. In both cases, the flexural mechanisms at the elastic and plastic limit states were induced by similar shear values. Specifically, in panel A, the mechanisms were activated at 110.7 kN and 111.1 kN, while in panel B at 204.0 kN and 205.4 kN. Finally, both panels exhibited the diagonal shear mechanism at the highest shear values, which were 123.5 kN and 224.4 kN for panels A and B, respectively.

Table 8 Failure hierarchy for the examined wall panels
Full size table

3.3.2 Capacity curves

To accurately describe the behaviour of each wall under different loading conditions, its capacity curves were developed. The curves typically establish the relationship between the shear force \(V\) and the dual displacement \(\delta\). Augenti and Parisi (2019) show that the horizontal component of the linear displacement of the section at the top of the panel, \({\delta }_{l}\), is a function of both shear displacement, \({\delta }_{lV}\), and flexural displacement, \({\delta }_{lM}\). This relationship is described by Eq. (16), which includes parameters such as the shear coefficient \(\upchi\), the shear threshold \(V\), the panel height \(H\), the shear modulus \(G\), the masonry elastic modulus \(E\) and the cross-section inertia \(I\):

$$\delta_{l} = \delta_{lV} + \delta_{lM} = \chi \cdot \frac{{V \cdot {\text{H}}}}{{G \cdot {\text{A}}}} + \frac{{V \cdot H^{3} }}{{12 \cdot {\text{E}} \cdot {\text{I}}}}$$
(16)

Here, the shear coefficient, \(\upchi\), is a constant value of 1.2, while \(G\) is assumed as \(0.4\cdot E\). The capacity displacement thresholds at the cracking \({\delta }_{f}\) (post-elastic phase) and ultimate limit states \({\delta }_{u}\) were consequently defined as \(1.2{\delta }_{l}\) and \(1.5{\delta }_{l}\), respectively (Augenti and Parisi 2019).

Considering the shear thresholds V for each specific limit state obtained from the strength domains, capacity curves were therefore developed for panels A and B. As shown in Table 8 and Fig. 17, the displacements observed in the masonry panels increased accordingly to their capacity. In simpler terms, as the capacity of the panel increased, the corresponding displacement increase proportionally.

Fig. 17
figure 17

Capacity curves: a panel A; b panel B

Full size image

3.3.3 Fragility curves

Fragility curves describe the likelihood of exceeding a specific damage level (\({D}_{s}\)) concerning a defined value of intensity measurement, and thus defining the damage limit states (Lamego et al. 2017). Specifically, the probability of a given damage to be reached or exceeded is evaluated using a cumulative lognormal distribution. In this specific case, the intensity measure is the displacement \({S}_{d}\), considering the following equation:

$$P\left[ {D_{s} \left| {S_{d} } \right.} \right] = \Phi \left[ {\frac{1}{{\beta_{Ds} }} \cdot \ln \left( {\frac{{S_{d} }}{{\overline{{S_{d,Ds} }} }}} \right)} \right]$$
(17)

where \(\Phi\) refers to the standard normal cumulative distribution function, \({\beta }_{Ds}\) is the standard deviation of the log-normal distribution and \(\overline{{S }_{d,Ds}}\) is the median value of displacement corresponding to a specific damage state \({D}_{s}\). Four damage states, proposed in FEMA and NIBS (2003) and commonly used in studies (Lamego et al. 2017; Lantada et al. 2004), are considered: \({D}_{1}\) slight damage, \({D}_{2}\) moderate damage, \({D}_{3}\) severe damage, and \({D}_{4}\) complete damage or collapse. As proposed in Cattari et al. (2004), the damage states can be defined in terms of displacements, specifically the yielding (\({\Delta }_{y}\)) and ultimate (\({\Delta }_{u}\)) displacements, which are known from the capacity curves discussed in the previous section. The displacement values for each damage state are then calculated based on the equations provided in Table 9.

Table 9 Damage thresholds and standard deviation
Full size table

Similarly, the standard deviation \({\beta }_{Ds}\) is calculated for all damage states to account for the uncertainty in the model. It worth noting that \({\beta }_{Ds}\) is dependent on the wall’s ductility \(\mu\), which is estimated as the ratio between \({\Delta }_{u}\) and \({\Delta }_{y}\). Equations for computing the standard deviation for each damage state are given in Table 9. On this assumption, Fig. 18 shows the fragility curves plotted for panels A and B. The displacement values were calculated from the capacity curve related to the expected ultimate failure mechanism. For instance, the fragility curve of panel A shows a high probability of damage starting from displacements \({S}_{d}\) equal to 0.2 mm. Slight \({D}_{1}\) and moderate \({D}_{2}\) damage then occur with a probability of 100% for \({S}_{d}\) values of 0.6 and 0.9 mm, respectively. The probability for damage \({D}_{4}\) reaches 100% at the small displacement \({S}_{d}\) of 1.6 mm, increasing from 0.3 mm. The range of displacements in which the probability of occurrence of the different damage types varies is, therefore, quite narrow. On the other hand, when comparing results, the fragility curve of panel B provides lower or null probabilities of damage for the same displacements. Indeed, the probability of slight damage (\({D}_{1}\)) begins at a displacement of 0.8 mm and reaches 100% at 3 mm. Moderate \({D}_{2}\) and severe \({D}_{3}\) damage occur with increasing probability for \({S}_{d}\) values ranging from 1.1 to 4.2 mm, and from 1.4 to 5.1 mm, respectively. Finally, the probability of complete damage or collapse (\({D}_{4}\)) varies between 1.3 and 7.7 mm.

Fig. 18
figure 18

Fragility curves: a wall panel A; b wall panel B

Full size image

4 Final remarks

In conclusion, this study presented a simplified and easy-to-use methodological approach for assessing the seismic vulnerability of archaeological sites. Due to the fragile state of ruins, usually characterised by detached structural elements, these sites are particularly susceptible to damage from seismic events. Numerical analyses are often complex, unreliable and time-consuming, making them impractical for large-scale evaluations. To address this challenge, the proposed approach has adapted empirical index-based methods for archaeological sites, to provide a rapid and easy-to-use tool for assessing their seismic vulnerability. The methodological approach was successfully applied to the Wupatki Pueblo archaeological site, in Arizona (US), which consists of two SAs, namely the South and North Units, with 12 and 4 SUs, respectively. The following considerations emerged from the application:

  • The comparison of index-based methods, including GNDT, Formisano and Vicente methods, showed that the GNDT method provided the most reliable vulnerability values. Most of the SUs were classified as having medium-high vulnerability with an index between 0.5 and 0.8. This method’s parameters, originally defined for isolated buildings, are indeed better suited for detached structural elements commonly found in archaeological sites, where walls behave as independent panels. However, the Formisano et al. (2010) and Vicente (2008) methods may provide a more accurate vulnerability assessment if the site exhibits significant interactions between adjacent SUs. Finally, the Ferreira method, which provides a single vulnerability value for the entire aggregate, is considered unsuitable for archaeological sites due to the limited number of parameters that can be generally applied (Ferreira et al. 2012);

  • The proposed formulation for estimating the conventional strength parameter performs well if walls behave as individual panels due to poor connections. In the case study application, the formulation provided good results and vulnerability classes that were more consistent with reality. Indeed, for most SUs, the parameter was estimated in vulnerability class B or C.

  • The damage vulnerability curves can vary significantly depending on the index-based method adopted. Considering the GNDT method as the most reliable approach in this specific case, the expected damage corresponding to the maximum PGA of 0.16 g (Unified Hazard Tool 2023) would be minimal, i.e. lower than a slight damage level (D1).

  • The need to analyse the local response of individual walls is emphasised for archaeological sites since, due to the construction characteristics and state of conservation, a global box behaviour cannot be assumed. The strength domains, capacity curves, and fragility curves can serve as valuable tools for this purpose. As an example, the local analysis was performed on two wall panels. The strength domains provided the following failure hierarchy for both panels: (i) flexural mechanism at the cracking limit state, (ii) shear limit mechanism, (iii) flexural mechanism at the elastic state, (iv) flexural mechanism plastic limit state, and finally (v) diagonal shear mechanism at shear values of 123.5 kN and 224.4 kN. As expected, the characteristic curves showed an increase in the displacements of the masonry panels according to their capacity. On the other hand, the fragility curves revealed a high probability of damage, even severe, at low displacement values. As future goals, the local analysis should be extended to a larger number of panels to provide a comprehensive overview of the site. Furthermore, it should be noted that the analyses were performed under static conditions, thus further studies should be conducted to assess the out-of-plane behaviour.

As a final note, it should be noted that the methodological procedure herein presented needs to be tailored to the specific characteristics of each archaeological site, involving the selection of parameters suitable for evaluation in each index-based method. An important aspect of advancing the proposed methodology lies in validating the scores and weights attributed to each parameter. For this purpose, as part of future developments, new vulnerability assessments based on a multi-criteria approach, MCDM, are expected to be formulated. These methods will incorporate novel evaluation criteria and customized weights, determined on a case-by-case basis to accommodate the unique characteristics of each site. Initially, this approach will be tailored to the specific archaeological site under investigation, facilitating comparison with outcomes from established index-based methods. Subsequently, it is anticipated to extend the approach to other archaeological sites to evaluate its reliability across diverse contexts. Furthermore, additional research developments can focus on creating correlation curves for the graphic determination of the C-factor, which is used to evaluate the conventional strength parameter, for different masonry types with varying specific gravity. It is also important to acknowledge that this study represents an initial step to adapt methods originally developed for buildings to archaeological sites, and improvements can be made by applying the approach to a larger number of cases. Primarily, the numerous sites within the same area as the case study represent potential scenarios where the methodology could be effectively applied with minimal adjustments, given their shared architectural and conservation characteristics. Overall, the findings demonstrated the effectiveness of the proposed approach in assessing the seismic vulnerability of archaeological sites and providing useful outcomes in the decision-making process for their conservation.