A parametric study in reinforced concrete frames with different infill wall materials

Abstract

Understanding the behavior of structures during earthquakes is crucial for ensuring safety. Despite their significant impact on buildings, infill walls are often overlooked in seismic assessments, contributing to the complexity of a structure. Because of their intricate nature and modeling difficulties, infill walls are frequently excluded from seismic models. However, given the prevalence of reinforced concrete buildings with various infill wall materials in earthquake-prone areas, it is essential to incorporate infill walls for a more realistic evaluation of seismic behavior. This study scrutinizes a building that sustained damage in the Izmir earthquake in Turkey. The building was represented in four distinct models using the SAP2000 V24 finite element program: without infill walls, with porotherm clay blocks, burnt clay brick, and autoclaved aerated concrete blocks. Real parameters of the building were utilized in the modeling process. Upon comparing the results of the time history analysis, it was observed that the presence of infill walls had a positive impact on various building properties, including period, ground floor shear force, column bearing capacity, and inter-story drift ratio. Additionally, infill walls increased base shear forces on the ground floors and the overall base shear force. Notably, similar outcomes were obtained with porotherm clay blocks and burnt clay brick as infill wall types, while autoclaved aerated concrete blocks exhibited lower stiffness than other infill wall models.

1 Introduction

The country of Turkey is located on active fault lines, and upon examination of the building stock, it has been observed that reinforced concrete buildings with infill walls are present (Uysal 2023; Onat, 2020). It is important to note that while infill walls are typically considered dead loads in building modeling, their ability to resist earthquake forces should not be disregarded (Sancıoğlu et al. 2022). To properly understand how structures behave during earthquakes and ensure their ability to withstand seismic loads safely, it is essential to model them as realistically as possible. This includes modeling structural elements such as columns, beams, floors, and foundations for infill walls in a manner consistent with the rest of the structure (Onat, 2020). According to the Turkish building earthquake code (TBDY-2018), the equivalent diagonal compression struts is recommended for modeling infill walls. This code provides elastic modulus, compressive strength, and shear strength values for three different types of infill walls (porotherm clay blocks, burnt clay brick, and autoclaved aerated concrete blocks) that comply with the code (TBDY 2018).

Literature review reveals that it has been proven that infill walls can effectively mitigate the damaging effects of earthquakes (Dolšek and Fajfar 2008; Sattar and Liel 2016; Mulgund and Kulkarni 2011; Nwofor and Chinwah 2012; Wakchaure and Ped 2012; Hermanns et al. 2014; Bolea 2016; Misir et al. 2016; Morfidis and Kostinakis 2017; Ning et al. 2017; Baghi et al. 2018). In addition to exploring the impact of infill walls on a structure's seismic behavior, experts have also simulated various infill wall designs to compare their effectiveness. The objective of these studies is to evaluate and contrast the seismic effects of different infill wall types on a structure. For example, Korkmaz and Uçar (2006), modeling and static pushover analysis were utilized to examine the influence of infill walls on building structures. A 10-story reinforced concrete building was used as the subject of the study, both with and without infill walls. The results of the analysis indicated the formation of plastic sections in the infill walls of the model featuring infill walls. Additionally, the base shear force was observed to occur more frequently in the infilled wall models (Korkmaz and Uçar 2006). Sattar and Liel (2010), evaluates the seismic performance of reinforced concrete frames with and without masonry infill. It finds that frames with full masonry infill have significantly lower collapse risks during earthquakes compared to bare frames. Infill increases structural stiffness and strength but introduces brittle failure mechanisms. This research highlights how infill configuration affects seismic safety, with full infill providing notable protective benefits in seismic regions (Sattar and Liel 2010). Pujol and Fick (2010), full-scale three-story reinforced concrete structures were tested with and without infill walls constructed from solid clay bricks. The walls filled the voids and extended continuously from the foundation to the roof. The study revealed that the walls significantly enhanced the strength and durability of the structures. Moreover, it was determined that the walled structures had a drift capacity of 1.5% (Pujol and Fick 2010). Uysal and Özkul (2013) analyzed the impact of infill walls on a building's load-bearing system. They used the SAP2000 program to create models of two reinforced concrete buildings, one six-storey, and one twelve-storey, both with and without brick and aerated concrete infill walls. Their analysis using the Equivalent Seismic Load Method revealed that models with infill walls had lower periods, higher base shear forces, decreased storey displacements, and increased storey stiffness compared to models without infill walls (Uysal and Özkul 2013). Dilmac et al. (2018) explored the effects of infill walls on reinforced concrete buildings. Utilizing the SAP2000 program, they simulated a range of existing structures between 2 and 5 stories, incorporating different infill wall setups to assess their nonlinear behavior. The results of the analysis led the researchers to conclude that infill walls have a significant impact on the buildings' ability to carry lateral loads (Dilmac et al. 2018). Furtado et al. (2020) examined the mechanical properties of infill masonry walls. The research involved conducting eighty tests on walls made with different types of masonry units. The findings showed that horizontally perforated clay bricks led to fragile behavior without the propagation of cracks, while concrete blocks exhibited the development of vertical cracks under increased vertical pressure (Furtado et al., 2020). Shan et al. (2019) examines how partial infill walls influence the structural integrity of reinforced concrete frames under collapse scenarios, using both experimental data and finite element simulations. It tests two frame specimens—with and without infill walls—to understand how variations in wall configurations impact collapse behavior, focusing on load distribution, resistance force, and failure mechanisms. Factors such as the type of infill wall, the size of openings, and the properties of the mortar and masonry significantly affect collapse resistance. The study also introduces a simplified analytical approach for predicting collapse resistance, offering a practical tool for structural engineers to enhance design and safety assessments (Shan et al. 2019). Wijaya et al. (2020) explored the impact of infill wall material and modeling methods on the seismic behavior of reinforced concrete frame structures. The research focused on the seismic performance of reinforced concrete buildings with 3, 6, and 9 stories, constructed with calcarenite masonry, clay masonry, and lightweight concrete masonry. The study revealed that walls significantly enhanced the seismic capacity of structures, particularly in low-rise buildings (Wijaya et al. 2020). Pouraminian (2022) analyzes the structural resilience of the Gaskar brick minaret in northern Iran to wind and earthquake hazards using a finite element model. The study demonstrates that the minaret can withstand design wind loads and resists significant seismic impacts with only slight potential damage. It highlights the importance of incorporating both wind and seismic considerations in the conservation strategies for historical structures (Pouraminian, 2022). Rahgozar et al. (2021) explores the effectiveness of controlled rocking steel cores (CRSCs) in reducing damage from earthquakes. It uses detailed nonlinear dynamic analyses to examine factors such as structure geometry, material characteristics, and the design of post-tensioned cables and energy dissipators. By employing Monte Carlo simulations, the study evaluates how these factors influence the seismic resilience of CRSCs. The findings suggest that while CRSCs enhance seismic safety overall, mid-rise structures with CRSCs exhibit higher failure probabilities than low-rise ones due to larger lateral displacements (Rahgozar et al. 2021). Kong et al. (2022) conducted a study to investigate the impact of vertical arrangement and masonry material of infill walls on the seismic performance of reinforced concrete (RC) frames. The study revealed that frames with vertically irregularly arranged infill experienced more severe damage than bare frames, indicating that such arrangements should be limited in the seismic design process. Additionally, the study emphasized the importance of considering the drawbacks associated with the elastic modulus of masonry materials when designing and assessing frames with vertically irregularly arranged infill (Kong et al. 2022). Sancıoğlu et al. (2022) conducted simulations of ten-storey symmetrical buildings utilizing two distinct types of infill wall materials perforated brick and aerated concrete block—and various wall layouts within the SAP2000 program. Their findings indicate that the placement and material of infill walls have a noteworthy impact on the horizontal load-carrying capacity and horizontal drifts of the structures (Sancıoğlu et al. 2022). Demirel et al. (2023) evaluates the seismic performance of infill wall systems in ductile reinforced concrete frames, focusing on different construction techniques like isolation joints, mesh overlays, and sliding joints. Through cyclic tests on seven half-scale RC frame specimens, it compares the seismic responses of frames with hollow clay bricks and aerated concrete blocks against bare frames. The findings show that the choice of infill material and construction technique greatly impacts strength, stiffness, energy dissipation, and damage progression. Systems using isolation joints and mesh coverings have been found to be significantly more effective in maintaining structural integrity and enhancing energy dissipation (Demirel et al. 2023). Grubišic et al. (2023) evaluated six reinforced concrete frames that were ductile and had minimal damage. The frames were strengthened with three different techniques and utilized two types of masonry units-hollow clay and solid clay units. Additionally, two reference samples were included in the analysis. The results showed an increase in hardness, strength, and hysteretic damping of the reinforced filled frame structures (Grubišic et al., 2023). Usta et al. (2023) delved into the impact of infill walls on reinforced concrete buildings when subjected to earthquake forces. Using the SAP2000 finite element program, they simulated earthquake-damaged buildings both with and without infill walls. Upon comparing the analysis results, the researchers observed that infill walls had a beneficial effect on the building's characteristics, including period, ground floor shear force, column bearing capacity, inter-storey drift ratio, and base shear forces on the ground storeys, ultimately increasing the base shear force (Usta et al. 2023).

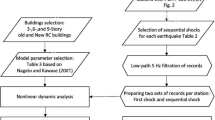
This study focuses on modeling a building damaged during the Izmir earthquake using the SAP2000 finite element program. The building was initially modeled without infill walls and subsequently with three different types of infill wall materials. Seven distinct earthquake records were then applied to the building to investigate its seismic behavior under various conditions. Chapter 2 delves into the seismicity of the Izmir Aegean region where the building is situated, while Chapter 3 details the methodology employed in modeling infill walls. Section 4 outlines the characteristics of the modeled building, followed by Chapter 5, which provides information on the earthquake records and scaling utilized for the nonlinear time history analysis. The analysis results, accompanied by graphics, are sequentially presented in the latter part of Chapter 5. Finally, Chapter 6 concludes the study by summarizing the findings obtained from the analysis.

2 Seismicity of Türkiye and the Aegean region

Turkey is situated within the expansive Alpine-Himalayan earthquake zone, one of the largest seismic regions globally. With its significant earthquake risk, Turkey faces a paramount concern. Factors such as its geological positioning, close proximity to active fault lines, and historical records of major seismic events contribute to Turkey's heightened vulnerability to earthquakes (Artindal et al., 2021).

Turkey is traversed by several active fault lines and experiences tectonic movements. Notably, the country is encompassed by three primary seismic zones: the Northern Anatolian Seismic Zone, the Southeastern Anatolian Seismic Zone, and the Western Anatolian Seismic Zone (Karimzadeh et al. 2024).

The North Anatolian Fault Line stands out as one of Turkey's most crucial seismic zones. Originating from the eastern Black Sea region, it stretches to the Marmara Sea. Over the years, significant and devastating earthquakes have occurred along this fault line. Particularly concerning is the segment passing beneath Istanbul, given its dense population and extensive infrastructure (Artindal et al., 2021).

In eastern Turkey, the Eastern Anatolian Fault Line presents the second-highest earthquake risk in the country. Extending from Erzurum to Southeastern Anatolia, this fault line poses a threat of significant and sometimes catastrophic earthquakes in the Eastern Anatolia Region (Karimzadeh et al. 2018).

Located along the Aegean Sea in western Turkey, the Western Anatolian Fault Line generates numerous earthquakes, some of which can be notably intense. Earthquakes originating from this fault line have the potential to inflict substantial damage and loss of life in the Aegean Region and Western Anatolia (Roumelioti et al. 2021).

The Aegean Region, situated in the western part of Turkey, is recognized as a highly active earthquake zone. Particularly notable is the region of Western Anatolia, encompassing Izmir and its environs, which experiences significant seismic activity due to the presence of active faults. These seismic events stem from the ongoing tectonic movements resulting from the convergence and interaction of the African and Eurasian plates (Usta et al. 2023).

Several significant tectonic structures characterize this region, including the Bursa-Gonen, Gemlik-Iznik-Edremit, Bakırcay, Bergama, Simav, Gediz, Buyuk Menderes, Kucuk Menderes, and Alasehir grabens. The tectonic framework of the Aegean region also features depression basins, with Büyük Menderes, Kucuk Menderes, Alasehir, Simav, Bergama, and Edremit being the primary depression areas (Durak 2008).

Among the prominent fault lines in the Aegean Region, the Western Anatolian Fault Line stands out. This fault line runs parallel to the Aegean Sea and branches off into several subsidiary fault lines. Earthquakes occurring along these fault lines typically manifest at the surface and have the potential to cause significant damage along their rupture zones (Usta 2016). Figure 1. shows the earthquake map of Türkiye and the seismicity of the Aegean region.

Fig. 1

Turkey earthquake map and Aegean region seismicity a Turkey earthquake map (AFAD 2018) b Active faults in Aegean Region (MTA 2023) c Devastating historical earthquakes around the Aegean region (AFAD, 2024)

3 Modeling of different infill walls

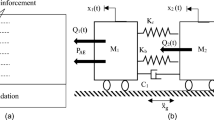
There are two distinct approaches to modeling infill walls: micro and macro models. Micromodeling involves enlarging the dimensions of masonry elements by half the thickness of the mortar layer towards the top and sides. Masonry units are separated by average interface lines, with possible cracks assumed to occur along these lines. The Poisson ratio of the mortar is neglected in this approach, and the mortar layer is disregarded as the binding agent. On the other hand, macro modeling treats masonry units as integral components, such as adobe, brick, and stone. In this approach, the mechanical properties of masonry building elements are homogenized, forming a composite material considered as a unified whole in the modeling process. Macro modeling simplifies the modeling of large-scale structures by not specifying the mechanical properties and details of each material separately, making it an efficient method in terms of time. This approach stands out as the most successful in terms of both time and efficiency, offering practical applicability (Usta 2016). During the 1950s, researchers conducted experimental and analytical studies to create models of infill walls and evaluate their effects on building performance. In 1956, Polyakov proposed a method of representing infill walls using a diagonal pressure bar, which was chosen because it acknowledged that infill walls transmit loads to the supporting system along the diagonal axis of the wall (Polyakov 1956).

Illustrated in Fig. 2. is the deformation of the infill wall in a reinforced concrete frame under horizontal loads. The infill wall passes the load to the frame through points 1 and 4, while points 2 and 3 become detached from the frame. A diagonal pressure bar can be used to conceptualize infill walls, which transmit force between points 1 and 4 (Onat, 2020).

Fig. 2

Infill wall under the influence of horizontal load (Onat, 2020)

The macro modeling technique was utilized in this article to represent three unique infill walls. An equivalent link element, designed to operate under pressure, was used to represent the infill walls in the modeling approach. Specifically, the calculated stiffness was established through the use of an equivalent pressure bar, which was modeled as a link element. To determine the necessary parameters, equations from Annex 15C of TBDY (2018) were employed. These equations allowed for the calculation of the equivalent pressure bar width of the infill walls, as well as the axial rigidity of the equivalent pressure bar and the shear force resistance of the infill walls. The equations given below were used to calculate the shear strength of infill walls.

$$a_{d} = 0.175\left( {\lambda_{d} \times h_{k} } \right)^{ - 0.4} r_{d}$$

(1)

The parameter 'ad' represents the width of the equivalent diagonal compression struts, measured in millimeters. 'λd' denotes a dimensionless parameter. 'hk' stands for the height of the column between the centerlines of beams, expressed in millimeters. Finally, 'rd' signifies the diagonal length of the infill wall, also in millimeters.

$$\lambda_{d} = \left( {\frac{{E_{d} \times t_{d} \times \sin 2\theta }}{{4 \times E_{c} \times I_{k} \times h_{d} }}} \right)^{\frac{1}{4}}$$

(2)

The parameter 'λd' represents a dimensionless factor. 'Ed' denotes the Young’s modulus of the infill, measured in units such as Pascal. 'td' signifies the thickness of the infill, expressed in millimeters. 'θ' stands for the angle, where the tangent is the ratio of infill height to length. 'Ec' represents the Young’s modulus of the column, also typically measured in units such as Pascal. 'Ik' denotes the moment of inertia of the column, measured in square millimeters. Lastly, 'hd' signifies the height of the infill, expressed in millimeters.

$$k_{d} = \frac{{a_{d} \times t_{d} \times E_{d} }}{{r_{d} }}$$

(3)

The parameter 'kd' represents the axial stiffness of equivalent compression struts. 'ad' denotes the width of equivalent compression struts, measured in millimeters. 'td' signifies the thickness of the infill wall, expressed in millimeters. 'Ed' stands for the modulus of elasticity of the frame concrete, typically measured in units such as Pascal. Lastly, 'rd' signifies the diagonal length of the infill wall, also measured in millimeters."

The values of Ed (Young's modulus of the infill), fd (compressive strength of the infill wall), and τd (shear strength of the infill wall) mentioned in the equations, as per Annex 15C.2.2 of TBDY (2018), are provided in Table 1.

Table 1 Values for E_d, f_d, and τ_d for different types of bricks

4 RC building

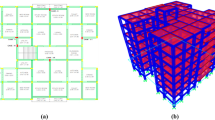
In this study, an existing building located in Izmir province of the Aegean Region of Turkey, which is very sensitive to earthquakes, was examined. The actual dimensions and material properties of the building have been utilized. The building structure is a reinforced concrete building that includes ground storeys and seven standard storeys. The ground storeys of the building is home to shops and a doorman's office, while the remaining 28 flats are evenly distributed across the seven standard storeys with four flats on each floor. The ground storeys stands at a height of 3.65 m, while each normal storeys is 2.70 m high, giving the building a total height of 22.55 m. The building does not have a basement and is supported by a strip foundation. The building site's soil classification is designated as ZD.

The project's shear walls are all 20 cm thick, with each floor incorporating nine shear walls. The building has three distinct column cross-sections: 30 × 70 cm, 30 × 80 cm, and 30 × 90 cm, with the dimensions of the columns decreasing by 10 cm as one moves from the ground storeys to the standard storeys. This reduction continues up to the seventh storeys. The project also utilizes two beam sizes: 25 × 50 cm and 20 × 50 cm. Exterior beams are 25 cm wide, while interior beams are 20 cm wide. The building has three different storey thicknesses: 20 cm for balconies, 12 cm for middle storeys, and 15 cm for other storeys. The floor plan of the building is given in Fig. 3.

Fig. 3

The floor plan of the building

In the building test results, the concrete compressive strength was determined to be C8.27, with fco = 8.27 MPa. The formulas given in 5A.1 Confined and Unconfined Concrete Models in TBDY-2018 were used to model the reinforced concrete material in the SAP2000 V24 finite element program. The material strenght of C8.27 concrete class is given in Fig. 4. Longitudinal reinforcements are made up of 420 MPa deformed steel, while confinement reinforcements are 220 MPa. The formula given in 5A.2 Reinforcement Steel Models in TBDY-2018 were used to model steel material in SAP 2000 finite element program. The material graphics of S420 steel and S220 steel are given in Figs. 5 and 6. The building was modeled using the SAP2000 V24 finite element program, with columns and beams represented as rod elements, shear walls as shell elements, and infill walls as link elements.

Fig. 4

The material strength of C8.27 concrete

Fig. 5

Stress- strain curves for S420

Fig. 6

Stress- strain curves for S220

The building's load-bearing elements were calculated using the SAP2000 V24 finite element program. The weight of each floor's elements was automatically computed and labeled as a two-way load acting on the floor area. The dead load for regular floors was set at 2 kN/m², while the attic floor had a dead load of 2.5 kN/m².

As a component of the architectural project, a comprehensive evaluation was completed to identify the load-bearing wall requirements. This involved a meticulous analysis of the wall placement and dimensions, with two distinct wall types measured at 20 cm and 10 cm. Since the reinforced concrete building design excluded walls, they were designated as a distributed load on the beams. The wall loads were determined to be 2.4 kN/m² for 20 cm walls and 2.0 kN/m² for 10 cm walls.

Live loads were defined based on floor types. Normal floors had a load of 2.0 kN/m², floors with walls had 3.5 kN/m², and attic floors had 1.5 kN/m².

Using the SAP2000 V24 finite element program, a detailed three-dimensional model of the designated building was generated. Link elements were utilized to represent the infill walls, which were analyzed via the equivalent pressure bar method. The model incorporated three different types of infill wall materials: Porotherm Clay Blocks, Burnt Clay Bricks, and Autoclaved Aerated Concrete blocks. The Fig. 7. displays images of modeled buildings with and without infill walls, using three different materials for the infill walls.

Fig. 7

4 different models a without infill wall; b model using porotherm clay blocks; c model using burnt clay bricks; d model using autoclaved aerated concrete blocks

5 Nonlinear dynamic time history analysis of building

The process of assessing how structural systems respond to earthquakes is referred to as nonlinear structural analysis. In this specific study, nonlinear dynamic time history analysis was utilized to examine the behavior of structures under earthquake conditions. The analysis was conducted nonlinearly using the SAP2000 finite element program. Seven distinct earthquake ground motions were selected from the AFAD website, with details provided in Table 2. When choosing these earthquakes, careful consideration was given to ensure they were earthquakes that occurred in Turkey and were likely to impact the same region. Additionally, the selected earthquakes had magnitudes ranging between 6.5 and 7.7, were within 23 km of the active fault plane, and were compatible with the local ground class (ZD).

Table 2 Used for nonlinear dynamic time history analysis of earthquakes

The seismic ground motions sourced from the AFAD website were organized based on the elastic design acceleration spectrum (S_ae(T)) outlined in the 2018 earthquake regulation (TBDY 2018). This spectrum is influenced by the natural vibration period in gravitational terms, along with the parameters of the short-period design spectral acceleration coefficient (S_DS) and the design spectral acceleration coefficient (S_D1) for a one-second period. Utilizing these parameters, the arrangement was tailored to suit the specific ground conditions at the building's location. Using the SAP2000 finite element program, the acceleration-time graphs for the earthquake were defined. Acceleration-time graphs and scaled acceleration-time graphs taken from the AFAD website are given in Fig. 8.

Fig. 8

Scaling of acceleration time graphs

After establishing the earthquake acceleration-time graphs, where the e-direction corresponds to the x-direction, n-direction to the y-direction, and u-direction to the z-direction, analyses were performed in the nonlinear time history for four distinct models.

5.1 Analysis results

Modal analysis was conducted before performing nonlinear time history analysis on the structure. The analysis focused on the first 12 modes. Figure 9 illustrates the period values of the models.

Fig. 9

Period values of the models

When examining the building model without infill walls, the 1st mode had the highest period at 3.01 s. On the other hand, when infill walls were included using Porotherm clay blocks, the highest period observed in the 1st mode was 1.69 s. Burnt clay bricks and autoclaved aerated concrete blocks were also used to create infill walls for other structures, resulting in the highest periods of 1.68 s and 1.94 s, respectively, observed in the 1st mode.

Through the use of nonlinear time history analysis, the total base shear forces for each model were determined. Figures 10 and 11 visually represent the resulting base shear forces.

Fig. 10

Base shear forces of models in x-direction

Fig. 11

Base shear forces of models in y-direction

Upon reviewing the results, it is revealed that the burnt clay brick model experienced the highest base shear force in the x-direction, reaching 12,700 kN following the Kahramanmaras (Pazarcık) earthquake. In the y-direction, the model lacking infill walls recorded the highest base shear force at 14,104 kN after the Duzce earthquake. Upon examining all models post-earthquake, it was obtained that the Kahramanmaras (Pazarcık) earthquake resulted in the highest average base shear force.

After analyzing the earthquake data, the interstorey drift values for the models were calculated, adhering to the Turkish Building Earthquake Regulation (TDBY, 2018). Figures 12 and 13 provide a visual representation of the interstorey drift values for the models.

Fig. 12

Interstorey drift value of models in x-direction

Fig. 13

Interstorey drift value of models in y-direction

Positive values in relative storey drift indicate a forward movement in the direction of measurement, while negative values represent a backward shift. When examining the average relative storey drifts in the X direction, notable observations emerge for different building models. In the model without infill walls, the earthquake producing the highest average drift occurred at 0.03357 following the Maraş-Elbistan earthquake. For the porotherm clay blocks model, the most significant average drift, 0.02611, was recorded after the Kocaeli earthquake. Similarly, in the burnt clay bricks model, the Kocaeli earthquake also resulted in the maximum average drift of 0.02611. Lastly, in the model using autoclaved aerated concrete blocks, the earthquake with the highest average drift was 0.03475, again following the Kocaeli earthquake. In an analysis of average relative storey drifts in the Y direction, significant findings were observed across different building models. For the model without infill walls, the earthquake that generated the highest average drift, measured at 0.02926, occurred following the Maraş-Pazarcık earthquake. In the porotherm clay blocks model, the largest recorded average drift was 0.02705, also following the Maraş-Pazarcık earthquake. In contrast, for the burnt clay bricks model, the Kocaeli earthquake led to the maximum average drift, registering at 0.02779. Similarly, the autoclaved aerated concrete blocks model recorded its highest average drift of 0.02779 after the Kocaeli earthquake.

According to TDBY (2018), the interstorey drift limit should not exceed 0.008. It appears that all the observed drifts during the earthquakes significantly exceed this threshold.

Following the earthquake analyses, the total shear forces acting on each floor of the models were determined. Graphs illustrating the storey shear force values of the models can be found in Figs. 14, 15, 16, 17, 18, 19, 20 and 21.

Fig. 14

Storey shear forces of the model without infill wall in the x-direction

Fig. 15

Storey shear forces of the model without infill wall in the y-direction

Fig. 16

Storey shear forces of the model with porotherm clay blocks in the x-direction

Fig. 17

Storey shear forces of the model with porotherm clay blocks in the y-direction

Fig. 18

Storey shear forces of the model with burnt clay bricks in the x-direction

Fig. 19

Storey shear forces of the model with burnt clay bricks in the y-direction

Fig. 20

Storey shear forces of the model with autoclaved aerated concrete blocks in the x-direction

Fig. 21

Storey shear forces of the model with autoclaved aerated concrete blocks in the y-direction

Upon reviewing the floor shear forces, it was observed that in the model without infill walls, the highest shear force was 11,883 kN in the x-direction on the ground floor following the Kahramanmaras(Pazarcık) earthquake. Similarly, for the model using Porotherm clay blocks, the highest floor shear force measured 13,273 kN in the x-direction on the ground floor after the Kahramanmaras(Elbistan) earthquake. Likewise, in the model employing burnt clay bricks, the highest floor shear force reached 13,114 kN in the x-direction on the ground floor post Kahramanmaras(Elbistan) earthquake. Furthermore, for the model incorporating autoclaved aerated concrete blocks, the highest floor shear force observed was 12,867 kN in the x-direction on the ground floor following the Kahramanmaras(Elbistan) earthquake.

Upon analysis of the ground floor x-direction shear forces, it was noted that the model without infill walls experienced, on average, a 21% higher shear force value following the Kahramanmaras(Pazarcık) earthquake compared to other earthquakes. Similarly, for the model utilizing Porotherm clay blocks, the shear force value was, on average, 44% higher after the Kahramanmaras(Elbistan) earthquake compared to other earthquakes. Additionally, the model employing burnt clay bricks exhibited a 43% higher shear force value on average post Kahramanmaras(Elbistan) earthquake compared to other earthquakes. Moreover, the model incorporating autoclaved aerated concrete blocks displayed, on average, a 36% higher shear force value following the Kahramanmaras(Elbistan) earthquake compared to other earthquakes.

Upon examination of the floor shear forces, it was found that in the model without infill walls, the highest shear force was 13,847 kN in the y-direction on the ground floor after the Duzce earthquake. Similarly, for the model utilizing Porotherm clay blocks, the highest floor shear force was 13,299 kN in the y-direction on the ground floor post Izmit earthquake. Likewise, the model employing burnt clay bricks exhibited its highest floor shear force as 13,290 kN in the y-direction on the ground floor after the Izmit earthquake. Moreover, the model incorporating autoclaved aerated concrete blocks recorded its highest floor shear force as 14,200 kN in the y-direction on the ground floor following the Kahramanmaras(Pazarcık) earthquake.

Analyzing the ground floor y-direction shear forces, it was observed that the model without infill walls experienced an average of 25% greater shear force value after the Duzce earthquake compared to other earthquakes. Similarly, for the model using Porotherm clay blocks, the shear force value was on average 30% higher after the Izmit earthquake compared to other earthquakes. Additionally, the model utilizing burnt clay bricks showed a 31% higher shear force value on average after the Izmit earthquake compared to other earthquakes. Furthermore, the model employing autoclaved aerated concrete block displayed a 38% higher shear force value on average after the Kahramanmaras(Pazarcık) earthquake compared to other earthquakes.

Following the earthquake analyses, shear force values acting on the shear walls were determined. The layout of the shear walls is illustrated in Fig. 22. Maximum shear forces that the shear walls can withstand were calculated. The calculated shear force limit values for each shear wall were as follows: 720 kN for shear wall 1, shear wall 2, and shear wall 3; 576 kN for shear wall 4, shear wall 5, shear wall 6, and shear wall 7; and 290 kN for shear wall 8 and shear wall 9. Upon analyzing the shear forces acting on the shear walls, it was observed that shear walls 1, 2, and 3 experienced forces exceeding their capacity to withstand. Conversely, the shear forces acting on the remaining shear walls remained below their maximum capacity. Consequently, only the shear force graphs for shear walls 1, 2, and 3 are provided. Shear wall 1 was assessed in the x-direction, shear wall 2 in the y-direction, and shear wall 3 in the y-direction. Detailed information regarding the shear forces acting on shear walls 1, 2, and 3 can be found in Figs. 23, 24, and 25, respectively.

Fig. 22

Location of shear walls

Fig. 23

SW1 floor shear values of the models

Fig. 24

SW2 floor shear values of the models

Fig. 25

SW3 floor shear values of the models

Upon examining the maximum shear forces on the shear walls, it was found that the shear force limit values for shear walls 1, 2, and 3 were exceeded. For instance, in the model without infill walls, the maximum shear force for shear wall 1 reached 4208 kN after the Izmit earthquake. Similarly, in the same model, shear wall 2 experienced a maximum shear force of 2843 kN after the Izmit earthquake, and shear wall 3 faced a maximum shear force of 2703 kN after the Kahramanmaras(Pazarcık)earthquake.

Similarly, in models using Porotherm clay blocks, burnt clay bricks, and autoclaved aerated concrete blocks for shear walls, maximum shear forces were observed. For instance, in the model utilizing Porotherm clay blocks, shear wall 1 experienced a maximum shear force of 3995 kN after the Kahramanmaras(Elbistan) earthquake, shear wall 2 faced a maximum shear force of 2663 kN after the Izmit earthquake, and shear wall 3 encountered a maximum shear force of 2687 kN after the Kahramanmaras(Pazarcık)earthquake.

In the model utilizing filled burnt clay brick for shear wall 1, the highest recorded shear force was 4031 kN, occurring after the Kahramanmaras(Elbistan) earthquake. Similarly, for shear wall 2, constructed with burnt clay brick, the maximum shear force reached 2636 kN after the Izmit earthquake. Following the same pattern, shear wall 3, also constructed with burnt clay brick, experienced its maximum shear force of 2667 kN after the Kahramanmaras(Pazarcık)earthquake.

For shear wall 1 using autoclaved aerated concrete blocks, the highest shear force recorded was 4512 kN after the Kahramanmaras(Elbistan) earthquake. Shear wall 2, constructed with the same material, encountered its maximum shear force of 2509 kN following the Izmit earthquake. Finally, shear wall 3, also built with autoclaved aerated concrete blocks, experienced its highest shear force of 2880 kN after the Kahramanmaras(Pazarcık) earthquake.

Following the earthquake analysis, the unit elongation and shortening values for shear walls 1, 2, and 3, which exceeded the shear wall force limit, were computed. Figures 26, 27, and 28 depict the unit elongation and shortening values for the shear walls.

Fig. 26

SW1 strain values at the left and right ends of the models

Fig. 27

SW2 strain values at the left and right ends of the models

Fig. 28

SW3 strain values at the left and right ends of the models

The calculations adhered to TBDY (2018) guidelines, which specify limit values of 0.0035 for concrete unit shortening and 0.01 for reinforcement unit elongation. Upon examination of the graphs, it is evident that the unit strain remains below the specified limit values.

6 Conclusions

When examining the construction of buildings in Turkey, it is apparent that many structures are built with reinforced concrete and infill walls. These buildings are often subjected to a number of earthquakes throughout their lifespan and can be susceptible to damage or even collapse. Consequently, it is crucial to investigate and comprehend the seismic behavior of such constructions. With this in mind, a study was conducted in which an earthquake-damaged building was modeled using three different types of infill walls (namely porotherm clay blocks, burnt clay bricks, and autoclaved aerated concrete blocks). The modeled building was then subjected to nonlinear earthquake analyses using time history methods.

The results of the conducted modal analysis have been meticulously examined and the period values of the models have been scrutinized. Based on the findings, it has been calculated that the first period of the model without infill walls was 3.01 s, while the first period of the model utilizing Porotherm clay blocks was 1.69 s, that of burnt clay bricks was 1.68 s, and of autoclaved aerated concrete blocks was 1.94 s. Furthermore, considering the model without infill walls as the standard, it has been observed that the first period of the model using Porotherm clay blocks decreased by 44%, that of burnt clay bricks decreased by 44.3%, and that of autoclaved aerated concrete blocks decreased by 35.5%. Upon closer examination, it can be inferred that the installation of infill walls in the model fortifies the building structure.

Upon examining the base shear forces exerted on the buildings, it was observed that the seismic force experienced by the buildings modeled with infill walls was notably higher, except for the Van earthquake in the x-direction. Conversely, in the y-direction, the model devoid of infill walls experienced higher seismic force, except for the Izmit earthquake.

All the building models exhibit average relative storey drifts in both the X and Y directions that far exceed the TDBY (2018) limit of 0.008 during significant earthquakes. This indicates that these buildings might not comply with current seismic standards and could be at risk of structural damage during strong seismic events. Each model's highest drifts, notably higher than the regulatory threshold, suggest that enhancements in earthquake resilience or retrofitting may be necessary to improve safety and compliance. The substantial exceedance of the drift limits across all models emphasizes the need for a thorough structural evaluation and possibly strengthened design measures to withstand future earthquakes.

Upon examining the storey shear forces, it was observed that the maximum forces were experienced in the y-direction. Notably, structures that were modeled with infill walls were found to have received an average of 33% more shear force than those models without any such walls. These findings highlight the significance of infill walls as a crucial structural element that can significantly influence the overall shear resistance of a building.

The comprehensive analysis conducted revealed that the shear forces exerted on shear walls 1, 2, and 3 significantly exceeded their design capacities, reaching levels 375% greater than the stipulated limit values. This substantial overshoot suggests a critical structural vulnerability under seismic loads that could potentially compromise the building's integrity in a real-world earthquake scenario. Notably, despite the immense shear forces, the observed deformations of these walls remained within acceptable limits, a condition that typically characterizes brittle fracture behavior.

Brittle fracture in shear walls is particularly concerning because it indicates a failure mode where the walls might lose their load-bearing capacity suddenly without significant prior warning in terms of large deformations. This type of failure is less ductile, meaning that the energy absorption capacity is lower, and the potential for sudden catastrophic failure is higher. Such outcomes emphasize the necessity for a reevaluation of the design and reinforcement strategies used for these critical structural elements.

Further investigation into the material properties and the interaction between different structural components could shed light on why these shear walls experienced such high shear forces yet exhibited minimal deformation. Analyzing the composition of the concrete, the configuration and quality of reinforcement, and the connection details between the walls and other structural members might reveal insights into the anomalous behavior observed. Additionally, simulation of different earthquake scenarios and the corresponding responses of these shear walls could help in designing more resilient structures capable of withstanding seismic forces without approaching brittle failure thresholds.

In seismic design, the presence of infill walls is a critical factor that significantly affects the behavior of the modeled structures under earthquake effect. The judicious selection of infill wall material is crucial for understanding the seismic behavior of structures. Studies have shown that modeling with infill walls can alter the results considerably. Notably, structures modeled with porotherm clay blocks and burnt clay bricks yield similar outcomes, while the structure modeled using autoclaved aerated concrete blocks exhibits values between the other two brick structures and the structure without infill walls. Therefore, it is imperative to acknowledge the significance of infill walls in seismic design and carefully select the infill wall material to achieve a comprehensive understanding of the seismic behavior of structures.

Furthermore, while this study focuses primarily on the impact of infill walls on seismic responses, the strength of mortar joints represents a potentially significant aspect that warrants further investigation. Understanding how mortar joint strength influences the overall seismic performance of structures could provide deeper insights into the optimization of building designs in earthquake-prone regions. Therefore, it is recommended that future studies consider the role of mortar joint strength as a critical parameter in their models to enhance the predictive accuracy and reliability of seismic assessments.

Moreover, the results discussed in this article stem from analyses specific to a single building. The study lacks discussion on how these findings might be applicable to other buildings with similar designs or material properties, limiting its broader relevance. Future studies should consider analyzing additional buildings with comparable characteristics to validate and compare these results. Furthermore, it would be beneficial to offer specific engineering recommendations based on these findings. Such recommendations could provide actionable insights and help guide subsequent research and engineering practices, particularly in regions susceptible to earthquakes.