1 Introduction

In the framework of the mitigation of the seismic risk, Geotechnical Seismic Isolation (GSI) is an innovative low-cost technique for protecting structures in earthquake-prone areas, alternative to traditional seismic isolation systems, such as: elastomeric bearings, sliding elements, and friction–pendulum systems (Kelly 1990; Naeim and Kelly 1999), whose installation and maintenance are considered quite expensive economically and technically for conventional buildings; moreover, these solutions are almost prohibited in developing countries where the financial resources are limited. The main idea of GSI is to improve the foundation soil so that seismic energy will be partially dissipated within GSI before being transmitted to the structure (Tsang 2009; Tsang et al. 2012; Mavronicola et al. 2010; Pitilakis et al. 2015; Pistolas et al. 2010; Forcellini 2020; Forcellini and Alzabeebee 2022). Among other materials proposed for foundation soil improvement, gravel-rubber mixtures (GRMs) have attracted significant research thanks to their good static and dynamic properties: low specific weight, wide range of elastic behaviour, low shear modulus, and high damping (Anastasiadis et al. 2012; Senetakis et al. 2012a, 2012b; Senetakis and Anastasiadis 2015; Pistolas et al. 2018; Tsiavos et al. 2019; Tasalloti et al. 2021a, b, c). Furthermore, their use has immediate advantageous ecological effects because the rubber grains for the mixtures are manufactured from end-of-life tires (ELTs), the disposal of which has become a severe environmental problem worldwide over the last years (Fig. 1).

Fig. 1
figure 1

Origin of the gravel-rubber mixtures (GRMs) from end-of-life tires (ELTs)

Full size image

GRMs suitability and advantages as GSI in the form of a layer underlying the foundation of structures have been investigated numerically over recent years (Tsang 2009; Tsang et al. 2012; Pitilakis et al. 2015; Pistolas et al. 2010; Forcellini and Alzabeebee 2022; Tsang and Pitilakis 2019; Dhanya et al. 2020; Chiaro et al. 2020). On the other hand, only a few experimental studies are available in the literature, mainly limited to laboratory and small-scale testing (Kaneko et al. 2013; Xiong and Li 2013; Chiaro et al. 2021; Tsang et al. 2020; Bandyopadhyay et al. 2015; Tsiavos et al. 2019; Tasalloti et al. 2021a). Just one experimental campaign on a full-scale prototype structure was recently performed in Thessaloniki (Greece) in the framework of the Research Program SOFIA-SERA (Pitilakis et al. 2021; Abate et al. 2022). Ambient noise was recorded, and free-, and forced-vibration tests were carried out on the EuroProteas structure located in the Euroseistest experimental facility after replacing the foundation soil with three different GRMs for a thickness of B/6, being B the width of the foundation. The full-scale tests demonstrated that a GRM with 30% rubber content per weight effectively isolates the structure.

The present study investigated numerically the effect of a GRM layer on the response of a real structure subjected to different seismic inputs. The static behaviour of the GRM-structure system was also evaluated, focusing on the movements at the foundation level. The adopted GRM was characterised by a rubber content per weight equal to 30% because of the good performance of the full-scale tests developed at Thessaloniki (Pitilakis et al. 2021; Abate et al. 2022). The recycled rubber included in the GRMs could trap the dynamic wave, thus avoiding its passage from the foundation to the soil and vice versa. The structure was a typical reinforced concrete building in southern Italy (Fiamingo et al. 2023). Three 2D FEM models were developed. The first model reproduced the actual configuration of the structure, so without the GRM layer underneath the foundation. In the second and third models, an uppermost layer of the foundation soil was replaced with the GRM backfill for a thickness equal to 0.80 m and 1.50 m, respectively.

To consider soil nonlinearity, the soil and the GRMs were modelled using an equivalent visco-elastic behaviour according to Eurocode 8 Part 5 (2004). The structure was modelled, assuming a visco-inelastic behaviour. Several seismic inputs were used, considering both recorded accelerograms (during the recent 26th December 2018 earthquake in Catania, Italy) and spectrum-compatible accelerograms. The comparisons among the models allowed us to assess the overall performance of the GRMs underneath foundations as a new eco-sustainable solution for mitigating the seismic risk of structures.

2 The reference soil–structure system

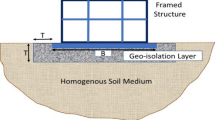
The building chosen for the analyses is a reinforced concrete framed structure with three elevations designed according to the 1976 Italian Technical Code (D.M. 1976) for gravity loads only (Fig. 2). The chosen frame for the FEM modelling is highlighted by the red box in Fig. 2a. The landings of a winding staircase are sustained by supporting beams belonging to the outer frame close to the street (Fig. 2b).

Fig. 2
figure 2

The analysed building: a plan view and, b chosen frame for the FEM modelling. Measurements are expressed in meters (modified after Fiamingo et al. 2023)

Full size image

Based on the allowable stress method, a simulated design was carried out to define beam and column cross-sections and reinforcements (D.M. 1976). The dimensions of the obtained cross-sections were compared to the available design drawings. Cross-sections of 30 × 60 cm and 50 × 70 cm were considered for the superstructure beams and the foundation beam, respectively, whereas the column cross-section varies along with the structure's height. More specifically, a cross-section of 30 × 50 cm was considered for the inside columns on the first and second elevations. In contrast, a cross-section of 50 × 30 cm was considered for the outside columns. Cross-sections of 30 × 40 cm and 40 × 30 cm were considered for inside and outside columns on the third elevation, respectively. Having no information on the resistant characteristics of the concrete and of the rebars and having not carried out any tests on the materials, it was decided to use a resistance class of concrete C20/25 and steel bars FeB38k, usual for the construction practice of the time. The area of rebars was evaluated considering gravity loads only. For more details, see Fiamingo et al. (2023).

The structure rests on volcanic soil (scoriaceous lava and volcanoclastic in the first layers, compact lavas at the bedrock). By the data provided by an MASW test carried out near the building, it was possible to identify three different layers of 2.4 m (Vs = 209 m/s), 4.6 m (Vs = 320 m/s) and 12 m (Vs = 460 m/s) respectively. The bedrock was found at a depth equal to 19 m. So, the subsoil is of type B, and the stratigraphic amplification coefficient is SS = 1.16 according to the in-force Italian Technical Code (NTC 2018). According to the site morphology, the topographic category T1 was attributed, and the topographic amplification coefficient is ST = 1. The peak horizontal rock acceleration concerning a probability of exceeding 10% in 50 years is ag = 0.225 g.

To consider the soil nonlinearity in the FEM analyses, in the absence of specific dynamic laboratory tests, the values of the soil shear velocity, the shear modulus and the damping ratio were modified according to Eurocode 8 Part 5 (2004), achieving Vs*, Gs* and Ds*, depending on the peak acceleration at the soil surface ag·S. So, using the value ag·S = 0.26 g (for the investigated area), reduction factors equal to 0.64 and 0.42 were estimated for Vs and Gs0, respectively, and Ds* = 8.5% was established. The soil's mechanical properties are shown in Table 1.

Table 1 Main geotechnical parameters of the foundation soil
Full size table

3 The adopted mixture for the GSI

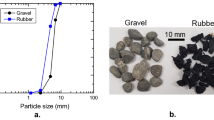
The mixture used for the numerical analyses consisted of two components: gravel (G) and rubber (R) (Fig. 3), whose mechanical properties determined by laboratory tests, are summarised in Table 2 in terms of specific density (Gs), maximum and minimum diameter of the particles (Dmax and Dmin), diameter D50, coefficient of uniformity (Cu), maximum and minimum void index (emax and emin). The mixture for the GSI layer underneath the foundations contains a gravel content per weight equal to 70% and a rubber content per weight equal to 30%. As for the main properties, the mass density was equal to 1.20 t/m3, and the angle of shear strength and the Poisson's ratio were φ' = 23.6°and ν = 0.4, respectively (Mikes 2019).

Fig. 3
figure 3

a Gravel and b rubber used in the reference tests; c grain size distribution curves of the gravel (G) and the rubber (R) used in the reference tests (after Pitilakis et al. 2021)

Full size image
Table 2 Main mechanical parameters of gravel and rubber
Full size table

Two GRM layers were supposed to be underneath the foundation for the numerical analyses. The first GRM layer was characterised by a thickness equal to 0.80 m, corresponding to B/16, being B = 12 m the foundation width (Tsang 2008); the second GRM layer was approximatively characterised by a double thickness equal to 1.5 m.

Through the above-mentioned mechanical properties, it was possible to obtain useful information for the dynamic characterisation of the mixture based on the Pistolas equations (Pistolas 2015). The curves G(γ)/G0 and D(γ) for the mixture used in the two GRM thicknesses of 0.80 m and 1.50 m, corresponding to the two confinement pressures σ0’ = 95.48 kPa and σ0’ = 99.70 kPa, respectively, are shown in Fig. 4. The shear modula at small strains (G0) are respectively equal to 5897.15 kPa and 6059.11 kPa for the two GRM thicknesses of 0.80 m and 1.50 m, according to the confinement pressures.

Fig. 4
figure 4

Curves G(γ)/G0 e D(γ) for the mixture GRM70-30 utilised

Full size image

4 The seismic inputs chosen for the FEM analyses

The city of Catania is characterised by medium–high seismicity given by the tectonic activity of the Ibleo-Maltese fault below the Ionian Sea and the activity of Mount Etna, the highest volcano in Europe (Capilleri and Massimino 2019; Caruso et al. 2016; Ferraro et al. 2018). In particular, the many faults along the eastern flank of Mount Etna cause frequent seismic events with considerable damage despite their moderate magnitude (Azzaro 2004; Alparone et al. 2013).

On 26 December 2018, an earthquake having Mw = 4.9 (Ml = 4.8) and hypocentre at a depth of less than 1 km struck the southeastern flank of Mount Etna, producing severe damage in the towns and villages of the area (Civico et al. 2019). Zafferana Etnea, a town of roughly 9,000 inhabitants, and its neighbouring village, Fleri (2.65 km from the epicentre), suffered the most damage. The SVN and EVRN accelerometer stations, about 1 km from each other, were the closest to the epicentre, respectively 4.5 km and 5.3 km away. The building chosen for the proposed analyses is in Fleri, 4.04 km from the SVN station and 4.90 km from the EVRN station.

Nine accelerograms were utilised for the FEM analyses. Two accelerograms (ID SVN, ID EVRN) recorded on 26 December 2018 at the SVN mentioned above and EVRN stations, respectively, were considered. Moreover, seven spectrum-compatible accelerograms (ID 4675, ID 0651, ID 7187, ID 0198xa, ID 7156, ID 0198ya, ID 0287) were added, the selection of which was made through the Rexel 3.5 code (Iervolino et al. 2009), following the indications of the current Italian Technical Code (NTC 2018). These seven accelerograms are obtained through Rexel 3.5. They are compatible with the target response spectrum (NTC 2018) and with the disaggregation of the seismic hazard (Stucchi et al. 2011) in terms of magnitude M and epicentral distance R, referred to a specific interval (M = 4.0–7.0, R = 0–30 km; Fig. 5a). More precisely, the target response spectrum was developed according to the following parameters: Site Class: A, Topographic category: T1, Nominal Life: 50 years, Functional Type: II and the Limit State of interest: SLV. Moreover, each of the seven accelerograms was linearly scaled (by a scale factor SF) to obtain an average spectrum with a 10% lower tolerance and a 30% upper tolerance in the range of periods 0.15–2 s, compared to the reference response spectrum.

Fig. 5
figure 5

a Range values for the disaggregation of the seismic hazard for Zafferana Etnea (Stucchi et al. 2011); b scaled Response Spectra of the seven selected accelerograms achieved by Rexel 3.5 (Iervolino et al. 2009); c response Spectra of the two accelerograms recorded by the SVN ed EVRN stations

Full size image

Figure 5b shows the output of the results obtained by Rexel on the spectrum compatibility of the 7 selected accelerograms; the average scale factor SF is 1.16. Figure 5c shows the elastic spectra of the accelerograms recorded by the SVN and EVRN stations. Table 3 shows the nine accelerograms' main properties and acceleration time histories.

Table 3 Main properties of the selected seismic inputs for the FEM analyses
Full size table

5 The numerical modelling

The parametric analyses were performed by the ADINA code (Bathe 1999) developing three different FEM models: (i) a first FEM model without the GRM layer (Model 1); (ii) a second FEM model with a 0.80 m GRM layer (Model 2); (iii) a third FEM model with a 1.50 m GRM layer (Model 3). Comparing the three numerical models allows us to evaluate the performance of the soil-GRM-structure system in static and dynamic conditions and the effectiveness of the GRM in terms of seismic energy reduction. The main characteristics of the 3 FEM models are described below.

For all the three FEM models, the height of the soil deposit (H = 19 m) was derived from the soil profile discussed in Sect. 2. The width of the soil deposit (100 m) was chosen to minimise boundary effects as far as possible (Fig. 6). Plane strain 4-node 2D-solid elements for the soil and the GRM and 2-node Hermitian beam elements for the structure were used, respectively.

Fig. 6
figure 6

The FEM model of the soil-structure system, without the GRM layer (Model 1), modified by Fiamingo et al. 2023

Full size image

The structure beams’ horizontal displacements along the y-direction were linked by “constraint equations” that imposed the same y-translation to reproduce an axial rigid diaphragm. The nodes of the lateral boundaries of the soil were connected by “constraint equations” that imposed the same y- and z-translation at the same depth. The nodes at the base of the model were constrained only in the vertical direction. Dashpots were implemented in the horizontal direction at the base of the model to simulate the bedrock, according to Lysmer and Kuhlemeyer (1969). The coefficient of each dashpot was evaluated as \(c= \rho \bullet {V}_{s}\bullet A\), where ρ is the bedrock mass density, and VS is the shear wave velocity of the bedrock, and A is the ‘effective’ area of each dashpot to maintain proportional results for any horizontal element size. Contacts between the foundation and the soil (for Model 1) or GRM (for Models 2 and 3) were defined to model uplifting and sliding phenomena. The friction angle between the foundation and the soil (for Model 1) or the GRM layer (for Models 2 and 3) was fixed as δ = 2φ'/3 (Sheng et al. 2007; Ilori et al. 2017), due to no availability of field tests, being φ' the angle of shear strength of the soil for Model 1 and the GRM for Models 2 and 3, respectively.

The maximum mesh element size, hmax, was chosen, as a first attempt, equal to hmax ≤ Vs*/(7 fmax), according to Kuhlemeyer and Lysmer (1973) and Lanzo and Silvestri (1999), where Vs* is the soil shear wave velocity modified according to Eurocode 8 (see Sect. 2) and fmax is the maximum significant frequency of the dynamic input. Then, to guarantee an even dense mesh, the Authors fixed an element size of 0.40 m for all the soil elements far from the frame and 0.25 m for those near the frame. The mesh element sizes selected are also in very well agreement with the suggestion provided by IAEA TECDOC (1990) for time-domain analyses using 4-node quadrilateral linear elements.

Regarding the materials' constitutive modelling, the soil was modelled using an equivalent linear viscoelastic constitutive model to consider the soil nonlinearity, so adopting the parameters Gs* and Ds* previously described in Sect. 2 (Table 1).

Elastic members modelled the beams and columns of the structure with finite-length plastic hinges at the two ends. The plastic hinge length was set equal to the height of the member cross-section. Within the plastic hinge region, the moment–curvature M–θ curves were assigned. Several M–θ curves can be given to a single cross-section for prefixed axial force values. These curves were preliminarily determined by the M–θ analysis carried out by the OpenSees code (Mazzoni et al. 2006). For details, see Fiamingo et al. (2023). Figure 7 shows the M-θ curves for the sections of the columns and beams. For columns, the M-θ curves were determined considering bending about either the strong or weak axis of the cross-section and for eight prefixed values of the axial force. Instead, for the beams, the M-θ curves were evaluated only about the strong axis for each cross-section. The values of the material parameters (elastic modulus Ec, compressive strength fcm, concrete strain εc0 at maximum strength, concrete strain εcu at crushing strength and tensile strength fctm) used for the moment–curvature M–θ curves are different for concrete fibres constituting the cover or the core of the cross-section (Table 4). Based on the values of strength directly obtained from cores extracted from about 400 buildings in Italy (Masi et al. 2004), an average compressive strength, fcm, was assumed equal to 20 MPa for the cover region. The properties of the confined concrete were obtained by considering the confinement effectiveness factor for each cross-section (Eurocode 8 Part 3 2004).

Fig. 7
figure 7

a–d Moment–curvature curves for the 30 × 50 cm, 30 × 40 cm column section; e moment–curvature curves for the 30 × 60 cm beam section (modified by Fiamingo et al. 2023)

Full size image
Table 4 Main parameters of the concrete of the investigated building for the M–θ curves
Full size table

The material viscosity was modelled according to the Rayleigh damping. The Rayleigh damping coefficients were estimated according to the following well-known equations (Chopra 1999):

$$\alpha = \left( {\xi \cdot \omega_{1} \cdot \omega_{2} } \right)/\left( {\omega_{1} + \omega_{2} } \right)$$
(1)
$$\beta = 2\xi /\left( {\omega_{1} + \omega_{2} } \right)$$
(2)

For the soil, the first natural angular frequency (ω1 = 22.10 rad/s, corresponding to the frequency of 6.28 Hz) was estimated using the following equation:

$$\omega_{1} = 2\pi \cdot \frac{{V_{s,av} }}{4H}$$
(3)

where H is the total thickness of the soil and Vs, av is the weighted average of the shear wave velocities of the whole soil. The second frequency (ω2 = 66.25 rad/s, corresponding to 18.84 Hz) was assumed to be three times the first one (Kwok et al. 2007). The damping ratio ξ was assumed to be equal to the values Ds* = 8.5% shown in Table 1.

For the structure, the first and the second angular fundamental frequencies (ω1 = 8.60 rad/s and ω2 = 25.12 rad/s, corresponding to f1 = 1.37 Hz and f2 = 4.00 Hz) were evaluated through the modal analysis of the frame fixed at the base including the nonlinear moment-rotation curves at the extremities. A damping ratio ξ = 5% was assigned to the first and second frequencies of the R.C. framed structures (Ghobarah and Biddah 1999; Bosco et al. 2015; Mazza 2016). The nonlinearities induced by the non-linear moment-rotation curves at the extremities of the beam elements could decrease the first frequency with the consequence that Rayleigh damping will overshoot the target value of 5%. Nevertheless, while the elastic behaviour is influenced mainly by viscous damping, the inelastic behaviour is mainly affected by the hysteretic damping and the contribution of the viscous damping is less significant (Bosco et al. 2023).

As for the loading conditions, distributed loads in the seismic design combination were applied to the beams. Furthermore, vertical forces were applied to the columns to consider gravity loads sustained by beams orthogonal to the frame under consideration. The mass of all the elements was also considered. The seismic inputs were applied to the dashpots located at the base of the soil deposit using the acceleration time histories shown in Sect. 4, which the code transforms into force time histories required by the damper boundary conditions.

Model 2 and Model 3 have, respectively, a 0.80 m and a 1.50 m (Fig. 8) GRM layer under the foundations, which replaced a portion of the first soil layer. Below the GRM layer, the soil stratigraphy remains unchanged compared to Model 1. The width of the GRM layer measured from the frame’s foundation beam toward the end of the GRM layer was fixed as 1/4 of the total width of the frame (Tsang 2008), i.e. equal to 3.0 m. Therefore, the overall width of the GRM footprint is equal to 18.10 m. As made for the soil, this GRM layer was modelled by 2D solid elements with equivalent linear visco-elastic behaviour. But the parameters G and D were updated step by step, according to the curves G(γ)/G0 and D(γ) shown in Fig. 4, considering the effective strain level γ obtained for each input through an iterative sub-routine. As an example, Fig. 9 reports the evolution of the shear modulus (G) and damping ratio (D) with the shear strain at each step (denoted as “st.” in Fig. 9) for Model 2 and Model 3, considering the seismic input ID 4675. As expected, the strain level induced by the GRM layer with a thickness of 1.50 m is more significant than that with a thickness of 0.80 m. This effect leads to a more pronounced decrease in shear modulus and an increase in the damping ratio, clarifying the beneficial effect of the GRM on the structure response, as will be discussed in the following.

Fig. 8
figure 8

A zoomed view (near the building) of the two FEM models: a Model 2 and b Model 3, including the GRM layer underneath the structure

Full size image
Fig. 9
figure 9

Evolution of the shear modulus (G) and damping ratio (D) with the shear strain at each step (denoted as “st.”) for: a Model 2 and b Model 3, considering the seismic input ID 4675

Full size image

The fundamental frequency of the soil profile, including the GRM, depends on the thickness of the GRM layer: it is, on average, 4.99 Hz and 3.36 Hz in the case of GRM layer thickness equal to 0.80 m and 1.50 m, respectively. This effect is due to the increase in the mixture's deformability.

6 The effectiveness of the investigated GRM layers

To evaluate the performance of the investigated GRM layers as GSI technique, the dynamic response of the two full-coupled systems (Model 2 and 3) was evaluated in terms of: dominant frequencies of the foundation input motions; fundamental frequencies of the structure based whether on the original soil or the GRM layers; elastic response spectra at the foundation of the structure; envelopes of the elastic response spectra in acceleration at the foundation and the roof of the structure; percentage reduction of the spectral ordinates as a function of the periods, thanks to the presence of the GRM. Finally, the ratio between the maximum shear force and the shear strength was evaluated for a representative column of the structure.

The dominant frequencies of the foundation input motions (fFIM), evaluated for all the seismic inputs and the three models (Model 1, Model 2 and Model 3), are reported in Table 5. It is evident that the GRM layer influences the values of fFIM; for all the seismic inputs, the presence of the GRM layers causes a decrease of fFIM (see Model 1 results vs Models 2 and 3 results); moreover, fFIM decreases by increasing the thickness of the GRM layer (see Model 2 results vs Model 3 results).

Table 5 Dominant frequencies of the foundation input motions (fFIM) for the investigated accelerograms and models
Full size table

Table 6 reports the first fundamental frequencies of the fixed-base structure and the structure placed whether on the original soil or the GRM layer (f*). These frequencies were obtained by computing the transfer function as the ratio between the Fast Fourier Transform (FFT) of the acceleration time histories at the roof and the foundation of the structure. Due to the soil-structure interaction effects, the fundamental frequencies of the structure on the original soil profile (Model 1) are lower than the frequency of the fixed-base structure. In addition, the GRM layer led to an increase in the fundamental frequency of the structure resting on the original soil (see Models 2 and 3 results vs Model 1 results). The higher the GRM layer thickness, the more frequency will be increased.

Table 6 First fundamental frequencies of the fixed-base structure and the structure placed, whether on the original soil or the GRM layers
Full size table

The frequency of the structure placed on the original soil is 1.11 Hz. The average frequency of the structure placed on the GRM layer with a thickness of 0.80 m and 1.50 m equals 0.90 Hz and 0.80 Hz, respectively. Therefore, the decrease of the fundamental frequency for the structure without and with base isolation compared to the fixed-base structure is 20% (Model 1), 34% (Model 2) and 41% (Model 3).

Figure 10 shows the elastic response spectra at the foundation of the structure resting on the original soil (Model 1) and the GRM layer (Model 2 and Model 3). These spectra were obtained for each seismic input, considering a damping ratio of 5%. However, to better highlight the difference between the models without and with GRM, varying the thickness of the mixture layer (Model 1 vs Model 2 and Model 1 vs Model 3), Fig. 11 reports the envelopes of the elastic response spectra. These envelopes at the foundation level (Foundation Motion) and the roof of the structure (Roof Motion) were obtained by referring to the elastic response spectra of all the seismic inputs, considering a damping ratio equal to 5%.

Fig. 10
figure 10

Elastic response spectra in acceleration at the foundation for the structure resting on the original soil (Model 1) and on the GRM layer having a thickness h = 0.80 m and h = 1.50 m (Model 2 and Model 3, respectively)

Full size image
Fig. 11
figure 11

Envelope of the elastic response spectra in acceleration at the foundation and the roof of the structure resting on the GRM layer having a thickness h = 0.80 m (Model 2) and of the structure resting on the GRM layer having a thickness h = 1.50 m (Model 3)

Full size image

As reported in Fig. 10 for the configuration without GRM (Model 1), it is possible to highlight that the behaviour of the original soil determines a significant increase in the spectral acceleration compared to those according to the NTC (2018) for the soil category of the present study (type B). However, for periods greater than 0.5 s, the spectral accelerations are generally lower than those reported in NTC (2018). The presence of the GRM layer leads to a general decrease in the spectral acceleration. The higher the GRM layer thickness, the more spectral acceleration will be decreased; this effect is due to the mobilization of a higher material damping that leads to more energy dissipation, as depicted in Fig. 9. The decrease of the spectral accelerations can also be noticed in Fig. 11, considering the envelope of the spectral acceleration. It is clearer that the GRM produces a reduction in the spectral acceleration peaks and a translation of these peaks towards higher periods for both the two investigated GRM-structure systems (Model 1 vs Model 2 and Model 1 vs Model 3). This result is typical of all those systems where valuable phenomena of dynamic soil-structure interaction (DSSI) occur (Eurocode 8 Part 3 2004).

Figure 12 shows the percentage reduction of the spectral accelerations at the foundation and the roof of the structure. Figure 13 reports the Fourier Spectrum (FAS) achieved for the reference seismic input “ID 0287” at the foundation and the roof of the structure. The “ID 0287” input was chosen because it agrees with the average trend of the percentage reduction of the spectral accelerations achieved for the nine seismic inputs. Figure 12 compares the average trends of the percentage variation of the spectral accelerations at the foundation and the roof of the structure. Finally, Fig. 14 shows the ratio Vmax/VRd, being Vmax the maximum shear force and VRd the shear strength, evaluated for the third column of the structure without the GRM layer underneath the foundation and with both the 0.80 m and 1.50 m GRM layers.

Fig. 12
figure 12

a–d Percentage variation of the spectral accelerations at the foundation and the roof of the structure resting on the GRM layer having a thickness h = 0.80 m and of the structure resting on the GRM layer having a thickness h = 1.50 m and e and f comparison between the average trends of percentage reduction of the spectral accelerations at the foundation and the roof of the structure for the two analysed GRM-structure systems

Full size image
Fig. 13
figure 13

Fourier Amplitude Spectrum for the ID 0287 input at the foundation and at the roof of the structure resting on the GRM layer having a thickness h = 0.80 m (Model 2) and of the structure resting on the GRM layer having a thickness h = 1.50 m (Model 3). (“f” is the frequency evaluated for the system “without GRM” and “f*” is the frequency evaluated for the system “with GRM”)

Full size image
Fig. 14
figure 14

Shear force along the third column for the adopted seismic inputs

Full size image

The percentage reduction of the spectral accelerations is shown in Fig. 12: a negative percentage reduction means a “de-amplification” of the spectral acceleration; conversely, a positive percentage reduction means an “amplification” of the spectral acceleration. As for the structure resting on the GRM layer having a thickness of 0.80 m (Figs. 12a and b, Model 2), considering the foundation level, there was a de-amplification of the spectral accelerations equal to about 30% in the period's ranges T = 0–0.25 s and equal to about 15% for T = 0.45–0.88 s. Nevertheless, for T = 0.25–0.45 s and T = 0.88–2.0 s, an amplification of the spectral acceleration equal to about 20% was achieved. At the roof of the structure, there was a significant de-amplification of the spectral accelerations equal to about 40% for T = 0–0.82 s and an amplification equal to about 20% for T = 0.82–2 s. As for the structure resting on the GRM layer having a thickness of 1.50 m (Fig. 12c, d Model 3), at the foundation level there was a de-amplification of the spectral accelerations equal to about 30% for T = 0–0.28 s and equal to 20% for T = 0.52–0.94 s. Nevertheless, for T = 0.28–0.52 s and for T = 0.94–2.0 s, an amplification of the spectral acceleration equal to about 20% was achieved. At the roof of the structure there was a significant de-amplification of the spectral accelerations equal to about 40% for T = 0–0.93 s and an amplification equal to about 20% for T = 0.93–2 s.

Figure 13 shows the Fourier Amplitude Spectra (FAS) for the input ID 0287. For the structure resting on the GRM layer having a thickness of 0.80 m (Model 2), at the foundation level, the peaks of the FAS for the system “with GRM” (green line) move towards lower frequencies, in comparison with the FAS for the system “without GRM” (red line). So the first and second natural frequencies move from f1 = 1.48 Hz towards f*1 = 0.80 Hz and from f2 = 4.84 Hz towards f*2 = 3.96 Hz, respectively. For a fixed low frequency, the FAS for the system “with GRM” is greater than the FAS for the system “without GRM”. In fact, from Fig. 12a it is possible to notice, for the same investigated seismic input ID 0287, an increase in the spectral acceleration at 1.25 s (i.e. at f*1 = 0.80 Hz). For a fixed high frequency, the FAS for the system “with GRM” is lower than the FAS for the system “without GRM”. On the contrary, from Fig. 12a, it is possible to highlight a decrease in the spectral acceleration at 0.25 s (i.e. at f*2 = 3.96 Hz). At the roof of the structure, the same trend of the peaks of the FAS was achieved for the first fundamental frequency, which moves from f1 = 1.89 Hz for the system “without GRM” to f*1 = 1.10 Hz for the system “with GRM”; as for the second fundamental frequency, it changes from f2 = 5.36 Hz towards a slightly higher frequency equal to f*2 = 5.86 Hz. A significant decrease in the amplitude of the Fourier spectrum was achieved for the system “with GRM”, as also highlighted in Fig. 12b in terms of spectral acceleration percentage variation. For the structure resting on the GRM layer having a thickness of 1.50 m (Model 3), the same results obtained for the previous GRM layer were achieved at the foundation level. The peaks of FAS move towards lower frequencies and lower values, comparing the system in the absence of mixture (“without GRM”: red line) with the system in the presence of mixture (“with GRM”: green line) and so the first and second natural frequencies move from f1 = 1.48 Hz towards f*1 = 0.80 Hz and from f2 = 4.84 Hz towards f*2 = 2.60 Hz, respectively. As discussed above, from Fig. 12c can be observed an increase in the spectral acceleration at 1.25 s (i.e. at f*1 = 0.80 Hz) and a decrease in spectral acceleration at 0.38 s (i.e. at f*2 = 2.60 Hz). At the roof of the structure, f1 = 1.89 Hz for the system “without GRM” shifts f*1 = 1.10 Hz for the system “with GRM”, as well as f2 = 5.36 Hz slightly shifts towards a lower frequency equal to f*2 = 4.81 Hz (Fig. 12d).

Then, the 1.50 m GRM layer provided a slightly greater reduction in spectral acceleration than the 0.80 m GRM layer for both the foundation level and the roof level, as well as a translation of the period ranges for which a reduction of the spectral accelerations occurred. This result is highlighted in Figs. 12e, f, which show the average trends of the percentage variation of the spectral accelerations for the two investigated GRM layers.

Based on the results achieved at the foundation level, this mixture could be used as a GSI technique for all structures having a period lower than about 0.28 s, as well as for all structures having a period in the range 0.52–0.94 s, thanks to the good reduction of the spectral accelerations. A GRM layer having a minor thickness lead to the translation of these ranges towards minor periods (and a minor decrease in spectral acceleration, as previously discussed).

It must be stressed that the effects of soil-GRM-structure interaction cannot always be beneficial. For structures characterised by fundamental periods in the ranges 0.28–0.52 s and 0.94–2.0 s (or slightly shifted for minor values), resting on a soil comparable to the investigated soil (basically a class B soil for NTC 2018), the effect of the GRM layer would be to increase the spectral ordinates at the foundation level. Based on the results achieved at the roof level, the beneficial effect of the GRM layer is observed for T from 0 s to approximately 0.9 s, i.e., for a valuable range of periods for many structures.

Finally, Fig. 14 shows the ratio Vmax/VRd, being Vmax the maximum shear force and VRd the shear strength, evaluated for the third column of the structure, the most stressed one (highlighted in the left corner in Fig. 14), per each adopted seismic input, and for the three different configurations, i.e., without the GRM layer and with the GRM layers having different thicknesses. This third column suffered severe damage at the second-floor level during the 26 December 2018 earthquake. Due to the unavoidable uncertainties, it has been established that shear failure occurs when Vmax/VRd ≥ 0.9. This value was reached exactly for ID SVN, i.e., the seismic event of 26 December 2018 recorded by the station closest to the analysed building. Comparing the values of Vmax/VRd for the three Models 1, 2, and 3, it is possible to affirm that using the GRM layer underneath the foundation reduced the shear force by about 50%. The best reductions are obtained with the 1.50 GRM layer.

7 Some final considerations about the static and dynamic behaviour of the GRM-structure systems

This section shows the FEM movements at the foundation level under the static and dynamic conditions for the two investigated GRM-structure systems (Models 2 and 3). In particular, the absolute vertical displacement smax, the differential vertical displacement δs,max and the maximum relative rotation βmax were evaluated (Maugeri et al. 1998). As for the dynamic movements, they depend on the time for which dynamic inputs cause the greatest movement. The most severe condition was considered in terms of the absolute vertical displacement: it was defined by the time in which one of the four columns suffered, firstly, the greatest vertical displacement. This time was used to evaluate the vertical displacement of the remaining three columns. The so evaluated numerical movements were compared with the following allowable values: allowable smax equal to 50 mm (Eurocode 7 Part 1 2004); allowable δs,max equal to 75% of the absolute vertical displacement (Terzaghi and Peck 1948); allowable δs,max equal to 20 mm (Eurocode 7 Part 1 2004); allowable βmax equal to 1/1000 (Skempton et al. 1956). Table 7 shows the achieved numerical movements at the foundation level. The values ​​that exceed the allowable ones are highlighted in bold.

Table 7 Static and dynamic absolute vertical displacement smax, differential vertical displacement δs,max and maximum relative rotation βmax for the analysed GRM-structure systems
Full size table

As for the static movements, they were always lower than the allowable ones for both of the investigated GRM-structure systems.

As for the dynamic movements, for the GRM-structure system with the 0.80 m GRM layer (Model 2), smax was always lower than the allowable one; δs,max slightly exceeds that allowable for the ID 0198xa, ID 0198ya, ID 0287, ID 4675, ID SVN and ID EVRN inputs; βmax only for the event ID EVRN exceeds the allowable value. For the GRM-structure system with the 1.50 m GRM layer (Model 3), the smax due to the ID 0198ya, ID 0287, ID EVRN inputs exceeding the allowable value; δs,max was greater than the allowable value for some seismic events; βmax does not exceed the allowable value. Finally, as an example, Fig. 15a, b shows the deformed and undeformed configurations of the structure resting on the 0.80 m GRM layer, as well as Fig. 15c-d shows the deformed and undeformed configurations of the structure resting on the 1.50 m GRM layer for the selected ID EVRN and ID 7187 inputs. For the ID EVRN input (Fig. 15a, c), the vertical displacement of Column 4 was considerably smaller than that of Column 2. For the ID 7187 input (Fig. 15b, d), the vertical displacement of the four columns is quite similar, thus limiting the maximum relative rotations (as shown in Table 7).

Fig. 15
figure 15

Original and deformed frame for the two investigated GRM-structure systems subjected to two different seismic inputs

Full size image

In addition, the applied forces in the beam foundation were successfully checked with respect to the bearing capacity, according to Paolucci and Pecker (1997).

8 Conclusive remarks

The present study investigated numerically the effect of a gravel-rubber mixture (GRM) layer, located underneath the shallow foundations of a real structure typical in Southern Italy, on its dynamic response under different seismic inputs to detect the capability of the GRM layer as geotechnical seismic isolation (GSI) system. Some considerations were carried out also for the static behaviour, evaluating the movements at the foundation level considering and not the GRM layer underneath the foundation. The adopted GRM was characterised by a rubber content equal to 30%, because of its good performance found by the first large tests recently developed at Thessaloniki (Greece) on a prototype structure laying on three different gravel-rubber mixtures (Transnational Research Project SERA-SOFIA; Pitilakis et al. 2021). The rubber grains were manufactured from end-of-life tires, so the proposed use of the investigated GRM represents a valuable eco-sustainable GSI solution.

The structure investigated in the present paper is a typical reinforced concrete building in southern Italy. Three FEM models were developed. The first model reproduced the actual configuration of the soil. The second model was characterised by an uppermost layer of the foundation soil replaced with a GRM layer having a thickness equal to B/16 (0.80 m), being B = 12 m the width of the foundation. The third model was characterised by an uppermost layer of the foundation soil replaced with a GRM layer having a quite double thickness, equal to 1.50 m. Several seismic inputs were applied to the models. The inputs are representative of the medium–high seismicity of the investigated area.

The comparisons among the FEM models allowed us to assess the overall performance of the GRM layers underneath the foundations to mitigate the seismic risk of the structure and to furnish some general information about GRM as GSI. The dynamic response of the full-coupled systems was evaluated in terms of: envelopes of the elastic response spectra in acceleration at the foundation and the roof of the structure; percentage reductions of the spectral accelerations in the period range 0–2 s; Fourier Amplitude Spectra (FAS) at the foundation and the roof of the structure. Moreover, the shear forces due to the different adopted seismic inputs along the structure and the movements at the foundation level were evaluated in terms of absolute vertical displacement, differential vertical displacement and maxima relative rotations. These movements were evaluated also considering just the static conditions.

The main findings are as in the following:

  • The GRM determined at the roof of the structure an excellent reduction (average value = 40%, maximum value = 60%) of the spectral accelerations for the period range 0–0.82 s and 0–0.93 s, by using the 0.80 m and the 1.50 m GRM layer, respectively. At the foundation level, a significant reduction of the spectral accelerations was achieved for periods lower than 0.25 s and 0.28 s, as well as for periods in the range 0.45–0.88 s and 0.52–0.94 s, by using the 0.80 m (average value = 15%, maximum value = 40%) and the 1.50 m GRM layer (average value = 25%, maximum value = 50%), respectively. But the effects of soil-GRM-structure interaction could not always be beneficial: for period ranges equal to 0.25–0.45 s and 0.88–2 s by using the 0.80 m GRM layer, as well as for period ranges equal to 0.28–0.52 s and 0.94–2.0 s by using the 1.50 m GRM layer, there was an increase (up to 20%) in the spectral accelerations at the foundation, the more significant, the higher the GRM layer thickness.

  • The GRM layer determined a slight increase in the amplitude of the FAS at very low frequencies and a valuable decrease at high frequencies. The peaks of the FAS move towards lower frequencies, comparing the system in the absence of the mixture with the system in the presence of the mixture. The 1.50 m GRM layer brought the first two fundamental frequencies closer together.

  • The use of the GRM also reduced the shear forces along the structures by about 50%. The best performance is reached with the 1.50 GRM layer.

  • As for the movements at the foundation level, considering the static conditions, they were always lower than the allowable ones. Under the adopted seismic inputs, the foundation movements were sometimes greater than the allowable ones.

Thus, GRM layers underneath foundations appear to be a valuable GSI solution even with reduced thicknesses. Nevertheless, careful attention should be devoted to the frequency ranges inside which GRM have irrefutable positive effects and foundation movements in static and dynamic conditions. Further Authors’ studies will be aimed at parametric analyses involving different site seismicity, soil types and structures, as well as analyses concerning the static behaviour of GRM-structure systems, also considering the durability of the overall performance over time.