1 Introduction

Probing the photospheric magnetic fields can be reliably determined from the induced Stokes profiles of polarization signals, as described in (Hale 1908; Stenflo 2017). Recently, space- and ground-based telescopes have permitted in the understanding fine structure of sunspots and pores regions of strong Zeeman signals, which include the internal structures of umbra and penumbrae regions (i.e., umbra dots, penumbra grains, light bridges, spines) and some studies have been performed toward the upper atmospheric layers above sunspots (e.g., Trujillo Bueno et al. 2017; Wiegelmann et al. 2017). Some previous analyses on the fine structure of sunspots were presented in several investigations (e.g., Spruit 1981; Solanki 2003; Borrero and Ichimoto 2011). Sunspots are a prominent manifestation of solar activity (Solanki 2003; Schlichenmaier 2009; Borrero and Ichimoto 2011). The magnetic fields of the penumbra were recognized by the uncombed configurations on small-scale fine structures along the azimuthal direction (Lites et al. 1993; Solanki and Montavon 1993; Title et al. 1993; Martínez Pillet 2000; Schlichenmaier and Collados 2002; Bellot Rubio et al. 2004; Tiwari et al. 2015; Murabito et al. 2019). Recently a possible configuration of the presence of super-strong magnetic fields (>7 kG) in the penumbra has been discovered by (Siu-Tapia et al. 2019). Van Noort et al. (2013) found strong magnetic fields (reaching over 7 kG) at the outer edge of the penumbra. Van Noort et al. (2013) also detected a large red-shifted velocity at the outer boundary of the penumbra, which reported values up to 20 km sec−1. Okamoto and Sakurai (2018) reported strong magnetic fields located in a light bridge of opposite polarities umbra (\(\delta \) sunspots). Livingston et al. (2006) found strong magnetic fields in sunspots of about 6100 G using statistics from 1917 to 2004.

The uncombed magnetic configurations of the penumbra have been proposed by two components inversions, which are commonly so-called spines and intra-spines systems (e.g., Solanki and Montavon 1993; Solanki 2003; Borrero et al. 2004; Ichimoto et al. 2008; Schlichenmaier 2009; Borrero and Ichimoto 2011; Guglielmino et al. 2019). For the details, the penumbra intra-spine region (Lites et al. 1993) is referred to as the flux-tube component (i.e., horizontal weak field strength) that carries the magnetized Evershed flows, while the penumbra spine region (Guglielmino et al. 2019) is indicated to the background component (i.e., more vertical field) that harbors stronger magnetic fields. To infer the physical quantities in sunspots, several inversions in the Local Thermodynamical Equilibrium (LTE) techniques have been applied (Skumanich and Lites 1987; Ruiz Cobo and Toro Iniesta 1992; Socas-Navarro et al. 1998; Frutiger et al. 2000; Lagg et al. 2004; Asensio Ramos et al. 2008; Borrero et al. 2011; Del Toro Iniesta and Ruiz Cobo 2016; De La Cruz Rodríguez and Van Noort 2017). For instance, various analyses of the vector magnetic field in sunspots have been studied (Westendorp Plaza et al. 2001a,b; Bellot Rubio et al. 2007; Beck 2008; Balthasar and Gömöry 2008; Tiwari et al. 2015; Felipe et al. 2016; Castellanos Durán et al. 2020; Trujillo Bueno and Pino Alemán 2022). Castellanos Durán et al. (2020) detected the presence of the strongest magnetic field in a sunspot light bridge, where the field strength reached 8.2 kG. A recent review on the magnetic field in the solar upper atmosphere was provided by Trujillo Bueno and Pino Alemán (2022), giving more details on the development of magnetic field measurements. In addition, some spectropolarimetric inversions on small-scale structures in sunspots are performed with Hinode SOT-SP data (Kubo et al. 2008; Franz and Schlichenmaier 2009; Tiwari 2009, 2011; Tiwari et al. 2009; Borrero and Ichimoto 2011; Van Noort et al. 2013). Similar studies along the dark lanes are analyzed (Scharmer et al. 2002; Spruit and Scharmer 2006; Borrero 2007; Bellot Rubio et al. 2007; Langhans et al. 2007; Rimmele 2008; Ruiz Cobo and Bellot Rubio 2008; Tiwari et al. 2013; Schlichenmaier et al. 2016).

Here we analyze Hinode SP-SOT data for the AR 12546 to infer the vector magnetic field quantities in the penumbra and its surrounding regions from the pair Fe I visible lines at 6301.5 Å and 6302.5 Å. The observational data is found in Sect. 2. Here we used the LTE treatment applying the SIR (Stokes Inversion based on Response functions; Ruiz Cobo and Toro Iniesta 1992) inversion code. The physical quantities are obtained by solving the radiative transfer equation under certain simplifying assumptions. The atmospheric models, as deduced from the SIR inversion, are taken into account in the entire sub-field of view area, focusing on the temperature, magnetic field strength, inclination field, and LOS velocity for a high-resolution data of Fe I lines at 6301.5 Å and 6302.5 Å. We extend further the debate to the vertical gradients of temperature (\(\Delta T\)), magnetic strength (\(\Delta B\)), inclination field (\(\Delta \gamma \)), and LOS velocity (\(\Delta V_{LOS}\)) using two selected optical depths. We study the NCP and Stokes V area asymmetry of Fe I 6302.5 Å spectral line of Hinode data for comparing the observed and best-fit values. We provide a 3D structure of the magnetic field for the AR 12546. Inversion analysis and results are explained in Sect. 3. Discussion and conclusions are summarized in Sect. 4.

2 Observations and methods

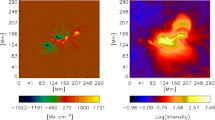
We analyze high-resolution observations with the spectropolarimeter (Lites et al. 2013) instrument of the Solar Optical Telescope (Tsuneta et al. 2008) onboard the Hinode satellite (Kosugi et al. 2007) in the couple Fe I lines at 6301.5 Å and 6302.5 Å. We studied a positive polarity sunspot AR (NOAA 12546), being currently the most prominent features in sunspot included from the quiet Sun, umbra, and penumbra inside the field of view. The observational data were acquired on 22 May 2016 in the period from 13:37:32 to 14:40:42 UT, in an interval time of 62 minutes with a field of view of (995 × 512) pixel2 area. The Hinode SOT-SP data has a single fast mode of observation. The heliocentric angle of AR is 27∘ located at (X = 416″, Y = −150″; [S07, W35]; \(\mu = 0.89\)) on the solar disk. In fact, the AR is slightly far away from the disk center of the sunspot. The present data have full Stokes profiles (IQUV) in the Fe I lines at 6301.5 Å (effective Landé factor \(g_{eff} = 1.67\)) and 6302.5 Å (\(g_{eff} = 2.5\)). Here the SP scan has a step cadence of 3.8 sec and a spectral sampling of 21.6 mÅ. The polarization sensitivity is 10−3 for the continuum intensity. The sequence of SP data has a step size of 0.32″ and an exposure time of 1.6 sec per slit position (fast map mode). The original field of view of SP was about (295″ × 162″), see here Fig. 1. Guglielmino et al. (2019) investigated the physical quantities of the vector magnetic field in the umbral filament of sunspots using a fast mode of a Hinode spacecraft. The Level 1 SP data are provided in the Flexible Image Transport System (fits) format and are from the available website (http://www2.hao.ucar.edu/csac/csac-data/) in calibrated 3D data (spectral × spatial × 4 Stokes parameters) which is ready for the scientific analysis. For Level 2 Hinode SOT-SP data, we used the very fast inversion of the Stokes vector code (VFISV; Borrero et al. 2011). The VFISV code performs a least-squares fitting of the Stokes profiles using the Milne-Eddington (ME) approximation. The ME-inversion codes assumed the physical quantities constant in the range of optical depths of a line formation, see a review by Borrero and Ichimoto (2011).

Fig. 1
figure 1

The photospheric Fe I 6301.5 Å and 6302.5 Å lines data is from the Hinode SOT-SP for a sunspot AR 12546. Top panel: the Stokes I, Q images in the polarimetric signals observations. Lower panel: the Stokes U and V. The North is up, and West is right. The arrow in the continuum intensity map refers to the disk center direction. The continuum map (top-left) shows the inverted pixels (red plus marks) which are shown in Figs. 3, 4, and 5

Full size image

Using the Hinode SOT-SP, we measure the Stokes V area asymmetry (\(\delta a\)) of Fe I 6302.5 Å line as follows:

$$ \delta a = \frac{\int V(\lambda ) d\lambda}{\int |V(\lambda )| d\lambda} $$
(1)

In addition, the Stokes V area asymmetries were studied in several investigations (Illing et al. 1974a,b; Makita and Ohki 1986; Sánchez Almeida and Lites 1992; Schlichenmaier and Collados 2002; Müller et al. 2002; Borrero et al. 2004). In addition, the NCP of spectral lines were analyzed in several investigations (Borrero et al. 2006; Tritschler et al. 2007; Ichimoto et al. 2008; Beck 2011; Carlin 2019; Kaithakkal et al. 2020; Siu-Tapia et al. 2020). The NCP of sunspots provides more information on the vector magnetic field (e.g., Beck 2011; Shaltout and Ichimoto 2015, and references therein). The NCP property is measured as usual:

$$ NCP = \int \frac{V(\lambda )}{I_{c}}d\lambda $$
(2)

In Fig. 2, the observed Stokes (I: top panel and V: bottom panel) profiles in the umbra (left), penumbra (middle), and quite Sun (right) regions are presented within a small area of (20 × 20 pixel2) from the original map. The continuum intensity (I) in the umbra reaches a maximum level of 0.45, where the normalization level agrees well with that normalized (Westendorp Plaza et al. 1998; see Fig. 13 therein).

Fig. 2
figure 2

The Stokes I (top) and V (bottom) profiles in the umbra (left), penumbra (middle) and quiet Sun (right) regions of a Hinode SOT-SP data. The Stokes profiles are shown within an area of (20 × 20 pixel2) in the original sub-field of view map, where the Stokes (I and V) spectra are normalized for the mean continuum quiet Sun intensity

Full size image

3 Inversion results

3.1 Vector magnetic field

We use the Stokes Inversion based on Response functions (SIR) code (Ruiz Cobo and Toro Iniesta 1992) for studying the vector magnetic field in the sunspot AR 12546. The original Hinode SOT data observed with a field of view of (995 × 512 pixel2), with a fast mode map. We chose a sub-field of view region (87″ × 103″) for the SIR inversion, as shown in the continuum intensity map of Fig. 1. The sub-field of view area is given in a pixel scale with (271 × 321 pixel2). We obtain the physical properties of the vector magnetic field in the quiet Sun, umbra and penumbra of a sunspot. We adopted the temperature stratification of the Harvard-Smithsonian Reference Atmosphere (HSRA; Gingerich et al. 1971) in standard optical depths between log \(\tau = [ -4, 0]\). The ME inversion atmospheres are obtained using the VFISV code. These atmospheres are used as an initial guess for the magnetic strength, LOS velocity, azimuth, and inclination angles in the target area, i.e., where each pixel has different initial guess values with the SIR inversion. In the inversion mode, we assume three nodes for the temperature, magnetic strength, LOS velocity, azimuth, and inclination fields. We also select a single node for the height independent of microturbulence, macroturbulence and stray light factor. The number of free parameters is 18 in the SIR inversion. The physical quantities are the LOS velocity, magnetic strength, and inclination and azimuth angles in the LOS reference frame, as retrieved from the inversion. In total, we have inverted 86991 pixels with the SIR inversion application. The inclination and azimuth angles are transformed into a local reference frame (LRF). The SP data of AR 12546 was taken far from the disk center; for a detailed explanation method for solving the 180∘ degree ambiguity, see the review of Metcalf et al. (2006). In this case, the solution of the 180∘ degree ambiguity was converted by adopting the acute angle with the potential extrapolated field, where the azimuth angle obtained produces an acute angle between the extrapolated and inverted fields (Metcalf et al. 2006). As a result, the LOS inclination and corrected azimuth angles were converted into the LRF using the transformations described by Gary and Hagyard (1990).

Based on the LTE calculations, we used the SIR inversion with the observed profiles of Hinode SP data. We apply a single component atmosphere in depth dependent in a sunspot AR 12546. The physical quantities of vector magnetic field change with the depth in the line forming region. The single-component atmospheres allow for gradients in the physical parameters along the LOS (e.g., Bellot Rubio et al. 2002; Mathew et al. 2003; Borrero et al. 2004; Shaltout and Ichimoto 2015; Guglielmino et al. 2019, and references therein). Similar studies were performed using the single-component atmospheres (e.g., Westendorp Plaza et al. 1997, 2001a,b; Cuberes et al. 2005; Bellot Rubio and Suárez 2019). We analyze high-quality data observed by the Hinode SOT satellite, see the observed Stokes images in Fig. 1. All Stokes profiles (I, Q, U, and V) are normalized to the mean continuum quiet Sun intensity at each pixel in the field of view map. We compare the observed and synthetic profiles in the umbra, penumbra, and quiet Sun regions inside the sub-field of view (87″ × 103″). We show the results of the vector magnetic field calculated at the standard optical depth of \(\lambda =\) 500 nm, see the 3rd and 4th columns in Figs. 3, 4, and 5. The chosen inverted pixels are revealed in Fig. 1 (top-left) by red plus marks in the continuum intensity image. Some inverted pixels in the sunspot are presented in Figs. 3, 4, and 5 at the 1st and 2nd columns. For more details, Fig. 3 (1st and 2nd columns) displays the observed Stokes (gray line) and synthetic (solid line) profiles for the inverted pixel in the penumbra located at x = 206 and y = 177 in the sub-field of view region. The synthetic spectra show a better reproduction of the Stokes profiles; however, we obtain a reliable fitting in the linear polarization (Q and U) profiles. The Stokes V area asymmetry (\(\delta{a}\)) and NCP of spectral lines are fitted well in the calculated and observed values for the Fe I 6302.5 Å line, and, in fact, they are presented in Fig. 3 (top). The physical parameters for the field strength, temperature, field inclination in LRF and LOS velocity as a function of the optical depth are exhibited, as can be seen in Fig. 3 (3rd and 4th columns). For comparison, the vertical (dashed lines) in the physical parameters display the two chosen optical depths at log \(\tau = 0\) and at log \(\tau = -1.5\). The field strength (3rd column, bottom) decreases from a value of B ≃ 3100 G to B ≃ 1800 G in the deeper (log \(\tau = 0\)) and higher (log \(\tau = -1.5\)) layers, with a strong strength at the deep level, this result agrees with previous studies (Borrero and Solanki 2008; Shaltout and Ichimoto 2015). The temperature stratification is enhanced by (T ∼ 4.3–5.8 kK) from those layers (3rd column, top). The inclination field (4th column, bottom) is \(\gamma \sim \) 110∘–140∘ between the two optical depths. For the penumbra, the horizontal field is localized with a positive velocity in the deep layer (\(v_{LOS} \sim \) 5.0 km sec−1 and a negative velocity in the higher layer (\(v_{LOS} \sim \) 0.5 km sec−1) (see, 4th column, top). In general, the single-component inversion successfully matches the Stokes profiles, and it might be a more realistic representation of the magnetic configurations.

Fig. 3
figure 3

The first and the second columns represent the Stokes profiles in the pair of Fe I 6301.5 Å and 6302.5 Å lines for the observed (gray line) and synthetic (black line) spectral lines (IQUV) in the penumbra using a Hinode SP data for a pixel located at (x = 206 and y = 177). The third and fourth columns contain the physical parameters as a function of the standard optical depth for the magnetic strength, temperature, field inclination and LOS velocity in a sunspot penumbra. The vertical dashed lines in the physical parameters display the atmospheric heights at log \(\tau = 0\) and log \(\tau = -1.5\) in comparing between both optical depths. At the top of the plot, we show the Stokes V area asymmetry (\(\delta{a}\)) and NCP between the calculated and observed values of the Fe I line at 6302.5 Å. Also the vertical dashed lines in the Stokes profiles show the location of central wavelengths of the pair Fe I lines at 6301.5 Å and 6302.5 Å of a Hinode SP data

Full size image
Fig. 4
figure 4

Same as Fig. 3, but for a pixel in the quiet Sun located at x = 236 and y = 107

Full size image
Fig. 5
figure 5

Same as Fig. 3, but for a pixel in the umbra located at x = 164 and y = 168

Full size image

For a quiet Sun region, the inverted pixel is located at (x = 236 and y = 107) in the sub-field of view area. The synthetic (solid line) and observed (gray line) Stokes profiles are shown in Fig. 4 (1st and 2nd columns). The vector magnetic field (temperature, strength, inclination, and velocity) are also illustrated in the 3rd and 4th columns in Fig. 4. The noise level in Stokes (Q and U) profiles is \(\sigma = 4.5 \times \) 10−3 in units of Ic. The field inclination is about \(\gamma \simeq 60^{\circ }- 125^{\circ}\) (bottom panel, right side), showing a quite inclined field in the deep layers. The single-component atmosphere has a weak field strength of B ≃ (500–700 G) between the optical depths at log \(\tau = 0\) and log \(\tau = -1.5\). We find a blue-shifted velocity of \(V_{LOS} \simeq \) 2.5 km sec−1 in the deep photosphere, while in the higher layers, we detect a small blue-shifted velocity of \(V_{LOS} \simeq \) 1.0 km sec−1. The temperature structure is almost T ∼ 6000 K in the deep layers, while in the higher layers, the temperature is about T ∼ 5100 K. The physical quantities in the quiet Sun are given in Figs. 6 and 7, and it confirms the results of other studies (Orozco Suárez et al. 2007; Bellot Rubio and Suárez 2019). A consistent topology exists with previously obtained of MHD simulations (e.g., Danilovic et al. 2016; see Fig. 10 therein) in the quiet Sun. The inverted pixel in the umbra is located at (x = 164 and y = 168) position, as can be shown by (red plus mark) in the continuum intensity map (Fig. 1, top-left). The field strength in the deep photosphere (log \(\tau = 0\)) is nearly 3800 G, and the higher layer has a strength of about 3200 G, with the less inclined field of (\(\gamma \simeq 50^{\circ}\)) associated with blue- and red-shifted velocities of (\(V_{LOS} \simeq \) 1.0 km sec−1) in the two atmospheric layers. These results agree with that found by Cheung et al. (2010) in which they obtained horizontal fields contributed with a blue-shifted velocity of \(V_{LOS} = 1.0\text{ km}\) sec−1 in the photosphere. In the umbral part, the temperature stratification is about T = 3950 K in the deep layers, and it decreases with depth to be nearly (T = 3000 K) in the upper layers. The observed Stokes (I) profile in the umbral pixel clearly reveals strong magnetic signatures (left-upper). Interestingly, the initial guess of ME-like atmospheres in each pixel can reproduce various Stokes shapes, showing reliable fitting spectra with a single component inversion. The inverted profiles are seen in the 1st and 2nd columns in Figs. 3, 4, and 5.

Fig. 6
figure 6

The physical quantities deduced from the SIR inversion of AR 12546, observed on 2016 May 22 at 13:37:32-14:40:42 UT. Top: Maps of the temperature stratification (left) and magnetic field strength (right) for the continuum optical depth at the visible solar surface (log \(\tau = 0\)) for a sub-field of view area (87″ × 103″) in the quiet Sun, umbra and penumbra regions. Bottom: Maps of the field inclination (left) and LOS velocity (right), as retrieved from the inversion. For the velocity map, the red color indicates the red shift velocity and the blue color is for the blue shift velocity. The inclination angle is expressed in a local reference frame

Full size image
Fig. 7
figure 7

Same as Fig. 6, but for the continuum optical depth at higher layer (log \(\tau = -1.5\))

Full size image

In Figs. 6 and 7, we obtain the physical quantities of the vector magnetic field from the observed Stokes profiles in a positive polarity sunspot AR 12546. The inclination angle is converted to a local reference solar frame. We used the SIR inversion selecting the sub-field of view area (87″ × 103″) for this purpose, see the continuum intensity image in Fig. 1 (top-left). In particular, from top to bottom and from left to right, we present the maps of temperature, magnetic field strength, and inclination field in the local reference frame to the solar surface. All physical quantities are performed in the deep layer (at log \(\tau = 0\); Fig. 6) and higher layer (at log \(\tau = -1.5\); Fig. 7). We detect strong blue- and red-shifted velocities in the disk center-side and limb-side penumbrae, respectively. We notice a small temperature variation (T = 5800 K) in the penumbra, as revealed in the temperature map in Fig. 6 (top-left) at the optical depth of unity, which is basically consistent with analyses (e.g., Van Noort et al. 2013; Tiwari et al. 2015). The temperature map shows a rapid decrease with the depth (at log \(\tau = -1.5\); see Fig. 7), with temperature values basically between T = 4100–4350 K around the penumbra. The inclination topology exhibits the opposite polarity of magnetic fields to the adjacent region of the umbra, see Figs. 6 and 7 (bottom-left) as deduced from the two atmospheric layers at (log \(\tau = 0\)) and (log \(\tau = -1.5\)). The physical quantities explain the observed data in a satisfactory way, see the synthetic spectrum in the penumbra, umbra, and quiet Sun regions in Figs. 2, 3, and 4. Our results are consistent with the previous investigations (e.g., Kubo et al. 2008; Franz and Schlichenmaier 2009; Tiwari 2009, 2011; Tiwari et al. 2009; Venkatakrishnan and Tiwari 2009, 2010; Bharti et al. 2010; Katsukawa and Jurčák 2010; Borrero and Ichimoto 2011; Franz 2011; Riethmüller et al. 2013; Van Noort et al. 2013; Tiwari et al. 2013, 2015; Shaltout and Ichimoto 2015; Joshi et al. 2017; Okamoto and Sakurai 2018). The LOS velocity map shows a rapid decrease for the red-shifted velocities (at log \(\tau = -1.5\)) in the limb-side penumbra (Fig. 7, bottom-right), with small blue-shifted velocities in the disk center-side penumbra.

3.1.1 Vertical gradients

We study the vertical gradients of the temperature (\(\Delta T\)), magnetic field strength (\(\Delta B\)), inclination field (\(\Delta \gamma \)), and LOS velocity (\(\Delta V_{LOS}\)) in optical depths variations, as described by Joshi et al. 2017; Balthasar 2018; Murabito et al. 2019.

$$ (\frac{\Delta B}{\Delta \log \tau})_{a,b}=\frac{B(b)-B(a)}{b-a} $$
(3)

where \(a\) and \(b\) are the lower and upper optical depths used in the estimations. For other parameters, we apply the same method for the temperature, inclination field, and LOS velocity as usual:

$$ (\frac{\Delta T}{\Delta \log \tau})_{a,b}=\frac{T(b)-T(a)}{b-a} $$
(4)
$$ (\frac{\Delta \gamma}{\Delta \log \tau})_{a,b}= \frac{\gamma (b)-\gamma (a)}{b-a} $$
(5)
$$ (\frac{\Delta V_{LOS}}{\Delta \log \tau})_{a,b}= \frac{V_{LOS}(b)-V_{LOS}(a)}{b-a} $$
(6)

Figure 8 gives the vertical gradients of \(\Delta T\), \(\Delta B\), \(\Delta \gamma \), and \(\Delta V_{LOS}\) maps calculated at optical depths of \([a,b]=[\log \tau = 0.0, \log \tau = -1.5]\) in a sub-field of view area.

Fig. 8
figure 8

The vertical gradients of vector magnetic field are calculated at two optical depths of log \(\tau = 0.0\) and log \(\tau = -1.5\) for the sub-field of view area, this sunspot was observed on 22 May, 2016 by a Hinode SP-SOT. The physical quantities for the temperature (top, left), magnetic strength (top, right), field inclination in LRF (bottom, left) and LOS velocity (bottom, right)

Full size image

The magnetic field shows significant negative gradients in the penumbral regions, see Fig. 8 (2nd column, top). For comparison, we detect a negative gradient of \(\Delta B \sim -0.4\text{ G}\,\text{km}^{-1}\) in the umbral region. However, this study reveals negative gradients ranging from \(\Delta B \sim -0.5\) to −0.9 G km−1 in the penumbra. In fact, these results are consistent with Balthasar (2018). He estimated the penumbral gradients using the divergence-free condition and determined \(\Delta B \sim -0.5\text{ G}\,\text{km}^{-1}\) or even shallower. Balthasar (2018) also studied the magnetic gradient using different methods of formation height in the photosphere, whereas the gradient was calculated by \(\Delta B = -2 G\text{ km}^{-1}\) and \(\Delta B = -3 G\text{ km}^{-1}\). Adopting the Hinode SOT data, Joshi et al. (2017) have found a rough positive value of \((\Delta B/\Delta \log \tau )_{0.0,-0.9} = 150 G/\log \tau \), but, mainly, they have applied different formation heights with a value of \((\Delta B/\Delta \log \tau )_{-0.9,-2.5} = 100 G/\log \tau \). Balthasar and Gömöry (2008) studied the vertical gradient in the umbra of a \(\delta \)-sunspot, with those values were given by −2 G km−1 and −4.5 G km−1. Murabito et al. (2019) detected a magnetic gradient of 0.3 G km−1 using the spectral line of Ca II 8542 Å line. Joshi and Cruz Rodríguez (2018) studied the magnetic field gradient, with values of [\(\Delta B/ \log \tau = 100\)–270 G, 50–100 G], from the Ca II 8542 Å spectral line. Westendorp Plaza et al. (2001a) deduced larger values by \((\Delta B/\Delta z) = -1.5\) or −2.0 G km−1 in the umbral part of a sunspot; these values are much higher than the current estimate. In fact, our magnetic gradient is lower than that reported from other studies, but it is quite well with the value of Balthasar (2018) using the divergence-free condition.

Here we study the vertical gradient of inclination in this AR, see Fig. 8 (bottom-left). Our results show negative gradients in the limb-side penumbra, indicating that values are between \((\Delta \gamma /\Delta z) = -9 \times 10^{-3}\) deg km−1 to \(-3.5 \times 10^{-2}\) deg km−1. In particular, the inclination gradient in the disk center-side penumbra is \((\Delta \gamma /\Delta z)_{0.0,-1.5}= 0.2 - 1.5 \deg \text{ km}^{-1}\) (i.e., positive values). The umbral part reveals gradient in a range of \((\Delta \gamma /\Delta z) = -5 \times 10^{-3}\) deg km−1 and \(3 \times 10^{-3}\) deg km−1. Westendorp Plaza et al. (2001a) obtained a higher gradient of inclination, which was about \((\Delta \gamma /\Delta z) = - 6.4 \times 10^{-2}\) deg km−1 in the penumbra of a sunspot. In fact, their results were calculated at a height level of 100 km per decade of optical depth. On the other hand, Sánchez Almeida (1998) detected a positive gradient in the penumbra of \(3.8 \times 10^{-3}\) deg km−1 and \(2.4 \times 10^{-3}\) deg km−1. Our values are different from those reported by Sánchez Almeida (1998) and Westendorp Plaza et al. (2001a).

Interestingly, the vertical gradient of velocity exhibits smaller values \((\Delta V_{LOS}/\Delta \log \tau )_{0.0,-1.5}= -0.13\) to −0.30 km sec−1 in the limb-side penumbra and shows positive values \((\Delta V_{LOS}/\Delta \log \tau )_{0.0,-1.5}= 0.11\) to 0.29 km sec−1 in the disk center-side part. The positive and negative values take place in large patches in the two penumbral regions, see Fig. 8 (bottom-right). The gradient of velocity in umbral part is approximately \((\Delta V_{LOS}/\Delta \log \tau )_{0.0,-1.5}= -0.2\text{ km}\) sec−1. Joshi and Cruz Rodríguez (2018) found the velocity gradient of [\(V_{LOS}\) = 5–12, 0.5–1.5] km \(sec^{-1}\). We mainly obtain a positive temperature structure in the umbra, reaching up to \((\Delta T/\Delta \log \tau )_{0.0,-1.5}= 50\text{ K}\). However, the temperature in the penumbra is \((\Delta T/\Delta \log \tau )_{0.0,-1.5}= -130\text{ K}\) (i.e., a negative value). On the other hand, different results were obtained by Joshi and Cruz Rodríguez (2018); they have reported the temperature gradient by [\(\Delta T = 500\)–\(1500\text{ K}\), 200–\(500\text{ K}\)]. In the end, we report a new findings for the vertical gradient of magnetic field, inclination field, flow velocity, and temperature in the umbral and penumbral regions of a sunspot, supporting that the SIR inversion application for the AR 12546 gave reliable interpretations.

3.1.2 Asymmetries

The NCP and the Stokes V area asymmetry are interesting techniques to learn about the presence of gradients in the magnetic field and LOS velocity along the optical depth. Those techniques serve as a strong signature for the presence of discontinuities in the magnetic field and flow velocity along the LOS (Auer and Heasley 1978; Tritschler et al. 2007; Ichimoto et al. 2008; Beck 2011; Shaltout and Ichimoto 2015). The NCP and area asymmetry are significant indicators for estimating the vector magnetic field and LOS velocity in the line-forming region. In other words, we take into account those techniques for the consistency between the observed and calculated NCPs or \(\delta a\) measurements would lead to complete confidence in the vector magnetic field results, as returned from the SIR inversion. We present a relationship between the observed and calculated NCPs in the Fe I line at 6302.5 Å in all pixels in the sub-field of view region; this result is given in Fig. 9 (left panel).

Fig. 9
figure 9

Left: Scatter plot shows the relation between the observed and best-fit NCPs for the Fe I line at 6302.5 Å in a sub-field area. Right: Scatter plot reveals the relation between the observed and best-fit Stokes V area asymmetries (\(\delta a\)) in the Fe I line at 6302.5 Å. The best-fit NCP and \(\delta a\) values are calculated from the inverted Stokes V profiles. The solid line shows the linear fit between the scattered data

Full size image

We obtain a linear fit relation along all inverted pixels in the selected region, with a coefficient parameter of (a = 0.65). The majority of pixels (about 95\(\%\) of pixels) are fitted well using the inversion technique, and we also notice a small difference in magnitude between the observed and calculated NCPs in all pixels, meaning that the inversion scheme applied here is significant progress. This result is apparently reliable and provides new extensive detail about the vector magnetic field, thermal and LOS velocity derived. We also exhibit a relation between the observed and inverted \(\delta a\) in the Fe I line inversion, see Fig. 9 (right panel). It is obvious that the calculated or inverted NCP is perfectly correlated with the observed NCP in most pixels (or relatively in all pixels), leading to linear fit with a coefficient parameter of (a = 1.0). This result is consistent with Borrero et al. 2004; Beck 2011; Shaltout and Ichimoto 2015. A better correlation between the observed and calculated NCPs was obtained. We have obtained the magnetic properties above a sunspot AR 12546, the new result is the description of the vector magnetic field based on the \(\delta a\) and NCP properties.

3.1.3 3D Magnetic picture

Figures 6 and 7 present the magnetic field strengths (top-right panel) and inclination fields (bottom-left panel) resulting from the SIR inversion at two chosen optical depths (log \(\tau = 0\) and log \(\tau = -\)1.5) in the photosphere. To visualize the 3-D picture of a sunspot it depends on two physical quantities, e.g., field strength and inclination as corrected from the normal to the solar surface. The magnetic component (\(b_{z}\)) can be defined as usual \(b_{z} = B\) cos(\(\gamma \)), where the B is the magnetic field strength (in G), and \(\gamma \) is the inclination field (in degrees), as additional information for the next run. The \(b_{z}\) component can be used as an initial input for the Boocock and Tsiklauri (2019) code, namely, is “BooTsik.f90” for the potential calculator. This code has been designed to calculate the potential magnetic field by extrapolating the normal field using the Green function method, and then the magnetic field components can be obtained from the potential field. We finally obtain the magnetic field components (\(b_{x}\), \(b_{y}\), and \(b_{z}\)) for the possible magnetic configurations in the photosphere. We visualize the 3-D magnetic structure as normal to the photospheric surface with the IDL visualization routine “Boobox.pro”, also written by Boocock and Tsiklauri 2019. The three magnetic components were obtained from the previous step using the Fortran code.

Figure 10 shows the 3-D magnetic picture of the AR 12546 in two photospheric layers at \(\log\tau = 0\) (top) and \(\log\tau = -1.5\) (bottom). The previous successful scenarios of 3-D magnetic pictures have been suggested by Solanki and Montavon 1993; Westendorp Plaza et al. 1997; Thomas et al. 2002, in which they proposed an interlocking-comb or uncombed penumbral structures of the magnetic field. The penumbral components were given by intra-spine (weaker flux-tube field; Lites et al. 1993) and spine (stronger background field; Guglielmino et al. 2019) configurations. In this work, we present a 3-D structure of the magnetic field for the studied sunspot. The umbral fields are stacked in the vertical direction with strengths of up to 4 kG. The penumbra magnetic fields lie horizontally next to each other. The Evershed flow is highly correlated with strong magnetic field strength (i.e., mostly of 3200 G), with large red-shifted velocities of 10 km sec−1 in the deep layer of the limb-side penumbra. Also, the penumbra shows a strong correlation between the magnetic field strength and LOS velocity. Moreover, the inner part of the disk center-side penumbra leads to magnetic strength of about 3700 G and 8 km sec−1 (at log \(\tau = 0\)). The NCP pointed out the presence of physical gradients in the LOS velocity and magnetic field strength (e.g., Borrero et al. 2004; Ichimoto et al. 2008; Beck 2011; Shaltout and Ichimoto 2015), where the NCP has been contributed as the reason for the gradients along the physical parameters in line forming region.

Fig. 10
figure 10

Top: the 3-D picture of the magnetic field in the sunspot AR 12546 at the deep layer (\(\log\tau = 0.0\)), since the magnetic strength in the deep layer is found in Fig. 6 (top-right). Bottom: same as displayed in top panel but for the magnetic field at the higher layer (log \(\tau = -1.5\)), where the magnetic field in the higher layer is presented in Fig. 7 (top-right). The 3-D structure of the magnetic field shows the field lines above a sunspot AR 12546

Full size image

4 Discussion and Conclusions

We present the three-dimensional stratification of the magnetic field, inclination field, temperature, and plasma flow for a sunspot and its surrounding areas. This study is a depth-dependent inversion retrieved between the solar optical depths at log \(\tau =(0,-1.5)\). We obtained a coherent magnetic field topology in the deep layer (at log \(\tau = 0\)) and higher layer (at \(\log \tau = -1.5\)) by applying the SIR inversion for a sunspot AR 12546.

We present a spatial study for the Stokes V area asymmetry (\(\delta a\)) and net circular polarization (NCP) for the Fe I 6302.5 Å line, showing a reliable fitting between the observed and synthetic spectra in the selected area. In Fig. 9, the \(\delta a\) (right panel) and NCP (left panel) scatter plots exhibit quite well-fitted spectra, with significant confidence for the vector magnetic field calculated from the inversion. There exist opposite signs of \(\delta a\) in the penumbra, with a large positive area asymmetry in the limb-side penumbra. We also detected negative and positive \(\delta a\) in the disk center-side of the penumbra. Our results are confirmed by many investigations (e.g., Borrero and Solanki 2008; Tiwari et al. 2013; Van Noort et al. 2013; Shaltout and Ichimoto 2015; Tiwari et al. 2015; Siu-Tapia et al. 2019; Löptien et al. 2021).

For the present SIR inversion, we summarize the physical quantities of the vector magnetic field, temperature, and plasma velocity in the AR 12546 as follows:

  • We detect supersonic red-shifted velocities in a penumbra, where the vector magnetic fields are nearly inclined. The SIR inversion of the observed spectra reveals red-shifted velocities of 10 km sec−1 (at log \(\tau = 0\)), associated with strong magnetic strengths between 2–3.2 kG in the limb-side penumbra. The disk center-side penumbra also exhibits strong magnetic fields up to 3.7 kG at the inner penumbra (see Fig. 6 of the top-right panel), where the magnetic field vector changes its orientation to be less inclined, with blue-shifted velocities up to 8 km sec−1. At the higher layers (log \(\tau = -1.5\)), we find positive (red-shifted) and negative (blue-shifted) velocities of 5 km sec−1 in the penumbral regions, whereas the flow velocity is decreasing with the height in the photosphere.

  • In the deep layers, some places show a horizontal field, with even opposite polarity (\(\gamma > 90^{\circ}\)) in the penumbra. These places originally have strong red-shifted velocity in the photosphere (\(V_{LOS} = 10\text{ km}\) sec−1), and it agrees with analyses by Van Noort et al. 2013; Tiwari et al. 2013, 2015, and references therein. There are also some places near the border of penumbra being less inclined fields, which are most likely to be spine regions. On the other hand, the disk center-side penumbra is fully enhanced by less inclined fields (\(\gamma \leq 60^{\circ}\)), which are associated with blue-shifted velocities.

  • The magnetic fields of the penumbra show more intense fields, with strengths reaching 3200 G in the deep layers, except for the outer parts of the limb-side penumbra, where some patches have fields of about 1200 G. In higher layers, the magnetic field strength is weak compared to that of deep layers, which agrees with the analysis by Shaltout and Ichimoto 2015.

  • The temperature stratification in the penumbra is cooler than in the umbra parts, with a temperature reaching 5500 K in the deep layer of the photosphere. While the temperature in the higher layer is cooler compared to the deep layers, exhibiting a temperature of about 4600 K.

We derive the vertical gradients of the magnetic field strength, inclination field, temperature, and LOS velocity in the penumbral and umbral regions using two optical depths (at log \(\tau = 0.0\)) and (at log \(\tau = -1.5\)). We find a small difference in the penumbral temperature of −130 K, resulting from the two atmospheric layers. A magnetic gradient in the umbral region is about \(\Delta B \sim -0.4\text{ G}\,\text{km}^{-1}\). However, the penumbral regions have a higher magnetic gradient than the umbra; our analysis reveals a result of \(\Delta B \sim -0.5\) to −0.9 G km−1. The inclination gradient in the limb-side penumbra is in a range of \((\Delta \gamma /\Delta z) = -9 \times 10^{-3}\) deg km−1 to \(-3.5 \times 10^{-2}\) deg km−1. In particular, we detect a higher positive inclination gradient in the disk center-side penumbra \((\Delta \gamma /\Delta z)= 0.2 \text{--} 1.5 \deg \text{ km}^{-1}\). The umbral part reveals an inclination field gradient with a tabulated result of \((\Delta \gamma /\Delta z) = -5 \times 10^{-3}\) deg km−1 to \(3 \times 10^{-3}\) deg km−1. While the vertical gradient of velocity is \((\Delta V_{LOS}/\Delta \log \tau )= -0.13\) to −0.30 km sec−1 in the limb-side penumbra, and the disk center-side penumbra is enhanced by \((\Delta V_{LOS}/\Delta \log \tau )= 0.11\) to 0.29 km sec−1. The umbra gradient velocity is given by \((\Delta V_{LOS}/\Delta \log \tau )= -0.2\text{ km}\,\text{sec}^{-1}\). We report new findings for the vertical gradients in the umbral and penumbral regions in the photosphere.

The physical consequences are as follows: The magnetic field strength in the disk center-side penumbra is up to 3.7 kG, which is associated with a supersonic blue-shifted flow of (\(V_{LOS} = 8\text{ km}\,\text{sec}^{-1}\)) at the deep layer. We also detect a supersonic red-shifted velocity (with high concentration flows) arriving at 10 km sec−1 in the limb-side penumbra. On the other hand, we found the magnetic field strength is smaller in magnitude in the limb-side penumbra than that in the disk center-side, and its value is almost 3 kG at the inner limb-side. In the outer layer, the magnetic field strengths are between 2 to 2.8 kG, with an inclined field at the disk center-side and a vertical field at the limb-side penumbra. For the LOS velocity, we found high concentrations of blue-shifted and red-shifted velocities (5 km sec−1) in the disk center-side and limb-side, respectively. The result of a strong magnetic field in the penumbra (i.e., at the disk center-side) is possible with the presence of blue-shifted Evershed flows at the deep layer. The possible variations in field strength configurations in different penumbral regions indicate complex and dynamic magnetic field structures. The presence of blue-shifted Evershed flows in the deep photosphere points out the existence of a plasma motion associated with a sunspot magnetic field. The inclination gradient is positive at the inner part and negative in a few patches at the outer part of the penumbra. A concentration of negative inclination gradient \(( \Delta \gamma /\Delta z)\) in the limb-side penumbra was obtained.

We provide a 3-D picture of a sunspot from spectropolarimetric data of a Hinode spacecraft using a single component inversion. The sunspot penumbra displays a clear pattern of convective nature. We detect supersonic red-shifted velocities in the penumbra due to the high quality of spatial resolution of the Hinode satellite. Our results demonstrate that the NCP of sunspots is a significant indicator to extract the vector magnetic field in the photosphere. Further studies with a complex topology in sunspots light bridges and umbral dots using the Hinode SOT data are required.