Investigation of Sidewall and Reynolds Number Effects in a Ribbed Square Duct

Abstract

This paper presents a comprehensive three-dimensional Direct Numerical Simulation (DNS) investigation of flow characteristics over a roughened wall in a duct, exploring bulk Reynolds number variations from 4400 to 13,200 and considering the influence of side walls. Notably, a significant increase in friction factor highlights heightened resistance to flow due to surface roughness, emphasizing the importance of considering surface conditions in engineering applications. The study reveals three recirculation zones in the streamwise direction, indicating intricate separation phenomena caused by the interaction between the ribbed wall and the flow. Furthermore, the presence of sidewalls creates two major vortices perpendicular to the flow direction, highlighting the complexity of the vortical structures in this configuration, crucial for predicting flow behavior and optimizing system performance. The study demonstrates that the influence of the Reynolds number on these vortices is not well-scalable with respect to outer units, in contrast with respect to smooth ducts. Investigating side-wall effects, increased turbulent production rate, and non-equilibrium turbulence along the side walls highlight the sensitivity of turbulent stresses to Reynolds number and side-wall proximity. In conclusion, the paper provides novel insights into the interplay between Reynolds numbers, roughened surfaces, and boundary conditions in turbulent flows, laying a foundation for a deeper understanding of the flow in duct with high roughness.

1 Introduction

Surface roughness within internal flows has emerged as one of the most appealing topics in engineering applications, with broad-ranging implications spanning the mechanical, aerospace, and electronic industries. This phenomenon is present at different scales and fields, from nano-channels in electrical circuits to micro-channels in turbine blades and slightly larger cooling channels in rocket engines. While new manufacturing techniques have allowed designers to freely choose the channels’ shape and dimensions, they also have to deal with new challenges. Specifically, these techniques introduce high roughness to the internal channels, which significantly impacts the flow patterns and thermal exchanges with the fluid. Understanding these alterations becomes of paramount importance for localized phenomena that may jeopardize system reliability. Direct Numerical Simulation (DNS) offers a powerful tool to advance research in this context by providing precise assessments of all the properties at every point within the channel. Since roughness is usually a micro-scale phenomenon, the variations in the flow pattern are complicated to resolve within coarser frames, as RANS (Reynolds–Averaged–Navier–Stokes) simulations or in experiments, where the dimension of the measurement probes overcome the dimension of the phenomena.

Nevertheless, many experiments and simulations have been run for smooth circular or planar channels to characterize canonical flows. However, more complex geometries like ducts with square or rectangular sections are under scrutiny because of the many applications in which they are involved. Square ducts were first studied in Brundrett and Burroughs (1967) in which bulk Reynolds numbers $Re_b=Hu_b/\nu$ (with H being the hydraulic diameter, $u_b$ the bulk velocity and $\nu$ the kinematic viscosity) of 33.000 and 67.000 were considered: the resulting ratio between average friction factor and heat transfer coefficient appeared to be approximately the same as the one in circular pipes.

Since the well-known work from Kim et al. (1986), the available computational power rapidly increased, allowing the computation of more complex geometries or higher Reynolds numbers; relevant examples are the wall-bounded flows computed in Lee and Moser (2015) and Del Alamo (2004) with friction Reynolds number up to 4000 and 5000, and the pipe flow in Wu and Moin (2008) up to 1000, where the friction Reynolds number has been defined in terms of h, which is the channel half-height or the pipe radius, and the friction velocity $u_{\tau} =\sqrt{\tau _w/\rho }$.

Once the main features of canonical flows were understood, attention was paid on more complex dynamics and geometries: it has been known since the beginning of the last century that the presence of corners creates secondary motions, as presented by Prandtl (1926) and Nikuradse (1930), who explained that secondary motions are indicators of non-zero streamwise vorticity which in turns is caused by a Reynolds stress gradient near the corner (non-circular cross sections). In square ducts, the secondary motions are known to come in the form of eight counter-rotating vortices, which bring high-momentum flow from the core region to the corners, and low-velocity flow from the near wall region to the core flow and are characterized by an intensity in the order of 1–2% of the bulk velocity, Prandtl (1926). The experimental investigation in Brundrett and Baines (1964) found that the bulk Reynolds number does not affect secondary flows. However, other experiments in Gessner and Jones (1965) showed that the ratio of secondary eddies intensity over the bulk velocity decreases with increasing Reynolds number. Numerically, secondary flows can only be caught if all the walls are simulated through no-slip boundary conditions. The first DNS of a square duct is recalled to be the one from Gavrilakis (1992) using a bulk Reynolds number of 4410. Higher Reynolds numbers were studied in Vinuesa (2014), Zhu (2009), and more recently in Pirozzoli (2018), Modesti (2018), Zhang (2015). In particular, in Pirozzoli (2018), Modesti and Pirozzoli (2022), Pirozzoli and Modesti analyzed the relation between secondary flows and the bulk Reynolds number by creating a wide database of square duct flows, ranging from a Reynolds number of 4.400 to 84.000. They simulated a square duct using DNS and suggested a differentiation between a “core recirculation”, characterized by a velocity scale that is associated with the bulk velocity of the flow and a length scale with the half-channel height, and a “corner recirculation” whose velocity-scale is still similar to the bulk velocity but with a length-scale which matches the inner-wall scaling length. At low bulk Reynolds numbers, the two circulations coincide, whereas at higher Reynolds numbers, the corner circulation moves nearer and nearer to the duct corners, while the core circulation emerges in the bulk flow.

Rectangular ducts and the effect of the aspect ratio (AR) of the duct were investigated in Vinuesa (2014), Vinuesa (2016), where aspect ratios up to 7 have been simulated, showing the variations of flow statistics and recirculation zones with respect to the height of the channel. In Nasuti et al. (2021), a conjugate heat transfer problem was solved for a rectangular duct, and both the friction factor and the Nusselt number were compared against RANS simulations, focusing on the effect of thermal conductivity of the wall.

Furthermore, increasing interest is attracted from the effect of rough surfaces and how each rough element can alter the turbulence behavior, enhancing the momentum and heat transfer.

The geometry of a rough surface is difficult to simulate due to the high frequencies in the roughness profile, which are introduced by the scanning process, as explained in Busse et al. (2015); thus, discrete roughness elements are often employed in numerical simulations to recreate the roughness protrusions inside the boundary layer: for this scope, riblets, cubes, or cones are used. Many have been the efforts to characterize the effects of such discrete elements in terms of heat transfer enhancement and momentum loss. However, most of these works did not simulate the side walls and only applied periodic boundary conditions on the side of the duct, reducing the complexity of the simulation to a 2D case. A few examples are the simulations performed in Leonardi et al. (2007), Nagano et al. (2004), Orlandi et al. (2016), Jelly (2022), Miyake et al. (2000), Miyake et al. (2001). The results of these works highlight new recirculation zones between rough elements which bring to the enhancement of the diffusion mechanism from the wall to the core fluid region. In order to quantify the variation of the most important dimensionless numbers over rough surfaces, in Bons (2005), experimental data in a low-speed wind tunnel are gathered at various flow conditions and Reynolds numbers to propose a suitable “Reynolds analogy factor” to estimate the relative increase of friction factor with respect to heat transfer coefficient; they defined $RA = 2St/C_f$ and showed that the momentum transfer is more enhanced with respect to the heat transfer and that RA usually assumes values between 0.5 and 0.7.

To the author’s knowledge, the only works in which a ribbed wall is simulated in a duct with four walls is Mahmoodi-Jezeh and Wang (2020): Mahmoodi-Jezeh and Wang simulated the same square duct three times, with different riblet dimensions, showing how the statistics of the flow vary with varying blockage ratio (BR) and how this influences the recirculation between riblets. Their simulations were run with an incompressible fluid and a constant bulk Reynolds number equal to 5600; their analysis pointed out a significant increment in the secondary turbulent motions, leading to an augmentation of the stresses near the rib crest, whose intensity is increasing along with the blockage ratio. They also presented the same case with heat transfer, Mahmoodi-Jezeh and Wang (2021) highlighting the effects of riblets on the flow development and the local increase of the Nusselt number up to 5 times more with respect to the smooth case. However, a major understanding of the effects of the interaction between the riblets and the side walls is missing, and although the influence of the Reynolds number has been thoroughly investigated for turbulent flows in smooth ducts, its influence on these newly generated vortices has never been unveiled before, and major phenomena dealing with the transport of matter and energy have to be quantified once again accounting for more complex wall geometries. Indeed, if for smooth wall ducts, it is well-known that the turbulent structures are not subject to significant variations, Pirozzoli (2018), this might not be true when the geometry becomes more complex and the interaction between walls is stronger.

In this work, a similar setup to the one implemented in Mahmoodi-Jezeh and Wang (2020) is used: an incompressible fluid is simulated through DNS in a square duct with transversal riblets on one wall, and the bulk Reynolds number is varied from 4400 to 13200.

In the next section, a more detailed overview of the numerical frame that has been employed is given, with information about the dimension of the simulated domain, the solver, the mesh, and other essential settings of the simulation setup. In Sect. 3, our results are presented: new recirculation zones have been found with respect to the smooth case, in streamwise and cross-flow direction, which arise due to the presence of the rough elements. Their intensity is found to be in the order of the 10% of the bulk velocity, thus, one order of magnitude larger than the corner-vortices characteristic of smooth ducts. Besides, their intensity and extension appear dependent on the Reynolds number when moving near the side walls, contrary to the smooth-walls case. The influence of the bulk Reynolds number is also visible on the vorticity and the statistics of the flow when both inner and outer scaling of the flow are used. Lastly, we compare a convergence index for the ribbed wall simulation and the smooth case, discovering a faster convergence of the ribbed case due to the stronger intensity of the vortices. In Sect. 4, we conclude our analysis with a summary of the results and an outlook on the potential development of this research.

2 Numerical Procedure

2.1 Numerical Setup

Each test case has been solved with the EBI (Engler-Bunte-Institut)-DNS code, Zirwes (2018), Zirwes (2019), Zirwes (2021), based on the open-source code OpenFOAM, Weller (1998), which solves the conservation equations for mass and momentum using a finite volume method (FVM). The code was initially developed for turbulent reacting flows, thus, the reaction mechanism has been shut off, and the coolant inside the duct has been simulated as a non-reactive fluid. The same solver has already been widely used in previous works of our research group to simulate turbulent combustion flows Martinez-Sanchis (2022), Martinez-Sanchis (2022), Martinez-Sanchis (2023), Sternin (2022). In addition, we inserted a switch in the code such that the reaction mechanism can easily be activated again to study cracking of methane and pyrolysis phenomena (Fuqiang 2018), which will be the focus of future works.

The continuity and the momentum equation are solved as reported in Eq. (1).

$$\begin{aligned} \frac{\partial u_i}{\partial x_i} = 0 \ \ ;\ \ \ \ \ \ \ \ \frac{\partial u_i}{\partial t}+\frac{\partial u_i u_j }{\partial x_j} = -\frac{1}{\rho } \frac{\partial p}{\partial x_j}+\frac{\partial ^2 u_i }{\partial x_j \partial x_j} + \Gamma \end{aligned}$$

(1)

In this work, we will use u, v and w for the velocity vector components, $\rho$ for the density, and p for the pressure; The equations are solved in OpenFOAM using the well-known PIMPLE algorithm with two correctors and two outer-correctors loops. The numerical algorithm is based on the finite-volume method, in which a second-order accuracy is achieved concerning spatial and temporal discretizations. The discretized equations are iteratively solved until the residuals drop below $10^{-6}$, the Courant number never exceeds 0.9, and the timestep is automatically adjusted at every iteration based on the maximum allowed Courant number. For more information on the solver, see Zirwes (2021). Regarding the simulation setup, periodicity has been imposed between the inlet and outlet, and the term $\Gamma$ is a time-varying pressure-gradient, which is added to the momentum equation to compensate for friction so that the volume-averaged streamwise velocity in the whole computational domain reaches the desired mean velocity, $u_b = 1/A \int u \ dA$. As mentioned, the objective of the simulations is to study the interaction of the walls and the riblets with the fluid; thus, all the sides of the domain are simulated through no-slip boundary conditions. The velocity field has been initialized with a uniform streamwise velocity component, and artificial turbulence has been used to assign values to the wall-normal and spanwise velocity components. This artificial turbulence model has been developed in our research group and presented in detail in Martinez-Sanchis (2021); it elaborates the strategy proposed by in Shur (2014), with a superposition of randomized harmonics following a reference spectrum as initially proposed by Kraichnan (1970), so that the synthetically generated velocity field respects the statistics of a generic turbulent flow. More details on the statistical description of the harmonics and their validation are given in Martinez-Sanchis (2021) and further used in Martinez-Sanchis (2022), Martinez-Sanchis (2023), Martinez-Sanchis (2022), Sternin (2022). This artificial turbulence is imposed in the all domain, only at the first time step of the simulation to allow a faster transition to a fully turbulent flow; then, the velocity field develops for 200 convective times ($T_a = h/u_b$) as suggested in Vinuesa (2016). As explained in more detail in Sect. 3, duct simulations require extremely long averaging time to converge properly and correctly capture the flow statistics and the secondary flows, which have weak intensities. Once the averaging interval is selected, the time average is evaluated using Reynolds averaging, which will be indicated with the overbar, $\bar{(\cdot )}$; the Reynolds average is defined as $\overline{q}=\left( 1/t_{end}\right) \int _{0}^{t_{end}}q\left( t\right) dt$.

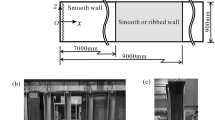
To facilitate understanding of the turbulence pattern and allow comparison with previous studies, the fluid is considered incompressible and has uniform properties (density and viscosity). The simulated domain is shown in Fig. 1.

Fig. 1

The contour of a generic instantaneous velocity field is presented along with the simulated domain and the relevant dimensions

A square channel is considered with the short sides of length 2h, and length of 20h, where h is the half-duct height. The riblets are placed only on one wall, from now on referred to as “bottom wall”; they are squared with side k equal to 0.2h and spacing w equal to 1.8h between each other, resulting in a repetition of the same geometry with a period of 2h. The length of the channel had to be chosen such that typical large-scale turbulent structures of the flow are properly captured; accordingly to previous studies, which undertook iterative procedures to understand how much space is needed to fully develop the flow, a length of $4\pi h$ is enough and was used in Mahmoodi-Jezeh and Wang (2020), Mahmoodi-Jezeh and Wang (2021), Pinelli (2010), while $6\pi h$ was utilized in Pirozzoli (2018), 25h in Vinuesa (2014), similarly to what was done in Gavrilakis (1992). Thus, the length we chose is considered enough.

In addition, to confirm this choice, the streamwise two-point correlation $R_{uu}$ is computed: due to the complexity of the flow in a ribbed duct, the usual approach through fast Fourier transform is not applicable. Consequently, we use the two-point auto-correlation coefficient as defined in Eq. (2), and previously used in Mahmoodi-Jezeh and Wang (2020) Violino et al. (2009), Townsend (1980).

$$\begin{aligned} R_{uu}(x_{ref}, \Delta x) = \frac{\overline{u'(x_{ref})u'(x_{ref}+\Delta x) } }{\sqrt{ \overline{u'^2(x_{ref})} \ \ \overline{u'^2(x_{ref}+\Delta x)} }} \end{aligned}$$

(2)

Where the notation $(\cdot )'$ stands for the instantaneous fluctuation of a certain quantity with respect to its time-averaged value. The correlation has been evaluated considering the vertical center line of the section at the center of the domain, namely $x = 10\,h$ and $z=0$. Different points along this line have been taken as reference points for evaluating the streamwise two-point autocorrelation. Results are shown on the left in Fig. 2. The value of $R_{uu}$ drops to values close to 0 in a portion of the domain, which is less than a quarter of the total length of the domain. This allows us to state that the domain is long enough to let the turbulent structures develop completely, and, at the same time, we can defend that the remaining part of the domain is not in excess: indeed the longer the domain, the faster the statistics will converge, as pointed out in Vinuesa (2016), where the “normalized eddy turnover time” is introduced to take into account also the length of the control-box when comparing different simulations and different convergence criteria.

The dimension of the mesh cells has been decided based on the results we got from precursor simulations presented in Santese (2023); due to the complex geometry and the strong ejection of fluid resulting when hitting on the riblets, a uniform mesh has been preferred; as investigated in Moser and Moin (1987), the cell size has to be of the same order of the Kolmogorov length, $\eta =\left( \frac{\nu ^3}{\varepsilon }\right) ^{0.25}$, with $\epsilon = \nu (\partial u_i' /\partial x_j \partial u_i' /\partial x_j)$ being the dissipation rate, Pope (2000). The ratio between the resolution and the Kolmogorov scale is shown on the right of Fig. 2, on a $y-z$ plane located at $x/h = 0.625$; it is visible that the ratio never exceeds a value of 4, and assumes its highest values near the crest of the riblet, where the flow is shed in small vortices. The same analysis has been carried out at different streamwise positions of the domain, pointing out that the ratio under scrutiny never exceeds the value of 4.

Fig. 2

Streamwise two-point autocorrelation for the smooth (solid-line) and the ribbed (dashed-line) duct simulation (on the left); the contour of the ratio between resolution and Kolmogorov scale, at $x/h = 0.625$

In total four simulations have been run within the same square duct: one simulation has four smooth walls and has been used for validation and comparison purposes; the other three present a ribbed wall, whose geometry is kept constant along the three runs, while the bulk Reynolds number has been varied; more details on the mesh used, the Reynolds number, the convergence indicators, and the Kolmogorov length are provided in Table 1 for each simulation. The validation of the solver is provided in Appendix 1.

Table 1 Simulations data: $N_x,N_y,N_z$ are the number of cells in each direction, $\varepsilon _p$ is defined in Eq. (4), $\eta$ is the Kolmogorov length, while $\Delta x$ is the resolution and the $()^*$ stands for global wall units; $t_s$ is the simulation time

3 Results

3.1 Velocity Field and Drag Coefficient

The main objective of this chapter is to highlight the features that characterize the flow, with particular attention to the effects of the side walls, the influence of the bulk Reynolds number, and the comparison between a smooth wall and a wall with transverse riblets.

Figure 3 presents the flow pattern in the region between two riblets: the section is taken at $z=0$ and shows the contour of the velocity magnitude underneath the streamlines of the flow. Between the two riblets, three major recirculation regions can be distinguished: a bigger bubble is evident after the riblet, whose center of rotation is called “A”, and two smaller vortices are created in the corners right after the first riblet and right before the following riblet, with centers of rotation respectively “B” and “C”. The cascade of smaller vortices generated by the interaction of these larger recirculations is not presented here due to the resolution of the contour-lines. After the big recirculation zone, the flow re-attaches on the bottom of the channel, as it happens for k-type roughness, Leonardi et al. (2007), and then starts rotating in the smaller vortex before the next riblet.

Fig. 3

Recirculation region in the middle of two consecutive riblets: contour of the ratio between the velocity magnitude and the bulk velocity, and superposition of streamlines for simulation R1. Points “A–B–C” highlight the center of the recirculations

The results are very similar to what has been found in Mahmoodi-Jezeh and Wang (2020), where the recirculation zones for different riblet heights have been investigated. In this work, instead, we find that the position of the three vortices does not change with respect to the Reynolds number, being the centers of rotation “A”, “B”, and “C” always in the same position, thus depending only on the geometry dimensions of the roughness elements.

Although it has not been found any influence of the Reynolds number on the shape of these vortices, which develop in a streamwise direction between the riblets, the Q-criterion has been used to visualize the effects of the riblet on the vortical structures that form those recirculations. More detailed on the Q-criterion are given in Appendix 1, while the results are presented in Fig. 4.

Fig. 4

Visualization of the vertical structures near a riblet, for simulations R1, R2 and R3, from “a” to “c”. Isosurfaces of the scalar Q with increasing value from grey to red

In Fig. 4 it is evident that the position of the three vortices already identified in Fig. 3 stays the same when increasing the bulk Reynolds number; however, the same recirculation area is dominated by smaller and smaller vortical structures, generated by the shredding of the flow when it impacts on the riblet.

As well explained in Jimenez (2004), the blockage ratio $k/\delta$, where k is the height of the rough element and $\delta$ the diameter of the channel, has profound importance in differentiating the flow over rough surfaces and the flow over obstacles. Indeed, this ratio measures the influence of the roughness on the logarithmic layer. It is suggested that ratios of $\delta /k$ higher than 40 should be considered in order to retrieve any similarity of the near-wall flow with canonical flows.

However, the same riblet dimension has been used in Leonardi (2003), Leonardi (2004), Leonardi et al. (2007), and the authors found that the similarity law of the dimensionless velocity profile was respected: indeed, accounting for the expected shift of the velocity profile, the slope of the logarithmic layer is still preserved. In order to assess if our simulations can still be addressed as flow over rough surfaces, the velocity profile is presented in Fig. 5a. In the figure, the quantities are made dimensionless with respect to wall units, namely the friction velocity $u_{\tau}$ and wall scale $l^+ = \nu /u_{\tau}$. Figure 5a shows that the logarithmic region can still be found, and the results agree well with previous works.

Fig. 5

a Non-dimensional velocity profile for simulation R1, R2 and R3 and results from Leonardi (2004), at different w/k ratios. Dashed lines are $u^+ = 1/0.41 \ln y^+ + C$, with C being 2.9, $-$6.2, $-$7.7, -11. b Roughness function $\Delta U^+$ against the roughness Reynolds number $k^+$, and compared with results from Leonardi et al. (2007)

Additionally, the roughness function $\Delta U^+$ is presented in Fig. 5b, again compared with the results from Leonardi et al. (2007). The results are presented as a function of the roughness Reynolds number $k^+ = k u_{\tau} / \nu$, characteristic for non-smooth wall flows, and are reasonably close to the results from the simulations from Leonardi et al. (2007), especially the ones with the same w/k ratio. However, the side walls simulated in our work increase the calculated friction velocity, leading to higher roughness numbers, with respect to the work from Leonardi et al. (2007), where a similar bulk Reynolds number range was simulated, however, periodicity was implemented on the sides of the simulated domain.

It is important to underline that the friction velocity is evaluated following the approach used by in Leonardi (2003), defining $u_{\tau} = (\bar{P_d} + \bar{C_f})^{0.5}$, where $\bar{P_d}$ stands for the pressure drag while $\bar{C_f}$ is the skin friction drag. It is found that for a duct with riblets on one wall, the skin friction drag can be evaluated as $1/w \int _w 1/Re_b^{-1} (\partial \bar{u}/\partial y)_{y=0} dx$, being w the distance between two riblets. The pressure drag instead, in case of periodicity in x and constant mass flow can be derived as $1/w \int _w 1/Re_b^{-1} (\partial \bar{u}/\partial y)_{y=k} dx -1/w \int _w (\overline{uv})_{y=k} dx -1/w \int _w 1/Re_b^{-1} (\partial \bar{u}/\partial y)_{y=0} dx$, Leonardi (2003).

Moving back to the recirculation zones presented in Fig. 3, if the averaged dimension of the streamwise vortices does not change with respect to Re, a significant impact has been detected on the secondary flows visible on the plane perpendicular to the direction of the flow. Figure 6 presents the contour of the cross-flow velocity magnitude divided by the bulk velocity, $\sqrt{\overline{v}^2 + \overline{w}^2}/u_b$, for the simulations R1 and R3 on the left, namely the lowest and highest Re of this work, and the same representation is given on the right for two simulations taken from the work in Pirozzoli (2018), with bulk Reynolds number equal to 4410 and 17800.

The presence of the riblets causes the flow to start recirculating, and the vortex occupies the entire channel, as pointed out by the arrows, which represent the direction of the in-plane velocity vectors. When varying the bulk Reynolds number, it becomes evident that the cross-flow velocity near the walls experiences a pronounced augmentation, even when scaled by the bulk velocity. This is particularly evident close to the top wall, the sidewall, and the bottom corners.

Fig. 6

Contour of the dimensionless cross-velocity magnitude, $\sqrt{\overline{v}^2 + \overline{w}^2}/u_b$, with superimposed arrows presenting the in-plane velocity vector, on the plane perpendicular to the flow direction and passing through the vortex-center “A” for a simulations R1, for $z/h <0$, and R3, for $z/h >0$, b smooth square duct flow from Pirozzoli (2018), at $Re_b = 4410$ for $z/h <0$ and $Re_b = 17800$ for $z/h >0$

It can be seen in Fig. 6a, that these currents become more robust with the increase of the Reynolds number. The most affected region of the duct is the side wall, where the current intensifies from a value of approximately 8% to the 15% when increasing the Reynolds number from 4400 to 13200. Furthermore, the typical secondary flows observed within smooth duct flows, manifesting as two counter-rotating vortices near the corners, are presented in the same figure at a similar Re for comparison. The symmetric rotating structures observed in Fig. 6b, are not observable in the simulations run in the frame of the current work, where riblets are added on the bottom wall. This relative absence can be attributed to their average intensity, which typically hovers around 1–3% of the bulk velocity, as presented for two Reynolds numbers in Fig. 6b. In contrast, the vortices generated by the presence of riblets are remarkably stronger, with a strength which is one order of magnitude greater than those in the smooth case, as can be seen from the dark red regions of Fig. 6a, where the cross-flow velocity reaches a value of 16% of the bulk velocity for the highest Reynolds number case. Consequently, the conventional secondary flows originating near the corners are only partially discernible near the smooth top wall. They are destroyed and replaced by bigger vortices near the ribbed wall.

This finding underscores the growing significance of investigating rough surfaces. Traditionally, corner vortices have been recognized for their ability to transfer momentum from the core flow to the corners. Therefore, the emergence of these new flow patterns resulting from rough elements necessitates thorough exploration. Furthermore, such new features were never presented before as a function of the Reynolds number: a similar analysis was conducted in Mahmoodi-Jezeh and Wang (2020), in which the vorticity was found to decrease with an increasing blockage ratio. However, the dependence on the Reynolds number points out that these new secondary flows might be crucial in applications with very high Re.

Figure 7 shows the vertical component of the velocity vector, scaled with respect to the bulk velocity, on the plane passing through the vortex-center, denoted “A” in Fig. 3, and in two spanwise positions, $z/h = -0.95$ to depict the “near-side-wall” behavior, and $z/h =-0.5$ to show the transition from the wall towards a region where the core flow is dominating. These spanwise positions will be recurrent in the rest of the paper to present the effects of the interaction with both the ribbed and the side walls. Additionally, the same quantities from the smooth simulations in Pirozzoli (2018) are presented for comparison.

Fig. 7

Vertical velocity component for different Reynolds number along the vertical direction, on the plane passing through $x/h = 0.625$ and for spanwise position, a $z/h = -0.5$ and b $z/h = -0.95$. The smooth case results from Pirozzoli (2018) are overimposed for comparison

In Fig. 7a, the vertical component of the velocity vector is shown at $z/h = -0.5$; the side wall effects are far away, and the profiles seem to collapse in the center part of the duct, in particular for $-0.5<y/h<0.5$, where the Reynolds number does not affect significantly the flow. However, near the top and bottom wall, the profiles are not aligning anymore and present peaks on both ends, whose magnitudes are decreasing with the increase in Re. This happens because the core flow gets bigger and stronger with increasing Re, pushes all the side effects closer and closer to the walls, and is less influenced by their presence. Additionally, when comparing with the smooth results, it can be understood that the presence of the riblet augments the peak close to the ribbed wall while the peak close to the top wall resembles the same behavior of the smooth simulations, however, with a more pronounced Re dependence.

In Fig. 7b, the same quantity is presented for all three simulations at $z/h = -0.95$, where the side-wall effects are dominant: indeed, the profiles look unaffected by the Reynolds number for $y/h <-0.5$, where the geometry of the riblet is the dominant criteria and decides the location and the intensity of the recirculation region, Mahmoodi-Jezeh and Wang (2020), while the profiles look consistently influenced by the Re for $y/h >0.5$. It can be appreciated that the intense vortex that was already visible in Fig. 6a, becomes significantly more powerful as the Reynolds number is increased. We take this chance to underline the magnitude of this quantity, which fluctuates between the 2% and the 4% of the bulk velocity near the core region and reaches peaks of more than 15% when analyzed close to the side-wall; further, this high value is not a local event but is maintained throughout the entire height of the duct. In contrast, in smooth ducts, the vertical and spanwise components of the velocity only assume value in the order of the 2% near the corners, and lower values everywhere else, as well documented presented by the dotted lines in Fig. 7b, whose values look negligible with respect to the fluctuations that are present in the ribbed wall simulations.

These newly discovered motions may play a determining role in applications where mass transfer is relevant since they will enhance the mixing processes in the cross-section of the duct.

The focus is now moved to evaluating the effects of these recirculations on bulk properties, such as the skin friction coefficient, which is often used as a design parameter in engineering applications. Figure 8 presents the riblet’s effect on the flow’s frictional behavior. The local skin friction coefficient will now be evaluated based on the local wall shear stress, as $C_f = 2 \tau _w / \rho u_b^2$ where $\tau _w = \mu ( \frac{du}{dy}|_{wall}^2 + \frac{dw}{dy}|_{wall}^2)^{0.5}$.

Fig. 8

Skin friction coefficient $C_f$, presented on the bottom wall of the ribbed duct (left), and on the smooth side wall of the duct (right)

With respect to a smooth duct, the distribution of the friction coefficient is remarkably non-uniform and depends on the periodical repetition of the riblets; besides, very different behaviors are found on the bottom wall and the side wall; the two walls have indeed been affected differently by the recirculation of the flow. In a smooth duct instead, the skin friction coefficient appears uniform in the streamwise direction and only dependent on the distance from the side wall; in a square duct, any side would present the same distribution, as documented in Agrawal et al. (2022)

For what concerns the bottom wall, in Fig. 8a, a direct connection between the recirculation regions created by the presence of the riblet and the area where the friction coefficient is more significant is evident; comparing Figs. 3 and  8a, the skin friction coefficient appears to be larger where a vortex is distinguished, which is in agreement with what was found in Casarsa and Arts (2005), where the authors conducted an experimental study of turbulent flow in a square duct with square ribs and a high blockage ratio, mounted on one wall in a wind tunnel. The behavior of the $C_f$ in Fig. 8 shows the main feature of k-type roughness, with a flow detachment after the riblet, which causes a low friction region and then the reattachment of the flow in a later stage. Considering the side wall, the in-plane recirculation presented in Fig. 6a is accelerating the flow near the side walls, which then experience a significant increase in friction coefficient close to the riblet, as presented in Fig. 8b.

By adjusting the dimensions and the position of the riblets, it is possible to take advantage of the region between the vortices, which experiences a lower friction coefficient, and obtain surfaces that minimize the overall drag increase, which is due to the riblets themselves, as summarized in Soleimani and Eckels (2021), where a deeper analysis on the influence of the riblet dimensions is carried out, underlining how significant the influence of rough elements can be on the overall friction behavior.

Lastly, an overall friction coefficient has been evaluated, averaging over the surface area of all the duct walls. The resulting trend is presented in Fig. 9, against the Dean-law for smooth pipes, Dean (1978), which has been widely used for comparison with square and rectangular ducts as well, Nasuti et al. (2021), with a simple adaptation of the hydraulic diameter. A general increase in friction factor has been found as expected, with the ribbed simulation having a skin coefficient almost double the predicted one for smooth pipes, in particular a $+61\%$, $+47\%$ and $+42\%$ has been evaluated with respect to the Dean’s law.

Fig. 9

Skin friction coefficient $C_f$ evaluation in the present work against the empirical law from Dean Dean (1978), for smooth pipes

3.2 Vorticity

In this section, it is presented the behavior of the streamwise vorticity, that in our reference system, defined in Fig. 1, is defined as $\overline{\omega _x} = \partial \overline{v} / \partial z - \partial \overline{w} / \partial y$. In order to conduct a thorough comparison with respect to the smooth case, we first recall some features of the vorticity structures in square smooth ducts. As explained in Brundrett and Baines (1964), the time-averaged secondary motions consist of eight eddies with obvious symmetry properties, which redistribute the momentum excess from the duct core towards the corners. When scaled in outer units ($u_b$ and h), the vortices do not show any dependence on the Reynolds number, as presented by Pirozzoli et al. in Pirozzoli (2018), with a range of Reynolds number which spans from 4410 to 40,000. For what concerns the vorticity instead, its behavior looks more complex than the streamlined contours, as explained in Pinelli (2010); already at a low Reynolds number, a negative vorticity patch appears in the duct core, while a positive vortex emerges near the corner as a result of the rebound near the wall due to the no-slip boundary condition, Orlandi (1990). As the Reynolds number is increased, the “corner-vorticity” becomes stronger and progressively more confined near the corner, while the “core-vorticity”, which scales well in outer units, stays at roughly constant value. In a recent work, Pirozzoli (2018), investigated the behavior of the more interesting corner-vorticity and demonstrated that a mixed scale approach, using $u_b$ and $l^*$, with $l^* = \nu /u_{\tau} ^*$ and the $(-)^*$ meaning global wall units, yields a good collapse of the vorticity profiles at different Reynolds number; this proved that, when expressed in outer units, the associated motions become progressively confined to the duct corners as the Reynolds number increases and their strength increases.

We can now focus on what happens in the case of a ribbed wall; Fig. 10a shows the streamwise vorticity distribution in the case of the three different Reynolds numbers.

Fig. 10

a Contour lines of the streamwise vorticity $\overline{\omega }_x/(u_b/h)$, black for R1, red for R2 and blue for R3. Contours are shown for $-5.5<\overline{\omega }_x/(u_b/h)<4.5$. For every simulation, the quarter of the domain in $-1< z/h <0$ and $-0.5<y/h < 0$ has been analyzed. b Vertical values of the streamwise vorticity at $z/h = -0.5$ (red lines) and $z/h = -0.95$ (black lines)

The contour lines are presented in the duct section passing through the biggest vortex previously identified with the letter “A”, and the vorticity values are made dimensionless with respect to outer units. In all the ribbed wall simulations, a positive vorticity peak is visible in the duct core, near the wall, and a negative peak right above it, approximately in the region of $-0.5< z/h < 0.5$; however, the positive peak appears to become stronger and stronger with the increase of the Reynolds number, while the negative peak stays more or less unchanged in strength but elongates to the center of the duct as the Reynolds number increases. This vorticity, which can be seen as the “core-vorticity” of the smooth duct, is caused by the wide recirculation bubble which is found right after the riblet, presented in Fig. 3, whose shape looks unaffected by the Reynolds number. This is also visible in Fig. 10b, in which the $\overline{\omega _x}$ profiles are presented as a function of the vertical coordinate y, in two spanwise positions: red lines are taken in $z/h = -0.5$ and show that the core vorticity behavior is sensible to the Reynolds number only very close to the wall, where the positive vorticity peak becomes stronger as Re is increased; when moving further from the wall the three simulations immediately collapse. Thus, it looks clear that apart from a difference in magnitude of the first peak, the peak’s position and shape do not significantly change with the Reynolds number, proving satisfactory scaling in outer units.

For what concerns the corner vorticity, in Fig. 10a, it consists of a large positive peak near the corner, sided by two stronger negative peaks close to the nearby walls. Differently from what has been found in Pirozzoli (2018) for smooth ducts, the corner vorticity looks roughly unaffected in shape and position by the Reynolds number when expressed in outer units. However, the scaling is still not perfect: also, the vortex near the side wall stretches with increasing Reynolds number, and the intensity of the vortices increases, as shown in Fig. 10b, where the $\overline{\omega _x}$ profiles are presented very close the side walls, at $z/h = -0.95$ (black lines). Comparing red and black lines, the Reynolds number influence looks heavier near the side wall because both the negative and the positive vorticity peaks of the black lines present a stronger magnitude as Re is increased; the curves collapse again altogether when moving sufficiently far away from the ribbed wall, $y/h>-0.5$.

To verify that the outer scale is the best scaling for such simulations, the mixed scale approach suggested in Pirozzoli (2018) is presented in Fig. 11.

Fig. 11

a Contour lines of the streamwise vorticity $\overline{\omega }_x/(u_b/l^*)$, black for R1, red for R2 and blue for R3. Contours are shown for $-0.02<\overline{\omega }_x/(u_b/l^*)<0.016$ (labels are multiplied by $10^3$). The same corner close to the bottom wall has been analyzed for every simulation. b Vertical values of the streamwise vorticity at $z^* = 120$ (red lines) and $z^* = 25$ (black lines)

The same representation is used, with a contour on the left presenting the vorticity distribution for the three simulations with different Reynolds numbers. The global wall units indicated with $(-)^*$ have been calculated from the global friction velocity, $u_{\tau} ^* = h \Gamma /2$. On the right of the image, vertical profiles are presented for spanwise positions at $z^*=25$ (black lines) and $z^*=120$ (red lines).

Although the approximate shape of the vortices is well presented also in mixed units, a more sensible variation is visible for the intensity and for the location of the maxima; the peaks of both the core and the corner vorticity flatten with respect to the Reynolds number, which is the opposite of what happens in outer units, and additionally, the vortex in the corner influences a wider and wider area with increasing Re which does not seem to be the case when looking at the vortices in Fig. 10a. Additionally, even though we have not performed a simulation with a Re as high as the highest in the work from Pirozzoli (2018), namely around 40,000, our three simulations present a Re very close to the first three simulations performed in that work; nonetheless, the enlargement of the vortices when presented in mixed units, was not visible in the work from in Pirozzoli (2018), and the simulations with the same Reynolds number as ours, presented almost perfectly collapsing vorticity contours.

The authors believe that this does not happen in a ribbed wall duct, because the $l*$ scales with respect to the Reynolds number much faster than the streamwise vorticity; thus, scaling with respect to outer units suits better the data of a ribbed channel since the increased intensity of the vortices is in this case comparable to bulk quantities.

Going back to what has been discovered in Fig. 10 and investigate the increase of vorticity magnitude on the near-side-wall region. The near-side-wall region was already presented in Fig. 7 because of the most significant variation of the vertical velocity component with respect to the Reynolds number. After this analysis, looking at the streamwise vorticity behavior and at the vertical velocity component, we can then postulate that with increasing Re, the corner recirculation becomes more intense increasing the momentum transport not only towards the corner but also towards the side of the ducts, where the fluid is slower; differently from the smooth duct case, where the corner vorticity does not significantly influence the secondary motions, due to its scaling with $u_b$ and $l^*$, Pirozzoli (2018), now the corner vorticity plays a fundamental role in making the secondary motions stronger with increasing Re, creating stronger fluctuations as will be shown in the next section, and redistributing the enhanced turbulence from the ribbed wall region to the upper part of the duct, through the secondary motions occurring along the side walls.

To sustain this statement, the vertical profile of the TKE (turbulent kinetic energy) production rate, $P_k = - \overline{u_i' u_j'} \partial \overline{u_i} / \partial x_j$, and dissipation rate, $\varepsilon$ are calculated and presented in Fig. 12: once again we present in red the values of quantities in spanwise position $z/h = -0.5$ and in black the near-side-wall quantities, at $z/h = -0.95$.

Fig. 12

a TKE production rate $P_k$, b dissipation rate $\varepsilon$, and c their ratio along $z/h = -0.5$ (red lines) and $z/h = -0.95$ (black lines) on the plane passing through $x/h = 0.625$, for three different Reynolds number

In all cases, dissipation and production present a peak very close to the height of the rib, which is a characteristic of ribbed-wall flows, as already analyzed in Nagano et al. (2004), Orlandi et al. (2016), Mahmoodi-Jezeh and Wang (2020), and how it easily visible also in the visualization of Fig. 4, where it is shown how the flow is shredded into small vortices when impacting onto the riblet. However, the near rib peak is not the absolute maximum assumed by the production. It can be seen that the production significantly increases near the side wall (black lines) and, despite the fact that the dissipation increases as well, the latter does not balance the former anymore, and their ratio assumes values much higher than 1, which is a clear indication of non-equilibrium turbulence; values much closer to the unity can instead be found far from the side wall (red lines), where the ratio between production and dissipation is just slightly higher than 1. This energy imbalance will be redistributed on the stresses, as shown in the next paragraph. Although the Reynolds number seems to attenuate the production, this is only true if looking at it in outer coordinate: even if not shown here, with increasing Re, the production peak increases and moves as expected closer to the side wall.

As expected, the analysis of the TKE production and dissipation rates confirms the increased activity near the side walls due to the presence of riblets on the bottom wall and the monotonic increase of these turbulence quantities in the investigated range of Reynolds numbers, in contrast with what has been presented in Vinuesa et al. (2015), Vinuesa et al. (2018), in which several smooth ducts with different aspect ratio were investigated. In that work, Vinuesa et al. (2015), highlighted that production and dissipation are different from zero near the wall but well-balanced, such that their ratio is very close to unity.

3.3 Turbulent Stresses

Fluctuations around the average are essential parameters in turbulent flows, and in order to quantify them, the fluctuations of the second order, or Reynolds stresses, are commonly used. In Fig. 13, the profiles of normal and shear stresses along the same vertical lines we investigated in the previous sections, namely $z/h = -0.5$ (red lines) and $z/h = -0.95$ (black lines) are presented, made dimensionless with respect to the turbulent kinetic energy, k, and again within the plane intersecting the largest recirculation vortex denoted as “A” in Fig. 3. Additionally, the same quantities from the smooth simulations at similar Reynolds numbers in Pirozzoli (2018) are presented for comparison.

Fig. 13

Normal and shear stresses along $z/h = -0.5$ (red lines) and $z/h = -0.95$ (black lines) on the plane passing through $x/h = 0.625$, for three different Reynolds numbers. Smooth simulations (squares and circles) presented for comparison from the results from Pirozzoli (2018)

These stress profiles are depicted for three different Reynolds numbers, facilitating an examination of their influence on the flow while also being compared to the results obtained with a smooth wall. Notably, both normal and shear stresses exhibit a conspicuous peak over the crest of the riblet. This phenomenon arises due to the disturbance caused by the riblet itself and can be easily explained by looking at the vortices distribution in Fig. 4. The geometric protrusion into the flow generates unsteady eddies that reverse within the flow above the riblet and are subsequently transported downward, as confirmed in Nagano et al. (2004).

In the case of a smooth wall, the normal stresses exhibit symmetry with respect to the duct’s centerline (Atzori et al. 2021), while the shear stress demonstrates antisymmetry. However, the presence of a riblet markedly disrupts this symmetry, rendering the flow notably asymmetric. Furthermore, the average magnitude of the stresses on the vertical plane at $z/h = -0.5$ is increased with respect to the smooth case, due to the intense motions showed previously in Fig. 6, which affect the entire cross-section of the duct. This phenomenon is particularly noticeable when considering the shear stress $\overline{v'v'}/k$, whose red lines present values very close to 0 for the smooth case and much higher for the simulations with a ribbed wall.

All of these findings align closely with previous research conducted in PIV experiments on ribbed duct flows using similar setups, as reported in Wang et al. (2007), Coletti (2012), Fang (2017), as well as with LES simulations discussed in Fang (2015).

What is even more interesting is the comparison between the behavior of the stresses in $z/h = -0.5$ and in $z/h = -0.95$ when the Re is varied: nearer to the core of the flow (red lines), the stresses are still affected by the riblets, noticing the difference with respect to the smooth case, but they are almost not affected by the Reynolds number variation. Closer to the side wall instead (black lines), the Reynolds number plays a significant role, as all the stresses, apart from the streamwise normal stress, sensibly increase with increasing Re. In particular, this increment is visible in $\overline{v'v'}$ and $\overline{w'w'}$, which are the main causes of the increased turbulence we have investigated in the previous sections. Noticeably, $\overline{v'v'}$ presents a high value throughout the entire vertical direction, with a value in $y/h = 0$, which has a stronger magnitude than the initial peak due to the riblet and keeps this high value for a wider and wider region, as the Re increases, and its behavior resembles the one of the production rate near the side wall, as visible in Fig. 12b.

It is worth noting that the observations presented in Fig. 13 pertain to the behavior of Reynolds stresses along two different spanwise positions.

In order to assess the effects of the side walls on the behavior of the stresses, Fig. 14 is presented.

Fig. 14

Normal and shear stresses on a plane passing through the vortex center “A”; along the vertical line of the duct, at $z=0$, with a solid black line, and in lighter grey for z coordinate going from the center line towards one of the side walls

The presence of the side walls exerts a significant influence on the flow statistics, and two discernible trends emerge. Near the ribbed wall, when transitioning from $z/h = 0$ to $z/h = \pm 1$, indicating a shift from the core flow region to the side walls, the Reynolds stress values exhibit a decrease of the near wall peak; conversely, an increase of the Reynolds stresses for vertical coordinates $y/h>0.5$ is visible. This movement results in a more flattened profile with a higher average value. Here, we are departing from the core region of the flow and entering a region where the in-plane velocity components display greater intensity, as observed in the prominent near-wall secondary flow highlighted in Fig. 6. The near-side-wall region is characterized by more pronounced gradients of the in-plane velocity components, leading to higher values of the Reynolds stresses, particularly for $\overline{v'v'}/u_b^2$. Importantly, these nuances in the flow behavior would not be captured if periodic boundary conditions had been employed for the side walls.

3.4 Convergence Analysis

As said, in smooth ducts, cross-flow velocities are characterized by a magnitude in the order of 2% of the bulk velocity; consequently, their weak intensity requires a very long averaging time to be captured properly. A first guess on the correct length of the time interval to get converged statistics was given in Klewicki and Falco (1990), in which a time interval of at least 6000 convective time units was suggested (defined as the ratio of boundary-layer thickness and free-stream velocity); although other noticeable studies are available on the uncertainties in statistics in DNS, Oliver (2014), we mostly recall the work of Vinuesa (2016), who firstly mathematically defined the converged state, based on the linearity of the total shear stress, then came up with a convergence indicator, and finally evaluated this indicator for many previous simulations from different authors and research groups to compare the convergence of their works. For ducts, the indicator that is used to establish convergence of the simulation is the residual of the momentum balance in the streamwise direction, as in Eq. (3).

$$\begin{aligned} \varepsilon _{v} = - \frac{\partial \overline{p}^+}{\partial x^+} + Re^{-1} \frac{\partial ^2 \overline{u}^+}{\partial y^{+2}} - \frac{\partial \overline{u}\overline{v}^+}{\partial y^+} - V^+ \frac{\partial \overline{u}^+}{\partial y^+} + Re^{-1} \frac{\partial ^2 \overline{u}^+}{\partial x^{+2}} \end{aligned}$$

(3)

In Vinuesa (2016), the authors presented the decay of the convergence indicator as a function of two parameters, $T_a$ and $T_s$, which are, respectively, the averaging time interval and the time at which the averaging should start, which is made dimensionless with respect to the convective time, defined using bulk velocity and duct half-height. The lowest convergence rate for square ducts, around $1\cdot 10^{-3}$ is achieved at $T_s=200$ and $T_a = 5400$; however, they also show that after the first 1000 convective times, the decay of the index is very slow, and in literature more moderate values of convergence are found, for example the same indicator has been evaluated for different works, finding a value of around $3.3\cdot 10^{-3}$ for (Gavrilakis 1992) and $2\cdot 10^{-3}$ for (Pinelli 2010), which are still reasonably good values and allow to save a consistent amount of computational time.

A second indicator has been proposed in Pirozzoli (2018), which is based on the required symmetry of the flow. This second indicator is presented in Eq. (4), and its value is reported as well in Table 1.

$$\begin{aligned} \varepsilon _{p}\ =\frac{1}{u_b}\left[ \frac{1}{d_H^2\ }\int _{0}^{2h}\int _{0}^{2h}{{\ \left( \overline{u}\left( z,y\right) -\overline{u_{sym}}\left( z,y\right) \right) }^2dxdy}\right] ^{0.5} \end{aligned}$$

(4)

In Eq. (4), $\overline{u_{sym}}\left( z,y\right)$ is the mean velocity averaged over the four quadrants of the smooth square section, or over the two vertical halves of the ribbed duct. In his work, Pirozzoli (2018) create a database of simulation for square smooth ducts at several Reynolds numbers and evaluates both the indicators; apparently, the one in Eq. (4) converges slower than the other one, thus we undertake a conservative approach choosing the indicator in Eq. (4) as reference for the convergence of our simulations. However, the turbulent patterns in a ribbed duct, and in general over rough surfaces, are very different with respect to the smooth case, and as we have discovered in the previous paragraphs, the traditional corner eddies with an intensity of 2% of the bulk velocity are destroyed and replaced by stronger vortices which are dependent on the geometry of the rough elements, and in literature nothing can be found yet on the convergence criteria of ribbed or rough walls duct simulations. Thus, we propose hereafter the first evaluation of the convergence indicator proposed by Pirozzoli (2018), evaluated in a ribbed duct. Due to the more pronounced recirculation regions that we have presented in this paper, it is natural to think that the convergence of the simulation should be faster with respect to the one of a smooth duct. In Fig. 15, we present our results.

Fig. 15

Contour plot of $\varepsilon _P$ as a function of $T_a$ and $T_s$, for the simulation R1 (left); Convergence of the indicator $\varepsilon _P$ compared between the simulation S (continuous line) and R1 (dashed line)

Firstly the influence of the time interval $T_a$ and $T_s$ as defined in Vinuesa (2016) is analyzed; it can be seen in the contour plot on the left in Fig. 15 that a darker region can be reached if the averaging period starts after $T_s>200$ which is still in good agreement with what has been found in Vinuesa (2016).

Secondly, the convergence indicator is compared for the smooth and the ribbed case, noticing, as expected, that the stronger eddies, characteristic of a rough duct, influence positively the trend of the indicator $\varepsilon _P$, allowing the simulation to reach a converged state much faster. Indeed, as stated in Table 1, accounting for a similar number of convective times, the smooth and the ribbed simulations reach respectively an indicator equal to 0.0069, 0.0017, 0.0015 and 0.002. This opens up the possibility of shorter simulation times, with respect to the long and consuming simulation for smooth ducts, where the weak secondary flows need more than 4000 convective timesteps in order to be fully resolved and for the convergence indicator to go as low as $10^{-3}$.

4 Conclusions

In this study, we conducted three-dimensional DNS simulations to investigate the characteristics of flow over a roughened wall in a duct, focusing on the variation of the Reynolds numbers from 4400 to 13,200 and examining the influence of the side wall. Our findings offer valuable insights into the complex behavior of such flows and have important implications for a wide range of engineering applications.

First and foremost, we observed a significant increase in the friction factor with respect to the smooth case, indicating heightened resistance to flow due to surface roughness. This result underscores the importance of considering surface conditions when designing and analyzing fluid transport systems. Understanding how surface roughness affects friction is essential for optimizing energy efficiency and performance in engineering applications. This increase was due to a remarkable deviation of the flow patterns with respect to the smooth case: three recirculation zones in the streamwise direction were identified which highlight the intricate separation phenomena caused by the presence of a roughened wall. These zones play a crucial role in altering flow patterns and can impact heat transfer, mixing, and mass transport processes in practical systems. Additionally, the presence of two major vortices on the plane perpendicular to the flow reveals the intricate vortical structures formed in this configuration. Understanding the formation and evolution of these vortices is critical for predicting flow behavior and optimizing system performance in situations where flow control is necessary. Furthermore, the influence of the Reynolds number on these vortices seems to be not well-scalable with respect to the bulk velocity, as usually happens for smooth ducts. Indeed, these vortices present an increasing near-wall intensity as the Re is increased, and this is further demonstrated by the streamwise vorticity distribution, which has its peak on the bottom wall and in the bottom corners but assumes important values also further away along the side wall. The streamwise vorticity has proven to be not scalable with respect to mixed units ($u_b$ and $l^*$), thus, is “promoted” to the outer-scale intensity level and significantly affects the secondary motions in the duct section.

The influence of the side walls has been further investigated: an increased turbulent production rate is found along the side walls, where the secondary motions are stronger, and the dissipation rate is not enough to balance the TKE, resulting in non-equilibrium turbulence. Also, turbulent normal and shear stresses are found to be highly sensible to the Reynolds number and to the side wall, increasing when moving towards the side wall and when the Re is increased; in all cases, the symmetry (or antisymmetry) of the stresses is lost, due to the presence of the riblet which causes a significant peak of the stresses near the ribbed wall, which once again, becomes even stronger when Re is increased.

Lastly, a convergence analysis is carried out for the first time, giving meaningful insights on the convergence behavior of a ribbed wall simulation against a smooth wall one; the convergence is found to happen quicker, probably due to the stronger intensity of the vortex which can be captured with less convective timesteps.

In conclusion, our study sheds light on the intricate interplay between Reynolds numbers, roughened surfaces, and boundary conditions in turbulent flows. The insights gained from this research enhance our fundamental understanding of flow over roughened walls and pave the way for improved design and control of engineering systems involving such flows. These findings provide a foundation for future investigations and engineering applications, ultimately contributing to more efficient and effective fluid transport systems. Looking ahead, it is imperative to revisit this analysis while incorporating heat transfer phenomena, as this will further enhance the applicability and relevance of our findings in engineering scenarios.

Appendices

Appendix A: Validation with a Smooth Square Duct

Although the same code was widely used in our research group, Martinez-Sanchis (2021), Martinez-Sanchis (2022), Martinez-Sanchis (2022), Martinez-Sanchis (2023), the application case was different, and some features of the code have been modified; thus a new validation was considered necessary. Simulations of smooth square ducts have been considered as a reference test for our solver, and the case of a square duct with friction Reynolds number $Re_{\tau} =hu_{\tau} /\nu = 110$ was selected as test-case since this relatively low Reynolds number allows us to compare and validate a fully turbulent simulation without the high computational cost of higher Reynolds numbers. In this way, we are able to use this validation case as a comparison case for the results of a ribbed duct presented in the previous section of the paper. Available data on this test case can be found in previous work from Pinelli (2010), who created a database of simulations for square ducts spanning a range of low bulk Reynolds numbers. The same dataset has been widely used for validation in many other works, as in Vinuesa (2014), Pirozzoli (2018), Mahmoodi-Jezeh and Wang (2020)

For this simulation, a control box of dimensions $2\,h \text { x } 2\,h \text { x } 20\,h$ is used, and periodic boundary conditions are enforced on the inlet and outlet as it has been done for the ribbed case, explained in Sect. 2.1; for both the smooth and the ribbed wall simulations, the same solver and boundary conditions have been used.

When simulating wall-bounded ducts, the accurate prediction of secondary flow is the most challenging phenomenon to be captured because the very weak intensity of the recirculation regions requires a very long averaging interval to be properly calculated, and, as pointed out in Oliver (2014), statistical errors due to poor convergence may be dominant over the numerical error itself. For this reason, the in-plane velocity components are often used for validating purposes: if the simulation is well converged, both the exact position of secondary flows and their magnitude are captured correctly.

In Fig. 16 we present the spanwise velocity component, along with results from previous works.

In addition, the more difficult-to-catch second-order statistics are presented on the right of Fig. 16. The comparison of the turbulent normal stresses with (Pinelli 2010), is carried out in inner-wall scaling, namely using $u_{\tau}$ and $l^+ = u_{\tau} / \nu$ to make near-wall quantities dimensionless.

The good agreement with previous simulations from other authors is clear and assures us that the computation technique is correct; the slight deviation that is visible between the present simulation and data from Pinelli has to be attributed to the different averaging time: Pinelli averaged his simulation for 4160 convective times ($h/u_b$), while in this work, we averaged the validation case over an interval of $\approx 1900$ convective times, saving more than half of the computational time but still getting very satisfactory results.

Fig. 16

The spanwise velocity component (on the left) is presented on the planes located at $y=-0.75h$ (continuous line) and at $y=-0.25h$ (dashed line). The turbulent normal stresses (on the right) are shown after scaling with respect to inner-wall characteristic length and velocity. Our results are compared with results from Pinelli (2010)

Appendix B: Vortical Structures Visualization

In Sect. 3 the streamwise vorticity $\omega _x$ is used to analyze the vertical structure of the flow; this quantity has been chosen such that a more direct comparison with the wide literature of smooth ducts can be carried out. However, several methods for vortex identifications have been developed in the past years, and for this reason, we use a second method in order to assess if the streamwise vorticity is well suited to correctly capture the analyzed features. The Q-criterion, developed by Hunt et al. (1988), uses the second invariant of the velocity gradient tensor to evaluate a quantity Q which is positive in areas of the flow dominated by the vorticity, and negative in areas dominated by the strain rate. In Fig. 17 we present the vortical structures that are generated near the side wall: from left to right, increasing the shown Q-value, only the strongest vortices stay visible.

Fig. 17

Vortical structures near the riblet and near the side wall, obtained using the Q-criterion. Q-values increased from left to right

We can understand that the riblet creates a very strong recirculation zone right before itself, while the recirculation immediately after the riblet looks weaker, as visible in the most right figure, where the vortex has disappeared. Additionally, an ejection of flow can be seen over the riblet and very close to the side wall, proving the enhanced near-wall activity we have presented in the paper. Finally, at the highest Q-value, namely when only the strongest vortices are shown, we can clearly distinguish very close to the side wall, and at a streamwise location that corresponds to the position of the vortex “A”, in Fig. 3, a big recirculation region; this proves to be at the same coordinate of the “corner vorticity” that has been presented in Sect. 3 by using the streamwise vorticity.