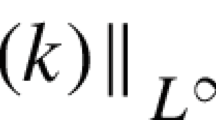1 Introduction

Turbulent length and time scales are very important for characterizing, analysing and modelling turbulent fluid flow (Pope 2000): As an example (i) the turbulent viscosity in the well-known two equation models is typically considered to be proportional to the product of a length scale and a velocity scale; (ii) For the estimation of statistical errors the confidence interval can be given as \(CI=[\varphi -k\sqrt{{\sigma }^{2}\left(\varphi \right)},\varphi +k\sqrt{{\sigma }^{2}\left(\varphi \right)}]\), where \(k=1\) for a confidence level of \(68.3\mathrm{\%}\) and \(k=2\) for a confidence level of \(95.4\mathrm{\% }.\) The variance \({\sigma }^{2}\left(\varphi \right)\) of the estimator of quantity \(\varphi \) is a function of the number of independent samples \(N\). For example assuming a Gaussian distribution we have \({\sigma }^{2}\left({\varphi }_{mean}\right)=\langle {\varphi }^{{\prime}2}\rangle /N\) for the mean value and \({\sigma }^{2}\left({\varphi }_{var}\right)=2{\langle {\varphi }^{{\prime}2}\rangle }^{2}/N\) for the variance of \(\varphi \), where as usual \(\langle \cdot \rangle \) denotes a suitable averaging operation and \(\varphi =\langle \varphi \rangle +{\varphi }{\prime}\) (Benedict and Gould 1996). It is common practice to estimate the number of statistically independent samples \(N\) in a homogeneous direction (or in time) as being proportional to the length of the domain (the length of the time interval) divided by the integral length scale (integral time scale), the so called decorrelation length (time). Accurate estimation of the latter is therefore of paramount importance for assessing the statistical error in Direct Numerical (DNS) or Large Eddy Simulations (LES) where the domain size and simulation time are limited or alternatively for determining the required run time to reach a given error threshold. However, strictly speaking statistical errors of each variable (or moments of the variable) should be analysed by using its individual integral scale. In fact one motivation for the present work was driven by the author’s subjective observation that estimates for statistical errors of the variance in DNS appeared to be too conservative; (iii) The ratio of the largest to the smallest turbulent scales, the so called Kolmogorov scale \({\eta }_{K}\), I is proportional to the Reynolds number to the power \(3/4\) which is a fundamental equation for describing the “degrees of freedom” of turbulence and for estimation the computational requirements of Direct Numerical Simulations (DNS) of turbulent flows. While \({\eta }_{K}\) scales with viscosity (as the Taylor scale), the large energy carrying scales of the flow, considered in this work, depend on the dimension of the flow geometry; (iv) Finally, the energy carrying length scales are also frequently needed for dimensioning the computational domain in numerical experiments.

For the sake of brevity the following discussion is limited to integral length scales but it applies equally well to integral time scales. While there is a large amount of literature regarding the characterization and calculation of turbulent length scales of velocity (or a scalar quantity), the length scales of higher order moments have not been studied according to the best knowledge of the author. As a motivation consider a harmonic function \(\mathrm{sin}\left(x\right).\) From the trigonometric theorems we know \({sin(x)}^{2}=0.5\left(1-cos\left(2x\right)\right)\) which illustrates that the frequency is doubled and suggests a shorter length scale for higher order moments.

The rest of the paper is structured as follows: the methodology for testing the equations suggested in this work is presented first. This is followed by the mathematical derivations for expressing the covariance of higher order moments in terms of the covariance of the variables themselves. Next, the methodology is illustrated for two different synthetic pseudo-turbulent signals as well as for a DNS database. Finally, some conclusions close the paper.

2 Methodology

The analysis in the results section relies on synthetic turbulence generated with two different methods and a DNS database for a turbulent plane jet which are described briefly in the following. The well-known ARMA process (Trenberth 1984) \({u}_{\alpha +1}=\Phi {u}_{\alpha }+\sqrt{{u}_{var}(1-{\Phi }^{2})} {r}_{\alpha }\) establishes a series with exponentially decaying autocorrelation function \(\mathrm{exp}\left(-x/L\right)\). Here \({r}_{\alpha }\) is a series of random numbers with zero mean and unit variance, \({u}_{var}\) is the desired variance of the synthetic signal and \(\Phi =1-\Delta x/L\) is a parameter related to the ratio of grid spacing and integral length scale. In the digital filter approach (Klein et al. 2003a) a series of random number \({r}_{\alpha }\) with zero mean and unit variance is filtered with suitable filter coefficients \({b}_{\beta }\), \({u}_{\alpha }={\sum }_{\beta =-N }^{N}{b}_{\beta }{r}_{\alpha +\beta }\) to obtain a pseudo turbulent velocity signal, where the obtained autocorrelation function obeys a Gaussian shape of the form \(\mathrm{exp}(-\pi {/4\cdot x}^{2}/{L}^{2})\). The ARMA process has often been used as a substitute for pseudo turbulent fluctuations (Trenberth 1984), while the Gaussian autocorrelation corresponds to homogeneous turbulence in a late stage (Batchelor 1953). Synthetic turbulence has the advantage that it allows for an arbitrary number of statistical samples and in particular to check the equations presented later under exactly the conditions they were derived.

In addition DNS data for a plane turbulent jet has been used (Vocke et al. 2023) in analogy to the work in Klein et al. (2003b) but featuring a higher Reynolds number of \(Re={U}_{0}D/\nu =10000\) with the bulk inlet velocity \({U}_{0},\) the nozzle width \(D\) and the kinematic viscosity \(\nu \). The incompressible Navier–Stokes equations have been solved on a Cartesian staggered grid with second-order central differences for spatial discretization and a low-storage Runge–Kutta method for temporal advancement. After reaching a statistically steady state the simulations have been run for 22 more flow through times to collect statistics. For more details the reader is referred to Vocke et al. (2023); Klein et al. (2003b).

2.1 Statistical Considerations

The following derivation assumes a Gaussian probability distribution of turbulent variables. More precisely it will make use of the central moments of a Gaussian distribution. In principal it might be possible to generalize the derivation for different moments and non-symmetric distributions (i.e. non zero skewness), but this is beyond the scope of the present work. According to She et al. (1988) it has been well verified that the probability distribution of the full velocity field of turbulent flows is often Gaussian and deviation from a Gaussian distribution become significant only at small scales. Since we are here interested in the large scales of a turbulent flow it is assumed that the non-Gaussian behaviour of turbulence has only a small effect on their estimation. It will be shown later that the assumption seems to be reasonable for a turbulent jet flow.

Consider now two jointly normally distributed random variables \(X,Y\) with zero mean, covariance \(c\) and variance \({\sigma }^{2}\). As usual the covariance and variance can be defined using the expectation value \(E\) as follows: \(c=Cov\left(X,Y\right)=E\left(XY\right)-E\left(X\right)E\left(Y\right), {\sigma }^{2}=Var\left(X\right)=E\left({X}^{2}\right)-E{\left(X\right)}^{2}\). This gives rise to the definition of the correlation for higher order moments as

$$Corr\left({X}^{n},{Y}^{n}\right)=\frac{Cov\left({X}^{n},{Y}^{n}\right)}{\sqrt{Var\left({X}^{n}\right)Var({Y}^{n})}}$$
(1)

where \(n\) is a natural number and the standard correlation between two variables is obtained for \(n=1\). In order to find relations between \(Cov\left(X,Y\right)\) and \(Cov\left({X}^{n},{Y}^{n}\right)\) one can write \((X,Y)\) as a linear combination of independent and identically distributed random variables \((X,Z)\) (Wolfies 2019) such that \(Cov\left(X,Y\right)=Cov\left(X,Z\right)=c\). It can be easily shown that \(Y=c/{\sigma }^{2}X+aZ\) with \({a}^{2}=1-{c}^{2}/{\sigma }^{4}\) gives \(E\left(c/{\sigma }^{2}X+aZ\right)=0\), as well as

$$Var\left(\frac{c}{{\sigma }^{2}}X+aZ\right)=E\left({\left(\frac{c}{{\sigma }^{2}}X+aZ\right)}^{2}\right)=\frac{{c}^{2}}{{\sigma }^{4}}E\left({X}^{2}\right)+{a}^{2}E\left({Z}^{2}\right)={\sigma }^{2}$$
(2)

where the facts have been used that for independent random variables \(E\left(XZ\right)=E\left(X\right)E\left(Z\right)=0\), \(E\left(X+Z\right)=E\left(X\right)+E\left(Z\right)=0\), and that the central moments of a Gaussian distribution are given by \(E\left( {\left( {X - \mu } \right)^{p} } \right) = \sigma^{p} \left( {p - 1} \right)!!\) if \(p\) is even and zero otherwise. Here the double factorial provides the values \({\sigma }^{2},3{\sigma }^{4},{15\sigma }^{6},{105\sigma }^{8}\) for the \({2}^{nd},{4}^{th},{6}^{th},{8}^{th}\) central moment of the Gaussian. In a similar manner one confirms:

$$Cov\left(X,\frac{c}{{\sigma }^{2}}X+aZ\right)=E\left(X\left(\frac{c}{{\sigma }^{2}}X+aZ\right)\right)=\frac{c}{{\sigma }^{2}}E({X}^{2})=c$$
(3)

For the second moment similar arguments lead to

$$ \begin{gathered} Cov\left( {X^{2} ,\left( {\frac{c}{{\sigma^{2} }}X + aZ} \right)^{2} } \right) = E\left( {X^{2} \left( {\frac{c}{{\sigma^{2} }}X + aZ} \right)^{2} } \right) - E\left( {X^{2} } \right)E\left( {\left( {\frac{c}{{\sigma^{2} }}X + aZ} \right)^{2} } \right) = \hfill \\ E\left( {X^{2} \left( {\frac{{c^{2} }}{{\sigma^{4} }}X^{2} + 2\frac{ca}{{\sigma^{2} }}XZ + a^{2} Z^{2} } \right)^{2} } \right) - \sigma^{4} = \frac{{c^{2} }}{{\sigma^{4} }}X^{4} + \left( {1 - \frac{{c^{2} }}{{\sigma^{4} }}} \right)X^{2} Z^{2} - \sigma^{4} = \hfill \\ 3c^{2} + \sigma^{4} - c^{2} - \sigma^{4} = 2c^{2} \hfill \\ \end{gathered} $$
(4)

For the third and fourth order moments the above calculation method provides

$$ \begin{gathered} Cov\left( {X^{3} ,\left( {\frac{c}{{\sigma^{2} }}X + aZ} \right)^{3} } \right) = 15c^{3} + 9a^{2} \sigma^{4} c = 6c^{3} + 9\sigma^{4} c \hfill \\ Cov\left( {X^{4} ,\left( {\frac{c}{{\sigma^{2} }}X + aZ} \right)^{4} } \right) = 105c^{4} + 90a^{2} \sigma^{4} c^{2} + 9a^{4} \sigma^{8} - 9\sigma^{8} = 24c^{4} + 72\sigma^{4} c^{2} \hfill \\ \end{gathered} $$
(5)

In summary, the following formulas are obtained to approximate the higher order covariances in terms of \(Cov\left(X,Y\right)\):

$$ \begin{gathered} Cov\left( {X^{2} ,Y^{2} } \right) = 2Cov\left( {X,Y} \right)^{2} \hfill \\ Cov\left( {X^{3} ,Y^{3} } \right) = 6Cov\left( {X,Y} \right)^{3} + 9\sigma^{4} Cov\left( {X,Y} \right) \hfill \\ Cov\left( {X^{4} ,Y^{4} } \right) = 24Cov\left( {X,Y} \right)^{4} + 72\sigma^{4} Cov\left( {X,Y} \right)^{2} \hfill \\ \end{gathered} $$
(6)

By putting \(X=u\left(x\right), Y=u(x+r)\) the above relations can be applied to the autocorrelation of a random, Gaussian distributed signal \(u\). For the (normalised) autocorrelation function of order \(n\) we define (see also Eq. (1)):

$${R}_{{u}^{n},{u}^{n}}\left(r\right)=\frac{Cov\left({u}^{n}\left(x\right),{u}^{n}\left(x+r\right)\right)}{Cov\left({u}^{n}\left(x\right),{u}^{n}\left(x\right)\right)}$$
(7)

where homogeneity has been assumed, i.e. \({R}_{{u}^{n},{u}^{n}}\left(x,r\right)={R}_{{u}^{n},{u}^{n}}(r)\). This equation gives rise to the definition of an integral length scale of higher order moments as follows:

$${L}_{{u}^{n},{u}^{n}}={\int }_{0}^{\infty }{R}_{{u}^{n},{u}^{n}}(r)dr$$
(8)

In the following relations (6) will be applied to two different generic autocorrelation functions. We start with a decaying exponential shape:

$${R}_{u,u}\left(r\right)=exp\left(-\frac{r}{{L}_{u,u}}\right) {L}\,\,_{u,u}={\int }_{0}^{\infty }exp\left(-\frac{r}{{L}_{u,u}}\right)dr$$
(9)

As a result of this we have \(c\left(r\right):=Cov\left(u\left(x\right),u\left(x+r\right)\right)={\sigma }^{2} exp\left(-r/{L}_{u,u}\right)\) and it follows

$$ \mathop \smallint \limits_{0}^{\infty } Cov\left( {u^{2} \left( x \right),u^{2} \left( {x + r} \right)} \right)dr = \mathop \smallint \limits_{0}^{\infty } 2Cov\left( {u\left( x \right),u\left( {x + r} \right)} \right)^{2} dr = \sigma^{4} \mathop \smallint \limits_{0}^{\infty } 2exp\left( { - \frac{2r}{{L_{uu} }}} \right)dr = 2\sigma^{4} \frac{{L_{uu} }}{2} $$
(10)

Hence one obtains after normalization with \(Cov\left( {u^{2} \left( x \right),u^{2} \left( x \right)} \right) = 2\sigma^{4} exp\left( { - 0/L_{uu}} \right)^{2}\)

$$ L_{{u^{2} ,u^{2} }} = 2\sigma^{4} \frac{{L_{uu} }}{2}/\left( {2\sigma^{4} } \right) = \frac{{L_{uu} }}{2} $$
(11)

Following the same procedure gives the length scales for the third

$$ \begin{gathered} \mathop \int \nolimits_{0}^{\infty } Cov\left( {u^{3} \left( x \right),u^{3} \left( {x + r} \right)} \right)dr = \mathop \int \nolimits_{0}^{\infty } 6c\left( r \right)^{3} + 9c\left( r \right)\sigma^{4} dr = \hfill \\ \sigma^{6} \mathop \int \nolimits_{0}^{\infty } 6exp\left( { - \frac{3r}{{L_{u,u} }}} \right) + 9exp\left( { - \frac{r}{{L_{u,u} }}} \right)dr = \sigma^{6} \left( {6\frac{{L_{u,u} }}{3} + 9L_{u,u} } \right) = 11\sigma^{6} L_{u,u} \hfill \\ \quad\quad\quad\quad\quad\quad\quad\quad \Rightarrow L_{{u^{3} ,u^{3} }} = \frac{{11\sigma^{6} }}{{\left( {6 + 9} \right)\sigma^{6} }}L_{u,u} = \frac{11}{{15}}L_{uu} \hfill \\ \end{gathered} $$
(12)

and fourth order moments

$$ \begin{gathered} \mathop \smallint \limits_{0}^{\infty } Cov\left( {u^{4} \left( x \right),u^{4} \left( {x + r} \right)} \right)dr = \mathop \smallint \limits_{0}^{\infty } 24c\left( r \right)^{4} + 72c\left( r \right)^{2} \sigma^{4} dr = \hfill \\ \sigma^{8} \mathop \smallint \limits_{0}^{\infty } 24exp\left( { - \frac{4r}{{L_{u,u} }}} \right) + 72exp\left( { - \frac{2r}{{L_{u,u} }}} \right)dr = \sigma^{8} \left( {24\frac{{L_{u,u} }}{4} + 72\frac{{L_{u,u} }}{2}} \right) = 42\sigma^{8} L_{u,u} \hfill \\ \Rightarrow L_{{u^{4} ,u^{4} }} = \frac{{42\sigma^{8} }}{{\left( {24 + 72} \right)\sigma^{8} }}L_{u,u} = \frac{7}{16}L_{uu} \hfill \\ \end{gathered} $$
(13)

Now let us consider an autocorrelation function given by a Gaussian:

$${R}_{u,u}\left(r\right)=exp\left(-\frac{\pi }{4}\frac{{r}^{2}}{{L}_{u,u}^{2}}\right) {L}\,\,_{u,u}={\int }_{0}^{\infty }exp\left(-\frac{\pi }{4}\frac{{r}^{2}}{{L}_{u,u}^{2}}\right)dr$$
(14)

We find for \(n=2\)

$$ \begin{gathered} \mathop \smallint \limits_{0}^{\infty } Cov\left( {u^{2} \left( x \right),u^{2} \left( {x + r} \right)} \right)dr = \mathop \smallint \limits_{0}^{\infty } 2Cov\left( {u\left( x \right),u\left( {x + r} \right)} \right)^{2} dr = \hfill \\ \sigma^{4} \mathop \smallint \limits_{0}^{\infty } 2exp\left( { - \frac{\pi }{4}\frac{{r^{2} }}{{L_{u,u}^{2} }}} \right)^{2} dr = 2\sigma^{4} \frac{{L_{uu} }}{\sqrt 2 } \Rightarrow L_{{u^{2} ,u^{2} }} = 2\sigma^{4} \frac{{L_{uu} }}{\sqrt 2 }/\left( {2\sigma^{4} } \right) = \frac{{L_{uu} }}{\sqrt 2 } \hfill \\ \end{gathered} $$
(15)

and for \(n=\mathrm{3,4}\)

$$ \begin{gathered} \Rightarrow L_{{u^{3} ,u^{3} }} = \frac{{\left( {6/\sqrt 3 + 9} \right)\sigma^{6} }}{{\left( {6 + 9} \right)\sigma^{6} }}L_{u,u} = \frac{2\sqrt 3 + 9}{{15}}L_{uu} \hfill \\ \Rightarrow L_{{u^{4} ,u^{4} }} = \frac{{\left( {12 + 36\sqrt 2 } \right)\sigma^{8} }}{{96\sigma^{8} }}L_{u,u} = \frac{1 + 3\sqrt 2 }{8}L_{uu} \hfill \\ \end{gathered} $$
(16)

Table 1 summarizes the results for the ratios of integral scales:

3 Results

Figure 1a–c shows the autocorrelation function \({R}_{{u}^{n}{u}^{n}}\) for \(n=\mathrm{2,3},4\) obtained from the 1D synthetic signal (which could reflect a space or time dependence) of the ARMA process (Eq. 9), while \({R}_{{u}^{2}{u}^{2}}\) obtained by the digital filter method (Eq. 14) is discussed in Fig. 1d.

Fig. 1
figure 1

Autocorrelation functions \({R}_{u,u}\) and \({R}_{{u}^{n}{,u}^{n}}\) obtained from the 1D synthetic signal obtained by the ARMA process (see Eq. 9) for a \(n=2\), b \(n=3\), c \(n=4.\) Subfigure d depicts \({R}_{u,u}\) and \({R}_{{u}^{2},{u}^{2}}\) obtained by the digital filter method (see Eq. 14). The blue line illustrates the result when \({R}_{{u}^{n}{,u}^{n}}\) is expressed in terms of the first order covariance. The term \({c}_{norm}\) denotes the appropriate normalisation

Full size image

It is evident that there is a perfect agreement with the formulas in Eq. (6). It is also worth mentioning that the length scale ratios in Table 1 have been confirmed numerically. Figure 2 shows similar findings for the second order moments on the centreline of a plane turbulent jet at two axial positions.

Table 1 Ratio of \({L}_{u,u}/{L}_{{u}^{n},{u}^{n}}\) for \(n=\mathrm{2,3},4\) assuming a decaying exponential or Gaussian shape of the autocorrelation function
Full size table
Fig. 2
figure 2

Autocorrelation functions \({R}_{u,u}\) and \({R}_{{u}^{2},{u}^{2}}\) of the axial velocity component with spatil separation at the centre line of a plane jet (Vocke et al. 2023; Klein et al. 2003b) at two different axial positions: a \(x/D=5.0\), b \(x/D=12.5\). c Autocorrelation with spanwise separation at \(x/D=12.5\). The blue line illustrates the result when \({R}_{{u}^{n}{,u}^{n}}\) is expressed in terms of the first order covariance. The term \({c}_{norm}\) denotes the appropriate normalisation

Full size image

The jet breakup point is close to \(x/D=5\) which explains the oscillation observed for, \({R}_{u,u}\) caused by the large coherent structures in the near field\(.\) Notwithstanding this complication we find good agreement with the theory outlined in the previous chapter, i.e. \({R}_{{u}^{2},{u}^{2}}\) can be reasonably accurate predicted by the square of the first order covariance. The position \(x/D=12.5\) is located in the fully developed (approximately self-similar) region of the jet. In agreement with the observations by Birch et al. (1978), one confirms that the autocorrelation function is closely approximated by a decaying exponential. Figure 2c exemplarily also shows one autocorrelation with spanwise separation. Despite the number of samples being more limited for the DNS data, compared to the synthetic turbulence, the agreement with the theory assuming a Gaussian distribution (not to be confused with the Gaussian shape of \({R}_{u,u}\)) is very accurate. It is important to understand that Eq. (6) is correct only under the assumptions of a Gaussian velocity PDF and it does not hold true for statistical estimators of these quantities in the case of finite sample size, which likely explains the small deviations between the green and the blue curves. Further, as a note of caution, there can be considerable deviations from a Gaussian PDF e.g. close to walls or for bounded scalars.

4 Conclusions

Assuming a Gaussian distribution of the velocity PDF, relations have been derived to express the covariance of higher order velocity moments by algebraic expressions of the covariance of velocity itself. While this assumption is not always met in reality the present work provides a mathematical theory for the behaviour of integral scales for higher order moments. This has been used to derive the ratio of the integral length scale to corresponding higher order integral length scales for different assumed shapes (exponential and Gaussian) of the autocorrelation function. The result has implications for estimating the statistical error in computational studies which scales with the inverse of the square root of the number of independent samples (in DNS being inherently limited), in particular when averaging is performed in more than one homogeneous direction. As an example the exponentially decaying autocorrelation function, characteristic for e.g. fully developed turbulence in shear layers, yields a length scale for the variance which is half the length scale of velocity. This implies a statistical error smaller by a factor of \({\left(1/\sqrt{2}\right)}^{k}\) for averaging in \(k\) appropriate space or time coordinates. Finally, it is believed that these relations might be also useful in terms of RANS based turbulence modelling involving higher order moments. While the present work suggests shorter length scales for higher order velocity statistics and provides quantitative relations for Gaussian velocity statistics, this has to be assessed in future for different flow configurations and for turbulent signals violating the assumptions used in this work.