1 Introduction

In today's combustion community, modeling of turbulence-chemistry interactions in gaseous flames is still a very active research field. Premixed and non-premixed combustion are the two combustion modes which have been studied deeply and most combustion models are exclusively developed for only one of these regimes (Masri 2020). In practice, however, inhomogeneities in the fuel–air ratio field due to insufficient mixing create situations which cannot be characterized clearly by one of these categories. Hence, our first focus is to analyse combustion models for partially premixed flames.

To study phenomena occurring in partially premixed combustion situations, new burner designs have been developed and tested to provide data for a better understanding of turbulence-chemistry interaction (TCI) in such situations, to improve combustion models and to validate them. The International Workshop on Measurement and Computation of Turbulent Flames (TNF Workshop) has built a flame library for comparison of experimental and numerical data. Several TNF workshops have featured the well-known Sydney compositionally inhomogeneous flames (Proceedings of the TNF 14 2018), one of which will be considered in this work. The burner was investigated by Barlow et al. (Barlow et al. 2015) and Meares et al. (Meares et al. 2015), who conducted experiments at Sandia to investigate the effects of the partial premixing. Because of its simple shape and the various combustion regimes possible, the burner has been explored in a number of numerical studies (Perry and Mueller 2019; Galindo et al. 2017; Hansinger et al. 2017; Kleinheinz et al. 2017; Lampmann et al. 2019).

Specifically, we perform LESs for the inhomogeneous test case FJ200-5GP-Lr75-57 (Masri 2020). One of the challenges in this configuration is the accurate prediction of the experimental scatter plots, which indicate a premixed combustion mode in the upstream region, transforming into a typical non-premixed shape further downstream. FSD models have been developed for (and are typically applied to) the simulation of turbulent premixed flames. They can be extended straightforwardly to the case of partially premixed flames by introducing a mixture fraction dependence into all model parameters notably the laminar flame speed, temperature, density and species mass fractions. Investigation of the performance of such extended FSD models in partially and non-premixed regions is of high interest. Here also the influence of stretch effects in the FSD modeling, applied to the present configuration, is analyzed. The ATF simulations of Lampmann et al. (2019) serve as numerical reference.

The second motivation for this analysis is based on the fact that, according to Kuhlmann et al. (2022) comparisons of combustion LES models (see e.g. Fiorina et al. 2015) are often conducted using different codes, with different numerical schemes and computational resources, which does not allow for a comprehensive and complete analysis of their respective performances. We compare ATF and FSD models using the same computational mesh, numerical scheme and boundary conditions.

The paper is structured as follows: The governing equations and closure assumptions are presented first, which is followed by detailing the test case and numerical setup. The presentation of the results is split into two parts: The first part represents the initial FSD and ATF simulations on the baseline mesh. Based on the deficiencies of the ATF model when compared to the FSD model these shortcomings are analysed and possible remedies are discussed in the second part of the results. A summary and conclusions finally close the paper.

2 Governing Equations

In this section we summarize the Keppeler FSD model as implemented in our inhouse version of the OpenFOAM-Solver, FSD LES. A documentation of the model is published in Keppeler (2013) and Keppeler et al. (2014). The model has, among other configurations, been successful in the simulation of high-pressure premixed Bunsen flames [Kobayashi burner setup (Keppeler et al. 2014), (Kobayashi et al. 1996)]. Here we extend the FSD LES solver to partially premixed flames.

The Favre filtered continuity, momentum and energy equations read (Poinsot and Veynante 2005):

$$\frac{{\partial \overline{\rho }}}{\partial t} + \frac{{\partial \overline{\rho }\tilde{u}_{i} }}{{\partial x_{i} }} = 0$$
(1)
$$\frac{{\partial \overline{\rho }\tilde{u}_{j} }}{\partial t} + \frac{{\partial \overline{\rho }\tilde{u}_{j} \tilde{u}_{i} }}{{\partial x_{i} }} = \frac{\partial }{{\partial x_{i} }}\left( {\overline{\tau }_{ij} - \overline{\rho }\left( {\widetilde{{u_{j} u_{i} }} - \tilde{u}_{j} \tilde{u}_{i} } \right)} \right) - \frac{{\partial \overline{p}}}{{\partial x_{j} }}$$
(2)

where \(\tilde{u}_{i}\) is the Favre filtered velocity in i-direction, \(\overline{\rho }\) the filtered fluid density, \(\overline{\tau }_{ij}\) the filtered stress tensor.

2.1 Flame Surface Density Based Modelling

It is possible to describe the thermochemistry of partially premixed turbulent combustion through a progress variable \(c\)

$$c = \frac{{Y_{f} - Y_{f}^{u} \left( z \right)}}{{ Y_{f}^{b} \left( z \right) - Y_{f}^{u} \left( z \right)}}$$
(3)

with mixture fraction \(z\). The transport equation for the Favre filtered mixture fraction \(z\) with a gradient diffusion assumption is that of a conserved scalar:

$$\frac{{\partial \overline{\rho }\tilde{z}}}{\partial t} + \nabla \cdot \left( {\overline{\rho }\tilde{u}\tilde{z}} \right) = \nabla \cdot \left[ {\overline{\rho }D_{eff} } \right]\nabla \tilde{z}$$
(4)

where \(D_{eff} = \tilde{D}_{z} + D_{sgs}\) implies effective diffusivity.

The transport equation for \(c\) can be derived (Bray et al. 2005; Lipatnikov 2017) using the relation between the species transport equation \(Y\) and \(c\)

$$\frac{{\partial \overline{\rho }\tilde{c}}}{\partial t} + \frac{{\partial \overline{\rho }\tilde{u}_{i} \tilde{c}}}{{\partial x_{i} }} + \frac{\partial }{{\partial x_{i} }} \left( {\overline{\rho }\left( {\widetilde{{u_{i} c}} - \tilde{u}_{i} \tilde{c}} \right)} \right) = \frac{\partial }{{\partial x_{i} }}\left( {\overline{{\rho D\frac{\partial c}{{\partial x_{i} }}}} } \right) + \overline{{\dot{\omega }_{c} }} + T_{\chi }$$
(5)

where \(\dot{\omega }_{c}\) is reaction source term. The additional term on the right-hand side contains cross dissipation terms and terms associated with diffusion flamelets. The first order approximation to the last term is given by \(T_{\chi } = 2\overline{\rho }\overline{D}\nabla \tilde{c} \cdot \nabla \tilde{z}/\tilde{z}\) for lean conditions (Lipatnikov 2017) and by \(T_{\chi } = 2\overline{\rho }\overline{D}\nabla \tilde{c} \cdot \nabla \tilde{z}/\left( {\tilde{z} - 1} \right)\) for rich conditions. The transport equation contains several unclosed terms. Modelling approaches to close these terms are presented in the following. Using a gradient assumption (Poinsot and Veynante 2005) the unclosed scalar flux is expressed as

$$\overline{\rho }\left( {\widetilde{{u_{i} c}} - \tilde{u}_{i} \tilde{c}} \right) = - \frac{{\mu_{SGS} }}{{Sc_{t} }}\frac{{\partial \tilde{c}}}{{\partial x_{i} }}$$
(6)

where \(\mu_{SGS}\) is the subgrid scale viscosity and \(Sc_{t} = 0.7\) is turbulent Schmidt number. A similar approach is taken to model the turbulent flux of enthalpy. The first two terms on the right-hand side of Eq. (5) are approximated by (Hawkes and Cant 2000; Boger et al. 1998)

$$\frac{\partial }{{\partial x_{i} }}\left( {\overline{{\rho D\frac{\partial c}{{\partial x_{i} }}}} } \right) + \overline{{\dot{\omega }}}_{c} = \overline{{\left( {\rho s_{d} } \right)_{s} }} \overline{{\left| {\nabla c} \right|}} = \rho_{u} s_{cs} {\Sigma }$$
(7)

where \({\Sigma } = \overline{{\left| {\nabla c} \right|}}\) denotes the generalized flame surface density,\(\overline{{\left( {\rho s_{d} } \right)_{s} }}\) is the density weighted surface-averaged displacement speed and \(s_{cs}\) is the average flame consumption speed along the surface, which has to be approximated (Boger et al. 1998). Here the assumption of thin flames and weak curvature effects \(\rho_{u} s_{cs} = \rho_{u} s_{L}\) is used. The resulting FSD formulation (Hawkes and Cant 2000) is given by:

$$\frac{\partial }{{\partial x_{i} }}\left( {\overline{{{\uprho }D\frac{\partial c}{{\partial x_{i} }}}} } \right) + \overline{{{\dot{\omega }}_{c} }} \approx {\uprho }_{u} s_{L} {\Sigma }$$
(8)

where \(\rho_{u}\) is density of the unburnt fluid. Subgrid flame wrinkling increases the flame surface density. This is considered through use of a flame wrinkling factor \({\Xi }\):

$${\Xi } = \frac{{\Sigma }}{{\left| {\nabla \overline{c}} \right|}}$$
(9)

which is modelled by a fractal approach based on the work of Fureby (2005) and Gouldin (1987).

$${\Xi } = \left( {1 + \frac{{\epsilon_{o} }}{{\epsilon_{i} }}} \right)^{{D_{f} - 2}}$$
(10)

\(D_{f}\) is a fractal dimension approximated as

$$D_{f} = \frac{{8/3 Ka_{{\Delta }} + 2c_{D} }}{{Ka_{{\Delta }} + c_{D} }}$$
(11)

with the constant \(c_{D}\) set to 0.03, and \(\epsilon_{o}\) and \(\epsilon_{i}\) are the outer and inner cut-off scales. In the context of Keppeler’s FSD model the expression translates into (Keppeler et al. 2014)

$${\Sigma } = C_{R} \left( {\frac{{2.2{\Delta }}}{{\max \left( {l_{F} Ka_{{\Delta }}^{ - 0.5} ,2l_{F} } \right)}}} \right)^{{D_{f} - 2}} \tilde{c}\left( {1 - \tilde{c}} \right)F\left( {\tilde{c}} \right)^{ - 1} \left| {\nabla \tilde{c}} \right|$$
(12)

the function \(F\left( {\tilde{c}} \right)\) is approximated by a polynomial (Keppeler et al. 2014), \(\left| {\nabla \tilde{c}} \right|\) is evaluated by the instantaneous resolved field and \(C_{R} = 4.5\) is a model constant (Keppeler et al. 2014). Finally, the subgrid Karlovitz number is defined as

$$Ka_{{\Delta }} = \left( {\frac{{u_{{\Delta }}{\prime} }}{{s_{L}^{0} }}} \right)^{\frac{3}{2}} \left( {\frac{{\Delta }}{{l_{F} }}} \right)^{ - 0.5}$$
(13)

with the sgs velocity fluctuation \(u_{{\Delta }}{\prime}\). Here the laminar flame thickness is defined by

$$l_{F} = \frac{{D_{th} }}{{s_{L}^{0} }}$$
(14)

where \(D_{th}\) is the thermal diffusivity of the unburnt mixture and \(s_{L}^{0} \left( {\phi ,T_{u} ,p_{u} } \right)\) is the unstretched laminar flame speed, while \(s_{L}\) represents the stretched laminar flame speed, which again requires modelling. It is approximated via the Markstein number (Ma) and a strain rate \(\kappa\)

$$s_{L} = s_{L}^{0} - Ma \cdot \kappa \cdot l_{F} \;\;\;\;{\text{or}}\;\;\;\;s_{L} = s_{L}^{0} \left( {1 - \frac{{Ma \cdot \kappa \cdot l_{F} }}{{s_{L}^{0} }}} \right)$$
(15)

The unstretched laminar flame speed \(s_{L}^{0}\) is calculated from an empirical correlation, which considers the dependence on overall pressure and unburnt temperature through a power law:

$$s_{L}^{0} \left( {\phi ,T_{u} ,p_{u} } \right) = s_{L,ref}^{0} \left( {\frac{{T_{u} }}{{T_{0} }}} \right)^{\alpha } \left( {\frac{{p_{u} }}{{p_{0} }}} \right)^{\beta }$$
(16)

\(s_{L,ref}^{0}\) is the flame speed at standard pressure and temperature (\(T_{u} = T_{0}\) and \(p_{u} = p_{0} )\) and \(\alpha\) and \(\beta\) are constants or mixture dependent parameters. The equivalence ratio dependence of \(s_{L,ref}^{0}\) is modelled following Gülder (1984):

$$s_{L,ref}^{0} \left( \phi \right) = Z W \phi^{\eta } e^{{ - \xi \left( {\phi - \sigma } \right)^{2} }}$$
(17)

where \(W,\eta ,\sigma\) and \(\xi\) are constants for the given fuel shown in Table 1, and \(Z = 1\) for single constituent fuels. The correlation is shown in Fig. 1 for methane/air at 300 K and a pressure of 1 bar.

Table 1 Coefficients for Eq. 17
Full size table
Fig. 1
figure 1

Laminar flame speed correlation (left) and Markstein number (right) witequivalence ratio

Full size image

The Markstein number is the ratio of the Markstein length and the flame thickness, typically based on correlations (Müller et al. 1997). In this work the model due to Driscoll et al. (2008) is used:

$$Ma\left( \phi \right) = 3.3 \phi - 2.3$$
(18)

The stretch \(\kappa\) effect is modeled by considering only strain rate effects and by neglecting curvature contributions, using the modified efficiency function \({\Gamma }\) from Hawkes et al. (2001) \(\kappa \approx \kappa_{s} = \kappa_{mean} + \kappa_{SGS}\)

$$\kappa_{mean} = \left( {\delta_{ij} - n_{ij} } \right)\frac{{\partial \tilde{u}_{i} }}{{\partial x_{j} }} ; \kappa_{SGS} = {\Gamma }\left( {\frac{{k_{SGS} }}{{s_{L}^{0} }},\frac{{l_{F} }}{{\Delta }}} \right)\frac{{\sqrt {k_{SGS} } }}{{\Delta }}$$
(19)

The species mass fraction for \({\text{CO}}_{2}\) and \({\text{H}}_{2} {\text{O}}\) are approximated here simply through a Burke-Schumann model (Lipatnikov 2017), assuming a linear relationship on mixture fraction \(z\) and progress variable \(c\):

$$\begin{gathered} z < z_{st} : Y_{{{\text{CO}}_{2} ,b}} = Y_{{{\text{CO}}_{2} ,st }} \frac{zc}{{Z_{st} }} , Y_{{{\text{H}}_{2} {\text{O}},b}} = Y_{{{\text{H}}_{2} {\text{O}},st}} \frac{zc}{{Z_{st} }} \hfill \\ z > z_{st} : Y_{{{\text{CO}}_{2} ,b}} = Y_{{{\text{CO}}_{2} ,st }} \frac{{\left( {1 - z} \right)c}}{{1 - z_{st} }} , Y_{{{\text{H}}_{2} {\text{O}},b}} = Y_{{{\text{H}}_{2} {\text{O}},st}} \frac{{\left( {1 - z} \right)c}}{{1 - z_{st} }} \hfill \\ \end{gathered}$$
(20)

where \(z_{st}\) is the stoichiometric mixture fraction and \(Y_{{{\text{CO}}_{2} ,st }} Y_{{{\text{H}}_{2} {\text{O}}, st}}\) are stoichiometric mass fractions of \({\text{CO}}_{2}\) and \({\text{H}}_{2} {\text{O}}\). In the context of LES subgrid effects are neglected due to a reasonably fine mesh used in the analysis.

Artificially Thickened Flame Model.

In this model a dynamic thickening factor thickens the premixed flame to approximately 5 computational cells (\(F = 5\)) based on the grid-adaptive technique (Charlette et al. 2002; Veynante et al. 2012; Jaravel 2016) and using a flame sensor derived by Durand (2007). The idea follows the philosophy that the flame thickness is proportional to \(D/S_{L}\). The formulation is further extended to multi-step chemistry by Guo et al. (2018), (Legier et al. 2000). The formulation of the dynamic thickening factor reads as follows:

$$F_{dyn} = 1 + S\left( {\max \left( {F\frac{{\Delta }}{{l_{F} }},1} \right) - 1} \right) ; S = {\text{tanh}}(C_{1} 16\left[ {c\left( {1 - c} \right)]^{2} } \right)$$
(21)

where \({\Delta }\) is LES filter size, \(S\) is the dynamic sensor function ensuring that that flame thickening is only applied in the flame region because the expression \(c\left( {1 - c} \right)\) is zero outside the flame and \(C_{1} = 100\) (Guo et al. 2018), (Legier et al. 2000).

The resolved wrinkling of the flame is reduced by the thickening, which is compensated through an increase in burning rate by introducing the efficiency function \(E\) which is based on the approach of Charlette et al. (2002) with the extension of Veynante et al. (2012):

$$E = \left( {\frac{{\Delta }}{{l_{F} }}} \right)^{\beta } = F_{dyn}^{\beta }$$
(22)

with \(\beta\) = 0.5. The modelled species and enthalpy equations after applying the thickening process and the gradient hypothesis (Lipatnikov 2017), as well as the assumption of unity Lewis-number, read:

$$\frac{{\partial \overline{\rho }\widetilde{{Y_{k} }}}}{\partial t} + \frac{{\partial \overline{\rho }\widetilde{{u_{j} }}\widetilde{{Y_{k} }}}}{{\partial x_{j} }} = \frac{\partial }{{\partial x_{j} }}\left[ {\overline{D}F_{dyn} E\frac{{\partial \widetilde{{Y_{k} }}}}{{\partial x_{j} }} + \left( {1 - S} \right)\frac{{\mu_{SGS} }}{{Sc_{t} }} \frac{{\partial \widetilde{{Y_{k} }}}}{{\partial x_{j} }}} \right] + \frac{E}{{F_{dyn} }}\overline{{\dot{\omega }_{k} }}$$
(23)
$$\frac{{\partial \overline{\rho }\tilde{h}}}{\partial t} + \frac{{\partial \overline{\rho }\tilde{h}\widetilde{{u_{j} }}}}{{\partial x_{j} }} = \frac{{\overline{Dp} }}{Dt} + \frac{\partial }{{\partial x_{j} }}\left[ {\overline{D}F_{dyn} E\frac{{\partial \tilde{h}}}{{\partial x_{j} }} + \left( {1 - S} \right)\frac{{\mu_{SGS} }}{{Sc_{t} }}\frac{{\partial \tilde{h}}}{{\partial x_{j} }}} \right] + \overline{\tau }_{ij} \frac{{\partial \widetilde{{u_{j} }}}}{{\partial x_{j} }} + \frac{\partial }{{\partial x_{j} }}\left[ {\overline{\rho }\mathop \sum \limits_{k = 1}^{N} h_{k} ,Y_{k} } \right] + \frac{E}{{F_{dyn} }}\overline{{\dot{\omega }_{h} }}$$
(24)

Here \(\widetilde{{Y_{k} }}\), \(\overline{{\dot{\omega }_{k} }}\), \(\overline{{\dot{\omega }_{h} }}\) are filtered mass fraction and reaction source terms in the transport equation for species \(k\) and enthalpy, respectively. Part of the ATF results shown here were already presented in Lampmann et al. (2019).

3 Test Case

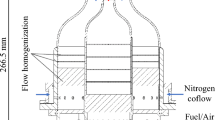
The burner has a concentric injector, the inner tube (\(d = 4 \;{\text{mm }}\)) of the injector is supplied with methane and is surrounded by an annular air flow (\(D = 7.5 \;{\text{mm }}\)). They are surrounded by a coaxial hot pilot and slow co-flow air streams. The axial position of the inner tube of the concentric injector tube is adjustable, allowing the combustion regime to change continuously from non-premixed to fully premixed (Barlow et al. 2015). The pilot coaxial stream consists of a stoichiometric mixture of nitrogen, acetylene, oxygen, hydrogen and carbon dioxide. It has similar C/H ratio as a stoichiometric methane/air mixture. The details of the simulated test case from Barlow’s experiments FJ200-5GP-Lr75-57 are provided in Table 2.

Table 2 Experimental SETUP
Full size table

4 Numerical Setup

The numerical simulations with the FSD model and ATF model are run on a 1 million cells hexahedral mesh. The cell size is about 0.5 mm at the inlet plane. The mesh is coarsened up to a cell size of 1 mm in the axial direction, starting at about 7D downstream of the evaluation plane (\(x/D = 20\)). An initial grid quality study has been performed in (Hansinger 2021) where it has been shown that, apart from a local region in the shear layer close to the nozzle, more than \(80\%\) of the (estimated) turbulent kinetic energy are resolved by the “coarse” mesh used in the present work. Combined with the fact that first FSD results were very promising compared to experimental data this mesh has been chosen as the baseline. The length and diameter of the simulated domain are 500 mm and 50 mm, respectively. Stoichiometric conditions of a fully burnt methane/air mixture are used in the simulations to model the pilot stream.

The inlet boundary conditions for instantaneous velocity and species composition of the fuel injector are taken from DNS results of inert mixing of the fuel and air (Zirwes et al. 2020). All combustion models are implemented into the open-source solver framework OpenFOAM [3430]. Temporal and spatial discretization schemes are second-order. The vanLeer scheme is used for convective terms of species and enthalpy equations. An adaptive time step is considered not exceeding a CFL number of 0.3. The WALE model is used to close the unresolved sgs terms (Nicoud and Ducros 1999).

We used two different chemical reaction mechanisms considering unity Lewis number (\(Le = 1\)) in combination with the ATF model for this study. The first one is an analytically reduced methane mechanism comprising 19 species and 184 reactions (Lu and Law 2008), not considering \({\text{NO}}_{x}\) formation. The second one is a reduced two-step mechanism (BFER). The chemical reaction rates are calculated by CANTERA (Goodwin et al. 2018) subroutines as described by Zirwes et al. (2020).

5 Results for the Baseline Mesh and Setup

Figure 2 compares snapshots of instantaneous velocity, temperature and \({\text{CO}}_{2} + {\text{H}}_{{2}} {\text{O}}\) mass fraction fields from FSD and ATF-Lu19 simulations in the central plane. The evaluation planes used in the line plots are located at \(x/D = 1, 5, 10, 15, 20, 30\) and are illustrated with white lines. There are noticeable qualitative differences between the results from both models.

Fig. 2
figure 2

Velocity magnitude, temperature and \({\text{CO}}_{2} + {\text{H}}_{2} {\text{O}}\) mass fraction with evaluation planes at \(x/D = 1, \,5,\, 10,\, 15, \,20\) for ATF (top) and FSD (bottom) [Domain sliced in radial-axial direction]

Full size image

One can clearly see higher velocity magnitudes in the core region of the ATF instantaneous velocity field for \(x/D > 20\) whereas the FSD results depict a faster decrease of centerline velocity indicating higher turbulence intensity and earlier jet breakup in the case of the FSD simulation. This induces an increased diffusive heat exchange between pilot and jet stream for the ATF model compared to FSD. The products mass fraction field (\({\text{CO}}_{2} + {\text{H}}_{2} {\text{O}}\)) is similar for both models close to inlet. Further downstream, the ATF mass fractions spread wider in the radial direction which is not seen in the case of the FSD model, again hinting at a larger effective ATF diffusivity.

5.1 Mean and RMS Flow Quantities

Figure 3 shows the temporally and circumferentially Favre-averaged mean and RMS profiles of temperature \(T\), mixture fraction \(z\) and \({\text{CO}}_{2} + {\text{H}}_{{2}} {\text{O}}\) mass fraction for all models together with the experimental results at different axial positions, normalized with burner pipe diameter \(D\). Mean flow quantities and their corresponding RMS values have been obtained from the simulations by averaging over 10 ms following earlier work (Lampmann et al. 2019; Hansinger 2021). Results have not only been averaged in time but also in circumferential direction and it has been ensured that halving or doubling the integration time did not change any of the findings reported in this paper. Next, the FSD and ATF model radial profiles are compared to experimental data (Barlow et al. 2015).

Fig. 3
figure 3

Favre- averaged mean and RMS values in radial direction for temperature \(T\), mixture fraction \(z\) and \({\text{CO}}_{2} + {\text{H}}_{2} {\text{O}}\) mass fraction at different axial positions. The dashed gray line in the mixture fraction profiles indicates the value \(z_{st} .\)

Full size image

While the ATF simulations considerably overpredict the mean temperature and underpredict the temperature fluctuations, the FSD-S (i.e. FSD including Stretch) temperature profiles at all planes are in very satisfactory agreement with experiment. The overprediction of temperature in the ATF simulations are assumed to be caused by the overprediction of mixture fraction in the outer flame region, which is closer to \(z_{st}\) (compared to FSD-S) and hence results in higher temperatures. Similar to (and consistent with) the temperature profile, the formation of product species \({\text{CO}}_{2} + {\text{H}}_{2} {\text{O}}\) is overpredicted by the ATF-Lu19 and ATF-2step, the maximum being skewed towards larger radii, while the FSD model predictions of \({\text{CO}}_{2} + {\text{H}}_{2} {\text{O}}\) again are rather accurate. The correlation between T and \({\text{CO}}_{2} + {\text{H}}_{2} {\text{O}}\) behavior is expected because \({\text{CO}}_{2}\) and \({\text{H}}_{2} {\text{O}}\) reactions are responsible for the major heat release.

All models show a similar behavior of mixture fraction close to the inlet plane (\(x/D\) = 1, 5). In the core jet stream, \(z\) is overpredicted and a sharp decline towards the pilot is observed. The problem in accurate prediction of mixture fraction particularly close to chamber axis has been reported by other groups, even with a quasi-DNS approach (Zirwes et al. 2020). Further downstream, mean mixture fraction is predicted very well by the FSD-S model. Similar to experiments, one can observe an axial decline in mixture fraction, notably in the core jet stream, which is slower in case of the ATF models.

The stretch effects play an important role in the present FSD model of the partially premixed flame. This can be illustrated by removing the stretch effects and the corresponding model will be called FSD-UN. The FSD-S and the FSD-UN models differ only by the stretched and unstretched laminar burning speed, profiles of which are shown in Figs. 4 and 5.

Fig. 4
figure 4

Favre- averaged mean values of flame speed in radial direction using FSD-S and FSD-UN models

Full size image
Fig. 5
figure 5

Mean flame speed (stretched and unstretched) conditioned on mixture fraction \(z\) using FSD-S and FSD-UN models

Full size image

The mean stretched laminar flame speed is smaller by about 15–20% at all axial positions which illustrates the sensitivity of the model to stretch effects. Figure 5 shows that the FSD-S flame speed is particularly decreased towards the rich side of the flame which is expected from the Markstein correlation shown in Fig. 1, while the peak flame speed does not change for FSD-UN and remains at a magnitude of 0.4 m/s.

Another important observation is that stretch effects are predominant in the shear layer between the central jet and the pilot, where highest variance in the temperature peaks is observed.

5.2 Scatter Plots

Figure 6 illustrates instantaneous snapshots of the temperature in an entire cut plane conditioned on the mixture fraction. Scatter plots offer qualitative assessment of the underlying combustion modes and flame structure specific to the used combustion model.

Fig. 6
figure 6

Temperature scatter plots \(T\) over mixture fraction \(z\) at different axial locations

Full size image

Each row depicts all models including experimental data at a different axial location \(x/D\). The first column shows the experimental data, followed by FSD models and ATF models. One can clearly see the flame transition from a premixed flame at the inlet (\(x/D = 1\)) to a diffusion flame (non-premixed) towards the exit in the experimental data. At stoichiometry \(z = 0.055\), we observe a kink and too high maximum temperatures in FSD and two-step ATF model results, typical for one/two-step chemistries. A similar effect is not present in the ATF-Lu19 multi-step chemistry result and in the experiment. At \(z < 0.1\), the FSD-S and to a lesser extent the FSD-UN simulations capture some extinction and re-ignition while it is hardly noticeable in both ATF results. The extinction effect in FSD-S intensifies as \(x/D\) increases similar to the experiment.

Figure 7 illustrates the mean temperature plots conditioned on the mixture fraction \(z\) for each evaluation plane have been obtained from the scatter date by averaging the scatter data over mixture fraction in bins of \({\Delta } z = 0.001\) based on the scatter plots respectively. At small \(x/D\), near stoichiometric temperatures are only well predicted by the ATF-Lu19 simulation consistent with the scatter plots. On the rich side (\(z > 0.055\)) FSD-S predicts the most accurate conditional temperatures while FSD-UN and also both ATF models overestimate it here. In case of the ATF models the reason may be the lack of local extinction seen in the scatter plots in contrast to experiment and FSD-S model results.

Fig. 7
figure 7

Mean temperature \(T\) conditioned on mixture fraction \(z\)

Full size image

The possible explanations for the less accurate ATF predictions are (i) the increased diffusivity inherent in the model, (ii) the unity Lewis number assumption that has been made (\(Le_{k} = 1\)) which results in the wrong laminar flame speed even on asymptotically refined meshes and (iii) the absence of stretch effects in the model. These possible deficiencies of the ATF more are further analysed and possible remedies are discussed in the second part of results.

6 Results for Refined Mesh and Improved Simulation Setup

We further investigated the setup by doing local mesh refinement and also considering differential diffusion in the species transport equations with Lu19 mechanism. The refined mesh contains 4.8 million cells. The local refinement is applied in the core region of the fuel jet and where the shear layers between jet and pilot feature strong velocity gradients that should be reasonably resolved. The comparison of cell size \({\Delta }\) is shown in Fig. 8 calculated as \({\Delta } = \sqrt[3]{V}\), where \(V\) represents the cell volume. The index M15 represents the baseline mesh used already in the first part of the results and the index M48 represents the refined mesh. The simulations have been repeated on the refined mesh also considering differential diffusion. Table 3 gives an overview of the different case setups.

Fig. 8
figure 8

Filter width \({\Delta }\) of meshes over radial position \(r\) at different axial planes

Full size image
Table 3 Overview of numerical setups with refined mesh and differential diffusion
Full size table

6.1 Mean and RMS Flow Quantities

Figure 9 presents Mean and RMS profiles of temperature, mixture fraction, \({\text{CO}}_{2} + {\text{H}}_{2} {\text{O}}\) and exemplarily mass fractions \({\text{CO}}\) and \({\text{H}}_{2}\) for the cases presented in Table 3. Mean temperature profiles improved after considering differential diffusion in the species transport. This effect might be due to a more correct prediction of the flame speed when using differential diffusion. Using a detailed methane mechanism with Le = 1, the laminar flame speed can be underpredicted by 20%, see Pfitzner et al. (2021). It is also noted that magnitude of turbulent diffusion is very low compared to laminar diffusion, so the differential diffusion effect will be felt in the simulations in particular on fine meshes and for lean species that strongly deviate from the unity Lewis number assumption. The results using mesh refinement together with the differential diffusion Lu19, ATF model shows very good agreement with the experiments especially in the downstream region. The refined grid reduces the sub-grid contributions, leading to an increase in ATF model accuracy. The agreement of RMS fluctuations with experiment also improved with mesh resolution to a satisfactory level.

Fig. 9
figure 9

Favre averaged mean and RMS values in radial direction for temperature \(T\), mixture fraction \(z\), \({\text{CO}}_{2} + {\text{H}}_{2} {\text{O}}\), \({\text{CO}}\) and \({\text{H}}_{2}\) mass fraction at different axial positions

Full size image

The flame surface density model simulated on the refined mesh (FSD-S-M48) gives nearly the same results as FSD-S presented in the Fig. 3 on the coarser mesh. This illustrates that the FSD model is less dependent on mesh resolution compared to the ATF model. For case ATF19-Diff-M48, mean mixture fraction magnitudes, notably at the jet center, are predicted very well and decline sharply similar to the experiment. Similar to (and consistent with) the temperature profile, the formation of product species \({\text{CO}}_{2} + {\text{H}}_{2} {\text{O}}\) is predicted well by the ATF-19-Diff-M48. The mean mass fraction profiles of \({\text{CO}}\) and \({\text{H}}_{2}\) are also predicted well in cases ATF19-Diff-M15 and ATF19-Diff-M48 at all axial planes. However, we observe huge differences in mass fraction profiles between the unity Lewis simulation ATF19-Le1-M15 and simulations considering non-equal Lewis numbers, i.e. ATF19-Diff-M15.

Figure 10 illustrates the scatter plots for the cases presented in the Table 3. In the rich region \(z > 0.05\), we observe increased scattering for case ATF19-Diff-M15 compared to the unity Lewis number case ATF19-Le1-M15. Using the refined mesh with differential diffusion (ATF19-Diff-M48) we observe similar amount of scatter as in the experiments. At \(z < 0.1\), the ATF19-Diff-M48 and to a lesser extent the ATF19-Diff-M15 simulations capture some extinction and re-ignition. The extinction effect in ATF19-Diff-M48 intensifies as \(x/D\) increases similar to the experiment.

Fig. 10
figure 10

Temperature scatter plots \(T\) over mixture fraction \(z\) at different axial locations

Full size image

Figure 11 illustrates the mean temperature plots conditioned on the mixture fraction \(z\) for each evaluation plane. On the rich side (\(z > 0.055\)) ATF19-Diff-M15 and ATF19-Diff-M48 predict more accurate conditional temperatures compared to ATF19-Le1-M15. The reason might be the increased prediction of extinction in the scatter plots, similar to the experiment. FSD-S-M48 results are in good agreement with experiments and similar to FSD-S in Fig. 7.

Fig. 11
figure 11

Mean temperature \(T\) conditioned on mixture fraction \(z\)

Full size image

The CO scatter data in Fig. 12 indicate similar behavior for \({\text{CO}}\) mass fraction as observed for \(T\) in Fig. 10. The CO scatter plots for ATF19-Diff-M15 and ATF19-Diff-M48 are in very good agreement with experiments. As \(x/D\) increases, the scattering also intensifies for case ATF19-Diff-M48 similar to experiment. The conditioned mean mass fractions for \({\text{CO}}\) and \({\text{H}}_{2}\) are presented in Figs. 13 and 14, respectively. The peaks in \({\text{CO}}\) and \({\text{H}}_{2}\) at small \(x/D\), near stoichiometry are underpredicted in models with differential diffusion and over predicted for unity Lewis number. At rich regions \(z > 0.05\), the cases ATF19-Diff-M15 and ATF-Diff-M48 predict accurate conditional mean \({\text{CO}}\) and \({\text{H}}_{2}\) mass fractions while ATF19-Le1-M15 overpredicts the peaks at all axial planes and remains inaccurate at the rich side, possibly caused by the lack of scattering seen in Fig. 11.

Fig. 12
figure 12

\({\text{CO}}\) scatter plots over mixture fraction \(z\) at different axial locations

Full size image
Fig. 13
figure 13

Mean CO mass fraction conditioned on mixture fraction \(z\)

Full size image
Fig. 14
figure 14

Mean H2 mass fraction conditioned on mixture fraction \(z\)

Full size image

6.2 Wasserstein Metric

After the qualitative assessment of the results an additional quantitative comparison between different ATF simulations is provided by using the Wasserstein metric proposed by Johnson et al. (2017). The analysis concentrates on comparing the scatter plots of temperature \(T\) and species mass fractions of \({\text{CO}}_{2} , {\text{CO}}\) and \(H2\) at five axial locations \(x/D = \left( {1, 5, 10, 15, 20, 30} \right)\). The Wasserstein metric W2(\({\text{T}},{\text{YCO}}_{2} ,{\text{YCO}},{\text{YH}}_{2}\)) in Fig. 15 shows the cumulative contributions of each scalar quantity to the overall stacked error of these particular scalar quantities. It provides a direct representation of the error: a numerical value of W2 = 0.6 corresponds to an error of 0.6 times the standard deviation of that particular quantity with respect to the experimental data. It can be observed that the ATF model with unity Lewis number ATF19-Le1-M15 exhibits a small error contribution from temperature relative to the contributions from \({\text{CO}}\) and \({\text{H}}_{2}\) mass fraction. In contrast, the simulations with differential diffusion show smaller error contributions from \({\text{CO}}\) and \({\text{H}}_{2}\) mass fraction. Another observation can be drawn by considering the axial evolution of the W2 metric. Especially for simulations ATF19-Diff-M15 and ATF19-Diff-M48 the error reduces with increasing axial distance, while the large errors at \(x/D = 1\) might be attributed to uncertainties in the boundary conditions, as remarked in Pfitzner and Breda (2021). It is noted that the improved temperature prediction seen in the radial plots in Fig. 9 is not clearly visible in the Wasserstein metric which does not account for distribution in space.

Fig. 15
figure 15

Comparison and contribution of single quantities to stacked W2 metric at different axial positions for ATF simulations

Full size image

6.3 Computational Times

Finally, the simulation times for all cases are compared in Fig. 16. All simulations have been carried out on a local inhouse compute cluster with 12 nodes on 24 CPU cores made of Intel Xenon E5 v1- v4. All simulation setups are decomposed into 336 processors and simulated for same amount of time. As expected we observe that both simulations on the refined mesh consume proportionally more computational time than the increase in total mesh size, but this effect is more pronounced for the ATF model. Further, it becomes evident that the ATF model consumes roughly a factor of 4 more computational time than the FSD model on the refined mesh. Finally, we observe a small computational overhead when considering differential diffusion compared to a unity Lewis number assumption (14.09%).

Fig. 16
figure 16

Comparison of computational times of simulations

Full size image

7 Summary and Conclusion

An LES study employing a flame surface density model has been performed for the Sydney piloted, inhomogeneous inlet, methane/air configuration FJ200-5GP-Lr75-57. FSD results are compared to results from two simulations using the artificially thickened flame model with two-step and detailed chemistry as well as experimental results. The FSD model including the modelled stretch effects yielded more accurate results both in premixed and non-premixed zones compared to the ATF model with multi-step and two-step chemistry. While all models perform reasonably well in the premixed region, the ATF model accuracy decreases further downstream and particularly for rich conditions. As expected, too high maximum temperatures are seen when using one-step and two-step chemistry. It is speculated that the deficiencies of the ATF models for this configuration are due to the increased diffusivity inherent in the model, delaying mixing and jet breakup, as well as the absence of stretch effects which seems to be of particular importance towards the rich side of the flame. These deficiencies are further addressed by considering differential diffusion in ATF model. The new ATF simulations with differential diffusion improved model accuracy in the downstream region dominated by non-premixed combustion. In addition, a mesh refinement study revealed the high sensitivity of the ATF model to mesh resolution. ATF model on refined mesh together with differential diffusion overcame the deficiencies and showed improved accuracy and performance of model. The FSD model performed very well and showed little change in results when increasing the mesh resolution. The application of Wasserstein metric allowed to identify competing contributions to model deviations and model deficiencies in case of the ATF model. It helped to condense multi scalar differences within the ATF data and the experiments into a single quantitative error measure. The FSD model consumed less computational time compared to the ATF model setups on similar grids while yielding mesh converged solutions on coarser grids already.

In summary the key findings of the present analysis can be summarized as follows:

  1. 1.

    Simple FSD model, when combined with suitable flame speed and stretch expressions, can be quite successful in prediction partially premixed flames including to some extent local extinction events.

  2. 2.

    Compared to the FSD model the ATF model requires a finer computational mesh to achieve the same level of accuracy, which can be attributed to the artificial thickening

  3. 3.

    For skeletal or detailed chemical mechanisms the assumption of unity Lewis number can lead to wrong laminar flame speeds which affects the overall accuracy of the results.

This work initiates potential future investigations on different burner configurations and different fuels such as hydrogen blends, featuring non-unity Lewis number effects.