1 Introduction

The clustering of intertial particles in incompressible turbulent flow has been established using experimental, numerical and theoretical investigations. Much of the early observation of the preferential concentration of inertial particles in turbulent flow was through observing the particle concentration field from direct numerical simulations (DNS) (Maxey 1987; Squires and Eaton 1991; Wang and Maxey 1993; Eaton and Fessler 1994). Particle clustering was also observed in a variety of experimental studies (Fessler et al. 1994; Wood et al. 2005; Aliseda et al. 2002; Salazar et al. 2008). The DNS and experimental studies have been complemented by numerous theoretical studies that have focused on describing and predicting the mechanisms behind the clustering of particles at sub-Kolmogorov scales. (Chun et al. 2005; Balkovsky et al. 2001; Bec 2003; Zaichik and Alipchenkov 2003; Gustavsson and Mehlig 2011). Understanding the dynamics of particles suspended in turbulent flows is valuable for a wide range of problems, with a majority of studies dedicated to understanding atmospheric cloud formation. In clouds, the implications of particle clustering may be significant; standard microphysics models are unable to explain the rapid cloud droplet growth in the intermediate size range of 15–40 μm where neither condensational growth or growth due to gravitational collision-coalescence are effective (Grabowski and Wang 2013). It has been shown that turbulence intermittencies and an interplay between turbulence and gravity increases the inertial effects leading to an accelerated formation of larger droplets (Falkovich et al. 2002). However many open questions still remain, making this an active field of research.

The physical mechanism behind particle clustering was first discussed by Maxey (1987) who showed that the velocity divergence of the particle flow field was positive in regions of high vorticity and negative in regions of high strain rate. Maxey (1987) predicted that (weakly) inertial particles would hence be ’centrifuged’ out of vortex cores and accumulate preferentially in regions of low vorticity or high strain rate. Studies have since suggested alternative mechanisms by which particle clustering occurs, which includes (among others) the ergodic-non-ergodic mechanism (Duncan et al. 2005; Gustavsson and Mehlig 2011) and the ’sweep-stick’ mechanism (Chen et al. 2006; Goto and Vassilicos 2006). More recently, in a series of papers (Bragg and Collins 2014a, b; Bragg et al. 2015a, b), the physical mechanism behind the clustering of inertial particles have been studied in detail across the dissipative and inertial scales. It was shown that the centrifuging mechanism is dominant for \(St \ll 1\) where \(St = \tau _p/\tau _\eta\) is the Stokes number based on the particle response time \(\tau _p\) and the Kolmogorov time scale \(\tau _\eta\). A non-local, symmetry breaking path-history mechanism takes over for higher Stokes numbers. This was also confirmed by DNS studies of inertial particles in isotropic turbulence by Ireland et al. (2016b) who observed preferential sampling for \(St < 0.1\) and non-local effects for \(St>0.2\).

Different methods have been used to quantify and characterize inertial particle clustering, with a few popular examples being bin counting (Wang and Maxey 1993; Eaton and Fessler 1994; Wood et al. 2005), radial distribution functions (RDF) (Sundaram and Collins 1997; Reade and Collins 2000), Lyapunov exponents (Bec et al. 2006) and Voronoi analyses (Monchaux et al. 2010; Baker et al. 2017; Huck et al. 2018; Petersen et al. 2019; Momenifar and Bragg 2020). In this work, we will be working extensively with the RDF which is defined as the ratio of the probability of finding particle pairs at a certain separation distance to the probability of finding particle pairs at the same separation in a uniformly distributed particle field, and is one of the most widely used tools to study particle clustering. The RDF is an important tool as it provides a scale dependent quantification of clustering and also appears as a correction to the kinematic collision kernel. Sundaram and Collins (1997) quantified the role of particle clustering on droplet collisions by multiplying the collision kernel calculated by Saffman and Turner (1956) with the RDF calculated at the point of collision for a monodisperse distribution of particles in homogeneous isotropic turbulence. DNS studies have shown that turbulence can enhance the collision kernel relative to stagnant flow through an increase in both the relative velocities of the colliding droplets as well as the increase in the RDF (Franklin et al. 2005, 2007; Ayala et al. 2008b). Reade and Collins (2000) showed that the RDF can have values up to a 100 at separation distances equal to the collision radius further highlighting the importance of clustering towards the collision process. They modelled the monodisperse RDF \(g_{11}\) using DNS data (at Taylor Reynolds number \(Re_{\lambda } = 54.5\)) of non-sedimenting particles in homogeneous isotropic turbulence and suggested the following function:

$$\begin{aligned} g_{11}({\hat{r}},St) = 1 + c_0 {\hat{r}}^{-c_1}\text {exp}[-c_2{\hat{r}}]. \end{aligned}$$
(1)

Here \({\hat{r}} = r/\eta\) where r is the inter-particle separation distance and \(\eta\) is the Kolmogorov length scale. The coefficients \(c_0\), \(c_1\) and \(c_2\) are all functions of St in principle. The study reveals an inverse power-law of the form \({\hat{r}}^{-c_1}\) at small \({\hat{r}}\), and transitions into an exponentially decaying tail at higher \({\hat{r}}\). Chun et al. (2005) derived an analytical expression for the RDF of a monodisperse collection of particles with \(St \ll 1\) as

$$\begin{aligned} g_{11}(r) = c_0 {\hat{r}}^{-c_1}, \end{aligned}$$
(2)

which is equivalent to Eq. (1). They showed that in a monodisperse distribution, the power-law dependence arises from a balance between an inward drift velocity caused by the particle inertia (inertial particles sample more strain than rotation giving rise to a net inward drift velocity) and a diffusion due to the random nature of the flow. For particles with different Stokes numbers, an additional diffusion arises due to the different particle response times to the local turbulent accelerations. This tends to homogenise the particle pair concentration leading to a reduction in the RDF. The additional acceleration diffusion term is independent of \({\hat{r}}\) and the resulting behaviour of the RDF is a power law dependence (\({\hat{r}}^{-c_1}\)) at larger scales and a transition to a plateau (independent of \({\hat{r}}\)) at smaller scales. An expression is also derived for the cross-over length scale \(r_c\) at which this transition occurs.

There are also numerous studies on particle clustering using tools from dynamical systems. These studies reveal that preferential concentration follows from the dissipative nature of particle dynamics (due to the Stokes drag) and in the position-velocity phase space, the particle trajectories converge to a dynamically evolving fractal attractor (Bec 2003; Bec et al. 2006, 2007). In such studies, the correlation dimension (\(D_2\)) of the spatial distribution is often used to quantify particle clustering and is also related to the exponent \(c_1\). This is an important quantity and has been investigated in detail in Gustavsson et al. (2015).

The presence of gravity adds complexity and breaks the spherical symmetry in particle pair concentration as well as relative velocities between two neighbouring particles. The effect of gravity on two-point particle statistics is extremely important for cloud microphysics and has been studied using DNS for monodisperse distributions recently by Bec et al. (2014); Gustavsson et al. (2014); Ireland et al. (2016a); Baker et al. (2017), and for bidisperse distributions by Ayala et al. (2008a); Woittiez et al. (2009); Dhariwal and Bragg (2018); Momenifar et al. (2019). The effect of gravity is quantified by the Froude number Fr which is defined as the ratio between the turbulent acceleration and the acceleration due to gravity. Bec et al. (2014) studied the interactions between turbulence, gravity and particle sizes by combining DNS with theoretical results based on their asymptotic analysis. They observed that gravity acted in a non-uniform manner depending on the values of Fr and St. For \(Fr \ll 1\), gravity suppresses clustering for \(St \lesssim 1\) and increases clustering for \(St \gtrsim 1\) whereas for moderate values of Fr and St, clustering is enhanced. Gustavsson et al. (2014) analyzed the effect of gravity by using perturbation theory in the Kubo number (a dimensionless correlation time) and derived a theory to describe the clustering of particles falling through a turbulent flow. A model system was analyzed where particles are subject to gravity in a random two-dimensional velocity field. The inertial particle response to turbulence fluctuations and gravity are not found to the additive. They found a similar non-uniform effect of gravity behaviour and found that particles at small and intermediate values of St falling at finite Fr tend to cluster less due to the reduced correlation between particles and flow structures whereas for particles with higher values of St, clustering of settling particles is enhanced.

Ayala et al. (2008a) extended the relations from Chun et al. (2005) for monodisperse sedimenting particles in a turbulent flow. The power law coefficients were assumed to be functions of a non-dimensional parameter for gravity \({g}/(u_\eta /t_\eta )\) (this can also be interpreted as the inverse Froude number—\(Fr^{-1}\), where g is the acceleration due to gravity, \(u_{\eta }\) and \(t_{\eta }\) are the Kolmogorov velocity and time scales respectively) in addition to St and the Taylor Reynolds number \(Re_{\lambda }\), and empirical expressions were generated by curve-fitting to DNS data. A similar procedure was followed to obtain expressions for the bidisperse distribution and the cross over length scale \(r_c\). In addition to particle clustering, the effect of gravity on the relative velocities and preferential concentration of colliding particles was explored by Woittiez et al. (2009), Ireland et al. (2016a) and Dhariwal and Bragg (2018) using DNS. The rate of collisions of sedimenting particles was found to be lower than non-sedimenting particles for a monodisperse distribution. For a bidisperse distribution, the higher relative velocities due to gravity enhanced particle accelerations resulted in a higher rate of collisions.

In this study, particle clustering is analysed in decaying turbulence. In the unique setup adopted here, turbulent flow structures are evolving in both time and space and accordingly particles interact with evolving flow scales. Previous works mentioned in this section were carried out using deterministic forcing schemes which generated statistically stationary turbulence. The RDF which appears as a correction to the collision kernel is explored in significant detail in this work. This study marks the first time an attempt has been made to study the RDF across a range of scales in decaying turbulence to our knowledge. Additionally, we generate models for the kinematic collision kernel for both non-sedimenting and sedimenting particles. This is a significant contribution of this work. A complete analytical model is of course not created, however we have created a framework with a robust set of carefully chosen functions which can help determine the particle statistics. For this, we have relied on previously existing analytical and also generated new empirical relations using a series of non-linear regression analyses utilizing the significant DNS data generated specially for this work.

The paper is structured as follows. In Sect. 2, the case setup is presented along with the characteristics of the turbulence and the relevant droplet parameters. In Sect. 3, the results for both monodisperse and bidisperse RDFs are presented with comparisons to theoretical predictions. In Sect. 4, the effect of gravity on the geometric collision kernel is presented and models are created for the collision kernels. Section 5 includes a discussion of the results along with concluding remarks.

2 Simulations

2.1 Case Setup

A novel decaying turbulence case is presented that closely resembles the flow in wind tunnel experiments. In wind tunnel experiments, grid-generated turbulence decays as the fluid moves downstream. The numerical case setup in this study aims to simulate the decaying turbulence by capturing the temporal evolution of a fluid section exiting the grid. Hence the simulations are temporal flow experiments and are similar to observing and following a fluid section through a camera which is being translated along an axis \({\tilde{x}}\) at a velocity equal to the mean flow speed U.

The wind tunnel setup used by Bateson and Aliseda (2012) is taken as a reference for flow characteristics and grid dimensions. Simulating the motion of an active grid is difficult to achieve numerically. We circumvent this by simulating the turbulent flow just downstream of a passive grid with mesh spacing \(G = {0.1016}\,{m}\). The average fluid velocity \({\tilde{u}}\) just downstream of the grid is \(U_g = Q/(A - A_{obs})\) between the grid, and zero at the grid. Here Q is the flow rate and \(A_{obs}\), A are the obstructed and total area of the grid respectively. The frame of reference for the numerical simulation is obtained by applying a Galilean transformation \(x \rightarrow {x} - U{t}\) where \(U = Q/A\). In the moving frame of reference, the initial condition u is given by

$$\begin{aligned} u = {\left\{ \begin{array}{ll} -U &{} \text {at grid } \\ U_g - U &{} \text {otherwise. } \end{array}\right. } \end{aligned}$$

The flow is then perturbed with random white noise and allowed to transition with time into isotropic, homogeneous turbulence.

The governing equations of the flow are given by the continuity equation and the incompressible Navier–Stokes equations

$$\begin{aligned} \nabla \cdot {\textbf {u}}&= 0, \end{aligned}$$
(3a)
$$\begin{aligned} \frac{\partial {\textbf {u}}}{\partial t} + {\textbf {u}} \cdot \nabla {\textbf {u}}&= - \nabla P + \nu \nabla ^2 {\textbf {u}}, \end{aligned}$$
(3b)

where \({\textbf {u}}\) = (u, v, w) is the velocity vector, P is the kinematic pressure and \(\nu\) is the kinematic viscosity. Particle motion is governed by the simplified Maxey-Riley equations (Maxey and Riley 1983)

$$\begin{aligned} \frac{\text {d}{\textbf {v}}(t)}{\text {d} t}&= \frac{{\textbf {u}}({\textbf {x}}(t),t) - {\textbf {v}}(t)}{\tau _p} + {{\textbf {g}}}, \end{aligned}$$
(4)
$$\begin{aligned} \frac{\text {d}{\textbf {x}}(t)}{\text {d} t}&= {\textbf {v}}(t), \end{aligned}$$
(5)

where \({\textbf {x}}(t)\) and \({\textbf {v}}(t)\) are the particle position and velocity vector respectively, \(\tau _p = 2\rho _p R^2/9\rho \nu\) is the particle inertial relaxation time with R the particle radius, \(\rho _p\) the particle density and \(\rho\) the fluid density. Also, \({\textbf {g}} = g{\textbf {e}}_x\) where g is the acceleration due to gravity and \({\textbf {e}}_x\) is the unit vector along \({\hat{x}}\). Here, \({\hat{x}}\) was chosen instead of the more conventional \({\hat{z}}\), as choosing \({\hat{z}}\) caused heavy droplets to rain out in our smaller domain (compared to the wind tunnel cross-section) due to the non-periodicity in \({\hat{z}}\) (more on this in the following subsection). Since the turbulence is homogeneous and isotropic, gravity can be defined in any direction.

2.2 Numerical Simulation Details

The DNS code SPARKLE is used, which solves the incompressible Navier–Stokes equations under the Boussineq approximation, and transport equations for scalars to fourth-order accuracy. Details of the numerical method used in SPARKLE and other details can be found in Craske and van Reeuwijk (2015). A tricubic Hermite interpolation scheme is used to interpolate the Eulerian flow velocities to the particle locations. A third order Adams-Bashforth time-stepping scheme is used to advance the particle locations and velocities at each time step. The particles on processor boundaries are communicated across processors after each time integration step following the flow field (Perrin and Jonker 2015; Nair et al. 2021). The collision algorithm implemented in SPARKLE follows the general scheme in Allen and Tildesley (1987) where hard sphere molecular dynamics is solved. More details of the numerical implementation of the particle routine can be found in Nair (2021). Only particles that can collide within one time step are considered as prospective colliding pairs. Also, only binary collisions are considered and colliding particles are allowed to geometrically overlap post-collision (ghost collisions), i.e. no post-collision dynamics are calculated for the particles. Since we only look at geometric collisions, the effects of collision efficiencies are ignored. The code also calculates the kinematic collision kernel (using Eq. 16). The kinematic collision kernel has been validated against the dynamic collision kernel using DNS (Nair 2021, P. 67).

Table 1 Turbulence parameters at \(x = Ut\) for a simulation with an isotropic grid spacing \(\Delta x\)
Full size table

A cubic domain is discretized using 1024\(^3\) grid cells. Time-steps are dynamically calculated with a Courant–Friedrichs–Lewy (CFL) number of 0.4. The kinematic viscosity of air \(\nu = {1\times 10^{-5}}\hbox {m}^2\hbox {s}^{-1}\). Periodic boundary conditions are imposed along the \({\hat{x}}\) and \({\hat{y}}\) axes, and a free slip condition is imposed along the \({\hat{z}}\) axis. The domain thus resembles a wind tunnel with frictionless side walls. The simulation was run for 1.1s. The computational domain is parallelized in the \({\hat{x}}\) and \({\hat{y}}\) directions using 4096 processors.

The number of particles required to reach a target droplet volume fraction of \({\mathcal {O}}(10^{-5})\) in a numerical domain whose sizes matches that of the wind-tunnel test section would be prohibitive (in terms of computational cost). Hence we calculate the two-point spatial correlation by determining the normalized spatial correlation tensor \(R_{ij}(r) = \displaystyle {\overline{u_i'({\textbf {x}})u_j'({\textbf {x}}+r)}}/{(\overline{u_i'^2u_j'^2})^{1/2}}\), where \(u'_i\) is the fluctuation from the mean for the instantaneous velocity field u. A length scale \(L_{11}\) indicative of the size of the largest eddies in the flow can then be calculated by \(L_{11} = \displaystyle \int _{0}^{L}R_{11} \, dr\), hence allowing us to determine domain sizes accordingly. We find that the value of \(L_{11} = {0.06}\,\hbox {m}\) at \(t = {1}\hbox {s}\) in a simulation without particles and a numerical domain of size \({1.2}\,\hbox {m} \times {1.2}\,\hbox {m} \times {1.2}\,\hbox {m}\). Accordingly, a numerical domain with a side length of \({0.509}\,\hbox {m}\) is chosen which is around ten times the length scale \(L_{11}\) and which is also almost half the size of the wind tunnel cross-section. This allows us to reach the target volume fraction with a computationally reasonable number of particles and also avoid any confinement effects due to the size of the domain.

Fig. 1
figure 1

a Volume averaged values for the velocity fluctuations, b normalized dissipation rates for the turbulence in the numerical domain and c Froude number Fr, Taylor Reynolds number (\(Re_{\lambda }\)) and Stokes number (St) for a droplet of radius \({15}\,\upmu \hbox {m}\) as a function of time

Full size image

2.3 Turbulence and Droplet Characterization

Table 1 shows characteristic values of the turbulent flow at \(x = Ut\). The mean turbulent kinetic energy in the domain can be characterized as \(\displaystyle {\overline{k}} = \frac{1}{2}\overline{ u'_iu'_i}\), where summation is implied over repeated indices. The large-scale eddies of the flow are characterized by the integral velocity (\(u_e\)) and length (\(L_e\)) scales. The integral velocity scale is given by the root-mean square value of the velocity fluctuations, \(u_{e} = u_{rms} = \displaystyle {2}/{3}{\overline{k}}^{1/2}\). The integral length scale is given by \(L_e = \displaystyle {\overline{k}}^{3/2}/{\overline{\varepsilon }}\) where \({\overline{\varepsilon }}\) is the mean kinetic energy dissipation rate, and the large-eddy turnover time \(\tau _e = u_e/L_e\). The small-scale turbulence can be characterized by the Kolmogorov length \(\eta = (\nu ^3/{\overline{\varepsilon }})^{1/4}\), velocity \(u_{\eta } = (\nu {\overline{\varepsilon }})^{1/4}\) and time \(\tau _{\eta } = (\nu / {\overline{\varepsilon }})^{1/2}\) scales. The velocity profiles averaged over the \({\hat{y}}-{\hat{z}}\) plane and over a time interval \(\Delta t = {0.1}\hbox {s}\) evolves and the effects of the grid slowly fade with time. After \(t = {0.6}\hbox {s}\), the flow can be considered to be isotropic. Also shown in Table 1 is the Taylor Reynolds number \(Re_{\lambda } = u_{rms}\lambda /\nu\), with the Taylor micro-scale \(\lambda = \sqrt{15\nu u_{rms}^2 /{\overline{\varepsilon }}}\) and the Froude number \(Fr = u_{\eta }/t_{\eta }g\).

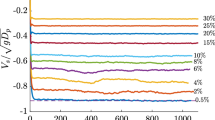
The evolution of the velocity variances \(\overline{u'^2}\), \(\overline{v'^2}\), and \(\overline{w'^2}\) with time are plotted in Fig. 1a. For isotropic homogeneous turbulence, these variances are equal to each other. The figure shows that the values are very close to each other after \(t = {0.5}\hbox {s}\) thus attesting to the isotropy of the flow. The initial high values for \(u'\) compared to \(v'\) and \(w'\) are due to the effects of the initial conditions. Figure 1b shows \({\overline{\varepsilon }}\) normalized with the classical scaling \(u_e^3/L_e\). This value has been shown to be constant for decaying grid-turbulence in experiments (Sreenivasan 1984) and in forced as well as decaying DNS simulations of turbulence (Sreenivasan 1998). The magnitude of the constant \(C_E = {\overline{\varepsilon }} L_e/u_e^3 \approx 1.8\) shown in Fig. 1b is comparable with those from other DNS data where it falls in the range \(1 - 3\) (see Fig. 1 in the review by Vassilicos 2015). Figure 1c also shows the change of \(Re_\lambda\), Fr and St (for a droplet of radius \({15}\upmu \hbox {m}\)) as a function of time.

A polydisperse distribution of droplets with 36 different discrete radii between 10 and 55\(\,\upmu \hbox {m}\) are randomly distributed across the whole computational domain at \(t = {0.4}\,\hbox {s}\). This size range is selected since these are the most important sizes in the problem of the size-gap bottleneck in warm rain initiation. The number of droplets in each size category is decided by a volume-weighted distribution (such that the total volume of droplets in each size category is the same). Using such a distribution, a target volume fraction of 5\(\times\)10\(^{-5}\) is achieved by introducing a total of 62.5 million droplets. We assume that the system is well within the dilute limit and any modulation of fluid turbulence due to two-way coupling with the particles can be neglected. We also neglect particle-particle aerodynamic interactions.

Table 2 Parameters for particle turbulence interaction at \(\varepsilon = 215 \ \textrm{cm}^2\textrm{s}^{-3}\) (\(t = 1s\))
Full size table

The simplified form of the Maxey-Riley equations is valid only in the case where \(R/\eta \ll 1\). Table 2 shows the values of \(R/\eta\) of six radius categories in the polydisperse system at \({\overline{\varepsilon }} = {215}\,\hbox {cm}^2\hbox {s}^{-3}\) and \(t = {1}\,\hbox {s}\). The values for all the categories are well within this limit. The added-mass, Basset history force and pressure forces are neglected under the assumption that \(\rho _p/\rho \gg 1\). Since we are considering water droplets (\(\rho _p = {1000}\,\hbox {kg m}^{-3}\)) dispersed in air (\(\rho = {1.1436}\,\hbox {kg m}^{-3}\)), \(\rho _p/\rho \sim 1000\). Another important assumption is the Stokes-drag approximation for the viscous drag forces. This assumption is valid in the range where the particle Reynolds number \(Re_p \ll 1\). Ayala et al. (2008b) showed that for \(R > {30}\,\upmu \hbox {m}\), \(Re_p\) is large enough to warrant the inclusion of a non-linear factor to model the departure from Stokes drag law. However, as was done in both Ayala et al. (2008b) and Woittiez et al. (2009), we employ the linear Stokes drag formulation to focus on the effects of gravity. Two simulations with the same flow characteristics and droplet parameters, but one with non-sedimenting particles and another with sedimenting particles, are performed.

Droplet-turbulence interactions are characterised using a series of non-dimensional parameters: the Stokes number \(\displaystyle St = {\tau _p}/{\tau _{\eta }}\), the parameter \(\tau _p/\tau _e\) (to characterize the interaction between particles and the larger turbulent flow scales), the settling parameter \(\displaystyle Sv = {w_t}/{u_\eta }\) (to characterize the interaction between settling particles and the smaller scales of turbulence) where \(w_t = \tau _p g\) is the droplet terminal velocity, and the parameter \(\displaystyle V_T = {w_t}/{u_e}\) (to characterize the interaction between settling droplets and the larger scales of turbulence). The values of these parameters for six different radius categories are shown in Table 2 at \(t = {1}\hbox {s}\).

Fig. 2
figure 2

Monodisperse RDF for a non-sedimenting (square markers) and sedimenting droplets (plus markers) at \(\varepsilon = {215}\,\hbox {cm}^{2}\hbox {S}^{-3}\), \(Fr =0.09\) and \(t = {1}\,\hbox {s}\), b droplets of radius 40.8 \(\upmu\) m

Full size image

3 Radial Distribution Function

The three-dimensional RDF is calculated during the simulations using

$$\begin{aligned} g_{12}(r;t) = \frac{\psi _{12}/V_s}{N_1 N_2/ V}, \end{aligned}$$
(6)

where \(\psi _{12}\) is the total number of droplet pairs with radii \(R_1\) and \(R_2\) with separation distance r detected in a spherical shell of inner radius equal to \(r - \delta\), outer radius equal to \(r + \delta\), and volume \(V_s\). Also, \(N_1\) and \(N_2\) are the total number of droplets of size \(R_1\) and \(R_2\) respectively. In this paper, \(\delta = 0.02\textit{r}\). For an RDF of same-sized droplets, \(g_{11}\), \(N_2\) is replaced with \((N_1 - 1)/2\). The RDF \(g_{12}(r;t)\) is further averaged over time to obtain \(g_{12}(r)\). The calculation of the RDF and collision statistics is started at \(t = 0.5\,s\) and averaged over every 0.1s thereafter. The very large number of particles ensures that converged particle statistics are obtained with this low averaging time. The maximum value of the inter-particle separation distance r over which the RDF is calculated is \(4\Delta x\). Considering particles at larger distances (beyond 4 cells in a direction) is restricted by the fact that the computational domain is parallelized in the \({\hat{y}}\) and \({\hat{z}}\) directions. Calculating particle separations at the processor boundaries requires exchange of data in the corresponding boundary cells of the neighbouring processor(s) which is a memory- and time-intensive procedure.

3.1 Monodisperse RDFs

As mentioned in the introduction, the RDF for same-sized particles can be expressed in terms of a power law. Figure 2a shows three dimensional RDFs in log-log coordinates for selected same-sized (\(g_{11}\)), non-sedimenting (square markers) and sedimenting (plus markers) particles at \(t = 1\) s (\(\varepsilon = 215 \ \textrm{cm}^2\,\textrm{s}^{-3},\, Fr = 0.09\)). The RDFs for both non-sedimenting and sedimenting particles reach a saturation at \(r/\eta < 1\) at \(St = 0.62\) (yellow squares and plus markers) after which the values start decreasing for higher St. However the magnitude of the maximum is higher in the absence of gravity. We observe a clear power law scaling for both cases for values of \(r/\eta\) upto 4. The RDF at \(r/\eta < 1\) remains the same up to \(Sv \approx 2\) after which sedimenting particles show a lower RDF. At these intermediate St, gravity clearly suppresses particle clustering. At higher Stokes numbers, gravity increases the RDF for \(r\ll \eta\) as can be seen for \(St = 1.03\). To explore this in detail, the RDFs \(g_{11}\) for droplets of size 40.8 \(\upmu\) m are shown as a function of time Fig. 2b.

The figure shows how a droplet of a particular size interacts with the evolving flow scales of decaying turbulence. The power law is maintained throughout decaying turbulence with the slopes of the straight line changing as a function of time. As the particle is suspended in decaying turbulence the Stokes numbers vary from 1.97 at \(t=0.6\) s (\(Fr = 0.34\)) to 0.81 at \(t=1\) s (\(Fr = 0.09\)). The rate of change of the slopes is high corresponding to the change (of almost an order of magnitude) in \(\varepsilon\) from 0.1245\(\ \textrm{m}^2\,\textrm{s}^{-3}\) (at \(t = 0.6\,\textrm{s}\)) to 0.0712 \(\ \textrm{m}^2\,\textrm{s}^{-3}\)(\(t = 0.7\,\textrm{s}\)). From \(t = 0.8\textrm{s}\) to \(1\textrm{s}\), the change in \(\varepsilon\) is very small which corresponds to a small change in the slope. An interesting feature from these plots is the role gravity plays on the clustering or RDF as a function of both Fr and St. For small values of Fr, which indicates a larger effect of gravity accelerations, the clustering is lesser (cyan and pink plus markers) as opposed to the non-sedimenting case (\(Fr = \infty\), cyan and pink squares). As Fr increases, indicating weaker gravity accelerations compared to higher turbulent accelerations, particle clustering is higher for sedimenting particles (red, black and blue markers) for \(r/\eta < 1\). Gravity reduces both preferential concentration and the path-history effects (Ireland et al. (2016a)). At low St, gravity weakens the preferential sampling drift effect leading to a reduction in the overall clustering. At higher Stokes numbers, gravity increases the RDF slightly by weakening the path-history effect whose effect is normally to decrease clustering.

Fig. 3
figure 3

Coefficients for monodisperse RDF: a, b pre-factor \(c_0\), c, d clustering exponent \(c_1\). The left and right columns represents non-sedimenting and sedimenting particles respectively. The circles show the coefficients obtained by fitting Eq. 2 to the DNS data from \(t = {0.7}\,{s}\) to \(t = {1}\,{s}\). The blue lines are the predicted values at \(t = 1\,s\) using the empirical formulas (Eq. (7) for a and c, Eq. (8) for b, and Eq. (9) for d)

Full size image

The coefficients \(c_0\) and \(c_1\) of the power law from Eq. (2) for the RDF values from \(t = 0.7\textrm{s}\) to \(t = 1.0\textrm{s}\) are shown in Fig. 3 for non-sedimenting (a, c) and sedimenting (b, d) particles. These are obtained by fitting Eq. (2) to the DNS data. The theory behind Eq. (2) was developed for steady-state realised by driven turbulence. Figure 2 clearly shows that a power law behaviour exists for decaying turbulence as well and Fig. 3 shows the coefficients \(c_0\) and \(c_1\) for the same. The dependency of the coefficients \(c_0\) and \(c_1\) on St is similar to that shown in Reade and Collins (2000). At low Stokes numbers, the coefficients are similar for both sedimenting and non-sedimenting particles. However it is interesting to note that for the coefficient \(c_0\), the peaks decrease with time for sedimenting particles (Fig. 3b), i.e. particles with the same Stokes number cluster to a lesser degree. The corresponding Fr decreases with time, indicating an increase in the gravitational accelerations compared to turbulent accelerations leading to a reduction in clustering in the intermediate St range of 0.3–1.

An empirical fit for the coefficients \(c_0\) and \(c_1\) was performed by Reade and Collins (2000) by curve fitting the following functions to their DNS data

$$\begin{aligned} c_0 = \frac{d_0 \, St^{d_1}}{d_2 + St^{d_3}} \quad , \quad c_1 = \frac{d_4\, St^{d_5}}{d_6 + St^{d_7}}, \end{aligned}$$
(7)

with \(c_2 =0.25\) assumed to be a constant. We use the same functions to curve fit \(c_0\) and \(c_1\) (the data shown in Fig. 3a, c). A very good fit was obtained as shown by the blue line in these figures with the following coefficients: \(d_0 = 6.8884, d_1 = 0.7840, d_2 = 0.8455,\) and \(d_3 = 2.1755\) for \(c_0\) and \(d_4= 0.5056, d_5 = 1.0944, d_6 = 0.1787\), and \(d_7 = 2.5626\) for \(c_1\).

The analytical solution developed by Chun et al. (2005) was extended to sedimenting particles by Ayala et al. (2008a) who developed an empirical model using DNS results to quantify the RDF. In order to account for the effects of gravity, they assumed the coefficients \(c_0\) and \(c_1\) to be a function of St, \(Re_{\lambda }\) and a dimensionless gravity parameter \(|g|/(u_\eta /\tau _\eta )\). An empirical expression for \(c_1\) for sedimenting particles was then obtained by curve-fitting to the DNS data with \(c_0 = 1\). However, Fig. 3 clearly shows that \(c_0\) is a function of St. Even though the range of \(Re_{\lambda }\) is small in our simulations, there is a clear change in the maxima for \(c_0\) (Fig. 3b) as the simulation progresses. This behaviour can be well represented by the empirical relation

$$\begin{aligned} c_0 = {f_1(Re_\lambda )} St^{b_2}\exp (-b_3St), \end{aligned}$$
(8)

where

$$\begin{aligned} f_1(Re_\lambda )&= b_0 \exp \left( \frac{b_1}{Re_\lambda }\right) , \end{aligned}$$

Curve-fitting this function with the data plotted in Fig. 3b gives the following parameters: \(b_0 =11.7825, b_1 = -9.3844, b_2 = 0.8338\) and \(b_3 = 0.9738\). The behaviour of coefficient \(c_1\) is captured by (Ayala et al. 2008a)

$$\begin{aligned} c_1 = \frac{f_2(St)}{(1/Fr)^{f_3(Re_\lambda )}}, \end{aligned}$$
(9)

where

$$\begin{aligned} f_2(St)&= b_4St^4 + b_5St^3 +b_6St^2 + b_7St,\\ f_3(Re_\lambda )&= b_8 \exp \left( \frac{b_9}{Re_\lambda }\right) . \end{aligned}$$

This function is fitted to the data shown in Fig. 3d for \(c_1\) and results in the following parameters: \(b_4 = -0.2817, b_5 = 1.6703, b_6 = -3.3334, b_7 = 2.3639, b_8 = -0.0632\) and \(b_9 = -9.9914\). These values vary from those obtained by Ayala et al. (2008a), however the parameters for \(c_1\) are of the same sign. The potential of using these empirical formulas for \(c_0\) and \(c_1\) to predict the RDF of colliding droplets will be explored in Sect. 4.

Figure 3 also shows how the the coefficients change as the droplets interact with decaying turbulence. Collins and Keswani (2004) reported that with increasing \(Re_{\lambda }\) (their study reached \(Re_\lambda\) values up to 152), the RDF saturates and approaches a plateau which was in contrast to the linear growth with \(Re_\lambda\) that was reported by Wang et al. (2000a). Falkovich and Pumir (2004) also reported an increase in the exponential coefficient \(c_1\) with increasing \(Re_\lambda\) and dissipation \(\varepsilon\). This was attributed to an increase in intermittency in the gradients of the turbulent velocities with increasing \(Re_{\lambda }\). However, Saw et al. (2008, 2012b) showed using wind tunnel experiments that there is a strong saturation in \(c_1\) in the limit of large \(Re_{\lambda }\) and the good agreement between experimental (\(Re_{\lambda }=440\)) and DNS results (\(Re_{\lambda } = 140\), Saw et al. 2012a) is also attributed to this saturation and the weaker dependence on \(Re_{\lambda }\) as compared to St. A Stokes number ’similarity’ was also observed in the RDFs measured in Saw et al. (2008, 2012b) where the plots of RDF for droplets with different sizes but same St (from measurements taken at different downstream locations of the wind tunnel) coincided even though these were calculated from different flow conditions. We see a similar St similarity for the exponential coefficient \(c_1\) which is the slope of the RDF. It is possible that this reinforces the observation from Saw et al. (2012b) that particle clustering occurs at scales that are well separated from the inhomogeneity in the larger scales. But we are hesitant to present this as a conclusion as we do not attain the maximum or the range of \(Re_{\lambda }\) in our numerical simulations (\(\sim\) 50–67) as in the experiments. Most of the previously stated DNS studies used different simulations of forced turbulence (at different turbulence intensities and hence \(Re_{\lambda }\)) to study the \(Re_{\lambda }\) dependence. Future studies where results from our novel setup will be compared to experimental data has been planned where we will aim for the range of \(Re_{\lambda }\) seen in wind tunnel flows. An attempt to provide a definitive answer for the Reynold’s number dependence to clustering will be made in the future.

Fig. 4
figure 4

The correlation dimension \(D_2 = d - c_1\) for non-sedimenting droplets (\(Fr =\infty\) shown by square markers) and sedimenting droplets (shown by plus markers)

Full size image

To conclude the analysis of the monodisperse RDFs, we plot the correlation dimension which is used extensively in dynamical systems theory (Bec et al. 2008; Gustavsson et al. 2015) in Fig. 4. The correlation dimension \(D_2\) can be related to the exponent \(c_1\) as \(D_2 = d - c_1\) where \(d = 3\) is the number of spatial dimensions. At low St, there is a decrease in the value of \(D_2\) with increasing St which points to an increasing spatial correlation, i.e. a higher degree of clustering. This decrease is followed by the value of \(D_2\) reaching a minimum between \(St = 0.4{-}0.6\) indicating maximum particle clustering which is consistent with results from experiments (Monchaux et al. 2012). The effect of gravity is clearly seen at the intermediate St range where the value of \(D_2\) is higher for sedimenting droplets (plus markers) indicating a lower spatial correlation and hence a lower degree of clustering. At high St, we see lower values of \(D_2\) indicating a higher spatial correlation and hence a higher degree of clustering for non-sedimenting droplets (square markers) compared to sedimenting droplets.

Fig. 5
figure 5

Bidisperse RDF with \(St_1\) = 0.50 (fixed) and (a, b) \(St_2 < St_1\) (c, d) \(St_2 > St_1\) at \(t = 1\,\textrm{s}\) and \(\varepsilon = {215}\,\hbox {cm}^{2}\,\hbox {s}^{-3}\). The left column represents non-sedimenting particles and right column represents sedimenting particles

Full size image

3.2 Bidisperse RDFs

The analytical theory of Chun et al. (2005) predicts the RDF for inertial particles of different sizes using the following expression at \(r \ll \eta\)

$$\begin{aligned} g_{12}(r) = c_0 \left[ \frac{\eta ^2 + r_c^2}{r^2 + r_c^2}\right] ^{c_1/2}, \end{aligned}$$
(10)

where \(c_0\) and \(c_1\) are interpreted similarly as in the monodipserse case (Eq. (2)) and \(r_c\) is a cross-over length scale. They showed that shear-driven diffusion dominates for \(\eta \gg r \gg r_c\) with the resulting RDF exhibiting a power law behaviour, while an acceleration-driven diffusion dominates for \(r \ll r_c\) resulting in an RDF which is independent of r. Hence \(r_c\) can be considered to be a length scale below which the power-law behaviour of the RDF crosses over to a plateau. A semi-empirical relation for \(r_c\) (for \(Re_{\lambda } = 47.1\)) is given by (Chun et al. 2005)

$$\begin{aligned} \frac{r_c}{\eta } \approx 5.0 |St_2 - St_1 |\end{aligned}$$
(11)

and for \(c_1\) as

$$\begin{aligned} c_1(St_1,St_2) = 6.6 St_1 St_2. \end{aligned}$$
(12)

For the monodisperse case, \(r_c = 0\) and Eq. (10) reduces to Eq. (2). Ayala et al. (2008a) modified the expression for \(r_c\) for sedimenting particles to

$$\begin{aligned} \left( \frac{r_c}{\eta }\right) ^2 = |St_2 - St_1 |F(a_{0g}, Re_{\lambda }), \end{aligned}$$
(13)

where

$$\begin{aligned} a_{0g}&= a_0 + \frac{\pi }{8}\left( \frac{1}{Fr}\right) ^2,\nonumber \\ a_0&= \frac{11 + 7Re_{\lambda }}{205 + Re_{\lambda }},\nonumber \\ F(a_{0g}, Re_{\lambda })&= 20.115\left( \frac{a_{0g}}{ Re_{\lambda }}\right) ^{1/2}. \end{aligned}$$
(14)

This is purely an empirical form which gave a reasonable fit to their DNS data. Figure 5 shows RDFs of droplets of different sizes at \(t = 1\) s with \(\varepsilon = 215 \ \textrm{cm}^2\textrm{s}^{-3}\). These bidisperse RDFs are calculated by fixing the size of one droplet at \(St_1 = 0.50\) and varying the size of the second droplet from \(St_2 = 0.42\) to \(St_2 = 0.81\). Figure 5a, c show RDFs for non-sedimenting droplets with \(St_2 \le St_1\) and \(St_2 \ge St_1\) respectively, while Fig. 5b, d show the same for sedimenting droplets. Also shown in dashed lines are the values of \(r_c\) obtained from Eqs. (11) and (13) for different \(\Delta St\). The bidisperse RDFs exhibit a power law at relatively larger scales which taper off to a plateau at smaller scales. It is also clear that this transition to a plateau where the RDF is independent of r clearly happens at much larger scales for sedimenting droplets (for the same \(\Delta St\)). We observe a similar asymmetry in \(g_{12}\) for non-sedimenting droplets when \(St_2\) is increased or decreased relative to the fixed \(St_1\), as was shown by Saw et al. (2012a). Interestingly, a symmetry is observed in \(g_{12}\) for sedimenting droplets. Any small deviation from a monodisperse distribution results in a sharp change in the RDF slope due to the difference in settling velocities for droplets with different sizes (or for small \(\Delta St = St_2 - St_1\)) irrespective of \(St_2\) being greater or lesser than \(St_1\). This is explored in detail for colliding droplets in Sect. 4.

Fig. 6
figure 6

Cross-over scale \(r_c\) for non-sedimenting particles as a function of \(\Delta St = St_2 - St_1\) where \(St_1 = 0.5\) is fixed. The black line in is the analytical solution given by Eq. (11)

Full size image

Saw et al. (2012a) observed that for non-sedimenting droplets, the power-law coefficient \(c_1\) can be recovered only at sufficiently small scales such that \(r \ll \eta\), which makes the retrieval of \(c_1\) difficult when the value of \(r_c\) approaches \(\eta\) for very small \(\Delta St\). This happens in our study as well, as is evident by the dashed lines in Fig. 5. Saw et al. (2012a) extended the bidisperse theory and proposed a new power-law coefficient \(c'_1\) which corresponds to the slope of the RDF in the range of scales between \(r_c\) and the large-scale flattening of the RDF (\(r/\eta \approx 1 - 6\) in their study) and approximated this as the lesser of the two corresponding monodisperse values, i.e.

$$\begin{aligned} c'_{1,bi}(St_1,St_2) = \min \left[ c'_{1,mono}(St_1),c'_{1,mono}(St_2) \right] . \end{aligned}$$
(15)

This relation was shown to hold for \(\Delta St = |St_2 - St_1 |\) of the order of 0.01–0.1 and arises as a result of a saturation effect (with \(c'_1\) increasing with \(St_2\) to a maximum and thereafter remaining constant) which suggests that the value of \(c'_1\) is always limited by the least clustered particles. We replace \(c_1\) with \(c'_1\) in Eq. (10) and calculate \(r_c\) for non-sedimenting droplets by performing a nonlinear fit of Eq. (10) to the DNS data for bidisperse RDFs (for the entire range of r). The resulting values of \(r_c\) are shown in Fig. 6 for different \(St_1\) at \(t = 1s\) and are compared with the theoretical values (Eq. (11)). There is a very good agreement between the two values suggesting that the extension proposed by Saw et al. (2012a) to the theory of Chun et al. (2005) works well even for \(r/\eta < 1\). This is important as Eq. (15) can be used to determine the collision kernel as will be done in Sect. 4. Unfortunately, extending this theory to sedimenting droplets is not straightforward and an attempt to do so failed since \(r_c/\eta\) approaches 1 for really small \(\Delta St\), and we do not see a power-law behaviour at larger scales (within 4\(\eta\)) as is clear in Fig. 5b, d.

We also highlight alternate results from Bec et al. (2005); Meibohm et al. (2017a, 2017b); Bhatnagar et al. (2018) which points towards \(r_c\) scaling as \({{|St_1 - St_2|}/{(St_1 + St_2)}}\). We performed an alternate analysis to retrieve \(r_c\) from the DNS data as before but with \(c_1 = c_{1,mono}({\overline{St}})\) where \({\overline{St}} = {2St_1St_2}/{(St_1 + St_2)}\) is the harmonic mean of the two Stokes numbers (again motivated by results from Bec et al. 2005; Meibohm et al. 2017a, b; Bhatnagar et al. 2018). The resulting values for \(r_c\) is similar to that obtained above at small \(\Delta St\) and the same issue with \(r_c\) approaching \(\eta\) at small \(\Delta St\) prevented us from looking at the actual scaling of \(r_c\) at larger range of \(\Delta St\) for non-sedimenting particles and for any \(\Delta St\) for sedimenting particles.

4 Geometric Collision Kernel

In this section, we analyse the effect of gravity on the collision kernel. The most common kinematic formulation for the geometric collision rate of a bidisperse distribution is given by (Sundaram and Collins 1997; Wang et al. 2000b, 1998),

$$\begin{aligned} \Gamma ^{K}_{12} = 2\pi R^2_c \langle |w_r(r = R_c)|\rangle g_{12}(r = R_c). \end{aligned}$$
(16)

where \(R_c = R_1 + R_2\) is the collision radius for two colliding droplets of radius \(R_1\) and \(R_2\). The radial relative velocity \(w_r\) is defined in terms of the relative velocity w between two droplets with separation vector r as \(\ w_r = {\textbf {w}}\cdot {\textbf {r}}/|{\textbf {r}}|\). The mean radial relative velocity \(\langle |w_r(r = R_c)|\rangle\) is then the conditional average, i.e. the mean of \(|w_r |\) conditional on \(r=R_c\).

Figure 7 shows contour plots for the collision kernel \(\Gamma ^K\)(a, d), RDF \(g(R_c)\) (b, e) and the magnitude of the mean radial relative velocities \(\langle |w_r(R_c) |\rangle\) (c, f) for all colliding droplets in the polydisperse distribution. For all the plots in this section, the statistics are shown for \(t = 1\,s\). It should be noted that for this figure, the DNS data for the RDF \(g(R_c)\) is calculated separately in the collision routine of SPARKLE and is not extracted from the RDF data used in Sect. 3 (details in Nair (2021)). All the figures show a striking symmetry which confirms the fact that the statistics for collisions between droplets of radii \(R_1\) and \(R_2\) are the same as those between \(R_2\) and \(R_1\).

Fig. 7
figure 7

Comparisons between the polydisperse distribution of non-sedimenting droplets (top row) and sedimenting droplets (bottom row) for the (a, d) kinematic collision kernel \(\Gamma ^K\), (b, e) RDF and (c, f) radial relative velocity \(\langle |w_r |\rangle\)

Full size image

Figure 7a, d show that sedimentation enhances the collision kernel except when collisions are between droplets of the same size. For collisions between same-sized particles (along the leading diagonal), the kernel is higher for non-sedimenting droplets (Fig. 7a) compared to sedimenting droplets (Fig. 7d), noticeably so for \(R > 25 \upmu m\). For collisions between unequal-sized droplets (either side of the leading diagonal), the enhancement observed in Fig. 7d is obvious for \(R_1>25\,\upmu \textrm{m}, R_2 > 25 \upmu \textrm{m}\). The higher velocity decorrelation due to the differential settling velocities for unequal-sized droplets becomes significant at sizes greater than \(25 \upmu \textrm{m}\) as can be seen by comparing Fig. 7c, f in the same size range. The figures reveal a difference of at least an order of magnitude between \(\langle |w_r |\rangle\) for non-sedimenting and sedimenting colliding droplets. For both cases, bands are observed within which the collision kernels have a similar order of magnitude. Detailed analysis of the kernels are done later in the section using a cross-section from the contour plot.

A detailed analysis of the RDF at scales extending up to \(4\eta\) was performed in Sect. 3. In Fig. 7b, e, we look at the effect of gravity on the RDF of colliding droplets, i.e. at \(r = R_c\). Figure 7b suggests that the gradient from the monodisperse peak is much more gradual for non-sedimenting colliding droplets when compared to sedimenting colliding droplets. In Fig. 7e, the RDF of sedimenting droplets falls rapidly from the monodisperse value for even a small \(\Delta R = R_2 - R_1\). This is due to the rapid decorrelation of the droplet concentrations for different droplet sizes (Zhou et al. 2001). The decorrelation arises from the fact that particles with different inertia tend to cluster in different (slightly-offset) regions with respect to the flow. Differential sedimentation enhances this decorrelation leading to a very sharp diagonal with high values of RDF and the values dropping to one even for a small \(\Delta R\). In Fig. 7c, f, the plots are symmetric indicating that \(\langle |w_r |\rangle\) depends on \(\Delta R\) (or \(\Delta St\)), the difference in inertia, rather than \(R_1\) or \(R_2\). The value of \(\langle |w_r |\rangle\) reaches a minimum for same-sized droplets and increases with \(\Delta R\) for both cases. The effect of gravity is an overall increase in \(\langle |w_r |\rangle\) of almost an order of magnitude for unequal-sized droplets.

The RDFs are now analysed separately in Fig. 8 by comparing the DNS data with values predicted from different analytical/empirical models for both non-sedimenting and sedimenting droplets. The DNS data in Fig. 8a for the monodisperse RDF \(g_{11}(R_c)\) corresponds to the leading diagonal of Fig. 7b and that for the bidisperse RDF \(g_{12}(R_c)\) in Fig. 8b corresponds to a slice through the contour plots at \(R_1 = 31.9 \upmu \textrm{m} (St = 0.5)\). For \(g_{11}(R_c)\), the obvious model to predict the RDF would be using Eq. (2) where the coefficients \(c_0\) and \(c_1\) are calculated using the equations and fitted parameters from Sect. 3, i.e. Eq. (7) for non-sedimenting droplets and Eqs. (8) and (9) for sedimenting droplets. The fitted parameters \(d_0 - d_7\) and \(b_0 - b_9\) for these equations remain the same as in Sect. 3. Similarly, the bidisperse RDF \(g_{12}(R_c)\) can be predicted using Eq. (10) where \(r_c\) is calculated using Eq. (11) for non-sedimenting droplets and (13) for sedimenting droplets. The coefficients \(c_0\) and \(c_1\) are selected from the corresponding monodisperse values as \(\min (c_0(St_1),c_0(St_2))\) and \(\min (c_1(St_1),c_1(St_2))\) for non-sedimenting droplets. For sedimenting droplets these are calculated using Eqs. (8) and (9) with \(St = \max [St_1,St_2]\). This model is referred to as model M1. The corresponding values obtained using model M1 (dashed lines) are compared with the DNS data (circles) in Fig. 8.

For the monodisperse case, there is very good agreement between the DNS data and model M1 for colliding non-sedimenting (red) and sedimenting droplets (black) as shown in Fig. 8a. For sedimenting droplets (black dashed lines), a good agreement is observed for smaller St even though the peak seems to be shifted with the model slightly over predicting for \(St > 1\). For the bidisperse case, there is a good agreement for the non-sedimenting case for all sizes except for when \(R_2 > 35\) which corresponds to \(\Delta St > 0.3\). Note that this is much better behaviour than expected since the relation given by Eq. (15) was shown to be valid for \(\Delta St\) up to 0.1 only. However, for sedimenting droplets, there is a marked disagreement for even small \(\Delta St\). This is due to the values of \(r_c/\eta\) rapidly approaching 1 even for small \(\Delta St\) which renders the retrieval of the power-law coefficient (and ultimately the RDF) using the model impossible.

Fig. 8
figure 8

Monodisperse (a) and bidisperse (b) RDF from DNS and models. Redlines represent non-sedimenting and black lines sedimenting colliding particles

Full size image
Fig. 9
figure 9

Monodisperse (top row) and bidisperse (bottom row) values of the (a, d) kinematic collision kernel \(\Gamma ^K\), (b, e) RDF and (c, f) radial relative velocity \(\langle |w_r |\rangle\). Red represents non-sedimenting and black sedimenting colliding particles. The circles in figure (b) are the RDF predicted from the empirical formulas, while lines indicate RDF from DNS

Full size image

We proceed to model the RDF using the procedure described in Ayala et al. (2008a) to investigate if this gives a better agreement with DNS results. This model will be named M2. We first curve-fit Eq. (2) to our DNS data for the monodisperse RDF \(g_{11}(R_c)\) setting \(c_0 = 1\) and \(c_1\) following Eq. (7) for non-sedimenting droplets, and Eq. (9) for sedimenting droplets. This fit results in a new set of parameters for \(c_1\) which are: \(d'_4 = 1.2993, d'_5 = 1.1487, d'_6 = 0.2264, d'_7 = 2.0458, b'_4 = -0.9125, b'_5 = 4.4471, b'_6 = -7.6730, b'_7 = 5.1852, b'_8 = 0.0095, b'_9 = 30\). For bidisperse RDF \(g_{12}(R_c)\), this process is extended by assuming that \(r_c\) follows Eq. (13) for both cases but with \(F(a_{0g},Re_{\lambda })\) replaced by \(F(Re_{\lambda }) = \displaystyle 11.5283{\left( {a_0}/{Re_{\lambda }}\right) }^{1/2}\) and \(a_0 =\displaystyle {(9.5686 +0.1303Re_{\lambda })}/{(205.29 + Re_{\lambda })}\) for non-sedimenting droplets. For sedimenting droplets, \(F(a_{0g},Re_{\lambda })\) has the same form and parameters as Eq. (14). The coefficient \(c_0 = 1\), and \(c_1\) is calculated similar to model M1. Very good agreement is observed for the monodisperse case for non-sedimenting droplets (red dotted lines) and sedimenting droplets (black dotted lines). An excellent agreement is observed for the bidisperse case for both non-sedimenting and sedimenting droplets. Details of both models and the respective equations and parameters are summarized in Table 3.

To obtain a clearer picture of the droplet collision process, the kinematic collision kernel \(\Gamma ^K_{11}\), the RDF \(g_{11}\), and the radial relative velocities \(\langle |w_r|\rangle\) for colliding droplets of the same size are plotted in Fig. 9a–c. These plots correspond to the leading diagonals of Fig. 7a–c respectively. Figure 9d–f show the collision statistics \(\Gamma ^K_{12}\), the RDF \(g_{12}\) and \(\langle |w_r |\rangle\) for unequal-sized droplets where \(St_1 = 0.5\) and \(St_2\) is varied. This corresponds to a slice through the contour plots at \(R_1 = 31.9 \mu m\) in Fig. 7. Also plotted are the theoretical/model values for comparison. Model M2 is used for comparison with the RDF values obtained from DNS in Fig. 9b, e. The values of \(\langle |w_r |\rangle\) obtained from DNS are compared with models from Wang et al. (2000a) for non-sedimenting droplets and Ayala et al. (2008a) for sedimenting droplets. For non-sedimenting droplets, this is given by

$$\begin{aligned} \langle |w_r |\rangle&= {\left( \frac{2}{\pi }\right) }^{1/2}\sqrt{w_{shear}^2 + w_{accel}^2}, \end{aligned}$$
(17)

where

$$\begin{aligned} w_{shear}^2&= \frac{1}{15}R_c^2\frac{{\overline{\varepsilon }}}{\nu },\quad \frac{w_{accel}^2}{u_e^2} = \frac{1}{3}C_w(\alpha )\left( \frac{w_{accel}^2}{u_e^2}\right) , \\ C_w(\alpha )&= 1.0 + 0.6\exp [-(\alpha - 1)^{1.5}], \end{aligned}$$

where \(\alpha = \max [\theta _2/\theta _1, \theta _1/\theta _2]\), \(\theta = 2.5\tau _p/T_e\) and \(w_{shear}\), \(w_{accel}\) are the radial relative velocities due to the shear and acceleration mechanism respectively. For sedimenting droplets, the following expression for the formula from Ayala et al. (2008a) for \(\langle |w_r |\rangle\) is used

$$\begin{aligned} \langle |w_r |\rangle = \sqrt{\frac{2}{\pi }}\left( \sigma ^2 + \frac{\pi }{8}(\tau _{p1} - \tau _{p2})^2 |{\textbf {g}} |^2\right) ^{1/2} \end{aligned}$$
(18)

where \(\sigma ^2 = \langle (v'^{(2)})^2\rangle + \langle (v'^{(1)})^2\rangle - 2\langle (v'^{(1)}v'^{(2)})\rangle\) and \(\langle (v'^{(i)})^2 \rangle ^{1/2}\) is the rms fluctuation velocity of the ith particle. The kinematic collision kernels \(\Gamma ^K_{11}\) and \(\Gamma ^K_{12}\) can then be predicted using model M2 to calculate the RDF, and Eqs. (17) and (18) for \(\langle |w_r |\rangle\) for non-sedimenting and sedimenting droplets respectively.

Figure 9b shows that for same-sized colliding droplets, the RDF reaches a maximum at around \(St = 0.5\) after which it reduces steadily. In the range \(St = 0.28\) to \(St = 0.86\), gravity clearly suppresses particle clustering due to reasons discussed in Sect. 3.1. Figure 9e shows the RDFs for the bidisperse case for \(St_1\). The sharp fall of the RDF values from a maximum to one is clearly visible for sedimenting droplets (black circles) when compared to the more gradual fall for non-sedimenting droplets (red circles). Again, model M2 shows very good agreement with the DNS values.

Sedimenting droplets of the same size have a lower \(\langle |w_r |\rangle\) than their non-sedimenting counterparts as shown in Fig. 9c. Gravity effects the relative velocities of colliding particles through preferential sampling of the fluid velocity field and the temporally non-local path-history of the particle pair (Ireland et al. 2016a; Dhariwal and Bragg 2018). Due to particles preferentially sampling the fluid velocity field, they experience high differences in fluid velocities. When \(\Delta St = 0\), and for small values of St, gravity reduces the preferential sampling effect which leads to particles having dynamics closer to that of the fluid and a resulting reduction in the relative velocities. At higher St, non-sedimenting droplets experience a higher influence of the path-history effects. The particles remember the interactions with the different turbulent scales which are significantly different from that at the current separation. The contribution to the relative velocities for a particle pair will be dominated by the fluid velocities at larger separations along their path histories. This results in relative velocities that are higher than the local fluid velocity difference at the point of collision. At higher St, gravity reduces the path-history effect causing a lower relative velocity value for sedimenting particles compared to non-sedimenting particles. This can be seen by the higher difference between the two cases for \(St > 1\). When \(\Delta St > 0\), gravity can enhance inertial particle accelerations leading to values of relative velocities higher than in the non-sedimenting case (Dhariwal and Bragg 2018). This is clear from the order of magnitude difference between the values in Fig. 9f. The enhancements have been shown to be due to large settling velocities of particles with finite St and low Fr, which causes a rapid change in the fluid velocities experienced by the particles. Studies by Ireland et al. (2016a), Dhariwal and Bragg (2018), Momenifar and Bragg (2020) have explored these in detail.

A very good agreement between the model and DNS data is observed for same-sized droplets in Fig. 9c for both the non-sedimenting and sedimenting cases. An excellent agreement is observed for sedimenting droplets for unequal-sized droplets, whereas for the non-sedimenting case, the semi-empirical formula from Wang et al. (2000a) seems to over-predict the values of \(\langle |w_r |\rangle\) for small sizes.

The kinematic collision kernel calculated using (16) is shown in Fig. 9a. Gravity clearly decreases the monodisperse collision kernel for \(St > 0.3\) by influencing the accumulation effect(particle clustering) and the turbulence transport effect (particle relative velocities). The model for the monodisperse kinematic collisions kernel \(\Gamma ^K_{11}\) works very well for both cases. For the bidisperse case, there is a slight over-prediction of \(\Gamma ^K_{11}\) for \(St_2 < 0.5\) as a result of the model for \(\langle |w_r |\rangle\) not exactly matching the DNS values. However, for the sedimenting case, there is an excellent agreement between the model and DNS.

It is important to highlight that even though the formulation of the kinematic collision kernel according to Eq. (16) suggests that particle clustering explicitly enhances the collision rates, an analysis by Gustavsson and Mehlig (2014) suggests this may not be the case. Gustavsson and Mehlig (2014) show that the collision rate is equal to \(m_1(R_c)/2\) where \(m_p\) is the p-th moment of \(w_r\). They argue that since \(\langle |w_r |\rangle\) is defined as a conditional average (conditional to \(r = R_c\)), \(\langle |w_r |\rangle\) can be expressed as \(m_1(R_c)/m_0(R_c)\) and with \(g(R_c) \approx m_0(R_c)/R^{d-1}\) (where d is the number of spatial dimensions), by definition (Eq. 16), any direct enhancement to the collision kernel from clustering through \(g(R_c)\) will be cancelled by the probability that is present in the formulation of \(\langle |w_r(r+R_c) |\rangle\) and the actual collision rate will be given by \(m_1(R_c)\). Also, any contribution from spatial clustering g(R) will be indirect; as the fractal evolves in phase space, the velocity moment \(m_1\) may be influenced by the same degree of fractal clustering in velocity. This could explain why in Fig. 9d, the collision kernel appears to be smoother compared to \(g_{12}\) and \(\langle |w_r |\rangle\), i.e. the non-smooth parts are cancelled out. For sedimenting particles, we speculate that the contributions of differential settling likely makes \(m_1(R_c)\) and hence the collision rates non-smooth as seen in Fig. 9d. An analysis to confirm this is reserved for future work.

Fig. 10
figure 10

a Turbulence enhancement of the geometric collision kernel \(\Gamma ^K\), b RDF and c Turbulence enhancement of the radial relative velocity \(\langle |w_r |\rangle\)

Full size image

The enhancement of the geometric collision kernel due to air turbulence relative to the gravitational kernel is shown in Fig. 10a. The figure shows the ratio \(\Gamma ^K/\Gamma ^g\) where \(\Gamma ^g\) is the gravitational collision kernel. Also shown is the RDF (Fig. 10b) and the enhancement of the average radial relative velocity with respect to the purely gravitational case (Fig. 10c). Turbulence-induced enhancements of up to a factor of 3 are observed, especially for collisions between droplets with a small size difference. Devenish et al. (2012) showed enhancements between 1.5 and 4 at similar \(\varepsilon\) and size range. The value of \(\Gamma ^K/\Gamma ^g\) is not defined for particles of the same size (since \(\Gamma _g = 0\)), however Fig. 10b shows that particle clustering can lead to enhancement in collisions up to 12 times that in the purely gravitational case. For larger droplets, as particle inertia increases, the effect of radial relative velocity is the significant contributor to the turbulence enhancement of the collision process. A difference in radial relative velocities between colliding particles can lead to enhancements of up to a factor of 2 for droplets of unequal size as shown in Fig. 10c.

5 Concluding Remarks

In this paper, we investigated the effect of gravity on the preferential concentration and geometric collisions of a polydisperse distribution of water droplets in decaying homogeneous isotropic turbulence. A polydisperse distribution of water droplets with radii ranging from \(R = 10\) to \(R = 55\upmu\) m was randomly distributed in isotropic turbulent flow. The radial distribution function (RDF) was used to quantify particle clustering and simulations were performed with both non-sedimenting and sedimenting droplets.

Analyses of the RDFs for same-sized droplets reveal a power law behaviour for both non-sedimenting and sedimenting droplets in decaying turbulence. As the flow decays, droplets encounter and interact with flow scales that are evolving with time. As a result, the flow Froude number Fr and droplet Stokes numbers St change, and gravity plays a different role depending on the magnitudes of Fr and St. We see that the power law is maintained throughout the decay. For small values of Fr, clustering is less compared to the non-sedimenting case. At higher Fr, gravity enhances clustering. Empirical models have been generated for the exponential coefficients for the power law for both non-sedimenting and sedimenting droplets. We refrain from making conclusions on the dependence of particle clustering on the Reynolds number due to the small range of values of \(Re_\lambda\) the flow attains during the time the particle statistics are calculated. Future studies will focus on attaining a higher maximum value as well as a wider range of \(Re_\lambda\) when particle statistics are calculated.

For clustering in droplets of unequal sizes, the cross-over scale at which the power-law behaviour of the RDF tapers to a plateau is calculated from theoretical predictions for both non-sedimenting and sedimenting droplets. Excellent agreement is observed between the \(r_c\) recovered from the DNS data and the theoretical formula of Chun et al. (2005) for non-sedimenting droplets. However, due to the difficulty in recovering the power-law coefficient \(c_1\) when the value of \(r_c\) approaches \(\eta\), comparison of \(r_c\) with the empirical formula of Sundaram and Collins (1997) was not possible. Contrary to non-sedimenting droplets, we show that sedimenting droplets of unequal sizes exhibit a symmetric behaviour in RDF with droplets smaller and larger in size. The asymmetry in non-sedimenting droplets is due to the differential sedimenting velocities for particles of unequal sizes.

The effect of gravity on geometric collisions is analysed by looking at the kinematic collision kernel, the RDF and radial relative velocity at the point of collision (\(r = R_c\)) of droplets. For same-sized droplets, gravity reduces the collision kernel for bigger droplets. This is mainly due to a reduction in relative velocity once the effects of droplet settling velocities dominate the particle inertial effects resulting in the droplet velocities being increasingly correlated. In the case of collisions between droplets of unequal sizes, gravity results in a significant increase in the kernel magnitude. A model to predict the kinematic collision kernel is developed by combining the models for the RDF and the already existing models for the conditional radial relative velocities in literature. Very good agreement is observed when compared with the DNS data. However, a smooth distribution of the kinematic collision kernel compared to the RDF and the conditional radial relative velocities suggest that any contribution due to particle clustering via the RDF is cancelled due to the definition of the conditional radial relative velocities (which includes a probability of the separation distance being at \(R_c\)) as was shown in Gustavsson and Mehlig (2014). This causes the non-smooth contribution to cancel out leading to the collisional kernel being determined by the first moment of the relative velocities. However confirmation of this has been reserved for future studies. We also explore the turbulence enhancement of the geometric collision kernel. Enhancement of up to factors of 3 is observed especially for monodisperse collisions.

Numerical studies involving a polydisperse distribution of droplets in decaying homogeneous isotropic turbulence are quite rare. The contour plots for the geometric collision kernel show how gravity plays an important role in enhancing collision between unequal sized droplets with radii greater than 30\(\,\upmu\)m. The results of this study can help in developing models of the collision kernel based on actual cloud conditions where gravity plays an important role. The value of typical mean turbulence dissipation rates in clouds is around \({400}\,\hbox {cm}^{2}\hbox {s}^{-3}\). The simulations in this study consider a droplet size distribution which is comparable to cloud droplet size distributions. However, the simulations are at a much lower Reynolds number than in actual clouds. Establishing a saturation of the RDF with respect to growing Reynolds numbers would have allowed us to comment on the suitability for using these models for actual cloud conditions. However, past studies such as those by Collins and Keswani (2004), Rosa et al. (2013) have found that the RDF and the radial relative velocities reach a plateau with increasing \(Re_\lambda\). This suggests that these models can be applied to study the evolution of droplet size distribution in clouds. We also plan to compare the DNS data with data from wind tunnel experiments for similar turbulence and droplet parameters.

Table 3 Different models used for predicting RDFs for colliding droplets
Full size table