1 Introduction

Today, sustainability is a strong driver forcing companies to achieve a more sustainable business structure. For example, the world’s largest asset manager, BlackRock, has announced its intention to invest only in climate-neutral companies by 2050 (see www.blackrock.com). Improving the carbon footprint of their electricity consumption is a key lever for industrial companies seeking to become more sustainable; see, for example, Dong et al. (2016) or Yenipazarli and Vakharia (2017). However, current events—i.e. the war in Ukraine and related political decisions—pose major challenges for utilities and energy consumers, as energy prices and volatility have increased significantly. So-called renewable or green power purchase agreements (PPAs), which are seen as a tool to improve corporate sustainability performance, may also be affected by this price and volatility explosion because of the risk transfers they contain. The use of such green PPAs as electricity price tariffs has recently been increasingly discussed in politics and business in Europe, especially due to the amended European Commission guidelines on state aid for climate, environmental protection and energy published in 2022. According to these guidelines, aid in the form of reduction of electricity levies for energy-itensive companies may be granted, if, for example, “at least 50% of their electricity consumption [is] from carbon-free sources, out of which either at least 10% will be covered by a forward instrument such as a power purchase agreement \(\left[ \text {or} \dots \right] \)”; EU-COM (2022, p. 76). For example, Google is currently one of the largest corporate buyers of green electricity provided by PPAs in Europe; cf. WBCSD (2016). Up till now, PPAs have been an instrument that has received insufficient attention in the literature of energy-efficient production planning (EEPP). Usually, price-dynamic electricity tariffs such as Real-Time-Pricing (RTP) or Time-Of-Use (TOU) are considered and tradeoffs between electricity costs and some other economic related criterion, e.g. makespan, are examined in a respective production planning approach, e.g. lot-sizing and/or scheduling; cf. Wang et al. (2022), Chen et al. (2020), Schulz et al. (2019) or Wichmann et al. (2019a). Additionally, according to the “Energy Efficiency First” principle of the EU (cf. EU-COM 2022), companies shall strive to reduce their electricity consumption. However, tradeoffs between electricity costs and electricity consumption have only been scarcely studied in the respective EEPP literature, and this is especially true with the additional consideration of a battery storage system (BSS). In this context, the main research questions of this study are:

  • How do RTP, TOU and PPA affect production planning?

  • Does it always make sense—regardless of the price tariffs—to use a battery storage system in production planning?

  • Does a battery storage system exacerbate or mitigate the potential conflict between energy costs and energy consumption?

Aiming at answering these questions, we are investigating a single-stage parallel machine lot-sizing and scheduling problem in the presence of an onsite BSS studying tradeoffs between electricity costs and electricity consumption under different electricity pricing schemes, i.e. RTP, TOU and PPA. A real BSS for industrial applications is considered, that is, a redox flow BSS, which is expected to be a BSS of the future; cf. BMBF (2022). Such a BSS has not yet been taken into account in the respective EEPP literature.

The remainder of the article is organized as follows: Sect. 2 is devoted to a description of RTP, TOU and PPAs as well as a literature overview of EEPP. The problem description, especially the description of a redox flow BSS, and model formulation are part of Sects. 3 and 4. Section 5 presents selected results of the scenario analysis we conducted. Section 6 is devoted to heuristic developments in order to cope with complex instances of our model. Section 7 concludes this work.

2 Energy-efficient production planning considering a battery storage system

2.1 Price-dynamic electricity tariffs and PPAs

Real-Time-Pricing (RTP) and Time-Of-Use (TOU) are well known electricity tariffs that companies can use as levers to reduce production-related electricity costs, for example; cf. Baboli et al. (2011) and Albadi and El-Saadany (2008). See Duarte et al. (2020), Keller et al. (2015) or Shrouf and Miragliotta (2015) for more details on these schemes. RTP and TOU can be understood as follows (cf. Eid et al. 2016):

  • RTP

    An hourly rate that depends on the day-ahead electricity price, i.e., the electricity price fluctuates hourly. See Fig. 1 for a corresponding example.

  • TOU

    Fixed electricity prices for different blocks of time within a specified period, e.g. a high electricity price at peak times (8–20 h) and a low electricity price at off-peak times (22–0 h and 0–9 h) as visualized in Fig. 2.

Fig. 1
figure 1

Real-time-pricing (RTP)

Full size image
Fig. 2
figure 2

Time-of-use (TOU)

Full size image

In contrast to these “classical” pricing schemes, so-called green power purchase agreements (PPAs) have recently attracted increasing attention. A green PPA is a renewable electricity delivery contract between an electricity seller and a buyer over a pre-agreed contractual period, e.g. 3 years; cf. DENA (2019). For industrial companies as buyers—i.e., a corporate PPA—green PPAs offer the opportunity, among other things, to improve the carbon footprint of electricity consumption, and thus improve sustainability performance; cf. PwC (2018) and DENA (2019).

There are various types and forms of PPAs in Europe DENA (2019). However, we will solely focus on virtual PPAs (VPPAs) including a Contract for Difference (CfD) as hedging instrument as described in the following (cf. BEIS 2022; DENA 2019):

  • VPPA including a CfD

    A fixed electricity price per kWh is agreed between the contracting parties for a defined amount of green electricity, i.e. between a wind farm operator and an industrial buyer. The green electricity is not delivered physically to the buyer. Instead, the producer sells, and the buyer procures, its electricity on the wholesale market. With a CfD, the two PPA partners agree to make compensation payments if the prices they achieve on the market differ from the fixed price negotiated in the PPA, see Figs. 3 and 4.

Fig. 3
figure 3

Conceptualization of a VPPA

Full size image
Fig. 4
figure 4

Operationalization of a VPPA

Full size image

2.2 Literature review

In this section, the related work for this article will be briefly discussed. For a detailed overview, cf. Bänsch et al. (2021) or Weitzel and Glock (2017).

In the research area of energy-efficient production planning (EEPP), electricity consumption and electricity costs are common themes and tradeoffs between one of these two criteria and an economic criterion such as makespan are studied in a certain production setting (e.g. flowshop etc.); cf. e.g. Mansouri et al. (2016) or Ding et al. (2016). Hereby, electricity consumption or electricity costs are typically leveraged by the variation of machine states (e.g. “idle”, “off”, etc.) and/or different production speed levels and/or parallel machines with different electricity consumption levels; cf. Giglio et al. (2017), Liu et al. (2017), Rager et al. (2015), Fang and Lin (2013) and Ji et al. (2013). In order to analyze electricity cost reduction potentials, dynamic electricity price tariffs are considered. Most often, a TOU tariff is used as the basis for the studies, more rarely RTP; cf. Schulz et al. (2019). As examples, the articles of Wichmann et al. (2019a), Ho et al. (2022), Dellnitz (2020) and Ding et al. (2021) can be named. However, none of the above articles considered an additional battery storage system (BSS), which nevertheless plays an important role for this article. Relevant articles are named in the following.

Wichmann et al. (2019b) studied a lot-sizing and scheduling approach considering a BSS. They showed the benefits of a BSS in terms of potential cost savings. Time-dependent electricity prices, electricity purchase and sale, and deterministic onsite renewable energy generation are also considered, but without further technical specifications of the BSS other than the capacity. Mikhaylidhi et al. (2015) also neglected technical aspects of the BSS other than capacity in their study. They studied a production planning problem under TOU considering a BSS without the possibility of onsite renewable electricity generation. The authors in Khalaf and Wang (2018) proposed a flow shop scheduling problem for minimizing electricity costs under RTP. Onsite renewable electricity supply and energy storage are considered, which were shown to have a significant impact on cost reduction. They modelled a BSS considering maximum charge and discharge rates and constant charge and discharge efficiencies. A more realistic model formulation for a BSS without the possibility of onsite electricity generation can be found in Weitzel and Glock (2019). Beside charge and discharge efficency rates, these authors also considered self discharging and battery aging and thus battery wear. Among other things, tradeoffs between total weighted completion time and electricity costs were studied taking variable electricity prices into account.

There are further articles worth mentioning considering battery storages, either with or without the possibilty of onsite renewable energy generation, cf. Scholz and Meisel (2022), Dong and Ye (2022), Duarte et al. (2020), Wu et al. (2018), Zhang et al. (2018), Golpîra et al. (2018), Liu (2016) and Moon and Park (2014). However, Bänsch et al. (2021) point out that especially bicriteria optimization for parallel machine environments considering an energy storage system have been insufficiently studied in literature, in particular in the context of lot-sizing and scheduling [see also Meng et al. (2020) or Maecker and Shen (2020) for details on parallel machine problems]. Furthermore, the technical specifications of a BSS are often neglected, e.g. the self-discharge of a battery is ignored or a constant factor for discharging efficiency is assumed, if at all. In practice, however, a proportional relationship between the discharge rate and the efficiency of a battery storage is not typical, i.e. the higher the discharge rate, the less stored energy can be used. Moreover, articles that consider electricity consumption and electricity costs simultaneously and analyze tradeoffs between them are rare and neither of the articles mentioned considered PPAs explicitly. Consequently, motivated by the literature, we intend to close this gap by studying tradeoffs between electricity consumption and electricity costs in a parallel machine environment under RTP, TOU and PPA. Additionally, a real BSS for industrial applications is also taken into account, that is a redox flow system which none of the mentioned articles considered.

3 Problem definition

3.1 General problem setting

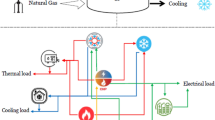
We set out to study a bicriteria single-stage parallel machine lot-sizing and scheduling problem minimizing total electricity costs (TEC) and total power consumption (TPC) simultaneously. A setting overview can be found in Fig. 5. However, the following assumptions are made:

  • The planning horizon consists of 5 days (Mon-Fri) and is decomposed into 120 intervals (1 h each).

  • Different electricity price tariffs are considered:

    • RTP: The hourly day-ahead prices of EPEX SPOT in Germany are used, which are valid from Nov. 22–26 of 2021 (41st CW, see www.smard.de).

    • TOU: Two price blocks (peak and off-peak) are considered. The peak price is in effect from 9 a.m. to 9 p.m., inclusive, and the off-peak price otherwise. For simplification, the average values of the corresponding day-ahead prices were taken [cf. Albadi and El-Saadany (2008) for justification].

    • PPA: The price for the 41st CW of 2021 for a 5-year PPA for wind offshore energy is taken as fixed reference price (see www.energybrainpool.com).

  • The single-stage parallel machine environment consists of several machines with non-identical electricity coefficients.

  • Different machine states and discrete production speed levels that allow for integer output in a period are taken into account. For the machine states, it holds: \(\text {off } [kW]< \text {standby } [kW]< \text {ramp up } [kW] < \text {production } [kW].\) Corresponding coefficients are randomly generated.

  • The change in electricity consumption with variation of the production speed is calculated using the conversion formula in Schulz et al. (2020).

  • A machine state or the selected production speed level cannot change within a time interval.

  • All jobs are available at the beginning of the planning horizon and have to be fulfilled at the end of the week (identical due dates).

  • For simplicity, backlog, warehousing and set-up effort are neglected.

  • Each machine can process at most one job at a time.

  • Preemption and lot-splitting is possible.

  • An onsite redox flow BSS is considered, which is operated in parallel with the grid supply. See Sect. 3.2 for details on the BSS.

Fig. 5
figure 5

Setting overview

Full size image

3.2 Redox flow BSS and related model-theoretic aspects

Redox flow BSS are expected to play an important role in the energy grids of the future. This is because of several advantages, e.g., power and storage capacity are separately scalable, capability of deep discharge, very long lifetime (10 to 20 years), theoretically unlimited cycle stability, high operational reliability, good energy efficiency (60 to over 75 percent), only low self-discharge; cf. BMBF (2022).

However, the redox flow BSS considered is available on the market mainly for industrial applications and its technical specifications can be found at https://pdf.archiexpo.de/pdf/gildemeister/cellcube/108571-246574.html. Here, a BSS consisting of several modules with a capacity of 400 kWh each and a charge and discharge power of up to 200 kW each. Due to the scalability of redox flow BSS, more than one module can be purchased to increase capacity as well as charging or discharging power, e.g., 2 modules for a maximal storage capacity of 800 kWh, etc. Furthermore, the efficiency of a charging and discharging cycle is \(\approx 70\%\), the BSS is suitable for 100% deep discharge, and the self-discharge is \(\approx 200\) W in standby mode. It is important to note that, as the literature review showed, maximal charge and discharge power as well as self-discharge cannot be neglected. Neglecting the self-discharge, for example, may lead to situations in which the maximal amount of energy is stored for a long time before being discharged. This might not be an optimal policy when cosidering self-discharge. Furthermore, in the literature a constant discharge power coefficient is usually assumed; cf., e.g., Weitzel and Glock (2017). However, as the technical data show, the higher the discharge rate, the more inefficient the BSS get, see Fig. 6.

Fig. 6
figure 6

Discharge intensity rate \(y_{kt}\) and its model-theoretic operationalization

Full size image

The piecewise linear curve in the lefthandside of Fig. 6—consisting of the line segments I,\(\dots \),IV— reflects this technical property. In this Fig. 6, \(0\le y_{kt} \le 1\) describes the discharge intensity rate of the storage module (BS) k in period t. In order to operationalize such a monotonous increasing and convex curve, we extend these four line segments to four different straight lines (\(L_I,\dots ,L_{IV}\)) and represent those as constraints in our model (refer to righthandside of Fig. 6). Consequently, the reduction [in kWh] of stored capacity in BS k at intensity rate \(y_{kt}\) is just obtained by calculating \(\max \lbrace L_{I}(y_{kt}),\ldots ,L_{IV}(y_{kt})\rbrace \).

4 Model setup

4.1 Formulation of MINLP

Table 1 contains the symbolics used in our nonlinear mixed-integer optimization problem (MINLP) given by equations (1)–(19). The nonlinearity occurs due to equations (14) and (15). However, linearization aspects will be discussed in the next subsection.

Table 1 Indices, parameters and variables
Full size table
$$\begin{aligned}&{\textbf {min}} \qquad \text {TEC} = \sum \limits _{t=1}^T c^{elec}_t \cdot \left( s^{buy}_t + \sum \limits _{k=1}^K s_{kt}^{buy\_BS}\right)&\end{aligned}$$
(1)
$$\begin{aligned}&{\textbf {min}} \qquad \text {TPC} = \sum \limits _{t=1}^T \left( s^{buy}_t + \sum \limits _{k=1}^K s_{kt}^{buy\_BS}\right)&\end{aligned}$$
(2)
$$\begin{aligned}&{\textbf {s.t.}}&\nonumber \\&\sum \limits _{\nu =1}^N\sum \limits _{t=1}^T \sum \limits _{m=1}^M a_{\nu j}^{prod}\cdot x_{jmt \nu } = d_j&\forall \ j \in \mathcal {J} \end{aligned}$$
(3)
$$\begin{aligned}&\sum \limits _{i=0}^I \delta ^{state}_{imt} = 1&\forall \ m \in \mathcal {M},\ t \in \mathcal {T} \end{aligned}$$
(4)
$$\begin{aligned}&\widehat{\delta }^{state\_I}_{mt \nu }-\sum \limits _{j=1}^J x_{jmt \nu } = 0&\forall \ t \in \mathcal {T}, \ m \in \mathcal {M},\ \nu \in \mathcal {N} \end{aligned}$$
(5)
$$\begin{aligned}&\delta ^{state}_{Imt} - \sum \limits _{\nu =1}^N \widehat{\delta }^{state\_I}_{mt \nu } = 0&\forall \ t \in \mathcal {T}, \ m \in \mathcal {M} \end{aligned}$$
(6)
$$\begin{aligned}&\delta ^{state}_{imt} + \delta ^{state}_{hm,t+1} \le 1 + \gamma ^{tran}_{ih}&\forall \ i,h {\in } \mathcal {I},\ m {\in } \mathcal {M},\ t {\in } \mathcal {T}\setminus \lbrace T \rbrace \end{aligned}$$
(7)
$$\begin{aligned}&\sum \limits _{m=1}^M \left( \sum \limits _{\nu =1}^N \widehat{a}^{elec\_I}_{\nu m} \cdot \widehat{\delta }^{state\_I}_{mt \nu } + \sum \limits _{i=0}^{I-1} a^{elec}_{im} \cdot \delta ^{state}_{imt}\right) = \widetilde{s}_t&\qquad \forall \ t \in \mathcal {T} \end{aligned}$$
(8)
$$\begin{aligned}&\sum \limits _{k=1}^K \eta ^{max} \cdot y_{kt}+ s_t^{buy} =\widetilde{s}_t&\forall \ t \in \mathcal {T} \end{aligned}$$
(9)
$$\begin{aligned}&m_l \cdot y_{kt} + b_l \le \alpha _{kt}&\forall \ l\in \mathcal {L},\ k\in \mathcal {K},\ t \in \mathcal {T} \end{aligned}$$
(10)
$$\begin{aligned}&BS_{kt}^{cap} + \eta ^{eff} \cdot s_{kt}^{buy\_BS} - \alpha _{kt}-\eta ^{self} = BS_{k,t+1}^{dummy}&\quad \forall \ t \in \mathcal {T}\setminus \lbrace T \rbrace ,\ k \in \mathcal {K} \end{aligned}$$
(11)
$$\begin{aligned}&s_{kt}^{buy\_BS} \le \eta ^{max}&\forall \ t\in \mathcal {T},\ k\in \mathcal {K} \end{aligned}$$
(12)
$$\begin{aligned}&\alpha _{kt} \le BS_{kt}^{cap}&\forall \ t\in \mathcal {T},\ k\in \mathcal {K} \end{aligned}$$
(13)
$$\begin{aligned}&\alpha _{kt}\cdot s_{kt}^{buy\_BS} = 0&\forall \ t\in \mathcal {T},\ k \in \mathcal {K} \end{aligned}$$
(14)
$$\begin{aligned}&\max \lbrace 0,\ BS_{kt}^{dummy} \rbrace = BS_{kt}^{cap}&\quad \forall \ k \in \mathcal {K},\ t \in \mathcal {T} \end{aligned}$$
(15)
$$\begin{aligned}&BS_{k1}^{cap}=0;\ \delta ^{state}_{0m1}+\delta ^{state}_{1m1}=1&\forall \ k \in \mathcal {K},\ m\in \mathcal {M} \end{aligned}$$
(16)
$$\begin{aligned}&x_{jmt \nu },\ \delta ^{state}_{imt}, \ \widehat{\delta }^{state\_I}_{mt \nu } \in \{0,1\}&\!\!\!\!\forall t{\in } \mathcal {T},\ j{\in } \mathcal {J},\ i {\in } \mathcal {I}, m \!{\in }\! \mathcal {M},\! \nu \! {\in } \mathcal {N} \end{aligned}$$
(17)
$$\begin{aligned}&s^{buy}_t,\ s_{kt}^{buy\_BS},\ \widetilde{s}_t,\ \alpha _{kt},\ BS_{kt}^{cap} \ge 0&\forall \ t \in \mathcal {T},\ k\in \mathcal {K} \end{aligned}$$
(18)
$$\begin{aligned}&BS_{kt}^{dummy} \in \left[ -\eta ^{self}, \kappa ^{max} \right] ;\ y_{kt} \in \left[ 0, 1\right]&\forall \ k\in \mathcal {K},\ t\in \mathcal {T} \end{aligned}$$
(19)

In MINLP, we simultaneously minimize total electricity costs TEC and total electricity consumption TPC, see (1) and (2). Here, the electricity to be purchased in period t is decomposed into the electricity purchased without charging the BSS, \(s_t^{buy}\), and the electricity purchased for charging the K modules of the BSS, \(\sum \limits _{k=1}^{K} s_{kt}^{buy\_BS}\). Aggregation over all periods results in the TPC and additional consideration of the electricity cost rate \(c_t^{elec}\) results in the TEC.

The equality constraints in (3) ensure the exact coverage of demand \(d_j\) with respect to each order j. Equations (4) ensure that a machine has exactly one machine state i in each period t. Equations (5) in combination with (6) are coupled and control the production state I (here, \(I=3\)) and the selection of a speed level. More precisely, equations (5) ensure that \(\widehat{\delta }^{state\_I}_{mt\nu }\) equals 1 if any \(x_{jmt\nu }\) is equal to 1. If so, that machine m has to be in production state at speed level \(\nu \). The Eq. (6) state that if a machine m is in the production state I in period t, \(\delta _{Imt}=1\), then exactly one speed level \(\nu \) must be selected. In order to control the state transitions of a machine, we use the constraints in (7). Either a machine retains a state with \(h=i\), or it can change it with \(h\ne i\), if feasible. Equations (8) determine the total amount of electricity required in period t. Here, the electricity consumption for the production state of each machine m \((\sum \nolimits _{\nu =1}^N \widehat{a}^{elec\_I}_{\nu m} \cdot \widehat{\delta }^{state\_I}_{mt \nu })\) is treated separately from the other states \((\sum \nolimits _{ i=0}^{I-1} a^{elec}_{im} \cdot \delta ^{state}_{imt})\) due to the finer-grained decomposition regarding the speed levels. Because of the equations’ length, the required amount of electricity \(\widetilde{s}_t\) in period t is decomposed in (9) into the electricity to be purchased without charging the BSS in period t, \(s_t^{buy}\), and the electricity obtained from the BSS in period t (\(\sum \nolimits _{k=1}^{K} \eta ^{max}\cdot y_{kt}\)).

Together with (9), Eqs. (10)–(15) control the operation of the BSS. Equations (10) are a linearised version of \(a_{kt}=\max \lbrace L_{I}(y_{kt}),\ldots ,L_{IV}(y_{kt})\rbrace \) mentioned in the prior section. However, (10) determine the reduction of the stored capacity in module k when discharged with a certain power intensity \(0\le y_{kt}\le 1\), see again Fig. 6. Here, e.g., \(y_{kt}=1\) means that BS k is discharged in period t at \(100\%\) of the maximum discharge rate. Equations (11)–(15) balance the stored capacity of BS k in period \(t+1\). The stored capacity of BS k in period \(t+1\) is given by the stored capacity of BS k in the previous period t plus the charged amount of electricity in period t (\(\eta ^{eff}\cdot s_{kt}^{buy\_BS}\)) minus the discharged amount of electricity (\(\alpha _{kt}\)) in period t and the losses due to self discharge \(\eta ^{self}\). Here, the purchased electricity \(s_{kt}^{buy\_BS}\) for charging the BS k in period t cannot exceed the maximal amount of electricity when charging at rate \(\eta ^{max}\) on the one hand, see (12). On the other hand, the reduction of the stored capacity \(\alpha _{kt}\) due to discharging cannot exceed the amount of stored capacity in BS k in period t, see (13). However, applying equations (14), in a period t, either a BS k is charged or discharged, but not both at a time. Moreover, due to self-discharge, the stored capacity in a BS may become negative. To avoid this, the dummy variables \(BS_{k,t+1}^{dummy}\)—which can take on negative values (see (19))—are used in (11) and together with equations (15), the stored capacity of BS k in period t is either 0 or strictly positive, but never negative.

Equations (16) are used for initialization. In period \(t=1\), there is no stored energy in the BSS. With \(\delta ^{state}_{0m1}+\delta ^{state}_{1m1}=1\), each machine is either in the off state or ramps up in period \(t=1\). (17)–(19) are typical binary, non-negativity and interval-value conditions.

4.2 Linearization of MINLP

MINLP is nonlinear due to (14) and (15). These equations are to be linearized in the following such that the resulting mixed-integer problem (MIP) can be solved as such, which is always preferred to nonlinear programming; cf. Kallrath (2021).

  • Linearizations of equations: (14)

    It is sufficient to replace (14) by the following constraints (20)–(22):

    $$\begin{aligned}&\alpha _{kt} - \beta _{kt}\cdot M \le 0&\forall \ k\in \mathcal {K},\ t\in \mathcal {T}&\end{aligned}$$
    (20)
    $$\begin{aligned}&s_{kt}^{buy\_BS} - (1-\beta _{kt})\cdot M \le 0&\forall \ k\in \mathcal {K},\ t\in \mathcal {T}&\end{aligned}$$
    (21)
    $$\begin{aligned}&\beta _{kt} \in \lbrace 0,1 \rbrace&\forall \ k\in \mathcal {K},\ t\in \mathcal {T}&\end{aligned}$$
    (22)

    Here, (20)–(22) form a switching mechanism (indicator constraints) with a sufficiently large number \(M>0\). Due to (13), \(M=\kappa ^{max}\) is sufficiently large. However, if \(\alpha _{kt}>0\) then \(\beta _{kt}\) must be 1 to satisfy (20). But then, \(s_{kt}^{buy\_BS} \le 0\) have to apply in (21) and thus \(s_{kt}^{buy\_BS}=0\) due to (18), and vice versa.

  • Linearizations of equations: (15)

    The nonlinearity arises from the \(\max \)-operator. Equations (23)–(26) yield a sufficient linearization:

    $$\begin{aligned}&BS_{kt}^{cap} \ge BS_{kt}^{dummy}&\forall \ k\in \mathcal {K},\ t\in \mathcal {T}&\end{aligned}$$
    (23)
    $$\begin{aligned}&BS_{kt}^{cap} - \widetilde{\beta _{kt}}\cdot M \le BS_{kt}^{dummy}&\forall \ k\in \mathcal {K},\ t\in \mathcal {T}&\end{aligned}$$
    (24)
    $$\begin{aligned}&BS_{kt}^{cap} - (1-\widetilde{\beta _{kt}})\cdot M \le 0&\forall \ k\in \mathcal {K},\ t\in \mathcal {T}&\end{aligned}$$
    (25)
    $$\begin{aligned}&\widetilde{\beta _{kt}} \in \lbrace 0,1 \rbrace&\forall \ k\in \mathcal {K},\ t\in \mathcal {T}&\end{aligned}$$
    (26)

    \(BS_{kt}^{cap}\) must be larger than both components of the \(\max \)-operator, so \(BS_{kt}^{cap}\) must be larger than 0 (which is the case due to (18)) and larger than \(BS_{kt}^{dummy}\), see (23). At the same time, however, \(BS_{kt}^{cap}\) must also be smaller than either component of the \(\max \)-operator due to the switching mechanism in (24) and (25). Thus, the larger component of the max-operator is chosen.

In total, MIP (1)–(13), (16)–(26) is the linearized version of MINLP (1)–(19).

5 Results and discussion

Now, we compute representations of Pareto fronts for the MIP considering RTP, TOU and PPA. The setting consists of 4 machines and 5 jobs with equal quantities for each job (\(\approx 75\)% machine utilization at the highest production speed). Furthermore, different numbers of modules for the redox flow BSS (0–2 modules) are taken into account. \(K=0\) modules means that there is no storage considered, and e.g. \(K=1\) module, there is a BSS with \(K\cdot 400\) kWh capacity and a maximum charge and discharge power of \(K\cdot 200\) kW. Representations of Pareto fronts are obtained via GAMS using CPLEX, applying the modified weighted Tchebycheff approach with weights \(0\le w_{TEC},w_{TPC} \le 1\) satisfying the convex combination \(w_{TEC}+w_{TPC}=1\). Cf. Miettinen (1988) for details on the method.

5.1 Results in the context of RTP and TOU

Fig. 7
figure 7

Baseline scenario, RTP

Full size image
Fig. 8
figure 8

Baseline scenario, TOU

Full size image

Figures 7 and 8 show representations of Pareto fronts under RTP and TOU for the cases without a BSS (\(K=0\)) and with different sized BSS (\(K=1\), \(K=2\)). First of all, it can be seen that there is a conflict between electricity costs and electricity consumption when considering RTP or TOU; thus, electricity costs should be considered an economic criterion under price-dynamic tariffs. However, under RTP, the following cases can be distinguished:

  • Case I (RTP):

    In area I of Fig. 7, the three point clouds (black, \(K=0\); red, \(K=1\); blue, \(K=2\)) overlap. Here, the 3 settings (\(K=0,1,2\)) lead to similar results for the considered criteria (TEC, TPC). The reason for this is that a BSS is not 100% efficient, and due to the energy losses involved, it is not TPC effective, i.e. the minimum electricity consumption for production cannot be reduced further than in the case of \(K=0\).

  • Case II-III (RTP):

    These areas are of particular interest. It can be see that in II the red points dominate the black points and the blue points dominate the red and black points—III can be interpreted analogously. Although there is no onsite generation and energy losses occur when a BSS is used, the inherent flexibility potentials of the manufacturing system (e.g., production speed levels and machine states) can be more fully exploited via a BSS. This, what we call TEC-TPC-efficiency, leads to dominant production schedules with lower TEC and lower (or similar) TPC compared to a setting without a BSS.

  • Case IV (RTP):

    The greater the capacity and the charging and discharging power of a BSS, the lower the electricity costs that can be achieved, but at the cost of increased electricity consumption (see, for example, the non-comparable blue dots in the northwest in Fig. 7). A BSS is thus what we call TEC-effective.

In case of the TOU-tariff under consideration, we obtain quite similar results, but not as pronounced as in the case of RTP. That said, in Fig. 8 we see that the point clouds overlap for the most part (I and II), which is most probably due to the relatively small price gaps of the respective two-block TOU-tariff. However, the largest-size BSS (\(K=2\)) results in lowest electricity costs, see III, but again at the cost of high electricity consumption. While flexibility potentials such as those shown in II and III in Fig. 7 could not be used to create dominant production schedules in the presence of a BSS, no general conclusions can be drawn from this, as this is probably due to tariff design.

Figures 9, 10, 11 and 12 show how a BSS (\(K=1\)) operates under RTP and TOU. In order not to overload this article, we have limited ourselves to showing the results for two different weighting combinations, \(w=(w_{TEC},w_{TPC})\) with \(w=(0.75,0.25),\ w=(1,0)\). Again, note that the modified weighted Tchebycheff approach was applied with different weighting vectors.

Fig. 9
figure 9

RTP, \(w=(0.75,0.25)\)

Full size image
Fig. 10
figure 10

RTP, \(w=(1,0)\)

Full size image

From Figs. 9, 10, 11 and 12, it is clear that more weighting on TEC (in the algorithmic computation; see again Fig. 7) leads to more use of the BSS. More precisely, for both RTP and TOU, more power is purchased in the market to load the BSS. We can further observe that, under TOU and a weight combination of (0.75, 0.25), the BSS is already not used anymore due to its efficiency \(<100\%\) and the associated energy loss. However, when the BSS is operated under both RTP and TOU, it is at times when electricity prices are relatively low (e.g., at night under RTP and during off-peak hours under TOU). It is also worth noting that a BSS is charged most of the time just before the start of peak periods (TOU) or high price periods (RTP) due to its strictly positive self-discharge rate. However, in a production environment like that described in the preceding and a BSS with an efficiency rate of \(<100\%\), it follows that energy waste is desirable from an economic point of view in order to achieve minimal TEC. However, this can be criticized from an ecological point of view.

5.2 Results in the context of PPA

Given the production planning problem at hand in the presence of a BSS and no onsite generation, there is no tradeoff between TEC and TPC. More precisely, due to the fact that a BSS does not have an efficency rate of 100% and there is no variability in electricity prices, a BSS will not be utilized at all. It is of particular interest that the application of such an instrument proposed by the EU in a given planning problem with the two criteria considered, TEC and TPC, leads to a minimization of both TEC and TPC. More precisely, the instrument here implies a minimization of electricity consumption in production. This reflects the “Energy Efficiency First” principle promoted by the EU, according to which companies should (among other things) become more energy efficient; cf. EU-COM (2022). Hereafter, energy efficiency as defined in Article 2, point 4, of Directive 2012/27/EU shall mean the “ratio of output of performance, service, goods or energy, to input of energy”; EU-COM (2012). Overall, the use of fixed-price PPAs thus implicitly contributes to this principle.

Fig. 11
figure 11

TOU, \(w=(0.75,0.25)\)

Full size image
Fig. 12
figure 12

TOU, \(w=(1,0)\)

Full size image

Of course, if onsite generation (e.g., from photovoltaic or wind power; Fig. 13) is taken into account, then a BSS in this case would result in a reduction of TPC and TEC, see Fig. 14. For the calculation results, deterministic onsite generation with power generation levels selected in advance for specific hours of the day was chosen (see Fig. 13), as was done by Moon and Park (2014) or Wichmann et al. (2019a). However, the implications drawn would not change if a stochastic approach were used.

The results of Sect. 5 are summarized in Table 2. These also apply to the simulation study we conducted, in which over 90 different randomly generated demand scenarios were considered for different numbers of jobs, machines and modules of the BSS. However, to avoid overloading the article, the respective results have been omitted.

It is time to pause a bit and reflect on the findings and conclusions. Considering dynamic electricity prices generally implies a conflict between minimizing energy costs and energy consumption, and this conflict can be exacerbated when operating a battery storage system in such an environment. However, the observations of Table 2 cannot be thoughtlessly transferred to arbitrary production processes, since they naturally depend on the parameter constellations. Still, it is important to recognize that the benefits of a battery storage system must always be evaluated in conjunction with the company’s electricity price tariff.

6 Heuristic procedures

6.1 A problem-specific heuristic approach in the context of fixed-price electricity tariffs

When considering fixed electricity prices as in the case of the selected PPA, the complexity of the problem at hand is reduced in comparison with price-dynamic tariffs. First, a BSS will not be used at all if no onsite generation or reselling of stored electricity is considered. This is due to the general storage inefficiency of a BSS. Second, there is then no tradeoff between the two objective functions (1) and (2), i.e. minimizing electricity costs also minimizes electricity consumption and vice versa. Third, the machine state “standby” becomes redundant since it is not worth switching a machine in standby mode due to a constant electricity price. These arguments are exploited in the following heuristic procedure for finding a solution within an acceptable time frame when dealing with large problem instances (see Table 3).

Fig. 13
figure 13

Daily onsite generation

Full size image
Fig. 14
figure 14

PPA and onsite generation

Full size image
Table 2 Summary of results
Full size table
Table 3 Energy-efficient allocation procedure
Full size table

Note here that Algorithm 1 can be further expanded by including ramp up checks, for example, if it is even worthy to ramp up a machine. However, due to the length of Algorithm 1, this is omitted since the ramp up costs are usually negligible in contrast to the power requirements of the production state.

Fig. 15
figure 15

Numerical example of Algorithm 1

Full size image

A numerical example of the procedure is given in Fig. 15. In the example, two machines (\(m=1,2\)) are considered with ramp up costs of 15 kWh for \(m=1\) and 10 kWh for \(m=2\). The demand amounts to 15 quantities of job 1, 7 of job 2 and 12 of job 3, i.e. \(d_1=15,d_2=7\) and \(d_3=12\). The electricity coefficients of the machines are provided in Table 4, which reflects a typical curve of the electricity consumption change at variable production speed. The time horizon is 5 periods, but \(t=1\) is used for the eventual ramp up of a machine.

Table 4 Electricity coefficients used for the example given in Fig. 15
Full size table

In step 1, the orders are assigned to the machines successively with as few slots occupied as possible, starting with the machine that performs best in terms of the electricity consumption of the production state (here machine \(m=1\)). This initial allocation is then reallocated in step 2 on a job-by-job basis and in an energy-efficient manner, but only to the slots that were also occupied in step 1. In step 3, a check is made to determine whether a slot on the best remaining not fully occupied machine should be occupied by one of the jobs. This lot-splitting approach is checked for each job, and the job that gives the best overall energy consumption reduction (if any) is taken. If no improvement is found, the schedule remains as it was up to that point. Step 4 is an improvement strategy for the schedule constructed so far. Subsets with at least two elements of \(\lbrace \text {job 1},\text {job 2},\text {job 3}\rbrace \) are formed and the jobs in these subsets are batched. Then it is checked whether the schedule can be improved by such a batching strategy and whether such a schedule would be feasible with the original job structure. It should be noted that the general assignment of the slots on the machines remains the same as before the batching check. If this general assignment were dropped, then such a batching check would lead to different results. E.g. in the example given in Fig. 15, batching of jobs 1, 2, 3 and treating it as one job would yield an optimal schedule of 6 quantities in \(t=2,3\) each and 5 quantities in \(t=4,5\) each on machine 1, 4 quantities in \(t=2,3,4\) and 0 quantities in \(t=5\) on machine 2. But such a schedule would not be feasible with the original job structure. However, Step 4 can be seen as optional because of its computational costs compared to step 1–3. In the worse case, it is checked for all possible subsets whether one of these is feasible and improves the schedule constructed so far. This leads to \(\sum \nolimits _{k=2}^J \left( {\begin{array}{c}J\\ k\end{array}}\right) =\sum \nolimits _{k=0}^J \left( {\begin{array}{c}J\\ k\end{array}}\right) \cdot 1^{J-k}\cdot 1^k-(J+1)=2^J-(J+1)\) iterations, which is exponential in the number J of jobs.

Table 5 depicts the results of a scenario analysis performed to show the advantages of Algorithm 1. The energy coefficients and demanded quantities were randomly generated. The algorithm was coded in MATLAB and compared to an exact solution via GAMS using CPLEX. It can be seen that the algorithm leads to an optimal solution in all scenarios and significantly reduces the computation time in all but one scenario compared to GAMS/CPLEX.

Table 5 Computation times in seconds and optimality gaps
Full size table

6.2 Fix-relax-and-optimize in the context of price-dynamic electricity tariffs

Under price-dynamic tariffs such as RTP or TOU, the problem under consideration is more challenging to solve, which usually is the case when conducting scheduling and/or lot-sizing under price-dynamic tariffs; cf. Rapine et al. (2018). However, fix-and-relax (F &R) and/or fix-and-optimize (F &O) strategies can be applied and usually show good results in the context of computation time and solution accuracy for such problems; cf., e.g., Copil et al. (2017) or Masmoudi et al. (2016). F &R is a constructive heuristic, its main idea is to decompose the global problem into smaller subproblems that are easier to solve from a computational point of view. Three time windows can be distinguished: the Frozen Window (FW) where values are partially or completely assigned to the decision variables; the Observation Window (OW) where the original model is considered; and the Approximation Window (AW) where some variables or constraints are relaxed; cf. Rodoplu et al. (2019). A sketchy illustration of the F &R procedure is given in Fig. 16.

Fig. 16
figure 16

Exemplary illustration of an F &R procedure

Full size image

The performance of F &R is significantly influenced by the choice of the length \(\sigma _k\) of the OW and the number of overlapping periods \(\delta _k\) in consecutive iterations. The smaller the OW, the easier it is to solve the subproblems, but at the cost of the number of iterations needed. Eventually, this may even generates infeasible solutions. A similar reasoning can be used for the overlapping time periods. If \(\delta _k\) is chosen too small, more iterations are needed. However, the value of \(\delta _k\) affects the solution accuracy. A value that is too large could lead to poor solution accuracy. Hence, defining the best size of \(\delta _k\) and \(\sigma _k\) is important to obtain a good performance of an F &R heuristic. More details on F &R can be found in Rodoplu et al. (2019) and Masmoudi et al. (2016).

In contrast to F &R, F &O is an improvement heuristic initialized with an initial solution. Based on a given solution, some subsets of binary variables are released and reoptimized while the other variables are fixed to their current values. This procedure is repeated by varying the subset of variables to be released until some stopping criterion is met. If the initial solution is feasible, then of course any newly generated solution is also feasible and no worse than the previous solution; Copil et al. (2017). In fix-relax-and-optimize (FR &O), the initial solution is generated via F &R.

Beside of these heuristic strategies, decomposition approaches are sometimes applied to tackle lot-sizing and/or scheduling problems; cf. Ho et al. (2022), Meyr and Mann (2013) or Liang et al. (2019). Since we are also considering a BSS, decomposing the problem into a part that concerns the BSS and a part that concerns the production processes could boost computation time.

In the following, using the modified weighted Tchebycheff approach, we solve a series of scalarized single-objective problems to determine a Pareto front representation for the respective MIP under RTP and considering a BSS with one module (\(K=1\)). In total, 6 weighting combinations are considered (\(w_1=1,\ w_2=0; w_1=0.8,\ w_2=0.2, etc.\)) thus calculating 6 points of the Pareto front. For each weighting combination, we solve the scalarized subproblem with an FR &O approach and with an FR &O approach mixed with a simple decomposition strategy. The results are compared with an exact solving method via GAMS using CPLEX. Overall, the following strategies are applied:

  • F &R strategy 1:

    All binary variables are fixed in FW and relaxed in AW. In OW, the original model is considered.

  • F &R strategy 2 mixed with a decomposition approach:

    The MIP is decomposed in a first step, i.e. the BSS is neglected (set \(K=0\)). For the reduced problem, F &R is conducted by fixing and relaxing all remaining binary variables in FW and AW. In OW, the reduced problem is considered. After F &R, the solution variables without reference to the BSS are fixed to their current values and the original model (with \(K=1\)) is reoptimized.

  • F &O strategy 1:

    An initial solution is given by F &R strategy 1 or 2. In every iteration, a uniform distributed random number \(rn \in \lbrace 2,\ldots ,T-2\rbrace \) is generated and all variables within the periods \(\left[ rn, rn+0.1\cdot T\right] \) are released. All other variables are fixed. This is repeated until no improvement in two consecutive iterations could be found.

  • F &O strategy 2:

    An initial solution is given by F &R strategy 1 or 2. Subsets are formed that contain combinations of two machines. All variables related to the machines in a subset are released; the other variables are fixed. This is done for all subsets, using the solution generated in the previous iteration.

In the following scenario analysis, different demand scenarios are randomly generated for different machine settings (\(M=5,\ M=6\)). In order to find good configurations for \(\sigma _k\) and \(\delta _k\) in the F &R procedures, different parameter choices were tested with \(\sigma =\sigma _k\) and \(\delta =\delta _k\) \(\forall \ k\), i.e. the values are the same in each iteration. A selection of respective computational results can be found in Tables 6 and 7. Since we are computing Pareto front representations (for 6 weighting combinations), we aggregate the time needed to compute the respective points. Regarding the solution quality, we averaged the solution gaps over every point found by the heuristics. The solution gap (in %) for a single point is calculated using the following formula:

$$\begin{aligned} \text {Gap} = 50\cdot \left( \dfrac{TEC_{heuristic}-TEC_{exact}}{TEC_{exact}} + \dfrac{TPC_{heuristic}-TPC_{exact}}{TPC_{exact}} \right) \end{aligned}$$
(27)

with \(TEC_{exact},TPC_{exact}\) the best solution found by GAMS using CPLEX within the time limit of 3600 s and \(TEC_{heuristic},TPC_{heuristic}\) the solution found either by F &R or FR &O.

After several tests and considering both solution quality and CPU time, we conclude that applying relatively large values for \(\sigma \) relative to the total number of periods T (\(\ge 0.5\cdot T\)) and values for \(\delta \) around \(0.5\cdot \sigma \) lead to overall good performance of the heuristics. Overall, it can be seen in Tables 6 and 7 that both the F &R strategies and the F &O strategies and thus the four FR &O approaches lead to good solutions in terms of solution quality and CPU compared to GAMS/CPLEX. When comparing F &R strategy 1 and 2, the second strategy including the decomposition approach leads to better gaps and lower computation times. Consequently, F &R 2 is to be preferred over F &R 1. With F &O strategy 1 or 2, it is shown that the generated output solution can be further improved, but at the expense of computation time. For example, F &R 1 with F &O 2 leads to the best solution gaps compared to the other approaches, but with significantly higher computation times. Overall, we propose to use F &R mixed with the decomposition approach and further improve the solution by F &O strategy 1, since it gives good results in both computation time and solution quality. However, since F &O is very computationally time intensive and the two F &R strategies already produce good solutions, F &O could also be omitted.

Table 6 Simulation results for F &R strategy 1 and 2 with F &O strategy 1
Full size table
Table 7 Simulation results for F &R strategy 1 and 2 with F &O strategy 2
Full size table

7 Conclusion

In this article, we studied a bicriteria lot-sizing and scheduling approach in a single-stage parallel machine environment in the presence of an onsite redox flow battery storage system (BSS). Different electricity pricing schemes were taken into account: Green Power Purchase Agreement (PPA), Real-Time-Pricing (RTP) and Time-Of-Use (TOU). Under these schemes, tradeoffs between electricity costs and electricity consumption are examined. In the case of price-dynamic tariffs, it could be shown that a redox flow BSS can lead to a significant electricity cost reduction, but mainly at the expense of high electricity consumption levels. This effect increases as the capacity of the BSS increases. In summary, as electricity costs become more favored over electricity consumption, the BSS is more heavily used. Thus, energy waste is desirable, making elctricity costs an economic criterion. However, it could also be shown that in the presence of a BSS, flexibility potentials inherent in the production system (different machine states and different production speed levels) can be better exploited to produce dominant schedules compared to a setting without a BSS. In contrast to RTP and TOU, under a fixed-price PPA, the BSS is not occupied at all and there is no tradeoff between electricity costs and electricity consumption. Consequently, under a fixed-price PPA, electricity costs can be considered an ecological criterion.

To cope with large instances of the model, we developed an energy-efficient allocation procedure for the case of a PPA and several fix-relax-and-optimize strategies for the case of an RTP. All heuristics show good performance in terms of computation times and solution accuracy. However, in the case of an RTP, Fix-and-Relax combined with a simple decomposition strategy and solution reoptimization leads to the most promising results.

Several aspects could be useful for further research. Since green PPAs can include certificates of origin, trading of such certificates could be included in production policies. Additionally, the use of a BSS not only to store and use electricity but also to sell electricity could lead to further profit benefits for companies, a possibility that merits further study.