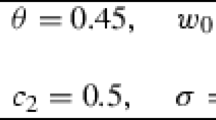Dynamic history-dependent tax and environmental compliance monitoring of risk-averse firms

Abstract

Firms may misreport income or fail to comply with environmental regulations. This study contributes to the growing literature that analyzes dynamic history-dependent compliance monitoring, under which penalties or monitoring frequency are selected on the basis of recent compliance history. The current study develops methods for evaluating and comparing explicit solutions under given monitoring costs and income distributions, using a commonplace utility-penalty scenario under which firms never comply fully with regulations if statically monitored (regardless of their income distribution), but find it to their benefit, if dynamically monitored, to comply fully when their income is sufficiently high. In most examples tried, dynamic monitoring is superior even when constrained to monitor all firms at rates below the optimal static rate. The model is applied to actual IRS 2010 tax-report monitoring and compliance data partitioned by income bracket. This allows, in particular, to deduce degrees of risk aversion.

1 Introduction

Importers must declare the contents of their containers and pay customs accordingly. Firms are required to declare annual income and pay the appropriate tax. Polluting firms are subject to compliance regulations that impose taxes and technology expenditures. Mass transit passengers are obligated to pay the required fare. Evasion and non-compliance may arise in these situations and many others. Compliance monitoring authorities maintain profiling data on firms, which may be used to determine the frequency and intensity of auditing. These profiles tend to include static information on the firm, but may also summarize the extent of compliance of the firm in recent history. The current study contributes to the literature on the merits of this dynamic, history-dependent monitoring strategy (Landsberger & Meilijson, 1982; Greenberg, 1984; Friesen, 2003; Solan & Zhao, 2021).

Static models of monitoring may suggest setting the static auditing probability p by maximizing $E[\text{ Fiscal } \text{ Revenue}]-c p$, where $c>0$ is the authority’s auditing cost per monitored firm. Alternatively, firms may be classified in terms of their compliance record, and the severity of violations may determine auditing probabilities and penalties in a dynamic manner. Under the model to be adopted in the current study, initiated by Landsberger and Meilijson (1982) (hereafter L & M), firms are to be dichotomously identified as type-1 or type-2 depending on full or partial compliance in the last auditing episode, a variant of what Friesen (2003) terms “non-target” and “target” groups. Type-1 firms are audited with probability $p_1$ and type-2 firms with higher probability $p_2$, and the label is re-defined at every auditing episode. Unlike the one-period nature of expected utility under static monitoring, expected utility under dynamic monitoring incorporates a discounted present value of future income. The main issue under study is the extent to which future welfare considerations could motivate improved firm compliance, without increasing the fiscal monitoring budget. Specifically, the following research questions are addressed:

• To what extent is the advantage of dynamic over static monitoring manifested for non-vanishing static auditing probability?

• What is the optimal compliance response of agents to dynamic monitoring?

• Can dynamic monitoring assist the authority in improving compliance behaviour and increasing average revenue while conducting fewer inspections?

These and other pertinent questions are answered in full, by constructing a game theoretic model between the authority and the firms under “laboratory conditions” - a particular type of penalty function (proportional underpayment penalty) employed by the authority and a particular family of concave utility functions (Constant Absolute Risk Aversion, CARA) to model the risk attitude of the firms.

The proportional underpayment penalty is commonly used in practice, for example by the U.S. IRS and U.S. Customs and Border Protection. Specifically, the regulations of the latter state the following: “if first offense, where there is knowledge of the declaration requirements, the undeclared articles are discovered by the Customs officers, and there are no mitigating or aggravating factors: Three times duty...” USCBP (2004). Such penalties have also been considered in the literature for environmental applications, as in Oestreich (2015) and Oestreich (2017). Also, to enforce the Clean Air Act Amendments, the regulatory actions of the U.S. Environmental Protection Agency (EPA) are a function of the plant’s history of past actions Blundell et al. (2020). Specifically, the EPA chooses dynamic enforcement because it avoids over-fining firms before they have the chance to fix violations. It uses the threat of high fines as an incentive for firms to make costly investments in pollution abatement.

The CARA assumption, widely applied in practice, is not too restrictive: it is reasonable to assume that the economic attitude toward compliance with tax or environmental regulations is relatively consistent in a homogeneous population of firms (that is, firms characterized by a relatively narrow wealth range); in other words, $\log (U'(x))$ may be approximated by a linear function, leading to constant absolute risk aversion. The penalty is B times the evaded amount, and the utility function is $U(x)=-e^{-\gamma x}$. The pair of parameters $B>1$ and $\gamma >0$ provides enough structure to develop policies in depth, optimizing monitoring rates in the static and dynamic cases.

It will be seen that under static monitoring, the firms never comply fully, and evade by an amount that depends on the parameters of the model (monitoring probability p, Arrow & Pratt index of risk aversion $\gamma$ (Arrow 1970, Pratt 1964), and penalty load B), but is independent of the tax level and mechanism, as well as of the gross income and the net full-compliance income R and its distribution. In contrast, the best response of expected-utility maximizing firms to dynamic monitoring is to comply fully when R exceeds a certain threshold, which is higher for type-1 than for type-2 firms. These two thresholds are sensitive to the distribution of R and to the discount factor $\beta$ as well as to other parameters of the model. It will be shown that, generally, the expected revenue of the authority under dynamic monitoring exceeds that under static monitoring with a smaller budget.

To support these theoretical statements, the model is applied to the monitoring and compliance data in the IRS 2010 tax-report. These data allow estimation of the risk-aversion parameters for the various homogeneous income brackets in the report. In their empirical studies, Dubin and Wilde (1988) reported, for each of six audit classes (low, middle and high income ; business and non-business), the audit rate for the previous year and the degree of compliance in the current year. These authors showed that while audit rates increase with income bracket ($2.5\%, 4\%, 10\%$), the degree of compliance is highest in the middle-income bracket, and is higher for non-business than business firms throughout the income range. This indicates that indices of risk aversion differ between audit classes. The heterogeneity of these indices is also reported by Babcock et al. (1993). The IRS 2010 report IRS (2011) plays a significant role, revealing the variability of the index of risk aversion across tax brackets.

As will be illustrated via the high-risk exponential loss distribution, there is no bound to the advantage of dynamic over static monitoring when either the Arrow & Pratt index of risk aversion (Arrow 1970, Pratt 1964) or the discount factor are allowed to vary. However, as illustrated via the exponential gain distribution, there may be an advantage of dynamic over static monitoring even when firms are subjected to moderate risk. Surprisingly, dynamic monitoring can allow the authority to improve compliance behaviour and increase average revenue with truly less inspections. That is, in some cases, there exist pairs $(p_1, p_2)$ such that $0 \le p_1 < p_2 \le p$, where p is the optimal static monitoring fraction, with smaller revenue loss for the authority than in the case of static p. This will be illustrated using IRS data (IRS, 2011). The implication is that auditing can in some sense be counter-productive: e.g., instead of auditing $5\%$ of all firms (the static case), the authority can improve compliance and increase its revenue by implementing the policy of reducing the auditing fraction to $2.5\%$, for firms that were fully compliant on their last auditing occasion, while the auditing fraction for the other firms remains the same.

The remainder of the paper is organized as follows. Following a literature review, Sect. 3 introduces CARA utility functions and the proportional underpayment penalty, the optimal firm’s compliance strategy and the optimal static rate of monitoring by the authority, which curbs evasion, illustrated on the IRS 2010 compliance data. Section 4 extends the analysis to dynamic monitoring, where both the distribution of income and the firm’s discount factor (ignored under static monitoring) play a role. Section 5 presents numerical examples comparing static and dynamic monitoring. Section 6 extends the analysis to an environmental setting, where it is assumed that the evading firm engenders additional societal costs that affect the authority’s loss function.

2 Literature review

How can a regulatory agency achieve acceptable levels of compliance with minimum cost of enforcement? This challenge confronts regulators in areas as diverse as tax collection, policing, customs and immigration, workplace health and safety, and natural resource management. Economists beginning with Becker (1968) have attempted to answer this question using the rational choice framework. Individuals facing regulation will comply when the expected benefit of doing so exceeds the expected cost, and enforcement mechanisms must be set accordingly. To minimize enforcement costs, economists have proposed simple random audit regimes.

In current practice, tax authorities such as the IRS may determine whom to audit strategically, such that the audit probability depends also on the past behavior of the taxpayer and the tax authority (Cronshaw & Alm, 1995; Alm, 2019). Conditional audit regimes exploit observable signals about firms or individuals. For example, a conditional future audit rule may stipulate that taxpayers found to be noncompliant may be audited more frequently in the future. L &M were the first to study a dynamic two-state policy under which firms that discount future utility exponentially in time with discount factor $\beta \in (0,1)$ are classified into type-1 and type-2 firms depending on whether they fully complied with regulations at their previous monitoring episode. Type-i firms are sampled with probability $p_i$, and the pair $p_1,p_2$ (with $p_1 \le p_2$) is chosen optimally from among those pairs that yield a steady-state monitoring probability equal to the value of p under static monitoring. Classification is dynamic in the sense that it is updated at every monitoring episode. The main finding of L &M is that as $p \downarrow 0$, ignoring the sampling cost, the authority’s revenue under dynamic monitoring is at least double that under static monitoring. The dynamic compliance monitoring model implemented in the current study goes beyond vanishing monitoring rates by effectively taking monitoring costs into account.

Greenberg (1984) extended the two-state model of L &M by adding a third state, called the penalty state, and showed that the three-state scheme is optimal for infinitely patient players. Experimental methods used by Alm et al. (1993) and by Rivas (1997) revealed that such history-dependent monitoring schemes are more effective than random audit selection rules at deterring noncompliance. Recently, Shimshack and Ward (2022) studied the optimal punishment mechanism of two types of heterogeneous entities, frequent and infrequent violators, and showed empirically the relative importance of factors driving optimal decisions (using data from a Clean Water Act regulatory setting).

While the above research focused on tax-evasion monitoring, dynamic auditing has also been considered in the context of environmental protection, where agencies need to inspect firms who generate air or water pollution; see for example Harrington (1988); Harford and Harrington (1991); Harford (1991); Friesen (2003); Eckert (2004); Weikard and Dellink (2014); Cason et al. (2021); Wu et al. (2022).

The literature on monitoring policies with respect to environment pollution has also considered the (competitive) interaction between firms subjected to targeted inspections. Colson and Menapace (2012) showed that the authority can utilize the added information from monitoring multiple agents to induce improved environmental compliance through the creation of strategic interactions among firms. Weikard and Dellink (2014) studied the terms for establishing a stable international climate agreement by developing a game model where a single agreement is proposed that can either be signed or not. The authors suggested a transfer scheme specifically designed to increase the incentive to join the coalition. Oestreich (2017) considered competition among firms, allowing the probability of being audited to depend on the relative difference between the firm’s emissions report and a reference value for the reported emissions of other firms. So, the optimal audit mechanism is a contest that exploits the strategic interdependence between firms. Recently, Wu et al. (2022) considered a competitive firm that faces a pollution tax and may evade taxes by concealing its actual pollution emissions. The authors developed a Nash bargaining model in order to study the effect of wage bargaining on the environmental effectiveness of tax enforcement.

Studies on effective enforcement and monitoring systems have employed a game theoretic formulation, in the form of an inspection game (originally proposed by Dresher (1962) and treated in greater generality by Maschler (1966)). Arguedas et al. (2012) studied a firm’s compliance decisions and the inspection agency’s monitoring strategy by means of a signaling game that incorporates dynamic enforcement and learning. Deutsch et al. (2019) considered a two-stage game in which the inspector first commits to a global monitoring technology, and then, in the second stage, an n-firm inspection game is played. Analysis of numerical examples yielded the counterintuitive result that monitoring may encourage pollution.Varas et al. (2020) provided insight into the effectiveness of surprise versus announced inspections. The authors developed a dynamic model of inspections to determine the principal’s optimal dynamic monitoring scheme. They found that unannounced inspections provided strong incentives for compliance while announced inspections were more effective for gathering information about the agent’s type.

Solan and Zhao (2021) studied a discounted repeated inspection game with two agents and one principal. The goal of the principal, who is assumed to have a Stackelberg leader advantage, is to minimize the discounted number of violations under the limitation of being able to inspect up to one agent in each time period. Whereas L &M only considered compliance behaviour at the previous auditing episode, these authors took into account the observed agent actions (either adherence or violation) at all previous inspection points up to the current time period. Optimal inspection strategies of the principal are described in two phases, the second being a cyclical rewarding scheme in which the principal inspects with variable inspection probabilities (some of them zero) that recur with some period d.

Most previous research assumes risk-neutral agents. Exceptions are Ravikumar and Zhang (2012), Goumagias et al. (2018) (and to some extent, L &M). The current study hinges on risk aversion and assumes that firms (agents) have constant absolute risk-averse preferences. Empirical estimation of risk-aversion parameters based on tax evasion was carried out by Goumagias et al. (2018), who applied a neural network methodology to Greek tax data as a case study. In the current paper, based on IRS 2010 data, coefficients of absolute and relative risk aversion are estimated, and their impact on the decisions of the agents is analyzed.

This paper is in line with the stochastic operations research (OR) literature in that it offers explicit, detailed, mathematically derived solutions to the problem of dynamic monitoring, under “laboratory” conditions (CARA utility functions, proportional underpayment penalty). This OR approach complements the economic theory outlook of L& M and the game theoretic outlook of Solan and Zhao (2021). The model can be applied both to tax-evasion monitoring, where firms may misreport income, and to an environmental setting where the evading firm may engender additional societal costs.

3 The non-compliance and monitoring model

A firm with taxable income Z has to pay t(Z) in taxes, so that the after-tax income under full compliance is $R=Z-t(Z)$. Under non-compliance, the firm misreports its taxable value with the result that the actual after-tax income, prior to a possible audit, is $R+D$ where D is the evaded amount. If monitoring is applied and $D>0$, the authority uncovers the value of (Z, D) and imposes on the firm a penalty or fine $f=f(D,Z)>D$ that brings the net income to $R+D-f$.

It is assumed throughout that time is discrete, in units that may be called “years”, although in the case of an importer, these units may actually correspond to shipments or physical containers. Taxable amounts, compliance behaviour, monitoring and penalties refer to each year separately. Firms are modeled as risk averse with (concave) utility function U. The expected utility of a firm is, in principle, a function of the taxable amounts Z, the full-compliance net income R, the evaded amount D and the audit probability p,

$$\begin{aligned} G(R,D,p,Z)=U(R+D)(1-p) + U(R+D-f(D,Z)) p \end{aligned}$$

(1)

In the current study, compared with previous work that generally assumes risk neutrality, firms are risk averse with CARA utility function $U(x)=-e^{-\gamma x}$, where $\gamma$ is the Arrow & Pratt index of absolute risk aversion. The evasion penalty is $f(D,Z)=B D$ with penalty load $B>1$. Expected utility is thus freed from dependence on Z.

Parenthetically, if the proportional underpayment penalty is applied to risk-neutral firms, then unless $p B \ge 1$ (in which case full compliance is dominant), expected-utility maximizing firms should evade by infinite amounts. Whether B is 1.5, 2 or 3, sampling the large proportion $p={1 \over B}$ is too costly in practice. Hence, analysis of the commonly applied proportional underpayment penalty relies on risk aversion by firms.

3.1 The authority’s loss under static monitoring

The authority’s loss (with respect to full compliance) from a firm that chooses to evade by amount D and is audited with probability p is

$$\begin{aligned} L(D,p)=c p + (1-\xi )(m D - p f(D)) \end{aligned}$$

(2)

where $c>0$ is the cost of monitoring a firm, $\xi$ is the proportion of firms that comply unconditionally with the regulations, and $m \ge 1$ is a multiplier that reflects the monetary cost to the authority or society as a result of the firm’s evasion: the excess proportion $m-1$ corresponds to the additional cost to society associated with the evaded amount D. The loss excluding the cost of monitoring is given by ${\widehat{L}}(D,p) = L(D,p) - cp$.

While $m=1$ is typical for income tax and customs duties, $m>1$ could be more appropriate for emissions taxes: due to the “tragedy of the commons” and externalities (Mas-Colell et al., 1995, Chapter 11), the firm’s evaded amount inflicts additional damages on the environment and society. Although this additional cost may not be linear in real settings, the linear relationship assumed by this model captures parsimoniously the co-monotonicity of D and the cost to society. The objective of the authority is to minimize the sum of the monitoring cost and the expected unpaid tax. The authority is naturally expected to foot at least some of the bill for the damage inflicted on society; for example, the authority’s national healthcare and/or health insurance program would incur the cost of illnesses caused by pollution.

It is reasonable to take the societal expenditure or loss into account in the design of monitoring strategies and penalties, by properly calibrating the multiplier m. Yet, to keep mathematical derivations as transparent as possible, this multiplier will be set at $m=1$ and the unconditional full-compliance proportion will be set at $\xi =0$ for the remainder of the paper, except in a special section at the end dedicated to the case $m>1$. A non-zero $\xi$ can be treated as though $\xi =0$ by recalibrating c to the higher cost ${c \over {1-\xi }}$.

In the same vein, a possible generalization to heterogeneously risk-averse firms (with a distribution of $\gamma$ values in the population of firms), will not be considered, and the authority’s monitoring policy will be designed with respect to fixed $\gamma$. Firms differ in terms of their after-tax income, shipment values or emissions, and in theory, the input data should include a probability model for the variability in this parameter, in particular the distribution of the full-compliance after-tax income R. In the absence of such information, particular Gaussian or exponential full-compliance net income scenarios will be used as illustrations.

3.2 Introduction to dynamic state-dependent compliance monitoring

Firms are labeled as either type-1 or type-2 every time the firm is monitored. Type-i firms are monitored with frequency $p_i$, satisfying $0 < p_1 \le p_2 \le {1 \over B}$. The full-compliance net income R is assumed to be i.i.d. across firms and years, with some distribution assumed to be common knowledge. Labels and monitoring frequencies are assumed to be common knowledge too. Two events $\mathcal{R}_1$ and $\mathcal{R}_2$ are singled out, and type-i firms comply fully with regulations during years with $R \in \mathcal{R}_i$, underpaying taxes otherwise. The state of the firm is a Markov chain with states 1 and 2 and transition matrix with diagonal entries $1-p_1+p_1 P(R \in \mathcal{R}_1)$ and $1-p_2+p_2 (1-P(R \in { \mathcal{R}_2)})$, as depicted in Fig. 1. The stationary probability $\mu _1$ of state 1 is

$$\begin{aligned} \mu _1={{p_2 P(R \in \mathcal{R}_2)} \over {p_2 P(R \in \mathcal{R}_2)+p_1 (1-P(R \in \mathcal{R}_1))}} \end{aligned}$$

(3)

and the mean monitoring proportion in the dynamic model is ${\bar{p}} =\mu _1p_1+(1-\mu _1)p_2$.

Fig. 1

The Markov chain in state-dependent monitoring (Landsberger & Meilijson, 1982)

It is assumed that the firms know the monitoring rates $p_1$ and $p_2$, and determine the two events $\mathcal{R}_i$ as a best response to $(p_1,p_2)$ in the sense of the maximal discounted sum of expected utilities across time. As will be seen, under CARA utility and a proportional underpayment penalty, firms monitored at rate $p_i$ that choose to underpay taxes (an event with probability $1-P(R \in \mathcal{R}_i)$) underpay by an amount D (see (8)) that depends on $p_i, B$ and $\gamma$, but is independent of R, whether monitoring is static or dynamic. Hence, the authority is indifferent to the choice of event $\mathcal{R}_i$ with given probability $P(R \in \mathcal{R}_i)$. The choice of events is a prerogative of the firm. It will be seen that it is in the firm’s interest to comply fully in high-income years; i.e., $\mathcal{R}_i$ is the $P(R \in \mathcal{R}_i)$-upper quantile of the distribution of R (possibly randomized if R has atoms with positive probability).

The authority determines the pair $(p_1,p_2)$ under this assumption, taking into account monitoring costs, so as to minimize expected total loss (underpayment plus monitoring cost minus collected penalties),

$$\begin{aligned} {\mathcal {L}}(p_1,p_2) ~~=~~&\mu _1 (D(p_1)P(R_1\notin \mathcal R_1) -p_1(f(D(p_1)P(R_1\notin \mathcal {R}_1))-c))\nonumber \\ {}&+(1-\mu _1) ( D(p_2)P(R_2\notin \mathcal R_2)-p_2(E[f(D(p_2)P(R_2\notin \mathcal R_2))-c))\nonumber \\ ~~ = ~~&\mu _1 (D(p_1)P(R_1\notin \mathcal R_1)-p_1f(D(p_1)P(R_1\notin \mathcal R_1)))\nonumber \\&+(1-\mu _1) (D(p_2)P(R_2\notin \mathcal R_2)-p_2f(D(p_2)P(R_2\notin \mathcal R_2))) + {\bar{p}} c \end{aligned}$$

(4)

which generalizes the expected loss for static monitoring ($p_1=p_2=p$) shown in (2) to the case of dynamic monitoring ($p_1<p_2$).

As the static loss function (2), the loss function in (4) can also be extended to model societal costs using the parameter m, which will be considered in Sect. 6. First, the best response of firms to a given monitoring rate is analyzed, the results of which are relevant to both the static and dynamic models. Subsequently, static monitoring will be studied in detail, followed by dynamic monitoring.

3.3 The response of firms to monitoring rate p

Evidently, for a given p, G(R, D, p) in (1) is maximized by D that satisfies

$$\begin{aligned} f_D'(D,\cdot )={1 \over p} - {{1-p} \over p}\left[ 1-{{U'(R+D)} \over {U'(R+D-f(D,\cdot ))}}\right] < {1 \over p} \end{aligned}$$

(5)

As explained earlier, for proportional underpayment penalty $f(D)=B D$ with penalty load $B>1$, evading can only occur if $p<{1 \over B}$. The ratio ${{U'(R+D)} \over {U'(R+D-f(D,\cdot ))}}$ can be approximated as

$$\begin{aligned} e^{\log (U'(R+D))-\log (U'(R+D-f(D,\cdot )))}&\approx e^{-f(D,\cdot ){{-U''(R+D-f(D,\cdot ))} \over {U'(R+D-f(D,\cdot ))}}} \nonumber \\ {}&= e^{-f(D,\cdot ) I_{AP}(R+D-f(D,\cdot ))} \end{aligned}$$

(6)

Thus, firms do not necessarily comply with regulations, and as expected, the extent of non-compliance is dictated by the Arrow-Pratt (Arrow 1970, Pratt 1964) index of absolute risk aversion $I_{AP}(\cdot )={{-U''(\cdot )} \over {U'(\cdot )}}$.

Absolute and relative indices of risk aversion. It seems to be challenging to pinpoint $I_{AP}(\cdot )$, as can be evidenced from the high variability reported by Babcock et al. (1993). The index may vary from firm to firm and even from application to application, since the rationale in Sect. 1 for its constancy is only local. A discussion on whether the absolute risk aversion (ARA) index $I_{AP}(x)$ or the relative risk aversion (RRA) index $x I_{AP}(x)$ should be considered globally constant, is deferred to Sect. 3.5. Throughout this paper, a constant ARA is denoted by $\gamma$. A constant RRA is denoted by $\lambda$ in Sect. 3.5, in the context of the IRS 2010 data (IRS, 2011).

CARA utility and proportional underpayment penalty. For CARA (constant absolute risk-averse) firms, with utility function $U(x)=-e^{-\gamma x}$ defined by the Arrow-Pratt index of risk aversion $\gamma >0$, approximation (6) is an equality, and the firm’s expected utility may be expressed in terms of a function S(p, D), which evidently does not depend on R

$$\begin{aligned} G(R,D,p)= & {} U(R+D)(1-p) + U(R+D-f(D))p \nonumber \\= & {} -e^{-\gamma R} \left( (1-p) e^{-\gamma D} + pe^{-\gamma (D-f(D))}\right) \nonumber \\= & {} -e^{-\gamma R} S(p,D) \end{aligned}$$

(7)

Thus, a best-response D for given (fixed) p is a minimizer of $S(p,\cdot )$, which does not depend on R.

Full compliance would occur only if $p \ge {1 \over {f'(0)}}$. For lower monitoring rates, firms adhering to the expected-utility maximization paradigm never comply, and evade by a fixed amount D. Under the assumed penalty scenario $f(D)=B D$ with $B>1$, for $p< \hat{p}\equiv {1 \over B}$, $S(p,\cdot )$ is convex and the evaded amount D that maximizes (7) can be expressed in closed form as

$$\begin{aligned} D(p)={1 \over {B \gamma }}\log \Big ({{1-p} \over {(B-1)p}}\Big ) \end{aligned}$$

(8)

Since $\gamma$ and B are fixed, the dependence of the function D(p) on these two parameters is left tacit. The minimal expected utility multiplier

$$\begin{aligned} S(p,D(p))=\left( {{p} \over \hat{p}}\right) ^{\hat{p}} ({{1-{p}} \over {1-\hat{p}}})^{1-\hat{p}}= e^{-{{\,\textrm{KLD}\,}}({\hat{p}},p)} \end{aligned}$$

(9)

depends only on B and p, free of $\gamma$, expressed in terms of the Kullback-Leibler divergence ${{\,\textrm{KLD}\,}}(q,p)$ of the dichotomous distribution with probabilities $(p, 1-p)$ from the distribution with probabilities $(q,1-q)$, which shows the increasing function S of p to be zero at zero and one at ${\hat{p}}$.

D (in (8)) and S (in (9)) clearly define the roles of risk aversion, penalty and monitoring frequency in determining underpayment. Static compliance monitoring shows its pitfalls: there is no “tomorrow” and there is no role for the distribution of R. As will be shown in the next section, a properly designed history-dependent compliance monitoring policy takes advantage of these extra features and can motivate the firm to drastically improve its compliance behavior.

To crisply see the effect of history-dependent $(p_1, p_2)$ compliance monitoring, let $R \equiv 0$ be deterministic. If type-1 firms underpay taxes by $D(p_1)$ and type-2 firms comply fully rather than underpaying taxes by $D(p_2)$, firms will comply fully a fraction ${{p_1} \over {p_1+p_2}}$ of the time (the stationary probability of being a type-2 firm).

To achieve this, the authority should compute pairs $p_1<p_2$ that equate the expected utilities under $(p_1,p_2)$-dynamic and $p_2$-static monitoring, satisfying

$$\begin{aligned} {{S(p_1,D(p_1)) p_2+p_1} \over {p_1+p_2}}=S(p_2,D(p_2)) \end{aligned}$$

and then apply pairs with a slightly smaller $p_1$ and slightly larger $p_2$.

3.4 The authority’s optimal choice of p in static monitoring

The response of CARA firms to proportional penalty is to underpay taxes by the fixed amount D(p) given by (8). The working assumptions of CARA utility function with given $\gamma$ and proportional penalty with globally-set B are meant only as a tractable mathematical basis for analysis, not as real-world knowledge of the authority about the firms’ behavior. As such, these assumptions lead to the clear-cut solution presented by the next theorem, easy to interpret and to serve as benchmark for the performance assessment of dynamic monitoring.

Theorem 1

Expected-utility optimizing CARA firms with Arrow & Pratt index of risk aversion $\gamma$, statically monitored at rate p and subjected to evasion penalty load $B>1$, underpay taxes by the amount $D(p)={1 \over {B \gamma }}\log \Big ({{1-p} \over {(B-1)p}}\Big )$ given by (8). The authority sets the monitoring rate $p=p^*$, the unique root of the equation

$$ c\gamma - {{1-pB} \over {B (1-p)p}} -\log \Big ({{1-p} \over {(B-1)p}}\Big )=0 $$

Proof

The authority’s revenue loss with respect to full compliance by firms, given by (8), is

$$\begin{aligned} {\mathcal {L}}(p)=L(D(p),p)=c p + D(p)-p B D(p) \end{aligned}$$

Since $D(\cdot ,\gamma ,B)$ is a decreasing function of p, and p should not exceed $\hat{p}={1 \over B}$, differentiation yields

$$\begin{aligned} {\mathcal {L}}'(p)=c -B D(p)+D'(p)(1-p B) < c-B D(p) \end{aligned}$$

(10)

As previously observed, optimal monitoring expenditure exceeds collected penalties. Since firms observe the authority’s monitoring rate p and respond by evading in the amount D, (8) can be substituted into (10) and the optimal value $p^*$ of p must be a solution of

$$\begin{aligned} \gamma {\mathcal {L}}'(p)=c\gamma - {{1-pB} \over {B (1-p)p}} -\log \Big ({{1-p} \over {(B-1)p}}\Big )=0 \end{aligned}$$

(11)

The function ${\mathcal {L}}'$ is continuous on the interval (0, 1/B) and its derivative ${\mathcal {L}}''(p)=(1/p+B-2)/(\gamma B(1-p)^2p)$ is positive throughout this interval for all $B>1$, implying that ${\mathcal {L}}$ is strictly convex and that $\gamma {\mathcal {L}}'$ increases in p. Since it increases from $-\infty$ to $\gamma c>0$, (0, 1/B) must contain the root of (11), the unique minimizer of ${\mathcal {L}}(p)$. $\square$

In numerical experiments, the unique solution $p^*$ of of (11), referred to in Theorem 1, is determined by straightforward bisection over the interval (0, 1/B).

3.5 Empirical illustration: The IRS 2010 compliance data

The US Internal Revenue Service divides firms into disjoint income brackets, and for each bracket, reports the audit proportion p and data from which it is possible to extract the mean underpayment D of firms that did not fully comply with regulations. For a menu of three penalty loads B (1.75, 2, 2.25), Table 1 displays, by tax bracket and penalty load, the values of p and D, as well as the Arrow-Pratt index of ARA $\gamma$ derived from (8), assuming that D maximizes the expected CARA utility in response to static audit proportion p. The table also displays the Arrow-Pratt index of relative risk aversion RRA $\lambda =w \gamma$. The central wealth level w of the i’th income bracket has been (reasonably but arbitrarily) taken as the left endpoint of the bracket divided by $1+{{i-2} \over 20}$, to represent net income as minimal gross income gradually adjusted from an excess of $5\%$ to a deduction of $35\%$.

Since the dimension of $\gamma$ is ${1 \over \text{ money }}$ while $\lambda$ is dimension-free, the relative stability of $\lambda$ across income brackets lends credence to the analysis. However, the values of $\lambda$, in the tens, are higher than the single-digit values commonly reported for investors. This suggests that either firms’ aversion to evasion risk is stronger than their standard risk aversion, or that the actual value of D is higher than the value that is derived from these data, or a combination of the two.

Let $\mathcal{D}$ be the underpayment dichotomous random variable with values D and $-(B-1) D$. Observe that (8), (9) and (11) remain unchanged if the utility function $U(R+\mathcal{D})=-e^{-\gamma (R+\mathcal{D})}$ is generalized to a utility function of the form $U(R,\mathcal{D})=-V(R) e^{-\gamma \mathcal{D}}$. In particular, V(R) could be $e^{-\gamma _1 R}$, where the ARA index $\gamma _1$ conforms with more standard risk aversion levels.

Table 1 Analysis of the IRS 2010 data: Underpayment D and static sampling frequency p for each income bracket.

Table 2 Analysis of the IRS 2010 data: Evaded amount D and static sampling frequency p for each income bracket.

Looking ahead and providing motivation for the following sections, Table 1 also displays the response of firms to a reduction by a factor of two in the monitoring frequency of type-1 firms (those found to comply fully on their last audit) relative to the audit rate under static monitoring. The immediate observation is that static monitoring can be counter-productive: a judicious reduction in monitoring to part of the firms can improve compliance. Sampling costs have been ignored, but these have certainly been reduced by dynamic monitoring. The table reports for each income bracket and a menu of underpayment penalty factors B: the authority’s loss (D minus collected penalties) under static and dynamic monitoring; the steady-state proportion $\mu _1$ of type-1 firms; the proportions of type-1 and type-2 firms that fully comply with regulations in a typical year. Table 1 also displays the mean dynamic sampling proportion ${\bar{p}}=p(1-{\mu _1 \over 2})$, which falls somewhere between ${p \over 2}$ and p depending on the effectiveness of dynamic auditing.

A salient feature displayed in Table 1 is that under static monitoring, the authority’s loss decreases as B increases, as this loss seems to be mostly due to the effect of the higher penalty BD, while in contrast, under dynamic monitoring, the authority’s loss increases with B, as the loss is more greatly affected by the increased risk aversion of firms when the same underpayment D must be explained by a smaller value of B. Another salient feature shown in Table 1 is that the advantage of dynamic over static monitoring, in particular the degree of compliance, appears to increase with income. Given that Table 1 provides clear evidence that the findings are qualitatively insensitive to the choice of B, B will henceforth be set to 1.75.

The IRS 2010 data provide no indication of the distribution of the full-compliance net income R. Table 1 assumes that R has a shifted exponential distribution with standard deviation $\sigma$ that is $20\%$ of the mid income of the bracket. Table 2 is the same as Table 1, except that $\sigma$ has been set to $4\%$ of the mid income of the bracket. Besides illustrating the influence of income volatility on the advantage of dynamic over static auditing, Table 2 can serve another role: keeping $\sigma$ as $20\%$ of the mid income as in Table 1, Table 2 effectively demonstrates the consequences of allowing the standard market-economy ARA, $\gamma _1$, to be one fifth of the evasion ARA, $\gamma$, derived from the IRS 2010 static auditing data.

4 Dynamic, history-dependent compliance monitoring

This section analyzes in depth the application of a history-dependent model for compliance monitoring to CARA firms subjected to proportional underpayment penalties. Under this model, firms are monitored with probability $p_1>0$ if they complied fully at the last monitoring episode (type-1 firms) and with probability $p_2 \ge p_1$ if they were found to be non-compliant at the previous audit (type-2 firms).

Time-additive reward utility model. The working paradigm for time aggregation to be adhered to is the neoclassical growth model by Ramsey (1928), Cass (1965) and Koopmans (1965), under which the social planner maximizes a social welfare function that consists of the aggregated stream of exponentially discounted instantaneous utilities from consumption. In our setting, for a discount factor $0< \beta <1$, the long-run utility of the firm is the infinite sum of period-by-period utilities, tapered geometrically with weights $\beta ^n$. The firm’s current decision affects not only current welfare, but future benefits as well.

The above presentation of static, random compliance monitoring did not make explicit reference to the distribution of the full-compliance net income R, although this distribution acts tacitly in the background. In the dynamic case, it is essential to consider the discount factor $\beta$ and this distribution as integral parts of the model.

Delinquent firms underpay taxes by the evaded amount D defined in (8), and are fined according to penalty load B. Let $\mathcal{R}_i$ be the set of R values for which type-i firms fully comply (possibly empty, possibly the whole space), and let $V_i$ be their overall discounted reward utility. Then the objective function of a type-i firm is the sum of three terms: current welfare when complying fully, current welfare when failing to comply fully, and total discounted future welfare as a result of current compliance behavior.

$$\begin{aligned} W_i (R)= & {} U(R) I_{\mathcal{R}_i}(R)+((1-p_i)U(R+D)+p_i U(R+D-f(D))) (1-I_{\mathcal{R}_i}(R)) \nonumber \\+ & {} \beta ((1-p_i) V_i + p_i (I_{\mathcal{R}_i} V_1 + (1-I_{\mathcal{R}_i}) V_2)) \end{aligned}$$

(12)

It is clear from (12) that if a firm fails to comply, the evaded amount D will be $D(p_i)$, the same as in static random compliance monitoring with $p=p_i$ and the applicable B. The rewards $V_i$ (for i=1,2) are the expectations of $W_i(R)$,

$$\begin{aligned} V_i= & {} E[U(R) I_{\mathcal{R}_i}(R)]+(1-p_i)E[U(R+D(p_i))(1-I_{\mathcal{R}_i}(R))]\nonumber \\ {}{} & {} +p_i E[U(R+D(p_i)-f(D(p_i)))(1-I_{\mathcal{R}_i}(R))] + \beta ((1-p_i) V_i\nonumber \\ {}{} & {} + p_i (P(R \in \mathcal{R}_i) V_1 + (1-P(R \in \mathcal{R}_i)) V_2)) \end{aligned}$$

(13)

For $i=1,2$, let

$$\begin{aligned} A_i= & {} E[U(R) I_{\mathcal{R}_i}(R)]+(1-p_i)E[U(R+D(p_i))(1-I_{\mathcal{R}_i}(R))]\nonumber \\{} & {} +p_i E[U(R+D(p_i)-f(D(p_i)))(1-I_{\mathcal{R}_i}(R))] \end{aligned}$$

(14)

The Bellman equation (13) can be rewritten as

$$\begin{aligned} V_1-V_2= {{A_1-A_2} \over {1-\beta + \beta (p_1 (1-P(R \in \mathcal{R}_1)) + p_2 P(R \in \mathcal{R}_2))}} \end{aligned}$$

(15)

In particular, for the 1-optimal version, substituting $\beta =1$,

$$\begin{aligned} V_1-V_2= {{A_1-A_2} \over {p_1 (1-P(R \in \mathcal{R}_1)) + p_2 P(R \in \mathcal{R}_2)}} \end{aligned}$$

(16)

but formal analysis is performed for $\beta <1$.

Equation (15) is the starting point of a multi-state, history-dependent compliance monitoring study. As was seen to follow from (12), if a firm fails to comply, the evaded amount is $D(p_i)$, the same as in static random compliance monitoring with $p=p_i$ and the applicable B. However, the decision as to whether to comply is affected by history. The expression $W_i(R)$ in (12) is higher under compliance than under failure to comply if and only if its value of $R \in \mathcal{R}_i$ is higher than in the complement. That is,

$$\begin{aligned} \mathcal{R}_i = \{y | (1-p_i)U(y+D(p_i))+p_i U(y+D(p_i)-f(D(p_i))) \!-\! U(y) \!<\! \beta p_i (V_1\!-\!V_2) \}\nonumber \\ \end{aligned}$$

(17)

which, for the generalized CARA utility $-e^{-\gamma _1 y}e^{-\gamma {\mathcal {D}}}$ (defined in the second paragraph of Sect. 3.5) and proportional penalty $B=1/q$, takes the form

$$\begin{aligned} \mathcal{R}_i=\{y | 1 - \left( {p_i \over q}\right) ^q ({{1-p_i} \over {1-q}})^{1-q}< \beta p_i (V_1-V_2)e^{\gamma _1 y} \} \end{aligned}$$

(18)

Without much loss of generality, henceforth $\gamma _1$ is taken to be $\gamma$.

Since $V_1>V_2$ when dynamic auditing is an improvement over static auditing, it is clear that each $\mathcal{R}_i$ is a right ray $(R_i,\infty )$, with left endpoint

$$\begin{aligned} R_i = \frac{1}{\gamma }\log \left( \frac{1-e^{-{{\,\textrm{KLD}\,}}({1 \over B},p_i)}}{\beta p_i(V_1-V_2)}\right) \end{aligned}$$

(19)

Iteratively applying (15) corresponds to the policy improvement method of discounted infinite-horizon dynamic programming (DP) (Bertsekas, 2005). Since the state payoff functions $A_i$ are bounded, and $V_1>V_2$, the control function $I(R\in R_i)$ is well defined, and standard theory of convergence for policy improvement should yield the result that the iterations (15) converge to the unique fixed point (Bertsekas, 2005). The proof of the following theorem contains a direct formal argument based on more elementary finite-action, finite-state discounted DP (see further comments in Appendix A).

Theorem 2

Consider firms with Arrow & Pratt index of risk aversion $\gamma$ that discount future income with discount factor $\beta$, penalized if under-reporting income with penalty load $B>1$. Assume that their income is independent and identically distributed over time periods, with $E[e^{-\gamma R}]<\infty$. Firms dynamically monitored at rates $p_1$ and $p_2$ comply with regulations in periods with full-compliance net income R exceeding the respective thresholds $R_1$ and $R_2$ given by (19). For lower values of R, these firms do not comply and underpay taxes by the respective constant amounts $D(p_1)$ and $D(p_2)$ given by (8), as in static monitoring. The authority sets the monitoring rates $p_1$ and $p_2$ that maximize the objective function (4) subject to policy constraints.

Proof

Derivation (19) proves the stated property that for each type, there is a threshold income such that agents fully comply if the full-compliance net income R exceeds this threshold; otherwise, they evade taxes to the same extent as when subject to (static) random sampling at the corresponding rate.

A fixed-point method for determining the firms’ response $R_1, R_2$ for an arbitrary pair $p_1 < p_2$ is now apparent: a value $DV_1=V_1-V_2$ substituted into (18) determines $\mathcal{R}_1$ and $\mathcal{R}_2$, i.e., $R_1$ and $R_2$. This determines uniquely the expressions $A_1$ and $A_2$ in (14), and then also $DV_2=V_1-V_2$ in (15). If the mapping T that maps $DV_1$ to $DV_2$ has a unique fixed point, this fixed point identifies the optimum. As shown next, the mapping T is a $\beta$-contraction, so its iterates converge to the unique fixed point from an arbitrary initial value of $DV_1$. Note first that the mapping T can be considered continuous. That is, even if the distribution of R has atoms, randomization can be incorporated in (18) and (19) as quantile thresholds instead of R-thresholds. If $p_1<p_2$ and $DV_1=0$, then $DV_2>0=DV_1$. E.g., the function T has $T(0)>0$. On the other hand, T is bounded from above (so $T(DV)<DV$ for DV large enough): since utility was chosen to be negative ($U(x)=-e^{-\gamma x}$), $V_1-V_2< -V_2 < {1 \over {1-\beta }}E[e^{-\gamma R}]e^{\gamma D(p_2)}$. Hence, T has fixed points. The question is whether T has a unique fixed point. Assuming the contrary, take an arbitrary finite set $\mathcal{R}$ of potential $R_i$ values, including the three or four values corresponding to two different fixed points of T, to be the set of actions. There are two states, type-1 and type-2. This is a discounted dynamic programming (DDP) problem with finitely many actions and states. The mapping from the pair $(V_1,V_2)$ of $DV_1$ to the pair $(V_1,V_2)$ of $DV_2$ (allowing only actions $R_i$ in $\mathcal{R}$) corresponds to the Howard improvement routine. By standard DDP arguments (Blackwell, 1962, 1965), this mapping is a $\beta$-contraction, which, by the Banach fixed point theorem on $L_{\infty }$, has a unique fixed point that attracts from every initial $V_1,V_2$. Hence, there cannot exist two different fixed points of the transformation T.

Once the firm’s behavior has been determined for an arbitrary pair $(p_1, p_2)$, these two compliance monitoring probabilities are determined by the authority in terms of the monitoring unit cost c (defined in (11)). To this end, recall (see paragraph before (3)) that the “type” of a firm is a two-state Markov chain with stationary probability $\mu _1$ for type-1 firms, as shown in expression (3). Since the pertinent regret revenue of the authority is $p f(D)-D$, the authority loss $L(p_1,p_2)$ to be minimized over the pairs $(p_1,p_2)$ is given by expression (4). This function may be minimized over all triples $(p_1,p_2,B_1)$ or over those constrained by $p_2 \le p^*$, $B_1=B$, etc. $\square$

Remark on indices. Indices (15) and (16) are reminiscent of the Gittins index (1989). The 1-optimal version yields a maintenance policy that is optimal in a long-run, steady-state sense, a case that may be fitting for environmental compliance monitoring, where checkups are carried out more frequently. It is certainly appropriate for customs duties, where the time scale of a “year” corresponds to the authority’s monitoring of a single container imported by the agent. Needless to say, the closer $\beta$ is to 1, the greater the advantage of history-dependent compliance monitoring over static random sampling, but for robustness purposes, it is desirable that the mere presence of $\beta >0$ should induce compliant behaviour, not only values very close to 1. As will be seen, this is indeed the case.

Heterogeneous degrees of risk aversion. The Arrow-Pratt index of risk aversion may vary from firm to firm in the population, and the expectations in (4) may be thought of as taken with respect to the distribution of $\gamma$ in the population and the conditional distribution of R given $\gamma$, as derived above. The terms $D(p_i)$ tacitly depend on $\gamma$. Roughly speaking, the harmonic mean of $\gamma$ can be considered to represent the global Arrow-Pratt index.

Table 3 The IRS 2010 data analyzed for $B=1.75$ and $\sigma$ set to $20\%$ of the mid-income level in the top half of the table and $4\%$ in the bottom half.

In the experimental section that follows, the unconstrained and $p^*$-constrained cases are explored, corresponding, respectively, to the following optimal authority losses:

$$\begin{aligned} {\mathcal {L}}^*&=\min \left\{ {\mathcal {L}}(p_1,p_2) \; \left| \;\; 0\le p_1\le p_2\le \min \{1,1/B\} \right. \right\}{} & {} \text {and}{} & {} \\ \bar{\mathcal L}^*&=\min \left\{ {\mathcal {L}}(p_1,p_2) \; \left| \;\; 0\le p_1\le p_2\le p^* \right. \right\} . \end{aligned}$$

To illustrate the theorem, explicit forms for the probabilities $P(R_i > y_i)$ and expectations $E[U(R_i+b)I_{R_i>y_i}]$ are provided for three different settings.

Illustration 1: The Gaussian full-compliance net income. If $R=\sigma W$ where $W \sim N(0,1)$ with survival function $\Phi ^*$, then $P(R>y)=\Phi ^*({y \over \sigma })$ and

$$\begin{aligned} E[U(R+b)I_{R>y}]= & {} -E[e^{-\gamma (R+b)} I_{R>y}] \nonumber \\= & {} -e^{-\gamma b+{{\gamma ^2 \sigma ^2} \over 2} } \Phi ^*({y \over \sigma }+\gamma \sigma ) \end{aligned}$$

(20)

Illustration 2: The shifted exponential gain full-compliance net income. $R = \sigma W$ where W is exponentially distributed with mean 1. For $y \ge 0$, $P(R>y)=e^{-{y \over \sigma }}$ yields directly $P(R \in \mathcal{R}_i)=P(R>y_i)$. The expectations needed for the evaluation of $A_i$ are of the form

$$\begin{aligned} E[U(R+b)I_{R>y}]= & {} -E[e^{-\gamma (R+b)} I_{R>y}] \nonumber \\= & {} -{1 \over {1+\gamma \sigma }}e^{-\gamma b } e^{-(1+\gamma \sigma ) {y \over \sigma }} \end{aligned}$$

(21)

where $y \ge 0$ may be $y_1$ or $y_2$ and b may be $D(p_i,\gamma )$ (see (8)) or $-(B-1)D(p_i,\gamma )$.

Illustration 3: The shifted exponential loss full-compliance net income. $R= -\sigma W$, where W is exponentially distributed with mean 1 and $\gamma \sigma <1$. Thus, for $y \le 0$, $P(R>y)=1-e^{{y \over \sigma }}$ yields directly $P(R \in \mathcal{R}_i)=P(R>y_i)$.

$$\begin{aligned} E[U(R+b)I_{R>y}]= & {} -E[e^{-\gamma (R+b)} I_{R>y}] \nonumber \\= & {} -{1 \over {1-\gamma \sigma }} e^{-\gamma b } (1-e^{(1-\gamma \sigma ) {y \over \sigma }}) \end{aligned}$$

(22)

Table 4 Analysis of the IRS 2010 data: The loss functions ${\mathcal {L}}=\widehat{{\mathcal {L}}}+c \overline{p}$ (in $K\$$) include the monitoring costs c shown in Table 3).

Fig. 2

Exponential loss distribution with $\sigma =1$. Penalty load $B=3$, Arrow-Pratt index $\gamma =95\%$ of ${1 \over \sigma }$ and discount factor $\beta =0.95$. All graphs are functions of the monitoring cost c, on the horizontal axis, ranging from 0 to $20 \sigma$. Graph (d) includes the fraction $\mu _1$ of type-1 firms

5 Numerical results

Determining ${\mathcal {L}}^*$ and $\bar{{\mathcal {L}}}^*$ involves optimizing the non-smooth function ${\mathcal {L}}$ over a relatively simple and bounded two-dimensional set. This optimization problem has been solved by a global derivative-free pattern search method (Conn et al., 2009). Experiments have used Matlab’s global optimization toolbox implementation of a mesh adaptive direct search algorithm (Audet et al., 2006), which appears to be quite a robust and efficient method for computing ${\mathcal {L}}^*$ and $\bar{\mathcal {L}}^*$ in practice.

Tables 1, 2 illustrate the advantage of dynamic over static monitoring (ignoring monitoring costs) by means of actual IRS data (IRS, 2011), even without optimizing the monitoring rates $p_1$ and $p_2$, but just taking $p_1={p \over 2}$ and $p_2={p}$. Dynamic losses $\widehat{{\mathcal {L}}}(p_1,p_2)$ are consistently smaller than static losses $\widehat{{\mathcal {L}}}(p)$ (with one exception at the highest income bracket with a small difference in losses).

The top half of Table 3 shows that the further reduction in the authority’s loss does not appear to be overwhelming when optimizing $p_1$ and $p_2$ using the same data as Table 1 under the assumption of an exponential gain distribution of income. The comparison requires some further explanation. The sampling cost c has been determined for each income bracket from expression (11) such that the static monitoring rate p would be optimal. Table 4 displays the total authority loss $\widehat{{\mathcal {L}}}(p_1,p_2) + c \overline{p}$ for the sub-optimal dynamic pair $({p \over 2}, p)$ of Table 1 and the optimal pair $(p_1, p_2)$ of Table 3.

We now examine more closely the effects of different choices for the income distribution, including exponential loss and exponential gain. We conduct a more extensive sensitivity analysis that includes a wide range of choices for the difficult-to-estimate monitoring cost c.

Fig. 3

Exponential loss distribution with $\sigma =1$. Penalty load $B=3$, Arrow-Pratt index $\gamma =95\%$ of ${1 \over \sigma }$ and discount factor $\beta =0.95$. Dynamic monitoring is constrained such that the static monitoring proportion is not exceeded

Exponential loss distribution. Figure 2 (unconstrained) and Fig. 3 ($0 \le p_1 \le p_2 \le p$) display the sensitivity analysis under a risky shifted exponential loss distribution (whatever the shift may be) with standard deviation (without loss of generality) $\sigma =1$, discount factor $95\%$ and Arrow-Pratt index $\gamma$ such that $\gamma \sigma =0.95$ (for $\gamma \sigma \ge 1$, the expected utility is $-\infty$). The advantage of dynamic over static monitoring is apparent: for small c, dynamic monitoring tends to yield a smaller authority loss with a much smaller auditing budget. As c increases, static auditing becomes ineffective in the sense that the auditing budget remains bounded and even decreases, while the authority loss increases at high rate. The advantage of constrained dynamic monitoring over static monitoring prevails throughout the range, and for $c \le 2.167$, the constrained and unconstrained solutions are the same.

Figure 4 corresponds to the same model as Fig. 2, except that $\gamma \sigma =0.995$ and $\beta =0.999$, meaning that the net income is very risky and the firms place equal importance on the present and the future. The purpose of this graph is to demonstrate the possibility that dynamic monitoring rates can be substantially lower than their static counterpart, throughout the cost range, when no constraints are applied. The graph also exhibits the relative insensitivity of the firms to their degree of risk aversion under static monitoring, compared to the decisive effect of this parameter under dynamic monitoring.

Fig. 4

Exponential loss distribution with $\sigma =1$. Penalty load $B=3$, Arrow-Pratt index $\gamma =99.5\%$ of ${1 \over \sigma }$ and discount factor $\beta =0.999$. The unconstrained and constrained solutions are identical

It is possible to set parameters (e.g., discount factor $\beta =0.9$ and Arrow-Pratt index $\gamma =0.8$) for which the unconstrained dynamic policy constitutes an improvement over static monitoring throughout the cost range, while, for the same parameters, the best constrained policy coincides with static monitoring for high c.

There is no bound to the advantage of dynamic over static monitoring. The values of the expected authority loss and expected misreporting (evaded amount) in Fig. 4 under static monitoring are observed to be approximately 8 times those under dynamic monitoring. By letting $\gamma$ increase from 0.995 to 0.996, 0.997, 0.998, the corresponding improvement ratios become approximately 9, 11, 14, respectively. The squares of the values of the expected authority loss and average evaded amount decrease roughly linearly in $\gamma$, reaching 0 when approaching the critical value $\gamma =1$, where firms give up on evading.

Exponential gain distribution. This a very safe distribution, with a stop-loss bound. To induce some reaction to risk, firms will be assumed to have an Arrow-Pratt index $10+$ times that of the firms subjected to exponential loss. The feature chosen for illustration is the non-monotonicity of the monitoring rate as a function of cost, which requires the constraint $p_2 \le p$ to be abolished. Figure 5 shows that $p_2 < p$ under low cost, but $p_2>p$ for higher cost, in a peculiar way. Figure 6 shows the effect of the constraint $p_2 \le p$. The compliance proportions $R_1$, $R_2$ and the type-1 fraction $\mu _1$ change rather drastically, but the overall authority loss and evaded amounts are practically unchanged.

Finally, Figure 7 illustrates that the unconstrained optimal monitoring policy when firms are less concerned about the future can be quite drastic. The parameters are the same as in Fig. 5 except that the discount factor $\beta$ has been reduced from 0.85 to 0.65. For mid to high costs, there are almost no type-2 firms, but the few that exist are monitored heavily.

Fig. 5

Exponential gain distribution with $\sigma =1$. Penalty load $B=3$, Arrow-Pratt index $\gamma =10 \times {1 \over \sigma }$ and discount factor $\beta =0.85$. Dynamic monitoring is unconstrained

Fig. 6

Exponential gain distribution with $\sigma =1$. Penalty load $B=3$, Arrow-Pratt index $\gamma =10 \times {1 \over \sigma }$ and discount factor $\beta =0.85$. Dynamic monitoring is constrained such that the static monitoring proportion is not exceeded

Fig. 7

Exponential gain distribution with $\sigma =1$. Penalty load $B=3$, Arrow-Pratt index $\gamma =10 \times {1 \over \sigma }$ and discount factor $\beta =0.65$. Dynamic monitoring is unconstrained

Dynamic monitoring seems very robust. As observed in all the above examples, very different policies lead to practically the same authority loss and firms’ evaded amounts, both of which are considerably lower than in the case of static monitoring.

The following section illustrates the extension of the model to the case where $m>1$.

6 Extending the model to environmental regulation and taxation

As described in Sect. 1 and 3, a key feature of our model in the case of environmental applications is a nonzero payoff structure, such that obtained by setting $m>1$ in (2).

The firm’s best-response evaded amount given monitoring rate p, D(p), is unchanged by the value of m and is given by (8). Then, for the static model, the authority’s revenue loss incorporating m and D(p) is

$$\begin{aligned} {\mathcal {L}}(p)=L(D(p),p)=c p + {m}D(p)-p B D(p)\end{aligned}$$

and its derivative is

$$\begin{aligned} {\mathcal {L}}'(p)=c -B D(p)+D'(p)({m}-p B). \end{aligned}$$

Substituting (8) into the above equation, the optimal value $p^*$ of p is 1/B if $c\le \frac{m-1}{\gamma (1-1/B)}$, and otherwise it is the unique root of the equation

$$\begin{aligned} {\mathcal {L}}'(p)=c-{{{m}-pB} \over {\gamma B(1-p)p}}-\frac{1}{\gamma }\log \Big ({{1-p} \over {(B-1)p}}\Big )=0 \end{aligned}$$

(23)

Similar to the case where $m=1$, the optimal p can then be determined using bisection. In the dynamic model, the authority loss, which generalizes (4) for $m\ge 1$, is

$$\begin{aligned} {\mathcal {L}}(p_1,p_2)&= \mu _1 ({m}E[D(p_1)]-p_1 (E[f(D(p_1))]-c))\\&\quad +(1-\mu _1) ({m}E[D(p_2)])-p_2 (E[f(D(p_2))]-c) \end{aligned}$$

The functions $E[D(\cdot ,\gamma ,B)]$ and $E[f(D(\cdot ,\gamma ,B))]$, and their evaluation using fixed-point iterations, are unchanged relative to the model with $m=1$ that is detailed in Sect. 4. Figure 8 displays the authority losses, evaded amounts, monitoring fractions and compliance proportions for values of the monitoring cost c ranging from 0 to $20\sigma$. It becomes evident from this figure, when compared with Fig. 2, that as m increases, the advantage of dynamic monitoring becomes even more evident, not only in terms of the difference in the social and authority losses, but, in particular, with regard to the difference in the monitoring rates. It appears that, on average, dynamic monitoring involves much less monitoring than that required for smaller values of m, such as $m=1$ in Fig. 2. Figure 8 shows a somewhat unexpected result for the static model, different from the analysis for $m=1$, where, under low monitoring costs c and relatively high monitoring rates p, no evasion takes place. In Fig. 8, the evaded amount is initially zero in the static model, and remains less than in the dynamic model up to approximately $c=6$, beyond which the evaded amount continues to increase rapidly under static monitoring, while the corresponding increase under dynamic monitoring is much more gradual.

Fig. 8

Exponential loss distribution with $\sigma =1$. Penalty load $B=3$, evaded amount multiplier $m=4$, Arrow-Pratt index $\gamma =95\%$ of ${1 \over \sigma }$ and discount factor $\beta =0.95$. All graphs are functions of the monitoring cost c, ranging from 0 to $20\sigma$

7 Conclusions

Tax or environmental control authorities can classify firms into type-1 or type-2 depending on recent tax or technology-expenditure compliance behavior. This classification gives rise to dynamic monitoring policies, with state-dependent monitoring frequency. Assuming a risk-neutral authority that applies a penalty proportional to the evaded amount, and CARA (constant absolute risk averse) firms, the effects of such a dynamic policy have been analyzed and compared to those of a static one, where firms are audited with fixed frequency.

It has been shown that, under the static policy, expected-utility maximizing firms never comply fully, displaying myopic behaviour insensitive to income. In contrast, the dynamic policy takes better advantage of the degree of risk aversion and the potential for future planning, which motivates firms to comply fully in periods of higher income. Surprisingly, static monitoring can be counter-productive: there are cases where the authority can achieve improved firm compliance and higher authority revenues, with monitoring frequencies steadily smaller than the optimal static monitoring frequency.

The significant advantage of two-state dynamic policy over static monitoring, shown in earlier literature to apply in the limit of vanishing monitoring rate, has been quantified and broadly illustrated in the current study under normal operational conditions. In particular, substantial lower bounds have been illustrated for the advantage afforded by history-dependent incentives to comply.

The two-state dynamic policy under the dichotomous type-1, type-2 sampling scheme was analyzed under firm homogeneity and utility-penalty assumptions that afforded a theoretical analysis. Future research should extend the analysis to take account of the degree of non-compliance, based on distributional data hitherto unavailable. Future work should also include monitoring policies of a more general nature, based not only on detection and punishment but also on incentives offered by the authorities to motivate agents to comply.

Dynamic state-dependent compliance monitoring as a mathematical program

Following the analysis of Sect. 4, dynamic two-state dependent compliance monitoring with CARA utility and $f(D)=BD$ could be considered as the mathematical program,

$$\begin{aligned} \min&\qquad \mu _1(p_1,p_2) (1-p_1B)D_1+(1-\mu _1(p_1,p_2)) (1-p_2B)D_2 \\&\qquad + c(\mu _1(p_1,p_2)(p_1-p_2)+p_2)\\ \text {subject to}&\qquad V_i = E[e^{-\gamma R} I_{\mathcal{R}_i}(R)]+(1-p_i)E[e^{-\gamma (R+D_i)}(1-I_{\mathcal{R}_i}(R))]\\&\qquad +p_i E[e^{-\gamma (R+(1-B)D_i)}(1-I_{\mathcal{R}_i}(R))] + \beta ((1-p_i) V_i \\&\qquad + p_i (P(R \in \mathcal{R}_i) V_1 + (1-P(R \in \mathcal{R}_i)) V_2)) \quad i=1,2\\&\qquad \ 0 \le p_1 \le p_2 \le \frac{1}{B}, \end{aligned}$$

where

$$\begin{aligned} D_i&= {1 \over {B \gamma }}\log \Big ({{1-p_i} \over {(B-1)p_i}}\Big ) \quad i=1,2\\ R_i&= \frac{1}{\gamma }\log \left( \frac{1-e^{-{{\,\textrm{KLD}\,}}({1 \over B},p_i)}}{\beta p_i(V_1-V_2)}\right) \quad i=1,2\\ {\mathcal {R}}_i&= (R_i,\infty ) \quad i=1,2\\ \mu _1(p_1,p_2)&= {{p_2 P(R \in \mathcal{R}_2)} \over {p_2 P(R \in \mathcal{R}_2)+p_1 (1-P(R \in \mathcal{R}_1))}} \end{aligned}$$

and the expectations in the constraints defining $V_i$ take the form (20), (21), or (22). However, this formulation is nonconvex and highly nonlinear. Further, both the objective and constraint functions need not be continuously differentiable. Hence, it may not be possible to solve this formulation directly using general purpose nonlinear programming solvers. On the other hand, for fixed $(p_1,p_2)$, dynamic programming DP (Blackwell, 1962; Bertsekas, 2005) is a standard and efficient approach to evaluate the value functions $V_i$ for $i=1,2$. Optimizing over such pairs $(p_1,p_2)$, even if nonconvex and nondifferentiable, is a two-dimensional optimization problem involving only simple linear/bound constraints, a task that can be carried out effectively by global derivative free methods (Conn et al., 2009) using DP as a “black box” subroutine. This is the theoretical and computational approach adopted in the current paper.