Coordination of social welfare, collecting, recycling and pricing decisions in a competitive sustainable closed-loop supply chain: a case for lead-acid battery

Abstract

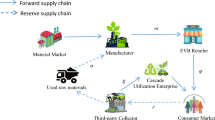
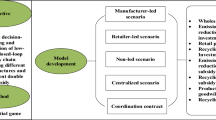
In order to attain competitive advantage, it is of high importance for firms to move towards sustainability. In practice, an efficient sustainable closed-loop supply chain (SCLSC) can reduce the negative effects of hazardous wastes and consequently improve the environmental dimension of sustainability. Besides the environmental dimension, the social aspect of sustainability can be achieved through initiating corporate social responsibility and enhancing social welfare of customers. Different from the existing literature, this paper proposes an analytical coordination model to not only cover all three dimensions of sustainability in a SCLSC but also to align different decisions made in competitive forward and reverse logistics. The proposed SCLSC is modeled under decentralized, centralized, and coordinated decision-making structures considering different game behaviors in the forward and reverse links. The results reveal that the proposed two-way two-part tariff (TWTPT) contract is of high benefit to the sustainable CLSC as it is able to simultaneously enhance the environmental, economic, and social performances. To be more precise, the proposed model improves the collection rate, consumer surplus, social welfare, and profits of all CLSC members. In addition, our findings demonstrate the applicability and efficiency of the proposed TWTPT contract in motivating the agents of both competitive forward and reverse chains to participate in the coordination scheme.

Appendices

Appendix A (Proof of Theorem 3)

To prove the concavity of the remanufacturer’s profit w.r.t. $w_{rm}$ and $t_{rm}$ under Cournot game structure, the Hessian matrix of $\pi_{rm} \left( {w_{rm} ,t_{rm} } \right)$ is investigated as follows. If the Hessian matrix is negative definite, then $\pi_{rm} \left( {w_{rm} ,t_{rm} } \right)$ is concave w.r.t. $w_{rm}$ and $t_{rm}$.

$$ H\left( {\pi_{rm} \left( {w_{rm} ,t_{rm} } \right)} \right) = \left[ {\begin{array}{*{20}c} {\frac{{\partial^{2} \pi_{rm} }}{{\partial t_{rm}^{2} }}} & {\frac{{\partial^{2} \pi_{rm} }}{{\partial t_{rm} \partial w_{rm} }}} \\ {\frac{{\partial^{2} \pi_{rm} }}{{\partial w_{rm} \partial t_{rm} }}} & {\frac{{\partial^{2} \pi_{rm} }}{{\partial w_{rm}^{2} }}} \\ \end{array} } \right] $$

(1a)

The first principal minor is negative:

$$ H_{11} = \frac{{\partial^{2} \pi_{rm} }}{{\partial t_{rm}^{2} }} = - \frac{{2\left( {1 - \emptyset } \right)}}{K}\left( {\frac{{\alpha_{1} + \alpha_{2} }}{2} + \left( {\gamma - \beta } \right)w_{rm} } \right)^{2} < 0 $$

(2a)

The second principle minor is positive when:

$$ \begin{aligned} & \left( {\left( {2m_{rm} - 2r_{rm} - 4t_{rm} + a_{1} + a_{2} } \right)\frac{{\left( {1 - \emptyset } \right)\left( {\gamma - \beta } \right)\left( {\frac{{\alpha_{1} + \alpha_{2} }}{2} + \left( {\gamma - \beta } \right)w_{rm} } \right)}}{K}} \right)^{2} \\ & \quad < \left( { - \frac{{2\left( {1 - \emptyset } \right)}}{K}\left( {\frac{{\alpha_{1} + \alpha_{2} }}{2} + \left( {\gamma - \beta } \right)w_{rm} } \right)^{2} } \right) \\ & \quad \quad \times \left( {2\left( {\gamma - \beta } \right) + \frac{{\left( {m_{rm} - r_{rm} - t_{rm} } \right)\left( {1 - \emptyset } \right)\left( {2t_{rm} - a_{1} - a_{2} } \right)\left( {\gamma - \beta } \right)^{2} }}{K} + \frac{{\omega \left( {\gamma - \beta } \right)^{2} }}{2\beta }} \right) \\ \end{aligned} $$

(3a)

The above condition is numerically checked to ensure that it is always positive under a wide range of parameters and all the test problems as well.

Appendix B

$$ Z\left( 1 \right) = \frac{{2\beta m_{rm} \left( {\gamma - \beta } \right) - \beta \left( {\alpha_{1} + \alpha_{2} } \right)}}{2\beta - \gamma } - \frac{{\omega \left( {\beta \gamma - \beta^{2} } \right)\left( {\alpha_{1} + \alpha_{2} } \right)}}{{\left( {2\beta - \gamma } \right)^{2} }} $$

(1b)

$$ Z\left( 2 \right) = - \frac{{2\beta^{2} \left( {\gamma - \beta } \right)\left( {1 - \emptyset^{2} } \right)\left( {\alpha_{1} + \alpha_{2} } \right)}}{{K\left( {2\beta - \gamma } \right)^{2} }} $$

(2b)

$$ Z\left( 3 \right) = \frac{{4\beta \left( {\gamma - \beta } \right)}}{2\beta - \gamma } + \frac{{2\omega \left( {\beta \gamma - \beta^{2} } \right)\left( {\gamma - \beta } \right)}}{{\left( {2\beta - \gamma } \right)^{2} }} $$

(3b)

$$ Z\left( 4 \right) = \frac{{4\beta^{2} \left( {\gamma - \beta } \right)^{2} \left( {1 - \emptyset^{2} } \right)}}{{K\left( {2\beta - \gamma } \right)^{2} }} $$

(4b)

$$ Z\left( 5 \right) = \frac{{\left( {\frac{{m_{rm} - r_{rm} }}{2} + \frac{{a_{1} + a_{2} }}{4}} \right)\left( {m_{rm} - r_{rm} - \frac{{a_{1} + a_{2} }}{2}} \right)\left( {1 - \emptyset } \right)\left( {\gamma - \beta } \right)\left( {\alpha_{1} + \alpha_{2} } \right)}}{2K} $$

(5b)

$$ Z\left( 6 \right) = \frac{{\left( {\frac{{m_{rm} - r_{rm} }}{2} + \frac{{a_{1} + a_{2} }}{4}} \right)\left( {m_{rm} - r_{rm} - \frac{{a_{1} + a_{2} }}{2}} \right)\left( {1 - \emptyset } \right)\left( {\gamma - \beta } \right)^{2} }}{K} $$

(6b)

$$ Z\left( 7 \right) = \left( {1 - \emptyset^{2} } \right)\left( {\left( {\frac{{m_{rm} - r_{rm} }}{2} + \frac{{a_{1} + a_{2} }}{4}} \right) - a_{1} } \right) $$

(7b)

$$ Z\left( 8 \right) = \left( {1 - \emptyset^{2} } \right)\left( {\left( {\frac{{m_{rm} - r_{rm} }}{2} + \frac{{a_{1} + a_{2} }}{4}} \right) - a_{2} } \right) $$

(8b)

$$ Z\left( 9 \right) = \left( {1 - \emptyset } \right)\left( {\left( {\frac{{m_{rm} - r_{rm} }}{2} + \frac{{a_{1} + a_{2} }}{4}} \right) - a_{1} } \right) $$

(9b)

$$ Z\left( {10} \right) = \left( {1 - \emptyset } \right)\left( {\left( {\frac{{m_{rm} - r_{rm} }}{2} + \frac{{a_{1} + a_{2} }}{4}} \right) - a_{2} } \right) $$

(10b)

$$ U\left( 1 \right) = \alpha_{1} - \omega \alpha_{1} + \frac{\omega \gamma }{\beta }\alpha_{2} - m_{rm} \left( {\gamma - \beta } \right) $$

(11b)

$$ U\left( 2 \right) = 2\gamma - 2\omega \gamma $$

(12b)

$$ U\left( 3 \right) = \left( {\gamma - \beta } \right)\left( { - a_{1} + m_{rm} - r_{rm} } \right) $$

(13b)

$$ U\left( 4 \right) = \left( {\gamma - \beta } \right)\left( { - a_{2} + m_{rm} - r_{rm} } \right) $$

(14b)

$$ U\left( 5 \right) = 2\beta - \omega \beta - \frac{{\omega \gamma^{2} }}{\beta } $$

(15b)

$$ U\left( 6 \right) = \alpha_{2} - \omega \alpha_{2} + \frac{\omega \gamma }{\beta }\alpha_{1} - m_{rm} \left( {\gamma - \beta } \right) $$

(16b)

$$ U\left( 7 \right) = \left( {\alpha_{1} + \alpha_{2} } \right)\left( { - a_{1} + m_{rm} - r_{rm} } \right) $$

(17b)

$$ U\left( 8 \right) = \frac{2K}{1 - \emptyset } $$

(18b)

$$ U\left( 9 \right) = \left( {\alpha_{1} + \alpha_{2} } \right)\left( { - a_{2} + m_{rm} - r_{rm} } \right) $$

(19b)

$$ U\left( {10} \right) = U\left( 7 \right)\left( {\frac{{\left( {\left( {U\left( 5 \right)U\left( 8 \right)} \right) - \left( {U\left( 3 \right)^{2} } \right) - \left( {U\left( 4 \right)^{2} } \right)} \right) - \left( {\left( {U\left( 2 \right)U\left( 8 \right)} \right) + \left( {U\left( 3 \right)^{2} } \right) + \left( {U\left( 4 \right)^{2} } \right)} \right)}}{U\left( 5 \right)U\left( 8 \right)}} \right) $$

(20b)

$$ U\left( {11} \right) = U\left( 8 \right)\left( {\frac{{\left( {\left( {U\left( 5 \right)U\left( 8 \right)} \right) - \left( {U\left( 3 \right)^{2} } \right) - \left( {U\left( 4 \right)^{2} } \right)} \right) - \left( {\left( {U\left( 2 \right)U\left( 8 \right)} \right) + \left( {U\left( 3 \right)^{2} } \right) + \left( {U\left( 4 \right)^{2} } \right)} \right)}}{U\left( 5 \right)U\left( 8 \right)}} \right) $$

(21b)

$$ U\left( {12} \right) = U\left( 3 \right)\left( {\frac{{\left( {\left( {U\left( 1 \right)U\left( 8 \right)} \right) + \left( {U\left( 3 \right)U\left( 7 \right)} \right) + \left( {U\left( 4 \right)U\left( 9 \right)} \right)} \right) + \left( {\left( {U\left( 6 \right)U\left( 8 \right)} \right) + \left( {U\left( 3 \right)U\left( 5 \right)} \right) + \left( {U\left( 4 \right)U\left( 9 \right)} \right)} \right)}}{U\left( 5 \right)U\left( 8 \right)}} \right) $$

(22b)

$$ U\left( {13} \right) = U\left( 9 \right)\left( {\frac{{\left( {\left( {U\left( 5 \right)U\left( 8 \right)} \right) - \left( {U\left( 3 \right)^{2} } \right) - \left( {U\left( 4 \right)^{2} } \right)} \right) - \left( {\left( {U\left( 2 \right)U\left( 8 \right)} \right) + \left( {U\left( 3 \right)^{2} } \right) + \left( {U\left( 4 \right)^{2} } \right)} \right)}}{U\left( 5 \right)U\left( 8 \right)}} \right) $$

(23b)

$$ U\left( {14} \right) = U\left( 4 \right)\left( {\frac{{\left( {\left( {U\left( 1 \right)U\left( 8 \right)} \right) + \left( {U\left( 3 \right)U\left( 7 \right)} \right) + \left( {U\left( 4 \right)U\left( 9 \right)} \right)} \right) + \left( {\left( {U\left( 6 \right)U\left( 8 \right)} \right) + \left( {U\left( 3 \right)U\left( 5 \right)} \right) + \left( {U\left( 4 \right)U\left( 9 \right)} \right)} \right)}}{U\left( 5 \right)U\left( 8 \right)}} \right) $$

(24b)

$$ U\left( {15} \right) = \left( {\frac{{\left( {\left( {U\left( 1 \right)U\left( 8 \right)} \right) + \left( {U\left( 3 \right)U\left( 7 \right)} \right) + \left( {U\left( 4 \right)U\left( 9 \right)} \right)} \right)\left( {\left( {U\left( 5 \right)U\left( 8 \right)} \right) - \left( {U\left( 3 \right)^{2} } \right) - \left( {U\left( 4 \right)^{2} } \right)} \right)}}{{\left( {U\left( 5 \right)U\left( 8 \right)} \right)^{2} }}} \right) $$

(25b)

$$ U\left( {16} \right) = \left( {\frac{{\left( {\left( {U\left( 6 \right)U\left( 8 \right)} \right) + \left( {U\left( 3 \right)U\left( 5 \right)} \right) + \left( {U\left( 4 \right)U\left( 9 \right)} \right)} \right)\left( {\left( {U\left( 2 \right)U\left( 8 \right)} \right) + \left( {U\left( 3 \right)^{2} } \right) + \left( {U\left( 4 \right)^{2} } \right)} \right)}}{{\left( {U\left( 5 \right)U\left( 8 \right)} \right)^{2} }}} \right) $$

(26b)

$$ U\left( {17} \right) = \left( {\frac{{\left( {U\left( 5 \right)U\left( 8 \right)} \right) - \left( {U\left( 3 \right)^{2} } \right) - \left( {U\left( 4 \right)^{2} } \right)}}{{\left( {U\left( 5 \right)U\left( 8 \right)} \right)}}} \right)^{2} - \left( {\frac{{\left( {U\left( 2 \right)U\left( 8 \right)} \right) + \left( {U\left( 3 \right)^{2} } \right) + \left( {U\left( 4 \right)^{2} } \right)}}{{\left( {U\left( 5 \right)U\left( 8 \right)} \right)}}} \right)^{2} $$

(27b)

$$ U\left( {18} \right) = \left( {\frac{{\left( {\left( {U\left( 6 \right)U\left( 8 \right)} \right) + \left( {U\left( 3 \right)U\left( 5 \right)} \right) + \left( {U\left( 4 \right)U\left( 9 \right)} \right)} \right)\left( {\left( {U\left( 5 \right)U\left( 8 \right)} \right) - \left( {U\left( 3 \right)^{2} } \right) - \left( {U\left( 4 \right)^{2} } \right)} \right)}}{{\left( {U\left( 5 \right)U\left( 8 \right)} \right)^{2} }}} \right) $$

(28b)

$$ U\left( {19} \right) = \left( {\frac{{\left( {\left( {U\left( 1 \right)U\left( 8 \right)} \right) + \left( {U\left( 3 \right)U\left( 7 \right)} \right) + \left( {U\left( 4 \right)U\left( 9 \right)} \right)} \right)\left( {\left( {U\left( 2 \right)U\left( 8 \right)} \right) + \left( {U\left( 3 \right)^{2} } \right) + \left( {U\left( 4 \right)^{2} } \right)} \right)}}{{\left( {U\left( 5 \right)U\left( 8 \right)} \right)^{2} }}} \right) $$

(29b)

Appendix C (Proof of Theorem 4)

To prove the concavity of the third party collectors’ profit w.r.t. $\theta_{1}$ and $\theta_{2}$ under Collusion game structure, the Hessian matrix of $\pi_{T} \left( {\theta_{1} ,\theta_{2} } \right)$ is as follows. If the Hessian matrix is negative definite, then $\pi_{T} \left( {\theta_{1} ,\theta_{2} } \right)$ is concave w.r.t. $\theta_{1}$ and $\theta_{2}$.

$$ H\left( {\pi_{T} \left( {\theta_{1} ,\theta_{2} } \right)} \right) = \left[ {\begin{array}{*{20}c} {\frac{{\partial^{2} \pi_{T} }}{{\partial \theta_{1}^{2} }}} & {\frac{{\partial^{2} \pi_{T} }}{{\partial \theta_{1} \partial \theta_{2} }}} \\ {\frac{{\partial^{2} \pi_{T} }}{{\partial \theta_{2} \partial \theta_{1} }}} & {\frac{{\partial^{2} \pi_{T} }}{{\partial \theta_{2}^{2} }}} \\ \end{array} } \right] $$

(1c)

The first principal minor is negative:

$$ H_{11} = \frac{{\partial^{2} \pi_{T} }}{{\partial \theta_{1}^{2} }} = - 2\frac{K}{1 - \emptyset } < 0 $$

(2c)

The second principle minor is always positive:

$$ H_{22} = 4\frac{{K^{2} }}{{\left( {1 - \emptyset } \right)^{2} }} > 0 $$

(3c)

Appendix D (Proof of Theorem 5)

To prove the concavity of the retailers’ profit w.r.t. $p_{1}$ and $p_{2}$ under Collusion game structure, the Hessian matrix of $\pi_{R} \left( {p_{1} , p_{2} } \right)$ is as follows. If the Hessian matrix is negative definite, then $\pi_{R} \left( {p_{1} , p_{2} } \right)$ is concave w.r.t. $p_{1}$ and $p_{2}$.

$$ H\left( {\pi_{R} \left( {p_{1} , p_{2} } \right)} \right) = \left[ {\begin{array}{*{20}c} {\frac{{\partial^{2} \pi_{R} }}{{\partial p_{1}^{2} }}} & {\frac{{\partial^{2} \pi_{R} }}{{\partial p_{1} \partial p_{2} }}} \\ {\frac{{\partial^{2} \pi_{R} }}{{\partial p_{2} \partial p_{1} }}} & {\frac{{\partial^{2} \pi_{R} }}{{\partial p_{2}^{2} }}} \\ \end{array} } \right] $$

(1d)

The first principal minor is negative:

$$ H_{11} = \frac{{\partial^{2} \pi_{R} }}{{\partial p_{1}^{2} }} = - 2\beta < 0 $$

(2d)

The second principle minor is always positive, since the assumption $\beta > \gamma .$

$$ H_{22} = 4\left( {\beta^{2} - \gamma^{2} } \right) > 0 $$

(3d)

Appendix E (Proof of Theorem 6)

To prove the concavity of the remanufacturer’s profit w.r.t. $w_{rm}$ and $t_{rm}$ under Collusion game structure, the Hessian matrix of $\pi_{rm} \left( {w_{rm} ,t_{rm} } \right)$ is investigated as follows. If the Hessian matrix is negative definite, then $\pi_{rm} \left( {w_{rm} ,t_{rm} } \right)$ is concave w.r.t. $w_{rm}$ and $t_{rm}$.

$$ H\left( {\pi_{rm} \left( {w_{rm} ,t_{rm} } \right)} \right) = \left[ {\begin{array}{*{20}c} {\frac{{\partial^{2} \pi_{rm} }}{{\partial t_{rm}^{2} }}} & {\frac{{\partial^{2} \pi_{rm} }}{{\partial t_{rm} \partial w_{rm} }}} \\ {\frac{{\partial^{2} \pi_{rm} }}{{\partial w_{rm} \partial t_{rm} }}} & {\frac{{\partial^{2} \pi_{rm} }}{{\partial w_{rm}^{2} }}} \\ \end{array} } \right] $$

(1e)

The first principal minor is negative:

$$ H_{11} = \frac{{\partial^{2} \pi_{rm} }}{{\partial t_{rm}^{2} }} = - \frac{{2\left( {1 - \emptyset^{2} } \right)}}{K}\left( {\frac{{\beta \left( {\alpha_{1} + \alpha_{2} } \right)}}{2\beta - \gamma } + \frac{{2\beta \left( {\gamma - \beta } \right)}}{2\beta - \gamma }w_{rm} } \right)^{2} < 0 $$

(2e)

The second principle minor is positive when:

$$ \begin{aligned} & \left( {\left( {2m_{rm} - 2r_{rm} - 4t_{rm} + a_{1} + a_{2} } \right)\frac{{2\beta \left( {1 - \emptyset^{2} } \right)\left( {\gamma - \beta } \right)\left( {\frac{{\beta \left( {\alpha_{1} + \alpha_{2} } \right)}}{2\beta - \gamma } + \frac{{2\beta \left( {\gamma - \beta } \right)}}{2\beta - \gamma }w_{rm} } \right)}}{{K\left( {2\beta - \gamma } \right)}}} \right)^{2} \\ & < \left( { - \frac{{2\left( {1 - \emptyset^{2} } \right)}}{K}\left( {\frac{{\beta \left( {\alpha_{1} + \alpha_{2} } \right)}}{2\beta - \gamma } + \frac{{2\beta \left( {\gamma - \beta } \right)}}{2\beta - \gamma }w_{rm} } \right)^{2} } \right) \\ & \quad \times \left( {\frac{{4\beta \left( {\gamma - \beta } \right)}}{2\beta - \gamma } + \frac{{2\omega \left( {\beta \gamma - \beta^{2} } \right)\left( {\gamma - \beta } \right)}}{{\left( {2\beta - \gamma } \right)^{2} }} + \frac{{4\beta^{2} \left( {\gamma - \beta } \right)^{2} \left( {1 - \emptyset^{2} } \right)\left( {m_{rm} - r_{rm} - t_{rm} } \right)\left( {2t_{rm} - a_{1} - a_{2} } \right)}}{{K\left( {2\beta - \gamma } \right)^{2} }}} \right) \\ \end{aligned} $$

(3e)

Appendix F (Proof of Theorem 7)

To prove the concavity of the closed-loop supply chain’s profit w.r.t. $\theta_{1} ,\theta_{2} ,p_{1} ,$ and $p_{2}$ under centralized decision-making structure, the Hessian matrix of $\pi_{SC} \left( {\theta_{1} ,\theta_{2} ,p_{1} ,p_{2} } \right)$ is as follows. If the Hessian matrix is negative definite, then $\pi_{SC} \left( {\theta_{1} ,\theta_{2} ,p_{1} ,p_{2} } \right)$ is concave w.r.t. $\theta_{1} ,\theta_{2} ,p_{1} ,$ and $p_{2}$.

$$ H\left( {\pi_{SC} \left( {\theta_{1} ,\theta_{2} ,p_{1} ,p_{2} } \right)} \right)\left[ {\begin{array}{*{20}c} {\frac{{\partial^{2} \pi_{SC} }}{{\partial \theta_{1}^{2} }}} & {\frac{{\partial^{2} \pi_{SC} }}{{\partial \theta_{1} \partial \theta_{2} }}} & {\frac{{\partial^{2} \pi_{SC} }}{{\partial \theta_{1} \partial p_{1} }}} & {\frac{{\partial^{2} \pi_{SC} }}{{\partial \theta_{1} \partial p_{2} }}} \\ {\frac{{\partial^{2} \pi_{SC} }}{{\partial \theta_{2} \partial \theta_{1} }}} & {\frac{{\partial^{2} \pi_{SC} }}{{\partial \theta_{2}^{2} }}} & {\frac{{\partial^{2} \pi_{SC} }}{{\partial \theta_{2} \partial p_{1} }}} & {\frac{{\partial^{2} \pi_{SC} }}{{\partial \theta_{2} \partial p_{2} }}} \\ {\frac{{\partial^{2} \pi_{SC} }}{{\partial p_{1} \partial \theta_{1} }}} & {\frac{{\partial^{2} \pi_{SC} }}{{\partial p_{1} \partial \theta_{2} }}} & {\frac{{\partial^{2} \pi_{SC} }}{{\partial p_{1}^{2} }}} & {\frac{{\partial^{2} \pi_{SC} }}{{\partial p_{1} \partial p_{2} }}} \\ {\frac{{\partial^{2} \pi_{SC} }}{{\partial p_{2} \partial \theta_{1} }}} & {\frac{{\partial^{2} \pi_{SC} }}{{\partial p_{2} \partial \theta_{2} }}} & {\frac{{\partial^{2} \pi_{SC} }}{{\partial p_{2} \partial p_{1} }}} & {\frac{{\partial^{2} \pi_{SC} }}{{\partial p_{2}^{2} }}} \\ \end{array} } \right] $$

(1f)

where

$$ H_{11} = \frac{{\partial^{2} \pi_{SC} }}{{\partial \theta_{1}^{2} }} = - 2\frac{K}{1 - \emptyset } < 0 $$

(2f)

The second principle minor is always positive:

$$ H_{22} = 4\frac{{K^{2} }}{{\left( {1 - \emptyset } \right)^{2} }} > 0 $$

(3f)

The third principle minor is negative when:

$$ \begin{aligned} & \left[ {\left( {\left( {\gamma - \beta } \right)\left( { - a_{2} + m_{rm} - r_{rm} } \right)} \right)^{2} - \left( {\frac{2K}{1 - \emptyset }\left( {2\beta - \omega \beta - \frac{{\omega \gamma^{2} }}{\beta }} \right)} \right)} \right] \\ & \quad < \left( {\gamma - \beta } \right)\left( { - a_{1} + m_{rm} - r_{rm} } \right) \\ \end{aligned} $$

(4f)

The fourth principle minor is positive when:

$$ \begin{aligned} & \frac{2K}{1 - \emptyset }\left( {\left( {\gamma - \beta } \right)\left( { - a_{2} + m_{rm} - r_{rm} } \right)} \right)^{2} \left( {\left( {2\gamma - 2\omega \gamma } \right) + \frac{2K}{1 - \emptyset }} \right) \\ & \quad < \frac{2K}{1 - \emptyset }\left( {\left( {2\beta - \omega \beta - \frac{{\omega \gamma^{2} }}{\beta }} \right) + \left( {2\gamma - 2\omega \gamma } \right)} \right) \\ & \quad \quad \times \left[ {\left( {2\beta - \omega \beta - \frac{{\omega \gamma^{2} }}{\beta }} \right) - \left( {2\gamma - 2\omega \gamma } \right) - \left( {\left( {\gamma - \beta } \right)\left( { - a_{2} + m_{rm} - r_{rm} } \right)} \right)^{2} } \right] \\ \end{aligned} $$

(5f)