1 Introduction

Fuzzy set theory, defined by Peng and Selvachandran (2019), was considered as a map of \(X\longrightarrow [0,1]\) for a set of X with a degree of membership to every element of X in a unit interval of [0, 1]. The concept of fuzzy relation on a set (Aliev et al. 2021) is a map of \(X\times X\) on [0, 1]. Tamura et al. derived some features of fuzzy relation (Xu et al. 2021). Rosenfeld indicated important and basic properties of fuzzy relation and utilized them in graph theory (Kalampakas et al. 2014; Ali et al. 2021). He established the notion of fuzzified graph theory as the generalization of ordinary graph theory. Later, Bhattacharya et al. investigated the fuzzy relation and fuzzy groups (Mohammadzadeh and Borzooei 2018).

The theory of hyperstructure is considered as the generalization of classical structures including hypergroup, hyperring, hypermodule, etc. This notion is based on a hyperoperation that appoints a pair of a set’s elements to a nonempty subset (Corsini and Leoreanu 2013). n-Ary hyperstructures are regarded as an extension of algebraic hyperstructures, which consist of n-ary hypergroups, (m, n)-ary hyperrings and (m, n)-ary hypermodules. n-Ary hypergroups were initially founded by authors (Yamak et al. 2008), after that Mirvakili et al. introduced the notion of (m, n)-ary hyperrings (Leoreanu-Fotea et al. 2015). Then, the concept of (m, n)-ary hypermodules was provided by Anvariyeh et al. over Krasner (m, n)-ary hyperrings (Ameri and Norouzi 2015). Leoreanu-Fotea presented a new kind of fuzzy n-ary hyperstructures as the generalization of n-ary hyperstructures, in particular fuzzy n-ary hypergroups and fuzzy (m, n)-ary hyperrings (Leoreanu-Fotea 2009). Sun et al. studied fuzzy hypergroups related to fuzzy relation according to a given fuzzy hyperoperation (Sun et al. 2010). With a general approach, fuzzy hyperalgebra theory was defined and improved by Ameri et al., that was the generalization of hyperalgebraic systems and ordinary algebraic systems. This theory was formed based on the n-ary fuzzy hyperoperation to obtain basic and important properties (Ameri and Nozari 2011).

Fuzzy set theory has many applications in various fields, including linguistics, decision-making, cluster analysis, bioinformatic, economics, management, physics etc. The authors presented a novel class of fuzzy hyperalgebra and fundamental relation with applications in biological structures (Firouzkouhi et al. 2021). Mohammedali et al. 2021 applied fuzzy set notion in solar cells. Grag utilized number-based q-rung orthopair fuzzy set in a decision-making process (Garg 2021). There is a variety of other applications with respect to algebraic hyperstructures in geometry, lattices, graphs and hypergraphs, fuzzy and rough sets, automata, computer coding, cryptography, and artificial intelligence (Corsini and Leoreanu 2013).

In 2019, coronavirus disease (COVID-19) emerged and significantly changed the precautionary lifestyle of human beings. One of the critical impacts of such global issue appeared in educational sectors where most of the schools and universities faced closure or forced to change their traditional systems. To mitigate the consequences of mutated COVID, a majority of colleges and universities implemented online/blended educational platforms to adapt instructors and students to the existing situation (Harada et al. 2020; Fox et al. 2021). In fact, online training can be regarded as a feasible and cheap gadget and an indispensable part of future educational systems (Panigrahi et al. 2018) beyond prevailing lockdowns.

With the ever-developing online learning environment, AI-techniques can be embedded for various goals in different gadgets, e.g., chatbots, dashboard, automated assessment system and intelligent tutoring systems. The automated assessment systems distinguish and automatically calculate and analyze the answers of students (Celik 2023). This is very important because AI-techniques can play a key role in evaluating and advancing students’ performance. For example, the automated AI-systems assist instructors to assess learners speaking and writing in the assignments and exams (Hu 2023) or the advanced AI prediction model can control the data of students’ learning process and manage their academic performance (Jiao et al. 2022).

According to a survey on online distance learning, a total of one hundred students who participated in questionnaires, acknowledged some of the advantages of such platform, for instance convenient accessibility at anytime and anywhere (32 percent), time and cost efficiency (22 percent) and sustainability (56 percent). Nevertheless, there were some complaints against the remote systems including network instability (39 percent), unilateral interaction and limited communication (18 percent), reduced concentration (29 percent), and the rest on declining the quality and educational satisfaction (Agarwal and Kaushik 2020; Fatonia et al. 2020). The IT (information technology) mindfulness and techno-eustress were theorized to facilitate the productivity and creativity of students in an online learning setup during COVID (Shirish et al. 2021). Meanwhile, the online courses have shown their benefits for the training of staff in industry and academia (Chang 2016) as well as helping their perspectives for career choices (Ray et al. 2019). Even after elapsing the current pandemic, the transition of education systems from traditional to online/blended phase is required for elevating learning/teaching efficiency, minimizing the costs, and increasing sustainability. With all these, there is not yet a solid and comprehensive theory to address such a learning/teaching platform at the local or global scale.

During the COVID-19 pandemic, the impact of e-learning was investigated with a theoretical approach to evaluate differences between dental schools before and after lockdown (Chang et al. 2021). With a fuzzy view, cluster analysis was conducted by applying fuzzy C-Means classifying students’ abilities in the e-learning process based on their learning outcomes (Sari et al. 2021). In K-S, fuzzy analytic hierarchy process (AHP) was utilized in constructing a blended learning measurement system. In another study, an advanced evaluation model was presented for online learning based on fuzzy mathematics to analyze the impact of virtual learning (Tao 2021).

In fact, fuzzy mathematical approach has a strong potential to evaluate/optimize multiple connections among entities (individuals or cores). Classical fuzzy binary relation has major drawbacks for effectively dealing with the uncertain behavior of entities and linkages. Indeed, classical fuzzy relations merely focus on binary connections of elements, however, complex systems possess multiple relations of elements that are disregarded in fuzzy analysis. Nonetheless, the conventional fuzzy relation method cannot tackle the systems with vagueness and imprecision among multiple elements; this approach is not beneficial for the analysis of complicated correlated entities. Also, the dependence values in classical fuzzy relation are devoted to the strength of relations (i.e., edges in fuzzy graph) between a pair of elements, while dependence values in the present theory comprehensively describe the strength of interrelated elements as it is the generalized version of the classical approach. In this way, the presented theory can be applicable for multidimensional fuzzy relations in real large-scale problems.

Despite advances in online learning systems, there is no well-established methodology to theoretically and functionally evaluate multi-facet intercomponent connections among elements. The goal of this study is extending the classical fuzzy relation into an advanced fuzzy system in order to establish the Global Online Learning (GOL) theory. This approach provides a powerful tool with many capabilities, for instance, exploring the fuzzy membership degree of complex correlations of components in virtual training systems with uncertainty. The presented theory concurrently considers 2-ary, 3-ary, \(\ldots\), n-ary relations of variables for multi-aspects interrelated components in dynamic systems with uncertain information. Compared to the existing theoretical and experimental achievements in e-learning systems, this pattern has supremacy as it applies a multi-facet fuzzy-based framework with a novel methodical graphical display.

In this study, a comprehensive soft computing methodology is extended to meticulously assess complex interconnected components (two or multiple interconnections between elements) with a graphical representation. It aims at generalizing classical relation and binary fuzzy relation in fuzzy mathematics called n-ary relation and fuzzy n-ary relation by developing new definitions and notations. A systematic connection between t-cut and Cartesian product is discussed in a generalized fuzzy relation format to configure complicated correlation of components. The proposed model is systematically framed into an AI-base “GOL theory” to solve fuzzy problems in terms of uncertain-based information in blended training. With the obtained symbols, a novel n-ary fuzzy hyperoperation is presented to construct fuzzy hyperalgebra with a new approach. The AI-base GOL theory is constructed in terms of uncertain-based information to intelligently analyze the learning/comprehension rate of taught courses for students in digital education at a local or global scale. Additionally, the theoretical and graphical architecture of the developed strategy outperforms the evaluation of components and interconnections.

After the Sect. 1, the basic and primary notions of the proposed method are briefly provided in Sect. 2. In Sect. 3, we present a new kind of relation called n-ary and n-ary fuzzy relations, with important results associated to reflexive, symmetric, transitive, composition, t-cut, support and Cartesian products. Also, the systematic relevance between Cartesian product and cut property is studied. In Sect. 4, through the declared n-ary fuzzy relation, we establish an n-ary fuzzy hyperoperation parameter “\(\circ _{\rho }\)” to achieve fuzzy hyperalgebra along with illustrative examples. The parametric connection between support property and derived hyperalgebra is investigated, along with determining the relevance between fuzzy hyperalgebra and hyperalgebra through the constructed notation \((\circ _{\rho })_{t}.\) In Sect. 5, the AI-base “GOL theory” is initiated using the n-ary fuzzy relation to address the online/blended training systems (Fig. 1).

Fig. 1
figure 1

AI-base GOL theory is constructed based on \(x_{i}\) as individuals, \(\mu\) as learning rate of each Individual, and \(\rho\) as learning rate of conjoint individuals (n-ary) in global online networks

Full size image

2 Preliminaries

Definition 2.1

A fuzzy set \(\zeta\) of a set V is a function of V on a unit interval [0, 1],  that is \(\zeta : V \longrightarrow [0, 1],\) which appoints a membership degree to every element of V. A fuzzy relation \(\theta\) on a set V is a fuzzy set of \(V\times V,\) i.e., \(\theta : V\times V\longrightarrow [0, 1],\) that assigns a membership degree to every pair of elements of V. In addition, \(\theta\) is considered as a fuzzy relation on a fuzzy set \(\zeta ,\) if \(\theta (x,y) \le \zeta (x)\wedge \zeta (y)\) for all \((x,y)\in V\times V.\) By considering \(\theta\) as a fuzzy relation on \(\zeta ,\) we say that \(\theta\) is a reflexive fuzzy relation provided \(\theta (x,x)= \zeta (x),\) and if \(\theta (x,y)= \theta (y,x),\) then we call \(\theta\) a symmetric fuzzy relation. Additionally, support \(\theta\) is defined as \(\theta ^{*}=\{(x,y)\in V\times V\mid \theta (x,y)>0\}\) while t-cut is determined as \(\theta ^{t}=\{(x,y)\in V\times V \mid \theta (x,y)\ge t\}\) (Binu et al. 2021).

Definition 2.2

\((G,*)\) is called a hypergroupoid if G is a nonempty set with a hyperoperation \(*,\) which is a mapping of \(*: G\times G\rightarrow P^{*}(G),\) where \(P^{*}(G)\) is the category of all nonempty subsets of G. Consider \(e*f\) as the hyperproduct of e and f for every \(e,f\in G.\) Besides, a hypergroupoid \((G,*)\) is introduced as a semihypergroup supposing that G is associative, i.e., \((e*f)*g=e*(f*g)\) for all \(e,f,g\in G.\) A hypergroup is a semihypergroup \((G,*)\) along with reproducibility axiom, symbolically \(g*G=G*g=G\) for all \(g\in G.\) The hypergroup is called commutative provided \(e *f = f *e\) for all \(e, f \in G.\) Meanwhile, a nonempty set L of a hypergroup G is called a subhypergroup of G,  if \(\forall z\in L\) we have \(z*L=L*z=L.\) By considering R and T as two nonempty subsets of G,  we have \(R *T =\bigcup \limits _{r\in R,\ t\in T } r*t.\) In addition, for \(g \in G, \ E\subseteq G,\) then \(g *E =\bigcup \nolimits _{e\in E} g*e.\) Describe the hyperproduct of components \(x_{1},\ldots ,x_{n}\) of G as \(\prod \nolimits _{i=1}^{n} x_{i}:=x_{1}*\prod \nolimits _{i=2}^{n} x_{i}\) (Corsini and Leoreanu 2013).

Definition 2.3

An n-ary hyperoperation \(\gamma\) on set G is a mapping of \(\gamma : G^{n}\longrightarrow P^{*}(G),\) where \(P^{*}(G)\) stands for the class of all nonempty subsets of G and \(G^{n}\) denotes the set of n tuples over G. A binary structure \({\textbf {G}} =\left\langle G, (\gamma _{i}: i \in I)\right\rangle\) is a hyperalgebra, where \((\gamma _{i}: i \in I)\) is a category of hyperoperations on G (Ameri and Nozari 2011).

Definition 2.4

The operation \(\delta _{i}\) is a fuzzy \(m_{i}\) -ary hyperoperation of G if a nonzero fuzzy subset \(\delta _{i} (b_{1},\ldots , b_{m_{i}})\) is corresponded to every m-tuple \((b_{1},\ldots , b_{m_{i}})\) of components of G,  i.e., a map of \(\delta _{i}: G \times \ldots \times G \longrightarrow F ^{*}(G)\) with \((b_{1},\ldots , b_{m_{i}})\longrightarrow \delta _{i} (b_{1},\ldots , b_{m_{i}}).\) The couple \(\left\langle G, \delta _{i}\right\rangle\) is considered as a fuzzy \(m_{i}\) -ary hypergroupoid (Ameri and Nozari 2011). Moreover, a fuzzy nullary hyperoperation on G is a nonzero fuzzy subset of G.

Let \(G\ne \emptyset\) and \(\forall i \in I,\) and \(\delta _{i}\) be a fuzzy \(m_{i}\)-ary hyperoperation on G. Then, \({\textbf {G}} =\left\langle G, (\delta _{i}: i \in I)\right\rangle\) is a fuzzy hyperalgebra, with \((m_{i}: i \in I)\) as a type of fuzzy hyperalgebra. Assume \(\lambda _{1}, \ldots , \lambda _{m_{i}}\) are nonzero fuzzy subsets of G,  and suppose \({\textbf {G}} =\left\langle G, (\delta _{i}: i \in I)\right\rangle\) is a fuzzy hyperalgebra, and for \(g \in G,\) the fuzzy subset \(\delta _{i}(\lambda _{1}, \ldots , \lambda _{m_{i}})\) is determined by

$$\begin{aligned} \delta _{i}(\lambda _{1}, \ldots , \lambda _{m_{i}})(g) = \bigvee \limits _{(x_{1},\ldots ,x_{m_{i}}) \in G^{m_{i}}} \left( \lambda _{1}(x_{1})\wedge \ldots \wedge \lambda _{m_{i}}(x_{m_{i}})\wedge \delta _{i}(x_{1},\ldots , x_{m_{i}})(g)\right) \end{aligned}$$

3 Basic characteristics of n-ary fuzzy relation

Definition 3.1

Let U be a set and \(A\subseteq U,\) and let R be an n -ary relation on U,  that is \(R\subseteq \overbrace{U\times U\times \ldots \times U}^{n}\) (Cristea and Ştefǎnescu 2010). R is an n-ary relation on A if \((u_{1},u_{2}, \ldots , u_{n})\in R,\) then \(u_{1}\in A, \ldots , u_{n}\in A.\) Also, R is n-ary equivalence relation if the following statements are held:

  1. (i)

    R has reflexive property if \((u,u,\ldots , u)\in R,\)

  2. (ii)

    R has symmetric property if for every \(i, u_{i}\) is permuted with \(u_{j}\) for \(i\ne j,\) i.e., \((u_{1},u_{2}, \ldots , u_{i-1}, u_{i},u_{i+1}, \ldots , u_{n})\in R\Longleftrightarrow (u_{i},u_{2}, \ldots , u_{i-1}, u_{1},u_{i+1}, \ldots , u_{n})\in R\Longleftrightarrow \ldots \Longleftrightarrow (u_{1},u_{2}, \ldots , u_{i-1}, u_{n},u_{i+1}, \ldots , u_{i})\in R\)

  3. (iii)

    R has transitive property if \((u_{1},u_{2}, \ldots , u_{n-1},z)\in R,\ (z,u_{2}, \ldots , u_{n})\in R,\) then \((u_{1},u_{2}, \ldots , u_{n})\in R.\)

Let \(R_{1}\) and \(R_{2}\) be two n-ary relations on U. Thus, the composition \(R_{1}\circ R_{2}\) is defined as follows:

$$\begin{aligned} (u_{1},u_{2}, \ldots , u_{n-1},y)\in R_{1}, (y,u_{2}, \ldots , u_{n})\in R_{2}\Longrightarrow (u_{1},u_{2}, \ldots , u_{n})\in R_{1}\circ R_{2} \end{aligned}$$

Definition 3.2

Let U be a set. An n-ary fuzzy relation on U is a fuzzy subset of \(\overbrace{U\times U\times \ldots \times U}^{n},\) i.e., a map \(\rho :\overbrace{U\times U\times \ldots \times U}^{n}\longrightarrow [0,1]\) that appoints a degree of membership to each ordered n components of \((u_{1},u_{2}, \ldots , u_{n}),\) that is \(0\le \rho (u_{1},u_{2}, \ldots , u_{n})\le 1,\) for all \(u_{i}\in U\) (Firouzkouhi et al. 2024). Suppose \(\mu\) is a fuzzy subset on a set U,  i.e., \(\mu :U\longrightarrow [0,1].\) Thus, a mapping \(\rho :\overbrace{U\times U\times \ldots \times U}^{n}\longrightarrow [0,1]\) is considered as an n-ary fuzzy relation on \(\mu ,\) if for all \(u_{i}\in U, i\in [1,n],\) we have \(\rho (u_{1},u_{2}, \ldots , u_{n})\le \mu (u_{1})\wedge \mu (u_{2}) \wedge \ldots \wedge \mu (u_{n}).\)

Definition 3.3

Assume \(\rho\) is an n-ary fuzzy relation. Thus,

  1. (i)

    \(\rho\) is reflexive if for every \(u\in U,\ \rho (u,u, \ldots , u)=\mu (u),\)

  2. (ii)

    \(\rho\) is symmetric if for every \(i\in [1,n],\) any \(u_{i}\) is permuted with all elements, i.e., \(\rho (u_{1},u_{2}, \ldots , u_{i-1}, u_{i},u_{i+1}, \ldots , u_{n})=\rho (u_{i},u_{2}, \ldots , u_{i-1}, u_{1},u_{i+1}, \ldots , u_{n})=\ldots = \rho (u_{1},u_{2}, \ldots , u_{i-1}, u_{n},u_{i+1}, \ldots , u_{i})\)

  3. (iii)

    \(\rho\) is transitive if \(\rho ^{2}\subseteq \rho ,\) i.e., for all \(u_{1},u_{2},\ldots , u_{n},z\in U,\) we have

    $$\begin{aligned} \bigvee \limits _{z\in U} (\rho (u_{1},u_{2}, \ldots , u_{n-1},z)\wedge \rho (z,u_{2}, \ldots , u_{n}))\le \rho (u_{1},u_{2}, \ldots , u_{n}) \end{aligned}$$

For two given n-ary fuzzy relations \(\rho ,\sigma\) on U,  the composition \(\rho \circ \sigma\) is described as:

$$\begin{aligned} (\rho \circ \sigma )(u_{1},u_{2}, \ldots , u_{n})=\bigvee \limits _{y\in U} (\rho (u_{1},u_{2}, \ldots , u_{n-1},y)\wedge \sigma (y,u_{2}, \ldots , u_{n})) \end{aligned}$$

For all \(t\in [0,1],\) consider t-cut as the set \(\mu _{t}=\{x\in U\mid \mu (x)\ge t\}\) which is the subset of U and the set \(\rho _{t}\) is defined as:

$$\begin{aligned} \rho _{t}=\{(u_{1},u_{2}, \ldots , u_{n})\in U\times U\times \ldots \times U\mid \rho (u_{1},u_{2}, \ldots , u_{n})\ge t\} \end{aligned}$$

The support \(\rho\) is defined in the following way:

$$\begin{aligned} supp(\rho )=\{(u_{1},u_{2}, \ldots , u_{n})\in U\times U\times \ldots \times U\mid \rho (u_{1},u_{2}, \ldots , u_{n})\ne 0\} \end{aligned}$$

Proposition 3.4

The following conditions are held:

  1. (i)

    If \(\rho ,\sigma\) are two n-ary fuzzy relations on \(\mu ,\) then the composition \(\rho \circ \sigma\) is an n-ary fuzzy relation on \(\mu .\)

  2. (ii)

    Assume \(\rho ,\sigma ,\nu\) are n-ary fuzzy relations, hence the composition of n-ary fuzzy relations is associative, i.e., \(\nu \circ (\rho \circ \sigma )=(\nu \circ \rho )\circ \sigma .\)

  3. (iii)

    For \(t\in [0,1],\) we have \(\rho _{t}\subseteq \mu _{t}\times \ldots \times \mu _{t}.\)

  4. (iv)

    Suppose \(\rho ,\sigma\) are n-ary fuzzy relations, and for all \(t\in [0,1],\) then \((\rho \circ \sigma )_{t}=\rho _{t}\circ \sigma _{t}.\)

Proof

Proof of (i): Since \(\rho\) and \(\sigma\) are n-ary fuzzy relations on \(\mu ,\) so, for all \(u_{i},y\in U, i\in [1,n],\) we have

$$\begin{aligned} \rho (u_{1},u_{2}, \ldots , u_{n-1},y)\le \mu (u_{1})\wedge \mu (u_{2}) \wedge \ldots \wedge \mu (u_{n-1})\wedge \mu (y), \\ \sigma (y,u_{2}, \ldots , u_{n})\le \mu (y)\wedge \mu (u_{2}) \wedge \ldots \wedge \mu (u_{n}) \end{aligned}$$

therefore,

\(\rho (u_{1},u_{2}, \ldots , u_{n-1},y)\wedge \sigma (y,u_{2}, \ldots , u_{n})\le \mu (u_{1})\wedge \mu (u_{2}) \wedge \ldots \wedge \mu (u_{n})\wedge \mu (y)\le \mu (u_{1})\wedge \mu (u_{2}) \wedge \ldots \wedge \mu (u_{n}),\)

for every \(y\in U,\) we have

\((\rho \circ \sigma )(u_{1},u_{2}, \ldots , u_{n})=\bigvee \limits _{y\in U} (\rho (u_{1},u_{2}, \ldots , u_{n-1},y)\wedge \sigma (y,u_{2}, \ldots , u_{n}))\le \mu (u_{1})\wedge \mu (u_{2}) \wedge \ldots \wedge \mu (u_{n}).\)

Then, the composition is an n-ary fuzzy relation on \(\mu .\)

Proof of (ii):

$$\begin{aligned} (&\nu \circ (\rho \circ \sigma ))(u_{1},u_{2}, \ldots , u_{n})=\bigvee \limits _{y\in U} (\nu (u_{1},u_{2}, \ldots , u_{n-1},y)\wedge (\rho \circ \sigma )(y,u_{2}, \ldots , u_{n}))\\&= \bigvee \limits _{y\in U} (\nu (u_{1},u_{2}, \ldots , u_{n-1},y)\wedge (\bigvee \limits _{z\in U}\rho (y,u_{2},\ldots , u_{n-1},z)\wedge \sigma (z,u_{2}, \ldots , u_{n})))\\&= \bigvee \limits _{z\in U} (\bigvee \limits _{y\in U}\nu (u_{1},u_{2}, \ldots , u_{n-1},y)\wedge \rho (y,u_{2},\ldots , u_{n-1},z))\wedge \sigma (z,u_{2}, \ldots , u_{n})\\&= \bigvee \limits _{z\in U} (\nu \circ \rho )(u_{1},u_{2}, \ldots , u_{n-1},z)\wedge \sigma (z,u_{2}, \ldots , u_{n})\\&=((\nu \circ \rho )\circ \sigma )(u_{1},u_{2}, \ldots , u_{n}). \end{aligned}$$

Proof of (iii): For \((u_{1},u_{2}, \ldots , u_{n})\in \rho _{t},\) we have \(\rho (u_{1},u_{2}, \ldots , u_{n})\ge t.\) As \(\rho\) is an n-ary fuzzy relation on \(\mu ,\) so \(\rho (u_{1},u_{2}, \ldots , u_{n})\le \mu (u_{1})\wedge \mu (u_{2}) \wedge \ldots \wedge \mu (u_{n}).\) Therefore, \(\mu (u_{1})\wedge \mu (u_{2}) \wedge \ldots \wedge \mu (u_{n})\ge t,\) which yields that for every i,  we have \(\mu (u_{i})\ge t.\) Then, \(u_{1}\in \mu _{t},\ldots , u_{n}\in \mu _{t}.\) Thus, \((u_{1},u_{2}, \ldots , u_{n})\in \mu _{t}\times \ldots \times \mu _{t}.\)

Proof of (iv):

$$\begin{aligned}&(u_{1},u_{2}, \ldots , u_{n})\in (\rho \circ \sigma )_{t}\Longleftrightarrow (\rho \circ \sigma )(u_{1},u_{2}, \ldots , u_{n})\ge t\\&\Longleftrightarrow \bigvee \limits _{y\in U} (\rho (u_{1},u_{2}, \ldots , u_{n-1},y)\wedge \sigma (y,u_{2}, \ldots , u_{n}))\ge t\\&\Longleftrightarrow \rho (u_{1},u_{2}, \ldots , u_{n-1},y)\ge t, \ \sigma (y,u_{2}, \ldots , u_{n})\ge t,\ \mathrm {for\ some\ y}\\&\Longleftrightarrow (u_{1},u_{2}, \ldots , u_{n-1},y)\in \rho _{t},\ (y,u_{2}, \ldots , u_{n})\in \sigma _{t}\\&\Longleftrightarrow (u_{1},u_{2}, \ldots , u_{n})\in \rho _{t}\circ \sigma _{t}. \end{aligned}$$

  

Proposition 3.5

Assume \(\rho\) is a reflexive n-ary fuzzy relation on \(\mu .\) The following statements are satisfied:

  1. (i)

    For all \(u_{i}\in U, i\in [1,n],\) we have \(\rho (u_{1},u_{2}, \ldots , u_{n})\le \rho (u_{i},u_{i},\ldots , u_{i}).\)

  2. (ii)

    For \(t\in [0,1],\) \(\rho _{t}\) is reflexive n-ary relation on \(\mu _{t}.\)

  3. (iii)

    The powers of \(\rho ^{i}\) are reflexive n-ary fuzzy relations, i.e., \(\rho \circ \rho =\rho ^{2},\ldots , \rho ^{n-1}\circ \rho =\rho ^{n}.\)

  4. (iv)

    Assume \(\sigma\) is reflexive, then \(\rho \circ \sigma\) is reflexive n-ary fuzzy relation.

  5. (v)

    For every \(\sigma ,\) as an n-ary fuzzy relation, we have \(\rho \circ \sigma \ge \sigma .\)

  6. (vi)

    For every \(n\in N,\) we have \(\rho \le \rho ^{2}\le \ldots \le \rho ^{n}.\)

Proof

Proof of (i): Since \(\rho\) is a reflexive n-ary fuzzy relation, thus \(\rho (u,u, \ldots ,u)=\mu (u).\) Then, \(\rho (u_{1},u_{2}, \ldots , u_{n})\le \mu (u_{1})\wedge \mu (u_{2})\wedge \ldots \wedge \mu (u_{n})\le \mu (u_{i})= \rho (u_{i},u_{i},\ldots , u_{i}).\)

Proof of (ii): For \(u\in \mu _{t},\) we have \(\mu (u)\ge t.\) Since \(\rho\) is reflexive, so \(\rho (u,u, \ldots ,u)=\mu (u)\ge t.\) Then, we have \((u,u, \ldots ,u)\in \rho _{t},\) so \(\rho _{t}\) is a reflexive n-ary relation on \(\mu _{t}.\)

Proof of (iii): For all \(u\in U,\)

\(\rho \circ \rho (u,u, \ldots ,u)=\bigvee \limits _{y\in U} \rho (u,u, \ldots ,y)\wedge \rho (y,u, \ldots ,u)\ge \rho (u,u, \ldots ,u)\wedge \rho (u,u, \ldots ,u)=\mu (u)\wedge \mu (u)=\mu (u).\) So, \(\rho \circ \rho (u,u, \ldots ,u)=\mu (u),\) this yields that \(\rho \circ \rho\) is reflexive and so on.

Proof of (iv): Since \(\rho ,\sigma\) are reflexive, \(\forall u\in U,\) we have

\(\rho \circ \sigma (u,u, \ldots ,u)=\bigvee \limits _{y\in U} \rho (u,u, \ldots ,y)\wedge \sigma (y,u, \ldots ,u)\ge \rho (u,u, \ldots ,u)\wedge \sigma (u,u, \ldots ,u)=\mu (u)\wedge \mu (u)=\mu (u).\) Then, \(\rho \circ \sigma (u,u, \ldots ,u)=\mu (u),\) so \(\rho \circ \sigma\) is reflexive.

Proof of (v): For all \(u\in U,\)

\(\rho \circ \sigma (u,u, \ldots ,u)=\bigvee \limits _{y\in U} \rho (u,u, \ldots ,y)\wedge \sigma (y,u, \ldots ,u)\ge \rho (u,u, \ldots ,u)\wedge \sigma (u,u, \ldots ,u)=\mu (u)\wedge \sigma (u,u, \ldots ,u).\) Since \(\sigma\) is fuzzy n-ary relation, thus \(\sigma (u,u, \ldots ,u)\le \mu (u)\) and we have \(\mu (u)\wedge \sigma (u,u, \ldots ,u)=\sigma (u,u, \ldots ,u).\) Then, \(\rho \circ \sigma (u,u, \ldots ,u)\ge \sigma (u,u, \ldots ,u).\) Therefore, \(\rho \circ \sigma \ge \sigma .\)

Proof of (vi): From the equation of proof (v) in Proposition 3.5, it is straightforward.   

Proposition 3.6

If \(\rho\) is a symmetric n-ary fuzzy relation. The following statements are held:

  1. (i)

    The powers of \(\rho\) are symmetric n-ary fuzzy relation.

  2. (ii)

    Let \(\sigma\) be symmetric n-ary fuzzy relation. Then, \(\sigma \circ \rho\) is symmetric if and only if \(\rho \circ \sigma =\sigma \circ \rho .\)

Proof

Proof of (i): It is obvious.

Proof of (ii): \((\Longrightarrow )\) Assume \(\rho , \sigma\) are symmetric n-ary fuzzy relation. Thus,

$$\begin{aligned}&(\rho \circ \sigma )(u_{1},u_{2}, \ldots , u_{n})=\bigvee \limits _{y\in U} (\rho (u_{1},u_{2}, \ldots , u_{n-1},y)\wedge \sigma (y,u_{2}, \ldots , u_{n}))\\&=\bigvee \limits _{y\in U} ( \sigma (u_{n},u_{2}, \ldots , u_{n-1} ,y)\wedge \rho (y,u_{2}, \ldots , u_{n-1},u_{1})), \ \mathrm {since\ \sigma , \rho \ are\ symmetric}\\&=(\sigma \circ \rho )(u_{n},u_{2}, \ldots , u_{n-1},u_{1})\\&=(\sigma \circ \rho )(u_{1},u_{2}, \ldots , u_{n-1},u_{n}),\ \mathrm { since\ \sigma \circ \rho \ is\ symmetric}. \end{aligned}$$

Therefore, \(\rho \circ \sigma =\sigma \circ \rho .\) The proof of converse is straightforward.   

Proposition 3.7

The following statements are held:

  1. (i)

    If \(\rho\) is symmetric and transitive n-ary fuzzy relation, hence for all \(u,y\in U,\) we have \(\rho (u,u,\ldots ,u, y)\le \rho (u,u,\ldots , u).\)

  2. (ii)

    Let \(\rho\) be transitive n-ary fuzzy relation on \(\mu .\) Then, \(\rho _{t}\) is transitive n-ary relation on \(\mu _{t}\) for \(t\in [0,1].\)

  3. (iii)

    If \(\rho\) is transitive n-ary fuzzy relation, and \(\sigma ,\nu \le \rho ,\) hence \(\nu \circ \sigma \le \rho .\)

  4. (iv)

    Assume \(\rho\) is transitive and \(\sigma\) is reflexive, and \(\sigma \le \rho .\) Thus, \(\sigma \circ \rho =\rho \circ \sigma =\rho .\)

  5. (v)

    Suppose \(\rho\) is reflexive and transitive n-ary fuzzy relation, hence \(\rho =\rho ^{2}=\ldots =\rho ^{n}.\)

  6. (vi)

    Let \(\rho ,\sigma\) be transitive n-ary fuzzy relations, and \(\rho \circ \sigma =\sigma \circ \rho .\) Then, \(\rho \circ \sigma\) is transitive.

Proof

Proof of (i):

$$\begin{aligned} (\rho \circ \rho )(u,u, \ldots , u)&=\bigvee \limits _{y\in U} \rho (u,u, \ldots , u,y)\wedge \rho (y,u,\ldots , u)\\&=\bigvee \limits _{y\in U} \rho (u,u, \ldots , u,y), \ \mathrm {since \ \rho \ is\ symmetric}\\&\ge \rho (u,u, \ldots , u,y) \end{aligned}$$

Since \(\rho\) is transitive, thus \((\rho \circ \rho )(u,u, \ldots , u)\le \rho (u,u, \ldots , u).\) Therefore, \(\rho (u,u,\ldots ,u, y)\le \rho (u,u,\ldots , u).\)

Proof of (ii): It is straightforward.

Proof of (iii):

$$\begin{aligned}&(\nu \circ \sigma )(u_{1},u_{2}, \ldots , u_{n})=\bigvee \limits _{y\in U} \nu (u_{1},u_{2}, \ldots , u_{n-1},y)\wedge \sigma (y,u_{2}, \ldots , u_{n})\\&\le \bigvee \limits _{y\in U} \rho (u_{1},u_{2}, \ldots , u_{n-1},y)\wedge \rho (y,u_{2}, \ldots , u_{n}), \ \mathrm {since\ \sigma ,\nu \le \rho }\\&\le \rho (u_{1},u_{2}, \ldots , u_{n}), \mathrm {\ since\ \rho \ is\ transitive}. \end{aligned}$$

Proof of (iv): By (iii) and Proposition 3.5 part (v), it is proved.

Proof of (v): Consider \(\sigma =\rho\) in part (iv), the proof is concluded.

Proof of (vi): Applying the associativity and commutativity of \(\rho ,\sigma ,\) and transitivity of \(\rho ,\sigma ,\) we have:

$$\begin{aligned} (\rho \circ \sigma )\circ (\rho \circ \sigma )=\rho \circ (\sigma \circ \rho )\circ \sigma = \rho \circ (\rho \circ \sigma )\circ \sigma = (\rho \circ \rho )\circ (\sigma \circ \sigma )\le (\rho \circ \sigma ). \end{aligned}$$

Definition 3.8

Assume \(\mu\) and \(\mu ^{\prime }\) are two fuzzy subsets on U,  thus the Cartesian product \((\mu \times \mu ^{\prime })(x,y)=\mu (x)\wedge \mu ^{\prime }(y)\) is fuzzy relation on U,  for every \(x,y\in U\) (Mohammadzadeh and Borzooei 2018).

Proposition 3.9

Suppose \(\rho\) is n-ary fuzzy relation on \(\mu ,\) and \(\rho ^{\prime }\) is n-ary fuzzy relation on \(\mu ^{\prime }.\) Then, the Cartesian product \(\rho \times \rho ^{\prime }\) is determined by

$$\begin{aligned} (\rho \times \rho ^{\prime })((u_{1},u_{2}, \ldots , u_{n}),(u^{\prime }_{1},u^{\prime }_{2}, \ldots , u^{\prime }_{n}))=\rho (u_{1},u_{2}, \ldots , u_{n})\wedge \rho ^{\prime }(u^{\prime }_{1},u^{\prime }_{2}, \ldots , u^{\prime }_{n}) \end{aligned}$$

which is n-ary fuzzy relation on \(\mu \times \mu ^{\prime }.\)

Proof

Let \(\rho\) and \(\rho ^{\prime }\) be n-ary fuzzy relations over universe sets of U and \(U^{\prime },\) respectively. Since \(\rho\) and \(\rho ^{\prime }\) are n-ary fuzzy relations on \(\mu\) and \(\mu ^{\prime },\) respectively, we have

$$\begin{aligned}&\rho (u_{1},u_{2}, \ldots , u_{n})\le \mu (u_{1})\wedge \mu (u_{2}) \wedge \ldots \wedge \mu (u_{n})\\&\rho ^{\prime }(u_{1}^{\prime },u_{2}^{\prime }, \ldots , u_{n}^{\prime })\le \mu ^{\prime }(u_{1}^{\prime })\wedge \mu ^{\prime }(u_{2}^{\prime }) \wedge \ldots \wedge \mu ^{\prime }(u_{n}^{\prime }) \end{aligned}$$

for all \(u_{i}\in U,\ u_{i}^{\prime }\in U^{\prime }\) and \(1\le i\le n.\) Then, by the definition of Cartesian product \(\rho \times \rho ^{\prime }\) and Definition 3.8, we follow

$$\begin{aligned}&(\rho \times \rho ^{\prime })((u_{1},u_{2}, \ldots , u_{n}),(u^{\prime }_{1},u^{\prime }_{2}, \ldots , u^{\prime }_{n}))\\&\quad =\rho (u_{1},u_{2}, \ldots , u_{n})\wedge \rho ^{\prime }(u^{\prime }_{1},u^{\prime }_{2}, \ldots , u^{\prime }_{n})\\&\quad \le \mu (u_{1})\wedge \mu (u_{2}) \wedge \ldots \wedge \mu (u_{n})\wedge \mu ^{\prime }(u_{1}^{\prime })\wedge \mu ^{\prime }(u_{2}^{\prime }) \wedge \ldots \wedge \mu ^{\prime }(u_{n}^{\prime })\\&\quad = [\mu (u_{1})\wedge \mu ^{\prime }(u_{1}^{\prime })] \wedge [\mu (u_{2})\wedge \mu ^{\prime }(u_{2}^{\prime })]\wedge \ldots \wedge [\mu (u_{n})\wedge \mu ^{\prime }(u_{n}^{\prime })]\\&\quad = (\mu \times \mu ^{\prime })(u_{1},u_{1}^{\prime }) \wedge (\mu \times \mu ^{\prime })(u_{2},u_{2}^{\prime })\wedge \ldots \wedge (\mu \times \mu ^{\prime })(u_{n},u_{n}^{\prime }) \end{aligned}$$

This yields that \(\rho \times \rho ^{\prime }\) is n-ary fuzzy relation on \(\mu \times \mu ^{\prime }.\)

Proposition 3.10

Let \(\rho\) and \(\rho ^{\prime }\) be n-ary fuzzy relations on \(\mu\) and \(\mu ^{\prime },\) respectively. Hence,

$$\begin{aligned} (\rho \times \rho ^{\prime })_{t}=\rho _{t}\times \rho ^{\prime }_{t} \end{aligned}$$

Proof

$$\begin{aligned}&((u_{1},u_{2}, \ldots , u_{n}),(u^{\prime }_{1},u^{\prime }_{2}, \ldots , u^{\prime }_{n}))\in (\rho \times \rho ^{\prime })_{t}\Longleftrightarrow (\rho \times \rho ^{\prime })((u_{1},u_{2}, \ldots , u_{n}),(u^{\prime }_{1},u^{\prime }_{2}, \ldots , u^{\prime }_{n}))\ge t\\&\quad \Longleftrightarrow \rho (u_{1},u_{2}, \ldots , u_{n})\wedge \rho ^{\prime }(u^{\prime }_{1},u^{\prime }_{2}, \ldots , u^{\prime }_{n})\ge t\\&\quad \Longleftrightarrow \rho (u_{1},u_{2}, \ldots , u_{n})\ge t,\ \rho ^{\prime }(u^{\prime }_{1},u^{\prime }_{2}, \ldots , u^{\prime }_{n})\ge t\\&\quad \Longleftrightarrow (u_{1},u_{2}, \ldots , u_{n})\in \rho _{t},\ (u^{\prime }_{1},u^{\prime }_{2}, \ldots , u^{\prime }_{n})\in \rho ^{\prime }_{t}\\&\quad \Longleftrightarrow ((u_{1},u_{2}, \ldots , u_{n}),(u^{\prime }_{1},u^{\prime }_{2}, \ldots , u^{\prime }_{n}))\in \rho _{t}\times \rho ^{\prime }_{t}. \end{aligned}$$

 

4 Fuzzy hyperalgebra based on n-ary fuzzy relation

Definition 4.1

Let \(\rho\) be n-ary fuzzy relation on A. Denote for all \(u_{i},z\in A,\)

$$\begin{aligned} M_{u_{1},u_{2}, \ldots , u_{n-1}}^{\rho }: A\longrightarrow (0,1]\\ M_{u_{1},u_{2}, \ldots , u_{n-1}}^{\rho }(z)=\rho (u_{1},u_{2}, \ldots , u_{n-1},z) \end{aligned}$$

An n-ary fuzzy hyperoperation "\(\circ _{\rho }\)" is defined as:

$$\begin{aligned} u_{1}\circ _{\rho } u_{2}\circ _{\rho }\ldots \circ _{\rho }u_{n}=M_{u_{1},u_{2}, \ldots , u_{n-1}}^{\rho }\cup M_{u_{1},u_{2}, \ldots , u_{n-2},u_{n}}^{\rho }\cup \ldots \cup M_{u_{2},u_{3}, \ldots , u_{n}}^{\rho } \end{aligned}$$

where for every z,  we have

$$\begin{aligned} (u_{1}\circ _{\rho } u_{2}\circ _{\rho }&\ldots \circ _{\rho }u_{n})(z)=M_{u_{1},u_{2}, \ldots , u_{n-1}}^{\rho }(z)\vee M_{u_{1},u_{2}, \ldots , u_{n-2},u_{n}}^{\rho }(z)\vee \ldots \vee M_{u_{2},u_{3}, \ldots , u_{n}}^{\rho }(z)\\&=\rho (u_{1},u_{2}, \ldots , u_{n-1},z)\vee \rho (u_{1},u_{2}, \ldots ,u_{n-2}, u_{n},z)\vee \ldots \vee \rho (u_{2}, \ldots , u_{n},z) \end{aligned}$$

Particularly, for all \(u\in A,\) we have

$$\begin{aligned} u\circ _{\rho } u \circ _{\rho }\ldots \circ _{\rho }u=M_{u,u, \ldots , u}^{\rho } \end{aligned}$$

Consider \(\mu _{1},\mu _{2},\ldots , \mu _{n}\) as nonzero fuzzy subset of A. Thus, \(\mu _{1}\circ _{\rho }\mu _{2}\circ _{\rho }\ldots \circ _{\rho } \mu _{n}\) is determined as follows:

\((\mu _{1}\circ _{\rho }\mu _{2}\circ _{\rho }\ldots \circ _{\rho } \mu _{n})(z)=\bigvee \limits _{u_{i}\in supp (\mu _{i})} (\rho (u_{1},u_{2}, \ldots , u_{n-1},z)\vee \rho (u_{1},u_{2}, \ldots ,u_{n-2}, u_{n},z)\vee \ldots \vee \rho (u_{2}, \ldots , u_{n},z))\)

Example 4.2

Assume A is a nonvoid set. Let \(\mu\) be nonzero fuzzy subset of A,  (which is 1-ary fuzzy relation). For all \(u_{1},u_{2}, \ldots , u_{n}\in A,\) define \(u_{1}\circ _{\rho } u_{2}\circ _{\rho }\ldots \circ _{\rho }u_{n}=\mu .\) It can be seen that \(\left\langle A, \circ _{\rho } \right\rangle\) is fuzzy hyperalgebra.

Example 4.3

Suppose A is a nonvoid set, and \(\rho\) is an n-ary fuzzy relation on \(\mu ,\) and for all \(i\in [1,n],n\in N, t_{i}\in (0,1].\) Introduce n-ary fuzzy hyperoperation for all \(u_{i},z\in A,\) in the following way:

$$\begin{aligned} (u_{1}\circ _{\rho } u_{2}\circ _{\rho }\ldots \circ _{\rho }u_{n})(z)= \left\{ \begin{array}{cc} \bigvee \limits _{1\le i \le n} t_{i} &{} \ if \ \rho (u_{1},u_{2}, \ldots ,u_{i-1},z,u_{i+1},\ldots , u_{n})=t_{i}\\ 0 &{} otherwise \\ \end{array} \right. \end{aligned}$$

where, \(\rho (u_{1},u_{2}, \ldots ,u_{i-1},z,u_{i+1},\ldots , u_{n}) \le \mu (u_{1})\wedge \ldots \mu (u_{i-1}) \wedge \mu (z)\wedge \mu (u_{i+1})\wedge \mu (u_{n}).\) Thus, \(\left\langle A, \circ _{\rho } \right\rangle\) is fuzzy hyperalgebra.

Proposition 4.4

Let \(\rho\) be a reflexive n-ary fuzzy relation on \(\mu .\) Thus, \((u\circ _{\rho } u \circ _{\rho }\ldots \circ _{\rho }u)(u)=\mu (u),\) for all \(u\in A.\)

Proof

Since \(\rho\) is a reflexive n-ary fuzzy relation, thus \(\rho (u, u,\ldots ,u)=\mu .\) Therefore, \(\rho (u, u,\ldots ,u)=M_{u,u, \ldots , u}^{\rho }(u)=(u\circ _{\rho } u \circ _{\rho }\ldots \circ _{\rho }u)(u),\) hence \((u\circ _{\rho } u \circ _{\rho }\ldots \circ _{\rho }u)(u)=\mu (u).\) \(\square\)

Theorem 4.5

Assume \(\rho\) is reflexive, symmetric and transitive n-ary fuzzy relation on A. Thus, \(\textbf{A}=\left\langle A, \circ _{\rho } \right\rangle\) is fuzzy hyperalgebra.

Proof

Since \((u_{1}\circ _{\rho } u_{2}\circ _{\rho } \ldots \circ _{\rho }u_{n})(z) =\rho (u_{1},u_{2}, \ldots , u_{n-1},z)\vee \rho (u_{1},u_{2}, \ldots ,u_{n-2}, u_{n},z)\vee \ldots \vee \rho (u_{2}, \ldots , u_{n},z)\) and \(\rho (u_{1},u_{2}, \ldots , u_{n-1},z)\in (0,1]\) and so forth, then \((u_{1}\circ _{\rho } u_{2}\circ _{\rho } \ldots \circ _{\rho }u_{n})(z)\in F^{*}(A).\) It concludes that \(\textbf{A}=\left\langle A, \circ _{\rho } \right\rangle\) is fuzzy hyperalgebra. Note that the assumption of reflexive, symmetric and transitive property would strengthen the theorem for the subcategories of fuzzy hypergroup, fuzzy hyperring, fuzzy hypermodule, etc.

Theorem 4.6

The following statements are satisfied for all \(u_{1},u_{2},\ldots , u_{n}\in A:\)

  1. (i)

    Assume \(\left\langle A, \circ \right\rangle\) is hyperalgebra. Hence, \(\left\langle A, \circ _{\rho } \right\rangle\) is fuzzy hyperalgebra provided \(u_{1}\circ _{\rho } u_{2}\circ _{\rho }\ldots \circ _{\rho }u_{n}=\chi _{u_{1}\circ u_{2}\circ \ldots \circ u_{n}}.\)

  2. (ii)

    Suppose \(\left\langle A, \circ _{\rho } \right\rangle\) is fuzzy hyperalgebra. Thus, \(\left\langle A, \circ \right\rangle\) is hyperalgebra if \(u_{1}\circ u_{2}\circ \ldots \circ u_{n}=supp (u_{1}\circ _{\rho } u_{2}\circ _{\rho } \ldots \circ _{\rho } u_{n}).\)

Proof

Proof of (i): For every \(z,u_{i}\in A,\) we have

$$\begin{aligned} (u_{1}\circ _{\rho } u_{2}\circ _{\rho }\ldots \circ _{\rho }u_{n})(z)=\chi _{u_{1}\circ u_{2}\circ \ldots \circ u_{n}}(z)=\left\{ \begin{array}{cc} 1 &{} \ if \ z\in u_{1}\circ u_{2}\circ \ldots \circ u_{n}\\ 0 &{} otherwise \\ \end{array} \right. \end{aligned}$$

Since \(\left\langle A, \circ \right\rangle\) is hyperalgebra, so \(u_{1}\circ u_{2}\circ \ldots \circ u_{n}\in P^{*}(A).\) Thus, there exists z such that \(z\in u_{1}\circ u_{2}\circ \ldots \circ u_{n},\) this results \((u_{1}\circ _{\rho } u_{2}\circ _{\rho }\ldots \circ _{\rho }u_{n})(z)=1\in F^{*}(A).\) This concludes that \(\left\langle A, \circ _{\rho } \right\rangle\) is fuzzy hyperalgebra.

Proof of (ii): Let \(\left\langle A, \circ _{\rho } \right\rangle\) be fuzzy hyperalgebra. Then, \((u_{1}\circ _{\rho } u_{2}\circ _{\rho } \ldots \circ _{\rho } u_{n})(z)>0\) for every \(z,u_{i}\in A\) which indicates \(z\in supp(u_{1}\circ _{\rho } u_{2}\circ _{\rho } \ldots \circ _{\rho } u_{n}).\) Because \(supp (u_{1}\circ _{\rho } u_{2}\circ _{\rho } \ldots \circ _{\rho } u_{n})=u_{1}\circ u_{2}\circ \ldots \circ u_{n},\) therefore, \(z\in u_{1}\circ u_{2}\circ \ldots \circ u_{n}.\) This proves that \(\left\langle A, \circ \right\rangle\) is hyperalgebra. \(\square\)

Let A be a nonempty set, endowed with a fuzzy hyperoperation \(\circ _{\rho },\) consider the t-cuts, \((u_{1}\circ _{\rho }u_{2}\circ _{\rho } \ldots \circ _{\rho } u_{n})_{t}=\{ w\in A \mid (u_{1}\circ _{\rho }u_{2}\circ _{\rho } \ldots \circ _{\rho } u_{n})(w)\ge t\}\) where \(t\in [0,1].\)

Denote n-ary hyperoperation as follows:

$$\begin{aligned} u_{1}(\circ _{\rho })_{t}\ u_{2}(\circ _{\rho })_{t} \ldots (\circ _{\rho })_{t} \ u_{n}=(u_{1}\circ _{\rho }u_{2}\circ _{\rho } \ldots \circ _{\rho } u_{n})_{t} \end{aligned}$$
(1)

Theorem 4.7

\(\left\langle A, \circ _{\rho } \right\rangle\) is fuzzy hyperalgebra if and only if for all \(t\in (0,1], \left\langle A, (\circ _{\rho })_{t} \right\rangle\) is hyperalgebra.

Proof

By considering Definitions 2.3, 2.4 and Eq. 1, it is straightforward.

5 AI-base GOL theory derived from the generalized n-ary fuzzy relation

5.1 AI-base GOL theory methodology

This section inaugurates a primitive and significant introduction to a novel well-established framework of graph theory that is a generalized format of classical fuzzy graph. Using standard mathematical definitions and principles, GOL theory is constructed to configure a strategic pattern for AI-based learning mechanism in an uncertain environment. Our purpose is to deal with the imprecision and ambiguity behavior of certain correlated elements and linkages in complex dynamic networks, and to furnish platforms with extensive diversity of applications in real-life problems. As a matter of fact, business affairs, sport activities, social skills, scientific and engineering proficiency, and medical sectors can be included in GOL theory applications. In these platforms, when individuals are organized and coordinated as a group under common training activities, their performance (i.e., content learning rate during the teaching process) evaluations are important and beneficial for employers, teachers and managers to assist decision-making procedures and promote e-learning process. Through GOL theory, learners are evaluated based on quantitative values. In fact, the efficiency measures of correlated and conjoint individuals are analyzed in an uncertain space. According to the theorized n-ary fuzzy relation, it is observed that group-wise performance is reduced compared to single performances in an online learning environment.

Here, a new automated assessment system called AI-base “GOL theory” is established on the basis of generalized n-ary fuzzy relation (Fig. 2) for the next generation online educational mega-systems. In Fig. 2, we consider the set X as participants in an electronic exam together with the defined fuzzy set of \(\mu\) on X,  that indicates the learning rate of each individual. The generalized n-ary fuzzy relation is introduced on \(\mu\) for specifying the learning rate of correlated n individuals, and designating group-wise performances in an online learning environment. The t-cut method as the clustering technique and support property of unary and n-ary relations as the coverage of system are characterized. In addition, the corresponding graphical pattern is executed for the proposed GOL theory platform to optimize multiple connections among entities (individuals). For this purpose, the mathematical concepts of Definitions of 3.2 and 3.3 are employed as follow:

  • Fuzzy relation \(\rho\) on \(\mu ,\) that is \(\rho :\overbrace{U\times U\times \ldots \times U}^{n}\longrightarrow [0,1]\) such that \(\rho (u_{1},u_{2}, \ldots , u_{n})\le \mu (u_{1})\wedge \mu (u_{2}) \wedge \ldots \wedge \mu (u_{n})\) for all \(u_{i}\in U, i\in [1,n].\)

  • t-cut \(\rho\) is defined as follows:

    $$\begin{aligned} \rho _{t}=\{(u_{1},u_{2}, \ldots , u_{n})\in U\times U\times \ldots \times U\mid \rho (u_{1},u_{2}, \ldots , u_{n})\ge t\} \end{aligned}$$

  • Support \(\rho\) is introduced as follows:

    $$\begin{aligned} supp(\rho )=\{(u_{1},u_{2}, \ldots , u_{n})\in U\times U\times \ldots \times U\mid \rho (u_{1},u_{2}, \ldots , u_{n})\ne 0\} \end{aligned}$$
Fig. 2
figure 2

The diagram of AI-base GOL theory

Full size image

In reality, fuzzy set \(\mu\) can be defined as the degree membership of the content learning rate (performance measure of a person) through individual online AI system, and \(\rho\) as the degree membership of the content learning rate (performance measure of n-persons) remotely as a group. The evaluation of students is performed via online test in academic centers. For the sample size, as per the nature of the generalized parametric approach in the presented theory, an unlimited number of students who participate in an online educational AI system can be included. Table 1 exemplifies the varying measurement results of a course assigned by letters A to F.

Table 1 The grading scheme (measure) of final exam
Full size table

5.2 Dataset

The advanced AI-base GOL theory in Application 1 is tested on real dataset collected from (Zhang et al. 2023). As depicted in Table 2, different academic performances (scores) of medical students were used during COVID-19 pandemic in various levels namely, Freshman students, Sophomores, Juniors, Seniors and Fifth grade.

Table 2 Online learning average scores of medical students under the effects of pandemic
Full size table

In this scheme, the individuals are categorized based on the analogous level.

  • Individual \(u_{1}\) is considered with the grade of 65 as Freshman students in Class 1, which is equivalent to the fuzzy membership value of 0.65 in our model.

  • Individual \(u_{2}\) is selected from Class 2 of Freshman students with the grade of 76, that is the counterpart of membership degree 0.76 in our developed model.

  • Individual \(u_{3}\) is chosen from Freshman students from Class 3 with the academic score of 84, the equivalent grade of 0.84 as the fuzzy membership value.

  • Individual \(u_{4}\) is regarded as Freshman students from Class 4 with the score of 95, equal to the fuzzy membership degree of 0.95.

To analyze the uncertain-based performance of online learning students in single, double, ternary and so forth, we employ the mentioned fuzzy membership degrees (academic grades) in the subsequent step.

In the second case study, the available dataset from Bossman and Agyei (2022) is used that addresses the academic performance of e-learning students in Ghana. Table 3 shows different learners’ performances in which the following individuals are selected for our model.

  • Individual \(a_{1}\) is chosen from Class 2 based on the performance value of \(0.827\simeq 0.8\) as the fuzzy membership degree.

  • Individual \(a_{2}\) belongs to Class 3 with the performance value of \(0.938 \simeq 0.9\) that is the fuzzy membership degree.

  • Individual \(a_{3}\) is included in Class 6 with the performance value of \(0.802 \simeq 0.8\) as the fuzzy dependence value.

Table 3 Performance metrics of distance learning (e-learning) students during COVID-19 pandemic in Ghana
Full size table

The ultimate application is executed on a large dataset, namely E-learning dataset of Jordan university of science and technology (E-LearningDJUST) that studied a sample of 9,246 students from 11 faculties during spring/summer 2020 and fall 2021 semester in COVID-19 pandemic (Abdullah et al. 2021).

These selected samples are used for the assessment of learners’ grades in multidimensional environment with uncertainty during the e-learning process. In the next section, we implement a theoretical basis for students who participated in online learning to investigate their learning rates in a multi-individual space.

5.3 Application 1

Suppose that U is a finite quantity of individuals participating in an electronic exam under artificial intelligent system in a university. Assume \(U=\{ u_{1},u_{2}, u_{3}, u_{4}\},\) and \(\mu\) is fuzzy subset of U that represents the performance measure of individuals in an online educational system, as depicted in Table 4. The dependence value of individual \(u_{4}\) with the level A is higher than others (learning the topic more than others), since \(\mu (u_{4})=0.95.\)

Table 4 Fuzzy set \(\mu\)
Full size table

The n-ary relation \(\rho :\overbrace{U\times U\times \ldots \times U}^{n}\longrightarrow [0,1]\) in Table 5 is considered as the membership values of n-elements which represents the performance measures of a group via remote distance learning.

Table 5 Fuzzy relation \(\rho\) for \(n=1,2,3,4\)
Full size table
Fig. 3
figure 3

Corresponding graphs for generalized fuzzy relations of \(n=1,2,3,4\)

Full size image

It is seen that \(\rho\) is a fuzzy relation on \(\mu\) for \(n=2,3,4,\) since \(\rho (u_{1},u_{2}, \ldots , u_{n})\le \mu (u_{1})\wedge \mu (u_{2}) \wedge \ldots \wedge \mu (u_{n})\) for all \(u_{i}\in U, i\in [1,4].\) For \(n=2,\) the fuzzy relation \(\rho (u_{i},u_{j})\) represents the learning rate in double space \(u_{i}\) and \(u_{j}\) for \(i,j=\{1,2,3,4\}.\) Thus, the comprehension degree of \(u_{3}\) and \(u_{4}\) is stronger, because \(\rho (u_{3},u_{4})=0.82.\) The corresponding graph is shown in Fig. 3 which is a regular graph. This graph demonstrates that the relation \(\rho\) is reflexive and symmetric. From the declared discussion, we remark some points as follow:

  • t-cut for \(\mu ,\rho\) is attained, which represents a partition that the elements \(u_{2},u_{3},u_{4}\) can be grouped into \(\mu _{0.75}\) at the level \(t=0.75,\) and \(\rho _{0.75}=\{(u_{3},u_{4}),(u_{2},u_{3},u_{4}),(u_{2},u_{2}),(u_{3},u_{3}), (u_{4},u_{4})\}\) which represents a hypergraph with a set of vertices \(\{u_{2},u_{3},u_{4}\}\) and hyperedges \(\{E_{1}=\{u_{3},u_{4}\}, E_{2}=\{u_{2}\},E_{3}=\{u_{3}\},E_{4}=\{u_{4}\},E_{5}=\{u_{2},u_{3},u_{4}\}\} \}.\)

  • \(supp(\mu )=V,\) and \(supp(\rho )=\overbrace{V\times V\times \ldots \times V}^{n}\) for \(n=1,2,3,4,\) that is a coverage of the system.

In relation to the performed fuzzy hyperalgebraic system, the performances of the group-wise individuals are corresponded to the fuzzy values of fuzzy n-ary hyperoperations on U. Indeed, for binary, ternary, and quaternary relations of correlated elements, we present this for some parameters and the rest is similar. In double space \(n=2\) and \(u_{1},u_{2}\in U\) and every z,  we have

$$\begin{aligned} (u_{1}\circ _{\rho }u_{2})(z)=\rho (u_{1},z)\vee \rho (u_{2},z) \end{aligned}$$

Then,

$$\begin{aligned}&For\ z=u_{1}: (u_{1}\circ _{\rho }u_{2})(u_{1})=\rho (u_{1},u_{1})\vee \rho (u_{2},u_{1})=0.65\vee 0.6=0.65\\&For\ z=u_{2}: (u_{1}\circ _{\rho }u_{2})(u_{2})=\rho (u_{1},u_{2})\vee \rho (u_{2},u_{2})=0.6\vee 0.76=0.76\\&For\ z=u_{3}: (u_{1}\circ _{\rho }u_{2})(u_{3})=\rho (u_{1},u_{3})\vee \rho (u_{2},u_{3})=0.5\vee 0.72=0.72\\&For\ z=u_{4}: (u_{1}\circ _{\rho }u_{2})(u_{4})=\rho (u_{1},u_{4})\vee \rho (u_{2},u_{4})=0.65\vee 0.7=0.7\\ \end{aligned}$$

Thus for \(z=u_{2},\) the highest membership degree of 0.76 is attained, while the lowest membership value of 0.65 is found for \(z=u_{1}.\)

For triplet space \(n=3\) and \(u_{1},u_{2},u_{3}\in U\) and every z,  we follow:

$$\begin{aligned}{} & {} (u_{1}\circ _{\rho }u_{2}\circ _{\rho }u_{3})(z)=\rho (u_{1},u_{2},z)\vee \rho (u_{1},z,u_{3})\vee \rho (z,u_{2},u_{3}) \\{} & {} For\ z=u_{1}: (u_{1}\circ _{\rho }u_{2}\circ _{\rho }u_{3})(u_{1})\\{} & {} \quad =\rho (u_{1},u_{2},u_{1})\vee \rho (u_{1},u_{1},u_{3})\vee \rho (u_{1},u_{2},u_{3})=0.6\vee 0.5\vee 0.62=0.62\\{} & {} For\ z=u_{2}: (u_{1}\circ _{\rho }u_{2}\circ _{\rho }u_{3})(u_{2})\\{} & {} \quad =\rho (u_{1},u_{2},u_{2})\vee \rho (u_{1},u_{2},u_{3})\vee \rho (u_{2},u_{2},u_{3})=0.6\vee 0.62\vee 0.72=0.72\\{} & {} For\ z=u_{3}: (u_{1}\circ _{\rho }u_{2}\circ _{\rho }u_{3})(u_{3})\\{} & {} \quad =\rho (u_{1},u_{2},u_{3})\vee \rho (u_{1},u_{3},u_{3})\vee \rho (u_{3},u_{2},u_{3})=0.62\vee 0.5\vee 0.72=0.72\\{} & {} For\ z=u_{4}: (u_{1}\circ _{\rho }u_{2}\circ _{\rho }u_{3})(u_{4})\\{} & {} \quad =\rho (u_{1},u_{2},u_{4})\vee \rho (u_{1},u_{4},u_{3})\vee \rho (u_{4},u_{2},u_{3})=0.6\vee 0.64\vee 0.75=0.75\\ \end{aligned}$$

It is observed that the highest membership degree (0.75) is obtained for \(z=u_{4},\) whereas the lowest membership value (0.62) belongs to \(z=u_{1}\) in the triplet space.

In quaternary setting \(n=4\) and for \(u_{1},u_{2},u_{3},u_{4}\in U\) and every z,  the following results are obtained:

$$\begin{aligned}{} & {} (u_{1}\circ _{\rho }u_{2}\circ _{\rho }u_{3}\circ _{\rho }u_{4})(z)\\{} & {} \quad =\rho (u_{1},u_{2},u_{3},z)\vee \rho (u_{1},u_{2},z,u_{4})\vee \rho (u_{1},z,u_{3},u_{4})\vee \rho (z,u_{2},u_{3},u_{4}) \\{} & {} For\ z=u_{1}: (u_{1}\circ _{\rho }u_{2}\circ _{\rho }u_{3}\circ _{\rho }u_{4})(u_{1})=0.64\\{} & {} For\ z=u_{2}: (u_{1}\circ _{\rho }u_{2}\circ _{\rho }u_{3}\circ _{\rho }u_{4})(u_{2})=0.75\\{} & {} For\ z=u_{3}: (u_{1}\circ _{\rho }u_{2}\circ _{\rho }u_{3}\circ _{\rho }u_{4})(u_{3})=0.75\\{} & {} For\ z=u_{4}: (u_{1}\circ _{\rho }u_{2}\circ _{\rho }u_{3}\circ _{\rho }u_{4})(u_{4})=0.75\\ \end{aligned}$$

According to the obtained results, the highest membership degree of 0.75 is corresponded to \(u_{2},u_{3},u_{4}\) and the lowest (0.64) is affiliated to \(u_{1},\) in quadric setting.

Remark 5.1

According to Proposition 3.4, for the value \(t=0.75,\) since

\(\rho _{0.75}=\{(u_{3},u_{4}),(u_{2},u_{3},u_{4}),(u_{2},u_{2}),(u_{3},u_{3}), (u_{4},u_{4})\}\) and \(\mu _{0.75}=\{u_{2},u_{3},u_{4}\},\) the inclusion is satisfied for \(n=2,3\) in the following way:

$$\begin{aligned} \rho _{0.75}\subseteq \overbrace{\mu _{0.75}\times \ldots \times \mu _{0.75}}^{n} \end{aligned}$$

Remark 5.2

Considering Definition 3.1 and Proposition 3.5, it is concluded that \(\rho _{0.75}\) is reflexive n-ary relation on \(\mu _{0.75}.\)

Remark 5.3

From Propositions 3.5 and 3.6, it is concluded that the powers of \(\rho\) (i.e., \(\rho ^{i}\)) are reflexive and symmetric n-ary fuzzy relation.

5.4 Application 2

In another numeric example, assume U is the set of students and \(U=\{a_{1},a_{2},a_{3}\}.\) In Table 6, the individual \(a_{2}\) with the level A has the membership value of 0.9, which is higher than others and thus is ranked in the first row of learners.

Table 6 Fuzzy set \(\mu\)
Full size table
Table 7 Fuzzy relation \(\rho\) for \(n = 1,2,3\)
Full size table

It is verified that \(\rho\) is a (symmetric and reflexive) fuzzy relation on \(\mu\) (Table 7). When \(\rho (a_{1},a_{2},a_{3})=0.7,\) it means that the learning rate by these three persons in online training system, has the membership value of 0.7. Also, the lowest learning rate is between \(a_{2}\) and \(a_{3},\) with the degree membership of \(\rho (a_{2},a_{3})=0.65\) (Fig. 4).

Fig. 4
figure 4

Corresponding graph for generalized fuzzy relations of \(n=1,2,3\)

Full size image

5.5 Application 3

In this scheme, we choose 44 students from the eleven faculties based on the standard compulsory courses in semester spring 2020, where different classes of grades (performance scores) are designated (Table 8). Table 9 displays details of faculties, offered courses, and corresponding membership values of \(\mu\) and \(\rho\) in spring 2020. \(\mu\) stands for student’s performance in single online learning space and \(\rho\) refers to the students’ performance in correlated group-wise online learning space. Note that each individual of each faculty may participate in online classes along with individuals from other schools.

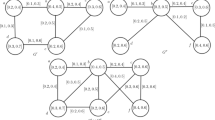
Figure 5 represents the graphical pattern of extracted generalized fuzzy relation in terms of unary, binary, ternary, quaternary, and quinary linkages (edges) where colored links of red, green, black, and blue are respectively associated to General Chemistry, Biochemistry, Computer skills, and General Physics. The results indicate 44 unary relations, 5 binary relations, 10 ternary relations, 7 quaternary relations, and 2 quinary relations in eleven faculties. The interval boundaries of [0.3, 1], [0.3, 0.8], [0.3, 0.8], [0.2, 0.5] and [0.5, 0.5] are respectively obtained for unary, binary, ternary, quaternary, and quinary links.

Table 8 Courses with their corresponding overall grades and percentage of students’ level for different group scale of grades
Full size table
Table 9 Faculties and registered elective courses along with associated membership values in spring 2020 semester
Full size table
Fig. 5
figure 5

Corresponding graph of generalized fuzzy relations for eleven faculties and elective courses (colored)

Full size image

5.6 Performance score assessment

To analyze and identify the learners’ academic performances within e-learning systems using GOL theory methodology, the performance score (PS) and overall performance score (OPS) are formulated as follow:

$$\begin{aligned}{} & {} PS(u_{i})=\dfrac{\mu (u_{i})+\sum \limits _{j} \rho _{j}(u_{1},\ldots , u_{i}, \ldots , u_{n})}{1+\mid \rho _{j}\mid } \end{aligned}$$
(2)
$$\begin{aligned}{} & {} OPS=\dfrac{\sum \nolimits _{i=1}^{n} PS(u_{i})}{\mid U\mid } \end{aligned}$$
(3)

\(PS(u_{i})\) is referred to the performance score of individual \(u_{i},\) and the membership degrees of \(\mu\) and \(\rho\) are allocated to the learning rate (final score) of individuals in unary and n-tuple spaces, respectively. \(\mid \rho _{j}\mid\) stands for the cardinality of n-ary fuzzy relation, and \(\mid U\mid\) is the cardinality of universe set of U. Note that \(\rho _{j}(u_{1},\ldots , u_{i}, \ldots , u_{n})\) is the membership value of generalized fuzzy relation including element \(u_{i}.\) Indeed, \(PS(u_{i})\) is the aggregation of all values in the row column of element \(u_{i}\) corresponded to the incidence matrix of fuzzy relation \(\rho .\)

In application 1, PS and OPS are calculated for every \(u_{i}\in U, i\in [1,4], \mid U\mid =4,\) as follow:

$$\begin{aligned}&PS(u_{1})=\dfrac{0.65+0.6+0.5+0.65+0.62+0.6+0.64+0.55}{1+7}=0.6\\&PS(u_{2})=\dfrac{0.76+0.6+0.72+0.7+0.62+0.55+0.6+0.75}{1+7}=0.66\\&PS(u_{3})=\dfrac{0.84+0.5+0.72+0.82+0.62+0.75+0.64+0.55}{1+7}=0.68\\&PS(u_{4})=\dfrac{0.95+0.65+0.7+0.82+0.6+0.75+0.64+0.55}{1+7}=0.7 \\&OPS=\dfrac{0.6+0.66+0.68+0.7}{4}=0.66 \end{aligned}$$

The resultant PS and OPS of the performed application 2 for every \(a_{i}\in U, i\in [1,3], \mid U\mid =3,\) are listed:

$$\begin{aligned}&PS(a_{1})=\dfrac{0.8+0.8+0.8+0.7}{1+3}=0.77\\&PS(a_{2})=\dfrac{0.9+0.65+0.7+0.8}{1+3}=0.76\\&PS(a_{3})=\dfrac{0.8+0.65+0.7+0.8}{1+3}=0.73\\&OPS=\dfrac{0.77+0.76+0.73}{3}=0.75 \end{aligned}$$

Table 10 shows the resultant PS and OPS for \(\mid U\mid =44\) in Sect. 5.5.

Table 10 Calculated PS and OPS for eleven faculties
Full size table

5.7 GOL theory approach assisting artificial intelligent e-learning systems

The following bullet points briefly discuss how the present approach can assist AI e-learning systems:

  • The performance knowledge of conjoint learners (\(\rho\)) can be carried out in a trained sequential machine learning algorithm on learners’ performance data.

  • Two PS and OPS metrics can be used for AI system through machine learning algorithms to analyze and identify students’ performances on any collected data. This model would provide paradigmatic implications for upcoming advancement of AI-generated learning assessment.

  • Learning rate of each student (membership degree \(\mu\)) can be evaluated via automated AI tools with detailed analytics.

  • Through developed n-ary fuzzy relation, a dynamic strategy can be accomplished to map out the learners’ interactions in group-based e-learning systems via graph neural network (GNN)-based classification system.

Table 11 depicts the parameters of GOL theory which can serve Artificial Intelligence for e-learning environments.

Table 11 GOL theory parameters for AI e-learning systems
Full size table

5.8 Comparison of methods

To address the superiority of the present method, we briefly compare the results with other existing methodologies. To predict and analyze the students’ performances, a methodical Machine Learning (ML) attitude was proposed to enhance the modality assurance of the online education programs with the accuracy of 93.2% better than the methods of k-Nearest Neighbor, Naive Bayes, and Decision Tree. A descriptive-analytical approach, inferential statistical methods and Statistical Package for the Social Sciences (SPSS), was used for data analysis in Maharat platform (Alsubaie 2023). The assessment of determinants of students’ performances was conducted in terms of empirical set-up data using structural equation (multivariate regression) model (Castillo-Merino and Serradell-Lopez 2014). A fuzzy model was used with standard test statistics and fuzzy membership functions which was constituted on the basis of confidence interval in order to eliminate the problems of sampling error and the convolution of accumulating fuzzy linguistic information. The model characterized performance indices and performance evaluation matrix with the validity and reliability of sample data, based on SPSS analysis (Lee et al. 2019). Also, a theoretical formative assessment technique was presented by merging the computational intelligent approaches namely, fuzzy association rule mining, fuzzy inference, grey relational assessment, and K-means on the basis of learning portfolio of learners in an online environment (Chen et al. 2007). Through fuzzy miner algorithm, the behavior analytics, process modeling and group performance analysis were carried out for the e-learning logs (Premchaiswadi et al. 2018). In another study, a systematic fuzzy graph approach was characterized by conventional binary fuzzy relation which considered the fuzziness strength of two related entities. This was useful in modeling and analyzing diverse real-life problems (Mathew et al. 2018). Our theory simultaneously copes with uncertainty of multi-facet interconnected learners to evaluate their academic performances in local and global e-learning systems regarding fuzzy membership degrees. Table 12 shows the advantages of the developed methodology against other approaches. This has confirmed the comprehensiveness of our theoretical and, at the same time, applicable framework using the generalized fuzzy relation that structures the GOL theory.

Table 12 Superiority of AI-based GOL theory compared to existing methods
Full size table

The comparison of clustering performance of the generalized fuzzy relation scheme with the only-available classical binary fuzzy relation is presented in Table 13. It is observed that our method has the best and most accurate performance on the used datasets in identifying unary, binary, ternary, quaternary, quinary and so forth relationships among entities, while the performance of fuzzy binary relation is inaccurate and unreliable due to the waiver of high-order relationships. In contrast to classical fuzzy relation, the developed n-ary fuzzy relation is the ensemble of correlated relations of entities to achieve better clustering performance. In the derived experimental results, in application 1, 6 links are identified based on the binary relations while 15 links are recognized with generalized fuzzy relation over 4 elements. For application 2, there are 3 links in classical binary relation, whereas 7 links are obtained among three elements. In application 3, a tremendous difference is shown between classical binary relation and generalized fuzzy relation with 5 and 68 links, respectively.

To validate the modality of the formulated PS for the assessment of learners’ performance, we examine and compare our method along with the available method, i.e., fuzzy inference method (\(Grade _{COG}\) metric) (Chen et al. 2007), on the three different classes of experimental data. As shown in Table 14, the group-wise performance of the correlated learners is neglected in \(Grade _{COG}\), and thus the performance score of each learner is merely based on single performances. According to our results, more precise and reliable values are obtained when the individuals are grouped in online classes. As seen in application 1, individuals’ performance scores (final grades) are 0.65, 0.76, 0.84, 0.95 by fuzzy inference method, while the individuals’ PSs of our developed method are 0.6, 0.66, 0.68, 0.7 in the e-learning platform. In application 2, individuals’ performance scores (final grades) are 0.8, 0.8, 0.9 using fuzzy inference approach, but the results of individuals’ PSs are 0.77, 0.76, 0.73 via GOL theory methodology. In application 3, the performance score only covers individual setups in fuzzy inference method, but the dependable results include both individual and group setups in the context of GOL theory.

Table 13 Superiority of the generalized fuzzy relation (GOL theory) to the classical binary relation on three different sets of experimental data
Full size table
Table 14 Supremacy of PS in GOL theory methodology to the proposed method over three different categories of experimental data
Full size table

6 Conclusion

The main contribution of this study is to establish AI-base “Global Online Learning (GOL) theory” based on the generalized n-ary fuzzy relations. As per the uncertain behavior of educational systems, the analysis of complex correlations between entities (individuals) is carried out with a comprehensive approach. The mathematical concepts of n-ary relation and n-ary fuzzy relation are introduced as the extension of classical binary relation and binary fuzzy relation. Certain characteristics are obtained, i.e., reflexive, symmetric, transitive, composition, t-cut, support and Cartesian products, to configure parametric connections between t-cut and Cartesian product. Based on the n-ary fuzzy relation model, the symbol “\(\circ _{\rho }\)” is defined to construct fuzzy hyperalgebra using new parameters, where the systematic relevance between fuzzy hyperalgebra and hyperalgebra is indicated as “\(\circ _{\rho }\)”, supp and t-cut notations. Also, an applicable theoretical infrastructure is established to present graphical attitudes of soft fuzzy graph and intuitionistic fuzzy graph. As the training systems are now transforming from traditional to virtual methodology, AI-base “GOL theory” is initiated to declare a theoretical platform for such a transition as a new generation of artificial intelligent educational system. Based on the generalized n-ary fuzzy relation, the evaluation of entities and correlations is carried out to tackle the uncertainty derived from the group-wise learning rate of individuals in educational systems. Multiple relationships of targets are investigated in terms of fuzzy information with seamless graphical presentation. By the implementation of generalized fuzzy relation, a methodical platform is constituted to use basic notions such as t-cut and support within the AI-base “GOL theory” framework. As such, the corresponding hypergraph is derived based on the t-cut method to assess the components in a simpler way. Also, the self-evaluation of components is carried out which is accompanied with the group-wise correlation, where the coverage of system is derived in terms of support property. The AI-base “GOL theory” and its evaluation approach can be used in other fields such as vocational businesses to model the virtual global, local training, social interactions among employees, students, and job seekers. Owing to the generality and comprehensiveness of the developed theory, it can be used to intelligently assess the behavioral trend of users, specifically when it is translated into coding for quantum computers for global online educational platforms and social media systems.