Subgraphs of BV functions on RCD spaces

Abstract

In this work, we extend classical results for subgraphs of functions of bounded variation in $\mathbb R^n\times \mathbb R$ to the setting of ${\textsf{X}}\times \mathbb R$, where ${\textsf{X}}$ is an ${\textrm{RCD}}(K,N)$ metric measure space. In particular, we give the precise expression of the push-forward onto ${\textsf{X}}$ of the perimeter measure of the subgraph in ${\textsf{X}}\times \mathbb R$ of a ${\textrm{BV}}$ function on ${\textsf{X}}$. Moreover, in properly chosen good coordinates, we write the precise expression of the normal to the boundary of the subgraph of a ${\textrm{BV}}$ function f with respect to the polar vector of f, and we prove change-of-variable formulas.

1 Introduction

This short note is about the study of functions of bounded variation in the setting of ${\textrm{RCD}}$ spaces. The study of analytic and geometric properties of ${\textrm{RCD}}$ metric measure spaces $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ flourished in the last decade, see the account in [3] and the references [5, 6, 10, 20, 29, 32, 38, 43, 44]. The geometric structure of these spaces up to ${\textsf{m}}$-negligible sets is pretty well understood after the works [19, 25, 34, 36, 42]. Recently, the research on these spaces has been focusing also on the study of structure results for sets of (locally) finite perimeter, and of fine properties of functions of (locally) bounded variation, see [4, 15, 17, 18].

We stress that this theory has recently found interesting applications in the study of the isoperimetric problem on non-compact smooth Riemannian manifolds with Ricci curvature bounded from below, see [14], and in the proof of the rank-one theorem in this low regularity setting [13]. We refer the reader to Sect. 2.2 for more details.

We fix from now on an ${\textrm{RCD}}(K,N)$ metric measure space $({\textsf{X}},{\textsf{d}},{\textsf{m}})$. Here $K\in \mathbb R$ plays the role of (synthetic) lower bound on the Ricci curvature, and $N\in [1,\infty )$ plays the role of synthetic upper bound on the dimension. Given a function of locally bounded variation $f\in {\textrm{BV}}_{\textrm{loc}}({\textsf{X}})$ (see Sect. 2.1.1), we consider in ${\textsf{X}}\times \mathbb R$ the subgraph

$$\begin{aligned} \mathcal {G}_f\mathrel {\mathop :}=\{(x,t)\in {\textsf{X}}\times \mathbb {R}:\,t<f(x)\}. \end{aligned}$$

Notice that, under the sole assumption of f being measurable, $f\in {\textrm{BV}}_{\textrm{loc}}({\textsf{X}})$ if and only if $\mathcal {G}_f$ is of locally finite perimeter, see the first part of the main Theorem 3. In this note, we are concerned with studying the relation of the measure on ${\textsf{X}}\times \mathbb R$ with the measure $|\textrm{D}f|$ on ${\textsf{X}}$. We will denote with $\pi ^1:{\textsf{X}}\times \mathbb R\rightarrow {\textsf{X}}$ the projection map onto ${\textsf{X}}$, and with $\pi ^2:{\textsf{X}}\times \mathbb R\rightarrow \mathbb R$ the projection map onto $\mathbb R$.

In the Euclidean setting, this study can be dated back at least to [40]. There, the author was concerned with the study of Cartesian surfaces, i.e., subsets of $\mathbb R^n\times \mathbb R$ that can be written as $\{(x,t)\in \mathbb R^n\times \mathbb R:x\in \Omega ,\,t=f(x)\}$, where $\Omega \subseteq \mathbb R^n$ is open, and $f\in \textrm{BV}_{\textrm{loc}}(\Omega )$. A systematic study of Cartesian surfaces and subgraphs of functions of locally bounded variation in Euclidean spaces can be found in [31, Section 4.1.5]. In fact, our results are the generalization of the results contained in [31, Section 4.1.5] to the setting of finite-dimensional ${\textrm{RCD}}$ spaces.

The results of [31, Section 4.1.5] have been used in the short proof of the rank-one theorem in the Euclidean setting of [39]. Moreover, outside the Euclidean setting, they have also been recently generalized in the setting of arbitrary Carnot groups in [28, Theorem 1.3, Theorem 4.2, and Theorem 4.3]. The latter generalization has been exploited to prove the rank-one theorem for a subclass of Carnot groups, see [28, Theorem 1.1 and Theorem 1.2].

We aim now at stating the main results of this note. We recall some terminology and notation. We refer the reader to Definition 11 and Definition 12 for more details. Given $f\in \textrm{BV}_{\textrm{loc}}({\textsf{X}})$, we can define in a natural way (see Definition 11) the approximate lower and upper limits $f^\wedge (x)$, $f^\vee (x)$ of f(x) at $x\in {\textsf{X}}$, and the precise representative ${\bar{f}}(x):=(f^\wedge (x)+f^\vee (x))/2$. The set of points $x\in {\textsf{X}}$ where $f^\wedge (x)<f^\vee (x)$ is called the jump set $J_f$. In the setting of finite-dimensional ${\textrm{RCD}}$ spaces it always holds ${\textsf{m}}(J_f)=0$.

We can write $|\textrm{D}f|$ as $|\textrm{D}f|^a+|\textrm{D}f|^s$, where $|\textrm{D}f|^a\ll {\textsf{m}}$ and $|\textrm{D}f|^s\perp {\textsf{m}}$. We also have $|\textrm{D}f|^s=|\textrm{D}f|^j+|\textrm{D}f|^c$, where the jump part is given by , while the Cantor part is given by , so that we can write with ${\textsf{m}}(C_f)=0$. Finally, we call $g_f$ the Borel function such that $|\textrm{D}f|^a=g_f{\textsf{m}}$.

We stress that in the low regularity setting of finite-dimensional ${\textrm{RCD}}$ spaces we cannot give a pointwise meaning to $\textrm{D}f$ for a function f of locally bounded variation. This also prevents us from proving the verbatim analogues of the results in [31, Section 4.1.5] in our setting. Nevertheless, with the Calculus developed in the ${\textrm{RCD}}$ setting, one can give a meaning to the polar vector $\nu _f$, that in the classical setting is $\textrm{D}f/|\textrm{D}f|$ ( [15], after [18]). This $\nu _f$ belongs to the capacitary module $L^0_{{\textrm{Cap}}}(T{\textsf{X}})$ (see [26]), and it is defined through a divergence theorem with sufficiently smooth test vector fields, see Theorem 25. When for a locally finite perimeter set E, we denote .

In the non-smooth setting of finite-dimensional ${\textrm{RCD}}$ spaces, there are no canonical local coordinates. Anyway, in a lot of situations, one can use the so-called splitting maps, see Definition 28. Roughly speaking, a splitting map is a vector-valued harmonic map whose Jacobian matrix is close to be the identity in an integral sense and whose Hessian matrix is close to be null in an integral sense. Splitting maps have been used to detect geometric properties of spaces with Ricci lower bounds since the seminal works [22, 23]. They have also been used in the recent [16,17,18,19, 24]. We also used the splitting maps in the proof of the rank-one theorem in finite-dimensional ${\textrm{RCD}}$ spaces [13]. The next definition is borrowed and inspired from the studies in [13, 17] and gives a good notion of local chart. Notice that as a consequence of Proposition 6 every function f of locally bounded variation has total variation that is supported on the countable union of domains of good splitting maps.

Definition 1

(Good splitting map) Let $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ be an ${\textrm{RCD}}(K,N)$ space of essential dimension n. Take $\eta \in (0,n^{-1})$. Fix $y\in {\textsf{X}}$ and $r_y>0$. We say that an n-tuple of harmonic $C_{K,N}$-Lipschitz maps $u=(u^1,\dots ,u^n):B_{2 r_y}(y)\rightarrow \mathbb {R}^n$ is a good $\eta$-splitting map on $D\subseteq \ B_{r_y}(y)$ if for every $x\in D$ and $s\in (0,r_y)$, u is an $\eta$-splitting map on $B_s(x)$. We simply write good splitting map if the value of $\eta \in (0,n^{-1})$ is not important.

For the notion of essential dimension, we refer the reader to Sect. 2.2. Given a good splitting map, following [13, Definition 3.6], we give the following definition. We are essentially reading the normals $\nu _f$ and $\nu _{\mathcal {G}_f}$ in charts.

Definition 2

Let $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ be an ${\textrm{RCD}}(K,N)$ space of essential dimension n, and let u be a good splitting map on $D\subseteq B_{r_y}(y)$. Let $f\in {\textrm{BV}}_\textrm{loc}({\textsf{X}})$. Then we define

• (1) the $|\textrm{D}f|$-measurable map $\nu _f^u$ defined at $|\textrm{D}f|$-a.e. $x\in B_{2r_y}(y)$ as

  $$\begin{aligned} \nu _f^u(x)\mathrel {\mathop :}=((\nu _f\,\cdot \, \nabla u^1)(x),\dots ,(\nu _f\,\cdot \, \nabla u^n)(x)), \end{aligned}$$

• (2) the -measurable map $\nu _{\mathcal {G}_f}^u$ defined at -a.e. $p:=(x,t)\in B_{2r_y}(y)\times \mathbb R$ as

  $$\begin{aligned} \nu _{\mathcal {G}_f}^u(p)\mathrel {\mathop :}=((\nu _{\mathcal {G}_f}\,\cdot \, \nabla u^1)(p),\dots ,(\nu _{\mathcal {G}_f}\,\cdot \, \nabla u^n)(p),(\nu _{\mathcal {G}_f}\,\cdot \, \nabla \pi ^2)(p)). \end{aligned}$$

We are now ready to state the main theorems of this note. In the first result, we explicitly compute in ${\textsf{X}}$ in terms of $|\textrm{D}f|$. Theorem 3 is the generalization in the setting of finite-dimensional ${\textrm{RCD}}$ spaces of [31, Theorem 1 in Section 4.1.5].

Theorem 3

Let $K\in \mathbb R$ and $N<\infty$. Let $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ be an ${\textrm{RCD}}(K,N)$ space, and let $f\in L^0({\textsf{m}})$. Then the following are equivalent:

• $f\in {\textrm{BV}}_\textrm{loc}({\textsf{X}})$,

• $\mathcal {G}_f$ has finite perimeter on cylinders.

If this is the case, then

In Theorem 4, we explicitly compute the normal to the boundary of the subgraph $\nu _{\mathcal {G}_f}^u$ in coordinates, with respect to the polar vector $\nu _f^u$ in coordinates, and the density $g_f$ of $|\textrm{D}f|^a$ with respect to ${\textsf{m}}$. For the sake of reference, the analogous result in the non-Euclidean setting of Carnot groups is obtained in [28, Theorem 4.3].

Theorem 4

Let $K\in \mathbb R$ and $N<\infty$. Let $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ be an ${\textrm{RCD}}(K,N)$ space, and let $f\in {\textrm{BV}}_\textrm{loc}({\textsf{X}})$. Let u be a good splitting map on $D\subseteq B_{r_y}(y)$, where $y\in {\textsf{X}}$ and $r_y>0$.

Then, for -a.e. $(x,t)\in D\times \mathbb {R}$, it holds that

$$\begin{aligned} \nu _{\mathcal {G}_f}^{{ u}}(x,t)= {\left\{ \begin{array}{ll} \Big (\sqrt{\frac{1}{1+g_f^2}}g_f\nu _f^{ u},-\sqrt{\frac{1}{1+g_f^2}}\Big )(x)\quad &{}\text {if }x\in D\setminus (J_f\cup C_f), \\ (\nu _f^{ u},0)(x)\quad &{}\text {if }x\in D\cap (J_f\cup C_f). \end{array}\right. } \end{aligned}$$

In Theorem 5, we extend [31, Theorem 2 and Theorem 3 in Section 4.1.5] in the setting of finite-dimensional ${\textrm{RCD}}$ spaces.

Theorem 5

Let $K\in \mathbb R$ and $N<\infty$. Let $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ be an ${\textrm{RCD}}(K,N)$ space of essential dimension n, and let $f\in {\textrm{BV}}_\textrm{loc}({\textsf{X}})$. Let u be a good splitting map on $D\subseteq B_{r_y}(y)$, where $y\in {\textsf{X}}$ and $r_y>0$. Let also $\varphi :D\times \mathbb {R}\rightarrow \mathbb {R}$ be a bounded Borel function. Then

• (i) for every $i=1,\dots ,n$,

  

• (ii) it holds

  

• (iii) for every $i=1,\dots ,n$,

  

  where we set $\Theta _n({\textsf{m}},x):=\lim _{r\rightarrow 0}{\textsf{m}}(B_r(x))/r^n$,

• (iv) it holds

  

In Theorem 4 and Theorem 5, we compare $\nu _{\mathcal {G}_f}^u$ and $\nu _f^u$ only for a single good splitting map u, on its domain D. This, however, still allows us to have a complete picture (i.e., the comparison for -a.e. (x, t)), thanks to the following result, taken from [13, Lemma 2.28], which, in turn, is inspired by the techniques introduced in [18]. The last part of the forthcoming statement is not explicitly written in [13], but it is a direct consequence of (12).

Proposition 6

Let $K\in \mathbb R$ and $N<\infty$. Let $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ be an ${\textrm{RCD}}(K,N)$ space of essential dimension n. Let also $\eta \in (0,n^{-1})$. Then there exists a family $\varvec{u}_\eta =\{u_{\eta ,k}\}_{k\in \mathbb N}$, where, for every $k\in \mathbb N$, $u_{\eta ,k}$ is a good $\eta$-splitting map on $D_k\subseteq B_{r_k}(x_k)$, for some $x_k\in {\textsf{X}}$ and $r_k>0$, and moreover,

$$\begin{aligned} |\textrm{D}f|\bigg ({\textsf{X}}\setminus \bigcup _k D_k\bigg )=0,\qquad \text {for every }f\in {\textrm{BV}}_\textrm{loc}({\textsf{X}}). \end{aligned}$$

In particular, it holds that

We spend a few lines about the strategy of the proof of Theorem 4, as once it is obtained, Theorem 5 follows quite easily. The classical strategy of [31] seems not suitable for our context, as we do not have a canonical way to decompose the distributional derivatives $\textrm{D}f$ and along different directions. This also causes the need to define the ‘components’ $\big (\nu _{f}^u\big )_{i}$ $\big (\nu _{\mathcal {G}_f}^u\big )_{i}$ exploiting maps that look like charts. The drawback is that these charts are defined only on Borel subsets; hence, it is not clear the distributional nature of the objects $\big (\nu _{f}^u\big )_{i}$ and $\big (\nu _{\mathcal {G}_f}^u\big )_{i}$. Nevertheless, in our main result we compare $\big (\nu _{f}^u\big )_{i}$ with $\big (\nu _{\mathcal {G}_f}^u\big )_{i}$. In order to do so, a new strategy has to be exploited, and we therefore employ a blow-up procedure, which is more compatible with the use of geometric measure theory results and does not need the distributional meaning of such objects. This strategy is in Sect. 3, after Sect. 2 in which some preliminary facts are discussed.

2 Preliminaries

Given $n\in \mathbb N$ and non-empty sets ${\textsf{X}}_1,\dots ,{\textsf{X}}_n$, for any $i=1,\ldots ,n$ we will denote by $\pi ^i$ the projection of the Cartesian product ${\textsf{X}}_1\times \dots \times {\textsf{X}}_n$ onto its $i^\textrm{th}$ factor:

$$\begin{aligned} \pi ^i:{\textsf{X}}_1\times \dots \times {\textsf{X}}_n\rightarrow {\textsf{X}}_i,\qquad (x_1,\dots ,x_n)\mapsto x_i. \end{aligned}$$

2.1 Metric measure spaces

We say that a metric measure space $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ is uniformly locally doubling if for every radius $R>0$ there exists a constant $C_D>0$ such that

$$\begin{aligned} {\textsf{m}}(B_{2r}(x))\le C_D{\textsf{m}}(B_r(x)),\qquad \text { for every }x\in {\textsf{X}}\text { and }r\in (0,R). \end{aligned}$$

Moreover, we say that $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ supports a weak local (1, 1)-Poincar inequality if there exists a constant $\lambda \ge 1$ for which the following property holds: Given any $R>0$, there exists a constant $C_P>0$ such that for any function $f\in \textrm{LIP}_{\textrm{loc}}({\textsf{X}})$ it holds that

where, for every $x\in {\textsf{X}}$,

$$\begin{aligned} \textrm{lip}f(x):=\varlimsup _{y\rightarrow x}\frac{|f(x)-f(y)|}{{\textsf{d}}(x,y)}, \end{aligned}$$

which has to be understood as 0 if x is isolated.

Uniformly locally doubling spaces supporting a weak local (1, 1)-Poincaré inequality are usually called ${\textrm{PI}}$ spaces.

2.1.1 BV calculus

We recall the notions of function of bounded variation and of finite perimeter set in the metric measure setting following [41].

Definition 7

(Function of bounded variation) Let $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ be a metric measure space. Let $f\in L^1_{\textrm{loc}}({\textsf{X}},{\textsf{m}})$ be given. Then we define

for any open set $\Omega \subseteq {\textsf{X}}$. We declare that a function $f\in L^1_\textrm{loc}({\textsf{X}},{\textsf{m}})$ is of local bounded variation, briefly $f\in \textrm{BV}_\textrm{loc}({\textsf{X}})$, if $|\textrm{D}f|(\Omega )<+\infty$ for every $\Omega \subseteq {\textsf{X}}$ open bounded. In this case, it is well known that $|\textrm{D}f|$ extends to a locally finite measure on ${\textsf{X}}$. Moreover, a function $f \in L^1({\textsf{m}})$ is said to belong to the space of functions of bounded variation $\textrm{BV}({\textsf{X}})=\textrm{BV}({\textsf{X}},{\textsf{d}},{\textsf{m}})$ if $|\textrm{D}f|({\textsf{X}})<+\infty$.

Definition 8

(Set of finite perimeter) Let $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ be a metric measure space. Let $E\subseteq {\textsf{X}}$ be a Borel set and $\Omega \subseteq {\textsf{X}}$ an open set. Then we define the perimeter of E in $\Omega$ as

in other words, . We say that E has locally finite perimeter if $P(E,\Omega )<+\infty$ for every $\Omega \subseteq {\textsf{X}}$ open bounded. Moreover, we say that E has finite perimeter if $P(E,{\textsf{X}})<+\infty$.

The following coarea formula is taken from [41].

Theorem 9

(Coarea) Let $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ be a metric measure space. Let $f\in L^1_\textrm{loc}({\textsf{m}})$ be given. Then for any open set $\Omega \subseteq {\textsf{X}}$, it holds that $\mathbb {R}\ni t\mapsto P(\{f>t\},\Omega )\in [0,+\infty ]$ is Borel measurable and

$$\begin{aligned} |\textrm{D}f|(\Omega )=\int _\mathbb {R}P(\{f>t\},\Omega )\,\textrm{d}t. \end{aligned}$$

(1)

In particular, if $f\in L^1({\textsf{m}})$, then $f\in {\textrm{BV}}({\textsf{X}})$ if and only if $\{f>t\}$ is a set of finite perimeter for a.e. $t\in \mathbb {R}$ and the function $t\mapsto P(\{f>t\},{\textsf{X}})$ belongs to $L^1(\mathbb {R})$. In this case, we have that $\mathbb {R}\ni t\mapsto P(\{f>t\},E)$ is Borel and $|\textrm{D}f|(E)=\int _\mathbb {R}P(\{f>t\},E)\,\textrm{d}t$ for every Borel set $E\subseteq {\textsf{X}}$.

The Borel measurability of $\mathbb {R}\ni t\mapsto P(\{f>t\},\Omega )\in [0,+\infty ]$ follows from the observation that is right-continuous and $L^1_\textrm{loc}({\textsf{m}})\ni g\mapsto |\textrm{D}g|(\Omega )$ is lower semicontinuous.

We remark that the weak local (1, 1)-Poincaré inequality of $\mathrm PI$ spaces holds for ${\textrm{BV}}_\textrm{loc}({\textsf{X}})$ functions f in the following form: For every bounded open set $\Omega \subseteq {\textsf{X}}$ and every $R>0$,

In the particular case of sets of (locally) finite perimeter, the (1, 1)-Poincaré inequality reads as a local isoperimetric inequality, as can be shown with classical computations:

(2)

The following proposition summarizes results about sets of finite perimeter that are now well known in the context of PI spaces and are proved in [2, 30], see also [1].

Proposition 10

Let $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ be a $\mathrm PI$ space and let $E\subseteq {\textsf{X}}$ be a set of locally finite perimeter. Then, for -a.e. $x\in {\textsf{X}}$ the following hold:

• (i) E is asymptotically minimal at x, i.e., there exist $r_x>0$ and a function $\omega _x:(0,r_x)\rightarrow (0,\infty )$ with $\lim _{r\searrow 0}\omega _x(r)=0$ satisfying

  

• (ii) is asymptotically doubling at x, i.e.,

  

• (iii) we have the following estimates:

  

• (iv) the following holds:

  $$\begin{aligned} \liminf _{r\searrow 0} \min \bigg \{\frac{{\textsf{m}}( B_r(x)\cap E)}{{\textsf{m}}(B_r(x))},\frac{{\textsf{m}}( B_r(x)\setminus E)}{{\textsf{m}}(B_r(x))}\bigg \}>0. \end{aligned}$$

We recall the following classical definition.

Definition 11

(Precise representative) Let $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ be a metric measure space, and let $f:{\textsf{X}}\rightarrow \mathbb {R}$ be a Borel function. Then we set the approximate lower and upper limits to be

$$\begin{aligned} f^{\wedge }(x)&\mathrel {\mathop :}={{\,\mathrm{ap\,\varliminf }\,}}_{y\rightarrow x} f(y)\mathrel {\mathop :}=\sup \left\{ t\in \bar{\mathbb {R}}\,:\,\lim _{r\searrow 0} \frac{{\textsf{m}}(B_r(x)\cap \{f<t\})}{{\textsf{m}}(B_r(x))}=0\right\} , \\ f^{\vee }(x)&\mathrel {\mathop :}={{\,\mathrm{ap\,\varlimsup }\,}}_{y\rightarrow x} f(y)\mathrel {\mathop :}=\inf \left\{ t\in \bar{\mathbb {R}}\,:\,\lim _{r\searrow 0} \frac{{\textsf{m}}(B_r(x)\cap \{f>t\})}{{\textsf{m}}(B_r(x))}=0\right\} , \end{aligned}$$

for every $x\in {\textsf{X}}$. Here we are assuming by convention that

$$\begin{aligned} \inf \varnothing =+\infty \qquad \text {and}\qquad \sup \varnothing =-\infty . \end{aligned}$$

Moreover, we define the precise representative $\bar{f}:{\textsf{X}}\rightarrow \bar{\mathbb {R}}$ of f as

$$\begin{aligned} \bar{f}(x):=\frac{f^\wedge (x)+f^\vee (x)}{2},\qquad \text { for every }x\in {\textsf{X}}, \end{aligned}$$

where we declare that $+\infty -\infty =0$.

We define the jump set $J_f\subseteq {\textsf{X}}$ of the function f as the Borel set

$$\begin{aligned} J_f:=\big \{x\in {\textsf{X}}:\,f^\wedge (x)<f^\vee (x)\big \}. \end{aligned}$$

It is known that if $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ is a PI space and $f\in {\textrm{BV}}({\textsf{X}})$, then ${\textsf{m}}(J_f)=0$, see [9, Proposition 5.2]. Moreover, as proved in [37, Lemma 3.2], it holds that

$$\begin{aligned} |\textrm{D}f|({\textsf{X}}\setminus {\textsf{X}}_f)=0,\qquad \text { where }{\textsf{X}}_f:=\big \{x\in {\textsf{X}}\;\big |\;-\infty<f^\wedge (x)\le f^\vee (x)<+\infty \big \}, \end{aligned}$$

thus in particular $-\infty<\bar{f}(x)<+\infty$ holds for $|\textrm{D}f|$-a.e. $x\in {\textsf{X}}$.

Definition 12

(Decomposition of the total variation measure) Let $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ be a PI space and let $f\in {\textrm{BV}}_\textrm{loc}({\textsf{X}})$. We write $|\textrm{D}f|$ as $|\textrm{D}f|^a+|\textrm{D}f|^s$, where $|\textrm{D}f|^a\ll {\textsf{m}}$ and $|\textrm{D}f|^s\perp {\textsf{m}}$. We can decompose the singular part $|\textrm{D}f|^s$ as $|\textrm{D}f|^j+|\textrm{D}f|^c$, where the jump part is given by , while the Cantor part is given by , so that we can write with ${\textsf{m}}(C_f)=0$. Finally, we write $|\textrm{D}f|^a=g_f{\textsf{m}}$.

We recall the definition of subgraph and [13, Lemma 2.11].

Definition 13

Let $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ be a metric measure space and let $f:{\textsf{X}}\rightarrow \mathbb {R}$ be Borel. Then we define the subgraph of f as the Borel set $\mathcal {G}_f\subseteq {\textsf{X}}\times \mathbb {R}$ given by

$$\begin{aligned} \mathcal {G}_f\mathrel {\mathop :}=\big \{(x,t)\in {\textsf{X}}\times \mathbb {R}:\,t<f(x)\big \}. \end{aligned}$$

Before stating the next result, we remind that the essential boundary $\partial ^*E$ of $E\subseteq {\textsf{X}}$ Borel is

$$\begin{aligned} \partial ^*E:=\bigg \{x\in {\textsf{X}}\;\bigg |\;\limsup _{r\searrow 0}\frac{{\textsf{m}}(B_r(x)\cap E)}{{\textsf{m}}(B_r(x))}>0,\, \limsup _{r\searrow 0}\frac{{\textsf{m}}(B_r(x)\setminus E)}{{\textsf{m}}(B_r(x))}>0\bigg \}. \end{aligned}$$

Lemma 14

Let $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ be a uniformly locally doubling metric measure space and $f\in {\textrm{BV}}_\textrm{loc}({\textsf{X}})$. Then it holds that

$$\begin{aligned} ({x},{t})\in \partial ^*\mathcal {G}_f&\quad \Rightarrow \quad t\in [f^\wedge (x),f^\vee (x)],\\ t\in (f^\wedge (x),f^\vee (x))&\quad \Rightarrow \quad (x,t)\in \partial ^*\mathcal {G}_f. \end{aligned}$$

In particular, if $x\in {\textsf{X}}_f\setminus J_f$, then it holds that $\partial ^*\mathcal {G}_f\cap (\{x\}\times \mathbb {R})\subseteq \{(x,\bar{f}(x))\}$.

2.2 RCD spaces

We assume the reader is familiar with the theory of ${\textrm{RCD}}(K,N)$ spaces. Recall that an ${\textrm{RCD}}(K,N)$ space is an infinitesimally Hilbertian metric measure space verifying the curvature dimension condition $\textrm{CD}(K,N)$, in the sense of Lott–Villani–Sturm, for some $K\in \mathbb {R}$ and $N\in [1,\infty ]$. In this paper, we only consider finite-dimensional ${\textrm{RCD}}(K,N)$ spaces; namely, we assume $N<\infty$. Finite-dimensional ${\textrm{RCD}}$ spaces are PI. If not otherwise stated, through this note we will work in the setting of finite-dimensional ${\textrm{RCD}}$ spaces.

2.2.1 Pointed measured Gromov–Hausdorff convergence and tangents

Let us recall some classical facts about pointed measured Gromov–Hausdorff convergence and tangents in the setting of ${\textrm{RCD}}(K,N)$ spaces. The exposition here is equivalent to the classical one in more general settings (see, e.g., [33]), due to the result in [8, Theorem 4.1]. See also the introduction given in [13, Section 2.1.2].

Definition 15

(Pointed measured Gromov–Hausdorff convergence) Let $({\textsf{X}},{\textsf{d}},{\textsf{m}},p),({\textsf{X}}_i,{\textsf{d}}_i,{\textsf{m}}_i,p_i)$, for $i\in \mathbb N$, be ${\textrm{RCD}}(K,N)$ spaces with $K\in \mathbb R$ and $N<\infty$. Then we say that $({\textsf{X}}_i,{\textsf{d}}_i,{\textsf{m}}_i,p_i)\rightarrow ({\textsf{X}},{\textsf{d}},{\textsf{m}},p)$ in the pointed measured Gromov–Hausdorff sense (briefly, in the pmGH sense) provided there exist a proper metric space $({\textsf{Z}},{\textsf{d}}_{\textsf{Z}})$ and isometric embeddings $\iota :{\textsf{X}}\rightarrow {\textsf{Z}}$ and $\iota _i:{\textsf{X}}_i\rightarrow {\textsf{Z}}$ for $i\in \mathbb N$ such that $\iota _i(p_i)\rightarrow \iota (p)$ and $(\iota _i)_*{\textsf{m}}_i\rightharpoonup \iota _*{\textsf{m}}$ in duality with $C_\textrm{bs}({\textsf{Z}})$, meaning that $\int f\circ \iota _i\,\textrm{d}{\textsf{m}}_i \rightarrow \int f\circ \iota \,\textrm{d}{\textsf{m}}$ for every $f\in C_\textrm{bs}({\textsf{Z}})$. The space ${\textsf{Z}}$ is called a realization of the pmGH convergence $({\textsf{X}}_i,{\textsf{d}}_i,{\textsf{m}}_i,p_i)\rightarrow ({\textsf{X}},{\textsf{d}},{\textsf{m}},p)$.

For brevity, we will identify $(\iota _i)_*{\textsf{m}}_i$ with ${\textsf{m}}_i$ itself. It is possible to construct a distance ${\textsf{d}}_\textrm{pmGH}$ on the collection (of equivalence classes) of ${\textrm{RCD}}(K,N)$ spaces whose converging sequences are exactly those converging in the pointed measured Gromov–Hausdorff sense. Moreover, the class of ${\textrm{RCD}}(K,N)$ metric measure spaces is compact in the pmGH topology.

Definition 16

(pmGH tangent) Let $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ be an ${\textrm{RCD}}(K,N)$ metric measure space. For every $r>0$ and every $x\in {\textsf{X}}$, we define

$$\begin{aligned} {\textsf{m}}_x^r:={\textsf{m}}(B_r(x))^{-1}{\textsf{m}}. \end{aligned}$$

Then, for every $p\in {\textsf{X}}$,

$$\begin{aligned} \textrm{Tan}_p({\textsf{X}},{\textsf{d}},{\textsf{m}}):=\bigg \{({\textsf{Y}},{\textsf{d}}_{\textsf{Y}},{\textsf{m}}_{\textsf{Y}},q)\;\bigg |\; \exists \,r_i\searrow 0:\,({\textsf{X}},r_i^{-1}{\textsf{d}},{\textsf{m}}_p^{r_i},p)\overset{\textrm{pmGH}}{\longrightarrow }({\textsf{Y}},{\textsf{d}}_{\textsf{Y}},{\textsf{m}}_{\textsf{Y}},q)\bigg \}. \end{aligned}$$

It is known that $\textrm{Tan}_p({\textsf{X}},{\textsf{d}},{\textsf{m}})$ is (well defined and) non-empty.

2.2.2 Structure results for ${\textrm{RCD}}$ spaces

Let us recall the definition of the regular set and some well-known structure results in the setting of ${\textrm{RCD}}$ spaces.

Definition 17

(Regular set) Let $n\in \mathbb N$ be given. Let ${\textsf{d}}_e$ stand for the Euclidean distance ${\textsf{d}}_e(x,y):=|x-y|$ on $\mathbb {R}^n$, while $\underline{\mathcal {L}}^n$ is the normalized measure $\underline{\mathcal {L}}^n=\frac{n+1}{\omega _n}\mathcal L^n$, where $\omega _n$ is the volume of the unit ball in $\mathbb R^n$. Then the set of n-regular points of an ${\textrm{RCD}}(K,N)$ space $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ is defined as

$$\begin{aligned} \mathcal R_n=\mathcal R_n({\textsf{X}}):=\Big \{x\in {\textsf{X}}\;\Big |\;\textrm{Tan}_x({\textsf{X}},{\textsf{d}},{\textsf{m}})=\big \{(\mathbb {R}^n,{\textsf{d}}_e,\underline{\mathcal {L}}^n,0)\big \}\Big \}. \end{aligned}$$

A Borel set $A\subseteq {\textsf{X}}$ is said to be $({\textsf{m}},n)$-rectifiable for some $n\in \mathbb {N}$ if there exist Borel subsets $(A_i)_{i\in \mathbb N}$ of A such that each $A_i$ is bi-Lipschitz equivalent to a subset of $\mathbb {R}^n$ and ${\textsf{m}}(A\setminus \bigcup _i A_i)=0$. As proved in [19, 25, 34, 36, 42], the following structure theorem holds.

Theorem 18

Let $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ be an ${\textrm{RCD}}(K,N)$ space. Then there exists a (unique) number $n\in \mathbb N$ with $1\le n\le N$, called the essential dimension of $({\textsf{X}},{\textsf{d}},{\textsf{m}})$, such that ${\textsf{m}}({\textsf{X}}\setminus \mathcal R_n)=0$. Moreover, the regular set $\mathcal R_n$ is $({\textsf{m}},n)$-rectifiable and it holds that ${\textsf{m}}\ll \mathcal H^n$.

More precisely, it is proved in [42] that $\mathcal R_k$ is $({\textsf{m}},k)$-rectifiable for every $k\in \mathbb {N}$ with $k\le N$ and that ${\textsf{m}}({\textsf{X}}{\setminus }\bigcup _{k\le N}\mathcal R_k)=0$. The fact that holds for every $k\le N$ was shown in [25, 34, 36], independently. Finally, the existence of a number $n\le N$ satisfying ${\textsf{m}}({\textsf{X}}\setminus \mathcal R_n)=0$ is proved in [19].

Definition 19

Let $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ be an ${\textrm{RCD}}(K,N)$ space having essential dimension n. Then we define the set $\mathcal R_n^*=\mathcal R_n^*({\textsf{X}})\subseteq \mathcal R_n$ as

$$\begin{aligned} \mathcal R_n^*:=\left\{ x\in \mathcal R_n\;\bigg |\;\exists \Theta _n({\textsf{m}},x):=\lim _{r\rightarrow 0}\frac{{\textsf{m}}(B_r(x))}{{\omega _n}r^n}\in (0,+\infty )\right\} . \end{aligned}$$

Notice that the set $\mathcal R_n^*$ is Borel, see [13, Remark 2.5]. As shown in [8, Theorem 4.1], it holds that ${\textsf{m}}({\textsf{X}}\setminus \mathcal R_n^*)=0$.

2.2.3 Structure results for sets of finite perimeter in ${\textrm{RCD}}$ spaces

Let us now recall some structure results for sets of finite perimeter in ${\textrm{RCD}}(K,N)$ spaces. We assume the reader to be familiar with [4, 15, 17, 18].

Definition 20

(Tangents to a set of finite perimeter) Let $({\textsf{X}},{\textsf{d}},{\textsf{m}},p)$ be a pointed ${\textrm{RCD}}(K,N)$ space, $E\subseteq {\textsf{X}}$ a set of locally finite perimeter. Then we define $\textrm{Tan}_p({\textsf{X}},{\textsf{d}},{\textsf{m}},E)$ as the family of all quintuplets $({\textsf{Y}},{\textsf{d}}_{\textsf{Y}},{\textsf{m}}_{\textsf{Y}},q,F)$ that verify the following two conditions:

• i) $({\textsf{Y}},{\textsf{d}}_{\textsf{Y}},{\textsf{m}}_{\textsf{Y}},q)\in \textrm{Tan}_p({\textsf{X}},{\textsf{d}},{\textsf{m}})$,

• ii) $F\subseteq {\textsf{Y}}$ is a set of locally finite perimeter with ${\textsf{m}}_{\textsf{Y}}(F)>0$ for which the following property holds: Along a sequence $r_i\searrow 0$ such that $({\textsf{X}},r_i^{-1}{\textsf{d}},{\textsf{m}}_p^{r_i},p)\rightarrow ({\textsf{Y}},{\textsf{d}}_{\textsf{Y}},{\textsf{m}}_{\textsf{Y}},q)$ in the pmGH sense, with realization ${\textsf{Z}}$, it holds that $E^i\rightarrow F$ in $L^1_\textrm{loc}$ (cf. with [4, Definition 3.1]), where $E^i$ is intended in the rescaled space $({\textsf{X}},r_i^{-1}{\textsf{d}})$. If this is the case, we write

  $$\begin{aligned} ({\textsf{X}},r_i^{-1}{\textsf{d}},{\textsf{m}}_p^{r_i},p,E)\rightarrow ({\textsf{Y}},{\textsf{d}}_{\textsf{Y}},{\textsf{m}}_{\textsf{Y}},q,F). \end{aligned}$$

Definition 21

(Reduced boundary) Let $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ be an ${\textrm{RCD}}(K,N)$ space. Let $E\subseteq {\textsf{X}}$ be a set of locally finite perimeter. Then we define the reduced boundary $\mathcal F E\subseteq \partial ^* E$ of E as the set of all those points $x\in \mathcal R_n^*$ satisfying all the four conclusions of Proposition 10 and such that

$$\begin{aligned} \textrm{Tan}_x({\textsf{X}},{\textsf{d}},{\textsf{m}},E)=\big \{(\mathbb {R}^n,{\textsf{d}}_e,\underline{\mathcal {L}}^n,0,\{x_n>0\})\big \}, \end{aligned}$$

(3)

where $n\in \mathbb N$, $n\le N$ stands for the essential dimension of $({\textsf{X}},{\textsf{d}},{\textsf{m}})$. We recall that the set of all points $x\in {\textsf{X}}$ that satisfy (3) was denoted by $\mathcal {F}_nE$ in [4].

We recall here, for the reader’s convenience, [13, Remark 2.22].

Remark 22

By the proof of [4, Corollary 4.10], by [4, Corollary 3.4], and by the membership to $\mathcal R_n^*$, we see that for any $x\in \mathcal {F}E$ the following hold.

• (i) If $r_i\searrow 0$ is such that

  $$\begin{aligned} ({\textsf{X}}, r_i^{-1}{\textsf{d}},{\textsf{m}}_x^{r_i},x)\rightarrow (\mathbb {R}^n,{\textsf{d}}_e, \underline{\mathcal {L}}^n,0)\end{aligned}$$

  (4)

  in a realization $({\textsf{Z}},{\textsf{d}}_{\textsf{Z}})$, then, up to not relabeled subsequences and a change of coordinates in $\mathbb {R}^n$,

  $$\begin{aligned} ({\textsf{X}}, r_i^{-1}{\textsf{d}},{\textsf{m}}_x^{r_i},x,E)\rightarrow (\mathbb {R}^n,{\textsf{d}}_e, \underline{\mathcal {L}}^n,0,\{x_n>0\}), \end{aligned}$$

  in the same realization $({\textsf{Z}},{\textsf{d}}_{\textsf{Z}})$. Notice that, given a sequence $r_i\searrow 0$, it is always possible to find a subsequence satisfying (4).

• (ii) If $r_i\searrow 0$ is such that

  $$\begin{aligned} ({\textsf{X}}, r_i^{-1}{\textsf{d}},{\textsf{m}}_x^{r_i},x,E)\rightarrow (\mathbb {R}^n,{\textsf{d}}_e, \underline{\mathcal {L}}^n,0,\{x_n>0\}) \end{aligned}$$

  in a realization $({\textsf{Z}},{\textsf{d}}_{\textsf{Z}})$, then 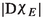weakly converges to in duality with $C_{\textrm{bs}}(Z)$.

• (iii) We have

  

  (5)

$\square$

We now recall [13, Theorem 3.3], which follows along the techniques of [17] and builds upon [27].

Theorem 23

Let $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ be an ${\textrm{RCD}}(K,N)$ space having essential dimension n. Then

$$\begin{aligned} |\textrm{D}f|({\textsf{X}}\setminus \mathcal R_n^*)=0,\quad \text { for every }f\in {\textrm{BV}}_{\textrm{loc}}({\textsf{X}}). \end{aligned}$$

The following is [13, Theorem 3.4].

Theorem 24

(Representation formula for the perimeter) Let $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ be an ${\textrm{RCD}}(K,N)$ space having essential dimension n. Let $E\subseteq {\textsf{X}}$ be a set of locally finite perimeter. Then

(6)

In particular, it holds that for $\mathcal {H}^{n-1}$-a.e. $x\in \mathcal {F} E$.

2.2.4 Good coordinates and good splitting maps

In this section, we recall the notion of good coordinates studied in [17] and good splitting maps introduced in [13]. First, we recall the following, which comes from [15, Theorem 4.13], see also [18, Theorem 2.4]. We assume the reader to be familiar with the Sobolev calculus on RCD spaces and with the notion of capacitary tangent module $L^0_{\textrm{Cap}}(TX)$. We refer to [13, Section 2.2.1] and references therein.

Theorem 25

Let $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ be an ${\textrm{RCD}}(K,N)$ space and let $f\in {\textrm{BV}}({\textsf{X}})$. Then there exists a unique, up to $|\textrm{D}f|$-a.e. equality, element $\nu _f\in L^0_{\textrm{Cap}}(T{\textsf{X}})$ such that $|\nu _f|=1\ |\textrm{D}f|$-a.e. and

$$\begin{aligned} \int _{\textsf{X}}f\textrm{div}(v)\,\textrm{d}{{\textsf{m}}}=-\int _{\textsf{X}}\pi _{|\textrm{D}f|}(v)\cdot \nu _f\,\textrm{d}{|\textrm{D}f|},\quad \text { for every } v\in {\textrm{TestV}}({\textsf{X}}). \end{aligned}$$

In particular, if E is a set of locally finite perimeter, we naturally have a unique, up to -a.e. equality, element $\nu _E\in L^0_{\textrm{Cap}}(T{\textsf{X}})$, where we understand by locality.

Definition 26

(Good coordinates) Let $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ be an ${\textrm{RCD}}(K,N)$ space of essential dimension n. Let $E\subseteq {\textsf{X}}$ be a set of locally finite perimeter and let $y\in \mathcal F E$ be given. Then we say that an n-tuple $u=(u^1,\ldots ,u^n)$ of harmonic functions $u^i:B_{r_y}(y)\rightarrow \mathbb {R}$ is a system of good coordinates for E at y provided the following properties are satisfied:

• (i) For any $i,j=1,\ldots ,n$, it holds that

  

  (7)

• (ii) For any $i=1,\ldots ,n$, it holds that

  

  (8)

• (iii) The resulting vector $\nu (y):=(\nu _1(y),\ldots ,\nu _n(y))\in \mathbb {R}^n$ satisfies $|\nu (y)|=1$.

It follows from [17, Proposition 3.6] that good coordinates exist at -a.e. $y\in \mathcal F E$.

Remark 27

Let $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ be an ${\textrm{RCD}}(K,N)$ space of essential dimension n, let $x\in {\textsf{X}}$ and let $u=(u^1,\dots ,u^n)$ be an n-tuple of harmonic functions satisfying

Given a sequence of radii $r_i\searrow 0$ such that

$$\begin{aligned} ({\textsf{X}},r_i^{-1}{\textsf{d}},{\textsf{m}}_x^{r_i},x)\rightarrow (\mathbb {R}^n,{\textsf{d}}_e,\underline{\mathcal {L}}^n,0) \end{aligned}$$

and fixed a realization of such convergence, it follows from the results recalled in [18, Section 1.2.3] (see the references therein, see also [18, (1.22)], consequence of the improved Bochner inequality in [35]) that, up to extracting a not relabeled subsequence, the functions in

$$\begin{aligned} \{r_i^{-1} (u^j-u^j(x))\}_i\qquad \text {for }j=1,\dots ,n \end{aligned}$$

converge locally uniformly to orthogonal coordinate functions $(y_j)$ of $\mathbb {R}^n$. If in addition $E\subseteq {\textsf{X}}$ is a set of locally finite perimeter, $x\in \mathcal {F}E$ and u is a system of good coordinates for E at x, then the blow-up of E at x coincides with $H=\{y\in \mathbb {R}^n\,|\,y\cdot \nu (x)\ge 0\}$, where we are denoting by

the vector given by (8). See [17, Proposition 4.8] for a proof of this last claim. $\square$

Let us now recall the notion of $\delta$-splitting map. We follow the presentation in [18, Definition 3.4], see also [13, Section 2.2.3].

Definition 28

(Splitting map) Let $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ be an ${\textrm{RCD}}(K,N)$ space. Let $y\in {\textsf{X}}$, $k\in \mathbb N$, and $r_y,\delta >0$ be given. Then a map $u=(u_1,\ldots ,u_k):B_{r_y}(y)\rightarrow \mathbb {R}^k$ is a $\delta$-splitting map if the following three properties hold:

• (i) $u_i$ is harmonic, meaning that, for every $i=1,\dots ,k$, $u_i\in D(\Delta ,B_{r_y}(y))$ and $\Delta u_i=0$; and moreover $u_i$ is $C_{K,N}$-Lipschitz for every $i=1,\dots ,k$,

• (ii) for every $i=1,\ldots ,k$,

• (iii) 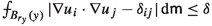for every $i,j=1,\ldots ,k$.

For what follows, recall the definition of good splitting map, compare with [13, Definition 2.29] and Definition 1.

Remark 29

Let u be a good splitting map on $D\subseteq B_{r_y}(y)$. Due to [17, Remark 2.10], for every $x\in B_{r_y}(y)$ there exists a Borel matrix $M(x)=\{M(x)_{i,j}\}_{i,j=1,\dots ,n}\in \mathbb {R}^{n\times n}$ satisfying

(9)

Then, from item iii) of Definition 28 and since $\eta <n^{-1}$, we have that for every $x\in D$

$$\begin{aligned} |M(x)_{i,j}-\delta _{ij}|\le \eta < n^{-1}. \end{aligned}$$

(10)

Hence, by applying the Gram–Schmidt orthogonalization algorithm to $\{\nabla u^i(x)\}_{i=1,\dots ,n}$ for every $x\in D$, we find a matrix-valued function $A\in L^{\infty }(D;\mathbb R^{n\times n})$ such that, for every $x\in D$,

$$\begin{aligned} A(x) M(x)A(x)^T=\mathrm Id.\ \end{aligned}$$

(11)

The membership $A\in L^{\infty }(D;\mathbb R^{n\times n})$ is due to (10). $\square$

Let $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ be an ${\textrm{RCD}}(K,N)$ space of essential dimension n, and let $f\in {\textrm{BV}}({\textsf{X}})$. Recall that [11, Theorem 5.1] and its proof (compare with [9, Proposition 4.2] and [13, Proposition 2.13]) yield that $\mathcal {G}_f$ has locally finite perimeter and

(12)

Also, by [13, Theorem 3.4], it holds that

(13)

so that, taking into account Lemma 14 and Theorem 18, we see that

(14)

Before going on, we stress a couple of remarks.

Remark 30

Taking into account Definition 2, it holds that $\nu _{\mathcal {G}_f}^u$ is well defined at $(x,\bar{f}(x))$ for $|\textrm{D}f|$-a.e. $x\in D{\setminus } J_f$ and ${\textsf{m}}$-a.e. $x\in D{\setminus } J_f$, as a consequence of (12) and (14), respectively, together with Lemma 14. $\square$

Remark 31

We isolate here an argument which will frequently appear during the paper, and that is essentially contained in [17, Proposition 3.6]. Let $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ be an ${\textrm{RCD}}(K,N)$ space of essential dimension n, and let $E\subseteq X$ be a set of locally finite perimeter.

Let $u: B_{2r_y}(y)\rightarrow \mathbb R^n$ be a good splitting map on $D\subseteq B_{r_y}(y)$. We claim that, for -almost every point $x\in \mathcal {F}E\cap D$, the function $v:=A(x)u:B_{2r_{y}}(y)\rightarrow \mathbb R^n$ is a system of good coordinates for E at x, where the matrix-valued function A is defined as in (11). In addition, if $\nu _E^u:B_{2r_y}(y)\rightarrow \mathbb R^n$ is the -measurable map

$$\begin{aligned} \nu _E^u(x):=((\nu _E\cdot \nabla u^1)(x),\ldots ,(\nu _E\cdot \nabla u^n)(x)), \end{aligned}$$

then the normal $\nu _E^v$ associated with the system of good coordinates v for E at x (see item ii) of Definition 26) is

$$\begin{aligned} \nu _E^v=A(x)\nu _E^u. \end{aligned}$$

Indeed, let us fix $x\in \mathcal {F}E\cap D$ that is, for every $i,j=1,\dots ,n$, a Lebesgue point of all the functions $\nabla u^i \cdot \nabla u^j$, $\nu _E\cdot A\nabla u^i$, $\nu _E\cdot \nabla u^i$, and A, with respect to the asymptotically doubling measure . Let us denote $v^i:=A(x) u^i$. We aim at showing that $(v^i)_{i=1,\dots ,n}:B_{2r_y}(y)\rightarrow \mathbb R^n$ are good coordinates for E at x.

First, $v^i$ are harmonic. Second, by the very definition of A and M, see (11) and (9), and by the fact that x is a Lebesgue point of $\nabla u^i \cdot \nabla u^j$ with respect to , we have the two equalities in (7) at x with $v^i$. Third, by denoting $a_i(x)$ the Lebesgue value of $\nu _E\cdot \nabla (A u)^i$ at x with respect to , and since by definition $\nabla (A u^i)\cdot \nabla (A u^j)=\delta _{ij}$ everywhere on D, we conclude that $\nu _E=\sum _{i=1}^n a_i\nabla (A u^i)$ holds -almost everywhere on D. Now, since $|\nu _E|=1$ in $L^2_E(T{\textsf{X}})$, and since $\nabla (A u^i)$ are pointwise orthonormal on D, we conclude that the vector $(a_i)_{i=1,\dots ,n}$ has norm 1. Hence, by finally taking into account that x is also a Lebesgue point of $\nu _E\cdot \nabla u^i$ and A with respect to , (8) and item ii) in Definition 26 hold. How the normal transforms is clear from (8). Thus, the claim is proved. $\square$

3 Main results

In this section, we are going to prove the main results of this note, i.e., Theorem 4 and Theorem 5. First, we start with some auxiliary results.

3.1 Auxiliary results

In this section, we fix an ${\textrm{RCD}}(K,N)$ space of essential dimension n $({\textsf{X}},{\textsf{d}},{\textsf{m}})$ and $f\in {\textrm{BV}}({\textsf{X}})$. We fix also u, a good splitting map on $D\subseteq B_{r_x}(x)$ for some $x\in {\textsf{X}}$ and $r_x>0$.

The following proposition can be proved exactly as [13, Proposition 3.7]. Recall the definition of the reduced boundary in use in this note, see Definition 21.

Proposition 32

In the above setting, there exists a Borel set $D_f\subseteq D$ satisfying the following properties:

• (i) $|\textrm{D}f|^c(D{\setminus } D_f)=0$ and ${\textsf{m}}(D{\setminus } D_f)=0$.

• (ii) .

• (iii) $D_f\subseteq \mathcal R_n^*({\textsf{X}}){\setminus } J_f$ and $\mathcal F\mathcal {G}_f\cap (D_f\times \mathbb {R}) =(\textrm{id}_{\textsf{X}},\bar{f})(D_f)$.

• (iv) Given any $x\in D_f$, for $A(x)\in \mathbb {R}^{n\times n}$ as in (11), we have that $(A(x) u,\pi ^2)$ is a system of good coordinates for $\mathcal {G}_f$ at $(x,\bar{f}(x))$.

• (v) If $v=(v^1,\ldots ,v^{n+1}):B_{r_x}(x,\bar{f}(x))\rightarrow \mathbb {R}^{n+1}$ is a system of good coordinates for $\mathcal {G}_f$ at $(x,\bar{f}(x))$ for some $x\in D_f$ and the coordinates $(x_i)$ on the (Euclidean) tangent space to ${\textsf{X}}\times \mathbb {R}$ at $(x,\bar{f}(x))$ are chosen so that the maps $(v^i)$ converge to $(x_i):\mathbb {R}^{n+1}\rightarrow \mathbb {R}^{n+1}$ (when properly rescaled, see Remark 27), then the blow-up of $\mathcal {G}_f$ at $(x,\bar{f}(x))$ can be written as

  $$\begin{aligned} H:=\big \{y\in \mathbb {R}^{n+1}\;\big |\;y\cdot \nu (x,\bar{f}(x))\ge 0\big \}, \end{aligned}$$

  where the unit vector $\nu (x,\bar{f}(x)):=\big (\nu _1(x,\bar{f}(x)),\ldots ,\nu _{n+1}(x,\bar{f}(x))\big )$ is given by (8) for v.

Proof

The proof follows along the lines of [13, Proposition 3.7]. We need some auxiliary sets:

• We define $\mathcal D$ as the set of all those points $(x,t)\in (D\times \mathbb {R})\cap \mathcal {F}\mathcal {G}_f$ of density 1 with respect to . The Lebesgue differentiation theorem ensures that .

• We define $\mathcal A$ as the set of all $(x,t)\in {\textsf{X}}\times \mathbb {R}$ where item v) of the statement holds. Notice that thanks to the final part of Remark 27.

• We define $\mathcal T$ as the set of all those $(x,t)\in (D\times \mathbb {R})\cap \mathcal {F}\mathcal {G}_f$ such that $(A(x)u,\pi ^2)$ is a system of good coordinates for $\mathcal {G}_f$ at (x, t). Notice that by Remark 31.

Let us now define the set $D_f\subseteq D$ as

$$\begin{aligned} D_f:=D\cap {\textsf{X}}_f\cap (\mathcal R_n^*({\textsf{X}})\setminus J_f)\cap \pi ^1(\mathcal {F}\mathcal {G}_f\cap \mathcal D\cap \mathcal A\cap \mathcal T). \end{aligned}$$

By exploiting (12) and (14), one can then prove that $D_f$ fulfills all the required properties. $\square$

Even though by definition $D_f\cap J_f=\varnothing$, we sometimes consider $D_f\setminus J_f$ to remind this fact. In our proofs, we will implicitly take as a representative of $\nu _{\mathcal {G}_f}^u$ (see Definition 2) its Lebesgue representative with respect to the asymptotically doubling measure . This will not make any difference in the end, due to the nature of the statements, but will allow us to exploit item v) of Proposition 32.

Lemma 33

The set $C_f$ (see Definition 12) such that and ${\textsf{m}}(C_f)=0$ can be taken as follows:

$$\begin{aligned} C_f\mathrel {\mathop :}=\left\{ x\in {D_f}\setminus J_f: \big (\nu _{\mathcal {G}_f}^u(x,\bar{f}(x))\big )_{n+1}=0\right\} .\end{aligned}$$

(15)

Proof

In this proof, we let $C_f$ be the set defined as in the right-hand side of (15). Let us first prove ${\textsf{m}}(C_f)=0$. By Theorem 18, we only have to show that . Then, by [12, Theorem 2.4.3] it is enough to show that

$$\begin{aligned} \liminf _{r\searrow 0} \frac{|\textrm{D}f|(B_r(x))}{r^n}=+\infty \end{aligned}$$

for $\mathcal {H}^n$-a.e. $x\in C_f$. Therefore, by (12), and by taking into account that $D_f\subseteq \mathcal {R}_n^*$, it is enough to show that

(16)

for $\mathcal {H}^n$-a.e. $x\in C_f$. The conclusion then follows from a blow-up argument. Now we follow the first part of the proof of [13, Theorem 3.8], and we sketch the argument. Take $x\in C_f$, let $p\mathrel {\mathop :}=(x,\bar{f}(x))$, and take a sequence $\{r_i\}_i\subseteq (0,\infty )$, $r_i\searrow 0$. We use repeatedly the membership $p\in \mathcal {F}\mathcal {G}_f$ and the implied properties as in Remark 22. We have that, up to subsequences,

$$\begin{aligned} ({\textsf{X}},r_i^{-1}{\textsf{d}},{\textsf{m}}_x^{r_i},x)\rightarrow (\mathbb {R}^n,{\textsf{d}}_e,\underline{\mathcal {L}}^n,0),\quad \text { in the pmGH topology.} \end{aligned}$$

Let $({\textsf{Z}},{\textsf{d}}_{\textsf{Z}})$ be a realization of such convergence. Then $({\textsf{Z}}\times \mathbb {R},{\textsf{d}}_{\textsf{Z}}\times {\textsf{d}}_e)$ is a realization of

$$\begin{aligned} \big ({\textsf{X}}\times \mathbb {R},r_i^{-1}({\textsf{d}}\times {\textsf{d}}_e),({\textsf{m}}\otimes \mathcal L^1)_p^{r_i},p,\mathcal {G}_f\big )\rightarrow (\mathbb {R}^{n+1},{\textsf{d}}_e,\underline{\mathcal {L}}^{n+1},0,H), \end{aligned}$$

(17)

where $H\subseteq \mathbb {R}^{n+1}$ is a half-space, and where we took a non-relabeled subsequence. We also know, as $p\in \mathcal {F}\mathcal {G}_f$, that the rescaled perimeters weakly converge, up to some dimensional constant, to in duality with $C_\textrm{bs}({\textsf{Z}}\times \mathbb {R})$. Moreover, by the definition of $C_f$ together with the item v) of Proposition 32, and the fact that the last coordinates of $\nu _{\mathcal {G}_f}^u$ and $\nu _{\mathcal {G}_f}^v$ are equal— where $v=(A(x)u,\pi ^2)$—we have that H can be written as $H'\times \mathbb {R}$, for some $H'\subseteq \mathbb {R}^n$ half-space. Then the claim follows from weak convergence of measures, taking into account also item iii) of Remark 22.

We give the details of the last conclusion, i.e., how the weak convergence of measures yields (16). Denote by $|\textrm{D}^i\chi _{\mathcal {G}_f}|$ the perimeter measure associated with $\mathcal {G}_f$ in the rescaled space as in (17). By weak convergence of measures (i.e., item ii) of Remark 22)), we have that $|\textrm{D}^i\chi _{\mathcal {G}_f}|$ weakly converges to $|\textrm{D}\chi _{H}|$. We can compute

$$\begin{aligned} \frac{|\textrm{D}\chi _{\mathcal {G}_f}|(B_{r_i}(x)\times \mathbb {R})}{{r_i}^n}=\frac{({\textsf{m}}\otimes \mathcal {L}^1)(B_{r_i}(p))}{r_i^{n+1}}|\textrm{D}^i\chi _{\mathcal {G}_f}|( B_{1}(x)\times \mathbb {R}), \end{aligned}$$

so that, by weak convergence,

$$\begin{aligned} \liminf _i\frac{|\textrm{D}\chi _{\mathcal {G}_f}|(B_{r_i}(x)\times \mathbb {R})}{{r_i}^n}&\ge \omega _{n+1}\Theta _n({\textsf{m}},x)|\textrm{D}\chi _H|(B^{\mathbb {R}^n}_1(0)\times \mathbb {R})=+\infty , \end{aligned}$$

where the last equality follows from $H=H'\times \mathbb {R}$. Then, being the sequence $\{r_i\}_i$ arbitrary, (16) follows.

Finally, as a direct consequence of [13, Theorem 3.8], and item i) of Proposition 32, we have that $|\textrm{D}f|^c$ is concentrated on ${C}_f$, so that . $\square$

Lemma 34

It holds that

$$\begin{aligned} \big (\nu _{\mathcal {G}_f}^{ u}(x,\bar{f}(x))\big )_{1,\dots ,n}=\sqrt{1-\Big (\nu _{\mathcal {G}_f}^u(x,\bar{f}(x))\Big )_{n+1}^2}\,\nu _f^{u}(x),\quad \text { for }|\textrm{D}f|\text {-a.e. }x\in D\setminus J_f \end{aligned}$$

and

$$\begin{aligned} \big (\nu _{\mathcal {G}_f}^{ u}(x,\bar{f}(x))\big )_{n+1}\le 0,\quad \text { for }|\textrm{D}f|\text {-a.e. }x\in D\setminus J_f. \end{aligned}$$

Proof

The proof follows the lines of the proof of [13, Lemma 3.9], but the conclusion is slightly different. We sketch here the argument.

For a.e. $t\in \mathbb {R}$, we have that $E_t\mathrel {\mathop :}=\{f>t\}$ is a set of finite perimeter (by Theorem 9) and that $\nu _f^u(x)=\nu _{E_t}^u(x)$ for $\mathcal {H}^{n-1}$-a.e. $x\in D\cap \mathcal {F}E_t$ (by (6) and [15, Lemma 4.27]). Recalling also Proposition 32, proving the statement amounts to showing for $\mathcal {H}^{n-1}$-a.e. $x\in D_f\cap \mathcal {F}E_t$ that

$$\begin{aligned} \big (\nu _{\mathcal {G}_f}^{u}(x,\bar{f}(x))\big )_{1,\dots ,n}=\sqrt{1-\Big (\nu _{\mathcal {G}_f}^u(x,\bar{f}(x))\Big )_{n+1}^2}\,\nu _{E_t}^{u}(x),\qquad \big (\nu _{\mathcal {G}_f}^{ u}(x,\bar{f}(x))\big )_{n+1}\le 0.\nonumber \\ \end{aligned}$$

(18)

In view of Remark 31 and Proposition 32 iv), for $\mathcal {H}^{n-1}$-a.e. $x\in D_f\cap \mathcal {F}E_t$ the following hold:

• A(x)u is a system of good coordinates for $E_t$ at x. Moreover, the unit vector $\nu =\nu (x)\in \mathbb {R}^n$ associated with A(x)u and $E_t$ as in (8) satisfies $\nu =A(x)\nu _{E_t}^u(x)$.

• $(A(x)u,\pi ^2)$ is a system of good coordinates for $\mathcal {G}_f$ at $p:=(x,\bar{f}(x))$. Moreover, the unit vector $\mu =\mu (p)\in \mathbb {R}^{n+1}$ associated with $(A(x)u,\pi ^2)$ and $\mathcal {G}_f$ as in (8) satisfies

  $$\begin{aligned} \mu =\Big (A(x)\big (\nu _{\mathcal {G}_f}^u(p)\big )_{1,\dots ,n},\big (\nu _{\mathcal {G}_f}^u(p)\big )_{n+1}\Big ). \end{aligned}$$

  (19)

Now choose coordinates $(y_i)$ on $\mathbb {R}^n$ such that the maps $(A(x)u^i)$ converge to $(y_i)$ (when properly rescaled, see Remark 27). We then deduce from the last part of Remark 27 and from Proposition 32 v) that the blow-up of $E_t$ at x and of $\mathcal {G}_f$ at $(x,\bar{f}(x))$ can be written as $H':=\{y\in \mathbb {R}^n\,|\,y\cdot \nu \ge 0\}$ and $H:=\{(y,s)\in \mathbb {R}^n\times \mathbb {R}\,|\,(y,s)\cdot \mu \ge 0\}$, respectively. Arguing exactly as in the proof of [13, Lemma 3.9], we thus obtain that

$$\begin{aligned} H'\times (-\infty ,0)\subseteq H\cap \{(y,s)\in \mathbb {R}^n\times \mathbb {R}\,|\,s<0\}. \end{aligned}$$

This forces the inequality $\mu _{n+1}\le 0$ and the identity $(\mu _1,\ldots ,\mu _n)=\alpha \nu$ for some $\alpha \in [0,1]$. Given that $\mu _{n+1}=(\nu _{\mathcal {G}_f}^u(p))_{n+1}$ by (19), the second formula in (18) is proved. Moreover, we have that

so that $\alpha =\sqrt{1-(\nu _{\mathcal {G}_f}^u(p))^2_{n+1}}$. Therefore, since the matrix A(x) is invertible, we conclude that also the first formula in (18) holds. $\square$

Lemma 35

It holds that

Proof

Recalling Proposition 32, we can reduce ourselves to show the conclusion only for ${\textsf{m}}$-a.e. $x\in D_f{\setminus } {( C_f\cup J_f)}$.

By Lemma 33, we know that

$$\begin{aligned} (\nu _{\mathcal {G}_f}^{{ u}})_{n+1}(x,\bar{f}(x))\ne 0,\quad \text { for } {\textsf{m}}{\mathrm{-a.e. }}\ x\in D_f\setminus {(C_f\cup J_f)}. \end{aligned}$$

(20)

We prove now that in fact

$$\begin{aligned} (\nu _{\mathcal {G}_f}^{{ u}})_{n+1}(x,\bar{f}(x))< 0,\quad \text { for } {\textsf{m}}\text { -a.e. } x\in D_f\setminus {( C_f\cup J_f)}. \end{aligned}$$

(21)

Fix $x\in D_f\setminus C_f$ satisfying (20), let $p\mathrel {\mathop :}=(x,\bar{f}(x))$ and take $\{r_i\}_i\subseteq (0,\infty )$ with $r_i\searrow 0$. Up to subsequences, we have that

$$\begin{aligned} \big ({\textsf{X}}\times \mathbb {R},r_i^{-1}({\textsf{d}}\times {\textsf{d}}_e),({\textsf{m}}\otimes \mathcal L^1)_p^{r_i},p,\mathcal {G}_f\big )\rightarrow (\mathbb {R}^{n+1},{\textsf{d}}_e,\underline{\mathcal {L}}^{n+1},0,H), \end{aligned}$$

in a realization $({\textsf{Z}}\times \mathbb {R},{\textsf{d}}_{{\textsf{Z}}\times \mathbb {R}})$, for some half-space H. Arguing as in the proof of Lemma 34, it holds that $H=\{z\in \mathbb {R}^{n+1}:z\,\cdot \,\mu \ge 0\}$, for

$$\begin{aligned} \mu =\Big (A(x)\big (\nu _{\mathcal {G}_f}^u(x,\bar{f}(x))\big )_{1,\dots ,n},\big (\nu _{\mathcal {G}_f}^u(x,\bar{f}(x))\big )_{n+1}\Big ). \end{aligned}$$

Let $\pm B_\epsilon \mathrel {\mathop :}=B_\epsilon ^{\textsf{Z}}(0_{\mathbb {R}^n})\times B_\epsilon ^{\mathbb {R}}(\pm 1_\mathbb {R})\subseteq {\textsf{Z}}\times \mathbb {R}$. Take $\epsilon >0$ small enough so that $(\pm B_{ \epsilon })\cap \partial H\ne \varnothing$. Such $\epsilon$ exists by (20). Now we compute, by convergence in $L^1_\textrm{loc}$,

$$\begin{aligned}&\underline{\mathcal {L}}^{n+1}(H\cap (-B_\epsilon ))-\underline{\mathcal {L}}^{n+1}(H\cap B_\epsilon )\\ {}&\quad =\lim _{i\rightarrow +\infty } \big (({\textsf{m}}\otimes \mathcal L^1)_p^{r_i}(\mathcal {G}_f\cap (-B_\epsilon ))-({\textsf{m}}\otimes \mathcal L^1)_p^{r_i}(\mathcal {G}_f\cap B_\epsilon )\big ). \end{aligned}$$

By Fubini’s theorem,

$$\begin{aligned}&({\textsf{m}}\otimes \mathcal L^1)_p^{r_i}(\mathcal {G}_f\cap (-B_\epsilon ))-({\textsf{m}}\otimes \mathcal L^1)_p^{r_i}(\mathcal {G}_f\cap B_\epsilon )\\ {}&\qquad =\frac{1}{({\textsf{m}}\otimes \mathcal L^1)(B_{r_i}(p))}\int _{B_\epsilon ^{\textsf{Z}}(0_{\mathbb {R}^n})} \bigg (\mathcal H^1\big ((\{x\}\times (-r_i-\epsilon ,-r_i+\epsilon ))\cap \mathcal {G}_f\big )\\ {}&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad -\mathcal H^1\big ((\{x\}\times (r_i-\epsilon ,r_i+\epsilon ))\cap \mathcal {G}_f\big ) \bigg )\textrm{d}{\textsf{m}}(x)\ge 0, \end{aligned}$$

where at the second member we have the image measure of ${\textsf{m}}$ corresponding to the $i^\textrm{th}$ rescaling. Therefore, $\underline{\mathcal {L}}^{n+1}(H\cap (-B_\epsilon ))-\underline{\mathcal {L}}^{n+1}(H\cap B_\epsilon )\ge 0$, so that (21) follows, taking into account also (20) and the defining expression for H.

Fix a ball ${\bar{B}}\subseteq {\textsf{X}}$. Define $C_\gamma (x,t)\mathrel {\mathop :}=\big \{(y,s)\in {\textsf{X}}\times \mathbb {R}: \gamma \,{\textsf{d}}(y,x)\ge |s-t|\big \}$ for every $\gamma >0$. We claim that for any $\epsilon >0$ there exist $\gamma =\gamma (\epsilon )>0$, $r_0=r_0(\epsilon )>0$ and $F_\epsilon \subseteq \mathcal {F}\mathcal {G}_f$ Borel such that:

• i) .

• ii) $F_\epsilon \cap (B_r(x)\times \mathbb {R})\subseteq C_{2\gamma }(x,{\bar{f}}(x))$ for every $(x,{\bar{f}}(x))\in F_\epsilon$ and $r<r_0$.

The proof of this claim follows along the lines of [13, Theorem 3.8]. First, we define ${\tilde{F}}^k_\epsilon$ as

$$\begin{aligned} {\tilde{F}}^k_\epsilon :=\big \{(x,{\bar{f}}(x))\;\big |\;x\in (\bar{B}\cap D_f)\setminus C_f,\,(\nu _{\mathcal {G}_f}^u)_{n+1}(x,{\bar{f}}(x))\le -1/k\big \}\subseteq \mathcal {F}\mathcal {G}_f,\quad \text { for every }k\in \mathbb {N}. \end{aligned}$$

Since $(({\bar{B}}\cap D_f){\setminus } C_f)\times \mathbb {R}=\bigcup _{k\in \mathbb {N}}{\tilde{F}}^k_\epsilon$ up to -null sets by (21), we can take $k_0\in \mathbb {N}$ large enough so that $\tilde{F}_\epsilon :={\tilde{F}}^{k_0}_\epsilon$ satisfies . Denote $\alpha :=1/k_0$. Up to discarding a -null set from ${\tilde{F}}_\epsilon$, we can also assume that for all $p\in {\tilde{F}}_\epsilon$; it follows from the Lebesgue differentiation theorem applied to , the second formula in (5) and $\Theta _n({\textsf{m}},x)=\Theta _{n+1}({\textsf{m}}\otimes \mathcal L^1,(x,\bar{f}(x)))$. Next we show that, denoting $\beta :=\sqrt{1-\alpha ^2}$,

(22)

The verification of (22) is a via a blow-up argument: if the half-space $H\subseteq \mathbb {R}^{n+1}$ is the blow-up of $\mathcal {G}_f$ at $p\in {\tilde{F}}_\epsilon$ in some realization, then Proposition 32 v) and $(\nu _{\mathcal {G}_f}^u)_{n+1}(p)\le -\alpha$ imply that $\partial H\cap B_1(0)\subseteq B_1(0)\times B_\beta (0)$, whence (22) follows. Denote $\gamma :=\sqrt{\frac{1+\beta }{1-\beta }}>1$. We now claim that

(23)

Indeed, for any $\delta >0$ we know from (22) that for some ${\bar{r}}>0$. Letting $\theta :=\beta \sqrt{(\gamma ^2+1)/\gamma ^2}<1$, we have that

$$\begin{aligned} B_{{\bar{r}}}(p)\setminus C_\gamma (p)\subseteq \bigcup _{j\in \mathbb {N}}B_{\theta ^j\bar{r}}(p)\setminus \big ({\textsf{X}}\times B_{\beta \theta ^j{\bar{r}}}(\bar{f}(x))\big ),\quad \text { for every }p=(x,{\bar{f}}(x))\in \tilde{F}_\epsilon , \end{aligned}$$

whence it follows, letting $\sigma :=\sum _{j\in \mathbb {N}}\theta ^{jn}<+\infty$, that for every $p=(x,{\bar{f}}(x))\in {\tilde{F}}_\epsilon$ it holds that

This proves (23). Now choose $\tilde{\delta }>0$ with $\tilde{\delta }<(1-\tilde{\delta })\frac{\eta ^n}{(1+\eta )^n}$, where $\eta :=\sin (\arctan (2\gamma )-\arctan (\gamma ))$. Applying Lusin’s theorem and Egorov’s theorem, we obtain a compact set $F_\epsilon \subseteq {\tilde{F}}_\epsilon$ and $r_1\in (0,1)$ such that $|$ (whence i) follows), ${\bar{f}}$ is (uniformly) continuous on $\pi ^1(F_\epsilon )$ and

(24)

for every $p\in F_\epsilon$ and $r<2r_1$; here, we exploited and (23). Next, we aim to show

$$\begin{aligned} F_\epsilon \cap B_{r_1}(p)\subseteq C_{2\gamma }(p),\quad \text { for every }p=(x,{\bar{f}}(x))\in F_\epsilon . \end{aligned}$$

(25)

To prove it, we argue by contradiction: Suppose there exists $q=(y,{\bar{f}}(y))\in (F_\epsilon \cap B_{r_1}(p)){\setminus } C_{2\gamma }(p)$. Then $B_{\tilde{\textsf{d}}(p,q)\eta }(q)\subseteq B_{\tilde{\textsf{d}}(p,q)(1+\eta )}(p){\setminus } C_\gamma (p)$, where we denote $\tilde{\textsf{d}}(p,q):=\big ({\textsf{d}}(x,y)^2+|{\bar{f}}(x)-\bar{f}(y)|^2\big )^{1/2}$. Combining this inclusion with (24), we deduce that $\tilde{\delta }\ge (1-\tilde{\delta })\frac{\eta ^n}{(1+\eta )^n}$, leading to a contradiction with our choice of $\tilde{\delta }$. Hence, (25) is proved. The uniform continuity of ${\bar{f}}|_{\pi ^1(F_\epsilon )}$ ensures that there exists $r_0\in (0,r_1/\sqrt{2})$ such that $|{\bar{f}}(y)-\bar{f}(x)|<r_1/\sqrt{2}$ for all $x\in \pi ^1(F_\epsilon )$ and $y\in \pi ^1(F_\epsilon )\cap B_{r_0}(x)$. By (25), we get $F_\epsilon \cap (B_{r_0}(x)\times \mathbb {R})\subseteq F_\epsilon \cap B_{r_1}(p)\subseteq C_{2\gamma }(p)$ for all $p=(x,{\bar{f}}(x))\in F_\epsilon$, proving ii).

We are now in a position to conclude the proof. We can and will assume that ${F}_\epsilon$ is made of points of density 1 with respect to . This will ensure that for $p\in {F}_\epsilon$, the rescaled measures and around p have the same weak limit. Let ${\hat{F}}_\epsilon \mathrel {\mathop :}=\pi ^1 (F_\epsilon )$. By a blow-up argument (taking into account Remark 22), for ${\textsf{m}}$-a.e. $x\in \big (( {\bar{B}}\cap D_f){\setminus } C_f\big )\cap {\hat{F}}_\epsilon$,

Here we exploited ii) and $\Theta _n({\textsf{m}},x)=\Theta _{n+1}({\textsf{m}}\otimes \mathcal L^1,(x,t))$. Notice that the left-hand side reads as

and, by (21), the right-hand side reads as

$$\begin{aligned} \omega _n\Theta _n({\textsf{m}},x)\big (-\nu _{\mathcal {G}_f}^{u}(x,\bar{f}(x))\big )_{n+1}^{-1}. \end{aligned}$$

Now we conclude recalling (14) and the arbitrariness of ${\bar{B}}$. $\square$

The first part of the following lemma can be proved also exploiting [11, Theorem 5.1]. Nevertheless, we give a different proof, tailored to this setting and more in the spirit of this paper.

Lemma 36

(Area formula) It holds that

Proof

Recall that by Lemma 35, for ${\textsf{m}}$-a.e. $x\in D_f{\setminus } (J_f\cup C_f)$ it holds that $\big (\nu _{\mathcal {G}_f}^u(x,\bar{f}(x))\big )_{n+1}<0$.

We start from the case $f\in {\textrm{BV}}({\textsf{X}})\cap {\textrm{LIP}}({\textsf{X}})$. First, recall [7, Proposition 6.3] and [21], which imply that $|\textrm{D}f|=(\textrm{lip}f){\textsf{m}}$. Also, by Proposition 32, we reduce ourselves to show the claim for ${\textsf{m}}$-a.e. $x\in D_f{\setminus } ( C_f\cup J_f)$. Take then $x\in D_f{\setminus } ( C_f\cup J_f)$ such that $p\mathrel {\mathop :}=(x, f(x))$ is a Lebesgue point for $\nu _{\mathcal {G}_f}^u$ with respect to . This choice can be made ${\textsf{m}}$-a.e. by (14).

We take $\{x_i\}\subseteq {\textsf{X}}$ with $x_i\rightarrow x$ and

$$\begin{aligned} \lim _{i\rightarrow +\infty } \frac{f(x_i)-f(x)}{{\textsf{d}}(x_i,x)}=\pm \textrm{lip}f(x). \end{aligned}$$

Set $r_i\mathrel {\mathop :}={\textsf{d}}(x,x_i)$, and notice that we can, and will, assume that $r_i\searrow 0$. Therefore, up to subsequences, we have that

$$\begin{aligned} \big ({\textsf{X}}\times \mathbb {R},r_i^{-1}({\textsf{d}}\times {\textsf{d}}_e),({\textsf{m}}\otimes \mathcal L^1)_p^{r_i},p,\mathcal {G}_f\big )\rightarrow (\mathbb {R}^{n+1},{\textsf{d}}_e,\underline{\mathcal {L}}^{n+1},0,H), \end{aligned}$$

where H is the half-space

$$\begin{aligned} H\mathrel {\mathop :}=\big \{y\in \mathbb {R}^{n+1}:y\,\cdot \,\nu _{\mathcal {G}_f}^{{v}}(p)\ge 0\big \}, \end{aligned}$$

for $v\mathrel {\mathop :}=(A(x)u,\pi ^2)$, see Proposition 32 and Remark 31. We assume that this convergence is realized in a proper metric space $({\textsf{Z}}\times \mathbb {R},{\textsf{d}}_{{\textsf{Z}}\times \mathbb {R}})$ and, up to taking a non-relabeled subsequence, we assume that the rescaled perimeters weakly converge to in duality with $C_\textrm{bs}({\textsf{Z}}\times \mathbb {R})$. Therefore, identifying $(x_i,f(x_i))$ with the corresponding point with respect to the $i^\textrm{th}$ isometric embedding, we have that, up to a non-relabeled subsequence, $(x_i,f(x_i))\rightarrow {\bar{q}}\mathrel {\mathop :}=({\bar{z}}, \pm \textrm{lip}f(x))\in \mathbb {R}^{n+1}$ with respect to ${\textsf{d}}_{{\textsf{Z}}\times \mathbb {R}}$, where ${\textsf{d}}_e({\bar{z}},0)=1$. Therefore, if we show that $\bar{q}\in \partial H$, it will follow that

$$\begin{aligned} \big (-\nu _{\mathcal {G}_f}^{ u}(x,{\bar{f}}(x)\big )_{n+1}^{-1}\ge \sqrt{\textrm{lip}f(x)^2+1}. \end{aligned}$$

(26)

Take ${\bar{q}}'=({\bar{z}},t)$ such that $\bar{q}'\in \partial H$. The claim will be proved by showing that ${\bar{q}}={\bar{q}}'$. By weak convergence of measures and Lemma 14, we find a sequence of points $\{(x_i',f(x_i'))\}_i$ with $(x_i',f(x_i'))\rightarrow {\bar{q}}'$ in ${\textsf{Z}}\times \mathbb {R}$, where we identified $(x_i',f(x_i'))$ with the corresponding point with respect to the $i^\textrm{th}$ isometric embedding. Now we compute, if L is the global Lipschitz constant of f,

$$\begin{aligned} |\pm \textrm{lip}f(x)-t|&=\lim _{i\rightarrow +\infty }\frac{ |f(x_i)-f(x_i')|}{r_i}\le \limsup _{i\rightarrow +\infty }L\frac{{\textsf{d}}(x_i,x_i')}{r_i}=\limsup _{i\rightarrow +\infty }L {\textsf{d}}_{\textsf{Z}}(x_i,x_i')\\ {}&\le \limsup _{i\rightarrow +\infty } L({\textsf{d}}_{\textsf{Z}}(x_i,\bar{z})+{\textsf{d}}_{\textsf{Z}}(x_i',{\bar{z}}))=0. \end{aligned}$$

Now we show the reverse inequality in (26). Take $\bar{q}\mathrel {\mathop :}=({\bar{z}},t)\in \partial H$ with ${\textsf{d}}_e({\bar{z}},0)=1$. As before, we find $(x_i,f(x_i))\rightarrow {\bar{q}}$ in ${\textsf{Z}}\times \mathbb {R}$. But then

$$\begin{aligned} |t|&= \lim _{i\rightarrow +\infty }\frac{ |f(x_i)-f(x)|}{r_i}=\lim _{i\rightarrow +\infty }\frac{ |f(x_i)-f(x)|}{{\textsf{d}}(x_i,x)}\frac{{\textsf{d}}(x_i,x)}{r_i}\\ {}&\le \limsup _{i\rightarrow +\infty } \frac{ |f(x_i)-f(x)|}{{\textsf{d}}(x_i,x)}\limsup _{i\rightarrow +\infty } {\textsf{d}}_{{\textsf{Z}}}(x_i,x)\le \textrm{lip}f(x){\textsf{d}}_e({\bar{z}},0)=\textrm{lip}f(x). \end{aligned}$$

This easily implies, by the arbitrariness of ${\bar{q}}$, that

$$\begin{aligned} \big (-\nu _{\mathcal {G}_f}^{ u}(x,{\bar{f}}(x))\big )_{n+1}^{-1}\le \sqrt{\textrm{lip}f(x)^2+1}. \end{aligned}$$

Now we pass to the general case. Take $\epsilon >0$ and, by [37, Proposition 4.3], take $h\in {\textrm{BV}}({\textsf{X}})\cap {\textrm{LIP}}({\textsf{X}})$ with ${\textsf{m}}(\{h\ne f\})<\epsilon$. Recall Proposition 32 and call $D_\epsilon \mathrel {\mathop :}=(D_f\cap D_h\cap \{h=f\}){\setminus } C_f$. It will be enough to prove the claim for ${\textsf{m}}$-a.e. $x\in D_\epsilon$. Notice that by [37, Proposition 3.7], $|\textrm{D}(f-h)|(D_\epsilon )=0$, in particular, $g_f=\textrm{lip}h\ {\textsf{m}}$-a.e. on $D_\epsilon$.

Now notice that for ${\textsf{m}}$-a.e. $x\in D_\epsilon$, it holds that ${\textsf{X}}\setminus \partial ^*\mathcal {G}_f$ is of n-density 0 for at (x, h(x)), by (12). Indeed,

whence the conclusion at density 0 points of $\{h\ne f\}$ follows, taking into account $|\textrm{D}h|\ll {\textsf{m}}$ and the fact that ${\textsf{m}}$ is concentrated on $\mathcal R_n^*$. At such points, and , properly rescaled, have the same weak limit. Hence, for ${\textsf{m}}$-a.e. $x\in D_\epsilon$, the blow-ups of $\mathcal {G}_f$ and $\mathcal {G}_h$ coincide at (x, h(x)), by a monotonicity argument (use also the last conclusion of Lemma 34). Now we use item v) of Proposition 32 together with Remark 31 to deduce that $\nu _{\mathcal {G}_h}^u (x,h (x))=\nu _{\mathcal {G}_f}^u (x,{\bar{f}} (x))$ holds for ${\textsf{m}}$-a.e. $x\in D_\epsilon$. Now, the claim follows from what proved in the first part of the proof. $\square$

Lemma 37

It holds that

$$\begin{aligned} \mathcal {H}^n\big (\big \{(x,t):x\in J_f,t=f^\vee (x)\big \}\big )=\mathcal {H}^n\big (\big \{(x,t):x\in J_f,t=f^\wedge (x)\big \}\big )=0. \end{aligned}$$

Proof

We only prove that

$$\begin{aligned} \mathcal {H}^n\big (\{(x,t):x\in J_f,t=f^\vee (x)\}\big )=0, \end{aligned}$$

the other statement being analogous. Also, we can reduce ourselves to prove that

$$\begin{aligned} \mathcal {H}^n\big (\big \{(x,t):x\in K,t=f^\vee (x)\big \}\big )=0, \end{aligned}$$

where $K\subseteq J_f$ is a compact set with $\mathcal {H}^{n-1}(K)<\infty$ and $f^\vee _{|K}:K\rightarrow \mathbb {R}$ is uniformly continuous. Indeed, notice first that $\mathcal {H}^n$ is $\sigma$-finite on

$$\begin{aligned} \{(x,t):x\in J_f,t=f^\vee (x)\}\subseteq J_f\times \mathbb {R}, \end{aligned}$$

as $\mathcal {H}^{n-1}$ is $\sigma$-finite on $J_f$. Then we can reduce ourselves to consider with ${\tilde{K}}\subseteq \{(x,t):x\in J_f,t=f^\vee (x)\}$ compact such that $K\mathrel {\mathop :}=\pi ^1({\tilde{K}})$ satisfies $\mathcal {H}^{n-1}( K)<\infty$. The continuity of $f^\vee _{|K}$ comes from the fact that it is the inverse of the continuous map $\pi ^1$ defined on a compact set into a Hausdorff space.

Now we conclude with a covering argument. Let $\epsilon >0$. Let also $\delta \in (0,\epsilon )$ be such that $|f^{\vee }(x)-f^\vee (y)|<\epsilon$ if $x,y\in K$ are such that ${\textsf{d}}(x,y)<\delta$. Now we find a sequence of balls $\{B_{r_i}(x_i)\}_i$ with $r_i<\delta$, $K\subseteq \bigcup _i B_{r_i}(x_i)$ and $\sum _i \omega _{n-1}{r_i}^{n-1}\le \mathcal {H}^{n-1}(K)+\epsilon$. Now notice that ${\tilde{K}}\cap (B_{r_i}(x_i)\times \mathbb {R})\subseteq B_{r_i}(x_i)\times (f^\vee (x_i)-\epsilon ,f^\vee (x_i)+\epsilon )$. It is easy to show that, as $r_i<\delta$,

$$\begin{aligned} \mathcal {H}^n_{\sqrt{2}\delta }\big ( B_{r_i}(x_i)\times (f^\vee (x_i)-\epsilon ,f^\vee (x_i)+\epsilon )\big )\le \omega _{n}(\sqrt{2}r_i)^n(2\epsilon /r_i+1). \end{aligned}$$

Therefore, if C denotes a constant that may vary from line to line,

$$\begin{aligned} \mathcal {H}_{\sqrt{2}\delta }^{n}({{\tilde{K}}})&\le C\sum _{i\in \mathbb {N}} (\sqrt{2}r_i)^n(\epsilon /(\sqrt{2}r_i)+1)\le C\sum _{i\in \mathbb {N}} \big (\epsilon r_i^{n-1}+ r_i^n\big )\le C(\epsilon +\delta )\sum _{i\in \mathbb {N}} r_i^{n-1}\\&\le C(\epsilon +\delta )(\mathcal {H}^{n-1}(K)+\epsilon ). \end{aligned}$$

The conclusion follows letting $\epsilon \searrow 0$. $\square$

Lemma 38

It holds that

Proof

Notice that, by (12), . Then, by Theorem 9, it suffices to show the claim for $x\in D\cap J_f\cap \mathcal {F}\{f>s\}$, for some $s\in \mathbb {R}$. By Lemma 37, we can use a partitioning argument to reduce ourselves to prove the claim on $K\times I$, where $K\subseteq D\cap J_f\cap \mathcal {F}\{f>s\}$ is compact with $\mathcal {H}^{n-1}(K)<\infty$ and $I=(a,b)\subseteq \mathbb {R}$ is an open interval such that for every $x\in K$, ${\bar{I}}\subseteq (f^\wedge (x),f^\vee (x))$ and $s\in I$. We can also assume, by [15, Lemma 4.27], that $\nu _f^u=\nu _{\{f>s\}}^u$ on K.

By a suitable modification of Remark 31, we see that for -a.e. (x, t) with $x\in D$, it holds that $v\mathrel {\mathop :}=(A(x)u,\pi ^2)$ is a system of good coordinates for $\mathcal {G}_f$ at (x, t). Also, for -a.e. (x, t) the conclusion of [17, Proposition 4.8] holds at (x, t). Also, for -a.e. x the analogous conclusions for $\{f>s\}$ are in place at x. Take a point $p=(x,t)\in \mathcal {F}\mathcal {G}_f$ of density 1 for $K\times I$ with respect to such that x is of density 1 for K with respect to and satisfying the above conclusions. Then for some sequence $\{r_i\}_i$, $r_i\searrow 0$,

$$\begin{aligned} \big ({\textsf{X}}\times \mathbb {R},r_i^{-1}({\textsf{d}}\times {\textsf{d}}_e),({\textsf{m}}\otimes \mathcal L^1)_p^{r_i},p,\mathcal {G}_f\big )\rightarrow (\mathbb {R}^{n+1},{\textsf{d}}_e,\underline{\mathcal {L}}^{n+1},0,H), \end{aligned}$$

in a realization $({\textsf{Z}}\times \mathbb {R},{\textsf{d}}_{{\textsf{Z}}\times \mathbb {R}})$, where

$$\begin{aligned} H:=\big \{y\in \mathbb {R}^{n+1}\;\big |\;y\cdot \nu (x,t)\ge 0\big \}, \end{aligned}$$

where $\nu (x,t)$ is given by (8) for v. Also, we have that

$$\begin{aligned} \big ({\textsf{X}},r_i^{-1}{\textsf{d}},{\textsf{m}}_x^{r_i},x,\{f>s\}\big )\rightarrow (\mathbb {R}^{n},{\textsf{d}}_e,\underline{\mathcal {L}}^{n},0,H'), \end{aligned}$$

where $H'$ is given by

$$\begin{aligned} H':=\big \{y\in \mathbb {R}^{n}\;\big |\;y\cdot \mu (x)\ge 0\big \}, \end{aligned}$$

where $\mu (x)$ is given by (8) for A(x)u. Our aim is then to show that

$$\begin{aligned} \nu (x,t)_{1,\dots ,n}=\mu (x,t) \qquad \text {and}\qquad \nu (x,t)_{n+1}=0, \end{aligned}$$

(27)

which will yield the conclusion. Indeed, at Lebesgue points,

$$\begin{aligned} \nu =\big (A(x)\big (\nu _{\mathcal {G}_f}^u(x,t)\big )_{1,\dots ,n},\nu _{\mathcal {G}_f}^u(x,t)_{n+1}\big )\qquad \text {and}\qquad \mu =A(x)\nu _{\{f>s\}}^u(x) \end{aligned}$$

and the matrix A(x) is invertible. Up to taking a non-relabeled subsequence, we assume that weakly converges to in duality with $C_\textrm{bs}({\textsf{Z}}\times \mathbb {R})$ and weakly converges to in duality with $C_\textrm{bs}({\textsf{Z}})$. We can now use the representation formula of Theorem 24 to combine the information (which we will prove below) together with the just mentioned convergences

in order to obtain that

Hence $H=\pm H'\times \mathbb {R}$ (with $-H'$ we mean the image of $H'$ through the map $\mathbb {R}^n\ni z\mapsto -z\in \mathbb {R}^n$).

We want to show that indeed $H=H'\times \mathbb {R}$, so that (27) will follow by the definitions of H and $H'$. There are two possible cases: either $s\ge t$ or $s< t$. In the former, $\{f\ge s\}\times (-\infty ,t]\subseteq \mathcal {G}_f$, and in the latter, $\{f<s\}\times [t,+\infty )\subseteq ({\textsf{X}}\times \mathbb {R})\setminus \mathcal {G}_f$. Thanks to stability with respect to $L^1_\textrm{loc}$ convergence (cf. the proof of [13, Lemma 3.9]), we obtain the monotonicity relations: $H'\times (-\infty ,0]\subseteq H$ in the first case, $-H'\times [0,\infty )\subseteq -H$, in the second. This is enough to conclude.

Now we prove the coarea formula claimed in the above paragraph exploiting the rectifiability result of [18] and the fact that $K\subseteq \mathcal {F}\{f>s\}$. Take E a set of finite perimeter. Fix $\epsilon >0$. We use [18, Theorem 4.1] (see also [18, Remark 4.3]) to write, up to $\mathcal {H}^{n-1}$-negligible subsets, $\mathcal {F}E=\bigcup _k E_k$, where $E_k$ are pairwise disjoint Borel subsets of $\mathcal {F}E$ such that, for every k, $E_k$ is $(1+\epsilon )$-bi-Lipschitz to some Borel subset of $\mathbb {R}^{n-1}$. Say that, for every k, there exists $g_k: E_k\rightarrow \mathbb {R}^{n-1}$ $(1+\epsilon )$-bi-Lipschitz with its image. Call also $f_k: E_k\times \mathbb {R}\rightarrow \mathbb {R}^{n-1}\times \mathbb {R}$ the map $(x,t)\mapsto (g_k(x),t)$. We have that, if $\psi :{\textsf{X}}\times \mathbb {R}\rightarrow [0,1]$ is Borel, then

$$\begin{aligned} \int _{\mathcal {F}E\times \mathbb {R}}\psi (x,t)\,\textrm{d}\mathcal {H}^n(x,t)&=\sum _{k\in \mathbb {N}} \int _{E_k\times \mathbb {R}}\psi (x,t)\,\textrm{d}\mathcal {H}^n(x,t) \\&=\sum _{k\in \mathbb {N}} \int _{g_k( E_k)\times \mathbb {R}} \psi (g_k^{-1}(y),t)\,\textrm{d}((f_k)_*\mathcal {H}^n)(y,t), \end{aligned}$$

where we used that if $N\subseteq \mathcal {F}E$ is $\mathcal {H}^{n-1}$-negligible, then $N\times \mathbb {R}$ is $\mathcal {H}^n$-negligible, thanks to a simple covering argument. Now notice that, as $g_k$ is $(1+\epsilon )$-bi-Lipschitz, we have that, on their natural domains,

$$\begin{aligned} \left( \frac{1}{1+\epsilon }\right) ^{n-1}\mathcal {H}^{n-1}\le (g_k)_*\mathcal {H}^{n-1}\le \left( \frac{1}{1-\epsilon }\right) ^{n-1}\mathcal {H}^{n-1} \end{aligned}$$

and

$$\begin{aligned} \left( \frac{1}{1+\epsilon }\right) ^{n}\mathcal {H}^n\le (f_k)_*\mathcal {H}^n\le \left( \frac{1}{1-\epsilon }\right) ^{n}\mathcal {H}^n. \end{aligned}$$

Therefore, using Fubini’s theorem in $\mathbb {R}^n$, setting $\tilde{\psi }(y,t)\mathrel {\mathop :}=\psi (g_k^{-1}(y),t)$ and denoting $C_\epsilon$ a constant, that may vary from line to line but that depends only on $\epsilon$ and n and such that $C_\epsilon \rightarrow 1$ as $\epsilon \searrow 0$,

$$\begin{aligned} \int _{g_k(E_k)\times \mathbb {R}} \tilde{\psi }(y,t)\,\textrm{d}((f_k)_*\mathcal {H}^n)(y,t)&\le C_\epsilon \int _{g_k( E_k)\times \mathbb {R}} \tilde{\psi }(y,t)\,\textrm{d}\mathcal {H}^n(y,t) \\&= C_\epsilon \int _{g_k(E_k) }\int _\mathbb {R}\tilde{\psi }(y,t)\,\textrm{d}\mathcal {H}^1(t)\,\textrm{d}\mathcal {H}^{n-1}(y) \\&\le C_\epsilon \int _{g_k( E_k) }\int _\mathbb {R}\tilde{\psi }(y,t)\,\textrm{d}\mathcal {H}^1(t)\,\textrm{d}{((g_k)_*\mathcal {H}^{n-1})}(y) \\&= C_\epsilon \int _{ E_k }\int _\mathbb {R}\psi (x,t)\,\textrm{d}\mathcal {H}^1(t)\,\textrm{d}\mathcal {H}^{n-1}(x). \end{aligned}$$

All in all,

$$\begin{aligned} \int _{ \mathcal {F}E\times \mathbb {R}}\psi (x,t)\,\textrm{d}\mathcal {H}^n(x,t)&\le \sum _k C_\epsilon \int _{ E_k }\int _\mathbb {R}\psi (x,t)\,\textrm{d}\mathcal {H}^1(t)\,\textrm{d}\mathcal {H}^{n-1}(x) \\&=C_\epsilon \int _{ \mathcal {F}E }\int _\mathbb {R}\psi (x,t)\,\textrm{d}\mathcal {H}^1(t)\,\textrm{d}\mathcal {H}^{n-1}(x). \end{aligned}$$

As $\epsilon >0$ was arbitrary, we obtain that

$$\begin{aligned} \int _{\mathcal {F}E\times \mathbb {R}}\psi (x,t)\,\textrm{d}\mathcal {H}^n(x,t)\le \int _{\mathcal {F}E}\int _\mathbb {R}\psi (x,t)\,\textrm{d}{\mathcal {H}^1(t)}\,\textrm{d}\mathcal {H}^{n-1}(x). \end{aligned}$$

The opposite inequality is obtained similarly. $\square$

3.2 Proof of the main results

We are now ready to prove the main theorems of this note.

Proof of Theorem 3

If $f\in {\textrm{BV}}_\textrm{loc}({\textsf{X}})$, then $\mathcal {G}_f$ has locally finite perimeter thanks to the proof of item (a) in [11, Theorem 5.1]. Conversely, assume that $\mathcal {G}_f$ has locally finite perimeter. Then, the argument in the proof of item (b) of [11, Theorem 5.1] yields that for any $x\in {\textsf{X}}$ and $r>0$,

Now we take $t_0\in (0,\infty )$ big enough so that ${\textsf{m}}(\{f>t_0\}\cap B_r(x))\le \min \{1,{\textsf{m}}(\{f\le t_0\}\cap B_r(x))\}$ and ${\textsf{m}}(\{f<-t_0\}\cap B_r(x))\le \min \{1,{\textsf{m}}(\{f\ge -t_0\}\cap B_r(x))\}$. This is possible as $f\in L^0({\textsf{m}})$. Thus, taking into account that for $\mathcal L^1$-a.e. t, , we obtain from the relative isoperimetric inequality (2) (that holds with $\lambda =1$ on finite-dimensional ${\textrm{RCD}}$ spaces) that

$$\begin{aligned} \int _{t_0}^\infty {\textsf{m}}(\{f>t\}\cap B_r(x))\,\textrm{d}t<\infty \qquad \text {and}\qquad \int _{-\infty }^{-t_0} {\textsf{m}}(\{f<t\}\cap B_r(x))\,\textrm{d}t<\infty . \end{aligned}$$

This implies $f\in L^1_\textrm{loc}({\textsf{X}})$ by Fubini’s theorem. By Theorem 9, it also follows that $f\in {\textrm{BV}}_\textrm{loc}({\textsf{X}})$.

The last conclusion is an immediate consequence of Lemma 36 and Proposition 6, for what concerns the absolutely continuous part. For what concerns the equality on the jump part and the Cantor part, it directly follows from (12). $\square$

Proof of Theorem 4

We first show that

Recall that (12) and Proposition 32 imply that we can reduce ourselves to show the claim for -a.e. $(x,t)\in (D_f{\setminus }(C_f\cup J_f))\times \mathbb {R}$.

For -a.e. $(x,t)\in \big (\{g_f=0\}\cap (D_f{\setminus }(C_f\cup J_f))\big )\times \mathbb {R}$, by Lemma 36, Lemma 35 and (12) it holds that $(\nu _{\mathcal {G}_f}^u(x,{\bar{f}}(x)))_{n+1}=-1$. The claim is then proved at -a.e. $(x,t)\in \big (\{g_f=0\}\cap (D_f{\setminus } C_f)\big )\times \mathbb {R}$ by the following fact. By Proposition 32, for $x\in D_f$, at $(x,\bar{f}(x))$, $v\mathrel {\mathop :}=(A(x)u,\pi ^2)$ is a system of good coordinates for $\mathcal {G}_f$, see also Remark 31. Also, if $\nu (x,{\bar{f}}(x))$ is computed as in item v) of Proposition 32, it holds that

and that $|\nu (p)|=1$. Recall that A(x) is invertible, whence the conclusion follows.

Now we show the claim at -a.e. (x, t) with $x\in \{g_f>0\}\cap \big (D_f\setminus (C_f\cup J_f)\big )$. Notice that on $\{g_f>0\}\cap \big (D_f\setminus (C_f\cup J_f)\big )$ it holds that ${\textsf{m}}\ll |\textrm{D}f|\ll {\textsf{m}}$. Therefore, by Lemma 34, taking into account Lemma 36, Lemma 35 and (12), we have the claim.

The fact that

is Lemma 38 together with [13, Theorem 3.8 and Lemma 3.9]. $\square$

Proof of Theorem 5

Items (i) and (ii) can be proved using Theorem 4, Theorem 3, and Lemma 14. Item (iv) follows from Lemma 38.

We show now item (iii). By the representation formula, we write

where we used that $\Theta _n({\textsf{m}},x)=\Theta _{n+1}\big ({\textsf{m}}\otimes \mathcal {H}^1,(x,t)\big )$ and Lemma 38. Now notice that if $N\subseteq J_f$ is such that $\mathcal {H}^{n-1}(N)=0$, then $\mathcal {H}^n(N\times \mathbb {R})=0$. This can be proved with an easy covering argument.

Therefore, taking into account also Lemma 14 and Theorem 9, we reduce ourselves to prove that for every $\psi :D\times \mathbb {R}\rightarrow [0,1]$ Borel, we have that for $\mathcal {H}^1$-a.e. $s\in \mathbb {R}$

$$\begin{aligned} \int _{(D\cap \mathcal {F}E_s\cap J_f)\times \mathbb {R}}\psi (x,t)\,\textrm{d}\mathcal {H}^n(x,t)=\int _{D\cap \mathcal {F}E_s\cap J_f}\int _\mathbb {R}\psi (x,t)\,\textrm{d}t\,\textrm{d}\mathcal {H}^{n-1}(x), \end{aligned}$$

where $E_s\mathrel {\mathop :}=\{f>s\}$. Fix s such that $E_s$ has finite perimeter. The claim is equivalent to , which has been proved at the end of the proof of Lemma 38. $\square$