Families of degenerating Poincaré–Einstein metrics on $\mathbb {R}^4$

Abstract

We provide the first example of continuous families of Poincaré–Einstein metrics developing cusps on the trivial topology $\mathbb {R}^4$. We also exhibit families of metrics with unexpected degenerations in their conformal infinity only. These are obtained from the Riemannian version of an ansatz of Debever and Plebański–Demiański. We additionally indicate how to construct similar examples on more complicated topologies.

1 Introduction

An Einstein metric satisfies for some real number $\Lambda$:

$$\begin{aligned} {{\,\mathrm{{\text {Ric}}}\,}}(g)=\Lambda g. \end{aligned}$$

(1)

This is a central equation in Geometry and in several instances of Physics, especially in dimension 4. A Poincaré–Einstein metric is a noncompact Einstein metric with a specific asymptotic behavior giving rise to a conformal boundary metric at infinity, the simplest example being the Poincaré model for hyperbolic space whose conformal infinity is the round sphere. Poincaré–Einstein metrics were first notably used to construct a number of conformal invariants of the boundary geometry; see [15, 16]. More recently, they have also played an important role in the physics literature in relationship with AdS/CFT correspondence; see [7, 31].

From several perspectives, dimension 4 is a threshold dimension in topology and geometry. In this dimension, there are three ways for compact Einstein or Poincaré–Einstein metrics on a given manifold to degenerate: orbifold singularity formation, collapsing and cusp formation.

Orbifold formation has been widely studied and is now reasonably understood. Numerous examples of curves of such degenerations have been produced in the Kähler and Poincaré–Einstein settings, see [8, 9, 25]. All such degenerations have moreover been reconstructed by gluing-perturbation [27, 28].

Despite deep general results such as [12], the collapsing and cusp formation remain comparatively mysterious. The collapsing situation has received a lot of attention, and many examples of curves of Einstein metrics collapsing have been produced on K3 surfaces, see for instance [17, 21]. The third situation of cusp formation has, however, never been observed except from “trivial” examples of (warped) products of degenerating surfaces and from sequences of metrics requiring infinitely many different topologies [5, 6]. More concretely, the following question was left open:

Question 0.1

[4] Another interesting open question is whether cusps can actually form within a given or fixed component of [the moduli space of Poincaré–Einstein metrics], on a fixed manifold M.

A simple but not so appealing example showing that this exists is the so-called topological black hole metric. The metric is $V(r)^{-1}dr^2 + V(r) d\theta ^2 +r^2 g_N$ for $V(r):= -1+r^2 -2\,m/r^2$ with m large enough and $g_N$ the metric of a hyperbolic surface. Letting $g_N$ degenerate creates a cusp that extends to the conformal infinity. This naive example answers Anderson’s question but, to the authors’ knowledge, does not seem to have been mentioned before. This is still a two-dimensional behavior, and we provide many more interesting examples here.

Another intriguing question is whether cusp formation requires some topology—like orbifold degeneration requires nontrivial 2-homology. Anderson conjectured that it was the case:

Question 0.2

[4] It would also be very interesting to know if the possible formation of cusps is restricted by the topology of the ambient manifold M. [...] One might conjecture for instance that on the 4-ball cusp formation is not possible.

We instead provide explicit examples of continuous families of smooth Poincaré–Einstein metrics on $\mathbb {R}^4$ developing different kinds of cusps. We moreover find curves of metrics without any degeneration in the bulk but forming various conical, cusp or naked singularities in their conformal infinity.

1.1 Debever and Plebański–Demiański’s local family of metrics

In this article, we study families of Poincaré–Einstein metrics exhibiting the above three types of degenerations focusing on the least understood case of cusp formation. These examples are surprisingly explicitly given in coordinates and are found in the families of Einstein metrics whose Lorentzian counterparts were discovered by Debever [14] and which were given in more convenient coordinates by Plebański–Demiański [29]. These metrics are known in the physics literature as Plebański–Demiański metrics (PD metrics). PD metrics are algebraically special of Petrov type D meaning (in the Riemannian setting) that at every point the selfdual and anti-selfdual parts of the Weyl curvature have repeated eigenvalues. This is also equivalent to the ambiKähler condition of [1]: the metric is conformally Kähler or Hermitian in both orientations. This curvature condition forces toric symmetry by [18].

The metrics of the PD family have a remarkably compact form (2) and depend solely on two related quartic polynomials P and Q of one variable. Still, despite their simplicity and their discovery in the early 70’s, these explicit metrics, once extended to the Riemannian setting contain in some limits most known examples of Einstein metrics ($\mathbb {S}^4$, $\mathbb {S}^2\times \mathbb {S}^2$, Fubini–Study, Page’s metric, Taub-NUT, Taub–Bolt, Eguchi–Hanson, Schwarzschild, Kerr and their AdS counterparts.) that were often discovered much later with complicated ansatz, see [24] where smooth Ricci-flat and compact Einstein PD metrics are conjecturally classified. Extensions of these families more generally solve the Einstein–Maxwell equations and include known metrics such as LeBrun’s earliest family of scalar-flat Kähler metrics [23].

This family also contains families developing orbifold singularities in the so-called AdS-Taub–Bolt family. It moreover contains continuous families of metrics exhibiting global collapsing bubbling out (Ricci-flat) Taub-NUT or Schwarzschild metrics in the so-called AdS-Taub-NUT (or Pedersen’s) metrics or AdS-Schwarzschild families. We will focus on cusp formation here.

1.2 Families of Poincaré–Einstein metrics forming cusps

1.2.1 Degeneration in the family of AdS C-metrics

It is now classical in the physics literature that a limit “without rotation or twisting” of the PD metrics leads to the well-known AdS C-metrics whose Ricci-flat versions were found by Levi-Civita [22] and Weyl [30] in the 1910 s(!). In this family, we first find a two-dimensional moduli space of smooth Poincaré–Einstein metrics on $\mathbb {R}^4$ containing the hyperbolic 4-metric and whose limiting behaviors include metrics forming one or two cusps. A significant asymptotic quantity of Poincaré–Einstein metrics is the renormalized volume defined in [20]. Despite the drastic degenerations presented in this article, the renormalized volume stays bounded.

Theorem A

(Sect. 2) There exists a smooth family of smooth Poincaré–Einstein metrics on $\mathbb {R}^4$ parametrized by an open region $\Omega$ in $\mathbb {R}^2$. Approaching some points at the boundary $\partial \Omega$, the metrics converge smoothly to the hyperbolic space or degenerate forming one or two codimension 2 cusps. These cusps have asymptotic behaviors:

$$\begin{aligned} dr_1^2+ae^{-r_1}d\theta _1^2+dr_2^2+ bd\theta _2^2 \;\;\text { for }\;\; r_1\in [0,+\infty ),\; r_2\in [0,1], \; \theta _1,\theta _2\in [0,2\pi ], \end{aligned}$$

for $a,b>0$ in the bulk of the manifold, and $dr^2+ae^{-r}d\theta _1^2+bd\theta _2^2$ at conformal infinity with $r\in [0,+\infty )$. These examples have uniformly bounded renormalized volume.

An important question left open is the following one.

Question 0.3

Does there exist a continuous family of Poincaré–Einstein metrics forming cusps separating the manifold into a complete finite volume piece and another complete Poincaré–Einstein metric?

Remark 0.4

Unfortunately, this is impossible in our family of metrics and there is little hope to find such a family of metrics explicitly given in coordinates. Indeed, in our case, one limit of such a degeneration has to be an Einstein metric with negative Ricci curvature and with at least one Killing vector field with finite length, which is impossible by Bochner’s formula; see [32] for instance.

1.2.2 Degeneration in the Carter–Plebański family of metrics

The limits “without acceleration” of the PD metrics constitute the Carter–Plebański family of metrics. In Sect. 3, we exhibit a subfamily of smooth Poincaré–Einstein metrics with topology $\mathbb{C}\mathbb{P}^2\backslash D^4$ forming cusp in some limits and discuss how other topologies may be reached.

1.2.3 Degeneration in the full Plebański–Demiański family of metrics

In the full family of PD metrics, we also obtain cusps as in Theorem A which are this time “twisted” as in (5). We additionally find families of smooth Poincaré–Einstein metrics on $\mathbb {R}^4$ where only the conformal infinity degenerates in some limit.

Theorem B

(Section  4) There exists a smooth family of Poincaré–Einstein metrics on $\mathbb {R}^4$ whose conformal infinity approaches one of the following behaviors in some limit: for $a,b>0$

• A conical (edge) singularity: $dr^2+ a^2r^2d\theta _1^2+b^2d\theta _2^2$ on $(r,\theta _1,\theta _2)\in [0,1]\times [0,2\pi ]\times [0,2\pi ]$,

• A naked singularity: $dr^2+ a^2r^6d\theta _1^2+b^2d\theta _2^2$ on $(r,\theta _1,\theta _2)\in [0,1]\times [0,2\pi ]\times [0,2\pi ]$, or

• A cusp end: $dr^2+ a^2e^{-4r}d\theta _1^2+b^2d\theta _2^2$ on $(r,\theta _1,\theta _2)\in [0,+\infty ]\times [0,2\pi ]\times [0,2\pi ]$.

While approaching these behaviors at conformal infinity, the metrics converge smoothly in the bulk metric in the pointed Cheeger–Gromov sense. These examples have uniformly bounded renormalized volume.

These degenerations can occur in various limits that we describe in Sect. 4.

2 Regularity and asymptotics of the Plebański–Demiański family of metrics

A “Euclideanized” Plebański–Demiański (PD) metric has the following form

$$\begin{aligned} g_{PD}= & {} \frac{1}{(x-y)^2}\left[ \frac{Q(y)}{1-a^2x^2y^2}(d\psi -ax^2d\varphi )^2 + \frac{1-a^2x^2y^2}{Q(y)}dy^2\right. \nonumber \\{} & {} \left. +\frac{P(x)}{1-a^2x^2y^2}(d\varphi -ay^2d\psi )^2+\frac{1-a^2x^2y^2}{P(x)}dx^2\right] \end{aligned}$$

(2)

where Q(y) and P(x) are polynomials of degree 4 which can be chosen depending on the value of $a\in \mathbb {R}$, physically understood as a rotation parameter, so that $g_{PD}$ is an Einstein metric with ${{\,\mathrm{{\text {Ric}}}\,}}_{g_{PD}} = -3g_{PD}$. This follows the Riemannian version of the computations in [29], see also [24]. We will ensure that the metric has the right Riemannian signature by choosing adapted ranges for the coordinates (x, y) where $Q(y)>0$ and $P(x)>0$. Up to rescaling, we can assume $a \in \{0,1\}$.

Let us first consider the larger family with $a =1$ from which the other ones can be obtained from various limiting procedures. The Einstein condition (1) with $\Lambda =-3$ is equivalent to P and Q having the form

$$\begin{aligned} P(x)= & {} bx^4 + cx^3 + dx^2 + ex + b + 1 \text { and }\nonumber \\ -Q(y)= & {} (b+1)y^4+cy^3+dy^2+ey+b, \end{aligned}$$

(3)

for $b,c,d,e\in \mathbb {R}$ where we note the identity $-Q(y) = P(y)+y^4-1$. The local metric (2) is then Einstein and Riemannian on ranges depending on roots of P and Q. When “closing-up” at roots of P and Q, it may have codimension 2 cone-edge singularities (which we will avoid) or cusp ends which are discussed in Sect. 1.3

These metrics are moreover Poincaré–Einstein (when they are smooth) since they are conformal to a metric with boundary: the boundary is given by $\{x=y\}$ and the conformal factor is $\frac{1}{(x-y)^2}$. The conformal infinity of these metrics is the conformal class of the metric induced on $\{x=y\}$ by $(x-y)^2g_{PD}$. We will see in different instances that these conformal infinities may degenerate. The possible such degenerations are collected in Sect. 4.

Without loss of generality, we can write $c = k_+ + k_-, e = k_+-k_-$ in (3), in which the set of eigenvalues of the ±-selfdual part of Weyl curvature $W_{g_{PD}}$ is proportional to $\frac{k_\pm }{(1 \pm x y)^3} (2,-1,-1)$, see the computations of [29] and the Riemannian version of [24]. The pointwise norm of the Riemannian tensor of $g_{PD}$ is then computed as

$$\begin{aligned} ||{{\,\mathrm{{\text {Rm}}}\,}}_{g_{PD}}||^2 = 24 + 24(x - y)^6\left( \frac{k_+^2}{(1 + x y)^6} + \frac{k_-^2}{(1-xy)^6}\right) . \end{aligned}$$

The volume element in these coordinates is $\frac{-1 + x^2 y^2}{(x - y)^4}dxdyd\varphi d\psi$, and one checks that $\Vert W_{g_{PD}}\Vert _{L^2(g_{PD})}$ is finite for the domains we consider, hence, by [3], the renormalized volume is controlled for our examples.

Let us describe here the possible asymptotics of our metrics and give the regularity conditions. The regularity conditions obtained for toric metrics are classical, and we focus on ruling our conical singularities.

2.1 At a simple root $x_1$ of P and a generic point y

As defined for instance in [2], a metric with cone-edge singularity of angle $2\pi \beta >0$ along a codimension 2 submanifold $\Sigma$ has the following asymptotic at $\Sigma$: for a $2\pi$-periodic $\theta$ and a 1-form $\omega$ on $\Sigma$

$$\begin{aligned} dr^2 + \beta ^2 r^2 (d\theta + \omega )^2 + g_\Sigma + \mathcal {O}(r^{1+\epsilon }), \text { for } \epsilon >0. \end{aligned}$$

(4)

Lemma 1.1

At a simple root $x_1$ of P and a generic point $y\notin \{-1/x_1,1/x_1\}$, our metric (2) with $a\in \{0,1\}$ has a cone-edge singularity whose angle is the period of $\frac{|P'(x_1)|}{2(1+a^2x_1^4)}\theta _1$, where $\theta _1:= \varphi + ax_1^2\psi$.

Proof

To do this, we first note that close to its root $x_1$, we have $P(x) = P'(x_1)(x-x_1) + O((x-x_1)^2)$ at first order. Close to the root $x=x_1$ and at $y\ne \pm x_1^{-1}$ which is not a root of Q, the metric therefore reads:

$$\begin{aligned} g_{PD} =&\frac{1}{(x_1-y)^2}\left[ \frac{Q(y)}{1-a^2x_1^2y^2}(d\psi -ax_1^2d\varphi )^2 + \frac{1-a^2x_1^2y^2}{Q(y)}dy^2\right. \\&\left. + \frac{P'(x_1)(x-x_1)}{1-a^2x_1^2y^2}(d\varphi -ay^2d\psi )^2+\frac{1-a^2x_1^2y^2}{P'(x_1)(x-x_1)}dx^2\right] + \mathcal {O}((x-x_1)^2). \end{aligned}$$

Our codimension 2 submanifold $\Sigma$ is given by $\{x=x_1\}$, hence $dx=0$ and $\theta _1:= \varphi + ax_1^2\psi =cst$, that is $d\theta _1=d\varphi + ax_1^2d\psi =0$ (this is chosen as the orthogonal of the 1-form $d\psi -ax_1^2d\varphi$). The local coframe on $\Sigma$ we will use is therefore dy and $\omega _1:=d\psi -ax_1^2d\varphi$. With these notations, the metric becomes:

$$\begin{aligned} g_{PD} =&\frac{1}{(x_1-y)^2}\left[ \frac{Q(y)}{1-a^2x_1^2y^2}\omega _1^2 + \frac{1-a^2x_1^2y^2}{Q(y)}dy^2\right. \\&\left. + (1-a^2x_1^2y^2)\left( \frac{P'(x_1)(x-x_1)}{(1+a^2x_1^4)^2}\left( d\theta _1 + f(y,x_1)\omega _1\right) ^2+\frac{dx^2}{P'(x_1)(x-x_1)}\right) \right] + \mathcal {O}((x-x_1)^2). \end{aligned}$$

where $f(y,x_1)=\frac{x_1^2+y^2}{1-x_1^2y^2}$ if $a= 1$ and $f(y,x_1)=0$ if $a=0$. The regularity of the metric close to $x=x_1$ therefore reduces to the regularity of $\frac{P'(x_1)(x-x_1)}{(1+x_1^4)^2}\left( d\theta _1 + f(y,x_1)\omega _1\right) ^2+\frac{1}{P'(x_1)(x-x_1)}dx^2$.

Considering a change of variables $x=x_1+\frac{P'(x_1)}{4}r^2$, we find the conical singularity metric:

$$\begin{aligned} \frac{|P'(x_1)|^2}{4(1+a^2x_1^4)^2}r^2\left( d\theta _1 + f(y,x_1)\omega _1\right) ^2+dr^2, \end{aligned}$$

of angle the period of $\frac{|P'(x_1)|}{2(1+a^2x_1^4)}\theta _1$ by comparison with (4). It will be smooth if and only if this period is $2\pi$. $\square$

The case of a simple root $y_2$ of Q is treated similarly and yields a cone-edge singularity whose angle is given by the period of $\frac{|Q'(y_2)|}{2(1+a^2y_2^4)}\theta _2$, where $\theta _2$ is $\psi + y_2^2\varphi$.

2.2 At $x_1$ simple root of P and $y_2$ simple root of Q

Let us now consider $y = y_2$, a simple root of Q, and still assume that $x_1^2\ne y_2^{-2}$ if $a=1$.

Lemma 1.2

Assume that $x_1$ is a simple root of P, and $y_2$ is a simple root of Q, and $1-a^2x_1^2y_2^2\ne 0$. Then, the metric (2) is smooth at $(x_1,y_2)$ if and only if both $\frac{|P'(x_1)|}{2(1+a^2x_1^4)}\theta _1$ and $\frac{|Q'(y_2)|}{2(1+a^2y_2^4)}\theta _2$ are $2\pi$-periodic, where $\omega _1=d\psi -ax_1^2d\varphi$ and $\omega _2=d\varphi -ay_2^2d\psi$.

Proof

Expanding the metric near $p=x_1$ and $q=y_2$, a first-order development of the metric gives:

$$\begin{aligned} g_{PD} =&\frac{1}{(x_1-y_2)^2}\left[ \frac{Q'(y_2)(y-y_2)}{1-a^2x_1^2y_2^2}(d\theta _2 + \tilde{\omega }_2)^2 + \frac{1-a^2x_1^2y_2^2}{Q'(y_2)(y-y_2)}dy^2\right. \\&\left. + (1-a^2x_1^2y_2^2)\left( \frac{P'(x_1)(x-x_1)}{(1+a^2x_1^4)^2}\left( d\theta _1 + \tilde{\omega }_1\right) ^2+\frac{1}{P'(x_1)(x-x_1)}dx^2\right) \right] \\&+ \mathcal {O}((x-x_1)^2 + (y-y_2)^2). \end{aligned}$$

for some 1-forms $\tilde{\omega }_1 = f_1(y,x_1)\omega _1$ and $\tilde{\omega }_2 = f_2(x,y_2)\omega _2$ for some smooth functions $f_1$ and $f_2$ whose explicit value does not affect the regularity ($f_1=f_2=0$ if $a=0$), and where $\omega _1=d\psi -ax_1^2d\varphi$ and $\omega _2=d\varphi -ay_2^2d\psi$.

The same change of variables as in Sect. 1.1 in both x and y ensures that the metric is smooth at $(x_1,y_2)$ if and only if $\frac{|P'(x_1)|}{2(1+a^2x_1^4)}\theta _1$ and $\frac{|Q'(y_2)|}{2(1+a^2y_2^4)}\theta _2$ are $2\pi$-periodic. $\square$

We conclude with the following regularity proposition.

Proposition 1.3

Let P and Q be polynomials such that $P>0$ and $Q>0$ on $(x_1,y_2)\subset \mathbb {R}$ and assume that: $x_1$ is a simple root of P, $y_2$ is a simple root of Q, and $1-a^2x^2y^2\ne 0$ for $x,y\in [x_1,y_2]$.

Then, the metric (2) is smooth if and only if the variables $\frac{|P'(x_1)|}{2(1+a^2x_1^4)}\theta _1$ and $\frac{|Q'(y_2)|}{2(1+a^2y_2^4)}\theta _2$ are $2\pi$-periodic where $\theta _1:= \varphi + ax_1^2\psi$ and $\theta _2:= \psi + ay_2^2 \varphi$.

2.3 At a double root $x_1$ of P and a generic y: separating cusp

Similarly, close to $x_1$ a double root of the polynomial, one has $P(x) \approx P''(x_1)(x-x_1)^2/2$. As in Sect. 1.1, we find that close to the same codimension 2 submanifold $\Sigma$, the metric is asymptotic to:

$$\begin{aligned} (1-a^2x_1^2y^2)\left( \frac{P''(x_1)(x-x_1)^2}{2(1+a^2x_1^4)^2}\left( d\theta _1 + f(y,x_1)\omega _1\right) ^2+\frac{2dx^2}{P''(x_1)(x-x_1)^2}\right) + g_\Sigma \end{aligned}$$

(5)

for some smooth $y\mapsto f(y,x_1)$ vanishing when $a=0$ which is an asymptotically cuspidal metric. This is a smooth complete metric, but it adds a cuspidal end to the manifold.

2.4 Approaching a cuspidal end

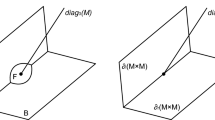
Let us now explain how one can approach a codimension 2 cuspidal end by smooth metrics. Assume that $x_1\pm i\epsilon$ are two complex conjugate roots of $P_\epsilon$ for $\epsilon >0$ that we will send to 0. This time, we have the following second-order approximation for $P_\epsilon (x)$ for x close to $x_1$: $P_\epsilon (x) \approx P''_\epsilon (x_1)\left( (x-x_1)^2+\epsilon ^2\right) /2 + \mathcal {O}((x-x_1)^3)$.

This implies that the metric is approximately

$$\begin{aligned}{} & {} (1-a^2x_1^2y^2)\left( \frac{P''_\epsilon (x_1)\left( (x-x_1)^2+\epsilon ^2\right) }{2(1+a^2x_1^4)^2}\left( d\theta _1 + f(y,x_1)\omega _1\right) ^2\right. \nonumber \\{} & {} \quad \left. +\frac{2dx^2}{P''_\epsilon (x_1)\left( (x-x_1)^2+\epsilon ^2\right) }\right) + g_\Sigma . \end{aligned}$$

(6)

This is a smooth metric, but along $\{x=x_1\}$ it is close to a thin cylinder, see the left picture of Fig. 1. As $\epsilon \rightarrow 0$, close to any $x\ne x_1$, the metric Cheeger–Gromov converges to the cuspidal metric (5) on compact sets, see the right image in Fig. 1.

Fig. 1

Stages of cusp formation. The cusp on the right is infinitely long

3 Degenerations of AdS C-metrics

3.1 Non-rotating limit: AdS C-metrics

For this section, we will follow [10] and will adopt their notation. Our study and goals are purely geometric and differ from theirs. The AdS C-metrics are obtained from the general Plebański–Demiański family (2) by taking the non-rotating limit $a \rightarrow 0$. These metrics are the Riemannian analogues of the metrics considered in [11] and have the form

$$\begin{aligned} g_{C} = \frac{1}{(x-y)^2} \left[ Q(y)d\psi ^2+\frac{dy^2}{Q(y)}+\frac{dx^2}{P(x)}+P(x)d\varphi ^2 \right] \end{aligned}$$

(7)

where we will assume that Q and P are parametrized by two variables $\mu ,\nu$ as

$$\begin{aligned} P(x)= & {} (1+x)\left( 1+\nu x+\mu x^2\right) ,\text { and }\nonumber \\ -Q(y)= & {} y\left[ 1+\nu +(\mu +\nu )y+\mu y^2\right] , \end{aligned}$$

(8)

Note the identity $-Q(y)=P(y)-1$. This ensures Einstein condition (1) is satisfied and the pointwise norm of the Riemannian tensor of $g_C$ is given by

$$\begin{aligned} \Vert {{\,\mathrm{{\text {Rm}}}\,}}_{g_C}\Vert _{g_C}^2 = 24+12(x-y)^6\mu ^2. \end{aligned}$$

More precisely, from the computations of [10], one has ${{\,\mathrm{{\text {Ric}}}\,}}(g_C)=-3g_C$ and the eigenvalues of both the selfdual and anti-selfdual parts of $W_{g_C}$ are equal to $\frac{\mu }{4} (y-x)^3(2,-1,-1)$. As expected, these eigenvalues go to zero as $x\rightarrow y$ and when $\mu =0$, the metric is locally hyperbolic. A direct computation ensures again that $\Vert W_{g_C}\Vert _{L^2(g_C)}^2$ is bounded. In particular, from [3], these examples have bounded renormalized volume.

3.2 Proof of Theorem A

In this section, we study a specific 2-dimensional family of AdS C-metrics on $\mathbb {R}^4$ forming one or two cusps in different limits. The cusps forming here effectively separate the manifold into two or three Poincaré–Einstein metrics with cusps ends in their bulk and their conformal infinities. We prove Theorem A.

As in Sect. 2.1, we consider the metric (7) where $-Q(y) = y\left[ 1+\nu +(\mu +\nu )y+\mu y^2\right]$ and $P(x) = (1+x)\left( 1+\nu x+\mu x^2\right)$. The roots of P and Q, respectively, are as follows

$$\begin{aligned} x_0= & {} -1, \quad x_{\pm }= \frac{-\nu \pm \sqrt{\nu ^2-4\mu }}{2\mu }, \text { and }\nonumber \\ y_0= & {} 0, \quad y_{\pm }= \frac{-(\mu +\nu ) \pm \sqrt{(\mu +\nu )^2-4\mu (1+\nu )}}{2\mu }. \end{aligned}$$

(9)

In order to approach metrics with cusp ends in this family by smooth metrics, we consider the case when $x_{\pm }, y_{\pm }$ are complex conjugate roots which we will let approach a real double root—leading to a cusp degeneration by Sect. 1.4. In the $(\mu ,\nu )$ plane, this condition means that $(\mu ,\nu )$ lies in the region bounded by the curves $\nu = 2 \sqrt{\mu }$ and $\nu = \mu - 2 \sqrt{\mu }$.

We then consider $-1<x<y<0$ where the conformal infinity is at $\{x=y\}$, see Fig. 2b. For the metric to be smooth, we require that $\frac{1-\nu + \mu }{2}\varphi$ and $\frac{1+\nu }{2}\psi$ be $2\pi$-periodic, see Proposition 1.3. We further impose that $\mu >\max (\nu /2,-\nu )$. This corresponds to forcing the real part of $x_\pm$ and $y_\pm$ to be in $(-1,0)$, this way the double root degeneration (when the imaginary part of the roots tends to zero) happens where the metric is defined and is geometrically meaningful. We end up with the region D4 in [10] shaded in Fig. 2a in the $\mu ,\nu$ plane bounded by the curves $\nu = 2 \sqrt{\mu }$, $\nu = \mu - 2 \sqrt{\mu }$, $\nu = 2\mu$ and $\nu = -\mu$.

Fig. 2

Parameter ranges considered. The dashed $\{x=y\}$ is the conformal infinity

Remark 2.1

In the limit $(\mu , \nu ) \rightarrow 0$ from our region shaded in Fig. 2a, our metrics converge smoothly to the hyperbolic 4-space. Indeed, the metric is already locally hyperbolic by our curvature computations and the change of variables $x = -\sin ^2\left( (u-\pi )/2\right) ,$ at the conformal infinity $\{x=y\}$, the restriction of the metric $(x-y)^2g_{C}$ with $\mu =\nu =0$ takes the form

$$\begin{aligned} du^2 + \cos \left( \frac{u-\pi }{2} \right) ^2d\varphi ^2+ \sin \left( \frac{u-\pi }{2} \right) ^2d\psi ^2. \end{aligned}$$

Thus, we recover the metric of the round 3-sphere in Hopf’s coordinates since $\varphi$ and $\psi$ are $4\pi$-periodic. This in particular ensures that the topology we consider is $\mathbb {R}^4$.

From (9), we see that, for $(\mu ,\nu )$ in the shaded region in Fig. 2a, if one of P, Q has a double root, then $(\mu ,\nu )$ lies on at least one of the boundary curves $\nu = 2 \sqrt{\mu }$ or $\nu = \mu -2\sqrt{\mu }$, respectively, in blue and red in Fig. 2, see the first two columns of Fig. 3 for the associated polynomials and geometric representation. The intersection of these curves, $(\mu ,\nu ) = (16,8)$, is the unique case when P and Q have double roots at $x = \frac{-1}{4}$ and $y=\frac{-3}{4})$ as described in Fig. 3c, f, respectively, leading to two cusps dividing the manifold in three regions, while the point $(\mu ,\nu )=(0,0)$ corresponds to hyperbolic 4-space from Remark 2.1. The possible double roots of P and Q, respectively, lie in the intervals $(-1,\frac{-1}{4}]$ and $[\frac{-3}{4},0)$.

Fig. 3

Different configurations of double roots

This completes the proof of Theorem A.

4 Degenerations in Carter–Plebański family of metrics

4.1 Non-accelerating limit: Carter–Plebański metrics

The Carter–Plebański family of metrics is a special limit of the Plebański–Demiański family of metrics (2) after a change of coordinates. To do this, start from (2) in the coordinates of [24] and perform a rescaling by $b>0$ (acceleration parameter) of coordinates as in [19, Section 2.2], which yields the following metric:

$$\begin{aligned} g_{PD}= & {} \frac{1}{(1-bpq)^2} \left[ \frac{p^2-q^2}{\mathcal {P}_b(p)}dp^2 + \frac{p^2-q^2}{\mathcal {Q}_b(q)}dq^2 + \frac{\mathcal {P}_b(p)}{p^2-q^2}\left( d\tau +q^2d\sigma \right) ^2\right. \nonumber \\{} & {} \left. +\frac{\mathcal {Q}_b(q)}{p^2-q^2}\left( d\tau +p^2d\sigma \right) ^2\right] \end{aligned}$$

(10)

for polynomials $\mathcal {P}_b$ and $\mathcal {Q}_b$ depending on $b>0$ chosen to satisfy (1) with $\Lambda = -3$. Taking the “no acceleration limit” $b \rightarrow 0$ as in [19, Section 5], we obtain from (10) the Carter–Plebański metric

$$\begin{aligned} g_{CP}:= \frac{p^2-q^2}{\mathcal {P}(p)}dp^2 + \frac{p^2-q^2}{\mathcal {Q}(q)}dq^2 + \frac{\mathcal {P}(p)}{p^2-q^2}\left( d\tau +q^2d\sigma \right) ^2 + \frac{\mathcal {Q}(q)}{p^2-q^2}\left( d\tau +p^2d\sigma \right) ^2,\nonumber \\ \end{aligned}$$

(11)

where the limiting polynomials $\mathcal {P}$ and $\mathcal {Q}$ are of the form:

$$\begin{aligned} \mathcal {P}(p)= & {} p^4 + E^2p^2 -2Np + \alpha \text { and }\nonumber \\ \mathcal {Q}(q)= & {} -q^4 - E^2q^2 +2Mq - \alpha \end{aligned}$$

(12)

following the notations of [26] for some real numbers E, M, N and $\alpha$.

We will consider intervals where $\mathcal {P}(p) \leqslant 0$ and $\mathcal {Q}(q)\leqslant 0$. This time, the range in p will be compact of the form $[p_-,p_+]$ for $p_\pm$ roots of $\mathcal {P}$ and the range in q will be of the form $[q_+,+\infty )$ for $q_+$ root of $\mathcal {Q}$.

This metric is Poincaré–Einstein and as $q \rightarrow + \infty$ (the infinity in these coordinates), the metric looks like

$$\begin{aligned} g_{CP} \approx \frac{dq^2}{q^2} + q^2\left( -\frac{dp^2}{\mathcal {P}(p)}-\mathcal {P}(p)d\sigma ^2+(d\tau + p^2d\sigma )^2\right) \end{aligned}$$

(13)

so the metric at conformal infinity is $-\frac{dp^2}{\mathcal {P}(p)}-\mathcal {P}(p)d\sigma ^2+(d\tau + p^2d\sigma )^2$.

4.2 An example with different topology

In this section, we indicate how to find families of metrics forming cusps with different topologies. We take the simplest example here on $\mathbb{C}\mathbb{P}^2\backslash D^4$ with conformal infinity $\mathbb {S}^3$. We follow [26, Sections 2.1, 2.2 and 2.3] for our regularity conditions: we impose $\tau$ and $\sigma$ to be as [26, Sections 2.13 and 2.17]. This also requires $N=M$, which is equivalent to the metric being self-dual, and forcing $\mathcal {P}=-\mathcal {Q}$.

We will moreover parametrize our polynomial by the roots and looking for a metric with a cusp, we will consider a polynomial with a double root: for $p_3,p_4,p_0\in \mathbb {R}$ (following notations of [26]):

$$\begin{aligned} \mathcal {P}(p) = (p-p_3)(p-p_4)(p-p_0)^2. \end{aligned}$$

(14)

We will then consider the range $(p,q)\in [p_3,p_4]\times [p_4,+\infty ]$, where the associated metric is indeed Riemannian (Fig. 4).

Fig. 4

Polynomial and range of coordinates

Remark 3.1

Recall that from Remark 0.4, we cannot have a double root in $\mathcal {Q}$ on $(p_4,+\infty )$. All we will find instead is a double root of $\mathcal {P}$ on $(p_3,p_4)$ corresponding to a cusp in the manifold extending to infinity.

We need our double root $p_0$, to lie in $(p_3,p_4)$ so that it is reflected in our metric. Since the sum of the roots is 0 (the cubic coefficient of the polynomial is zero), $p_0 = -\frac{p_3+p_4}{2}$ and so $p_0\in (p_3,p_4)$ imposes

$$\begin{aligned} p_3< 0< p_4,\; \text { and } \; \frac{1}{3}|p_3|< |p_4| < 3|p_3|. \end{aligned}$$

(15)

We can find this polynomial (14) as a limit of polynomials with two complex conjugate roots: for $\epsilon \geqslant 0$

$$\begin{aligned} \mathcal {P}_\epsilon (p) = (p-p_3)(p-p_4)\Big (\Big (p+\frac{1}{2}(p_3+p_4)\Big )^2+\epsilon ^2\Big ) \end{aligned}$$

(16)

where we get the double root mentioned above when $\epsilon \rightarrow 0$ and we also let $-\mathcal {Q}_\epsilon = \mathcal {P}_\epsilon$ to satisfy the above regularity condition of [26]. Since the roots of the polynomials are the same, the intervals in which these are defined stay the same. Geometrically, in the limit $\epsilon \rightarrow 0$, the metrics (11) associated with $-\mathcal {Q}_\epsilon = \mathcal {P}_\epsilon$ develop a cusp along $\{p=-(p_3+p_4)/2\}$ separating the manifold in two parts by an argument similar to Sect. 1.3.

The topology of the manifold is that of $\mathbb{C}\mathbb{P}^2$ minus a ball and the conformal infinity is $\mathbb {S}^3$. The “bolt” of the metric is reached at $[p_3,p_4]\times \{q=1\}$ which is a codimension 2 submanifold (a 2-sphere), see [26].

Remark 3.2

It is likely possible to obtain infinitely many different topologies from the Carter–Plebański family of metrics by having a larger and larger “self-intersection” for the 2-sphere while obtaining a conformal infinity $\mathbb {S}^3/\mathbb {Z}_k$ for $\mathbb {Z}_k$ a cyclic subgroup of SU(2) acting freely on $\mathbb {S}^3$. See [13, Section 5.1] for a discussion of the regularity conditions and possible topologies. In the larger Plebański–Demiański family of metrics, we believe that there is also a large class of additional possible topologies, with two “bolts” (and a “NUT”). The conformal infinity, could this time be an arbitrary lens space. See [13, Section 5.2] for a discussion of the regularity conditions and possible topologies.

5 Degenerations in the Plebański–Demiański family of metrics

We will now turn to the general PD family of metrics. The above degenerations of Sects. 2 and 3 can be found in the full family of Plebański–Demiański, but we focus on exhibiting new behaviors of complete metrics whose conformal infinities develop unexpected types of singularities. We prove Theorem B.

In this section, we consider a subfamily of metrics in (2) with $a=1$, parametrizing our polynomials as

$$\begin{aligned} P_{\infty }(x) = C_{\infty }(x-\alpha _1)((x-1+\alpha _2)^2+\alpha _3)(x-\alpha _4) \end{aligned}$$

(17)

with $C_{\infty } = (-1+\alpha _1\alpha _2^2\alpha _4+\alpha _1\alpha _4-2\alpha _1\alpha _2\alpha _4+\alpha _1\alpha _3\alpha _4)^{-1}$ and $-Q_{\infty }(y) = P_{\infty }(y)+y^4-1$. These metrics satisfy the Einstein Condition (1) with $\Lambda = -3$ for all $\alpha _1,\alpha _2,\alpha _3, \alpha _4\in \mathbb {R}$.

As for the bulk metric, the conformal infinity $\{x=y\}$ has different possible asymptotic behaviors close to roots of $P_{\infty }$ or $Q_{\infty }$. We consider (2), whose conformal metric at infinity is:

$$\begin{aligned} g_{bdry}= & {} (1-a^2x^4)\left( \frac{1}{P_{\infty }(x)}+ \frac{1}{Q_{\infty }(x)}\right) dx^2+\frac{Q_{\infty }(x)}{1-a^2x^4}(d\psi -ax^2d\varphi )^2\nonumber \\{} & {} + \frac{P_{\infty }(x)}{1-a^2x^4}(d\varphi -ax^2d\psi )^2. \end{aligned}$$

(18)

We will moreover assume that the regularity conditions for the bulk of Proposition (1.3) are satisfied whenever applicable. Simpler arguments than Sects. 1.1 and 1.3 imply the following result.

Fig. 5

Naked singularity, not infinitely long

Fig. 6

Example polynomials and region for metric with naked singularity at infinity

Proposition 4.1

Under the assumptions of Proposition 1.3, the conformal metric is smooth. Moreover, if $P_{\infty }$ (or $Q_{\infty }$) has a double root at $-1<x_0<1$, then the conformal boundary metric of (18) has a codimension 2 separating cusp as described in (5).

We will see that allowing the roots to be at $\pm 1$ leads to different degenerate behavior for the conformal infinity alone. Setting $\alpha _2 = \alpha _3 = 0$ and choosing distinct $\alpha _1,\alpha _4 \in \mathbb {R}$ in (17), the polynomial $P_{\infty }$ has a double root only at $x = 1$ while $Q_\infty$ has a simple root at 1. This will correspond to a Naked Singularity in the metric, which we describe in Sect. 4.1 once we ensure that our metric is smooth and Riemannian. We first need to verify that we have the correct signs $P_{\infty }>0$ and $Q_{\infty }>0$ on the region $\alpha _1 \leqslant x < y \leqslant 1$. Assume that $\alpha _1 < 1 \leqslant \alpha _4$, then the inequality $P_{\infty }'(\alpha _1) = \frac{(\alpha _1-1)^2(\alpha _1-\alpha _4)}{\alpha _1 \alpha _4-1 } > 0$, which is satisfied whenever $\alpha _1 < \alpha _4^{-1}$, guarantees that $P_{\infty } >0$ on $(\alpha _1,1)$. To guarantee that $Q_\infty$ has the right sign, it is enough to impose $-1< \alpha _1 < 0$.

Remark 4.2

This is true on a larger range of values of $\alpha _1$ which we do not attempt to describe.

Lastly, we assume that $\varphi$ and $\psi$ satisfy the periodicity conditions imposed in Proposition 1.3 to ensure that we find smooth metrics.

5.1 A naked singularity

Assuming that 1 is a double root of $P_{\infty }$ and a simple root of $Q_{\infty }$, at $x=1$, the metric (18) approaches

$$\begin{aligned} \frac{C_1}{(1-x)} dx^2 + C_2 \theta _1(x)^2 + C_3 (x-1)^3\theta _2(x)^2 \end{aligned}$$

(19)

for $\theta _1(x) \rightarrow d\varphi -d\psi$, $\theta _2(x)\rightarrow d\varphi +d\psi$ as $x\rightarrow 1$ and where $C_1 = \frac{8}{P_{\infty }''(1)}$, $C_2 = \frac{Q_{\infty }'(1)}{4}$ and $4C_2C_3 = \frac{P_{\infty }''(1)}{2}Q_{\infty }'(1)$ so $C_3 = \frac{P_{\infty }''(1)}{2}$. A change of variables $r=2\sqrt{1-x}$ in (19) yields the naked singularity metric: close to $r=0$,

$$\begin{aligned} C_1 dr^2 + C_2 \theta _1(x)^2 + \frac{C_3}{4} r^6\theta _2(x)^2. \end{aligned}$$

(20)

The metrics obtained in this way can be approached by perturbing the parameters $\alpha _2$ and $\alpha _3$ in various ways around (0, 0). This gives the following different types of degenerations, which we describe below (Figs. 5, 6).

5.2 Degeneration 1: from a smooth metric to a naked singularity.

By taking $\alpha _3 > 0$ and keeping $\alpha _2 = 0$, the double root of $P_{\infty }$ at 1 is replaced with two complex roots, see Fig. 7a. Taking the limit $\alpha _3\rightarrow 0$ yields the above naked singularity. Similarly, by taking $\alpha _2 < 0$ and $\alpha _3 = 0$, the double root of $P_{\infty }$ is moved past the conformal infinity $y=x$, see Fig. 7b. Taking the limit $\alpha _2\rightarrow 0$ yields the above naked singularity.

Both of these situations yield a smooth metric at conformal infinity by Proposition 4.1. Indeed, $P_\infty$ does not have any root close to the root of $Q_{\infty }$.

Fig. 7

Smooth metric to naked singularity

5.3 Degeneration 2: from a conical singularity to a naked singularity.

Let us assume that 1 is a simple root of both $P_{\infty }$ and $Q_{\infty }$ for the metric (18). The case of $-1$ is treated similarly. As $x\rightarrow 1$, we obtain that the metric (18) is asymptotic to

$$\begin{aligned} C_1 dx^2 + C_2 \theta _1(x)^2 + C_3 (x-1)^2\theta _2(x)^2 \end{aligned}$$

where $\theta _1(x) \rightarrow d\varphi -d\psi$, $\theta _2(x)\rightarrow d\varphi +d\psi$ as $x\rightarrow 1$, and $C_1 = 4 \left( \frac{1}{P_{\infty }'(1)} + \frac{1}{Q_{\infty }'(1)}\right)$, $C_2 = \frac{P_{\infty }'(1) + Q_{\infty }'(1)}{4}$ and $C_3 = \frac{P_{\infty }'(1)Q_{\infty }'(1)}{P_{\infty }'(1) + Q_{\infty }'(1)} = \left( \frac{1}{P_{\infty }'(1)} + \frac{1}{Q_{\infty }'(1)}\right) ^{-1}$. This yields a codimension 2 cone-edge singularity of angle $\frac{-P_{\infty }'(1)Q_{\infty }'(1)}{2(P_{\infty }'(1) + Q_{\infty }'(1))}$.

By taking $\alpha _3 < 0$ and $\alpha _2 = 0$, see Fig. 8a, the double root of $P_{\infty }$ at 1 is split in two real roots $x_-<1<x_+$. This changes the topology and creates a codimension 2 cone-edge singularity along $\{x=x_-\}$ by Lemma 1.1, extending to the conformal infinity $\{x=y\}$. As $\alpha _3\rightarrow 0$, the angle tends to zero and a naked singularity appears while the singularities in the bulk are “sent to infinity”.

By setting $\alpha _3 < 0$ and $\alpha _2 = -\sqrt{-\alpha _3}$ as in Fig. 8b, the double root of $P_{\infty }$ at 1 is split into a single root at 1 and a root larger than 1. This gives a conical singularity in the metric at the conformal infinity only this time. As $\alpha _3\rightarrow 0$, the angle tends to zero and a naked singularity appears in the limit.

Fig. 8

Conical singularity to naked singularity

Fig. 9

Cusp to naked singularity

5.4 Degeneration 3: from cusp to naked singularity

By taking $\alpha _2 > 0$ and $\alpha _3 = 0$, the double root $1-\alpha _2$ of $P_{\infty }$ is moved to the left of the root in $Q_\infty$. This creates a cusp in the bulk metric as well as in its infinity by Sect. 1.3 and Proposition 4.1.

As in Sect. 2.1, this cusp at $\{x=1-\alpha _2\}$ separates the manifold in two regions infinitely far apart, and the conformal infinity in two finite volume manifolds with cusp ends.

When $\alpha _2\rightarrow 0$, the volume of $\{1-\alpha _2<x=y<1\}$ tends to zero and the region disappears, and the metric on $\{\alpha _1<x=y<1-\alpha _2\}$ has infinite diameter for $\alpha _2>0$ but finite diameter in the limit $\alpha _2\rightarrow 0$ (these remarks do not depend on the representative of the conformal class) (Fig. 9).

This is a manifestation of cusp degenerations in the bulk manifold comparable to those of Sect. 2.1. Indeed, in the family of metrics obtained from (17), there is a four-dimensional family of smooth Poincaré–Einstein metrics with a (three-dimensional) boundary constituted of metrics with one cusp separating the manifold in two set, and a two-dimensional family with two cusps separating the manifold in three.

Remark 4.3

There are important differences with Sect. 2.1. The cusps from (2) for $a=1$ are “twisted” (see (5)) and do not look like mere products of surfaces in the limit. Moreover, as described above, as $\alpha _2\rightarrow 0$ the cusps “escapes” to infinity creating the above unexpected naked singularity at infinity. This was impossible in the family (7) because the double root in P could not approach 0 and the double root in Q could not approach $-1$.

Fig. 10

Two cusps at conformal infinity only

5.5 Two cusps at conformal infinity only

We finally assume that 1 is a triple root of $P_{\infty }$ and a simple root of $Q_{\infty }$. The metric (18) is asymptotic to

$$\begin{aligned} \frac{C_1}{(1-x)^2} dx^2 + C_2 \theta _1(x)^2 + C_3 (x-1)^4\theta _2(x)^2 \end{aligned}$$

(21)

where again, $\theta _1(x) \rightarrow d\varphi -d\psi$, $\theta _2(x)\rightarrow d\varphi +d\psi$ as $x\rightarrow 1$ and where $C_1 = \frac{24}{P_{\infty }^{(3)}(1)}$, $C_2 = \frac{Q_{\infty }'(1)}{4}$ and $C_3 = \frac{P_{\infty }^{(3)}(1)}{6}$. A change of variables $r=-\log (1-x)$ in (21) yields the cusp end metric: for r close to $+\infty$,

$$\begin{aligned} C_1 dr^2 + C_2 \theta _1(x)^2 + C_3 e^{-4r}\theta _2(x)^2. \end{aligned}$$

(22)

This time, we exhibit a metric with codimension 2 cusps ends at the conformal infinity only—in particular, the conformal infinity is not compact. Unlike the example of Sect. 2, these cusps do not cut the manifold in different pieces. Consider

$$\begin{aligned} P_{2,\infty }(x)= & {} -\frac{1}{2}(x-1)^3(x+1) \text { and}\nonumber \\ Q_{2,\infty }(y)= & {} -\frac{1}{2}(y-1)(y+1)^3 \end{aligned}$$

which are limit of the polynomials in (17) for $\alpha _1=-1$, $\alpha _2=0$, $\alpha _3=0$ and $\alpha _4=1$. These polynomials have the desired signs on the region $-1 \leqslant x \leqslant 1, -1 \leqslant y \leqslant 1$ making the metric (2) with $a=1$ Riemannian. Its infinity has two cusp ends at the points $(-1,-1)$ and (1, 1) thanks to (21). This is a limiting case for all the previous degenerations as well as a limit of naked singularities at either 1 or $-1$ (Fig. 10).

Remark 4.4

From Sect. 1, one moreover notices that this metric is anti-selfdual since the linear and cubic coefficients of $P_{2,\infty }$ are opposite.