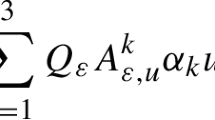1 Introduction

The application of microporous materials for mass separation and selective conversion is based on the intimate contact between the guest molecules and the internal surface of these materials, ensured with pore sizes close to the diameters of the molecules. This intimate contact, on the other side, gives rise to a notable reduction in the translational mobility of the involved molecules, impeding the rate of gain of value-added products. Over the last two decades, this impediment in performance has been progressively counteracted by the emergence of hierarchically porous materials. Such materials represent combinations of regions with various pore sizes, which may occur in quite different arrangements [29], (see also Sect. 5 of “Connecting Theory and Simulation with Experiment for the Study of Diffusion in Nanoporous Solids” by Coppens et. al. in this Thematic Issue). They may appear in manifold structural variants [32,33,34, 49, 72, 80, 89] and offer particular advantages when—as in the so-called mesoporous zeolites and MOFs—the microporous bulk phase is permeated by a network of transport pores [8, 12, 20, 23, 29, 56, 60, 61, 63,64,65, 81, 87]. Preserving the matter upgrading by separation and/or conversion in the micropores, incorporation of “transport pores” (in general mesopores, but also possibly with macropores [58]) enables a sufficiently fast exchange between the microporous regions and the surroundings. Following the IUPAC recommendation [86], pores with widths below 2 nm are called micropores, with widths between 2 and 50 nm mesopores and above 50 nm macropores. The term nanopores embraces these categories with an upper limit of 100 nm.

While, in the ideal case, quantitation of mass transfer in a purely microporous material may be based on already a sole parameter, namely the micropore diffusivity, for hierarchically porous materials a whole set of parameters is required. This notably complicates a theory-based description of the relevant scenarios of mass transfer [24, 25, 50, 67, 68, 82, 91].

Among the various patterns of pore architecture, microporous bulk phases permeated by a network of transport pores (as in meso/macro-porous zeolites and MOFs) are distinguished by allowing an analytical representation of their intrinsic mass transfer. Such a possibility is provided within the frame of the so-called two-region model of diffusion. Originally introduced for quantifying PFG NMR diffusion measurements (see [3, 40] in this Thematic Issue) in beds of zeolite crystallites [37, 38, 43], it has meanwhile found widespread application in compartmented systems quite in general [1, 5, 71, 90]. This refers, in particular, to its application to diffusion studies with assemblages of cells in organic tissues [27, 66, 93], where the term “Kärger model” [22, 70, 92] has been coined for this approach.

By assigning the two regions to, respectively, the spaces of the micro- and mesopores, in Ref. [36] the two-region model has now been shown to serve as a useful tool for investigating mass transfer in also hierarchically porous materials. In this way a formalism has been found in which—to the best of our knowledge for the first time—it became possible to represent mass transport in a hierarchically porous material in a closed analytical expression. After a general introduction in Sect. 2, this access is applied in Sect. 3 for establishing a set of correlations between the input parameters of the model and the overall transport patterns. Section 4 considers diffusion and reaction in the model system, ending up, in Sect. 5, with simple rules for correlating their influence on the effectiveness factor of catalytic reactions in hierarchically porous materials.

2 The two-region model and its application to diffusion in pore hierarchies

In the diffusion equation, considered in the two-region model, molecular concentrations are referred to unit volumes accommodating both micro- and transport pores. The unit volumes of a given material are, moreover, chosen to be large enough so that, in a statistical sense, they are of identical topography. This is exactly the condition presupposed in ref. [85] on demonstrating the broad applicability of Fick’s laws for mass transfer in nanoporous materials. Temporal variation of the concentration in transport pores (\({c}_{1}\)) and micropores (\({c}_{2}\)) is, correspondingly, expressed by the relations

$$\frac{\partial {c}_{1}}{\partial t}={D}_{1}\frac{{\partial }^{2}{c}_{1}}{\partial {x}^{2}}-\frac{{c}_{1}}{{\tau }_{1}}+\frac{{c}_{2}}{{\tau }_{2}}$$
(1)
$$\frac{\partial {c}_{2}}{\partial t}={D}_{2}\frac{{\partial }^{2}{c}_{2}}{\partial {x}^{2}}-\frac{{c}_{2}}{{\tau }_{2}}+\frac{{c}_{1}}{{\tau }_{1}}$$
(2)

with \({D}_{1(2)}\) and \({\tau }_{1(2)}\) denoting, respectively, diffusivities and mean lifetimes of molecules in the transport (micro-) pores. With these starting equations, we confine our treatment to one-dimensional diffusion as typically observed in plain-parallel slabs. The time dependence of molecular uptake and release is known to be largely independent of the shape of the adsorbent particles under study (see, e.g., Fig. 6.2 in [45]), so that the general message of our considerations will not be affected by this restriction.

The probabilities \({p}_{1(2)}\) to find, under equilibrium conditions, a molecule within the transport (micro-) pores are correlated with the respective mean lifetimes by the detailed balance equation

$$\frac{{p}_{1}}{{p}_{2}}=\frac{{\tau }_{1}}{{\tau }_{2}}$$
(3)

They follow, from the equilibrium concentrations, by the relation

$${p}_{1}=1-{p}_{2}=\frac{{c}_{1,\mathrm{ eq}}}{{c}_{1,\mathrm{ eq}}+{c}_{2,\mathrm{ eq}}}$$
(4)

While in the absence of any additional transport resistances (e.g. surface barriers, see [76] this volume) uptake in purely microporous materials is determined by a single parameter, namely the micropore diffusivities, with (1) to (4) uptake in the pore hierarchy is seen to depend on, altogether, four parameters, namely the diffusivity in each pore space, the relative population of the pore spaces and the exchange rate between them. In nuclear magnetic resonance literature, (1) to (4) are known to constitute the “Kärger model” [22, 70, 92].

For a detailed mathematical treatment we refer to [35]. A condensed version is also presented in its accompanying supporting information. In the following we restrict our discussion to the special case (referred to as the “third limiting case”) that the relative amount of molecules in the micropores significantly exceeds that in the transport pores

$${p}_{1}\ll {p}_{2}\approx 1$$
(5)

while the diffusivity in the micropores is significantly exceeded by that in the transport pores

$${D}_{1}\gg {D}_{2}$$
(6)

Under such conditions, the overall mass transfer is found to be controlled by only three parameters [35], namely the diffusivity \({D}_{2}\) and the mean lifetime \({\tau }_{2}\) in the space of micropores and \({p}_{1}{D}_{1}\) as a measure of the “efficiency” of mass transfer in the transport pores. Porosity does not explicitly appear in this model. It is rather implicitly contained in the relative populations.

Under the assumption that molecular exchange between the spaces of micropores and transport pores is not additionally affected by a resistance at their mutual interface, the molecular mean lifetime within the space of micropores may be, further on, correlated with the diffusivity \({D}_{2}\) in the micropores via the relation [35, 79]

$${\tau }_{2}=\frac{{R}_{2}^{2}}{15{D}_{2,\mathrm{bulk}}}$$
(7)

where

$${R}_{2}=\frac{3{V}_{2}}{{A}_{1}}=\frac{3\left({V}_{\mathrm{cryst}}-{V}_{1}\right)}{{A}_{1}}$$
(8)

appears as a measure of the extension of the space of micropores, filled or emptied in contact with the transport pores. \({V}_{\mathrm{cryst}}\), \({V}_{1}\) and \({V}_{2}\) are, respectively, the volume of the crystal (particle) and of the spaces filled by the transport pores and the micropores. \({A}_{1}\) stands for the area of their mutual interface. With Eqs. (7) and (8), we have exploited the fact that the sorption (or release) time of a body of any shape is approximately the same as the sorption time of a sphere with the same surface-to-volume ratio [45, 75].

It is worthwhile mentioning that the diffusivity \({D}_{2,\mathrm{bulk}}\) appearing in (7) is the diffusivity in a continuous microporous phase. Therefore, it cannot coincide with the diffusivity \({D}_{2}\) introduced with (2) as a parameter of the two-region model, which—for sufficiently large diffusion pathways through the space of micropores—must be implied to be affected by the presence of the transport pores. This is due in particular to the effect of the tortuosity experienced by the molecules in the space of the micropores when they have to bypass the transport pores (namely at sufficiently low temperatures) instead of benefiting from their presence [59]. In the following we imply that the space occupied by the transport pores is negligibly small in comparison with the space filled by the microporous bulk phase. Under such conditions, the effect of tortuosity by even a total blockage of the transport pores is easily seen to be negligibly small [15, 59]. Therefore, in our further discussion, we may use the approximation \({D}_{2,\mathrm{bulk}}\approx {D}_{2}\).

Under the assumption that the transport pores are formed by a network of cylindrical channels of diameter d, (8) may be transferred into

$${R}_{2}\approx \frac{3d}{4\epsilon }$$
(9)

with \(\epsilon \ll 1\) denoting the space fraction occupied by the transport pores. In this way, the magnitude of \({R}_{2}\) as a measure of the extension of the space of micropores within the hierarchically structured particles may be referred to more easily accessible structural parameters.

Following the formalism of the statistical moments [4, 18, 45, 52], the influence of additional transport resistances may be taken into account with the sum of the time constants corresponding to the various resistances. Thus, under the influence of a transport resistance (a “surface barrier” [59]) at the interface between the two pore spaces, the exchange time between the micro- and transport pores may be noted as [46]

$${\tau }_{2}=\frac{{R}_{2}^{2}}{15{D}_{2}}+\frac{{R}_{2}}{3\alpha }$$
(10)

with \(\alpha\) denoting the permeance (also referred to as the permeability [30, 31]) of the interface. It was a remarkable finding of the application of PFG NMR to diffusion studies with zeolites [41] that overall mass transfer is often controlled by surface barriers rather than by intracrystalline diffusion [42].

With (10), the influence of surface barriers in comparison with diffusion is seen to increase with decreasing extension \({R}_{2}\) of the microporous regions. Since the molecular exchange rate \({1/\tau }_{2}\) increases with decreasing \({R}_{2}\), this is the situation one is generally interested in for performance enhancement. In the development of novel nanoporous materials, this appears in a tendency towards increasing miniaturization [6, 10, 36, 54, 57, 60, 62, 69]. In hierarchically structured materials, due to the same reason, the extension of the microporous ranges should be kept as small as possible giving rise to a situation where \({\tau }_{2}\) is more and more controlled by the influence of surface resistances.

An introduction to the various techniques applicable for the measurement of surface barriers is provided by [76] in this Thematic Issue. They are, as a rule, based on a comparison of the influences of intracrystalline diffusion and surface barriers on the rates of molecular uptake or release. Among these techniques, microimaging via interference and IR microscopy [9, 39, 47] is distinguished by its ability to directly measure both the flux \(j\left(x=0\right)\) entering a nanoporous particle and the boundary concentration \(c\left(x=0\right)\). This allows the determination of the surface permeance (or permeability) through, immediately, the defining equation

$$j\left(x=0\right)=\alpha \left[{c}_{\mathrm{eq}}-c\left(x=0\right)\right]$$
(11)

with \({c}_{\mathrm{eq}}\) denoting the guest concentration in equilibrium with the surrounding atmosphere [13, 30, 31].

This access to experimentally determine transport resistances does, obviously, not apply to the interface between the space of micropores and the transport pores in hierarchically structured materials. Here novel concepts of measurement are required where the input from the modelling of surface barriers by molecular simulations shall be highly desirable [11, 19, 78, 88, 94, 95].

3 The intracrystalline mean lifetime as a function of the system parameters

3.1 Rigorous treatment

We are going to consider the intracrystalline mean lifetime of a guest molecule within a nanoporous solid particle as a key parameter for assessing its technological performance. For concentration-independent diffusivities as considered throughout this contribution, the intracrystalline mean lifetime coincides with the time constants of both uptake and release [14, 45]. It is defined by the first statistical moment [4, 18, 45, 52]

$${M}_{1}={\int }_{F=0}^{1}tdF={\int }_{0}^{\infty }\left[1-F\left(t\right)\right]dt$$
(12)

with

$$F\left(t\right)=\frac{\Delta m\left(t\right)}{\Delta m\left(\infty \right)}=\frac{\int \left[c\left(\mathbf{r}, t\right)-{c}_{0}\right]d\mathbf{r}}{\int \left[{c}_{\infty }-{c}_{0}\right]d\mathbf{r}}\equiv \frac{\overline{c}\left(t\right)-{c}_{0}}{{c}_{\infty }-{c}_{0}}$$
(13)

denoting the fractional uptake (or, respectively, release and exchange). \(c\left(\mathbf{r}, t\right)\) results from the solution of the diffusion equation for the relevant initial and boundary conditions. Integration is over the whole particle. Relation (13) may therefore, completely equivalently, be represented in terms of the mean concentration as with the last identity.

For a purely microporous slab of thickness \(L\) the intracrystalline mean lifetime is thus found to be [4, 18, 45, 52]

$${T}_{\mathrm{micro}}=\frac{{L}^{2}}{12{D}_{2}}$$
(14)

We are going to use this relation as a standard for quantifying the enhancement of molecular uptake and release in hierarchically porous materials. As a counterpart of this notation we as well introduce the quantity

$${T}_{\mathrm{macro}}=\frac{{L}^{2}}{12{({p}_{1}{D}_{1}+D}_{2})}$$
(15)

as the uptake time of a slab with an intrinsic diffusivity given by the mean of the diffusivities in the two pore spaces of the hierarchically porous material.

The determination of the intracrystalline mean lifetimes via Eqs. (12) and (13) is based on the solution of the diffusion Eqs. (1) and (2) under conditions (3) to (6) with the initial and boundary conditions

$${c}_{i}\left(x, t=0\right)=0, 0<x<L, i=1, 2$$
(16)
$${c}_{i}\left(x=0, t\right)={c}_{i}\left(x=L, t\right)={c}_{i,eq}=\left({c}_{1,eq}+{c}_{2,eq}\right){p}_{i}, 0\le t<\infty , i=1, 2$$
(17)

By division with, respectively, the slab thickness \(L\) and the uptake time \({T}_{\mathrm{micro}}\) of the purely microporous plate we introduce dimensionless space and time coordinates. The rate \({1/M}_{1}\) of molecular uptake as following with (12) and (13) will thus be obtained in terms of \(1/{T}_{\mathrm{micro}}=\frac{12{D}_{2}}{{L}^{2}}\). The only (dimensionless) parameters on which the (dimensionless) uptake rate \(\frac{{1/M}_{1} }{1/{T}_{\mathrm{micro}}}\equiv \frac{{T}_{\mathrm{micro}}}{{M}_{1}}=\frac{{1/M}_{1} }{\frac{12{D}_{2}}{{L}^{2}}}\) depends, are \(\frac{{p}_{1}{D}_{1}+{D}_{2}}{{D}_{2}}\) and \(\frac{{T}_{\mathrm{micro}}}{{\tau }_{2}}\).

The solution procedure is extensively described by [35] and, once again, summarized in its supporting information. Before the solution for selected parameter combinations shall be presented in Sect. 3.3, we first refer, in the subsequent section, to different limiting cases for mass transfer in hierarchical pore spaces. We shall end up with the suggestion of a generally applicable approach for correlating the first statistical moment M1 of molecular uptake, release and exchange with the system parameters.

3.2 Limiting cases and an approach of the general pattern

As a first extreme case, molecular exchange between the micro- and transport pores may be considered to be extremely slow that the space of micropores is, essentially exclusively, filled through the micropores, without any significant contribution by mass transfer through the transport pores. It is true that, in comparison with the micropores, the space of transport pores is essentially immediately filled by the guest molecules. The space of micropores, however, would remain unaffected by this in the given case, as a consequence of the negligibly small exchange rate implied. Such a situation is, obviously, characterized by the condition

$$\frac{{L}^{2}}{12{D}_{2}}\equiv {T}_{\mathrm{micro}}\le {\tau }_{2}$$
(18)

Since, in this case, the existence of transport pores does not lead to any transport enhancement, we discard it in our further discussion.

There are, obviously, two limiting cases where the presence of the transport pores may give rise to an acceleration of the overall uptake. In one limiting case, to which we refer as the case of “slow exchange”, the exchange time \({\tau }_{2}\) is, on the one hand side, short enough so that the space of micropores may be filled, via the mutual interface, from the space of transport pores long before it is filled exclusively via the micropores, yielding

$${T}_{\mathrm{micro}}\equiv \frac{{L}^{2}}{12{D}_{2}}\gg {\tau }_{2}$$
(19)

On the other hand, it still notably exceeds the time required for the filling of the total pore system via diffusion through both the transport and micropores yielding

$$\frac{{L}^{2}}{12{{(p}_{1}D}_{1}+{D}_{2})}\equiv {T}_{\mathrm{macro}}\ll {\tau }_{2}{\ll T}_{\mathrm{micro}}$$
(20)

The second inequality results as a consequence of (19), implying \({{p}_{1}D}_{1}\gg {D}_{2}\) as to be anyway required as a precondition of the transport pores for giving rise to transport enhancement. Thus, under “slow-exchange” conditions, the overall uptake time is determined by the exchange time, yielding

$${M}_{1,\mathrm{ slow ex}.}={\tau }_{2}=\frac{{R}_{2}^{2}}{15{D}_{2}}$$
(21)

The second equality results from (7), implying the absence of any surface barrier at the interface between the micro- and transport pores.

In the opposite limiting case of “fast exchange”, molecular exchange between the two pore spaces is very fast, so that molecular uptake proceeds as a continuum where the diffusion front propagates essentially parallel to each other within the micro- and transport pores, i.e. with an exchange time between the two pore spaces much shorter than the overall uptake time and a diffusivity given by the weighted mean of the diffusivities in the two regions, yielding

$$\frac{{L}^{2}}{12{{(p}_{1}D}_{1}+{D}_{2})}\equiv {T}_{\mathrm{macro}}\gg {\tau }_{2}$$
(22)

The time constant of the overall molecular uptake once again results from (14), now however with an effective diffusivity given by the weighted mean of the diffusivities in the two pore spaces:

$${M}_{1,\mathrm{ fast ex}.}={T}_{\mathrm{macro}}\equiv \frac{{L}^{2}}{12\left({p}_{1}{D}_{1}+{D}_{2}\right)}\approx \frac{{L}^{2}}{12{p}_{1}{D}_{1}}$$
(23)

The approximation is, again, due to the precondition that \({{p}_{1}D}_{1}\gg {D}_{2}\) has to be met for giving rise to transport enhancement.

Table 1 summarizes the conditions for the limiting cases and the corresponding expressions for mass transfer enhancement in pore hierarchies.

Table 1 The two limiting cases of transport enhancement in hierarchically porous materials and the respective uptake times \({M}_{1}\)
Full size table

The mechanisms giving rise to transport enhancement in the limiting cases of slow and fast exchange with the constants given by (21) and (23) operate in mutual interdependence: Uptake by the micropores can never be faster than allowed by the supply provided by the transport pores while, on the other hand, even the fastest infeed into the transport pores does not contribute to overall uptake if the micropores are not filled quickly enough. The time-determining process is, correspondingly, that with the larger time constant and summation of the two limiting time constants provides us with a first-order estimate of the overall time constant:

$${M}_{1 }\approx {M}_{1,\mathrm{slow ex}.}+{M}_{1, \mathrm{fast ex}.}$$
(24)

Normalization with the time constant (14) for the purely microporous system and insertion of (21) and (23) finally yields for the normalized uptake rate

$$\frac{{T}_{\mathrm{micro}}}{{M}_{1 }}\approx \frac{\frac{{L}^{2}}{12{D}_{2}}}{{\tau }_{2 }+\frac{{L}^{2}}{ 12{p}_{1}{D}_{1}}}$$
(25a)
$$= \frac{{\frac{{L^{2} }}{{12D_{2} }}}}{{\frac{{R_{2}^{2} }}{{15D_{2} }} + \frac{{L^{2} }}{{ 12p_{1} D_{1} }}}}$$
(25b)
$$= \frac{1}{{\frac{{4R_{2}^{2} }}{{5L^{2} }} + \frac{{D_{2} }}{{p_{1} D_{1} }}}} = \frac{1}{{\frac{{9d^{2} }}{{20\varepsilon^{2} L^{2} }} + \frac{{D_{2} }}{{p_{1} D_{1} }}}}$$
(25c)
$$= \frac{1}{{\frac{{\tau_{2} }}{{T_{{{\text{micro}}}} }} + \frac{{D_{2} }}{{p_{1} D_{1} }}}}$$
(25d)

where, with (25b) and (25c), the exchange between the two pore spaces is assumed to be controlled by exclusively diffusion, with the time constant as given by (7) and specified with structural parameters by using (9). With (25d), the normalized uptake rate is presented as a function of the (only) two dimensionless parameters that it depends on, i.e. the normalized exchange rate between the two pore spaces and the relative diffusivity enhancement brought about by the presence of the transport pores.

As the 3-d representation of (25d), Fig. 1 shows the normalized uptake rate \(\frac{{T}_{\mathrm{micro}}}{{M}_{1}}\) of a hierarchically structured slab (for concentration-independent diffusivities coinciding with the rates of molecular release or exchange with the surroundings) as a function of the two dimensionless parameters that it depends on, namely the exchange rate \(\frac{{T}_{\mathrm{micro}}}{{\tau }_{2}}\) between the two pore spaces and the ratio \(\frac{{p}_{1}{D}_{1}}{{D}_{2}}\) between the concentration-weighted diffusivities in the transport and micropores, normalized with the uptake rate of the purely microporous slab. The presentation allows an easy distinction between the two limiting cases. Under slow-exchange conditions (\(\frac{{p}_{1}{D}_{1}}{{D}_{2}}\gg \frac{{T}_{\mathrm{micro}}}{{\tau }_{2}}\), near the right corner in Fig. 1), the uptake rate \(\frac{{T}_{\mathrm{micro}}}{{M}_{1}}\) is seen to increase with increasing \(\frac{{T}_{\mathrm{micro}}}{{\tau }_{2}}\), while it remains unaffected by \(\frac{{p}_{1}{D}_{1}}{{D}_{2}}\). Just the opposite is true under fast-exchange conditions (\(\frac{{p}_{1}{D}_{1}}{{D}_{2}}\ll \frac{{T}_{\mathrm{micro}}}{{\tau }_{2}}\), near the left corner in Fig. 1), where \(\frac{{T}_{\mathrm{micro}}}{{M}_{1}}\) increases with increasing \(\frac{{p}_{1}{D}_{1}}{{D}_{2}}\), while a variation of \(\frac{{T}_{\mathrm{micro}}}{{\tau }_{2}}\) has no influence.

Fig. 1
figure 1

Enhancement \(\frac{{T}_{\mathrm{micro}}}{{M}_{1}}\) of molecular uptake by a hierarchically structured particle plotted as a function of the parameters \(\frac{{T}_{\mathrm{micro}}}{{\tau }_{2}}\) and \(\frac{{p}_{1}{D}_{1}}{{D}_{2}}\) as the origin of this enhancement. The presentation is based on the approach provided by (25d)

Full size image

As a straightforward and most simple way of parameter variation we are going to consider the influence of the temperature on \(\frac{{T}_{\mathrm{micro}}}{{M}_{1}}\). By implying that the experiments are performed with closed samples under excess micropore loading, a temperature variation will not lead to any substantial change in the micropore loading. The temperature dependence (“activation energy”) of \({p}_{1}{D}_{1}\) is then, essentially, given by the isosteric heat of adsorption which, as a rule, notably exceeds the activation energy \({E}_{\mathrm{diff}}\) of intracrystalline diffusion [45]. With varying temperature, the magnitude of \(\frac{{p}_{1}{D}_{1}}{{D}_{2}}\) will, correspondingly, vary with an “activation energy” given by the difference between the heat of adsorption and the activation energy of micropore diffusion. Implying, as a first-order approach, diffusion-limited exchange following (7) between the two pore spaces, the magnitude of \(\frac{{T}_{\mathrm{micro}}}{{\tau }_{2}}\) remains essentially unaffected by temperature variation. Temperature variation is thus found to serve as a valuable tool for determining the rate-determining mechanism of mass transfer in hierarchically porous materials.

The discussion in this Section was based on the application of the approach for the uptake (release and exchange) rate of hierarchically porous, slab-shaped materials given by (25a–d). In the subsequent Section we are going to confirm the validity of this relation by comparison with the outcome of rigorous calculations.

3.3 Proof of consistency

We are going to check the reliability of the estimates of the uptake rates of hierarchical pore systems as provided by (25a–d) and presented in Fig. 1 by comparison with the results of rigorous calculation, following the procedure described in Sect. 3.1. For this purpose, we have considered the accurate results obtained for \(\frac{{T}_{\mathrm{micro}}}{{M}_{1}}\) within an array of parameters \(\frac{{T}_{\mathrm{micro}}}{{\tau }_{2}}\) and \(\frac{{p}_{1}{D}_{1}}{{D}_{2}}\), each varying over four orders of magnitude from 101 up to 105, with their mutual spacing given by a factor of 10. The data are shown in Fig. 2, together with the results obtained with the approach given by (25a–d) and displayed in Fig. 1. Numerical values are summarized in a table in Supplementary Information. From the data presented in Fig. 2, the estimate of the uptake time in porous hierarchies via (25a–d) is seen to be in excellent agreement with the results of the more rigorous treatment. Relation (25a–d) is thus demonstrated to indeed provide a meaningful instrument for correlating the intraparticle lifetime in hierarchically porous materials, as one of the key data for their technological application, with their structural parameters.

Fig. 2
figure 2

Comparison of the enhancement \(\frac{{T}_{\mathrm{micro}}}{{M}_{1}}\) of molecular uptake in a hierarchically structured slab as resulting from rigorous calculation (points) along with the definition of the first statistical moment M1 via (12) and (13) and from the approach (solid lines) provided by (25d)

Full size image

It is worthwhile mentioning that the curves exhibited in Fig. 2 coincide with the curves on the surface shown in Fig. 1 with increasing \(\frac{{p}_{1}{D}_{1}}{{D}_{2}}\), for the chosen values of \(\frac{{T}_{\mathrm{micro}}}{{\tau }_{2}}\) as given on the right in Fig. 2. Following our discussion above, they are thus easily recognized to result by temperature enhancement, corresponding with an enhancement of \(\frac{{p}_{1}{D}_{1}}{{D}_{2}}\) while \(\frac{{T}_{\mathrm{micro}}}{{\tau }_{2}}\) remains unaffected. In agreement with our previous considerations, the curves in Fig. 2 with \(\frac{{T}_{\mathrm{micro}}}{{\tau }_{2}}\ll \frac{{p}_{1}{D}_{1}}{{D}_{2}}\) are seen to reach a plateau, while \(\frac{{T}_{\mathrm{micro}}}{{M}_{1}}\) gradually increases with increasing \(\frac{{p}_{1}{D}_{1}}{{D}_{2}}\), i.e. with increasing temperature, when \(\frac{{T}_{\mathrm{micro}}}{{\tau }_{2}}\gg \frac{{p}_{1}{D}_{1}}{{D}_{2}}\).

4 Chemical conversion in pore hierarchies

Following the classical treatises by, e.g., Thiele [83] and Riekert [73], we are going to consider the combined influence of mass transfer and conversion in hierarchically organized porous materials for a unimolecular, irreversible reaction \(A\stackrel{k}{\to }B\) of first order. The diffusivities of the reactant and product molecules are, moreover, assumed to coincide and to remain constant with varying concentration and composition. In [84], these conditions have been shown to apply for, e.g., the hydrogenation of benzene to cyclohexane in nanoporous glasses with dispersed nickel, where the transient concentration profiles predicted with these implications were in good agreement with the profiles recorded by IR microimaging. By transferring this concept to hierarchically organized porous materials with two interpenetrating pore spaces we arrive at

$$\frac{\partial {c}_{A1}}{\partial t}={D}_{1}\frac{{\partial }^{2}{c}_{A1}}{{\partial x}^{2}}-\frac{1}{{\tau }_{1}}{c}_{A1}+\frac{1}{{\tau }_{2}}{c}_{A2}-k{c}_{A1}$$
(26)
$$\frac{\partial {c}_{A2}}{\partial t}={D}_{2}\frac{{\partial }^{2}{c}_{A2}}{{\partial x}^{2}}-\frac{1}{{\tau }_{2}}{c}_{A2}+\frac{1}{{\tau }_{1}}{c}_{A1}-k{c}_{A2}$$
(27)
$$\frac{\partial {c}_{B1}}{\partial t}={D}_{1}\frac{{\partial }^{2}{c}_{B1}}{{\partial x}^{2}}-\frac{1}{{\tau }_{1}}{c}_{B1}+\frac{1}{{\tau }_{2}}{c}_{B2}+k{c}_{A1}$$
(28)
$$\frac{\partial {c}_{B2}}{\partial t}={D}_{2}\frac{{\partial }^{2}{c}_{B2}}{{\partial x}^{2}}-\frac{1}{{\tau }_{2}}{c}_{B2}+\frac{1}{{\tau }_{1}}{c}_{B1}+k{c}_{A2}$$
(29)

\({c}_{A1(2)}\) and \({c}_{B1(2)}\) denote the concentration of reactant (A) and product (B) molecules in transport pores (1) and micropores (2). It has been mentioned already at the beginning of Sect. 2 that the unit volumes, to which the concentrations are referred, are sufficiently large, comprising both micro- and transport pores [85]. In comparison with the starting relations (1) and (2), here the number of equations has been doubled, now with relations referring to both the reactant and product molecules. Each equation is, moreover, complemented by a further term, taking account of the loss or gain of molecules by the conversion \(A\stackrel{k}{\to }B\), with \(k\) denoting the (first-order) reaction rate constant. Just like the diffusivities in the two pore spaces, the exchange rates \(\frac{1}{{\tau }_{1}}\) and \(\frac{1}{{\tau }_{2}}\) between the two pore spaces are also implied to be identical for both molecular species. With (26) to (29) conversion \(A\stackrel{k}{\to }B\) is implied to occur in both pore spaces with the same rate constant \(k\). This somehow arbitrary implication, introduced for facilitating mathematical analysis, has no practical consequences in view of the relatively small number of molecules in the transport pores. While they do contribute to overall mass transfer as a consequence of their high diffusivity, it is very unlikely that their reactivity in the transport pores similarly significantly exceeds the reactivity in the micropores, thereby influencing the overall reaction substantially. One rather has to expect the opposite situation, namely a decrease in the reactivity in comparison with the micropores since it is only on the surface of the transport pores where reaction sites may be positioned so that, within the transport pores, the interaction between guest molecules and reactive sites is per se inferior to the interaction in the micropores.

We are going to investigate uptake and conversion in a hierarchical pore system as described with (26) to (29) by placing the initially activated system in an atmosphere of molecules A. Molecules A are provided in excess, so that the concentration of reactant molecules A at the system’s external surface is kept constant and the concentration of product molecules close to the surface is zero. (26) to (29) are to be solved, therefore, with the initial and boundary conditions

$${c}_{Ai}\left(x; t=0\right)={c}_{Bi}\left(x; t=0\right)=0, 0<x<L, i=1, 2$$
(30)
$${c}_{Ai}\left(x=0, t\right)={c}_{Ai}\left(x=L, t\right)={c}_{Ai,eq}=\left({c}_{A1,eq}+{c}_{A2,eq}\right){p}_{i}, 0\le t<\infty , i=1, 2$$
(31)
$${c}_{Bi}\left(x=0, t\right)={c}_{Bi}\left(x=L, t\right)=0, 0\le t<\infty , i=1, 2$$
(32)

With the appearance of the intrinsic reaction rate constant \(k\), the number of free parameters has increased by one, compared to mere molecular uptake as considered in Sects. 2 and 3. These parameters have been shown to yield, via (21) and (23), the time constants of molecular uptake in the limiting cases of fast and slow exchange, with the larger one serving as a reasonable estimate of the actual time constant. Under the additional influence of chemical conversion, the pattern of overall uptake and conversion should, correspondingly, depend on the relation between the two limiting time constants of uptake and the time constant 1/\(k\) of chemical conversion.

Typical examples of the evolution of the concentration profiles of the reactant and product molecules within a hierarchically structured porous catalyst as resulting from the solution of (26–29) with the initial and boundary conditions (30–32) are displayed in Fig. 3. They are shown together with the uptake curves of reactant and product molecules until establishment of stationarity, as resulting from integration over the concentration profiles for the considered instants of time. Further details are provided in Supplementary Information.

Fig. 3
figure 3figure 3

Evolution of the concentration profile during uptake and conversion of reactant molecules A (solid lines, left) to product molecules B (broken lines, left) and the corresponding uptake curves (right) during first-order reaction within a hierarchically organized pore system, resulting as a solution of the differential Eqs. (26–29) with the initial and boundary conditions (30–32) for the conditions as specified together with the representations

Full size image

We start our discussion with a closer look at the evolution of the profiles of the reactant molecules. As a common feature of all representations, the uptake under the conditions of “slow exchange” between the transport and micropores (Fig. 3a, c and e) is observed to proceed with intracrystalline concentrations increasing, essentially, uniformly over the whole system. This behavior can be easily rationalized as a consequence of the high efficiency of mass transfer through the transport pores under the slow exchange conditions (see Table 1, case \({M}_{1, \mathrm{ slow ex}.}\gg {M}_{1, \mathrm{ fast ex}.}\), i.e. \(\frac{{p}_{1}{D}_{1}}{{D}_{2}}\gg \frac{{T}_{\mathrm{micro}}}{{\tau }_{2}}\)), so that the uptake mainly occurs, uniformly over the particle, through the interface between the two pore systems.

Under the fast-exchange conditions (Fig. 3b, d and f), i.e. for \({M}_{1, \mathrm{ slow ex}.}\ll {M}_{1, \mathrm{ fast ex}.}\) or \(\frac{{p}_{1}{D}_{1}}{{D}_{2}}\ll \frac{{T}_{\mathrm{micro}}}{{\tau }_{2}}\)), on the opposite, the uptake predominantly proceeds with a diffusion front propagating essentially in parallel through the two pore spaces. Given the fact that, within the particle, the reactant molecules A are converted into the product molecules B, the reactant concentration must be expected to decrease towards the interior. Finally, under stationary conditions, the increase in product molecules due to conversion is exactly compensated by their efflux, following their concentration gradient toward the external surface.

Interestingly, for reaction rates notably exceeding the overall uptake rate (Fig. 3c and d), transient profiles of the product concentrations are seen to exhibit a maximum, before attaining stationary-state conditions with the concentrations continuously decreasing from the particle center to its surface. Such behavior is observable with also porous catalysts of mono-modal pore geometry (see, e.g., [84]). It is the straightforward consequence of the fact that the catalyst interior is initially free of any molecule and that, with the boundary condition (32), the concentration of the product molecules close to the external surface is as well vanishing. Such maxima are observable under the conditions of both slow (Fig. 3c) and fast (Fig. 3d) exchange. Simultaneously, in also both cases the final concentration of product molecules is seen to significantly exceed the reactant concentration.

The opposite situation (Fig. 3e and f) is observed when the rates of uptake and release notably exceed the reaction rates. Now the reactant concentration under stationary conditions is found to notably exceed the product concentration. This is, once again, observed in both the cases of slow (Fig. 3e) and fast (Fig. 3f) exchange. In between these two limiting cases, i.e. with the time constants of conversion and uptake comparable with each other, the total amount of reactant and product molecules finally attain similar values. This is the situation displayed in Fig. 3a and b, once again for both fast and slow exchange.

A slightly different perspective is provided by the representations of the time dependences of the total amount of reactant and product molecules on the right hand side of Fig. 3. Now, the pronounced differences between the limiting cases of fast and slow exchange as observable in the shape of the concentration profiles have been vanished. This is the situation known already from mere adsorption in hierarchical pore spaces [34], impeding confirmation of the relevant limiting processes by uptake measurement. The steady-state concentrations are seen to be approached by the reactant molecules at a faster rate than the product molecules. Also this is the behavior known from conversion in porous catalysts of mono-modal pore geometry [84]. It is, obviously, to be correlated with the fact that any conversion to a product molecule must be preceded by reactant uptake.

The mean values of the overall concentrations of reactant and product molecules finally attained determine the effectiveness factor of a catalytic reaction, which is in the focus of the subsequent Section.

5 The effectiveness factor of chemical conversion in pore hierarchies

The degree of replacement of the product molecules by “fresh” reactants is conventionally quantified by the effectiveness factor \(\eta\). It is defined as the ratio between the “efficient” (i.e. the actual) and the “intrinsic” (i.e. the maximum possible) reaction rate under stationary conditions

$$\eta =\frac{{r}_{\mathrm{eff}}}{{r}_{\mathrm{int}}}$$
(33)

It indicates the degree up to which, in a given chemical reaction, the conversion potential of a porous catalyst can be exploited [17, 45, 51, 73, 83].

For a first-order reaction \(A\stackrel{k}{\to }B\) we may note

$$\eta =\frac{{r}_{\mathrm{eff}}}{{r}_{\mathrm{int}}}=\frac{\int k{c}_{A,\infty }dV}{\int k{c}_{A,\mathrm{eq}}({p}_{A})dV}=\frac{{\overline{c}}_{A,\infty }}{{c}_{A,\mathrm{eq}}({p}_{A})}$$
(34)

with the integral taken over the whole catalyst particle. \({\overline{c}}_{A,\infty }\) stands for the mean concentration of the reactant molecules within the catalyst particle under stationary conditions. \({c}_{A,\mathrm{eq}}({p}_{A})\) is the reactant concentration in equilibrium with the external atmosphere. In the absence of any transport limitation, i.e. in the limiting case that, under stationary conditions, all product molecules are immediately replaced by fresh reactant molecules, \({c}_{A,\mathrm{eq}}({p}_{A})\) would coincide with the actual concentration of reactant molecules. In reality, however, a certain fraction of the emerging product molecules shall remain within the catalyst particle, giving rise to a decrease in the actual amount of reactant molecules in comparison with its equilibrium, i.e. maximum possible, value.

For an irreversible reaction of 1st order in a slab-shaped catalyst of thickness \(L\) and uniform porosity, the effectiveness factor \(\eta\) is known to be given by the relation [17, 45, 51, 73]

$$\eta =\frac{\mathrm{tanh}{\phi }_{L}}{{\phi }_{L}}$$
(35)

where the combined influence of thickness \(L\), reaction constant \(k\) and diffusivity \(D\) is contained in a single parameter

$$\phi _{L} = \frac{L}{2}\sqrt {\frac{k}{D}} ,$$
(36)

referred to as Thiele modulus. Further simplification may be based on (14), by which the combined influence of particle size and diffusivity appears in the intraparticle mean lifetime M1, yielding

$${\phi }_{L}=\sqrt{3k{M}_{1}}=\sqrt{\frac{3{M}_{1}}{{\tau }_{\mathrm{react}.}}}$$
(37)

With the second equality we have introduced the mean reaction time \({\tau }_{\mathrm{react}.}\equiv 1/k\) as the reciprocal value of the reaction rate. This equality visualizes the mechanism giving rise to a limitation of the effectiveness factor [48]. Since \(\frac{\mathrm{tanh}{\phi }_{L}}{{\phi }_{L}}=1\) for \({\phi }_{L}\ll 1\), approaching \(\frac{\mathrm{tanh}{\phi }_{L}}{{\phi }_{L}}=\frac{1}{{\phi }_{L}}\) for \({\phi }_{L}\gg 1\) (see Fig. 4 further below), the effectiveness factor is seen to be equal to one only in the limiting case that the mean reaction time \({\tau }_{\mathrm{react}.}\) significantly exceeds the mean lifetime \({M}_{1}\) of the molecules within the catalyst. As soon as the reaction time approaches the mean lifetime and, finally, becomes much shorter than it, the relative fraction of reactant molecules within the catalyst under stationary conditions is seen to decrease in proportion with the square root of the ratio of the respective time constants. Here we recognize the well-known limiting case of inverse proportionality between the effectiveness factor and the Thiele modulus as valid for strong diffusion resistances.

Fig. 4
figure 4

Effectiveness factor \(\eta\) as a function of Thiele modulus \({\phi }_{L}\) (solid line), following (35). As well shown are six special cases (points), with the abscissa given by the generalized Thiele modulus \(\sqrt{3k{M}_{1}}\) following (37) and the ordinate as resulting from the rigorous calculation of the effectiveness factor via (34). The special cases are the same as those considered in Fig. 3, indicated by the same color code as in the uptake curves in Fig. 3

Full size image

In [44] this concept, i.e. (35) with a generalization of the definition of the Thiele modulus via (37), has been applied for an estimate of the effectiveness factor of a catalytic reaction of 1st order quite in general by dropping the implication that overall mass transfer is controlled by normal diffusion. In this case, mass transfer has been controlled by single-file rather than by normal diffusion. Nevertheless, estimates of the effectiveness factors via (35) and (37) with the relevant mean lifetimes were found to be in reasonable agreement with the results of rigorous calculations via dynamic Monte Carlo simulations. Single-file diffusion occurs for channel pores with diameters matching the molecular diameters [16, 26, 28, 53, 77] where it has to be taken into consideration for properly reflecting the interplay of mass transfer and conversion [7, 21, 55, 74].

We are now going to apply the formalism as supplied with the relations (37) to catalysts with hierarchically ordered pore spaces. Though specified with the conditions as valid for slab-shaped catalyst particle, the results of such considerations are known to hold in at least a qualitative way for any particle shape [2, 17, 45, 51, 73].

Figure 4 compares the effectiveness factor determined via the classical Thiele relation (35) noted in terms of the intraparticle mean lifetime \({M}_{1}\), with the results of its rigorous calculation via (34) based on the solution of the diffusion–reaction equation for a two-region system (26–29) under stationary-state conditions as specified by (31) and (32). The cases considered are those appearing in also Fig. 3. The mean lifetimes \({M}_{1}\), which lead to the abscissa, i.e. \(\sqrt{3k{M}_{1}}\), were determined using (24). The rigorously determined effectiveness factors are seen to nicely agree with the predictions based on the approach (37). The intraparticle mean lifetime (coinciding with the uptake and release time under the simplifying condition of concentration-independent diffusivities) is thus recognized as the sole parameter determining, jointly with the intrinsic reaction rate constant, the effectiveness factor of a chemical conversion in a hierarchically porous catalyst. The governing mechanism giving rise to the particular value of the mean lifetime is found to be of negligible influence.

It is important to emphasize that, on the other hand, thorough understanding of the rate determining mechanism of mass transfer is indispensable for knowledge-based performance enhancement. While, with (23), particle miniaturization is seen to give rise to transport enhancement under fast-exchange conditions, with (21), uptake and release times under slow-exchange conditions are found to be independent of particle size (\(L\)). It is obvious that only in the latter case the metaphor of a reduction of the diffusion path describes the given microdynamic situation completely adequately. As a prerequisite of such a situation, the efficiency of mass transfer through the transport pores must by far exceed the rate of uptake by the micropores as specified by (20).

6 Conclusion

Working with hierarchically structured pore spaces has been recognized as a powerful tool for improving performance in the application of nanoporous materials for mass separation and conversion. Knowledge-based performance enhancement must be based on a critical assessment of all influencing parameters. In hierarchically porous materials, their number is dramatically increased in comparison with conventional materials of uniform porosity which, as a rule, are sufficiently precisely described with already a single diffusivity. An important class of hierarchically organized porous materials, including the so-called mesoporous zeolites, consist of a continuous microporous phase, permeated by a network of transport pores.

We have shown that mass transfer in such materials is ideally suited to be quantified with the so-called two-region (“Kärger”) model of diffusion. Parameters of this model are the diffusivity in the microporous bulk phase (\({D}_{2}\)), the diffusivity in the transport pores weighted with their occupation probability (\({p}_{1}{D}_{1}\)), and the exchange rate (\(\frac{1}{{\tau }_{2}}\)) between the two pore spaces. If this exchange is controlled by the rate of diffusion within the micropores rather than by an additional transport resistance at the mutual interface, this rate may be represented in terms of the micropore diffusivity \({D}_{2}\) and a length parameter \({R}_{2}\) as a measure of the dimensions of the micropores to be covered by the molecules on their diffusion path between subsequent displacements in the transport pores. These parameters allow covering a large spectrum of situations.

One may distinguish between two limiting cases. They depend on the relation between the mean molecular exchange time \({\tau }_{2}\) between the two pore spaces within the particle and the overall uptake time \({T}_{\mathrm{macro}}\) of the particle with an intrinsic diffusivity given by the weighted mean of the diffusivities in the two pore spaces. Under “fast-exchange” conditions (\({\tau }_{2}\ll\) \({T}_{\mathrm{macro}}\), corresponding with \(\frac{{p}_{1}{D}_{1}}{{D}_{2}}\ll \frac{{T}_{\mathrm{micro}}}{{\tau }_{2}}\), with \({T}_{\mathrm{micro}}\) denoting the uptake time of the purely microporous particle), the molecular mean lifetime \({M}_{1}\) within the particle (which, under the considered conditions, coincides with the uptake and release times) scales with the ratio \(\frac{{p}_{1}{D}_{1}}{{D}_{2}}\). Under “slow-exchange” conditions (\({\tau }_{2}\gg {T}_{\mathrm{macro}}\), corresponding with \(\frac{{p}_{1}{D}_{1}}{{D}_{2}}\gg \frac{{T}_{\mathrm{micro}}}{{\tau }_{2}}\)), on the other hand side, the transport enhancement scales with the ratio \(\frac{L}{{R}_{2}}\) between the particle size \(L\) and \({R}_{2}\) as a measure of the diffusion path length within the micropores in between periods of migration in the transport pores. It is in this case, where the transport enhancement may be referred to a “reduction of the diffusion path length” in the true sense of the word. The sum \({M}_{1 }\approx {M}_{1,\mathrm{slow ex}.}+{M}_{1, \mathrm{fast ex}.}\) of the time constants in the two limiting cases is found to serve as an impressively good approach of the uptake time constant quite in general.

Complemented by a first-order reaction term, the two-region model is shown to serve as also an excellent analytical approach for investigating the simultaneous influence of diffusion and reaction in hierarchically structured porous materials. It is, in particular, found that the classical Thiele concept formulated in terms of the intra-particle mean lifetime serves as an excellent tool for the prediction of the effectiveness factor in the hierarchically ordered pore spaces, with the intra-particle mean lifetime as following with the parameters of the two-region model. Among them, the determination of the exchange rate between the two pore spaces is the most challenging one. While under diffusion limitation it may easily be referred to more easily accessible parameters like the micropore diffusivity and the pore space characteristics, decreasing dimensions of the phase of micropores is likely to give rise to an increasing influence of surface barrier on the mutual interface between the space of micro- and mesopores. Their determination on already “simple” external surfaces is far from being trivial and shall be a challenging task for future studies.