1 Gas permeation through membranes and the role of diffusion

Membrane permeation is energy efficient and environmentally friendly in comparison to thermal separation processes like distillation as convincingly demonstrated by Sholl and Lively (2016). Therefore, growing applications of membrane technology in industrial gas separation can be observed. The main membrane materials are organic polymers as hollow fibres or spiral wound flat sheet modules. Increasingly, novel nanoporous membranes have been developed such as supported zeolites, metal–organic framework (MOF) and covalent organic framework (COF). The substitution of energy-intensive separation processes such as distillation by energy-efficient permeation and adsorption processes requires knowledge-based nanoporous membranes and adsorbents with designed diffusion-optimized pore geometry and size as well as adsorption sites.

The role of adsorption and diffusion in membrane science is a double-track: (i) Diffusion and adsorption studies are crucial for the development of novel membrane materials and are a prerequisite for ensuring optimum operational conditions. (ii) From membrane permeation studies, transport diffusion coefficients can be derived. While (ii) is in the focus of this contribution, first the importance of experimental diffusion studies for the development and the application of nanoporous membranes will be highlighted. Detailed knowledge on intrinsic mass transfer in nanoporous materials is of highest importance for nanoporous membranes and adsorbents. With the introduction of pulsed field gradient NMR as the first technique allowing “microscopic” diffusion measurements (Kärger 1971) it could be shown that the results of the traditional “macroscopic” techniques may deviate up to five orders of magnitude from the true values. A systematic evaluation of the pulsed field gradient NMR data showed their consistency (Kärger and Caro 1977). The NMR data have been confirmed by another “microscopic” technique, the Quasi Elastic Neutron Scattering (Jobic et al. 1990). Just recently, micro-imaging by IR microscopy and optical interference microscopy (Kärger et al. 2014) have been developed as powerful tools for the in situ detection of molecular transport. Their application allows for the in situ observation of molecular fluxes in multicomponent systems including uphill diffusion and overshooting (Lauerer et al. 2015). Even the simultaneous recording of diffusion and conversion of catalytic reactions became possible (Titze et al. 2015).

Parallel with the increasing application of the polymer membranes, there were attempts to predict novel polymers as membrane material with superior separation properties as structure–property relationship. The flux ji through a membrane is in direct proportion with the concentration gradient (Kärger and Ruthven 2016; Kärger et al. 2020) which leads to Fick’s 1st law of diffusion as Eq. (1)

$$ j_{i} = - D_{T} \frac{\partial c}{{\partial x}} $$
(1)

The proportionality factor DT between flux and the concentration gradient is called transport or Fickian diffusivity. It is the transport diffusion coefficient DT which can be derived from single component permeation studies. In the case of binary mixed gas permeation, the flux of component A can be influenced by the gradient of the chemical potential of component B. As described by (Eq. 9 in Kärger et al. 2020) for a multi-component diffusion system, the diffusion coefficient becomes a diffusion matrix. When we ignore all non-diagonal elements of this matrix, DT of a single and mixed gas system should be comparable. However, this is a rough estimate, which works only for small concentrations.

The permeability Pi of a membrane is a finger print for the performance of a membrane as a materials constant and following Eq. (2) it is defined as the flux ji of a gas i (as single component or in a mixture) passing the membrane of thickness δ per (partial) pressure difference Δpi

$$ P_{i} = \frac{{j_{i}\delta }}{\Delta{p_{i} }} $$
(2)

It was found empirically for organic polymer membranes that the permeability Pi of a gaseous component i can be expressed as the product of the solubility Si of gas i in the polymer (e.g., in the units cm3 gas (STP) per cm3 polymer per bar) and its diffusion coefficient Di (e.g. in the units m2 s−1) through the polymer as shown by Eq. (3)

$$ P_{i} = S_{i} \cdot D_{i} $$
(3)

As an example, according to this solubility–diffusivity model, the transport diffusion coefficients DT for CO2 and N2 under the testing condition (0.3 MPa, 25 °C) was determined after Eq. (3) by measuring the gas permeabilities Pi and using for the solubility Si the high-pressure adsorption isotherms (Wijmans and Baker 1995).

Assuming that we have a binary gas mixture of components A and B, the membrane selectivity αA,B can be described as the ratio of the permeabilities PA and PB with a solubility-selectivity αsol(A,B) and a diffusion-selectivity αdiff(A,B) as described by Eq. (4). Di, Si and the resulting Pi are considered as intrinsic properties of a membrane material as e.g. described by Kesting and Fritzsche (1993).

$$ \alpha_{A,B} = \frac{{P_{A} }}{{P_{B} }} = \frac{{S_{A} }}{{S_{B} }} \cdot \frac{{D_{A} }}{{D_{B} }} = \alpha_{{sol\left( {A,B} \right)}} \cdot \alpha_{{diff\left( {A,B} \right)}} $$
(4)

Usually, a trade-off between solubility-selectivity and diffusion-selectivity is observed. With the aim to optimize the membranes performance, independent studies of gas solubility and diffusivity in polymers have been performed. There are numerous studies with the aim to develop new polymer materials for membranes by increasing independently diffusion selectivity and solubility selectivity without decreasing plasticisation. However, on the opposite, from permeation studies also diffusion coefficients can be derived. However, we must accept that permeation studies will provide averaged estimated values of DT since the guest concentration in a membrane is sui generis at the feed side higher than on the permeate side. And it is well known that both permeability and diffusivity are function of the guest molecule loading of the polymer or of a nanoporous material. In principle, the concepts, which have been developed for the determination of diffusion coefficients from permeation studies through nonporous organic polymer membranes can be applied as well for porous membranes.

It is the aim of this critical review to highlight and comment different approaches to derive diffusion coefficients from experimental permeation measurements on micro- and nanoporous membranes. We will focus on diffusion in nanoporous materials such as zeolites or metal–organic frameworks (MOFs). Two principal geometries how to build a nanoporous membrane are used as shown in Fig. 1: (i) Thin films (< 1 µm) on a mechanically strong macroporous ceramic or metal support, and (ii) Mixed Matrix Membranes (MMMs) as a dispersion of nanoscale filler particles (zeolites, MOFs) in a continuous organic polymer matrix. The attempt will be discussed, to derive diffusion coefficients from permeation studies on these two geometries: Supported films and MMMs. To begin with, Table 1 shows definitions and fundamentals of gas permeation.

Fig. 1
figure 1

Typical nanoporous membranes: Thin supported MOF layer and nano-seized MOF crystals in a polymer as Mixed Matrix Membrane (MMM). a Supported MOF membrane showing an UiO-67 film on α-alumina as support prepared by solvothermal synthesis (Knebel et al. 2017). b Flat sheet of 100 nm seized ZIF-8 crystals in the polymer matrimid prepared by doctor blading (Diestel et al. 2015b)

Full size image
Table 1 IUPAC terminology for membranes and membrane processes as proposed by Koros et al. (1996)
Full size table

2 Methods to derive diffusion coefficients from permeation studies

2.1 The time lag method

If a single gas or a gas mixture is sent through a freshly activated membrane, it takes some time before the first gas molecules become released on the permeate side of the membrane, detected e.g. by pressure increase. This time lag is controlled by the thickness of the membrane and the diffusivity of the permeating molecules. In the interest of historical accuracy, it should be mentioned that the earliest article on the time lag method is given by Daynes 1920. Later, the time lag technique was applied by Barrer 1951 in a number of his early studies and is described in detail in his book “Diffusion in and through solids” in 1951. The classical book “The Mathematics of Diffusion” (Crank 1975) describes the case of one-dimensional diffusion through a plate which can be used for the determination of DT. As a solution of the 2nd Fickian Law, Crank obtains Eq. (5) for the total amount Qt which has passed the plate of thickness l after time t for the case that the concentration C1 of the starting side of the plate is constant and on the other side kept zero

$$ Q_{t} = D_{T} C_{1} \frac{t}{l} - \frac{{lC_{1} }}{6} - \frac{{2lC_{1} }}{{\pi^{2} }}\mathop \sum \limits_{n = 1}^{\infty } \frac{{\left( { - 1} \right)^{n} }}{{n^{2} }}\exp \left( {\frac{{ - D_{T} n^{2} \pi^{2} t}}{{l^{2} }}} \right) $$
(5)

Since the function exp(−DTn2π2t/l2) goes to zero for \( t \to \infty \), Eq. (5) becomes a linear function of time, as e.g. recently shown (Dudek and Borys 2019; Montelone et al. 2018; Bowen et al. 2004). From the time lag t = l2/6DT, the transport (or Fickian) diffusion coefficient DTcan be determined as shown in Eq. (6).

$$ Q_{t} = \frac{{D_{T} C_{1} }}{l} \left( {t - \frac{{l^{2} }}{{6D_{T} }}} \right) $$
(6)

In the case of a single component permeation, Qt can be easily recorded by the pressure increase in the permeate chamber. In case of mixed gas permeation, the partial pressures must be recorded by an in situ technique (spectroscopy, e.g. IR) or a technique that needs only tiny amounts of analyte (e.g. mass spectrometry).

The simple time lag approach works for both dense non-porous membranes such as organic polymers, oxygen ions or proton conducting ceramics, hydrogen transporting metals such as Pd (consider here Sieverts law) and nano/micro porous membranes such as zeolites, MOFs, COFs, GO or silica. The applications of the time lag method for the determination of diffusion coefficients DT from thin molecular sieve layers is based on the pioneering studies of Hayhurst and his student Paravar who applied this technique to measure the diffusivity along the long axis of a large silicalite-1 crystal embedded in a polymer (Hayhurst and Paravar 1988). Later, Shah used the time lag technique to determine the diffusivities of aromatics in a large silicalite-1 crystal in epoxy (Shah and Liou 1994). The time lag method was developed and adopted to zeolites membranes by Ruthven under special attention of the Langmurian type of adsorption (Ruthven 2007).

2.2 Approximation for steady state using Fick’s 1st law

Two approaches for the determination of diffusion coefficients from steady state permeation studies are common.

(i) As shown recently (Chmelik et al. 2018), Fick’s 1st law as given as Eq. (1) describes the flux density jx in x-direction against the concentration gradient dc/dx with DT as proportionality factor. When we approximate the gradient of the concentration by the concentration difference Δci divided by the membrane thickness δ, we obtain for the flux density j in x-direction Eq. (7)

$$ j_{x} = - D_{T} \frac{\partial c}{{\partial x}} \approx - D_{T} \frac{{C_{i} }}{\delta } $$
(7)

This means, from the measurement of the flux j and the knowledge of the concentrations in the membrane facing the feed and the permeate side, the transport diffusivity DT can be roughly estimated.

(ii) Following Eq. (3) Pi = Si⋅DT, from the independent measurement of the membrane permeability Pi and the adsorption constant (amounts of gas adsorbed per pressure, called solubility Si which can be derived from adsorption isotherms), the transport diffusion coefficient DT can be estimated.

Equation (3) holds true also for mixtures. Assuming a partial pressure difference Δpi of a binary mixture A/B across the membrane and linear adsorption isotherms (Henry) ci = Hi\(\cdot\)pi, the ratio of the flux densities ji is given in Eq. (8)

$$ \frac{{j_{A} }}{{j_{B} }} = \frac{{D_{A} }}{{D_{B} }}\frac{{c_{A} }}{{c_{B} }} = \frac{{D_{A} }}{{D_{B} }}\frac{{H_{A} p_{A} }}{{H_{B} p_{B} }} = \alpha_{{diff\left( {A,B} \right)}} \cdot \alpha_{{ads\left( {A,B} \right)}} $$
(8)

with the ratio of the diffusion coefficients as diffusion selectivity αdiff(A,B) = DA/DB and the ratio of the adsorbed guest molecules as an adsorption selectivity αads(A,B) = cA/cB = HApA/HBpB. The guest concentrations ci can be expressed through an adsorption isotherm, here Henry. However, due to the simplifications only effective diffusion coefficients can be evaluated. Since DT is loading dependent and there is a concentration difference Δci over the membrane, the lowest diffusivity controls the mass transport, which is usually the diffusivity in the low-loading area of the membrane since the transport diffusivity DT increases with loading (Krishna et al. 2004; Kärger et al. 2020).

2.3 Experimental techniques for the determination of diffusion coefficients from steady state permeation measurements

The simplest but most powerful method for the determination of the flux through a membrane is monitoring the pressure increase on the permeate side of the membrane in a steady state permeation study and evaluating the data according to the simplified Fickian 1st law acc. to Eq. (7). For small loading steps and for short permeation time, a linear increase of the pressure with permeation time on the permeate side is observed and justifies this procedure. This determination of the flux j is an easy standard method, the determination of diffusion coefficient DT is not correct due to the changing boundary conditions (the guest concentration in the porous membrane increases with increasing pressure in the permeate chamber) and the loading dependence of DT during the permeation experiment. On the other hand, also mixed gas data can be determined in this way if the gas atmosphere on the permeate side can be analysed by in situ techniques or techniques without extracting big gas volumes such as mass spectrometry.

Often, the so-called Wicke Kallenbach technique (Wicke and Kallenbach 1941) is applied for the study of multicomponent permeation. The characteristics of this technique is the identical gas pressure on feed and permeate side of the membrane with the flux induced by differences in the relevant partial pressures. However, this technique has its limits if it is not properly applied. In the classical experiment, the feed gas was a mixture CO2/N2 at 1 bar (pCO2 = 0.13 bar, pN2 = 0.87 bar). On the permeate side of the carbon membrane was pure N2 at 1 bar as sweep gas to transport the permeated CO2 to the TCD (thermal conductivity detector). This experimental setup was justified since the only major gradient in partial pressure is that for CO2. There is also a slight gradient in the partial pressure of N2 between the sweep side (pN2 = 1 bar) and the feed side (pN2 = 0.87 bar) which causes a counter flow of N2 but this slight N2 counter flow does not disturb the surface diffusion controlled CO2 transport since CO2 adsorbs much better on carbon surfaces than N2. These principles of the historic Wicke Kallenbach technique are often violated nowadays. As an example, if one has a 50%/50% H2/CH4 mix at 1 bar on the feed side of a molecular sieve membrane with 4 Å pores, and N2 as sweep gas on the other side of the membrane, hydrogen will permeate faster through the membrane than methane and a H2/CH4 selectivity > 1 can be determined. However, there will be also a flux of nitrogen from the sweep to the feed side. This counter flow situation increases the H2/CH4 selectivity but reduces the H2 flow. The effects of the counter flow of the sweep gas from the permeate to the feed side of the membrane can be suppressed to some extent when the feed gas is under elevated pressure of up to 5 bar.

The most practice-relevant but also scientifically healthy testing of a membrane, however, is simulating the technical permeation process with medium pressure of 5 to 15 bar on the feed side and without any sweep gas on the permeate side, operating at temperatures above room temperature. The pressure on the permeate side is caused by the permeated gas and can be kept at about 1 bar or slightly above. However, using this permeation protocol can result in a severe drop in the permeances. On the permeate side of the membrane, the porous membrane is in contact with the permeated gas at a pressure of about 1 bar. Due to the usually curved adsorption isotherm (Langmuir-type), at 1 bar and typical permeation temperatures slightly above room temperature, the permeated component is to a certain degree re-adsorbed by the nanoporous membrane which reduces the driving force for the flux according to 1st Fickian Law. Further, at high pore filling also the diffusion coefficients DA and DB can average out which means that the diffusion selectivity collapses. The elevated pressure on the feed side causes almost complete pore filling of the membrane in contact with the feed gas. Any further pressure increase cannot increase the pore filling.

3 Case studies

3.1 Diffusion coefficients from permeations studies through supported nanoporous membranes

Depending on the relationship between mean free path of a gas molecule which is determined by temperature and pressure, different diffusion mechanisms can govern the mass transport through a pore membrane. For mean free path < pore diameter, gas–gas collisions are dominant and the fluid flow is determined by the gas viscosity. If the free path becomes of the order of the pore diameter, gas-wall collisions become dominant and transport is described by Knudsen diffusion mechanism. If the size of the adsorbed atoms/molecules becomes comparable to the size of the pores of a membrane or an adsorbent (< 1 nm), we call the corresponding mass transport configurational diffusion. The interplay of adsorption and diffusion for the flux and selectivity of porous membranes is described in fundamental papers (Ruthven 2009; Krishna 2012).

In two pioneering papers (Bux et al. 2010, 2011) diffusion data from membrane permeation were correlated with directly measured diffusivities from IR sorption uptake microscopy. In both studies, diffusion coefficients could be obtained by measuring (i) the membrane permeability and in another independent study (ii) adsorption isotherms. Following Eq. (3) \(P_{i} = S_{i} \cdot D_{T}\) the diffusion coefficient DT (as single gas or in a mixture) could be derived as ratio of its permeability Pi and solubility Si. The transport diffusion coefficients DT calculated in this way can be compared with the transport diffusion coefficients calculated from IR sorption uptake microscopy.

Bux et al. 2010 studied the permeation behaviour of CO2/CH4 as binary mixture and as single components through the 30 µm thick ZIF-8 membrane shown in Fig. 2. Table 2 gives the measured permeabilities, measured loadings from adsorption isotherms and calculated transport diffusion coefficients acc. to Eq. (3) \(P_{i} = S_{i} \cdot D_{T}\) with Pi as permeability of a gaseous component i as the product of the solubility Si of gas i and its diffusion coefficient DTi. Despite the simplicity of the approach acc. to Eq. (3), the coincidence of the diffusion coefficients derived from membrane permeation and the corresponding transport diffusivity DT derived from IR sorption uptake microscopy is surprising. This agreement is found for single components as well as for the binary mixture. There is even a satisfactory agreement with the “corrected diffusivity” D0 derived from mixed matrix membrane permeation at 35 °C: D0 CO2 ≈1.5 10–10 m2 s−1, and D0 CH4 ≈ 0.3 10–10 m2 s−1 (see Zhang et al. 2012). At low loading, the transport diffusivity DT is comparable with the corrected diffusivity D0 (DT = D0dlnp/dlnc(p) which gives for a Langmuir isotherm DT = D0/(1-Θ). For pore systems with sufficiently narrow windows, self- and corrected diffusivities can be expected to coincide (Chmelik et al. 2016).

Fig. 2
figure 2

Cross section of a typical supported molecular sieve membrane. a While the top layer of technical membranes should be sub-µm thin, for mechanistic studies thick molecular sieve films are helpful since the rate limiting flow resistance is then the nthick anoporous top layer and not the support. Here a microporous titania support has been used to facilitate the growth of the 30 µm ZIF-8 layer (Bux et al. 2009). b The molecular sieve film is usually grown on a porous support with pores in the ultrafiltration range (10 … 100 nm) to avoid infiltration of the MOF or zeolite synthesis solution. To reduce flow resistance, the support is built asymmetrically

Full size image
Table 2 Calculation of transport diffusion coefficients DT of CO2 and CH4 in ZIF-8 from single gas and mixed gas permeation at room temperature and 1 bar. The permeabilities Pi were measured in membrane permeation studies (Bux et al. 2010), adsorption constants Si taken from published adsorption studies (McEwen et al. 2013) and DT was calculated acc. to Eq. (3) DT = Pi/Si
Full size table

Another example for the determination of transport diffusion coefficients of guest molecules in MOFs is from the permeation of ethene/ethane mixtures through a ZIF-8 membrane (Bux et al., 2011). Table 3 shows the permeability data from membranes permeation, the solubility data from adsorption studies, the diffusion coefficients derived from these data acc. to Eq. (3), and reference data for comparison. The supported 30 µm thick ZIF-8 membrane is shown in Fig. 2. For the single components, again a good accordance of the transport diffusion coefficients from single gas permeation and from IR sorption uptake microscopy as reference is found. The calculated data are also in good agreement with transport diffusion coefficients from classical sorption uptake studies (Verploegh et al. 2015) at 308K for a loading of about 5 molecules/u.c. with gravimetric/volumetric control: DT Ethene ≈ 10–10 m2 s−1 and DT Ethane ≈ 0.5 10–10 m2s−1. Also MD simulations (Krokidas et al. 2017) and (Verploegh et al. 2015) give transport diffusivities of the same order of magnitude. It is interesting to note that the self-diffusivity D of ethane in ZIF-8 was found in 13C PFG NMR studies (Mueller et al. 2015) under similar experimental conditions to amount to be D ≈ 0.8 10–10 m2s−1 which is again a good coincidence with the DT value of 10–10 m2 s−1 derived from membrane permeation. This finding is in agreement with the expectation that the corrected diffusivity D0 ≤ DT according to DT = D0/(1-Θ) for a Langmuir isotherm and, further, that for pore systems with sufficiently narrow windows, self-diffusion coefficient D and corrected diffusion coefficient D0 coincide (Chmelik et al. 2016).

Table 3 Calculation of diffusion coefficients Di of ethene and ethane in ZIF-8 from single gas and mixed gas permeation studies at room temperature and 6 bar
Full size table

However, while in a binary mixture the ethane and ethene diffusivities average out as observed in IR sorption uptake microscopy (Bux et al. 2011), this finding is not observed in membrane permeation. The ethene/ethane mixed gas permeation was conducted under a feed pressure of 6 bar with 1 bar on the permeate side. This big pressure gradient causes big differences in the loading of the guest molecules over the membrane and it is known that the diffusion of guest molecules in ZIF structures is extremely dependent on the loading.

3.2 Diffusion studies on mixed matrix membranes (MMMs)

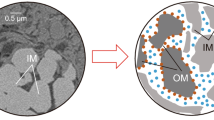
Supported thin (< 1 µm) film membranes (see Fig. 2) of nanoporous materials such as zeolites, MOFs or COFs are difficult to scale up, no technologies for a continuous production exist, the porous ceramic or metallic supports for the thin nanoporous membrane top layer are expensive to produce. Therefore, the concept of MMMs has been developed: The nanoporous material is given as powder (filler) to a polymer of known permeation ability (continuous phase). Using established organic polymer membrane technologies such as hollow fiber spinning or flat sheet technologies, membrane areas of the order of km2 per day can be produced. The working principle of an MMM is illustrated in Fig. 3. Assuming that the polymer shows a slight selectivity for the transport of component A in comparison with B (free volume theory), this selectivity in favor of A can be increased by the filler if (i) component A diffuses faster through the filler particle than B, and if (ii) the concentration of A in the filler is higher than that of B due to a preferred adsorptive enrichment of A.

Fig. 3
figure 3

Mixed Matrix Membranes (MMMs). a Preparation errors: 1: Some parts of the polymer protrude into the pore system of the filler thus blocking the surface of the filler particle like a “surface barrier”. 2: Ideal case, perfect preparation. 3: Due to insufficient interaction between polymer and filler (no wetting), a gap can occur where gas transport is non-selective. b Next generation MMM: Nanosheets allow the selective transport of component A but are impermeable for component B. The parallel orientation of the nanosheets can be easily achieved by tape casting (shrinking due to solvent evaporation) or extrusion/spinning (orientation due to shear forces)

Full size image

The development of MMMs is pushed by a large industrial interest and most of the MMM developments follow the principle “trial and error”: Give some powder of a promising nanoporous filler to a known polymer and hope for improvements of the A/B selectivity. However, the preparation of high-quality MMMs is not trivial. Figure 3a shows some preparation errors which might occur. However, our group has experience in the preparation of crack-free layers of different supported MOF membranes (Diestel et al. 2015a). Figure 3b gives the next generation of MMMs with oriented porous nanosheets in a polymer following Cusslers selective flake concept (Cussler 1990). There are some recent prominent papers to synthesize porous nanosheets and to arrange them as membrane stack as shown in Fig. 3b, zeolite nanosheets (Kumar et al. 2020), and MOF nanosheets (Rodenas et al. 2015 and Peng et al. 2014). The perspectives of such membrane structure have been recently highlighted recently (Caro and Kärger 2020).

There are only a few attempts to get a complete fundamental understanding of molecular diffusion inside an MMM (Hwang et al. 2018; Mueller et al. 2015). On the one hand, the independent study of diffusion in the filler as well as in the polymer can be helpful for the development of new MMMs. On the other hand, also from permeation studies on MMMs the transport diffusion coefficient DT of the permeating molecules in the nanoporous filler can be determined. It has to be mentioned that correct DT values can be only derived from permeation studies on MMMs in the absence of surface barriers (Saint Remy et al. 2015). In the case of an unproper preparation of MMMs, the polymer can block the pores of the filler as indicated in Fig. 3a.

It is clear that the selectivity of such MMM for a gas mixture A/B results from transport through the A-selective polymer and the highly A-selective filler. The permeation properties of an MMM can be predicted from the single gas permeabilities PA and PB through the pure polymer as continuous phase, PA,c and PB,c, and through the pure filler material, PA,d and PB,d as the dispersed phase as shown in Eq. (9). φd is the volume fraction of the dispersed filler. The permeability PMMM of an MMM for a single component gas is described by the so called Maxwell Equation (Monsalve-Bravo and Bhatia 2018; Gonzo et al. 2006; Mahajan and Koros 2002) originally derived for the electrical conductivity of particles in a matrix (Maxwell 1873). However, there is a close analogy between electrical/thermal conduction and membrane permeation (Pal 2008).

$$ P_{MMM} = P_{c} \left[ {\frac{{P_{d} + 2P_{c} - 2\varPhi_{d} (P_{c} - P_{d})}}{{P_{d} + 2P_{c} +\varPhi_{d} (P_{c} - P_{d} )}}} \right] $$
(9)

The role of diffusion becomes evident if the permeability coefficient P of the dispersed filler Pd and of the continuous polymer phase Pc are estimated as the product of diffusion coefficient and adsorption coefficient acc. to Eq. (3). If the volume fraction of the dispersed filler phase is zero (φd = 0), Eq. (9) predicts identical permeabilities for the MMM and the neat polymer membrane. For an impermeable non-porous filler (Pd = 0), PMMM is predicted from Pc as a polymer diluted by an inert material.

Like for single component permeation through MMs, also for gas mixtures the transport diffusion coefficient DT can be derived acc. to Eq. (3). The ratio of the measured permeabilities PMMM of the two single components A and B through an MMM give an ideal separation factor, also called ideal permselectivity αideal of the MMM for the binary gas mixture A/B. From the single gas permeabilities of components A and B acc. to Eq. (10), an ideal selectivity as the ratio of the single gas permeabilities through an MMM can be formed. Analog to Eq. (4), the membrane selectivity can be split in a diffusion selectivity and an adsorption selectivity. Also in the case of permeation through MMMs, this splitting of the selectivity into a diffusion and an adsorption selectivity works.

$$ \alpha_{MMM,A/B}^{ideal} = \frac{{P_{MMM,A}^{measured} }}{{P_{MMM,B}^{measured} }} $$
(10)

A fine example, how to derive diffusion coefficients DT of small molecules in the nanoporous filler of MMMs comes from the Koros group (Zhang et al. 2012). Based on the solution-diffusion model for permeation in MMMs and in conjunction with adsorption isotherms, the transport diffusivities DT, and using the Darken relation the corrected diffusion coefficients D0 have been calculated. The transport diffusion coefficients thus determined agree very well with the transport diffusivities determined from sorption uptake measurements on big single crystals of ZIF-8 with gravimetric/volumetric control or with those from IR microscopy (Bux et al. 2009 and Bux et al. 2010). At low loading or after the Darken correction, the transport diffusivities DT from membrane permeation agree with the self-diffusivities D from PFG NMR (Pantatosaki et al. 2011).

Just recently it was found (Knebel 2020) that the addition of the MOF nano-powder of ZIF-67 (ZIF-67 is the Co-variant of the Zn-containing ZIF-8) to the two standard membrane polymers (i) 6FDA-DAM and (ii) 6FDA-DHTM-Durene can improve the separation performance of the resulting MMM in the propylene/propane separation due to a modified diffusion behaviour. Adding the MOF powder to the polymers and producing an MMM, increased the propylene/propane permeation selectivity from 4 to 15 (for 6FDA-DAM) and from 7 to 20 (for 6FDA-DHTM-Durene). Having in mind Eq. (4), \(\alpha_{A/B} = \frac{{P_{A} }}{{P_{B} }} = \frac{{S_{A} }}{{S_{B} }} \cdot \frac{{D_{A} }}{{D_{B} }} = \alpha_{{sol\left( {A,B} \right)}} \cdot \alpha_{{diff\left( {A,B} \right)}}\) the increased propylene/propane selectivity can be either an adsorption or a diffusion effect.

Therefore, deconvolution of the permeability (P) into the product of sorption coefficient (solubility, S) and diffusion coefficient (diffusivity, DT) was performed based on the sorption–diffusion model to gain further insight into the separation mechanism. The transport diffusion coefficients DT for the MMM was determined from the time lag method using Eq. (6). The solubility coefficient of the MMM was determined by adsorption studies. In these adsorption studies, the isotherms of propylene and propane on the pure ZIF-67 powders were found to be identical. This means, that the addition of the MOF filler to the two polymers did not alter the adsorption selectivity of the polymers. This experimental finding is in complete accordance with the expectations. The Co2+ position in ZIF-67 is not accessible to the guest molecules. Therefore, the adsorption isotherms of propylen and propane on ZIF-67 are comparable. From the identical adsorption isotherms of propylene and propane on the pure filler ZIF-67 it can be concluded that the improvement of the MMM in olefin/paraffin separation must be due to a modified diffusion behaviour. This is the case indeed. Adding MOF powder to the two polymers, increases the diffusion selectivity propylene/propane from initially 1…2 for the pure polymers to about 20 …30 for the MMMs containing almost 50 wt.% MOF powder. This increased diffusivity for the MOF-containing MMMs is a clear molecular sieving effect: Propylene is slightly slimmer than propane, with both diameters being close to the diameters of the “windows” between adjacent cavities in ZIF-67. In, e.g., MOF ZIF-8 this difference has been found to give rise to an order-of-magnitude difference in the diffusivities (Chmelik 2015; Chmelik et al. 2016).

4 Conclusions

Surprisingly, the solution-diffusion model of permeation, which was developed for polymer membranes, can be successfully applied to gas transport through nanoporous membranes as well. With a relatively high accuracy, transport diffusion coefficients DT can be derived from single gas and mixed gas permeation studies on supported membrane layers as well as mixed matrix membranes. The diffusion coefficients derived from permeation experiments are transport diffusivities DT and agree well with those from sorption uptake studies, MD simulations and self-diffusion coefficients of pulsed field gradient NMR. However, it cannot be claimed that permeation experiments will become a standard technique for the determination of diffusion data. Due to the nature of a permeation experiment, the guest concentrations on the two sides of a membrane are different which results in averaged values of the loading-dependent diffusion data. Another problem is that even small preparation defects in a membrane cause huge effects in the permeation data and in the diffusion data derived from.