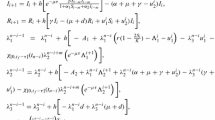1 Introduction

Mathematical models are often used to study disease spread, with the susceptible-infectious-recovered (SIR) model being preferred for disease spread via droplet and aerosol. For example, the SIR model has been used to study pandemic flu (Bootsma and Ferguson 2007; Carrat et al. 2006; Chowell et al. 2005; Mills et al. 2004), seasonal flu (Bridges et al. 2003; Cauchemez et al. 2004; Dushoff et al. 2004), SARS (Lipsitch et al. 2003; Riley et al. 2003; Wearing et al. 2005), HIV/AIDS (Magombedze et al. 2009; Okosun et al. 2013) and smallpox (Elderd et al. 2006; Kaplan et al. 2002; Riley and Ferguson 2007). These studies use SIR models to simulate the disease outbreak and evaluate the effectiveness of selected control measures under various predefined scenarios. Optimal control theory approaches based on mathematical models of epidemics can provide valuable information about how best to control infectious disease outbreaks, and in particular, can determine the optimal distribution of limited resources during epidemics. We refer to Abakuks (1974), Behncke (2000), Clancy (1999), Hansen and Day (2011), Lin et al. (2010), Morton and Wickwire (1974), Sethi and Staats (1978), Sethi (1978) and Wickwire (1975) for studies of SIR model based on optimal control that minimizes a prescribed objective function.

Some of the earlier work in this area was by Abakuks. Abakuks (1974) investigated the optimal control of a simple deterministic SIR model, and determined the optimal vaccination strategy under the assumption that, at any instant, either all or none of the susceptibles are vaccinated. Shortly after the publication of Abakuks (1974), Morton and Wickwire (1974) studied the same problem but with two notable differences. They found that the optimal vaccination policy is a Bang–Bang control from maximal vaccination to no vaccination. Behncke (2000) expanded Wickwire’s results to models with more general contact rates. Sethi & Staats (1978) and Sethi (1978) derived optimal closed-form results for isolation and immunization policies using an SI model. The control is to either isolate and vaccinate at a maximum rate or do nothing. Clancy (1999) studied the properties of optimal policies for isolation and immunization assuming that all infectious individuals can be immediately isolated and all susceptible individuals can be immediately immunized. The policy takes no action when the number of infectious is below an optimal threshold and immediately isolates and/or immunizes when the number exceeds the threshold. However, no analytical solution for an optimal control problem of epidemics was discussed. Hansen and Day (2011) extended that of Abakuks (1974), Behncke (2000), Clancy (1999), Morton and Wickwire (1974), Sethi and Staats (1978), Sethi (1978) by examining the kind of resource constraints mentioned earlier. Specifically, the simple SIR model with mass action contact is revisited, and the analytical solutions rather than numerical ones are obtained. For the vaccination model (Problem 2 in Hansen and Day 2011), under an assumption of total vaccine supply being limited, the optimal policy is to vaccinate with maximal effort until either all of the resources are used up or the epidemic is over.

However, in preparation for an outbreak, the allocated resources are sometimes limited at each day besides stockpiling a fixed amount of vaccine and other drugs over time. In order to find out the relation between a vaccination policy and environment factors, we will still consider a basic SIR epidemic model and suggest a vaccination program under the assumption of daily vaccine supply, rather than total vaccine supply in Hansen and Day (2011), being limited. Unlike Hansen and Day (2011), our objective is to minimize the total cost of disease with linear control, the purpose is also to study analytically and numerically how Bang–Bang control is influenced with the initial conditions, model parameters and constraint conditions.

2 Statement of the Optimization Problem

The following standard deterministic SIR model is used throughout this article (Anderson and May 1992; Hansen and Day 2011; Morton and Wickwire 1974)

$$\begin{aligned} \begin{array}{l} \dot{S}=-\beta SI-uS,\\ \dot{I}=\beta SI-\mu I, \end{array} \end{aligned}$$
(1)

where \(S\) and \(I\) are the numbers of susceptible and infected hosts (a dot indicating time derivative), \(\beta\) is the transmission rate, \(\mu\) is the per capita loss rate of infected individuals through both mortality and recovery, and \(u\) is the per capita rates of vaccination, \(0\le u\le u_{max}\). By definition, vaccination has a direct effect only on susceptible individuals.

The model (1) may be used to describe the diseases like small-pox, influenza, SARS and HIV/AIDS in a particular situation. Although the model presented is simple, it provides notation, concepts, intuition and foundation for considering more refined models.

From (1), we have

$$\begin{aligned} \begin{array}{l} S(t)=S(t_0)e^{-\int _{t_0}^{t_f}(\beta I+u)dt}>0,\,\forall \ t\in [t_0,t_f],\\ I(t)=I(t_0)e^{\int _{t_0}^{t_f}(\beta S-\mu )dt}>0,\,\forall \ t\in [t_0,t_f], \end{array} \end{aligned}$$
(2)

if the initial states \(S(t_0)>0, I(t_0)>0\).

Commonly, in preparation for an outbreak of epidemics, a fixed amount of vaccine are stockpiled and supplied at each day. In this paper, we will explore the impact of the following control inequality constraints (limited vaccine supply) on the optimal vaccination policies:

$$\begin{aligned} uS\le \omega , \end{aligned}$$
(3)

where \(\omega\) represents the total amount of vaccines available at the time \(t\in [t_0,t_f]\).

As in Behncke (2000), Castilho (2006), Greenhalgh (1988), Morton and Wickwire (1974), Sethi (1974, 1978), Wickwire (1975), our objective is to design a vaccination program intensity over time such that the total cost (intensity) of disease is minimized, i.e.

$$\begin{aligned} \min J=\int \limits _{t_0}^{t_f}(C_dI+k u))dt, \end{aligned}$$
(4)

where \(C_d\) is social cost per infective, \(k\) is cost per unit level of vaccination program. So, our optimal control problem can be formulated as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \min &{} J=\int _{t_0}^{t_f}(C_dI+k u))dt,\\ s.t. &{} \dot{S}=-\beta SI-uS, \\ &{} \dot{I}=\beta SI-\mu I,\\ &{} uS\le \omega ,\\ &{} S(0)=S_0, I(0)=I_0, u\in [0,u_{max}], \end{array}\right. \end{aligned}$$
(5)

and the corresponding optimal control problem without any constraints is

$$\begin{aligned} \left\{ \begin{array}{ll} \min &{} J=\int _{t_0}^{t_f}(C_dI+k u))dt,\\ s.t. &{} \dot{S}=-\beta SI-uS, \\ &{} \dot{I}=\beta SI-\mu I,\\ &{} S(0)=S_0, I(0)=I_0, u\in [0,u_{max}]. \end{array}\right. \end{aligned}$$
(6)

3 Lemma

For the sake of convenience, we state the Maximum Principle to be used in the sequel and we refer to Chiang and Wang (1999), Kamien and Schwartz (1991) for more details. We consider the following optimal control problem with control inequality constraints:

$$\begin{aligned} \begin{array}{ll} \min J &{}=\phi (t_f,x(t_f))+\int _{t_0}^{t_f}L(t,x,u)dt,\\ s.t.&{}\\ &{}\dot{x}=f(t,x,u), \ x(t_0)=x_0, u\in U,\\ &{}C(t,x,u)\le \omega ,\\ &{}\psi (t_f,x(t_f))=0, \end{array} \end{aligned}$$
(7)

where, \(x\in \mathbb {R}^n\) is the state vector, \(u\in \mathbb {R}^m\) is the control vector, \(\phi , L, C\) and \(\psi\) are vector functions of their respective variables, and have continuous partial derivatives with respect to all of their arguments, \(\omega\) is a constant vector, \(U\) is an admissible control region.

Lemma 3.1

For optimal control problem (7), if \(u(t)\) is an optimal control with \(x(t)\) being the corresponding optimal path, then there exist nontrivial vector functions \(\lambda\) and \(\xi ,\) nontrivial constant vectors \(\nu ,\) and a slack variable \(\alpha\) such that the following conditions are satisfied:

  • (1) For the off-boundary subarc (\(\xi =0\)),

    $$\begin{aligned}&\dot{x}=f,\, \dot{\lambda }=-H_x^T,\\&u \, \text{ is } \text{ determined } \text{ from }\ H_u=0,\,\alpha ^2=\omega -C,\\&\psi =0,\, \bar{H}|_{t=t_f}=-G_{t_f},\,\lambda (t_f)=G_{x(t_f)}, x(t_0)=x_0; \end{aligned}$$

  • (2) For the on-boundary subarc (\(\alpha =0\)),

    $$\begin{aligned}&\dot{x}=f,\,\dot{\lambda }=-\bar{H}_x^T,\\&u \,\text{ is } \text{ determined } \text{ from }\,C(t,x,u)=\omega ,\,\xi \,\text{ from }\,\bar{H}_u=0,\\&\psi =0,\,\bar{H}|_{t=t_f}=-G_{t_f},\,\lambda (t_f)=G_{x(t_f)}, x(t_0)=x_0; \end{aligned}$$

  • (3) For a corner point \(c\) where two subarcs joint,

    $$\begin{aligned} H|_{t=c+}=H|_{t=c-},\,\lambda (c+)=\lambda (c-), \end{aligned}$$

where, \(H(t,x,u,\lambda )=L(t,x,u)+\lambda ^T(t)f(t,x,u)\) is Hamiltonian, \(\bar{H}(t,x,u,\lambda ,\xi ,\alpha )=H(t,x,u,\lambda )+\xi ^T(C-\omega +\alpha ^2)\) is extended Hamiltonian, \(G(t_f,x(t_f))=\phi (t_f,x(t_f))+\nu ^T\psi (t_f,x(t_f))\).

Notice that, if the optimal system (7) is autonomous, then the Hamiltonian \(H\) is constant, i.e.

$$\begin{aligned} H(x,u,\lambda ,\lambda _1,\lambda _2)=\text{ const },\ \forall \ t\in [t_0,t_f]. \end{aligned}$$

4 Optimal Control, Analytical Results

It is not difficult to see that the optimal control problem (5) admits an optimal solution (see Bryson and Ho 1975; Geering 2007; Hull 2003). So, we need only find the necessary conditions.

This is an optimal control problem with a control inequality constraint. The key is to determined whether there exist any corner points for the optimal control problem (5).

4.1 Optimal Vaccination Policy Without Any Constraints

In this section, we study the optimal control problem (6) (without the control inequality constraint (3)). Denote Hamiltonian \(H(S,I,u,\lambda _S,\lambda _I)\) as

$$\begin{aligned} H=C_dI+ku+\lambda _S(-\beta SI-uS)+\lambda _I(\beta SI-\mu I), \end{aligned}$$
(8)

where \(\lambda _S,\lambda _I\) are co-state variables. By the Lemma 3.1, we have the following necessary conditions:

$$\begin{aligned}&\dot{S}=-\beta SI-u S,\end{aligned}$$
(9)
$$\begin{aligned}&\dot{I}=\beta SI-\mu I,\end{aligned}$$
(10)
$$\begin{aligned}&\dot{\lambda }_S=(\beta I+u)\lambda _S-\beta I\lambda _I,\end{aligned}$$
(11)
$$\begin{aligned}&\dot{\lambda }_I=-C_d+\beta S\lambda _S+(\mu -\beta S)\lambda _I,\end{aligned}$$
(12)
$$\begin{aligned}&H(S,I,u,\lambda _S,\lambda _I)\le H(S,I,u_1,\lambda _S,\lambda _I),\,\forall \ u_1\in [0,u_{max}],\end{aligned}$$
(13)
$$\begin{aligned}&S(t_0)=S_0,\,I(t_0)=I_0,\end{aligned}$$
(14)
$$\begin{aligned}&\lambda _S(t_f)=0,\,\lambda _I(t_f)=0,\end{aligned}$$
(15)
$$\begin{aligned}&H(S,I,u,\lambda _S,\lambda _I)\equiv 0, \,\forall \ t\in [t_0,t_f]. \end{aligned}$$
(16)

Thus,

$$\begin{aligned} H&= -I\dot{\lambda }_I+(k-\lambda _S S)u\nonumber \\&= -S\dot{\lambda }_S+ku+C_dI-\mu I\lambda _I\\&= 0,\ \forall \ t\in [t_0,t_f].\nonumber \end{aligned}$$
(17)

From (13), we have

$$\begin{aligned} u=\left\{ \begin{array}{ll} u_{max},&{}\quad k-\lambda _S S<0,\\ ?,&{}\quad k-\lambda _S S=0,\\ 0,&{}\quad k-\lambda _S S>0, \end{array}\right. \end{aligned}$$

and, by (17)

$$\begin{aligned} \dot{\lambda }_I(t)\le 0,\quad \forall \,t\in [t_0,t_f]. \end{aligned}$$
(18)

First, we will show that the optimal control of (6) is Bang–Bang (that is, has no singular components).

If, now, \(k-\lambda _S S=0\) on some sub-interval \(J\subset [t_0,t_f]\), then

$$\begin{aligned} \lambda _S=\frac{k}{S}>0,\,\dot{\lambda }_S=-\frac{k}{S^2}\dot{S}>0, \,\forall \,t\in J, \end{aligned}$$

i.e., \(\lambda _S>0\) and \(\lambda _S\) is increasing on \(J\), that is on the left of the final point \(t_f\), which implies that there exists an extremum point \(t_c\in (t_0,t_f)\) such that \(\dot{\lambda }_S(t_c)=0\) due to the differentiability of \(\lambda _S\) and \(\lambda _S(t_f)=0\). This, in turn, will results in

$$\begin{aligned} \dot{S}(t_c)=0. \end{aligned}$$

Thus, from (9), we get

$$\begin{aligned} I(t_c)=-\frac{u(t_c)}{\beta }, \end{aligned}$$

which contradict (2). Hence, the optimal control must be purely Bang–Bang.

Second, we will prove that the optimal control is as follows:

$$\begin{aligned} u=\left\{ \begin{array}{ll} u_{\max }, &{}\quad t\in [t_0,\tau ),\\ 0, &{}\quad t\in [\tau ,t_f]. \end{array}\right. \end{aligned}$$
  1. (1)

    Notice that \(k-\lambda _S S<0\) cannot occur on some final sub-interval \([t_e,t_f]\subset [t_0,t_f]\) due to \(\lambda _S(t_f)=0\), so \(u=u_{\max }\) is not optimal on final sub-interval \([t_e,t_f]\).

  2. (2)

    We will show that \(u\equiv 0\) is not optimal for the problem (6).

    In fact, \(u\equiv 0\) hints that \(\lambda _I\equiv 0\) due to (17) and (15). Thus, by (17) and (12), \(\dot{\lambda }_S=\frac{C_dI}{S}>0\) and \(\lambda _S=\frac{C_d}{\beta S}>0\), that is impossible owing to \(\lambda _S(t_f)=0\).

  3. (3)

    We show that the optimal control \(u=0\) cannot also begin in initial stages. If not, there exist two switches between 0 and \(u_{max}\), that is, there exist two times \(t_{c_1}, t_{c_2}: t_0\le t_{c_1}< t_{c_2}\le t_f\) such that

    $$\begin{aligned} u=\left\{ \begin{array}{ll} 0, &{}\quad t\in [t_0,t_{c_1})\,\left( \lambda _S -\frac{k}{S}<0\right) ,\\ u_{\max },&{}\quad t\in [t_{c_1},t_{c_2})\,\left( \lambda _S-\frac{k}{S}>0\right) ,\\ 0, &{}\quad t\in [t_{c_2},t_f]\,\left( \lambda _S-\frac{k}{S}<0\right) . \end{array}\right. \end{aligned}$$
    (19)

Then

$$\begin{aligned}&\left. \frac{d\left( \lambda _S-\frac{k}{S}\right) }{dt}\right| _{t=t_{c_1}}>0,\quad \left. \frac{d\left( \lambda _S-\frac{k}{S}\right) }{dt}\right| _{t=t_{c_2}}<0,\end{aligned}$$
(20)
$$\begin{aligned}&H(t_{c_i})=-S(t_{c_i})\dot{\lambda }_S+I(t_{c_i})(C_d-\mu \lambda _I(t_{c_i}))=0, \,i=1,2. \end{aligned}$$
(21)

From (20), (21) and (9), we have

$$\begin{aligned} \lambda _I(t_{c_1})<C_d+k\beta ,\quad \lambda _I(t_{c_2})>C_d+k\beta , \end{aligned}$$
(22)

which contradicts (18).

Therefor, We have the following result:

Theorem 4.1

For the optimal control problem (6), there exists a \(\tau \in [t_0,t_f]\) such that the optimal vaccination policy is

$$\begin{aligned} u=\left\{ \begin{array}{ll} u_{max},&{}\quad t\in [t_0,\tau ),\\ 0, &{}\quad t\in [\tau ,t_f]. \end{array}\right. \end{aligned}$$
(23)

That is, the optimal vaccination policy is to vaccinate with maximal effort until either all of the resources are used up or the epidemic is over.

Remark 1

The above Theorem 4.1 is similar with the Theorem 4.2 in Hansen and Day (2011), that is, the optimal vaccination policy without any constraints is similar to one with limited total vaccine supply, which implies that the impact of limited total resources on optimal vaccination policy (in Hansen and Day 2011) is indistinctive.

4.2 Optimal Vaccination Policy with Control Inequality Constraint

Next, we study the optimal control problem (5) (with a control inequality constraint (3)).

By (2), \(S(t)\) is decreasing and bounded, and the control inequality constraint (3) is inactive if \(\omega\) is large enough or \(u\) is sufficiently small. In this case, the optimal control problem (5) is one without any constraints, that is the case in Theorem 4.1.

We, now, suppose that \(S(t)\) and \(u(t)\) are the optimal path and the optimal control in Theorem 4.1 respectively. The optimal control problem (5) must fall into one of following two cases owing to the monotonicity and boundedness of \(S(t)\) and Bang–Bang of optimal control \(u(t)\):

Case I: \(\frac{\omega }{u_{\max }}\ge S(t_0)\) which implies that the inequality (3) is satisfied. This is equivalent to an optimal control problem without any constraints. This case is illustrated by the numerical simulation shown in the left panel of Fig. 1, where the parameters in (5) are taken as \(C_d=1, k=10, \beta =0.0003, \mu =0.03, S(0)=\hbox {1,000}, I(0)=10, \omega =55,\ t_f=60\) and \(u_{max}=0.05\).

Fig. 1
figure 1

The paths \(S(t)\) and the optimal control \(u(t)\) for the parameters \(C_d=1, k=10, \beta =0.0003, \mu =0.03, S(0)=\hbox {1,000}, I(0)=10, \omega =55, t_f=60\) and \(u_{max}=0.05\)

Full size image

Case II: \(S(\tau )\le \frac{\omega }{u_{\max }}< S(t_0)\) which hints that there exists a corner point \(t_c\in [t_0,\tau ]\). From Lemma 3.1, \(u(t)\) is determined from \(u(t)S(t)=\omega\) on the boundary subarc \([t_0,t_c]\). It follows that

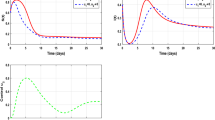
$$\begin{aligned} u(t)=\frac{\omega }{S(t)},\quad t\in [t_0,t_c]. \end{aligned}$$
(24)

This case is illustrated by the numerical simulation shown in the left panel of Fig. 2, where the parameters in (5) are taken as \(C_d=1, k=10, \beta =0.0003,\ \mu =0.03, S(0)=\hbox {1,000},\ I(0)=10,\ \omega =20,\ t_f=60\) and \(u_{max}=0.05\).

Fig. 2
figure 2

The paths \(S(t)\) and the optimal control \(u(t)\) for the parameters \(C_d=1, k=10, \beta =0.0003, \mu =0.03, S(0)=\hbox {1,000}, I(0)=10, \omega =20, t_f=60\) and \(u_{max}=0.05\)

Full size image

Therefor, We have the following Theorem 4.2.

Theorem 4.2

Depending on the initial conditions, model parameters and constraint conditions, we have the following optimal vaccination strategies for the optimal control problem (5):

  • (i) Let \(S(t)\) and \(u(t)\) be the optimal path and the optimal control in Theorem 4.1 respectively (without the constrain \(u(t)S(t)\le \omega\)). If \(\frac{\omega }{u_{\max }}\ge S(t_0)\), then optimal control is one in Theorem 4.1, i.e., there exists a \(\tau \in [t_0,t_f]\) such that the optimal vaccination policy is

    $$\begin{aligned} u=\left\{ \begin{array}{ll} u_{max},&{}\quad t\in [t_0,\tau ),\\ 0, &{}\quad t\in [\tau ,t_f] \end{array}\right. \end{aligned}$$
    (25)

    (In Fig. 1, \(\tau \approx 51.5\)).

  • (ii) Let \(S(t)\) and \(u(t)\) be the optimal path and the optimal control in Theorem 4.1 respectively (without the constrain \(u(t)S(t)\le \omega\)). If \(S(\tau )\le \frac{\omega }{u_{\max }}< S(t_0)\), then there exist a corner point \(t_c\) and a switch \(\tau\) with \(t_0\le t_c\le \tau \le t_f\) such that the optimal vaccination policy is

    $$\begin{aligned} u=\left\{ \begin{array}{ll} \frac{\omega }{S}, &{}\quad t\in [t_0,t_c),\\ u_{max}, &{}\quad t\in [t_c,\tau ),\\ 0, &{} t\in [\tau ,t_f] \end{array}\right. \end{aligned}$$
    (26)

    (In Fig. 2, \(t_c\approx 16.5, \tau \approx 49.5\)).

Remark 2

The Theorem 4.2 means that the limited vaccine supply has a distinct effect on optimal vaccination policies. This should be a more reasonable result using of limited resources.

5 Conclusion

The resources are usually limited. It is critical that the limited resources are administered in a time-optimal fashion. In this paper, we use analytical method and optimization tool to study optimal vaccination policies for a basic SIR epidemic model under the assumption of daily vaccine supply, rather than total vaccine supply, being limited. We find that the optimal vaccination strategies are closely associate with the initial conditions, model parameters and constraint conditions when daily vaccine supply is limited, which hints that the change of environment should be considered in making a vaccination program. These results are different from ones in Hansen and Day (2011). For the basic model, there are two different scenarios for optimal vaccination strategies. The optimal control policies are derived explicitly in terms of initial conditions, model parameters and resources for vaccination. With sufficient resources, the optimal control strategy is the normal Bang–Bang control, i.e., to vaccinate with maximal effort until either all of the resources are used up or the epidemic is over. However, with limited resources, the optimal control strategy requires to switch to time-variant vaccination, i.e., from increasing gradually vaccination to maximizing vaccination until either all of the resources are used up or the epidemic is over.

Dynamic of infection is certainly far more complicated and varied than the one captured by this mathematical model. But, it illustrate the role that mathematical methods can play in formulate treatment strategy.