Theoretical prediction for effective properties and progressive failure of textile composites: a generalized multi-scale approach

Abstract

A generalized analytical model is developed to predict progressive failure behavior of several types of textile composites, including plain weave composites, twill weave composites, two-dimensional tri-axially braided composites and warp-reinforced 2.5-dimensional braided composites. In this model, the unit cell (UC) of composite is firstly identified and reconstructed into a refined lamina structure with multiple equivalent lamina elements (ELEs) based on apt geometrical approximation and assumptions. Secondly, two-way coupled stress-strain responses within the UC (macro-scale) and ELE (meso-scale) are established through a universal series-parallel model (SPM). Finally, a progressive damage model, which consists of damage initiation criteria and a stiffness evolution strategy, is employed to predict damage behavior of the ELE. The analytical results including mechanical properties and progressive failure process are validated against the existing numerical and experimental ones in literature. The validated analytical model is then used to study the effects of global fiber volume fraction, braided angle, shear failure coefficient and selected failure criteria on stiffness, strength and failure process. The present results demonstrate the efficiency and generic capability of the present analytical model for predicting the mechanical responses of a range of textile composites.

Graphic Abstract

Appendices

Appendix A

The transformation matrix $[{\varvec{R}}_{\mathrm {i}}] (i=1,2 \text { and } 3)$ has the following structural form:

$$\begin{aligned}&\left[ {\varvec{R}}_{\mathrm {i}}\right] \nonumber \\&=\left[ \begin{array}{cccccc} l_{1}^{2} &{} l_{2}^{2} &{} l_{3}^{2} &{} 2 l_{2} l_{3} &{} 2 l_{3} l_{1} &{} 2 l_{1} l_{2} \\ m_{1}^{2} &{} m_{2}^{2} &{} m_{3}^{2} &{} 2 m_{2} m_{3} &{} 2 m_{3} m_{1} &{} 2 m_{1} m_{2} \\ n_{1}^{2} &{} n_{2}^{2} &{} n_{3}^{2} &{} 2 n_{2} n_{3} &{} 2 n_{3} n_{1} &{} 2 n_{1} n_{2} \\ m_{1} n_{1} &{} m_{2} n_{2} &{} m_{3} n_{3} &{} m_{2} n_{3}+m_{3} n_{2} &{} n_{3} m_{1}+n_{1} m_{3} &{} m_{1} n_{2}+m_{2} n_{1} \\ n_{1} l_{1} &{} n_{2} l_{2} &{} n_{3} l_{3} &{} l_{2} n_{3}+l_{3} n_{2} &{} n_{3} l_{1}+n_{1} l_{3} &{} l_{1} n_{2}+l_{2} n_{1} \\ l_{1} m_{1} &{} l_{2} m_{2} &{} l_{3} m_{3} &{} l_{2} m_{3}+l_{3} m_{2} &{} l_{1} m_{3}+l_{3} m_{1} &{} l_{1} m_{2}+l_{2} m_{1} \end{array}\right] \nonumber \\ \end{aligned}$$

(A1)

The relevant elements in the transformation matrix $[{\varvec{R}}_{\mathrm {1}}]$ can be expressed as:

$$\begin{aligned} \left\{ \begin{array}{lll} l_{1}=\cos \left( \beta _{K}^{M}(x)\right) &{} l_{2}=0 &{} l_{3}=-\sin \left( \beta _{K}^{M}(x)\right) \\ m_{1}=0 &{} m_{2}=1 &{} m_{3}=0 \\ n_{1}=\sin \left( \beta _{K}^{M}(x)\right) &{} n_{2}=0 &{} n_{3}=\cos \left( \beta _{K}^{M}(x)\right) \end{array}\right. \end{aligned}$$

(A2)

where $\sin (\beta _K^M(x))=\tan (\beta _K^M(x))/\sqrt{1+\tan ^2(\beta _K^M(x))}$ and $\cos (\beta _K^M(x))$ $=1/\sqrt{1+\tan ^2(\beta _K^M(x))}$, in which $\tan (\beta _K^M(x))$ is given by Eq. (4).

The relevant elements in the transformation matrix $[{\varvec{R}}_{\mathrm {2}}]$ can be expressed as:

$$\begin{aligned} \left\{ \begin{array}{lll} l_{1}=\cos \left( \theta _{K}^{M}\right) &{} l_{2}=-\sin \left( \theta _{K}^{M}\right) &{} l_{3}=0 \\ m_{1}=\sin \left( \theta _{K}^{M}\right) &{} m_{2}=\cos \left( \theta _{K}^{M}\right) &{} m_{3}=0 \\ n_{1}=0, &{} n_{2}=0, &{} n_{3}=1 \end{array}\right. \end{aligned}$$

(A3)

The relevant elements in the transformation matrix $[{\varvec{R}}_{\mathrm {3}}]$ can be expressed as:

$$\begin{aligned} \left\{ \begin{array}{lll} l_{1}=\cos \left( \theta _{K}^{M}\right) &{} l_{2}=\sin \left( \theta _{K}^{M}\right) &{} l_{3}=0 \\ m_{1}=-\sin \left( \theta _{K}^{M}\right) &{} m_{2}=\cos \left( \theta _{K}^{M}\right) &{} m_{3}=0 \\ n_{1}=0 &{} n_{2}=0 &{} n_{3}=1 \end{array}\right. \end{aligned}$$

(A4)

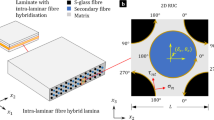
where $\theta _K^M$ denotes the braided angle, as shown in Fig.1.

Appendix B

The SPM for calculating the homogenized properties is presented here.

1.1 1. SPM-X model

The SPM-X model is used to obtain the homogenized properties of $N_{\alpha }$ subcells stacked in X direction, as shown in Fig. 15a. The stress and strain components based on the series-parallel assumption can be expressed as:

$$\begin{aligned} \begin{array}{lll} \epsilon _{YY}^{\alpha }=\epsilon _{YY} &{}\quad \epsilon _{ZZ}^{\alpha }=\epsilon _{ZZ} &{}\quad \gamma _{YZ}^{\alpha }=\gamma _{YZ}\\ \sigma _{XX}^{\alpha }=\sigma _{XX} &{}\quad \tau _{XY}^{\alpha }=\tau _{XY} &{}\quad \tau _{XZ}^{\alpha }=\tau _{XZ} \quad \alpha =1,2,\cdots , N_{\alpha }\nonumber \\ \end{array}\\ \end{aligned}$$

(A5)

which leads to the following equilibrium and compatibility conditions:

$$\begin{aligned} \begin{array}{lll} \sum _{\alpha =1}^{N_{\alpha }}k^{\alpha }\sigma _{YY}^{\alpha }=\sigma _{YY}&{}\quad \sum _{\alpha =1}^{N_{\alpha }}k^{\alpha }\sigma _{ZZ}^{\alpha }=\sigma _{ZZ}&{}\quad \sum _{\alpha =1}^{N_{\alpha }}k^{\alpha }\tau _{YZ}^{\alpha }=\tau _{YZ}\\ \sum _{\alpha =1}^{N_{\alpha }}k^{\alpha }\epsilon _{XX}^{\alpha }=\epsilon _{XX}&{}\quad \sum _{\alpha =1}^{N_{\alpha }}k^{\alpha }\gamma _{XY}^{\alpha }=\gamma _{XY}&{}\quad \sum _{\alpha =1}^{N_{\alpha }}k^{\alpha }\gamma _{XZ}^{\alpha }=\gamma _{XZ}\nonumber \end{array}\!\!\!\!\!\!\\ \end{aligned}$$

(A6)

where $k^{\alpha }$ denote the effective width ratios of each subcell. Solving these equations yields the formula for the effective stiffness matrix of the X model:

$$\begin{aligned} {\left\{ \begin{array}{ll} C_{11}&{}=P_1\prod _{\alpha =1}^{N_{\alpha }}C_{11}^{\alpha }\\ C_{12}&{}=P_1\sum _{\alpha =1}^{N_{\alpha }}k^{\alpha }C_{12}^{\alpha }\left( \dfrac{\prod _{m=1}^{N_{\alpha }}C_{11}^{m}}{C_{11}^{\alpha }}\right) \\ C_{13}&{}=P_1\sum _{\alpha =1}^{N_{\alpha }}k^{\alpha }C_{13}^{\alpha }\left( \dfrac{\prod _{m=1}^{N_{\alpha }}C_{11}^{m}}{C_{11}^{\alpha }}\right) \\ C_{21}&{}=P_1\sum _{\alpha =1}^{N_{\alpha }}k^{\alpha }C_{21}^{\alpha }\left( \dfrac{\prod _{m=1}^{N_{\alpha }}C_{11}^{m}}{C_{11}^{\alpha }}\right) \\ C_{22}&{}=\sum _{\alpha =1}^{N_{\alpha }}k^{\alpha }C_{22}^{\alpha }+P_1\sum _{\alpha =1}^{N_{\alpha }-1}\sum _{m=2}^{N_{\alpha }}k^{\alpha }k^{m} \\ &{} ~~\times \left[ \dfrac{\prod _{n=1}^{N_{\alpha }}C_{11}^{n}}{C_{11}^{\alpha }C_{11}^{m}}\right] \left( C_{21}^{\alpha }-C_{21}^{m}\right) \left( C_{12}^{m}-C_{12}^{\alpha }\right) \\ &{}\quad m\le \alpha , k^{\alpha }k^{m}=0 \\ C_{23}&{}=\sum _{\alpha =1}^{N_{\alpha }}k^{\alpha }C_{23}^{\alpha }+P_1\sum _{\alpha =1}^{N_{\alpha }-1}\sum _{m=2}^{N_{\alpha }}k^{\alpha }k^{m} \\ &{} ~~\times \left[ \dfrac{\prod _{n=1}^{N_{\alpha }}C_{11}^{n}}{C_{11}^{\alpha }C_{11}^{m}}\right] \left( C_{21}^{\alpha }-C_{21}^{m}\right) \left( C_{13}^{m}-C_{13}^{\alpha }\right) \\ &{}\quad m\le \alpha , k^{\alpha }k^{m}=0\\ C_{31}&{}=P_1\sum _{\alpha =1}^{N_{\alpha }}k^{\alpha }C_{31}^{\alpha }\left( \dfrac{\prod _{m=1}^{N_{\alpha }}C_{11}^{m}}{C_{11}^{\alpha }}\right) \\ C_{32}&{}=\sum _{\alpha =1}^{N_{\alpha }}k^{\alpha }C_{32}^{\alpha }+P_1\sum _{\alpha =1}^{N_{\alpha }-1}\sum _{m=2}^{N_{\alpha }}k^{\alpha }k^{m} \\ &{} ~~\times \left[ \dfrac{\prod _{n=1}^{N_{\alpha }}C_{11}^{n}}{C_{11}^{\alpha }C_{11}^{m}}\right] \left( C_{31}^{\alpha }-C_{31}^{m}\right) \left( C_{12}^{m}-C_{12}^{\alpha }\right) \\ &{} \quad m\le \alpha , k^{\alpha }k^{m}=0\\ C_{33}&{}=\sum _{\alpha =1}^{N_{\alpha }}k^{\alpha }C_{33}^{\alpha }+P_1\sum _{\alpha =1}^{N_{\alpha }-1}\sum _{m=2}^{N_{\alpha }}k^{\alpha }k^{m} \cdot \\ &{} ~~\left[ \dfrac{\prod _{n=1}^{N_{\alpha }}C_{11}^{n}}{C_{11}^{\alpha }C_{11}^{m}}\right] \left( C_{31}^{\alpha }-C_{31}^{m}\right) \left( C_{13}^{m}-C_{13}^{\alpha }\right) \\ &{} \quad m\le \alpha , k^{\alpha }k^{m}=0\\ C_{44}&{}=\sum _{\alpha =1}^{N_{\alpha }}k^{\alpha }C_{44}^{\alpha }\\ C_{55}&{}=P_2\prod _{\alpha =1}^{N_{\alpha }}C_{55}^{\alpha }\\ C_{66}&{}=P_3\prod _{\alpha =1}^{N_{\alpha }}C_{66}^{\alpha } \end{array}\right. } \end{aligned}$$

(A7)

with

$$\begin{aligned} {\left\{ \begin{array}{ll} P_{1}=\dfrac{1}{\left[ \sum _{\alpha =1}^{N_{\alpha }} k^{\alpha }\left( \frac{\prod _{m=1}^{N_{\alpha }}C_{11}^{m}}{C_{11}^{\alpha }}\right) \right] } \vspace{1mm}\\ P_{2}=\dfrac{1}{\left[ \sum _{\alpha =1}^{N_{\alpha }} k^{\alpha }\left( \frac{\prod _{m=1}^{N_{\alpha }}C_{55}^{m}}{ C_{55}^{\alpha }}\right) \right] }\vspace{1mm}\\ P_{3}=\dfrac{1}{\left[ \sum _{\alpha =1}^{N_{\alpha }} k^{\alpha }\left( \frac{\prod _{m=1}^{N_{\alpha }}C_{66}^{m}}{C_{66}^{\alpha }}\right) \right] } \end{array}\right. } \end{aligned}$$

(A8)

The strain components of each subcell can be expressed as:

$$\begin{aligned} {\left\{ \begin{array}{ll} \epsilon _{XX}^{\alpha }&{}=P_1\left( \frac{\prod _{m=1}^{N_{\alpha }}C_{11}^{m}}{C_{11}^{\alpha }}\right) \epsilon _{XX}\\ &{}~~+P_1\sum _{n=1}^{N_{\alpha }}k^{n}\left[ \frac{\prod _{l=1}^{N_{\alpha }}C_{11}^{l}}{C_{11}^{\alpha }C_{11}^n}\right] \\ &{}~~\times \left[ \left( C_{12}^{n}-C_{12}^{\alpha }\right) \epsilon _{YY}+\left( C_{13}^{n}-C_{13}^{\alpha }\right) \epsilon _{ZZ}\right] \\ &{} \quad n=\alpha , k^n=0,\\ \epsilon _{YY}^{\alpha }&{}=\epsilon _{YY}\\ \epsilon _{ZZ}^{\alpha }&{}=\epsilon _{ZZ}\\ \gamma _{YZ}^{\alpha }&{}=\gamma _{YZ}\\ \gamma _{XZ}^{\alpha }&{}=P_2\left( \dfrac{\prod _{m=1}^{N_{\alpha }}C_{55}^{m}}{C_{55}^{\alpha }}\right) \gamma _{XZ}\\ \gamma _{XY}^{\alpha }&{}=P_3\left( \dfrac{\prod _{m=1}^{N_{\alpha }}C_{66}^{m}}{C_{66}^{\alpha }}\right) \gamma _{XY}\\ \end{array}\right. } \end{aligned}$$

(A9)

1.2 2. SPM-Y model

The SPM-Y model is used to obtain the homogenized properties of $N_{\beta }$ subcells stacked in Y direction, as shown in Fig. 15b. The stress and strain components based on the series-parallel assumption can be expressed as:

$$\begin{aligned} \begin{array}{lll} \epsilon _{XX}^{\beta }=\epsilon _{XX} &{}\quad \epsilon _{ZZ}^{\beta }=\epsilon _{ZZ} &{}\quad \gamma _{XZ}^{\beta }=\gamma _{XZ}\\ \sigma _{YY}^{\beta }=\sigma _{YY} &{}\quad \tau _{XY}^{\beta }=\tau _{XY} &{}\quad \tau _{YZ}^{\beta }=\tau _{YZ} \quad \beta =1,2,\cdots N_{\beta } \end{array} \end{aligned}$$

(A10)

which leads to the following equilibrium and compatibility conditions:

$$\begin{aligned} \begin{array}{lll} \sum _{\beta =1}^{N_{\beta }}k^{\beta }\sigma _{XX}^{\beta }=\sigma _{XX}&{}\quad \sum _{\beta =1}^{N_{\beta }}k^{\beta }\sigma _{ZZ}^{\alpha }=\sigma _{ZZ}&{}\quad \sum _{\beta =1}^{N_{\beta }}k^{\beta }\tau _{XZ}^{\beta }=\tau _{XZ}\\ \sum _{\beta =1}^{N_{\beta }}k^{\beta }\epsilon _{YY}^{\beta }=\epsilon _{YY}&{}\quad \sum _{\beta =1}^{N_{\beta }}k^{\beta }\gamma _{XY}^{\beta }=\gamma _{XY}&{}\quad \sum _{\beta =1}^{N_{\beta }}k^{\beta }\gamma _{YZ}^{\beta }=\gamma _{YZ} \end{array}\nonumber \\ \end{aligned}$$

(A11)

where $k^{\beta }$ denote the effective width ratios of each subcell. Solving these equations yields the formula for the effective stiffness matrix of the Y model:

$$\begin{aligned} {\left\{ \begin{array}{ll} C_{11}=P_1\prod _{\beta =1}^{N_{\beta }}C_{11}^{\beta },\vspace{1mm}\\ C_{12}=P_1\sum _{\beta =1}^{N_{\beta }}k^{\beta }C_{12}^{\beta }\left( \dfrac{\prod _{m=1}^{N_{\beta }}C_{11}^{m}}{C_{11}^{\beta }}\right) \vspace{1mm}\\ C_{13}=P_1\sum _{\beta =1}^{N_{\beta }}k^{\beta }C_{13}^{\beta }\left( \dfrac{\prod _{m=1}^{N_{\beta }}C_{11}^{m}}{C_{11}^{\beta }}\right) \vspace{1mm}\\ \vspace{1mm}C_{21}=P_1\sum _{\beta =1}^{N_{\beta }}k^{\beta }C_{21}^{\beta }\left( \dfrac{\prod _{m=1}^{N_{\beta }}C_{11}^{m}}{C_{11}^{\beta }}\right) \\ C_{22}=\sum _{\beta =1}^{N_{\beta }}k^{\beta }C_{22}^{\beta }+P_1\sum _{\beta =1}^{N_{\beta }-1}\sum _{m=2}^{N_{\beta }}k^{\beta }k^{m}\left[ \dfrac{\prod _{n=1}^{N_{\beta }}C_{11}^{n}}{C_{11}^{\beta }C_{11}^{m}}\right] \cdot \\ ~~\left( C_{21}^{\beta }-C_{21}^{m}\right) \left( C_{12}^{m}-C_{12}^{\beta }\right) \quad m\le \beta , k^{\beta }k^{m}=0 \vspace{1mm}\\ C_{23}=\sum _{\beta =1}^{N_{\beta }}k^{\beta }C_{23}^{\beta }+P_1\sum _{\beta =1}^{N_{\beta }-1}\sum _{m=2}^{N_{\beta }}k^{\beta }k^{m}\left[ \dfrac{\prod _{n=1}^{N_{\beta }}C_{11}^{n}}{C_{11}^{\beta }C_{11}^{m}}\right] \cdot \\ ~~\left( C_{21}^{\beta }-C_{21}^{m}\right) \left( C_{13}^{m}-C_{13}^{\beta }\right) \quad m\le \beta , k^{\beta }k^{m}=0\vspace{1mm}\\ C_{31}=P_1\sum _{\beta =1}^{N_{\beta }}k^{\beta }C_{31}^{\beta }\left( \dfrac{\prod _{m=1}^{N_{\beta }}C_{11}^{m}}{C_{11}^{\beta }}\right) \\ C_{32}=\sum _{\beta =1}^{N_{\beta }}k^{\beta }C_{32}^{\beta }+P_1\sum _{\beta =1}^{N_{\beta }-1}\sum _{m=2}^{N_{\beta }}k^{\beta }k^{m}\left[ \dfrac{\prod _{n=1}^{N_{\beta }}C_{11}^{n}}{C_{11}^{\beta }C_{11}^{m}}\right] \cdot \\ ~~\left( C_{31}^{\beta }-C_{31}^{m}\right) \left( C_{12}^{m}-C_{12}^{\beta }\right) \quad m\le \beta , k^{\beta }k^{m}=0\vspace{1mm}\\ C_{33}=\sum _{\beta =1}^{N_{\beta }}k^{\beta }C_{33}^{\beta }+P_1\sum _{\beta =1}^{N_{\beta }-1}\sum _{m=2}^{N_{\beta }}k^{\beta }k^{m}\left[ \dfrac{\prod _{n=1}^{N_{\beta }}C_{11}^{n}}{C_{11}^{\beta }C_{11}^{m}}\right] \cdot \\ ~~\left( C_{31}^{\beta }-C_{31}^{m}\right) \left( C_{13}^{m}-C_{13}^{\beta }\right) , \quad m\le \beta , k^{\beta }k^{m}=0\vspace{1mm}\\ C_{44}=\sum _{\beta =1}^{N_{\beta }}k^{\beta }C_{44}^{\beta }\vspace{1mm}\\ C_{55}=P_2\prod _{\beta =1}^{N_{\beta }}C_{55}^{\beta }\vspace{1mm}\\ C_{66}=P_3\prod _{\beta =1}^{N_{\beta }}C_{66}^{\beta } \end{array}\right. }\nonumber \\ \end{aligned}$$

(A12)

with

$$\begin{aligned} {\left\{ \begin{array}{ll} P_{1}=\dfrac{1}{\left[ \sum _{\beta =1}^{N_{\beta }} k^{\beta }\left( \frac{\prod _{m=1}^{N_{\beta }} C_{11}^{m}}{C_{11}^{\beta }}\right) \right] } \\ P_{2}=\dfrac{1}{\left[ \sum _{\beta =1}^{N_{\beta }} k^{\beta }\left( \frac{\prod _{m=1}^{N_{\beta }} C_{55}^{m}}{C_{55}^{\beta }}\right) \right] } \\ P_{3}=\dfrac{1}{\left[ \sum _{\beta =1}^{N_{\beta }} k^{\beta }\left( \frac{\prod _{m=1}^{N_{\beta }} C_{66}^{m}}{C_{66}^{\beta }}\right) \right] } \end{array}\right. } \end{aligned}$$

(A13)

The strain components of each subcell can be expressed as:

$$\begin{aligned} {\left\{ \begin{array}{ll} \epsilon _{XX}^{\beta }=\epsilon _{XX}\\ \epsilon _{YY}^{\beta }=P_1\left( \frac{\prod _{m=1}^{N_{\beta }}C_{22}^{m}}{C_{22}^{\beta }}\right) \epsilon _{YY}+P_1\sum _{n=1}^{N_{\beta }}k^{n}\left[ \frac{\prod _{l=1}^{N_{\beta }}C_{22}^{l}}{C_{22}^{\beta }C_{22}^n}\right] \cdot \\ ~~~~\left[ \left( C_{21}^{\beta }-C_{21}^{m}\right) \epsilon _{XX}+\left( C_{23}^{\beta }-C_{13}^{m}\right) \epsilon _{ZZ}\right] \quad n=\beta , k^n=0\\ \epsilon _{ZZ}^{\beta }=\epsilon _{ZZ}\\ \gamma _{YZ}^{\beta }=P_2\left( \dfrac{\prod _{m=1}^{N_{\beta }}C_{44}^{m}}{C_{44}^{\beta }}\right) \gamma _{YZ}\\ \gamma _{XZ}^{\beta }=\gamma _{XZ}\\ \gamma _{XY}^{\beta }=P_3\left( \dfrac{\prod _{m=1}^{N_{\beta }}C_{66}^{m}}{C_{66}^{\beta }}\right) \gamma _{XY} \end{array}\right. } \end{aligned}$$

(A14)

1.3 3. SPM-Z model

The SPM-Z model is used to obtain the homogenized properties of $N_{\gamma }$ subcells stacked in Z direction, as shown in Fig. 15c. The stress and strain components based on the series-parallel assumption can be expressed as:

$$\begin{aligned} \begin{array}{lll} \epsilon _{XX}^{\gamma }=\epsilon _{XX} &{}\quad \epsilon _{YY}^{\gamma }=\epsilon _{YY} &{}\quad \gamma _{XY}^{\gamma }=\gamma _{XY}\\ \sigma _{ZZ}^{\gamma }=\sigma _{ZZ} &{}\quad \tau _{XZ}^{\gamma }=\tau _{XZ} &{}\quad \tau _{YZ}^{\gamma }=\tau _{YZ} \quad \gamma =1,2\cdots N_{\gamma }\,\,\,\,\,\,\,\,\,\, \end{array}\nonumber \\ \end{aligned}$$

(A15)

which leads to the following equilibrium and compatibility conditions:

$$\begin{aligned} \begin{array}{lll} \sum _{\gamma =1}^{N_{\gamma }}k^{\gamma }\sigma _{XX}^{\gamma }=\sigma _{XX}&{}\quad \sum _{\gamma =1}^{N_{\gamma }}k^{\gamma }\sigma _{YY}^{\alpha }=\sigma _{YY}&{}\quad \sum _{\gamma =1}^{N_{\gamma }}k^{\gamma }\tau _{XY}^{\gamma }=\tau _{XY}\\ \sum _{\gamma =1}^{N_{\gamma }}k^{\gamma }\epsilon _{ZZ}^{\gamma }=\epsilon _{ZZ}&{}\quad \sum _{\gamma =1}^{N_{\gamma }}k^{\gamma }\gamma _{XZ}^{\gamma }=\gamma _{XZ}&{}\quad \sum _{\gamma =1}^{N_{\gamma }}k^{\gamma }\gamma _{YZ}^{\gamma }=\gamma _{YZ} \end{array}\nonumber \\ \end{aligned}$$

(A16)

Table 6 Fiber mechanical properties as input for calculation

Table 7 Matrix mechanical properties as input for calculation

Table 8 Strength of equivalent laminate elements for PWC

where $k^{\gamma }$ denote the effective width ratios of each subcell. Solving these equations yields the formula for the effective stiffness matrix of the Z model:

$$\begin{aligned} {\left\{ \begin{array}{ll} C_{11}=\sum _{\gamma =1}^{N_{\gamma }}k^{\gamma }C_{11}^{\gamma }+P_1\sum _{\gamma =1}^{N_{\gamma }-1}\sum _{m=2}^{N_{\gamma }}k^{\gamma }k^{m}\left[ \dfrac{\prod _{n=1}^{N_{\gamma }}C_{33}^{n}}{C_{33}^{\gamma }C_{33}^{m}}\right] \\ ~~~~\left( C_{13}^{\gamma }-C_{13}^{m}\right) \left( C_{31}^{m}-C_{31}^{\gamma }\right) \quad m\le \gamma , k^{\gamma }k^{m}=0 \\ C_{12}=\sum _{\gamma =1}^{N_{\gamma }}k^{\gamma }C_{12}^{\gamma }+P_1\sum _{\gamma =1}^{N_{\gamma }-1}\sum _{m=2}^{N_{\gamma }}k^{\gamma }k^{m}\left[ \dfrac{\prod _{n=1}^{N_{\gamma }}C_{33}^{n}}{C_{33}^{\gamma }C_{33}^{m}}\right] \\ ~~~~\left( C_{13}^{\gamma }-C_{13}^{m}\right) \left( C_{32}^{m}-C_{32}^{\gamma }\right) \quad m\le \gamma , k^{\gamma }k^{m}=0\\ C_{13}=P_1\sum _{\gamma =1}^{N_{\gamma }}k^{\gamma }C_{13}^{\gamma }\left( \dfrac{\prod _{m=1}^{N_{\gamma }}C_{33}^{m}}{C_{33}^{\gamma }}\right) \\ C_{21}=\sum _{\gamma =1}^{N_{\gamma }}k^{\gamma }C_{21}^{\gamma }+P_1\sum _{\gamma =1}^{N_{\gamma }-1}\sum _{m=2}^{N_{\gamma }}k^{\gamma }k^{m}\left[ \dfrac{\prod _{n=1}^{N_{\gamma }}C_{33}^{n}}{C_{33}^{\gamma }C_{33}^{m}}\right] \\ ~~~~\left( C_{23}^{\gamma }-C_{23}^{m}\right) \left( C_{31}^{m}-C_{31}^{\gamma }\right) \quad m\le \gamma , k^{\gamma }k^{m}=0,\\ C_{22}=\sum _{\gamma =1}^{N_{\gamma }}k^{\gamma }C_{22}^{\gamma }+P_1\sum _{\gamma =1}^{N_{\gamma }-1}\sum _{m=2}^{N_{\gamma }}k^{\gamma }k^{m}\left[ \dfrac{\prod _{n=1}^{N_{\gamma }}C_{33}^{n}}{C_{33}^{\gamma }C_{33}^{m}}\right] \\ ~~~~\left( C_{23}^{\gamma }-C_{23}^{m}\right) \left( C_{32}^{m}-C_{32}^{\gamma }\right) \quad m\le \gamma , k^{\gamma }k^{m}=0\\ C_{23}=P_1\sum _{\gamma =1}^{N_{\gamma }}k^{\gamma }C_{23}^{\gamma }\left( \dfrac{\prod _{m=1}^{N_{\gamma }}C_{33}^{m}}{C_{33}^{\gamma }}\right) \\ C_{31}=P_1\sum _{\gamma =1}^{N_{\gamma }}k^{\gamma }C_{31}^{\gamma }\left( \dfrac{\prod _{m=1}^{N_{\gamma }}C_{33}^{m}}{C_{33}^{\gamma }}\right) \\ C_{32}=P_1\sum _{\gamma =1}^{N_{\gamma }}k^{\gamma }C_{32}^{\gamma }\left( \dfrac{\prod _{m=1}^{N_{\gamma }}C_{33}^{m}}{C_{33}^{\gamma }}\right) \\ C_{33}=P_1\prod _{\gamma =1}^{N_{\gamma }}C_{33}^{\gamma }\\ C_{44}=P_2\prod _{\gamma =1}^{N_{\gamma }}C_{44}^{\gamma }\\ C_{55}=P_3\prod _{\gamma =1}^{N_{\gamma }}C_{55}^{\gamma }\\ C_{66}=\sum _{\gamma =1}^{N_{\gamma }}k^{\gamma }C_{66}^{\gamma }\nonumber \end{array}\right. }\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\\ \end{aligned}$$

(A17)

where

$$\begin{aligned} {\left\{ \begin{array}{ll} P_{1}=\dfrac{1}{\left[ \sum _{\gamma =1}^{N_{\gamma }} k^{\gamma }\left( \frac{\prod _{m=1}^{N_{\gamma }} C_{33}^{m}}{C_{33}^{\gamma }}\right) \right] } \vspace{1mm}\\ P_{2}=\dfrac{1}{\left[ \sum _{\gamma =1}^{N_{\gamma }} k^{\gamma }\left( \frac{\prod _{m=1}^{N_{\gamma }} C_{44}^{m}}{ C_{44}^{\gamma }}\right) \right] } \vspace{1mm}\\ P_{3}=\dfrac{1}{\left[ \sum _{\gamma =1}^{N_{\gamma }} k^{\gamma }\left( \frac{\prod _{m=1}^{N_{\gamma }} C_{55}^{m}}{C_{55}^{\gamma }}\right) \right] } \end{array}\right. } \end{aligned}$$

(A18)

The strain components of each ELE can be expressed as:

$$\begin{aligned} {\left\{ \begin{array}{ll} \epsilon _{XX}^{\gamma }=\epsilon _{XX}\\ \epsilon _{YY}^{\gamma }=\epsilon _{YY}\\ \epsilon _{ZZ}^{\gamma }=P_1\left( \frac{\prod _{m=1}^{N_{\gamma }}C_{33}^{m}}{C_{33}^{\gamma }}\right) \epsilon _{ZZ}+P_1\sum _{n=1}^{N_{\gamma }}k^{n}\left[ \frac{\prod _{l=1}^{N_{\gamma }}C_{33}^{l}}{C_{33}^{\gamma }C_{33}^n}\right] \cdot \\ ~~~~\left[ \left( C_{31}^{n}-C_{31}^{\gamma }\right) \epsilon _{XX}+\left( C_{32}^{n}-C_{32}^{\gamma }\right) \epsilon _{YY}\right] \quad n=\gamma , k^n=0\\ \gamma _{YZ}^{\gamma }=P_2\left( \dfrac{\prod _{m=1}^{N_{\gamma }}C_{44}^{m}}{C_{44}^{\gamma }}\right) \gamma _{YZ}\\ \gamma _{XZ}^{\gamma }=P_3\left( \dfrac{\prod _{m=1}^{N_{\gamma }}C_{55}^{m}}{C_{55}^{\gamma }}\right) \gamma _{XZ}\\ \gamma _{XY}^{\gamma }=\gamma _{XY} \end{array}\right. } \end{aligned}$$

(A19)

Appendix C

The fiber and matrix properties used for the studied composites are listed in Tables 6 and 7. Tables 8, 9, 10 and 11 present the strength of equivalent laminate elements for PWC, TWC, WR-2.5DBC and 2DTBC, respectively.

Table 9 Strength of equivalent laminate elements for TWC

Table 10 Strength of equivalent laminate elements for WR-2.5DBC

Table 11 Strength of equivalent laminate elements for 2DTBC