Wall shear-stress extraction by an optical flow algorithm with a sub-grid formulation

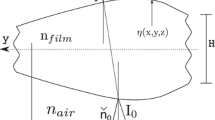
Abstract

In this study, we developed a novel optical-flow algorithm for determining the wall shear-stress on the surface of objects. The algorithm solves the thin-oil-film equation using a numerical scheme that recovers local features neglected by smoothing filters. A variational formulation with a smoothness constraint was applied to extract the global shear-stress fields. The algorithm was then applied to scalar images generated using direct numerical simulation (DNS) method, which revealed that the errors were smaller than those of conventional methods. The application of the proposed algorithm to recover the wall shear-stress on a low-aspect-ratio wing and on an axisymmetric boattail model taken as examples in this study showed a strong potential for analysing shear-stress fields. Compared to the methods used in previous studies, proposed method reveals more local features of separation line and singular points on object surface.

Graphic abstract

Appendices

Appendix A. Effect of pressure gradient on wall shear-stress results

The current study neglects the effects of pressure gradient and gravity on the wall shear-stress. This assumption holds in principle for most results except those near the separation position, where pressure is highly variable and the wall shear-stress is close to zero. Clearly, the pressure gradient can affect the shear-stress value as well as streamline around the surface. However, for most cases of two-dimensional flow, the pressure gradient in the direction normal to the flow fields is often small and its effect on the normal flow can be neglected. The oil flow in the normal direction can be considered to follow the direction of the boundary-layer motion. In this section, the effect of pressure on the shear-stress component, which is parallel with the flow direction, is evaluated.

Experiments were conducted on a boattail model of 20º at two velocities of V_∞ = 22 m/s and V_∞= 45 m/s. The experimental setup for the shear-stress measurement was the same as that for the boattail model of 18º in Sect. 4.2. Additionally, the pressure on the vertical surface was measured by silicon tubes. Details of the experimental setup are available in the paper by Tran et al. [49].

Figure 13 shows the pressure distribution on the boattail surface for the different velocities. Clearly, the minimum pressure occurs near the shoulder, where the flow separated. The change in pressure leads to a high pressure gradient in this region, as shown in Fig. 14. By comparison to the case of V_∞ = 22 m/s, the pressure gradient at V_∞ = 45 m/s changes greatly. It should be noted that the pressure gradient at V_∞ = 45 m/s is much higher for a conventional flow in subsonic conditions, ranging within the region of 10²–10⁴ Pa/m [50].

Fig. 13

Pressure coefficient on boattail surface

Fig. 14

Pressure gradient on boattail surface

In flow measurement technique, the maximum thickness of oil film layer is often in from 30 µm to 100 µm [25]. To estimate the effect of the pressure gradient, the oil thickness of 50 µm was used in this study, which yields a constant parameter κ of κ = 2 × 10⁻⁵. The oil viscosity is µ = 0.0276 (kg/ms) and the oil density is ρ = 895 kg/m³. From Eq. (3), the wall shear-stress can be estimated as follows:

$$ {{\tau }}_{{{\text{w,}}{\mathbf{s}}}} = \frac{2\mu }{\kappa I}{\text{u + }}\frac{2\kappa I}{3}\left( {\nabla p - \rho {\text{g}}} \right). $$

(A1)

In other words, we write the wall shear-stress as the sum of ${{\tau }}_{{{\text{w,}}s}} = {{\tau }}{}_{{{\text{w}},0}} + {{\tau }}_{{{\text{w,}}pg}}$. Here, ${{\tau }}_{{{\text{w}},0}} = \frac{2\mu }{\kappa I}{\text{u}}$ is the shear-stress term neglecting the effect of the pressure gradient and gravity terms, and ${{\tau }}_{{{\text{w,}}pg}} = \frac{2\kappa I}{3}\left( {\nabla p - \rho {\text{g}}} \right)$ is the shear-stress term formed by pressure gradients and gravity.

Figure 15 shows the results obtained using the two skin-friction components for different velocities. The main effect occurs near the separation position, where the pressure gradient is high and the wall shear-stress is close to zero. The effects of pressure and gravity are very small and have a negligible effect on the wall shear-stress at V_∞ = 22 m/s. However, at V_∞ = 45 m/s, the effect of the pressure is very high near the separation position, which causes the separation position to move forward. These results are highly consistent with previous observations by Zhang [50] and Squire [51], whereby the separation positions changed less than 5% in a region with a high pressure gradient. Clearly, the effect of pressure gradient leads to early flow separation. However, the change in the shear-stress tendency is negligible. The effect of the pressure gradient can be reduced by the use of a thinner oil layer. To obtain a more highly accurate skin-friction calculation, further experimental setups and numerical schemes should be considered.

Fig. 15

Wall shear-stress with consideration of the pressure gradient effect: a V_∞ = 22 m/s, b V_∞ = 45 m/s

Appendix B. Divergence-free of optical-flow velocity vectors

In this study, the optical-flow velocity vectors were considered as divergence-free parameters. However, this assumption is not always satisfied. The divergence-free optical-flow velocity can be tested by the relation between the wall shear-stress and the luminescent intensity. Specifically, the relation between the optical-flow velocity, luminescent intensity and wall shear-stress is as follows:

$$ \nabla \cdot {\text{u}} = \nabla \cdot \left( {\frac{\kappa I}{2\mu }{{\tau }}_{\text{w}} } \right), $$

(B1)

or

$$ \nabla \cdot {\text{u}} = \frac{\kappa I}{2\mu }\nabla \cdot {{\tau }}_{\text{w}} { + }\left[ {\nabla \left( {\frac{\kappa I}{2\mu }} \right)} \right] \cdot {{\tau }}_{\text{w}} . $$

(B2)

This relation can be used to determine whether the optical-flow velocity is in fact divergence-free.

To obtain the above relation, we used the data of low-aspect-ratio wing presented in Sect. 4.1. Here, the skin-friction fields and luminescent intensity is averaged in the region of x/c = 0 to 1 and y/c = − 0.15 to 0.15. Figure 16 shows the magnitude of the mean velocity, which was calculated by ${\text{u}} = \frac{\kappa I}{2\mu }{{\tau }}_{\text{w}} ,$ and the mean divergence of the velocity obtained using Eq. (B2). The results clearly show that the divergence of the velocity is sufficiently small and can be neglected in the numerical process.

Fig. 16

Magnitude of mean optical-flow velocity and mean divergence of velocity in the region of x/c = 0 to 1 and y/c = − 0.15 to 0.15

Appendix C. Lagrange multipliers and sub-grid coefficient selections

Although Lagrange multipliers are very important parameters for numerical schemes, there is no criteria for their selection. These parameters are often selected based on the numerical results, which should be consisted with experimental observations and previous knowledge. Woodiga [6] showed that the skin-friction fields on a wing surface are not sensitive to the Lagrange multipliers. The problem could occur when the Lagrange multipliers are too small or too large, which could lead to some artificial features or smoothing of the flow, respectively.

To evaluate the effect of the Lagrange multipliers on the numerical results, we conducted tests on two systematic images at t₁ = 0.39 s and t₂ = 0.40 s, as shown in Sect. 3. In that case, the vorticity regulation coefficient is set to α₂ = 0, while divergence regulation is changed from α₁ = 10⁻⁴ to 10⁴. Figure 16 shows the effect of the Lagrange multipliers on the AAE. Generally, Lagrange multipliers play as smoothing function, which has less effect on the solution than the observation term [36]. Consequently, a change in the Lagrange multipliers in the range from 1 to 100 has only a small effect on the AAE. However, the problem will occur when the Lagrange multipliers are sufficiently large, which affects the solution and leads to a high AAE (Fig. 17).

Fig. 17

Effect of Lagrange multiplier on the AAE

In the next step, the effect of c_s and Pr_sgs on the solution is considered. By changing c_s and Pr_sgs in the ranges of c_s = 0.1–0.2 and Pr_sgs = 0.1–1, we obtained the turbulence diffusion coefficient D_t changed from 0.01 to around 0.25. Here, the smallest and highest values of D_t correspond to (c_s, Pr_sgs)=(0.1, 1) and (c_s, Pr_sgs)=(0.2, 0.1), respectively. Figure 18 shows the AAE as a function of D_t. The AAE at D_t= 0 (c_s = 0), which corresponds to the Horn–Struck solution, is also plotted.

Fig. 18

Effect of the final turbulent diffusion coefficient D_t on the AAE

From these results, it is clear that AAE decreases with increases in D_t up to D_t= 0.22, which corresponds to (c_s, Pr_sgs)=(0.19, 0.1), and then it increases again. These results strongly agree with those observed by Cassisa (2011), where the minimum AAE corresponded to D_t= 0.2. Note that the coefficient c_s= 0.19 has also been used in previous studies by Chen et al. [36] on particle-image velocimetry data to recover local features.

Appendix D. Numerical scheme for extraction of optical-flow velocity vectors

To solve Eq. (12), we apply a variational formulation. The velocity vectors is denoted as u = (u, v). Equation (12) can be rewritten as follows:

$$\begin{aligned} J(\bar{u}) &= \int\limits_{{{\varOmega }}} {\left( {\bar{u}\overline{{I_{x} }} + \bar{v}\overline{{I_{y} }} + \overline{{I_{t} }} - D_{t} \Delta \bar{I}} \right)^{2} } {\text{d}}x{\text{d}}y \\ &\quad+ \int\limits_{{{\varOmega }}} {\left[ {\alpha_{1} \left( {\bar{u}_{x} + \bar{v}_{y} } \right)^{2} + \alpha_{2} \left( {\bar{u}_{y} - \bar{v}_{x} } \right)^{2} } \right]} {\text{d}}x{\text{d}}y.\end{aligned} $$

(D1)

The Euler–Lagrange equation for the function $J({\bar{\text{u}}})$ is as follows:

$$ \begin{aligned} & \frac{\partial J}{{\partial \bar{u}}} - \frac{\partial }{\partial x}\frac{\partial J}{{\partial \bar{u}_{x} }} - \frac{\partial }{\partial y}\frac{\partial J}{{\partial \bar{u}_{y} }} = 0, \\ & \frac{\partial J}{{\partial \bar{v}}} - \frac{\partial }{\partial x}\frac{\partial J}{{\partial \bar{v}_{x} }} - \frac{\partial }{\partial y}\frac{\partial J}{{\partial \bar{v}_{y} }} = 0. \\ \end{aligned} $$

(D2)

The application of from Eq. (D1) to Eq. (D2) yields:

$$ \begin{aligned} & \bar{I}_{x} \left( {\bar{u}\bar{I}_{x} + \bar{v}\bar{I}_{y} + \bar{I}_{t} - D_{t} \Delta \bar{I}} \right) = \alpha_{1} \left( {\bar{u}_{xx} + \bar{v}_{xy} } \right) + \alpha_{2} \left( {\bar{u}_{yy} - \bar{v}_{xy} } \right){\mathbf{,}} \\ & \bar{I}_{y} \left( {\bar{u}\bar{I}_{x} + \bar{v}\bar{I}_{y} + \bar{I}_{t} - D_{t} \Delta \bar{I}} \right) = \alpha_{1} \left( {\bar{u}_{xy} + \bar{v}_{yy} } \right) - \alpha_{2} \left( {\bar{u}_{xy} - \bar{v}_{xx} } \right). \\ \end{aligned} $$

(D3)

To calculate the derivative, we used the following relations:

$$ \begin{aligned} & \bar{u}_{xx} \approx \left( {\bar{u}_{m + 1,n} + \bar{u}_{m - 1,n} - 2\bar{u}_{m,n} } \right)/h^{2} , \\ & \bar{u}_{xy} \approx \left( {\bar{u}_{m + 1,n + 1} - \bar{u}_{m - 1,n + 1} - \bar{u}_{m + 1,n - 1} + \bar{u}_{m - 1,n - 1} } \right)/(4h^{2} ), \\ & \bar{u}_{yy} \approx \left( {\bar{u}_{m,n + 1} + \bar{u}_{m,n - 1} - 2\bar{u}_{m,n} } \right)/h^{2} , \\ & \bar{v}_{xx} \approx \left( {\bar{v}_{m + 1,n} + \bar{v}_{m - 1,n} - 2\bar{v}_{m,n} } \right)/h^{2} , \\ & \bar{v}_{xy} \approx \left( {\bar{v}_{m + 1,n + 1} - \bar{v}_{m - 1,n + 1} - \bar{v}_{m + 1,n - 1} + \bar{v}_{m - 1,n - 1} } \right)/(4h^{2} ), \\ & \bar{v}_{yy} \approx \left( {\bar{v}_{m,n + 1} + \bar{v}_{m,n - 1} - 2\bar{v}_{m,n} } \right)/h^{2} , \\ \end{aligned} $$

(D4)

where h is the spatial step.

By applying the above relations to Eq. (D3), the velocity components at iteration p + 1 can be calculated from p using Eq. (D5):

$$\begin{aligned} \left( {\begin{array}{*{20}c} {\bar{u}^{p + 1} } \\ {\bar{v}^{p + 1} } \\ \end{array} } \right) &= \left( {\begin{array}{*{20}c} {\bar{I}_{x}^{2} + 2\left( {\frac{{\alpha_{1} }}{{h^{2} }} + \frac{{\alpha_{2} }}{{h^{2} }}} \right)} & {\bar{I}_{x} \bar{I}_{y} } \\ {\bar{I}_{x} \bar{I}_{y} } & {\bar{I}_{y}^{2} + 2\left( {\frac{{\alpha_{1} }}{{h^{2} }} + \frac{{\alpha_{2} }}{{h^{2} }}} \right)} \\ \end{array} } \right)^{ - 1} \\ & \left( {\begin{array}{*{20}c} {\left( {\alpha_{1} \bar{u}_{1}^{p} + \alpha_{2} \bar{u}_{2}^{p} } \right)\bar{I}_{y}^{2} + 2\left( {\alpha_{1} + \alpha_{2} } \right)\left( {\alpha_{1} \bar{u}_{1}^{p} + \alpha_{2} \bar{u}_{2}^{p} } \right) - 2\left( {\alpha_{1} + \alpha_{2} } \right)\bar{I}_{x} \left( {\bar{I}_{t} - D_{t} \Delta \bar{I}} \right) - \bar{I}_{x} \bar{I}_{y} \left( {\alpha_{1} \bar{v}_{1}^{p} + \alpha_{2} \bar{v}_{2}^{p} } \right)} \\ {\left( {\alpha_{1} \bar{v}_{1}^{p} + \alpha_{2} \bar{v}_{2}^{p} } \right)\bar{I}_{x}^{2} + 2\left( {\alpha_{1} + \alpha_{2} } \right)\left( {\alpha_{1} \bar{v}_{1}^{p} + \alpha_{2} \bar{v}_{2}^{p} } \right) - 2\left( {\alpha_{1} + \alpha_{2} } \right)\bar{I}_{y} \left( {\bar{I}_{t} - D_{t} \Delta \bar{I}} \right) - \bar{I}_{x} \bar{I}_{y} \left( {\alpha_{1} \bar{u}_{1}^{p} + \alpha_{2} \bar{u}_{2}^{p} } \right)} \\ \end{array} } \right), \end{aligned}$$

(D5)

where $\bar{u}_{1}^{p} = \bar{u}_{xx}^{p} + \bar{v}_{xy}^{p} + 2\frac{{\bar{u}_{{}}^{p} }}{{h^{2} }}$; $\bar{u}_{2}^{p} = \bar{u}_{yy}^{p} - \bar{v}_{xy}^{p} + 2\frac{{\bar{u}_{{}}^{p} }}{{h^{2} }}$; $\bar{v}_{1}^{p} = \bar{v}_{yy}^{p} + \bar{u}_{xy}^{p} + 2\frac{{\bar{v}_{{}}^{p} }}{{h^{2} }}$; $\bar{v}_{2}^{p} = \bar{v}_{xx}^{p} + \bar{u}_{xy}^{p} + 2\frac{{\bar{v}_{{}}^{p} }}{{h^{2} }}$.

This interaction is repeated until the total error $\left( {\left\| {u^{p + 1} - u^{p} } \right\|^{2} + \left\| {v^{p + 1} - v^{p} } \right\|^{2} } \right)$ is smaller than the given error tolerance ε.