Introduction

Catastrophic rapid landslides have been extensively studied with the aim of understanding the failure mechanisms and predicting the time of failure. Early studies focused on extrapolating the inverse velocity of the sliding mass to predict the collapse time (Voight 1988; Saito 1965, 1969). However, this kind of prediction does not consider the mechanisms of failure, and gives a very short period of time (minutes) of early warning before the landslide collapses catastrophically. Recent studies have shifted the focus towards the behavior of the shear band (Kilburn and Petley 2003), which is one of the weakest parts of a landslide, as it is where all the thermo-mechanical phenomena occurs (Vardoulakis 2002b; Veveakis et al. 2010, 2007; Goren and Aharonov 2009). Researchers have investigated how external factors, like groundwater changes, affect the material behavior of the shear band and its friction coefficient (Alonso and Pinyol 2010; Alonso et al. 2016). Shear bands of deep-seated landslides are usually composed of clay or clayey materials that can undergo thermal softening and rate hardening (Vardoulakis 2002a, b; Hueckel and Baldi 1990), leading to a positive thermal feedback loop that increases the temperature and reduces the friction coefficient of the material (Anderson 1980; Vardoulakis 2002b; Voight and Faust 1982; Lachenbruch 1980; Rice 2006). This process can continue until the shearing resistance decreases uncontrollably, resulting in a thermal runaway instability that can trigger mechanical dissipation without any external influence (Gruntfest 1963).

New models have been developed to consider the role of temperature in landslides. Vardoulakis (2002b) presented a mathematical model that considers the counterbalance between thermal softening and rate hardening as the coupling mechanisms affecting the clay material of the landslide’s gouge. This model was applied to the Vaiont landslide by Veveakis et al. (2007), assuming only the maximum loading condition, whose results indicated that the landslide collapsed due to the positive thermal feedback loop reaching its critical value of basal temperature. Segui et al. (2020) applied the same model to two case studies, the Vaiont (collapsed) and the Shuping (active) landslides, to evaluate the critical point of stability and temperature. Seguí et al. (2021) tested and validated the assumption of the temperature’s role through field data collected from the El Forn landslide. In a more recent study, Seguí and Veveakis (2022) applied the model to four case studies, mapping all of them on a single stability curve (steady-state/bifurcation curve), showing its applicability to different deep-seated landslides, regardless of the nature of their instability and/or the data available (properties of the shear band material and field data).

In summary, these studies have advanced our understanding of the role of the basal temperature with the behavior of deep-seated landslides. The results of these studies have shown that temperature plays a crucial role in the stability of landslides and, that the model, which is simplified to the relationship between basal temperature and external loading, can be applied to different landslides.

The latter model by Vardoulakis (2002b), Veveakis et al. (2007), and Segui et al. (2020) proposed a partial differential equation (PDE) that is able to capture the interplay between the external loading (e.g., groundwater variations) and the basal (shear band material) temperature through the heat diffusion equation in dimensionless form. This equation depends on two parameters: the basal temperature and the Gruntfest number (Gruntfest 1963). These two parameters are plotted in a steady-state curve, which is also called a bifurcation curve, calculated through the heat diffusion equation in dimensionless form as steady-state, and applying the pseudo-arc-length continuation method. This PDE allows us to map the behavior of the landslide, in time, on the bifurcation curve, thus forecasting when the landslide will turn unstable (i.e., transitioning from secondary to tertiary phase) and collapse catastrophically. As mentioned above, the constitutive model considers that the shear band material behaves as rate hardening and thermal softening:

$$\begin{aligned} \frac{\partial \theta ^*}{\partial t^*} = \frac{\partial ^2 \theta ^*}{\partial {z^*}^2} + Gr e^{\theta ^*} \end{aligned}$$
(1)

where \(\theta\) is the temperature, t is time, z is the thickness of the shear band, and Gr is the Gruntfest number, which is the ratio of the mechanical work that is transformed to heat over the materials heat diffusion capacity. Gr contains information about the basal mean shear stress (including the effects of groundwater evolving in time), thermal conductivity, shear band thickness, and reference shear strain rates, among other parameters (see Segui et al. 2020 and Veveakis et al. 2007 for more information about the mathematical model). It is, therefore, a convenient way to encapsulate multiple data which benefits the work in this paper, as will be shown later.

Equation 1 is complex to solve, and current solutions involve using the pseudo-arc-length continuation method with spectral elements, using Fourier transforms instead of finite elements or other more traditional approaches (Veveakis et al. 2010; Chan and Keller 1982; Segui et al. 2020).

Artificial neural networks offer an alternative solution for making timely predictions and comparing them with observations. These networks have the potential to solve differential equations due to their universal approximation features (DeVore 1998; Tariyal et al. 2016; Hangelbroek and Ron 2010). To approximate the solution of a complex PDE, two essential factors are needed. The first one is a parameterized function that is both easy to train and evaluate, and robust enough to approximate the solution of a complex PDE. Modern deep neural network models (LeCun et al. 2015) provide these functions, which are made up of a number of linear transformations and component-wise non-linearities. Because of recent developments in paralleled hardware and automatic differentiation (Bergstra et al. 2010; Baydin et al. 2018; Ermoliev and Wets 1988), deep neural network models with numerous parameters can be trained and assessed rapidly. The other essential component is a loss objective or function. A loss function, when reduced, promotes that the parameterized function is a satisfactory approximation solution of the PDE.

This approach is now known as physics-informed neural networks (PINNs). It has been applied to numerous forms of PDEs, representing different phenomena in physics and engineering (see Raissi et al. 2019). Critical to this approach is the use of automatic differentiation (AD) which has made a significant contribution to enable this approach, as shown by Griewank (1989). It allows obtaining derivatives of the output variable, with regard to the input parameters. Other methods of calculating the derivatives suffer from rounding-off errors and, therefore, leading to inaccuracies (Baydin et al. 2018). This drawback of other approaches is avoided in PINNs, by using modern graph-based implementations, such as TensorFlow (Abadi et al. 2016) or PyTorch (Paszke et al. 2017). Using this automatic differentiation, exact expressions with floating values are applied, and no approximation error is found. In PINNs, the solution of the PDE is predicted without the need for an additional model, by including the PDE in the neural network loss function. Hence, during learning, the neural network (NN) learns to minimize the residual of the PDE by using the learned input parameters. Boundary and initial conditions are also included in the loss function in different ways to complete the boundary value problem.

The advantage is that PINN models may be used as a surrogate model for a range of input parameters, allowing for real-time simulations. PINNs also have other several advantages over the finite element method and other surrogate models: it does not require a mesh-based spatial discretization or laborious mesh generation; the derivatives of the solutions are available after training; it satisfies the strong form of the differential equations at all training points with known accuracy, and it allows data and mathematical models to be integrated within the same framework (Pang and Karniadakis 2020).

As mentioned previously, PINNs have been applied to a variety of problems, including fluid mechanics (Cai et al. 2022; Wu et al. 2018; Jin et al. 2021), solid mechanics (Haghighat et al. 2021; Rezaei et al. 2022; Harandi et al. 2023), heat transfer (Niaki et al. 2021; Cai et al. 2021b), and soil mechanics (Bandai and Ghezzehei 2021; Amini et al. 2022), including multiple ground-based problems (Amini et al. 2022). However, they have not been applied, to the authors knowledge, within the landslides field, more specifically to catastrophic deep-seated landslides, where the formulation of Eq. 1 allows us to apply this approach.

In this paper, thus, we present a new way of integrating a complex PDE into PINN to reproduce the behavior of deep-seated landslides. We provide field and calculated data from the Vaiont, Shuping, and Mud Creek landslides. We have chosen these three landslides to prove the validity of the model and the application of PINN for landslides that have collapsed due to different triggering factors, as Vaiont and Mud Creek, and active landslides, as Shuping. Also, it is important to notice that for these three landslides, the field and experimental data are not always available, and we have been able to simplify or generalize some of the needed parameters to solve the PDE, therefore, presenting a novel way to analyze the stability of deep-seated landslides in a quicker way that could be a very useful tool of early warning system.

Case studies

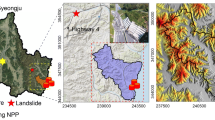
Three deep-seated landslides are used in this study: Vaiont, Shuping, and Mud Creek, which are briefly explained below. Detailed descriptions of the case studies can be found in Seguí (2020), Segui et al. (2020), Seguí and Veveakis (2022), Handwerger et al. (2019), and Alonso et al. (2016). The description below is simplified to the different trigger mechanisms, landslide volumes, and failure stages, to highlight the various conditions that can be covered. Interestingly for this paper, Fig. 1 shows the Gruntfest number calculated for each case study, as a function of dimensionless time (Seguí 2020; Seguí and Veveakis 2022). As will be shown later, the different order of magnitude, comparing Shuping (still in secondary creep) with Mud Creek and Vaiont (collapsed) could be a problem that will be overcome to obtain a good generalization. Table 1 presents a summary of the characteristics of each case study.

Fig. 1
figure 1

Gruntfest number in time with time-dependent external loadings history for different case studies (Seguí 2020; Seguí and Veveakis 2022). a The Vaiont landslide (Italy) that collapsed in 1963. b The Shuping landslide in the Three Gorges Dam (China) that remains active. c The Mud Creek landslide in California (USA) that collapsed in 2017

Full size image

Vaiont, Italy

The Vaiont landslide was an ancient landslide reactivated by the filling process of a dam constructed nearby (Semenza and Melidoro 1992). While the dam was working, the field data was showing that when the water level of the dam increased, the landslide accelerated. Thus, the engineers of the dam were controlling the accelerations of the landslide by reducing the water level of the dam (Muller 1964; Müller 1968). That happened because the material of the sliding mass was mainly calcarenite and limestone with high permeability (Ferri et al. 2011). On October 9th, 1963, the landslide catastrophically failed, mobilizing approximately 270 \(Mm^3\) of rock mass over a depth of 150 m (Muller 1964; Müller 1968). The material reached velocities in excess of 20 m/s resulting in a tsunami that over-topped the dam causing significant destruction downstream and 2000 casualties.

Shuping, China

The Shuping landslide was reactivated by the construction of the Three Gorges Dam in China. Additionally to the reservoir water level, the area is also subject to long periods of rainfall, which has been highlighted as another possible factor for triggering (Huang et al. 2016; Segui et al. 2020). The lithology of the area is mainly sandy mudstone and muddy sandstone (Wang et al. 2017). The thickness of the landslide is between 30 and 70 m and has a calculated volume of 27 \(Mm^3\). Conversely to Vaiont, this landslide accelerates during reservoir lowering and slows down during filling (Segui et al. 2020; Huang et al. 2016). The difference possibly resides in the different permeability of they layers of the sliding mass (Segui et al. 2020).

It is important to highlight that the Shuping landslide has not yet failed catastrophically, as indicated by the low Gruntfest numbers shown in Fig. 1. The fact that it shows also a different behavior (in terms of groundwater) to Vaiont reinforces the ability to capture different phenomena with this model.

Mud Creek, USA

Mud Creek was a landslide that like Vaiont catastrophically collapsed on May 20th of 2017 in California (USA) (Handwerger et al. 2019). The thickness of the sliding was 20 m and involved approximately 60 \(Mm^3\) that collapsed towards the sea and completely damaged a coastal road (Handwerger et al. 2019). The triggering mechanism of the failure of this landslide was mainly continuous heavy rainfalls during days that lead to an excessive pore water pressure inside the sliding mass (Handwerger et al. 2019).

Table 1 Case study summary
Full size table

PINNS basics and problem application

All neural networks consider three main general aspects: network architecture, loss functions, and training. These aspects are explained below, in the context of our application. A more detailed theoretical and methodological explanation for each aspect can be found, for example, in Haghighat and Juanes (2021) and Raissi et al. (2019).

Network architecture

The typical architecture of PINNs uses feed-forward neural networks (Schmidhuber 2015) (FFNNs), as presented in Fig. 2. It has Z as an input tensor and u as an output tensor, and it includes network trainable parameters, such as weights, W, and biases, b. In the application to Eq. 1, the input Z consists of three variables: z, t, and Gr. The output tensor u is the temperature, \(\theta\).

When deciding an architecture of NN, a decision needs to be made on the number of layers and the number of neurons in each layer. The number of hidden layers is an arbitrary, but very important aspect. It can be chosen based on the number of collocation points and the number of input and output parameters, but its selection remains largely a trial-and-error process. In some implementations, this number is considered a hyper-parameter, and therefore, can be fine-tuned during training. Equally, it can also be included as an additional variable so that its value is part of the learning process. However, the consensus is not clear as to what approach is more adequate, and therefore, lacking an established and rigorous way to do it, we propose later a systematic framework to choose what we consider a novel contribution to our paper.

In this type of fully connected neural network, neurons in a layer have no connection to each other (Bishop and Nasrabadi 2006). These FFNNs can be shown mathematically as shown in Eq. 2:

$$\begin{aligned} u^k = \sigma ^k (W^k Z^{k\mathop{-}1} + b^k) , k = 1, . . ., K \end{aligned}$$
(2)

where \(Z^0 = X\) is the input layer and \(u^k\) is the output layer. The values of the output layer are approximated as a function of the weights, W, and biases, b. Each connection between a neuron in layer k-1 and another neuron in layer k is assigned a weight W and a bias term b. Taking the weighted sum of its inputs, \(Z^k-1\), as well as a bias term, it delivers the output through an activation function \(\sigma\) that accommodates non-linearity (Sibi et al. 2013).

Loss function

In traditional FFNNs, the loss function can be calculated by minimizing the square of the difference of the predicted and given outputs (Schmidhuber 2015), or the so-called mean square error MSE (Eq. 3).

$$\begin{aligned} MSE = \sum _{i\mathop{=}1}^{n}(Y_i-\overline{Y}_i)^2 \end{aligned}$$
(3)

where n is the total number of collocation points, and Y and \(\overline{Y}\) are the ground truth values and the predicted values, respectively. As previously mentioned, in PINNs, the physics are included by adding the PDE to the loss function. Therefore, the total loss, \(\mathcal {L}\), becomes:

$$\begin{aligned} \mathcal {L} = \mathcal {L}_{data} + \mathcal {L}_{PDE} \end{aligned}$$
(4)

where \(\mathcal {L}_{data}\) is the loss function calculated from data points as in traditional FFNNs, and \(\mathcal {L}_{PDE}\) is the loss function from considering the physics using the PDE and the initial value. Generally, this will also involve adding boundary condition losses, but these do not apply to the problem we are solving here. Hence, the PDE loss function is:

$$\begin{aligned} \mathcal {L}_{PDE} = \mathcal {L}_\theta + \mathcal {L}_{\theta _0} \end{aligned}$$
(5)

Then, we can write Eq. 1 into the mean squared error loss function as:

$$\begin{aligned} \mathcal {L}_\theta = \frac{1}{n} \sum _{i\mathop{=}1}^{n} \left(\frac{\partial \theta ^*}{\partial t^*} \vert _{z_i} - \frac{\partial ^2 \theta ^*}{\partial {z^*}^2} \vert _{z_i} - Gr e^{\theta ^*} \vert _{z_i}\right)^2 \end{aligned}$$
(6)

The losses related to the initial condition are calculated as:

$$\begin{aligned} \mathcal {L}_{\theta _0} = \frac{1}{n} \sum _{i\mathop{=}1}^{n} {(\theta \vert _{t\mathop{=}0} - \theta _{0}(z))}^2 \end{aligned}$$
(7)

Finally, the network is trained by minimizing the losses for a different set of hyper-parameters, \(\theta\), at the collocation points, X:

$$\begin{aligned} \theta ^* = \arg \min _{\theta } \mathcal {L}_N(X;\, \theta ) \end{aligned}$$
(8)
Fig. 2
figure 2

A schematic of single neural network architecture with space, time, and Gruntfest number as input features (z; t; Gr). And the temperature, \(\theta\), as output with optimization of the total loss function, consisted of loss terms for the governing equation

Full size image

Training

Training is the third critical part of the PINNs. One of the critical parameters in the process of training PINNs is the activation function, which should be chosen considering the partial differential equation and the physical output quantities. After considering different activation functions, and comparing the final value of the loss function, we observed that tanh gave the best results with the lowest loss function. We also used tanh, sigmoid, swish, and softplus, although this comparison is not included in the paper. The tanh activation function can be defined as:

$$\begin{aligned} \tanh (n)=\frac{\exp ^n - \exp ^{-n}}{\exp ^n + \exp ^{-n}} \end{aligned}$$
(9)

We used the available algorithms in Keras (Chollet et al. 2015) and Adam’s optimization scheme (Kingma and Ba 2014) within the SciANN (Haghighat and Juanes 2021) framework for training. Due to the lack of a systematic approach, we defined the learning rate by using trial and error. The learning rate is a hyper-parameter worth tuning because of the use of the stochastic gradient descent algorithm. We reached the conclusion that 0.001 is a suitable value for the learning rate since the optimizer can reach the minimum value slowly, while avoiding getting stuck in local minima. It also needs to be considered that adaptive learning is included in SciANN, and the optimizer (in our case, Adam) reduces the value of the learning rate in case it is necessary. Hence, this value was not critical for this implementation.

Different hyper-parameters and architectures are investigated in this study. The hyper-parameters in the algorithm, which had a noticeable influence during the training of this problem, are batch-size, activation function, and number of epochs. Batch size is the number of collocation points from a data set, used to determine one gradient descend update (Ruder 2016). The batch size also influences the computational cost. This means that, for a larger batch size, the training becomes faster because fewer iterations are needed for one epoch to round the training on a data set. The minimum batch size is 1, which corresponds to a full stochastic gradient descent optimization. In this work, several different batch sizes were considered to find the best and optimal value, which in this case was 64.

The second important hyper-parameter is the number of epochs. At each epoch, before a new round of training (epoch) starts, the data set can be shuffled leading to an updated parameter. This occurs when the batch gradients are calculated on a new batch and therefore, it is affected by the number of batches. In PINNs, a value of 5000 epochs was used in several studies (Raissi et al. 2019; Niaki et al. 2021) and we have used it here after trial and error, using as criteria a predefined low-value of the loss function, as recommended by Raissi et al. (2019). In many cases, the total loss converges to a constant value after 3000 epochs. Shuffling of collocation points was also used during the training.

Since the aim of this study is to minimize the loss function, and since the optimizer is non-convex, the training needs to be tested from different starting points and, at the same time, with different directions. In this way, weights and biases are evaluated by minimizing the loss function, and patience is a limit that monitors the optimizer intended to stop the training.

Over-fitting during the training (Hawkins 2004) is always a concern, especially for forecasting unseen cases. Since the number of collocation points in this study is small, the over-fitting is examined by splitting the collocation points into three sets: train, test, and validation. Since validation data are available during training, the accuracy and loss function can be plotted in Keras (Chollet et al. 2015) for examination. This offers a great advantage to control over-fitting. If during training, the loss function increases, or the model starts to lose test accuracy, then the model is over-fitted.

There are several methods to train PINNs. In this research, calculated data from Segui et al. (2020) and Seguí and Veveakis (2022) are used for training, which is presented in the next section.

Synthetic data and network architecture

Synthetic data

The purpose of PINNs is to generate a model with good generalization properties. Initially, one typically trains the model by only using the PDE, without any data. In our case, the results of training without data were not satisfactory; hence, this approach was discarded. This is due to the complexity contained by the Gr, which is not captured when considering only the PDE. Hence, training with data was necessary.

Figure 3 shows the results where the training and testing have been performed individually for each case. As expected, the results are very close to the initial data, when training in the same case. Note that the architecture used for this case is 4 hidden layers and 10 neurons for each one. As Fig. 3 shows, this is not the optimal architecture; however, the temperature calculated reproduces the behavior of the ground truth with minor discrepancy.

Fig. 3
figure 3

Normalized temperature evolving in time for the three case studies applying the architecture of 4[10]. Here, the training and the testing have been performed individually for each case study. Note that the ground truth data is from Segui et al. (2020) and Seguí and Veveakis (2022): a ground truth and architecture data of the Vaiont landslide, b ground truth and architecture data of the Shuping landslide, c ground truth and architecture data of the Mud Creek landslide

Full size image

By using an optimal architecture with 3 layers and 20 neurons each, the results reproduce the ground truth with more accuracy, as shown in Fig. 4. However, one must understand that this is using training data selected randomly along the entire time domain (i.e., there is future prediction ability, but only interpolation) and within the same case study.

Fig. 4
figure 4

Normalized temperature in time for the three case studies with architectures of 3[20]. The training and the testing have been performed individually. Note that the ground truth data is from Segui et al. (2020) and Seguí and Veveakis (2022): a Ground truth and architecture data of the Vaiont landslide, b ground truth and architecture data of the Shuping landslide, c ground truth and architecture data of the Mud Creek landslide

Full size image

However, this approach hardly helps to generalize the behavior of all (unseen) case studies. As shown in Fig. 5, we have trained the model with two of the cases and tested the model on the third one. We repeat this for all three combinations (Fig. 5). As can be seen, the results are not as satisfactory. Critically, the model is not capable of forecasting the Shuping landslide behavior. This means that generalizing, by training the model with just one landslide, does not represent the behavior of the rest of the case studies.

Fig. 5
figure 5

Normalized temperature in time for the three case studies by training two different cases and testing on the other one. Note that the ground truth data is from Segui et al. (2020) and Seguí and Veveakis (2022). a Training the model with the Vaiont and Shuping landslides. b Testing of the Mud Creek landslide by the training of a. c. Training the model with the Vaiont and Mud Creek landslides. d Testing of the Shuping landslide by the training of c. e. Training the model with the Shuping and Mud Creek landslides. f Testing of the Vaiont landslide by the training of e

Full size image

Therefore, the next option is to resort to more data or create synthetic data. This approach has been followed by several authors (Bandai and Ghezzehei 2021; Cai et al. 2021a; Jagtap et al. 2022). Hence, this method has been implemented in our study, to define the best hyper-parameters and the optimal network architecture. The adequacy of this approach to represent real case studies is presented in the next section.

The synthetic data was generated by using the observations from Segui et al. (2020) and Veveakis et al. (2007). Those studies show that the Gruntfest number follows a sinusoidal wavy, increasing, pattern. This sinusoidal pattern is related to seasonal groundwater variation, which leads to an increase in the temperature of the shear band, and an acceleration of the sliding mass (Cecinato et al. 2008; Seguí et al. 2021). This behavior can be mathematically expressed as follows:

$$\begin{aligned} Gr = 0.8 t + exp(t)(0.07sin(c*t))\ 0 < t < 1 \end{aligned}$$
(10)

where Gr is the Gruntfest number and t is the time. The equation is defined so that the maximum value of Gr is 0.88, as the critical value stated by Segui et al. (2020). Meaning that, once the system reaches and overcomes this value, the system becomes unconditionally stable and the landslide enters the point of no return (i.e., tertiary creep and catastrophic collapse) (Segui et al. 2020). c covers the number of cycles or seasonal changes that the landslide experiences. Hence, by using an appropriate number of cycles and forcing it to fail by reaching a Gr equal to or higher than 0.88, we can control that all possible behaviors are generally covered in the synthetic data. A value of c equal to 32 is used, which corresponds to five seasonal changes, taken as the behavior of the Shuping landslide, which is the case study with more years of data. The temperature is calculated by using the method presented by Vardoulakis (2002b), Veveakis et al. (2007), Segui et al. (2020), Seguí et al. (2021), and Seguí and Veveakis (2022). The generated synthetic data are shown in Fig. 10a.

A critical aspect of using PINNs is the normalization of the data, in particular, in those cases where the variables show large differences in scale. For example, the Gruntfest number in Shuping only varies between 0.038 and 0.044, whereas in Vaiont it reached the critical value of 0.88. Equally, the time is also at a different scale. Hence, we normalized all of the input and output variables between 0 and 1. Without this normalization, none of the architectures and attempts was successful. In any event, this is generally a good practice (Haghighat and Juanes 2021; Raissi et al. 2019).

Remark 1

At the same time, the use of data-driven neural networks (DDNN) is common in a lot of fields of study, and the authors also considered this approach at the beginning of the research on landslides. PINN is basically an add-on to the DDNN approach to improving the performance of the network, by adding physical constraints. The DDNN approach showed promising results when we trained one case and tested it on the same case. However, in terms of generalization and extrapolation for other cases, it is not always robust and stable.

A DDNN neural network approach was conducted to train the synthetic data with 4 layers and 20 neurons, and the three case studies were predicted based on this model. The results are presented in Fig. 6, which show a good prediction for synthetic data (seen data set), and poor quantitative results for the other case studies (unseen data set). This shows the effectiveness of physics in improving the performance of the neural network.

Fig. 6
figure 6

Normalized temperature in time calculated by the network for the three case studies. This normalized temperature has been calculated by training the synthetic data with a DDNN approach with 4 layers and 20 neurons in each layer. Note that the ground truth data is from Segui et al. (2020) and Seguí and Veveakis (2022). a Fit of the ground truth (generated data) and calculated by the DDNN network synthetic data. b Fit of the ground truth data of the Vaiont landslide and the calculated data by the DDNN network. c Fit of the ground truth data of the Shuping landslide and the calculated data by the DDNN network. d Fit of the ground truth data of the Mud Creek landslide and the calculated data by the DDNN network

Full size image

Network architecture sensitivity analysis

In this section, we present an approach to select the network architecture by using a sensitivity analysis, where we considered the number of neurons and the number of hidden layers. We performed all of our training on the generated synthetic data, which contains 1510 collocation points. We always kept 10% of the data for testing after each training, and determine the convergence of the network in terms of over-fitting. We used the network hyper-parameters and activation function shown in the “Training” section.

To study the optimal network architecture, the criteria we used from the sensitivity analysis were three-fold: minimizing the loss function, reducing the standard deviation (stability) of network prediction for the unseen cases (which is due to the random processes associated with different initial values of weights and biases for each network), and avoiding over-fitting.

Figure 7 shows the standard deviation, based on 5 realizations, in the y-axis and the error in the x-axis. The error is calculated as the mean absolute difference of the forecast values to the ground truth. It only shows combinations of layers and neurons (layers[neurons]), where over-fitting was not observed. The number of neurons was kept equal for all hidden layers, which is common for different implementations of PINNs (Haghighat et al. 2021; Raissi et al. 2019). The plotted values in Fig. 7 show the results for the three case studies.

Fig. 7
figure 7

Comparison of mean absolute error and standard deviation of the different network architectures by training the synthetic data and forecasting the three case studies. (Black) the Vaiont landslide results, (red) the Shuping landslide results, and (blue) the Mud Creek landslide results. (Round) 3 hidden layers network, (triangle) 4 hidden layers, (square) 5 hidden layers

Full size image

Based on the results of the sensitivity analysis, the Vaiont case shows the highest stability of the network (i.e., each time the network is trained, the results are the same) among all cases. However, the accuracy of Vaiont almost remains constant throughout the different architectures. The case of Shuping is the most sensitive case to the architecture, and the standard deviation of different network architectures changed significantly. The case of Mud Creek shows the best accuracy of all cases. In general, the more neurons, the more accurate and network stable the results are. The upper bound of neurons is provided by the over-fitting consideration.

After examining all the cases, we conclude that the best two architectures are (1) using 3 hidden layers and 20 neurons per layer and (2) 4 hidden layers with 16 neurons each. We repeated the training with these architectures to calculate the value of the total loss function and validate our conclusion. Both networks show a good convergence in terms of the loss function, which is demonstrated in Fig. 8, and also confirms that the PDE is satisfied.

Fig. 8
figure 8

Evolution of the different loss functions in the training of the network for synthetic data. The graphs also include the total loss, the loss from temperature (\(\theta\)), and the loss from the governing equation (Eq. 5). a Joint network architecture applying 3 layers and 20 neurons. b Joint network architecture applying 4 layers and 16 neurons

Full size image

To further examine the robustness of these two network architectures (Fig. 8), we calculate the \(95\%\) confidence range of each network. As presented in Fig. 9, the repeated training on synthetic data shows satisfactory performance in terms of the calculated loss function. The network stability training is considered satisfactory and, based on this training, we calculate the basal temperature of the three landslides.

Fig. 9
figure 9

Evolution of the \(95\%\) total loss confidence band of training the synthetic data for a network architecture 3[20] and b network architecture 4[16]

Full size image

Remark 2

To address the computational efficiency of each training procedure, with Intel Xeon CPU @2.20 GHz, 13 GB RAM, the average time required to complete one epoch of 3 layers and 20 neurons, with an average epoch time of 0.1 s. The second configuration comprised four layers and 16 neurons, resulting in an average epoch time of 0.16 s. It is worth noting that the total training time can be influenced by multiple factors, such as batch size and the number of epochs. By varying these parameters, it is possible to alter the overall duration of the training process.

Results and discussion

Figure 10 shows the results of the calculated temperature, using only the synthetic data as training inputs, and the network architectures chosen in the previous section. These results expand on the parametric studies, and are validated by the fitting of the ground truth data from Segui et al. (2020, 2021), and Seguí and Veveakis (2022), with low absolute mean error as shown in Fig. 7. Moreover, we have validated the network in terms of trends and times at which changes occur. By training the proposed synthetic data, we are able to forecast the point of instability (i.e., when the landslide reaches the point of no return and enters the tertiary creep) of the landslide in both Vaiont and Mud Creek cases. At the same time, since the created synthetic data considers multiple seasonal changes, it could closely represent the real behavior of the Shuping landslide, although the network underestimates the temperature for the larger peak. The results of the network architecture with 3 layers and 20 neurons were slightly closer to the ground truth data. Since the suggested synthetic data can be regenerated for more seasonal changes, it is expected that by re-training the model, the core temperature of the shear band in other cases of deep-seated landslides could be also achievable. This is extremely important for practical purposes, if such a model is going to be used. For example, the model does not seem to reproduce the exact maximum temperature for all three cases. However, the calculated temperature by the network reproduces the changes of the landslide’s behavior in time.

Fig. 10
figure 10

Normalized temperature in time calculated by the network for the three case studies. This normalized temperature has been calculated by training the synthetic data for two different network architectures 3[20] and 4[16]. Note that the ground truth data is from Segui et al. (2020) and Seguí and Veveakis (2022). a Fit of the ground truth (generated data) and calculated by the network synthetic data. b Fit of the ground truth data of the Vaiont landslide and the calculated data by the network. c Fit of the ground truth data of the Shuping landslide and the calculated data by the network. d Fit of the ground truth data of the Mud Creek landslide and the calculated data by the network

Full size image

Conclusions

In this study, we have presented a physics-informed neural network framework for modeling large deep-seated landslides. The proposed PINN is a feed-forward neural network that tackles the solution of the partial differential equation. Physics-informed neural networks are promising tools for solving PDEs in multiple domains, including landslides.

In this study, we have considered three different case studies of deep-seated landslides triggered by different phenomena with different data available, and we have trained the network based on field data. Since the range of each input variable varies, data normalization has become crucial to achieve a more optimal training and forecast the behavior of each landslide.

Moreover, in this study, we have presented different network architectures, as well as different hyper-parameters. Showing that the combination of the number of layers and the number of neurons play an important role to  reach an accurate solution (i.e., reproducing the real behavior of the landslide). We have also explored the best solution to minimize the mean absolute error for the three case studies and its robustness (to cater to the random process). The results presented in this paper show that a good generalization can be achieved, which can help significantly in the development of real-time monitoring and early warning systems for catastrophic deep-seated landslides.