Introduction

Over the last few decades, the processing strategies for large GNSS networks have been an issue of concern in the GNSS community. With the extension of satellite constellations and the increasing number of ground stations, a dense network of GNSS data with long orbit arcs is usually used to guarantee orbital accuracy in multi-GNSS precise orbit determination (POD). In real-time applications, a fast update of the POD processing is also needed to reduce orbit prediction errors. Therefore, fast, dense, and large multi-GNSS POD solutions challenge computational efficiency in multi-GNSS data processing. In such a high-volume data processing, a huge number of parameters should be inevitable for achieving a more accurate and reliable parameter estimation (Steigenberger et al. 2006; Chen et al. 2014).

Eliminating parameters in the normal equation (NEQ) system has been widely recommended in GNSS data processing (Boomkamp and König 2004) to reduce the requirement on memory. Ge et al. (2006) accordingly proposed a new algorithm by only keeping the active parameters in the NEQ system, which indeed releases the computation burden for solving the NEQ. Since the advent of cached-based processors with a multi-layer memory, the matrix–matrix operations are provided by the basic linear algebra subprograms (BLAS) to amortize the cost of data movement between memory layers (Low and van de Geijn 2004). Using this tool, the block-partitioned algorithms, including the Cholesky and QR factorizations, are implemented in the linear algebra package (LAPACK) for solving NEQ (Gunter and van de Geijn 2005; Demmel et al. 2012; Gong et al. 2018). The computational cost of solving NEQ is negligible for parameter estimation through a combination of the blocked algorithm and the strategy of parameter elimination. However, the whole procedure of parameter estimation is still time-consuming at each epoch with the increasing number of satellites and ground stations even though the parameter elimination strategy is applied (Schönemann et al. 2011). The major reason for this turns out to be the huge computational burden for parameter elimination.

Higher computational power has already been exploited in many application areas with a continuous upgrade of computing systems. For the modern GNSS software, the coding of algorithms and processing procedures should be directed toward enhanced computing resources. In need for more computational power, developers of computing systems tried to use several existing computing machines joined, which is the origin of parallel machines (Gottlieb and Almasi 1989). As well-known in high-performance computing (HPC), parallel computing has become the dominant paradigm in computer architectures mainly in multi-core processors (Asanovic et al. 2006). In parallel computing, the most common forms of process interaction are message passing and shared memory, except for implicit interactions that are difficult to manage (Kessler and Keller 2007). In order to fully exploit the capabilities of multi-core shared-memory machines (El-Rewini and Abd-El-Barr 2005), individual hardware vendors developed their own standards of compiler directives and libraries. For a large agreement between compiler developers and hardware vendors, an important tool, i.e., Open Multiprocessing (OpenMP), has emerged to support the multi-platform shared memory multiprocessing programming (Costa et al. 2004; Mironov et al. 2017). The OpenMP and message passing interface (MPI) techniques have been applied in GNSS receiver software for accelerating GNSS signal acquisition and tracking (Sun and Jan 2008). The OpenMP-based parallelism has been introduced into the extended Kalman filter for real-time GPS network solutions (Kuang et al. 2019). In the message passing mode, a communication network is required to connect inter-processor memory. The memory address in one processor cannot be mapped to another processor. Therefore, unlike shared memory, there is no concept of global address across all the processors for distributed memory (i.e., message passing). The distributed memory computing techniques have been used for processing massive GPS network datasets (Serpelloni et al. 2006; Boomkamp 2010). For instance, one procedure, e.g., preprocessing, can be further separated into several independent subtasks, which are operated in parallel by all processors over a distributed communication network. Based on this distributed environment, some parallel processing strategies have been developed to speed up epoch-wise PPP or baseline solutions (Li et al. 2019; Cui et al. 2021).

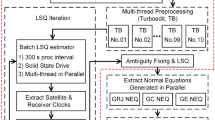
From the perspective of the parameter elimination principle, it is possible to parallelize this operation highly. Using the OpenMP parallel tool, an efficient parallel algorithm is therefore developed based on the multi-core processors to improve the computational efficiency of parameter estimation for GNSS network solutions. First, the principle of sequential least square (LSQ) estimation with parameter elimination is introduced. Then, the OpenMP-based parallelization and the parallel optimization are described for parallel programming, respectively. In the OpenMP-based parallel algorithm, the cache memory traffic optimizations and an optimized multi-thread scheduling scheme are developed to improve the computational performance of parameter elimination. Experiments are carried out to demonstrate the feasibility of the cache memory traffic optimization and the multi-thread scheduling scheme, respectively. Afterward, the multi-GNSS POD is taken as a typical case to further confirm the improvements in computational efficiency due to the proposed parallel algorithm. Finally, the contributions and several outlooks are summarized for GNSS software development.

Parallel processing algorithm for sequential LSQ

As mentioned above, most of the computational burden is from parameter elimination for sequential LSQ estimation. First, we provide the principle of sequential LSQ estimation with parameter elimination. Then, the feasibility of parallelizing the parameter elimination is confirmed from the perspective of principle. For the major time-consuming operations in the parameter elimination, parallel optimizations, including the cache memory traffic optimization and the multi-thread scheduling scheme, are finally introduced and implemented in the parallel processing algorithm.

Sequential LSQ estimation with parameter elimination

In the LSQ estimation, the number of parameters often accumulates with the observation time period. A great number of parameters would bring a huge computational burden for the estimation. However, many of the parameters are valid just over a specific time interval, such as parameters for only a single epoch, piece-wise constant, or piece-wise linear parameters. For saving computer memory and reducing the computational burden, these parameters could be only kept while they are active over a specific time period; otherwise, they are considered as inactive and will be removed immediately from the normal equations before and after the active status, respectively (Ge et al. 2006). For the time-dependent parameters such as the tropospheric zenith wet delays (ZWDs), additional state equations of the adjacent parameters will be introduced as pseudo observations for the LSQ estimation. The observation equations for the LSQ adjustment with the time-dependent state parameter x can be written as follows,

$$\left\{ {\begin{array}{*{20}l} {v_{{y_{0} }} = y - y_{0} ,} \hfill & {P_{{y_{0} }} } \hfill \\ {v_{{x_{0} }} = x(0) - x_{0} ,} \hfill & {P_{{x_{0} }} } \hfill \\ {v_{x} (i) = \Phi (i)x(i - 1) - x(i),} \hfill & {P_{x} (i)} \hfill \\ {v(i) = A(i)y + B(i)x(i) - l(i),} \hfill & {P_{l} (i)} \hfill \\ \end{array} } \right.$$
(1)

where the design matrices A and B are combined with the measurement l in the observation equation. y and x(i) represent the global parameters and the epoch-related parameters at the epoch i, respectively. x(0) stands for the parameter at the initial epoch. Absolute constraints are applied to the correction of y and x(0). In the state equation, \(\Phi (i)\) is the state transition matrix of x from epoch i − 1 to epoch i. Relative constraints are introduced between x(i − 1) and x(i). In some cases, absolute constraints can also be given on x(i), for instance, coa zero mean condition. After this transition, the active parameters x(i) and y are still kept for the current epoch i, while the adjacent parameter x(i − 1) at the previous epoch i − 1 becomes inactive. At the starting epoch, the initial values y0 and x0 are introduced with a priori weighting matrices Py0 and Px0, respectively.

After the new state parameter x(i) are introduced at epoch i, the contribution of new observational and state equations to the normal equation can be expressed as follows,

$$\begin{aligned} & \left[ {\begin{array}{*{20}c} {A^{T} (i)P_{l} (i)A(i)} & 0 & {A^{T} (i)P_{l} (i)B(i)} \\ 0 & {\Phi^{T} (i)P_{x} (i)\Phi (i)} & { - \Phi^{T} (i)P_{x} (i)} \\ {B^{T} (i)P_{l} (i)A(i)} & { - P_{x} (i)\Phi (i)} & {B^{T} (i)P_{l} (i)B(i) + P_{x} (i)} \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} y \\ {x(i - 1)} \\ {x(i)} \\ \end{array} } \right] \\ & = \left[ {\begin{array}{*{20}c} {A^{T} (i)P_{l} (i)l(i)} \\ 0 \\ {B^{T} (i)P_{l} (i)l(i)} \\ \end{array} } \right] \\ \end{aligned}$$
(2)
$$\Delta N(i)X(i) = \Delta w(i)$$
(3)

where the initialization condition of x0 and Px0, y0 and Py0 should also be introduced for the initial epoch. To simplify the notation, the above contribution to the normal equation is denoted by (3).

The accumulated normal equation at epoch i is written as follows before new observational and state equations are introduced,

$$\left[ {\begin{array}{*{20}c} {N_{11} (i - 1)} & {N_{12} (i - 1)} & 0 \\ {N_{21} (i - 1)} & {N_{22} (i - 1)} & 0 \\ 0 & 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} y \\ {x(i - 1)} \\ {x(i)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {w_{1} (i - 1)} \\ {w_{2} (i - 1)} \\ 0 \\ \end{array} } \right]$$
(4)
$$\overline{N}(i)X(i) = \overline{w}(i)$$
(5)

where (4) can be simplified and expressed as (5).

Considering the contribution of the new observational equations, the normal equation at epoch i becomes,

$$\left[ {\overline{N}(i) + \Delta N(i)} \right]X(i) = \overline{w}(i) + \Delta w(i)$$
(6)
$$\hat{N}(i)X(i) = \hat{w}(i)$$
(7)

where (6) is denoted as (7). To be more specific, Eq. (7) is rewritten as,

$$\left[ {\begin{array}{*{20}c} {\hat{N}_{11} (i)} & {\hat{N}_{12} (i)} & {\hat{N}_{13} (i)} \\ {\hat{N}_{21} (i)} & {\hat{N}_{22} (i)} & {\hat{N}_{23} (i)} \\ {\hat{N}_{31} (i)} & {\hat{N}_{32} (i)} & {\hat{N}_{33} (i)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} y \\ {x(i - 1)} \\ {x(i)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\hat{w}_{1} (i)} \\ {\hat{w}_{2} (i)} \\ {\hat{w}_{3} (i)} \\ \end{array} } \right]$$
(8)
$$x(i - 1) \, = - \left[ {\hat{N}_{22} (i)} \right]^{ - 1} \left[ {\hat{N}_{21} (i)y + \hat{N}_{23} (i)x(i) - \hat{w}_{2} (i)} \right]$$
(9)

where the parameter x(i − 1) that is to be eliminated can be derived as (9). Substituting (9) into (8), the normal equation is converted into,

$$\begin{gathered} \left[ {\begin{array}{*{20}c} {\hat{N}_{11} (i) - \hat{N}_{12} (i)[\hat{N}_{22} (i)]^{ - 1} \hat{N}_{21} (i)} & 0 & {\hat{N}_{13} (i) - \hat{N}_{12} (i)[\hat{N}_{22} (i)]^{ - 1} \hat{N}_{23} (i)} \\ {\hat{N}_{21} (i)} & {\hat{N}_{22} (i)} & {\hat{N}_{23} (i)} \\ {\hat{N}_{31} (i) - \hat{N}_{32} (i)[\hat{N}_{22} (i)]^{ - 1} \hat{N}_{21} (i)} & 0 & {\hat{N}_{33} (i) - \hat{N}_{32} (i)[\hat{N}_{22} (i)]^{ - 1} \hat{N}_{23} (i)} \\ \end{array} } \right] \hfill \\ \cdot \left[ {\begin{array}{*{20}c} y \\ {x(i - 1)} \\ {x(i)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\hat{w}_{1} (i) - \hat{N}_{12} (i)[\hat{N}_{22} (i)]^{ - 1} \hat{w}_{2} (i)} \\ {\hat{w}_{2} (i)} \\ {\hat{w}_{3} (i) - \hat{N}_{32} (i)[\hat{N}_{22} (i)]^{ - 1} \hat{w}_{2} (i)} \\ \end{array} } \right] \hfill \\ \end{gathered}$$
(10)

where the matrix at the left side of the NEQ is positive definite. Only the upper triangular part of the NEQ matrix is stored and available for parameter elimination. The parallel speedup for these large triangular matrices will be introduced in detail in the following sections.

Equation (10) is written as (11),

$$\left[ {\begin{array}{*{20}c} {N_{11} (i)} & 0 & {N_{12} (i)} \\ {\hat{N}_{21} (i)} & {\hat{N}_{22} (i)} & {\hat{N}_{23} (i)} \\ {N_{21} (i)} & 0 & {N_{22} (i)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} y \\ {x(i - 1)} \\ {x(i)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {w_{1} (i)} \\ {\hat{w}_{2} (i)} \\ {w_{2} (i)} \\ \end{array} } \right]$$
(11)
$$\left[ {\begin{array}{*{20}c} {N_{11} (i)} & {N_{12} (i)} & 0 \\ {N_{21} (i)} & {N_{22} (i)} & 0 \\ 0 & 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} y \\ {x(i)} \\ {x(i + 1)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {w_{1} (i)} \\ {w_{2} (i)} \\ 0 \\ \end{array} } \right]$$
(12)

where after x(i − 1) is removed, the normal equations of y and x(i) are taken as a priori condition at epoch i + 1 for new parameters x(i + 1), and the procedure starts again with (4) for the next epoch i + 1, as shown in (12).

Following the same pattern of (2–11), the recursion mentioned above is repeated until the last active parameter x(n) is introduced at epoch n. Finally, the following normal equation is solved for achieving the optimal estimate of x(n),

$$\left[ {\begin{array}{*{20}c} {N_{11} (n)} & {N_{12} (n)} \\ {N_{21} (n)} & {N_{22} (n)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} y \\ {x(n)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {w_{1} (n)} \\ {w_{2} (n)} \\ \end{array} } \right]$$
(13)
$$\begin{aligned} V^{T} PV = & l^{T} P_{l} l + y_{0}^{T} P_{{y_{0} }} y_{0} + x_{0}^{T} P_{{x_{0} }} x_{0} - y^{T} P_{{y_{0} }} y_{0} - x(0)^{T} P_{{x_{0} }} x_{0} \\ & - y^{T} \sum\limits_{i = 1}^{n} {\Delta w_{1} (i)} - \sum\limits_{i = 1}^{n} {x(i)^{T} \Delta w_{3} (i)} \\ \end{aligned}$$
(14)

where the performance metric VTPV needs to be computed for obtaining a posteriori error of unit weight. According to (1) and (3), it can be expressed at epoch n by (14).

As a consequence of (1, 6, 7, and 10), the following recurrence relations are achieved after x(n − 1) has been eliminated,

$$\begin{aligned} - y^{T} w_{1} (n) - x(n)^{T} w_{2} (n) = & - y^{T} [\hat{w}_{1} (n) - \hat{N}_{12} (n)[\hat{N}_{22} (n)]^{ - 1} \hat{w}_{2} (n)] \\ & - x(n)^{T} [\hat{w}_{3} (n) - \hat{N}_{32} (n)[\hat{N}_{22} (n)]^{ - 1} \hat{w}_{2} (n)] \\ = & [ - y^{T} \Delta w_{1} (n) - x(n)^{T} \Delta w_{3} (n)] + \hat{w}_{2} (n)^{T} [\hat{N}_{22} (n)]^{ - 1} \hat{w}_{2} (n) \\ & + [ - y^{T} w_{1} (n - 1) - x(n - 1)^{T} w_{2} (n - 1)] \\ \end{aligned}$$
(15)
$$\left\{ {\begin{array}{*{20}c} { - y^{T} w_{1} (n) - x(n)^{T} w_{2} (n) = \hat{w}_{2} (n)^{T} [\hat{N}_{22} (n)]^{ - 1} \hat{w}_{2} (n)} \\ {\,\,\,\,\,\,\, + [ - y^{T} \Delta w_{1} (n) - x(n)^{T} \Delta w_{3} (n)]} \\ {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + [ - y^{T} w_{1} (n - 1) - x(n - 1)^{T} w_{2} (n - 1)]} \\ \vdots \\ { - y^{T} w_{1} (1) - x(1)^{T} w_{2} (1) = \hat{w}_{2} (1)^{T} [\hat{N}_{22} (1)]^{ - 1} \hat{w}_{2} (1)} \\ {\,\,\,\,\,\,\, + [ - y^{T} \Delta w_{1} (1) - x(1)^{T} \Delta w_{3} (1)]} \\ {\,\,\, + [ - y^{T} w_{1} (0) - x(0)^{T} w_{2} (0)]} \\ { - y^{T} w_{1} (0) - x(0)^{T} w_{2} (0) = - y^{T} P_{{y_{0} }} y_{0} - x(0)^{T} P_{{x_{0} }} x_{0} } \\ \end{array} } \right.$$
(16)
$$\begin{aligned} - y^{T} w_{1} (n) - x(n)^{T} w_{2} (n) = & \sum\limits_{i = 1}^{n} {\hat{w}_{2} (i)^{T} [\hat{N}_{22} (i)]^{ - 1} \hat{w}_{2} (i)} - y^{T} P_{{y_{0} }} y_{0} - x(0)^{T} P_{{x_{0} }} x_{0} \\ & - y^{T} \sum\limits_{i = 1}^{n} \Delta w_{1} (i) - \sum\limits_{i = 1}^{n} {x(i)^{T} } \Delta w_{3} (i) \\ \end{aligned}$$
(17)

where the recurrence relation in (15) yields as results of (16) and (17) over a range from i = 0 to i = n.

Therefore, the alternative performance index at epoch n could be computed by substituting (17) into (14),

$$\begin{aligned} V^{T} PV\, = & l^{T} P_{l} l + y_{0}^{T} P_{{y_{0} }} y_{0} + x_{0}^{T} P_{{x_{0} }} x_{0} - y^{T} w_{1} (n) \\ & - x(n)^{T} w_{2} (n) - \sum\limits_{i = 1}^{n} {[\hat{w}_{2} (i)]^{T} [\hat{N}_{22} (i)]^{ - 1} \hat{w}_{2} (i)} \\ \end{aligned}$$
(18)

where the last term stands for the contribution of eliminating parameters n times.

The observational and state equations of eliminated parameters and their NEQs are saved to recover the observational residuals and estimates at every epoch. Based on (1) and (9), the related estimates and residuals could be computed backward for numerical analysis and quality control.

OpenMP-based parallelization

As an Application Program Interface (API), OpenMP has been widely used on multiple platforms, instruction set architectures, and operating systems for shared memory multiprocessing. OpenMP consists of a set of compiler directives, library routines, and environment variables. These instructions can be employed to build a portable, scalable model, which can provide developers with a simple, flexible interface for parallel processing based on multiple platforms. For implementing the parallel algorithm, the first step is to confirm the possibility of parallelizing the target operation and accordingly transform the source code into the form that can be identified by OpenMP. In parameter elimination, the major cost is caused by the computation in the NEQ system, and the NEQ should be defined as a shared memory accessed by multiple threads in parallel. Before the parameter elimination is performed, as shown in (10), the nonzero elements of the row or column vector associated with the eliminated parameter are stored in advance. In the NEQ system, access to these nonzero elements is read-only, and their impacts are removed from each row vector without any intervention from other elements. As shown in the NEQ transformation from (8 to 10), the second row vector for the eliminated parameter x(i − 1) is multiplied by \(\hat{N}_{12} (i)[\hat{N}_{22} (i)]^{ - 1}\) and subtracted from the first row vector. A similar computing pattern is adopted for each row vector. This indicates that the entire NEQ-level computation can be separated into sub-blocks row by row and the sub-blocks are distributed among the threads without data dependence. From the perspective of principle, it is possible to parallelize the parameter elimination in a row-wise manner.

OpenMP-based parallel optimization

In sequential least square estimation, epoch-related parameters are eliminated per epoch. The parameter elimination could effectively avoid the extension of NEQs due to the accumulation of epoch-related parameters and thus release the computational burden when computing the final inverse of the NEQs. However, a large number of non-epoch-related parameters and active epoch-related parameters are still valid for each epoch even after the parameter elimination. As a consequence, the computational costs of the matrix computation and the shifts of elements in the NEQ matrix are not negligible at all. The two major time-consuming parts for parameter elimination are the matrix computation, as shown in (10), for removing the contribution of the eliminated parameters and the shift of elements associated with eliminated parameters for compacting the NEQs. In what follows, the multi-core parallel optimizations are mainly implemented in the two parts for achieving the parallel speedup in the parameter elimination.

From (8 to 10), it can be seen that the NEQ-level matrix computations for eliminating parameters account for most of the computation time for LSQ estimation. OpenMP is employed to create work-sharing spaces where multiple threads run in parallel on the available cores for realizing the parallelization. A large problem can be divided into several work-sharing subtasks in the NEQ system. For each subtask, the whole process of matrix calculations is further divided into multiple smaller sub-blocks. Because of the symmetric property for the positive definite NEQ matrix, only its upper triangular part is saved in the program so as to reduce NEQ memory. Thus, the whole process of NEQ-level matrix calculations during parameter elimination can be considered as a manipulation of a large triangular matrix. Figure 1 shows the parallel optimization for the large subtask of triangular matrix computation. Taking the row and column associated with the parameter to be removed as boundaries, a large triangular work-sharing space is divided into three parts: one rectangular sub-block and two smaller triangular sub-blocks. The dimension of the matrix in each sub-block will vary due to the change in position of the parameter to be removed. In the work-sharing space, triangular and rectangular parallelized sub-blocks are executed one by one. There is no interaction between these parallelized sub-blocks. The cache memory traffic optimization and the optimized multi-thread scheduling scheme are implemented within the parallelized sub-blocks. Padding and loop tiling techniques are applied in the shift of elements for optimizing the cache memory traffic. On the other hand, an optimized multi-thread scheduling scheme is mainly employed in the operations of (10) during the parameter elimination.

Fig. 1
figure 1

Parallel optimization for a large triangular work-sharing space. Each sub-block is an independent parallelized space where available threads run in parallel

Full size image

To improve the memory traffic and avoid such cache misses as far as possible, this study uses a loop tiling technique to optimize the temporal locality of data accesses in nested loops (Wolfe 1989). Figure 2 shows a typical example for this cache memory traffic optimization for easy understanding. As shown in Fig. 2, the hypothetical algorithm has two nested loops j and i to perform a specific calculation on all pairs of the element of arrays a and b. Both arrays a and b have a length of six elements residing on the main memory and also have caches for this memory. A cache is large enough to fit five elements of either array a or array b. For intel Xeon or Xeon Phi caches, the least recently used (LRU) eviction policy is applied. This means that the cache stores every element fetched from the memory, and then a list of the recently used elements will be evicted from the cache to make room for new incoming elements if the cache is filled up. The algorithm without tiling has a cache hit ratio of 10 to 24. It is possible to improve the cache hit ratio if the memory accesses are reordered. As shown in Fig. 2, the optimization is implemented by strip mining the i-loop and permuting the outer two loops. This algorithm hits the cache 17 out of 24 times. In the optimized algorithm, the element of array b is revisited sooner while it is still in the cache, which improves the memory traffic and its performance. The operation that we performed is called loop tiling, and its strategy applied here is cache blocking.

Fig. 2
figure 2

Loop tiling based cache memory traffic optimization. Cache memory performance is measured in terms of cache hit ratio, i.e., a ratio of the number of cache hits to the number of total accesses

Full size image

For the parallelized standard square or rectangular matrices, all the i-loops are first padded by modifying an offset of their addresses in order to map them to different cache lines. In Fig. 3, the padding offset is indicated by ‘PADS’. In this study, only one thread is allocated per core for parallel computing. For each core, the loop tiling technique is employed to improve temporal locality and reuse cache more efficiently for every i-loop or j-loop iteration, as shown in Fig. 3. From the figure, it can be seen that the i-loop and j-loop are tiled with tile sizes denoted as TILE_i and TILE_j, respectively. The elements in the i-tile will be reused across the elements of the j-loop without being evicted from cache and vice versa. After the tile size is specified, a block of TILE_i × TILE_j is formed to fit the cache line in memory. For a specific cache architecture, different tile sizes can lead to significant variations in the performance of loop tiling. The optimal tile sizes need to be confirmed through actual experiments about the computational cost of nested loops.

Fig. 3
figure 3

Multi-thread parallel optimization for square or rectangular matrices. \(n{\text{thread}}\) denotes the number of available cores

Full size image

Figure 4 shows the parallel algorithm for triangular matrices within the OpenMP parallelized space. Before the vectorization is enforced in the inner loop, it is mandatory to ensure that there is no carried-loop dependence for available shared arrays in the parallelized space. For the parallelized triangular matrix, the j-loop iterations are distributed over the different threads, and the computational cost of these iterations for one thread is different from that for another one. Figure 5 shows the graphical representations of the working principle of scheduling methods including ‘static’, ‘dynamic’, and ‘guided’ clauses, respectively. As mentioned before, the pieces of work created from the iteration space are evenly distributed over the threads in the work following the ‘static’ scheduling law. The best computing performance is achievable with this simple scheduling option if all the pieces require the same computational time for all of the available threads. However, it turns out to be difficult to provide an optimal distribution of non-homogeneous iterations among the threads, for instance, in the triangular matrix. A possible solution would be to assign different pieces of work to the threads in a dynamic manner. In the ‘dynamic’ scheduling mode, each thread bears one piece of work at first. After they complete their previous subtask, another piece will be assigned to them until the last piece of work is finished. In general, the ‘dynamic’ scheduling method could efficiently enhance the capability of solving the problem of non-homogenous iterations compared to the previous ‘static’ method, whereas it adds overhead in computational cost due to the handling and distributing of the different iteration packages (Hermanns 2002). With the increase in the size of pieces of work (i.e., chunk size), this overhead can be reduced, but a larger non-equilibrium between different threads is, after that, possible. To achieve a better balance of workload among the threads, the ‘guided’ scheduling scheme begins with a big chunk size and then has pieces of work with decreasing size. The decreasing law is of exponential nature, which means the number of iterations for the following piece of work is halved after the previous one is finished. These scheduling types will be compared with each other for achieving an optimized solution.

Fig. 4
figure 4

Multi-thread parallel optimization for triangular matrices. The option of distributing the non-homogeneous iterations is expressed as \(selected\_mode\)

Full size image
Fig. 5
figure 5

Options of Scheduling for a multi-thread parallel algorithm based on OpenMP

Full size image

Hardware and software

To develop the multi-thread parallel algorithm, the server ‘srtg4’ is exclusively taken from the real-time GNSS group at German Research Centre for Geosciences (GFZ) as a hardware device. The information about the hardware resources is listed in Table 1 for this server. The PANDA (Positioning And Navigation Data Analyst) software package has been steadily improved over decades since it was developed at Wuhan University (Liu and Ge 2003). Currently, the software can support data processing for various purposes, for example GNSS or low earth orbit satellites POD, precise clock estimation, precise point positioning, and very-long-baseline interferometry (VLBI) with comparable accuracy as most of the IGS ACs software packages. In this study, the multi-GNSS experiment (MGEX) data (Montenbruck et al. 2017; Johnston et al. 2017) are processed by the PANDA software package. The POD is taken as a typical example for testing the computational efficiency of GNSS network solutions in this study. To be more precise, its processing strategy is listed in Table 2.

Table 1 CPU architecture information of the dedicated server
Full size table
Table 2 Processing strategy for multi-GNSS POD
Full size table

Validation

For the multi-thread parallel algorithm, the cache memory traffic optimization and the multi-thread scheduling scheme are implemented in rectangular and triangular parallelized sub-blocks. First, the advantages of these optimizations in parallelized sub-blocks are verified to justify the developed parallel algorithm. Afterward, the new parallel algorithm is implemented in the PANDA software and validated by processing MGEX data to demonstrate its improvements in the computational efficiency of parameter estimation.

Cache memory traffic optimization

For comparison, Fig. 6 shows the computational performances for the movements of elements relevant to the parameter to be eliminated in the rectangular matrix with different padding sizes. It is assumed that 2000 parameters are involved for this movement with different padding sizes. Padding of an array is an optimization of spatial locality for accessing memory. The optimal solution is to make sure that the offset between addresses of data accessed by multiple threads is as large as possible. Then, different threads do not use the same cache line to avoid false sharing. In this study, the cache line size is 64 bytes, which is equivalent to eight double-precision floating-point numbers. As shown in Fig. 6, the computational cost is relatively high if the padding size is less than eight. Under this circumstance, the same cache line is written by different threads. Consequently, the data will be fetched by individual threads from the main memory, which causes a lower speed of data access. Except for the false sharing, the overheads of the nested loop are increased when the padding size is smaller than \({{(m - 1)} \mathord{\left/ {\vphantom {{(m - 1)} {n{\text{thread}}}}} \right. \kern-\nulldelimiterspace} {n{\text{thread}}}}\). The workloads distributed among threads will be unbalanced if the padding size is larger than \({{(m - 1)} \mathord{\left/ {\vphantom {{(m - 1)} {n{\text{thread}}}}} \right. \kern-\nulldelimiterspace} {n{\text{thread}}}}\). The optimal padding size is, therefore, \({{(m - 1)} \mathord{\left/ {\vphantom {{(m - 1)} {n{\text{thread}}}}} \right. \kern-\nulldelimiterspace} {n{\text{thread}}}}\) for ‘nthread’ threads. The padding size of \({{(m - 1)} \mathord{\left/ {\vphantom {{(m - 1)} {n{\text{thread}}}}} \right. \kern-\nulldelimiterspace} {n{\text{thread}}}}\) is also much larger than the cache line size.

Fig. 6
figure 6

Computational performance of the multi-thread schemes with different padding sizes for movements of elements in a 1999 × 3000 rectangular matrix. Each item in legend denotes a multi-thread scheme with a different number of threads in parallel. The cases of padding sizes less than the cache line size are shown in the bottom panel

Full size image

Figure 7 shows the computational cost of the matrix operations with different TILE_i and TILE_j sizes for the innermost i-loop and j-loop in Fig. 3, respectively. The shift of elements is repeated 20 times for each tile size. The tile size in the innermost j-loop fits the corresponding cache line when the tile size in the innermost i-loop is tested. For the innermost i-loop, the optimal tile size is eight since the cache line size equals an array of eight double-precision floating-point numbers. For the innermost j-loop, the optimal is fifteen, as shown in Fig. 7. This is because the cache line size is equivalent to sixteen integer numbers, and the addresses of two adjacent columns are accessed inside the innermost i-loop. In Fig. 8, the improvements of the cache-aware scheme are also confirmed for the computations of matrices with different sizes. The padding strategy has been adopted for the matric computation without false sharing between threads. Therefore, the computational performance is improved by introducing more threads in multi-thread applications.

Fig. 7
figure 7

Computational performance of movements of elements in a 5000 × 8000 rectangular matrix with different tiling sizes in the innermost j-loop (top) and the innermost i-loop (bottom), respectively

Full size image
Fig. 8
figure 8

Computational performance of movements of elements in rectangular matrices with different sizes including: a 15,000 × 15,000, b 15,000 × 8000, c 8000 × 8000, and d 5000 × 8000, respectively

Full size image

Scheduling scheme

Figure 9 shows the variation in computational performance of the triangular matrix operation with the increasing minimum chunk size for the ‘static’, ‘dynamic’, and ‘guided’ scheduling schemes, respectively. It is assumed that fifty parameters to be eliminated are involved in the matrix computation of (10) to test the computational cost of these schemes. In this experiment, six threads are employed to parallelize the triangular block. For ‘static’ scheduling type, the computational cost is nearly linearly reduced to the minimum value of 489 ms as the minimum chunk size is increased to 60 loop iterations. The ‘dynamic’ scheduling type dynamically distributes chunks to the threads during the runtime so that its overhead may be higher than the ‘static’ scheduling type. The cost of the ‘dynamic’ scheme accordingly rises above that of the ‘static’ scheme and then gradually approaches the same level of the ‘static’ scheme with the increasing minimum chunk size. The ‘guided’ scheduling type provides a suitable approach to solving the unbalance existing in iterations. The initial chunk size is large enough to reduce the overhead due to the distribution of iterations. Small chunks are assigned among the threads toward the end of the computation in order to improve the load balancing. The best computational performance is achieved by using the ‘guided’ scheduling scheme when the minimum chunk size defaults to one. Although the default ‘dynamic’ scheduling scheme completes the computation at a small cost, its overall computational performance is worse than the ‘guided’ scheme when the chunk size is within 60 loop iterations. The computational burden grows with the increasing minimum chunk size for all the scheduling schemes if the minimum chunk size exceeds 60 loop iterations. The workload of the last chunk assigned to one thread will be heavier with the increase of the minimum chunk size, while other threads that have finished their works are waiting for the running thread in the final synchronization. To avoid this load imbalance during the end of the computation, a big minimum chunk size may be simply prohibited in the scheduling clause for the parallelized triangular block.

Fig. 9
figure 9

Computational performance of a 4000 × 4000 triangular matrix operation using the static, dynamic, and guided scheduling schemes with different minimum chunk sizes, respectively

Full size image

Computation efficiency

The multi-GNSS POD is taken as a typical GNSS network solution in order to demonstrate the improvements in the computational efficiency using the parallel algorithm. The total number of GPS, Galileo, and BDS satellites is about eighty in this GNSS network solution. Tracking networks containing different numbers of stations are used for the parameter estimation. In the POD processing, the percentage of the parameter elimination in the whole time consumption is at least 85% when the parallel algorithm is not used. For comparison, the parameter eliminations with and without the parallel algorithm are utilized in the parameter estimation, respectively.

Figure 10 shows the computation time of one iteration of the least square parameter estimation by using the serial scheme and the parallel scheme, respectively. The computational time increases gently and near-linearly with the number of stations for the multi-thread parallel strategy, whereas it exhibits quadratic growth for the serial strategy. In the network solution of 60 ground stations, the computation cost can be halved by applying the parallel algorithm in comparison with the serial scheme. With the increased number of stations, the improvement of the parallel algorithm compared to the serial scheme becomes more significant. Even for 200 ground stations, the computation of one iteration of the least square parameter estimation can be completed within 25 min with the parallel strategy. The time consumed for this estimation is three times higher if the serial scheme is used. This gives a promising potential for enhancing the efficiency of huge GNSS network solutions.

Fig. 10
figure 10

Comparison of computation times of serial and parallel strategies for one iteration of parameter estimation with different numbers of ground stations

Full size image

Figure 11 shows the comparison of the parallel strategies with different numbers of threads. In this experiment, the six-core hardware cannot allow more than one thread to run on each core since the processor is without hyper threading. Considering the limitation of architecture, the maximum speedup of parallel computing can be achieved only by allocating one thread per core and fully distributing subtasks among the six threads. For each case, about 100 ground stations and 80 satellites are involved in the parameter estimation. With the increase in the number of threads, the parallel algorithm reduces the computation time rapidly and linearly at first. After more than three threads are employed, the consumed cost gently reduces with the increase of threads. The percentage of the runtime for the parallelizable part exceeds 95% of the whole parameter estimation before parallelization. This implies that the current level of parallel speedup is far below the theoretical upper limit even if all the six threads are fully exploited (Amdahl 1967). Nowadays, Intel has released a series of the Intel Many Integrated Core (MIC) architecture-based Xeon Phi coprocessors to give a low-cost solution to parallel computing. As the instruments become commonplace in the HPC field, a more significant improvement in the performance is expected for the presented parallel algorithm.

Fig. 11
figure 11

Comparison of computation times of one iteration of parameter estimation for parallel strategies with different numbers of threads

Full size image

Conclusions and remarks

In this contribution, an effective multi-thread parallel algorithm is developed based on OpenMP and introduced into eliminating inactive parameters to accelerate the sequential LSQ parameter estimation highly. Concerning the multi-thread algorithm, we create two types of parallelized spaces, including the square or rectangular parallelized block and the triangular parallelized block, according to the feature of CPU architecture. The loop tiling technique is applied in the rectangular parallelized block to improve memory locality and fully reuse cache. In the multi-thread schemes, it has been demonstrated that the maximum parallel speedup can be achieved when tiles are evenly distributed among the threads. For a triangular parallelized block, a ‘guided’ scheduling scheme with the enforced vectorization is used to distribute chunks across the threads appropriately. Results confirm that the ‘guided’ scheduling strategy significantly reduces the overhead existing in the ‘dynamic’ scheduling type and avoids the final load imbalance occurring toward the ‘static’ distribution. Using six threads in parallel for the developed parallel algorithm, the computational performance in parameter estimation can be improved by a factor of about three compared to the traditional serial strategy. The performance of this architecture-oriented algorithm depends on the multi-core features of available processors. To ensure more efficient use of the high-performance instruments, Intel company recently has been developing various new series of multi-core Xeon Phi coprocessors with a well-documented set of new configurations and technical experiences. This also gives a low-cost solution for enhancing the efficiency of scientific computing. In the future, it is very likely to further improve the parallel computing algorithm by applying the MIC-architecture-based coprocessor.