New criteria for existence of solutions for equilibrium problems

Abstract

Equilibrium problems provide a mathematical framework which includes optimization, variational inequalities, fixed point and saddle point problems, and noncooperative games as particular cases. In this paper sufficient conditions for the existence of solutions of an equilibrium problem are given by weakening the assumption of quasiconvexity of the involved equilibrium bifunction. The existence of solutions is established both in presence of compactness of the feasible set as well with a coercivity assumption. The results are obtained in an infinite dimensional setting, and they are based on the so called finite solvability property which is weaker than the recently introduced finite intersection property and in turn, weaker than most common cyclic and proper quasimonotonicity. Some examples are presented to illustrate the various cases in which other existence results for equilibrium problems do not apply. Finally, applications to the solution of quasiequilibrium problems, quasioptimization problems and generalized quasivariational inequalities are discussed.

1 Introduction

The importance of equilibrium problems (so named by Muu and Oettli (1992) and adopted by a lot of researchers working on this topic) is justified by a great number of applications in various fields of mathematics, including game theory, complementarity problems, control theory, fixed point theory and so on. Over the time, equilibrium problems aroused increasing interest, and many aspects of these problems have been investigated (for a recent review see Bigi et al. (2019) and references therein). As in the case of other general models, a special attention was paid to the existence of solutions.

The origin of the equilibrium problem goes back to the paper of Fan (1972), in which an existence result has been established under the following assumptions: compactness and convexity of the feasible set, the nonnegativity of the equilibrium bifunction f on the diagonal, upper semicontinuity of $f(\cdot ,y)$ and quasiconvexity of $f(x,\cdot )$. Because Fan’s result is equivalent to his famous minimax inequality, the equilibrium problem is also called Ky Fan minimax inequality problem.

A major line of development in equilibrium theory, which has led in recent decades to a large number of articles, consisted in finding conditions, different or weaker than the usual ones, that guarantee the existence of the solutions. Our work fits in this group of papers. Its aim is to establish new existence criteria of the solutions for equilibrium problems, using a new concept related to the bifunction f, the so-called finite solvability property that generalizes the finite intersection property recently introduced in Cotrina and Svensson (2021).

The paper is organized as follows. Section 2 contains some considerations about equilibrium problems and recalls some needed notions and results. Section 3 is devoted to the equilibrium problems when the equilibrium bifunction enjoys the finite solvability property. The existence of solutions is investigated first, for the case when the feasible set is compact and then, in the absence of compactness. In the last section, we establish existence theorems for quasiequilibrium and quasioptimization problems. An application to the generalized quasivariational inequality problem is also discussed.

2 Preliminaries

Several optimization problems (minimization problems, variational inequalities, complementarity problems, Nash equilibria, saddle point problems are just a few examples) can be put in the following format:

$$\begin{aligned} \text {find } x_0\in X\text { such that } f(x_0,y)\ge 0,\ \forall y\in X\qquad \qquad \qquad {\text {(EP)}} \end{aligned}$$

where X is a nonempty convex subset of a Hausdorff topological vector space and f is a real bifunction defined on $X\times X$.

Usually, in an equilibrium problem it is required the bifunction f to satisfy an equilibrium condition which can be, either $f(x,x)=0$ for all $x\in X$ or a weaker one

$$\begin{aligned} f(x,x)\ge 0,\ \forall x\in X \end{aligned}$$

(1)

The well-known existence result due to Fan (1972) holds under the following assumptions:

• (i) X is a nonempty compact convex subset of a Hausdorff topological vector space;

• (ii) f is

  (ii₁):

  upper semicontinuous in the first variable, and

  (ii₂):

  quasiconvex in the second one;

• (iii) condition (1) holds.

Actually condition (ii$_2$) is too strong; the proof requires the convexity of the sublevel sets $\{y\in X:f(x,y)<0\}$ only. Moreover, in order to avoid any assumption of convexity both for the domain X and for the bifunction f, in Castellani and Giuli (2016) a different approach is proposed in which the existence of solutions for (EP) is obtained assuming the cyclical monotonicity of $-f$, that is,

$$\begin{aligned} f(x_0,x_1)+f(x_1,x_2)+\dots +f(x_m,x_0)\ge 0,\ \forall m\in {\mathbb {N}},\ x_0,x_1,\dots ,x_m\in X \end{aligned}$$

(2)

In this paper we establish equilibrium results avoiding the convexity of the sublevel sets $\{y \in X:f(x,y)<0\}$ and requiring that for any finite subset $A\subseteq X$ and $x\in {\text {conv}}A$, that is, x in the convex hull of the set A, it holds

$$\begin{aligned} f(x,y)<0\quad \Rightarrow \quad \exists a\in A\text { such that } f(y,a)>0 \end{aligned}$$

We will show that this condition comes down to the pseudomonotonicity of $-f$, if the sets $\{y\in X: f(x, y)\le 0\}$ are convex. It might be shown with several examples that the convexity of these sets is not comparable with the convexity of the sublevel sets $\{y\in X:f(x,y)<0\}$ but they both descend from the quasiconvexity of $f(x,\cdot )$. We recall that a bifunction $f:X\times X\rightarrow {\mathbb {R}}$ is said to be pseudomonotone (Bianchi and Schaible 1996, ) if

$$\begin{aligned} x,y\in X, f(x,y)\ge 0\quad \Rightarrow \quad f(y,x)\le 0 \end{aligned}$$

Clearly $-f$ is pseudomonotone if and only if

$$\begin{aligned} x,y\in X,\ f(x,y)<0\quad \Rightarrow \quad f(y,x)>0 \end{aligned}$$

(3)

It is easy to see that a bifunction f is nonnegative on the diagonal of $X\times X$, whenever it satisfies conditions (2) or (3). Notice further that condition (2) implies the pseudomonotonicity of $-f$. Indeed, if (2) holds and for some $x,y\in X$, $f(x,y)\le 0$, then:

$$\begin{aligned} f(y,x) \ge f(x,y)+f(y,x)\ge 0 \end{aligned}$$

One can easily find examples showing that the pseudomonotonicity of $-f$ does not implies (2). Let $f:[1,2]\times [1,2]\rightarrow {\mathbb {R}}$, $f(x,y)=2x(y-x)$. Then clearly $-f$ is pseudomonotone but nevertheless $f(1,2)+f(2,1)=-2<0$. Equilibrium theorems for pseudomonotone bifunctions can be found in Iusem and Sosa (2003) and Bianchi and Pini (2005) but, to the best of our knowledge, there is no such result for bifunctions f with $-f$ pseudomonotone.

We end this preliminary section by recalling some basic notions and facts concerning set-valued mappings (see Aliprantis and Border (2006) for more details). If X and Y are topological spaces, the graph of a set-valued mapping $F:X\rightrightarrows Y$ is denoted by ${\text {gr}}F=\{(x,y)\in X \times Y: y\in F(x)\}$. The mapping F is closed if its graph is a closed subset of $X\times Y$ and it is compact if its range F(X) is contained in a compact subset of Y. The mapping F is said to be closed-valued if F(x) is a closed set for any $x\in X$. The terms nonempty-valued, compact-valued and convex-valued are similarly defined. The mapping F is said to be lower semicontinuous if for any closed subset B of Y the set $\{x \in X: F(x)\subseteq B\}$ is closed or, equivalently, for each $x\in X$, for each convergent net $x_\alpha \rightarrow x$, and for each $y\in F(x)$ there exist a subnet $\{x_{\alpha _\lambda }\}$ of $\{x_\alpha \}$ and a net $\{y_\lambda \}$ in Y satisfying $y_\lambda \in F(x_{\alpha _\lambda })$ for each $\lambda$ and $y_\lambda \rightarrow y$. The mapping F is said to be upper semicontinuous if for any closed subset B of Y the set $\{x\in X: F(x)\cap B \ne \emptyset \}$ is closed. The mapping F is upper semicontinuous and compact-valued if and only if for every net $\{(x_\alpha ,y_\alpha )\}\subseteq {\text {gr}}F$, if $x_\alpha \rightarrow x$, then the net $\{y_\alpha \}$ has a limit point in F(x). The mapping is continuous, if it is both upper and lower semicontinuous.

If $X=Y$ is a subset of a vector space, the mapping F is called KKM mapping if ${\text {conv}}A\subseteq \bigcup _{x\in A}F(x)$ for each finite set $A\subseteq X$. Lastly, the following two lemmas are needed in the proof of the main theorems.

Lemma 1

(Aliprantis and Border 2006) Let X and Y be topological spaces and $F:X\rightrightarrows Y$ a set-valued mapping.

• (i) If Y is Hausdorff and F is compact, then F is closed if and only if it is upper semicontinuous and closed-valued.

• (ii) The intersection of a family of closed set-valued mappings is closed.

• (iii) If Y is a finite dimensional topological vector space and F is upper semicontinuous and compact-valued, then the convex hull mapping ${\text {conv}}F$, defined by $({\text {conv}}F)(x)={\text {conv}}F(x)$, is upper semicontinuous.

Lemma 2

(Mehta et al. 1997) Let X and Y be topological spaces and D be an open subset of X. Suppose that $F_1:D\rightrightarrows Y$ and $F_2:X \rightrightarrows Y$ are upper semicontinuous set-valued mappings such that $F_1(x)\subseteq F_2(x)$ for all $x\in D$. Then the mapping $F:X \rightrightarrows Y$ defined by

$$\begin{aligned} F(x)=\left\{ \begin{array}{ll} F_1(x) &{} \text {if } x\in D \\ F_2(x) &{} \text {if } x\in X\setminus D \end{array}\right. \end{aligned}$$

is also upper semicontinuous.

3 Equilibrium problems

In recent papers the existence of solutions of the problem (EP) has been obtained under some generalized monotonicity assumptions. We introduce the notion of finite solvability property for bifunctions, and we discuss its relation with some generalized monotonicity properties.

Definition 1

A bifunction $f:X\times X\rightarrow {\mathbb {R}}$ is said to have the finite solvability property on X if, for any finite subset $A\subseteq X$ such that there exists $x\in X$ with $f(x,a)<0$ for all $a\in A$, then there exists $y\in X$ such that $f(a,y)\le 0$ for all $a\in A$.

Since the finite solvability property seems difficult to check in concrete situations, it is desirable to compare it with stronger conditions, but easier to verify. Below we make some comments on such conditions. Let X be a nonempty convex subset of a topological vector space. A bifunction $f:X\times X\rightarrow {\mathbb {R}}$ is said

• to be properly quasimonotone (Bianchi and Pini 2001) or 0-diagonally quasiconcave in the second variable, in the terminology used by Zhou and Chen (1988), if for each finite set $A\subseteq X$ and any $y\in {\text {conv}}A$, there exists $a\in A$ such that $f(a,y)\le 0$;

• to be cyclically quasimonotone (Khanh and Quan 2019) if, for all $n\ge 1$ and all $x_0,x_1,\dots x_n\in X$, there exists $i \in \{0,1,\dots ,n\}$ such that $f(x_i,x_{i+1}) \le 0$, where $x_{n+1}=x_0$;

• to have the finite intersection property (Cotrina and Svensson 2021) on X if for any finite subset $A\subseteq X$, there exists $y\in X$ such that $f(a,y)\le 0$, for all $a\in A$.

Very recently (Cotrina and Svensson 2021) characterized the cyclic quasimonotonicity as follows: a bifunction f is cyclically quasimonotone if and only if, for any nonempty finite subset $A\subseteq X$, there exists $y\in A$ such that $f(a,y) \le 0$, for all $a\in A$. Hence cyclic quasimonotonicity implies the finite intersection property which in turn implies the finite solvability property.

Besides, the proper quasimonotonicity of f coincides with the affirmation that the mapping $F(x)=\{y\in X:f(x,y)\le 0\}$ is a KKM mapping. In particular, if F is closed-valued (for instance if $f(x,\cdot )$ is lower semicontinuous) and A is a finite subset of X, from the Fan-KKM theorem we have $\bigcap _{a\in A} F(a)\ne \emptyset$ which implies that f has the finite intersection property.

The example below proves that a bifunction with the property of finite solvability may not have the finite intersection property.

Example 1

Consider the bifunction $f:[0,2]\times [0,2]\rightarrow {\mathbb {R}}$ defined as $f(x,y)=x^2+2y-2$. This continuous bifunction has not the finite intersection property: indeed if $2\in A$ then $f(2,y)=2y+2>0$ for all $y\in [0,2]$. On the converse, since there exists $x\in [0,2]$ such that $f(x,a)<0$ for all $a\in A$ if and only if $\max A<1$, then $f(a,0)<1-2<0$ for each $a\in A$ and f has the finite solvability property.

The finite solvability property holds whenever there exists a function $h:X\rightarrow X$ such that

$$\begin{aligned} x,y\in X,\ f(x,y)<0\quad \Rightarrow \quad f(y,h(x))\le 0 \end{aligned}$$

Indeed, in this case, if $x\in X$ satisfies $f(x,a)<0$ for all $a\in A$, then $y=h(x)$ will be solution for the system $f(a,y)\le 0$ with $a\in A$. Notice that this property is verified by the bifunction in the previous example where $h:[0,2]\rightarrow [0,2]$ is $h(x)=x^2/2$.

The following theorem is one of our main results. Its method of proof has some similarities with that used by Brézis et al. (1972) to generalize the Ky Fan minimax principle. Recall that a subset X of a topological vector space is said to be finitely closed (Shioji 1991) if for each finite dimensional subspace V the set $X\cap V$ is closed.

Theorem 3

Let X be a nonempty compact convex subset of a Hausdorff topological vector space and f be a real bifunction defined on $X\times X$ that satisfies the following assumptions:

• (i) for each $y\in X$, the set $\{x\in X:f(x,y)\ge 0\}$ is finitely closed;

• (ii) for each $x\in X$, the set $\{y\in X:f(x,y)\le 0\}$ is finitely closed;

• (iii) for any finite subset $A\subseteq X$, $x\in {\text {conv}}A$ and $y\in X$ it holds

  $$\begin{aligned} f(x,y)<0\quad \Rightarrow \quad \exists a\in A \text { such that } f(y,a)>0; \end{aligned}$$

• (iv) for each finite dimensional subspace V, the bifunction f has the finite solvability property on section $D=X\cap V$;

• (v) for any finite dimensional section $D=X\cap V$ and for every net $\{x_\alpha \}\subseteq X$ converging to a point $x\in D$, the following implication holds

  $$\begin{aligned} f(x_\alpha ,y)\ge 0,\quad \forall y\in D,\ \forall \alpha \quad \Rightarrow \quad f(x,y)\ge 0,\quad \forall y\in D \end{aligned}$$

Then, there exists $x_0\in X$ such that $f(x_0,y)\ge 0$ for all $y\in X$.

Proof

Let $\{V_\alpha \}$ be the net of all finite dimensional subspaces of E that intersect the set X, ordered by inclusion, i.e. $\alpha \ge \beta$ means $V_\alpha \supseteq V_\beta$. For each $\alpha$ consider $X_\alpha =X\cap V_\alpha$. We claim that there exists $x_\alpha \in X_\alpha$ such that $f(x_\alpha ,y)\ge 0$ for all $y\in X_\alpha$. Assume by contradiction that for each $x\in X_\alpha$ there exists $y\in X_\alpha$ such that $f(x,y)<0$. Therefore $X_\alpha =\bigcup _{y\in X_\alpha } G_\alpha (y)$, where each

$$\begin{aligned} G_\alpha (y)=\{x\in X_\alpha :f(x,y)<0\} \end{aligned}$$

is open in $X_\alpha$ by assumption (i). Since $X_\alpha$ is compact, there exists a finite subcover $\{G_\alpha (y_1),\dots ,G_\alpha (y_n)\}$ of $X_\alpha$. Define the set-valued mapping $H_\alpha :X_\alpha \rightrightarrows X_\alpha$ by

$$\begin{aligned} H_\alpha (x)=\bigcap _{i\in I(x)}F_\alpha (y_i) \end{aligned}$$

where $I(x)=\{i\in \{1,\dots ,n\}:x\in G_\alpha (y_i)\}\ne \emptyset$ and

$$\begin{aligned} F_\alpha (y_i)=\{x\in X_\alpha :f(y_i,x)\le 0\} \end{aligned}$$

is a closed set, for every $i\in I(x)$. The mapping $H_\alpha$ is nonempty-valued from assumption (iv). Moreover,

$$\begin{aligned} H_\alpha =\bigcap _{i=1}^nH_i^\alpha \end{aligned}$$

where the set-valued mappings $H_i^\alpha$ are defined by

$$\begin{aligned} H_i^\alpha (x)=\left\{ \begin{array}{ll} F_\alpha (y_i) &{} \text {if } x\in G_\alpha (y_i) \\ X_\alpha &{} \text {if } x\in X_\alpha \setminus G_\alpha (y_i) \end{array}\right. \end{aligned}$$

Lemma 2 ensures that the maps $H_i^\alpha$ are upper semicontinuous. The mapping $H_\alpha$ is closed as intersection of closed mappings (Lemma 1). The convex hull of a closed set is closed in the finite dimensional space $V_\alpha$ and hence, again from Lemma 1 the set-valued mapping ${\text {conv}}H_{\alpha }$ is upper semicontinuous with nonempty, compact and convex values. Then there exists a fixed point $x\in {\text {conv}}H_\alpha (x)$. Consequently, there is a finite set $A\subseteq H_\alpha (x)$ such that $x\in {\text {conv}}A$ and $f(y_i,a)\le 0$ for all $i\in I(x)$ and $a\in A$. Fixing an $i\in I(x)$, we get $f(y_i,a)\le 0$, for all $a\in A$ and $f(x,y_i)<0$ which contradicts (iii). Therefore, there exists a net $\{x_\alpha \}$ such that for each $\alpha$, $x_\alpha \in X_\alpha$ and $f(x_\alpha ,y)\ge 0$, for all $y\in X_\alpha$. Since X is a compact set, without loss of generality, we may assume that the net $\{x_\alpha \}$ converges to a point $x_0 \in X$. Consider an arbitrary $y\in X$ and denote by $V_{\alpha _0}$ the linear space generated by $x_0$ and y. For any $\alpha \ge \alpha _0$ we get $f(x_\alpha ,z)\ge 0$ for all $z\in X\cap V_{\alpha _0}$, and $f(x_0,y)\ge 0$ derives from (v). $\square$

It is worthy to say that if all the sublevel sets $\{x\in X:f(x,y)\ge 0\}$ are closed, the limit condition (v) in Theorem 3 is verified. Therefore in the particular case where the domain X is a subset of a Euclidean space, and finitely closed sets are closed, we get the following as a direct consequence of Theorem 3.

Corollary 4

Let $X\subseteq {\mathbb {R}}^n$ be a nonempty compact convex set and f be a real bifunction defined on $X \times X$ that satisfies the following assumptions:

• (i) for each $y\in X$, the set $\{x\in X:f(x,y)\ge 0\}$ is closed;

• (ii) for each $x\in X$, the set $\{y\in X:f(x,y)\le 0\}$ is closed;

• (iii) for any finite subset $A\subseteq X$, $x\in {\text {conv}}A$ and $y\in X$ it holds

  $$\begin{aligned} f(x,y)<0\quad \Rightarrow \quad \exists a\in A\text { such that } f(y,a)>0; \end{aligned}$$

• (iv) the bifunction f has the finite solvability property on X.

Then, there exists $x_0\in X$ such that $f(x_0,y)\ge 0$ for all $y \in X$.

When the space is not finite dimensional, as in the proof of Theorem 3, the sublevel sets are intersected with a finite dimensional subspace V to ensure the closedness of convex hulls of closed sets. This can be avoided and the proof can be shortened considerably by assuming the sublevel sets in (ii) to be convex. Moreover, under this additional assumption, condition (iii) coincides with the pseudomonotonicity of $-f$. Condition (iii) implies the pseudomonotonicity of $-f$ by choosing $A=\{x\}$. Viceversa the pseudomonotonicity of $-f$ and the convexity of the sets $\{y\in X:f(x,y)\le 0\}$ guarantee condition (iii). Indeed, take a finite subset A, $x\in {\text {conv}}A$ and $y\in X$ such that $f(x,y)<0$. By contradiction assume that $f(y,a)\le 0$ for all $a\in A$. The convexity of the sublevel set implies that $f(y,x)\le 0$ which contradicts the pseudomonotonicity of $-f$.

Theorem 5

Let X be a nonempty compact convex subset of a locally convex Hausdorff topological vector space and f be a real bifunction defined on $X\times X$ that satisfies the following assumptions:

• (i) for each $y\in X$, the set $\{x \in X:f(x, y)\ge 0\}$ is closed;

• (ii) for each $x\in X$, the set $\{y \in X: f(x, y)\le 0\}$ is closed and convex;

• (iii) $-f$ is pseudomonotone;

• (iv) the bifunction f has the finite solvability property on X.

Then, there exists $x_0\in X$ such that $f(x_0,y)\ge 0$ for all $y\in X$.

Proof

By contradiction assume that $X=\bigcup _{y\in X}G(y)$, where the sets

$$\begin{aligned} G(y)=\{x\in X:f(x,y)<0\} \end{aligned}$$

are open in X. Let $G(y_1),\dots ,G(y_n)$ be a finite subcover and define

$$\begin{aligned} H_i(x)=\left\{ \begin{array}{ll} F(y_i)=\{z\in X:f(y_i,z)\le 0\} &{} \text {if } x\in G(y_i) \\ X &{} \text {if } x\in X\setminus G(y_i) \end{array} \right. \end{aligned}$$

The sets $F(y_i)$ are closed and convex and the set-valued mapping $H:X\rightrightarrows X$,

$$\begin{aligned} H(x)=\bigcap _{i=1}^nH_i(x) \end{aligned}$$

is upper semicontinuous, nonempty closed convex-valued from the compact convex set X to itself. The Kakutani-Fan-Glicksberg fixed point theorem guarantees the existence of a fixed point x of H. The fact that $x\in G(y_i)\cap F(y_i)$ for some index $i\in \{1,\dots ,n\}$ contradicts the pseudomonotonicity of $-f$. $\square$

Nasri and Sosa (2011) established an existence result (Theorem 2.3) for (EP) assuming that $g(x,y)=-f(y,x)$ is properly quasimonotone. This condition is guaranteed by the convexity of the sublevel set $\{y\in X:f(x,y)<0\}$ and $f(x,x)\ge 0$ for all $x\in X$. They showed that this assumption, together with the closedness of the sets $\{x\in X:f(x,y)\ge 0\}$, imply the existence of solutions of the Ky Fan inequality. Their result has been proved when the space is finite dimensional and a coercivity condition is verified; anyway the proof works also in a locally convex Hausdorff topological vector space if the domain is compact. Below we provide a simple example in which the assumptions of Theorem 5 are fulfilled but Theorem 2.3 in Nasri and Sosa (2011) is not applicable.

Example 2

Consider the bifunction $f:[-1,1]\times [-1,1]\rightarrow {\mathbb {R}}$ defined by

$$\begin{aligned} f(x,y)=\left\{ \begin{array}{ll} -1 &{} \text {if } x\in (-1,1) \text { and } y\in \{\pm 1\}\\ 1 &{} \text {if } x\in \{\pm 1\} \text { and } y\in [-1,1)\\ 0 &{} \text {otherwise} \end{array} \right. \end{aligned}$$

We prove that f satisfies all the assumptions of Theorem 5. The sublevel set

$$\begin{aligned} \{x\in [-1,1]:f(x,y)<0\}=\left\{ \begin{array}{ll} (-1,1) &{} \text {if } y\in \{\pm 1\}\\ \emptyset &{} \text {otherwise} \end{array} \right. \end{aligned}$$

is open in $[-1,1]$ and the sublevel set

$$\begin{aligned} \{y\in [-1,1]:f(x,y)\le 0\}=\left\{ \begin{array}{ll} \{1\} &{} \text {if } x\in \{\pm 1\}\\ {} [-1,1] &{} \text {otherwise} \end{array} \right. \end{aligned}$$

is closed and convex. Moreover $f(x,y)<0$ if and only if $(x,y)\in (-1,1)\times \{\pm 1\}$ and, for every $(x,y)\in \{\pm 1\}\times (-1,1)$, the bifunction $f(x,y)>0$. Finally, condition (iv) in Theorem 5 is fulfilled. Indeed, if system $f(x,y_i)<0$, $i=1,\dots ,n$, is compatible then $y_i\in \{\pm 1\}$ and $f(\pm 1,1)=0$ hence also the system $f(y_i,x)\le 0$, $i=1,\dots ,n$, is compatible. Hence all the assumptions of Theorem 5 hold and the points $x=\pm 1$ are solutions of the equilibrium problem. Instead, Theorem 2.3 in Nasri and Sosa (2011) is not applicable: if $A=\{\pm 1\}$ and $x=0\in (-1,1)$, then $f(0,\pm 1)=-1<0$.

We provide below an example in which the assumptions of Theorem 5 are fulfilled but Proposition 10 in Cotrina and Svensson (2021) is not applicable.

Example 3

Consider the bifunction $f:[0,1]\times [0,1]\rightarrow {\mathbb {R}}$

$$\begin{aligned} f(x,y)=\left\{ \begin{array}{ll} 1-x-y &{}\quad \text {if } x\in [0,1/2)\\ 1/2 &{}\quad \text {if } x=1/2 \\ x-y &{} \quad\text {if } x\in (1/2,1] \end{array}\right. \end{aligned}$$

It can be easily verified that

$$\begin{aligned} \{x\in [0,1]:f(x,y)\ge 0\}= & {} \left\{ \begin{array}{ll} [0,1] &{} \quad\text {if } y\in [0,1/2]\\ {} [0,1-y]\cup \{1/2\}\cup [y,1] &{}\quad \text {if } y\in (1/2,1] \end{array} \right. \\{} & {} \\ \{y\in [0,1]:f(x,y)\le 0\}= & {} \left\{ \begin{array}{ll} [1-x,1] &{} \quad\text {if } x\in [0,1/2)\\ \emptyset &{} \quad\text {if } x=1/2 \\ {} [x,1] &{} \quad\text {if } x\in (1/2,1] \end{array}\right. \end{aligned}$$

Consequently, the first two assumptions of Theorem 5 hold. Simple calculations lead to the following implication:

$$\begin{aligned} f(x,y)< 0\quad \Rightarrow \quad x\ne \frac{1}{2} \text { and } \max \{x,1-x\}<y\le 1 \end{aligned}$$

(4)

The bifunction $-f$ is pseudomonotone. Indeed, if $f(x,y)<0$, in view of (4), we have $f(y,x)=y-x>0$.

We prove that f has the finite solvability property. Assume that for a finite set $A\subseteq [0,1]$ there exists an $x\in [0,1]$ such that $f(x,a)<0$ for all $a\in A$. Then, from (4) we infer that $A \subseteq (1/2,1]$. Choosing $y_0=\max A$, we have $f(a,y_0)=a-y_0\le 0.$ Hence, all the requirements of Theorem 5 are fulfilled. On the other hand, since $f(1/2,y)=1/2$ for all $y\in [0,1]$, f does not have the finite intersection property. Note that the solution set for the associated equilibrium problem is $\{0,1\}$.

As usual, the absence of compactness of X can be overcome adding some coercivity conditions, as in the next theorem.

Theorem 6

Let X be a nonempty convex set in a locally convex Hausdorff topological vector space and $f:X\times X\rightarrow {\mathbb {R}}$ be a bifunction satisfying conditions (i), (ii) and (iii) of Theorem 5. Moreover, assume that X contains a compact convex set $C_0$ and a compact set $K_0$ such that

• (iv) has the finite solvability property on each compact convex set C such that $C_0\subseteq C\subseteq X$;

• (v) for each $x\in X\setminus K_0$ there exists $y\in C_0$ such that $f(x,y)<0$.

Then, there exists $x_0\in X$ such that $f(x_0,y)\ge 0$ for all $y\in X$.

Proof

The proof goes along the same lines as the one of Theorem 4.3 in Balaj (2013). Denote by

$$\begin{aligned} {\mathcal {C}}=\{C: C_0\subseteq C\subseteq X,\ C \text { is compact and convex}\} \end{aligned}$$

For every $C\in {\mathcal {C}}$, Theorem 5 provides a point $x_C\in C$ such that $f(x_C,y)\ge 0$, for all $y\in C$. In view of (v), $x_C\in K_0$.

If $C^{\prime },C^{\prime \prime }\in {\mathcal {C}}$, then the set ${\text {conv}}\big (C^{\prime }\cup C^{\prime \prime })$ belongs also to ${\mathcal {C}}$, because the convex hull of the union of a finite family of compact convex sets is compact (Aliprantis and Border 2006, Lemma 5.29). Consequently, ${\mathcal {C}}$ is a directed set relative to the order relation $\subseteq$. Since the set $K_0$ is compact, we may assume that the net $\{x_C\}_{C\in {\mathcal {C}}}$ converges to some $x_0\in K_0$.

We now prove that $f(x_0,y)\ge 0$, for all $y\in X$. Take an arbitrary $y\in X$ and denote by $C_y={\text {conv}}(C_0\cup \{y\})$. Clearly, $C_y\in {\mathcal {C}}$ and for every $C\in {\mathcal {C}}$ satisfying $C_y\subseteq C$, we have $f(x_C,y)\ge 0$. Since the set $\{x\in X:f(x,y)\ge 0\}$ is closed, it follows that $f(x_0,y)\ge 0$. $\square$

Remark 1

One of the most used coercivity conditions in proving existence results for equilibrium problems when the set X is not compact is the following given in Bianchi and Pini (2005): there exists a compact convex subset $K_0$ of X such that for each $x\in X\setminus K_0$ there exists $y\in K_0$ such that $f(x,y_0)<0$. Observe that the coercivity condition (v) of Theorem 6 reduces to the aforementioned condition when $K_0=C_0$.

The following example illustrates the applicability of Theorem 6.

Example 4

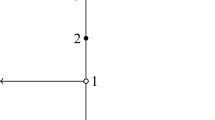
Consider the bifunction $f:(-\infty ,1]\times (-\infty ,1]\rightarrow {\mathbb {R}}$ defined by

$$\begin{aligned} f(x,y)=\left\{ \begin{array}{ll} 0 &{} \text {if } \vert x-y\vert \le 1\\ y^2(x-y) &{} \text {if } \vert x-y\vert >1 \end{array} \right. \end{aligned}$$

and take $C_0=K_0=[0,1]$. We prove that the assumptions of Theorem 6 are satisfied. The set

$$\begin{aligned} \{x\in (-\infty ,1]:f(x,y)\ge 0\}=[y-1,1] \end{aligned}$$

is closed, for each $y\in (-\infty ,1]$, and

$$\begin{aligned} \{y\in (-\infty ,1]:f(x,y)\le 0\}=[x-1,1] \end{aligned}$$

is a closed convex set, for every $x\in (-\infty ,1]$. The bifunction $-f$ is pseudomonotone, because

$$\begin{aligned} f(x,y)<0\Rightarrow & {} \vert x-y\vert>1,\ y\ne 0,\ y>x \\\Rightarrow & {} x<y-1\le 0 \\\Rightarrow & {} f(y,x)=x^2(y-x)>0 \end{aligned}$$

For every $x\in (-\infty ,1]$, $f(x,1)\le 0$. Consequently, on every compact interval $C\subseteq (-\infty ,1]$ containing the interval [0, 1], f has the finite intersection property and, implicitly, the finite solvability property.

Condition (v) is also verified, since for every $x<0$, $f(x,1)<0$. From Theorem 6, the associated equilibrium problem has solutions. It can be easily verified that the solution set is the interval [0, 1]. Note that, for every $x<-1$, the sublevel set

$$\begin{aligned} \{y\in (-\infty ,1]:f(x,y)<0\}=(1+x,0)\cup (0,1] \end{aligned}$$

is not convex. As the convexity of the sublevel sets is a standard condition, almost all known existence results do not work for this example. Let us also mention that f is not pseudomonotone, because $f(-2,0)=0$, $f(0,-2)>0$. Consequently, existence results in which the pseudomonotonicity of f is needed (for instance, Theorem 3.1 and Theorem 3.2 in Bianchi and Pini (2005), Theorem 3.12 in Iusem and Sosa (2003) and Proposition 4.1 in Bianchi and Schaible (1996)), are not applicable in this case.

4 Quasiequilibrium problems

Let X be a nonempty convex subset of a topological vector space, $f:X\times X\rightarrow {\mathbb {R}}$ and $T: X \rightrightarrows X$. The quasiequilibrium problem associated to X, f and T consists in finding a point $x_0$ which is simultaneously a fixed point for T and an equilibrium point for $f_{\mid T(x_0) \times T(x_0)}$. More precisely, this problem reads as follows:

$$\begin{aligned} \text {find } x_0\in X \text { such that } x_0\in T(x_0) \text { and } f(x_0,y)\ge 0,\ \forall y\in T(x_0)\qquad \qquad \quad {\text {(QEP)}} \end{aligned}$$

Often the proof of the existence of solutions for problem (QEP) is done by transforming this problem into a fixed point problem. For instance, (Aussel et al. 2017; Balaj and Khamsi 2019; Mosco 1976) and Tan (1985) obtain existence theorems for problem (QEP) exploiting the following observation: consider the set-valued mapping $S:X\rightrightarrows X$, defined by

$$\begin{aligned} S(x)=\{x^{\prime }\in T(x):f(x^{\prime },y)\ge 0,\ \forall y\in T(x)\} \end{aligned}$$

then, $x_0$ is a solution of the problem (QEP) if and only if it is a fixed point for S. The same idea will be used for proving Theorem 7.

Theorem 7

Assume that X is a nonempty convex subset of a locally convex Hausdorff topological vector space, $T:X\rightrightarrows X$ is a compact continuous set-valued mapping with nonempty closed and convex values and $f:X\times X\rightarrow {\mathbb {R}}$ is a bifunction satisfying the following conditions:

• (i) the set $\{(x,y)\in X\times X:f(x,y)\ge 0\}$ is closed in $X \times X$;

• (ii) for every $y \in X$, the set $\{x \in X: f(x, y) \ge 0\}$ is convex;

• (iii) for every $x \in X$ the set $\{y \in X: f(x, y) \le 0\}$ is closed and convex;

• (iv) $-f$ is pseudomonotone;

• (v) for each $x \in X$, the bifunction f has the finite solvability property on T(x).

Then, there exists $x_0\in X$ such that $x_0\in T(x_0)$ and $f(x_0,y)\ge 0$, for all $y \in T(x_0)$.

Proof

Fix an arbitrary $x \in X$. From the hypotheses it follows that the restriction of f to $T(x)\times T(x)$ fulfills the assumptions of Theorem 5. From the mentioned theorem, there exists $x^{\prime }\in T(x)$ such that $f(x^{\prime },y) \ge 0$, for all $y \in T(x)$. Consequently, $S(x)\ne \emptyset$. If $x^{\prime },x^{\prime \prime }\in S(x)$ and $\lambda \in [0,1]$, since T(x) is a convex set, $\lambda x^{\prime }+(1-\lambda )x^{\prime \prime }\in T(x)$. Moreover, from (ii), $f(\lambda x^{\prime }+(1-\lambda )x^{\prime \prime },y)\ge 0$ for any $y\in T(x)$, hence S(x) is a convex set.

Further, we prove that S is a closed mapping. Let $(x,x^{\prime })\in {\text {cl}}S$ and $\{(x_\alpha ,x^{\prime }_\alpha )\}$ be a net in the graph of S converging to $(x, x^{\prime })$. Then, for each index $\alpha$, $x^{\prime }_\alpha \in T(x_\alpha )$ and, since T is a closed mapping (by Lemma 1), $x^{\prime }\in T(x)$. If $y\in T(x)$, since T is lower semicontinuous, there exists a net $\{y_\alpha \}$ converging to y with $y_\alpha \in T(x_\alpha )$, for all $\alpha$. As $x^{\prime }_\alpha \in S(x_\alpha )$, $f(x^{\prime }_\alpha , y_\alpha ) \ge 0$. From (i), we infer that $f(x^{\prime }, y)\ge 0$, hence $x^{\prime } \in S(x).$

Reviewing what we proved until now, we see that S is a closed mapping with nonempty convex values. Moreover, since T is compact, so will be S. From the fixed point theorem in Himmelberg (1972), S has a fixed point and thus we get the desired conclusion. $\square$

Remark 2

It could be of interest to compare our previous result with Theorem 2 proved by Balaj (2021). In the mentioned theorem, instead of condition (iii), it is required the convexity of the sublevel sets $\{y\in X:f(x,y)<0\}$ and conditions (iv) and (v) are replaced by the following one:

$$\begin{aligned} x\in X,\ y\in T(x)\quad \Rightarrow \quad f(u,y)\ge 0, \text { for some } u\in T(x) \end{aligned}$$

The quasioptimization problem is an example of a quasiequilibrium problems, where the bifunction f is defined by $f(x,y)=\varphi (y)-\varphi (x)$. The next result can be derived from Theorem 7 and it improves slightly Corollary 3.2 in Cotrina and Zúñiga (2018) which in turn generalizes Propositions 4.2 and 4.5 in Aussel and Cotrina (2013). In the mentioned corollary, X is assumed to be compact, while in Theorem 8 is needed only that the mapping T is compact.

Theorem 8

Let X be a nonempty convex subset of a locally convex Hausdorff topological vector space, $T: X \rightrightarrows X$ be a compact continuous set-valued mapping with nonempty closed and convex values and $\varphi :X\rightarrow {\mathbb {R}}$ be a quasiconvex and continuous function. Then, there exists $x_0\in X$ such that $x_0\in T(x_0)$ and $\varphi (x_0)=\min _{y\in T(x_0)}\varphi (y)$.

We conclude the paper giving a particular application of Theorem 7 when the quasiequilibrum problem is a generalized quasivariational inequality which allows one to model and study several complex phenomena as generalized Nash equilibrium problems in economy or contact problems with deformation in mechanics.

In this last part, let E be a real normed space endowed with the norm topology, $E^*$ be its dual equipped with the weak$^*$ topology, and $\langle \cdot ,\cdot \rangle$ the duality pairing. Recall that, if X is a nonempty subset of E, a set-valued mapping $F:X\rightrightarrows E^*$ is said to be:

• pseudomonotone if for every $(x_1,x_1^*),(x_2,x_2^*)\in {\text {gr}}F$, the following implication holds:

  $$\begin{aligned} \langle x_1^*,x_2-x_1\rangle \ge 0 \quad \Longrightarrow \quad \langle x_2^*,x_2-x_1\rangle \ge 0; \end{aligned}$$

• properly quasimonotone if for each finite set $A\subseteq X$, and any $y\in {\text {conv}}A$ there exists $x\in A$ such that

  $$\begin{aligned} \langle x^*,y-x\rangle \le 0,\quad \forall x^*\in F(x); \end{aligned}$$

• cyclically quasimonotone if for every $x_0,x_1,\dots ,x_n \in X$, there exists an index $i\in \{0,1,\dots ,n\}$ such that

  $$\begin{aligned} \langle x_i^*,x_{i+1}-x_i\rangle \le 0,\quad \forall x^*_i\in F(x_i), \end{aligned}$$

  where $x_{n+1}=x_0$.

If F has compact values with respect to the weak$^*$ topology, the representative bifunction of F is defined by

$$\begin{aligned} f_F(x,y)=\max _{x^*\in F(x)}\langle x^*,y-x\rangle . \end{aligned}$$

Directly from the definition, F is pseudomonotone (properly quasimonotone, cyclically quasimonotone, respectively) if and only if $f_F$ is pseudomonotone (properly quasimonotone, cyclically quasimonotone, respectively).

Theorem 9

Let X be a convex subset of E and $T:X \rightrightarrows X$, $F:X\rightrightarrows E^*$ be two set-valued mappings. Assume that

• (i) T is compact, continuous and has nonempty closed and convex values;

• (ii) F is upper semicontinuous and compact-valued;

• (iii) for every $y \in X$, the set

  $$\begin{aligned} \{x\in X:\exists x^*\in F(x)\text { such that }\langle x^*,y-x\rangle \ge 0\} \end{aligned}$$

  is convex;

• (iv) $-F$ is pseudomonotone;

• (v) F is either properly quasimonotone or cyclically quasimonotone.

Then, there exists $(x_0,x_0^*)\in {\text {gr}}F$ such that $x_0\in T(x_0)$ and $\langle x_0^*,y-x_0\rangle \ge 0$ for all $y\in T(x_0)$.

Proof

We intend to apply Theorem 7 when the involved bifunction is the representative bifunction of F. Denote by $M =\{(x,y)\in X\times X:f_F(x,y) \ge 0\}$. Let $(x,y)\in {\text {cl}}M$ and $(x_\alpha , y_\alpha )$ be a net in M converging to (x, y). For each index $\alpha$, since $f_F(x_\alpha ,y_\alpha )\ge 0$, there is an $x^*_\alpha \in F(x_\alpha )$ such that $\langle x^*_\alpha ,y_\alpha -x_\alpha \rangle \ge 0$. Since F is upper semicontinuous and compact-valued, there is a subnet $\{x^*_{\alpha _\lambda }\}$ of $\{x^*_\alpha \}$ converging to some $x^*\in F(x)$. From (ii) we infer that F(X) is a compact subset of $E^*$ and particularly, norm bounded. From Lemma 4.3 in Balaj (2018), the duality pairing is continuous on $F(X)\times E$. Passing to the limit in $\langle x^*_{\alpha _\lambda },y_{\alpha _\lambda }-x_{\alpha _\lambda }\rangle \ge 0$, we get $\langle x^*,y-x\rangle \ge 0$. Summing up the above, the set M is closed, hence $f_F$ satisfies condition (i) of Theorem 7. By (iii), for every $y\in X$, the set $\{x\in X:f_F(x,y)\ge 0\}$ is convex. For every $x\in X$ the set $\{y\in X:f_F(x,y)\le 0\}$ is closed and convex, because

$$\begin{aligned} \{y\in X: f_F(x,y)\le 0\}=\bigcap _{x^*\in F(x)}\{y\in X:\langle x^*,y-x\rangle \le 0\}. \end{aligned}$$

Taking into account the aforementioned equivalence, the bifunction $f_F$ satisfies the last two conditions of Theorem 7.

From Theorem 7, there exists $x_0\in X$ such that $f_F(x_0,y)\ge 0$ for all $y\in T(x_0)$. This means that $\min _{y\in T(x_0)}\max _{x^*\in F(x_0)} \langle x^*, y - x_0\rangle \ge 0$. By Sion’s minimax theorem

$$\begin{aligned} \max _{x^*\in F(x_0)}\min _{y\in T(x_0)}\langle x^*,y-x_0\rangle = \min _{y\in T(x_0)}\max _{x^*\in F(x_0)}\langle x^*,y-x_0\rangle \ge 0, \end{aligned}$$

hence there exists $x_0^*\in F(x_0)$ such that $\langle x^*,y-x_0\rangle \ge 0$, for all $y\in T(x_0)$. $\square$

Theorem 10

Condition (iii) of Theorem 9 is fulfilled when F and $-F$ are both pseudomonotone.

Proof

For an arbitrary $y\in X$, define

$$\begin{aligned} A=\{x\in X:\exists x^*\in F(x)\text { such that } \langle x^*,y-x\rangle \ge 0\} \end{aligned}$$

and take $x_1,x_2\in A$ and $\lambda \in [0,1]$. Since F is pseudomonotone, for all $y^*\in F(y)$, $\langle y^*,y-x_1\rangle \ge 0$, $\langle y^*,y-x_2\rangle \ge 0$, whence $\langle y^*,y-(\lambda x_1+(1-\lambda )x_2)\rangle \ge 0$. As $-F$ is pseudomonotone, $\langle x^*,y-(\lambda x_1+(1-\lambda )x_2)\rangle \ge 0$ for every $x^*\in F(\lambda x_1+(1-\lambda )x_2)$. Consequently, the set A is convex. $\square$

The mappings F for which F and $-F$ are both pseudomonotone are called in Bianchi et al. (2003) pseudoaffine. Notice that a mapping $F:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n$ is pseudoaffine if and only if there exist a skew-symmetric linear mapping A, a vector u and a positive function $g:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ such that $F(x)=g(x)(Ax+u)$.

5 Conclusions

In this paper we show how it is possible to obtain some versions of the Ky Fan minimax inequality in finite and infinite dimensional setting avoiding the quasiconvexity of the function in its second variable. The results involve the so called finite solvability property which is weaker than the recently introduced finite intersection property and in turn, weaker than most common cyclic and proper quasimonotonicity. Some examples are presented to illustrate the various results and cases in which other existence results for equilibrium problems do not apply. An open topic for future work could be the use of the finite solvability property in case of variational inequalities.