Predictions of machine learning with mixed-effects in analyzing longitudinal data under model misspecification

Abstract

We consider predictions in longitudinal studies, and investigate the well known statistical mixed-effects model, piecewise linear mixed-effects model and six different popular machine learning approaches: decision trees, bagging, random forest, boosting, support-vector machine and neural network. In order to consider the correlated data in machine learning, the random effects is combined into the traditional tree methods and random forest. Our focus is the performance of statistical modelling and machine learning especially in the cases of the misspecification of the fixed effects and the random effects. Extensive simulation studies have been carried out to evaluate the performance using a number of criteria. Two real datasets from longitudinal studies are analysed to demonstrate our findings. The R code and dataset are freely available at https://github.com/shuwen92/MEML.

1 Introduction

Longitudinal data, which occur frequently in economics, finance, medical science and other fields, are measured repeatedly for each subject. The circumstances under which the measurements are taken cannot be exactly the same. For example, students could be sampled in different classrooms or patients by different doctors. Therefore, the assumption of longitudinal data is that measurements are correlated for the same subjects but independent among different subjects. If the number of measurements from each subject is the same, the datasets are said to contain balanced data; otherwise, the datasets contain unbalanced data. Laird and Ware (1982) introduced the random effects models for longitudinal data because they claimed that a general multivariate model with unrestricted covariance structure is not suited for the analysis of unbalanced data. Mixed-effects models that include both fixed and random effects can handle the correlation in longitudinal data. The fixed effects are parameters related to the levels of the entire population or certain repeatable experimental factors, while the random effects are related to individual experimental units randomly chosen from a population (Pinheiro and Bates 2000). An expectation-maximisation (EM) algorithm can be used to determine the maximum likelihood and restricted maximum likelihood estimation in the longitudinal data setting (Laird et al. 1987). Lindstrom and Bates (1988) developed an efficient and computationally stable implementation of the Newton-Raphson (NR) algorithm for obtaining the parameters in mixed-effects models for longitudinal data.

The misspecification of mixed-effects models can include the misspecification of fixed effects or random effects. Grilli and Rampichini (2015) first review the literature about the consequences of misspecifying the distribution of the random effects. McCulloch and Neuhaus (2011a) investigated the impact of misspecification of the distribution of the random effects and claimed that the prediction accuracy is little affected for mild-to-moderate violations of the assumptions. Their mild-to-moderate violations of random effects implies assumption of normal distribution of random effects has been misspecified to three different distributions: a skewed and truncated distribution, a heavy-tailed distribution, and a mixture distribution. Hui et al. (2021) focused on variance components when they studied the effects of random effects misspecification in linear mixed models. There are also other references (McCulloch and Neuhaus 2011b; Albert 2012; Drikvandi et al. 2017) investigated the misspecification of shape/distribution of random effects and they confirmed that the mean square error for random effects estimation is robust to the random effects misspecification. Misspecification of random components will lead to misspecified variance and correlation structures. Therefore, our work with a slightly different focus has been that of assessing random effects misspecification from the misspecification of correlation structure with simulated data generated from marginal model. Wang and Carey (2003) provided both asymptotic and numerical results in the GEE framework.

There have been very few comparison studies of statistical models and machine learning methods in the analysis of longitudinal data. One thing we can notice is that statistical models usually have more assumptions than machine learning methods. However, this is a double-edged sword. Machine learning methods are usually recognised as having a ‘black box’ aspect, which means there is less attention paid to the processes between their inputs and outputs. Real data sets are usually complex, and it is worthwhile to investigate more about the data before definitive decisions are made. Some papers have compared the predictive performance of statistical methods and machine learning methods in the area of health (Song et al. 2004; Venkatesh et al. 2020; Shin et al. 2021) and air quality (Wei et al. 2019; Berrocal et al. 2020). They confirmed that the nature of data is of primary importance rather than the learning technique.

Among the six machine learning methods (trees, bagging, random forest, boosting, support-vector machine and neural network) addressed in this work, the trees method is the most broadly applied for longitudinal data (Segal 1992; Hajjem et al. 2011, 2014; Berger and Tutz 2018; Kundu and Harezlak 2019). Sela and Simonoff (2012) presented the random effects expectation-maximisation (RE-EM) tree, which combined the structure of mixed-effects models with tree-based methods. They showed that the RE-EM tree had improved predictive power over traditional linear models with random effects and regression trees without random effects. However, Fu and Simonoff (2015) proposed what they claimed are unbiased RE-EM trees by using conditional inference trees instead of classification and regression trees (CARTs). In addition, Loh and Zheng (2013) had proposed an unbiased regression tree for longitudinal data based on a generalised, unbiased interaction detection and estimation (GUIDE) approach rather than the traditional CARTs. Later, Eo and Cho (2014) combined the decision tree and mixed-effects methods for longitudinal data based on GUIDE. Hajjem et al. (2014) have extended their methodology with the use of random forest instead of regression trees ,which called mixed effects random forest (MERF). A framework for predicting longitudinal change in glycemic control measured by hemoglobin A1c (HbA1c) using mixed effect machine learning is presented by Ngufor et al. (2019). The machine learning methods can be applied to regression as well as classification. There are some progress in the development of mixed-effects machine learning methods with application of classification, such as generalized mixed-effects regression trees (Hajjem et al. 2017), generalized mixed-effects random forest (Pellagatti et al. 2021) and neural networks for longitudinal data (Crane-Droesch. 2017; Xiong et al. 2019). Mangino and Finch (2021) utilised a Monte Carlo simulation to compare the prediction performance of several classification algorithms and they claimed the panel neural network and Bayesian generalized mixed effects models have the highest prediction accuracy. We focus on the regression in this work in order to compare the prediction performance of linear mixed models and machine learning methods with or without mixed effects when the model is specified correctly or missepcified.

Li and Wu (2015) claimed that the traditional linear mixed model is inferior to the machine learning methods for both long- and short-term prediction in milk protein data, which is apparently because the linear mixed model is not sufficient to fit this data. This milk protein data was also illustrated by Diggle et al. (2002) using a piecewise model at breakpoint three with an exponential correlation structure. However, we noticed that the quadratic term is not necessary, and a piecewise mixed-effects model would have better performance. Yang et al. (2016) illustrated the mathematical programming for a piecewise linear regression analysis. They showed that the piecewise regression method achieved better prediction performance than a number of state-of-the-art regression methods, such as random forest (RF), support-vector regression (SVR), K-nearest neighbour (KNN) and so on. Kohli et al. (2018) investigated the estimation of a piecewise mixed-effects model with unknown breakpoints using maximum likelihood. They found that the maximum likelihood estimates are reliable and accurate under the conditions that the observed variables had a small residual variance. The mixed-effects tree-based method is emphasized because it has shown strong prediction performance and it is explainable.

The estimation of parameters in the mixed-effects machine learning usually relied on two steps: estimation of mean function and random effect component, respectively. As far as we know, the literature lacks a comparison of the performance of statistical models and machine learning methods for longitudinal data when the fixed effects or random effect are misspecified. However, correctly specification of mean function/fixed effects and random effect components are very important in the longitudinal data analysis (Wang and Lin 2005). A new metric, true root mean square error (TRMSE) is defined to measure how close the predictions would be to the true values without noise error in the simulation. The differences between the TRMSE and RMSE are also presented according to the simulation parts. Two different ways are utilised to generate correlated data. One way is to generate data from mixed-effects models with fixed effects and random effects, the other is to generate data from a marginal model.

In this paper, we review and compare the performances of a mixed-effects model and six machine learning methods (tree, bagging, random forest, boosting, support-vector machine and neural network) and two mixed effects machine learning methods (RE-EM trees and MERF) in the prediction of longitudinal data. The remainder of this work is organized as follows. Section 2 describes the various methods that we compared in this work. In Sect. 3, a description is made of the extensive simulations that are carried out to evaluate the performance of the different methods. Two different kinds of real data (milk protein and wages) are considered as case studies in Sect. 4. Section 5 presents some conclusions and further discussion.

2 Methods

In this section, the details of the linear mixed-effects model, tree-based method (including the RE-EM tree), support-vector machine and neural network are introduced.

2.1 Linear mixed-effects models

Linear mixed-effects models are an extension of simple linear models by the inclusion of random effects that are used to account for the correlation among measurements within the same subject.

Let response vector ${\varvec{Y_i}}$ be the $n \times 1$ vector $(y_{i1},\ldots , y_{in})^T$, in which $y_{ij}$ is the jth measurement for the ith subject ($i=1,\ldots ,K$, $j=1,\ldots ,n$). The total number of subjects is K. ${\varvec{X_i}}$ (of dimension $n \times p$) and ${\varvec{Z_i}}$ (of dimension $n \times q$) are the separate fixed-effect and random-effect covariates. ${\varvec{\beta }}$ is a p-dimensional vector of the fixed effect, and ${\varvec{b_i}}$ is a q-dimensional vector of the random effect, which are assumed to be Gaussian distributed with mean zero and variance ${\varvec{\Psi }}$. The formulation of the linear mixed-effects model is as follows:

$$\begin{aligned} {\varvec{Y_i = X_i\beta +Z_i b_i+\epsilon _i}}, \nonumber \\ {\varvec{b_i}} \sim N(0,{\varvec{\Psi }}), {\varvec{\epsilon _i}} \sim N(0,\sigma ^2 {\varvec{\Lambda _i}}). \end{aligned}$$

(1)

The within-groups errors ${\varvec{\epsilon _i}}$ and the random effects ${\varvec{b_i}}$ are assumed to be independent. It is a special case if ${\varvec{\Lambda _i=I}}$. Then, it follows that ${\varvec{Y_i}} \sim N({\varvec{X_i\beta ,\Sigma _i}})$, where ${\varvec{\Sigma _i}}=\sigma ^2({\varvec{\Lambda _i+Z_i \Psi Z_i^T}})$. The matrix form for the model is as follows:

$$\begin{aligned} {\varvec{Y = X\beta +Z b+\epsilon }}, \end{aligned}$$

where ${\varvec{Y = \left[ {\begin{array}{*{20}{c}} Y_1 \\ Y_2 \\ \vdots \\ Y_K \end{array}} \right] }}$, ${\varvec{X =\left[ {\begin{array}{*{20}{c}} X_1 \\ X_2 \\ \vdots \\ X_K \end{array}} \right] }}$, ${\varvec{b =\left[ {\begin{array}{*{20}{c}} b_1 \\ b_2 \\ \vdots \\ b_K \end{array}}\right] }}$, ${\varvec{Z}}=\text{ diag }({\varvec{Z_1, Z_2, ..., Z_K}})$, ${\varvec{\Lambda }}=\text{ diag }({\varvec{\Lambda _1, \Lambda _2, ..., \Lambda _K}})$, ${\varvec{\Sigma }}=\text{ diag }({\varvec{\Sigma _1, \Sigma _2, ..., \Sigma _K}})$ and ${\varvec{{\tilde{\Psi }}}}=\text{ diag }({\varvec{\Psi ,\Psi ,...,\Psi }})$. It follows that ${\varvec{Y}}$ are independent multivariate normal vectors with mean ${\varvec{X\beta }}$ and the covariance matrix is ${\varvec{\Sigma }}=\sigma ^2({\varvec{\Lambda +Z {\tilde{\Psi }} Z^T}})$. Then, the likelihood function is

$$\begin{aligned} L({\varvec{\beta ,\theta }},{\sigma }^2 |{\varvec{Y}})=p({\varvec{Y |\beta ,\theta }},\sigma ^2)=\prod _{i=1}^{K} p({\varvec{Y_i |\beta ,\theta }},\sigma ^2), \end{aligned}$$

where

$$\begin{aligned} p({\varvec{Y_i |\beta ,\theta }},\sigma ^2)=(2\pi \sigma ^2)^{-\frac{n}{2}}\text{ exp }\frac{\left( {\varvec{Y_i-X_i\beta ^T)}}) {\varvec{\Sigma _i^{-1}}}({\varvec{Y_i-X_i\beta }}\right) }{-2\sigma ^2}) |{\varvec{\Sigma _i}} |^{-\frac{1}{2}} \end{aligned}$$

and ${\varvec{\theta }}$ represents the parameters in ${\varvec{{\tilde{\Psi }}}}$ and ${\varvec{\Lambda }}$. An EM algorithm can be used to obtain both the maximum likelihood and restricted maximum likelihood estimation according to Laird et al. (1987). The lme function of the R-package nlme is implemented to fit the linear mixed model (Pinheiro et al. 2020).

2.2 Piecewise linear mixed-effects models

Piecewise regression is a special type of linear regression that arises when a single line is not sufficient to model a data set. Piecewise regression breaks the domain into potentially many ‘segments’ and fits a separate line through each one. Breakpoints are the values where the slope of the linear function changes. The value of the breakpoints are unknown and must be estimated. In some cases, the breakpoints can be specified by us according to plots. In other words, it is obvious to the naked eyes when one linear trends give way to other. However, this is not fit for all the cases. For some data set, it is not easy to detect the breakpoints just from eyes. In statistics, the popular way is to compare the errors with different breakpoints, which means minimize the errors between each segment’s regression and the observed data points.

A piecewise linear mixed-effects (PLME) model is an extension of linear mixed-effects model. The PLME has been used in many areas, such as in analysing longitudinal educational and psychological data sets (Kohli et al. 2018, 2015). We introduced PLME in this work because of its flexibility for accommodating a different mean function in each phase. The mathematical forms of PLME are presented in Sect. 4.1 to analyse the milk protein data.

2.3 Tree-based methods

2.3.1 Decision trees

Tree-based methods, support-vector machine and neural network can be applied to regression as well as classification, and we focus on regression problems in this work. The decision tree, bagging, random forest, and boosting methods can be grouped together as they are all tree-based methods. CART (classification and regression tree) is a popular algorithm which was proposed by Breiman et al. (1984). In the tree method, the training data is used to construct a data tree starting at the root node. The predicted space is divided into non-overlapping M regions ($R_1, R_2,..., R_M$) determined by recursive splitting, which is a top-down and greedy approach (James et al. 2013). In each region, a constant $c_m$ would be the response. The model is as follows:

$$\begin{aligned} f(X)=\sum _{m=1}^M c_m I(X\in R_m). \end{aligned}$$

The splitting we choose will cause the largest reduction in the mean square error. We can split recursively until the mean square error reaches a defined threshold. Then it is easy to see that the best value is the average of ${\varvec{Y}}$ in region $R_m$:

$$\begin{aligned} {\hat{c}}_m=\text{ ave }({\varvec{Y}} |{\varvec{X}} \in R_m). \end{aligned}$$

The predicted response for a test data point is the mean of the training observations in the region to which that test point belongs. For each test data point that falls in the same region on a path starting from the root node until reaching a terminal (leaf) node, the response prediction would be the same. A usual strategy to fit a single tree is to grow a large tree and then trim it by weakest link pruning. The R-package tree is used to implement the above process in this work (Ripley 2019). Trees can be displayed graphically and are easy to explain but can be subject to overfitting. Also, trees are not robust, which means small changes in the training data can cause very different series of splits. Ensemble decision tree methods, including bagging, random forests and boosting, combine many decision trees to produce better predictive performances than a single decision tree.

2.3.2 Ensemble decision tree methods

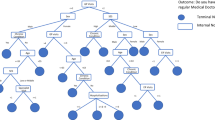
Bagging trees, random forest and boosting trees are called ensemble decision trees. The simple flowchart of these three different ensemble decision trees is presented in Fig. 1.

Bagging is the application of the bootstrap procedure to decision trees in order to lower the variance. There are three main steps: firstly, generate random sub-samples of the training data set with replacement; secondly, train the decision tree method on each sample; and thirdly, calculate the average prediction from each model using the test data. The average prediction would be the final prediction for each test data point. Bagging will improve the prediction accuracy compared to the tree method at the cost of interpretability.

Fig. 1

Three different ensemble trees

Random forest is a popular tree-based ensemble method that builds a large collection of de-correlated trees and then averages them based on the bagging (Breiman 2001). When building this algorithm, a random sample of features is chosen as split candidates from the full set of predictors rather than using all the features in bagging. This forces each split to consider only a subset of the predictors, which is reasonable, especially when there is a very strong predictor in the training data set. After a certain number of trees are grown, the predictor is obtained by the average (for regression) or the majority vote (for classification) (James et al. 2013). This algorithm contains four main parameters: total number of observations, total number of predictor variables, randomly chosen features for determining the decision tree and the total number of decision trees. The R-package randomForest is used to implement the algorithm of bagging and random forest (Liaw and Wiener 2002).

The different trees based on the bootstrapped data are independent in bagging. Boosting works in a similar way to bagging, but the difference is the trees are constructed sequentially, which means that the growth of each tree depends on the trees that have already been constructed. It is a forward stagewise approach. Boosting regression trees (BRT) have three parameters: the number of trees, the shrinkage parameter that controls the learning rate and the number of splits in each tree that determines the complexity of the boosted ensemble. The BRT algorithm has three main steps: firstly, a regression tree is fitted; secondly, another tree is fitted to the residuals of the first tree; and thirdly, the model is updated to have two trees with a shrinkage parameter (this last step is repeated hundreds or thousands of times). The final model is a linear combination of these trees. The R-package gbm is implemented for this algorithm (Greenwell et al. 2019).

2.4 Mixed-effects regression trees and random forest

Segal (1992) was the first to apply regression trees to longitudinal data. The mixed-effects tree method we have used in this work, the RE-EM tree, was proposed by Sela and Simonoff (2012). The notation in an RE-EM tree follows the linear mixed-effects model:

$$\begin{aligned} {\varvec{Y_i}}=f({\varvec{X_i}})+{\varvec{Z_ib_i+\epsilon _i}}, \end{aligned}$$

(2)

in which the ${\varvec{Y_i, X_i, Z_i, b_i}}$ and ${\varvec{\epsilon _i}}$ analogous to their use in equation (1). If f is a linear function, $f({\varvec{X_i}})={\varvec{X_i\beta }}$, then the model is a linear mixed model. Generally, this f function can be estimated by a tree method when the random effects ${{\varvec{b_i}}}$ are known. However, when neither the fixed effects nor the random effects are known, an iterative two-step process is utilised. Firstly, the random effects ${\hat{{\varvec{b}}}_i}$ are set to zero initially, and a regression tree is used to estimate function f based on ${\varvec{Y_i-Z_i {\hat{b}}_i}}$. A linear mixed-effects model is then fitted to estimate the random effects based on the tree regression results: $y_{ij}=Z_{ij}{\varvec{b_i}}+I({\varvec{X_{ij}}}\in g_p)\mu _p+\epsilon _{ij}$, in which $I({\varvec{X_{ij}}}\in g_p)\mu _p$ means the estimated value for $y_{ij}$ at terminal node $g_p$. The algorithm will not stop until the estimates of random effects ${\varvec{{\hat{b}}_i}}$ converge. We used R package REEMtree (Sela and Simonoff 2012) in this work.

Hajjem et al. (2014) proposed mixed-effects random forest (MERF) for clustered data which implemented using a standard random forest algorithm within the framework of the expectation-maximization (EM) algorithm. The notations of MERF are the same with Equation (2) and the random forest is used to estimate the fixed part of the model, i.e., the estimation of function f. The MERF algorithm is similar to the EM algorithm for the linear mixed-effects model and the detailed steps of the MERF algorithm can be found in Hajjem et al. (2014). Louis (2020) implemented this MERF algorithm in R package LongituRF.

2.5 Support-vector machine

The initial idea of a support-vector machine (SVM) is to construct a linear partition of the high-dimensional space into two sub-spaces for classification or regression (Scholkopf and Smola 2002). We will focus on the regression application in this work. Given the training data $({\varvec{X_1}},Y_1),({\varvec{X_2}},Y_2),...,({\varvec{X_N}},Y_N)$, the prediction is shown as a linear function $f({\varvec{X}})={\varvec{\omega ^T X}}+b_0$, and the error function is

$$\begin{aligned} \frac{1}{2}||{\varvec{\omega }}||^2+C\sum _{k=1}^N \ell _{\epsilon }(f({\varvec{X_k}})-Y_k), \end{aligned}$$

(3)

where $\ell _{\epsilon }(z)=\text{ max }\{0,|z|-\epsilon \}$ is the $\epsilon$-insensitive loss. After minimising the error function, the solution is

$$\begin{aligned} f({\varvec{X}})=\sum _{k=1}^N ({\hat{\alpha }}_k-\alpha _k){\varvec{X_k^TX}}+b_0, \end{aligned}$$

(4)

where ${\hat{\alpha }}_k$ and $\alpha _k$ are Lagrange multipliers. The nonzero Lagrange multipliers that indicate the training vector makes $({\hat{\alpha }}_k-\alpha _k)\ne 0$ in Equation (4) are called support-vectors. Obviously, the non-support-vectors do not contribute directly to the solution . Besides this linear case, the data are often not linearly separable. A kernel function is then used to transform the nonlinear system in the input space to a linear system in the feature space. Popular kernel functions are polynomial kernel, radial kernel, among others (James et al. 2013). We will also include the support-vector regression with a polynomial kernel in our simulations. The svm function of the R-package e1071 is used (Meyer et al. 2019).

2.6 Neural network

In this work, we consider the neural network as a multilayer perceptron (MLP), which is a class of feedforward artificial neural network. The multilayer perceptron is a popular network for classification and regression. The formula is as follows:

$$\begin{aligned} {\hat{Y}}=\sum _{k=0}^{NH} v_k g_k ({\varvec{X}}), \end{aligned}$$

where $v_k$ are the weights, $g_k({\varvec{X}})$ are the hidden functions (or hidden units), NH is the number of hidden nodes, ${\varvec{X}}$ is the input vector and ${\hat{Y}}$ is the output. Here, the hidden function $g_0$ takes a fixed value of one to allow a constant term in the equation. The sigmoid function is commonly used: $g_k(u)=1/(1+\text{ exp }(-u))$. Also, the tangent hyperbolicus function $\text{ tanh } x=(e^x-e^{-x})/(e^x+e^{-x})$ is used in the simulation. The general approach to fit this method is minimizing the sum-of-squared errors by gradient descent, which is called back-propagation. The R-package neuralnet is used to implement the neural network algorithm (Fritsch et al. 2019).

3 Simulation studies

In this section, we describe the investigation of the performances of linear mixed-effects models and machine learning methods through extensive simulations.

3.1 Design of simulations

There are two types of misspecification in the linear mixed model: misspecification of fixed effects and misspecification of random effects. Therefore, in our design of simulations, we generate the longitudinal data in two different ways to deal with these two different kinds of misspecification. To analyse misspecification of the fixed effects, we consider two different true mean functions: linear and quadratic in our setting. The performance of various models only with linear mean function would be investigated, which means the fixed effects are misspecified if the true mean function is quadratic. The longitudinal data can also be generated from the marginal model with different correlation structures, such as AR(1) or exchangeable correlation. This data generation aimed to reflect the misspecification of random effects. The data generated from the linear mixed-effects model with random intercept are equivalent to that generated from the marginal model with the same mean function and exchangeable correlation. If the data are generated with exchangeable correlation structure, the linear mixed effects model with random intercept is the true model. Otherwise, it could be considered as the misspecification of random effects. The details of data generation are provided in the following paragraph and Table 1.

Two different ways are used to generate the longitudinal data. One is from the mixed model:

$$\begin{aligned} y_{ij}=\beta _0+\beta _1x_{ij}+\beta _2 {g_i}+\beta _3 x_{ij}^2+{\varvec{b}}_i+\epsilon _{ij}, i=1,\ldots , K, j=1,\ldots , n, \end{aligned}$$

(5)

where $\mu _{ij}=\beta _0+\beta _1x_{ij}+\beta _2g_i+\beta _3 x_{ij}^2$ is the overall mean response, ${\varvec{b}}_i$ is the random effects from the normal distribution $N(0, \sigma _b^2)$ and $\epsilon _{ij}$ come from an iid normal distribution $N(0, \sigma ^2)$. In addition, $x_{ij}$ and $g_i$ are sampled from the uniform distribution (0, 1). In our simulation, there are two different true mean function: ${{\varvec{\beta }}}=(\beta _0,\beta _1,\beta _2,\beta _3)^T=(0.5,1,1.2,0)^T$ and ${{\varvec{\beta }}}=(\beta _0,\beta _1,\beta _2,\beta _3)^T=(0.5,1,1.2,-5)^T$, which demonstrate the true mean function is linear and quadratic respectively. In this simulation, we set $\sigma =1$ and $\sigma _b=2$.

Another way to generate the longitudinal data from the following marginal model:

$$\begin{aligned} y_{ij}=\beta _0+\beta _1x_{ij}+\beta _2 {s_i}+\beta _3x_{ij}^2+\epsilon _{ij},\ \ i=1,\ldots , K,\ \ j=1,\ldots , n, \end{aligned}$$

(6)

where $\mu _{ij}=\beta _0+\beta _1x_{ij}+\beta _2s_i+\beta _3x_{ij}^2$, $x_{ij}$ is sampled from the uniform distribution (0, 1), and $s_i$ is sampled from the binary distribution, which can represent the sex variable in the real dataset. In order to compare the performances between different methods under a scenario in which the mean function is correctly specified and misspecified, we have set different values for ${\varvec{\beta }}$. In the model in which the mean function is correctly specified, ${{\varvec{\beta }}}=(\beta _0,\beta _1,\beta _2,\beta _3)^T=(0,0.5,1,0)^T$. This indicates the true mean function of the simulated data is linear (without a quadratic term). In contrast, ${{\varvec{\beta }}}=(\beta _0,\beta _1,\beta _2,\beta _3)^T=(0,0.5,1,-5)^T$ is used when the mean function is misspecified, which indicates the data are generated from a quadratic model. We used the linear mean function in various prediction models. We had two different scenarios for $\epsilon _{ij}$: the first is $\epsilon _{ij}$ are correlated with an exchangeable structure, in other words, $\text{ cor }(\epsilon _{ij},\epsilon _{ij^{'}})=0.5$ if $j \ne j^{'}$; and the second is for each i, $(\epsilon _{i1},\ldots , \epsilon _{in})$ are correlated with an autoregressive AR(1) structure that also had a correlation coefficient of 0.5. It is worth noting that when the data are generated from the linear mean function with first scenario (i.e., the correlation structure is exchangeable), the linear mixed-effects model with a random intercept is the true model. Otherwise, when the data are correlated with the AR(1) structure, the linear mixed-effects model is not the true model even if the mean function of simulated data is linear.

Table 1 The design of simulations

3.2 Evaluation metrics

There are few references about how to measure the predictive power of methods for longitudinal data. The stratified cross-validation method cannot be used directly because the observations from longitudinal data contain sequences. Based on Sela and Simonoff (2012), three different ways are utilised: (1) predicting the future 30% of observations based on the previous 70% of observations for K different subjects, denoted as future observation; (2) predicting another new K/2 objects based on the previous K different subjects, denoted as new object; and (3) predicting a future 30% of observations for new K/2 objects based on the previous K different subjects and the previous 70% of observations in the new K/2 subjects, denoted as future new observation. In this case, there are 100 subjects (K = 100), and each subject is observed 10 times (n = 10).

We also proposed another one-step prediction and two-step prediction in order to see the performances of different methods in real-time prediction. In this case, $K=100$ and $n=5$. This is a bit similar to the future observation method described above but did not just consist of the overall prediction. We can obtain the prediction performance at the time of each observation. In the one-step prediction, we used the first observation to predict the second observation; the first two observations are then used to predict the third, and so on. In contrast, the first observation is used to predict the third observation in the two-step prediction. The results based on 1000 simulations are presented in Tables 2, 3,  4 and 5. The numerosity of the generated data is 1000 and 500 for the two different prediction performance evaluations, respectively.

Table 2 The one-step prediction for different methods in simulated data generated from a mixed-effects model

Table 3 The two-step prediction for different methods in simulated data generated from a mixed-effects model

Table 4 The one-step prediction for different methods in simulated data which correlated with the exchangeable and AR(1) structure

To measure the prediction performance of the different methods, the root mean square error (RMSE) is used:

$$\begin{aligned} \text{ RMSE }=\sqrt{\frac{\sum _{i=1}^K\sum _{j=1}^n(y_{ij}-{\hat{y}}_{ij})^2}{K*n}}, \end{aligned}$$

where $y_i$ is the measured value, and ${\hat{y}}_i$ is the predicted value. Because the true values of $\mu _i$ are known in the simulations and the curious is about how close the predictions would be to the true values without noise, we defined another metric, the true root mean square error (TRMSE), to measure the prediction performance as follows:

$$\begin{aligned} \text{ TRMSE }=\sqrt{\frac{\sum _{i=1}^K\sum _{j=1}^n(\mu _{ij}-{\hat{y}}_{ij})^2}{K*n}}. \end{aligned}$$

According to the formula of mean square error,

$$\begin{aligned} \text{ RMSE }= & {} \sqrt{ \text{ ave}_{x\in \text{ test }}({\hat{y}}-y)^2} {}\\= & {} {}\sqrt{\text{ ave}_{x\in \text{ test }}({\hat{y}}-(\mu + \mathbf {b}+ \epsilon ))^2}\\= & {} {}\sqrt{\text{ ave}_{x\in \text{ test }}[({\hat{y}}-\mu )^2-2({\hat{y}}-\mu )(\mathbf {b}+\epsilon )+(\mathbf {b}+\epsilon )^2]} \\= & {} {} \sqrt{\text{ ave}_{x\in \text{ test }}[({\hat{y}}-\mu )^2]+\text{ ave}_{x\in \text{ test }}[-2({\hat{y}}-\mu )(\mathbf {b}+\epsilon )+(\mathbf {b}+\epsilon )^2]} \end{aligned}$$

where ${\hat{y}}$ is the prediction value, y is the observed value, $\mu$ is the true value and $\epsilon$ is the error. Also, $\text{ ave}_{x\in \text{ test }}[({\hat{y}}-\mu )^2]$ is the square of TRMSE. If the data are generated from marginal model (i.e. $\mathbf {b}$ is zero) and error is independent of the observations (i.e. $\text{ ave}_{x\in \text{ test }}[-2({\hat{y}}-\mu )\epsilon ]=0$), the RMSE values would be larger than the TRMSE values, which is consistent with the simulation results from Tables 4 and 5.

Table 5 The two-step prediction for different methods in simulated data which correlated with the exchangeable and AR(1) structure

3.3 Simulation results

The objective of our extensive simulations is to compare the prediction performances among the different methods in the longitudinal data. The parameters in the linear mixed-effects model are estimated with maximum likelihood and they are varied according to the different sizes of training data. Ten-fold cross-validation was used to tune the parameters in tree-based methods. For the tree method, the common and default tree growth is limited to a depth of 31 by the use of integers to label nodes. Therefore, the range of tree maximum depth is from 20 to 40 for tuning. The random effect in RE-EM trees is the grouping variable (subject). We used 500 trees in total in bagging and random forest method. The number of variables randomly sampled as candidates at each split is 2 and 1 in bagging and random forest, respectively because we have two covariates $x_{ij}$ and $t_{i}$. Otherwise, the number of trees ranged from 200 to 5000 for tuning in the boosting method. In the SVM, the cost of constraints violation is 1 and the epsilon in the insensitive-loss function is 0.1 ($C=1$ and $\epsilon =0.1$ in Eq. 3). The degree of polynomial kernel in SVM is 3. For the parameters of neural network, there are one layer and the hidden neurons in each layer is 2. The threshold for the partial derivatives of the error function as stopping criteria is 0.1.

Fig. 2

The prediction results of future observation. RMSE root mean square error, TRMSE true root mean square error, lme linear mixed-effects model, tree decision tree method, re-em RE-EM trees with random intercept, bag bagging method, rf random forest method, merf mixed-effects random forest, boost boosting method, svm support-vector regression with linear kernel, svmk support-vector regression with polynomial kernel, nn neural network method with logistic activation function, nntanh neural network method with hyperbolic tangent activation function

Fig. 3

The prediction results of new objects. The notations are the same as Fig. 2

Figures 2, 3 and 4 presents the prediction results of future observation, new object and future new observation respectively when the fixed effects is specified correctly. Meanwhile, the boxplots of prediction results of future observation, new object and future new observation respectively when the fixed effects is misspecified can be found in Figs. 5, 6 and 7. We can see that the linear mixed model performed the best when the fixed effects/mean function is specified correctly in terms of predicting future observations and future new observations. However, the support vector machine and neural network methods have better performance when we need to predict the observations from new objects. It is expected that the support vector regression with polynomial kernel (‘svmk’) and neural network with hyperbolic tangent activation function (‘nntanh’) would also have better performance if the mean function is misspecified. However, it seems that we should be careful to choose the nonlinear function according to the data structure which is the quadratic in this case. The RE-EM trees and mixed effects random forest (MERF) performed better when the mean function is misspecified in terms of predicting future observations and future new observations. It is interesting to find that RE-EM trees and MERF performed worse than trees and RF in terms of predicting new objects (see Fig. 6), which means that mixed effects machine learning needs to be used in caution when predicting unseen data. The TRMSE values that measured the differences between the predictions and mean values without random effects and errors. According to the TRMSE values, the support-vector machine with a linear kernel had the best performance whether the mean function is correctly specified or misspecified.

Fig. 4

The prediction results of future new observations. The notations are the same as Fig. 2

Fig. 5

The prediction results of future observation under fixed effects misspecification. The notations are the same as Fig. 2. The results of ‘nntanh’ is omitted in the plots because the range of RMSE and TRMSE is too large (the maximum of RMSE and TRMSE is 38.79 and 38.68, respectively)

Fig. 6

The prediction results of new objects under fixed effects misspecification. The notations are the same as Fig. 2. The results of ‘nntanh’ is omitted in the plots because the range of RMSE and TRMSE is too large (the maximum of RMSE and TRMSE is 327.38 and 327.14, respectively)

Fig. 7

The prediction results of future new observations under fixed effects misspecification. The notations are the same as Fig. 2. The results of ‘nntanh’ is omitted in the plots because the range of RMSE and TRMSE is too large (the maximum of RMSE and TRMSE is 4909.26 and 4908.88, respectively)

Fig. 8

The results of future observations for the simulated data generated from marginal model with exchangeable correlation structure and AR(1) correlation structure. The notations are the same as Fig. 2

The performance of different methods in simulated data generated from the marginal model with exchangeable and AR(1) correlation structure is presented in Figs. 8, 9 and 10. In Figs. 8 and 10, because the linear mixed model is the true model when the correlation structure is exchangeable, it is not a surprise to see that the linear mixed model performed the best when the mean model is specified correctly and in terms of predicting future observations and future new observations. The support-vector machine with a linear kernel and the neural had good performances when predicting the observations from new object (see Fig. 9). However, when the correlation structure is AR(1), which means that the random effect component is misspecified, the random forest had better performance. RE-EM trees and MERF do not show an advantage because these two methods were not designed for this case of correlation structure misspecification.

Fig. 9

The results of new objects for the simulated data generated from marginal model with exchangeable correlation structure and AR(1) correlation structure. The notations are the same as Fig. 2

Fig. 10

The results of future new observations for the simulated data generated from marginal model with exchangeable correlation structure and AR(1) correlation structure. The notations are the same as Fig. 2

If the mean function is misspecified, the RE-EM trees and support-vector machine with a polynomial kernel had the advantages in terms of predicting future observations and future new observations regardless of whether the random effect component is misspecified or not (see Figs. 11, 12 and 13). It is not a surprise to see that the support-vector machine with a polynomial kernel had smaller RMSE values than when a linear kernel is used if the mean function is misspecified. The results according to TRMSE values are a slightly different from the conclusions according to RMSE values. The boost method had the best performance according to the TRMSE values.

Fig. 11

The results of future observations for the simulated data generated from marginal model with exchangeable correlation structure and AR(1) correlation structure under fixed effects misspecification. The notations are the same as Fig. 2

Fig. 12

The results of new objects for the simulated data generated from marginal model with exchangeable correlation structure and AR(1) correlation structure under fixed effects misspecification. The notations are the same as Fig. 2

Fig. 13

The results of future new observations for the simulated data generated from marginal model with exchangeable correlation structure and AR(1) correlation structure under fixed effects misspecification. The notations are the same as Fig. 2

The results from the one-step and two-step predictions are presented in Tables 2,  3, 4 and 5, respectively. Regardless of how the correlated data was generated, the linear mixed model had the best performance both in the one-step and two-step predictions when the mean function is correct. It is noted that in the simulated data generated from the mixed-effects model, support vector machine had better performance when the mean function is misspecified according to TRMSE values. We can also conclude that the RE-EM trees and support-vector machine with a polynomial kernel performed well when the mean function is misspecified. The performances between the one-step and two-step predictions are different when the mean function is specified correctly while the correlation structure is different, see Table 4(a)(ii) and Table 5(a)(ii). In the one-step prediction, the linear mixed model is still comparable but not for the two-step prediction. The support vector machine method had the best performance when the random effect component is misspecified in the two-step prediction.

4 Application to real data

Two real data sets are analysed using these different methods in this section.

4.1 Case study 1: milk protein data

In this data set, milk was collected weekly from 79 Australian cows and analyses for its protein content. There are three diets: 25 cows received a barley diet, 27 cows a mixture of barley and lupins, and 27 cows a diet of lupins only. The observation period of each cow is not necessarily the same and each cow is observed for between 12 weeks and 19 weeks (Fig. 14). There are 1337 observations of protein in total.

Fig. 14

The mean of protein for three different kinds of diet in milk protein data

It appears from the Fig. 14 that barely gives higher values than the mixture, which in turn have higher values than lupins alone. The mean response profiles are approximately parallel, showing an initial sharp decline associated with a settling-in period, followed by an approximately constant mean response through the following period and a slow rise towards the end.

Diggle et al. (2002) used the following mean response profiles model:

$$\begin{aligned} \mu _i = \left\{ \begin{array}{ll} \beta _{0i}+\beta _{1}t &{} \hbox { if}\ t \le 3,\\ \beta _{0i}+3\beta _{1}+\beta _{2}(t-3)+\beta _3(t-3)^2 &{} \text {if t>3}, \end{array} \right. \end{aligned}$$

where $i=1,2,3$ denotes treatment group with an exponential correlation function $\text{ Cov }(\epsilon _j,\epsilon _k)=\sigma ^2\text{ exp }(-\phi \vert t_j - t_k \vert )$. The covariates include time and quadratic of time.

However, the quadratic term is not significant and the breakpoint is not necessarily to be a integer. According to the mean square error, the breakpoint we chose for this milk protein data is 2.6. So we use the piecewise mixed model with the mean response profiles model as follows:

$$\begin{aligned} y_i = \left\{ \begin{array}{ll} \beta _{0i}+\beta _{1}t+b_{i1}+tb_{i2}+\epsilon _i &{} \hbox { if}\ t \le 2.6,\\ \beta _{0i}+2.6\beta _{1}+\beta _{2}(t-2.6)+b_{i1}+tb_{i2}+\epsilon _i &{} \hbox { if}\ t>2.6, \end{array} \right. \end{aligned}$$

where $i=1,2,3$ denotes treatment group and with the different mean function

$$\begin{aligned} \mu _i = \left\{ \begin{array}{ll} \beta _{0i}+\beta _{1}t &{} \hbox { if}\ t \le 2.6,\\ \beta _{0i}+2.6\beta _{1}+\beta _{2}(t-2.6) &{} \hbox { if}\ t>2.6. \end{array} \right. \end{aligned}$$

The $b_{i1}$ and $b_{i2}$ are the corresponding random effects for different groups. The estimated parameters of $\beta _{0i}, \beta _1, \beta _2, b_{i1}$ and $b_{i2}$ $(i=1,2,3)$ varied a bit according to the different size of training data in piecewise linear mixed-effects model. We focus on the predictive performance of the different models and the estimation of the parameters is not reported here. The one-step prediction and two-step prediction results are presented in Table 6(a). We can see that the piecewise linear mixed model has the best performance in one-step prediction. RE-EM trees also has advantages. Tree-based methods have smaller RMSE values than support-vector machine and neural network methods.

Table 6 The RMSE values for different methods in Milk data and Wages data

4.2 Case study 2: wages data

Wages data came from the National Longitudinal Survey of Youth (NLSY), which was previously studied by Singer and Willett (2003), Eo and Cho (2014) and Fu and Simonoff (2015). The data has the information of 888 individuals’ hourly wage. Each individual has the different observation times, ranged from 1 to 13. There are 6402 observations in total. In the linear mixed-effects model, the log of individual’s hourly wage (logwage) is the response variable, the covariates include exper, hgc and race. The individual’s races are White, Black and Hispanic. The variable hgc means the highest grade completed by the individual. Figure 15 present the plots of the time variable (exper, which is the duration of the working experience) and the log of wages at different race and hgc. The random intercept is included to indicate the differences between individuals. We used the eight cross-validation method to compare the prediction performances between statistical models and machine learning methods. According to Table 6(b), RE-EM methods has the smallest RMSE. Tree-based methods and support-vector machine have similar results while the average RMSE values of LME and neural network are close in this case.

Fig. 15

The wages data

5 Conclusions and discussion

We have presented the performances of the statistical models and six machine learning methods and two mixed effects machine learning methods for the longitudinal data analysis. The parameters in the machine learning methods we used in the work are indicated and justified. Overall, the simulation results showed that the linear mixed-effects model is comparable with the various machine leaning methods when the models are correctly specified, included the fixed effects and random effects because we knew the truth model in the simulations. The performances under the scenarios of the different mean function and the different correlation structures (exchangeable and AR(1)) are compared. Otherwise, even with the milk dataset (a real world dataset), the statistical model (especially, the piecewise linear mixed model) still performed better than the machine learning methods. This means that the piecewise linear mixed model provided an adequate fit to the original data. It can also be concluded that the model diagnostics are very important before making decisions regarding performance.

There are few references about how to measure the predictive power of methods in longitudinal data. The prediction accuracy according to a cross-validation method are not reasonable because longitudinal data are always sequential. In this work, we used one-step and two-step prediction along with future observation, new object and future new observation prediction. The performances of all kinds of methods are demonstrated comprehensively. In addition, we also presented the differences between RMSE and TRMSE values in the predictions. It is not surprising to see that the TRMSE values are smaller than the RMSE values in data generated from marginal model because we measured that differences between the predictions and true values without noise. However, this is not always true, which can be found from the predictions in the data generated from a mixed-effects model.

There are still some limitations in this study. The predictions between the different methods are discussed rather than the parameter estimates and inferences in the longitudinal data. Misspecified models, including the mean function are considered in this work. Wang and Lin (2005) also investigated the effects of variance function and correlation structure misspecification in the analysis of longitudinal data. In this work, we only investigated the popular exchangeable and AR(1) correlation structures that are appropriate for equally spaced (in time) longitudinal data. However, unequally spaced observations and time-dependent correlated errors deserves more attention by researchers (Nunez-Anton and Woodworth 1994). It would be of great interest to evaluate machine learning performance in these settings. There are also other modified methods that combine mixed-effects models and tree methods (Fu and Simonoff 2015; Loh and Zheng 2013; Eo and Cho 2014) that deserve further examination. An extended comparison with more recently developed machine learning methods, such as deep learning, would be of interest.