Valve-related modes of pump failure in collecting lymphatics: numerical and experimental investigation

Abstract

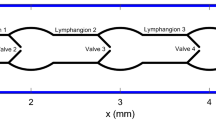
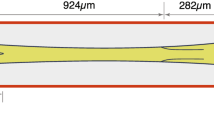
Lymph is transported along collecting lymphatic vessels by intrinsic and extrinsic pumping. The walls have muscle of a type intermediate between blood-vascular smooth muscle and myocardium; a contracting segment between two valves (a lymphangion) constitutes a pump. This intrinsic mechanism is investigated ex vivo in isolated, spontaneously contracting, perfused segments subjected to controlled external pressures. The reaction to varying afterload is probed by slowly ramping up the outlet pressure until pumping fails. Often the failure occurs when the contraction raises intra-lymphangion pressure insufficiently to overcome the outlet pressure, open the outlet valve and cause ejection, but many segments fail by other means, the mechanisms of which are not clear. We here elucidate those mechanisms by resort to a numerical model. Experimental observations are paired with comparable findings from computer simulations, using a lumped-parameter model that incorporates previously measured valve properties, plus new measurements of active contractile and passive elastic properties, and the dependence of contraction frequency on transmural pressure, all taken from isobaric twitch contraction experiments in the same vessel. Surprisingly, the model predicts seven different possible modes of pump failure, each defined by a different sequence of valve events, with their occurrence depending on the parameter values and boundary conditions. Some, but not all, modes were found experimentally. Further model investigation reveals routes by which a vessel exhibiting one mode of failure might under altered circumstances exhibit another.

Appendix—equations of the model

The basic equations are as follows.

Mass conservation:

$$\begin{aligned} \frac{\mathrm{d}D}{\mathrm{d}t}=\frac{2\left( {Q_1 -Q_2 } \right) }{\pi LD} . \end{aligned}$$

(1)

Momentum conservation:

$$\begin{aligned} p_{\mathrm{a}}- p_{0}= & {} R_{\mathrm{a}}Q_{1}; p_{0}- p_{1}=R_{\mathrm{V1}}Q_{1};\nonumber \\ p_1 -p_m= & {} \frac{64}{\pi }\frac{\mu LQ_1 }{D^{4}}; \end{aligned}$$

(2)

$$\begin{aligned} p_\mathrm{m} -p_2= & {} \frac{64}{\pi }\frac{\mu LQ_2 }{D^{4}}; \nonumber \\ p_{2}- p_{\mathrm{p}}= & {} R_{\mathrm{V2}}Q_{2}; p_{\mathrm{p}}- p_{\mathrm{b}}=R_{\mathrm{b}}Q_{2}; \end{aligned}$$

(3)

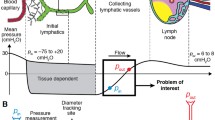
where $p_{1}$, $p_{\mathrm{m}}$, and $p_{2} =$ pressure at the upstream end, centre, and downstream end of the lymphangion, $p_{\mathrm{a}}$ and $p_{\mathrm{b}}$ are the upstream and downstream reservoir pressures, $p_{0}$ is the pressure upstream of the inlet valve but downstream of the inlet cannula, and $p_{\mathrm{p}}$ is the pressure downstream of the outlet valve but upstream of the outlet cannula; $Q_{1}$ and $Q_{2}$ are the flow–rates into and out of the lymphangion, and D is the lymphangion diameter. These are the principal time-variables of the problem, but $R_{\mathrm{V1}}$ and $R_{\mathrm{V2}}$, the resistances of the inlet and outlet valves, also both vary with time as a result of their dependence on the local trans-valvular pressure $\Delta p_{\mathrm{V}}$ and the local transmural pressure, as

$$\begin{aligned} R_{{\mathrm{V1}}}= & {} R_{{\mathrm{Vn}}} +\frac{R_{{\mathrm{Vx}}} }{1+\hbox {exp}\left[ {-s_{\mathrm{o}} \left( {\Delta p_{{\mathrm{V1}}} -\Delta p_{{\mathrm{o1}}} } \right) } \right] }\hbox { and }\nonumber \\ R_{{\mathrm{V2}}}= & {} R_{{\mathrm{Vn}}} +\frac{R_{{\mathrm{Vx}}} }{1+\hbox {exp}\left[ {-s_{{\mathrm{o}}} \left( {\Delta p_{\mathrm{V2}} -\Delta p_{\mathrm{o2}} } \right) } \right] }, \end{aligned}$$

(4)

where $\Delta p_{{\mathrm{V1}}}=p_{0}- p_{1}$, $\Delta p_{{\mathrm{V2}}}=p_{2}- p_{\mathrm{p}}$, the open/close threshold $\Delta p_{{\mathrm{o1}}}$ depends on either $p_{0}-p_{\mathrm{e}}$ or $p_{1}- p_{\mathrm{e}}$ according to the current valve state, and $\Delta p_{{\mathrm{o2}}}$ depends on either $p_{2}-p_{\mathrm{e}}$ or $p_{\mathrm{p}}-p_{\mathrm{e}}$; see Bertram et al. (2014b). The constants in eqns. 1-4 are the lymphangion length L (0.3 cm), the lymph viscosity $\mu$ (1 cP), the resistances of the inlet and outlet cannulae ($R_{\mathrm{a}}$ and $R_{\mathrm{b}}$, respectively), the minimum and maximum resistance of a valve ($R_{{\mathrm{Vn}}}$ and $R_{{\mathrm{Vn}}}+R_{{\mathrm{Vx}}}$, respectively), a parameter $s_{\mathrm{o}}$ which governs the steepness of the smooth transition between minimum and maximum valve resistance, and the external pressure $p_{\mathrm{e}}$. Values of $R_{{\mathrm{Vn}}}$, $R_{{\mathrm{Vx}}}$ and $s_{\mathrm{o}}$ used here are chosen to limit closing regurgitation and closed-valve leakage to reasonable amounts; $R_{{\mathrm{Vn}}}$ has been estimated experimentally and numerically, but further numerical work (not yet published) suggests that the earlier methods may have underestimated true values. The model can be modified to make $p_{\mathrm{e}}$ vary with time as a representation of extrinsic pumping, but this was not done here. Each valve resistance function $R_{\mathrm{V}}(\Delta p_{\mathrm{V}})$ also includes a term which provides for loss of valve resistance by prolapse (Bertram et al. 2011b) if a very large adverse $\Delta p_{\mathrm{V}}$ is exceeded, but this is not approached here. The outlet pressure $p_{\mathrm{b}}$ is raised in a linear ramp according to the following equations.

$$\begin{aligned} p_{\mathrm{b}}(t)= & {} p_{{\mathrm{b1}}},\quad t \le t_{\mathrm{b1}} \end{aligned}$$

(5a)

$$\begin{aligned} p_b \left( t \right)= & {} p_{{{b1}}} +\left( {p_{{b2}} -p_{{{ b1}}} } \right) \frac{t-t_{b1} }{t_{b2} -t_{b1} },\quad t_{{\mathrm{b1}}}< t< t_{{\mathrm{b2}}} \end{aligned}$$

(5b)

$$\begin{aligned} p_{\mathrm{b}}(t)= & {} p_{{\mathrm{b2}}}, \quad t \ge t_{{\mathrm{b2}}}, \end{aligned}$$

(5c)

where the ramp begins at pressure $p_{{\mathrm{b1}}}$ and time $t_{\mathrm{b1}}$ and ends at pressure $p_{\mathrm{b2}}$ and time $t_{\mathrm{b2}}$.

Time-course of active contraction: the waveform of contraction activation M(t) is a smooth (continuously differentiable) curve formed by application of the following equations between the times $t=t_{\mathrm{c}}$ and $t=t_{\mathrm{c}} + 1/f$, where $t_{\mathrm{c}}$ is the beginning of a contraction and 1 / f is its duration. M(t) is calculated in two steps; in the first,

$$\begin{aligned} M\left( t \right)= & {} 0.5\left\{ {1-\cos \left[ {2\pi f_m \left( {t-t_{\mathrm{c}} } \right) } \right] } \right\} ,\hbox { with }\nonumber \\ f_{m}= & {} {\textit{mf}},\hbox { and }m = 1\hbox { or }2; \end{aligned}$$

(6a)

in parallel a function $M_{\mathrm{j}}(t)$ is calculated and used to modify the preliminary M(t) to its final form.

$$\begin{aligned} M_{\mathrm{j}} \left( t \right)= & {} m_{\mathrm{g}} \left\{ {1-\cos \left[ {2\pi f\left( {t-t_{\mathrm{c}} } \right) } \right] } \right\} ,\hbox { with }\nonumber \\ m_{\mathrm{g}}= & {} 1\Big /\left( {1-\cos \frac{\pi }{m}} \right) ;\hbox { if }M_{\mathrm{j}}(t) > 1, M(t) = 1. \end{aligned}$$

(6b)

See fig. 3 of Bertram et al. (2016b) which shows how the resulting waveform of M(t) changes with m.

The constant m is a multiplier for the rate of onset and decay of the active state; with $m = 1$, M(t) increases sinusoidally and starts a similar decline as soon as it peaks; with $m= 2$, the onset and decay phases occur in half the time, and peak activation is maintained in between.

The duration of the period of relaxation $t_{\mathrm{r}}$ that starts at $t=t_{\mathrm{c}} + 1/f$ is

$$\begin{aligned} t_r =\frac{1}{f_{\mathrm{tw}} }-\frac{1}{f}, \end{aligned}$$

(7)

where $f_{\mathrm{tw}} =60y$, with y as defined in the text relating to Fig. 2. To evaluate y, the average transmural pressure over the immediately preceding systole is defined as

$$\begin{aligned} {\overline{{\Delta p}}} _{\mathrm{tm}} =\int _{t_c }^{t_c +1/f} \Delta p_{{\mathrm{tm}}} dt, \end{aligned}$$

(8)

where $\Delta p_{{\mathrm{tm}}}=p_{\mathrm{m}}- p_{\mathrm{e}}$ (in $\hbox {cmH}_{2}\hbox {O}$).

Constitutive relation: the two fitted curves shown in Fig. 1b can be described as

$$\begin{aligned} D_\mathrm{act} =f_\mathrm{act} \left( {\Delta p_{{\mathrm{tm}}} } \right) ; D_\mathrm{psv} =f_\mathrm{psv} \left( {\Delta p_{{\mathrm{tm}}} } \right) , \end{aligned}$$

(9)

where the subscripts act and psv indicate the peak twitch and pre-twitch states, respectively; see Sect. 2.3 for details of the derivation of the curves. Then

$$\begin{aligned} \Delta D_\mathrm{act} =D_\mathrm{psv} -D_\mathrm{act} ,\hbox { and }D=D_\mathrm{psv} -M\left( t \right) \Delta D_\mathrm{act} . \end{aligned}$$

Thus we have the curve family $D=f\left( {t,\Delta p_{{\mathrm{tm}}} } \right)$, or, inversely, $\Delta p_{{\mathrm{tm}}} =f^{-1}\left( {D,t} \right)$, where the inverse can be found either iteratively or by converting the function to a lookup table which is interpolated as needed.

Solution procedure: we combine Eqs. 1–3 to eliminate $Q_{1}$ and $Q_{2}$ and obtain

$$\begin{aligned} \frac{\mathrm{d}D}{\mathrm{d}t}=\frac{D^{3}}{32\mu L^{2}}\left( {p_{11} -2p_\mathrm{m} +p_{12} } \right) \quad . \end{aligned}$$

(10)

At each time-step we integrate this first-order ordinary differential equation (ODE) using a $4{{\mathrm{th}}}$-order Runga-Kutta scheme. The rest of the equations collectively provide algebraic constraints on the ODE, together making up a differential-algebraic equation (DAE) system. However, the system cannot be solved with conventional DAE solvers, because of the solution discontinuities arising from the valve hysteresis; see Bertram et al. (2014b).

The following describes solution procedure in models A7e, A8e and A8g. After advancing by one time-step we know ${}^{{\mathrm{old}}}\Delta p_{{\mathrm{tm}}}$, ${}^{{\mathrm{old}}}D$, ${}^{{\mathrm{curr}}}D$, and ${}^{{\mathrm{curr}}}t$; the new value of $\Delta p_{{\mathrm{tm}}}$ is then found iteratively as ${}^{{\mathrm{new}}}\Delta p_{{\mathrm{tm}}}=f^{-1}(^{{\mathrm{curr}}}D$, ${}^{{\mathrm{curr}}}t)$, using ${}^{{\mathrm{old}}}\Delta p_{{\mathrm{tm}}}$ as a starting value. Then ${}^{{\mathrm{new}}}p_{\mathrm{m}}={}^{{\mathrm{new}}}\Delta p_{{\mathrm{tm}}}+p_{\mathrm{e}}$, and the new values of $p_{1}$ and $p_{2}$ are again found iteratively as ${}^{{\mathrm{new}}}p_{1} = {f}({}^{{\mathrm{old}}}p_{1}, {}^{{\mathrm{new}}}p_{\mathrm{m}}, {}^{{\mathrm{curr}}}D)$ and ${}^{{\mathrm{new}}}p_{2} = {f}({}^{{\mathrm{old}}}p_{2},{}^{{\mathrm{new}}}p_{\mathrm{m}}, {}^{{\mathrm{curr}}}D)$.

In more detail for that last step, we iterate to find $p_{0}- p_{1} -R_{\mathrm{V1}}Q_{1} = 0$, where $Q_1 =\frac{\pi D^{4}}{64\mu L}\left( {p_1 -p_{\mathrm{m}} } \right)$, and $p_{0}=p_{\mathrm{a}}- R_{\mathrm{a}}Q_{1}$ . Similarly, we iterate to find $p_{2}- p_{\mathrm{p}}-R_{\mathrm{V2}}Q_{2} = 0$, where $Q_2 =\frac{\pi D^{4}}{64\mu L}\left( {p_{\mathrm{m}} -p_{2} } \right)$ and $p_{\mathrm{p}}=p_{\mathrm{b}}+R_{\mathrm{b}}Q_{2}$.

In model A8h the step ${}^{{\mathrm{new}}}\Delta p_{{\mathrm{tm}}}=f^{-1}({}^{{\mathrm{curr}}}D, {}^{{\mathrm{curr}}}t)$ is handled differently. The function to be solved has at most three segments if sigmoidal, or one if not. Each segment is separately interpolated from the lookup table to find $\Delta p_{{\mathrm{tm}}} =f^{-1}\left( {D,t} \right)$, then the solution closest to ${}^{{\mathrm{old}}}\Delta p_{{\mathrm{tm}}}$ is chosen.

Section 3.2 details how some behaviours in response to ramping can be transformed to others, by running the ramp simulation with a different value of one of the boundary pressures. Some of these results were obtained from model variants other than the main one (A8e/h). Model A8g differs from A8e/h in having valves with open/close $\Delta p_{\mathrm{V}}$-thresholds set by the current diameter instead of the local transmural pressure. The curves which constitute the two $\Delta p_{\mathrm{V}}(D)$ relations are fitted to the valve-switching data of Davis et al. (2011) shown in fig. 4 of Bertram et al. (2014a), with the closing data modified as therein, utilising the nonlinear relation $D_{psv} =f_\mathrm{psv} \left( {\Delta p_{{\mathrm{tm}}} } \right)$ detailed in appendix of Bertram et al. (2014a) to convert from transmural pressure to diameter; see Fig. 14. In order to give each valve an individual characteristic, a diameter is also calculated for the stub part-lymphangion beyond the outlet valve, based on the transmural pressure at that location and the same $D_\mathrm{psv} \left( {\Delta p_{{\mathrm{tm}}} } \right)$. Model A7e is that described previously (Bertram et al. 2014a).

Fig. 14

Opening and closure thresholds for the diameter-operated valves used in model A8g