Resonance properties of a closed rotating rectangular basin subject to space- and time-dependent wind forcing

Abstract

We present an idealised process-based model to study the possibly resonant response of closed basins subject to periodic wind forcing. Two solution methods are adopted: a collocation technique (valid for arbitrary rotation) and an analytical expansion (assuming weak rotation). The spectral response, as obtained from our model, displays resonance peaks, which we explain by linking them to the spatial pattern of the wind forcing, the along-wind and cross-wind basin dimensions as well as the influence of rotation. Increasing bottom friction lowers the peaks. Finally, we illustrate how the spectral response is reflected in the time-dependent set-up due to a single wind event.

1 Introduction

Wind blowing over coastal basins often induces high water levels that may threaten coastal safety (Pugh 1987). An overall practical goal is to be able to predict water levels for any type of wind event at any location. These water levels are generally sensitive to basin geometry and the type of wind forcing (Pugh 1987). In extreme cases, a phenomenon known as resonance may occur. Examples of unusual flooding events that have been linked to such resonant conditions are typhoon Winnie at the Korean coast of the Yellow Sea (Moon et al. 2003) and storm Xynthia in the Bay of Biscay (Bertin et al. 2012). However, it is difficult to identify the physics from these complex site-specific events. Achieving the practical goal mentioned above requires a more generic insight in the physical processes underlying this wind-driven resonance phenomenon.

For the equilibrium response to steady wind, it is the relative importance of rotation and friction that determines the way in which the wind stress is communicated through the water column (e.g. Ekman 1905; Csanady 1982). This balance is expressed in the Ekman number $\delta _{E}~=~h^{-1}\sqrt {2K/f}$ with water depth h, vertical eddy viscosity K, and Coriolis parameter f. Focusing on the circulation in closed basins, in shallow/highly turbulent basins (Mathieu et al. 2002; Winant 2004) (small δ _E ), cross-wind flows are weak, whereas they are strong in deep/weakly turbulent basins (large δ _E ). The general case requires a three-dimensional flow model.

Other studies focused on the time-dependency of the dynamics. Two approaches exist. The first is to study the transient evolution to equilibrium of a quiescent basin to a suddenly imposed spatially uniform wind (Csanady 1968; Birchfield 1969; Mohammed-Zaki 1980). The second is to study the response to a single wind event, characterised by not only a spin-up but also a spin-down stage. Such an event can be seen as the superposition of periodic wind forcings at various frequencies ω (Craig 1989). Assuming linear dynamics, also the response will be the superposition of the reponses at these individual frequencies. Hence, the basin’s response to a single wind event lies in its spectral response. For example, from his idealized model for elongated basins (B ≪ L) subject to periodic and spatially uniform wind, Ponte (2010) identified resonance peaks associated with along-basin standing waves. The oscillations associated with these peaks (eigenmodes) were investigated more generally by Rao (1966). His numerical study particularly demonstrated that the resonant frequencies strongly depend on B and L.

Other studies account for spatial variations in the wind field, which have been observed, e.g. in the Gulf of California (Ponte et al. 2012) and are known to affect the response (Pugh 1987). This was also found in theoretical studies, e.g. regarding the equilibrium response to steady wind in a shallow circular basin (Birchfield 1967) and the transient response to a suddenly imposed wind stress in deep circular basins (Mohammed-Zaki 1980).

From the above, we identify the following knowledge gap. There is no study systematically investigating the resonance properties of basins of arbitrary geometry, subject to arbitrary wind fields. The goal of the present study is to systematically investigate the resonance properties of wind-driven flow in closed rotating basins. Specifically, our research questions are as follows. How do the resonance properties depend on the following aspects: (1) basin dimensions, (2) the spatial structure of the wind forcing and (3) bottom friction?

As a first step to answering these question, we present a three-dimensional idealized process-based model of wind-driven flow in closed rectangular rotating basins of uniform depth. The vertical profile of the flow field is resolved fully analytically, and expressed in the free surface elevation. In turn, the free surface elevation pattern follows from solving an elliptic problem. To solve it, two methods are used: (i) a so-called collocation method, valid for arbitrary values of the dimensionless Coriolis parameter f/ω, and (ii) an analytical approximation valid for small values of f/ω to obtain physical insight in the influence of rotation. Spatial variations in the wind are accounted for in a schematized way, i.e. by allowing linear variation of wind stress amplitude and phase in the along-wind (nonzero divergence) and cross-wind direction (nonzero curl).

This paper is organised as follows. In Section 2, we present the model. Next, Section 3 contains the solution method, and in Section 4, we present the model results. Finally, Sections 5 and 6 present the discussion and conclusions, respectively.

2 Model formulation

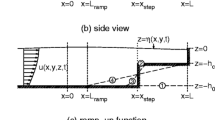
Consider a rectangular basin of length L, width B and uniform depth h on the f plane (see Fig. 1). Let x and y be the along-basin and cross-basin coordinates, such that the basin boundaries are located at x = 0,L and y = 0,B. The vertical coordinate z points upward, with z = η denoting the free surface elevation with respect to the undisturbed water level z = 0 and the bed level at z = −h. Let u = (u,v,w) represent the flow velocity vector, with components u, v and w in the x, y and z-direction, respectively. Assuming that the vertical displacement of the free surface is small compared to the water depth, conservation of momentum and mass is expressed by the three-dimensional linearised shallow water equations according to

$$\begin{array}{@{}rcl@{}} \frac{\partial u}{\partial t} - f v & =& -g \frac{\partial \eta}{\partial x} + \frac{\partial }{\partial z} \left[ K \frac{\partial u}{\partial z} \right] , \end{array} $$

(1)

$$\begin{array}{@{}rcl@{}} \frac{\partial v}{\partial t} + f u & =& -g \frac{\partial \eta}{\partial y} + \frac{\partial }{\partial z} \left[ K \frac{\partial v}{\partial z} \right] , \end{array} $$

(2)

$$\begin{array}{@{}rcl@{}} \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} &+& \frac{\partial w}{\partial z} = 0 . \end{array} $$

(3)

Here, $f~=~2{\Omega }\sin \vartheta$ is the Coriolis parameter (with Ω = 7.292 × 10⁻⁵ rad s⁻¹ the angular frequency of the Earth’s rotation and 𝜗 the latitude), g = 9.81 m s⁻² the gravitational acceleration and K the vertical eddy viscosity, assumed constant. Horizontal mixing of momentum is neglected.

Fig. 1

Definition sketch of the model geometry, showing a rectangular basin of uniform depth: a top view, b side view in along-basin direction displaying the vertical profile of one component of the three-dimensional flow field. The black dot in the left-hand image indicates the location used to evaluate the solution in Section 4. The dash-dotted lines denote the along-basin and cross-basin centrelines, used in the symmetry arguments in Section 5

Regarding boundary conditions, we impose a wind stress at the free surface and a partial-slip condition at the bottom. Along with the kinematic boundary conditions, this reads in linearised form:

$$\begin{array}{@{}rcl@{}} w & =& \frac{\partial \eta}{\partial t} , \quad K \left( \frac{\partial u}{\partial z} , \frac{\partial v}{\partial z} \right) = \frac{ (\tau^{(x)}_{\mathrm{w}},\tau^{(y)}_{\mathrm{w}} ) }{\rho} \quad \textnormal{at \(z=0\),} \end{array} $$

(4)

$$\begin{array}{@{}rcl@{}} w &=& 0 , \quad K \left( \frac{\partial u}{\partial z} , \frac{\partial v}{\partial z} \right) = s (u , v ) \quad \textnormal{at \(z=-h\).} \end{array} $$

(5)

The linearisation procedure causes the free surface condition to be imposed at z = 0 instead of at z = η. In Eq. 5, we have introduced the resistance parameter s, its value usually obtained from the analysis of field data. Two limiting cases are of interest. For large s, the bottom boundary condition effectively means no-slip, as used by, e.g. Ponte (2012). On the other hand, s = 0 corresponds to free-slip for which the flow becomes z-independent.

Furthermore, $(\tau ^{(x)}_{\mathrm {w}},\tau ^{(y)}_{\mathrm {w}})$ is the wind stress vector. The wind is assumed time-periodic with angular frequency ω, aligned with the x-direction. In addition to a spatially uniform contribution (Fig. 2a), we allow the wind to vary linearly in both the along-wind and the cross-wind direction. Along-wind variations lead to a nonzero divergence of the wind field, cross-wind variations to a nonzero curl (see Figs. 2b, c).

Fig. 2

Top view of the three contributions to the spatial wind pattern in Eq. 7: a spatially uniform part, b divergent part showing linear variation in the along-wind direction, c curl part showing linear variation in the cross-wind direction. These images are snapshots showing wind directions at a certain time: half a period later these directions are reversed

This means

$$ \frac{(\tau_{\mathrm{w}}^{(x)},\tau_{\mathrm{w}}^{(y)})}{\rho} = \Re \left\{ (T^{(x)},T^{(y)}) \exp(-i\omega t) \right\} , $$

(6)

with

$$ T^{(x)} = \hat{T} \left( 1+a\left[\frac{2x}{L}-1\right]+b\left[\frac{2y}{B}-1\right] \right) ,\!\!\!\! \qquad T^{(y)} = 0 . $$

(7)

The parameter $\hat {T}$ denotes the magnitude of the forcing (wind stress divided by density) at the basin’s centre. The complex coefficients a and b quantify the along-wind and cross-wind variation from this basin-averaged value. Importantly, the assumption of wind in x-direction only is not restrictive. The solution to a periodic wind in an arbitrary direction is the superposition of the separate solutions for wind in x- and y-direction only. The latter solution can be obtained by rotating the entire system 90 ^∘ in the clockwise direction (effectively interchanging L and B, wind now parallel to x-axis) and finally rotating the solution 90 ^∘ in the counterclockwise direction.

Finally, at the horizontal boundaries of the rectangular basin, we require the normal transports to vanish, i.e.

$$ \left< u \right> = 0 \quad \text{at \(x=0,L\)} \qquad \text{and} \qquad \left< v \right> = 0 \quad \text{at \(y=0,B\)} . $$

(8)

where angle brackets denote vertical integration from bottom to surface, i.e. $\left < \cdot \right >~=~{\int }_{-h}^{0} \cdot \mathrm {d}z$ (with the upper boundary z = 0 arising from the linearisation).

3 Solution method

3.1 Differential problem for surface elevation amplitude

First we write the solution in a time-periodic fashion according to

$$\begin{array}{@{}rcl@{}} \eta & =& \Re \left\{ N(x,y) \exp(-i\omega t) \right\} , \end{array} $$

(9)

$$\begin{array}{@{}rcl@{}} u & =& \Re \left\{ U(x,y,z) \exp(-i\omega t) \right\} , \end{array} $$

(10)

with complex amplitudes N and U. Similar expressions hold for v and w, with complex amplitudes V and W.

Next, we express the horizontal flow solution U and V in terms of surface slopes ∇N and wind stress. This is done using the so-called rotating flow components, for which we derive expressions; see Appendix A.1. Substituting these expressions into the continuity equation and integrating from bottom to surface gives the following elliptic equation for N (see Appendix A.2):

$$ \frac{\partial^{2} N}{\partial x^{2}} + \frac{\partial^{2} N}{\partial y^{2}} + k^{2} N = -\left[ \frac{\partial \left< R_{1} \right>}{\partial x} + \frac{\partial \left< R_{2} \right>}{\partial y} \right] , $$

(11)

in which k is a wave number satisfying

$$ k^{2} = \frac{-i\omega}{\left< C_{1} \right>} , $$

(12)

with the coefficient $\left < C_{1} \right >$ as specified in Appendix A.2. The forcing term on the right-hand side of Eq. 11 includes contributions arising from the divergence and curl of the wind stress field (see Appendix A.1); it is zero for spatially uniform wind. Moreover, k is a wave number, and the coefficient 〈C ₁〉 in Eq. 12 is as specified in Appendix A.2.

The boundary conditions in Eq. 8 imply

$$\begin{array}{@{}rcl@{}} \frac{\partial N}{\partial x} + \gamma \frac{\partial N}{\partial y} & =& -\left< R_{1} \right> \quad \textnormal{at \(x=0,L\)} , \end{array} $$

(13)

$$\begin{array}{@{}rcl@{}} -\gamma \frac{\partial N}{\partial x} + \frac{\partial N}{\partial y} & =& -\left< R_{2} \right> \quad \textnormal{at \(y=0,B\)} , \end{array} $$

(14)

with coefficient $\gamma ~=~\left < C_{2} \right >/\left < C_{1} \right >$ as well as forcing terms $\left < R_{1} \right >$ and $\left < R_{2} \right >$ associated with the wind stress at the cross-basin and along-basin boundaries, respectively; see Appendix A.2. Finally, the vertical flow amplitude W at any depth z can be expressed in terms of the free surface elevation N and the wind forcing. This follows from integration of the continuity equation over z; see Appendix A.3.

Finally, for ω = 0, the wave number in Eq. 11 reduces to k ² = 0, and as an additional condition the total water volume in the basin must be prescribed.

3.2 Collocation method

The solution, for arbitrary values of the dimensionless rotation parameter f/ω, will be written as

$$ N = N^{\text{unif}} + a N^{\text{div}} + b N^{\text{curl}} , $$

(15)

with three contributions associated with the spatially uniform part of the wind, the divergent part of the wind (a ≠ 0) and the curl part of the wind (b ≠ 0).

The first contribution N ^unif takes advantage of the fact that a function ϕ ^unif(y) exists satisfying both the differential Eq. 11 and the along-basin boundary conditions in Eq. 14, only regarding the forcing terms arising from the spatially uniform wind. See Appendix B.1 for an expression for ϕ ^unif. We thus write

$$ N^{\text{unif}} = \phi^{\text{unif}}(y) + \sum\limits_{m=0}^{M} c_{m}^{\oplus} N^{\oplus}_{m}(x,y) + \sum\limits_{m=0}^{M} c_{m}^{\ominus} N^{\ominus}_{m}(x,y) , $$

(16)

with $N^{\oplus }_{m}(x,y)$ and $N^{\ominus }_{m}(x,y)$ representing two families of so-called along-basin eigenmodes, consisting of Kelvin and Poincaré modes propagating or exponentially decaying in the positive or negative x-direction, respectively (see Appendix B.3). In Eq. 16, M is the truncation number. The coefficients $c_{m}^{\oplus }$ and $c_{m}^{\ominus }$ follow from applying a collocation technique. Herein, we require the boundary condition (13) to be satisfied at two sets of M + 1 collocation points, one at x = 0 and the other at x = L (see Fig. 3)¹. Note that this boundary condition includes a contribution due to ϕ ^unif.

Fig. 3

Sketch of the solution method outlined in Section 3.2. a To calculate N ^unif and N ^curl, a superposition of along-basin channel modes (white arrows) and a suitable particular solution (double arrow) is forced to satisfy $\left < U \right >~=~0$ at a set of collocation points at x = 0,L (white circles). b Alternatively, to obtain N ^div, a superposition of cross-basin channel modes and a particular solution is forced to satisfy $\left < V \right >~=~0$ at a set of collocation points at y = 0,B. By symmetry, the latter orientation also works for N ^unif, which is done in the convergence test (Appendix B.2)

The second contribution N ^div is found analogously, but now using a solution ϕ ^div(x) satisfying both the differential equation and the cross-basin boundary conditions, regarding the forcing terms proportional to a (see Appendix B.1). We thus write

$$ N^{\text{div}} = \phi^{\text{div}}(x) + \sum\limits_{m=0}^{\tilde{M}} a_{m}^{\oplus} \tilde{N}^{\oplus}_{m}(x,y) + \sum\limits_{m=0}^{\tilde{M}} a_{m}^{\ominus} \tilde{N}^{\ominus}_{m}(x,y) , $$

(17)

Also, this solution involves two families of cross-basin eigenmodes, but now propagating or exponentially decaying in the positive or negative y-direction, respectively. The $2(\tilde {M}~+~1)$ collocation points are now located at y = 0 and y = B. Please note that the value of $\tilde {M}$ may differ from the value of M used above.

Finally, the third contribution reads

$$ N^{\text{curl}} = \phi^{\text{curl}}(y) + \sum\limits_{m=0}^{M} b_{m}^{\oplus} N^{\oplus}_{m}(x,y) + \sum\limits_{m=0}^{M} b_{m}^{\ominus} N^{\ominus}_{m}(x,y) , $$

(18)

again involving along-basin eigenmodes and collocation points identical to those used in obtaining N ^unif (and involving ϕ ^curl, as given in Appendix B.1).

By symmetry, the contribution N ^unif due to the spatially uniform wind can just as well be obtained with an alternative form of Eq. 16, involving cross-basin eigenmodes and collocation points at y = 0 and y = B. This requires an alternative particular solution $\tilde {\phi }^{\text {unif}}(x)$ instead of ϕ ^unif(y). This symmetry property provides us with an opportunity to perform a convergence test; see Appendix B.2. This possibility does not exist for the other two contributions N ^div and N ^curl.

3.3 Analytical solution for small f/ω and free slip

In the case of weak Coriolis effects, we may obtain additional insight from expanding the solution in powers of 𝜖 = f/ω. For convenience we will do this for the case of free slip (s = 0), which makes the flow pattern z-independent. Let us write the complex amplitudes as

$$\begin{array}{@{}rcl@{}} N & =& N_{0} + \epsilon N_{1} + \epsilon^{2} N_{2} + {\dots} , \end{array} $$

(19)

$$\begin{array}{@{}rcl@{}} U & =& U_{0} + \epsilon U_{1} + \epsilon^{2} U_{2} + {\dots} , \end{array} $$

(20)

and the same for V, where U and V are the flow velocities.

At lowest order, i.e. at $\mathcal {O}(\epsilon ^{0})$, Coriolis effects is absent. For the uniform and divergent wind field, we then obtain a purely along-basin oscillation. Alternatively, due to its cross-basin dependency, the solution due to the curl part of the wind also displays cross-basin oscillations. Adopting a notation that is convenient to present also the higher-order solutions, the lowest-order solution reads

$$\begin{array}{@{}rcl@{}} \frac{N_{0}}{\hat{N}} & =& F_{k_{0}}^{-}(x) + a \left[ \frac{2}{k_{0}L} - F_{k_{0}}^{+}(x) \right] \\ && \qquad + b \sum\limits_{m\;\text{odd}} c_{m} F_{\tilde{\alpha}_{m}}^{-}(x) \cos \beta_{m} y , \end{array} $$

(21)

$$\begin{array}{@{}rcl@{}} \frac{U_{0}}{\hat{U}} & = &iG_{k_{0}}^{-}(x) + ia \left[ \frac{2x}{L} - G_{k_{0}}^{+}(x) \right] \\ && \qquad + ib \sum\limits_{m\;\text{odd}} c_{m} \frac{\tilde{\alpha}_{m}}{k_{0}} G_{\tilde{\alpha}_{m}}^{-}(x) \cos \beta_{m} y , \end{array} $$

(22)

$$\begin{array}{@{}rcl@{}} \frac{V_{0}}{\hat{U}} & =& ib \sum\limits_{m\;\text{odd}} c_{m} \frac{\beta_{m}}{k_{0}} F_{\tilde{\alpha}_{m}}^{-}(x) \sin \beta_{m} y . \end{array} $$

(23)

Here, we have introduced reference values of the elevation and velocity amplitudes given by $\hat {N}~=~\hat {T}/(ghk_{0})$ (with shallow water wave number $k_{0}~=~\omega /\sqrt {gh}$) and $\hat {U}~=~\hat {T}/(\omega h)$, respectively. Next, the curl-part has a cross-basin structure containing a cross-basin wave number β _m = m π/B and coefficients $c_{m}~=~-8k_{0}/[\tilde {\alpha }_{m}(m\pi )^{2}]$, only required for odd values of m. Moreover, we used the dimensionless functions $F_{k_{0}}^{\pm }(x)~=~\sin k_{0}x~\pm ~\xi _{k_{0}L}^{\pm }\cos k_{0}x$ and $G_{k_{0}}^{\pm }(x)~=~1~-~\cos k_{0}x~\pm ~\xi _{k_{0}L}^{\pm }\sin k_{0} x$ involving the coefficient $\xi _{k_{0}L}^{\pm }~=~(1~\pm ~\cos k_{0}L)/\sin k_{0}L$. Similarly, we introduce along-basin wave numbers $\tilde {\alpha }_{m}$ satisfying $\tilde {\alpha }_{m}^{2}~+~{\beta _{m}^{2}}~=~{k_{0}^{2}}$ as well as functions $F_{\tilde {\alpha }_{m}}^{\pm }(x)$ and $G_{\tilde {\alpha }_{m}}^{\pm }(x)$ involving a similar coefficient $\xi _{\tilde {\alpha }_{m}L}$.

The solutions at first order, i.e. at $\mathcal {O}(\epsilon ^{1})$ express how Coriolis effects modify the above oscillations. Mathematically, the Coriolis acceleration of the lowest order flow enters as the only forcing term at first order (the direct wind forcing being absent here). As a result, the solutions for a uniform and divergent wind field now experience a forcing in the cross-basin direction. Alternatively, the curl part is further modified in along-basin and cross-basin directions. Expressions for the first-order solutions are given in Appendix C.

4 Results

4.1 Collocation method

To present the results, we consider a reference basin with characteristics as shown in Table 1. This corresponds to a basin with dimensions roughly representing those of the Southern Bight of the North Sea. To investigate the role of bottom friction, we consider a frictional case with the resistance parameter equal to s = 10⁻⁴ m s⁻¹ as well as a frictionless case with s = 0.

Table 1 Overview of model parameters and their reference values

We will first present three examples (Fig. 4). The examples all deal with the reference basin, but differ with respect to the applied forcing. We have intentionally chosen our forcing frequencies such that they coincide with peaks in the spectral response, to be shown in Fig. 5. The first example is forced by a spatially uniform wind field with an angular frequency given by $\omega _{1}~=~1.52~\times ~10^{-4}~\;\text {rad}~\;\mathrm {s}^{-1}~=~0.49\omega _{\text {ref}}$ with reference frequency

$$ \omega_{\text{ref}} = \sqrt{gh} \frac{2\pi}{L} . $$

(24)

Fig. 4

Amphidromic charts for three examples of basin responses. a Uniform wind with ω = ω ₁. b Uniform wind with ω = ω ₂. c Divergent wind with ω = ω ₂. Colours indicate elevation amplitude; pink lines are the co-phase lines. Parameter values as in Table 1 (including bottom friction)

Fig. 5

Scaled elevation amplitude A at evaluation point (black dot in Fig. 1a), as a function of the dimensionless forcing frequency ω/ω _ref for three different types of wind forcing: a spatially uniform part, b divergent part and c curl part. Parameter values as in Table 1, with black and pink curves pertaining to the cases without and with bottom friction, respectively. As indicated, the three pink dots refer to the cases displayed in Fig. 4. Please note that all peaks of the black curve should reach to infinity, but due to the plotting resolution for ω this is not visible for all peaks

The reference frequency is the frequency for which the frictionless shallow water wave length equals the basin length $\lambda=\frac{2\pi\sqrt{gh}}{\omega}$ equals the basin length. The second example is forced by a spatially uniform wind field, as well, but now of angular frequency $\omega _{2}~=~2.95~\times ~10^{-4}~\;\text {rad}~\;\mathrm {s}^{-1}~=~0.95\omega _{\text {ref}}$. The same frequency is applied in the third example, but now using a divergent wind field. Since the solution is time-periodic, the elevation field can be visualised as an amphidromic system, displaying amplitudes and co-phase lines. As shown in Fig. 4a, the first examples display a rotating wave with one amphidromic point at the basin centre, and relatively high amplitudes near the coast. The other examples, shown in Figs. 4b,c, display qualitatively different patterns and much lower amplitudes. These examples already illustrate that the response depends on both types of forcing and forcing frequency.

To further investigate the dependency of the solution on the forcing frequency for the various types of wind forcing, we will focus on the location midway one of the cross-basin boundaries; see the black dot in Fig. 1a. The elevation amplitude at this location, scaled against the reference elevation amplitude $\hat {N}$ according to

$$ A = \frac{|N|}{\hat{N}} \qquad at (x,y)=(L,\frac{1}{2}B) with \ \hat{N} = \frac{\hat{T}}{ghk_{0}} , $$

(25)

will be used to evaluate the solution. Figure 5 shows the value of A as a function of the dimensionless forcing frequency ω/ω _ref. This is done for each of the three types of wind forcing, in each case distinguishing a case without (black line) and with bottom friction (thick pink line). First of all, the three examples presented before appear here as part of the spectral response, the first one clearly having the highest value. More generally, the spectral response shows a complex pattern of peaks at certain frequencies and lower responses in between. Comparison between panels a, b, and c of Fig. 5 shows that this pattern strongly depends on the type of wind forcing, e.g. at $\omega ~\approx ~\frac {1}{2}L/\lambda$ showing a peak for the spatially uniform wind, but not for the other types of forcing.

Increasing the resistance parameter (see Table 1) generally lowers the peaks, in certain cases causing it more or less to disappear. As a second-order effect, actually not visible in Fig. 5, the peaks shift to a slightly lower frequency. Further simulations, not shown here, suggest that the spectral response of the surface elevation hardly depends on the value of the vertical eddy viscosity K. However, the vertical structure of the flow velocity does depend on K.

The influence of basin width on the spectral response is shown in Fig. 6, for each of the three types of wind forcing. We kept the basin length to its default value, and varied basin width from B = 25 to 400 km, thus covering a width-over-length range from 0.1 to 3.5. For the solutions with collocation points along the cross-basin boundaries, the number of collocation points was adjusted to keep a collocation spacing to a constant value of about 3 km. The colour plots show that for elongated basins, i.e. for B/L ≪ 1, the spectral response is nearly B/L-independent for the frequency range plotted. In Fig. 6a, we particularly reproduce the peaks mentioned by Ponte AL (2010); and we now show that similar behaviour is found for the other spatial wind patterns. For non-elongated basins, i.e. for $B/L~=~\mathcal {O}(1)$ and larger, a more complicated pattern is obtained showing a strong width-dependence to be further interpreted in Section 5.2. The reference case for which $B/L~=~\frac {1}{2}$ is denoted by a dashed white line.

Fig. 6

Scaled elevation amplitude A at evaluation point (black dot in Fig. 1a), as a function of dimensionless forcing frequency ω/ω _ref and dimensionless basin width B/L, for three different types of wind forcing: a spatially uniform part, b divergent part and c curl part. This figure has been obtained by varying ω and B, while fixing the other parameters to the values listed in Table 1 (including bottom friction)

4.2 Analytical solution for small f/ω and free slip

In addition to the results from the collocation method, we now turn to the analytical solution in powers of f/ω. The spectral response at various orders of 𝜖 = f/ω is shown in Fig. 7 (for spatially uniform and divergent wind) and Fig. 8 (for wind with nonzero curl), again as a function of the scaled frequency L/λ. Analogous to Rao (1966), the resonance peaks have been labelled by bracketed numbers (m,n), with along-basin mode number m and cross-basin mode number n. As such, they correspond to an eigenmode with a specific spatial structure as presented by Rao (1966). For example, the mode associated with the (1,0)-peak at $L/\lambda ~=~\frac {1}{2}$ in Fig. 7a is actually the frictionless counterpart of the first example (Fig. 4a), in the limit of no rotation. Likewise, the mode associated with the (2,0)-peak at L/λ = 1 in Fig. 7a is the counterpart of the third example (Fig. 4c). Peaks are labelled only if they are new at a certain order in 𝜖, not if they are already present at a lower order for the same type of forcing. As noted by Rao (1966), all eigenmodes are either symmetric or antisymmetric about the center point of the basin.

Fig. 7

Scaled elevation amplitude A at evaluation point (black dotin Fig. 1a), as a function of the dimensionless forcing frequency L/λ according to the expansion in powers of 𝜖 = f/ω: a lowest order and b first order. The curves pertain to the solution due to the spatially uniform part (black) and the divergent part (red) of the wind field. Bracketed numbers (m,n) indicate the eigenmode with along-basin mode number m and cross-basin mode number n; see text. Parameter values as in Table 1 (free slip case and small f)

Fig. 8

Same as Fig. 7, but now for the solution due to the curl part of the wind field (blue), which is available at a the lowest order and b the first order

5 Discussion

5.1 Interpretation of the resonances

To interpret the complex patterns of peaks in the spectral response presented in Section 4.1, we will examine the physics behind the peaks appearing in the analytical solution for small f/ω and free slip presented in Section 4.2. To this end, we must turn to the concept of resonance. Resonance implies that, when starting from rest, the forcing continuously feeds energy into the system. This means that the net power supplied by the wind forcing, i.e. integrated over the basin and averaged over a forcing period, is positive. In our context with along-basin wind only and neglecting dissipation, this resonance condition can be expressed as

$$ \mathcal{P}_{\text{input}} = \frac{\omega}{2\pi} {\int}_{0}^{2\pi/\omega} \left[ \rho {{\int}_{0}^{B}} {{\int}_{0}^{L}} u \: \tau_{\mathrm{w}} \: \mathrm{d}x \: \mathrm{d}y \right] \mathrm{d}t > 0 . $$

(26)

Whether a certain mode can be excited depends on symmetry properties associated with the spatial structure of the wind field in relation to the spatial structure of the along-basin flow field.

Let us now focus on the lowest-order solution for spatially uniform and divergent wind (Fig. 7a), i.e. without rotation. The peaks occurring at $L/\lambda ~=~\frac {1}{2}~+~p$ for p = 0,1,2,..., associated with the odd modes (2p + 1,0) are the odd seiches of a closed basin that can be excited by a spatially uniform wind (Csanady 1982; Ponte 2010). In addition to this well-known result, the peaks at L/λ = p for p = 1,2,⋯ demonstrate that a divergent wind field may excite the even modes (2p,0). Symmetry arguments help to explain this from Eq. 26. Odd modes can be excited by a spatially uniform wind field, because both wind and along-basin flow are symmetric about the cross-basin centerline, thus giving a nonzero result in Eq. 26. Analogously, even modes can be excited by a divergent wind field, because both wind and along-basin flow are then antisymmetric about the cross-basin centerline. This is illustrated in Fig. 9a,b.

Fig. 9

Sketch of the symmetry argument showing the spatial structure of the forcing (left-hand panel) and the spatial structure of the along-basin flow field of three modes: (1,0), (2,0), and (1,1). Grey shades indicate positive values, white means negative. We consider three types of wind forcing: a spatially uniform part, b divergent part and c curl part. Whether a certain mode is resonant under these forcing conditions, is denoted in the figure

Next, let us discuss the lowest order solution due to the curl part of the wind field, also without rotation. As shown by the peaks in Fig. 8a, modes characterised by odd along-basin and odd cross-basin mode numbers can be resonant under this type of forcing. The following symmetry arguments show why this is the case. Modes with an even along-basin mode number cannot be resonant, because the along-basin flow on the left-hand side of the cross-basin centerline is then always opposite to that on the right-hand side. However, the wind forcing is symmetric about this cross-basin centerline. The power input by the wind in these two parts of the basin will thus always cancel, which causes the net power by the wind forcing to be zero. A similar argument holds for the modes with an even cross-basin mode number, but now with respect to the along-basin centerline. These modes cannot be resonant, because the along-basin flow is then symmetric about this line and the wind forcing is antisymmetric about this line. Hence, the power input by the wind in these situations. Such symmetry arguments do not apply to the modes characterised by odd along-basin and odd cross-basin mode numbers. The above reasoning is illustrated in Fig. 9c.

The first-order solutions for the uniform and divergent wind case show new resonances; see the peaks in Fig. 7b. To understand these peaks, it is crucial to realise that the first-order problem is actually similar to the lowest-order problem, but instead of by the wind, it is forced by the Coriolis acceleration of the lowest-order along-basin flow. This forcing acts in the cross-basin direction, it is uniform in this cross-basin direction and it has an along-basin structure that depends on the type of wind forcing. For spatially uniform wind, the lowest order along-basin flow in Eq. 22 and hence, the first-order forcing is symmetric about the cross-basin centerline. Alternatively, for divergent wind, the first-order forcing is antisymmetric about the cross-basin centerline. Symmetry arguments similar to those presented above for the lowest-order solution due to the curl part now explain why the uniform wind (divergent wind) gives rise to resonance at modes with an even (odd) along-basin mode number, and in each case an odd cross-basin mode number.

Similar symmetry arguments explain the new peaks arising in the first-order response to the curl part of the wind (Fig. 8b), but this is more complicated due to the spatial structure of the forcing.

5.2 Influence of basin dimensions

The modes identified in the previous subsection allow us to interpret the width-dependence of the (peaks in the) spectral response presented in Fig. 6. As noted earlier, for elongated basins, i.e. for B < L ≪ 1, the response is independent of B/L in the frequency range under consideration. This is because the cross-basin dynamics are weak. For non-elongated basins, i.e. for $B/L~=~\mathcal {O}(1)$ and larger, we see that these purely along-basin modes (e.g. (1,0) for the spatially uniform wind) are modified by Coriolis effects into a more rotary wave propagating around the basin, which has a longer travel distance and thus a lower resonant frequency. In addition to this, resonant peaks appear pertaining to purely cross-basin modes (e.g. (0,1)) as well as mixed along-/cross-basin modes (e.g. (2,1)). As can be expected, the peak frequency modes decrease with increasing basin width. In conclusion, we can say that for non-elongated basins, cross-wind dynamics produces peaks at frequencies significantly lower than those obtained by Ponte (2010).

5.3 Single wind event

We will now illustrate how the spectral response translates into time-dependent elevation patterns for a single wind event (Fig. 10). To this end, it is important to realise that any wind event can be represented as the superposition of periodic signals. This means that Eq. 6 must be extended according to

$$ \frac{(\tau_{\mathrm{w}}^{(x)},\tau_{\mathrm{w}}^{(y)})}{\rho} = \Re \left\{ {\sum}_{p=0}^{P} (T_{p}^{(x)},T_{p}^{(y)}) \exp(-i\omega_{p} t) \right\} , $$

(27)

with frequencies ω _p = p ω _min and corresponding wind amplitudes $T_{p}^{(x)}$ and $T_{p}^{(y)}$. As we must discretise the wind spectrum, there is a minimum frequency ω _min and hence a recurrence period T _recur = 2π/ω _min over which the event repeats itself. To realistically describe a ‘single’ wind event, this recurrence period must be sufficiently large such as to avoid unwanted interference. In this example, we have taken T _recur = 10 days. By linearity, the basin response to the forcing in Eq. 27 will be the superposition of the responses to the individual periodic forcings as calculated by our model.

Fig. 10

Response of surface elevation at evaluation point for two wind events that differ in duration: 10.3 h for event I (top), 6 h for event II (bottom). The plots on the left show the spectral representation of the wind (grey) as well as the amplification (pink), and the actual response (dashed). The plots on the right show the temporal representation of both forcing (grey) and response (black). Note that the grey curve represents the wind forcing as it is actually simulated using a superposition of Fourier modes. Parameter values as in Table 1, spatially uniform wind

Now, let us consider two wind events I and II, that impose a spatially uniform wind forcing of 3 N m⁻² onto our reference basin in the along-basin direction (parameter values in Table 1). According to standard empirical friction laws (Wu 1982), this corresponds to a wind speed of about 30 m s⁻¹ (at 10 m height). The two wind events differ in their duration: wind event I lasts 10.3 h, wind event II lasts 6 h. Regarding spin-up and spin-down of the forcing, we apply a smooth transition taking 1.2 h for both wind events (see grey curves in Fig. 10b, d).

The elevation at the evaluation point, as a function of time, shows quite different responses for the two wind events (see black curves in Fig. 10b, d). The strongest sloshing is observed after wind event II, whereas wind event I produces relatively little oscillations. This is as expected from comparing the wind spectrum with the spectral response of the basin (see Fig. 10a, c). It is the product of these two quantities that gives the spectral response to the wind event under consideration (blue curve). Indeed, the resonant frequency L/λ = 0.49 is not contained in the wind spectrum of event I, whereas it is present in event II.

6 Conclusions

We have developed an idealised process-based model to systematically investigate the resonance properties of closed rectangular rotating basins of uniform depth, subject to space- and time-dependent wind forcing. We focus on the spectral response of the surface elevation at an evaluation point midway one of the cross-basin boundaries.

Regarding the resonance peaks, we conclude that the spatial structure of the wind forcing matters. For example, without rotation, a spatially uniform wind produces the classical resonance peaks at $L/\lambda ~=~\frac {1}{2},\frac {3}{2}, ...$, whereas divergent wind also gives peaks at L/λ = 1,2,.... Including rotation shifts these peaks.

Next, because the cross-wind basin dimension B is not small, cross-wind dynamics produces peaks at frequencies significantly lower than obtained by Ponte (2010). These cross-wind dynamics can be triggered by several mechanisms. Firstly, a wind forcing with nonzero curl produces cross-wind variations in elevation and thus cross-basin flow and oscillations that may be resonant. Secondly, the Coriolis acceleration of the along-wind flow also produces cross-basin oscillations. As discussed above, this along-wind pattern depends on the spatial pattern of the wind forcing, so these rotation-induced peaks will be different for spatially uniform wind and divergent wind.

In each of the above cases, the main effect of increasing friction is a lowering of the peaks. Finally, we have illustrated how the spectral response analysed above manifests itself in the response to a single wind event, and particularly, how excitation of resonant frequencies produces sloshing in the basin. Extending this model approach with respect to geometry (realistic topography and coastlines) and atmospheric forcing is essential before making a detailed comparison with observations.

Appendices

Appendix

A Expressions for flow and problem for N

2.1 A.1 Vertical profiles from horizontal momentum equations

Here, we present the details of the vertical structure of the flow First we define rotating flow components according to q ^± = u ± i v with complex amplitudes Q ^±, such that U = (Q ⁺ + Q ⁻)/2 and V = (Q ⁺ − Q ⁻)/(2i). From Eqs.1–2, the differential equation for the complex amplitude Q ^± is given by

$$ \frac{\mathrm{d}^{2} Q^{\pm}}{\mathrm{d} z^{2}} - \lambda^{\pm2} Q^{\pm} = g \mathcal{L}^{\pm} N , $$

(28)

with complex operators $\mathcal {L}^{\pm }~=~\partial /\partial x~\pm ~i\partial /\partial y$. From Eqs.4–5, the boundary conditions are given by

$$ K \frac{\mathrm{d} Q^{\pm}}{\mathrm{d} z} = T^{\pm} \quad \text{at} \ z=0, \qquad\!\!\!\!\!\!\!\!\!\!\!\!\ \text{and} \qquad\!\!\!\!\!\!\!\!\!\! K \frac{\mathrm{d} Q^{\pm}}{\mathrm{d} z} = s Q^{\pm} \quad\!\! \text{at \(z=-h\),} $$

(29)

with rotating wind forcing amplitudes T ^± = T ^(x) ± i T ^(y) (wind stress divided by density). The two forcing terms in this nonhomogeneous differential problem imply that the rotating flow solution contains two contributions, proportional to the surface gradient and the wind stress, respectively:

$$ Q^{\pm}(z) = Q^{\pm}_{\eta}(z) \mathcal{L}^{\pm} N + Q^{\pm}_{\mathrm{w}}(z) T^{\pm} , $$

(30)

The vertical structures read

$$\begin{array}{@{}rcl@{}} Q_{\eta}^{\pm}(z) & =& \frac{g\left[\cosh\lambda^{+}z-\alpha_{\mathrm{c}}^{\pm}\right]}{\alpha_{\mathrm{c}}^{\pm} K\lambda^{\pm2}} , \end{array} $$

(31)

$$\begin{array}{@{}rcl@{}} Q_{\mathrm{w}}^{\pm}(z) & =& \frac{\alpha_{\mathrm{c}}^{\pm}\sinh\lambda^{\pm} z+\alpha_{\mathrm{s}}^{\pm}\cosh\lambda^{\pm} z}{\alpha_{\mathrm{c}}^{\pm} K\lambda^{\pm}} , \end{array} $$

(32)

with λ ^±2 = −i(ω ∓ f)/K and $\alpha ^{\pm }_{\mathrm {c}}~=~\cosh \lambda ^{\pm } h~+~s^{-1}K\lambda ^{\pm }\sinh \lambda ^{\pm } h$ and $\alpha ^{\pm }_{\mathrm {s}}~=~\sinh \lambda ^{\pm } h~+~s^{-1}K\lambda ^{\pm }\cosh \lambda ^{\pm } h$. The vertical integral is given by

$$ \left< Q^{\pm} \right> = \left< Q^{\pm}_{\eta} \right> \mathcal{L}^{\pm} N + \left< Q^{\pm}_{\mathrm{w}} \right> T^{\pm} , $$

(33)

with

$$\begin{array}{@{}rcl@{}} \left< Q^{\pm}_{\eta} \right> & =& \frac{g\left[ \sinh\lambda^{\pm} h - \alpha_{\mathrm{c}}^{\pm} \lambda^{\pm} h \right]}{\alpha_{\mathrm{c}}^{\pm} K \lambda^{\pm 3}}, \end{array} $$

(34)

$$\begin{array}{@{}rcl@{}} \left< Q^{\pm}_{\mathrm{w}} \right> & =& \frac{\alpha_{\mathrm{c}}^{\pm} \left[ 1 - \cosh\lambda^{\pm} h \right] + \alpha_{\mathrm{s}}^{\pm} \sinh\lambda^{\pm} h}{\alpha_{\mathrm{c}}^{\pm} K \lambda^{\pm 2}} . \end{array} $$

(35)

The two cases ω = ±f require alternative expressions for either Q ⁺ or Q ⁻. If ω = +f, we must replace the Q ⁻ expressions in Eqs.31–33; if ω = −f we must replace the Q ⁺ expressions. They must be replaced with

$$\begin{array}{@{}rcl@{}} Q_{\eta}^{\pm}(z) &=& \frac{gh^{2}}{K} \left[ \frac{1}{2} \left(\frac{z}{h}\right)^{2} - \frac{1}{2} - \frac{K}{sh} \right] ,\\ \qquad Q_{\mathrm{w}}^{\pm}(z) &=& \frac{h}{K} \left[ 1 + \left( \frac{z}{h} \right) + \frac{K}{sh} \right] , \end{array} $$

(36)

and

$$ \left< Q^{\pm}_{\eta} \right> = -\frac{gh^{3}}{K} \left[ \frac{1}{3} + \frac{K}{sh} \right] , \qquad \left< Q^{\pm}_{\mathrm{w}} \right> = \frac{h^{2}}{K} \left[ \frac{1}{2} + \frac{K}{sh} \right] . $$

(37)

2.2 A.2 Elliptical problem for N

Depth-integration of the continuity Eq. 3, with the aid of boundary conditions (4) gives, in terms of the complex amplitudes of surface elevation and the rotating velocity components.

$$ -i\omega N + \frac{\partial }{\partial x} \underbrace{\left( \frac{\left< Q^{+} \right>+\left< Q^{-} \right>}{2} \right) }_{\left< U \right>} + \frac{\partial }{\partial y} \underbrace{\left( \frac{\left< Q^{+} \right>-\left< Q^{-} \right>}{2i} \right) }_{\left< V \right>} = 0 , $$

(38)

Substitution of Eq. 30 gives the elliptical equation for N presented in Eq. 11 of the main text. The corresponding coefficients are given by

$$ C_{1} = \frac{1}{2} \left[ Q^{+}_{\eta} + Q^{-}_{\eta} \right] , \qquad C_{2} = \frac{1}{2i} \left[ Q^{+}_{\eta} - Q^{-}_{\eta} \right] , $$

(39)

The boundary conditions presented in Eqs.13–14 of the main text follow from depth-integration of the momentum Eqs. 1–2. The coefficients in there are given by $\gamma ~=~\left < C_{2} \right >/\left < C_{1} \right >$ and

$$\begin{array}{@{}rcl@{}} R_{1} &=& \frac{1}{2\left< C_{1} \right>} \left[ Q^{+}_{\mathrm{w}} T^{+} + Q^{-}_{\mathrm{w}} T^{-} \right] ,\\ \qquad R_{2} &=&\frac{1}{2i\left< C_{1} \right>} \left[ Q^{+}_{\mathrm{w}} T^{+} - Q^{-}_{\mathrm{w}} T^{-} \right] . \end{array} $$

(40)

2.3 A.3 Vertical flow velocity

The vertical flow velocity amplitudes at any depth z are given by

$$ W(z)~=~- \left\lfloor C_{1} \right\rfloor \left( \frac{\partial^{2} N}{\partial x^{2}} ~+~ \frac{\partial^{2} N}{\partial y^{2}} \right) ~-~ \left< C_{1} \right> \left( \left\lfloor \frac{\partial R_{1}}{\partial x} \right\rfloor + \left\lfloor \frac{\partial R_{2}}{\partial y} \right\rfloor \right) , $$

(41)

where floor brackets indicate integration from bottom to z, i.e. $\lfloor \cdot \rfloor ~=~{\int }_{-h}^{z}\cdot \mathrm {d}z$. This expression can be simplified further by using the differential Eq. 11 for N to eliminate the Laplacian of N.

B Details of the collocation method

1.1 B.1 Expressions for ϕ ^unif, ϕ ^div and ϕ ^curl

Our solution method uses functions that homogenize the differential Eq. 11 and either the along-basin or cross-basin boundary conditions in Eqs.13–14. For the three different parts of the wind field, these functions are given by

$$\begin{array}{@{}rcl@{}} \phi^{\text{unif}}(y) & =& -\frac{\left[\left< Q^{+}_{\mathrm{w}} \right>-\left< Q^{-}_{\mathrm{w}} \right>\right]\hat{T}}{2i\left< C_{1} \right>k} \left[ \sin ky-\chi^{-}_{k}\cos ky \right] , \end{array} $$

(42)

$$\begin{array}{@{}rcl@{}} \phi^{\text{div}}(x) & =& \frac{\left[\left< Q^{+}_{\mathrm{w}} \right>+\left< Q^{-}_{\mathrm{w}} \right>\right]\hat{T}}{4\left< C_{1} \right>k}\left[\sin kx+\xi_{k}^{+}\cos kx-\frac{2}{kL}\right], \end{array} $$

(43)

$$\begin{array}{@{}rcl@{}} \phi^{\text{curl}}(y) & =& \frac{\left[\left< Q^{+}_{\mathrm{w}} \right>-\left< Q^{-}_{\mathrm{w}} \right>\right]\hat{T}}{4i\left< C_{1} \right>k}\left[\sin ky+\chi_{k}^{+}\cos ky-\frac{2}{kB}\right] , \end{array} $$

(44)

with k as defined in Eq. 11 and $\chi ^{\pm }_{k}~=~(1~\pm ~\cos kB)/\sin kB$ and $\xi _{k}^{\pm }~=~(1~\pm ~\cos kL)/\sin kL$.

1.2 B.2 Convergence test for spatially uniform wind

As already pointed out in Section 3, the case of spatially uniform wind can be solved in two ways. The first is by combining along-basin modes with collocation points at the cross-basin boundaries (as in Fig. 3a and in the main text); the second by combining cross-basin modes and collocation points at the along-basin boundaries (Fig. 3b). The latter choice requires an alternative particular solution; Eq. 42 should be replaced with

$$ \tilde{\phi}^{\text{unif}}(x) = -\frac{\left[\left< Q^{+}_{\mathrm{w}} \right>+\left< Q^{-}_{\mathrm{w}} \right>\right]\hat{T}}{2\left< C_{1} \right>k} \left[ \sin kx-\xi^{-}_{k}\cos kx \right] . $$

(45)

The symmetry property mentioned above allows us to perform a convergence test by intercomparing the two solutions for different truncation numbers. Using superscripts to denote the two ways of solution, we calculate the difference

$$ \epsilon_{\text{conv}} = \frac{1}{M_{\text{colloc}}} \sum\limits_{m} |N^{\text{unif}}(x_{m},y_{m})^{(1)}-N^{\text{unif}}(x_{m},y_{m})^{(2)}| , $$

(46)

averaging over the combined set of M _colloc collocation points (x _m ,y _m ) along the boundaries (see circles in Fig. 3a, b). In doing so, we make sure that the collocation spacing for both solutions is equal, i.e. B/M equals $L/\tilde {M}$. The result of doing this for different values of the truncation number M is shown in Fig. 11. The figure displays second-order convergence (Boyd 2000).

Fig. 11

Difference 𝜖 _conv between two possible solution techniques available for the case with spatially uniform wind, as defined in Eq. 46. M is the truncation number used for the solution with along-basin modes. Parameter values as in Table 1

1.3 B.3 Channel modes: Kelvin and Poincaré waves

Here, we present expressions for the surface elevation amplitudes of the along-basin and cross-basin channel modes, used in Section 3.2.

First, along-basin channel modes are wave solutions in an infinitely long channel aligned with the x-axis, and of width B. This means that these modes satisfy the homogenised elliptic (11) for N as well as the homogenised cross-basin boundary conditions in Eq. 14, while having a harmonic along-basin structure $\exp (i\kappa _{m}x)$ with complex wave number κ _m . We thus identify infinitely many modes, characterised by

$$ {\kappa_{0}^{2}} = \frac{k^{2}}{1+\gamma^{2}} , \qquad {\kappa_{m}^{2}} = k^{2} - \left( \frac{m\pi}{B} \right)^{2} , \quad (m=1,2,\cdots) . $$

(47)

For each m, these quadratic relationships yield two wave numbers. We thus distinguish two families of modes. The modes having a wave number with a positive imaginary part I{κ _m } > 0 propagate and/or decay exponentially in the positive x-direction are termed positive modes and denoted with a superscript ⊕. The modes having a wave number with a negative imaginary part I{κ _m } < 0 propagate and/or decay exponentially in the negative x-direction are termed negative modes and denoted with a superscript ⊖.

Within each of these two families of modes, we identify a Kelvin wave (corresponding to m = 0) and infinitely many Poincaré waves (m = 1,2,...). The spatial structure of the Kelvin mode is given by

$$ N_{0}^{\oplus}(x,y) = \exp\left(\frac{-y}{R_{\text{def}}}\right) \exp(i\kappa_{0}^{\oplus} x) , \qquad\!\!\!\! R_{\text{def}} = \sqrt{\frac{1+\gamma^{2}}{\gamma^{2}k^{2}}} , $$

(48)

where, due to vertical friction, the Rossby deformation radius R _def is now a complex quantity. The spatial structure of the Poincaré modes is given by:

$$\begin{array}{@{}rcl@{}} N_{m}^{\oplus}(x,y) = \left[ \cos \left( \frac{m\pi y}{B} \right) - \frac{\gamma i k B}{m \pi} \sin \left( \frac{m\pi y}{B} \right) \right]\\ \exp(i\kappa_{m}^{\oplus} x) , \quad (m=1,2,\cdots) . \end{array} $$

(49)

Expressions for the negative Kelvin and Poincaré modes follow similarly.

Analogously, the cross-basin channel modes are wave solutions in an infinitely long channel aligned with the y-axis, and of width L. This means that these modes satisfy the homogenised elliptic ?? QevoleqN) for N as well as the homogenised along-basin boundary conditions in Eq. 13, while having an exponential cross-basin structure $\exp (i\tilde {\kappa }y)$ with wave number $\tilde {\kappa }$. The two families of cross-basin channel modes follow from the along-basin modes by replacing B with L and considering a rotated coordinate system.

1.4 B.4 Equilibrium response to steady wind forcing (ω = 0)

Here, we will solve the equilibrium response to a steady wind forcing (ω = 0). The free surface elevation amplitude satisfies a Poission problem:

$$ \frac{\partial^{2} N}{\partial x^{2}} + \frac{\partial^{2} N}{\partial y^{2}} = -\left[ \frac{\partial \left< R_{1} \right>}{\partial x} + \frac{\partial \left< R_{2} \right>}{\partial y} \right] , $$

(50)

with boundary conditions as in Eqs. 13–14.

For the solution due to the spatially uniform part of the wind field, the solution is a linear profile sloping in the along-basin direction only:

$$ N^{\text{unif}} = - {\Lambda} \left( x-\frac{L}{2} \right) , \qquad {\Lambda} = \frac{\left< Q_{\mathrm{w}}^{+}+Q_{\mathrm{w}}^{-} \right>}{\left< Q_{\eta}^{+}+Q_{\eta}^{-} \right>} \hat{T} . $$

(51)

The solution due to the divergent part of the wind field is solved by means of a collocation technique largely similar to the one presented in Section 3.2. However, there are three notable differences: (i) the particular solution ϕ ^div has a different form, (ii) the Kelvin modes must be replaced with a linearly sloping function ψ ^div and a constant function, (iii) the Poincaré modes are as in Appendix B.3 but now with k = 0 and (iv) the boundary condition at one of the collocation points must be replaced by the overall statement that water is conserved. We write

$$\begin{array}{@{}rcl@{}} N^{\text{div}} = & \phi^{\text{div}}(x) + a_{0}^{\text{sl}} \psi^{\text{div}}(x,y) + a_{0}^{\text{const}} + \\ & \sum\limits_{m=1}^{\tilde{M}} a_{m}^{\oplus} \tilde{N}_{m}^{\oplus}(x,y) + \sum\limits_{m=1}^{\tilde{M}} a_{m}^{\ominus} \tilde{N}_{m}^{\ominus}(x,y) , \end{array} $$

(52)

with $\phi ^{\text {div}}(x)~=~-\frac {1}{2}{\Lambda }(x~-~\frac {1}{2}L)^{2}$, ψ ^div(x,y) = γ x−y and associated coefficients $a_{0}^{\text {sl}}$ and $a_{0}^{\text {const}}$. We always use an even number for $\tilde {M}$, and we select the collocation point midway one of the collocation boundaries for the conservation condition. A second solution is then obtained by doing the same, but now selecting the collocation point midway as the other boundary. Averaging the two finally leads to a solution that is symmetric with respect to the collocation method.

For the solution due to curl part of the wind field, a similar approach is followed:

$$\begin{array}{@{}rcl@{}} N^{\text{curl}} = & \phi^{\text{curl}}(y) + b_{0}^{\text{sl}} \psi^{\text{curl}}(x,y) + b_{0}^{\text{const}} + \\ & \sum\limits_{m=1}^{M} b_{m}^{\oplus} N_{m}^{\oplus}(x,y) + \sum\limits_{m=1}^{M} b_{m}^{\ominus} N_{m}^{\ominus}(x,y) , \end{array} $$

(53)

with $\phi ^{\text {curl}}(x)~=~-\frac {1}{2}{\Lambda }(y~-~\frac {1}{2}B)^{2}$, ψ ^curl(x,y) = x + γ y and associated coefficients $b_{0}^{\text {sl}}$ and $b_{0}^{\text {const}}$.

C Details of the expansion in f/ω

At first order, i.e. at $\mathcal {O}(\epsilon )$ with 𝜖 = f/ω, the elevation amplitude and flow field are given by

$$\begin{array}{@{}rcl@{}} \frac{N_{1}}{\hat{N}} = i \sum\limits_{n\;\text{even}} d_{n} \cos(\alpha_{n} x)F_{\tilde{\beta}_{n}}^{-}(y) + ia \sum\limits_{n\;\text{odd}} e_{n} \cos(\alpha_{n} x)F_{\tilde{\beta}_{n}}^{-}(y) \\ & \quad - ib \left\{ \frac{2}{k_{0}B} + \sum\limits_{m\;\text{odd}} \sum\limits_{n\;\text{even}} \left( j_{mn} F_{\tilde{\alpha}_{n}}^{+}(x) \cos\beta_{n} y + k_{mn} \cos(\alpha_{n} x) F_{\tilde{\beta}_{n}}^{+}(y) \right) \right\} , \end{array} $$

(54)

$$\begin{array}{@{}rcl@{}} \frac{U_{1}}{\hat{U}} & = - \sum\limits_{n\;\text{even}} d_{n} \frac{\alpha_{n}}{k_{0}} \sin(\alpha_{n}x)F_{\tilde{\beta}_{n}}^{-}(y) - a \sum\limits_{n\;\text{odd}} e_{n} \frac{\alpha_{n}}{k_{0}} \sin(\alpha_{n} x)F_{\tilde{\beta}_{n}}^{-}(y) \end{array} $$

$$\begin{array}{@{}rcl@{}} & \quad + b \sum\limits_{m\;\text{odd}} \left( \sum\limits_{n\;\text{even}} j_{mn} \frac{\tilde{\alpha}_{n}}{k_{0}} I_{\tilde{\alpha}_{n}\alpha_{m}} (x) \cos\beta_{n} y + k_{mn} \frac{\alpha_{n}}{k_{0}} \sin(\alpha_{n}x) F_{\tilde{\beta}_{n}}^{+}(y) \right) , \\ \frac{V_{1}}{\hat{U}} & = - \sum\limits_{n\;\text{even}} d_{n} \frac{\tilde{\beta}_{n}}{k_{0}} \cos(\alpha_{n}x)G_{\tilde{\beta}_{n}}^{-}(y) - a \sum\limits_{n\;\text{odd}} e_{n} \frac{\tilde{\beta}_{n}}{k_{0}} \cos(\alpha_{n}x)G_{\tilde{\beta}_{n}}^{-}(y) \end{array} $$

(55)

$$\begin{array}{@{}rcl@{}} & \quad + b \left\{ \sum\limits_{m\;\text{odd}} \sum\limits_{n\;\text{even}} \left( j_{mn} \frac{\beta_{n}}{k_{0}} F_{\tilde{\alpha}_{n}}^{+}(x) \sin\beta_{n} y - k_{mn} \frac{\tilde{\beta}_{n}}{k_{0}} \cos(\alpha_{n}x) H_{\tilde{\beta}_{n}\beta_{m}}^{+}(y) \right) \right\} , \end{array} $$

(56)

respectively. Here, we have introduced wave numbers α _n = n π/L and $\tilde {\beta }_{n}$ satisfying ${\alpha _{n}^{2}}~+~\tilde {\beta }_{n}^{2}~=~{k_{0}^{2}}$. Next, the coefficients d _n and e _n are given by

$$ d_{0} = \frac{2\xi_{k_{0}L}^{-}}{k_{0}L} - 1, \qquad d_{n} = \frac{2k_{0}L\xi_{k_{0}L}^{-}}{(\tilde{\beta}_{n}L)^{2}} , $$

(57)

for n nonzero and even, as well as

$$ e_{n} = \frac{8\sin k_{0}L}{(\alpha_{n}L)^{2}} + \frac{4k_{0}L\xi_{k_{0}L}^{+}}{(\tilde{\beta}_{n}L)^{2}} , $$

(58)

for n odd. For m odd and n even, we have

$$\begin{array}{@{}rcl@{}} j_{m0} & =& c_{m} \frac{\beta_{m}}{k_{0}} \frac{2\xi_{\tilde{\alpha}_{m}L}^{-}}{m\pi} , \\\qquad j_{mn}& =& c_{m} \frac{\beta_{m}}{\tilde{\alpha}_{n}} \frac{4\xi_{\tilde{\alpha}_{m}L}^{-}m}{\pi(m^{2}-n^{2})} , \end{array} $$

(59)

$$\begin{array}{@{}rcl@{}} k_{m0} & =& c_{m} \frac{\tilde{\alpha}_{m}}{k_{0}} \left[ 1 - \frac{2 \xi_{\alpha_{n}L}^{-}}{\tilde{\alpha}_{m}L} \right] , \\\qquad k_{mn} &=& c_{m} \frac{\tilde{\alpha}_{m}}{\tilde{\beta}_{n}} \frac{4\xi_{\tilde{\alpha}_{m}L}^{-}\tilde{\alpha}_{m}L}{(\alpha_{n}L)^{2}-(\tilde{\alpha}_{m}L)^{2}} . \end{array} $$

(60)

As new functions, we have used $H_{\tilde {\beta }_{n}\beta _{m}}^{+}(y)~=~1~-~\cos \beta _{m}y-G_{\tilde {\beta }_{n}}^{+}(y)$ and $I_{\tilde {\alpha }_{n}\tilde {\alpha }_{m}}(x)~=~G_{\tilde {\alpha }_{n}}^{+}(x)~-~1~-~F_{\tilde {\alpha }_{m}}^{-}(x)/\xi _{\tilde {\alpha }_{m}L}$.