Non-integrally closed Kronecker function rings and integral domains with a unique minimal overring

Abstract

It is well-known that an integrally closed domain D can be expressed as the intersection of its valuation overrings but, if D is not a Prüfer domain, most of the valuation overrings of D cannot be seen as localizations of D. The Kronecker function ring of D is a classical construction of a Prüfer domain which is an overring of D[t], and its localizations at prime ideals are of the form V(t) where V runs through the valuation overrings of D. This fact can be generalized to arbitrary integral domains by expressing them as intersections of overrings which admit a unique minimal overring. In this article we first continue the study of rings admitting a unique minimal overring extending known results obtained in the 1970s and constructing examples where the integral closure is very far from being a valuation domain. Then we extend the definition of Kronecker function ring to the non-integrally closed setting by studying intersections of Nagata rings of the form A(t) for A an integral domain admitting a unique minimal overring.

1 Introduction

Let D be a local, integrally closed integral domain with maximal ideal ${\mathfrak {m}}$ and quotient field K. Let $\alpha \in K$ be such that $\alpha$ and $1/\alpha$ are not in D. A theorem of Seidenberg [36, Theorem 7] indicates that ${\mathfrak {m}}$ extends to a nonmaximal prime ideal in the ring $D[\alpha ]$ and gives details concerning the structure of the maximal ideals of $D[\alpha ]$ which contain ${\mathfrak {m}}$. Here, we only note that there are infinitely many. Clearly, these same results hold for $D[1/\alpha ]$. The fact that D is integrally closed insures that $D[\alpha ] \cap D[1/\alpha ] = D$. We can think of the introduction of $\alpha$ and $1/\alpha$ as being like striking a large crystal (the ring D) with a hammer and shattering it into many smaller pieces.

Of course, the scenario described above does not quite always work. In particular, it is impossible to choose the element $\alpha$ when D is a valuation domain. In accordance with the depiction above, a classical theorem by Krull states that every integrally closed domain is the intersection of all its valuation overrings. For this reason, valuation rings are the indivisible atoms in a canonical decomposition of an integrally closed domain. This makes it seem that valuation rings would be a powerful tool in studying the structure of rings. This is often true, but there are several things that can make it difficult.

First, note that it is hard to describe in a simple way all the valuation overrings of a given ring. For instance, let F be any field. The ring $D = F[x,y]$ of polynomials in two variables has uncountably many valuation overrings, but only few of them are easy to see when looking at the localizations of D. Krull provided an answer to this difficulty. The Kronecker function ring Kr(D) of D is an overring of the polynomial ring D[t] with the property that that there is an easy correspondence between the valuation overrings of D and the localizations of Kr(D) at prime ideals [16, 29, 30]. A second difficulty is harder to overcome. If one is inclined to analyze a ring by the means of studying its valuation overrings, it can be disconcerting to be faced with an integral domain that is not integrally closed. Of course, one can turn to tools of an entirely different nature. The aim of this paper is to generalize the notions of valuation ring and Kronecker function ring to a non-integrally closed setting.

When semistar operations were first introduced one of the major selling points was the possibility of using semistar operations to build a Kronecker function ring for a domain which is not integrally closed [11]. However, in this case the Kronecker function ring that is produced is simply a conventional Kronecker function ring of an integrally closed overring of D. Our real purpose is to produce a non-integrally closed Kronecker function ring which mirrors the non-integrally closed character of D. The first step in such a process is to generalize the notion of a valuation domain. We need two properties to hold for such a generalization.

• We need a generalized valuation ring to actually be a valuation ring if it is integrally closed.

• We need for a domain which is not integrally closed to be equal to the intersection of the generalized valuation rings that contain it.

Suppose now D is not integrally closed. Let $\alpha$ be an element of the quotient field K which is not in D. Let $A_\alpha$ be an overring of D which is maximal with respect to the property of not containing the element $\alpha$. Such a domain exists by application of Zorn’s Lemma and is necessarily local. We call $A_\alpha$ a maximal excluding domain. It has been observed that maximal excluding domains are exactly the integral domains admitting a unique minimal overring in the sense of [17] (see also [20]). This is our proposed notion for a generalization of valuation rings.

The structure of this paper is as follows. Section 2 is devoted to reviewing the already known facts concerning Kronecker function rings and maximal excluding domains. We provide in this section all the needed references.

Section 3 is devoted to constructing examples of maximal excluding domains. Almost all valuation rings are maximal excluding (specifically all those with branched maximal ideal). One might think that this fact, combined with the fact that we are specifically working with rings that are not integrally closed, would mean that the integral closure of a maximal excluding domain is a valuation ring, or at least a Prüfer domain. This is known to not be true [19]. Here we show how to construct maximal excluding domains using generalized power series rings. Our construction is interesting since the maximal excluding domains constructed can be farther from being Prüfer than examples that are already in the literature. We can indeed construct examples that have infinitely many incomparable prime ideals of the same height. We also construct maximal excluding domains of a more ordinary character using pullbacks.

In Sect. 4 we work in earnest on the theory of non-integrally closed Kronecker function rings. In the classical setting we begin with an integrally closed domain D. In this case, the key feature of Kr(D) is that if we localize at any prime ideal we get a ring of the form V(t) where V is a valuation overring of D and V(t) is what is known as the Nagata ring of V. Suppose that D is not integrally closed and is expressed as the intersection of a family of maximal excluding domains. We can define a new generalized version of the Kronecker function ring to be the intersection of the Nagata rings of the maximal excluding domains in this family. We should not expect in this setting to always recover all the maximal excluding domains back by localizing this generalized Kronecker function ring. For example, if the integral closure of D is a Prüfer domain then perhaps we should expect any of these generalized Kronecker function rings to be just equal to the Nagata ring D(t). We prove that this fact holds true in Theorem 4.8. Along the way we also study general properties about whether the operation of Nagata rings extension commutes with intersection of integral domains.

Finally, in Sect. 5 we explore various settings where: we start with a domain D, which is not integrally closed, we express D as an intersection of maximal excluding domains, and we intersect the rings A(t) where A runs through the maximal excluding rings in our collection. We first demonstrate that a localization of this intersection at a maximal ideal has the form C(t) where C is an overring of D (providing also several examples where this ring C is maximal excluding). Then, we demonstrate that the integral closure of this intersection is a classical Kronecker function ring of the integral closure of D. We analyze also a simpler construction of the form $R = Kr({\overline{D}}) \cap A(t)$ where ${\overline{D}}$ is the integral closure of a domain D and $D = {\overline{D}} \cap A$ for A a semilocal overring. We can study the properties of this ring R more in general without requiring A to be maximal excluding. To give examples and applications we involve the maximal excluding rings coming from the constructions in Sect. 3. Furthermore, throughout the paper, we leave several open questions for further research.

2 Preliminaries

We fix our notation for this article and recall all the definitions and results that we will need about Nagata rings, Kronecker function rings, and integral domains maximal with respect to excluding a given element of their quotient field.

All the rings we consider will be integral domains, having the same unit element 1. For an integral domain D, we denote its quotient field by ${\mathcal {Q}}(D)$. If D is local, we denote its unique maximal ideal by ${\mathfrak {m}}_D$. An overring of D is an integral domain A such that $D \subseteq A \subseteq {\mathcal {Q}}(D)$. If A is an overring and A and D are both local, we say that A dominates D if ${\mathfrak {m}}_A \supseteq {\mathfrak {m}}_D$. The set of all valuation overrings dominating D is standardly called Zar(D) (the name comes from Zariski’s definition). Given a valuation overring V we denote by v the associated valuation and by $G_V$ its value group. The integral closure of an integral domain D in a field $F \supseteq {\mathcal {Q}}(D)$ is denoted by ${\overline{D}}^{F}$. If $F = {\mathcal {Q}}(D)$, we simply use the notation ${\overline{D}}$.

2.1 Nagata rings and Kronecker function rings

The main reference we consider for Nagata rings and Kronecker function rings is Gilmer’s book [16]. For an historical introduction we refer to the paper [9] and to its bibliography. These subjects have been widely studied in the last 60 years. There are many other relevant references including [3, 10, 11, 22, 29, 30, 32].

Given an integral domain D and an indeterminate t over the quotient field of D, consider a polynomial $f(t) \in D[t]$. The content of f is the ideal $c(f) \subseteq D$ generated by the coefficients of f. The Nagata ring of D is defined as

$$\begin{aligned} D(t):= \left\{ \frac{f}{g} \,: \, f,g \in D[t], \, c(g)=D \right\} . \end{aligned}$$

This ring is the localization of the ring D[t] at the multiplicatively closed set consisting of the polynomials whose content is equal to the unit ideal.

We will use several known facts about the Nagata ring. When ${\mathfrak {m}}$ is a maximal ideal of D, the extension ${\mathfrak {m}}D(t)$ is a maximal ideal of D(t), and $D(t)_{{\mathfrak {m}}D(t)}= D_{{\mathfrak {m}}}(t)$ (cf. [26, Proposition 2.1]). Therefore, since $D= \bigcap _{{\mathfrak {m}}\subseteq D} D_{{\mathfrak {m}}}$, we get $D(t)= \bigcap _{{\mathfrak {m}}\subseteq D} D_{{\mathfrak {m}}}(t).$ We can thus say that the operation of Nagata ring extension commutes with the intersection of localizations at the maximal ideals. By [18, Theorem 3], Nagata ring extension commutes also with integral closure. We have that the integral closure of D(t) in its quotient field is ${\overline{D}}(t)$.

If V is a valuation domain, the ring V(t) is also a valuation domain, called the trivial extension of v to the field ${\mathcal {Q}}(V)(t)$. The value of a polynomial $f= \sum _{k=0}^n a_k t^k \in {\mathcal {Q}}(V)[t]$ with respect to this valuation is equal to $\textrm{min}_{k=0,\ldots , n} \lbrace v(a_k) \rbrace$.

Let D be an integrally closed domain. By a classical theorem of Krull, $D = \bigcap _{V \in \text{ Zar }(D)} V$. The Kronecker function ring of D can be defined as the intersection

$$\begin{aligned} Kr(D)=\bigcap _{V \in \text{ Zar }(D)} V(t). \end{aligned}$$

In the literature, the definition of Kronecker function ring is commonly given using the e.a.b star operations of the ring D, but for the purpose of this paper, where we study intersections of Nagata rings, we give this as an equivalent definition. It is well-known that the Kronecker function ring of D is always a Bezout domain (indipendently of the properties of D) and its localizations at the prime ideals are all the trivial extensions of the valuation overrings of D. Moreover, $Kr(D) \supseteq D(t)$ and they coincide if and only if D is a Prüfer domain. Given a subset ${\mathcal {F}} \subseteq \textrm{Zar }(D)$ such that $D = \bigcap _{V \in {\mathcal {F}}} V$, one can define another ring $Kr^{{\mathcal {F}}}(D)=\bigcap _{V \in {\mathcal {F}}} V(t).$ This last ring is an overring of the Kronecker function ring Kr(D). Also these overrings $Kr^{{\mathcal {F}}}(D)$ are commonly called Kronecker function rings of D.

2.2 Integral domains maximal with respect to excluding an element of their quotient field

In this paper we are interested in studying intersections of Nagata rings of overrings of an integral domain. For this reason we need to understand the properties of those integral domains which cannot be expressed as intersections of proper overrings. These rings have been already considered in the literature. Gilmer and Heinzer [17] consider integral domains admitting a unique minimal overring, in the sense that an integral domain D has an overring A such that for any other overring B of D there are inclusions $D \subseteq A \subseteq B$. Several properties of these domains have been studied in [17, 20] and other papers, but generally these rings are still quite mysterious and difficult to identify (in the case they are not integrally closed). It is observed that an integral domain D admits a unique minimal overring in the sense of Gilmer and Heinzer if and only if it is maximal with respect to the property of not containing some element $\alpha \in {\mathcal {Q}}(D)$ (obviously if D is maximal with respect to excluding $\alpha$, then $D[\alpha ]$ is the unique minimal overring of D). Clearly these properties are also equivalent to the fact that D cannot be written as an intersection of proper overrings. In particular, any such ring D has to be local and its maximal ideal a t-ideal (see [13] for information about the star operation t). It is also easy to observe that any integral domain can be written as the intersection of its overrings that are maximal with respect to excluding some element of the quotient field.

Papick [33] consider a slightly weaker notion of unique minimal overring. To avoid confusion with this notion we call an integral domain maximal with respect to excluding an element of its quotient field, a maximal excluding domain. For a survey about this topic and about the more general concept of minimal ring extensions we refer to [34].

If not otherwise specified, the proofs of all the results that we mention in the following paragraphs can be found in [17, 20]. The first important known fact is that an integrally closed maximal excluding domain is necessarily a valuation domain with branched maximal ideal (in particular any valuation domain of finite dimension is maximal excluding). Another relevant class of maximal excluding domains, not necessarily integrally closed, is the class of local domains such that every ideal is divisorial, for instance local Gorenstein noetherian domains of dimension one (cf. [5, 12, 24]).

If a domain D, maximal with respect to excluding an element $\alpha$, is not integrally closed, then the unique minimal overring $D[\alpha ]$ is an integral extension of D and is semilocal with at most two maximal ideals. Furthermore, ${\mathfrak {m}}_DD[\alpha ] \subseteq D$.

If $D[\alpha ]$ has exactly two maximal ideals, then the integral closure of D is a Prüfer domain obtained as the intersection of two valuation rings. In this case, if $D[\alpha ]= {\overline{D}}$, the structure of D has been described in [25, Theorem 14] with the use of pullback diagrams. Also if the maximal ideal ${\mathfrak {m}}_D$ of D coincides with the maximal ideal of $D[\alpha ]$, then the integral closure of D is a valuation overring V of D such that ${\mathfrak {m}}_V = {\mathfrak {m}}_D$. In the case $D[\alpha ]$ is local and its maximal ideal is strictly larger than ${\mathfrak {m}}_D$, the integral closure of D may not be a Prüfer domain. The most known example of this situation is the subject of the paper [19]. In this case D is one-dimensional and its integral closure is a PVD but not a valuation domain (a PVD is a local domain sharing its maximal ideal with a valuation overring [23]). A similar example appears here as Example 3.8.

Many questions about non-integrally closed maximal excluding domains are still open. Already in [25], one can find examples of maximal excluding domains whose prime ideals are not linearly ordered (but the integral closure is a Prüfer domain). In Sect. 3 of this paper we show that a maximal excluding domain of dimension at least 2 can have infinitely many prime ideals of the same height and its integral closure may not even be a PVD (see Theorem 3.13, Example 3.14).

The complete integral closure of a domain D is the ring of the elements $x \in {\mathcal {Q}}(D)$ for which there exists $d \in D$ such that $dx^n \in D$ for every $n \ge 1$. The complete integral closure of the example described by Gilmer and Hoffmann [19] is a valuation domain. The same happens for the classes of maximal excluding domains that we consider here in Sect. 3. We leave the following open questions.

Question 2.1

Let D be a maximal excluding domain. Is the complete integral closure of D always a Prüfer domain? If D is one-dimensional and ${\overline{D}}$ is local, is ${\overline{D}}$ a PVD?

3 Constructions of maximal excluding domains

In this section we characterize maximal excluding domains that can be obtained as pullbacks and as generalized power series rings over a field, defined by submonoids of the positive part of a totally ordered abelian group. In both cases, as a consequence of Theorems 3.1 and 3.10, we get that the complete integral closures of the rings in these families are valuation rings.

3.1 Maximal excluding domains obtained as pullbacks

Let T be a local domain with maximal ideal ${\mathfrak {m}}$ and let B be an integral domain having quotient field $\kappa := \frac{T}{{\mathfrak {m}}}.$ Let $\phi : T \rightarrow \kappa$ be the canonical surjective map. Define the ring $D:= \phi ^{-1}(B)$ as in the pullback diagram:

For exhaustive information about the properties of rings of this form the reader may consult [8, 14,15,16].

Theorem 3.1

The integral domain D is maximal excluding if and only if B is maximal excluding and T is a valution domain.

Proof

First suppose that B is not maximal excluding. Thus, there are two proper overrings $B_1, B_2$ of B such that $B= B_1 \cap B_2$. It follows that $D = \phi ^{-1}(B_1) \cap \phi ^{-1}(B_2)$ is an intersection of two proper overrings, hence is not maximal excluding.

Thus, suppose that B is maximal excluding with unique minimal overring $B[\alpha ']$. Let $\alpha$ be an element of T such that $\phi (\alpha ) = \alpha '.$ Clearly $\alpha$ is a unit in T.

Assume that T is a valuation ring and pick $z \in {\mathcal {Q}}(D) {\setminus } D$. In particular $z \not \in {\mathfrak {m}}$. We need to show that $\alpha \in D[z]$. If $z \not \in T$ then, $\frac{1}{z} \in {\mathfrak {m}}\subseteq D$. It follows that $\frac{\alpha }{z} \in {\mathfrak {m}}\subseteq D$ and $\alpha = z \frac{\alpha }{z} \in D[z]$. Next assume z to be a unit in T. Therefore $\phi (z) \in \kappa$. Since B is maximal excluding, we get $\alpha ' \in B[\phi (z)]$. Since ${\mathfrak {m}}\subseteq D$, we get $\alpha \in \phi ^{-1}(B[\phi (z)]) = D[z].$

Finally consider the case where T is not a valuation domain. Let V be a valuation overring of T such that ${\mathfrak {m}}\subseteq {\mathfrak {m}}_V$. By way of contradiction suppose that D is maximal with respect to excluding an element $\beta$. We must have $\beta \in D[\alpha ] \subseteq T$. If there exists $z \in {\mathfrak {m}}_V {\setminus } {\mathfrak {m}}$, then we find the contradiction $\beta \not \in D[z]$. Indeed, if $\beta \in D[z]$, then there exists $d_0 \in D$ such that $\beta - d_0 = z(d_1 + zd_2 + \cdots + z^{n-1}d_n) \in {\mathfrak {m}}_V \cap T = {\mathfrak {m}}\subseteq D$. This is a contradiction since $\beta \not \in D$. If instead ${\mathfrak {m}}_V = {\mathfrak {m}}$, let $\phi '$ be the canonical quotient map $V \rightarrow V/{\mathfrak {m}}_V$. Observe that $\phi '|_T = \phi$ and the image of $\phi '$ is a proper field extension of $\kappa$. We show that there exists an element $z \in V {\setminus } T$ such that $\kappa (\phi '(z)) \supsetneq \kappa$ and $\beta \not \in D[z]$. Setting $\theta := \phi '(z)$ for some $z \in V {\setminus } T$, this is equivalent to showing that $\alpha ' \not \in B[\theta ]$. If $\theta$ is transcendental over $\kappa$, this is obvious. If it is algebraic, let us assume it to be of degree n. Let f be the minimal polynomial of $\theta$ over F. Using that $\kappa$ is the quotient field of B, we can find $b \in B$ such that the constant term of the minimal polynomial of $b \theta$, which is equal to $b^nf(0)$, is in B. Replace $\theta$ by $b\theta$ to have $f(0) \in B$. Assume there exists a relation $\alpha ' = b_0 + b_1 \theta + b_2 \theta ^2 + \cdots + b_{t} \theta ^{t}$. For $k \ge n,$ using the relation given by $f(\theta )=0$, the term $\theta ^{k}$ can be replaced by a linear combination of $\theta , \ldots , \theta ^{n-1}$ with coefficient in $\kappa$ and constant term in B. This yields another equation of algebraic dependence of $\theta$ over $\kappa$ of degree at most $n-1$ but with constant term not in B. This is a contradiction. $\square$

Corollary 3.2

Consider the same notation of the previous theorem but assume that B is a field and $\kappa$ a field extension of B. Then D is maximal excluding if and only if T is a valuation domain and the extension $\kappa /B$ is a minimal field extension.

Proof

The condition that $\kappa /B$ is a minimal field extension is clearly necessary. The other conditions can be proved exactly as in Theorem 3.1 choosing $\alpha '$ to be any element of $\kappa {\setminus } B$. $\square$

3.2 Maximal excluding domains in generalized power series rings

In the following G will denote a totally ordered abelian group (with additive notation and order relation $\le$), ${\varvec{0}}$ will denote its unit element and $G_{\ge {\varvec{0}}}$ the subsemigroup of elements of G larger than or equal to ${\varvec{0}}$. We consider a family of generalized power series rings, defined according to [6]. The literature about generalized power series rings is very extensive, an interested reader can consult also [27, 28, 35] and several other papers by P. Ribemboim and other authors.

Let S be a subsemigroup of $G_{\ge {\varvec{0}}}$ containing ${\varvec{0}}$. A subset A of S is Artinian if it does not contain any infinite descending sequence of elements with respect to $\le$ (equivalently, if A admits a minimal element). Let K be any field. The generalized power series ring $[[K^S]]$ is defined formally as the set of all the maps $S \rightarrow K$ such that the set $\text{ supp }(f):= \lbrace s \in S \, | \, f(s) \ne 0 \rbrace$ is Artinian. The operations on this ring are pointwise addition and the convolution product defined as in [6, Section 2]. The ring $[[K^S]]$ is a commutative integral domain with unit element equal to the map e such that $e({\varvec{0}})= 1$ and $e(s)= 0$ for $s \ne {\varvec{0}}$. Notice that in [6] and in the subsequent papers, the authors consider a more general case of this construction where the group G is not necessarily totally ordered and K is replaced by an arbitrary commutative ring R. The classical semigroup ring $K[X^s, s \in S]$ can be embedded canonically in $[[K^S]]$ sending the homogeneous element $X^s$ to the map f such that $f(s)=1$ and $f(g) = 0$ for every $g \ne s$. For simplicity of notation we also denote the image of this element in $[[K^S]]$ by $X^s$ and we say that these elements are monomial elements. A general element of $[[K^S]]$ can be now expressed as a possibly infinite sum $f= \sum _{s \in S} u_s X^s$ with $u_s \in K$ and such that $\text{ supp }(f)$ is Artinian. The units of $[[K^S]]$ can be described using [6, Proposition 5] (which is based on a result proved in [21]). It turns out that f is a unit if and only if $f({\varvec{0}})$ is a nonzero element of K. This fact makes $[[K^S]]$ a local domain. It is easy to observe that, if $S = G_{\ge {\varvec{0}}}$, the ring $[[K^{G_{\ge {\varvec{0}}}}]]$ is a valuation domain with value group G and the value of an element $f \in [[K^{G_{\ge {\varvec{0}}}}]]$ is exactly the minimal element of $\text{ supp }(f)$. Let us set $V:= [[K^{G_{\ge {\varvec{0}}}}]]$.

We want to describe the maximal excluding domains of the form $[[K^S]]$ with $S \subseteq G_{\ge {\varvec{0}}}$. In the following we always assume that $[[K^S]]$ and V have the same quotient field. The first result we prove is inspired by the case $G= {\mathbb {Z}}$ which has been considered. If $G= {\mathbb {Z}}$, V is isomorphic to a standard power series ring in one variable over a the field K. The set S is a numerical semigroup and the subring $[[K^S]]$ is maximal excluding if and only if S is symmetric or pseudo-symmetric (cf. [12, 4, Lemma I.1.9]).

Theorem 3.3

Let S be a proper submonoid of $G_{\ge {\varvec{0}}}$ and let $D:= [[K^S]] \subsetneq V$. Assume that D and V have the same quotient field. Take $a \in G_{\ge {\varvec{0}}} {\setminus } S$. The following conditions are equivalent:

• (1) D is maximal with respect to excluding the element $X^a$.

• (2) For every $g \in G$, $g \ne \frac{a}{2}$, $X^g \in D$ if and only if $X^{a-g} \not \in D$.

Proof

Let v be the valuation associated to V and call ${\mathfrak {m}}_V$ the maximal ideal of V. Assume D to be maximal with respect to excluding the element $y= X^a$. Let us first show that $y{\mathfrak {m}}_V \subseteq D$. If there exists $z \in y{\mathfrak {m}}_V {\setminus } D$, then by definition of maximal excluding domain $y = d_0 + d_1z + \cdots + d_n z^n$ with $d_0, \ldots , d_n \in D$. Hence $v(y-d_0) \ge v(z)> v(y)$, implying that $d_0$ is an element of D of value $v(y)=a$. This is a contradiction. It follows that if $g > a$, then $X^{g} \in D$ and if $g < {\varvec{0}}$, then $X^{a-g} \in D$.

Consider now $g \in G$ such that ${\varvec{0}}< g < a$ and $2g \ne a$. If both $X^{g}, X^{a-g} \in D$, then $y =X^{g} X^{a-g} \in D$, contradicting the assumption. Suppose both $X^{g}, X^{a-g} \not \in D$. In this case we show that one among $D[X^{g}]$ and $D[X^{a-g}]$ is an overring of D not containing y. Suppose $y \in D[X^{g}]$. Hence

$$\begin{aligned} X^a = d_0 + d_1 X^{g} + d_2 X^{2g} + \cdots + d_n X^{ng}, \end{aligned}$$

with $d_0, \ldots , d_n \in D$. Using that $X^g \in D$ for every $g > a$, if $2g > a$ the equation reduces to $X^a = d_0 + d_1 X^g$. But this yields a contradiction since no term of $d_1$ can contain $X^{a-g}$ and no term of $d_0$ can contain $X^{a}$. If instead $2g < a$, we obtain that $y \not \in D[X^{a-g}]$. For this write

$$\begin{aligned} X^a = c_0 + c_1 X^{a-g} + c_2 X^{2a-2g} + \cdots + c_n X^{na-ng}, \end{aligned}$$

with $c_0, \ldots , c_n \in D$. Now observe that $2a-2g > a$ and conclude in the same way as before.

Assume now condition (2) and prove that D is maximal with respect to excluding y. Using that D is a subring of V, we know that D cannot contain $X^g$ with $g < 0$. Hence $X^g \in D$ for every $g > a$. In particular D contains all the elements of V of value larger than a, thus $y{\mathfrak {m}}_V \subseteq D$.

Let z be an element of the quotient field of D. We want to show that $y \in D[z]$. In the case $z \not \in V$, we get $\frac{y}{z} \in y{\mathfrak {m}}_V \subseteq D$. Thus $y = z \frac{y}{z} \in D[z]$. Otherwise, pick $z \in V {\setminus } D$. By subtracting elements of D, we reduce to the case where $v(z)= \text{ min } \text{ supp }(z)\in G_{\ge {\varvec{0}}} {\setminus } S.$ Set $b:=v(z)$. Then $z = uX^b + h$ with $u \in K$ and $v(h)> b$. By hypothesis $X^{a-b} \in D$, hence $X^{a-b}z = uy+h' \in D[z]$. But $v(h')> (a-b)+b=a$, implying $h' \in D$. It follows that $y \in D[z]$. $\square$

Example 3.4

Let G be equal to the additive group of real numbers $({\mathbb {R}}, +)$ and set $V= [[K^{G_{\ge {\varvec{0}}}}]]$. Let a be a positive real number. Set

$$\begin{aligned} S= \lbrace {\varvec{0}} \rbrace \cup \left\{ g \in G \, | \, \frac{a}{2}< g < a \right\} \cup \lbrace g \in G \, | \, g > a \rbrace . \end{aligned}$$

Clearly S is a monoid contained in $G_{\ge {\varvec{0}}}$ and every real number can be obtained as the difference of two elements in S. Thus the ring $D:= [[K^S]]$ has the same quotient field as V. By Theorem 3.3, D is maximal excluding with unique minimal overring $D[X^a]$. It is easy to check that the integral closure of D is V (for a precise proof see Corollary 3.6).

Before presenting more examples we describe how to compute the integral closure of certain domains of the form $[[K^S]]$. This result is similar to the corresponding case for semigroup rings, where the integral closure coincides with the root closure, see [1, 2]. For this, we need to introduce some new notation and from now on we assume $\dim (V)= n < \infty$. Write the group $G \cong G_1 \oplus \cdots \oplus G_n$. For $i=1, \ldots , n$ define the semigroup

$$\begin{aligned} \widehat{G_i}= \lbrace (g_1, \ldots , g_n) \in G \, | \, g_k = 0 \text{ for } k < i \text{ and } g_i > 0 \rbrace \subseteq G_{\ge {\varvec{0}}}. \end{aligned}$$

Set also $\widehat{G_0} = \lbrace {\varvec{0}} \rbrace$. Observe that $G_{\ge {\varvec{0}}}= \bigcup _{i=0}^n \widehat{G_i}$ and $\widehat{G_i} + \widehat{G_j} \subseteq {\widehat{G}}_{\textrm{min}(i,j)}$ for any i, j. Denote by ${\mathfrak {q}}_i$ the prime ideal of V of height i. Then $g \in \widehat{G_i}$ if and only if $X^g \in {\mathfrak {q}}_i {\setminus } {\mathfrak {q}}_{i-1}.$ Given any submonoid S of $G_{\ge {\varvec{0}}}$, we define $S_i:= S \cap \widehat{G_i}$. Clearly $S= \bigcup _{i=0}^n S_i$. Define also

$$\begin{aligned} {\overline{S}}:= \bigcup _{n \in {\mathbb {N}}} \lbrace g \in G \, | \, ng \in S \rbrace . \end{aligned}$$

Also ${\overline{S}}$ is a monoid contained in $G_{\ge {\varvec{0}}}$. It is straightforward to see that for every $i=1, \ldots , n$, $\overline{S_i}= {\overline{S}} \cap \widehat{G_i}$.

Proposition 3.5

Let $G \cong G_1 \oplus \cdots \oplus G_n$ be a totally ordered abelian group of finite rank. Let S be a proper submonoid of $G_{\ge {\varvec{0}}}$ such that $G= \langle S \rangle$. Let $D:= [[K^S]].$ Suppose that for every $i=1, \ldots , n$, there exists $a_i \in S_i$ such that $\lbrace g \in \overline{S_i} \, | \, g \ge a_i \rbrace \subseteq S_i.$ Suppose also that the ring $R = [[K^{{\overline{S}}}]]$ is integrally closed. Then R is the integral closure of D.

Proof

For $f \in R$, we show that f is integral over D. We can write $f= f_1+ \cdots + f_n$ in such a way that the support of $f_i$ is in $\overline{S_i} \cup \lbrace {\varvec{0}} \rbrace$. It is sufficient to show that any $f_i$ is integral over D. But for this, if $g_i$ is the minimum of the support of $f_i$, by the Archimedean property of real numbers, applied in the component $G_i$ of G, one can find a positive integer $e_i$ such that $e_ig_i \ge a_i$. In this way by assumption we get $f_i^{e_i} \in D$. $\square$

We will apply this proposition to study the integral closure of the domains defined in Examples 3.7, 3.8, 3.14. Moreover we can immediately use it to describe the integral closure in the case when V is one-dimensional, as for instance in Example 3.4.

Corollary 3.6

Let G be a subgroup of the additive group of real numbers $({\mathbb {R}}, +)$. Let S be a submonoid of $G_{\ge {\varvec{0}}}$ and let $D:= [[K^S]] \subseteq V:= [[K^{G_{\ge {\varvec{0}}}}]]$ (notice that $\dim (V)=1$). Suppose that D is maximal excluding and D and V have the same quotient field. Then V is the integral closure of D.

Proof

By Theorem 3.3, there exists $a \in G_{\ge {\varvec{0}}}$ such that $g \in S$, for every $g > a$. Given $s \in G_{\ge {\varvec{0}}}$, there exists some $n \in {\mathbb {N}}$ such that $ns > a$. Hence, ${\overline{S}} = G_{\ge {\varvec{0}}}$ and V is the integral closure of D by Proposition 3.5. $\square$

In the next two examples the valuation ring V has dimension 2.

Example 3.7

Let $G= {\mathbb {Z}}\times {\mathbb {Z}}$, ordered by lexicographic order, and let $V= [[K^{G_{\ge {\varvec{0}}}}]].$ Call X the monomial element of V of value (0, 1) and Y the monomial element of V of value (1, 0). The ring $V= K[[X]]+YK((X))[[Y]]$ is a discrete valuation ring of rank 2. Consider the submonoid

$$\begin{aligned} S= \left\{ (0,n) \, | \, n \ge 0 \right\} \cup \left\{ (1,n) \, | \, n \ge 1 \right\} \cup \left\{ (m,n) \, | \, m \ge 2, n \in {\mathbb {Z}}\right\} \subseteq G_{\ge {\varvec{0}}}. \end{aligned}$$

By Theorem 3.3 the ring $D= [[K^S]]= K[[Y{\mathfrak {m}}_V, X]]$ is maximal excluding with unique minimal overring D[Y]. The integral closure is clearly V by Proposition 3.5. Indeed, $S_2= \widehat{G_2}$ and $2(1,n) \in S_1$ for every $n \in {\mathbb {Z}}$. By an analogous argument also the ring D[Y] is maximal excluding with unique minimal overring $D[\frac{Y}{X}]$. Iterating, we observe that there exists an infinite ascending chain

$$\begin{aligned} D \subseteq D[Y] \subseteq D\left[ \frac{Y}{X}\right] \subseteq D\left[ \frac{Y}{X^2}\right] \subseteq \cdots \subseteq \bigcup _{n=0}^{\infty }D\left[ \frac{Y}{X^n}\right] = V, \end{aligned}$$

such that each ring is maximal excluding, the next one is the unique minimal overring, and the integral closure of all these ring is V. In this example, the ring D has dimension 2 and two nonzero prime ideals. The maximal ideal ${\mathfrak {m}}$ is generated by X and YX, the height one prime is $P= {\mathfrak {p}}\cap D$ where ${\mathfrak {p}}$ is the height one prime of V. The quotient D/P is a DVR with maximal ideal generated by the image of X. The localization $D_P$ coincides with the localization $V_{{\mathfrak {p}}}$. The quotient ring D/(X) is an Artinian ring having dimension 2 as K-vector space.

Example 3.8

This example is a sort of dual of the previous one. Again let $G= {\mathbb {Z}}\times {\mathbb {Z}}$, ordered by lexicographic order, let $V= [[K^{G_{\ge {\varvec{0}}}}]]$ and define X, Y as in Example 3.7. Set

$$\begin{aligned} S= \left\{ (0,0) \right\} \cup \left\{ (1,n) \, | \, n \in {\mathbb {Z}}{\setminus } \lbrace 0 \rbrace \right\} \cup \left\{ (m,n) \, | \, m \ge 2, n \in {\mathbb {Z}}\right\} \subseteq G_{\ge {\varvec{0}}}. \end{aligned}$$

It is easy to check that S is a monoid. The ring $D= [[K^S]]= K[[Y{\mathfrak {m}}_V, \frac{Y}{X}, \frac{Y}{X^2}, \ldots ]]$ is maximal excluding by Theorem 3.3 and the unique minimal overring is D[Y]. We notice that this ring D[Y] is equal to $K + YK((X))[[Y]]$, thus it is an integrally closed PVD but not a valuation domain ($X, X^{-1} \not \in D[Y]$). By Proposition 3.5, we observe that D[Y] is the integral closure of D. Indeed, Y is clearly integral over D while all the powers of X are not integral since for every $m, n \in {\mathbb {N}}$, $m(0, n) = (0, mn) \not \in S$ (hence $\overline{S_2}= S_2 = \emptyset$). Let W be the rank one valuation overring of V. The maximal ideal of W coincides with the height one prime ${\mathfrak {p}}$ of V and is also equal to the maximal ideal ${\mathfrak {m}}$ of D[Y]. Hence, in this example D is one-dimensional and its complete integral closure W is a valuation domain. This example is similar to the Gilmer–Hoffmann construction which appears in [19].

Remark 3.9

Consider the same notation used earlier through this section and assume V to have finite dimension. In the next part of this section we can always reduce to assuming that, if D is maximal excluding with unique minimal overring D[Y], then Y is an element of the height one prime of V. Indeed, given any non-maximal prime ideal ${\mathfrak {q}}$ of V, it is well-known that V is the pullback of the valuation ring $V/{\mathfrak {q}}$ with respect to the quotient map from $V_{{\mathfrak {q}}}$ to its residue field. The ring $V/{\mathfrak {q}}$ is maximal excluding, hence if the ideal YV has height $i > 1$, we can choose ${\mathfrak {q}}$ to be the prime ideal of height $i-1$ and apply Theorem 3.1, reducing to the case where the height of YV is 1.

In all the above examples, the complete integral closure of D is the rank one valuation overring of V. We prove now that this happens in general for all the maximal excluding rings in this family, provided that they share the same quotient field with V and V has finitely many prime ideals.

Theorem 3.10

Let S be a submonoid of $G_{\ge {\varvec{0}}}$ and let $D:= [[K^S]] \subseteq V= [[K^{G_{\ge {\varvec{0}}}}]]$. Suppose that D is maximal excluding, D and V have the same quotient field, and V has finite dimension. Then the rank one valuation overring W of V is the complete integral closure of D.

Proof

The ring W is completely integrally closed. Hence, it is sufficient to show that every element of W is almost integral over D. If $\dim (V)=1$, then $V=W$ and the result follows by Corollary 3.6. Assume $\dim (V) \ge 2$ and let ${\mathfrak {p}}$ be the height one prime ideal of V, which coincides with the maximal ideal of W. We can write $G \cong G_W \oplus G_{V/{\mathfrak {p}}}$ where $G_W$ is the rank one value group associated to W and $G_{V/{\mathfrak {p}}}$ is the value group of the valuation ring $V/{\mathfrak {p}}$.

Say that the unique minimal overring of D is D[y] with $y \in {\mathfrak {m}}_V$. Let $v(y)= (a_1, a_2)$ with $a_1 \ge 0$. Choose $f \in {\mathfrak {p}}$ such that $v(f) = (s_1, s_2)$ with $s_1 > a_1$. In particular $v(f) > v(y)$. Since by Theorem 3.3, $y{\mathfrak {m}}_V \subseteq D$ we get $f \in D$. Pick $h \in W$. If $h \in V$, then for every $n \ge 1$, $v(h^nf) \ge v(f) > v(y)$. If $h \not \in V$, then $v(h)= (0, -g)$, for g a positive element of $G_{V/{\mathfrak {p}}}$. Thus $v(h^nf) = (s_1, -ng+s_2) > (a_1, a_2) = v(y)$. In both cases this implies $h^nf \in D$. $\square$

We now analyze further the integral closure of $[[K^S]]$ to show that the integral closure of a maximal excluding domain can be very far from being Prüfer. We show that it does not even need to be a PVD and can have infinitely many incomparable prime ideals. For this, we assume $1< \dim (V)= n < \infty$. In the following, we let the semigroups $\widehat{G_i}$ and $S_i$ for $i=1, \ldots , n$ be defined as earlier in this section. We show how given arbitrary $S_2, \ldots , S_n$ we can construct a monoid S such that $D= [[K^S]]$ is maximal excluding. By Remark 3.9 we can restrict to consider only the case where the excluded element is in the height one prime of V.

Lemma 3.11

Let $G\cong G_1 \oplus \cdots \oplus G_n$ be a totally ordered abelian group of rank $n > 1$. For each $i=2, \ldots , n$, fix a (possibly empty) semigroup $S_i \subseteq \widehat{G_i}$. Suppose that $S_i + S_j \subseteq S_{\textrm{min}(i,j)}$ for any $i, j = 2, \ldots , n$. Also set $S_0:= \widehat{G_0} = \lbrace {\varvec{0}} \rbrace$. Then, it is possible to construct $S_1 \subseteq \widehat{G_1}$ such that $S:= \bigcup _{i=0}^n S_i$ is a monoid and the ring $D= [[K^S]]$ is maximal excluding. Moreover, D has the same quotient field of $V= [[K^{G_{\ge {\varvec{0}}}}]]$.

Proof

Fix $a= (a_1, \ldots , a_n) \in \widehat{G_1}$ (in particular $a_1 > 0$). Define $S_1 = S_1' \cup S_1'' \cup S_1^*$ where

$$\begin{aligned} S_1' = \lbrace g \in \widehat{G_1} \, | \, g > a \rbrace , \quad S_1'' = \lbrace g \in \widehat{G_1} \, | \, g < a, \, g_1= a_1, \text{ and } a-g \not \in S_2 \cup \cdots \cup S_n \rbrace , \end{aligned}$$

and $S_1^* \subseteq \lbrace g \in \widehat{G_1} \, | \, g_1 < a_1 \rbrace$ is empty if $\lbrace g \in \widehat{G_1} \, | \, g_1 < a_1 \rbrace = \emptyset$ or otherwise is constructed in such a way that:

• $g \in S_1^*$ if and only if $a-g \not \in S_1^*$.

• $S_1^* + S_1^* \subseteq S_1$.

• $S_j + S_1^* \subseteq S_1^*$ for every $j=2, \ldots , n$.

To get some ideas on how one can concretely construct such $S_1^*$ see Remark 3.12. We prove now that S is a monoid.

We have to show that for every $j=1, \ldots , n$, the set $S_j + S_1 \subseteq S_1$. Clearly $S_j + S_1' \subseteq S_1'$ for every j. Also $(S_1''+ S_1'') \cup (S_1''+ S_1^*) \subseteq S_1'$. By the hypothesis on $S_1^*$, to conclude we only need to check the inclusion $S_j + S_1'' \subseteq S_1$ for $j \ge 2$. Pick $g = (0, \ldots , 0, g_j, \ldots , g_n) \in S_j$ and $h=(a_1, h_2, \ldots , h_n) \in S_1''$. If $g+h > a$, then $g+h \in S_1' \subseteq S_1$. We cannot have $g+h=a$ since this would contradict the definition of $S_1''$. Hence, suppose $g+h < a$ and let us show that $g+h \in S_1''$. If by way of contradiction $a-(g+h) \in S_2 \cup \cdots \cup S_n$, we would have

$$\begin{aligned} a-h= g + (a-g-h) \in S_j + (S_2 \cup \cdots \cup S_n) \subseteq (S_2 \cup \cdots \cup S_n). \end{aligned}$$

Also this contradicts the definition of $S_1''$ and shows that S is a monoid.

Set $D: = [[K^S]]$. By construction $X^{2a}, X^{3a}$ are in D, hence $X^{-a}$ is in the quotient field of D. For every $g \in G_{\ge {\varvec{0}}}$, $X^{g} = X^{a+g} X^{-a}$. This implies that D has the same quotient field as V. Using Theorem 3.3, it is straightforward to check that D is maximal with respect to excluding the element $X^a$. $\square$

Remark 3.12

For the purpose of constructing examples, the conditions defining the set $S_1^*$ in the above proof are not very explicit. A good way to satisfy the third condition is assuming that, if $g_1 >0$, for every $g_2, \ldots , g_n$, the element $g=(g_1, g_2, \ldots , g_n) \in S_1^*$ if and only if $(g_1, 0, \ldots , 0) \in S_1^*$. For the first two conditions, one can choose a set such that the projection on the first component behaves as the set described in Example 3.4. An easier assumption, which can still produce many nice examples, is the following: set $G_1 = {\mathbb {Z}}$ and $a=(1, 0, \ldots , 0)$. In this way the set $S_1^* = \emptyset$ and the proof of Lemma 3.11 can be simplified. However, there are other possible choices to construct a set $S_1^*$ satisfying the required conditions.

We now prove the main theorem concerning the rings which occur as integral closure of a maximal excluding domain of the form $D= [[K^S]]$.

The notation for the next theorem is slightly different from that used until now. Let $n >1$ and let $G' \cong G_2 \oplus \cdots \oplus G_n$ be a totally ordered abelian group. Set $V':=[[K^{G'_{\ge 0}}]]$. Let H be any submonoid of $G'_{\ge 0}$ such that ${\overline{H}}=H$ and suppose that $A =[[K^H]] \subseteq V'$ is integrally closed and A and $V'$ have the same quotient field. Given another totally ordered abelian group $G_1$ of rank one, set $G:= G_1 \oplus G'.$ Define $V:=[[K^{G_{\ge {\varvec{0}}}}]]$. Let W be the rank one valuation overring of V and $\kappa$ be the residue field of W. Observe that by quotienting G with respect to $G_1$, the quotient field of $V'$ and A can be identified with $\kappa$ and V is the pullback of $V'$ with respect to the map $W \rightarrow \kappa$.

Theorem 3.13

With the notation and the assumptions stated above, there exists a submonoid S of $G_{\ge {\varvec{0}}}$ such that:

• (i) The ring $D =[[K^S]] \subseteq V$ is maximal excluding and has the same quotient field as V.

• (ii) The integral closure ${\overline{D}}$ of D occurs as the pullback in the following diagram:

  

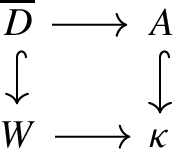
Conversely, if $D=[[K^{S'}]]\subseteq V$ is a maximal excluding domain having the same quotient field as V, then the integral closure of D is the pullback of some integrally closed local domain $A'$ with respect to the quotient map $W \rightarrow \kappa$.

Proof

For $i=0, \ldots , n$, define $\widehat{G_i}$ and $\widehat{G'_i}$ as above in this section. Decompose H as the union $H= H_0 \cup \bigcup _{i=2}^n H_i$, where $H_i = H \cap \widehat{G'_i}$. Since for $i \ge 2$ there exists a bijective map between $\widehat{G_i}$ and $\widehat{G'_i}$, we can identify $H_i$ with a subsemigroup of $\widehat{G_i}$.

To construct S, set $S_0= \lbrace {\varvec{0}} \rbrace$ and for $i=2, \ldots , n$, define $S_i = H_i$. Since H is a monoid, the semigroups $S_2, \ldots , S_n$ defined in this way obviously satisfy the hypothesis of Lemma 3.11. Use Lemma 3.11 to produce $S_1 \subseteq \widehat{G_1}$ such that $S:= \bigcup _{i=0}^n S_i$ is a monoid and the ring $D= [[K^S]]$ satisfies condition (i).

By construction, the ring D is maximal with respect to excluding an element $a \in \widehat{G_1}$ and the set $\lbrace g \in \widehat{G_1} \, | \, g > a \rbrace \subseteq S$. Given $g \in \widehat{G_1}$, since $G_1$ has rank one, there exists $n \ge 1$ such that $ng > a$. Thus $\overline{S_1}= \widehat{G_1}$. Clearly, ${\overline{S}}= \widehat{G_1} \cup H$ and $[[K^{{\overline{S}}}]]$ is integrally closed by standard properties of pullback diagrams. By Proposition 3.5, ${\overline{D}}= [[K^{{\overline{S}}}]]$. Let $\pi : W \rightarrow \kappa$ be the canonical quotient map. We show that ${\overline{D}} = \pi ^{-1}(A)$. Observe that, given $g \in G$, $\pi (X^g)=0$ if and only if $g_1 > 0$ and if $g_1 = 0$, $\pi (X^g)= X^{g'}$ where $g'$ is the component of g in $G'$. It easily follows that $\pi ({\overline{D}}) = A$. Since $\text{ ker }(\pi ) \subseteq {\overline{D}}$, we obtain ${\overline{D}} = \pi ^{-1}(A)$ and finally prove (ii).

Conversely, if $D=[[K^{S'}]]\subseteq V$ is a maximal excluding domain having the same quotient field as V, by Remark 3.9, we can assume D maximal with respect to excluding an element $X^a$ with $a \in \widehat{G_1}$. Using Theorem 3.3 and the same argument as above we get $\overline{S_1'} = \widehat{G_1}$. The thesis now follows setting $H':= \bigcup _{i=2}^n \overline{S_i} \cup \lbrace {\varvec{0}} \rbrace$ and letting $A'$ be the integral closure of $[[K^{H'}]]$. $\square$

The next example shows that both D and its integral closure can have infinitely many incomparable prime ideals.

Example 3.14

Using the notation of Theorem 3.13, let $G'= G_2 = {\mathbb {Z}}[\sqrt{2}]$ and $G_1= {\mathbb {Z}}$. Choose

$$\begin{aligned} H = \lbrace a+b\sqrt{2}, \, | \, a, b \ge 0 \rbrace \subseteq G'_{\ge 0}. \end{aligned}$$

We notice that $H= {\overline{H}}$. Indeed, if for some $n \ge 1$ and $a,b,c,d \in {\mathbb {Z}}$, $n(c+d\sqrt{2}) = a+\sqrt{2}b \in H$, using the irrationality of $\sqrt{2}$, we must have $nc=a$ and $nd=b$, forcing $c,d \ge 0$.

Define X to be the monomial element of V of value (0, 1) and Z to be the monomial element of V of value $(0,\sqrt{2})$. The ring $A =[[K^H]] \cong K[[X,Z]]$ is a regular local ring of dimension 2. Since $X^{-1}, Z^{-1}$ are in the quotient field of A, then the quotient field of A coincides with the quotient field of $V' =[[K^{G'}]]$.

Now construct S as in Theorem 3.13. Looking at the notation of Lemma 3.11 and at Remark 3.12, we notice that, if we choose $a=(1,0)$, we get $S_1^*= \emptyset$. Therefore Lemma 3.11 gives a precise way to construct S that does not require further choices. Let Y be the monomial element of V of value (1, 0). The ring $D = [[K^S]]$ is maximal with respect to excluding Y. The integral closure ${\overline{D}}$ is the pullback of A with respect to the map $W \rightarrow \kappa$. Hence, ${\overline{D}}$ is local and has infinitely many incomparable prime ideals (of height 2). Therefore it can be neither a PVD nor Prüfer. In this example we can identify W with K((X, Z))[[Y]]. Then, if ${\mathfrak {m}}_W$ is the maximal ideal of W, we have ${\overline{D}} \cong K[[X,Z]] + {\mathfrak {m}}_W$.

The prime ideals of height 2 of ${\overline{D}}$ are principal, generated by elements that are also elements of D as a consequence of the way S is defined in Theorem 3.13. For this reason, they all contract to distinct prime ideals of D. It follows that also D has infinitely many incomparable prime ideals.

4 Intersections of Nagata extensions of overrings

In this section we consider intersections of Nagata rings in order to extend the concept of Kronecker function rings to non-integrally closed domains. For simplicity we suppose all the rings in this section to have finite Krull dimension. In particular, as noted in Sect. 2.2, every integrally closed maximal excluding domain will be a valuation domain.

Let D be an integral domain. We say that a collection of overrings ${\mathcal {F}}= \lbrace D_i \rbrace _{i \in \Lambda }$ is a defining family for D if $\bigcap _{D_i \in {\mathcal {F}}} D_i = D.$ From what observed in Sect. 2, every integral domain always admits a defining family formed by maximal excluding overrings. Moreover we can always consider defining families of D where all the non-integrally closed rings do not contain the integral closure of D. Indeed D can be always expressed as

$$\begin{aligned} D = {\overline{D}} \cap \bigcap _{\alpha \in {\mathcal {Q}}(D) {\setminus } {\overline{D}}} A_{\alpha } \end{aligned}$$

where $A_{\alpha }$ is a non-integrally closed overring of D maximal with respect to excluding the element $\alpha$.

Definition 4.1

Let D be an integral domain and let ${\mathcal {F}}$ be a defining family of D. We say that the ring

$$\begin{aligned} Kr(D)^{{\mathcal {F}}}= \bigcap _{D_i \in {\mathcal {F}}} D_i(t) \end{aligned}$$

is the Kronecker function ring of D with respect to ${\mathcal {F}}$.

When D is integrally closed and the family ${\mathcal {F}}$ is contained in Zar(D), the ring $Kr(D)^{{\mathcal {F}}}$ is a classical Kronecker function ring. We already recalled in Sect. 2, that an integrally closed domain is Prüfer if and only if its Kronecker function ring Kr(D) is equal to the Nagata ring D(t) (in this case the Nagata ring is the unique Kronecker function ring). Also if D is a maximal excluding domain, since the only defining family of D is $\lbrace D \rbrace$, we get that the only Kronecker function ring, according to Definition 4.1 is D(t). However, in general Prüfer domains and maximal excluding domains may behave differently with respect to intersecting Nagata rings of overrings. For a Prüfer domain D, the operation of Nagata ring extension, mapping an overring A to its Nagata ring A(t), commutes with arbitrary intersection of overrings. Conversely, one may observe that if the integral closure of an arbitrary integral domain is not Prüfer, then the operation of Nagata ring extension does not commute with intersection for some collections of overrings. Indeed, if D is an integral domain such that ${\overline{D}}$ is not a Prüfer domain, choosing ${\mathcal {F}}= \text{ Zar }(D)$, we get

$$\begin{aligned} \bigcap _{V \in {\mathcal {F}}} V(t)= Kr({\overline{D}}) \ne \left( \bigcap _{V \in {\mathcal {F}}} V \right) (t) = {\overline{D}}(t). \end{aligned}$$

(1)

We dedicate this section to investigating whether an intersection of Nagata rings is a Nagata ring. The next section is dedicated to constructing relevant families of non-integrally closed Kronecker function rings that behave similarly to the classical integrally closed ones. The following question arises naturally:

Question 4.2

Let D be an integral domain and suppose that ${\overline{D}}$ is a Prüfer domain. If ${\mathcal {F}}$ is an arbitrary collection of overrings of D, then is $\bigcap _{A \in {\mathcal {F}}}A(t)= (\bigcap _{A \in {\mathcal {F}}}A) (t)$?

We answer positively to this question in Theorem 4.8. We start by proving a lemma, which points out a condition for an intersection of local domains to be local. Given two (non-necessarily local) integral domains $A \subseteq B$, we say that B dominates A if every maximal ideal of A is contained in some maximal ideal of B and every maximal ideal of B contracts to some maximal ideal of A. If A and B are local this means simply that ${\mathfrak {m}}_{A} \subseteq {\mathfrak {m}}_{B}$, returning to the classical definition.

We prove that an intersection of local domains dominated by a common valuation overring is local.

Lemma 4.3

Let D be an integral domain. Let $\lbrace D_i \rbrace _{i \in \Lambda }$ be a collection of local overrings of D such that $D= \bigcap _{i} D_i$. Suppose that there exists a valuation overring V that contains all the rings $D_i$ and dominates all of them, except at most one. Then D is local.

Proof

Call $D_1$ the ring in the family ${\mathcal {F}}$ possibly not dominated by V. Pick two non-units $x, y \in D$. Then $x, y \in \bigcup _{i \in \Lambda } ({\mathfrak {m}}_{D_i} \cap D)\subseteq ({\mathfrak {m}}_{D_1} \cap D) \cup ({\mathfrak {m}}_V \cap D) = {\mathfrak {m}}_{D_1} \cap D.$ It follows that $x+y \in {\mathfrak {m}}_{D_1} \cap D$ is not a unit in D. Notice also that if $D_1$ is dominated by V, then also D is dominated by V. $\square$

To illustrate the above lemma with an example, for every prime number p choose an algebraic complex number $\theta _p$ having degree p over ${\mathbb {Q}}$. Let F be the infinite algebraic extension of ${\mathbb {Q}}$ generated by all such $\theta _p$’s. Let t be an indeterminate over F and for every p let $D_p = {\mathbb {Q}}(\theta _p)+ tF[[t]].$ The rings $D_p$ are all local and dominated by the valuation overring F[[t]]. Their intersection is the local domain ${\mathbb {Q}}+ tF[[t]].$

Our next step is proving that in the situation described in Lemma 4.3, the intersection of the Nagata rings of the rings $D_i$ is equal to the Nagata ring of D. We actually aim to prove a more general result which will be useful also later. We want to involve in the intersection also semilocal domains. We are able to do this after adding a technical assumption on the residue fields.

Notice that the two following conditions are equivalent for a domain D: all the residue fields of D have cardinality at least $s+1$ if and only if D contains s units $u_1, \ldots , u_s$ such that $u_i-u_j$ is still a unit for every i, j. Clearly for all the integral domains containing an infinite field or containing ${\mathbb {Z}}(t)$, the next results can be proved without technical assumptions on the residue fields.

Lemma 4.4

Let D be a semilocal domain with s maximal ideals. Suppose that all the residue fields of D have cardinality at least s. Fix a set of units $U \subseteq D$, of cardinality at least $s-1$ and such that $u_i-u_j$ is a unit for every distinct $u_i, u_j \in U$. Let $x_1, \ldots , x_n \in D$ be elements such that $(x_1, \ldots , x_n)=D$. Then there exists a unit of D of the form $c = \sum _{k=1}^n \delta _k x_k$ with $\delta _k \in U \cup \lbrace 0 \rbrace$ for every k.

Proof

We prove it by induction on n. In the case $n=1$, we clearly must have that $x_1$ is a unit, and thus $\delta _1 x_1$ is a unit for every $\delta _1 \in U$. Thus assume the thesis true for every set of at most $n-1$ elements. Therefore if after reordering the generators $(x_1, \ldots , x_{n-1})=D$, we conclude by applying the inductive hypothesis and setting $\delta _n = 0$.

Call ${\mathfrak {m}}_1, \ldots , {\mathfrak {m}}_s$ the maximal ideals of D. Possibly relabeling, suppose that $x_1, \ldots , x_{n-1} \in {\mathfrak {m}}_s$, and there exist $1 \le s' < s$ such that $x_n \in ({\mathfrak {m}}_1 \cap \cdots \cap {\mathfrak {m}}_{s'}) {\setminus } ({\mathfrak {m}}_{s'+1} \cup \cdots \cup {\mathfrak {m}}_s)$. The ideal generated by $x_1, \ldots , x_{n-1}$ cannot be contained in any of the maximal ideals ${\mathfrak {m}}_1, \ldots , {\mathfrak {m}}_{s'}$. Consider the ring $A= S^{-1}D$ where $S = D {\setminus } ({\mathfrak {m}}_1 \cup \cdots \cup {\mathfrak {m}}_{s'})$. The ring A is semilocal and contains U. Moreover $(x_1, \ldots , x_{n-1})A=A$. By the inductive hypothesis there exists a unit of A of the form $c' = \sum _{k=1}^{n-1} \delta _k x_k$ with $\delta _k \in U \cup \lbrace 0 \rbrace$. Observing that $c' \in D$, we obtain $c' \not \in {\mathfrak {m}}_1 \cup \cdots \cup {\mathfrak {m}}_{s'}$.

Take now two elements of the form $d_1= c'+ux_n$, $d_2 =c'+vx_n$ with $u,v \in U$, $u \ne v$. We claim that $d_1, d_2$ cannot be contained in a common maximal ideal. Indeed if $d_1, d_2 \in {\mathfrak {m}}_i$, then we would have $d_1 - d_2 = (u-v)x_n \in {\mathfrak {m}}_i$ and $vd_1-ud_2= (v-u)c' \in {\mathfrak {m}}_i$, implying that $c', x_n \in {\mathfrak {m}}_i$, since $u-v$ is a unit. This is a contradiction with the choice of $c'$. Moreover any element of the form $c'+ux_n$ cannot be in a maximal ideal containing either $c'$ or $x_n$. Using now that U contains at least $s-1$ elements and D has only s maximal ideals we can find an element of the form $c' + \delta _n x_n$ which is a unit in D. $\square$

Proposition 4.5

Let D be an integral domain with quotient field K. Let ${\mathcal {F}}= \lbrace D_i \rbrace _{i \in \Lambda }$ be a defining family of D. Suppose that all the rings in ${\mathcal {F}}$ are contained in a common overring $T \ne K$ and one ring $D_1 \in {\mathcal {F}}$ is semilocal with s maximal ideals. Also suppose that all the residue fields of D have cardinality at least s and T dominates $D_i$ for every i, except possibly $D_1$. Then $D(t)= \bigcap _{i} D_i(t).$

Proof

As in Lemma 4.4, we can fix a set of units $U \subseteq D$, of cardinality at least $s-1$ such that $q_i-q_j$ is a unit for every distinct $q_i, q_j \in U$. Clearly the set U is also contained in $D_1$.

We always have the inclusion $D(t) \subseteq \bigcap _{i} D_i(t).$ To prove the opposite inclusion pick $\phi \in \bigcap _{i} D_i(t)$. Such an element $\phi$ can be always written as $\frac{f}{g}$ with $f,g \in D[t]$. Say that $f= \sum _{k=0}^m a_k t^k$ and $g= \sum _{k=0}^n b_k t^k$.

Since $\phi \in \bigcap _{i} D_i(t)$, for every i we can find $x_i \in K$ such that $\frac{a_k}{x_i}, \frac{b_k}{x_i} \in D_i$ for every k and the ideal $\frac{1}{x_i}(b_0, \ldots , b_n)D_i$ is the unit ideal. Hence we can choose an element $c_i \in (b_0, \ldots , b_n)D_i$ such that $c_i= x_iu_i$ with $u_i$ a unit in $D_i$. In particular $x_i \in D_i$. For $j \ne i$, since $\frac{b_k}{x_j} \in D_j$ for every k, we get $\frac{c_i}{x_j}= \frac{x_i}{x_j}u_i \in T$. Similarly, $\frac{c_j}{x_i}= \frac{x_j}{x_i}u_j \in T$ and, since $u_i, u_j$ are units in T, we obtain that also $\frac{x_i}{x_j}$ is a unit in T for every i, j.

Let us now consider the semilocal domain $D_1$. The ideal $\frac{1}{x_1}(b_0, \ldots , b_n)D_1 = D_1$. By Lemma 4.4 we can choose the element $c_1 = \sum _{l=0}^n \delta _l b_l$ with all $\delta _l \in U \cup \lbrace 0 \rbrace \subseteq D$. Thus $c_1 \in D$. For every i, $\frac{c_1}{x_i} \in D_i$ and from what said above $\frac{c_1}{x_i}= \frac{x_1}{x_i}u_1$ is a unit of T. Since, for $i \ne 1$, the overring T dominates $D_i$, then $\frac{c_1}{x_i}$ has to be a unit of $D_i$. It follows that for every i we can write $c_1 = x_iw_i$ with $x_i, w_i \in D_i$ and $w_i$ a unit in $D_i$ (for $i=1$, set $w_1= u_1$). Hence, $\frac{a_k}{c_1}, \frac{b_k}{c_1} \in \bigcap _i D_i = D$. This implies that $\frac{f}{c_1}, \frac{g}{c_1} \in D[t]$ and, since $c_1 \in (b_0, \ldots , b_n)D$ we get that the ideal of D generated by the coefficients of $\frac{g}{c_1}$ coincides with D. This implies $\phi = \frac{f}{g}\frac{c_1}{c_1} \in D(t)$. $\square$

Corollary 4.6

Let D be an integral domain and let ${\mathcal {F}}= \lbrace D_i \rbrace _{i \in \Lambda }$ be a family of local rings that is also a defining family of D. Suppose that there exists a valuation overring V that contains all the rings $D_i$ and dominates all of them, except at most one. Then $Kr^{{\mathcal {F}}}(D)= D(t)$.

Example 4.11 illustrates a case where exactly one ring in the family ${\mathcal {F}}$ is not dominated by the valuation overring V. The next easy lemma is needed to prove Theorem 4.8.

Lemma 4.7

Let D be an integral domain with quotient field K. Then $D(t) \cap K[t]= D[t]$.

Proof

The inclusion $D[t] \subseteq D(t) \cap K[t]$ is clear. Let $f \in K[t] \cap D(t)$ and write $f= \frac{f^*}{a}$ with $f^*\in D[t]$ and $a \in D$. There must exist $g,h \in D[t]$ such that $c(h)=D$ and $f^*h= ga$. By [31, Theorem 4], $c(f^*)= c(f^*h)= c(ag)= ac(g).$ Hence a divides in D all the coefficients of $f^*$ implying that $f \in D[t]$. $\square$

We now prove the main theorem about Kronecker function rings of integral domains having Prüfer integral closure.

Theorem 4.8

Let D be an integral domain such that ${\overline{D}}$ is a Prüfer domain. Let ${\mathcal {F}}$ be a defining family of D. Then $\bigcap _{A \in {\mathcal {F}}} A(t) = D(t)$.

Proof

By expressing any ring in ${\mathcal {F}}$ as the intersection of its localizations at the maximal ideals, we can assume every element of ${\mathcal {F}}$ to be local (as recalled in Sect. 2, Nagata ring extension commutes with the intersection of the localizations at the maximal ideals). For every valuation overring V of D denote by ${\mathcal {F}}_V$ the set of elements of ${\mathcal {F}}$ that are dominated by V. Clearly ${\mathcal {F}}= \bigcup _{V \supseteq D} {\mathcal {F}}_V$. By Corollary 4.6 we get $\bigcap _{A \in {\mathcal {F}}_V} A(t) = B_V(t)$ where $B_V= \bigcap _{A \in {\mathcal {F}}_V} A.$ Therefore, using that $Kr({\overline{D}})= {\overline{D}}(t)$ we get

$$\begin{aligned} \bigcap _{A \in {\mathcal {F}}} A(t) = \bigcap _{V \supseteq D} B_V(t) \subseteq \bigcap _{V \supseteq D} V(t) = {\overline{D}}(t). \end{aligned}$$

Pick now $F= \frac{g}{f} \in \bigcap _{A \in {\mathcal {F}}} A(t)$ such that $f,g \in {\overline{D}}[t]$ and $c(f)= {\overline{D}}$. We want to construct a polynomial $\psi \in {\overline{D}}[t]$ such that the product $\phi := f \psi \in D[t]$ and $c(\phi )=D$. After doing this we can write $F = \frac{g\psi }{\phi }$ and use that $\phi \in D(t) \subseteq \bigcap _{A \in {\mathcal {F}}} A(t)$ to get $g \psi \in \bigcap _{A \in {\mathcal {F}}} A(t) \cap K[t]$ where K is the quotient field of D. By Lemma 4.7,

$$\begin{aligned} \left( \bigcap _{A \in {\mathcal {F}}} A(t) \right) \cap K[t]= \bigcap _{A \in {\mathcal {F}}} (A(t) \cap K[t])= \bigcap _{A \in {\mathcal {F}}} A[t]= D[t]. \end{aligned}$$

This shows $F \in D(t)$.

To construct the polynomial $\psi$, we write $f= \sum _{i=0}^n a_i t^i$ and use the fact that $c(f)={\overline{D}}$ to find $z_0, \ldots , z_n \in {\overline{D}}$ such that $1= \sum _{i=0}^n a_i z_i$. Then we argue exactly as in the proof of [31, Theorem 4] to construct $\phi \in D[t]$ such that $c(\phi )=D$, $\phi = f \psi$, and $\psi \in K[t]$. By construction, as mentioned in the proof of [31, Theorem 4], the coefficients of $\psi$ are in the integral closure of D in some algebraic field extension E of K. Then $\psi \in K[t] \cap {\overline{D}}^E[t]= {\overline{D}}[t]$. This is sufficient to conclude the proof. $\square$

Recall that if the integral closure of D is a Prüfer domain, then also the integral closure of every overring of D is a Prüfer domain. Using this fact, the next corollary follows combining Theorem 4.8 with Eq. (1).

Corollary 4.9

Let D be an integral domain. The following conditions are equivalent:

• (1) The integral closure of D is a Prüfer domain.

• (2) For every collection ${\mathcal {F}}$ of overrings of D, $\bigcap _{A \in {\mathcal {F}}} A(t) = (\bigcap _{A \in {\mathcal {F}}} A)(t)$.

We pass now to study the case of an intersection of a semilocal domain A and a valuation domain V, having the same quotient field. This case is relevant for the results in Sect. 5. In the case A is local, the thesis of the next theorem holds without assumptions on the residue fields. In Example 4.11 are provided instances of interesting cases where the next theorem applies.

Theorem 4.10

Let V be a valuation domain of finite dimension and let A be a semilocal domain such that ${\mathcal {Q}}(A)= {\mathcal {Q}}(V)= {\mathcal {Q}}(V \cap A)$. Assume that A has s maximal ideals ${\mathfrak {m}}_1, \ldots , {\mathfrak {m}}_s$ and all the residue fields of $A \cap V$ have cardinality at least $s+1$. The following assertions hold:

• (i) $A \cap V$ is local if and only if A is local and is dominated by an overring of V. In this case ${\mathfrak {m}}_A$ is a common prime ideal of A and $A \cap V$, $A = (A \cap V)_{{\mathfrak {m}}_A}$, and $\frac{A \cap V}{{\mathfrak {m}}_A}$ is a valuation domain with quotient field $\frac{A}{{\mathfrak {m}}_A}$.

• (ii) If $A \cap V$ is not local, then $A_{{\mathfrak {m}}_i} = (A \cap V)_{{\mathfrak {m}}_i \cap V}$ for every $i=1, \ldots , s$.

• (iii) If A and V have no common proper overrings, then $V = (A \cap V)_{{\mathfrak {m}}_V \cap A}.$

• (iv) If $A \cap V$ is not local and $A \subseteq V_Q$ for some prime ideal Q of V, maximal with respect to this property, then $(A \cap V)_{{\mathfrak {m}}_V \cap A} = A_{Q \cap A} \cap V.$

• (v) $(A \cap V)(t)= A(t) \cap V(t)$.

Proof

We can assume $A \nsubseteq V$, otherwise all the results are obvious. The assumption on the residue fields of $A \cap V$ implies that if $z \in {\mathfrak {m}}_i$ for some i, then there exists a unit $q \in A \cap V$ such that $z + q$ is a unit in A.

• (i) If A is local and dominated by an overring of V, the implication follows by Lemma 4.3. Conversely if $A \cap V$ is local we claim that ${\mathfrak {m}}_i \subseteq V$ for every i. Indeed, if there exists $z \in {\mathfrak {m}}_i {\setminus } V$, we get $z^{-1} \in {\mathfrak {m}}_V {\setminus } A$. Choose a unit $q \in A \cap V$ such that $z + q$ is a unit in A. Observing that

  $$\begin{aligned} \frac{z}{q+z} = \frac{1}{qz^{-1}+1} \in {\mathfrak {m}}_i \cap (V {\setminus } {\mathfrak {m}}_V), \quad \frac{qz^{-1}}{1+qz^{-1}} = \frac{q}{z+q} \in {\mathfrak {m}}_V \cap \left( A {\setminus } \bigcup _{j=1}^s{\mathfrak {m}}_j\right) , \end{aligned}$$

  we find that $\frac{z}{q+z}$ and $\frac{q}{z+q}$ are two non-units of $A \cap V$ whose sum is a unit. This is a contradiction. Hence we have ${\mathfrak {m}}_i \subseteq V$ for every i. Pick an element $s \in A {\setminus } V$. For every $n \ge 1$ and every $x \in \bigcup _{j=1}^s{\mathfrak {m}}_j$ we get $s^nx \in V$, showing that the radical of xV is properly contained in the radical of $s^{-1}V$. Therefore, there exists a non-maximal prime ideal Q of V such that $\bigcup _{j=1}^s{\mathfrak {m}}_j \subseteq Q= QV_Q$ and $A \subseteq V_Q$. In particular the unique maximal ideal of A is ${\mathfrak {m}}_A= Q \cap A$ and A is dominated by $V_Q$. Using that ${\mathfrak {m}}_A \subseteq V$, we obtain that ${\mathfrak {m}}_A$ is a prime ideal of $A \cap V$. For $a \in A {\setminus } V$, we have $a^{-1} \in (A \cap V) {\setminus } {\mathfrak {m}}_A$, thus $A = (A \cap V)_{{\mathfrak {m}}_A}$. If $x,y \in (A \cap V) {\setminus } {\mathfrak {m}}_A$, then the fractions $\frac{x}{y}, \frac{y}{x}$ are in A and at least one of them is in V, implying that $\frac{A \cap V}{{\mathfrak {m}}_A}$ is a valuation domain.

• (ii) It is sufficient to show that $A\subseteq (A \cap V)_{{\mathfrak {m}}_i \cap V}$. For $z \in A {\setminus } V$, if $z^{-1} \in A$ then $z= \frac{1}{z^{-1}} \in (A \cap V)_{{\mathfrak {m}}_i \cap V}.$ If z is not a unit, pick again a unit $q \in A \cap V$ such that $q+z$ is a unit in A. Set $u = \frac{1}{q+z}$ and observe that u is a unit of A such that $uz = \frac{1}{qz^{-1}+1} \in V$ and $u \in V$. Hence $z = \frac{zu}{u} \in (A \cap V)_{{\mathfrak {m}}_i \cap V}$.

• (iii) For $x \in V {\setminus } A$, if $x^{-1} \in A$, we conclude that $x \in (A \cap V)_{{\mathfrak {m}}_V \cap A}$ as in item (ii) by choosing $u= \frac{1}{1+qx}$ with q a unit in $A \cap V$ such that $q+x^{-1}$ is a unit in A. Suppose that $x, x^{-1} \not \in A$ and write $x=\frac{a}{b}$ with a, b both non-units in A and $v(a) \ge v(b)$. We want to find a unit u of A such that $v(u)= - v(b)$. In this way we can write $x = \frac{au}{bu} \in (A \cap V)_{{\mathfrak {m}}_V \cap A}$. If there exists a unit t of A such that $v(t) > v(b)$, it is sufficient to set $u = \frac{1}{t+qb}$ where $q \in A \cap V$ is a unit such that $t+qb$ is a unit in A. Suppose by way of contradiction that there are no units of A with value larger than or equal v(b). This implies that $v(b) > 0$ (because 1 is a unit of both A and V). By assumption on the residue fields, every element of A can be expressed as the sum of at most two units, thus, since $A \nsubseteq V$, there exists some unit s of A such that $v(s) < 0$. For every such s, we get that the radical of $s^{-1}V$ properly contains the radical of bV. In particular all the units of A are contained in a proper overring $V_Q$ of V. This forces $A \subseteq V_Q$. This is a contradiction.

• (iv) Clearly $V_Q$ dominates $A_{Q \cap A}$. By Lemma 4.3, $A_{Q \cap A} \cap V$ is local and contains $A \cap V$. In particular it contains the localization $(A \cap V)_{{\mathfrak {m}}_V \cap A}.$ For $x \in A_{Q \cap A} \cap V$ we argue as we did for item (iii) to show that $x = \frac{au}{bu} \in (A \cap V)_{{\mathfrak {m}}_V \cap A}$. Now we can choose a, b non-units in A such that $b \not \in Q \cap A$. By the choice of Q, there exists some unit s of A such that the radical of sV is the unique prime ideal $Q'$ of V such that $\textrm{ht }(Q') = \textrm{ht }(Q)+1$. Hence, there exists a unit t of A such that $v(t) > v(b)$. We can conclude using the same proof as for item (iii).

• (v) We consider different cases. If $A \cap V$ is local, by item (i), A is dominated by a valuation overring of V. The thesis follows now by Proposition 4.5. If $A \cap V$ is not local and A and V have no common overrings, by items (ii)–(iii), all the rings $A_{{\mathfrak {m}}_i}$ and V are precisely the localizations of $A \cap V$ at the maximal ideals. The thesis follows since Nagata ring extension commutes with localizations at the maximal ideals. If instead we are in the situation described by item (iv), we use item (ii) and localization to say that $(A \cap V)(t)= A(t) \cap (A_{Q \cap A} \cap V)(t)$. Using that $A_{Q \cap A} \cap V$ is local we can split further $(A_{Q \cap A} \cap V)(t) = A_{Q \cap A}(t) \cap V(t)$ and conclude since $A \subseteq A_{Q \cap A}$. $\square$

We do not know whether the results of Theorem 4.10 hold if we remove the assumption on the cardinality of the residue fields.

Example 4.11

First consider $A = K((y))[[x^2, x^3]]$ and $V = K[[y]]+xK((y))[[x]]$. These two rings have a common overring, namely $W= K((y))[[x]]$, that dominates A. Hence Lemma 4.3 and Corollary 4.6 apply to show that $A \cap V$ is local and $(A \cap V)(t)= A(t) \cap V(t)$. Notice that in this case only A is dominated by W, V is contained in W but of course not dominated. Theorem 4.10(i) describes the structure of $A \cap V$.

To describe a case where A is semilocal, we can take $A = A_1 \cap A_2$ where $A_1 = K((y))[[x^2, x^3]]$, $A_2=K((x))[[y^2, y^3]]$ (A has two maximal ideal because $x^2y^{-2} \in {\mathfrak {m}}_{A_1}$ and $y^2x^{-2} \in {\mathfrak {m}}_{A_2}$ and moreover the localizations of A at the maximal ideals are exactly $A_1$ and $A_2$). Let V be the same as above. Theorem 4.10 applies to prove that $(A \cap V)(t)= A(t) \cap V(t)$ and that the localization of $A \cap V$ at the maximal ideals are $A_2$ and $A_1 \cap V$.

We conclude this section by showing that under some mild conditions, Nagata ring extension does not commute with intersection also in the non-integrally closed case. Various constructions of this kind will be analyzed in the next section (see Constructions 5.3 and 5.13).

Proposition 4.12

Let D be a local integral domain and let ${\mathcal {F}}= \lbrace D_i \rbrace _{i \in \Lambda }$ be a defining family of D. If there exists $z \in {\mathcal {Q}}(D)$ such that $z, z^{-1} \not \in D$ and for every i, $z \in D_i$ or $z^{-1} \in D_i$, then $D(t) \ne \bigcap _{i \in \Lambda } D_i(t).$ In particular if $D = T \cap A$ with T integrally closed, and there exists $z \in A$ such that $z, z^{-1} \not \in D$. Then $D(t) \ne \bigcap _{V \supseteq T} V(t) \cap A(t)$.

Proof

Consider

$$\begin{aligned} \phi = \frac{1}{t+z} = \frac{z^{-1}}{z^{-1}t+1}. \end{aligned}$$

Clearly $\phi \in \bigcap _{i \in \Lambda } D_i(t)$. Let us show that $\phi \not \in D(t)$. We can multiply by a common factor to have both numerator and denominator of $\phi$ inside D. Hence pick any $d \in D$ such that $dz \in D$ and write $\phi = \frac{d}{dt+dz}$. If $\phi \in D(t)$, since D is local we would have that either d or dz is a unit in D. But d cannot be a unit, since $dz \in D$ and $z \not \in D$. If dz were a unit, we would have $z^{-1} = d (dz)^{-1} \in D$. In any case this leads to a contradiction. $\square$

As an easy example, one can take $D= K[[x^2, x^3, y]]$, $A= K((y))[[x^2, x^3]]$ and notice that $D = {\overline{D}} \cap A$. We know that A is maximal excluding and the family ${\mathcal {F}}= \text{ Zar }(D) \cup \lbrace A \rbrace$ is a defining family for D. Observing that $x^2y^{-1} \in A {\setminus } D$ and its inverse is also not in D, we get $D(t) \subsetneq Kr^{{\mathcal {F}}}(D).$

Remark 4.13

For a local domain D that is not a valuation ring and an overring A, the existence of an element $z \in A$ such that $z, z^{-1} \not \in D$ is usually satisfied. Indeed, such an element z does not exist if and only if $A = D_Q$ for a prime ideal Q of D such that $Q=QD_Q$, and $\frac{D}{Q}$ is a valuation ring. For this pick $z \in A$ not a unit and observe that $z \in {\mathfrak {m}}_D$. Thus for x, y not units in A, if $x+y$ was a unit in A, we would get $1 = \frac{x}{x+y}+\frac{y}{x+y} \in {\mathfrak {m}}_D$, which is impossible and implies that A is local. The maximal ideal of A is equal to a prime ideal Q of D which forces $Q=QD_Q$ and $A=D_Q$. Finally, if u, v are element of $D {\setminus } Q$, then $\frac{u}{v}, \frac{v}{u}$ are units in A and at least one of them has to be in D, implying that $\frac{D}{Q}$ is a valuation domain. Notice that by Theorem 4.10-(i), a domain D of this form may arise as intersection $D= A \cap V$ for some valuation ring V which has an overring dominating A.

The above remark suggests an example of a local domain D not maximal excluding, such that ${\overline{D}}$ is not Prüfer, but still we have $Kr^{{\mathcal {F}}}(D)=D(t)$ for some defining family ${\mathcal {F}}$. However, Nagata ring extension clearly does not commute with intersection for all the overrings of D.

Example 4.14

Let T be the maximal excluding generalized power series ring of Example 3.8, defined over the field $K= {\mathbb {Q}}$. Set $D= {\mathbb {Z}}_{(p)}+ {\mathfrak {m}}_T$ for a prime number p. The integral closure of D is ${\overline{D}}= {\mathbb {Z}}_{(p)}+ {\mathfrak {m}}_{{\overline{T}}}$ and it is not Prüfer since ${\overline{T}}$ is not. Also D is not maximal excluding by Theorem 3.1 because T is not a valuation ring. We can write $D = {\overline{D}} \cap T$ and consider the defining family ${\mathcal {F}}= \textrm{Zar }(D) \cup \lbrace T \rbrace$, setting $Kr^{{\mathcal {F}}}(D) = Kr({\overline{D}}) \cap T(t)$. Let V be a valuation overring of D such that ${\mathfrak {m}}_{V}=pV$. Observing that there are no rings properly contained between D and T and $p^{-1} \in T {\setminus } V$, we get $V \cap T = D$ (of course T is dominated by an overring of V, as expected by Theorem 4.10-(i)). Now, Theorem 5.16-(i) from the next section applies to this setting to show that the localization of $Kr^{{\mathcal {F}}}(D)$ at the center of V(t) is equal to D(t). Thus $Kr^{{\mathcal {F}}}(D) = D(t)$.

We leave another open question.

Question 4.15

Is it possible to find an integral domain D not maximal excluding, such that ${\overline{D}}$ is not Prüfer but $Kr^{{\mathcal {F}}}(D)=D(t)$ for every defining family ${\mathcal {F}}$ of D? Is this true for the ring D defined in Example 4.14?

5 Constructions of non-integrally closed Kronecker function rings

In this section we construct non-integrally closed rings of the form $Kr^{{\mathcal {F}}}(D)$, according to the notation of Definition 4.1. The two main questions that we investigate for such rings are: understanding what the integral closure is and studying if they behave locally like classical Kronecker function rings, in the sense that the localizations at maximal ideals are Nagata ring extensions of some overring of the base ring D. We immediately observe that in general the integral closure of $Kr^{{\mathcal {F}}}(D)$ may not coincide with the Kronecker function ring $Kr({\overline{D}})$. Indeed we have:

Remark 5.1

Let D be an integral domain, ${\mathcal {F}}$ a defining family for D and set $R= Kr^{{\mathcal {F}}}(D)$. Suppose that ${\overline{R}}= Kr({\overline{D}}).$ Then the integral closure of every $A \in {\mathcal {F}}$ is a Prüfer domain. For this simply recall that $Kr({\overline{D}})$ is Prüfer and integral closure commutes with Nagata ring extension.

In the following we first consider cases where the integral closure of $Kr^{{\mathcal {F}}}(D)$ is equal to $Kr({\overline{D}})$. Then, recalling that the integral closure of a maximal excluding domain may not be a Prüfer domain, we give in Theorem 5.16 and Example 5.12, examples such that the integral closure is a proper non-Prüfer subring of $Kr({\overline{D}})$.

Regarding the local behavior of $Kr^{{\mathcal {F}}}(D)$, we find that in all our constructions, the localizations at the maximal ideals are Nagata ring extensions of overrings of D. For this reason we leave the following general question for further research:

Question 5.2

Let D be an integral domain and let ${\mathcal {F}}$ be any defining family of D. Let ${\mathfrak {p}}$ be a maximal ideal of the ring $R=\bigcap _{A \in {\mathcal {F}}} A(t)$. Is $R_{{\mathfrak {p}}}= C(t)$ for some overring C of D?

Our first construction is based on integral domains whose integral closure is obtained by adding the generators of a finite algebraic (Galois) field extension. We restrict to working with D a local domain, since one can always reduce from the global case to the local one by localizing at each maximal ideal.

Construction 5.3

Let D be a local domain with quotient field F. Let $F'$ be a subfield of F such that ${\mathbb {Q}} \subseteq F'$ and F is a finite Galois extension of $F'$, generated as $F'$-vector space by $\theta _1=1, \theta _2, \ldots , \theta _n$. Call K the field generated over ${\mathbb {Q}}$ by $\theta _1, \theta _2, \ldots , \theta _n$ and all their conjugates with respect to the action of Gal$(F/F')$. We assume any intermediate field extension $E/ E'$ such that $F' \subseteq E' \subseteq E \subseteq F$ to be a Galois extension generated by $\vartheta _1, \ldots , \vartheta _m$ and satisfying one of the following condition (see Examples 5.4 and 5.5 for examples):

($*_1$):

The field K is contained in ${\overline{D}}$.

($*_2$):

$\lbrace \vartheta _1, \ldots , \vartheta _m \rbrace = \lbrace 1, \vartheta , \vartheta ^2, \ldots , \vartheta ^{m-1} \rbrace$ where $\vartheta$ is a simple root of degree m over $E'$ and ${\overline{D}}$ contains $\xi \vartheta ^m$ for every m-th root of unity $\xi$.

Suppose there exists a local integrally closed domain $D'$ containing ${\mathbb {Q}}$, having quotient field $F'$ such that ${\mathfrak {m}}_{D'} \subseteq {\mathfrak {m}}_{D}$, $D= D'[{\mathfrak {m}}_D]_{{\mathfrak {m}}_D}$, and $\overline{D'}^F= {\overline{D}} = D[\theta _1, \ldots , \theta _n]$.

Given a valuation overring V of $D'$ such that ${\mathfrak {m}}_V \supseteq {\mathfrak {m}}_{D'}$, define $A_V:= V[{\mathfrak {m}}_D]_{({\mathfrak {m}}_{V}, {\mathfrak {m}}_D)}$. Clearly $D \subseteq \bigcap _{V \supseteq D'} A_V \subseteq {\overline{D}}$. Suppose that $\bigcap _{V \supseteq D'} A_V = D$, and in that case define ${\mathcal {F}}$ to be the defining family of D containing all the maximal excluding overrings A such that $A \supseteq A_V$ for some V valuation overring of $D'$. Set $R:=Kr^{{\mathcal {F}}}(D)$.

The main examples of rings D that we can obtain from Construction 5.3 are certain kinds of $K+{\mathfrak {m}}$ constructions and of algebras over fields, as shown in the next examples.

Example 5.4

Let $D'= K'+ {\mathfrak {n}}$ be an integrally closed domain with quotient field $F'$, such that ${\mathbb {Q}} \subseteq K'$. Let K be a finite Galois extension of $K'$ generated as $K'$-vector space by $\theta _1, \ldots , \theta _n$ and such that $K \cap F' = K'$. Call F the finite Galois extension of $F'$ generated by the same elements. Then define $D= K' + {\mathfrak {m}}$ with ${\mathfrak {m}}= \sum _{i=1}^n \theta _i {\mathfrak {n}},$ and observe that ${\overline{D}}= \overline{D'}^F= K+ {\mathfrak {m}}$. Clearly the field extension $F/F'$ satisfies condition ($*_1$). By construction the rings $A_V$ do not contain any element of $K {\setminus } K'$. Therefore $\bigcap _{V \supseteq D'} A_V = D$.

Example 5.5

Consider a K-algebra of the form $D= \sum _{i=1}^c K[[x_i^{e_{1i}}, \ldots , x_i^{e_{l_ii}}]]$ (or the corresponding localized polynomial ring version), where $x_1, \ldots , x_c$ are indeterminates over K, the exponents $1 \le e_{1i}< \cdots < e_{l_ii}$ generate a numerical semigroup, and K contains the $e_{1i}$-th cyclotomic field for all $i=1, \ldots , c$. In this case ${\overline{D}}= K[[x_1, \ldots , x_c]]$ and $D'= K[[x_1^{e_{11}}, \ldots , x_c^{e_{1c}}]].$ The field extension $F/F'$ satisfies condition ($*_2$). To see that $\bigcap _{V \supseteq D'} A_V = D$, observe that if V is a valuation overring of $D'$ (with ${\mathfrak {m}}_V \supseteq {\mathfrak {m}}_{D'}$) such that $x_1^{e_{11}}$ has infinitely larger value than all the other $x_i^{e_{1i}}$, then all the elements of the form $x_1^s f(x_2, \ldots , x_c)$ are not in $A_V$ if s is not in the semigroup generated by $e_{11}, \ldots , e_{l_11}$. Similarly one can show that each element of ${\overline{D}} {\setminus } D$ does not belong to some ring $A_V$. Simple examples that one may consider in this family are rings such as $K[[x^2,x^3,y]]$ and $K[[x^2,x^3,y^2,y^3]]$.

Lemma 5.6

Take the assumptions and notations of Construction 5.3. Let V be a valuation overring of $D'$. Then any element $\sum _{j=1}^n a_j \theta _j \in F$ with $a_j \in F'$ is integral over V if and only if each summand $a_j\theta _j$ is integral over V.

Proof

Let $\sigma _1, \ldots , \sigma _n$ be the elements of Gal$(F/F')$. By restricting each time to the automorphisms with fixed field $E'$, we can reduce to proving this result for only the main field extension $F/ F'$, assuming that it satisfies either condition $(*_1)$ or condition $(*_2)$.

Set $B_V:={\overline{V}}^{F}.$ Let $\alpha = \sum _{j=1}^n a_j \theta _j \in B_V$ with $a_j \in F'$. Since $F/ F'$ is a Galois extension, it is well-known that the integral closure of V in F is the intersection of all the extensions of V to the field F, and such extensions are all conjugates by the elements of Gal$(F/F')$ (see for instance [7, Section 3.2]). Therefore, also all the conjugates of $\alpha ,$ $\sigma _i(\alpha )$ are elements of $B_V.$ It follows that any linear combination of $\sigma _1(\alpha ), \ldots , \sigma _n(\alpha )$ with coefficients in $B_V$ is in $B_V.$ Now, set up a linear square system to express $a_j \theta _j$ as a linear combination of $\sigma _1(\alpha ), \ldots , \sigma _n(\alpha )$. The equations we obtain are of the form $a_j \theta _j = a_j \sum _{k=1}^n b_k \sigma _k(\theta _j)$ and $0=a_i\sum _{k=1}^n b_k \sigma _k(\theta _i)$ for $i \ne j$. These can be solved independently of $a_1, \ldots , a_n$ for a choice of coefficients $b_1, \ldots , b_n$ in the field K, which is generated over ${\mathbb {Q}}$ by the elements $\sigma _i(\theta _k)$. Assuming condition $(*_1)$, we have that $K \subseteq {\overline{D}} \subseteq B_V$. The square matrix defining the linear system is

$$\begin{aligned} \begin{bmatrix} 1 &{} 1 &{} \ldots &{} 1 \\ \theta _2 &{} \sigma _2(\theta _2) &{} \ldots &{} \sigma _n(\theta _2) \\ \vdots &{} \vdots &{} \ldots &{} \vdots \\ \theta _n &{} \sigma _2(\theta _n) &{} \ldots &{} \sigma _n(\theta _n) \end{bmatrix}. \end{aligned}$$

The determinant of this matrix lives in K and is equal to the square root of the discriminant of the field extension $F/F'$. This extension is separable, hence the discriminant is nonzero. Since $K \subseteq B_V$, the system can be solved over $B_V$ by Cramer’s rule yielding $a_j \theta _j \in B_V$ for every j. In case condition $(*_2)$ is satisfied, the field F is generated over $F'$ by simple roots, and by hypothesis we have $\theta _j= \theta _2^{j-1}$ for $j=1, \ldots , n$. Moreover, the n-th cyclotomic field ${\mathbb {Q}}(\xi )$ is contained in ${\overline{D}}$, hence in $B_V$. To solve the same linear system as above with respect to $a_j \theta _j$, we reduce to solve a linear square system in ${\mathbb {Q}}(\xi )$ whose matrix is a Vandermonde matrix in the entries $1, \xi , \ldots , \xi ^{n-1}$. Since ${\mathbb {Q}}(\xi ) \subseteq B_V$ we again obtain $a_j \theta _j \in B_V$ for every j. $\square$

The next lemma gives us a sufficient condition to have a localization of an overring of D(t) equal to the Nagata ring extension of an overring of D. We are going to use this lemma as a technical tool in the proofs of Theorems 5.8 and 5.16, showing instances of cases where its assumptions are satisfied.

Lemma 5.7

Let D be an integral domain and let A be a local overring. Suppose R to be an integral domain such that $D(t) \subseteq R \subseteq A(t)$. Let ${\mathfrak {p}}= {\mathfrak {m}}_{A(t)} \cap R$ and suppose $A \subseteq R_{{\mathfrak {p}}}$. Then $R_{{\mathfrak {p}}} = A(t)$.

Proof

By assumption $t \in R$, thus there are inclusions $A[t] \subseteq R_{{\mathfrak {p}}} \subseteq A(t)$. The ring A(t) is the localization of A[t] at the prime ideal ${\mathfrak {m}}_{A}[t] = {\mathfrak {m}}_{A(t)} \cap A[t]$. From the fact that ${\mathfrak {p}}R_{{\mathfrak {p}}} \subseteq {\mathfrak {m}}_{A(t)}$, it follows that ${\mathfrak {q}}:= {\mathfrak {p}}R_{{\mathfrak {p}}} \cap A[t] \subseteq {\mathfrak {m}}_{A}[t]$. This implies that $A(t) \subseteq (A[t])_{{\mathfrak {q}}} \subseteq R_{{\mathfrak {p}}}$. The thesis follows. $\square$

Theorem 5.8

Let R be defined as in Construction 5.3. Then ${\overline{R}}= Kr({\overline{D}})$ and all the localizations of R at the maximal ideals are of the form $R_{{\mathfrak {p}}} = A_V(t)$ where ${\mathfrak {p}}= {\mathfrak {m}}_{A_V(t)} \cap R$.

Proof

By construction, for every valuation overring V dominating $D'$, the integral closure of $A_V$ is $B_V:={\overline{V}}^F$, which is the intersection of all the extensions of V to F, of which there are finitely many. Hence $\overline{A_V}$ is a semilocal Prüfer domain. By Theorem 4.8, Nagata ring extension commutes with intersection for all the overrings of $A_V$. It follows that $R = \bigcap _{V \supseteq D'} A_V(t)$ and therefore

$$\begin{aligned} Kr(D')= \bigcap _{V \in \textrm{Zar}(D')} V(t) \subseteq R \subseteq Kr({\overline{D}})= \bigcap _{V \in \textrm{Zar}(D')} B_V(t). \end{aligned}$$

Pick now an element $\Phi \in Kr({\overline{D}})$. The field extension $F(t)/F'(t)$ is clearly a finite Galois extension generated by $\theta _1, \ldots , \theta _n$ and satisfies one of the conditions $(*_1)$, $(*_2)$, since so does the field extension $F/F'.$ Hence, there exist $\phi _1(t), \ldots , \phi _n(t) \in F'(t)$ such that

$$\begin{aligned} \Phi = \sum _{j=1}^n \phi _j(t) \theta _j \in Kr({\overline{D}})= \bigcap _{V \in \textrm{Zar}(D')} B_V(t). \end{aligned}$$

By Proposition 5.6, this yields $\phi _j(t) \theta _j \in Kr({\overline{D}})$ for every $j=1, \ldots , n$. If now all $\theta _j$ are units in ${\overline{D}}$, this gives

$$\begin{aligned} \phi _j(t) \in \bigcap _{V \in \textrm{Zar}(D')} B_V(t) \cap F'(t)= \bigcap _{V \in \textrm{Zar}(D')} V(t) = Kr(D') \subseteq R \end{aligned}$$

and shows that $\Phi$ is integral over R since so are all $\theta _j$. If instead all $\theta _j$ are simple roots, saying that $\theta _j^{e_j} \in D'$, we obtain $(\phi _j(t) \theta _j)^{e_j} \in Kr({\overline{D}}) \cap F'(t) \subseteq R,$ again showing that $\Phi$ is integral over R, being a sum of integral elements.

Now, using that ${\overline{R}}= Kr({\overline{D}})$, we obtain that all the maximal ideals of R are centers of trivial extensions of valuation overrings of D. In particular, since $R \subseteq A_V(t) \subseteq \overline{A_V}(t)= B_V(t)$, every maximal ideal of R is of the form ${\mathfrak {p}}= {\mathfrak {m}}_{A_V(t)} \cap R$. This proves the inclusions $R_{{\mathfrak {p}}} \subseteq A_V(t)$ and ${\mathfrak {p}}R_{{\mathfrak {p}}} \subseteq {\mathfrak {m}}_{A_V(t)}$. We show now that $A_V \subseteq R_{{\mathfrak {p}}}$. For this observe first that ${\mathfrak {m}}_D \subseteq {\mathfrak {m}}_{A_V} \cap R \subseteq {\mathfrak {p}}$. Then pick $\alpha \in V$. The fraction $\frac{1}{t+\alpha } \in Kr(D') \subseteq R$ but $v(\frac{1}{t+\alpha })=0$, hence $\frac{1}{t+\alpha } \not \in {\mathfrak {m}}_{V(t)}= {\mathfrak {m}}_{A_V(t)} \cap V(t)$. This implies $\frac{1}{t+\alpha } \not \in {\mathfrak {p}}$, thus $\alpha \in R_{{\mathfrak {p}}}$. It is clear that ${\mathfrak {m}}_{V(t)} \subseteq {\mathfrak {p}}$. It follows that $A_V \subseteq R_{{\mathfrak {p}}}$. The thesis now follows by Lemma 5.7. $\square$

The above theorem shows that the localizations of R at prime ideals coincide with the localizations of some Nagata ring extensions of overrings of D. Essentially by the same proof we can obtain the same result also for some integral extensions of R.

Corollary 5.9

Take the assumptions and notations of Construction 5.3. For each ring $A_V$, let $C_V$ be a local integral extension. Let $T= \bigcap _{V \supseteq D'} C_V$ and suppose $T \ne {\overline{D}}$. Let $R^*= \bigcap _{V \supseteq D'} C_V(t)$. Then the ring $R^*= Kr^{{\mathcal {F}}^*}(T)$ for some defining family ${\mathcal {F}}^*$ of T and the integral closure of $R^*$ is $Kr({\overline{D}})$. Moreover, let ${\mathfrak {p}}= {\mathfrak {m}}_{C_V(t)} \cap R$. If $C_V \subseteq R^*_{{\mathfrak {p}}}$, then $R^*_{{\mathfrak {p}}} = C_V(t)$.

Proof

The integral closure of any of the rings $C_V$ is semilocal and Prüfer. Hence, as in the proof of Theorem 5.8, the family ${\mathcal {F}}^*$ can be chosen to be the family of all the maximal excluding overrings of the rings $C_V$. By definition we have inclusions $R \subseteq R^* \subseteq R \subseteq Kr({\overline{D}})$, showing that $\overline{R^*}= {\overline{R}}= Kr({\overline{D}})$. The last part about localizations follows by Lemma 5.7. $\square$

Corollary 5.9 can be applied to the following situation.

Proposition 5.10

Let $D= K'+{\mathfrak {m}}$ be constructed as in Example 5.4. Let $C_V= V[\sum _{i=1}^n \theta _i {\mathfrak {m}}_{V}]$ and let ${\mathfrak {p}}= {\mathfrak {m}}_{C_V(t)} \cap R$. Then $C_V$ is local and $A_V \subseteq C_V \subseteq R^*_{{\mathfrak {p}}}$.

Proof

From the inclusions ${\mathfrak {m}}_D \subseteq \sum _{i=1}^n \theta _i {\mathfrak {m}}_{D'} \subseteq \sum _{i=1}^n \theta _i {\mathfrak {m}}_{V}$, it follows that $A_V \subseteq C_V$ and $\overline{C_V}= {\overline{V}}^F$. Let $\sigma _1, \ldots , \sigma _n$ be the elements of Gal$(F/F')$ with $\sigma _1$ equal to the identity. To see that $C_V$ is local, pick $\alpha = a + \sum _{i=1}^n \theta _i b_i$ with $b_i \in {\mathfrak {m}}_V$ and a a unit in V. Observe that $\sigma _j(\theta _i)b_i \in {\mathfrak {m}}_VC_V \subseteq \text{ Jac }({\overline{V}}^F)$ for every i, j. In particular the product $\prod _{i=1}^n \sigma _i(\alpha ) = a^n + z$, with $z \in {\mathfrak {m}}_VC_V$, is a unit in $C_V$. It follows that

$$\begin{aligned} \frac{1}{\alpha }= \frac{\prod _{i=2}^n \sigma _i(\alpha )}{\prod _{i=1}^n \sigma _i(\alpha )} \in C_V. \end{aligned}$$

Now let us prove that $C_V \subseteq R^*_{{\mathfrak {p}}}$. By the same argument used in the proof of Theorem 5.8, we obtain $V \subseteq R^*_{{\mathfrak {p}}}$. We need to show that $z\theta _i \in R^*_{{\mathfrak {p}}}$ for $z \in {\mathfrak {m}}_V$. For this consider the fraction $\phi =\frac{1}{t+z\theta _i}$. For all the valuation overrings $V'$ of $D'$ containing z, we have $\phi \in C_V(t)$. For the valuation overrings $V'$ not containing z, we have $z^{-1} \in {\mathfrak {m}}_{V'}$, $z^{-1}\theta _i^{-1} \in C_V$, and $\phi =\frac{z^{-1}\theta _i^{-1}}{z^{-1}\theta _i^{-1}t+1} \in C_V(t)$. Thus $\phi \in \bigcap _{V \supseteq D'} C_V(t) = R$. In particular, since $\phi$ is a unit in $C_V$, we obtain $\phi ^{-1} \in R^*_{{\mathfrak {p}}}$ and therefore $z\theta _i \in R^*_{{\mathfrak {p}}}$. $\square$

In general the rings $A_V$ may be too small for being maximal excluding. In particular if ${\overline{V}}^{F}$ has more than two maximal ideals we do not expect $A_V$ to be maximal excluding. In some cases it can be shown that $A_V$ is maximal excluding. For $D=K[[x^2, x^3, y]]$ and $D'=K[[x^2, y]]$, we have $A_V= V[x^3]_{{\mathfrak {m}}_V, x^3}$. For $V=K[[x^2, y, \frac{y}{x^{2}}, \frac{y}{x^{4}}, \ldots ]]$, the ring $A_V=K[[x^2, x^3, y, \frac{y}{x}, \frac{y}{x^{2}}, \ldots ]]$ is maximal excluding since it can be expressed as pullback as in Theorem 3.1. Also, if $V=K[[y, x^2, \frac{x^2}{y}, \frac{x^2}{y^2}, \ldots ]]$, the ring $A_V=K[[y, x^3, x^2, \frac{x^2}{y}, \frac{x^2}{y^2}, \ldots ]]$ is a generalized power series ring and is maximal with respect to excluding the element $\frac{x^3}{y}$ by Theorem 3.3. In the next examples we construct rings of the form $Kr^{{\mathcal {F}}}(D)$ such that the rings $A_V$ or $C_V$ are all maximal excluding.

Example 5.11

Adopting the same notation of Example 5.4 and Proposition 5.10, let $D'= {\mathbb {Q}}+ {\mathfrak {n}}$, $D= {\mathbb {Q}}+ {\mathfrak {m}}= {\mathbb {Q}}+ {\mathfrak {n}} + i {\mathfrak {n}}$ and ${\overline{D}}= {\mathbb {Q}}(i)+{\mathfrak {m}}$. For a valuation overring V of $D'$, set $C_V = V[i{\mathfrak {m}}_V]$. We show that $C_V$ is maximal with respect to excluding the element i. It is clear that $C_V \subseteq V(i)$ is a minimal ring extension. We have two possible cases. In the first $a^2 + 1 \not \in {\mathfrak {m}}_V$ for every $a \in V$. It is easy to check that in this case there is only one valuation W of F extending V, and $w(a+ib)= \textrm{min}(v(a), v(b))$. Hence, $W=V(i)$ and its residue field is isomorphic to $\frac{V}{{\mathfrak {m}}_V}(i)$. Now [17, Theorem 2.4], or alternatively our Corollary 3.2, shows that $C_V$ is maximal excluding. In the other case we have two distinct conjugated valuations $W_1$ and $W_2$ extending V to F. We observe that $V(i)=W_1 \cap W_2$, indeed for $a+ib \in W_1 \cap W_2$ we cannot have $v(a)= v(b)<0$, otherwise the conjugate $a-ib$ would not be in the same ring. Again [17, Theorem 2.4] shows that $C_V$ is maximal excluding. The structure of $C_V$ in this case is described by [25, Theorem 14].

In the next example we replace the intersection of all the valuation overrings of $D'$ by the intersection of a smaller collection, which still form a defining family for $D'$. The Kronecker function ring associated to this family is an overring of the canonical Kronecker function ring.

Example 5.12

Let $\kappa$ be a field, x an indetreminate over $\kappa$, and T a local integrally closed domain of the form $\kappa (x)+{\mathfrak {m}}$. Set $W=\kappa [[x]]$ and $B=\kappa [[x^2, x^3]]$ (one can also take any other maximal excluding domain having W as integral closure). Define D to be the pullback $B + {\mathfrak {m}}$. If we assume that T is not a valuation ring, the ring D is not maximal excluding by Theorem 3.1. For $F={\mathcal {Q}}(D)$, let $F'$ be the largest subfield of F containing $x^2$ but not x. The ring $D'$ in this case is set to be $\kappa [[x^2]]+ ({\mathfrak {m}}\cap F')$ and we set also $T'= D'_{{\mathfrak {m}}\cap F'}= \kappa (x^2)+({\mathfrak {m}}\cap F')$. The extension $F/F'$ satisfies the assumption of Construction 5.3. We can now express $D'$ as the intersection of the valuation overrings V of the form $V= \pi _V^{-1}(\kappa [[x^2]])$ where $\pi _V$ is the quotient map from a valuation overring $V'$ of $T'$ to its residue field. For any of such V, we can define as previously $A_V= V[{\mathfrak {m}}_D]_{{\mathfrak {m}}_V, {\mathfrak {m}}_D} = V[x^3, {\mathfrak {m}}]$. In particular $A_V$ is the pullback of B with respect to the quotient map from the valuation overring $V'(x)$ of T to its residue field. Therefore $A_V$ is maximal excluding by Theorem 3.1. Let ${\mathcal {F}}$ be the family of all the rings $A_V$. The same proof used for Theorem 5.8 shows that, if $R= Kr^{{\mathcal {F}}}(D)$, then ${\overline{R}}$ is the Kronecker function ring of ${\overline{D}}$ obtained by intersecting all the valuations of the form $V'(x)(t)$. Furthermore, all the localizations of R at the maximal ideals are of the form $A_V(t)$.

We now move on to discuss a second construction which produces rings that are very close the the Kronecker function ring of ${\overline{D}}$, in the sense that they locally coincide for almost all the maximal ideals. This construction allows also to describe cases where the integral closure of D is not finitely generated over D or where the integral closure of some overring in the defining family of D is not Prüfer. The idea is to express D as the intersection of its integral closure with a semilocal domain A. The rings we define here are not necessarily of the form $Kr^{{\mathcal {F}}}(D)$, if the integral domain A is neither maximal excluding nor has Prüfer integral closure. However, Theorem 4.10 give us the tools to study a more general situation.

Construction 5.13

Let D be an integral domain and suppose that there exists a semilocal overring A such that $D = {\overline{D}} \cap A$. Suppose that also ${\overline{A}}$ is semilocal with s maximal ideals and all the residue fields of D have cardinality at least $s+1$. Let $R'= Kr({\overline{D}}) \cap A(t)$.

Notice that if D arises as in Construction 5.3 and A contains an intersection of rings of the form $A_V$, then the above ring $R'$ is an overring of the ring R, contained in $Kr({\overline{D}})$. By Theorem 5.8, one immediately gets $\overline{R'}= Kr({\overline{D}})$. Easy examples that illustrate this construction are

$$\begin{aligned} D= K[[x^2, x^3, y]]= K[[x,y]] \cap K((y))[[x^2, x^3]], \end{aligned}$$

and the ring D defined in Example 4.14.

Before proving the main theorem about this construction, we need to investigate the integral closure of local rings of the form $A \cap V$ considered in Theorem 4.10-(i).

Remark 5.14

Let A and V be defined as above. Obviously there is an inclusion $\overline{A \cap V} \subseteq {\overline{A}} \cap V$. However, the containment may be strict: for instance take $A= {\mathbb {Q}}+ X{\mathbb {Q}}(i)[[X]]$ and $V= {\mathbb {Z}}_{(5)}[\frac{2+i}{5}] + X{\mathbb {Q}}(i)[[X]]$. These rings have the same quotient field and V is a valuation domain. We have $A \cap V = {\mathbb {Z}}_{(5)} + X{\mathbb {Q}}(i)[[X]]$, ${\overline{A}}= {\mathbb {Q}}(i)[[X]]$, and

$$\begin{aligned} \overline{A \cap V} = {\mathbb {Z}}_{(5)}(i) + X{\mathbb {Q}}(i)[[X]] \subsetneq {\overline{A}} \cap V = V. \end{aligned}$$

Next proposition analyzes the relation between $\overline{A \cap V}$ and ${\overline{A}} \cap V$.

Proposition 5.15

Let A be a local domain, V a valuation ring such that ${\mathcal {Q}}(A)= {\mathcal {Q}}(V)= {\mathcal {Q}}(A \cap V)$ and suppose that A is dominated by a localization $V_Q$ of V. Let ${\mathfrak {q}}=Q \cap {\overline{A}}$ be the center of $V_Q$ in ${\overline{A}}$ and set $B= \overline{A \cap V}$ and $C = {\overline{A}}_{{\mathfrak {q}}} \cap V$. Then the following assertions hold:

• (1) $B':= \frac{B}{Q \cap B}$ and $C':= \frac{C}{Q \cap C}$ are Prüfer domains with the same quotient field.

• (2) $C'$ is the localization of $B'$ at the maximal ideal defined as the center of the valuation ring $\frac{V}{Q}$.

Proof

Since $V_Q$ dominates A, then ${\mathfrak {q}}$ is a maximal ideal of ${\overline{A}}$ and $V_Q$ dominates ${\overline{A}}_{{\mathfrak {q}}}$. Thus C is local and its structure is described in Theorem 4.10-(i). In particular $Q \cap C = {\mathfrak {q}}{\overline{A}}_{{\mathfrak {q}}}$ and $C'$ is a valuation domain with quotient field $\kappa = \frac{{\overline{A}}_{{\mathfrak {q}}}}{{\mathfrak {q}}{\overline{A}}_{{\mathfrak {q}}} } = \frac{{\overline{A}}}{{\mathfrak {q}}}.$ For the same reason, again by Theorem 4.10-(i), we have that $A':= \frac{A \cap V}{{\mathfrak {m}}_A}$ is a valuation domain with quotient field $\kappa '= \frac{A}{{\mathfrak {m}}_A}$. By standard results on quotient rings of integral extensions, since $Q \cap (A \cap V)= {\mathfrak {m}}_A$, we get that $B'$ is an integral extension of $A'$ and $\kappa$ is an algebraic field extension of $\kappa '$. The integral closure of a valuation domain in an algebraic field extension of the quotient field is a Prüfer domain. The ring $B'$ is clearly integrally closed, thus is a Prüfer domain. It is clear that $B' \subseteq C'$. To prove (1) it remains to show that they have the same quotient field. For this we prove that ${\overline{A}} \cap V$ is contained in a ring of fractions $S^{-1}B$ for S a multiplicatively closed set of B with $S \cap Q = \emptyset$. Define $S= (A \cap V) {\setminus } {\mathfrak {m}}_A$. This set S is multiplicatively closed since ${\mathfrak {m}}_A$ is a prime ideal of $A \cap V$ and $S \cap Q = S \cap {\mathfrak {m}}_A= \emptyset$. Pick $x \in {\overline{A}} \cap V$. Then $x^n + a_{n-1}x^{n-1}+ \cdots + a_1x + a_0=0$ for $a_0, \ldots , a_{n-1} \in A$. If $a_0, \ldots , a_{n-1} \in V$ then $x \in B$. Thus suppose that at least one of them is not in V and set $a= \prod _{a_k \not \in V} a_k$. Since ${\mathfrak {m}}_A \subseteq Q \subseteq V$, we have that a is a unit in A and $a^{-1} \in V$. Multiplying the above equation of integral dependence of x by $a^{-n}$ yields an equation of integral dependence of $a^{-1}x$ over $A \cap V$. It follows that $a^{-1}x \in B$ and $x \in S^{-1}B$ because $a^{-1} \in S$. From this, going modulo the contraction of Q and observing that $\frac{{\overline{A}} \cap V}{{\mathfrak {q}}}$ and $C'$ have the same quotient field, we obtain that $B'$ and $C'$ have the same quotient field. Finally to prove (2), we simply notice that V dominates both $A \cap V$ and C, therefore it dominates the localization of B at the maximal ideal ${\mathfrak {m}}_V \cap B = {\mathfrak {m}}_C \cap B$. It follows that $C'$ dominates the localization of $B'$ at the center of $\frac{V}{Q}$. Since $B'$ and $C'$ are Prüfer domains with the same quotient field, $C'$ must be equal to that localization of $B'$. $\square$

Theorem 5.16

Let D, A and $R'$ be defined as in Construction 5.13. The following assertions hold:

• (i) For a valuation overring V of D, let ${\mathfrak {p}}= {\mathfrak {m}}_{V(t)} \cap R'$. Then $R'_{{\mathfrak {p}}}= (A \cap V)_{{\mathfrak {m}}_{V} \cap A}(t)$. Moreover, if A and V have no common proper overrings then $R'_{{\mathfrak {p}}} = V(t)$.

• (ii) For every valuation overring ${\mathcal {V}}$ of $R'$, there exists a valuation overring V of D such that ${\mathcal {V}} \supseteq (A \cap V)(t)$.

• (iii) The localizations of $R'$ at its maximal ideals are Nagata ring extensions of overrings of R.

• (iv) The integral closure of $R'$ is $Kr({\overline{D}}) \cap {\overline{A}}(t)$.

Proof

It is well-known that the number of maximal ideals of A is less or equal than the number of maximal ideals of ${\overline{A}}$. The assumption on the residue fields of D implies that also the residue fields of $A \cap V$ and ${\overline{A}} \cap V$ have cardinality at least s for every valuation overring V of D. Therefore the intersections $A \cap V$ and ${\overline{A}} \cap V$ satisfy the hypothesis of Theorem 4.10.

• (i) By Theorem 4.10-(iv) we immediately get $(A \cap V)(t)= A(t) \cap V(t)$. Hence, $R' \subseteq (A \cap V)(t)$ and ${\mathfrak {p}}$ is equal also to the contraction in $R'$ of the maximal ideal of $(A \cap V)_{{\mathfrak {m}}_{V} \cap A}$. This implies $R'_{{\mathfrak {p}}} \subseteq (A \cap V)_{{\mathfrak {m}}_{V} \cap A}(t)$. We only need to show $(A \cap V)_{{\mathfrak {m}}_{V} \cap A} \subseteq R'$ and apply Lemma 5.7. Let $a,s \in A \cap V$ with $s \not \in {\mathfrak {m}}_V$. Consider

  $$\begin{aligned} F = \frac{1}{t+ a}, \quad G = \frac{1}{t+ s^{-1}} = \frac{s}{st+1}. \end{aligned}$$

  Clearly $F,G \in Kr({\overline{D}}) \cap A(t) = R'$. Moreover, $v(a) \ge 0$, $v(s)=0$, and F, G are units in V(t). Thus $F^{-1}= t+a$ and $G^{-1}= t+s^{-1}$ are in $R'_{{\mathfrak {p}}}$. This proves $\frac{a}{s} \in R'_{{\mathfrak {p}}},$ because $t \in R'$. If A and V have no common proper overrings we get $R'_{{\mathfrak {p}}} = V(t)$ by Theorem 4.10-(iii).

• (ii) Set $V= {\mathcal {V}} \cap {\mathcal {Q}}(D)$ (of course we allow also the case $V={\mathcal {Q}}(D)$). Clearly $V \supseteq R' \cap {\mathcal {Q}}(D) \supseteq D(t) \cap {\mathcal {Q}}(D) = D$. Since $t \in R'$ we get $(A \cap V)[t] \subseteq V[t] \subseteq {\mathcal {V}}$. Pick a polynomial $f=\sum _{k=0}^m a_k t^k \in (A \cap V)[t]$ such that $c(f)= A \cap V$. Let $a_k$ be a coefficient of f. In every valuation overring of $Kr({\overline{D}})$, the value of $a_k$ is larger than or equal to the value of f. Hence $a_kf^{-1} \in Kr({\overline{D}}) \cap A(t) = R' \subseteq {\mathcal {V}}.$ Since $c(f)= A \cap V$ and A is semilocal, by Lemma 4.4 there exist $u_0, \ldots , u_m \in D$, that are either units or zeros, such that $a= \sum _{k=0}^m a_k u_k$ is a unit in $A \cap V$. It follows that $af^{-1} \in R' \subseteq {\mathcal {V}}$. Now a is a unit in $A \cap V$, hence a unit in ${\mathcal {V}}$. This implies $f^{-1} \in {\mathcal {V}}$ and shows $(A \cap V)(t) \subseteq {\mathcal {V}}$.

• (iii) Every prime ideal of $R'$ is the center of some valuation overring of $R'$. By item (ii), every valuation overring ${\mathcal {V}}$ of $R'$ contains an intersection of the form $(A \cap V)(t) = A(t) \cap V(t)$ for some valuation overring V of D. By item (i), $(A \cap V)_{{\mathfrak {m}}_{V} \cap A}(t)$ is the localization of $R'$ at the center of the valuation overring V(t). In particular, given a maximal ideal ${\mathfrak {m}}$ of A, the ring $A_{{\mathfrak {m}}}(t)$ is the localization of $R'$ at the center of any valuation overring V(t) such that V dominates $A_{{\mathfrak {m}}}$. Let ${\mathfrak {p}}= {\mathfrak {m}}_{{\mathcal {V}}} \cap R'$. By Theorem 4.10, since localization at the maximal ideals commutes with Nagata ring extension, ${\mathcal {V}}$ contains a ring C(t) which is equal either to $A_{{\mathfrak {m}}}(t)$ for ${\mathfrak {m}}$ a maximal ideal of A or to $(A \cap V)_{{\mathfrak {m}}_{V} \cap A}(t)$. For what said above, this ring C(t) is a localization of $R'$ at a prime ideal and, if ${\mathfrak {q}}= {\mathfrak {m}}_{{\mathcal {V}}} \cap C(t)$, then ${\mathfrak {q}}\cap R' = {\mathfrak {p}}$. Hence $R'_{{\mathfrak {p}}}$ is the localization of C(t) at ${\mathfrak {q}}$. In particular, since we already know that the rings C(t) are localizations of $R'$ at some prime ideal, it follows that the localizations of $R'$ at its maximal ideals are all of the form C(t) for some overring C of D.

• (iv) We argue showing that every valuation overring of $R'$ contains ${\overline{A}}(t) \cap V(t) = ({\overline{A}} \cap V)(t)$ for some valuation overring V of D. Let ${\mathcal {V}}$ be a valuation overring of $R'$ and let $V= {\mathcal {V}} \cap {\mathcal {Q}}(D)$. By item (ii) we already know that ${\mathcal {V}} \supseteq (A \cap V)(t)$. If ${\mathcal {V}} \supseteq A(t)$, we are done since then ${\mathcal {V}} \supseteq \overline{A(t)} = {\overline{A}}(t)$. Otherwise by Theorem 4.10, localizing at the maximal ideals of $A \cap V$ we find that ${\mathcal {V}} \supseteq (A \cap V)_{{\mathfrak {m}}_V \cap A}(t).$ If $(A \cap V)_{{\mathfrak {m}}_V \cap A} = V$ we can conclude. If not, again by Theorem 4.10, we reduce to the case where there exists a prime ideal Q of V such that $V_Q$ contains A and $(A \cap V)_{{\mathfrak {m}}_V \cap A} = A_{Q \cap A} \cap V.$ Without loss of generality, we simplify the notation possibly replacing A by $A_{Q \cap A}$, and reduce to the case where A and $A \cap V$ are local, $V_Q$ dominates A, and ${\mathcal {V}} \supseteq (A \cap V)(t)$. Obviously, using that Nagata ring extension commutes with integral closure, we get ${\mathcal {V}} \supseteq (\overline{A \cap V})(t)$. Now, if $\overline{A \cap V}= {\overline{A}} \cap V$ we are clearly done. If not we use the result of Proposition 5.15. Let ${\mathfrak {q}}=Q \cap {\overline{A}}$ and set $B= \overline{A \cap V}$ and $C = {\overline{A}}_{{\mathfrak {q}}} \cap V$. It is sufficient to prove that ${\mathcal {V}} \supseteq C(t)$. Since ${\mathcal {V}}$ contains V and t, then ${\mathcal {V}} \supseteq C[t]$. Notice also that the maximal ideal ${\mathfrak {m}}_V \cap B$ of B is contained in ${\mathfrak {m}}_{{\mathcal {V}}}$. Thus, by localization we find that ${\mathcal {V}} \supseteq B_{{\mathfrak {m}}_V \cap B}(t)$. Pick $f \in C[t]$ such that $c(f)= C$. We want to prove that $f^{-1} \in {\mathcal {V}}$. For $h \in C[t]$, if $h^{-1} \in {\mathcal {V}}$ and $g \in {\mathfrak {m}}_V[t] \subseteq {\mathfrak {m}}_{{\mathcal {V}}}$ we get $(h+g)^{-1} \in {\mathcal {V}}$. Hence, we want to find $g \in {\mathfrak {m}}_V[t]$ such that $f+g \in B_{{\mathfrak {m}}_V \cap B}[t]$ and $c(f+g)=B_{{\mathfrak {m}}_V \cap B}$. But Proposition 5.15 implies that $B_{{\mathfrak {m}}_V \cap B}$ and C coincide after going modulo the contractions of Q on both rings. In particular, if $x \in C$, then there exists $z \in Q \cap C \subseteq Q \subseteq {\mathfrak {m}}_V$ such that $x+z \in B_{{\mathfrak {m}}_V \cap B}$. Furthermore, if x is a unit in C then $x+z$ is a unit in $B_{{\mathfrak {m}}_V \cap B}$. Applying this procedure to all the coefficients of f that are not in $B_{{\mathfrak {m}}_V \cap B}$, one can construct a polynomial $g \in Q[t] \subseteq {\mathfrak {m}}_V[t]$ such that $f+g \in B_{{\mathfrak {m}}_V \cap B}[t]$ and $c(f+g)=B_{{\mathfrak {m}}_V \cap B}$. $\square$

Remark 5.17

With the setting of the above theorem, if ${\overline{A}}$ is Prüfer, we automatically have $\overline{R'}= Kr({\overline{D}})$. In this case, since we assume all the rings to have finite dimension, ${\overline{A}}$ has only finitely many valuation rings, hence all but finitely many localizations of $R'$ at prime ideals are valuation domains of the form V(t). The other localizations are localizations of A(t) or of domains of the form $(A \cap V)(t)$.

For instance, let $D= K[[x^2, x^3, y]]$, $A= K((y))[[x^2, x^3]]$, and $R'= Kr({\overline{D}}) \cap A(t)$. Then $\overline{R'}= Kr({\overline{D}})$ because ${\overline{A}}$ is Prüfer. In this case all but two localizations of $R'$ at its prime ideals are of the form V(t). The two remaining localizations are A(t) and $(A \cap W)(t)$ where W is the rank two valuation overring of D having ${\overline{A}}$ as unique minimal overring.

We construct now examples of Kronecker function ring of D of the form $Kr({\overline{D}}) \cap A(t)$ such that A is maximal excluding, but ${\overline{A}}$ is not a valuation. Therefore $\overline{R'} = Kr({\overline{D}}) \cap {\overline{A}}(t) \subsetneq Kr({\overline{D}})$.

Example 5.18

Let K be any field and let $D'= [[K^S]]$ be a maximal excluding generalized power series ring. Let z be an indeterminate over ${\mathcal {Q}}(D)$ and set $D = D'[[z]]$. Let A be the generalized power series ring over K obtained by adding to D all the elements of the form $\frac{z}{y}$ for $y \in {\mathfrak {m}}_{D'}$ a monomial element. This ring A can be represented as pullback of $D'$ with respect to the quotient map from ${\mathcal {Q}}(D')[[z]]$ to its residue field. Hence, by Theorem 3.1, A is maximal excluding. By standard properties of pullback diagrams (see [15, Theorem 1.2]), ${\overline{A}}$ is the pullback of $\overline{D'}$ with respect to the same quotient map. Moreover, $D = {\overline{D}} \cap A$. Let $R'= Kr({\overline{D}}) \cap A(t)$.

Notice that A and ${\overline{A}}$ are both local, therefore D, A and $R'$ satisfy the hypothesis of Construction 5.13 without restrictions on the field K. The generalized power series rings of Example 3.8 and Example 3.14 provide examples where ${\overline{A}}$ is not a Prüfer domain. Those from Examples 3.4 and 3.7 provide examples where ${\overline{D}}$ is not finitely generated as D-module.