Abstract
We show that contact reductions can be described in terms of symplectic reductions in the traditional Marsden–Weinstein–Meyer as well as the constant rank picture. The point is that we view contact structures as particular (homogeneous) symplectic structures. A group action by contactomorphisms is lifted to a Hamiltonian action on the corresponding symplectic manifold, called the symplectic cover of the contact manifold. In contrast to the majority of the literature in the subject, our approach includes general contact structures (not only co-oriented) and changes the traditional view point: contact Hamiltonians and contact moment maps for contactomorphism groups are no longer defined on the contact manifold itself, but on its symplectic cover. Actually, the developed framework for reductions is slightly more general than purely contact, and includes a precontact and presymplectic setting which is based on the observation that there is a one-to-one correspondence between isomorphism classes of precontact manifolds and certain homogeneous presymplectic manifolds.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Reductions of systems due to their symmetries are fundamental tools in almost all areas of physics, having strong links to important questions in the traditional classical mechanics of particles, rigid bodies, fields, fluids, plasmas, and elastic solids, as well as quantum and relativistic theories. A model appearance of reductions is that for Hamiltonian systems with the celebrated Marsden–Weinstein–Meyer theorem, defined for Hamiltonian group actions and with the use of momentum maps (see the historical survey [60]).
Hamiltonian systems are intensively studied recently in the context of contact structures replacing the symplectic ones in the traditional setting. The roots of contact geometry go back to 1872, when Sophus Lie introduced the concept of contact transformations for studying systems of differential equations, but then contact structures became objects of intensive studies in a purely geometric context, as well as a tool for numerous applications, like in Gibbs’ work on thermodynamics, Huygens’ work on geometric optics, Hamiltonian dynamics, fluid mechanics, etc. As a nice source for the history of contact geometry and topology with an extended list of references we recommend [31], and for comprehensive presentation of contact geometry we refer to classical monographs [3, 32, 55].
The standard Hamiltonian formulation describes exclusively isolated systems with reversible dynamics, while real systems are constantly in interaction with the environment, which introduces the phenomena of dissipation and irreversibility. Some of these phenomena can be described mathematically by means of contact geometry methods. There is a huge list of publications on contact Hamiltonian geometry, let us mention only a few recent ones describing mechanical dissipative systems, both in the Hamiltonian and Lagrangian setting [10, 19, 23,24,25, 29], but also quantum systems [15].
Unfortunately, almost all this literature deals with trivial (co-oriented) contact structures, where a global contact form \(\eta \) on a manifold M is given. This is fine for local calculations, but it hides the essence of the corresponding intrinsic geometry. The problem is that, even in co-orientable cases, dealing with contact Hamiltonian vector fields and the Reeb vector field associated with a particular contact form \(\eta \) depends strongly on the choice of \(\eta \) and does not make any sense for more general contact structures. The point is that, changing a local contact form defining the contact structure into another one in the same class of conformal equivalence, we have to change also the Reeb vector field (the new one is not even in the same conformal class) and the original Hamiltonian defined on the contact manifold. Actually, it is a student exercise to prove that if, for a contact distribution  , a tangent vector
, a tangent vector  is not in \(C_y\), then there is a local contact form \(\eta \) inducing C, i.e., \(C=\ker (\eta )\), such that \(v_y={{\mathcal {R}}}_\eta (y)\), where \({{\mathcal {R}}}_\eta \) is the Reeb vector field for \(\eta \).
is not in \(C_y\), then there is a local contact form \(\eta \) inducing C, i.e., \(C=\ker (\eta )\), such that \(v_y={{\mathcal {R}}}_\eta (y)\), where \({{\mathcal {R}}}_\eta \) is the Reeb vector field for \(\eta \).
In [34], we developed an essentially different picture for contact Hamiltonian mechanics and contact Hamilton–Jacobi theory which is geometrically intrinsic and valid for general contact structures. The main change of the view point is that contact structures on M are represented by 1-homogeneous symplectic forms \(\omega \) on \({{\mathbb {R}}^\times }\)-principal bundles \(\tau :P\rightarrow M\), where \({{\mathbb {R}}^\times }={\mathbb {R}}\setminus \{0\}={{\,\textrm{GL}\,}}(1,{\mathbb {R}})\) is the multiplicative group of nonzero reals. We call these structures symplectic \({{\mathbb {R}}^\times }\)-bundles and they are for us genuine contact structures (see [12, 34, 38]). In this sense, contact geometry is not an ‘odd dimensional version’ of symplectic geometry but rather a particular, namely homogeneous, symplectic geometry. To make it precise, let us mention that on every \({{\mathbb {R}}^\times }\)-principal bundle \(\tau :P\rightarrow M\) with respect to an action of the Lie group \({{\mathbb {R}}^\times }\),
a concept of homogeneity of tensor field is well defined. Namely, a vector field X (resp., a differential form \(\alpha \)) on P is homogeneous of degree \(k\in {\mathbb {Z}}\) if \((h_s)_*(X)=s^{-k}\cdot X\) (resp., \((h_s)^*(\alpha )=s^k\cdot \alpha \)). Putting \(\Phi =h_s\) in the general differential geometric formula
valid for any diffeomorphism \(\Phi :N_1\rightarrow N_2\), any differential form \(\alpha \) on \(N_2\), and any vector field X on \(N_1\), we immediately get that \(i_X\alpha \) is \((l+k)\)-homogeneous if only X is k-homogeneous and \(\alpha \) is l-homogeneous. It is also easy to see that then  is also l-homogeneous. Any symplectic \({{\mathbb {R}}^\times }\)-bundle associated with a given contact structure we call its symplectic cover. All these covers are canonically isomorphic, but a choice of a particular presentation of a symplectic cover may depend on our purposes. All this can be generalized to precontact structures and their presymplectic covers being presymplectic \({{\mathbb {R}}^\times }\)-bundles. The corresponding theory is developed in this paper.
is also l-homogeneous. Any symplectic \({{\mathbb {R}}^\times }\)-bundle associated with a given contact structure we call its symplectic cover. All these covers are canonically isomorphic, but a choice of a particular presentation of a symplectic cover may depend on our purposes. All this can be generalized to precontact structures and their presymplectic covers being presymplectic \({{\mathbb {R}}^\times }\)-bundles. The corresponding theory is developed in this paper.
Note that any \({{\mathbb {R}}^\times }\)-principal bundle \(P\rightarrow M\) can be viewed as an open submanifold \(L^\times _P\) of nonzero vectors in the suitable line bundle \(L_P\) with the action of \({{\mathbb {R}}^\times }\) being the multiplication by (nonzero) reals in \(L_P\). The line bundle \(L_P\) can be viewed as the line bundle associated with the principal bundle P and the standard action of \({{\mathbb {R}}^\times }\) on \({\mathbb {R}}\). In the case of a symplectic \({{\mathbb {R}}^\times }\)-principal bundle corresponding to a contact manifold (M, C), the line bundle \(L_P\) is dual to  . Contact Hamiltonians in this framework are not functions on M but 1-homogeneous functions on P, \(H:P\rightarrow {\mathbb {R}}\) (alternatively, sections of the line bundle \(L^C\)). Since the principal bundle may be nontrivial, there is generally no way to associate with them functions (Hamiltonians) on M. Canonical examples are contact structures on the bundles
. Contact Hamiltonians in this framework are not functions on M but 1-homogeneous functions on P, \(H:P\rightarrow {\mathbb {R}}\) (alternatively, sections of the line bundle \(L^C\)). Since the principal bundle may be nontrivial, there is generally no way to associate with them functions (Hamiltonians) on M. Canonical examples are contact structures on the bundles  of first jets of sections of a line bundle \(L\rightarrow Q\) which are nontrivial if only L is nontrivial. In this case,
of first jets of sections of a line bundle \(L\rightarrow Q\) which are nontrivial if only L is nontrivial. In this case,  with its canonical symplectic form and the so-called phase lift (see [11, 12, 34, 38, 43]) of the \({{\mathbb {R}}^\times }\)-principal bundle structure on \((L^*)^\times =L^*\setminus \{0_M\}\) consisting of nonzero vectors in L (cf. [34, 38]). Note that this phase lift is not the same as the standard cotangent lift of a group action. In [38], it was shown that these canonical examples are the only linear contact structures. This result is a contact analog of the well-known fact that every linear symplectic structure on a vector bundle \(E\rightarrow M\) is equivalent to the canonical symplectic structure on
with its canonical symplectic form and the so-called phase lift (see [11, 12, 34, 38, 43]) of the \({{\mathbb {R}}^\times }\)-principal bundle structure on \((L^*)^\times =L^*\setminus \{0_M\}\) consisting of nonzero vectors in L (cf. [34, 38]). Note that this phase lift is not the same as the standard cotangent lift of a group action. In [38], it was shown that these canonical examples are the only linear contact structures. This result is a contact analog of the well-known fact that every linear symplectic structure on a vector bundle \(E\rightarrow M\) is equivalent to the canonical symplectic structure on  .
.
Since the symplectic form \(\omega \) on a symplectic \({{\mathbb {R}}^\times }\)-bundle P is 1-homogeneous with respect to the \({{\mathbb {R}}^\times }\)-action, 1-homogeneous Hamiltonians are closed with respect to the symplectic Poisson (Lagrange) bracket \(\{ H_1,H_2\}_\omega \). This defines also a Jacobi bracket of sections of \(L^*_P\) which makes \(L^*_P\) into a local Lie algebra in the sense of Kirillov [45, 49, 58] or, equivalently, into a Jacobi bundle in the sense of Marle [58], or a Kirillov manifold in the sense of [12, 38]. For trivial principal (or line) bundles, we get a Jacobi structure on M, i.e., a Jacobi bracket on the \(C^\infty (M)\)-module \(C^\infty (M)\) in the sense of Lichnerowicz [21, 56]. A standard misunderstanding present in the literature is that the Jacobi bracket on \(C^\infty (M)\) is viewed as a bracket on the associative algebra \(C^\infty (M)\), and not on \(C^\infty (M)\) as a \(C^\infty (M)\)-module. The corresponding Jacobi structure on M is therefore understood as a pair \((\Lambda ,\Gamma )\), where \(\Lambda \) is a bivector field and \(\Gamma \) is a vector field on M (satisfying some additional conditions), that comes from taking the constant function 1 as the basic section for this module, while choosing another basic section leads to other tensors \((\Lambda ,\Gamma )\) for the same Jacobi bracket.
Note that our symplectic \({{\mathbb {R}}^\times }\)-bundles, being particular instances of symplectic Liouville manifolds in the terminology of [55], can be understood as more advanced symplectizations of contact structures which (at least for contact forms) are very well known in contact geometry. The use of the multiplicative group \({{\mathbb {R}}^\times }\) (which is non-connected) instead of the additive group \({\mathbb {R}}\) (or the multiplicative group \({\mathbb {R}}^+\) of positive reals), which appears in traditional symplectizations of contact forms, is crucial for including nontrivial contact structures into the picture. Traditional symplectizations of contact forms produce symplectic \({\mathbb {R}}^+\)-principal bundles (which are always trivializable) which are sometimes called symplectic cones. The same remains valid for Jacobi brackets and the corresponding poissonizations.
Contact reductions, as contact analogs of various symplectic reductions, and related questions (for a pure algebraic approach to Poisson and Jacobi reductions see [41, 48]) were already a subject of studies in numerous papers, let us mention [2, 7, 22, 30, 46, 52,53,54, 57, 79]. These reductions are mainly reductions by Lie group actions, and generally use contact forms as the starting point, even if in some cases (e.g., [79]) the final reduced structure does not depend on the choice of the contact form in its conformal (equivalence) class. Consequently, contact moment maps are usually defined on contact manifolds themselves, and associated with actions preserving the contact form, which is completely non-geometrical from the contact geometry point of view. An exception is the paper [80], which is devoted to generalized concepts of a reduction, and [57], where a concept of the moment map, although geometrically different, is equivalent to ours, but no symplectic geometry is used and only the zero-value of the moment map is considered (which is the trivial part in our setting). Note finally that contact reductions can be viewed as particular cases of reductions of Jacobi bundles. In [76], the authors propose a version of coisotropic reductions of contact structures in the language of Jacobi bundles and Jacobi brackets. Some reductions of Jacobi brackets on functions on manifolds (e.g., trivial Jacobi bundles) are developed in [62, 63, 65, 66].
In this paper we propose a completely different approach by viewing contact reductions as particular (homogeneous) symplectic reductions on symplectic \({{\mathbb {R}}^\times }\)-bundles. Therefore, we can use some well-known methods from symplectic geometry and the reductions are intrinsic from the very beginning, not referring to any auxiliary contact form representing the contact structure. Moreover, the proposed reduction procedure is very broad and includes not only contact analogs of the Marsden–Weinstein–Meyer reduction by a Lie group action, but also constant rank submanifold reductions. Our version of a contact Marsden–Weinstein–Meyer reduction is the following (cf. Theorem 6.3).
Theorem 1.1
Let (M, C) be a contact manifold with a symplectic cover \(\tau :P\rightarrow M\), let \(\rho :G\times M\rightarrow M\) be an action on M of a Lie group G by contactomorphisms, and let \(J:P\rightarrow {\mathfrak {g}}^*\) be the corresponding contact moment map. Let \(\mu \in {\mathfrak {g}}^*\) be a weakly regular value of J, so the connected Lie subgroup \(G_\mu ^0\) of G, corresponding to the Lie subalgebra
of the Lie algebra \({\mathfrak {g}}\) of G, acts on the submanifold \(M_\mu =\tau (J^{-1}(\mu ))\) of M. In particular, \(G^0_\mu =G\) if \(\mu =0\) and G is connected.
Suppose additionally that  is transversal to C and the \(G^0_\mu \)-action on \(M_\mu \) is free and proper. Then we have a canonical submersion \(\pi :M_\mu \rightarrow M(\mu )\) onto the orbit manifold \(M(\mu )=M_\mu /G^0_\mu \), which is canonically a contact manifold with the contact structure
is transversal to C and the \(G^0_\mu \)-action on \(M_\mu \) is free and proper. Then we have a canonical submersion \(\pi :M_\mu \rightarrow M(\mu )\) onto the orbit manifold \(M(\mu )=M_\mu /G^0_\mu \), which is canonically a contact manifold with the contact structure  .
.
Note that in the case \(\mu =0\) our contact reduction comes down to the standard Marsden–Weinstein–Meyer reduction on the symplectic cover of the contact manifold.
Actually, in the paper we consider a more general situation when a field of hyperplanes C on a manifold M is only precontact, i.e., the corresponding 2-form on C is of constant rank (this form is nondegenerate in the contact case). We associate with precontact structures (M, C) presymplectic \({{\mathbb {R}}^\times }\)-bundles, i.e., principal \({{\mathbb {R}}^\times }\)-bundles \(\tau :P\rightarrow M\) equipped with a 1-homogeneous presymplectic form \(\omega \). Note that we always understand presymplectic forms as closed 2-forms of constant rank and all objects are generally smooth. One exception are distributions understood as just fields of linear subspaces of tangent bundles (non-necessarily smooth). On the other hand, constant rank distributions are always assumed to be regular, i.e., of constant rank and smooth. In particular, when we speak about fields of hyperplanes, we always mean smooth fields of hyperplanes. Groups and precontact manifolds are connected, if not declared otherwise.
With every contact vector field on a precontact manifold (M, C), i.e., a vector field whose local flow preserves C, we associate a Hamiltonian vector field on the presymplectic cover \((P,\omega )\) of (M, C) and a unique 1-homogeneous Hamiltonian on P. In the case of a contact group action, this leads to a uniquely defined equivariant moment map \(J:P\rightarrow {\mathfrak {g}}^*\), so we can follow the ideas of Meyer, Marsden, and Weinstein [60, 61] if the reduction by symmetry group is concerned. Note finally that presymplectic reductions have been already studied by some authors (e.g., [13, 27]), including reductions of Dirac structures [6, 9]. The paper is organized as follows.
In the next section, we present basics of our understanding of precontact geometry, together with introducing presymplectic \({{\mathbb {R}}^\times }\)-bundles. Also fundamental theorems describing relations between precontact and presymplectic setting are proved there. In Sect. 3, we show a precontact analog of the presymplectic reduction, i.e., precontact-to-contact reduction, while Sect. 4 is devoted to precontact and contact Hamiltonian dynamics. Different types of submanifolds in precontact manifold are considered in Sect. 5, together with a contact analog of the constant rank reduction in symplectic geometry. The precontact analogs of the Marsden–Weinstein–Meyer reduction are proved in Sect. 6. We end up with concluding remarks, showing in part possible applications and follow-up studies.
2 Principles of precontact geometry
For our picture of contact geometry, we refer generally to [12, 34, 38]. It is easy to generalize the concepts developed there to a precontact setting.
Let M be a manifold of dimension m, and let  be a field of hyperplanes on M, i.e., a distribution with \((m-1)\)-dimensional fibers (corank 1 distribution). Such a distribution is, at least locally, the kernel of a nonvanishing 1-form \(\eta \) on M, i.e., \(C=\ker (\eta )\). Of course, the 1-form \(\eta \) is determined only up to conformal equivalence, since \(\ker (\eta ')=\ker (\eta )\) if and only if \(\eta '=f\eta \), where f is a nowhere-vanishing function. Denote with
be a field of hyperplanes on M, i.e., a distribution with \((m-1)\)-dimensional fibers (corank 1 distribution). Such a distribution is, at least locally, the kernel of a nonvanishing 1-form \(\eta \) on M, i.e., \(C=\ker (\eta )\). Of course, the 1-form \(\eta \) is determined only up to conformal equivalence, since \(\ker (\eta ')=\ker (\eta )\) if and only if \(\eta '=f\eta \), where f is a nowhere-vanishing function. Denote with  the canonical projection onto the line bundle
the canonical projection onto the line bundle  , and with \(\nu ^C:C\times _MC\rightarrow L^C\) the skew-symmetric bilinear map which for vector fields X, Y on M, taking values in C, reads \(\nu ^C(X,Y)=\rho ^C([X,Y])\).
, and with \(\nu ^C:C\times _MC\rightarrow L^C\) the skew-symmetric bilinear map which for vector fields X, Y on M, taking values in C, reads \(\nu ^C(X,Y)=\rho ^C([X,Y])\).
Definition 2.1
The distribution \(\ker (\nu ^C)\) we will denote simply \(\chi (C)\) and call the characteristic distribution of C. A hyperplane field  we call a precontact structure of rank \((2r+1)\) if the 2-form \(\nu ^C\) on C is of rank 2r, i.e., the distribution \(\chi (C)\) is regular of rank \((m-2r-1)\). Manifolds equipped with a precontact structure (of rank \((2r+1)\)) we will call precontact manifolds (of rank \((2r+1)\)). Any nonvanishing (local) 1-form which determines a precontact structure C of rank \((2r+1)\) as its kernel we call a precontact form of rank \((2r+1)\). If \((2r+1)\) is the dimension of M, then any precontact structure of rank \((2r+1)\) we call a contact structure and any (local) 1-form \(\eta \) such that \(C=\ker (\eta )\) we call a contact form.
we call a precontact structure of rank \((2r+1)\) if the 2-form \(\nu ^C\) on C is of rank 2r, i.e., the distribution \(\chi (C)\) is regular of rank \((m-2r-1)\). Manifolds equipped with a precontact structure (of rank \((2r+1)\)) we will call precontact manifolds (of rank \((2r+1)\)). Any nonvanishing (local) 1-form which determines a precontact structure C of rank \((2r+1)\) as its kernel we call a precontact form of rank \((2r+1)\). If \((2r+1)\) is the dimension of M, then any precontact structure of rank \((2r+1)\) we call a contact structure and any (local) 1-form \(\eta \) such that \(C=\ker (\eta )\) we call a contact form.
Remark 2.2
Of course, all 1-forms conformally equivalent to a precontact form \(\eta \) of rank \((2r+1)\) are also precontact forms of rank \((2r+1)\) and contactomorphisms, i.e., diffeomorphisms respecting the fields of hyperplanes, are possible only between precontact structures of the same rank. Note that a differential 2-form \(\beta \) is of (constant) rank 2r if and only if \(\beta ^{r}\) is nowhere vanishing and \(\beta ^{r+1}=0\). We will frequently use this fact in the sequel. We will denote the value of a differential form \(\beta \) at point y as \(\beta _y\) or \(\beta (y)\), depending on editorial needs.
Proposition 2.3
Let C be a field of hyperplanes on a manifold M of dimension m, and let \(\eta \) be a nonvanishing 1-form on M such that \(C=\ker (\eta )\). The following are equivalent:
-
(1)
the distribution C is a precontact structure of rank \((2r+1)\);
-
(2)
the 2-form
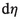 is of rank 2r on \(C=\ker (\eta )\);
is of rank 2r on \(C=\ker (\eta )\); -
(3)
the \((2r+1)\)-form
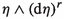 is nonvanishing and
is nonvanishing and 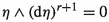 .
. -
(4)
the characteristic distribution
 of \(\eta \), defined by
of \(\eta \), defined by 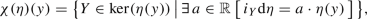
is regular of rank \((m-2r-1)\);
In any, thus all of these cases, \(\chi (C)=\chi (\eta )\) and \(\chi (C)\) is regular and involutive, so it determines a foliation \({\mathcal {F}}_C\) on M, whose leaves are maximal integral submanifolds of \(\chi (C)\).
Proof
\((1\Leftrightarrow 2)\) In the trivialization of \(L^C\) induced by \(\eta \),
we have, for vector fields \(X,Y\in C\),

so the rank of  equals the rank of \(\nu ^C\). Here, \(\big \langle \cdot ,\cdot \big \rangle \) denotes the canonical pairing between vectors and covectors.
equals the rank of \(\nu ^C\). Here, \(\big \langle \cdot ,\cdot \big \rangle \) denotes the canonical pairing between vectors and covectors.
\((2\Leftrightarrow 3)\) Suppose that  is nonvanishing at \(y\in M\). Then,
is nonvanishing at \(y\in M\). Then,  is nonvanishing on \(C_y\), so the rank of
is nonvanishing on \(C_y\), so the rank of  on \(C_y=\ker (\eta _y)\) is at least 2r. If this rank is greater than 2r, then it is at least \(2(r+1)\), so
on \(C_y=\ker (\eta _y)\) is at least 2r. If this rank is greater than 2r, then it is at least \(2(r+1)\), so  at y. Conversely, if the rank of
at y. Conversely, if the rank of  on \(\ker (\eta )\) is 2r, then clearly
on \(\ker (\eta )\) is 2r, then clearly  is nonvanishing and
is nonvanishing and  .
.
\((2\Leftrightarrow 4)\) Let us first show that for each \(y\in M\) we have  . If \(Y\in \chi (\eta )(y)\), then \(Y\in \ker (\eta (y))\) and
. If \(Y\in \chi (\eta )(y)\), then \(Y\in \ker (\eta (y))\) and  for some \(a\in {\mathbb {R}}\), so
for some \(a\in {\mathbb {R}}\), so  vanishes on \(C_y=\ker (\eta )(y)\), thus belongs to kernel of
vanishes on \(C_y=\ker (\eta )(y)\), thus belongs to kernel of  . Conversely, if
. Conversely, if  , then \(Y\in \ker (\eta (y))\) and the linear function
, then \(Y\in \ker (\eta (y))\) and the linear function  on
on  vanishes on \(\ker (\eta (y))\). Hence it is of the form \(a\eta (y)\) for some \(a\in {\mathbb {R}}\). Consequently,
vanishes on \(\ker (\eta (y))\). Hence it is of the form \(a\eta (y)\) for some \(a\in {\mathbb {R}}\). Consequently,  is of rank 2r if and only if the dimension of its kernel is \(m-2r-1\), that finishes the proof.
is of rank 2r if and only if the dimension of its kernel is \(m-2r-1\), that finishes the proof.
Finally, from the proof of \((2\Leftrightarrow 4)\) it follows that \(\chi (C)=\chi (\eta )\). The involutivity of \(\chi (C)\) is a well-known fact. \(\square \)
We have the following version of Darboux Theorem for precontact structures.
Theorem 2.4
(Precontact Darboux Theorem) Let C be a precontact structure of rank \((2r+1)\) on a manifold M of dimension m, and let \(y_0\in M\). Then, there are local coordinates \((z,p_i,q^i,u^j)\) in a neighborhood U of \(y_0\), with \(i=1,\dots ,r\) and \(j=1,\dots ,m-2r-1\), such that these coordinates vanish at \(y_0\) and C is on U the kernel of the 1-form

Proof
Consider a neighborhood U of \(y_0\) which is equipped with coordinates \((z^l,u^j)\) such that the foliation \({\mathcal {F}}_C\) is defined locally by the system of equations \(z^l=const\) and

is a local 1-form such that \(C=\ker (\eta )\). Of course, \(l=1,\dots ,2r+1\) and \(j=1,\dots ,m-2r-1\). Since \(\partial _{u^j}\in \chi (C)\), we have \(g_j=0\) and we can assume that \(f_1=1\), as \(\eta \ne 0\). Moreover, the condition  (Proposition 2.3 (4)) implies that
(Proposition 2.3 (4)) implies that
But for \(f_1=1\) we get \(a_j=0\), so \(\eta \) depends on the coordinates \((z^l)\) only. Since \(\eta \ne 0\) and  is of rank 2r on \(\ker (\eta )\), the 1-form \(\eta \) is actually a contact form in coordinates \((z^l)\), \(l=1\dots ,2r+1\). Using the contact Darboux Theorem, we get (3), and it is easy to see that we can additionally require that \(y_0=0\) in the Darboux coordinates. \(\square \)
is of rank 2r on \(\ker (\eta )\), the 1-form \(\eta \) is actually a contact form in coordinates \((z^l)\), \(l=1\dots ,2r+1\). Using the contact Darboux Theorem, we get (3), and it is easy to see that we can additionally require that \(y_0=0\) in the Darboux coordinates. \(\square \)
Note that the above theorem does not mean that any precontact form of rank \((2r+1)\) inducing C reads locally as in (3). Indeed,  is of rank 2r for \(\eta \) as in (3). On the other hand,
is of rank 2r for \(\eta \) as in (3). On the other hand,  is in the same conformal class as \(\eta \), but
is in the same conformal class as \(\eta \), but

is of rank \(2(r+1)\), not 2r.
Remark 2.5
We will call the foliation \({\mathcal {F}}_C\) on the precontact manifold (M, C) the characteristic foliation. Note that the characteristic distribution \(\chi (C)\) of a precontact structure C is trivial, i.e., \(2r+1=\dim (M)\), if and only if the precontact structure is actually a contact one. According to the Darboux classification of 1-forms [20] (see also [55, Ch. V.4]), the 1-form (3) can be characterized as a 1-form of class \((2r+1)\) on U, i.e., a 1-form \(\eta \) satisfying  and
and  .
.
Note that precontact structures are understood by many authors as just distributions of corank 1, and precontact forms as just nonvanishing 1-forms (e.g., [76, 77, 80]), which is too weak in our opinion. In practice and applications, even such authors put additional requirements which made the structures close to what we call precontact structures and precontact forms. In [25, 26], precontact forms of class \((2r+1)\) are defined as in the Darboux’ classification, so that the precontact manifolds in [25, 26] are trivial examples of the precontact structures in our sense (in which  can be nontrivializable).
can be nontrivializable).
In what follows, we will use also the concept of a presymplectic form after Souriau [74]: a 2-form \(\omega \) is presymplectic of rank \(2(r+1)\) if \(\omega \) is closed and its characteristic distribution \(\chi (\omega )\) has constant rank equal to \(2(r+1)\). Being automatically involutive, \(\chi (\omega )\) defines a foliation \({\mathcal {F}}_\omega \) which we call the characteristic foliation of \(\omega \). Again, some authors consider presymplectic forms simply as closed 2-forms, which is too weak for our purposes. As easily seen, our presymplectic forms are by definition nonzero.
Definition 2.6
A contactomorphism between precontact structures \((M_i,C_i)\), \(i=1,2\), is a diffeomorphism \(\varphi :M_1\rightarrow M_2\) such that  . A contact vector field on a precontact manifold (M, C) is a vector field whose local flow consists of contactomorphisms. For a vector field X on M and a distribution
. A contact vector field on a precontact manifold (M, C) is a vector field whose local flow consists of contactomorphisms. For a vector field X on M and a distribution  , we will write \(X\in D\) if X takes values in D.
, we will write \(X\in D\) if X takes values in D.
The following easy proposition states the properties of contactomorphisms and contact vector fields.
Proposition 2.7
A diffeomorphism \(\varphi :M_1\rightarrow M_2\) between precontact structures being locally the kernels of precontact forms \(\eta _i\), \(i=1,2\), is a contactomorphism if and only if \(\varphi ^*(\eta _2)\) is in the conformal class of \(\eta _1\), i.e., \(\varphi ^*(\eta _2)=f\eta _1\) for a nonvanishing function f. A vector field X on a precontact manifold (M, C) is a contact vector field if and only if \([X,Y]\in C\) for any vector field \(Y\in C\), and if and if and only if \({\pounds }_X\eta =g\eta \) for any (local) precontact form inducing C, where g is a function (not necessary nonvanishing) on M.
2.1 Presymplectic \({{\mathbb {R}}^\times }\)-bundles
Throughout the paper we will use the following notation: if \(L\rightarrow M\) is a vector bundle, then we denote with \(L^\times \) the open submanifold in L consisting of nonzero vectors, i.e., \(L^\times =L\, {\setminus }\, 0_M\), where \(0_M\) is the zero section of L. Of course, if L is a line bundle, i.e., the rank of L is 1, then \({L^\times }\rightarrow M\) is canonically an \({{\mathbb {R}}^\times }\)-principal bundle with respect to the multiplication by nonzero reals. In what follows, principal bundles with the structure group \({{\mathbb {R}}^\times }\) we will call simply \({{\mathbb {R}}^\times }\)-bundles. Any precontact structure (M, C) determines a line subbundle of the cotangent bundle  , namely the annihilator \(C^o\) of C. Any (local) precontact form \(\eta \) determining C induces a local trivialization of \(C^o\), represented by the line subbundle
, namely the annihilator \(C^o\) of C. Any (local) precontact form \(\eta \) determining C induces a local trivialization of \(C^o\), represented by the line subbundle  generated by \(\eta \), and given by
generated by \(\eta \), and given by

Note that under this trivialization, the pull-back of the canonical symplectic form \(\omega _M\) on  is
is

where \(\theta _M\) is the Liouville 1-form on  . Since the zero section of
. Since the zero section of  is a Lagrangian submanifold, we will consider exclusively the form \(\omega _\eta \) restricted to \(M\times {{\mathbb {R}}^\times }\), which corresponds to the restriction of \(\omega _M\) to \([\eta ]^\times \). Note that \(\tau :M\times {{\mathbb {R}}^\times }\rightarrow M\) is a trivial \({{\mathbb {R}}^\times }\)-bundle, and the opposite of the fundamental vector field of the \({{\mathbb {R}}^\times }\)-action and \(1\in {\mathbb {R}}\), where we understand \({\mathbb {R}}\) as the Lie algebra of \({{\mathbb {R}}^\times }\), is \(\nabla =s\partial _s\).
is a Lagrangian submanifold, we will consider exclusively the form \(\omega _\eta \) restricted to \(M\times {{\mathbb {R}}^\times }\), which corresponds to the restriction of \(\omega _M\) to \([\eta ]^\times \). Note that \(\tau :M\times {{\mathbb {R}}^\times }\rightarrow M\) is a trivial \({{\mathbb {R}}^\times }\)-bundle, and the opposite of the fundamental vector field of the \({{\mathbb {R}}^\times }\)-action and \(1\in {\mathbb {R}}\), where we understand \({\mathbb {R}}\) as the Lie algebra of \({{\mathbb {R}}^\times }\), is \(\nabla =s\partial _s\).
Of course, the map (4), thus the closed 2-form \(\omega _\eta \), is defined for any 1-form \(\eta \). The following proposition describes a relation between the characteristic distribution of \(\omega _\eta \),

and the characteristic distribution of \(\eta \),

Proposition 2.8
Let \(\eta \) be a 1-form on a manifold M. For any  and any \(a\in {\mathbb {R}}\), the vector
and any \(a\in {\mathbb {R}}\), the vector  is a characteristic vector of the closed 2-form \(\omega _\eta \) if and only if Y is a characteristic vector of the form \(\eta \).
is a characteristic vector of the closed 2-form \(\omega _\eta \) if and only if Y is a characteristic vector of the form \(\eta \).
In particular, the fibers of the characteristic distribution \(\chi (\omega _\eta )\) are projected by  onto the fibers of the characteristic distribution \(\chi (\eta )\) of \(\eta \). The projection
onto the fibers of the characteristic distribution \(\chi (\eta )\) of \(\eta \). The projection  is an isomorphism of vector spaces if and only if \(\eta (\tau (x))\) is nonvanishing, so a is uniquely determined. If \(\eta (y)=0\), then \(\partial _s\) is a characteristic vector of \(\omega _\eta (y,s)\) for all \(s\in {{\mathbb {R}}^\times }\).
is an isomorphism of vector spaces if and only if \(\eta (\tau (x))\) is nonvanishing, so a is uniquely determined. If \(\eta (y)=0\), then \(\partial _s\) is a characteristic vector of \(\omega _\eta (y,s)\) for all \(s\in {{\mathbb {R}}^\times }\).
Proof
The vector  is a characteristic vector of \(\omega _\eta \) if and only if
is a characteristic vector of \(\omega _\eta \) if and only if

This is clearly equivalent to \(Y\in \ker (\eta )\) and

which means, in turn, that Y is a characteristic vector of \(\eta \). The number \(a\in {\mathbb {R}}\) is uniquely determined if and only if \(\eta (y)\ne 0\), and arbitrary if \(\eta (y)=0\), that implies immediately the final statements. \(\square \)
A fundamental observation which connects precontact geometry with the presymplectic one, is the following (cf. [12, 38]).
Theorem 2.9
A nonvanishing 1-form \(\eta \) on a manifold M is a precontact form of rank \((2r+1)\) if and only if the closed 2-form (5) on \(M\times {{\mathbb {R}}^\times }\) is presymplectic of rank \(2(r+1)\) (in particular, \(\omega _\eta \) is symplectic on \(M\times {{\mathbb {R}}^\times }\) if and only if \(\eta \) is a contact form). In this case, the characteristic distribution \(\chi (\omega _\eta )\) of \(\omega _\eta \) is transversal to the fibers of the projection \(\tau :M\times {{\mathbb {R}}^\times }\rightarrow M\).
Remark 2.10
Before proving, let us explain the term ‘transversal to the fibers’ used in the above theorem. What we mean here and in several other places later on is that at each point the intersection of the distribution and the subspace of vectors vertical with respect to the projection \(\tau \) is trivial. This notion of transversality does not agree with the traditional one, we have nevertheless decided to use this terminology for purposes of this paper. We hope it will not lead to any misunderstanding.
Proof
(\(\Rightarrow \)) Let us assume that \(\eta \) is precontact of rank \((2r+1)\), which means that  , while
, while  . The 2-form \(\omega _\eta \) is clearly closed. We have
. The 2-form \(\omega _\eta \) is clearly closed. We have

The two summands are linearly independent and  , so \((\omega _\eta )^{r+1}\ne 0\). We have
, so \((\omega _\eta )^{r+1}\ne 0\). We have

The first summand vanishes, since  , and the second vanishes, since
, and the second vanishes, since

Therefore, \((\omega _\eta )^{r+2}=0\), thus \((\omega _\eta )\) is of rank \(2(r+1)\).
(\(\Leftarrow \)) Now we assume that \((\omega _\eta )\) is of rank \(2(r+1)\), i.e., \((\omega _\eta )^{r+1}\ne 0\) and \((\omega _\eta )^{r+2}=0\). From (7), we get that  , because the summands there are linearly independent. It remains to show that \((\omega _\eta )^{r+1}\ne 0\) implies now
, because the summands there are linearly independent. It remains to show that \((\omega _\eta )^{r+1}\ne 0\) implies now  . This is, of course, true at points in which the rank of
. This is, of course, true at points in which the rank of  is \(<2(r+1)\). Suppose that
is \(<2(r+1)\). Suppose that  . Hence, the rank of
. Hence, the rank of  is \(2(r+1)\) at y. Let us choose
is \(2(r+1)\) at y. Let us choose  such that
such that

We can assume additionally that \(X_1,\dots ,X_{2r+1}\in \ker (\eta _y)\) and \(\big \langle \eta _y,X_{2r+2}\big \rangle =1\) (\(\eta \) is nonvanishing). We have

Hence, at least one summand must be \(\ne 0\), i.e., for some k,

But then

a contradiction. \(\square \)
Remark 2.11
Let us note that Theorem 2.9 can be seen as a particular case of [77, Proposition 3.6], where precontact forms are understood as 1-forms with values in a line bundle. This language is better adapted to the work with general Jacobi bundles.
Corollary 2.12
Let C be a field of hyperplanes on a manifold M. Then, C is a precontact structure of rank \((2r+1)\) if and only if the restriction of the canonical symplectic form \(\omega _M\) on  to \((C^o)^\times \) is a presymplectic form of rank \(2(r+1)\), where
to \((C^o)^\times \) is a presymplectic form of rank \(2(r+1)\), where  is the annihilator of the subbundle
is the annihilator of the subbundle  . In particular, C is a contact structure if and only if \((C^o)^\times \) is a symplectic submanifold of
. In particular, C is a contact structure if and only if \((C^o)^\times \) is a symplectic submanifold of  .
.
Theorem 2.9 shows that with any precontact structure (M, C) of rank \((2r+1)\) there is canonically associated the principal \({{\mathbb {R}}^\times }\)-bundle \(P=(C^o)^\times \), with the \({{\mathbb {R}}^\times }\)-action \(s\mapsto h_s\) inherited from the vector bundle structure of  , \(h_s(\eta _y)=s\cdot \eta _y\), and the obvious projection \(\tau :P\rightarrow M\) inherited from the projection
, \(h_s(\eta _y)=s\cdot \eta _y\), and the obvious projection \(\tau :P\rightarrow M\) inherited from the projection  . Moreover, P is equipped with a presymplectic form \(\omega =\omega _M\,\big |_P\) of rank \(2(r+1)\) inherited from the canonical symplectic form \(\omega _M\) on
. Moreover, P is equipped with a presymplectic form \(\omega =\omega _M\,\big |_P\) of rank \(2(r+1)\) inherited from the canonical symplectic form \(\omega _M\) on  . Since the canonical symplectic structure \(\omega _M\) on
. Since the canonical symplectic structure \(\omega _M\) on  is linear, the presymplectic form \(\omega \) is 1-homogeneous with respect to the \({{\mathbb {R}}^\times }\)-action, \(h^*_s(\omega )=s\cdot \omega \). The characteristic distribution of \(\omega \) is transversal to the fibers of \(\tau _M:(C^o)^\times \rightarrow M\). An abstract counterpart of such a structure is therefore the following (cf. [11, 38]).
is linear, the presymplectic form \(\omega \) is 1-homogeneous with respect to the \({{\mathbb {R}}^\times }\)-action, \(h^*_s(\omega )=s\cdot \omega \). The characteristic distribution of \(\omega \) is transversal to the fibers of \(\tau _M:(C^o)^\times \rightarrow M\). An abstract counterpart of such a structure is therefore the following (cf. [11, 38]).
Definition 2.13
A presymplectic \({{\mathbb {R}}^\times }\)-bundle of rank \((2r+1)\) is an \({{\mathbb {R}}^\times }\)-bundle \(\tau :P\rightarrow M\) with respect to an \({{\mathbb {R}}^\times }\)-action
equipped additionally with a presymplectic form \(\omega \) of rank \(2(r+1)\) which is 1-homogeneous, \((h_s)^*(\omega )=s\cdot \omega \), and whose characteristic distribution \(\chi (\omega )\) is transversal to the fibers of \(\tau \). Such a structure we will denote \((P,\tau ,M,h,\omega )\). With every such a presymplectic \({{\mathbb {R}}^\times }\)-bundle there are canonically associated: a nonvanishing \({{\mathbb {R}}^\times }\)-invariant (0-homogeneous) vector field \(\nabla \), being the opposite \(\nabla =-\widetilde{1}\) of the fundamental vector field \(\widetilde{1}\) of the \({{\mathbb {R}}^\times }\)-action,

and a nonvanishing 1-form \(\theta =i_{\nabla }\omega \). If \(\omega \) is symplectic, then we speak about a symplectic \({{\mathbb {R}}^\times }\)-bundle.
An isomorphism of presymplectic \({{\mathbb {R}}^\times }\)-bundles \((P_i,\tau _i,M_i,h^i,\omega _i)\), \(i=1,2\), is an isomorphism

of \({{\mathbb {R}}^\times }\)-bundles such that \(\widetilde{\varphi }^*(\omega _2)=\omega _1\). A vector field X on a presymplectic \({{\mathbb {R}}^\times }\)-bundle we call an \({{\mathbb {R}}^\times }\)-presymplectic vector field if it generates a flow of local automorphisms of the presymplectic \({{\mathbb {R}}^\times }\)-bundle
Proposition 2.14
Let \((P,\tau ,M,h,\omega )\) be a presymplectic \({{\mathbb {R}}^\times }\)-bundle. Then
-
(1)
the 1-form \(\theta \) is a unique 1-homogeneous nonvanishing and semi-basic 1-form such that
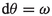 (in particular, \(\omega \) is always exact);
(in particular, \(\omega \) is always exact); -
(2)
the characteristic distribution
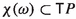 of \(\omega \) is involutive, \({{\mathbb {R}}^\times }\)-invariant, and induces an \({{\mathbb {R}}^\times }\)-invariant foliation \({\mathcal {F}}_\omega \) on P, with leaves transversal to the fibers of \(\tau \);
of \(\omega \) is involutive, \({{\mathbb {R}}^\times }\)-invariant, and induces an \({{\mathbb {R}}^\times }\)-invariant foliation \({\mathcal {F}}_\omega \) on P, with leaves transversal to the fibers of \(\tau \); -
(3)
any isomorphism (8) respects \(\nabla _i\) and \(\theta _i\), \(i=1,2\),
$$\begin{aligned} \widetilde{\varphi }_*(\nabla _1)=\nabla _2,\quad \text {and}\quad \widetilde{\varphi }^*(\theta _2)=\theta _1; \end{aligned}$$ -
(4)
a vector field X on P is \({{\mathbb {R}}^\times }\)-presymplectic if and only if X is \({{\mathbb {R}}^\times }\)-invariant (homogeneous of degree 0) and \({\pounds }_X\theta =0\).
Proof
-
(1)
Since \(\nabla \) is vertical, \(\theta \) is semi-basic. But \(\nabla \) is homogeneous of degree 0 (\({{\mathbb {R}}^\times }\)-invariant) and \(\omega \) is homogeneous of degree 1, therefore \(\theta \) is 1-homogeneous. Consequently,
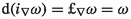 . If \(\theta _1\) is another 1-homogeneous and semi-basic potential for \(\omega \), then
. If \(\theta _1\) is another 1-homogeneous and semi-basic potential for \(\omega \), then 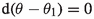 . But \(\theta -\theta _1\) is 1-homogeneous and semi-basic, so
. But \(\theta -\theta _1\) is 1-homogeneous and semi-basic, so 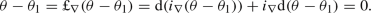
The first summand on the right-hand side is 0, because \(\theta -\theta _1\) is semi-basic.
-
(2)
The characteristic distribution is clearly of constant rank and involutive, so it induces an \({{\mathbb {R}}^\times }\)-invariant foliation \({\mathcal {F}}_\omega \) whose leaves are maximal integral submanifolds of \(\chi (\omega )\). The characteristic distribution \(\chi (\omega )\) is transversal to the fibers of \(\tau \) by definition, so are the leaves of the foliation \({\mathcal {F}}_\omega \).
-
(3)
If now \(\widetilde{\varphi }:P_1\rightarrow P_2\) is an isomorphism of presymplectic \({{\mathbb {R}}^\times }\)-bundles, it respects the \({{\mathbb {R}}^\times }\)-actions, so \(\widetilde{\varphi }_*(\nabla _1)=\nabla _2\). Since \(\widetilde{\varphi }^*(\omega _2)=\omega _1\), from (1) we get \(\widetilde{\varphi }^*(\theta _2)=\theta _1\).
-
(4)
Finally, a vector field X on P is \({{\mathbb {R}}^\times }\)-presymplectic if it is \({{\mathbb {R}}^\times }\)-invariant and the flow \(\varphi _t\) of X consists of (local) automorphisms of \((P,\tau ,M,h,\omega )\). This means that \(h_s\circ \varphi _t=\varphi _t\circ h_s\) and, as we have just shown, \(\varphi _t^*(\theta )=\theta \). It is a standard task to prove that \(h_s\circ \varphi _t=\varphi _t\circ h_s\) is equivalent to
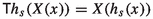 , thus invariance of X, and \(\varphi _t^*(\theta )=\theta \) is equivalent to \({\pounds }_X(\theta )=0\). \(\square \)
, thus invariance of X, and \(\varphi _t^*(\theta )=\theta \) is equivalent to \({\pounds }_X(\theta )=0\). \(\square \)
The 1-form \(\theta \) we will call the Liouville 1-form for the presymplectic \({{\mathbb {R}}^\times }\)-bundle, and the vector field \(\nabla \) - the Euler vector field. For the presymplectic \({{\mathbb {R}}^\times }\)-bundle \((C^o)^\times \) the Liouville 1-form \(\theta \) is the restriction to \((C^o)^\times \) of the canonical Liouville 1-form \(\theta _M\) on  . For simplicity, we will usually identify pull-backs of differential forms on M by \(\tau \) with the forms themselves, i.e., we write \(\tau ^*(\eta )=\eta \).
. For simplicity, we will usually identify pull-backs of differential forms on M by \(\tau \) with the forms themselves, i.e., we write \(\tau ^*(\eta )=\eta \).
Proposition 2.15
For a presymplectic \({{\mathbb {R}}^\times }\)-bundle \((P,\tau ,M,h,\omega )\) of rank \(2(r+1)\) and an open submanifold \(U\subset M\), there is a canonical one-to-one correspondence between trivializations of the principal bundle P over U and precontact forms \(\eta \) of rank \((2r+1)\) on U. The correspondence between \(\eta \) on U and \(\theta \) on \(U\times {{\mathbb {R}}^\times }\) is given by \(\theta (y,s)=s\cdot \eta (y)\), so that

Hence,

is a precontact structure on U.
Proof
Since the \({{\mathbb {R}}^\times }\)-action on \(U\times {{\mathbb {R}}^\times }\) is \(h_{s'}(y,s)=(y,s'\cdot s)\), we get \(\nabla =s\,\partial _s\) and \(\theta =s\cdot i_{\partial _s}\omega \). Since \(\theta \) is homogeneous of degree 1, the 1-form \(i_{\partial _s}\omega =\theta /s\) is \({{\mathbb {R}}^\times }\)-invariant and nowhere vanishing, and hence it is a pull-back \(\tau ^*(\eta )\) of a local nowhere-vanishing 1-form \(\eta \) on U. We will write simply \(\eta \) for \(\tau ^*(\eta )\) on \(U\times {{\mathbb {R}}^\times }\). Consequently,

Since \(\omega \) is presymplectic of rank \(2(r+1)\), from Theorem 2.9 we deduce that \(\eta \) is a precontact form of rank \(2r+1\). Of course, \(\ker (s\eta )=\ker (\eta )\) for \(s\ne 0\). Conversely, if \(\eta \) is a precontact form on U such that \(\ker (\tau ^*(\eta ))=\ker (\theta )\), then \(\theta (x)=F(x)\eta (\tau (x))\) for some nonvanishing function F on \(\tau ^{-1}(U)\). But \(\theta \) is 1-homogeneous, while \(\eta \) is 0-homogeneous, so F is 1-homogeneous. We will show that the map
is a local trivialization of the principal bundle P. Indeed,
In this trivialization \(F(x)=s\), so \(\theta =s\cdot \eta \) and \(C=\ker (\eta )\) is a precontact structure on U. \(\square \)
It is well known (cf. [34, Theorem 2.1]) that for every principal \({{\mathbb {R}}^\times }\)-bundle (or a line bundle) \(\tau :P\rightarrow M\) we can always find an atlas of local trivializations
with the transition functions
This is equivalent to the fact that we can always find a 2-sheet cover \(p:{\tilde{M}}\rightarrow M\) such that the pull-back principal bundle \(p^*P\) is trivializable. An analogous fact is true for line bundles. We get therefore from Proposition 2.3 the following corollary, which is very useful when dealing with precontact structures.
Corollary 2.16
For every precontact manifold (M, C), we can find an open covering \((U_\alpha )\) of M and local precontact forms \(\eta _\alpha \) inducing C on \(U_\alpha \), such that \(\eta _\alpha =\pm \eta _\beta \) on \(U_{\alpha \beta }=U_\alpha \cap U_\beta \). In other words, there exists a 2-sheet cover \(p:{\tilde{M}}\rightarrow M\) such that the pull-back precontact structure \(p^*C\) on \({\tilde{M}}\) admits a global precontact form.
We know already that with every precontact structure (M, C) there is a canonically associated presymplectic \({{\mathbb {R}}^\times }\)-bundle  , with the projection \(\tau =\pi _M\), the \({{\mathbb {R}}^\times }\)-action h, and the presymplectic form \(\omega \) inherited from the cotangent bundle
, with the projection \(\tau =\pi _M\), the \({{\mathbb {R}}^\times }\)-action h, and the presymplectic form \(\omega \) inherited from the cotangent bundle  . This presymplectic \({{\mathbb {R}}^\times }\)-bundle we will call the canonical presymplectic cover of (M, C). For contact structures, we refer to canonical symplectic covers. A fundamental result is the converse of this observation (cf. [38]).
. This presymplectic \({{\mathbb {R}}^\times }\)-bundle we will call the canonical presymplectic cover of (M, C). For contact structures, we refer to canonical symplectic covers. A fundamental result is the converse of this observation (cf. [38]).
Theorem 2.17
Any presymplectic \({{\mathbb {R}}^\times }\)-bundle \((P,\tau ,M,h,\omega )\) of rank \(2(r+1)\) induces canonically a precontact structure C of rank \((2r+1)\) on M, together with an isomorphism

of presymplectic \({{\mathbb {R}}^\times }\)-bundles. This precontact structure is given by  , where \(\theta \) is the Liouville 1-form on P. In other words, there is a one-to-one correspondence between precontact manifolds (M, C) of rank \((2r+1)\) and isomorphism classes of presymplectic \({{\mathbb {R}}^\times }\)-bundles of rank \(2(r+1)\) over M. As a principal \({{\mathbb {R}}^\times }\)-bundle, P can be therefore identified with \(\big [\left( L^C\right) ^*\big ]^\times \), where
, where \(\theta \) is the Liouville 1-form on P. In other words, there is a one-to-one correspondence between precontact manifolds (M, C) of rank \((2r+1)\) and isomorphism classes of presymplectic \({{\mathbb {R}}^\times }\)-bundles of rank \(2(r+1)\) over M. As a principal \({{\mathbb {R}}^\times }\)-bundle, P can be therefore identified with \(\big [\left( L^C\right) ^*\big ]^\times \), where  . Moreover, the projection \(\tau :P\rightarrow M\) maps locally diffeomorphically the leaves of the characteristic foliation \({\mathcal {F}}_\omega \) onto the leaves of the characteristic foliation \({\mathcal {F}}_C\). In other words, the projection \(\tau \) is on leaves of \({\mathcal {F}}_\omega \) a differentiable covering of the leaves of \({\mathcal {F}}_C\).
. Moreover, the projection \(\tau :P\rightarrow M\) maps locally diffeomorphically the leaves of the characteristic foliation \({\mathcal {F}}_\omega \) onto the leaves of the characteristic foliation \({\mathcal {F}}_C\). In other words, the projection \(\tau \) is on leaves of \({\mathcal {F}}_\omega \) a differentiable covering of the leaves of \({\mathcal {F}}_C\).
Proof
Since in Proposition 2.15 the local contact structure was defined as  , so without any reference to the local precontact form \(\eta \), this definition gives a global contact structure on M. Moreover, we infer from this proposition that, for every \(x\in P\), we have \(\theta (x)=\tau ^*(\Phi _P(x))\), where
, so without any reference to the local precontact form \(\eta \), this definition gives a global contact structure on M. Moreover, we infer from this proposition that, for every \(x\in P\), we have \(\theta (x)=\tau ^*(\Phi _P(x))\), where  . In particular, \(\pi _M\circ \Phi _P=\tau \), where
. In particular, \(\pi _M\circ \Phi _P=\tau \), where  is the canonical projection. The map \(\Phi _P\) takes values in \((C^o)^\times \). Indeed, since any \(X_0\in C_{\tau (x)}\) is of the form
is the canonical projection. The map \(\Phi _P\) takes values in \((C^o)^\times \). Indeed, since any \(X_0\in C_{\tau (x)}\) is of the form  for some \(X\in \ker (\theta (x))\), we have
for some \(X\in \ker (\theta (x))\), we have

Moreover, \(\Phi _P(x)\ne 0\), since \(\theta (x)\ne 0\), and so \(\Phi _P:P\rightarrow (C^o)^\times \) is a morphism of principal \({{\mathbb {R}}^\times }\)-bundles: as \(\theta \) is 1-homogeneous, we have \(\Phi _P(h_s(x))=s\cdot \Phi _P(x)\). This morphism induces the identity on the base, so it is an isomorphism. In other words, \(\Phi _P:P\rightarrow (C^o)^\times \) is a diffeomorphism such that \(\Phi _P\circ h_s=s\cdot \Phi _P\), where \(\tau _M\circ \Phi _P=\tau \). Of course, the annihilator  can be canonically identified with the dual line bundle of
can be canonically identified with the dual line bundle of  .
.
It remains to show that \(\Phi ^*(\omega _M)=\omega \). We will just show that \(\Phi ^*(\theta _M)=\theta \), where we denote for simplicity \(\Phi =\Phi _P\) and \(\theta _M\) for the canonical Liouville 1-form on  . Let
. Let  . We have
. We have

We used the coordinate-free definition of \(\theta _M\): for any  and any vector field Y on
and any vector field Y on  , we have
, we have

We already know from the local picture (Theorem 2.9) that the fibers of \(\chi (\omega )\) are mapped by  isomorphically onto the fibers of \(\chi (C)\). This immediately implies that the leaves of \({\mathcal {F}}_\omega \) are mapped by \(\tau \) locally diffeomorphically into the leaves of \({\mathcal {F}}_C\). The image of every leaf of \({\mathcal {F}}_\omega \) is therefore open in the corresponding leaf of \({\mathcal {F}}_C\). It is a student exercise to show that it is also closed, so it is the whole leaf. \(\square \)
isomorphically onto the fibers of \(\chi (C)\). This immediately implies that the leaves of \({\mathcal {F}}_\omega \) are mapped by \(\tau \) locally diffeomorphically into the leaves of \({\mathcal {F}}_C\). The image of every leaf of \({\mathcal {F}}_\omega \) is therefore open in the corresponding leaf of \({\mathcal {F}}_C\). It is a student exercise to show that it is also closed, so it is the whole leaf. \(\square \)
Any presymplectic \({{\mathbb {R}}^\times }\)-bundle \(\tau :P\rightarrow M\) inducing a given precontact structure C on M, we will call a presymplectic cover of (M, C). The reader could ask why we do not just stay with the canonical presymplectic cover \((C^o)^\times \). The point is that in many cases we deal with a structure which is clearly a presymplectic \({{\mathbb {R}}^\times }\)-bundle, while the corresponding contact structure C, thus \((C^o)^\times \), is not explicitly given. This is an easy way to define precontact structures.
Example 2.18
For a manifold M, the cotangent bundle  with the zero section removed, i.e.,
with the zero section removed, i.e.,  is clearly an \({{\mathbb {R}}^\times }\)-bundle with respect to the multiplication by reals in
is clearly an \({{\mathbb {R}}^\times }\)-bundle with respect to the multiplication by reals in  . The canonical symplectic form \(\omega _M\) restricted to
. The canonical symplectic form \(\omega _M\) restricted to  is still symplectic and 1-homogeneous, so we deal with a symplectic \({{\mathbb {R}}^\times }\)-bundle. According to Theorem 2.17, this defines a canonical contact structure on the projectivized cotangent bundle
is still symplectic and 1-homogeneous, so we deal with a symplectic \({{\mathbb {R}}^\times }\)-bundle. According to Theorem 2.17, this defines a canonical contact structure on the projectivized cotangent bundle  . In textbooks one usually uses much more space to define this contact structure. Our approach, however, can be found for the holomorphic case in [78, Example 55].
. In textbooks one usually uses much more space to define this contact structure. Our approach, however, can be found for the holomorphic case in [78, Example 55].
Proposition 2.19
Let \((P_i,\tau _i,M_i,h^i,\omega _i)\) be a presymplectic cover of a precontact structure \((M_i,C_i)\), \(i=1,2\). If (8) is an isomorphism of presymplectic \({{\mathbb {R}}^\times }\)-bundles, then \(\varphi \) is a contactomorphism of the corresponding precontact structures on \(M_1\) and \(M_2\). Conversely, any contactomorphism \(\varphi :M_1\rightarrow M_2\) is covered by a unique isomorphism

of presymplectic \({{\mathbb {R}}^\times }\)-bundles.
Proof
According to Proposition 2.14, we have \(\widetilde{\varphi }^*(\theta _2)=\theta _1\), hence  maps \(\ker (\theta _1(x))\) onto \(\ker (\theta _2(\widetilde{\varphi }(x))\). But
maps \(\ker (\theta _1(x))\) onto \(\ker (\theta _2(\widetilde{\varphi }(x))\). But  projects the kernels of \(\theta _i(x_i)\) onto \(C_i(\tau _i(x_i))\), thus
projects the kernels of \(\theta _i(x_i)\) onto \(C_i(\tau _i(x_i))\), thus  , that proves that \(\varphi \) is a contactomorphism.
, that proves that \(\varphi \) is a contactomorphism.
Conversely, for the canonical presymplectic covers  , \(i=1,2\), we can obtain \(\widetilde{\varphi }\) as
, \(i=1,2\), we can obtain \(\widetilde{\varphi }\) as  restricted to \((C_1^o)^\times \) (
restricted to \((C_1^o)^\times \) ( respects the precontact structures, so
respects the precontact structures, so  respects their annihilators). It remains to show that the isomorphism \(\widetilde{\varphi }\) of presymplectic \({{\mathbb {R}}^\times }\)-bundles covering the contactomorphism \(\varphi \) is unique. This is equivalent to proving that vertical (i.e., covering the identity) automorphisms \(\widetilde{\varphi }\) of any presymplectic \({{\mathbb {R}}^\times }\)-bundle \((P,\tau ,M,h,\omega )\) are trivial. Indeed, since \(\widetilde{\varphi }\) projects onto identity, it acts trivially on pull-backs \(\tau ^*(\eta )\) of forms \(\eta \) on M. Actually, since \(\widetilde{\varphi }\) is a vertical automorphism of the corresponding \({{\mathbb {R}}^\times }\)-bundle, it must be of the form \(\widetilde{\varphi }(x)=h_{f(\tau (x))}\) for a nowhere-vanishing function f on M. But if \(f\ne 1\), then \(\widetilde{\varphi }\) cannot preserve \(\omega \). This because if \(\widetilde{\varphi }^*(\omega )=\omega \), then one can prove as above that it preserves also the Liouville 1-form \(\theta =i_{\nabla }\omega \). But \(\theta \) is semi-basic and 1-homogeneous, so locally, in coordinates (s, y) associated with a local trivialization, it reads \(\theta (s,y)=s\cdot \eta (y)\) for a (pull-back of) 1-form \(\eta \) on M (we know already that it is a local precontact form for the precontact structure). Then,
respects their annihilators). It remains to show that the isomorphism \(\widetilde{\varphi }\) of presymplectic \({{\mathbb {R}}^\times }\)-bundles covering the contactomorphism \(\varphi \) is unique. This is equivalent to proving that vertical (i.e., covering the identity) automorphisms \(\widetilde{\varphi }\) of any presymplectic \({{\mathbb {R}}^\times }\)-bundle \((P,\tau ,M,h,\omega )\) are trivial. Indeed, since \(\widetilde{\varphi }\) projects onto identity, it acts trivially on pull-backs \(\tau ^*(\eta )\) of forms \(\eta \) on M. Actually, since \(\widetilde{\varphi }\) is a vertical automorphism of the corresponding \({{\mathbb {R}}^\times }\)-bundle, it must be of the form \(\widetilde{\varphi }(x)=h_{f(\tau (x))}\) for a nowhere-vanishing function f on M. But if \(f\ne 1\), then \(\widetilde{\varphi }\) cannot preserve \(\omega \). This because if \(\widetilde{\varphi }^*(\omega )=\omega \), then one can prove as above that it preserves also the Liouville 1-form \(\theta =i_{\nabla }\omega \). But \(\theta \) is semi-basic and 1-homogeneous, so locally, in coordinates (s, y) associated with a local trivialization, it reads \(\theta (s,y)=s\cdot \eta (y)\) for a (pull-back of) 1-form \(\eta \) on M (we know already that it is a local precontact form for the precontact structure). Then,
so \(f(y)=1\). \(\square \)
Corollary 2.20
Let \((P,\tau ,M,h,\omega )\) be a presymplectic cover of a precontact structure (M, C). Then, any action \(\rho :G\times M\rightarrow M\) of a Lie group G on M by contactomorphisms can be lifted to a unique action \(\widetilde{\rho }:G\times P\rightarrow P\) on the presymplectic \({{\mathbb {R}}^\times }\)-bundle P by its automorphisms such that \((\widetilde{\rho })_g=\widetilde{(\rho _g)}\). Conversely, any G-action on the presymplectic cover P by automorphisms projects to a G-action on M by contactomorphisms. It follows that there is a canonical one-to-one correspondence between contact vector fields \(X^c\) on M and \({{\mathbb {R}}^\times }\)-presymplectic vector fields X on P, given by \(X^c=\tau _*(X)\).
2.2 Remarks on Poisson \({{\mathbb {R}}^\times }\)-bundles
Note that the concept of a symplectic \({{\mathbb {R}}^\times }\)-bundle has an obvious generalization, namely a Poisson \({{\mathbb {R}}^\times }\)-bundle. The Poisson tensor on P should be \((-1)\)-homogeneous (the symplectic Poisson tensor \(\Lambda =\omega ^{-1}\) is homogeneous of degree \((-1)\) if \(\omega \) is 1-homogeneous). Of course, if the Poisson tensor is invertible, we deal with a symplectic \({{\mathbb {R}}^\times }\)-bundle, i.e., with a contact structure. The concept of a Poisson \({{\mathbb {R}}^\times }\)-bundle coincides with the concept of Kirillov’s local Lie algebra [49] (or Jacobi bundles in the terminology of Marle [58]), which provides a proper understanding of Jacobi brackets as local brackets on sections of line bundles. In other words, Jacobi brackets are closely related to homogeneous Poisson brackets, that is pretty well known in the literature (see, e.g., [12, 21, 40, 42, 45, 50, 51, 58]). In non-singular cases, the Lie algebra of Jacobi brackets completely determines the manifold M [37]. More information about Jacobi brackets and their generalizations, as well as various Lie brackets on manifolds, can be found in [36, 39, 77]. We will not go deeper into this subject in this paper.
3 Precontact-to-contact reduction
Let now C be a precontact structure of rank \((2r+1)\) on a manifold M of dimension m, and let \(\chi (C)=\ker (\nu ^C)\) be the characteristic distribution of C. Since \(\chi (C)\) is regular and involutive, by Frobenius Theorem we conclude that it induces a foliation \({\mathcal {F}}_C\) of M by maximal integral submanifolds of \(\chi (C)\) which we will call the characteristic foliation of C. The dimension of leaves of this foliation is the rank of \(\chi (C)\) which is \((m-2r-1)\). The assumption that the characteristic foliation is simple means that there is a smooth manifold structure on the space \(M_0=M/{\mathcal {F}}_C\) of leaves such that the canonical projection \(p_0:M\rightarrow M_0\), associating to points of a leaf F this leaf in the space of leaves, is a surjective submersion, i.e., \(p_0\) is a smooth fibration. Of course, the dimension of \(M_0\) is \((2r+1)\).
Theorem 3.1
If the characteristic foliation \({\mathcal {F}}_C\) is simple, then \(M_0\) carries a canonical contact structure \(C_0\) such that  . Moreover, if \(\eta \) is a precontact form defined in a neighborhood of \(y\in M\) and inducing C, then \(p_0^*(\eta _0)=f_{\eta }\eta \) for any contact form \(\eta _0\) defined in a neighborhood of \(p_0(y)\) and inducing \(C_0\), where \(f_{\eta }\) is a nonvanishing function.
. Moreover, if \(\eta \) is a precontact form defined in a neighborhood of \(y\in M\) and inducing C, then \(p_0^*(\eta _0)=f_{\eta }\eta \) for any contact form \(\eta _0\) defined in a neighborhood of \(p_0(y)\) and inducing \(C_0\), where \(f_{\eta }\) is a nonvanishing function.
Proof
Let us observe first that  is a correct definition of a field of hyperplanes \(C_0\) on \(M_0\). Since the leaves are connected by definition, it is enough to prove that this definition is correct in a neighborhood of any \(y\in M\), i.e.,
is a correct definition of a field of hyperplanes \(C_0\) on \(M_0\). Since the leaves are connected by definition, it is enough to prove that this definition is correct in a neighborhood of any \(y\in M\), i.e.,

Let us fix y. As \(p_0:M\rightarrow M_0\) is a fibration, it is locally trivial in a neighborhood of y, so there are local vector fields \(X_1,\dots ,X_m\) generating  in a neighborhood of y, which are projectable onto vector fields \(Y_1,\dots ,Y_m\) on \(M_0\). In other words, \(Y_i\) and \(X_i\) are \(p_0\)-related, \((p_0)_*(X_i)=Y_i\). We can also assume that \(X_1,\dots ,X_{m-1}\) span C and \(X_{2r+1},\dots ,X_{m-1}\) span \(\chi (C)\), i.e., tangent spaces of the leaves of \({\mathcal {F}}_C\). Then, \(Y_{2r+1}=\cdots =Y_{m-1}=0\) and \(Y_1,\dots ,Y_{2r},Y_m\) span
in a neighborhood of y, which are projectable onto vector fields \(Y_1,\dots ,Y_m\) on \(M_0\). In other words, \(Y_i\) and \(X_i\) are \(p_0\)-related, \((p_0)_*(X_i)=Y_i\). We can also assume that \(X_1,\dots ,X_{m-1}\) span C and \(X_{2r+1},\dots ,X_{m-1}\) span \(\chi (C)\), i.e., tangent spaces of the leaves of \({\mathcal {F}}_C\). Then, \(Y_{2r+1}=\cdots =Y_{m-1}=0\) and \(Y_1,\dots ,Y_{2r},Y_m\) span  . Let us show first that the local flow \(\varphi ^i_t\) of each \(X_i\), \(i=2r+1,\dots ,m-1\), preserves C. Let Y be a local vector field taking values in C. Since
. Let us show first that the local flow \(\varphi ^i_t\) of each \(X_i\), \(i=2r+1,\dots ,m-1\), preserves C. Let Y be a local vector field taking values in C. Since
we get that \([X_i,Y]\) again takes values in C, thus the local flow \(\varphi ^i_t\) of each \(X_i\) preserves C for each \(i=2r+1,\dots ,m-1\), i.e.,  . Hence, if \(y'=\varphi ^i_t(y)\), then
. Hence, if \(y'=\varphi ^i_t(y)\), then

since clearly \(p_0\circ \varphi ^i_t=p_0\) for such i. As \(X_{2r+1},\dots ,X_{m-1}\) span the involutive distribution \(\chi (C)\), compositions of local diffeomorphisms from their flows act locally transitively on the leaves of \({\mathcal {F}}_C\), that shows (9) for \(y'\) in a neighborhood of y in the leaf containing y.
Now, it is easy to see that \(C_0\) is a contact structure, since the map \(p_0\) kills the kernel of \(\nu ^C\). More precisely, the surjective morphism of vector bundles  induces canonically a surjective morphism \(p^C:L^C\rightarrow L^{C_0}\) by
induces canonically a surjective morphism \(p^C:L^C\rightarrow L^{C_0}\) by

We have
where \(i,j=1,\dots ,2r\). But \(\nu ^C\) is nondegenerate on the subbundle in C spanned by \(X_1,\dots ,X_{2r}\), so the matrix \(\Big (\rho ^C\big ([X_i,X_j]\big )\Big )\) is nondegenerate, that proves that \(\nu ^{C_0}\) is nondegenerate. Finally, it follows from (1) that \(\ker (p_0^*(\eta _0))=C\), so \(p_0^*(\eta _0)=f\eta \) for a nonvanishing function f (of course, f depends on the choice of \(\eta \)). \(\square \)
Definition 3.2
The contact structure \(C_0\) on \(M_0\) we call the reduced contact structure and the whole procedure—the precontact-to-contact reduction.
Remark 3.3
Note that the local 1-form \(p_0^*(\eta _0)\) on M generating C is automatically of class \((2r+1)\) (cf. Theorem 2.4). Moreover, Theorem 3.1 is very similar to contact coisotropic reductions proposed in [25, Theorem 14] and [76, Proposition 4.2]. Analogous reductions for general Jacobi structures are considered in [77, Section 7.2]. However, the situation in this case is much more complicated.
A natural question is now, what is the counterpart of precontact-to-contact reductions on the level of presymplectic covers.
3.1 Symplectic reduction of presymplectic \({{\mathbb {R}}^\times }\)-bundles
The well-known symplectic reduction of presymplectic manifolds (or constant rank submanifolds in symplectic manifolds) requires some additional caution in the case of presymplectic \({{\mathbb {R}}^\times }\)-bundles, in order to assure that the resulted symplectic manifold has a compatible \({{\mathbb {R}}^\times }\)-bundle structure.
Theorem 3.4
Let \((P,\tau ,M,h,\omega )\) be a presymplectic cover of a contact manifold (M, C) of rank \(2r+1\). Then, the characteristic foliation \({\mathcal {F}}_\omega \) is simple if and only if the characteristic foliation \({\mathcal {F}}_C\) is simple.
In this case, the manifold \(P_0=P/{\mathcal {F}}_\omega \) of \({\mathcal {F}}_\omega \)-leaves carries a canonical structure of a symplectic \({{\mathbb {R}}^\times }\)-bundle \((P_0,\tau _0,M_0,h^0,\omega _0)\) such that the canonical submersion \(p:P\rightarrow P_0\) is a submersive morphism of \({{\mathbb {R}}^\times }\)-bundles, i.e., \(h^0_s\circ p=p\circ h_s\), and \(\omega =p^*(\omega _0)\).
In particular, we have the following commutative diagram for a surjective morphism of \({{\mathbb {R}}^\times }\)-bundles:

Moreover, \(M_0=M/{\mathcal {F}}_C\) and \(M_0\) carries a canonical contact structure \(C_0\) such that  , where \(p_0\) is the canonical submersion onto the manifold of leaves of \({\mathcal {F}}_C\).
, where \(p_0\) is the canonical submersion onto the manifold of leaves of \({\mathcal {F}}_C\).
Proof
Suppose \({\mathcal {F}}_C\) is simple. According to Theorem 3.1, the manifold \(M_0=M/{\mathcal {F}}_C\) of \({\mathcal {F}}_C\)-leaves carries a canonical contact structure \(C_0\) such that  , where \(p_0:M\rightarrow M_0\) is the canonical submersion. Consider the canonical symplectic cover \((P_0,\tau _0,M_0,h^0,\omega _0)\) of the contact manifold \((M_0,C_0)\), the Liouville form \(\theta _0\) on \(P_0\), and the pull-back bundle \(P_1=p_0^*(P_0)\), with the commutative diagram
, where \(p_0:M\rightarrow M_0\) is the canonical submersion. Consider the canonical symplectic cover \((P_0,\tau _0,M_0,h^0,\omega _0)\) of the contact manifold \((M_0,C_0)\), the Liouville form \(\theta _0\) on \(P_0\), and the pull-back bundle \(P_1=p_0^*(P_0)\), with the commutative diagram

It is easy to see that \(P_1\) carries a canonical structure of a principal \({{\mathbb {R}}^\times }\)-bundle with the \({{\mathbb {R}}^\times }\)-action \(h^1\) inherited from \(P_0\), and the above diagram describes a submersive morphism of principal \({{\mathbb {R}}^\times }\)-bundles. The 1-form \(\theta _1=p^*_1(\theta _0)\) is clearly nonvanishing, 1-homogeneous, and  . Since \(p_1\) is a submersion, \(\omega _1\) is a closed form of rank \(2(r+1)\) and its characteristic distribution \(\chi (\omega _1)\) is mapped by
. Since \(p_1\) is a submersion, \(\omega _1\) is a closed form of rank \(2(r+1)\) and its characteristic distribution \(\chi (\omega _1)\) is mapped by  onto the trivial distribution, so \(\chi (\omega _1)\) is transversal to the fibers of \(\tau _1\). Moreover, since \(p_0\circ \tau _1=\tau _0\circ p_1\) and
onto the trivial distribution, so \(\chi (\omega _1)\) is transversal to the fibers of \(\tau _1\). Moreover, since \(p_0\circ \tau _1=\tau _0\circ p_1\) and  , we have
, we have

Hence,  and we have just proved that \((P_1,\tau _1,M,h^1,\omega _1)\) is a presymplectic cover of (M, C). But all presymplectic covers are isomorphic, so \((P,\omega )\simeq (P_1,\omega _1)\), thus the characteristic foliation \({\mathcal {F}}_\omega \) is simple, since \({\mathcal {F}}_{\omega _1}\) is simple by definition.
and we have just proved that \((P_1,\tau _1,M,h^1,\omega _1)\) is a presymplectic cover of (M, C). But all presymplectic covers are isomorphic, so \((P,\omega )\simeq (P_1,\omega _1)\), thus the characteristic foliation \({\mathcal {F}}_\omega \) is simple, since \({\mathcal {F}}_{\omega _1}\) is simple by definition.
Conversely, let us assume that \({\mathcal {F}}_\omega \) is simple. For a leaf F of \({\mathcal {F}}_\omega \), denote with [F] the corresponding point of \(P_0\) and with \(\omega _0\) the reduced symplectic form on \(P_0\). In other words, \(F=p^{-1}([F])\), where \(p:P\rightarrow P_0\) is the canonical surjective submersion onto the manifold of leaves (thus a fibration). From symplectic geometry, we know that \(P_0\) is equipped with a unique symplectic form \(\omega _0\) such that \(p^*(\omega _0)=\omega \). Since the \({{\mathbb {R}}^\times }\)-action h on P maps leaves onto leaves, it induces a smooth \({{\mathbb {R}}^\times }\)-action \(h^0\) on \(P_0\) by \(h^0_s([F])=[h_s(F)]\), i.e., \(h^0_s\circ p=p\circ h_s\), and the fibers of \(\tau \) are projected by p onto the orbits of \(h^0\). Since the leaves of \({\mathcal {F}}_\omega \) are transversal to the fibers of \(\tau \), the submersion p restricted to any fiber of \(\tau \) is a local diffeomorphism. Moreover, since \(h_s^*(\omega )=s\cdot \omega \), we have \((h^0_s)^*(\omega _0)=s\cdot \omega _0\), so \(\omega _0\) is 1-homogeneous. This easily implies that every leaf F intersects the fibers at no more than one point, that implies that the action \(h^0\) is free.
Indeed, if in a fiber F of \({\mathcal {F}}_\omega \) there are two different points of the fiber \(\tau ^{-1}(y_0)\), say \(x_0\) and \(x_1=h_{s_0}(x_0)\), \(s_0\ne 1\), then \(v=p(x_0)=p(x_1)\in P_0\), and \(h^0_{s_0}(v)=v\). Since \(h_{s_0}(h_s(x_0))=h_s(x_1)\), we have \(h^0_{s_0}(h^0_s(v))=h^0_s(v)\), so \(h^0_{s_0}\) is the identity on the whole \({{\mathbb {R}}^\times }\)-orbit of v.
Let us consider a local trivialization \(U\times {{\mathbb {R}}^\times }\) of P over a neighborhood U of \(y_0\in M\), which is equipped with coordinates \((z^i,u^j)\) such that \(y_0=(0,0)\) and the foliation \({\mathcal {F}}_C\) is defined locally by the system of equations \(z^i=const\). This system of coordinates on U gives a system of coordinates \((z^i,u^j,s)\) in \(\widetilde{U}=\tau ^{-1}(U)=U\times {{\mathbb {R}}^\times }\) such that \(s\in {{\mathbb {R}}^\times }\) and \(h_{s'}(z^i,u^j,s)=(z^i,u^j,s's)\). There is \(a\in {{\mathbb {R}}^\times }\) such that \(x_0=(0,0,a)\). These coordinates, reduced to a sufficiently small neighborhood of \(x_0\), induce local coordinates \((z^i,s)\) in a neighborhood of v in \(P_0\) such that \(v=(0,a)\). Note that \(z^i\) are invariant with respect to the \({{\mathbb {R}}^\times }\)-action on \(P_0\). We denote \(z^i\) and \(z^i\circ p\) with the same symbol, hoping that it is clear from the context on which manifold we are. On the \({{\mathbb {R}}^\times }\)-orbit of v, the diffeomorphism \(h^0_{s_0}\) is the identity, so \(h^0_{s_0}(z^i,s)=(z^i,f(z)s)\) for \(z=(z^i)\) sufficiently close to 0, and \(f(0)=1\). Hence, for the symplectic form \(\omega _0\) on \(P_0\), with

we have

The identity \((h^0_{s_0})^*(\omega _0(v))=s_0\cdot \omega _0(v)\), with \(s_0\ne 1\), would imply

a contradiction, since  (otherwise \(\omega _0\) would not be symplectic).
(otherwise \(\omega _0\) would not be symplectic).
We have just proved that the smooth \({{\mathbb {R}}^\times }\)-action \(h^0\) on \(P_0\) is free. Now, we will show that it is proper. To prove this, it is convenient to use Borel’s characterization of properness (see [68, Thm. 1.2.9 (5)], attributed there to Borel): a G-action on a manifold N is proper if and only if for every compact subset K of N the subset
of G is compact.
So, let us take a compact subset \(K\subset P_0\), and a sequence \(m_1,m_2,\dots \) of points from K which is dense in K. Let \(x_1,x_2,\dots \) be a sequence of points in P such that \(p(x_i)=m_i\), and let \(U_i\) be a neighborhood of \(x_i\) having compact closure \({\bar{U}}_i\), for all \(i=1,2,\dots \). Since p is an open map, the family of open sets \(\{p(U_i)\}_{i\in {\mathbb {N}}}\) covers K, so we can choose a finite covering, say \(U_1\cup U_2\cup \cdots \cup U_r\). But then \(\widetilde{K}={\bar{U}}_1\cup {\bar{U}}_2\cup \cdots \cup {\bar{U}}_r\) is a compact set and \(K\subset p(\widetilde{K})\). Consequently, \((K\big | K)\) is a closed subset of \((\widetilde{K}\big |\widetilde{K})\) which is compact, since the \({{\mathbb {R}}^\times }\)-action on P is proper. Moreover, \((P_0,\tau _0,M_0,h^0,\omega _0)\) is a symplectic \({{\mathbb {R}}^\times }\)-bundle and p is a submersive homomorphism of \({{\mathbb {R}}^\times }\)-bundles. Here, \(M_0=P_0/{{\mathbb {R}}^\times }\). The projection \(\tau :P\rightarrow M\) commutes with the \({{\mathbb {R}}^\times }\)-action, so induces a smooth map \(p_0:M\rightarrow M_0\) defined by \(p_0(\tau (x))=\tau _0(p(x))\). Let us observe that \(p_0(\tau (x))=p_0(\tau (x'))\) if and only if p(x) and \(p(x')\) belong to the same \({{\mathbb {R}}^\times }\)-orbit in \(P_0\), say \(p(x')=h^0_r(p(x))\), so if and only if \(p(x)=p(h_r(x'))\). This, in turn, is equivalent to the fact that x and \(h_r(x')\) belong to the same leaf of \({\mathcal {F}}_\omega \), and further that \(\tau (x)\) and \(\tau (x')\) belong to the same leaf of \({\mathcal {F}}_C\). This means that \(M_0\) is a manifold of leaves of \({\mathcal {F}}_C\), that finishes the proof. \(\square \)
Remark 3.5
The reduction (10) we call the symplectic reduction of a presymplectic \({{\mathbb {R}}^\times }\)-bundle. Since any foliation is locally trivial, thus locally simple, symplectic reductions as above can always be done locally, i.e., on presymplectic \({{\mathbb {R}}^\times }\)-bundles \(\tau ^{-1}(U)\subset P\), where U is an open submanifold of M on which the foliation \({\mathcal {F}}_C\) is trivial.
If actions of Lie groups by contactomorphisms are concerned, it is easy to see that such actions ‘commute’ with the contact (equivalently, symplectic) reductions. Namely, as the contact actions of Lie groups on precontact manifolds (equivalently, actions on presymplectic \({{\mathbb {R}}^\times }\)-bundles by automorphisms) respect the characteristic distribution, Theorem 3.4, together with Corollary 2.20, immediately imply the following.
Proposition 3.6
Let \((P,\tau ,M,h,\omega )\) be a presymplectic cover of a precontact manifold (M, C), let \(\rho :G\times M\rightarrow M\) be an action of a Lie group G on M by contactomorphisms, and let \(\widetilde{\rho }:G\times P\rightarrow P\) be the canonical lift to a G-action on P by automorphisms. Suppose that the characteristic foliation \({\mathcal {F}}_C\) (equivalently, the characteristic foliation \({\mathcal {F}}_\omega \)) is simple, so we have the contact (symplectic) reduction (10). Then, the G-actions \(\rho \ \text {and}\ \widetilde{\rho }\) induce canonically actions \(\rho ^0:G\times M_0\rightarrow M_0\) and \(\widetilde{\rho }^0:G\times P_0\rightarrow P_0\) by contactomorphisms and automorphisms, respectively, according to the formulae
In particular, \(\tau _0\circ \widetilde{\rho }^0_g=\rho ^0_g\).
3.2 Precontact and presymplectic reductions
Sometimes we have to deal with reductions of precontact and presymplectic manifolds with respect to foliations smaller than the characteristic foliations. In particular, we have the following obvious generalization of the standard symplectic reduction of presymplectic manifolds.
Proposition 3.7
Let \((P,\omega )\) be a presymplectic manifold of rank 2r. If \({\mathcal {F}}\) is a simple foliation of P, whose leaves are integral submanifolds of the characteristic distribution \(\chi (\omega )\), then the manifold \(P_0=P/{\mathcal {F}}\) of leaves of \({\mathcal {F}}\) carries a canonical presymplectic form \(\omega _0\) of rank 2r such that \(p^*(\omega _0)=\omega \), where \(p:P\rightarrow P_0\) is the canonical submersion.
In the context of precontact manifolds and their presymplectic covers, we can proceed exactly like in Theorems 3.1 and 3.4 for foliations \({\mathcal {F}}_M\) and \({\mathcal {F}}_P\) replacing \({\mathcal {F}}_C\) and \({\mathcal {F}}_\omega \), respectively, where the leaves of \({\mathcal {F}}_P\) cover the leaves of \({\mathcal {F}}_M\) (thus \({\mathcal {F}}_P\) is \({{\mathbb {R}}^\times }\)-invariant), if only their leaves are integral submanifolds of the corresponding characteristic foliations. The proofs are essentially the same, the ranks of the reduced \(\omega _0\) and \(C_0\) remain the same, only the reduced manifolds \(P_0\) and \(M_0\) are generally of dimensions greater than the dimensions obtained for contact and symplectic reductions. Hence, we can formulate the following theorem on precontact/presymplectic reductions.
Theorem 3.8
Let \((P,\tau ,M,h,\omega )\) be a presymplectic cover of a precontact manifold (M, C) of rank \((2r+1)\). Then, there is a canonical one-to-one correspondence between regular \({{\mathbb {R}}^\times }\)-invariant involutive distributions \(\chi _P\) of rank k on P such that \(\chi _P\subset \chi (\omega )\), and regular involutive distributions \(\chi _M\) of rank k on M such that \(\chi _M\subset \chi (C)\), given by  . Let \({\mathcal {F}}_P\) and \({\mathcal {F}}_M\) be the corresponding foliations. Then, \({\mathcal {F}}_P\) is simple if and only if \({\mathcal {F}}_M\) is simple.
. Let \({\mathcal {F}}_P\) and \({\mathcal {F}}_M\) be the corresponding foliations. Then, \({\mathcal {F}}_P\) is simple if and only if \({\mathcal {F}}_M\) is simple.
In this case, the manifold \(P_0=P/{\mathcal {F}}_P\) of \({\mathcal {F}}_P\)-leaves carries a canonical structure of a presymplectic \({{\mathbb {R}}^\times }\)-bundle \((P_0,\tau _0,M_0,h^0,\omega _0)\) of rank \(2(r+1)\) such that the canonical submersion \(p:P\rightarrow P_0\) is a submersive morphism of \({{\mathbb {R}}^\times }\)-bundles, i.e., \(h^0_s\circ p=p\circ h_s\), and \(\omega =p^*(\omega _0)\).
In particular, we have the following commutative diagram of a surjective morphism of \({{\mathbb {R}}^\times }\)-bundles:

Moreover, \(M_0=M/{\mathcal {F}}_M\), and \(M_0\) carries a canonical precontact structure \(C_0\) of rank \((2r+1)\) such that  , where \(p_0\) is the canonical submersion onto the manifold of leaves of \({\mathcal {F}}_M\).
, where \(p_0\) is the canonical submersion onto the manifold of leaves of \({\mathcal {F}}_M\).
4 Hamiltonian dynamics on precontact manifolds
4.1 Precontact Hamiltonians
A vector field on a presymplectic manifold \((P,\omega )\) we will call a Hamiltonian vector field if there is a function H (called a Hamiltonian of X) on P such that  . It is easy to check that a function H is a Hamiltonian if and only if H is constant on the leaves of the characteristic foliation \({\mathcal {F}}_\omega \). Note that there is no guarantee that such functions are not just constants. Moreover, if \(\omega \) is not symplectic, then a Hamiltonian H does not determine X uniquely: Hamiltonian vector fields \(X_H\) with the same Hamiltonian H differ by a vector field taking values in the characteristic distribution \(\chi (\omega )\). On the other hand, we have the following.
. It is easy to check that a function H is a Hamiltonian if and only if H is constant on the leaves of the characteristic foliation \({\mathcal {F}}_\omega \). Note that there is no guarantee that such functions are not just constants. Moreover, if \(\omega \) is not symplectic, then a Hamiltonian H does not determine X uniquely: Hamiltonian vector fields \(X_H\) with the same Hamiltonian H differ by a vector field taking values in the characteristic distribution \(\chi (\omega )\). On the other hand, we have the following.
Proposition 4.1
On every presymplectic manifold \((P,\omega )\), there exists a Hamiltonian vector field \(X_H\) for each Hamiltonian H (i.e., a function on P which is constant on the leaves of \({\mathcal {F}}_\omega \)). Two such Hamiltonian vector fields differ by a vector field taking values in the characteristic distribution \(\chi (\omega )\). Moreover, we have a well-defined ‘Poisson bracket’ of Hamiltonians, given by
where \(X_H,X_{H'}\) are Hamiltonian vector fields with Hamiltonians \(H,H'\).
Proof
For any \(x_0\in P\), there is a neighborhood U of \(x_0\) and a vector field \(X^U_H\) on U such that  for \(x\in U\). This is because we can choose U such that \({\mathcal {F}}_\omega \) is trivial on U, so we can pass locally to the symplectic reduction \(p:U\rightarrow U_0=U/{\mathcal {F}}_\omega \) such that \(\omega =p^*(\omega _0)\) for a symplectic form \(\omega _0\) on \(U_0\). Then, \(H=H_0\circ p\) for some Hamiltonian \(H_0\) on the symplectic manifold \((U_0,\omega _0)\), and as \(X^U_H\) we can take any vector field on U which projects via
for \(x\in U\). This is because we can choose U such that \({\mathcal {F}}_\omega \) is trivial on U, so we can pass locally to the symplectic reduction \(p:U\rightarrow U_0=U/{\mathcal {F}}_\omega \) such that \(\omega =p^*(\omega _0)\) for a symplectic form \(\omega _0\) on \(U_0\). Then, \(H=H_0\circ p\) for some Hamiltonian \(H_0\) on the symplectic manifold \((U_0,\omega _0)\), and as \(X^U_H\) we can take any vector field on U which projects via  onto the Hamiltonian vector field \(X_{H_0}\) on \(U_0\). This is possible, since p is a trivial fiber bundle. Of course, any two such vector fields \(X^U_H\) differ by a vector field whose projection on \(U_0\) is 0. What we have just proved is that the submanifold
onto the Hamiltonian vector field \(X_{H_0}\) on \(U_0\). This is possible, since p is a trivial fiber bundle. Of course, any two such vector fields \(X^U_H\) differ by a vector field whose projection on \(U_0\) is 0. What we have just proved is that the submanifold  , defined by
, defined by

is a smooth locally trivial affine subbundle in  . By topological reasons (the fibers of A are contractible), there is always a global section \(X_H\) of A. Finally, the definition of the Poisson bracket is correct, since (11) does not depend on the choice of the Hamiltonian vector fields. \(\square \)
. By topological reasons (the fibers of A are contractible), there is always a global section \(X_H\) of A. Finally, the definition of the Poisson bracket is correct, since (11) does not depend on the choice of the Hamiltonian vector fields. \(\square \)
From Corollary 2.20, we deduce now the following.
Proposition 4.2
Let \((P,\tau ,M,h,\omega )\) be a presymplectic cover of a precontact manifold (M, C), and let X be an \({{\mathbb {R}}^\times }\)-presymplectic vector field, i.e., X is an \({{\mathbb {R}}^\times }\)-invariant vector field such that \({\pounds }_X\theta =0\). Then, X admits a unique 1-homogeneous Hamiltonian H defined by \(H=i_X\theta \). Consequently, any contact vector field \(X^c\) on M determines a unique 1-homogeneous Hamiltonian H on P and a unique \({{\mathbb {R}}^\times }\)-invariant Hamiltonian vector field X on P such that  and \(\tau _*(X)=X^c\).
and \(\tau _*(X)=X^c\).
Proof
Since X and \(\theta \) are homogeneous of degrees 0 and 1, respectively, \(H=i_X\theta \) is homogeneous of degree 1. Moreover,

so H is a Hamiltonian for X. If \(H_1\) is another 1-homogeneous Hamiltonian for X, then  . But \(H-H_1\) is 1-homogeneous, so
. But \(H-H_1\) is 1-homogeneous, so

\(\square \)
We will call \(H=i_X\theta \) the contact Hamiltonian of \(X^c\). Of course, a contact Hamiltonian can be associated with many contact vector fields \(X^c\).
Remark 4.3
H associated with \(X^c\) can be described directly by \(H(x)=\iota _{\sigma _{X^c}}(x)\), where \(\iota _{\sigma _{X^c}}\) is the linear function on \(\left( L^C\right) ^*\) defined by the section \(\sigma _{X^c}\) of  , \(\sigma _{X^c}(y)=\rho ^C(X^c(y))\), where we identify P with \(\big [\left( L^C\right) ^*\big ]^\times \) (cf. Theorem 2.17).
, \(\sigma _{X^c}(y)=\rho ^C(X^c(y))\), where we identify P with \(\big [\left( L^C\right) ^*\big ]^\times \) (cf. Theorem 2.17).
4.2 Contact Hamiltonian mechanics
In this section, we will concentrate on contact manifolds and their symplectic covers. In this case, any function on the symplectic cover is a Hamiltonian and determines a unique Hamiltonian vector field. Note first that we are using the convention in which the canonical symplectic form \(\omega _N\) on  is
is  in canonical coordinates, i.e.,
in canonical coordinates, i.e.,  for
for  being the Liouville 1-form on
being the Liouville 1-form on  , and Hamiltonian vector fields are uniquely defined by
, and Hamiltonian vector fields are uniquely defined by

This gives the correct Hamilton’s equations and the map \(H\mapsto X_H\) is a morphism of the symplectic Poisson bracket
into the Lie bracket of vector fields, \(X_{\{ H_1,H_2\}_\omega }=[X_{H_1},X_{H_2}]\).
The commonly accepted approach to contact Hamiltonian dynamics in the physics literature is constructed almost exclusively only for trivial contact manifolds, i.e., manifolds M equipped with a globally defined contact 1-form \(\eta \) (cf. [10, 25, 28, 44, 64, 69, 73]), although a more general approach is also known, especially in the context of Jacobi geometry (see, e.g., [34, 35, 51, 58, 75]).
For a real valued function \({{\hat{H}}}\) (contact Hamiltonian) on a trivial contact manifold \(({M},\eta )\), the corresponding contact Hamiltonian vector field \(X^c_{{\hat{H}}}\) is a vector field on M defined as the unique one satisfying

where \({\mathcal {R}}\) is the Reeb vector field for \(\eta \), i.e., \({{\mathcal {R}}}\) is uniquely determined by \(i_{{\mathcal {R}}}\eta =1\) and  . In this sense, a contact Hamiltonian system is the triple \(({M},\eta ,{{\hat{H}}})\). Since
. In this sense, a contact Hamiltonian system is the triple \(({M},\eta ,{{\hat{H}}})\). Since

\(X^c_{{\hat{H}}}\) is a contact vector field on M with the conformal factor \(\lambda =-{\mathcal {R}}({{\hat{H}}})\). In this realization, the contact Jacobi bracket of two smooth functions on M is defined by
According to (13), the flow of a contact Hamiltonian vector field preserves the contact structure, but it does not preserve neither the contact one-form nor the Hamiltonian function. Instead, we obtain
Referring to contact Darboux coordinates \((z,q^i,p_j)\) in which  , the Hamiltonian vector field determined in (12) is computed to be
, the Hamiltonian vector field determined in (12) is computed to be
whereas the contact Jacobi bracket (14) is
So, the Hamilton’s equations for \({{\hat{H}}}\) read
In our setting, contact Hamiltonians for a contact manifold (M, C) are 1-homogeneous Hamiltonians \(H:P\rightarrow {\mathbb {R}}\) on the corresponding symplectic cover \(\tau :P\rightarrow M\) equipped with a 1-homogeneous symplectic form \(\omega \). As we already mentioned, 1-homogeneous Hamiltonians on P can be viewed as sections of the line bundle \(L^C\rightarrow M\), where  . The section corresponding to a Hamiltonian H we will denote \(\sigma _H\), and the Hamiltonian corresponding to a section \(\sigma \) will be denoted \(H_\sigma \). Since \(\omega \) is 1-homogeneous, the 1-homogeneous Hamiltonians are closed with respect to the symplectic Poisson (Lagrange) bracket \(\{ H,H'\}_\omega \). This corresponds to a Jacobi bracket \(\{\sigma ,\sigma '\}_J\) on sections of \(L^C\) via
. The section corresponding to a Hamiltonian H we will denote \(\sigma _H\), and the Hamiltonian corresponding to a section \(\sigma \) will be denoted \(H_\sigma \). Since \(\omega \) is 1-homogeneous, the 1-homogeneous Hamiltonians are closed with respect to the symplectic Poisson (Lagrange) bracket \(\{ H,H'\}_\omega \). This corresponds to a Jacobi bracket \(\{\sigma ,\sigma '\}_J\) on sections of \(L^C\) via
The corresponding Hamiltonian vector fields \(X_H\) (or \(X_\sigma \)) on P are homogeneous of degree 0, i.e., they are \({{\mathbb {R}}^\times }\)-invariant, therefore they project onto the vector fields \(X^c_H=X^c_{\sigma _H}=\tau _*(X_H)\) on M, called contact Hamiltonian vector fields. Contact Hamiltonian vector fields are actually contact vector fields, i.e., their flows preserve the contact structure (cf. Proposition 2.19), and \(H\mapsto X^c_H\) is a one-to-one correspondence between contact Hamiltonians and contact vector fields.
Note that the above understanding of Hamiltonians as sections of certain line bundles is present already in [58] (see also [51]) and valid for an arbitrary Jacobi bundle.
Example 4.4
Let \(P={\mathbb {R}}^\times \times M\) be the trivial \({\mathbb {R}}^\times \)-principal bundle with coordinates \((s,y=(y^a))\). Any trivial contact structure on P consists of the symplectic form \(\omega _\eta \) associated with a contact 1-form \(\eta \) on M and defined by  . If \({{\mathcal {R}}}\) is the Reeb vector field for \(\eta \), then \({{\mathcal {R}}}\), viewed as homogeneous vector field of weight 0 on P, \({{\mathcal {R}}}(s,y)={{\mathcal {R}}}(y)\), is the Hamiltonian vector field with respect to \(\omega _\eta \) with the Hamiltonian \(H=s\),
. If \({{\mathcal {R}}}\) is the Reeb vector field for \(\eta \), then \({{\mathcal {R}}}\), viewed as homogeneous vector field of weight 0 on P, \({{\mathcal {R}}}(s,y)={{\mathcal {R}}}(y)\), is the Hamiltonian vector field with respect to \(\omega _\eta \) with the Hamiltonian \(H=s\),  . Let us take a function \({\hat{H}}\) on M and consider the homogeneous Hamiltonian (the sign depends on conventions)
. Let us take a function \({\hat{H}}\) on M and consider the homogeneous Hamiltonian (the sign depends on conventions)
The function \({\hat{H}}\) we will call a reduced contact Hamiltonian (it is defined only for trivial \({{\mathbb {R}}^\times }\)-bundles). The corresponding Hamiltonian vector field \(X_H\) is homogeneous of weight 0, so that \(X_H(s,y)=F(y)\,s\cdot \partial _s+Y(y)\), where F is a (pull-back of a) function on M and  , so that the vector field Y can be viewed as tangent to M and therefore identified with the contact Hamiltonian vector field \(X^c_H=\tau _*(X_H)\). In other words,
, so that the vector field Y can be viewed as tangent to M and therefore identified with the contact Hamiltonian vector field \(X^c_H=\tau _*(X_H)\). In other words,
We have

so that \(i_{X^c_H}\eta =-{\hat{H}}\) and

Contracting both sides with \({{\mathcal {R}}}\), we get \(F={{\mathcal {R}}}({\hat{H}})\), so
and in this way we reconstructed equations (12) for the reduced contact Hamiltonian \({\hat{H}}\). In Darboux coordinates \(y=(z,q^i,p_j)\) for \(\eta \), we recover the contact Hamilton equations (15).
5 Contact reductions
5.1 Isotropic, coisotropic, and Legendrian submanifolds
Let us fix a contact manifold (M, C) and its symplectic cover \((P,\tau ,M,h,\omega )\). It is obvious that there is a canonical one-to-one correspondence between submanifolds N of M and \({{\mathbb {R}}^\times }\)-subbundles \({\widetilde{N}}\) of P, given by \(N=\tau ({\widetilde{N}})\) and \({\widetilde{N}}=\tau ^{-1}(N)\).
Since in our language contact structures are understood as certain homogeneous symplectic structures, objects in contact geometry are consequently homogeneous objects in symplectic geometry. For instance, a submanifold N of the contact manifold M we call isotropic (resp., coisotropic, Legendre) if the inverse image \({\widetilde{N}}=\tau ^{-1}(N)\) is isotropic (resp., coisotropic, Lagrangian) in \((P,\omega )\). These concepts are well known in the literature even for general Jacobi structures, although often defined in other languages. For some deeper studies on contact coisotropic submanifolds, see, e.g., [51, 71, 75, 76].
Proposition 5.1
Let N be a submanifold of a contact manifold (M, C). Then,
-
1.
N is isotropic if and only if
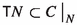 . Equivalently, the restriction \(\eta \,\big |_N\) of any local contact form \(\eta \) associated with C vanishes.
. Equivalently, the restriction \(\eta \,\big |_N\) of any local contact form \(\eta \) associated with C vanishes. -
2.
N is coisotropic if and only if the contact vector fields \(X^c_H\) on M, associated with contact Hamiltonians \(H:P\rightarrow {\mathbb {R}}\) vanishing on \({\widetilde{N}}\), are tangent to N.
-
3.
N is a Legendre submanifold if and only if it is simultaneously isotropic nad coisotropic.
Proof
1. Let \(\eta \) be a local contact form on \(U\subset M\) such that \(C=\ker (\eta )\). We can assume that P over U is trivial and we can write \(\omega \) on \(\widetilde{U}=\tau ^{-1}(U)\) as

where \(y\in U\). Assume that \({\widetilde{N}}\) is isotropic in P. Since \(\partial _s\) is tangent to \({\widetilde{N}}\), we get that \(i_{\partial _s}\omega \) vanishes on  . But, for \(y_0\in N\), the vector space
. But, for \(y_0\in N\), the vector space  is spanned by \(\partial _s\) and
is spanned by \(\partial _s\) and  , so \(i_{\partial _s}\omega (y_0,s)=\eta (y_0)\). Hence, \(\eta (y_0)\) vanishes on
, so \(i_{\partial _s}\omega (y_0,s)=\eta (y_0)\). Hence, \(\eta (y_0)\) vanishes on  . Conversely, if \(\eta \) vanishes on
. Conversely, if \(\eta \) vanishes on  , then taking vectors
, then taking vectors  we get
we get

This is because if \(\eta \,\big |_N=0\), then  .
.
2. Since contact Hamiltonians are particular Hamiltonians on P, and projectable vector fields tangent to \({\widetilde{N}}\) project onto vector fields on M which are tangent to N, the implication ‘\(\Rightarrow \)’ follows easily. Conversely, suppose that the contact vector fields associated with Hamiltonians vanishing on \({\widetilde{N}}\) are tangent to N. This implies that the Hamiltonian vector fields \(X_H\) on P associated with 1-homogeneous Hamiltonians vanishing on \({\widetilde{N}}\) are tangent to \({\widetilde{N}}\). We have to show that it is true for all Hamiltonians on P vanishing on \({\widetilde{N}}\). Since the statement is local, we can assume that \(P={{\mathbb {R}}^\times }\times M\) and  , where \(y\in M\). Consider an arbitrary Hamiltonian \(H=H(y,s)\) on P, \(H(y_0,s)=0\) if \(y_0\in N\). For a fixed \(s_0\in {{\mathbb {R}}^\times }\), let \({\hat{H}}(y)=H(y,s_0)/s_0\). It is a function on M, so \(H'(y,s)=s\cdot {\hat{H}}(y)\) is a 1-homogeneous Hamiltonian on P. Let us take \(y_0\in N\). Since
, where \(y\in M\). Consider an arbitrary Hamiltonian \(H=H(y,s)\) on P, \(H(y_0,s)=0\) if \(y_0\in N\). For a fixed \(s_0\in {{\mathbb {R}}^\times }\), let \({\hat{H}}(y)=H(y,s_0)/s_0\). It is a function on M, so \(H'(y,s)=s\cdot {\hat{H}}(y)\) is a 1-homogeneous Hamiltonian on P. Let us take \(y_0\in N\). Since

the vectors \(X_H(y_0,s_0)\) and \(X_{H'}(y_0,s_0)\) coincide. But the latter is tangent to \({\widetilde{N}}\), that completes the proof.
3. It follows from the well-known fact that Lagrangian submanifolds in a symplectic manifold can be characterized as being simultaneously isotropic and coisotropic. \(\square \)
Note that \({\widetilde{N}}\) being \({{\mathbb {R}}^\times }\)-invariant is actually an \({{\mathbb {R}}^\times }\)-principal bundle itself, \(\tau _N:{\widetilde{N}}\rightarrow N\), where \(\tau _N=\tau \,\big |_{\widetilde{N}}\), equipped additionally with a 1-homogeneous closed 2-form \(\omega \,\big |_{\widetilde{N}}\). Here, we understand \(\omega \,\big |_{\widetilde{N}}\) as \(i_{\widetilde{N}}^*(\omega )\), where \(i_{\widetilde{N}}:{\widetilde{N}}\hookrightarrow P\) is the canonical inclusion map. We will write simply \(\tau \) instead of \(\tau _N\), that should not lead to any misunderstanding.
The above concepts can be formulated also in the precontact/presymplectic case, although the concept of Legendrian/Lagrangian submanifolds in noncontact/nonsymplectic case are used less frequently. For instance, if \({\widetilde{N}}\) is a submanifold in a precontact manifold \((P,\omega )\) of rank 2r, then
-
1.
\({\widetilde{N}}\) is isotropic if \(\omega \,\big |_{\widetilde{N}}=0\), i.e.,
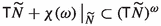 ;
; -
2.
\({\widetilde{N}}\) is coisotropic if
 ;
; -
3.
\({\widetilde{N}}\) is Lagrangian if it is isotropic and coisotropic, i.e.,
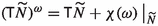 ,
,
where  denotes the ’orthogonal complement’ of
denotes the ’orthogonal complement’ of  with respect to \(\omega \), i.e., for \(x\in {\widetilde{N}}\),
with respect to \(\omega \), i.e., for \(x\in {\widetilde{N}}\),

Since we always have a local symplectic reduction to a symplectic manifold of dimension 2r, any Lagrangian submanifold \({\widetilde{N}}\) is locally projected by the reduction to a Lagrangian submanifold of the reduced symplectic manifold, so the rank d of the intersection  is locally constant and \(\dim {{\widetilde{N}}}=r+d\) (cf. [47, Definition 2.2]). For precontact manifolds, we have the following analog of Proposition 5.1.
is locally constant and \(\dim {{\widetilde{N}}}=r+d\) (cf. [47, Definition 2.2]). For precontact manifolds, we have the following analog of Proposition 5.1.
Proposition 5.2
Let N be a submanifold of a precontact manifold (M, C). Then,
-
1.
N is isotropic if and only if
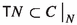 .
. -
2.
N is coisotropic if and only if the contact vector fields \(X^c_H\) on M, associated with contact Hamiltonians \(H:P\rightarrow {\mathbb {R}}\) vanishing on \({\widetilde{N}}\), take values in
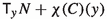 for \(y\in N\).
for \(y\in N\). -
3.
N is a Legendre submanifold if and only if it is simultaneously isotropic nad coisotropic.
5.2 Constant rank reduction
For general symplectic reductions, we refer to [4, 5, 55]. For symplectic reductions by Hamiltonian actions of Lie groups to [1, 3, 55, 59, 61].
Constant rank submanifolds in a symplectic manifold are defined as those submanifolds \({\widetilde{N}}\) for which the restriction of the symplectic form to \({\widetilde{N}}\) is a closed 2-form of constant rank (recall that we decided to call such 2-forms presymplectic forms). It could suggest that this leads naturally to the definition of constant rank submanifolds of a contact manifold M as those submanifolds \(N\subset M\) for which \({\widetilde{N}}=\tau ^{-1}(N)\) is a constant rank submanifold in \((P,\omega )\), i.e., the closed 2-form \(\omega \,\big |_{\widetilde{N}}\) is of constant rank. There is, however, a problem with such a definition, especially if we want to work with reductions, since constant rank \({{\mathbb {R}}^\times }\)-subbundles \({\widetilde{N}}\) in symplectic \({{\mathbb {R}}^\times }\)-bundles \((P,\tau ,M,h,\omega )\) need not to be presymplectic \({{\mathbb {R}}^\times }\)-bundles themselves. This is because the characteristic distribution of \(\omega \,\big |_{\widetilde{N}}\) need not to be transversal to the fibers of \(\tau :{\widetilde{N}}\rightarrow N\).
Let us start with looking closer at corresponding characteristic distributions. Let \((P,\tau ,M,h,\omega )\) be a presymplectic cover of a precontact manifold (M, C) of rank \((2r+1)\), with the 2-form \(\nu ^C:C\times _MC\rightarrow L^C\) on C of rank 2r, the Euler vector field \(\nabla \), and the Liouville 1-form \(\theta \), so  . Let N be a submanifold of M. If we denote
. Let N be a submanifold of M. If we denote  , then it is clear that the dimension of
, then it is clear that the dimension of  may jump at some points \(y\in N\), so generally
may jump at some points \(y\in N\), so generally  is not even a smooth distribution.
is not even a smooth distribution.
For \(x\in {\widetilde{N}}\) and \(y\in N\), denote with  the kernel of \(\omega \,\big |_{\widetilde{N}}(x)\), and with
the kernel of \(\omega \,\big |_{\widetilde{N}}(x)\), and with  the kernel of \(\left( \nu ^C_N\right) (y)\), where
the kernel of \(\left( \nu ^C_N\right) (y)\), where  . The dimensions of these kernels we denote \(k({\widetilde{N}})(x)\) and k(N)(y), respectively. We know that if a 1-form \(\eta \) generates the precontact structure \(C=\ker (\eta )\) locally on \(U\subset M\), then we have a local trivialization \(\widetilde{U}=U\times {{\mathbb {R}}^\times }\) in which \(\omega =\omega _\eta \). From Proposition 2.8, we know that
. The dimensions of these kernels we denote \(k({\widetilde{N}})(x)\) and k(N)(y), respectively. We know that if a 1-form \(\eta \) generates the precontact structure \(C=\ker (\eta )\) locally on \(U\subset M\), then we have a local trivialization \(\widetilde{U}=U\times {{\mathbb {R}}^\times }\) in which \(\omega =\omega _\eta \). From Proposition 2.8, we know that  maps \(\chi ({\widetilde{N}})(x)\) onto \(\chi (N)(y)\), where \(y=\tau (x)\), so \(k({\widetilde{N}})(x)\ge k(N)(y)\) and these dimensions are equal if and only if \(\eta \,\big |_N(y)\ne 0\). The latter is equivalent to
maps \(\chi ({\widetilde{N}})(x)\) onto \(\chi (N)(y)\), where \(y=\tau (x)\), so \(k({\widetilde{N}})(x)\ge k(N)(y)\) and these dimensions are equal if and only if \(\eta \,\big |_N(y)\ne 0\). The latter is equivalent to  , and to the fact that \(\omega _{\widetilde{N}}\) has no vertical characteristic vectors (the characteristic distribution is transversal to the fibers of \(\tau \)). A submanifolds N of M we will call transversal if
, and to the fact that \(\omega _{\widetilde{N}}\) has no vertical characteristic vectors (the characteristic distribution is transversal to the fibers of \(\tau \)). A submanifolds N of M we will call transversal if  for all \(y\in N\). In general it could be \(k({\widetilde{N}})(x)=k(N)(y)+1\) even if \(k({\widetilde{N}})\) is constant or k(N) is constant, which shows that we cannot work with constant rank submanifolds in the traditional meaning.
for all \(y\in N\). In general it could be \(k({\widetilde{N}})(x)=k(N)(y)+1\) even if \(k({\widetilde{N}})\) is constant or k(N) is constant, which shows that we cannot work with constant rank submanifolds in the traditional meaning.
Example 5.3
Consider the contact form  on \(M={\mathbb {R}}^3\) and the submanifold \(N\subset M\) defined by the equation \(z=0\), so the tangent bundle
on \(M={\mathbb {R}}^3\) and the submanifold \(N\subset M\) defined by the equation \(z=0\), so the tangent bundle  is spanned by vector fields \(\partial _{q},\partial _{p}\) and the contact form restricted to N reads
is spanned by vector fields \(\partial _{q},\partial _{p}\) and the contact form restricted to N reads  . Hence,
. Hence,  and
and  is spanned by \(\partial _p\) if \(p\ne 0\), and
is spanned by \(\partial _p\) if \(p\ne 0\), and  . Consequently, \(\chi (N)(p,q)\) is spanned by \(\partial _p\) if \(p\ne 0\), and is trivial if \(p=0\), so the generalized distribution \(\chi (N)\) is not regular. However, \({\widetilde{N}}\) is of constant rank. Indeed, the submanifold \({\widetilde{N}}\) on \(P=M\times {{\mathbb {R}}^\times }\) with adapted coordinates (z, p, q, s) is defined by the same equation \(z=0\). Since the symplectic form reads
. Consequently, \(\chi (N)(p,q)\) is spanned by \(\partial _p\) if \(p\ne 0\), and is trivial if \(p=0\), so the generalized distribution \(\chi (N)\) is not regular. However, \({\widetilde{N}}\) is of constant rank. Indeed, the submanifold \({\widetilde{N}}\) on \(P=M\times {{\mathbb {R}}^\times }\) with adapted coordinates (z, p, q, s) is defined by the same equation \(z=0\). Since the symplectic form reads

its restriction to \({\widetilde{N}}\) is

Its kernel is generated by \(s\partial _s-p\partial _p\). It is a nowhere vanishing vector field on \({\widetilde{N}}\), so \(\chi ({\widetilde{N}})\) is of constant rank 1. Actually, \({\widetilde{N}}\) is coisotropic. Indeed, the vector field \(X(p,q,s)=s\partial _s-p\partial _p\) is the restriction to \({\widetilde{N}}\) of the vector field \(s\partial _s-p\partial _p-z\partial _z\) which is the Hamiltonian vector field for the 1-homogeneous Hamiltonian \(H(z,p,q,s)=s\cdot z\). Note that \(X(0,q,s)=s\partial _s\) is vertical, so \(\chi ({\widetilde{N}})(0,q,s)\) is the vertical part of the tangent space  .
.
Example 5.4
Consider the standard contact form  on \(M={\mathbb {R}}^5\). Let a submanifold N in M be defined by the equations \(z=0, q^1=q^2\), so we can take \((p_1,p_2,q=q^1+q^2)\) as coordinates on N in which the contact form restricted to N reads
on \(M={\mathbb {R}}^5\). Let a submanifold N in M be defined by the equations \(z=0, q^1=q^2\), so we can take \((p_1,p_2,q=q^1+q^2)\) as coordinates on N in which the contact form restricted to N reads  . Hence,
. Hence,  is spanned by \(\partial _{p_1},\partial _{p_2}\) if \(p_1+p_2\ne 0\) and equals
is spanned by \(\partial _{p_1},\partial _{p_2}\) if \(p_1+p_2\ne 0\) and equals  if \(p_1+p_2=0\). Since
if \(p_1+p_2=0\). Since  , the kernel of
, the kernel of  as a bilinear form on
as a bilinear form on  is in both cases spanned by \(\partial _{p_1},\partial _{p_2}\) (cf. (2)), so N is of constant rank.
is in both cases spanned by \(\partial _{p_1},\partial _{p_2}\) (cf. (2)), so N is of constant rank.
The above examples show that even if \({\widetilde{N}}\) is of constant rank in \((P,\omega )\), the distribution  can be of non-constant rank, and vice versa. As Example 5.3 shows, even coisotropic submanifolds can be non-transversal. This is, of course, a very bad situation if we want to use this distribution for a reduction, and suggests the following definition.
can be of non-constant rank, and vice versa. As Example 5.3 shows, even coisotropic submanifolds can be non-transversal. This is, of course, a very bad situation if we want to use this distribution for a reduction, and suggests the following definition.
Definition 5.5
A submanifold N of a contact manifold (M, C) is of constant rank if N is transversal and the characteristic distribution \(\chi (N)\) is of constant rank. An \({{\mathbb {R}}^\times }\)-subbundle \(\tau :{\widetilde{N}}\rightarrow N\) of a symplectic \({{\mathbb {R}}^\times }\) principal bundle \(\tau :P\rightarrow M\) we call constantly transversal if the characteristic distribution  has constant rank and it is transversal to the fibers of \(\tau \) (has no vertical vectors).
has constant rank and it is transversal to the fibers of \(\tau \) (has no vertical vectors).
The following is now obvious.
Proposition 5.6
Let \((P,\tau ,M,h,\omega )\) be a symplectic cover of a contact manifold (M, C), and let N be a submanifold of M. Then, N is of constant rank, if and only \({\widetilde{N}}=\tau ^{-1}(N)\) is constantly transversal. This is equivalent to the fact that  is a precontact manifold of rank \((2r+1)\), and to the fact that \(({\widetilde{N}},\tau ,N,h,\omega \,\big |_{\widetilde{N}})\) is its presymplectic \({{\mathbb {R}}^\times }\)-bundle of rank \(2(r+1)\), where \(2r=\dim (N)-k(N)\). In this case, the characteristic distributions \(\chi (N)\) and \(\chi ({\widetilde{N}})\) are regular and involutive, so define the corresponding foliations \({\mathcal {F}}_N\) and \({\mathcal {F}}_{\widetilde{N}}\), respectively.
is a precontact manifold of rank \((2r+1)\), and to the fact that \(({\widetilde{N}},\tau ,N,h,\omega \,\big |_{\widetilde{N}})\) is its presymplectic \({{\mathbb {R}}^\times }\)-bundle of rank \(2(r+1)\), where \(2r=\dim (N)-k(N)\). In this case, the characteristic distributions \(\chi (N)\) and \(\chi ({\widetilde{N}})\) are regular and involutive, so define the corresponding foliations \({\mathcal {F}}_N\) and \({\mathcal {F}}_{\widetilde{N}}\), respectively.
The foliations \({\mathcal {F}}_N\) and \({\mathcal {F}}_{\widetilde{N}}\) we call the characteristic foliations of N and \({\widetilde{N}}\), respectively. Theorem 3.4 immediately implies the following result on contact constant rank reduction.
Theorem 5.7
(contact constant rank reduction) Let \((P,\tau ,M,h,\omega )\) be a symplectic cover of a contact manifold (M, C), and let N be a constant rank submanifold of M such that its characteristic foliation \({\mathcal {F}}_N\) is simple, with the canonical submersion \(p_0:N\rightarrow N_0=N/{\mathcal {F}}_N\). Then,  is a precontact manifold, \(p_0\) is a precontact-to-contact reduction, and \({\widetilde{N}}=\tau ^{-1}(N)\) is a presymplectic \({{\mathbb {R}}^\times }\)-subbundle of \((P,\tau ,M,h,\omega )\), with all structures inherited from the latter. Moreover, the characteristic foliation \({\mathcal {F}}_{\widetilde{N}}\) is also simple, with the canonical submersion \(p:{\widetilde{N}}\rightarrow {\widetilde{N}}_0={\widetilde{N}}/{\mathcal {F}}_{\widetilde{N}}\), and we have the commutative diagram
is a precontact manifold, \(p_0\) is a precontact-to-contact reduction, and \({\widetilde{N}}=\tau ^{-1}(N)\) is a presymplectic \({{\mathbb {R}}^\times }\)-subbundle of \((P,\tau ,M,h,\omega )\), with all structures inherited from the latter. Moreover, the characteristic foliation \({\mathcal {F}}_{\widetilde{N}}\) is also simple, with the canonical submersion \(p:{\widetilde{N}}\rightarrow {\widetilde{N}}_0={\widetilde{N}}/{\mathcal {F}}_{\widetilde{N}}\), and we have the commutative diagram

in which the right-hand side is a symplectic \({{\mathbb {R}}^\times }\)-bundle and the horizontal maps form a symplectic reduction of the presymplectic \({{\mathbb {R}}^\times }\)-bundle \({\widetilde{N}}\).
6 Contact Marsden–Weinstein–Meyer reduction
6.1 Precontact moment maps
Let \((P,\tau ,M,h,\omega )\) be a presymplectic cover of a precontact manifold (M, C) of rank \((2r+1)\), and let
be an action of a Lie group G on M by contactomorphisms. This induces a homomorphism \(\xi \mapsto \xi ^c\) of the Lie algebra \({\mathfrak {g}}\) of G into the Lie algebra of contact vector fields on M, where \(\xi ^c\) is the fundamental vector field associated with the action \(\rho \) and \(\xi \in {\mathfrak {g}}\). The group action \(\rho \) is covered by an action (see Corollary 2.20)
of G on P by automorphisms of the presymplectic \({{\mathbb {R}}^\times }\)-bundle structure, i.e.,
Moreover, any contact vector field \(\xi ^c\) is covered by a unique \({{\mathbb {R}}^\times }\)-invariant Hamiltonian vector field \({{\hat{\xi }}}\) on P, with 1-homogeneous Hamiltonian \(H_\xi =i_{{\hat{\xi }}}\theta \) on P. Therefore, we do not have the problems with defining the moment map, coming from non-uniqueness of Hamiltonians in the standard symplectic setting.
Let \({\hat{{\mathfrak {g}}}}\) be the Lie algebra of vector fields spanned by \({{\hat{\xi }}}\) (the infinitesimal action of G). It is easy to see that \({\hat{{\mathfrak {g}}}}(x)\) is the tangent space to the G-orbit \(G.x=\{\widetilde{g}(x)\,\big |\,g\in G\}\) at \(x\in P\),

Of course, \(\tau :P\rightarrow M\) maps G-orbits in P onto G-orbits in M. We define the map
which we will call the contact moment map associated with the action \(\rho \) of G on M by contactomorphisms. Actually, in the context of moment maps and reductions, only the Lie algebra of vector fields \({\hat{{\mathfrak {g}}}}\) (a \({\mathfrak {g}}\)-action) is needed if G is connected. Note that, in contrast to the majority of existing literature (cf. [2, 25, 31, 52, 79]), our contact moment map is defined on P, not on M. This moment map is known to be \(\text {Ad}\)-equivariant. The equivariance means that
so
In our case, the moment map is not only equivariant, but it intertwines additionally the corresponding \({{\mathbb {R}}^\times }\)-actions,
Indeed,
since \(H_\xi \) is 1-homogeneous. For any vector subspace  , with \(V^\omega \) we denote the ’orthogonal complement’ of V with respect to \(\omega \), i.e.,
, with \(V^\omega \) we denote the ’orthogonal complement’ of V with respect to \(\omega \), i.e.,  .
.
Proposition 6.1
Let  be the kernel of
be the kernel of  . Then,
. Then,

In particular, \(\chi (\omega )\subset K(J)\), so the moment map J is constant along the leaves of the characteristic foliation \({\mathcal {F}}_\omega \). In the case when the foliation \({\mathcal {F}}_\omega \) (equivalently, \({\mathcal {F}}_C\)) is simple, the map J induces the moment map \(J^0:P_0\rightarrow {\mathfrak {g}}^*\) for the induced G-action (the \({\mathfrak {g}}\)-action is enough) on the reduced symplectic \({{\mathbb {R}}^\times }\)-bundle \(P_0=P/{\mathcal {F}}_\omega \) (cf. Proposition 3.6) by \(J^0(p(x))=J(x)\), where \(p:P\rightarrow P_0\) is the canonical submersion.
Proof
Let \(X\in K(J)(x_0)\), and let \(\gamma :{\mathbb {R}}\rightarrow P\) be a smooth curve representing X, i.e., \(\gamma (0)=x_0\) and \({\dot{\gamma }}(0)=X\). For any \(\xi \in {\mathfrak {g}}\), we have

The rest is obvious. \(\square \)
The above proposition shows that, in the case of simple \({\mathcal {F}}_C\) (e.g., if C is a contact structure) we can reduce our considerations to the standard Marsden–Weinstein–Meyer Hamiltonian reduction.
6.2 The precontact Marsden–Weinstein–Meyer theorem
Our construction will be modeled on the standard Marsden–Weinstein–Meyer reduction, with some necessary adaptation to the case of presymplectic \({{\mathbb {R}}^\times }\)-bundles. We will assume that G is connected. Let us fix \(\mu \in {\mathfrak {g}}^*\). The inverse image \(P_\mu =J^{-1}(\mu )\), considered in the standard approach, is \({{\mathbb {R}}^\times }\)-invariant only if \(\mu =0\), so for \(\mu \ne 0\) we consider
which is the smallest \({{\mathbb {R}}^\times }\)-subbundle in P containing \(P_\mu \). Here, \([\mu ]^\times =\{s\mu \,\big |\,s\ne 0\}\). Of course, \(P_{s\mu }=h_s(P_\mu )\) and \(P_{[s\mu ]}=P_{[\mu ]}\) for \(s\ne 0\) (cf. (16)).
We say that \(\mu \) is a weakly regular value of J if \(P_\mu \) is a submanifold and for every \(x\in P_\mu \) we have  . Of course, due to (16), \(\mu \) is a weekly regular value if and only if \(s\mu \) is a weakly regular value, where \(s\ne 0\), and any regular value is also weakly regular. In what follows we always assume that \(\mu \) is a weakly regular value. Then,
. Of course, due to (16), \(\mu \) is a weekly regular value if and only if \(s\mu \) is a weakly regular value, where \(s\ne 0\), and any regular value is also weakly regular. In what follows we always assume that \(\mu \) is a weakly regular value. Then,  and (17) implies that all Hamiltonians \(H_\xi \), \(\xi \in {\mathfrak {g}}\), are constant on \(P_\mu \), thus on all \(P_{s\mu }\), \(s\in {{\mathbb {R}}^\times }\). Moreover, due to the equivariance of the moment map, the subgroup
and (17) implies that all Hamiltonians \(H_\xi \), \(\xi \in {\mathfrak {g}}\), are constant on \(P_\mu \), thus on all \(P_{s\mu }\), \(s\in {{\mathbb {R}}^\times }\). Moreover, due to the equivariance of the moment map, the subgroup
of G acts on \(P_\mu \). Denote its Lie algebra with \({\mathfrak {g}}_\mu \), and the distribution spanned by \({\hat{\xi }}\) for \(\xi \in {\mathfrak {g}}_\mu \) with \({\hat{{\mathfrak {g}}}}_\mu \).
The cases \(\mu =0\) and \(\mu \ne 0\) are essentially different, so we will consider them separately. Let us start with the case \(\mu \ne 0\) which is more sophisticated. In this case, the submanifold \(P_{[\mu ]}\) of P is foliated by 1-codimensional submanifolds \(P_{s\mu }\), \(s\ne 0\), which are transversal to the \(\tau \)-fibers, so \(\tau (P_{[\mu ]})=\tau (P_\mu )=M_\mu \) is a submanifold in M, and the subgroup \(G_\mu \) acts on \(M_\mu \). We will describe the characteristic distribution of the submanifold \(P_{[\mu ]}\).
Let us first look at the characteristic distribution \(\chi (\omega _\mu )\), where \(\omega _\mu \) is the restriction of \(\omega \) to \(P_{\mu }\). We know that, for \(x\in P_\mu \), the tangent space  equals \(K(J)(x)=({\hat{{\mathfrak {g}}}}(x))^\omega \) (17). Assume first that \(\omega \) is symplectic. Then,
equals \(K(J)(x)=({\hat{{\mathfrak {g}}}}(x))^\omega \) (17). Assume first that \(\omega \) is symplectic. Then,  , so
, so

Using a local symplectic reduction of the presymplectic \({{\mathbb {R}}^\times }\)-bundle P and the corresponding reduction of the moment map (Proposition 6.1), we can infer that in the general presymplectic case we have

Note that we are actually interested in the characteristic distribution of \(\omega _{[\mu ]}=\omega \,\big |_{P_{[\mu ]}}\)of \(\omega \) restricted to \(P_{[\mu ]}\) rather than \(\chi (\omega _\mu )\). As the \({{\mathbb {R}}^\times }\)-action allows for identifying each \(P_{s\mu }\) with \(P_\mu \), we have  , where \([\nabla ]\) is the line subbundle of vertical vectors in
, where \([\nabla ]\) is the line subbundle of vertical vectors in  , thus generated by the Euler vector field \(\nabla \).
, thus generated by the Euler vector field \(\nabla \).
First of all, \(\nabla (x)\in \chi (\omega _{[\mu ]})(x)\) if and only if \(i_{\nabla (x)}\omega =\theta (x)\) vanishes on  , so
, so  . We can exclude this case assuming that \(M_\mu \) is a transversal submanifold in (M, C). It remains to check for which \(X\in \chi (\omega _\mu )(x)\) we have \(0=\omega (\nabla (x),X)=\big \langle \theta (x),X\big \rangle \). But \(\chi (\omega _\mu )(x)={\hat{{\mathfrak {g}}}}_\mu (x)+\chi (\omega )(x)\) (18), so it is enough to take \(X={\hat{\xi }}(x)\) for \(\xi \in {\mathfrak {g}}_\mu \). We have then
. We can exclude this case assuming that \(M_\mu \) is a transversal submanifold in (M, C). It remains to check for which \(X\in \chi (\omega _\mu )(x)\) we have \(0=\omega (\nabla (x),X)=\big \langle \theta (x),X\big \rangle \). But \(\chi (\omega _\mu )(x)={\hat{{\mathfrak {g}}}}_\mu (x)+\chi (\omega )(x)\) (18), so it is enough to take \(X={\hat{\xi }}(x)\) for \(\xi \in {\mathfrak {g}}_\mu \). We have then
which means that \(\mu \) annihilates \(\xi \), i.e., \(\xi \in \ker (\mu )\). It is easy to see that \({\mathfrak {g}}^0_\mu ={\mathfrak {g}}_\mu \cap \ker (\mu )\) is an ideal in the Lie algebra \({\mathfrak {g}}_\mu \). Indeed, \(\xi \in {\mathfrak {g}}_\mu \) if and only if \(\textrm{ad}^*_\xi (\mu )=0\). Hence, for \(\xi ,\xi '\in {\mathfrak {g}}_\mu \) we have
i.e., \([{\mathfrak {g}}_\mu ,{\mathfrak {g}}_\mu ]\subset {\mathfrak {g}}^0_\mu \). The corresponding connected Lie subgroup in \(G_\mu \) we denote \(G^0_\mu \). We conclude that in the case when \(M_\mu \) is transversal, we have
on \(P_{[\mu ]}\).
Let us pass to the case \(\mu =0\). Now, \(P_0=P_{[0]}\) is automatically an \({{\mathbb {R}}^\times }\)-subbundle in P over a certain submanifold \(M_0=\tau (P_0)\) of M. Similarly as in (18), we have

Note that in this case \({\mathfrak {g}}^0_0={\mathfrak {g}}_0={\mathfrak {g}}\). Summarizing these observations, we get the following.
Theorem 6.2
For any weekly regular value \(\mu \in {\mathfrak {g}}^*\) of the moment map J such that \(M_\mu \) is a transversal submanifold of (M, C), the characteristic distribution \(\chi (\omega _{[\mu ]})\) of the closed 2-form \(\omega _{[\mu ]}=\omega \,\big |_{P_{[\mu ]}}\) on \(P_{[\mu ]}\) is
and the characteristic distribution \(\chi (C_\mu )\) of the field of hyperplanes  on \(M_\mu \) is
on \(M_\mu \) is  and equals
and equals
where \({\hat{{\mathfrak {g}}}}^0_\mu \) (resp., \(({\mathfrak {g}}^0_\mu )^c\)) is the distribution on \(P_{[\mu ]}\) (resp. \(M_\mu \)) spanned by the Hamiltonian vector fields \({\hat{\xi }}\) (resp., by the contact vector fields \(\xi ^c\)), where \(\xi \in {\mathfrak {g}}^0_\mu \) and \({\mathfrak {g}}^0_\mu ={\mathfrak {g}}_\mu \cap \ker (\mu )\) is a Lie ideal in \({\mathfrak {g}}_\mu \).
In particular, if the distribution \({\hat{{\mathfrak {g}}}}^0_\mu +\chi (\omega )\) (equivalently, \(({\mathfrak {g}}^0_\mu )^c+\chi (C)\)) is of constant rank on \(P_{[\mu ]}\) (resp., \(M_\mu \)), then \((P_{[\mu ]},\tau ,M_\mu ,h,\omega _{[\mu ]})\) is a presymplectic \({{\mathbb {R}}^\times }\)-bundle covering the precontact manifold \((M_\mu ,C_\mu )\), where  .
.
Under the assumptions of Theorem 6.2, we can carry out the presymplectic reduction (Theorem 3.8), provided that the action of \(G_\mu ^0\) on \(M_\mu \) is free and proper. In this case, the orbits of the subgroup \(G^0_\mu \) on \(M_\mu \) (resp., on \(P_{[\mu ]}\)) form a regular simple foliation, spanned by \(({\mathfrak {g}}^0_\mu )^c\) (resp., \({\hat{{\mathfrak {g}}}}^0_\mu \)). The characteristic foliation \(\chi (C_\mu )\) (resp., \(\chi (\omega _{[\mu ]})\)) is then of constant rank if and only if the intersection \(({\mathfrak {g}}^0_\mu )^c\cap \chi (C)\) (equivalently, \({\hat{{\mathfrak {g}}}}^0_\mu \cap \chi (\omega )\)) is of constant rank, e.g., \(\chi (C)\subset ({\mathfrak {g}}^0_\mu )^c\) (resp., \(\chi (\omega )\subset {\hat{{\mathfrak {g}}}}^0_\mu \)). The latter condition is automatically satisfied for C being contact (resp., \(\omega \) being symplectic). Therefore, we can formulate the following precontact/presymplectic version of the Marsden–Weinstein–Meyer theorem.
Theorem 6.3
Let \((P,\tau ,M,h,\omega )\) be a presymplectic cover of a precontact manifold (M, C), let \(\rho :G\times M\rightarrow M\) be an action on M of a Lie group G by contactomorphisms, and let \(\widetilde{\rho }:G\times P\rightarrow P\) be the Hamiltonian cover of this action, associating with every element \(\xi \) of the Lie algebra \({\mathfrak {g}}\) of G the contact vector field \(\xi ^c\) on (M, C) and the Hamiltonian vector field \({{\hat{\xi }}}\) on \((P,\omega )\).
Let \(J:P\rightarrow {\mathfrak {g}}^*\) be the corresponding contact moment map, and let \(\mu \in {\mathfrak {g}}^*\) be a weakly regular value of J, so that \(P_{[\mu ]}=J^{-1}([\mu ]^\times )\) is an \({{\mathbb {R}}^\times }\)-subbundle of P, covering a submanifold \(M_\mu =\tau (P_{[\mu ]})\) of M. Then the connected Lie subgroup \(G_\mu ^0\) of G, corresponding to the Lie subalgebra
of \({\mathfrak {g}}\), acts on \(P_{[\mu ]}\) and \(M_\mu \).
Suppose that \(M_\mu \) is a transversal submanifold in (M, C) and the \(G^0_\mu \)-action on \(M_\mu \) is free and proper, so that we have a canonical submersion \(\pi :M_\mu \rightarrow M(\mu )\) onto the orbit manifold \(M(\mu )=M_\mu /G^0_\mu \). Suppose additionally that the distribution \(({\mathfrak {g}}^0_\mu )^c\cap \chi _C\) (equivalently, \({\hat{{\mathfrak {g}}}}^0_\mu \cap \chi (\omega )\)) is regular (e.g., C is contact/\(\omega \) is symplectic), where \(({\mathfrak {g}}^0_\mu )^c\) is the distribution on \(M_\mu \) spanned by the contact vector fields \(\xi ^c\) with \(\xi \in {\mathfrak {g}}^0_\mu \).
Then, \(M(\mu )\) is canonically a precontact manifold with the precontact structure  . Moreover, the \(G^0_\mu \)-action on \(P_{[\mu ]}\) is also free and proper, so that we have a canonical submersion \(p:P_{[\mu ]}\rightarrow P(\mu )\) onto the orbit manifold \(P(\mu )=P_{[\mu ]}/G^0_\mu \), and \(P(\mu )\) carries a presymplectic \({{\mathbb {R}}^\times }\)-bundle structure \((P(\mu ),\tau _\mu ,M(\mu ),h^\mu ,\omega (\mu ))\) such that
. Moreover, the \(G^0_\mu \)-action on \(P_{[\mu ]}\) is also free and proper, so that we have a canonical submersion \(p:P_{[\mu ]}\rightarrow P(\mu )\) onto the orbit manifold \(P(\mu )=P_{[\mu ]}/G^0_\mu \), and \(P(\mu )\) carries a presymplectic \({{\mathbb {R}}^\times }\)-bundle structure \((P(\mu ),\tau _\mu ,M(\mu ),h^\mu ,\omega (\mu ))\) such that

is a morphism of \({{\mathbb {R}}^\times }\)-bundles and \(p^*(\omega (\mu ))=\omega \,\big |_{P_{[\mu ]}}\). Moreover, \(C(\mu )\) is a contact structure (resp., \(\omega (\mu )\) is symplectic) if only C is contact (resp., \(\omega \) is symplectic).
An obvious consequence of the above theorem in the case when (M, C) is a contact manifold, i.e., a contact Marsden–Weinstein–Meyer theorem, is Theorem 1.1. A particular case of the latter is Theorem 1 in [79]. Note that if the action of \(G_\mu \) is free and proper, then the action of \(G_\mu ^0\) is free and proper if and only if \(G^0_\mu \) is closed in \(G_\mu \) (\(G_\mu \) is always a closed subgroup of G), thus closed in G. A characterization of closeness of \(G_\mu ^0\) for compact G is given in the following proposition.
Proposition 6.4
If G is compact and connected, then \(G_\mu ^0\) is a closed (thus compact) subgroup in \(G_\mu \) if and only if \(a\mu \) induces a character on \(G_\mu \) for some \(a\ne 0\), i.e., the linear map \(a\mu :{\mathfrak {g}}_\mu \rightarrow {\mathbb {R}}\) gives rise to a group homomorphism
for all \(v\in {\mathfrak {g}}_\mu \). In other words, \(a\mu \in {\mathfrak {g}}^*\) takes integer values on the kernel of \(\exp :{\mathfrak {g}}_\mu \rightarrow G_\mu \).
Proof
Since for G being compact and connected the subgroup \(G_\mu \) is always connected (see, e.g., [8]), the normal subgroup \(G_\mu ^0\) of \(G_\mu \) is closed in \(G_\mu \) if and only if \(G_\mu /G_\mu ^0\simeq S^1\). Let \(\varphi :G_\mu \rightarrow S^1=G_\mu /G_\mu ^0\) be the canonical group homomorphism. Since \({\mathfrak {g}}_\mu ^0=\ker (\mu )\), the corresponding morphism \(D\varphi :{\mathfrak {g}}_\mu \rightarrow {\mathfrak {g}}_\mu /{\mathfrak {g}}_\mu ^0\simeq {\mathbb {R}}\) has the form \(D\varphi (v)=a\langle \mu ,v\rangle \) for some \(a\in {\mathbb {R}}\), \(a\ne 0\), so \(\varphi =\varphi _{a\mu }\). \(\square \)
Example 6.5
A simple numerical example for the above contact Marsden–Weinstein–Meyer reduction is the following. Consider  with the contact structure determined by the Darboux contact form
with the contact structure determined by the Darboux contact form  . In other words, this is the canonical contact structure on the first jet bundle
. In other words, this is the canonical contact structure on the first jet bundle  . Hence, \(\tau :P=M\times {{\mathbb {R}}^\times }\rightarrow M\) is the trivial \({{\mathbb {R}}^\times }\)-bundle and
. Hence, \(\tau :P=M\times {{\mathbb {R}}^\times }\rightarrow M\) is the trivial \({{\mathbb {R}}^\times }\)-bundle and

Moreover, \(\nabla =s\,\partial _s\) and  . Consider the 1-dimensional Lie algebra \({\mathfrak {g}}={\mathbb {R}}\) and its realization in vector fields on M given by \(\xi \mapsto \xi ^c=\xi \cdot (\partial _q-p\,\partial _p-z\,\partial _z)\). This is the infinitesimal part of the action of the group \(G={\mathbb {R}}\) by \(t.(z,p,q)=(e^{-t}z,e^{-t}p,q+t)\) on M by contactomorphisms. The vector fields \(\xi ^c\) are contact vector fields, \({\pounds }_{\xi ^c}\,\eta =0\), and the corresponding 1-homogeneous Hamiltonians read \(H_\xi =\xi \cdot s\cdot (p+z)\). Indeed, the Hamiltonian vector field \({{\hat{\xi }}}=X_{H_\xi }\) on P reads
. Consider the 1-dimensional Lie algebra \({\mathfrak {g}}={\mathbb {R}}\) and its realization in vector fields on M given by \(\xi \mapsto \xi ^c=\xi \cdot (\partial _q-p\,\partial _p-z\,\partial _z)\). This is the infinitesimal part of the action of the group \(G={\mathbb {R}}\) by \(t.(z,p,q)=(e^{-t}z,e^{-t}p,q+t)\) on M by contactomorphisms. The vector fields \(\xi ^c\) are contact vector fields, \({\pounds }_{\xi ^c}\,\eta =0\), and the corresponding 1-homogeneous Hamiltonians read \(H_\xi =\xi \cdot s\cdot (p+z)\). Indeed, the Hamiltonian vector field \({{\hat{\xi }}}=X_{H_\xi }\) on P reads
so its projection onto M is exactly \(\xi ^c\). The moment map \(J:P\rightarrow {\mathbb {R}}^*\) satisfies
so \(J(s,z,q,p)=s\cdot (p+z)\) with every \(\mu \in {\mathbb {R}}^*\) as a regular value.
Let us consider first the case \(\mu =0\), so that \(P_0=J^{-1}(0)\) is the 3-dimensional and \({{\mathbb {R}}^\times }\)-invariant submanifold in P, defined by the equation \(p+z=0\). We can take (s, z, q) as global coordinates parameterizing \(P_0\), \((s,z,q)\mapsto (s,z,q,-z)\), in which

The submanifold \(M_0=\tau (P_0)\) in M is of dimension 2 and it is defined by the same equation \(p+z=0\), so that \(M_0\) is a transversal submanifold and (z, q) serve as coordinates in \(M_0\). The rank of \(\omega \,\big |_{P_0}\) is clearly 2, so the rank of the distribution \(D=\ker (\omega \,\big |_{P_0})\) is 1. The distribution D is thus generated by the vector field \(X=\partial _q-z\,\partial _z+s\,\partial _s\), as X is nonvanishing and \(i_X(\omega \,\big |_{P_0})=0\). Note that X is the restriction of the Hamiltonian vector field \(\hat{1}=\partial _q-p\,\partial _p-z\,\partial _z+s\,\partial _s\) to \(P_0\). This vector field is nowhere vanishing, so it spans D, and the corresponding \({\mathbb {R}}\)-action on \(P_0\) is
As 1-dimensional submanifolds, the trajectories of this action are described by the system of equations \(s\,e^{-q}=s'\) and \(z\,e^q=z'\), where \((z',s')\in {\mathbb {R}}\times {{\mathbb {R}}^\times }\), so that \((z',s')\) are coordinates in \(P(0)=P_0/{\mathbb {R}}\). The reduced principal \({{\mathbb {R}}^\times }\)-action on P(0) is clearly \(s.(z',s')=(z',s\,s')\), and the reduced symplectic form reads (cf. (19))

The trivial \({{\mathbb {R}}^\times }\)-bundle \(P(0)={\mathbb {R}}\times {{\mathbb {R}}^\times }\) with the symplectic form \(\omega (0)\) is the symplectic cover of the unique (trivial) contact structure  on \({\mathbb {R}}\), which is associated with the contact form
on \({\mathbb {R}}\), which is associated with the contact form  . Note that the analog of the above procedure can be done for
. Note that the analog of the above procedure can be done for  equipped with the canonical contact form. If we view
equipped with the canonical contact form. If we view  as
as  with coordinates \((z,q,p,q^i,p_j)\), then formally the same contact vector field \({{\hat{\xi }}}\) can be used as the infinitesimal part of the \({\mathbb {R}}\) action involving only coordinates (z, q, p, s). The whole procedure will give the canonical contact structure on
with coordinates \((z,q,p,q^i,p_j)\), then formally the same contact vector field \({{\hat{\xi }}}\) can be used as the infinitesimal part of the \({\mathbb {R}}\) action involving only coordinates (z, q, p, s). The whole procedure will give the canonical contact structure on  as the reduced structure.
as the reduced structure.
Our procedure is intrinsic, so does not depend on the particular choice of the (local) contact form generating the contact structure. For instance, if we start in our example from

where f is a nowhere vanishing function on  , then we have another trivialization of P with \({\tilde{s}}=f\cdot s\) and the rest of coordinates unchanged. In these coordinates, the procedure is the same, and we end up finally with another trivialization of P(0) with coordinates \((z',q^i,p_i,{\tilde{s}}')\), where \({\tilde{s}}'=f(z,0,-z,q^i,p_j)\cdot s'\). This corresponds to the new contact form
, then we have another trivialization of P with \({\tilde{s}}=f\cdot s\) and the rest of coordinates unchanged. In these coordinates, the procedure is the same, and we end up finally with another trivialization of P(0) with coordinates \((z',q^i,p_i,{\tilde{s}}')\), where \({\tilde{s}}'=f(z,0,-z,q^i,p_j)\cdot s'\). This corresponds to the new contact form
which is clearly equivalent to \(\eta \), so that it induces the same reduced contact structure.
If now \(\mu \in {\mathbb {R}}^*\), \(\mu \ne 0\), then \(P_\mu \) is the submanifold in \(P=M\times {{\mathbb {R}}^\times }\) defined by the equation \(s=\mu /(p+z)\), \(p+z\ne 0\), and \(P'=P_{[\mu ]}=J^{-1}(({\mathbb {R}}^*)^\times )\) is an open-dense submanifold in P of those  such that \((p+z)\ne 0\). The action of \({\mathbb {R}}\) on P preserves \(P'\), so its action on M preserves the open-dense submanifold \(M'=\tau (P')\) defined by \((p+z)\ne 0\). The group \(G={\mathbb {R}}\) is commutative, so \({\mathfrak {g}}_\mu ={\mathfrak {g}}\) and \({\mathfrak {g}}_\mu ^0=\{ 0\}\). Hence, \(M'\) and \(P'\) with restricted contact (resp., symplectic) structures are the reduced structures in this case.
such that \((p+z)\ne 0\). The action of \({\mathbb {R}}\) on P preserves \(P'\), so its action on M preserves the open-dense submanifold \(M'=\tau (P')\) defined by \((p+z)\ne 0\). The group \(G={\mathbb {R}}\) is commutative, so \({\mathfrak {g}}_\mu ={\mathfrak {g}}\) and \({\mathfrak {g}}_\mu ^0=\{ 0\}\). Hence, \(M'\) and \(P'\) with restricted contact (resp., symplectic) structures are the reduced structures in this case.
In the next example, we consider first jet prolongations of group actions on line bundles which can serve as canonical examples of group actions by contactomorphisms on nontrivial contact manifolds.
Example 6.6
In this example, we show how to produce a contact analog of the Marsden–Weinstein–Meyer reduction for the cotangent lifts of group actions on a manifold (see, e.g., [1, 67, 70]).
Let \(\tau _0:L\rightarrow Q\) be a line bundle, \(\pi _0:L^*\rightarrow Q\) be its dual, and G be a Lie group. Note first that, similarly to the case of cotangent bundles, any G-action \({\hat{\rho }}:G\times L\rightarrow L\) on L by vector bundle automorphisms can be canonically lifted to a contact G-action  on the first jet bundle
on the first jet bundle  of sections \(\sigma :Q\rightarrow L^*\) of \(L^*\), equipped with its canonical contact structure. Indeed, if \({\hat{\rho }}^*:G\times L^*\rightarrow L^*\) is the dual action on \(L^*\) and the vector bundle isomorphisms \({\hat{\rho }}_g\) reads
of sections \(\sigma :Q\rightarrow L^*\) of \(L^*\), equipped with its canonical contact structure. Indeed, if \({\hat{\rho }}^*:G\times L^*\rightarrow L^*\) is the dual action on \(L^*\) and the vector bundle isomorphisms \({\hat{\rho }}_g\) reads

then \(\rho \) is uniquely determined by

Recall that infinitesimal automorphisms of a vector bundle consist of linear vector fields on the bundle and the symplectic cover of the contact manifold  is
is  , with the phase lift of the \({{\mathbb {R}}^\times }\)-action on \({L^\times }\) and the canonical symplectic structure of the cotangent bundle [34, 38]. The Hamiltonian action of G on
, with the phase lift of the \({{\mathbb {R}}^\times }\)-action on \({L^\times }\) and the canonical symplectic structure of the cotangent bundle [34, 38]. The Hamiltonian action of G on  , lifted from the contact action on
, lifted from the contact action on  , is the standard cotangent lift of the G action on L, thus on \({L^\times }\).
, is the standard cotangent lift of the G action on L, thus on \({L^\times }\).
If \(\xi \in {\mathfrak {g}}\) is an element in the Lie algebra \({\mathfrak {g}}\) of G and \({{\hat{\xi }}}_0\) is the corresponding linear vector field on L (thus a 1-homogeneous vector field on \({L^\times }\)), associated with the G-action \({\hat{\rho }}\) on L by vector bundle automorphisms, then the contact Hamiltonian \(H_\xi \) on  is \(H_\xi =\iota _{{{\hat{\xi }}}_0}\), where \(\iota _{{{\hat{\xi }}}_0}\) is the linear function on
is \(H_\xi =\iota _{{{\hat{\xi }}}_0}\), where \(\iota _{{{\hat{\xi }}}_0}\) is the linear function on  , thus on
, thus on  , associated with the vector field \({{\hat{\xi }}}_0\) on L. Since \({{\hat{\xi }}}_0\) is a linear vector field on L, it is easy to see that the function \(\iota _{{{\hat{\xi }}}_0}\) on
, associated with the vector field \({{\hat{\xi }}}_0\) on L. Since \({{\hat{\xi }}}_0\) is a linear vector field on L, it is easy to see that the function \(\iota _{{{\hat{\xi }}}_0}\) on  is additionally 1-homogeneous with respect to the lifted principal \({{\mathbb {R}}^\times }\)-bundle structure, thus a contact Hamiltonian. The corresponding Hamiltonian vector field \({{\hat{\xi }}}=X_{H_\xi }\) is therefore the well-known cotangent lift of the vector field \({{\hat{\xi }}}_0\) on L, and the contact moment map reads
is additionally 1-homogeneous with respect to the lifted principal \({{\mathbb {R}}^\times }\)-bundle structure, thus a contact Hamiltonian. The corresponding Hamiltonian vector field \({{\hat{\xi }}}=X_{H_\xi }\) is therefore the well-known cotangent lift of the vector field \({{\hat{\xi }}}_0\) on L, and the contact moment map reads

where  , \(v\in {L^\times }\).
, \(v\in {L^\times }\).
For \(0=\mu \in {\mathfrak {g}}^*\), we can proceed now with the traditional Marsden–Weinstein–Meyer reduction, which is known to yield the reduced symplectic manifold  . Since clearly \({L^\times }/G=(L/G)^\times \), the corresponding reduced contact manifold is
. Since clearly \({L^\times }/G=(L/G)^\times \), the corresponding reduced contact manifold is  with its canonical contact structure. The case \(\mu \ne 0\) is more complicated even in the standard situation and leads to the so-called fibration cotangent bundle reduction [67, Theorem 6.6.8]. The studies on corresponding contact analogs of the latter we postpone to a separate paper.
with its canonical contact structure. The case \(\mu \ne 0\) is more complicated even in the standard situation and leads to the so-called fibration cotangent bundle reduction [67, Theorem 6.6.8]. The studies on corresponding contact analogs of the latter we postpone to a separate paper.
7 Conclusions and outlook
We presented in this paper a fully intrinsic geometric approach to reductions of contact manifolds, which serves for general (also nontrivial) contact structures. This approach is closely related to symplectic reductions, due to a one-to-one correspondence between contact manifolds and symplectic manifolds of a special type (symplectic \({{\mathbb {R}}^\times }\)-bundles). Actually, all tools can be easily adapted to the precontact/presymplectic structures introduced in the paper. We obtained precontact-to-contact reductions, as well as precontact versions of the celebrated Marsden–Weinstein–Meyer theorem. The presentation was concentrated on introducing geometric concepts and tools. A next step will be devoted to closer analysis of important examples coming from physics and other potential applications.
The precontact/presymplectic framework can be crucial for these aims, since presymplectic structures play a fundamental rôle in various problems of physics origins, especially related to constrained systems (e.g., [14, 33, 70, 72]) or time-dependent mechanics [47]. For instance, the presymplectic approach is a crucial step in the relativistic theory, e.g., the equations of motion of a charged spinning particle moving in a space-time (with or without torsion) in the presence of an electromagnetic field. The power of presymplectic formulation resides in the fact that it is manifestly covariant and does not require non-relativistic concepts, like absolute time, to describe dynamics. Also the space of solutions of first-order Hamiltonian field theories is a presymplectic manifold, that was exploited in a series of papers [16,17,18] describing covariant variational evolution and Poisson/Jacobi brackets on the space of functions on the solutions to a variational problem. We plan to carry out studies in these directions and publish them in forthcoming papers.
Availability of data and material
The manuscript has no associated data.
Code availability
No code required.
References
Abraham, R., Marsden, J.E.: Foundations of Mechanics, 2nd edn. Benjamin-Cummings, New York (1978)
Albert, C.: Le théorème de réduction de Marsden-Weinstein en géométrie cosymplectique et de contact. J. Geom. Phys. 6, 627–649 (1989)
Arnold, V.I.: Mathematical Methods of Classical Mechanics. Springer, 2nd ed (1989)
Benenti, S.: The category of symplectic reductions. In Proceedings of the International Meeting on Geometry and Physics. (Florence, 1982), pp. 11–41, Pitagora, Bologna (1983)
Benenti, S., Tulczyjew, W.M.: Remarques sur les réductions symplectiques. C. R. Acad. Sci. Paris Ser. I Math. 294, pp. 561–564 (1982)
Blankenstein, G., van der Schaft, A.J.: Symmetry and reduction in implicit generalized Hamiltonian systems. Rep. Math. Phys. 47, 57–100 (2001)
Boyer, C.P., Galicki, K.: A note on toric contact geometry. J. Geom. Phys. 35, 288–298 (2000)
Borel, A.: Kählerian coset spaces of semisimple Lie groups. Proc. Nat. Acad. Sci. U.S.A. 40, 1147–1151 (1954)
Brahic, O., Fernandes, R.-L.: Integrability and reduction of Hamiltonian actions on Dirac manifolds. Indag. Math. (N.S.) 25, 901–925 (2014)
Bravetti, A., Cruz, H., Tapias, D.: Contact Hamiltonian mechanics. Ann. Phys. 376, 17–39 (2017)
Bruce, A.J., Grabowska, K., Grabowski, J.: Linear duals of graded bundles and higher analogues of (Lie) algebroids. J. Geom. Phys. 101, 71–99 (2016)
Bruce, A. J., Grabowska, K., Grabowski, J.: Remarks on contact and Jacobi geometry. SIGMA Symmetry Integrability Geom. Methods Appl.13 (2017), Paper No. 059, 22 pp
Bursztyn, H., Cabrera, A.: Symmetries and reduction of multiplicative 2-forms. J. Geom. Mech. 4, 111–127 (2012)
Cantrijn, F., de León, M., Marrero, J.C., de Martín, D.: Diego: reduction of constrained systems with symmetries. J. Math. Phys. 40, 795–820 (1999)
Ciaglia, F.M., Cruz, H., Marmo, G.: Contact manifolds and dissipation, classical and quantum. Ann. Phys. 398, 159–179 (2018)
Ciaglia, F.M., Di Cosmo, F., Ibort, A., Marmo, G., Schiavone, L.: Covariant variational evolution and Jacobi brackets: particles. Mod. Phys. Lett. A 35, 2020001 (2020)
Ciaglia, F.M., Di Cosmo, F., Ibort, A., Marmo, G., Schiavone, L.: Covariant variational evolution and Jacobi brackets: fields. Mod. Phys. Lett. A 35, 2050206 (2020)
Ciaglia, F.M., Di Cosmo, F., Ibort, A., Marmo, G., Schiavone, L., Zampini, A.: Symmetries and covariant Poisson brackets on presymplectic manifolds. Symmetry 14, 70 (2022)
Cruz, H.: Contact Hamiltonian mechanics. An extension of symplectic Hamiltonian mechanics. J. Phys.: Confer. Ser. 1071, 012010 (2018)
Darboux, G.: Sur le probléme de Pfaff, I, II. Bull. Sci. Math. \(2^e\) série 6, 14–36 and 49–68 (2018)
Dazord, P., Lichnerowicz, A., Marle, Ch.-M.: Structure locale des variétés de Jacobi. J. Math. Pures et Appl. 70, 101–152 (1991)
Drǎgulete, O., Ornea, L., Ratiu, T.S.: Cosphere bundle reduction in contact geometry. J. Symplectic Geom. 1, 695–714 (2003)
de León, M., Gaset, J., Lainz Valcázar, M., Rivas, X., Román-Roy, N.: Unified Lagrangian–Hamiltonian formalism for contact systems. Fortschr. Phys. 68, 2000045 (2020)
de León, M., Gaset, J., Gràcia, X., Muñoz-Lecanda, M.C., Rivas, X.: Time-dependent contact mechanics. Monatshefte für Mathematik. https://doi.org/10.1007/s00605-022-01767-1
de León, M., Lainz Valcázar, M.: Contact Hamiltonian systems. J. Math. Phys. 60, 102902 (2019)
de León, M., Lainz Valcázar, M.: Singular Lagrangians and precontact Hamiltonian systems. Int. J. Geom. Methods Mod. Phys. 16, 1950158 (2019)
Echeverría-Enríquez, A., Muñoz-Lecanda, M.C., Román-Roy, N.: Reduction of presymplectic manifolds with symmetry. Rev. Math. Phys. 11, 1209–1247 (1999)
Esen, O., Lainz Valcázar, M., de León, M., Marrero, J.C.: Contact dynamics: Legendrian and Lagrangian submanifolds. Mathematics 9, 9 (2021)
Gaset, J., Gràcia, X., Muñoz-Lecanda, M.C., Rivas, X., Román-Roy, N.: New contributions to the Hamiltonian and Lagrangian contact formalisms for dissipative mechanical systems and their symmetries. Int. J. Geom. Methods Mod. Phys. 17, 2050090 (2020)
Geiges, H.: Constructions of contact manifolds. Math. Proc. Cambridge Philos. Soc. 121, 455–464 (1997)
Geiges, H.: A brief history of contact geometry and topology. Expo. Math. 19, 25–53 (2001)
Geiges, H.: An Introduction to Contact Topology, Cambridge Studies in Advanced Mathematics 109. Cambridge University Press, Cambridge (2008)
Gotay, M.J., Nester, J.M., Hinds, G.: Presymplectic manifolds and the Dirac-Bergmann theory of constraints. J. Math. Phys. 19, 2388–2399 (1978)
Grabowska, K., Grabowski, J.: A novel approach to contact Hamiltonians and contact Hamilton–Jacobi Theory. J. Phys. A 55, 435204 (2022)
Grabowska, K., Grabowski, J.: Contact geometric mechanics: the Tulczyjew triples, arXiv:2209.03154
Grabowski, J.: Quasi-derivations and QD-algebroids. Rep. Math. Phys. 32, 445–451 (2003)
Grabowski, J.: Local Lie algebra determines base manifold, From geometry to quantum mechanics, pp. 131–145. Progr. Math. 252, Birkhäuser Boston, Boston, MA, 2007
Grabowski, J.: Graded contact manifolds and contact Courant algebroids. J. Geom. Phys. 68, 27–58 (2013)
Grabowski, J.: Brackets. Int. J. Geom. Methods Mod. Phys. 10, 1360001 (2013)
Grabowski, J., Iglesias, D., Marrero, J.C., Padrón, E., Urbański, P.: Poisson-Jacobi reduction of homogeneous tensors. J. Phys. A 37, 5383–5399 (2004)
Grabowski, J., Landi, G., Marmo, G., Vilasi, G.: Generalized reduction procedure: symplectic and Poisson formalism. Forts. Phys. 42, 393–427 (1994)
Grabowski, J., Marmo, G.: The graded Jacobi algebras and (co)homology. J. Phys. A 36, 161–181 (2003)
Grabowski, J., Rotkiewicz, M.: Higher vector bundles and multi-graded symplectic manifolds. J. Geom. Phys. 59, 1285–1305 (2009)
Grmela, M.: Contact geometry of mesoscopic thermodynamics and dynamics. Entropy 16, 1652–1686 (2014)
Guédira, F., Lichnerowicz, A.: Géométrie des algébres de Lie locales de Kirillov. J. Math. Pures Appl. 63, 407–484 (1984)
Guillemin, V., Sternberg, S.: Homogeneous quantization and multiplicities of group representations. J. Funct. Anal. 47, 344–380 (1982)
Guzmán, E., Marrero, J.C.: Time-dependent mechanics and Lagrangian submanifolds of presymplectic and Poisson manifolds. J. Phys. A 43, 505201 (2010)
Ibort, A., de León, M., Marmo, G.: Reduction of Jacobi manifolds. J. Phys. A 30, 2783–2798 (1997)
Kirillov, A.A.: Local Lie algebras. Russian Math. Surv. 31(4), 55–75 (1976)
Vân Lê, Hông, Tortorella, A.G., Vitagliano, L.: Jacobi bundles and the BFV-complex. J. Geom. Phys.121 (2017), 347–377
Lê, H.V., Oh, Y.-G., Tortorella, A.G., Vitagliano, L.: Deformations of coisotropic submanifolds in Jacobi manifolds. J. Symplectic Geom. 16, 1051–1116 (2018)
Lerman, E., Willett, C.: The topological structure of contact and symplectic quotients. Internat. Math. Res. Notices 2001, 33–52 (2001)
Lerman, E.: Geodesic flows and contact toric manifolds, Symplectic geometry of integrable Hamiltonian systems (Barcelona, 2001), pp. 175–225. Adv. Courses Math. CRM Barcelona, Birkhäuser, Basel (2003)
Lerman, E.: Contact fiber bundles. J. Geom. Phys. 49, 52–66 (2004)
Libermann, P., Marle, C.-M.: Symplectic Geometry and Analytical Mechanics, Mathematics and its Applications 35. D. Reidel Publishing Co., Dordrecht (1987)
Lichnerowicz, A.: Les variétés de Jacobi et leurs algébres de Lie associées. J. Math. Pures Appl. 57, 453–488 (1978)
Loose, F.: Reduction in contact geometry. J. Lie Theory 11, 9–22 (2001)
Marle, C. M.: On Jacobi manifolds and Jacobi bundles, in Symplectic geometry, groupoids, and integrable systems (Berkeley, CA, 1989), pp. 227–246, Math. Sci. Res. Inst. Publ.20, Springer, New York, 1991
Marsden, J.E., Weinstein, A.: Reduction of symplectic manifolds with symmetry. Rep. Math. Phys. 5, 121–130 (1974)
Marsden, J. E., Weinstein, A.: Comments on the history, theory, and applications of symplectic reduction, in Quantization of singular symplectic quotients, 1–19, Progr. Math.198, Birkhäuser, Basel, 2001
Meyer, K.R.: Symmetries and integrals in mechanics, Dynamical systems (Proc. Sympos., Univ. Bahia, Salvador, 1971), pp. 259–272. Academic Press, New York (1973)
Mikami, K.: Local Lie algebra structure and momentum mapping. J. Math. Soc. Japan 39, 233–246 (1978)
Mikami, K.: Reduction of local Lie algebra structures. Proc. Amer. Math. Soc. 105, 686–691 (1989)
Mrugała, R., Nulton, J.D., Schön, J.C., Salamon, P.: Contact structure in thermodynamic theory. Rep. Math. Phys. 29, 109–121 (1991)
Nunes da Costa, J.M.: Réduction des variétés de Jacobi, C. R. Acad. Sci. Paris Sér. I Math. 308 (1989), 101–103
Nunes da Costa, J.M.: Une généralisation, pour les variétés de Jacobi, du théorème de réduction de Marsden-Weinstein. C. R. Acad. Sci. Paris Sér. I Math. 310, 411–414 (1990)
Ortega, J.-P., Ratiu, T.S.: Momentum maps and Hamiltonian reduction, Progress in Mathematics 222. Birkhäuser Boston Inc, Boston, MA (2004)
Palais, R.: On the existence of slices for actions of non-compact Lie groups. Ann. Math. 73, 295–323 (1961)
Rajeev, S.G.: A Hamilton-Jacobi formalism for thermodynamics. Ann. Phys. 323, 2265–2285 (2008)
Reyes, E.G.: On the motion of particles and strings, presymplectic mechanics, and the variational bicomplex. Gen. Relat. Gravit. 37, 437–459 (2005)
Rosen, D., Zhang, J.: Chekanov’s dichotomy in contact topology. Math. Res. Lett. 27, 1165–1193 (2020)
Rothe, H.J., Rothe, K.D.: Classical and quantum dynamics of constrained Hamiltonian systems, World Scientific Lecture Notes in Physics 81, World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ (2010)
van der Schaft, A., Maschke, B.: Geometry of thermodynamic processes. Entropy 20, 925 (2018)
Souriau, J.-M.: Structure des systèmes dynamiques. Maîtrises de mathématiques, Dunod, Paris (1970)
Tortorella, A.G.: Deformations of coisotropic submanifolds in Jacobi manifolds, PhD. thesis 2017, arXiv:1705.08962
Tortorella, A.G.: Rigidity of integral coisotropic submanifolds of contact manifolds. Lett. Math. Phys. 108, 883–896 (2018)
Vitagliano, L.: Dirac-Jacobi bundles. J. Symplectic Geom. 16, 485–561 (2018)
Vitagliano, L., Wade, A.: Holomorphic Jacobi manifolds, Internat. J. Math. 31, 2050024 (2020)
Willett, C.: Contact reduction. Trans. Amer. Math. Soc. 354, 4245–4260 (2002)
Zambon, M., Zhu, C.: Contact reduction and groupoid actions. Trans. Amer. Math. Soc. 358, 1365–1401 (2006)
Acknowledgements
The authors thank Witold Respondek for his useful comments on the classification of hyperplane fields.
Funding
None.
Author information
Authors and Affiliations
Contributions
All authors equally contributed to this work.
Corresponding author
Ethics declarations
Conflict of interest
No conflicts of interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Grabowska, K., Grabowski, J. Reductions: precontact versus presymplectic. Annali di Matematica 202, 2803–2839 (2023). https://doi.org/10.1007/s10231-023-01341-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10231-023-01341-y
Keywords
- Contact structures
- Symplectic structures
- Principal bundles
- Hamiltonian group action
- Symplectic reduction
- Contactomorphisms



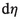 is of rank 2r on
is of rank 2r on 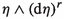 is nonvanishing and
is nonvanishing and 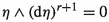 .
. of
of 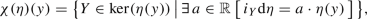
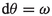 (in particular,
(in particular, 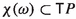 of
of 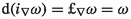 . If
. If 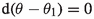 . But
. But 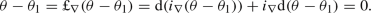
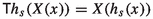 , thus invariance of X, and
, thus invariance of X, and 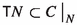 . Equivalently, the restriction
. Equivalently, the restriction 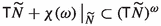 ;
; ;
;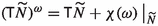 ,
,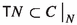 .
.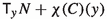 for
for