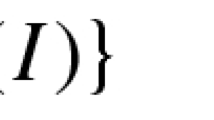On an elastic flow for parametrized curves in $\mathbb {R}^{n}$ suitable for numerical purposes

Abstract

In Pozzi and Stinner (ESAIM: M2AN 57:445–466, 2023) a variant of the classical elastic flow for closed curves in $\mathbb {R}^{n}$ was introduced, that is more suitable for numerical purposes. Here we investigate the long-time properties of such evolution demonstrating that the flow exists globally in time.

1 Introduction

Let $f:I \rightarrow \mathbb {R}^{n}$, $f=f(x)$, $I=[0, 2\pi ] \simeq S^{1}$, be the parametrization of a closed (i.e. periodic) regular smooth curve, $\textrm{d}s=|f_{x}| \textrm{d}x$ its length element, $\mathbf {\kappa }=f_{ss}$ its curvature vector, $\tau =f_{s}=\partial _{s} f=\frac{f_{x}}{|f_{x}|}$ its unit tangent vector. Recall that the length $\mathcal {L}$, Dirichlet $\mathcal {D}$ and bending energy $\mathcal {E}$ are defined by

$$\begin{aligned} \mathcal {L}(f)&:= \int _{I} \textrm{d}s= \int _{I} |f_{x}| \textrm{d}x, \qquad \mathcal {D}(f):= \frac{1}{2} \int _{I} |f_{x}|^{2} \textrm{d}x,\\ \mathcal {E}(f)&:= \frac{1}{2} \int _{I} |\mathbf {\kappa }|^2 \textrm{d}s =\frac{1}{2} \int _{I} |\mathbf {\kappa }|^2 |f_{x}| \textrm{d}x. \end{aligned}$$

The study of evolution equations associated to the bending energy $\mathcal {E}$ has attracted a lot of attention in recent years: for motivation and extended references we refer here simply to [6], which has inspired a lot of the work presented here, and to a recent survey [9], where several recent results are discussed. Here we only remark that the study of the bending energy is very old and essentially goes back to Bernoulli, who in 1691 investigated the problem of a bent beam. Some years later Euler provided a first treatise on the equilibria of bent rods ([11]). Since then the analysis of $\mathcal {E}$ has never ceased to awake the interest of many mathematicians, one of the reason being that it provides a challenging fourth order problem.

Because of the scaling properties of $\mathcal {E}$ one usually penalizes the growth of the curve in some way, a length constraint being quite a typical and natural choice. In this paper our attention is focused on the evolution towards stationary points of the bending energy augmented with a penalization term. Thus, for some positive given $\lambda >0$ we set

$$\begin{aligned} \mathcal {E}_{\lambda }(f):=\mathcal {E}(f)+ \lambda \mathcal {L}(f) \ge 0, \qquad \mathcal {D}_{\lambda }(f):=\mathcal {E}(f)+ \lambda \mathcal {D}(f) \ge 0. \end{aligned}$$

The corresponding $L^{2}$-gradient flow are given by

$$\begin{aligned} f_{t} = -\nabla _{s}^{2} \mathbf {\kappa } -\frac{1}{2} |\mathbf {\kappa }|^{2} \mathbf {\kappa } +\lambda \mathbf {\kappa }, \end{aligned}$$

(1.1)

for $\mathcal {E}_{\lambda }$ (cf. [6], where the evolution problem for $\mathcal {E}_{\lambda }$ is thoroughly studied) and

$$\begin{aligned} f_{t}&= -\nabla _{s}^{2} \mathbf {\kappa } -\frac{1}{2} |\mathbf {\kappa }|^{2} \mathbf {\kappa } +\lambda \frac{f_{xx}}{|f_{x}|}\nonumber \\&= -\nabla _{s}^{2} \mathbf {\kappa } -\frac{1}{2} |\mathbf {\kappa }|^{2} \mathbf {\kappa } +\lambda \mathbf {\kappa } |f_{x}| + \lambda (|f_{x}|)_{s} \tau \end{aligned}$$

(1.2)

for $\mathcal {D}_{\lambda }$ (see Sect. 2.1 below). Here $\nabla _{s} \mathbf {\phi } =\partial _{s} \mathbf {\phi } - \langle \partial _{s} \mathbf {\phi }, \tau \rangle \tau$ denotes the normal component of the derivative with respect to arc length for a given vector field $\mathbf {\phi }: [0,2\pi ] \rightarrow \mathbb {R}^{n}$ along the curve. The study of the evolution of $\mathcal {E}_{\lambda }$ is by now classical and is presented in [6]: there it is shown that given a smooth regular closed curve the flow (1.1) exists globally in time. The case where $\lambda =0$ is also contemplated in their [6, Theorem 3.2]: however, in this case the curve might “disappear” at infinity (a circle whose radius increases to infinity drives the energy $\mathcal {E}$ to zero). The case where the length of the curve is kept fixed along the evolution is also studied in [6]. A global existence result holds again, but the analysis is more subtle as in this case $\lambda =\lambda (t)$ is time dependent (see [6, Theorem 3.3]).

Note that the energy $\mathcal {E}_{\lambda }$ is invariant under reparametrization of the curve and that the flow associated to $\mathcal {E}_{\lambda }$ has a velocity vector that is entirely normal to the curve. The latter observation is quite crucial for numerical analysts, especially when a curve must undergo strong deformations, since great grid deformations might occur. Grid degeneration is very detrimental from a numerical point of view. This is why the author, together with B. Stinner, tackled in [10] the problem of numerically studying alternatives to (1.1) which provide good grid properties and at the same time are amenable for (finite element) numerical analysis (a more detailed discussion on this delicate point can be found in [10]). In this respect the flow associated to $\mathcal {D}_{\lambda }$ yields the kind of numerical properties that one usually looks for.

Therefore, motivated by the numerical investigation undertaken in [10], we study here analytically the long-time existence properties for the $L^{2}$-gradient flow associated to $\mathcal {D}_{\lambda }$.

In [10] we demonstrate that $\mathcal {E}_{\lambda }$ and $\mathcal {D}_{\lambda }$ share common sets of critical points (in a suitable sense), thus motivating the choice of $\mathcal {D}_{\lambda }$ as an alternative to the study of $\mathcal {E}_{\lambda }$. From a numerical point of view, the minimization of the energy $\mathcal {D}_{\lambda }$ (via $L^{2}$-gradient flow) presents major advantages. Indeed the presence of a specific tangential component (see (1.2)) makes it possible to avoid the aforementioned grid-degeneration problems; moreover the numerical analysis is significantly simplified as opposed to [5] (see [10] and related discussion in there). In [10] one can also find interesting simulations of the evolution (1.2), as well as comparisons with other schemes depicting the evolution associated to (1.1).

As mentioned above, long-time existence properties for the geometric $L^{2}$-gradient flow generated by $\mathcal {E}_{\lambda }$ are well known and investigated in [6]. Since $\mathcal {D}$ dominates the length functional, in the sense that $\mathcal {L}(f) \le \sqrt{2\pi } \sqrt{2 \mathcal {D}(f)}$, one is inclined to believe that the $L^{2}$- gradient flow for $\mathcal {D}_{\lambda }$ should also exist for all times. However, this must be proved rigorously. This is the purpose of this work. Our method of proof is similar to that employed in [6], which is based on $L^{2}$- curvature estimates combined with Gagliardo-Nirenberg type inequalities. However, our evolution is not geometric (the functional $\mathcal {D}_{\lambda }$ is not invariant under reparametrizations of the curves) and we must take care of the specific tangential component that appears in (1.2). Therefore new arguments are needed. In particular, upon observing a strong relation between length element and tangential component, we exploit the second order PDE solved by the length element. Our main result, whose proof is given in Sect. 3, is the following:

Theorem 1.1

Let $\lambda \in (0, \infty )$ and let $f_{0}:I \rightarrow \mathbb {R}^{n}$ be smooth and regular. Assume that for any smooth regular initial data $f_{0}$ the flow (1.2) exists for some (small) time [0, T] and is smooth and regular on $[0,T] \times I$. Then: the flow (1.2) has a global solution.

This results hinges on a short-time existence result for the flow, which is outside the scope of the paper and will be tackled elsewhere. On this matter let us here only remark, that a short-time existence results holds for (1.1) (see [6, § 3], and also [3] where classical techniques are discussed in detail). The differences between (1.1) and (1.2) are to be found only in the lower order term multiplying $\lambda$, therefore it is safe to assume that a short-time existence result holds also in our setting. However, note that since the flow (1.2) is no longer geometric, one can not factor out the degeneracy of the high order operator $\nabla _{s}^{2}$ in the usual way (i.e. by reparametrization), therefore some extra care must be taken in the arguments.

2 Preliminaries

We can write the (non-geometric) flow (1.2) as

$$\begin{aligned} \partial _{t}f =\textbf{V} + \varphi \tau \end{aligned}$$

with normal component of the velocity vector given by

$$\begin{aligned} \textbf{V}:=-\nabla _{s}^{2} \mathbf {\kappa } -\frac{1}{2} |\mathbf {\kappa }|^{2} \mathbf {\kappa } +\lambda \mathbf {\kappa } |f_{x}| =-\nabla _{s}^{2} \mathbf {\kappa } -\frac{1}{2} |\mathbf {\kappa }|^{2} \mathbf {\kappa } +\lambda \textbf{w} \end{aligned}$$

(2.1)

where

$$\begin{aligned} \textbf{w}:= \mathbf {\kappa } |f_{x}|, \end{aligned}$$

and (scalar) tangential component

$$\begin{aligned} \varphi :=\lambda \left\langle \frac{f_{xx}}{|f_{x}|} , \tau \right\rangle = \lambda \left\langle \frac{f_{xx}}{|f_{x}|^{2}} , f_{x}\right\rangle = \lambda \frac{1}{|f_{x}|} \left( \frac{|f_{x}|^{2}}{2} \right) _{s} =\lambda (|f_{x}|)_{s}. \end{aligned}$$

(2.2)

Here and in the following $\langle , \rangle$ denotes the Euclidean scalar product in $\mathbb {R}^{n}$. For partial derivatives we use both notations $f_{x}$ and $\partial _{x}f$.

Before diving into computations, let us comment on the strategy of the proof of Theorem 1.1 in a very informal way, so that the reader might find it easier to follow the steps outlined below. Theorem 1.1 is proved by a contradiction argument: we assume that the flow exists only for some finite maximal time $0<T < \infty$, then we derive uniform estimates for the parametrization f and its derivatives $\partial _{x}^{m} f$ on the time interval [0, T) so that we can extend f smoothly up to T. Restarting the flow yields the wished contradiction to the maximality of T.

To derive estimates for f and its derivatives, we first of all observe that

$$\begin{aligned} f_{x}=|f_{x}| \partial _{s}f, \qquad f_{xx}= (|f_{x}| \partial _{s}f)_{x}= (|f_{x}|)_{x} \partial _{s}f + |f_{x}|^{2} \partial _{s}^{2}f, \end{aligned}$$

and so on. In other words

• a control of the length element $|f_{x}|$ (and its derivatives) and

• a control of the derivatives of f with respect to arc-length

yield a control of f and its derivatives $\partial _{x}^{m} f$ in the original parametrization. This motivates why in a first instance we try to obtain uniform bounds the curvature $\mathbf {\kappa }$ and its derivatives $\partial _{s}^{m}\mathbf {\kappa }$ (indeed recall that $\partial ^{m}_{s} f= \partial _{s}^{m-2} \mathbf {\kappa }$). On the other hand, the natural operator governing the PDE (1.2) is $\nabla _{s}$ and not $\partial _{s}$: the relation between the two operators is considered in Lemma 2.4, where it is shown that the “two derivatives entails essentially the same information up to lower order terms”. By Lemma 2.9 and the fact that $\mathcal {E}(f)=\frac{1}{2} \Vert \mathbf {\kappa }\Vert _{L^{2}}^{2}$ remains bounded along the flow, we infer that it is sufficient to obtain uniform control of $\nabla _{s}^{m} \mathbf {\kappa }$.

Finally, to control $\nabla _{s}^{m} \mathbf {\kappa }$ we study the evolution in time of its $L^{2}$-norm. This is described in an abstract way in Lemma 2.3. When we choose $\phi =\nabla _{s}^{m} \mathbf {\kappa }$ in Lemma 2.3, we observe that in trying to control the right-hand side of (2.16) (with the help of interpolation inequalities) a big role is played by the term $Y= (\nabla _{t} + \nabla _{s}^{4}) \phi = (\nabla _{t} + \nabla _{s}^{4})\nabla _{s}^{m} \mathbf {\kappa }$, a quantity that is studied in Lemma 2.5. Again here the main observation lies in the PDE itself, which written as $\partial _{t}f + \nabla _{s}^{2}\mathbf {\kappa }= l.o.t$ yields the ideas that “one derivative in time plus four derivatives in space” give terms of lower order.

In the following we proceed as follows; after identifying the evolution of all relevant geometric quantities in Lemma 2.1 as well as some important uniform bounds (which are fundamental to apply interpolation inequalities later on), we divide our study in two sections: one is concerned with the evolution of the length element (and its derivatives) and one is concerned with the evolution of the curvature vector (and its derivatives). Interpolation inequalities and important embeddings are recalled in Sect. 2.2. All preliminaries results are then strung together in the proof of the main Theorem 1.1 in Sect. 3 where we obtain the wished uniform estimates by a rather technical induction procedure.

2.1 Evolution of geometric quantities

For $\mathbf {\phi }$ any smooth normal field along f and h a scalar map we have that for any $m \in \mathbb {N}$

$$\begin{aligned}&\nabla _{s}(h \mathbf {\phi }) = (\partial _{s } h ) \mathbf {\phi } + h\nabla _{s} \mathbf {\phi }, \qquad \qquad \nabla _{s}^{m}(h \mathbf {\phi }) = \sum _{r=0}^{m}\left( {\begin{array}{c}m\\ r\end{array}}\right) \partial _{s}^{m-r}h \nabla _{s}^{r} \mathbf {\phi } \end{aligned}$$

(2.3)

where recall that $\nabla _s \mathbf {\phi } = \partial _s \mathbf {\phi } - \langle \partial _s \mathbf {\phi }, \partial _s f \rangle \partial _s f$. Similarly we write $\nabla _t \mathbf {\phi } = \partial _t \mathbf {\phi } - \langle \partial _t \mathbf {\phi }, \partial _s f \rangle \partial _s f$.

Lemma 2.1

(Evolution of geometric quantities) Let $f:[0, T)\times I \rightarrow \mathbb {R}^{n}$ be a smooth solution of $\partial _{t} f = \textbf{V} + \varphi \tau$ for $t \in (0, T)$ with $\textbf{V}$ the normal velocity. Given $\mathbf {\phi }$ any smooth normal field along f, the following formulas hold.

$$\begin{aligned} \partial _{t}(\textrm{d}s)&=(\partial _{s} \varphi - \langle \mathbf {\kappa }, \textbf{V} \rangle ) \textrm{d}s \end{aligned}$$

(2.4)

$$\begin{aligned} \partial _{t} \partial _{s}- \partial _{s}\partial _{t}&= (\langle \mathbf {\kappa }, \textbf{V} \rangle -\partial _{s} \varphi ) \partial _{s} \end{aligned}$$

(2.5)

$$\begin{aligned} \partial _{t} \tau&= \nabla _{s} \textbf{V} + \varphi \mathbf {\kappa } \end{aligned}$$

(2.6)

$$\begin{aligned} \partial _{t} \mathbf {\phi }&= \nabla _{t} \mathbf {\phi }- \langle \nabla _s \textbf{V} + \varphi \mathbf {\kappa }, \mathbf {\phi } \rangle \tau \end{aligned}$$

(2.7)

$$\begin{aligned} \partial _{t} \mathbf {\kappa }&= \partial _{s} \nabla _{s} \textbf{V} + \langle \mathbf {\kappa }, \textbf{V}\rangle \mathbf {\kappa } + \varphi \partial _{s} \mathbf {\kappa } \end{aligned}$$

(2.8)

$$\begin{aligned} \nabla _{t} \mathbf {\kappa }&= \nabla _{s}^{2} \textbf{V} + \langle \mathbf {\kappa }, \textbf{V}\rangle \mathbf {\kappa } + \varphi \nabla _{s} \mathbf {\kappa }\ \end{aligned}$$

(2.9)

$$\begin{aligned} (\nabla _{t}\nabla _{s}- \nabla _{s}\nabla _{t}) \mathbf {\phi }&=(\langle \mathbf {\kappa },\textbf{V} \rangle -\partial _{s }\varphi ) \nabla _{s}\mathbf {\phi } +[\langle \mathbf {\kappa }, \mathbf {\phi }\rangle \nabla _{s}\textbf{V} -\langle \nabla _{s} \textbf{V}, \mathbf {\phi } \rangle \mathbf {\kappa }]. \end{aligned}$$

(2.10)

Proof

The proof follows by straightforward computation: see for instance [6, Lemma 2.1] or [4, Lemma 2.1]. $\square$

The above lemma holds in fact for any smooth evolution equation that can be written in the form $\partial _{t} f = \textbf{V} + \varphi \tau$ with $\textbf{V}$ the normal velocity. It allows to compute the first variation of $\mathcal {D}_{\lambda }$ and derive (1.2) (cf. [4, Lemma A.1]). Another important application is the following verification that the energy $\mathcal {D}_{\lambda }$ decreases along the flow.

Decrease in energy along the flow. To retrieve some fundamental bounds it is important to notice that the energy decreases along the flow (1.2). Precisely, using (2.9), (2.4), and integration by parts we obtain

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t} \mathcal {D}_{\lambda } (f)&{=} \int _{I} \langle \mathbf {\kappa }, \nabla _{s}^{2} \textbf{V} {+} \langle \mathbf {\kappa }, \textbf{V}\rangle \mathbf {\kappa } {+} \varphi \nabla _{s} \mathbf {\kappa } \rangle \textrm{d}s {+} \int _{I} \frac{1}{2} |\mathbf {\kappa }|^{2} (\partial _{s} \varphi {-} \langle \mathbf {\kappa }, \textbf{V} \rangle ) \textrm{d}s {+} \lambda \int _{I} \langle f_{x}, f_{xt}\rangle \textrm{d}x\\&{=} \int _{I} \langle \mathbf {\kappa }, \nabla _{s}^{2} \textbf{V} {+} \frac{1}{2}\langle \mathbf {\kappa }, \textbf{V}\rangle \mathbf {\kappa } \rangle \textrm{d}s {-} \int _{I} \langle \lambda f_{xx}, f_{t} \rangle \textrm{d}x\\&{=} \int _{I} \langle \nabla _{s}^{2} \mathbf {\kappa } {+}\frac{1}{2} |\mathbf {\kappa }|^{2} \mathbf {\kappa } , \textbf{V} \rangle \textrm{d}s {-} \int _{I} \langle ( \varphi |f_{x}| \tau {+} \lambda \mathbf {\kappa } |f_{x}|^{2} ), (\textbf{V} {+}\varphi \tau ) \rangle \textrm{d}x\\&{=} {-}\int _{I} |\textbf{V}|^{2} \textrm{d}s {-} \int _{I} \varphi ^{2} \textrm{d}s \le 0. \end{aligned}$$

Uniform bounds along the flow. As a consequence of the energy decrease we infer that the following uniform bounds hold for as long the the flow exists:

$$\begin{aligned} \mathcal {D}_{\lambda } (f(t))&\le \mathcal {D}_{\lambda } (f(0)),\\ \Vert \mathbf {\kappa }\Vert _{L^{2}(I)}^{2}(t)&= \int _{I} |\mathbf {\kappa }|^{2} \textrm{d}s \le 2 \mathcal {D}_{\lambda } (f(0)),\\ \mathcal {D}(f(t))&=\frac{1}{2} \int _{I} |f_{x}|^{2} \textrm{d}x \le \frac{1}{\lambda }\mathcal {D}_{\lambda } (f(0)),\\ \mathcal {L}(f(t))&\le 2\sqrt{\frac{\pi }{\lambda } \mathcal {D}_{\lambda } (f(0))}. \end{aligned}$$

Moreover, as observed in [6, (2.18)], since the curve is closed, the Poincaré inequality for $\partial _{s} f=\tau$ implies

$$\begin{aligned} 2\pi \le \sqrt{\mathcal {L} (f(t))} \Vert \mathbf {\kappa }\Vert _{L^{2}}, \end{aligned}$$

so that in view of the uniform bound from above for the curvature we obtain a uniform bound for the length from below. Hence along the flow we have that

$$\begin{aligned} 0< C^{-1} < \mathcal {L}(f(t)) \le C \end{aligned}$$

where $C=C(\mathcal {D}_{\lambda } (f(0)), \lambda )$. Last but not least we have that for any time t where the flow is well defined

$$\begin{aligned} \int _{0}^{t} \Vert \varphi \Vert _{L^{2}}^{2} \textrm{d}t' {+} \int _{0}^{t} \Vert \textbf{V}\Vert _{L^{2}}^{2} \textrm{d}t'{=} \int _{0}^{t} \int _{I} \varphi ^{2} \textrm{d}s \textrm{d}t' {+}\int _{0}^{t} \int _{I} |\textbf{V}|^{2} \textrm{d}s \textrm{d}t' \le \mathcal {D}_{\lambda } (f(0)). \end{aligned}$$

(2.11)

PDEs for the length element $|f_{x}|$ and tangential component $\varphi$. Next we derive and investigate the evolution equation satisfied by the length element $|f_{x}|$ and the tangential component $\varphi$. Note that in view of (2.2) there is a strong relation between the two of them.

We start by considering the length element. For as long as $|f_{x}| \ge C >0$, classical embedding theory yields that

$$\begin{aligned} \Vert \, |f_{x}|\, \Vert _{C^{0}[0, 2\pi ]} \le \int _{I} ||f_{x}|_{x} | \textrm{d}x + \frac{1}{2\pi } \int _{I} |f_{x}| \textrm{d}x. \end{aligned}$$

Using the uniform bounds on the length and the fact that $\lambda$ is a fixed contant, it follows then that

$$\begin{aligned} \Vert \,|f_{x}|\, \Vert _{L^{\infty }} \le C + \int _{I} \frac{|\varphi |}{\lambda } \textrm{d}s \le C (1 + \Vert \varphi \Vert _{L^{2}}) \end{aligned}$$

(2.12)

where $C=C(\mathcal {D}_{\lambda } (f(0)), \lambda )$.

Next, let us have a closer look at the evolution equation satisfied by the length element. Using the definition of the tangential component (2.2) we can write

$$\begin{aligned} \partial _{t} (|f_{x}|)&= \langle \tau , f_{tx} \rangle = \varphi _{x} - \langle \mathbf {\kappa }, f_{t} \rangle |f_{x}|=\lambda ((|f_{x}|)_{s})_{x} - \langle \mathbf {\kappa }, \textbf{V}\rangle |f_{x}|\\&=\frac{\lambda }{|f_{x}|} (|f_{x}|)_{xx} + \lambda (|f_{x}|)_{x} \left( \frac{1}{|f_{x}|}\right) _{x} - \langle \mathbf {\kappa }, \textbf{V}\rangle |f_{x}|. \end{aligned}$$

Note that to apply a maximum principle we would need some uniform bounds on $\textbf{V}$ and $\mathbf {\kappa }$, which at the moment are out of reach.

Now we turn to the tangential component (2.2). We first explain some useful notation. In the following we write $B_{2}^{a,c} (\varphi )$ for any linear combination of terms of type

$$\begin{aligned} (\partial _{s}^{i_{1}}\varphi ) ( \partial _{s}^{i_{2}}\varphi ), \qquad \text { with } i_{1}+i_{2} =a \text { and } \max i_{j} \le c \end{aligned}$$

with universal, constant coefficients. Notice that a records the total number of derivatives and c gives the highest number of derivatives falling on one factor. We have that $\partial _{s} B_{2}^{a,c} (\varphi )= B_{2}^{a+1,c+1} (\varphi )$. Similarly we write $M_{2}^{a,c}(\langle \mathbf {\kappa }, \textbf{V}\rangle , \varphi )$ for any linear combination of terms of type

$$\begin{aligned} \partial _{s}^{i_{1}}( \langle \mathbf {\kappa }, \textbf{V} \rangle ) \, \partial _{s}^{i_{2}} \varphi , \qquad \text { with } i_{1}+i_{2} =a \text { and } \max i_{j} \le c \end{aligned}$$

with universal, constant coefficients. Note that $\partial _{s} M_{2}^{a,c} (\langle \mathbf {\kappa }, \textbf{V}\rangle , \varphi )= M_{2}^{a+1,c+1}(\langle \mathbf {\kappa }, \textbf{V}\rangle , \varphi )$.

Using (2.5), the previous computations, and recalling that $\varphi =\lambda (|f_{x}|)_{s}$ we immediately infer

$$\begin{aligned} \partial _{t} \varphi&= \lambda \partial _{t} \partial _{s} (|f_{x}|) = \lambda \partial _{s} \partial _{t} (|f_{x}|) + (\langle \mathbf {\kappa }, \textbf{V} \rangle - \varphi _{s}) \partial _{s} (\lambda |f_{x}|) \nonumber \\&=\lambda \partial _{s} ( \varphi _{x} - \langle \mathbf {\kappa }, f_{t} \rangle |f_{x}|) +(\langle \mathbf {\kappa }, \textbf{V} \rangle - \varphi _{s}) \varphi \nonumber \\&=\lambda (|f_{x}| \varphi _{s})_{s} - \lambda (\langle \mathbf {\kappa }, \textbf{V} \rangle |f_{x}|)_{s} +(\langle \mathbf {\kappa }, \textbf{V} \rangle - \varphi _{s}) \varphi . \end{aligned}$$

(2.13)

This gives also

$$\begin{aligned} \partial _{t} \varphi&= \varphi \varphi _{s} + \lambda |f_{x}| \varphi _{ss} - (\langle \mathbf {\kappa }, \textbf{V} \rangle )_{s} \lambda |f_{x}| - \langle \mathbf {\kappa }, \textbf{V} \rangle \varphi + \langle \mathbf {\kappa }, \textbf{V} \rangle \varphi -\varphi \varphi _{s} \\&= \lambda |f_{x}| \varphi _{ss} - (\langle \mathbf {\kappa }, \textbf{V} \rangle )_{s} \lambda |f_{x}|. \end{aligned}$$

Next we compute in a similar manner

$$\begin{aligned} \partial _{t} ( \varphi _{s} )&= \partial _{t} \partial _{s}\varphi = \partial _{s} \partial _{t} \varphi +( \langle \mathbf {\kappa }, \textbf{V} \rangle - \varphi _{s}) \varphi _{s} \nonumber \\&= (\lambda |f_{x}| \varphi _{ss})_{s} - \left( (\langle \mathbf {\kappa }, \textbf{V} \rangle )_{s} \lambda |f_{x}| \right) _{s} +( \langle \mathbf {\kappa }, \textbf{V} \rangle - \varphi _{s}) \varphi _{s}\\&=(\lambda |f_{x}| \varphi _{ss})_{s} - \left( (\langle \mathbf {\kappa }, \textbf{V} \rangle )_{s} \lambda |f_{x}| \right) _{s} + M_{2}^{1,1} (\langle \mathbf {\kappa }, \textbf{V}\rangle , \varphi ) + B_{2}^{2,1} (\varphi ) \nonumber . \end{aligned}$$

(2.14)

This gives also

$$\begin{aligned} \partial _{t} ( \varphi _{s} )&= \lambda |f_{x}| \partial _{s}^{3} \varphi + \varphi \partial _{s}^{2}\varphi -\lambda |f_{x}| \partial _{s}^{2} (\langle \mathbf {\kappa }, \textbf{V} \rangle ) - \varphi \partial _{s} (\langle \mathbf {\kappa }, \textbf{V} \rangle ) + \langle \mathbf {\kappa }, \textbf{V} \rangle \varphi _{s} - (\varphi _{s})^{2}\\&=\lambda |f_{x}| \partial _{s}^{3} \varphi -\lambda |f_{x}| \partial _{s}^{2} (\langle \mathbf {\kappa }, \textbf{V} \rangle ) + M_{2}^{1,1} (\langle \mathbf {\kappa }, \textbf{V}\rangle , \varphi ) + B_{2}^{2,2} (\varphi ). \end{aligned}$$

Proceeding inductively one finds:

Lemma 2.2

For any $m \in \mathbb {N}$ we have

$$\begin{aligned} \partial _{t} ( \partial _{s}^{m}\varphi )&=(\lambda |f_{x}| \partial _{s}^{m{+}1} \varphi )_{s} {-} \left( \lambda |f_{x}| \partial _{s}^{m} (\langle \mathbf {\kappa }, \textbf{V} \rangle ) \right) _{s} {+}M_{2}^{m,m} (\langle \mathbf {\kappa }, \textbf{V}\rangle , \varphi ) {+}B_{2}^{m{+}1,m} (\varphi )\nonumber \\&= \lambda |f_{x}| \partial _{s}^{m+2} \varphi - \lambda |f_{x}| \partial _{s}^{m+1} (\langle \mathbf {\kappa }, \textbf{V} \rangle ) +M_{2}^{m,m} (\langle \mathbf {\kappa }, \textbf{V}\rangle , \varphi ) +B_{2}^{m+1,m+1} (\varphi ). \end{aligned}$$

(2.15)

On the curvature vector and its derivatives. For geometric terms such as the curvature vector and its derivatives we will make use of the following lemma, which is a straight-forward generalisation of [6, Lemma 2.2].

Lemma 2.3

Suppose $\partial _{t}f =\textbf{V}+\varphi \tau$ on $(0,T) \times I$. Let $\mathbf {\phi }$ be a normal vector field along f and $Y=\nabla _{t} \mathbf {\phi } + \nabla _{s}^{4} \mathbf {\phi }$. Then

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t} \frac{1}{2}\int _{I} |\mathbf {\phi }|^{2} \textrm{d}s + \int _{I} |\nabla _{s}^{2} \mathbf {\phi }|^{2 } \textrm{d}s&= \int _{I} \langle Y + \frac{1}{2} \mathbf {\phi } \, \varphi _{s}, \mathbf {\phi } \rangle \textrm{d}s - \frac{1}{2} \int _{I} |\mathbf {\phi }|^{2} \langle \mathbf {\kappa }, \textbf{V} \rangle \textrm{d}s , \end{aligned}$$

(2.16)

Proof

The claim follows using (2.4) and integration by parts. $\square$

As in [2, Sec. 3], [6, Lem.2.3] and [4, Sec. 3] we denote by $\mathbf {\phi }_1 * \mathbf {\phi }_2 * \cdots * \mathbf {\phi }_k$ the product of k normal vector fields $\mathbf {\phi }_i$ ($i=1,..,k$) defined as $\langle \mathbf {\phi }_1,\mathbf {\phi }_2 \rangle \cdot .. \cdot \langle \mathbf {\phi }_{k-2},\mathbf {\phi }_{k-1} \rangle \mathbf {\phi }_{k}$ if k is odd and as $\langle \mathbf {\phi }_1,\mathbf {\phi }_2 \rangle \cdot .. \cdot \langle \mathbf {\phi }_{k-1},\mathbf {\phi }_{k} \rangle$, if k is even. The expression $P_b^{a,c}(\mathbf {\kappa })$ stands for any linear combination of terms of the type

$$\begin{aligned} (\nabla _{s}^{i_1} \mathbf {\kappa }) * \cdots * (\nabla _{s}^{i_b} \mathbf {\kappa }) \text { with }i_1 + \cdots + i_b = a \text { and }\max i_j \le c \end{aligned}$$

with universal, constant coefficients. Thus a gives the total number of derivatives, b denotes the number of factors and c gives a bound on the highest number of derivatives falling on one factor. Using (2.3) we observe that for $b \in \mathbb {N}$, b odd, we have $\nabla _s P^{a,c}_b (\mathbf {\kappa })= P^{a+1,c+1}_b (\mathbf {\kappa }).$ With a slight abuse of notation, $|P^{a,c}_b(\mathbf {\kappa })|$ denotes any linear combination with non-negative coefficients of terms of type

$$\begin{aligned} |\nabla _{s}^{i_1} \mathbf {\kappa }|\cdot |\nabla _{s}^{i_2} \mathbf {\kappa }| \cdot \cdot | \nabla _{s}^{i_{b}} \mathbf {\kappa }| \text{ with } i_1 + \cdots +i_{b}= a \text{ and } \max i_{j} \le c . \end{aligned}$$

Similarly we write $Q_b^{a,c}(\mathbf {\kappa }, \textbf{w})$ for any linear combination of terms of the type

$$\begin{aligned} (\nabla _{s}^{i_1} \textbf{w}) *(\nabla _{s}^{i_2} \mathbf {\kappa }) * \cdots * (\nabla _{s}^{i_b} \mathbf {\kappa } ) \text { with }i_1 + \cdots + i_b = a \text { and }\max i_j \le c \end{aligned}$$

with universal, constant coefficients. Also in this case for odd $b \in \mathbb {N}$ we have $\nabla _s Q^{a,c}_b (\mathbf {\kappa }, \textbf{w})= Q^{a+1,c+1}_b (\mathbf {\kappa }, \textbf{w}).$ For sums we write

$$\begin{aligned} \sum _{\begin{array}{c} [[a,b]] \le [[A,B]]\\ c\le C \end{array}} P^{a,c}_{b} (\mathbf {\kappa }):=\sum _{a=0}^{A}\sum _{b=1}^{2A+B-2a} \sum _{c=0}^C\text { } P_{b}^{a,c}(\mathbf {\kappa }) \text {.} \end{aligned}$$

(2.17)

Similarly we set $\sum _{\begin{array}{c} [[a,b]] \le [[A,B]]\\ c\le C \end{array}}| P^{a,c}_{b} (\mathbf {\kappa })|: = \sum _{a=0}^{A} \sum _{b=1}^{2A+B-2a} \sum _{c=0}^{C} | P^{a,c}_{b}(\mathbf {\kappa }) |\,.$

With this notation we can state the following result, which relates the operator $\nabla _{s}^{m}$ to the full derivative $\partial _{s}^{m}$. Loosely speaking one can say that $\partial _{s}^{m} \mathbf {\kappa }$ and $\nabla _{s}^{m} \mathbf {\kappa }$ “are the same” up to lower order terms.

Lemma 2.4

We have the identities

$$\begin{aligned}&\partial _{s} \mathbf {\kappa }= \nabla _{s}\mathbf {\kappa } -|\mathbf {\kappa }|^{2}\tau ,\\&\partial _{s}^{m} \mathbf {\kappa } = \nabla _{s}^{m} \mathbf {\kappa } +\tau \sum _{\begin{array}{c} [[a,b]] \le [[m-1,2]]\\ c \le m-1, \ b \ even \end{array}} P^{a,c}_{b} (\mathbf {\kappa }) + \sum _{\begin{array}{c} [[a,b]] \le [[m-2,3]]\\ c \le m-2\ b \ odd \end{array}} P^{a,c}_{b} (\mathbf {\kappa }) \quad \text { for } m\ge 2 \, . \end{aligned}$$

Proof

The proof can be found for instance in [4, Lemma  4.5] (see also [6, Lemma 2.6]). The first claim is obtained directly using that

$$\begin{aligned} \partial _s \mathbf {\kappa }= \nabla _s \mathbf {\kappa } + \langle \partial _s \mathbf {\kappa }, \tau \rangle \tau = \nabla _s \mathbf {\kappa } - |\mathbf {\kappa }|^2 \tau . \end{aligned}$$

The second claim follows by induction. $\square$

We are now able to describe in detail the evolution of the curvature vector and its derivatives.

Lemma 2.5

Suppose $\partial _t f= -\nabla _s^2 \mathbf {\kappa } - \frac{1}{2} |\mathbf {\kappa }|^2 \mathbf {\kappa } + \lambda \textbf{w}+ \varphi \tau$, where $\lambda =\lambda (t)$. Then for $m \in \mathbb {N}_0$ we have

$$\begin{aligned} \nabla _t \nabla _s^m \mathbf {\kappa }+ \nabla _s^4 \nabla _s^m \mathbf {\kappa }&= P^{m+2,m+2}_3 (\mathbf {\kappa })+ \lambda (\nabla _s^{m+2} \textbf{w} + Q^{m,m}_3 (\mathbf {\kappa }, \textbf{w})) +P^{m,m}_5 (\mathbf {\kappa }) + \varphi \nabla _s^{m+1} \mathbf {\kappa }. \end{aligned}$$

Proof

For $m=0$ the claim follows directly from (2.9). For $m=1$ it follows using (2.10) and (2.9), namely

$$\begin{aligned} \nabla _t \nabla _s \mathbf {\kappa }+ \nabla _s^5 \mathbf {\kappa }&= \nabla _s \nabla _t \mathbf {\kappa } + (\langle \mathbf {\kappa },\textbf{V} \rangle -\partial _{s }\varphi ) \nabla _{s}\mathbf {\kappa } +[\langle \mathbf {\kappa }, \mathbf {\kappa }\rangle \nabla _{s}\textbf{V} -\langle \nabla _{s} \textbf{V}, \mathbf {\kappa } \rangle \mathbf {\kappa }] + \nabla _s^5 \mathbf {\kappa }\\&= \nabla _{s} (-\nabla _s^4 \mathbf {\kappa } + P^{2,2}_3 (\mathbf {\kappa })+ \lambda (\nabla _s^{2} \textbf{w} + Q^{0,0}_3 (\mathbf {\kappa }, \textbf{w})) +P^{0,0}_5 (\mathbf {\kappa }) + \varphi \nabla _s \mathbf {\kappa })\\&\quad + (\langle \mathbf {\kappa },\textbf{V} \rangle -\partial _{s }\varphi ) \nabla _{s}\mathbf {\kappa } +[\langle \mathbf {\kappa }, \mathbf {\kappa }\rangle \nabla _{s}\textbf{V} -\langle \nabla _{s} \textbf{V}, \mathbf {\kappa } \rangle \mathbf {\kappa }] + \nabla _s^5 \mathbf {\kappa }. \end{aligned}$$

Since $\nabla _{s} (\varphi \nabla _s \mathbf {\kappa }) = \varphi _{s} \nabla _s \mathbf {\kappa } + \varphi \nabla _s^{2} \mathbf {\kappa }$ and

$$\begin{aligned} \langle \mathbf {\kappa }, \textbf{V}\rangle \nabla _{s} \mathbf {\kappa }&= P_3^{3,2}(\mathbf {\kappa })+ P_5^{1,1}(\mathbf {\kappa })+ \lambda Q_3^{1,1}(\mathbf {\kappa }, \textbf{w}) \, \\ \text{ and } \qquad |\mathbf {\kappa }|^2 \nabla _s \textbf{V}&= P_3^{3,3}(\mathbf {\kappa })+ P_5^{1,1}(\mathbf {\kappa })+ \lambda Q_3^{1,1}(\mathbf {\kappa }, \textbf{w}), \end{aligned}$$

we infer

$$\begin{aligned} \nabla _t \nabla _s \mathbf {\kappa }+ \nabla _s^5 \mathbf {\kappa }&= P^{3,3}_3 (\mathbf {\kappa })+ \lambda (\nabla _s^{3} \textbf{w} + Q^{1,1}_3 (\mathbf {\kappa }, \textbf{w})) +P^{1,1}_5 (\mathbf {\kappa }) + \varphi \nabla _s^{2} \mathbf {\kappa } \,, \end{aligned}$$

noticing that the terms appearing in $P^{3,2}_3 (\mathbf {\kappa })$ can be collected in $P^{3,3}_3 (\mathbf {\kappa })$. The general statement follows with an induction argument. $\square$

2.2 Interpolation inequalities and embeddings

We start by recalling some fundamental interpolation inequalities. Consider the scale invariant norms for $k \in \mathbb {N}_{0}$ and $p \in [1, \infty )$

$$\begin{aligned} \Vert \mathbf {\kappa }\Vert _{k,p}:= \sum _{i=0}^{k} \Vert \nabla _s^{i} \mathbf {\kappa }\Vert _{p} \quad \text{ with } \quad \Vert \nabla _s^{i} \mathbf {\kappa } \Vert _{p}:= \mathcal {L}(f)^{i+1-1/p} \Big ( \int _I |\nabla _s^{i} \mathbf {\kappa }|^p \, \textrm{d}s \Big )^{1/p} , \end{aligned}$$

(cf. [6]) and the usual $L^p$- norm $\Vert \nabla _s^{i} \mathbf {\kappa } \Vert _{L^p}^p:= \int _I |\nabla _s^{i} \mathbf {\kappa }|^p \, \textrm{d}s$.

Most of the following results can be found in several papers (e.g. [4, 6, 7]). We provide reference to the papers where complete proofs can be found.

Lemma 2.6

(Lemma 4.1 [4]) Let $f: I \rightarrow \mathbb {R}^n$ be a smooth regular curve. Then for all $k \in \mathbb {N}$, $p \ge 2$ and $0 \le i<k$ we have

$$\begin{aligned} \Vert \nabla _s^{i} \mathbf {\kappa }\Vert _{p} \le C \Vert \mathbf {\kappa }\Vert _{2}^{1-\alpha } \Vert \mathbf {\kappa }\Vert _{k,2}^{\alpha } , \end{aligned}$$

with $\alpha = (i+\frac{1}{2} -\frac{1}{p})/k$ and $C=C(n,k,p)$.

Corollary 2.7

(Corollary 4.2 [4]) Let $f: I \rightarrow \mathbb {R}^n$ be a smooth regular curve. Then for all $k \in \mathbb {N}$ we have

$$\begin{aligned} \Vert \mathbf {\kappa }\Vert _{k,2} \le C ( \Vert \nabla ^{k}_{s}\mathbf {\kappa }\Vert _{2} + \Vert \mathbf {\kappa }\Vert _{2}) , \end{aligned}$$

with $C=C(n,k)$.

Lemma 2.8

(Lemma 3.4 [1]) Let $f: I \rightarrow \mathbb {R}^n$ be a smooth regular curve. For any $a,c,\ell \in \mathbb {N}_0$, $b \in \mathbb {N}$, $b\ge 2$, $c \le \ell +2$ and $a < 2(\ell +2)$ we find

$$\begin{aligned} \int _I |P^{a,c}_{b} (\mathbf {\kappa })| \, \textrm{d}s \le C \mathcal {L}(f)^{1-a-b} \Vert \mathbf {\kappa }\Vert _{2}^{b-\gamma } \Vert \mathbf {\kappa }\Vert _{\ell +2,2}^{\gamma } , \end{aligned}$$

(2.18)

with $\gamma =(a+\frac{1}{2} b-1)/(\ell +2)$ and $C=C(n,\ell ,a, b)$. Further if $a+\frac{1}{2} b<2\ell +5$, then for any $\varepsilon >0$

$$\begin{aligned} \int _I |P^{a,c}_{b}(\mathbf {\kappa })| \, \textrm{d}s&{\le } \varepsilon \int _I |\nabla _s^{\ell {+}2} \mathbf {\kappa }|^2 \, \textrm{d}s {+}C \varepsilon ^{{-}\frac{\gamma }{2{-}\gamma }} (\Vert \mathbf {\kappa }\Vert ^2_{L^{2}})^{\frac{b-\gamma }{2-\gamma }} {+} C \mathcal {L}(f)^{1{-}a{-}\frac{b}{2}} \Vert \mathbf {\kappa }\Vert _{L^{2}}^{b} \, , \end{aligned}$$

(2.19)

with $C=C(n,\ell ,a, b)$.

We finish this section with some important results that are based on classical embedding theory.

Lemma 2.9

(Lemma 2.7 [6]) Assume that the bounds $\Vert \mathbf {\kappa }\Vert _{L^{2}} \le \Lambda _{0}$ and $\Vert \nabla _{s}^{m} \mathbf {\kappa }\Vert _{L^{1}} \le \Lambda _{m}$ for $m \ge 1$. Then for any $m \ge 1$ one has

$$\begin{aligned} \Vert \partial _{s}^{m-1} \mathbf {\kappa } \Vert _{L^{\infty }} + \Vert \partial _{s}^{m} \mathbf {\kappa }\Vert _{L^{1}} \le c_{m}(\Lambda _{0}, \ldots , \Lambda _{m}). \end{aligned}$$

(2.20)

Lemma 2.10

For any smooth scalar map $h:I \rightarrow \mathbb {R}$ and normal vector field $\mathbf {\phi }:I \rightarrow \mathbb {R}^{n}$ along f we have that

$$\begin{aligned} \Vert \mathbf {\phi } \Vert _{\infty } \le C (\Vert \mathbf {\phi } \Vert _{L^{2}} + \Vert \nabla _{s} \mathbf {\phi } \Vert _{L^{2}})\\ \Vert h \Vert _{\infty } \le C (\Vert h \Vert _{L^{2}} + \Vert \partial _{s} h \Vert _{L^{2}})\ \end{aligned}$$

where $C=C(\frac{1}{\mathcal {L}(f)})$.

Proof

The proof of both statements can be found in the proof of [2, Lemma 3.7]. It is an application of classical embedding theory to the map $|\mathbf {\phi }|^{2}$ respectively $h^{2}$. $\square$

More generally we can state the following.

Lemma 2.11

(Lemma 3.7 [2]) We have that for any $x \in I$ there holds

$$\begin{aligned} | P^{a,c}_{b}(\mathbf {\kappa })(x)|^{2} \le C \int _{I} \big ( |P^{2a+1,c+1}_{2b}(\mathbf {\kappa })| + |P^{2a,c}_{2b} (\mathbf {\kappa })|\big ) \textrm{d}s, \quad \text { if}\; b\; \text { is odd},\end{aligned}$$

(2.21)

$$\begin{aligned} | P^{a,c}_{b}(\mathbf {\kappa })(x)| \le C \int _{I} \big (|P^{a+1,c+1}_{b}(\mathbf {\kappa })| + |P^{a,c}_{b} (\mathbf {\kappa })| \big ) \textrm{d}s, \quad \text { if}\; b\; \text {is even}, \end{aligned}$$

(2.22)

where $C=C(\frac{1}{\mathcal {L}(f)})$.

3 Long-time existence

This section is devoted to the proof of Theorem 1.1. By assumption we know that given any smooth regular initial data $f_{0}$, there exists a smooth regular solution $f: [0,T) \times I \rightarrow \mathbb {R}^{n}$ of (1.2) with $f(0, \cdot ) = f_{0}$. Assume by contradiction that the solution does not exist globally in time and let $0<T<\infty$ be the maximal time. Recall that on [0, T) the uniform bounds listed in Sect. 2.1 hold (with constants that depend on $\lambda$ and the initial energy but not on T). In particular

$$\begin{aligned} \Vert \mathbf {\kappa } (t)\Vert _{L^{2}} \le C, \qquad \frac{1}{C} \le \mathcal {L}(f(t)) \le C, \qquad t \in [0, T) \end{aligned}$$

(3.1)

with $C =C(\lambda , \mathcal {D}_{\lambda }(f_{0}))$. These bounds are essential in order to be able to apply interpolation inequalities. In the following a constant C may vary from line to line, but we will indicate what it depends on.

Our first task is to derive uniform bounds for $\mathbf {\kappa }$, $\varphi$ and their derivatives. This is performed in several steps, using an induction procedure.

First Step - Part A: bound on $\Vert \nabla _{s} \mathbf {\kappa }\Vert _{L^{2}}$. Recalling (2.1), using Lemma 2.3 with $\mathbf {\phi }:=\nabla _{s}\mathbf {\kappa }$, Lemma 2.5, and exploiting the fact that $\varphi \langle \nabla _{s}^{2} \mathbf {\kappa }, \nabla _{s} \mathbf {\kappa } \rangle + \frac{1}{2} \varphi _{s} |\nabla _{s} \mathbf {\kappa }|^{2} = \partial _{s} \left( \frac{1}{2} \varphi |\nabla _{s} \mathbf {\kappa }|^{2}\right)$ we obtain

$$\begin{aligned}&\frac{\textrm{d}}{\textrm{d}t} \left( \frac{1}{2}\int _{I} |\nabla _{s} \mathbf {\kappa }|^{2} \textrm{d}s\right) + \int _{I} |\nabla _{s}^{3} \mathbf {\kappa }|^{2} \textrm{d}s + \frac{1}{2}\int _{I} |\nabla _{s} \mathbf {\kappa }|^{2} \textrm{d}s \\&\quad =\int _{I}\langle (\nabla _{t}+ \nabla _{s}^{4}) \nabla _{s} \mathbf {\kappa },\nabla _{s} \mathbf {\kappa } \rangle + \frac{1}{2} \varphi _{s} |\nabla _{s} \mathbf {\kappa }|^{2} \textrm{d}s - \frac{1}{2} \int _{I} |\nabla _{s} \mathbf {\kappa }|^{2} \langle \mathbf {\kappa }, \textbf{V} \rangle \textrm{d}s + \frac{1}{2}\int _{I} |\nabla _{s} \mathbf {\kappa }|^{2} \textrm{d}s\\&\quad = \int _{I} \langle P^{3,3}_3 (\mathbf {\kappa })+ \lambda (\nabla _s^{3} \textbf{w} + Q^{1,1}_3 (\mathbf {\kappa }, \textbf{w})) +P^{1,1}_5 (\mathbf {\kappa }), \nabla _{s} \mathbf {\kappa } \rangle \textrm{d}s \\&\qquad - \frac{1}{2} \int _{I} |\nabla _{s} \mathbf {\kappa }|^{2} \langle \mathbf {\kappa }, \textbf{V} \rangle \textrm{d}s + \frac{1}{2}\int _{I} |\nabla _{s} \mathbf {\kappa }|^{2} \textrm{d}s \\&\quad =\int _{I} P_{4}^{4,3} (\mathbf {\kappa }) + P^{2,1}_6 (\mathbf {\kappa }) + P_{2}^{2,1} (\mathbf {\kappa }) + P_{4}^{4,2} (\mathbf {\kappa }) \textrm{d}s + \lambda \int _{I} \langle \nabla _s^{3} \textbf{w} + Q^{1,1}_3 (\mathbf {\kappa }, \textbf{w}), \nabla _{s} \mathbf {\kappa } \rangle \textrm{d}s\\&\quad =\int _{I} P_{4}^{4,3} (\mathbf {\kappa }) {+} P^{2,1}_6 (\mathbf {\kappa }) {+} P_{2}^{2,1} (\mathbf {\kappa }) \textrm{d}s {+} \lambda \int _{I} \langle \nabla _{s} \textbf{w}, \nabla _{s}^{3} \mathbf {\kappa } \rangle \textrm{d}s {+} \lambda \int _{I} \langle Q^{1,1}_3 (\mathbf {\kappa }, \textbf{w}), \nabla _{s} \mathbf {\kappa } \rangle \textrm{d}s\\&\quad =J_{1}+J_{2}+J_{3}, \end{aligned}$$

where we have used integration by parts in the last step and absorbed the terms $P_{4}^{4,2} (\mathbf {\kappa })$ into $P_{4}^{4,3} (\mathbf {\kappa })$. By applying Lemma 2.8 and (3.1) we find

$$\begin{aligned} |J_{1}|&=|\int _{I} P_{4}^{4,3} (\mathbf {\kappa }) + P^{2,1}_6 (\mathbf {\kappa }) + P_{2}^{2,1} (\mathbf {\kappa }) \textrm{d}s | \le \epsilon \int _{I} |\nabla _{s}^{3} \mathbf {\kappa }|^{2} \textrm{d}s + C(\epsilon , n, \lambda , \mathcal {D}_{\lambda }(f_{0}) ) . \end{aligned}$$

Since

$$\begin{aligned} \nabla _{s}(\textbf{w})= \nabla _{s} (|f_{x}| \mathbf {\kappa })= |f_{x}| \nabla _{s} \mathbf {\kappa } + (|f_{x}|)_{s} \mathbf {\kappa }= |f_{x}| \nabla _{s} \mathbf {\kappa } +\frac{\varphi }{\lambda } \mathbf {\kappa } \end{aligned}$$

(3.2)

we can write

$$\begin{aligned} J_{2} =\lambda \int _{I} \langle \nabla _{s} \textbf{w}, \nabla _{s}^{3} \mathbf {\kappa } \rangle \textrm{d}s =\lambda \int _{I} |f_{x}| \langle \nabla _{s} \mathbf {\kappa }, \nabla _{s}^{3} \mathbf {\kappa }\rangle \textrm{d}s + \int _{I} \varphi \langle \mathbf {\kappa }, \nabla _{s}^{3} \mathbf {\kappa }\rangle \textrm{d}s=J_{2,1}+J_{2,2}. \end{aligned}$$

We have

$$\begin{aligned} J_{2,1}&\le \epsilon \int _{I} |\nabla _{s}^{3} \mathbf {\kappa }|^{2} \textrm{d}s + C_{\epsilon } \Vert |f_{x}|\Vert _{\infty }^{2} \int _{I} | \nabla _{s} \mathbf {\kappa }|^{2} \textrm{d}s \\&\le \epsilon \int _{I} |\nabla _{s}^{3} \mathbf {\kappa }|^{2} \textrm{d}s + C_{\epsilon }(1 +\Vert \varphi \Vert _{L^{2}}^{2})\int _{I} | \nabla _{s} \mathbf {\kappa }|^{2} \textrm{d}s \end{aligned}$$

where we have used (2.12) in the last step. Note that here $C_{\epsilon }= C(\epsilon , \lambda , \mathcal {D}_{\lambda }(f_{0}))$. Next, we compute

$$\begin{aligned} J_{2,2}&=\int _{I} \varphi \langle \mathbf {\kappa }, \nabla _{s}^{3} \mathbf {\kappa }\rangle \textrm{d}s \le \Vert \mathbf {\kappa }\Vert _{L^{\infty }} \Vert \varphi \Vert _{L^{2}} \Vert \nabla _{s}^{3} \mathbf {\kappa }\Vert _{L^{2}} \le \epsilon \int _{I} |\nabla _{s}^{3} \mathbf {\kappa }|^{2} \textrm{d}s + C_{\epsilon } \Vert \mathbf {\kappa }\Vert ^{2}_{L^{\infty }} \Vert \varphi \Vert _{L^{2}}^{2}. \end{aligned}$$

Since $\Vert \mathbf {\kappa }\Vert _{L^{\infty }}^{2} \le C (\Vert \mathbf {\kappa }\Vert _{L^{2}}^{2} + \Vert \nabla _{s} \mathbf {\kappa }\Vert _{L^{2}}^{2})$ by Lemma 2.10 and (3.1) we obtain

$$\begin{aligned} J_{2,2} \le \epsilon \int _{I} |\nabla _{s}^{3} \mathbf {\kappa }|^{2} \textrm{d}s + C_{\epsilon } (1 + \Vert \nabla _{s} \mathbf {\kappa }\Vert _{L^{2}}^{2}) \Vert \varphi \Vert _{L^{2}}^{2}. \end{aligned}$$

Using the definition of $Q^{1,1}_3 (\mathbf {\kappa }, \textbf{w})$, $\textbf{w}$, (3.2), and (2.18) we observe that

$$\begin{aligned} J_{3}&=\lambda \int _{I} \langle Q^{1,1}_3 (\mathbf {\kappa }, \textbf{w}), \nabla _{s} \mathbf {\kappa } \rangle \textrm{d}s=\int _{I} \lambda |f_{x}| P_{4}^{2,1}(\mathbf {\kappa }) + \varphi P_{4}^{1,1}(\mathbf {\kappa }) \textrm{d}s\\&\le |\lambda |\Vert |f_{x}| \Vert _{L^{\infty }} \int _{I} | P_{4}^{2,1}(\mathbf {\kappa })| \textrm{d}s +\Vert \varphi \Vert _{L^{2}} \left( \int _{I} |P_{8}^{2,1} (\mathbf {\kappa })| \textrm{d}s \right) ^{\frac{1}{2}}\\&\le C |\lambda | \Vert |f_{x}| \Vert _{L^{\infty }} \mathcal {L}(f)^{-5} \Vert \mathbf {\kappa }\Vert _{2}^{3} \Vert \mathbf {\kappa }\Vert _{3,2} + C\Vert \varphi \Vert _{L^{2}} \mathcal {L}(f)^{-9/2} \Vert \mathbf {\kappa }\Vert _{2}^{\frac{8-5/3}{2}} \Vert \mathbf {\kappa }\Vert _{3,2}^{\frac{5}{6}}. \end{aligned}$$

Using the bounds for the length and curvature (3.1), Corollary 2.7, Young inequality, and (2.12) we obtain

$$\begin{aligned} J_{3}&\le C\Vert |f_{x}| \Vert _{L^{\infty }} (1 + \Vert \nabla _{s}^{3} \mathbf {\kappa }\Vert _{L^{2}}) + C \Vert \varphi \Vert _{L^{2}}^{2} + C\Vert \mathbf {\kappa }\Vert _{3,2}^{\frac{5}{3}} \\&\le \epsilon \int _{I} |\nabla _{s}^{3} \mathbf {\kappa }|^{2} \textrm{d}s +C_{\epsilon } (1+ \Vert \varphi \Vert _{L^{2}}^{2}) . \end{aligned}$$

Collecting all estimates found so far for $J_{1}$, $J_{2}$, $J_{3}$, and choosing $\epsilon$ appropriately we find

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}&\left( \frac{1}{2}\int _{I} |\nabla _{s} \mathbf {\kappa }|^{2} \textrm{d}s\right) + \frac{1}{2}\int _{I} |\nabla _{s}^{3} \mathbf {\kappa }|^{2} \textrm{d}s + \frac{1}{2}\int _{I} |\nabla _{s} \mathbf {\kappa }|^{2} \textrm{d}s \\&\le C(1 +\Vert \varphi \Vert _{L^{2}}^{2}) + C(1 +\Vert \varphi \Vert _{L^{2}}^{2})\int _{I} | \nabla _{s} \mathbf {\kappa }|^{2} \textrm{d}s \end{aligned}$$

where $C=C(n,\lambda , \mathcal {D}_{\lambda }(f_{0}))$. On the other hand using again Lemma 2.8 we can write

$$\begin{aligned} \int _{I} | \nabla _{s} \mathbf {\kappa }|^{2} \textrm{d}s = \int _{I} |P_{2}^{2,1} (\mathbf {\kappa })| \textrm{d}s \le \epsilon \int _{I} |\nabla _{s}^{3} \mathbf {\kappa }|^{2} \textrm{d}s + C(\epsilon , n, \lambda , \mathcal {D}_{\lambda }(f_{0}) ), \end{aligned}$$

so that, upon choosing $\epsilon$ small enough, we can finally write

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}&\left( \frac{1}{2}\int _{I} |\nabla _{s} \mathbf {\kappa }|^{2} \textrm{d}s\right) + \frac{1}{4}\int _{I} |\nabla _{s}^{3} \mathbf {\kappa }|^{2} \textrm{d}s + \frac{1}{2}\int _{I} |\nabla _{s} \mathbf {\kappa }|^{2} \textrm{d}s \\&\le C(1 +\Vert \varphi \Vert _{L^{2}}^{2}) + C\Vert \varphi \Vert _{L^{2}}^{2}\int _{I} | \nabla _{s} \mathbf {\kappa }|^{2} \textrm{d}s \end{aligned}$$

where $C=C(n,\lambda , \mathcal {D}_{\lambda }(f_{0}))$. It follows for $\xi (t):= e^{t}\int _{I} |\nabla _{s} \mathbf {\kappa }|^{2}(t) \textrm{d}s$ that

$$\begin{aligned} \xi '(t) \le C e^{t}(1 +\Vert \varphi \Vert _{L^{2}}^{2}) + C \Vert \varphi \Vert _{L^{2}}^{2} \xi (t). \end{aligned}$$

Using that $\int _{0}^{t} e^{t'}(1 +\Vert \varphi \Vert _{L^{2}}^{2}) \textrm{d}t' \le e^{t} + e^{t} \int _{0}^{t}\Vert \varphi \Vert _{L^{2}}^{2} \textrm{d}t' \le C e^{t}$ by (2.11) we infer

$$\begin{aligned} \xi (t) \le \xi (0) + Ce^{t} + C\int _{0}^{t}\Vert \varphi \Vert _{L^{2}}^{2}(t') \xi (t')\, \textrm{d}t' \end{aligned}$$

and a Gronwall Lemma gives that $\xi (t) \le C (\xi (0) + Ce^{t})$, that is

$$\begin{aligned} \sup _{[0,T)}\Vert \nabla _{s} \mathbf {\kappa }\Vert _{L^{2}}^{2}(t) \le C_{1} =C_{1}(n, \lambda , \mathcal {D}_{\lambda }(f_{0}), f_{0}). \end{aligned}$$

(3.3)

Note that the above bound together with (2.11), (3.1), Lemma 2.10 yields

$$\begin{aligned} \sup _{[0,T)} \Vert \mathbf {\kappa }(t) \Vert _{L^{\infty }}&\le C_{1} =C_{1}(n, \lambda , \mathcal {D}_{\lambda }(f_{0}), f_{0}), \end{aligned}$$

(3.4)

$$\begin{aligned} \sup _{[0,T)} \int _{0}^{t} \Vert \nabla _{s}^{3} \mathbf {\kappa } \Vert _{L^{2}}^{2} \textrm{d}t'&\le C_{1,1} =C_{1,1}(n, \lambda , \mathcal {D}_{\lambda }(f_{0}), f_{0},T). \end{aligned}$$

(3.5)

First Step-Part B: Bound on $\Vert \varphi \Vert _{L^{2}}$. Although we know already that the $L^{2}$-norm of the tangential component behaves well in time (in the sense of (2.11)), we need to refine this information. To that end we consider

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t} \left( \frac{1}{2} \int _{I} \varphi ^{2} \textrm{d}s \right)&= \int _{I} \varphi \varphi _{t} \textrm{d}s + \frac{1}{2} \int _{I} \varphi ^{2} (\varphi _{s} - \langle \mathbf {\kappa }, \textbf{V} \rangle ) \textrm{d}s\\ \quad&= \int _{I} \varphi \lambda (|f_{x}| \varphi _{s})_{s} - \lambda \varphi (\langle \mathbf {\kappa }, \textbf{V} \rangle |f_{x}|)_{s} +(\langle \mathbf {\kappa }, \textbf{V} \rangle - \varphi _{s}) \varphi ^{2} \textrm{d}s \\&\quad + \frac{1}{2} \int _{I} \varphi ^{2} (\varphi _{s} - \langle \mathbf {\kappa }, \textbf{V} \rangle ) \textrm{d}s \end{aligned}$$

where we have used (2.4) and (2.13). Integration by parts and the fact that $\int _{I} \varphi ^{2} \varphi _{s} \textrm{d}s =0$ (this can be seen using integration by parts) yields

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t} \left( \frac{1}{2} \int _{I} \varphi ^{2} \textrm{d}s \right) + \lambda \int _{I} (\partial _{s} \varphi )^{2} |f_{x}| \textrm{d}s&= \lambda \int _{I} \varphi _{s}\langle \mathbf {\kappa }, \textbf{V} \rangle |f_{x}| \textrm{d}s +\frac{1}{2} \int _{I} \langle \mathbf {\kappa }, \textbf{V} \rangle \varphi ^{2} \textrm{d}s\\&=A_{1}+A_{2}. \end{aligned}$$

Using the $L^{\infty }$-bound on the curvature (3.4) we can write

$$\begin{aligned} A_{1}&=\lambda \int _{I} \varphi _{s}\langle \mathbf {\kappa }, \textbf{V} \rangle |f_{x}| \textrm{d}s \le \epsilon \lambda \int _{I} (\partial _{s} \varphi )^{2} |f_{x}| \textrm{d}s + \lambda C_{\epsilon } \int _{I}|\textbf{V}|^{2} |f_{x}| \textrm{d}s\\&\le \epsilon \lambda \int _{I} (\partial _{s} \varphi )^{2} |f_{x}| \textrm{d}s + \lambda C_{\epsilon } (1 + \Vert \varphi \Vert _{L^{2}}^{2}) \Vert \textbf{V}\Vert _{L^{2}}^{2} \end{aligned}$$

where we have used (2.12) in the last step. For the second term $A_{2}$ we obtain, using (3.4), (2.12), and (2.1), that

$$\begin{aligned} A_{2}&=\frac{1}{2} \int _{I} \langle \mathbf {\kappa }, \textbf{V} \rangle \varphi ^{2} \textrm{d}s \le C\int _{I} |P_{2}^{2,2} (\mathbf {\kappa })| \varphi ^{2} \textrm{d}s + C (1 + \Vert |f_{x}|\Vert _{\infty }) \int _{I}\varphi ^{2} \textrm{d}s \\&\le C (\Vert |P_{2}^{2,2} (\mathbf {\kappa })| \Vert _{\infty } +1 + \Vert \varphi \Vert _{L^{2}}^{2} ) \int _{I}\varphi ^{2} \textrm{d}s. \end{aligned}$$

Using (2.22), (2.19), (3.1), we obtain

$$\begin{aligned} |P_{2}^{2,2} (\mathbf {\kappa })|&\le C \int _{I} |P_{2}^{3,3} (\mathbf {\kappa })|+ |P_{2}^{2,2} (\mathbf {\kappa })| \textrm{d}s \le C ( \Vert \nabla _{s}^{3} \mathbf {\kappa } \Vert _{L^{2}}^{2} +1 ) , \end{aligned}$$

so that

$$\begin{aligned} A_{2} \le C(1+ \Vert \nabla _{s}^{3} \mathbf {\kappa } \Vert _{L^{2}}^{2} + \Vert \varphi \Vert _{L^{2}}^{2} ) \int _{I}\varphi ^{2} \textrm{d}s. \end{aligned}$$

Putting all estimates together we obtain (recall that $|f_{t}|^{2} =|\textbf{V}|^{2} +\varphi ^{2}$)

$$\begin{aligned} A_{1}+A_{2} \le \epsilon \lambda \int _{I} (\partial _{s} \varphi )^{2} |f_{x}| \textrm{d}s + C_{\epsilon } \Vert \textbf{V}\Vert _{L^{2}}^{2} + C_{\epsilon } ( \Vert \nabla _{s}^{3} \mathbf {\kappa } \Vert _{L^{2}}^{2} +1 + \Vert f_{t} \Vert _{L^{2}}^{2}) \int _{I}\varphi ^{2} \textrm{d}s \end{aligned}$$

with $C_{\epsilon }= C_{\epsilon }(n, \lambda , \mathcal {D}_{\lambda }(f_{0}), f_{0})$. Choosing $\epsilon$ appropriately we can write

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}&\left( \frac{1}{2} \int _{I} \varphi ^{2} \textrm{d}s \right) + \frac{1}{2} \int _{I} \varphi ^{2} \textrm{d}s + \frac{\lambda }{2} \int _{I} (\partial _{s} \varphi )^{2} |f_{x}| \textrm{d}s \\ {}&\le C( \Vert \textbf{V}\Vert _{L^{2}}^{2} + \Vert \varphi \Vert _{L^{2}}^{2}) + C ( \Vert \nabla _{s}^{3} \mathbf {\kappa } \Vert _{L^{2}}^{2} + \Vert f_{t} \Vert _{L^{2}}^{2}) \int _{I}\varphi ^{2} \textrm{d}s \end{aligned}$$

where $C =C(n, \lambda , \mathcal {D}_{\lambda }(f_{0}), f_{0})$. Recalling (2.11) and (3.5), a Gronwall argument (as performed in First Step -Part A) gives

$$\begin{aligned} \sup _{ t \in [0,T)} \Vert \varphi \Vert _{L^{2}}^{2}(t) \le {\tilde{C}}_{1} = {\tilde{C}}_{1}( n, \lambda , \mathcal {D}_{\lambda }(f_{0}), f_{0}, T). \end{aligned}$$

(3.6)

Note that the dependence of the constant on T is caused by (3.5). As a consequence we obtain also

$$\begin{aligned} \sup _{ t \in [0,T)} \int _{0}^{t} \int _{I} (\partial _{s} \varphi )^{2} |f_{x}| \textrm{d}s \textrm{d}t' \le {\tilde{C}}_{1} ={\tilde{C}}_{1}( n, \lambda , \mathcal {D}_{\lambda }(f_{0}), f_{0}, T). \end{aligned}$$

(3.7)

Moreover recalling (2.12), the definition of $\textbf{w}$, and (3.4) we can state

$$\begin{aligned} \sup _{ t \in [0,T)} \Vert \,|f_{x}| \Vert _{\infty } + \Vert \textbf{w} \Vert _{\infty } \le {\tilde{C}}_{1}={\tilde{C}}_{1}( n, \lambda , \mathcal {D}_{\lambda }(f_{0}), f_{0}, T). \end{aligned}$$

(3.8)

From the expression (3.2) together with the bounds (3.3), (3.4), (3.6) and (3.8) it follows

$$\begin{aligned} \sup _{ t \in [0,T)} \Vert \nabla _{s}w\Vert _{L^{2}}^{2}(t) \le {\tilde{C}}_{1}={\tilde{C}}_{1}( n, \lambda , \mathcal {D}_{\lambda }(f_{0}), f_{0}, T). \end{aligned}$$

(3.9)

Finally note that since $f_{xx}= |f_{x}|^{2} \mathbf {\kappa } + \frac{\varphi }{\lambda } |f_{x}| \tau$ we derive

$$\begin{aligned} \sup _{ t \in [0,T)} \int _{I} |f_{xx}|^{2} \textrm{d}x \le {\tilde{C}}_{1}={\tilde{C}}_{1}( n, \lambda , \mathcal {D}_{\lambda }(f_{0}), f_{0}, T). \end{aligned}$$

Intermezzo: bound from below for the length element $|f_{x}|$. In Sect. 2.1 we computed

$$\begin{aligned} \partial _{t} (|f_{x}|)&=\frac{\lambda }{|f_{x}|} (|f_{x}|)_{xx} + \lambda (|f_{x}|)_{x} \left( \frac{1}{|f_{x}|}\right) _{x} - \langle \mathbf {\kappa }, \textbf{V}\rangle |f_{x}|. \end{aligned}$$

Hence, using [8, Lemma 2.1.3] and the uniform bound on the curvature (3.4) we infer that $g(t):= \min _{I} |f_{x} (x,t)|$ is a positive map that satisfies

$$\begin{aligned} g_{t} \ge - g \langle \mathbf {\kappa }, \textbf{V} \rangle \ge -C g \Vert \textbf{V}\Vert _{L^{\infty }}. \end{aligned}$$

Since $\nabla _{s} \textbf{V}= -\nabla _{s}^{3} \mathbf {\kappa } + P_{3}^{1,1}(\mathbf {\kappa }) +\lambda \nabla _{s}\textbf{w}$, Lemma 2.10, (3.1), (3.4), (3.3), and (3.9) yield

$$\begin{aligned} \Vert \textbf{V} \Vert _{\infty } \le C (\Vert \textbf{V} \Vert _{L^{2}} + \Vert \nabla _{s} \textbf{V} \Vert _{L^{2}}) \le C (1+ \Vert \textbf{V} \Vert _{L^{2}}^{2} + \Vert \nabla _{s}^{3} \mathbf {\kappa } \Vert _{L^{2}}^{2} ), \end{aligned}$$

(3.10)

so that, upon recalling (3.5) and (2.11), we can state that

$$\begin{aligned} \sup _{ t \in [0, T)} \int _{0}^{t} \Vert \textbf{V} \Vert _{\infty }(t') \textrm{d}t' \le C \end{aligned}$$

where $C=C ( n, \lambda , \mathcal {D}(f_{0}), f_{0}, T)$. Thus, integrating in time the inequality $(\ln g)_{t} \ge -C \Vert \textbf{V}\Vert _{L^{\infty }}$ gives

$$\begin{aligned} g(t) \ge e^{-C} g(0) \end{aligned}$$

with $C=C ( n, \lambda , \mathcal {D}_{\lambda }(f_{0}), f_{0}, T)$. This yields

$$\begin{aligned} \inf _{ t \in [0, T)} |f_{x}| \ge C=C ( n, \lambda , \mathcal {D}_{\lambda }(f_{0}), f_{0}, T). \end{aligned}$$

(3.11)

An important consequence iss that (3.7) now yields

$$\begin{aligned} \sup _{ t \in [0,T)} \int _{0}^{t} \int _{I} (\partial _{s} \varphi )^{2} \textrm{d}s \textrm{d}t' \le {{\tilde{C}}}_{1}= {\tilde{C}}_{1} ( n, \lambda , \mathcal {D}_{\lambda }(f_{0}), f_{0}, T). \end{aligned}$$

(3.12)

Induction step: Assume that for some $m \ge 1$ we have the following induction hypothesis:

$$\begin{aligned} \left\{ \begin{array}{r} \sup _{t \in [0,T)} ( \sum _{j=0}^{m} \Vert \nabla _{s}^{j} \mathbf {\kappa } \Vert _{L^{2}} + \int _{0}^{t} \Vert \nabla _{s}^{m+2} \mathbf {\kappa } \Vert _{L^{2}}^{2} \textrm{d}t' ) \le C_{m}, \\ \sup _{t \in [0,T)} ( \sum _{j=0}^{m-1} \Vert \partial _{s}^{j}\varphi \Vert _{L^{2}} +\int _{0}^{t} \Vert \partial _{s}^{m}\varphi \Vert _{L^{2}}^{2} \textrm{d}t' + \sum _{j=0}^{m} \Vert \nabla _{s}^{j} \textbf{w}\Vert _{L^{2}}) \le {\tilde{C}}_{m}, \end{array} \right. \end{aligned}$$

(IP)

with $C_{m}=C_{m}( n, \lambda , \mathcal {D}(f_{0}), f_{0}, T)$, ${\tilde{C}}_{m}={\tilde{C}}_{m}( n, \lambda , \mathcal {D}(f_{0}), f_{0}, T)$.

Note that by Lemma 2.10 this means in particular that

$$\begin{aligned} \left\{ \begin{array}{r} \sup _{t \in [0,T)} ( \sum _{j=0}^{m-1} \Vert \nabla _{s}^{j} \mathbf {\kappa } \Vert _{L^{\infty }} + \Vert \nabla _{s}^{m}\mathbf {\kappa }\Vert _{L^{2}}+ \int _{0}^{t} \Vert \nabla _{s}^{m+2} \mathbf {\kappa } \Vert _{L^{2}}^{2} \textrm{d}t' ) \le C_{m}, \\ \sup _{t \in [0,T)} ( \sum _{j=0}^{m-2} \Vert \partial _{s}^{j}\varphi \Vert _{L^{\infty }} + \Vert \partial _{s}^{m-1}\varphi \Vert _{L^{2}}+\int _{0}^{t} \Vert \partial _{s}^{m}\varphi \Vert _{L^{2}}^{2} \textrm{d}t') \le {\tilde{C}}_{m}, \\ \sup _{t\in [0,T)} (\Vert \nabla _{s}^{m} \textbf{w}\Vert _{L^{2}} + \sum _{j=0}^{m-1} \Vert \nabla _{s}^{j} \textbf{w}\Vert _{L^{\infty }}) \le {\tilde{C}}_{m}. \end{array} \right. \end{aligned}$$

(3.13)

Induction Step - Part A: Using Lemma 2.3 with $\mathbf {\phi }:=\nabla _{s}^{m+1}\mathbf {\kappa }$, Lemma 2.5, and exploiting the fact that $\varphi \langle \nabla _{s}^{m+1} \mathbf {\kappa }, \nabla _{s}^{m+2} \mathbf {\kappa } \rangle + \frac{1}{2} \varphi _{s} |\nabla _{s}^{m+1} \mathbf {\kappa }|^{2} = \partial _{s} \left( \frac{1}{2} \varphi |\nabla _{s}^{m+1} \mathbf {\kappa }|^{2}\right)$ we obtain

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}&\left( \frac{1}{2}\int _{I} |\nabla _{s}^{m+1} \mathbf {\kappa }|^{2} \textrm{d}s\right) + \int _{I} |\nabla _{s}^{m+3} \mathbf {\kappa }|^{2} \textrm{d}s + \frac{1}{2}\int _{I} |\nabla _{s}^{m+1} \mathbf {\kappa }|^{2} \textrm{d}s \\&=\int _{I}\langle (\nabla _{t}+ \nabla _{s}^{4}) \nabla _{s}^{m+1} \mathbf {\kappa },\nabla _{s}^{m+1} \mathbf {\kappa } \rangle + \frac{1}{2} \varphi _{s} |\nabla _{s}^{m+1} \mathbf {\kappa }|^{2} \textrm{d}s \\&\quad - \frac{1}{2} \int _{I} |\nabla _{s}^{m+1} \mathbf {\kappa }|^{2} \langle \mathbf {\kappa }, \textbf{V} \rangle \textrm{d}s + \frac{1}{2}\int _{I} |\nabla _{s}^{m+1} \mathbf {\kappa }|^{2} \textrm{d}s\\&= \int _{I} \langle P^{m+3,m+3}_3 (\mathbf {\kappa })+ \lambda (\nabla _s^{m+3} \textbf{w} + Q^{m+1,m+1}_3 (\mathbf {\kappa }, \textbf{w})) +P^{m+1,m+1}_5 (\mathbf {\kappa }), \nabla _{s}^{m+1} \mathbf {\kappa } \rangle \textrm{d}s\\&\quad - \frac{1}{2} \int _{I} |\nabla _{s}^{m+1} \mathbf {\kappa }|^{2} \langle \mathbf {\kappa }, \textbf{V} \rangle \textrm{d}s + \frac{1}{2}\int _{I} |\nabla _{s}^{m+1} \mathbf {\kappa }|^{2} \textrm{d}s\\&=\int _{I} P_{4}^{2m+4,m+3} (\mathbf {\kappa }) + P^{2m+2,m+1}_6 (\mathbf {\kappa }) + P_{2}^{2m+2,m+1} (\mathbf {\kappa }) + P_{4}^{2m+4,m+1} (\mathbf {\kappa }) \textrm{d}s \\&\quad + \lambda \int _{I} \langle \nabla _s^{m+3} \textbf{w} + Q^{m+1,m+1}_3 (\mathbf {\kappa }, \textbf{w}), \nabla _{s}^{m+1} \mathbf {\kappa } \rangle \textrm{d}s\\&= \int _{I} P_{4}^{2m+4,m+3} (\mathbf {\kappa }) + P^{2m+2,m+1}_6 (\mathbf {\kappa }) + P_{2}^{2m+2,m+1} (\mathbf {\kappa }) \textrm{d}s \\&\quad + \lambda \int _{I} \langle \nabla _{s}^{m+1} \textbf{w}, \nabla _{s}^{m+3} \mathbf {\kappa } \rangle \textrm{d}s + \lambda \int _{I} \langle Q^{m+1,m+1}_3 (\mathbf {\kappa }, \textbf{w}), \nabla _{s}^{m+1} \mathbf {\kappa } \rangle \textrm{d}s\\&=J_{1}+J_{2}+J_{3}, \end{aligned}$$

where we have used integration by parts in the last step and absorbed the terms $P_{4}^{2m+4,m+1} (\mathbf {\kappa })$ into $P_{4}^{2\,m+4,m+3} (\mathbf {\kappa })$. Using (3.1) we find by applying Lemma 2.8

$$\begin{aligned} |J_{1}|&=|\int _{I} P_{4}^{2m+4,m+3} (\mathbf {\kappa }) + P^{2m+2,m+1}_6 (\mathbf {\kappa }) + P_{2}^{2m+2,m+1} (\mathbf {\kappa }) \textrm{d}s |\\&\le \epsilon \int _{I} |\nabla _{s}^{m+3} \mathbf {\kappa }|^{2} \textrm{d}s + C(\epsilon , n, \mathcal {D}_{\lambda }(f_{0}) ) . \end{aligned}$$

Using (2.3) and the expression for $\varphi$ we can write for $m \ge 1$

$$\begin{aligned} \nabla _{s}^{m+1} \textbf{w}&= \nabla _{s}^{m+1}( |f_{x}| \mathbf {\kappa }) = \sum _{r=0}^{m+1}\left( {\begin{array}{c}m+1\\ r\end{array}}\right) \partial _{s}^{m+1-r} (|f_{x}|) \nabla _{s}^{r} \mathbf {\kappa }\nonumber \\&=|f_{x}| \nabla _{s}^{m+1} \mathbf {\kappa } + \frac{d_{m}}{\lambda }\varphi \nabla _{s}^{m} \mathbf {\kappa } \nonumber \\&\quad +\frac{1}{\lambda }\left( d_{m-1} \partial _{s} \varphi \nabla _{s}^{m-1} \mathbf {\kappa } + \cdots +d_{2} \partial _{s}^{m-2} \varphi \nabla _{s}^{2} \mathbf {\kappa } \right) \nonumber \\&\quad + \frac{d_{1}}{\lambda }\partial _{s}^{m-1} \varphi \nabla _{s}\mathbf {\kappa } + \frac{1}{\lambda }\mathbf {\kappa }\partial _{s}^{m} \varphi \nonumber \\&=|f_{x}| \nabla _{s}^{m+1} \mathbf {\kappa }+\frac{d_{m} }{\lambda }\varphi \nabla _{s}^{m} \mathbf {\kappa } + \frac{d_{1}}{\lambda }\partial _{s}^{m-1} \varphi \nabla _{s}\mathbf {\kappa } + \frac{1}{\lambda }\mathbf {\kappa }\partial _{s}^{m} \varphi +\frac{1}{\lambda } W \end{aligned}$$

(3.14)

(for appropriate coefficients $d_{j}$ which we do not specify for notation purposes) where

$$\begin{aligned} W:= d_{m-1} \partial _{s} \varphi \nabla _{s}^{m-1} \mathbf {\kappa } + \cdots +d_{2} \partial _{s}^{m-2} \varphi \nabla _{s}^{2} \mathbf {\kappa } \end{aligned}$$

and with the convention that $W=0$ if $m=1,2$. Note that if $m \ge 3$ then $|W| \le C$ by (3.13), so in what follows we can treat W as a bounded term. Therefore we can write

$$\begin{aligned} J_{2}&=\lambda \int _{I} \langle \nabla _{s}^{m+1} \textbf{w}, \nabla _{s}^{m+3} \mathbf {\kappa } \rangle \textrm{d}s =\lambda \int _{I} |f_{x}| \langle \nabla _{s}^{m+1} \mathbf {\kappa } , \nabla _{s}^{m+3} \mathbf {\kappa }\rangle \textrm{d}s + \int _{I} \partial _{s}^{m}\varphi \langle \mathbf {\kappa }, \nabla _{s}^{m+3} \mathbf {\kappa }\rangle \textrm{d}s\\&\quad + \int _{I} d_{1} \partial _{s}^{m-1}\varphi \langle \nabla _{s} \mathbf {\kappa }, \nabla _{s}^{m+3} \mathbf {\kappa }\rangle \textrm{d}s +\int _{I} d_{m} \varphi \langle \nabla _{s}^{m} \mathbf {\kappa }, \nabla _{s}^{m+3} \mathbf {\kappa } \rangle \textrm{d}s+ \int _{I} \langle W,\nabla _{s}^{m+3} \mathbf {\kappa }\rangle \textrm{d}s \\&=J_{2,1}+J_{2,2} + J_{2,3} + J_{2,4} + J_{2,5}. \end{aligned}$$

Using (3.1), (3.8), (3.13), Young inequality, and Lemma 2.8, one can verify that

$$\begin{aligned} J_{2,1} + J_{2,5} \le \epsilon \int _{I} |\nabla _{s}^{m+3} \mathbf {\kappa }|^{2} \textrm{d}s + C(\epsilon , n, \mathcal {D}_{\lambda }(f_{0}), f_{0},T ) . \end{aligned}$$

Young inequality, (3.4), (IP), (3.13), and Lemma 2.10 yield

$$\begin{aligned} J_{2,2}&+ J_{2,3} + J_{2,4}\\&\le \epsilon \int _{I} |\nabla _{s}^{m+3} \mathbf {\kappa }|^{2} \textrm{d}s + C_{\epsilon } (\Vert \partial _{s}^{m} \varphi \Vert _{L^{2}}^{2} + \Vert \partial _{s}^{m-1} \varphi \Vert _{L^{\infty }}^{2} \Vert \nabla _{s} \mathbf {\kappa } \Vert _{L^{2}}^{2} + \Vert \varphi \Vert _{L^{\infty }}^{2} \Vert \nabla _{s}^{m} \mathbf {\kappa } \Vert _{L^{2}}^{2} )\\&\le \epsilon \int _{I} |\nabla _{s}^{m+3} \mathbf {\kappa }|^{2} \textrm{d}s + C_{\epsilon } (\Vert \partial _{s}^{m} \varphi \Vert _{L^{2}}^{2} + \Vert \partial _{s}^{m-1} \varphi \Vert _{L^{2}}^{2} + \Vert \varphi \Vert _{L^{2}}^{2} + \Vert \partial _{s} \varphi \Vert _{L^{2}}^{2} )\\&\le \epsilon \int _{I} |\nabla _{s}^{m+3} \mathbf {\kappa }|^{2} \textrm{d}s + C_{\epsilon } (\Vert \partial _{s}^{m} \varphi \Vert _{L^{2}}^{2} +\Vert \partial _{s}^{m-1} \varphi \Vert _{L^{2}}^{2} + 1). \end{aligned}$$

Next, observe that (neglecting here for simplicity the coefficients multiplying each term)

$$\begin{aligned} Q^{m+1,m+1}_3 (\mathbf {\kappa }, \textbf{w})&= \nabla _{s}^{m+1} \textbf{w} *\mathbf {\kappa }* \mathbf {\kappa } + \nabla _{s}^{m} \textbf{w} *\mathbf {\kappa }* \nabla _{s}\mathbf {\kappa } + R_{m+1} + \textbf{w} * \nabla _{s}\mathbf {\kappa }* \nabla _{s}^{m}\mathbf {\kappa } \\&\quad + \nabla _{s}\textbf{w} * \nabla _{s}^{m}\mathbf {\kappa }* \mathbf {\kappa } + \textbf{w} * \mathbf {\kappa }* \nabla _{s}^{m+1}\mathbf {\kappa } \end{aligned}$$

where $R_{m+1}$ contains all terms of type $\nabla _{s}^{i_{1}} \textbf{w} * \nabla _{s}^{i_{2}}\mathbf {\kappa } * \nabla _{s}^{i_{2}}\mathbf {\kappa }$ with $i_{1}+i_{2}+i_{3} =m+1$ and $i_{1} \le m-1$, $i_{2}, i_{3} \le m-1$ (In case $m=1$, $R_{m+1}=0$). Due to (3.13) we see that $|R_{m+1}| \le C$. Thus, using (3.13) we can write

$$\begin{aligned} |\lambda \langle Q^{m+1,m+1}_3 (\mathbf {\kappa }, \textbf{w}), \nabla _{s}^{m+1} \mathbf {\kappa } \rangle |&\le C(|\nabla _{s}^{m+1}\textbf{w}||\nabla _{s}^{m+1} \mathbf {\kappa }|+ |\nabla _{s}^{m} \textbf{w} *\mathbf {\kappa }* \nabla _{s}\mathbf {\kappa }* \nabla _{s}^{m+1} \mathbf {\kappa }|\\&\quad + |\nabla _{s}^{m+1} \mathbf {\kappa }| + |\textbf{w} * \nabla _{s}\mathbf {\kappa }* \nabla _{s}^{m}\mathbf {\kappa } * \nabla _{s}^{m+1} \mathbf {\kappa }|\\&\quad + |\nabla _{s}\textbf{w} * \nabla _{s}^{m}\mathbf {\kappa }* \mathbf {\kappa } *\nabla _{s}^{m+1} \mathbf {\kappa }| +|\nabla _{s}^{m+1} \mathbf {\kappa }|^{2}). \end{aligned}$$

Taking into account the expression (3.14) derived above, (3.8), and (3.13) we obtain

$$\begin{aligned} |\nabla _{s}^{m+1}\textbf{w}||\nabla _{s}^{m+1} \mathbf {\kappa }|&\le C (|\nabla _{s}^{m+1} \mathbf {\kappa }|^{2} + | \varphi | |\nabla _{s}^{m} \mathbf {\kappa }| |\nabla _{s}^{m+1} \mathbf {\kappa }| + |\nabla _{s}^{m+1} \mathbf {\kappa }| \\&\qquad + |\partial _{s}^{m-1} \varphi ||\nabla _{s} \mathbf {\kappa } ||\nabla _{s}^{m+1} \mathbf {\kappa }| + |\partial _{s}^{m}\varphi | |\nabla _{s}^{m+1} \mathbf {\kappa }|)\\&\le C (|\nabla _{s}^{m+1} \mathbf {\kappa }|^{2} + \Vert \varphi \Vert _{\infty }^{2} |\nabla _{s}^{m} \mathbf {\kappa }|^{2} + 1 + \Vert \partial _{s}^{m-1}\varphi \Vert _{\infty }^{2} |\nabla _{s} \mathbf {\kappa }|^{2} + | \partial _{s}^{m} \varphi |^{2}). \end{aligned}$$

Similarly

$$\begin{aligned} |\nabla _{s}\textbf{w} * \nabla _{s}^{m}\mathbf {\kappa }* \mathbf {\kappa } *\nabla _{s}^{m+1} \mathbf {\kappa }|&\le C(\Vert \varphi \Vert _{\infty }^{2} |\nabla _{s}^{m} \mathbf {\kappa }|^{2} + |\nabla _{s}^{m+1} \mathbf {\kappa }|^{2} + |P_{3}^{2m+2, m+1}(\mathbf {\kappa })| ),\\ |\textbf{w} * \nabla _{s}\mathbf {\kappa }* \nabla _{s}^{m}\mathbf {\kappa } * \nabla _{s}^{m+1} \mathbf {\kappa }|&\le C|P_{3}^{2m+2, m+1}(\mathbf {\kappa })|, \end{aligned}$$

and for $m \ge 2$ (note that if $m=1$ the following term has already been dealt with, since for $m=1$ we have $\nabla _{s}^{m} \textbf{w} *\mathbf {\kappa }* \nabla _{s}\mathbf {\kappa }* \nabla _{s}^{m+1} \mathbf {\kappa }= \nabla _{s}\textbf{w} * \nabla _{s}^{m}\mathbf {\kappa }* \mathbf {\kappa } *\nabla _{s}^{m+1} \mathbf {\kappa }$ )

$$\begin{aligned} |\nabla _{s}^{m}&\textbf{w} *\mathbf {\kappa }* \nabla _{s}\mathbf {\kappa }* \nabla _{s}^{m+1} \mathbf {\kappa }|\\&\le C (|P_{3}^{2m+2, m+1}(\mathbf {\kappa })| + |\varphi | |\nabla _{s}^{m-1}\mathbf {\kappa }|| \nabla _{s}^{m+1}\mathbf {\kappa }| +|\nabla _{s}^{m+1}\mathbf {\kappa }| + |\partial _{s}^{m-1} \varphi || \nabla _{s}^{m+1}\mathbf {\kappa }|)\\&\le C (|P_{3}^{2m+2, m+1}(\mathbf {\kappa })| + \Vert \varphi \Vert _{\infty }^{2} |\nabla _{s}^{m-1} \mathbf {\kappa }|^{2} + 1 + |\nabla _{s}^{m+1} \mathbf {\kappa }|^{2} + | \partial _{s}^{m-1} \varphi |^{2} ) \end{aligned}$$

so that using (IP), (3.13), (3.1), Lemma 2.8 and Lemma 2.10 we obtain that

$$\begin{aligned} J_{3}&=\int _{I}\lambda \langle Q^{m+1,m+1}_3 (\mathbf {\kappa }, \textbf{w}), \nabla _{s}^{m+1} \mathbf {\kappa } \rangle \textrm{d}s \le \epsilon \int _{I} |\nabla _{s}^{m+3} \mathbf {\kappa }|^{2} \textrm{d}s + C_{\epsilon }\\&\quad + C( \Vert \varphi \Vert _{L^{2}}^{2} + \Vert \partial _{s} \varphi \Vert _{L^{2}}^{2}+ \Vert \partial _{s}^{m-1}\varphi \Vert _{L^{2}}^{2} + \Vert \partial _{s}^{m} \varphi \Vert _{L^{2}}^{2})\\&\le \epsilon \int _{I} |\nabla _{s}^{m+3} \mathbf {\kappa }|^{2} \textrm{d}s + C_{\epsilon } + C(\Vert \partial _{s}^{m-1}\varphi \Vert _{L^{2}}^{2} + \Vert \partial _{s}^{m} \varphi \Vert _{L^{2}}^{2}). \end{aligned}$$

Collecting the estimates for $J_{1}$, $J_{2}$ and $J_{3}$ we find

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}&\left( \frac{1}{2}\int _{I} |\nabla _{s}^{m+1} \mathbf {\kappa }|^{2} \textrm{d}s\right) + \int _{I} |\nabla _{s}^{m+3} \mathbf {\kappa }|^{2} \textrm{d}s + \frac{1}{2}\int _{I} |\nabla _{s}^{m+1} \mathbf {\kappa }|^{2} \textrm{d}s \\&= J_{1}+ J_{2}+J_{3} \le \epsilon \int _{I} |\nabla _{s}^{m+3} \mathbf {\kappa }|^{2} \textrm{d}s + C_{\epsilon } ( 1 + \Vert \partial _{s}^{m-1}\varphi \Vert _{L^{2}}^{2}+ \Vert \partial _{s}^{m}\varphi \Vert _{L^{2}}^{2}). \end{aligned}$$

Choosing $\epsilon$ appropriately and using (IP), a Gronwall Lemma yields

$$\begin{aligned} \sup _{ t \in [0,T)} \Vert \nabla _{s}^{m+1} \mathbf {\kappa } \Vert _{L^{2}} + \sup _{ t \in [0,T)} \int _{0}^{t} \Vert \nabla _{s}^{m+3} \mathbf {\kappa }\Vert _{L^{2}}^{2} \textrm{d}t'\le C_{m+1} \end{aligned}$$

(3.15)

with $C_{m+1}=C_{m+1}(n,\lambda , \mathcal {D}_{\lambda }(f_{0}), T, f_{0}).$ Together with Lemma 2.10 and (IP) we also infer that

$$\begin{aligned} \sup _{ t \in [0,T)} \Vert \nabla _{s}^{m} \mathbf {\kappa } \Vert _{L^{\infty }} \le C_{m+1}=C_{m+1}(n,\lambda , \mathcal {D}_{\lambda }(f_{0}), T, f_{0}). \end{aligned}$$

(3.16)

Induction Step - Part B: We compute

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t} \left( \frac{1}{2} \int _{I} (\partial _{s}^{m}\varphi )^{2} \textrm{d}s \right)&= \int _{I} \partial _{s}^{m}\varphi \, \partial _{t} \partial _{s}^{m}\varphi \textrm{d}s + \frac{1}{2} \int _{I} (\partial _{s}^{m}\varphi )^{2} (\varphi _{s} - \langle \mathbf {\kappa }, \textbf{V} \rangle ) \textrm{d}s\\&= \int _{I} \partial _{s}^{m}\varphi \left( (\lambda |f_{x}| \partial _{s}^{m+1} \varphi )_{s} - ( \lambda |f_{x}| \partial _{s}^{m} (\langle \mathbf {\kappa }, \textbf{V} \rangle ))_{s}\right. \\&\quad \left. +M_{2}^{m,m} (\langle \mathbf {\kappa }, \textbf{V}\rangle , \varphi ) {+}B_{2}^{m{+}1,m{+}1} (\varphi ) \right) \textrm{d}s \\&\quad + \frac{1}{2} \int _{I} (\partial _{s}^{m}\varphi )^{2} (\varphi _{s} {-} \langle \mathbf {\kappa }, \textbf{V} \rangle ) \textrm{d}s \end{aligned}$$

where we have used (2.4) and (2.15). Integration by parts gives

$$\begin{aligned}&\frac{\textrm{d}}{\textrm{d}t} \left( \frac{1}{2} \int _{I} (\partial _{s}^{m}\varphi )^{2} \textrm{d}s \right) + \int _{I} \lambda |f_{x}| (\partial _{s}^{m+1}\varphi )^{2} \textrm{d}s= \int _{I} (\partial _{s}^{m+1}\varphi ) \lambda |f_{x}| \partial _{s}^{m} (\langle \mathbf {\kappa }, \textbf{V} \rangle ) \textrm{d}s \\&\qquad +\int _{I} (\partial _{s}^{m}\varphi ) \, M_{2}^{m,m} (\langle \mathbf {\kappa }, \textbf{V}\rangle , \varphi ) \textrm{d}s +\int _{I} (\partial _{s}^{m}\varphi ) \,B_{2}^{m+1,m+1} (\varphi ) \textrm{d}s =A_{1}+A_{2}+A_{3}. \end{aligned}$$

Note that exploiting the bound from below for the length element (3.11) we can write

$$\begin{aligned}&\frac{\textrm{d}}{\textrm{d}t} \left( \frac{1}{2} \int _{I} (\partial _{s}^{m}\varphi )^{2} \textrm{d}s \right) + C\int _{I} (\partial _{s}^{m+1}\varphi )^{2} \textrm{d}s + \frac{1}{2}\int _{I} \lambda |f_{x}| (\partial _{s}^{m+1}\varphi )^{2} \textrm{d}s \nonumber \\&\le \int _{I} (\partial _{s}^{m+1}\varphi ) \lambda |f_{x}| \partial _{s}^{m} (\langle \mathbf {\kappa }, \textbf{V} \rangle ) \textrm{d}s \nonumber +\int _{I} (\partial _{s}^{m}\varphi ) \, M_{2}^{m,m} (\langle \mathbf {\kappa }, \textbf{V}\rangle , \varphi ) \textrm{d}s \nonumber \\&\quad +\int _{I} (\partial _{s}^{m}\varphi ) \,B_{2}^{m+1,m+1} (\varphi ) \textrm{d}s =A_{1}+A_{2}+A_{3}. \end{aligned}$$

(3.17)

Observing that by (3.13) and (3.16)

$$\begin{aligned} |\partial _{s}^{m} (\langle \mathbf {\kappa }, \textbf{V} \rangle )|&\le C (|\textbf{V}| + \cdots +|\nabla _{s}^{m} \textbf{V}|) \le C (1 +|\nabla _{s}^{m+1} \mathbf {\kappa }| +|\nabla _{s}^{m+2} \mathbf {\kappa }| + |\nabla _{s}^{m}\textbf{w}|)\\ |\partial _{s}^{m-1} (\langle \mathbf {\kappa }, \textbf{V} \rangle )|&\le C (1+ |\nabla _{s}^{m+1} \mathbf {\kappa }|)\\ |\partial _{s}^{m-2} (\langle \mathbf {\kappa }, \textbf{V} \rangle )|&\le C, \end{aligned}$$

and recalling (3.8) we derive immediately that

$$\begin{aligned} A_{1}&\le \epsilon \int _{I} \lambda |f_{x}| (\partial _{s}^{m+1}\varphi )^{2} \textrm{d}s + C_{\epsilon } \int _{I} (1 +|\nabla _{s}^{m+1} \mathbf {\kappa }|^{2} +|\nabla _{s}^{m+2} \mathbf {\kappa }|^{2} + |\nabla _{s}^{m}\textbf{w}|^{2}) \textrm{d}s \\&\le \epsilon \int _{I} \lambda |f_{x}| (\partial _{s}^{m+1}\varphi )^{2} \textrm{d}s + C_{\epsilon } (1 + \Vert \nabla _{s}^{m+2} \mathbf {\kappa } \Vert _{L^{2}}^{2}) \end{aligned}$$

where we have used the induction hypthesis, (3.1), and (3.15) in the last step. Using the definition of $M^{m,m}_{2}$, the calculation above for $|\partial _{s}^{m} (\langle \mathbf {\kappa }, \textbf{V} \rangle )|$, (3.16), and (3.13) we infer that for any $m \ge 1$ there holds

$$\begin{aligned} |M_{2}^{m,m} (\langle \mathbf {\kappa }, \textbf{V}\rangle , \varphi ) |&\le C (1 +|\nabla _{s}^{m+1} \mathbf {\kappa }| +|\nabla _{s}^{m+2} \mathbf {\kappa }| + |\nabla _{s}^{m}\textbf{w}|) |\varphi | \\&\quad + C (1 + |\nabla _{s}^{m+1} \mathbf {\kappa }|) |\partial _{s} \varphi | + C + C( |\partial _{s}^{m-1} \varphi | + |\partial _{s}^{m} \varphi |). \end{aligned}$$

Thus together with Lemma 2.10, (3.13), and (3.15) we obtain

$$\begin{aligned} A_{2}&\le C \big (\Vert \varphi \Vert _{L^{2}} \Vert \partial _{s}^{m}\varphi \Vert _{L^{2}} +\Vert \varphi \Vert _{L^{2}}\Vert \partial _{s}^{m}\varphi \Vert _{L^{2}} \left[ \Vert \nabla _{s}^{m+1}\mathbf {\kappa }\Vert _{L^{\infty }} + \Vert \nabla _{s}^{m+2}\mathbf {\kappa }\Vert _{L^{\infty }} \right] \\&\quad +\Vert \varphi \Vert _{L^{\infty }}\Vert \partial _{s}^{m}\varphi \Vert _{L^{2}} \Vert \nabla _{s}^{m}\textbf{w}\Vert _{L^{2}} \big )\\&\quad + C \big ( \left[ \Vert \partial _{s}\varphi \Vert _{L^{2}} + \Vert \partial _{s}^{m-1}\varphi \Vert _{L^{2}} \right] \Vert \partial _{s}^{m}\varphi \Vert _{L^{2}} \big ) + C\Vert \partial _{s}^{m}\varphi \Vert _{L^{2}}^{2} \\&\quad + C\Vert \nabla _{s}^{m+1}\mathbf {\kappa }\Vert _{L^{\infty }} \Vert \partial _{s}^{m}\varphi \Vert _{L^{2}} \Vert \partial _{s}\varphi \Vert _{L^{2}} +C\\&\le C + C( \Vert \varphi \Vert _{L^{2}}^{2} + \Vert \partial _{s}\varphi \Vert _{L^{2}}^{2} + \Vert \partial _{s}^{m-1}\varphi \Vert _{L^{2}}^{2} +\Vert \partial _{s}^{m}\varphi \Vert _{L^{2}}^{2} ) \\ {}&\quad + C \Vert \varphi \Vert _{L^{2}}\Vert \partial _{s}^{m}\varphi \Vert _{L^{2}} [\Vert \nabla _{s}^{m+1}\mathbf {\kappa }\Vert _{L^{2}} + \Vert \nabla _{s}^{m+2}\mathbf {\kappa }\Vert _{L^{2}} + \Vert \nabla _{s}^{m+3}\mathbf {\kappa }\Vert _{L^{2}}] \\ {}&\quad + C\Vert \partial _{s}^{m}\varphi \Vert _{L^{2}} \Vert \partial _{s}\varphi \Vert _{L^{2}} (\Vert \nabla _{s}^{m+1}\mathbf {\kappa }\Vert _{L^{2}} + \Vert \nabla _{s}^{m+2}\mathbf {\kappa }\Vert _{L^{2}} )\\&\le C + C(\Vert \partial _{s}^{m-1}\varphi \Vert _{L^{2}}^{2} +\Vert \partial _{s}^{m}\varphi \Vert _{L^{2}}^{2} ) + C (\Vert \nabla _{s}^{m+2}\mathbf {\kappa }\Vert _{L^{2}}^{2} + \Vert \nabla _{s}^{m+3}\mathbf {\kappa }\Vert _{L^{2}}^{2} ) \int _{I} |\partial _{s}^{m}\varphi |^{2} \textrm{d}s. \end{aligned}$$

Finally, recalling the definition of $B^{m+1,m+1}_{2}(\varphi )$ we see that every term appearing in $A_{3}$ is of type

$$\begin{aligned} \int _{I} (\partial _{s}^{m} \varphi ) (\partial _{s}^{i_{1}} \varphi ) (\partial _{s}^{i_{2}} \varphi ) \textrm{d}s \end{aligned}$$

with $i_{1}+i_{2} = m+1$ and $0 \le i_{j} \le m+1$. Each such term can be estimated using Lemma 2.10, (3.1) and (3.13) as follows: if $i_{1}=m+1$ (hence $i_{2}=0$) then

$$\begin{aligned} |\int _{I} (\partial _{s}^{m} \varphi ) (\partial _{s}^{m+1} \varphi ) \,\varphi \textrm{d}s |&\le \epsilon \Vert \partial _{s}^{m+1} \varphi \Vert _{L^{2}}^{2} + C_{\epsilon }\Vert \varphi \Vert _{L^{\infty }}^{2} \int _{I} |\partial _{s}^{m} \varphi |^{2} \textrm{d}s\\&\le \epsilon \Vert \partial _{s}^{m+1} \varphi \Vert _{L^{2}}^{2} + C_{\epsilon }(\Vert \varphi \Vert _{L^{2}}^{2} +\Vert \partial _{s} \varphi \Vert _{L^{2}}^{2}) \int _{I} |\partial _{s}^{m} \varphi |^{2} \textrm{d}s\\&\le \epsilon \Vert \partial _{s}^{m+1} \varphi \Vert _{L^{2}}^{2} + C_{\epsilon }(1 +\Vert \partial _{s}^{m} \varphi \Vert _{L^{2}}^{2}) \int _{I} |\partial _{s}^{m} \varphi |^{2} \textrm{d}s \end{aligned}$$

where we have used (3.13) in the last step (note that for $m \ge 2$ we actually have $\Vert \partial _{s} \varphi \Vert _{L^{2}}^{2} \le C$). If $i_{1}=m$, $i_{2}=1$ with $m \ge 2$ then we write using Lemma (2.10) and (3.13)

$$\begin{aligned} \int _{I} (\partial _{s}^{m} \varphi ) (\partial _{s}^{m} \varphi ) (\partial _{s}\varphi ) \textrm{d}s&\le \Vert \partial _{s}\varphi \Vert _{L^{\infty }}\int _{I} |\partial _{s}^{m} \varphi |^{2} \textrm{d}s \le C (\Vert \partial _{s}\varphi \Vert _{L^{2}} +\Vert \partial _{s}^{2}\varphi \Vert _{L^{2}})\int _{I} |\partial _{s}^{m} \varphi |^{2} \textrm{d}s \\&\le C(1 + \Vert \partial _{s}^{m-1}\varphi \Vert _{L^{2}}^{2} +\Vert \partial _{s}^{m}\varphi \Vert _{L^{2}}^{2})\int _{I} |\partial _{s}^{m} \varphi |^{2} \textrm{d}s. \end{aligned}$$

On the other hand if $i_{1}=m$, $i_{2}=1$ with $m =1$ then integration by parts yields

$$\begin{aligned} \int _{I} (\partial _{s}^{m} \varphi ) (\partial _{s}^{m} \varphi ) (\partial _{s}\varphi ) \textrm{d}s&= \int _{I} (\partial _{s}^{m}\varphi )^{3} \textrm{d}s =- 2\int _{I} (\partial _{s}^{m} \varphi ) (\partial _{s}^{m-1} \varphi ) (\partial _{s}^{m+1} \varphi ) \textrm{d}s \\&\le \epsilon \Vert \partial _{s}^{m+1} \varphi \Vert _{L^{2}}^{2} + C_{\epsilon } \Vert \partial _{s}^{m-1} \varphi \Vert _{L^{\infty }}^{2} \int _{I} |\partial _{s}^{m} \varphi |^{2} \textrm{d}s\\&\le \epsilon \Vert \partial _{s}^{m+1} \varphi \Vert _{L^{2}}^{2} + C_{\epsilon }(\Vert \partial _{s}^{m-1} \varphi \Vert _{L^{2}}^{2} +\Vert \partial _{s}^{m} \varphi \Vert _{L^{2}}^{2}) \int _{I} |\partial _{s}^{m} \varphi |^{2} \textrm{d}s. \end{aligned}$$

If $i_{1}=m-1$, $i_{2}=2$ and $m=1$ then similar arguments as above yield

$$\begin{aligned} \int _{I} (\partial _{s}^{m} \varphi ) (\partial _{s}^{m-1} \varphi ) (\partial _{s}^{2}\varphi ) \textrm{d}s&= \int _{I} (\partial _{s}^{m} \varphi ) (\partial _{s}^{m-1} \varphi ) (\partial _{s}^{m+1}\varphi ) \textrm{d}s\\&\le \epsilon \Vert \partial _{s}^{m+1} \varphi \Vert _{L^{2}}^{2} + C_{\epsilon }(\Vert \partial _{s}^{m-1} \varphi \Vert _{L^{2}}^{2} +\Vert \partial _{s}^{m} \varphi \Vert _{L^{2}}^{2}) \int _{I} |\partial _{s}^{m} \varphi |^{2} \textrm{d}s. \end{aligned}$$

On the other hand if $i_{1}=m-1$, $i_{2}=2$ and $m \ge 2$ then

$$\begin{aligned} \int _{I} (\partial _{s}^{m} \varphi ) (\partial _{s}^{m-1} \varphi ) (\partial _{s}^{2}\varphi ) \textrm{d}s&\le \Vert \partial _{s}^{2}\varphi \Vert _{L^{2}}^{2} + \Vert \partial _{s}^{m-1}\varphi \Vert _{L^{\infty }}^{2}\int _{I} |\partial _{s}^{m} \varphi |^{2} \textrm{d}s\\&\le C + C(1+\Vert \partial _{s}^{m-1}\varphi \Vert _{L^{2}}^{2} +\Vert \partial _{s}^{m}\varphi \Vert _{L^{2}}^{2})\int _{I} |\partial _{s}^{m} \varphi |^{2} \textrm{d}s. \end{aligned}$$

Finally if $i_{1} \le m-2$ $i_{2}=m+1-i_{1}$, then by (3.13) we know that $| \partial _{s}^{i_{1}} \varphi | \le C$ and therefore we can write

$$\begin{aligned} |\int _{I} (\partial _{s}^{m} \varphi ) (\partial _{s}^{i_{1}} \varphi ) (\partial _{s}^{i_{2}} \varphi ) \textrm{d}s |&\le C \Vert \partial _{s}^{i_{2}} \varphi \Vert _{L^{2}} \Vert \partial _{s}^{m} \varphi \Vert _{L^{2}} \le \Vert \partial _{s}^{i_{2}} \varphi \Vert _{L^{2}}^{2} + \int _{I} |\partial _{s}^{m} \varphi |^{2} \textrm{d}s\\&\le C + \int _{I} |\partial _{s}^{m} \varphi |^{2} \textrm{d}s \end{aligned}$$

where we have taken (IP) and $i_{2} < m$ into account. According to all considerations outlined so far we can state that

$$\begin{aligned} |A_{3}|&\le \epsilon \Vert \partial _{s}^{m+1} \varphi \Vert _{L^{2}}^{2} + C_{\epsilon }(1+\Vert \partial _{s}^{m-1} \varphi \Vert _{L^{2}}^{2} +\Vert \partial _{s}^{m} \varphi \Vert _{L^{2}}^{2}) \int _{I} |\partial _{s}^{m} \varphi |^{2} \textrm{d}s + C. \end{aligned}$$

Fron (3.17) together with the obtained estimates for $A_{1}$, $A_{2}$, $A_{3}$, (IP), and choosing $\epsilon$ appropriately we obtain

$$\begin{aligned}&\frac{\textrm{d}}{\textrm{d}t} \left( \frac{1}{2} \int _{I} (\partial _{s}^{m}\varphi )^{2} \textrm{d}s \right) + C\int _{I} (\partial _{s}^{m+1}\varphi )^{2} \textrm{d}s \\&\le C(1 + \Vert \nabla _{s}^{m+2} \mathbf {\kappa } \Vert _{L^{2}}^{2}) + C ( 1 +\Vert \partial _{s}^{m} \varphi \Vert _{L^{2}}^{2} +\Vert \nabla _{s}^{m+2}\mathbf {\kappa }\Vert _{L^{2}}^{2} + \Vert \nabla _{s}^{m+3}\mathbf {\kappa }\Vert _{L^{2}}^{2} ) \int _{I} |\partial _{s}^{m}\varphi |^{2} \textrm{d}s. \end{aligned}$$

A Gronwall argument that takes into account (IP) and (3.15) finally yields

$$\begin{aligned} \sup _{t \in [0,T)} ( \Vert \partial _{s}^{m}\varphi \Vert _{L^{2}} +\int _{0}^{t} \Vert \partial _{s}^{m+1}\varphi \Vert _{L^{2}}^{2} \textrm{d}t' ) \le {\tilde{C}}_{m+1}, \end{aligned}$$

with ${\tilde{C}}_{m+1}={\tilde{C}}_{m+1}( n, \lambda , \mathcal {D}_{\lambda }(f_{0}), f_{0}, T)$. The uniform $L^{2}$-bound for $\nabla _{s}^{m+1}\textbf{w}$ follows from (3.14) and the uniform bounds obtained so far. The induction step is now completed.

Final steps: As observed in [6, Thm 3.1], for a function $h:I \rightarrow \mathbb {R}$ we have that $\partial _{x}^{m} h = |f_{x}|^{m} \partial _{s}^{m} h + P_{m} (|f_{x}|, \ldots , \partial _{x}^{m-1}(|f_{x}|), h, \ldots , \partial _{s}^{m-1}h)$ where $P_{m}$ is a polynomial. With $h=|f_{x}|$ and (2.2) it follows $\partial _{x}^{m} (|f_{x}|) = \frac{1}{\lambda }|f_{x}|^{m} \partial _{s}^{m-1} \varphi + P_{m} (|f_{x}|, \ldots , \partial _{x}^{m-1}(|f_{x}|), \varphi , \ldots , \partial _{s}^{m-2}\varphi )$, so that taking into account (3.8), and the uniform bounds obtained for $\varphi$ and its derivatives (recall that (3.13) holds for any m), we obtain uniform bounds for the derivatives of the length element in the original parametrization. Similarly, using Lemma 2.9 and (3.13) we can also state that on [0, T) we have for any $m \in \mathbb {N}$

$$\begin{aligned} \Vert \partial _{x}^{m} f \Vert _{L^{\infty }} \le C(m, n, \lambda , \mathcal {D}(f_{0}), f_{0}, T). \end{aligned}$$

Moreover $\Vert f \Vert _{L^{\infty }} \le C(n, \lambda , \mathcal {D}(f_{0}), f_{0}, T)$. Therefore we can extend f smoothly over $[0,T] \times I$ and even beyond by short-time existence contradicting the maximality of T. This proves that the flow exists globally in time.