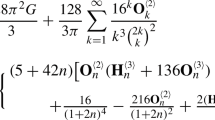Abstract
In this paper, we introduce a formula for the exact number of zeros of every partial sum of the Riemann zeta function inside infinitely many rectangles of the critical strips where they are situated.
Similar content being viewed by others
1 Introduction
The zeros of exponential polynomials are a topic which appeared in the first third of the twentieth century in relation to the development of the theory of differential equations. At this point, we must quote Wilder [14]. Here, it can be found one of the first formulae to determine the number of zeros of an exponential sum inside a rectangle of the critical strip where its zeros are located. On the line which Wilder had indicated are the works of Tamarkin [11, 12] and Langer [6]. Analogous results can be found in [13], where Turan attributes to Pólya [10] a formula for the number of the zeros of an exponential sum where the coefficients are algebraic polynomials. Also, certain ideas considered by Tamarkin, Wilder and Langer were developed in the sixties by Dickson [3, 4].
Similar formulae on the number of zeros of functions much more general than exponential polynomials are provided in Levin’s book [7]. For instance, if the convex hull of the spectrum of an almost-periodic function \(f(z)\) is a segment of the imaginary axis, the formula is, for sufficiently large values of \(\left| y_{1}\right| \) and \(\left| y_{2}\right| \),
where \(d\) is the length of the segment and \(N(x_{1},x_{2},y_{1},y_{2})\) denotes the number of zeros of \(f(z)\) inside the rectangle \(x_1\le x\le x_2,\ y_1\le y\le y_2\) [7, Chapter 6, Th. 9].
Recently, for the partial sums,
with \(s=\sigma +it\) a complex variable and \(X\) a real number greater than or equal to \(2\), Gonek and Ledoan prove in [5, Theorem 2] the formula
which determines the number of zeros \(N_{X}(T)\) of \(\zeta _{X}(s)\) for the special case when these zeros have ordinates in \(\left[ 0,T\right] \). Here, \( \left[ x\right] \) is used to denote the largest integer not exceeding the real number \(x\). It is worth to note here that the term \(O(1)\) of formula (1.1), which essentially depends on \(f(z)\), has been specified for the functions \(\zeta _X(s)\).
As we have just seen, in the extensive literature on the related question with the topic of the zeros, the formulae for the number of zeros in certain regions, mainly rectangles, have a common thing: all them contain either the error term \(O(1)\) or a bound which expresses the maximum error with respect to the exact number of zeros inside those regions. For the partial sums of the Riemann zeta function, we established in [9, Theorem 6] a formula for the number of their zeros inside certain rectangles in the critical strip. In fact, for every integer \(n\ge 2\), we proved the existence of infinitely many rectangles \(\{R_{n,T}\}\) bounded by the lines \(y=0\) and \(y=T\), \(T>0\), such that the number of zeros, \(N_n(T)\), of \(\zeta _{n}(s)\) inside each \(R_{n,T}\) satisfies
In this paper, we deal with the problem of the existence of rectangles in the critical strip of every \(\zeta _{n}(s)\) for which the error in the formula for the number of zeros can be reduced to \(0\). In terms of the last paper of Gonek and Ledoan [5], the question would be expressed as follows: are there rectangles in the critical strip given by the lines \(y=0\) and \(y=T\) for which the formula (1.2) is exact? We have just proved that the answer is yes; in fact, we demonstrate the existence of infinitely many values of \(T\) where the zeros, of every partial sum \(\zeta _{n}(s)\) inside each rectangle \(R_{n,T}\), are counted by the formula
It is worthwhile to remark that this result improves that of [9, Theorem 6].
2 The formula
For each integer, \(n\ge 2\), \(\zeta _{n}(s)\) is an entire function of order \(1\), exponential type \(\ln n\), and it has infinitely many zeros not all of them are situated on the imaginary axis, except for the case \(n=2\) [9] whose zeros \(z_{k}\) are explicitly given by
Therefore, \(n=2\) is the trivial case, and we will assume that \(n>2\).
On the other hand, since for any \(t\), we have
and
there exist two values of \(\sigma \), \(\sigma _{n_{1}}<0<\sigma _{n_{2}}\), such that
and
Therefore the functions \(\zeta _{n}(s)\) have all their zeros comprised in vertical strips \(S_{n}\), called critical strips, defined by
where the bounds
and
have been estimated by means of the expressions
and
by Balazard and Velazquez-Castañon [2] and Montgomery [8], respectively.
Remark 1
We first take a rectangle, denoted by \( R_{n,T}\), defined by the right-lines \(x=a_{n}^{\prime }\), \(x=b_{n}^{\prime }\); \(y=0\) and \(y=T\), where \(a_{n}^{\prime }\) and \(b_{n}^{\prime }\) are arbitrary real numbers satisfying \(a_{n}^{\prime }<a_{n}\), \(b_{n}^{\prime }>b_{n}\), and \(T>0\) is so that \(\zeta _{n}(s)\) has no zero on the line \(y=T\). The values of \(T\) for which formula (1.3) is valid will be specified in the proof of the next theorem.
Theorem 2
For every integer \(n\ge 2\), there exist infinitely many rectangles \(R_{n,T}\) such that the number of zeros, \(N_{n}(T)\), of the function \(\zeta _{n}(s)\) inside each one of them is given by the formula
Proof
For \(n=2\), we consider a rectangle \(R_{2,T}\) with \(T\in \left[ \tfrac{2\pi k}{ \log 2},\tfrac{\pi (2k+1)}{\log 2}\right) \) for some integer \(k\ge 0\). Then, \(k\le \frac{T\log 2}{2\pi }<k+\frac{1}{2}\), therefore, \(\left[ \frac{ T\log 2}{2\pi }\right] =k\). Noticing (2.1) the number of zeros inside \( R_{2,T}\) satisfies
and this means that the formula (1.3) follows. Therefore, from now on we assume that \(n>2\). Consider a rectangle \(R_{n,T}\); we observe that \(\zeta _{n}(s)\) is never \(0\) on the boundary of \(R_{n,T}\); therefore, we can apply the argument principle [1, p. 87] on it. For a given \(0<\epsilon <\dfrac{1}{6}\), by virtue of (2.2) and (2.3), we determine two values \(a_{n}^{\prime \prime }\), \( b_{n}^{\prime \prime }\), with \(a_{n}^{\prime \prime }<a_{n}^{\prime }\) and \( b_{n}^{\prime \prime }>b_{n}^{\prime }\), satisfying
and
Let \(R_{n,T}^{\prime }\) be a new rectangle defined by the right-lines \( x=a_{n}^{\prime \prime }\), \(x=b_{n}^{\prime \prime }\); \(y=0\), \(y=T\). Noticing \(\mathrm{Re }\,s\le a_{n}^{\prime }\) and \(\mathrm{Re }\,s\ge b_{n}^{\prime } \) are zero-free regions, we conclude that \(\zeta _{n}(s)\) has the same number of zeros inside both rectangles \(R_{n,T}\) and \(R_{n,T}^{\prime }\). Then, for the above \(\epsilon \), we claim that there exist infinitely many values of \( T \) such that the variation of the argument of \(\zeta _{n}(s)\) on the boundary of \(R_{n,T}^{\prime }\), denoted by \(VA(\zeta _{n}(s);R_{n,T}^{\prime })\), satisfies
Indeed, by writing
and according to (2.4), we infer that the variation of the argument of \(\zeta _{n}(s)\) on the side of the rectangle \(R_{n,T}^{\prime }\) defined by the line \(x=a_{n}^{\prime \prime }\), denoted by \(VA(\zeta _{n}(s);x=a_{n}^{\prime \prime })\), is given by
Now, from (2.5), we conclude that the variation of the argument of \( \zeta _{n}(s)\) on the side of the rectangle \(R_{n,T}^{\prime }\) defined by the line \(x=b_{n}^{\prime \prime }\), denoted by \(VA(\zeta _{n}(s);x=b_{n}^{\prime \prime })\), satisfies
On the other hand, because \(\zeta _{n}(s)>0\) for all real \(s\), the variation of the argument of \(\zeta _{n}(s)\) on the side of the rectangle \(R_{n,T}^{\prime }\) defined by the line \(y=0\), denoted by \(VA(\zeta _{n}(s);y=0)\), is
Finally, it only remains to prove that there exist infinitely many values of \(T\) such that the variation of the argument of \(\zeta _{n}(s)\) on the side of the rectangle \(R_{n,T}^{\prime }\) defined by the line \(y=T\), \(VA(\zeta _{n}(s);y=T)\), satisfies
Indeed, let \(\left\{ p_{1},p_{2},\ldots ,p_{k_{n}}\right\} \) be the set of all prime numbers less than or equal to \(n\); noticing for each integer \(1\le m\le n\), there exist non-negative integers \(l_{mj}\) such that
the functions \(\mathrm{Re }\,\zeta _{n}(s)\) and \(\mathrm{Im }\,\zeta _{n}(s)\) can be considered as polynomial in
Given the preceding \(\epsilon \), by continuity, there exists \(\delta >0\) such that for any real number \(\sigma \in \left[ a_{n}^{\prime \prime },b_{n}^{\prime \prime }\right] \), one has
provided that
for all \(j=1,\ldots ,k_{n}\). Given \(\delta >0\), determine a positive number \(\eta <\epsilon \) so that for any \(\eta _{j}\) satisfying \(\left| \eta _{j}\right| \le \eta \), the conditions (2.13) to be fulfilled, that is
Now, since for any \(s=\sigma +it\)
by using (2.11) we can write, for \(\sigma \in \left[ a_{n}^{\prime \prime },b_{n}^{\prime \prime }\right] \),
where \(f_{j}(t,\sigma )\) is a uniformly bounded function on \( \mathbb {R} \times \left[ a_{n}^{\prime \prime },b_{n}^{\prime \prime }\right] \). Let \( M>0\) be such that \(\left| f_{j}(t,\sigma )\right| \le M\) for all \( j=1,\ldots ,k_{n}\). Define a positive number
and let us take
Then, as the numbers \(\dfrac{1}{\alpha _{j}}\) are linearly independent over the rationals, by applying a lemma of Kronecker and Bohl [11, p. 68], there exists a positive real number \(l\) such that any real interval of the form
contains an interval \(I_{p}\) of length \(\lambda \) which contains at least one point of each set
Let \(T\) be an arbitrary point of some \(I_{p}\) with \(p\ge 0\). For each \(j\in \left\{ 1,2,\ldots ,k_{n}\right\} \) determine \(\gamma _{j}\in I_{p}\cap A_{j}\) and define \(\eta _{j}=T-\gamma _{j}\). Since \(p_{k_{n}}\ge 3\), because (2.16) we can assure that \(\left| \eta _{j}\right| \le \eta \), and according to each \(\gamma _{j}=\dfrac{2\pi q}{\log p_{j}}\), with \(q\) integer, by substituting the values of \(\eta _{j}\) into (2.14), we get
and, consequently, (2.12) is true for \(t=T\). Then, according to \(\mathrm{Re }\, \zeta _{n}(\sigma )>1\) for all \(\sigma \in \mathbb {R} \), one has
for all \(\sigma \in \left[ a_{n}^{\prime \prime },b_{n}^{\prime \prime } \right] \).
About the imaginary part of \(\zeta _{n}(s)\), by setting \(s=\sigma +iT\) with \( \sigma \in \left[ a_{n}^{\prime \prime },b_{n}^{\prime \prime }\right] \) in (2.15), because of (2.16), we have
From (2.17) and (2.18), it deduces that the variation of the argument of \( \zeta _{n}(s)\) on the side of the rectangle \(R_{n,T}^{\prime }\) defined by the line \(y=T\), \(VA(\zeta _{n}(s);y=T)\), satisfies
Now, recalling that we have chosen \(\epsilon \) so that \(0<\epsilon <\dfrac{1 }{6}\) and taking into account that \(\arctan x\le x\), for all \(x\in \mathbb {R} \), the above inequality implies that
and then (2.10) is true, as claimed. Now, according to (2.7), (2.8), (2.9) and (2.10), it follows (2.6) for any point \(T\) of every \(I_{p}\) with \(p\ge 0\) and, in consequence, the formula (1.3) is true. \(\square \)
References
Ash, R.B.: Complex Variables. Academic Press, New York (1971)
Balazard, M., Velásquez-Castañón, O.: Sur l’infimum des parties réelles des zéros des sommes partielles de la fonction zêta de Riemann. C. R. Acad. Sci. Paris Ser. I 347, 343–346 (2009)
Dickson, D.G.: Asymptotic distribution of zeros of exponential sums. Publ. Math. Debrecen 11, 297–300 (1964)
Dickson, D.G.: Zeros of exponential sums. Proc. Am. Math. Soc. 16(1), 84–89 (1965)
Gonek, S.M., Ledoan, A.H.: Zeros of partial sums of the Riemann Zeta-function. Int. Math. Res. Not. 10, 1775–1791 (2010)
Langer, R.E.: On the zeros of exponential sums and integrals. Bull. Am. Math. Soc. 37, 213–239 (1931)
Levin, B.J.: Distribution of Zeros of Entire Functions. American Mathematical Society, Providence (1980)
Montgomery, H.L.: Zeros of Approximations to the Zeta Function, Studies in Pure Mathematics: To the Memory of Paul Turán, pp. 497–506. Birkhäuser, Basel (1983)
Mora, G., Sepulcre, J.M.: On the distribution of zeros of a sequence of entire functions approaching the Riemann zeta function. J. Math. Anal. Appl. 350, 409–415 (2009)
Pólya, G.: Problem. Jber. Deutch. Math. Verein, 3, 97 (1925); 24
Tamarkin, J.D.: The zeros of certain integral functions. J. Lond. Math. Soc. 2, 66–69 (1927)
Tamarkin, J.D.: Some general problems of the theory of ordinary linear differential equations and expansions of an arbitrary function in series of fundamental functions. Math. Z. 27, 1–54 (1928)
Turán, P.: On some approximative Dirichlet-polynomials in the theory of the zeta-function of Riemann, Danske Vid. Selsk. Mat.-Fys. Medd. 24(17), 3–36 (1948)
Wilder, C.E.: Expansion problems of ordinary linear differential equations with auxiliary conditions at more than two points. Trans. Am. Math. Soc. 18, 415–442 (1917)
Acknowledgments
The authors wish to thank the referees for their helpful comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Mora, G., Sepulcre, J.M. Computing the zeros of the partial sums of the Riemann zeta function. Annali di Matematica 194, 1499–1504 (2015). https://doi.org/10.1007/s10231-014-0430-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10231-014-0430-6