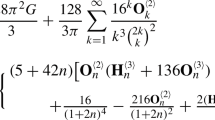Counting Real Roots in Polynomial-Time via Diophantine Approximation

Abstract

Suppose $A\!=\!\{a_1,\ldots ,a_{n+2}\}\!\subset \!\mathbb {Z}^n$ has cardinality $n+2$, with all the coordinates of the $a_j$ having absolute value at most d, and the $a_j$ do not all lie in the same affine hyperplane. Suppose $F\!=\!(f_1,\ldots ,f_n)$ is an $n\times n$ polynomial system with generic integer coefficients at most H in absolute value, and A the union of the sets of exponent vectors of the $f_i$. We give the first algorithm that, for any fixed n, counts exactly the number of real roots of F in time polynomial in $\log (\textrm{d}H)$. We also discuss a number-theoretic hypothesis that would imply a further speed-up to time polynomial in n as well.

1 Introduction

Solving sparse polynomial systems remains a challenging problem, even 40 years after the dawn of fewnomial theory [61, 62]. More recently, connections have emerged between fewnomial theory over finite fields, cryptography, and number theory [26, 32, 37], and sparse polynomial systems over the real numbers continue to form the foundation of applications including computational biology and biochemistry [18, 19, 42, 43] and circuit complexity [64]. However, efficiently counting the number of real roots and even just finding a reasonably tight upper bound on the number of real roots are still open problems. Here, we focus on the problem of exactly counting real roots and roots in any given orthant. In what follows, all O-constants and o-constants are absolute (and can be made explicit), time will refer to the number of (deterministic) bit operations in the classical Turing model of computation, and we will use $\#S$ for the cardinality of a set S.

Assuming $A\!=\!\{a_1,\ldots ,a_t\}\!\subset \!\mathbb {Z}^n$, $x^{a_j}\!:=\!x^{a_{1,j}}_1 \cdots x^{a_{n,j}}_n$, and $f(x)\!=\!\sum ^t_{j=1}c_j x^{a_j}\!\in \!\mathbb {Z}\!\left[ x^{\pm 1}_1,\ldots , x^{\pm 1}_n\right]$, we define the support of f to be $\textrm{Supp}(f)\!:=\!\{a_j \; | \; c_j\!\ne \!0\}$. We then call a system of the form $F\!:=\!(f_1,\ldots ,f_n) \!\in \!\mathbb {Z}\!\left[ x^{\pm 1}_1,\ldots ,x^{\pm 1}_n\right] ^n$, with $f_i(x)\!:=\!\sum ^t_{j=1} c_{i,j}x^{a_j}$ for all i and $\#\bigcup ^n_{i=1} \textrm{Supp}(f_i)\!=\!t$, a t-nomial $n\times n$ system (over $\mathbb {Z}$) supported on A. We denote the positive orthant by $\mathbb {R}^n_+$, $\mathbb {R}^*\!:=\!\mathbb {R}\setminus \{0\}$ and call a root of F in $\mathbb {R}^n_+$ a positive root.

If the $a_j$ do not all lie in the same affine hyperplane, then we clearly have $t\!\ge \!n+1$. It is natural to assume that the exponent vectors are non-coplanar in this sense, and we will do so, for otherwise one could use a monomial change of variables to reduce F to a system in fewer variables: See Remark 2.6 from Sect. 2. Our main theorem gives a dramatic new speed-up for counting the exact number of real roots of F in the special case $t\!=\!n+2$.

Theorem 1.1

Following the notation above, assume further that $t\!\le \!n+2$, $A\!\subset \!\{-d,\ldots ,d\}^n$, and the coefficient matrix $[c_{i,j}]$ lies in $\{-H,\ldots ,H\}^{n\times (n+2)}$ and is generic. Then, in time $(n^2\log (\textrm{d}H))^{(2+o(1))n}$, we can determine the number of roots of F in $\mathbb {R}^n$, ${(\mathbb {R}^*)}^n$, and $\mathbb {R}^n_+$. Furthermore, if $t\!=\!n+1$, then we can do the same in time $n^{3.373}\log ^{1+o(1)}(\textrm{d}H)$.

We prove Theorem 1.1 in Sect. 5.1, based mainly on Algorithms 4.1 and 4.3 from Sect. 4. A key new ingredient is diophantine approximation over number fields.

Remark 1.2

We count roots without multiplicity. In particular, degenerate¹ isolated roots are not a problem and are counted correctly by our algorithms. $\diamond$

A sufficient genericity condition for our faster counts in ${(\mathbb {R}^*)}^n$ and $\mathbb {R}^n_+$ is the non-singularity of the $n\times n$ sub-matrices of $[c_{i,j}]$. This condition is checkable in time $O\!\left( n^{4.373}\log ^{1+o(1)}(nH)\right)$: See Lemma 2.15 and Corollary 2.18 of Sect. 2.3. In particular, the fraction of coefficient matrices failing to satisfy this genericity condition is no greater than $\frac{n(n+2)(n+1)}{4H+2}$. A sufficient genericity condition for faster counting in $\mathbb {R}^n$ is detailed in Sect. 5 and also holds practically often: Probability $1-\varepsilon$ when H has $\Omega \!\left( n\log (nd)+ \log \frac{1}{\varepsilon }\right)$ bits (see Remark 5.8 of Sect. 5.1).

Root counting without genericity assumptions is rather non-trivial: Deciding finiteness for the number of real (or positive) roots in time $(n\log (\textrm{d}H))^{O(n)}$ (i.e., roughly as fast as our main algorithms), when $t\!=\!n+2$ and $f_2\!=\cdots \!=\!f_n$ identically, is still an open problem [15, 22]. Furthermore, for any fixed $\varepsilon \!>\!0$, deciding whether the non-generic system $F\!=\!(f_1,\ldots ,f_1)$ has any real (or positive) roots is ${\textbf{NP}}$-hard already for $t\!=\!n+n^\varepsilon$ [22]: With our underlying measure of size being $nt(\log (H)+n\log (d))$ (which has asymptotically the same order as the number of bits needed to write down all the monomial terms of F), the existence of an algorithm with complexity $(n\log (\textrm{d}H))^{O(1)}$, for just one $\varepsilon \!>\!0$, would imply $\textbf{P}\!=\!{\textbf{NP}}$.

Other than an algorithm for the very special case $(n,t)\!=\!(1,3)$ from [22], the best previous deterministic complexity bound for $t\!=\!n+2$ appears to have been $(n^{n\log n}d^n)^{O(\log ^2 n)}$ arithmetic operations [9], via an algorithm solving the harder problem of computing roadmaps (see, e.g., [8, Ch. 15]) for arbitrary real algebraic sets. One can also speed up to a $(d\log H)^{O(n)}$ arithmetic complexity bound via [85] if one assumes the complex zero set is finite. (All of these works build upon the seminal works [12, 33, 38, 89]. See also [95] for more recent speed-ups via randomization.) There have also been important recent advances from the point of view of numerical conditioning (e.g., [40, 41]), even enabling practical computation of homology of real projective sets, but work in this direction has not yet focused on speed-ups like Theorem 1.1: With few exceptions, earlier work on solving polynomial systems over the real numbers focused on coarser complexity bounds that ignored the finer monomial term structure.

Example 1.3

Consider the 7-nomial $5\times 5$ system $F\!=\!(f_1,\ldots ,f_5)$ defined by

Then, Algorithm 4.3 from Sect. 4 (simulated in a few lines of Maple code²) tells us in under a second that F has exactly 2, 6, 6, 2, 2, or 0 positive roots, respectively, when c is $\frac{1}{20731}$, $\frac{1}{20730}$, $\frac{1}{14392}$, $\frac{1}{14391}$, $\frac{1}{13059}$, or $\frac{1}{13058}$. (All roots in $(\mathbb {R}^*)^5$ of these F happen to lie in $\mathbb {R}^5_+$.) One can also easily check that each these F has infinitely many roots in $\mathbb {R}^5$, since they each vanish identically on the 3-plane $\{x_1\!=\!x_4\!=\!0\}$. We will return to this family in Sect. 2.3, and see another example there as well. It is interesting to observe that Maple’s Solve command (which employs Gröbner bases) gives no useful information about any of these systems, even after 3 hours.$^2$ Bertini (a state-of-the-art homotopy solver, Version 1.4 [11]), on each of the preceding systems, immediately returns a message stating

“ERROR: The system is numerically zero 0! Please input a non- degenerate system. Bertini will now exit due to this error.”

This is partially because each such F has³ over 245 million roots in $(\mathbb {C}^*)^5$, and older polynomial system solving techniques have complexity super-linear, or worse, in the number of complex roots. $\diamond$

The main intent of Theorem 1.1 is to set the stage (building on the framework of [48, 49, 83]) for more practical improvements in real-solving such as complexity sub-exponential in n, in the average-case/smoothed analysis setting, for sparse systems. In particular, just as binomial systems are a building block for polyhedral homotopy algorithms for arbitrary $n\times n$ systems [58, 69, 102], $(n+2)$-nomial $n\times n$ systems are a building block behind recent optimization techniques such as SONC/SAGE-optimization (see, e.g., [35, 44, 84]). While tackling the remaining exceptional cases (e.g., infinitely many real roots in ${(\mathbb {R}^*)}^n$) is important, such cases are provably rare for random coefficients.

1.1 Connection to Fewnomial Bounds Over $\mathbb {R}$

There has been growing interest in generalizing Descartes’ Rule of Signs (see, e.g., [53, 100]) from univariate polynomials to $n\times n$ polynomial systems. This began with Khovanski’s seminal Theorem on Real Fewnomials [62] which, in our notation, asserted an upper bound of $2^{\left( {\begin{array}{c}t\\ 2\end{array}}\right) }(n+1)^t$ for the number of non-degenerate positive roots of any t-nomial $n\times n$ system. It was then shown in [71] that Khovanski’s bounds could be greatly improved for various structured systems, e.g., the correct tight upper bound on the number of isolated⁴ positive roots for $2\times 2$ systems of trinomials is 5 — far less than the best previous bound of 248832. Sharper upper bounds for new families of systems, including a tight upper bound of $n+1$ (resp. $(n+1)2^n$) non-degenerate roots in $\mathbb {R}^n_+$ (resp. ${(\mathbb {R}^*)}^n$) for the case $t\!=\!n+2$ were then derived in [14]. Explicit families of systems attaining these bounds for each n were then given in [86] (see also [15, 21]). Khovanski’s general upper bound was vastly improved to $\frac{e^2+3}{4}2^{\left( {\begin{array}{c}t-n-1\\ 2\end{array}}\right) }n^{t-n-1}$ positive roots in [23], and a remarkable (sometimes much sharper) bound for curve intersections was derived later in [63]. More recently, an elegant and near-optimal average-case upper bound of $\frac{1}{2^{n-1}}\cdot \frac{t!}{n!(t-n)!}$ for the number of positive roots was proved in [31], using independent real Gaussians for the coefficients.

Fewnomial bounds so far have not made significant use of the signs of the coefficients (much less their values) when $n\!\ge \!2$, and such refined bounds remain elusive: see, e.g., [10, Thm. 2.1] and [16, 17, 20]. The latter works, particularly [17], culminated in a refined characterization of the maximal number of positive roots — incorporating the signs of $n\times n$ sub-determinants of the coefficient matrix $[c_{i,j}]$ and the matroidal structure of $\mathcal {A}$ —in the case $t\!=\!n+2$. Nevertheless, no algorithm for exactly counting the real or positive roots, faster than combining more general results on rational univariate reduction (see, e.g., [66, 90, 94]) with the computation of real dimension (see, e.g., [7]) or real root isolation (see, e.g., [96]), appears to have been known before Theorem 1.1.

Exactly counting the real or positive roots of F, and even formulating a reasonable generalization of Descartes’ Rule, appears to be much harder for $t\!\ge \!n+3$. This is why there is much recent attention on the case $t\!=\!n+2$ to develop further intuition. An even harder open question is the complexity of actually approximating the real roots of such F and we hope to address this in future work. For instance, finding real approximate roots (in the sense of Smale [24]) in deterministic time $(\log (\textrm{d}H))^{O(1)}$, just for the special case $(n,t)\!=\!(1,3)$, is still an open problem [27, 59, 92].

Our main tools are reduction to a canonical form (a special case of Gale Dual Form from [23]) and a careful application of diophantine approximation to the critical values of this reduction. In particular, the locus of F with degenerate roots forms a discriminant variety which partitions the coefficient space into connected open regions we call chambers (see, e.g., [52, Ch. 11]). Classical topological results, such as Hardt’s Triviality Theorem [55], tell us that counting the real roots of F is tantamount to identifying the chamber in which F lies. Such a calculation is challenging, since the theory of $\mathcal {A}$-discriminants [52] does not directly provide a tractable description of our chambers. However, applying Rolle’s Theorem to the resulting Gale Dual Form allows one to replace chamber identification by the determination of signs of the critical values and poles of a single univariate rational function.

A new obstacle is that the usual univariate root-finding algorithms, combined with classical height bounds on polynomial roots, do not yield a useful complexity bound. Indeed, the degree of the resulting univariate reduction can be so high that a naive use of real root isolation would lead to complexity super-linear in $n^{n/2} d^n$. So we leverage the special structure of the derivative of our univariate reduction to apply a powerful theorem from diophantine approximation: A refinement of an estimate of Baker and Wustholtz on linear forms in logarithms of algebraic numbers (see, e.g., [4, 6, 30, 77]).

1.2 Linking Diophantine Approximation and Algorithmic Complexity

A nice warm-up to the Baker–Wustholtz Theorem is the following problem:

Rational Binomial Sign Problem (RBSP). Given positive rational numbers $\alpha _1,\ldots ,\alpha _m$ with numerators and denominators no greater than $\mathscr {A}$, and integers $b_1,\ldots ,b_m$ with absolute value at most B, what is the sign ($+$, −, or 0) of the binomial $\left( \prod ^m_{i=1}\alpha ^{b_i}_i\right) -1$?

While the RBSP is a fundamental real algebraic question, there is a still an exponential gap between its best current lower and upper complexity bounds. [22] applied the theory of $\mathcal {A}$-discriminants [52] to show that determining the isotopy type of the real zero set of a single n-variate $(n+2)$-nomial over $\mathbb {Z}$ is (under mild assumptions) equivalent to the RBSP. A consequence of this connection between the RBSP and real zero sets was then the first polynomial-time algorithm to decide non-emptiness for the real zero sets of (single) n-variate $(n+2)$-nomials with n fixed [22].

Note that the RBSP is clearly equivalent to deciding the sign of the linear combination of logarithms $\Lambda (\alpha ,b)\!:=\!\sum ^m_{i=1}b_i\log \alpha _i$. Indeed, since simply evaluating the binomial can lead to numbers with huge bit-length, it makes sense to solve the RBSP by instead approximating the linear combination of logarithms $\Lambda (\alpha ,b)$ to sufficient accuracy. However, this is feasible only if we know a sufficiently good (and explicit!) lower bound on the minimum of $|\Lambda (\alpha ,b)|$ over all such $\alpha _i$ and $b_i$. Alan Baker won a Fields medal in 1970, due in large part to finding such a bound—over arbitrary number fields—and deriving numerous landmark results in number theory as a consequence [4]: The most recent refinements of his bound [77, 80], in the special case of $\mathbb {Q}$, can be coarsely summarized as follows.

$$\begin{aligned} \Lambda (\alpha ,b)\!\ne \!0 \Longrightarrow \log |\Lambda (\alpha ,b)|\!>\!-[O(\log \mathscr {A})]^m\log B \ \ \ \mathrm{(Coarse ~Baker's ~Bound)} \end{aligned}$$

(1)

Combined with classical results on quickly approximating logarithms [13, 28, 29, 97], Bound (1) readily implies that the RBSP can be solved in time $[O(\log \mathscr {A})]^m\log B$ [22], and thus polynomial-time if m is fixed.

Remark 1.4

It is perhaps surprising that efficiently distinguishing between $\Lambda (\alpha ,b)\!=\!0$ and $\Lambda (\alpha ,b)\!\ne \!0$ (neglecting positivity or negativity) has already been known for decades: This simplification of the RBSP can be solved in time $(m\log (\mathscr {A}B))^{O(1)}$ via gcd-free bases (see, e.g., [23, Ch. 4] and [22]). $\diamond$

Sadly, little is known about the true asymptotics of $\log |\Lambda (\alpha ,b)|$. However, around 1978, Lang and Waldschmidt conjectured that a much sharper bound of the shape

$$\begin{aligned}{} & {} \Lambda (\alpha ,b)\!\ne \!0 \Longrightarrow \log |\Lambda (\alpha ,b)|\!>\!-O(m\log (\mathscr {A}B)) \nonumber \\{} & {} \quad \mathrm{(Lang-Waldschmidt ~Conjecture)} \end{aligned}$$

(2)

should hold [68, Pg. 213] and this conjecture remains open. Later, Baker proved [5] that a bound of the form

$$\begin{aligned}{} & {} \Lambda (\alpha ,b)\!\ne \!0 \Longrightarrow \log |\Lambda (\alpha ,b)|\!>\!-O(m\log (\mathscr {A})\log B) \nonumber \\{} & {} \quad \mathrm{(Consequence~ of ~Refined ~abc)} \end{aligned}$$

(3)

follows from a refined version [5] of the famous Masser-Oesterle abc-Conjecture [76, 81, 82]. Unfortunately, the latter refinement also appears out of reach.

Such conjectures are important not just in diophantine geometry but also in real algebraic geometry:

Theorem 1.5

[50]⁵ The truth of either of the Lang–Waldschmidt Conjecture or Baker’s refined abc-Conjecture implies that we can decide non-emptiness for the positive zero set of any $f\!\in \!\mathbb {Z}\!\left[ x^{\pm 1}_1,\ldots ,x^{\pm 1}_n\right]$—with coefficients in $\{-H,\ldots ,H\}$, and support of cardinality $n+2$ lying in $\{-d,\ldots ,d\}^n$ not contained in any affine hyperplane—in time $(n\log (\textrm{d}H))^{O(1)}$. $\square$

Our framework here implies an even deeper conditional speed-up: Sufficiently sharp lower bounds for linear forms in logarithms of real algebraic numbers imply that root counting in $\mathbb {R}^n$, for the $(n+2)$-nomial $n\times n$ systems from Theorem 1.1, can be sped up to time polynomial in n as well. We formalize this through a conjecture, and a theorem, below:

Real Algebraic Log Conjecture (RALC)

Suppose K is a real, degree d algebraic extension of $\mathbb {Q}$, $\alpha _1,\ldots ,\alpha _m\!\in \!K$, $b_1,\ldots ,b_m\!\in \!\mathbb {Z}\setminus \{0\}$, $\log \mathscr {A}$ is the maximum of the logarithmic heights⁶ of the $\alpha _i$, and $B\!:=\!\max _i|b_i|$. Then, there are constants $x_0,C\!>\!0$ such that $\Lambda (\alpha ,b)\!\ne \!0$ $\Longrightarrow \log |\Lambda (\alpha ,b)|\!>\!-(dm\log (\mathscr {A}B))^{C}$ for all $d,m,\mathscr {A},B\!\ge \!x_0$.

Note that the latest refinement of the Baker–Wustholtz Theorem by Matveev [77, Cor. 2.3] (stated as Theorem 2.25 in Sect. 2.4) can be coarsely summarized as

$$\begin{aligned} \Lambda (\alpha ,b)\!\ne \!0 \Longrightarrow \log |\Lambda (\alpha ,b)|\!>\!-d^2\log (d)[O(\log \mathscr {A})]^m\log B. \end{aligned}$$

Note also that the special case $d\!=\!1$ of the RALC (with $C\!\le \!2$) is implied by the truth of either of the Lang–Waldschmidt Conjecture or Baker’s Refined abc-Conjecture.

The special case $d\!=\!1$ case of the RALC (with any $C\!>\!0$) is an even weaker hypothesis that still implies the speed-up for fewnomial hypersurfaces from Theorem 1.5 above. If we have the RALC true in full, then we also obtain the following speed-up for fewnomial systems:

Theorem 1.6

If the RALC is true then the complexity bound from Theorem 1.1, for counting roots in $\mathbb {R}^n$, ${(\mathbb {R}^*)}^n$, and $\mathbb {R}^n_+$, in the hardest case $t\!=\!n+2$, can be replaced by $(n\log (\textrm{d}H))^{O(1)}$.

We prove Theorem 1.6 in Sect. 6. It is tantalizing to speculate that some kind of converse may hold, i.e., sufficiently fast real root counting for sparse polynomial systems may imply a strengthenings of Baker’s Theorem on linear forms in logarithms. Such an implication is still not clear, and it seems natural that information like the underlying real root-spacing is also needed. It would indeed be worthwhile to prove new root-spacing bounds for $(n+2)$-nomial $n\times n$ systems, in order to apply them to improving Baker’s Theorem. However, the current state of the art goes in the opposite direction: [65, 93] prove new root-spacing bounds in the case $n\!=\!1$ over $\mathbb {C}$ (and even $\mathbb {C}_p$), but heavily use Baker’s Theorem (and its p-adic cousin, Yu’s Theorem [103]).

What is clearer (and true) is the contrapositive of Theorem 1.6: If counting real roots for generic $(n+2)$-nomial $n\times n$ systems (as in Theorem 1.1) is not doable in time $(n\log (\textrm{d}H))^{O(1)}$, then the RALC is false. Similarly, if deciding non-emptiness for real zero sets of n-variate $(n+2)$-nomials (as in Theorem 1.5) is sufficiently hard, then we can falsify both the Lang–Waldschmidt Conjecture and Baker’s Refined abc-Conjecture. These are curious examples of how proving complexity lower bounds in real algebraic geometry is as hard as falsifying conjectures from diophantine approximation.

The hardness of proving new diophantine approximation bounds is one reason that new average-case speed-ups, using geometric numerical conditioning techniques (e.g., [48, 49]) instead of diophantine approximation, may arrive sooner than new worst-case speed-ups.

2 Background

2.1 The Complexity of Linear Algebra Over $\mathbb {Z}$

Let $\omega$ denote the well-known matrix multiplication exponent, i.e., the infimum over all $\omega$ such that there exists an algorithm that can multiply an arbitrary pair of $n\times n$ matrices, in any field K, using $O(n^\omega )$ field operations in K. The best current upper bound is $\omega \!<\!2.3728596$ [2, 70]. Recall the notions of reduced row echelon form and leading entries of a matrix, from basic linear algebra (see, e.g., [87]). For any nonzero rational number $\frac{p}{q}$ with $p,q\!\in \!\mathbb {Z}$ and $\gcd (p,q)\!=\!1$, its (absolute) logarithmic height is $h(p/q)\!:=\!\max \{\log |p|,\log |q|\}$. (We set $h(0)\!:=\!0$.) We will first need a result on the bit complexity of row reduction for matrices:

Lemma 2.1

[101, Pg. 17 & Cor. 2.12]⁷ Suppose $M\!\in \!\mathbb {Z}^{n\times t}$ has rank r and all the entries of M have absolute value at most H. Then, in deterministic time

$$\begin{aligned} O\!\left( ntr[r^{\omega -2}\log \log (r\log (rH))+\log (r)\log ^2(r\log (rH))] \log (rH)\right) \end{aligned}$$

we can find the reduced row echelon form $R\!\in \!\mathbb {Q}^{n\times t}$ of M. Furthermore, every nonzero entry of R has logarithmic height $O(r\log (rH))$. $\square$

An illuminating alternative discussion of the bit complexity of linear algebra can be found in [24, Ch. 15, Sec. 15.5].

Via Cramer’s Rule and Hadamard’s classical inequality on the absolute values of determinants [78, Thm. 1], we can easily obtain the following related bound:

Lemma 2.2

If $\mathcal {A}\!\in \!\mathbb {Z}^{n\times (n+1)}$ has rank n and all the entries of the ith row of $\mathcal {A}$ have absolute value at most $d_i$, then any generator $(b_1,\ldots ,b_{n+1})^\top \!\in \!\mathbb {Z}^{(n+1)\times 1}$ of the right-null space of $\mathcal {A}$, with $\gcd (b_1,\ldots ,b_{n+1})\!=\!1$, satisfies $|b_j|\!\le \!n^{n/2}\prod \limits ^n_{i=1} d_i$ for all j. $\square$

Definition 2.3

[57, 98] We call a matrix $U\!\in \!\mathbb {Z}^{n\times n}$ with determinant $\pm 1$ unimodular. Given any matrix $M\!\in \!\mathbb {Z}^{n\times t}$, we then call any identity of the form $UM\!=\!R$, with $U\!\in \!\mathbb {Z}^{n\times n}$ unimodular and R upper-triangular with all leading entries positive, a Hermite factorization. Finally, we call any identity of the form $UMV\!=\!S$, with $U\!\in \!\mathbb {Z}^{n\times n}$ and $V\!\in \!\mathbb {Z}^{t\times t}$ both unimodular, and S with diagonal entries $s_1,\ldots ,s_n$ satisfying $s_1|s_2, \ldots , s_{n-1}|s_n$, a Smith factorization of M. $\diamond$

We will also need the following complexity bound on Smith factorization:

Theorem 2.4

[101, Ch. 8, Prop. 8.10] Suppose $M\!\in \!\mathbb {Z}^{n\times t}$ has rank r and all its entries having absolute value at most d. Then, a Smith factorization $UMV\!=\!S$ for M can be found in deterministic time

$$\begin{aligned} O\!\left( ntr[r^{\omega -2}\log \log (r\log (rd))+\log ^2(r\log (rd))] \log (nt)\log (rd)\right) \end{aligned}$$

with all the entries of U, V, S having logarithmic height $O(r\log (rd))$. $\square$

The bound above also assumes that we use an $O(h\log h)$-time algorithm for h-bit integer multiplication, e.g., [56].

2.2 Binomial and $(n+1)$-Nomial Systems Over ${(\mathbb {R}^*)}^n$

A simple, folkloric algebraic/analytic fact we will need is the following:

Proposition 2.5

Suppose $\mathcal {A},\mathcal {B}\!\in \!\mathbb {Z}^{n\times n}$ and $x\!=\!(x_1,\ldots ,x_n)$ is a vector of indeterminates. Let us define $x^{\mathcal {A}}$ to be the vector of monomials $\left( x^{a_{1,1}}_1\cdots x^{a_{n,1}}_n, \ldots ,x^{a_{1,n}}_1\cdots x^{a_{n,n}}_n\right)$, where $\mathcal {A}\!=\![a_{i,j}]$. Then, $(x^{\mathcal {A}})^{\mathcal {B}}\!=\!x^{\mathcal {A}\mathcal {B}}$ and, if $\mathcal {A}$ is unimodular, the function defined by $x\mapsto x^{\mathcal {A}}$ defines an analytic group automorphism of ${(\mathbb {C}^*)}^n$ that restricts to an analytic group automorphism of $\mathbb {R}^n_+$. $\square$

Remark 2.6

A simple consequence of Proposition 2.5 is that if $f\!\in \!\mathbb {R}\!\left[ x^{\pm 1}_1,\ldots ,x^{\pm 1}_n\right]$ is an n-variate t-nomial with support A, and d is the dimension of the smallest affine subspace containing A, then there is a monomial change of variables $x\!=\!y^U$ (with U unimodular), and a monomial $y^b\!\in \!\mathbb {R}\!\left[ y^{\pm 1}_1,\ldots ,y^{\pm 1}_d\right]$, such that $g(y)\!:=\!y^b f\!\left( y^U\right) \!\in \!\mathbb {R}\!\left[ y^{\pm 1}_1, \ldots ,y^{\pm 1}_d\right]$ is a d-variate t-nomial, and the zero set of f in ${(\mathbb {R}^*)}^n$ is analytically isomorphic to the Cartesian product of $(\mathbb {R}^*)^{n-d}$ and the zero set of g in $(\mathbb {R}^*)^d$. So A in an affine hyperplane implies that the zero set of f in ${(\mathbb {R}^*)}^n$ can be easily characterized by the zero set of another t-nomial in fewer variables. $\diamond$

Another consequence of Lemma 2.1 is that we can almost trivially count the positive roots of binomial systems, provided the exponent vectors are in general position.

Proposition 2.7

Suppose $c\!=\!(c_1,\ldots ,c_n)\!\in \!{(\mathbb {R}^*)}^n$, $a_1,\ldots ,a_n\!\in \!\mathbb {Z}^n$, $\mathcal {A}$ is the $n\times n$ matrix with jth column $a_j$ for all j, $U\mathcal {A}V\!=\!S$ is a Smith factorization of $\mathcal {A}$, and $c'\!:=\!\left( c'_1,\ldots ,c'_n\right) \!:=\!c^V$. Let $s_j$ be the (j, j) entry of S. Then, $G\!:=\!(x^{a_1}-c_1,\ldots ,x^{a_n}-c_n)$ and $\left( y^{s_1}_1-c'_1,\ldots ,y^{s_n}_n-c'_n\right)$ have the same number of roots in $\mathbb {R}^n_+$ (resp. ${(\mathbb {R}^*)}^n$, ${(\mathbb {C}^*)}^n$). In particular, G has exactly 0, 1, or infinitely many roots in $\mathbb {R}^n_+$ under the following respective conditions: : Some $c_i$ is negative or [$\textrm{Rank}(\mathcal {A})\!=\!j\!<\!n$ and $c'_i\!\ne \!1$ for some $i\!\in \!\{j+1,\ldots ,n\}$].

: $c\!\in \!\mathbb {R}^n_+$ and $\det \mathcal {A}\!\ne \!0$.

: $c\!\in \!\mathbb {R}^n_+$, $\textrm{Rank}(\mathcal {A})\!=\!j\!<\!n$, and $c'_{j+1}\!=\cdots =\!c'_n\!=\!1$. $\square$

Proposition 2.7 follows directly from Proposition 2.5. Both facts are folkloric in the toric geometry/Lie group literature (see, e.g., [58] and [25, Ch. 3]). A more in-depth discussion of binomial systems can be found in [34, 36, 83].

Counting roots in ${(\mathbb {R}^*)}^n$ is slightly more complicated but still admits efficient formulae.

Proposition 2.8

Following the notation of Proposition 2.7, assume the exponent vectors $a_1,\ldots ,a_n$ are linearly independent. Let r denote the rank, over the field $\mathbb {F}_2$, of the mod 2 reduction of $\mathcal {A}$. Then, the map $m : {(\mathbb {R}^*)}^n\longrightarrow {(\mathbb {R}^*)}^n$ defined by $m(x)\!:=\!x^{\mathcal {A}}$ is $2^{n-r}$-to-1, and the ith coordinate of the range of $m^V$ is $\mathbb {R}^*$ (resp. $\mathbb {R}_+$) if and only if $i\!\le \!r$ (resp. $i\!\ge \!r+1$). In particular, F has exactly 0 (resp. $2^{n-r}$) roots in ${(\mathbb {R}^*)}^n$ if and only if $c'_i\!<\!0$ for some (resp. no) $i\!\ge \!r+1$.

Proof

First note that by the definition of Smith factorization, we have that the diagonal entries $s_i$ of S are such that $s_1,\ldots ,s_r$ are odd and $s_{r+1},\ldots ,s_n$ are even. By Proposition 2.5, exponentiating by U or V induces a permutation of the open orthants of $\mathbb {R}^n$. In particular, we see that the range of $x\mapsto x^S$ is exactly $(\mathbb {R}^*)^r\times \mathbb {R}^{n-r}_+$. So the pre-image assertion on m is proved.

Now, note that the range of m must be $\left( (\mathbb {R}^*)^r\times \mathbb {R}^{n-r}_+\right) ^{V^{-1}}$ thanks to Proposition 2.5. So now we know the range of m.

The final remaining assertion follows from our earlier definition $c'\!:=\!c^V$ and our earlier assumption that $c\!\in \!{(\mathbb {R}^*)}^n$. $\square$

We can now state more explicitly how we deal with positive root counting for t-nomial systems in the case $t\!=\!n+1$.

Lemma 2.9

If $F\!=\!(f_1,\ldots ,f_n)\!\in \!\mathbb {Z}\!\left[ x^{\pm 1}_1,\ldots ,x^{\pm 1}_n \right] ^n$ is an $(n+1)$-nomial $n\times n$ system, with union of supports $A\!=\!\{a_1,\ldots ,a_{n+1}\}$ not lying in an affine hyperplane, and the coefficient matrix of F has rank n, then the number of positive roots of F is either 0 or 1. Furthermore, if all the coefficients of all the $f_i$ have absolute value at most H, then we can determine the number of positive roots of F in time $n^{3.373}\log ^{1+o(1)}(nH)$.

Remark 2.10

The reader disturbed by the complexity bound being independent of A may be reassured to know that (a) checking the hyperplane condition takes time dependent on A and (b) the analogue of our lemma for counting roots in ${(\mathbb {R}^*)}^n$ (Corollary 2.11) has complexity depending on A. $\diamond$

Proof of Lemma 2.9:

By our assumption on the coefficient matrix, we may reorder monomials so that the left-most $n\times n$ minor of the coefficient matrix has nonzero determinant. So we may divide every $f_i$ by $x^{a_{n+1}}$ without changing the roots of F in ${(\mathbb {C}^*)}^n$, and assume $a_1,\ldots ,a_n$ are linearly independent and $a_{n+1}\!=\!\textbf{O}$.

From Lemma 2.1 (and the fact that $\omega \!<\!2.373$ [2]), it is then clear that we can reduce the coefficient matrix of F, $[c_{i,j}]\!\in \!\mathbb {Z}^{n\times (n+1)}$, to a reduced row echelon form in $\mathbb {Q}^{n\times (n+1)}$, in time $n^{3.373}\log ^{1+o(1)}(nH)$. The underlying linear combinations of rows can then be applied to the equations $f_i\!=\!0$ so that $F\!=\!\textbf{O}$ can be reduced to a binomial system of the form $x^{\mathcal {A}}\!=\!\gamma$ where $\gamma \!=\!(\gamma _1,\ldots ,\gamma _n)$, $\mathcal {A}\!\in \!\mathbb {Z}^{n\times n}$, and the solutions of $x^{\mathcal {A}}\!=\!\gamma$ in ${(\mathbb {C}^*)}^n$ are the same as the roots of F in ${(\mathbb {C}^*)}^n$.

Clearly then, $\gamma _i\!\le \!0$ for any i implies that F has no positive roots. In which case, we simply report that F has 0 positive roots and conclude, having taken time $n^{3.373}\log ^{1+o(1)}(nH)$.

Otherwise, $\gamma \!\in \!\mathbb {R}^n_+$ implies that F has exactly 1 positive root by Proposition 2.7, and we are done. $\square$

A simple consequence of our development so far is a method to efficiently count roots in $(\mathbb {R}^*)^n$ for generic $(n+1)$-nomial systems.

Corollary 2.11

Following the notation and assumptions of Lemma 2.9 and its proof, the number of roots of F in ${(\mathbb {R}^*)}^n$ is either 0 or $2^{n-r}$, where r is the rank, over the field $\mathbb {F}_2$, of the mod 2 reduction of $\mathcal {A}$. In particular, we can determine the number of roots of F in ${(\mathbb {R}^*)}^n$ in time $n^{3.373}\log ^{1+o(1)}(n\textrm{d}H)$, where d is the maximum absolute value of any entry of A.

Proof

Continuing from the proof of Lemma 2.9 (and having already reduced our input $(n+1)$-nomial $n\times n$ system to a binomial system), it is clear that Proposition 2.8 tells us that we can easily count the roots of F in ${(\mathbb {R}^*)}^n$: We merely need to check the signs of $\gamma '_{r+1},\ldots ,\gamma '_n$ where $\gamma '\!:=\!\gamma ^V$ and $U\mathcal {A}V\!=\!S$ is a Smith factorization of $\mathcal {A}$. More precisely, instead of computing $\gamma ^V$, we compute $\textrm{sign}(\gamma )^{(V \text { mod } 2)}$. Computing the mod 2 reduction of V takes time $O(n^2)$ and then computing the resulting vector of signs clearly takes time just $O(n^2)$. So the only remaining work (after applying Lemma 2.1 to the coefficient matrix of F) is extracting the Smith factorization of $\mathcal {A}$ via, say, Theorem 2.4. So our final complexity bound is $n^{3.373}\log ^{1+o(1)}(nH) +n^{3.373}\log ^{1+o(1)}(nd)$, which is no greater than our stated bound. $\square$

2.3 Circuits, $(n+2)$-Nomial Systems, and Gale Dual Form with Heights

We now show how to reduce root counting in ${(\mathbb {R}^*)}^n$ for F to root counting in certain sub-intervals of $\mathbb {R}$ for a linear combination of logarithms in one variable. This reduction dates back to [23], if not earlier, but our statement here includes height and computational complexity bounds that appear to be new. Before proving our reduction, however, let us recall the combinatorial/geometric notion of a circuit⁸:

Definition 2.12

Given any subset $A\!=\!\{a_1,\ldots ,a_{m+2}\}\!\subset \!\mathbb {Q}^n$ with $\#A\!=\!m+2$, we define $\widehat{\mathcal {A}}\!\in \!\mathbb {Z}^{(n+1)\times (m+2)}$ to be the unique matrix with jth column $\begin{bmatrix}1\\ a_j\end{bmatrix}$ for all j. We then call A a circuit if and only if $\widehat{\mathcal {A}}$ has right nullspace of dimension one. In which case, we call any generator $b\!\in \!\mathbb {Z}^{(m+2)\times 1}\setminus \{\textbf{O}\}$ for the right nullspace of $\widehat{\mathcal {A}}$, with 1 for its gcd of coordinates, a (minimal) circuit relation of A. We also call A a degenerate circuit if and only if b has at least one zero coordinate. $\diamond$

Note that $m\!\le \!n$ if A as above is a circuit, since $m\!\ge \!n+1$ would imply $\widehat{\mathcal {A}}$ has a right nullspace of dimension at least 2. Note also that all circuit relations for a fixed circuit (other than the trivial relation $\textbf{O}$) have zero entries occuring at the same set of coordinates. More precisely, the following proposition is elementary.

Proposition 2.13

Any circuit $A\!=\!\{a_1,\ldots ,a_{m+2}\}\!\subset \!\mathbb {Z}^n$ has a unique subset $\Sigma \!=\!\{a_{i_1},\ldots ,a_{i_{\ell +2}}\}$ with $\Sigma$ a non-degenerate circuit of cardinality $\ell +2$. In particular, $\{i_1,\ldots ,i_{\ell +2}\}$ is exactly the set of indices of the nonzero coordinates of any (non-trivial) circuit relation for A. Furthermore, if $J\!\subseteq \!\{i_1,\ldots ,i_{\ell +2}\}$ and $\sum _{j\in J} a_j\!=\!\textbf{O}$, then $J\!=\!\{i_1,\ldots ,i_{\ell +2}\}$. $\square$

We call $\Sigma$ the unique non-degenerate sub-circuit of A. Note that any $A\!=\!\{a_1,\ldots ,a_{n+2}\}\!\subset \!\mathbb {Z}^n$ with cardinality $n+2$, and A not lying in any affine hyperplane, is a circuit.

Example 2.14

It is easily checked that $A\!=$ $\left\{ \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}, \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix}, \begin{bmatrix} 2 \\ 0 \\ 0 \\ 0 \end{bmatrix}, \begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \end{bmatrix}, \begin{bmatrix} 0 \\ 0 \\ 1 \\ 0 \end{bmatrix}, \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \end{bmatrix}\right\}$$\subset \!\mathbb {R}^4$ is a degenerate circuit, and that letting $\Sigma$ consist of the first 3 points of A yields the unique non-degenerate sub-circuit of A. In particular, $\Sigma$ has the same minimal circuit relation (up to sign) as the non-degenerate circuit $\{0,1,2\}$ in $\mathbb {R}^1$. $\diamond$

Lemma 2.15

Suppose $F\!=\!(f_1,\ldots ,f_n)\!\in \!\mathbb {Z}\!\left[ x^{\pm 1}_1, \ldots ,x^{\pm 1}_n\right] ^n$ is an $(n+2)$-nomial $n\times n$ system supported on a circuit $A\!=\!\{a_1,\ldots ,a_{n+2}\}\!\subset \!\{-d,\ldots , d\}^n$ for some $d\!\in \!\mathbb {N}$. Suppose also that F has coefficient matrix $[c_{i,j}]\!\in \!\{-H,\ldots ,H\}^{n\times (n+2)}$ with all of its $n\times n$ sub-matrices non-singular. Then in time $n^{3.373}\log ^{1+o(1)}(n\textrm{d}H)$, we can give either a true declaration that F has no positive roots, or find $\gamma _{1,0}, \gamma _{1,1}, \ldots , \gamma _{n+1,0}, \gamma _{n+1,1}\!\in \!\mathbb {Q}$ and $b_1,\ldots ,b_{n+1}\!\in \!\mathbb {Z}$ such that:

• 1. The number of roots of the function $L(u)\!:=\!\sum ^{n+1}_{i=1} b_i\log |\gamma _{i,1}u +\gamma _{i,0}|$ in the open interval $I\!:=\!\left\{ u\!\in \!\mathbb {R}\; | \; \gamma _{i,1}u+\gamma _{i,0}\!>\!0 \text { for all } i\!\in \!\{1,\ldots ,n+1\}\right\}$ is finite and exactly the number of positive roots of F.

• 2. I is non-empty and, for each $i\!\in \!\{1,\ldots ,n+1\}$, we have $\max \{\gamma _{i,1},\gamma _{i,0}\}\!>\!0$.

• 3. L is a non-constant real analytic function on I.

• 4. We have height bounds $h(b_i)\!=\!O(n\log (nd))$ and $h(\gamma _{i,j})\!=\!O(n\log (nH))$ for all i and j.

Example 2.16

Returning to Example 1.3, one can easily apply Gauss-Jordan elimination to the underlying linear combinations of monomials, and then divide every equation by the last monomial $x^{166}_3 x^{68}_4 x^{343}_5$, to reduce $F\!=\!\textbf{O}$ to the following system having the same roots in $(\mathbb {R}^*)^5$:

$$\begin{aligned} x^{36}_1 x^{194}_2 x^{-116}_3 x^{14}_4 x^{-283}_5= & {} 16384cx^{58}_1 x^{194}_2 x^{-142}_3 x^{-32}_4 x^{-318}_5 + \frac{1}{4}\\ x^{76}_1 x^{240}_2 x^{-166}_3 x^{-27}_4 x^{-342}_5= & {} 4096cx^{58}_1 x^{194}_2 x^{-142}_3 x^{-32}_4 x^{-318}_5 + 1 \\ x^{74}_1 x^{179}_2 x^{-141}_3 x^{-68}_4 x^{-286}_5= & {} 256cx^{58}_1 x^{194}_2 x^{-142}_3 x^{-32}_4 x^{-318}_5 + 1 \\ x^{25}_1 x^{203}_2 x^{-122}_3 x^{-67}_4 x^{-343}_5= & {} 16cx^{58}_1 x^{194}_2 x^{-142}_3 x^{-32}_4 x^{-318}_5 + 1 \\ x^{20}_1 x^{167}_2 x^{-102}_3 x^{-56}_4 x^{-275}_5= & {} cx^{58}_1 x^{194}_2 x^{-142}_3 x^{-32}_4 x^{-318}_5 + 1 \end{aligned}$$

Note that this new system reveals why all the roots of F in $(\mathbb {R}^*)^5$ (for our earlier chosen values of c) must in fact lie in $\mathbb {R}^5_+$: The right-hand sides are all positive on $(\mathbb {R}^*)^5$. The underlying circuit relation for the exponent vectors above is the same as the circuit relation for the exponent vectors of F: $b\!=\!(-2,2,-2,2,-2,1,1)^\top$. Part of the proof of Lemma 2.15, applied to our example here, will imply that the resulting linear combination of logarithms L(u) can be easily read from b and the right-hand sides of our reduced system:

$$\begin{aligned} -2\log \left| 16384cu+\frac{1}{4}\right| +2\log \left| 4096cu+1\right| -2\log \left| 256cu+1\right| +2\log \left| 16cu+1 \right| -2\log |cu+1| +\log |u|. \end{aligned}$$

In particular, for any $c>0$, the number of roots of L in $I=\mathbb {R}_+$ is the same as the number of roots of F in $\mathbb {R}^5_+$. Our family of examples here is in fact an obfuscated version of a family derived in [86], thus accounting for the nice coefficients and high number of positive roots (6) for $c\!\in \!\left[ \frac{1}{20730}, \frac{1}{14392}\right]$. A more realistic example of coefficient growth can be found in Example 2.21 (see also Example 3.2 from Sect. 3). $\diamond$

Example 2.17

Even if $\Sigma \!=\!A$ (so that $m\!=\!n$), we still need enough non-singular minors to guarantee that F has just finitely many roots in $\mathbb {R}^n_+$. For instance, the 4-nomial $2\times 2$ system

$$\begin{aligned} x_1 \quad \quad -1= & {} 0 \\ x_1x_2 - x_2 \quad \quad= & {} 0, \end{aligned}$$

has $\begin{bmatrix}c_{1,1} &{}\quad c_{1,2}\\ c_{2,1} &{}\quad c_{2,2} \end{bmatrix}$ and $\begin{bmatrix}c_{1,3} &{}\quad c_{1,4}\\ c_{2,3} &{}\quad c_{2,4} \end{bmatrix}$ non-singular (among other $2\times 2$ sub-matrices), but has infinitely many positive solutions: (1, t) for all $t\!>\!0$. In particular, we are missing the non-singularity of $\begin{bmatrix}c_{1,2} &{}\quad c_{1,3}\\ c_{2,2} &{}\quad c_{2,3} \end{bmatrix}$. $\diamond$

Proof of Lemma 2.15:

First let $b\!\in \!\mathbb {Z}^{(n+2)\times 1}$ be the unique (up to sign) minimal circuit relation of A. By identifying the nonzero entries of b, we can then reorder the $a_i$ so that the unique non-degenerate circuit in A is $\Sigma \!=\!\{a_1,\ldots ,a_m,a_{n+1},a_{n+2}\}$. (So $\Sigma$ has cardinality $m+2$ and $b_{m+1},\ldots ,b_n$ are the only 0 entries of b.) Note that the coordinates of b are of logarithmic height $O(n\log (nd))$, and the computation of b takes time $n^{3.373}\log ^{1+o(1)}(nd)$, thanks to Lemmata 2.1 and 2.2 (and the fact that $\omega \!<\!2.373$ [2]).

We can then divide $f_1,\ldots ,f_n$ by $x^{a_{n+2}}$ without affecting the positive roots of F. So we may assume further that $a_{n+2}\!=\!\textbf{O}$ and, since this at worst doubles our original d, our O-estimates will be unaffected. We can then apply Lemma 2.1, thanks to our assumption on the $n\times n$ sub-matrices of $[c_{i,j}]$, to reduce $F\!=\!\textbf{O}$ to a system of equations of the form $G\!=\!\textbf{O}$, having the same solutions in $\mathbb {R}^n$ as F, where $G\!:=\!(g_1,\ldots ,g_n)$,

$$\begin{aligned} g_i(x)= & {} x^{a_i}-\gamma _{i,1}x^{a_{n+1}}-\gamma _{i,0} \text { for all } i, \end{aligned}$$

and the $\gamma _{i,j}$ are rational with logarithmic height $O(n\log (nH))$. This reduction takes time just $n^{3.373} \log ^{1+o(1)}(nH)$, by Lemma 2.1 (and our earlier observations on $\omega$). To complete our notation, let us also set $\gamma _{n+1,1}\!:=\!1$, $\gamma _{n+1,0}\!:=\!0$, $\gamma _{n+2,1}\!:=\!0$, and $\gamma _{n+2,0}\!:=\!1$.

Clearly, if there is an i such that both $\gamma _{i,0}$ and $\gamma _{i,1}$ are non-positive, then G (and thus F) has no positive roots, and we can simply stop, having spent time just $n^{3.373} \log ^{1+o(1)}(nH)$. So we may assume the following:

$$\begin{aligned} \text {For each } i\!\in \!\{1,\ldots ,n+1\} \text { we have } \max \{\gamma _{i,1},\gamma _{i,0}\}\!>\!0. \end{aligned}$$

(4)

We can easily check whether I is non-empty after sorting the (possibly infinite) numbers $-\gamma _{i,0}/\gamma _{i,1}$, using just $O(n\log n)$ comparisons of integers with $O(n\log (nH))$ bits (via, say, merge sort [39]). If I is empty, then we can conclude that F has no positive roots and stop (having spent time just $n^{3.373}(\log ^{1+o(1)}(nd)+\log ^{1+o(1)}(nH))$). So we may also assume the following:

$$\begin{aligned} I \text { is non-empty.} \end{aligned}$$

(5)

We now establish Assertions (1)–(4) via G and $\Sigma$: Observe that any root $\zeta \!\in \!{(\mathbb {R}^*)}^n$ of G must satisfy

$$\begin{aligned} 1= & {} (\zeta ^{a_1})^{b_1}\cdots (\zeta ^{a_m})^{b_m}(\zeta ^{a_{n+1}})^{b_{n+1}} \nonumber \\= & {} (\gamma _{1,1}\zeta ^{a_{n+1}}+\gamma _{1,0})^{b_1} \cdots (\gamma _{m,1}\zeta ^{a_{n+1}}+\gamma _{m,0})^{b_m} (\zeta ^{a_{n+1}})^{b_{n+1}} 1^{b_{n+2}}, \end{aligned}$$

(6)

So let $P(u)\!:=\!(\gamma _{1,1}u+\gamma _{1,0})^{b_1} \cdots (\gamma _{m,1}u+\gamma _{m,0})^{b_m}u^{b_{n+1}}-1$. Note that $n\!=\!1\Longrightarrow (\gamma _{1,1}, \gamma _{1,0})\!=\!(-c_2/c_1,-c_3/c_1)\!\in \!(\mathbb {R}^*)^2$ and thus P is a non-constant real rational function when $n\!=\!1$. So L(u) is a non-constant real analytic function on I when $n\!=\!1$. Let us then assume $n\!\ge \!2$. By Cramer’s Rule, and our assumption on the $n\times n$ sub-matrices of $[c_{i,j}]$, we have $\gamma _{i,0}\!\ne \!0$ and $\gamma _{i,1}\!\ne \!0$ for all i. P is then a non-constant real rational function since $b_{n+1}\!\ne \!0$ (thanks to $\Sigma$ being a non-degenerate circuit and Proposition 2.13), and there is thus no way to cancel the $u^{b_{n+1}}$ factor in the product term of P. So L(u) is a non-constant real analytic function on I.

Now observe that any root $\zeta \!\in \!\mathbb {R}^n_+$ of F yields $\zeta ^{a_{n+1}}\!\in \!I$ as a root of P by Equation (6). Moreover, by Proposition 2.5, any root $\zeta '\!\in \!\mathbb {R}^n_+$ of F with $(\zeta ')^{a_{n+1}}\!=\!\zeta ^{a_{n+1}}$ must satisfy $\zeta '\!=\!\zeta$, since G reduces to a binomial system with a unique positive root once the value of $x^{a_{n+1}}$ is fixed. (This is because the vectors $a_1,\ldots ,a_n$ are linearly independent, thanks to $\{a_{n+1},\textbf{O}\}\!\subset \!\Sigma$ and A being a circuit.) So P has at least as many roots in I as F has in $\mathbb {R}^n_+$.

Conversely, Proposition 2.5 tells us that any root $u\!\in \!I$ of P yields a unique $\zeta \!\in \!\mathbb {R}^n_+$ satisfying $\left( \zeta ^{a_1}, \ldots ,\zeta ^{a_n}\right) \!=\!(\gamma _{1,1}u+\gamma _{1,0},\ldots ,\gamma _{n,1}u +\gamma _{n,0})$. Recall that $b_{n+1}\!\ne \!0$. So we also obtain $\zeta ^{a_{n+1}}=\left( (\gamma _{1,1}u+\gamma _{1,0})^{-b_1} \cdots (\gamma _{m,1}u+\gamma _{m,0})^{-b_m}\right) ^{1/b_{n+1}} \!=\!u^{b_{n+1}/b_{n+1}}\!=\!u$ by the definition of P. So $\zeta$ is in fact a root of G. Similarly, a root $u'\!\in \!I$ of P with $u'\!\ne \!u$ would yield a positive root of $\left( (\zeta ')^{a_1}, \ldots ,(\zeta ')^{a_n}\right) \!=\!(\gamma _{1,1}u'+\gamma _{1,0}, \ldots ,\gamma _{n,1}u' +\gamma _{n,0})$ with $(\zeta ')^{a_{n+1}}\!\ne \!\zeta ^{a_{n+1}}$ and thus a root $\zeta '\!\ne \!\zeta$ of F. So F has at least as many roots in $\mathbb {R}^n_+$ as P has in I.

Observing that $P(u)\!=\!0 \Longleftrightarrow L(u)\!=\!0$ (for $u\!\in \!I$), and recalling Assumptions (4) and (5), we thus obtain Assertions (1)–(4). Noting that $m\!\le \!n$, we are done. $\square$

Our sub-matrix condition from Lemma 2.15 in fact holds for a large fraction of integer coefficients:

Corollary 2.18

The fraction of matrices $[c_{i,j}]\!\in \!\{-H,\ldots ,H\}^{n\times (n+2)}$ with all $n\times n$ sub-matrices of $[c_{i,j}]$ non-singular is at least $1-\frac{n(n+2)(n+1)}{4H+2}$. Also, the fraction of matrices $[c_{i,j}]\!\in \!\{-H,\ldots ,H\}^{n\times (n+1)}$ with leftmost $n\times n$ sub-matrix of $[c_{i,j}]$ non-singular is at least $1-\frac{n}{2H+1}$.

Proof

The DeMillo–Lipton–Schwartz–Zippel (DLSZ) Lemma [73, 99, 104] is a classic result that tells us that if $f\!\in \!\mathbb {C}[z_1,\ldots ,z_n]$ has degree d and $S\!\subset \!\mathbb {C}$ is a set of finite cardinality N, then f vanishes at no more than $dN^{n-1}$ points of $S^n$. The condition stated in our corollary is then equivalent to the non-vanishing of a product of $\left( {\begin{array}{c}n+2\\ 2\end{array}}\right)$ many $n\times n$ sub-determinants of $[c_{i,j}]$. The resulting polynomial clearly has degree $\frac{n(n+2)(n-1)}{2}$. Taking $S\!=\!\{-H,\ldots ,H\}$ (which has cardinality $2H+1$) and applying the DLSZ Lemma, we obtain our first bound. Our second bound follows almost identically, just considering one determinant instead. $\square$

Recall that a critical point of a function $L : \mathbb {R}\longrightarrow \mathbb {R}$ is a root of the derivative $L'$.

Proposition 2.19

Following the notation and assumptions of Lemma 2.15, let $u_0\!:=\!\inf I$, $u_k\!:=\!\sup I$, and suppose $u_1\!<\cdots <\!u_{k-1}$ are the critical points of L in I ($k\!=\!1$ implying no critical points). Then, the number of positive roots of F is exactly the number of $i\!\in \!\{0,\ldots ,k-1\}$ such that $\left( \lim _{u\rightarrow u^+_i} L(u)\right) \left( \lim _{u\rightarrow u^-_{i+1}} L(u)\right) \!<\!0$, plus the number of degenerate roots of L in I.

Proof

It is clear that L is strictly monotonic on any open sub-interval $(u_i,u_{i+1})$ of I. So the image of $(u_i,u_{i+1})$ under L is

$$\begin{aligned} L_i\!:=\!\left( \min \left\{ \lim _{u\rightarrow u^+_i} L(u), \lim _{u\rightarrow u^-_{i+1}} L(u)\right\} , \max \left\{ \lim _{u\rightarrow u^+_i} L(u), \lim _{u\rightarrow u^-_{i+1}} L(u)\right\} \right) , \end{aligned}$$

and we see by the Intermediate Value Theorem that $L_i$ does not contain $0 \Longleftrightarrow [\lim _{u\rightarrow u^+_i} L(u)$ and $\lim _{u\rightarrow u^-_{i+1}} L(u)$ are both non-positive or both non-negative]. So by Lemma 2.15, we are done. $\square$

We can now state analogues of Lemma 2.15 and Proposition 2.19 for roots in ${(\mathbb {R}^*)}^n$.

Lemma 2.20

Following the notation and assumptions of Lemma 2.15, assume further that $b_{n+1}$ is odd, $a_{n+2}\!=\!\textbf{O}$, and let $\mathcal {A}\!:=\![a_1,\ldots ,a_n]$. Let $U\mathcal {A}V\!=\!S$ be a Smith factorization of $\mathcal {A}$, and r the rank, over the field $\mathbb {F}_2$, of the mod 2 reduction of $\mathcal {A}$. Also, for any $u\!\in \!\mathbb {R}$, let $\varepsilon _i\!:=\!\textrm{sign}(\gamma _{i,1}u +\gamma _{i,0})$, $\Lambda (u)\!:=\!\prod \limits ^m_{i=1}\varepsilon ^{b_i\textrm{mod} \; 2}_i$, and $(\Gamma '_1(u),\ldots ,\Gamma '_n(u))\!:=\!(\varepsilon _1,\ldots , \varepsilon _n)^{V \textrm{mod} 2}$. Then, the number of roots of F in ${(\mathbb {R}^*)}^n$ is exactly $2^{n-r}$ times the number of roots $u\!\in \!\mathbb {R}$ of L satisfying both $\Lambda (u)\!=\!\textrm{sign}(u)$ and $\Gamma '_{r+1}(u),\ldots ,\Gamma '_n(u)\!>\!0$.

Example 2.21

Consider the 6-nomial $4\times 4$ system $F\!=\!(f_1,\ldots ,f_4)$ defined by

$$\begin{aligned} \left( -12x^{8}_1 x^{18}_2 x^{16}_4 -5x^{4}_1 x_2 x^3_3 x^8_4 +17x^{11}_1 x^{19}_2 x_3 x^{17}_4 -4x^{11}_1 x^9_2 x^{14}_3 +2 x^{18}_2 x^{13}_3 x^{17}_4 +3x^5_1 x^{14}_3 x^{16}_4, \right. \\ -9x^{8}_1 x^{18}_2 x^{16}_4 +14x^{4}_1 x_2 x^3_3 x^8_4 -8x^{11}_1 x^{19}_2 x_3 x^{17}_4 +3x^{11}_1 x^9_2 x^{14}_3 +12 x^{18}_2 x^{13}_3 x^{17}_4 - x^5_1 x^{14}_3 x^{16}_4, \\ 5x^{8}_1 x^{18}_2 x^{16}_4 +4x^{4}_1 x_2 x^3_3 x^8_4 +11x^{11}_1 x^{19}_2 x_3 x^{17}_4 -16x^{11}_1 x^9_2 x^{14}_3 +18 x^{18}_2 x^{13}_3 x^{17}_4 -19x^5_1 x^{14}_3 x^{16}_4, \\ \left. -x^{8}_1 x^{18}_2 x^{16}_4 +2x^{4}_1 x_2 x^3_3 x^8_4 +11x^{11}_1 x^{19}_2 x_3 x^{17}_4 -17x^{11}_1 x^9_2 x^{14}_3 -14 x^{18}_2 x^{13}_3 x^{17}_4 -6x^5_1 x^{14}_3 x^{16}_4 \right) . \end{aligned}$$

Proceeding as in Lemmata 2.15 and 2.20, we see that Gauss–Jordan elimination on the coefficient matrix, and computing the circuit relation underlying the exponent vectors, yields the following linear combination of logarithms:

$$\begin{aligned} L(u)= & {} 54667\log \left| \frac{39898}{27281}-\frac{84556}{27281}u\right| -16978 \log \left| \frac{47210}{27281}-\frac{125680}{27281}u\right| \\{} & {} -43727 \log \left| \frac{42139}{27281}-\frac{126754}{27281}u\right| +5123\log \left| \frac{20845}{27281}-\frac{114296}{27281}u\right| -10129\log |u|. \end{aligned}$$

In particular, L is an analytic function on

$$\begin{aligned} \mathbb {R}\setminus \{0,0.182377...,0.332447...,0.375636...,0.471852...\} \end{aligned}$$

whose roots encode the roots of F in $(\mathbb {R}^*)^4$: Observing that

$$\begin{aligned} \Lambda (u)\!=\!\textrm{sign}\!\left( 39898-84556u\right) \textrm{sign}\!\left( 42139 -126754u\right) \textrm{sign}\!\left( 20845-114296u\right) , \end{aligned}$$

we see that the only open intervals containing u satisfying $\Lambda (u)\!=\!\textrm{sign}(u)$ are

$$\begin{aligned} (0,0.182377...), (0.332447...,0.375636...), (0.375636...,0.471852...). \end{aligned}$$

(The mod 2 reduction in our $\mathcal {A}$ here has full rank $r\!=\!4$ and thus the condition involving the $\Gamma '_i(u)$ becomes vacuously true.) It is then easily checked that L is strictly decreasing, with range $\mathbb {R}$, on the first and third intervals; and L is positive on the second interval. (See also Corollary 2.22.) So L has exactly 2 roots in $\mathbb {R}^*$ satisfying the sign conditions⁹ of Lemmata 2.20, and thus F has exactly 2 roots in $(\mathbb {R}^*)^4$: The roots in $(\mathbb {R}^*)^4$ respectively lie in the $++++$ and $+-++$ orthants. (It is also easily checked that F has infinitely many roots in $\mathbb {R}^4$, since F vanishes on the entire subspace defined by $x_1\!=\!x_2\!=\!0$.) PHCpack (a state-of-the-art polyhedral homotopy solver [102]) confirms our root count for this F in about 15 minutes, along with a count of 70834 for the total number of roots in $(\mathbb {C}^*)^4$, as well as approximations of all these roots to 14 decimal places. Our Maple code counts the roots of F in $(\mathbb {R}^*)^4$ and $\mathbb {R}^4_+$ in under one second. $\diamond$

Proof of Lemma 2.20:

Continuing the notation of the proof of Lemma 2.15, we need to revisit the properties of the rational function P defined earlier. In particular, whereas before we had a natural bijection between the roots of F in $\mathbb {R}^n_+$ and the roots of P in a particular interval I, we now need to consider roots of F with negative coordinates and roots of P throughout $\mathbb {R}$. In particular, a key difference from our earlier lemma is the following simple equivalence, valid for all $u\!\in \!\mathbb {R}$: $P(u)\!=\!0 \Longleftrightarrow [L(u)\!=\!0$ and $\Lambda (u)\!=\! \textrm{sign}(u)]$. (Indeed, we could encounter u with $P(u)\!=\!-2$ without the condition involving $\Lambda (u)$.) Note also that by construction, P(0) is either $-1$ or undefined.

So let $\zeta \!\in \!{(\mathbb {R}^*)}^n$ be a root of F. By Relation (6), $\zeta ^{a_{n+1}}$ must be a nonzero real root of P and, by the definition of G and the $\gamma _{i,j}$ (and Proposition 2.8), we must have $\Gamma '_{r+1}\!\left( \zeta ^{a_{n+1}}\right) , \ldots ,$ $\Gamma '_n\!\left( \zeta ^{a_{n+1}}\right) \!>\!0$. By Proposition 2.8, there must also be exactly $2^{n-r}$ many roots $\zeta '\!\in \!{(\mathbb {R}^*)}^n$ of F with $(\zeta ')^{a_{n+1}}\!=\!\zeta ^{a_{n+1}}$, because G reduces to a binomial system once the value of $\zeta ^{a_{n+1}}$ is fixed. So F has no more than $2^{n-r}$ times as many roots in ${(\mathbb {R}^*)}^n$ as P has in $\mathbb {R}^*$.

Conversely, if $u\!\in \!\mathbb {R}^*$ is a root of P, then Proposition 2.8 tells us that $\Gamma '_{r+1}(u), \ldots ,\Gamma '_n(u)\!>\!0$ implies that there are exactly $2^{n-r}$ many $\zeta \!\in \!{(\mathbb {R}^*)}^n$ satisfying

$$\begin{aligned} (\zeta ^{a_1},\ldots ,\zeta ^{a_n})\!=\!(\gamma _{1,1}u+\gamma _{1,0},\ldots , \gamma _{n,1}u+\gamma _{n,0}). \end{aligned}$$

(Note also that $\gamma _{i,1}u+\gamma _{i,0} \!\ne \!0$ for all i since $P(u)\!\ne \!0$ when $\gamma _{i,1}u+\gamma _{i,0}\!=\!0$.) We then also obtain $\zeta ^{b_{n+1}a_{n+1}}=(\gamma _{1,1}u+\gamma _{1,0})^{-b_1} \cdots (\gamma _{m,1}u+\gamma _{m,0})^{-b_m} \!=\!u^{b_{n+1}}$ by Relation (6). Since $b_{n+1}$ is odd, all our resulting $\zeta$ must satisfy $\zeta ^{a_{n+1}}\!=\!u$ and therefore be roots of G (and thus of F). Similarly, a real root $u'$ of P with $u'\!\ne \!u$ would yield a collection of $2^{n-r}$ many $\zeta '\!\in \!{(\mathbb {R}^*)}^n$ that are roots of F but with $(\zeta ')^{a_{n+1}}\!\ne \!\zeta ^{a_{n+1}}$, since $b_{n+1}$ is odd and $u\!\in \!\mathbb {R}^*$. So the number of roots of F in ${(\mathbb {R}^*)}^n$ is at least $2^{n-r}$ times the number of roots of P in $\mathbb {R}^*$.

Our stated root count for F in ${(\mathbb {R}^*)}^n$ is thus correct. $\square$

The following variant of Proposition 2.19 can be proved almost the same as Proposition 2.19, simply using Lemma 2.20 instead of Lemma 2.15:

Corollary 2.22

Following the notation and assumptions of Lemma 2.20, let $w_1\!<\cdots <\!w_{\ell -1}$ be the critical points and poles of L in $\mathbb {R}$, and set $w_0\!:=\!-\infty$ and $w_\ell \!:=\!+\infty$. Let $\mathcal {N}$ be the number of $i\!\in \!\{0,\ldots ,\ell -1\}$ such that $\Lambda (u)\!=\!\textrm{sign}(u)$ and $\Gamma '_{r+1}(u),\ldots ,\Gamma '_n(u)\!>\!0$ for all $u\!\in \!(w_i,w_{i+1})$, and $\left( \lim _{u\rightarrow w^+_i} L(u)\right) \left( \lim _{u\rightarrow w^-_{i+1}} L(u)\right) \!<\!0$. Then, the number of roots of F in ${(\mathbb {R}^*)}^n$ is exactly $\mathcal {N}$ plus the number of degenerate roots of L in $\mathbb {R}$. $\square$

2.4 Heights of Algebraic Numbers and Linear Forms in Logarithms

Recall that if $\beta$ is in the algebraic closure $\overline{\mathbb {Q}}$ of $\mathbb {Q}$, with minimal polynomial $m(x_1):=c_0+\cdots +c_dx^d_1\!\in \!\mathbb {Z}[x_1]$ satisfying $\gcd (c_0,\ldots ,c_d)\!=\!1$, then we may define the (absolute) logarithmic height of $\beta$ to be

$$\begin{aligned} \displaystyle {h(\beta )\!:=\!\frac{1}{d}\left( \log |c_d|+\sum \limits ^d_{i=1}\log \max \{|\beta _i|,1\}\right) }, \end{aligned}$$

where $\beta _1,\ldots ,\beta _d$ (among them, $\beta$) are all the roots of m. This definition in fact agrees with our earlier definition for rational numbers. Since m must be irreducible we have $\#\{\beta _1,\ldots ,\beta _d\}\!=\!d$.

Proposition 2.23

(See, e.g., [25, Prop. 1.5.15, pg. 18].) If $\alpha _1,\ldots ,\alpha _k\!\in \!\overline{\mathbb {Q}}$, then $h\!\left( \sum \limits ^k_{i=1}\alpha _i\right)$ is no greater than $\log (k)+\sum \limits ^k_{i=1} h(\alpha _i)$. Also, $h\!\left( \prod \limits ^k_{i=1}\alpha _i\right) \!\le \!\sum \limits ^k_{i=1} h(\alpha _i)$. $\square$

Letting $\left| c_0+c_1x_1+\cdots +c_dx^d_1\right| _2\!:=\!\sqrt{\sum ^d_{i=0}|c_i|^2}$, we recall the following classical inequality:

Landau’s Inequality

[78] If $\beta \!\in \!\overline{\mathbb {Q}}$ has minimal polynomial $g\!\in \!\mathbb {Z}[x_1]$ with relatively prime coefficients then $\displaystyle {h(\beta )\!\le \!\frac{\log |g|_2}{\deg g}}$. $\square$

It will also be useful to have a mildly refined version of Liouville’s classic bound [72] on the separation between rational numbers and irrational algebraic numbers.

Theorem 2.24

Suppose $\beta \!\in \!\overline{\mathbb {Q}}$, with minimal polynomial $m\!\in \!\mathbb {Z}[x_1]$ of degree $d\!\ge \!2$. Then,

$$\begin{aligned} \displaystyle {\left| \beta -\frac{p}{q}\right| <1\Longrightarrow \left| \beta -\frac{p}{q}\right| \ge \frac{\left( |m'(\beta )|+ \left| \frac{m''(\beta )}{2!}\right| +\cdots +\left| \frac{m^{(d)}(\beta )}{d!} \right| \right) ^{-1}}{q^d}} \end{aligned}$$

for all $p,q\!\in \!\mathbb {Z}$ with $q\!>\!0$.

Proof

First note that the parenthesized expression in the numerator of the large fraction above is positive since m is the minimal polynomial of $\beta$ and thus $m'(\beta )\!\ne \!0$.

Via Taylor expansion we then obtain the following:

$$\begin{aligned} |m(p/q)|= & {} \left| m(\beta )+m'(\beta )\left( \frac{p}{q}-\beta \right) + \frac{m''(\beta )}{2!}\left( \frac{p}{q}-\beta \right) ^2+\cdots + \frac{m^{(d)}(\beta )}{d!}\left( \frac{p}{q}-\beta \right) ^d\right| \\= & {} \left| \beta -\frac{p}{q}\right| \left| 0 +m'(\beta ) + \frac{m''(\beta )}{2!} \left( \frac{p}{q}-\beta \right) +\cdots +\frac{m^{(d)}(\beta )}{d!}\left( \frac{p}{q}-\beta \right) ^{d-1}\right| \\\le & {} \left| \beta -\frac{p}{q}\right| \left( |m'(\beta )|+\left| \frac{m''(\beta )}{2!}\right| \left| \frac{p}{q} -\beta \right| +\cdots +\left| \frac{m^{(d)}(\beta )}{d!}\right| \left| \frac{p}{q}-\beta \right| ^{d-1}\right) \\< & {} \left| \beta -\frac{p}{q}\right| \left( |m'(\beta )|+\left| \frac{m''(\beta )}{2!}\right| +\cdots +\left| \frac{m^{(d)}(\beta )}{d!}\right| \right) . \end{aligned}$$

Since m is irreducible and of degree $\ge \!2$, m has no rational roots, and thus $q^d m(p/q)$ must be a nonzero integer. So we obtain $q^d|m(p/q)|\!\ge \!1$ and thus $|m(p/q)|\!\ge \!1/q^d$. Combined with our last Taylor series inequalities, we are done. $\square$

Finally, we recall the following paraphrase of a bound of Matveev [77, Cor. 2.3], considerably strengthening earlier bounds of Baker and Wustholtz [6]. (See also [30, Thm. 9.4].)

Theorem 2.25

Suppose K is a degree d real algebraic extension of $\mathbb {Q}$, $\alpha _1,\ldots ,\alpha _m\!\in \!K\setminus \{0\}$, and $b_1,\ldots ,b_m\!\in \!\mathbb {Z}\setminus \{0\}$. Let $B\!:=\!\max \{|b_1|, \ldots ,|b_m|\}$ and $\log \mathscr {A}_i\!:=\!\max \{\textrm{d}h(\alpha _i),|\log \alpha _i|,0.16\}$ for all i. Then, $\sum ^m_{i=1} b_i\log \alpha _i\!\ne \!0$ implies that

$$\begin{aligned} \displaystyle {\log \left| \sum ^m_{i=1} b_i\log \alpha _i \right| >- 1.4\cdot m^{4.5} 30^{m+3}d^2(1+\log d)(1+\log B)\prod ^m_{i=1}\log \mathscr {A}_i}. \end{aligned}$$

$\square$

2.5 Bounds on Coefficients, Roots, and Derivatives of Univariate Polynomials

Letting $\left| c_0+c_1x_1+\cdots +c_dx^d_1\right| _\infty \!:=\!\max _i|c_i|$, recall the following classic bounds on the size and minimal spacing of roots of polynomials:

Proposition 2.26

(See, e.g., [88, Thm. 8.1.4 & Thm. 8.1.7, (i), (8.1.3)].) If $f\!\in \!\mathbb {Z}[x_1]$ satisfies $|f|_\infty \!\le \!H$ and $\zeta \!\in \!\mathbb {C}$ is a nonzero root of f, then $\frac{1}{1+H}\!<\!|\zeta |\!<\!1+H$. $\square$

Mahler’s Theorem

[74] Suppose $f\!\in \!\mathbb {Z}[x_1]$ is square-free, has degree d, and $|f|_\infty \!\le \!H$. Then, any two distinct complex roots $\zeta _1,\zeta _2$ of f satisfy

$$\begin{aligned} \displaystyle {|\zeta _1-\zeta _2|\!>\!\sqrt{3}(d+1)^{-(2d+1)/2} H^{-(d-1)}}. \end{aligned}$$

In particular, $|\log |\zeta _1-\zeta _2||\!=\!O(d\log (\textrm{d}H))$. $\square$

Letting $\left| c_0+c_1x_1+\cdots +c_dx^d_1\right| _1\!:=\!\sum ^d_{i=0}|c_i|$, recall also the following nice bound on the coefficients of divisors of polynomials:

Lemma 2.27

[78, Thm. 4] Suppose $f,g\!\in \!\mathbb {C}[x_1]$ have respective leading coefficients c and $\gamma$, and g|f. Then, $|g|_1\!\le \!2^{\deg g}\left| \frac{\gamma }{c}\right| |f|_2$. $\square$

Recall that the content of a polynomial $r(x)\!:=\!c_0+\cdots +c_dx^d\!\in \!\mathbb {Z}[x_1]$ is $\textrm{con}(r)\!:=\!\gcd (c_0,\ldots ,c_d)$, and that we call such an r primitive if and only if $\textrm{con}(r)\!=\!1$. We will need the following consequence of the classical Gauss’ Lemma for polynomials (see, e.g., [46, Ex. 3.4, pg. 109]):

Lemma 2.28

If $f,h\!\in \!\mathbb {Z}[x_1]$ with h primitive, $g\!\in \!\mathbb {Q}[x_1]$, and $f\!=\!gh$ identically, then $g\!\in \!\mathbb {Z}[x_1]$. $\square$

We can now prove the following extension of Mahler’s bound to the case of polynomials with degenerate roots.

Corollary 2.29

Suppose $f\!\in \!\mathbb {Z}[x_1]$ has degree d and $|f|_\infty \!\le \!H$. Then, any two distinct complex roots $\zeta _1,\zeta _2$ of f satisfy $|\log |\zeta _1-\zeta _2||\!=\! O(d^2+d\log H)$.

Proof

Let $g\!:=\!\gcd (f,f')$, where we compute the gcd of two polynomials in $\mathbb {Q}[x_1]$ via the Euclidean Algorithm. (So $g\!\in \!\mathbb {Q}[x_1]$ and g is monic.) In particular, since $\gamma g$ is primitive for some minimal $\gamma \!\in \!\mathbb {N}$, Lemma 2.28 tells us that $f/(\gamma g)\!\in \!\mathbb {Z}[x_1]$. Moreover, since g is monic, $\gamma$ must divide the leading coefficient of f and thus $\gamma \!\le \!H$.

Recall that the square-free part of f is $p\!:=\!f/\gcd (f,f')$. It is then elementary that p has the same roots in $\mathbb {C}$ as f, p is square-free, and $p\!\in \!\mathbb {Q}[x_1]$. In particular, from the last paragraph, we see that $p\!\in \!\mathbb {Z}[x_1]$, with the same leading coefficient as that of f since g is monic. Lemma 2.27 then tells us that $|p|_1\!\le \!2^d|f|_2$. So then, $|p|_\infty \!\le \!2^d \sqrt{d}|f|_\infty \!\le \!\sqrt{d}H2^d$. Applying Mahler’s Theorem, we see that $\log |\zeta _1-\zeta _2|\!=\!O(d\log (d\sqrt{d}H2^d)) \!=\!O(d[\log (d)+d+\log H])\!=\!O(d^2+d\log H)$. $\square$

We will also need the following bound on the coefficients of products of polynomials:

Lemma 2.30

If $f_1,\ldots ,f_k\!\in \mathbb {Z}[x_1]$ then $\left| \prod \limits ^k_{i=1}f_i\right| _\infty \!\le \! \prod \limits ^k_{i=1} (1+\deg f_i)|f_i|_\infty$.

Proof

Via direct expansion (and the Triangle Inequality) it is clear that the 1-norm for polynomials is sub-multiplicative, i.e., $\left| \prod \limits ^k_{i=1} f_i\right| _1 \!\le \!\prod \limits ^k_{i=1} |f_i|_1$. It is also immediate that $|f|_\infty \!\le \!|f|_1$ and $|f|_1\!\le \!(1+\deg f)|f|_\infty$ for any polynomial. So we obtain

$$\begin{aligned} \left| \prod \limits ^k_{i=1} f_i\right| _\infty \le \left| \prod \limits ^k_{i=1} f_i\right| _1 \le \prod \limits ^k_{i=1} |f_i|_1 \le \prod \limits ^k_{i=1}(1+\deg f_i)|f_i|_\infty . \end{aligned}$$

$\square$

Finally, we will need the following bound on higher derivatives of polynomials, dating back to work of Duffin and Schaeffer [45], based on a classic bound of A. A. Markov [75]:

Corollary 2.31

Suppose $f\!\in \!\mathbb {C}[x_1]$ has degree d and $t\!>\!0$. Then,

$$\begin{aligned} \displaystyle {\underset{-t\le x_1 \le t}{\max } \left| f^{(j)}(x_1)\right| \le \frac{d^2(d^2-1^2)\cdots (d^2-(j-1)^2)}{1\cdot 3 \cdots (2j-1)}\cdot \frac{\underset{-t\le x_1 \le t}{\max }|f(x_1)|}{t^j}}. \end{aligned}$$

$\square$

After rescaling the variable so it ranges over $[-1,1]$, the statement above follows immediately from [88, Thm. 15.2.6 & Cor. 15.2.7, Sec. 15.2]. The latter results in fact include conditions for equality in the bound above.

3 Critical Values of Linear Forms in Logarithms and Their Signs

We are now ready to prove two key lemmata 3.1 and 3.4 that enable our new complexity bounds.

Lemma 3.1

Suppose $m\!\ge \!2$, $b_i\!\in \!\mathbb {Z}\setminus \{0\}$ and $\gamma _{i,1},\gamma _{i,0}\!\in \!\mathbb {Q}$ with $h(\gamma _{i,j})\!\le \!\log H$ (for some integer $H\!\ge \!3$) for all $i\!\in \!\{1,\ldots ,m\}$, $B\!:=\!\max _i|b_i|$, and $L(u):=\sum ^m_{i=1}b_i\log |\gamma _{i,1}u+\gamma _{i,0}|$ is non-constant and differentiable on some non-empty open interval. Then, the critical points of L in $\mathbb {R}$ are exactly the real roots of a polynomial $g\!\in \!\mathbb {Z}[u]$ of degree at most $m-1$ with $|g|_\infty \!\le \!m2^{m-1}BH^{2m}$. In particular, $\log |g|_\infty \!=\!O(\log (B)+m\log H)$, L has at most m roots in any open interval I not containing a pole of L, and L has at most 2m real roots.

Example 3.2

Example 2.21 is more representative (than Example 2.16) of the coefficient growth one encounters when converting F into a univariate linear combination of logarithms L: There we saw an input 6-nomial $4\times 4$ system F with coefficients and exponents having at most 2 digits, resulting in an L with coefficients having 6 or fewer digits. In particular, the polynomial encoding the critical points of L is

$$\begin{aligned} g(u):= & {} -85015812446550320118784u^4 +160578806134338659719072u^3\\{} & {} -78932164016242868100268u^2\\{} & {} +13833463598904597755876u -837930167824219163155, \end{aligned}$$

which has coefficients with at most 24 digits, and 2 real roots, neither of which lies in the sub-intervals of $\mathbb {R}$ contributing to the root count of F in $(\mathbb {R}^*)^4$. So in Example 2.21, it is the signs of the poles of L, instead of the signs of the critical values that determine the number of roots of F in $(\mathbb {R}^*)^4$. $\diamond$

Example 3.3

Returning to Example 2.16, which had L(u) being

$$\begin{aligned}{} & {} -2\log \left| 16384cu+\frac{1}{4}\right| +2\log \left| 4096cu+1\right| -2\log \left| 256cu+1\right| \\ {}{} & {} \quad +2\log \left| 16cu+1 \right| -2\log |cu+1| +\log |u|, \end{aligned}$$

it is easily checked via Maple that this L has exactly 5 critical values, alternating in sign, and the underlying critical points interlace the 6 positive roots of L. $\diamond$

Proof of Lemma 3.1:

First observe that $L'(u)\!=\!\sum \limits ^m_{i=1} \frac{b_i\gamma _{i,1}}{\gamma _{i,1}u +\gamma _{i,0}}$. Thanks to our non-constancy assumption, $L'$ has at most m distinct poles. Letting $\nu _i$ be the least common multiple of the denominators of $\gamma _{i,1}$ and $\gamma _{i,0}$, and setting

$$\begin{aligned} \displaystyle {g_i(u)\!:=\! \left( b_i\gamma _{i,1}\nu _i \prod \limits ^m_{j=1}(\gamma _{j,1}u +\gamma _{j,0})\nu _j\right) /((\gamma _{i,1}u +\gamma _{i,0})\nu _i)}, \end{aligned}$$

let us define $g(u)\!:=\!\sum ^m_{i=1}g_i(u)$. Clearly, $g_i\!\in \!\mathbb {Z}[u]$ for all i, $g\!\in \!\mathbb {Z}[u]$, and g(u) is nothing more than $L'(u)\prod ^m_{j=1} (\gamma _{j,1}u+\gamma _{j,0})\nu _j$. So we clearly obtain the statement on the real critical points of L being the real roots of g, and it is clear that $\deg g\!\le \!m-1$. Lemma 2.30 implies that $|g_i|_\infty \!\le \! BH^2\left( 2^{m-1}H^{2(m-1)}\right)$. Clearly then, $|g|_\infty \!\le \!m2^{m-1}BH^{2m}$. That L has at most m roots in I is immediate from Rolle’s Theorem, since $\deg g\!\le \!m-1$. We similarly obtain at most 2m roots in $\mathbb {R}$ since L has no more than m poles (as well as no more than $m-1$ critical points). $\square$

Recall that a critical value of a function $L : \mathbb {R}\longrightarrow \mathbb {R}$ is the value of L at a critical point of L.

Lemma 3.4

Following the notation and assumptions of Lemma 3.1, let I be any open interval defined by consecutive real poles of L, let $\varepsilon$ denote any nonzero critical value of L, and let $\delta$ (resp. $\eta$) be the minimum of $|\zeta _1-\zeta _2|$ over all distinct roots $\zeta _1,\zeta _2\!\in \!I$ of L (resp. the derivative $L'$). Finally, let $\Delta$ denote the minimum of $|\zeta -\mu |$ as $\zeta$ (resp. $\mu$) ranges over the critical points (resp. poles) of L. Then:

• 1. $\log \eta >-O(m\log (B)+m^2\log H)$.

• 2. $\log |\varepsilon | > -O\!\left( 61^m\log ^{m+1}\left( \sqrt{B}H^{2m-1}\right) \right)$.

• 3. $\log \Delta > -O\!\left( m\log (B)+m^2\log H\right)$.

• 4. $\log \delta > -O\!\left( 61^m\log ^{m+1}\left( \sqrt{B}H^{2m-1}\right) \right)$.

Proof

If L has no critical points then, by Rolle’s Theorem, L has at most 1 root in I and Assertions (1)–(3) are vacuously true. So let us assume L has exactly $k-1$ critical points (with $k\!\ge \!2$) in the open interval I, $u_0\!:=\!\inf I$, $u_k\!:=\!\sup I$, and suppose $u_1\!<\cdots <\!u_{k-1}$ are the critical points of L in I. Also let g denote the polynomial from Lemma 3.1. Below, we illustrate a coarse approximation of what the graph of L can look like, along with some of our notation:

Assertion (1) then follows immediately by applying Corollary 2.29 to g, thanks to Lemma 3.1. In particular, we get $|\log \eta |\!=\!O((m-1)^2+(m-1)\log ( m2^{m-1}BH^{2m}))$

$$\begin{aligned} =\!O(m^2+m[\log (m)+m+\log (B)+m\log H]), \end{aligned}$$

which clearly reduces to the stated bound.

Assertion (2) then follows routinely from Theorem 2.25 upon observing that $|\varepsilon |$ is nothing more than the absolute value of a linear combination of logarithms of real algebraic numbers. In particular, the arguments of the logarithms constituting $L(u_j)$ at a critical point $u_j\!\in \!I$ (for some $j\!\in \!\{1,\ldots ,k-1\}$) all lie in the same real algebraic extension: $\mathbb {Q}(u_j)$. Noting that the minimal polynomial, p, of $u_j$ has degree $\le \!m-1$, Lemmata 2.27 and 3.1 then tell us that $|p|_\infty \!\le \!2^{m-1}\left( \frac{\gamma _p}{\gamma _g}\right) |g|_2$ (since p|g), where $\gamma _p$ and $\gamma _g$ are, respectively, the leading coefficients of p and g. Moreover, since $p,g\!\in \!\mathbb {Z}[u]$, we have that $\gamma _p|\gamma _g$ and thus

$$\begin{aligned} |p|_\infty \le 2^{m-1}\cdot 1\cdot (\sqrt{m}(mB2^{m-1}H^{2m})) = m^{3/2}4^{m-1}B H^{2m}. \end{aligned}$$

(7)

So $\log |p|_2\!\le \!\log \left( \sqrt{m}\cdot m^{3/2}4^{m-1}BH^{2m}\right)$, and thus Landau’s Inequality tells us that

$$\begin{aligned} \deg (p)h(u_j) \le \log \left( m^2 4^{m-1} B H^{2m}\right) . \end{aligned}$$

(8)

Proposition 2.26 and Lemma 3.1 then tell us that $|u_j|< 1+|g|_\infty \le 1+m2^{m-1}B H^{2m}$. Also, $h(\gamma _{i,1}u_j+\gamma _{i,0})\!\le \!\log (2)+(h(\gamma _{i,1})+ h(u_j))+h(\gamma _{i,0})$, thanks to Proposition 2.23. So then, by Inequality (8),

$$\begin{aligned}{} & {} \deg (p)h(\gamma _{i,1}u_j+\gamma _{i,0}) \\{} & {} \quad \le (m-1)\log (2)+(m-1)\log (H) +\log \!\left( m^2 4^{m-1}BH^{2m}\right) +(m-1)\log H\\{} & {} \quad \le \log \!\left( m^2 8^{m-1}BH^{4m-2}\right) . \end{aligned}$$

Theorem 2.25 then tells us that

$$\begin{aligned} \log |\varepsilon |> & {} -1.4\cdot 30^{m+3}m^{4.5}(m-1)^2 (1+\log (m-1))(1+\log B)\left( \log \!\left( m^2 8^{m-1}B H^{4m-2} \right) \right) ^m \nonumber \\> & {} -1.4\cdot 30^3\cdot 30^m m^{6.5} (1+\log m)(1+\log B)\log ^m\!\left( m^2 8^{m-1}B H^{4m-2}\right) \nonumber \\= & {} -O\!\left( 30^m m^{6.5}\log (m)\log (B) \log ^m\!\left( m^2 8^{m-1}B H^{4m-2}\right) \right) . \end{aligned}$$

(9)

Now observe that $m^{6.5}\log m\!=\!O\!\left( (1+\theta _1)^m\right)$ for any $\theta _1\!>\!0$, and $m^2 8^{m-1}\!\le \!(BH^{4m-2})^{\theta _2}$ when $H\!\ge \!8.08^{\frac{1}{4\theta _2}}$, $m\!\ge \!1467$, and $\theta _2\!>\!0$. So then, if we pick $\theta _1\!=\!\theta _2\!=\!\sqrt{30.5/30}-1\!=\!0.00829...$ we obtain: $\log |\varepsilon | > -O\!\Big (30^m (1+\theta _1)^m \log (B) \log ^m \left( \left( B H^{4m-2}\right) ^{1+\theta _2}\right) \Big )$

$$\begin{aligned}{} & {} \displaystyle {=-O\!\left( (30(1+\theta _1)(1+\theta _2))^m \log ^{m+1}\!\left( \left( BH^{4m-2}\right) \right) \right) }\\{} & {} =-O\!\left( 30.5^m 2^{m+1} \log ^{m+1}\!\left( \sqrt{B}H^{2m-1}\right) \right) \\{} & {} = -O\!\left( 61^m \log ^{m+1}\!\left( \sqrt{B}H^{2m-1}\right) \right) , \end{aligned}$$

thus proving Assertion (2).

To prove Assertion (3), observe that $\Delta \!=\!\min \{u_1-u_0,u_k-u_{k-1}\}$, i.e., $\Delta \!=\!|u_{j'}-u_\ell |$ for some $j'\!\in \!\{1,k-1\}$ and $\ell \!\in \!\{0,k\}$, by our earlier definitions. If $\Delta \!=\!\infty$, then there is nothing to prove, so let us assume $\Delta \!<\!\infty$. If $u_{j'}\!\in \!\mathbb {Q}$, then Assertion (3) follows easily from Proposition 2.23, since $u_\ell$ has logarithmic height no greater than $2\log H$ and $u_{j'}$ must have logarithmic height no greater than $O(\log (B)+m\log H)$. So we may assume that $u_{j'}$ is algebraic of degree at least 2 over $\mathbb {Q}$.

We can then apply Theorem 2.24 and Lemma 3.1 to obtain that $\Delta$ must be bounded from below by

$$\begin{aligned} \min \left\{ \frac{\left( |p'(u_{j'})|+ \left| \frac{p''(u_{j'})}{2!}\right| +\cdots +\left| \frac{p^{(m-1)}(u_{j'})}{(m-1)!}\right| \right) ^{-1}}{H^{2(m-1)}},1\right\} . \end{aligned}$$

(10)

We know that $|u_{j'}|< 1+m2^{m-1}B H^{2m}$ by Proposition 2.26, so it is enough to minimize the preceding sum of derivative norms over the interval $J\!:=\!\left[ -1-m2^{m-1}B H^{2m},1+m2^{m-1}B H^{2m}\right]$.

Noting the easy inequality $\displaystyle {\underset{-t\le x_1 \le t}{\max }\ \left| f(x_1)\right| \le |f|_1\max \left\{ 1,|t|^d\right\} }$ for any $f\!\in \!\mathbb {R}[x_1]$ of degree d and $t\!\in \!\mathbb {R}$, we then have:

$$\begin{aligned} \underset{x_1 \in J}{\max }|g(x_1)|\le & {} |g|_1 \max \left\{ 1,(1+m2^{m-1}BH^{2m})^{m-1}\right\} \nonumber \\\le & {} m|g|_\infty \left( 1+m2^{m-1}BH^{2m}\right) ^{m-1}, \nonumber \\\le & {} m\cdot m2^{m-1}BH^{2m}\left( 1+m2^{m-1}BH^{2m}\right) ^{m-1}, \end{aligned}$$

(11)

and Corollary 2.31 then implies

$$\begin{aligned} |p^{(r)}(u_{j'})|\le & {} \underset{x_1 \in J }{\max }\left| p^{(r)}(x_1)\right| \\\le & {} \frac{(m-1)^2((m-1)^2-1^2)\cdots ((m-1)^2-(r-1)^2)}{1\cdot 3\cdots (2r-1)}\cdot |p|_1\\{} & {} \cdot \left( 1+m2^{m-1}BH^{2m}\right) ^{m-1}, \\ \end{aligned}$$

since p has degree $\le \!m-1$. Since $|p|_1\!\le \!m|p|_\infty$, Inequality (7) tells us that $\left| p^{(r)}(u_{j'})\right|$ is bounded from above by

$$\begin{aligned}{} & {} \frac{(m-1)^2((m-1)^2-1^2)\cdots ((m-1)^2-(r-1)^2)}{1\cdot 3 \cdots (2r-1)}\cdot m \cdot \left( m^{3/2}4^{m-1}B H^{2m}\right) \\{} & {} \quad \left( 1+m2^{m-1} B H^{2m}\right) ^{m-1}\\\le & {} \left( {\begin{array}{c}(m-1)^2\\ r\end{array}}\right) m \cdot \left( m^{3/2}4^{m-1} B H^{2m}\right) \left( 1+m2^{m-1} B H^{2m}\right) ^{m-1} \\\le & {} \left( \frac{(m-1)^2e}{r}\right) ^r m^{5/2}4^{m-1}B H^{2m} \left( 1+m2^{m-1} B H^{2m}\right) ^{m-1}, \\ \end{aligned}$$

where the last inequality follows easily from Stirling’s classical estimate for the factorial function. So then, $|p'(u_{j'})|+ \left| \frac{p''(u_{j'})}{2!}\right| +\cdots +\left| \frac{p^{(m-1)}(u_{j'})}{(m-1)!}\right|$ is strictly less than

$$\begin{aligned}{} & {} \left[ (m-1)^2e+\frac{((m-1)^2e/2)^2}{2!}+\cdots +\frac{((m-1)^2e/(m-1))^{m-1}}{(m-1)!}\right] \\{} & {} \quad m^{5/2}4^{m-1} B H^{2m} \left( 1+m2^{m-1} B H^{2m}\right) ^{m-1}. \end{aligned}$$

Now, by the Maclaurin series for $e^x$, the bracketed factor above is strictly less than $e^{(m-1)^2e}$. So then, $|p'(u_{j'})|+ \left| \frac{p''(u_{j'})}{2!}\right| +\cdots +\left| \frac{p^{(m-1)}(u_{j'})}{(m-1)!}\right|$ is strictly less than

$$\begin{aligned}{} & {} e^{(m-1)^2e} m^{5/2}4^{m-1} B H^{2m}\left( 1+m2^{m-1} B H^{2m}\right) ^{m-1}\\\le & {} e^{m(m-1)e} m^{5/2}4^{m-1} B H^{2m}\left( 1+m2^{m-1} B H^{2m}\right) ^{m-1} \\= & {} O\!\left( \left( e^{e+\theta _3}\right) ^{m(m-1)} B H^{2m}\left( 2^{(1+\theta _4)(m-1)} B H^{2m}\right) ^m\right) \\= & {} O\!\left( \left( 2^{1+\theta _4}e^{e+\theta _3}\right) ^{m(m-1)}B^{m+1}H^{2m^2+2m}\right) , \end{aligned}$$

for any $\theta _3,\theta _4\!>\!0$. Observing that $2e^e\!<\!30.31$, we can then clearly pick $\theta _3$ and $\theta _4$ to obtain

$$\begin{aligned} |p'(u_{j'})|+\left| \frac{p''(u_{j'})}{2!}\right| +\cdots +\left| \frac{p^{(m-1)}(u_{j'})}{(m-1)!} \right|= & {} O\!\left( 31^{m(m-1)}B^{m+1}H^{2m^2+2m}\right) , \end{aligned}$$

and thus, combining with Inequality (10), $\frac{1}{\Delta }\!=\!O\!\left( 31^{m(m-1)}B^{m+1}H^{2m^2+4m-2}\right)$, and we obtain Assertion (3) by taking logarithms.

To prove Assertion (4), we merely use the mean value theorem. First, let $\delta '$ be the minimum distance between any critical point $u_j$ of L (with nonzero critical value) and $\zeta '$, where $\zeta '$ is any root of L. Clearly, $\delta \!\ge \!2\delta '\!>\!0$ (thanks to Rolle’s Theorem), so it is enough to prove a sufficiently good lower bound on $\delta '$. Note in particular that if $\delta '\!>\!\Delta /2$, then we are done, thanks to Assertion (3). So let us assume $\delta '\!\le \!\Delta /2$.

Recall that from the proof of Lemma 3.1, we have $L'(u)\!=\!g(u)/\prod \limits ^m_{i=1} (\gamma _{i,1}u+\gamma _{i,0})\nu _i$ where $\nu _i$ is the least common multiple of the denominators of $\gamma _{i,1}$ and $\gamma _{i,0}$.

Clearly, if $\gamma _{i,1}\!\ne \!0$, then $|(\gamma _{i,1}u+\gamma _{i,0})\nu _i|\!=\! \left| u-\frac{-\gamma _{i,0}}{\gamma _{i,1}}\right| |\gamma _{i,1}\nu _i|\!>\! |\gamma _{i,1}\nu _i|\Delta /2\!\ge \!\Delta /2$ for all $u\!\in \!\left[ u_j-\delta ',u_j+\delta '\right]$, since $\zeta '\!\in \!I$, $\frac{-\gamma _{i,0}}{\gamma _{i,1}}$ is a pole of L, and $\gamma _{i,1}\nu _i$ is a nonzero integer. On the other hand, if $\gamma _{i,1}\!=\!0$, then $|(\gamma _{i,1}u+\gamma _{i,0})\nu _i|\!=\!|\gamma _{i,0}\nu _i|\!\ge \!1$ since $\gamma _{i,0}\nu _i$ is a nonzero integer. So then,

$$\begin{aligned} \prod \limits ^m_{i=1}(\gamma _{i,1}u+\gamma _{i,0})\nu _i>\Delta ^m/2^m \text { for all }u\!\in \!\left[ u_j-\delta ',u_j+\delta '\right] . \end{aligned}$$

(12)

By the mean value theorem, we must have $|L'(\xi )|\!=\left| \frac{\varepsilon }{\delta '}\right|$ for some $\xi \!\in \!\left( u_j-\delta ',u_j+\delta '\right)$. So then, thanks to Inequalities (11) and (12), we obtain

$$\begin{aligned} |L'(\xi )|= & {} \left| g(\xi )\bigg /\prod \limits ^m_{i=1}(\gamma _{i,1}\xi +\gamma _{i,0})\nu _i\right| \nonumber \\< & {} m^2 2^{m-1}BH^{2m}\left( 1+m2^{m-1}BH^{2m}\right) ^{m-1}\frac{2^m}{\Delta ^m} \nonumber \\\le & {} m^2 2^{2m-1}BH^{2m}\left( 1+m2^{m-1}BH^{2m}\right) ^{m-1}O\!\left( 31^{m(m-1)}B^{m+1} H^{2m^2+4m-2}\right) ^m\nonumber \\ \end{aligned}$$

(13)

Since $\delta '\!=\!|\varepsilon /L'(\xi )|$ we thus obtain that $\log \delta ' = \log |\varepsilon |-\log |L'(\xi )|$, which is then bounded from

$$\begin{aligned}{} & {} \text {below by}-O\!\left( 61^m\log ^{m+1}\left( \sqrt{B}H^{2m-1}\right) \right) \\{} & {} \quad -O\!\left( \log (m)+m+\log (B)+m\log (H) +m\log \!\left( m2^{m-1}BH^{2m}\right) \right) \\{} & {} \quad -mO\!\left( m^2\log (31)+m\log (B)+m^2\log H\right) , \end{aligned}$$

which reduces to $-O\!\left( 61^m\log ^{m+1}\left( \sqrt{B}H^{2m-1}\right) \right)$. $\square$

3.1 The Complexity of Approximating Logarithms and Real Roots of Polynomials

Any real number can be expressed in binary. Since $2^{\left\lfloor \log _2 x\right\rfloor }\!\le \!x\!\le \!2^{1+\left\lfloor \log _2 x\right\rfloor }$ for any $x\!\in \!\mathbb {R}_+$, it is easy to check that $1+\left\lfloor \log _2 x\right\rfloor$ is the number of bits for the integer part of x. It then makes sense to call the binary expansion of $\left\lfloor 2^{\ell -1-\left\lfloor \log _2 x\right\rfloor }x\right\rfloor$ the $\ell$ most significant bits of an $x\!\in \!\mathbb {R}_+$. Clearly, knowing the $\ell$ most significant bits of x means that one knows x within a multiple of $(1+2^{-\ell })^{\pm 1}$.

Let us recall the following classical fact on approximating logarithms via arithmetic–geometric Iteration:

Theorem 3.5

[13, Sec. 5] Given any positive $x\!\in \!\mathbb {Q}$ of logarithmic height h, and $\ell \!\in \!\mathbb {N}$ with $\ell \!\ge \!h$, we can compute $\left\lfloor \log _2 \max \{1,\log |x|\}\right\rfloor$ and the $\ell$ most significant bits of $\log x$ in time $O(\ell \log ^2\ell )$. $\square$

The underlying technique dates back to Gauss and was refined for computer use in the 1970s by many researchers (see, e.g., [28, 29, 97]). We note that in the complexity bound above, we are applying the recent $O(n\log n)$ algorithm of Harvey and van der Hoeven for multiplying two n-bit integers [56]. Should we use a more practical (but asymptotically slower) integer multiplication algorithm, then the time can still be kept at $O\!\left( \ell ^{1.585}\right)$ or lower.

Recall that bisection is the ancient technique of approximating a root of a continuous function $f : [r_1,r_2] \longrightarrow \mathbb {R}$ by the following trick: If $\textrm{sign}(f(r_1)f(r_2))\!<\!0$, then f must have a root in the open interval $(r_1,r_2)$, and this root lies in the left half-interval $\left( r_1,\frac{r_1+r_2}{2}\right)$ if and only if $\textrm{sign}\!\left( f(r_1)f\!\left( \frac{r_1+r_2}{2}\right) \right) \!<\!0$. Bisection thus allows one to extract an extra bit of precision for a root of f at the cost of one more evaluation of f. Put another way, bisection allows one to halve the size of an isolating interval at the cost of one more evaluation of f.

We will also need the following result on the bit complexity of approximating the real roots of a polynomial in $\mathbb {Z}[x_1]$ by rational numbers.

Lemma 3.6

Suppose $f\!\in \!\mathbb {Z}[x_1]$ has degree d, $|f|_\infty \!\le \!H$, and $\ell \!\in \!\mathbb {N}$ with $\ell \!\ge \!2$. Let $\delta (f)$ denote the minimum of $|\zeta _1-\zeta _2|$ over all distinct real roots $\zeta _1,\zeta _2$ of f. Then, in time

$$\begin{aligned} O\!\left( d^4[\log ^2(H)+\ell (\ell +d^2+d\log H)\log (d \ell \log H)]\right) , \end{aligned}$$

we can find a collection of disjoint non-empty open intervals $\{J_i\}^k_{i=1}$ with the following properties:

• (a) k is the number of real roots of f.

• (b) Each $J_i$ contains exactly one root of f.

• (c) The endpoints of all the $J_i$ are rational numbers with logarithmic height $O(\ell +d^2+d\log H)$.

• (d) All the $J_i$ have width no greater than $2^{-\ell }\delta (f)$.

Proof

The case $\ell \!=\!0$ is well-known in the computational algebra community and is elegantly described in [96]. (In fact, [96] even allows polynomials with real coefficients known only up to a given tolerance.) In particular, we merely apply the real root isolation algorithm from Theorem 24 of [96] to the square-free part, $p\!:=\!f/\gcd (f,f')$, of f: From the proof of Corollary 2.29, we know that $p\!\in \!\mathbb {Z}[x_1]$. Also, by [51, Cor. 11.20] and fast integer multiplication [56] (and the development of [51, Ch. 6]), $\gcd (f,f')$ can be computed within time $O(d^2\log ^2(d)\log (\textrm{d}H)\log ^2(d\log (\textrm{d}H)))$, and this dominates the complexity of the division needed to compute $f/\gcd (f,f')$. Moreover, the coefficients of p have logarithmic height $\log H'\!=\!O(d+\log H)$, thanks to Lemma 2.27. So an overall complexity bound of $O(d^4(d+\log H)^2)$ holds, via the $O(d^4\log ^2 H')$ bit-complexity bound (in our notation) from [96, Thm. 24].

The case of arbitrary $\ell \!\ge \!2$ can be derived simply by applying bisection after using the $\ell \!=\!0$ case to start with isolating intervals that are likely larger than desired, but correct in number, for the real roots of f: One first observes that if $\alpha \!\in \!\mathbb {Q}$ has logarithmic height L, then Proposition 2.23 implies that $f(\alpha )$ has height $O(d\log (H)+d^2L)$. So we can correctly find the sign of $f(\alpha )$ by, say, Horner’s Rule [51], using $O(d\log (H)+d^2L)$ bits of accuracy in all intermediate calculations. Since there are at most d roots, and each application of Horner’s Rule takes O(d) multiplications and additions, we see that the complexity of one step of bisection, applied to all of our initial isolating intervals (to halve the size of each interval), is dominated by $O(d^2)$ many multiplications of integers of height $O(d\log (H)+d^2 L)$. Assuming we use the fast multiplication algorithm of [56], this will take time

$$\begin{aligned}{} & {} O(d^2\cdot (d\log (H)+d^2L)\cdot \log (d\log (H)+d^2L))\nonumber \\{} & {} \quad = O(d^3(\log (H)+dL)\cdot \log (d\log (H)+d^2L)). \end{aligned}$$

(14)

Corollary 2.29 then tells us that $|\log \delta (f)|\!=\!O(d^2+d\log H)$. This means that our bisection must start with at least $L\!=\!O(d^2+d\log H)$ bits of accuracy, and this accuracy will successively increase to $L+\ell$ bits when we finish. So then, by Equality (14), getting $\ell$ additional bits of accuracy beyond the minimum root separation will require time

$$\begin{aligned}&\sum ^{\ell }_{i=0}O\!\left( d^3(\log (H)+d(L+i)) \log (d\log H+d^2(L+i))\right) .&\end{aligned}$$

(15)

Note that $\log (H)+d(L+i)\!=\!O(d^3+d^2\log (H)+di)\!=\!O(d^3(\log (H)+i))$ and thus $\log (d(\log (H)+d(L+i)))\!=\!O(\log (id\log H))$. So each term of the sum (15) admits an upper bound of

$$\begin{aligned} O([d^6+d^5\log (H)+d^4\ell ]\log (\ell d\log H)). \end{aligned}$$

So our final bound is $O(d^4(d+\log H)^2)+\ell \cdot O(d^4(d^2+d\log (H)+\ell )\log (d\ell \log H))$. Cancelling dominant terms, we get our stated bound. $\square$

Remark 3.7

We have opted for a streamlined proof at the expense of a larger complexity estimate. In particular, the exponent of d in our bound can likely be lowered slightly if one uses more sophisticated techniques, some of which are discussed further in [96] and the references therein. $\diamond$

4 Our Main Algorithms and Their Complexity

Our central algorithm for counting roots in ${(\mathbb {R}^*)}^n$ is conceptually simple but ultimately somewhat laborious: Reduce to computing the signs of a linear combination of m logarithms, evaluated at its critical points and poles. To compute the signs at the critical points, we approximate the input to each logarithm, and each resulting summand, to extremely high accuracy. The devil is in the level of accuracy, but thanks to our earlier development, the required accuracy can be estimated explicitly, and the resulting complexity bound is quadratic in $(n^2\log (\textrm{d}H))^{(1+o(1))n}$. We will see an even better conditional speed-up in Sect. 6, but let us first explore what is provable with current technology.

Algorithm 4.1

Input Integers $b_1,\ldots ,b_m$, rational numbers $\gamma _{1,1},\gamma _{1,0},\ldots ,\gamma _{m,1}, \gamma _{m,0},u_0,u_\infty$, with $m\!\ge \!2$, $\gamma _{i,1}u+\gamma _{i,0}\!>\!0$ for all $u\!\in \!(u_0,u_\infty )$ and $i\!\in \!\{1, \ldots ,m\}$, and $\displaystyle {L(u)\!=\!\sum \limits ^m_{i=1}b_i \log \left| \gamma _{i,1} u+\gamma _{i,0}\right| }$ non-constant and differentiable on some non-empty open interval.

Output The signs of L at all its critical points in $(u_0,u_\infty )$.

Description

0.:

Let $B\!:=\!\max _i |b_i|$, $\log H\!:=\!\max \left\{ 1,\max _{i,j} h\!\left( \!\gamma _{i,j}\!\right) \!\right\}$, $\mathscr {A}:= m^2 8^{m-1}BH^{4m-2}$,

$$\begin{aligned} \mathcal {E}:= & {} 1.4\cdot m^{6.5} 30^{m+3}(1+\log m)(1+\log B)\log ^m\mathscr {A},\\ \mathcal {D}:= & {} m^2e+(m+2)\log \left( 8+m2^{m+2}BH^{2m} \right) , \end{aligned}$$

and $\rho \!:=\!1.443(\mathcal {D}+\log (12m)+\mathcal {E})$.

1.:

Compute the polynomial $\displaystyle {g(u)\!:=\!\sum ^m_{i=1}{b_i\gamma _{i,1}\nu _i \prod \limits ^m_{j=1}(\gamma _{j,1}u +\gamma _{j,0})\nu _j/ ((\gamma _{i,1}u+\gamma _{i,0})\nu _i)}}$,where $\nu _i$ denotes the least common multiple of the denominators of $\gamma _{i,1}$ and $\gamma _{i,0}$.

2.:

Via Lemma 3.6, find respective isolating intervals $J_1,\ldots ,J_{k-1}$ to the roots $u_1\!<\cdots <\!u_{k-1}$ of g in $(u_0,u_\infty )$ such that each $J_i$ has width no greater than $2^{-\rho }$.

3.:

For all $i\!\in \!\{1,\ldots ,k-1\}$ do:

4.:

Let $\bar{u}_i\!:=\!\frac{\sup J_i+\inf J_i}{2}$.

5.:

For all $j\!\in \!\{1,\ldots ,m\}$ do:

6.:

Compute, via Theorem 3.5, a rational number $L_j$ agreeing with $\log |\gamma _{j,1}\bar{u_i}+\gamma _{j,0}|$          in its first $\left\lceil 1.443\mathcal {E}+\log _2(6m)\right\rceil$ most significant bits.

7.:

End For

8.:

Let $\mathscr {L}_i\!:=\!\sum \limits ^m_{j=1}b_jL_j$ and$\theta _i\!:=\!\textrm{sign}(\mathscr {L}_i)$.

9.:

If $|\mathscr {L}_i|\!>\!\frac{1}{2}2^{-1.443\mathcal {E}}$ then

10.:

Output “The sign of L at $u_i$ is $\theta _i$.”

11.:

Else

12.:

Output “$L(u_i)\!=\!0$.”

13.:

End If

14.:

End For

Lemma 4.2

Algorithm 4.1 is correct and runs in time

$$\begin{aligned} O\!\left( 901^m (\log (B)+m\log H)^{2m}\log ^2(B)\log ^2(\log (B)+m\log H)\right) . \end{aligned}$$

Proof

The correctness of our algorithm follows directly from Theorem 2.25 and Lemmata 3.1 and 3.4. First note that the classical inequality $1-\frac{1}{x}\le \log x \le x-1$ (for all $x\!>\!0$), yields $\frac{s}{v+s} \le \log (v+s)-\log v \le \frac{s}{v}$ (for all $v\!>\!0$ and $s\!>\!-v$), upon setting $x\!=\!\frac{v+s}{v}$. Setting $v\!=\!\gamma _{j,1}\bar{u}_j+\gamma _{j,0}$ and $s\!=\!\gamma _{j,1}(u_j-\bar{u}_j)$, and assuming $\gamma _{j,1}u_j+\gamma _{j,0},\gamma _{j,1}\bar{u}_j+\gamma _{j,0}\!>\!0$, we then obtain

$$\begin{aligned} \frac{(u_j-\bar{u}_j)\gamma _{j,1}}{\gamma _{j,1}u_j+\gamma _{j,0}} \le \log (\gamma _{j,1}u_j+\gamma _{j,0})- \log (\gamma _{j,1}\bar{u}_j+\gamma _{j,0}) \le \frac{(u_j-\bar{u}_j)\gamma _{j,1}}{\gamma _{j,1}\bar{u}_j+\gamma _{j,0}}.\nonumber \\ \end{aligned}$$

(16)

The proof of Assertion (4) of Lemma 3.4 tells us that $\frac{|\gamma _{j,1}u_j+\gamma _{j,0}|}{|\gamma _{j,1}|}\!\ge \!\Delta /2$. Since $1/\log 2\!<\!1.443$, we have $\Delta \!>\!2^{-1.443\mathcal {D}}$, thanks to the definition of $\mathcal {D}$. So the definition of s tells us that $|u_j-\bar{u}_j|\!\le \!\frac{1}{2} 2^{-1.443\mathcal {D}}$ is sufficient to guarantee that $\frac{|\gamma _{j,1}\bar{u}_j+\gamma _{j,0}|}{|\gamma _{j,1}|}\!\ge \!\Delta /2$. So, by Inequality (16), we obtain that $|u_j-\bar{u}_j|\!\le \!2^{-\rho }$ guarantees $|\log (\gamma _{i,1}u_i+\gamma _{i,0})-\log (\gamma _{i,1}\bar{u}_i+\gamma _{i,0})| \!\le \!\frac{1}{6m}2^{-1.443\mathcal {E}}$. Should $\gamma _{i,1}u+\gamma _{i,0}\!<\!0$ we can repeat our preceding argument, with a sign flip, to obtain that $|u_j-\bar{u}_j|\!\le \!2^{-\rho }$ guarantees $|\log |\gamma _{i,1}u_i+\gamma _{i,0}|-\log |\gamma _{i,1}\bar{u}_i+\gamma _{i,0}|| \!\le \!\frac{1}{6m}2^{-1.443\mathcal {E}}$. So then, thanks to Step 6 and the Triangle Inequality, we see that our algorithm computes, for each $i\!\in \!\{1,\ldots ,k-1\}$, a rational $\mathscr {L}_i$ such that $|L(u_i)-\mathscr {L}_i|\!\le \!\frac{1}{3}2^{-1.443\mathcal {E}}$.

Theorem 2.25 then tells us that $|L(u_i)|$ is either 0 or strictly greater than $2^{-1.443\mathcal {E}}$. So the threshold on $|\mathscr {L}_i|$ from Step 9 indeed correctly distinguishes between $L(u_i)$ being nonzero or zero, and the signs of $L(u_i)$ and $\mathscr {L}_i$ also match when $L(u_i)\!\ne \!0$ thanks to our chosen accuracy. In other words, our algorithm is correct.

We now analyze the complexity of our algorithm. First note that H, $\mathscr {A}$, $\mathcal {E}$, $\mathcal {D}$, and $\rho$ need not be computed exactly: it is sufficient to work with the ceilings of these quantities, or even the smallest powers of 2 respectively greater than these quantities. In particular, these parameters can easily be computed via standard efficient methods for computing the exponential function [1] (along with Theorem 3.5) and thus the complexity of Step 0 is negligible, and in fact asymptotically dominated by Steps 2 and beyond.

Likewise, Step 1 is easily seen to take time within $O(m^2(\log ^2(B)+m\log ^2 H))$, by combining the fast polynomial multiplication method from, say, [51, Sec. 8.4] with the fast integer multiplication method of Harvey and van der Hoeven [56].

Lemma 3.1 tells us that the complexity of Step 2 can be estimated by replacing $(d,H,\ell )$ in the statement of Lemma 3.6 by $(m-1,m2^{m-1}BH^{2m},\rho )$. Noting that $\rho \!=\!O(\mathcal {E})$ and $m^r,\log ^r B, \log ^r H\!=\!O(\mathcal {E})$ for any $m\!\ge \!r\!>\!0$, Lemma 3.6 then tells us that Step 2 takes time

$$\begin{aligned}{} & {} O(m^4[\log ^2(m2^{m-1}BH^{2m})+\rho (\rho +m^2 +m\log (m^2 2^{m-1}BH^{2m})) \nonumber \\{} & {} \quad \log (\rho m\log (m\cdot m2^{m-1}B^{2m}))]) \nonumber \\{} & {} \quad = O(m^4\mathcal {E}^2\log ^2\mathcal {E}). \end{aligned}$$

(17)

Thanks to Theorem 3.5, a simple over-estimate for the complexity of Step 6 is $O(\mathcal {E}\log ^2\mathcal {E})$, so then the time spent in (each run of) Steps 4–7 in total is $O(m\mathcal {E}\log ^2\mathcal {E})$. Since $k-1\!\le \!m-1$, Steps 3–14 then take time no greater than $O(m^2\mathcal {E}\log ^2 \mathcal {E})$.

We thus see, from comparison to Estimate (17), that Step 2 in fact dominates the asymptotic complexity of our entire algorithm. Since $m^r\!=\!O((1+\varepsilon )^m)$ for any fixed $r,\varepsilon \!>\!0$, we have that $\mathcal {E}\!=\!O(\log (B)(30+\varepsilon )^m(\log (B)+m\log H)^m)$. Since $\log \mathcal {E}\!=\!O(m\log (\log (B)+m\log H))$, we see similarly that the complexity of our algorithm is

$$\begin{aligned} O\!\left( (900+\varepsilon )^m (\log (B)+m\log H)^{2m}\log ^2(B) \log ^2(\log (B)+m\log H)\right) \end{aligned}$$

which is dominated by our stated bound. $\square$

We can now state our algorithm for counting the positive roots of circuit systems:

Algorithm 4.3

Input Polynomials $f_1,\ldots , f_n\!\in \!\mathbb {Z}\!\left[ x^{\pm 1}_1,\ldots , x^{\pm 1}_n\right]$ with $A\!:=\!\bigcup _i \textrm{Supp}(f_i)$ a circuit and $\#A\!=\!n+2$.

Output The number of roots of $F\!=\!(f_1,\ldots ,f_n)$ in $\mathbb {R}^n_+$.

Description

• 0. Find the unique (up to sign) minimal circuit relation $b\!\in \! \mathbb {Z}^{(n+2)\times 1}$ of A, and re-index the points of b and A so that $b_{m+1}\!=\cdots =\!b_n\!=\!0$ and the unique non-degenerate sub-circuit $\Sigma$ of A is $\Sigma \!=\!\{a_1,\ldots ,a_m,a_{n+1},a_{n+2}\}$. Then, translate $a_1,\ldots ,a_{n+1}$ by $-a_{n+2}$, and set $a_{n+2}\!:=\!\textbf{O}$.

• 1. Letting $[c_{i,j}]$ be the coefficient matrix of F, check whether all the $n\times n$ sub-matrices of $[c_{i,j}]$ are non-singular. If not, then output

“Your system might have infinitely many roots but I’m not sure: Please check if there are any updates to this algorithm, addressing the cases of vanishing minors for the coefficient matrix.”

and STOP.

• 2. Reduce $F\!=\!\textbf{O}$ to a system of equations of the form $G\!=\!\textbf{O}$, where $G\!:=\!(g_1,\ldots ,g_n)$ and $g_i(x)\!:=\!x^{a_i}-\gamma _{i,1}x^{a_{n+1}}-\gamma _{i,0}$ for all i.

• 3. Let $\displaystyle {L(u)\!:=\!b_{n+1}\log |u| +\sum \limits ^m_{i=1} b_i\log |\gamma _{i,1}u+\gamma _{i,0}|}$ and

  $$\begin{aligned} \displaystyle {I\!:=\!\left\{ u\!\in \!\mathbb {R}_+ \; | \; \gamma _{i,1}u+\gamma _{i,0}\!>\!0 \text { for all } i\!\in \!\{1,\ldots ,n\}\right\} }. \end{aligned}$$

• 4. Via Algorithm 4.1 and Proposition 2.19, compute the number, N, of roots of L in I, and output N.

Example 4.4

Depending on the coefficient matrix of F, the number of poles of L can certainly be smaller than $m+1$: For instance, one can directly build a $4\times 4$ circuit system $F\!\in \!(\mathbb {Z}[x_1,x_2,x_3,x_4])^4$ yielding, say,

$$\begin{aligned} L(u)\!=\!2\log |u|+\log |u+1|+2\log |2u+2|+3\log |9u+9|-5\log |7u+7| \end{aligned}$$

and $b\!=\![1,2,3,-5,2,-3]^\top$. This L clearly has just 2 poles: 0 and $-1$. $\diamond$

Lemma 4.5

Algorithm 4.3 is correct and runs in time

$$\begin{aligned} O\!\left( (31n^2\log (n\textrm{d}H))^{2n+2}(\log (nd)\log (n\log (\textrm{d}H)))^2\right) , \end{aligned}$$

where d is the largest absolute value of an entry of A and $H\!:=\!\max _i|f_i|_\infty$.

Proof

First note that Step 1 tests a natural genericity condition mentioned earlier, and the algorithm proceeds to Step 2 if and only if the genericity condition holds. So let us assume we have proceeded to Step 2.

Observe then that the sum L from Step 3 is non-constant and differentiable on a non-empty open sub-interval $J\!\subseteq \!\mathbb {R}_+$: By the sub-matrix non-singularity assumption of Step 1, the $\gamma _{i,j}$ must all be nonzero, and thus any cancellation between terms of L can not affect the term $b_{n+1}\log |u|$. So then $J\!=\!\mathbb {R}_+$ if $\gamma _{i,j}\!>\!0$ for all i and j, and $J\!=\!\left( 0,\min \limits _{\gamma _{i,1}\gamma _{i,0}<0} \{-\gamma _{i,0}/\gamma _{i,1}\}\right)$ otherwise.

Letting $u_0\!:=\!\inf I$, $u_\infty \!:=\!u_k\!:=\!\sup I$, and letting $u_1\!<\cdots <\!u_{k-1}$ be the critical points of L in I as before, note that the sign of $\lim _{u\rightarrow u^+_0} L(u)$ is either $-\textrm{sign}(b_{n+1})$ (if $u_0\!=\!0$) or $-\textrm{sign}\left( \sum \limits _{u_0=-\gamma _{i,0}/\gamma _{i,1}} b_i \right)$. Similarly, the sign of $\lim _{u\rightarrow u^-_k} L(u)$ is simply $-\textrm{sign}\left( \sum \limits _{u_k=-\gamma _{i,0}/\gamma _{i,1}} b_i \right)$ (resp. $-\textrm{sign}(b_{n+2})$) if $u_k\!<\!\infty$ (resp. $u_k\!=\!+\infty$). So the use of Proposition 2.19 is clear.

The correctness of Algorithm 4.3 then follows directly from Lemmata 2.15, Proposition 2.19, and Lemma 4.2. So we now analyze the complexity of our algorithm.

Thanks to Lemmata 2.1 and 2.2, it is clear that Steps 0–3 are doable in time $n^{3.373}\log ^{1+o(1)}(nd)+ n^{4.373}\log ^{1+o(1)}(nH)$. This will not be the dominant part of the algorithm: Observing that $h(\gamma _{i,j})\!=\!O(n\log (nH))$ and $h(b_i)\!=\!O(n\log (nd))$ for all i, j (simply by Hadamard’s Inequality and Cramer’s Rule), the proof of Lemma 4.2 tells us that applying Algorithm 4.1 and Proposition 2.19 (with $m\!\le \!n+1$) takes time

(18)

for any fixed $\varepsilon \!>\!0$. Note in particular that the underlined expressions are clearly bounded from above by:

$$\begin{aligned} n^2+n^2\log (d)+n^2\log (nH)\!\le \!n^2(1+\log (n\textrm{d}H)), \end{aligned}$$

provided $n,d,H\!\ge \!1$. So the O-estimate from (18) is bounded from above by

$$\begin{aligned} O\!\left( ((30+\varepsilon ')(n^2\log (n\textrm{d}H))^{2n+2}\log ^2(nd) \log ^2(n^2\log (n\textrm{d}H))\right) \end{aligned}$$

for any $\varepsilon '\!>\!\varepsilon$. Since $n^2\log (n\textrm{d}H)\!=\!n^2\log (n)+n^2\log (\textrm{d}H) \!\le \!n^3+n^3\log ^3(\textrm{d}H)\!=\!O((n\log (\textrm{d}H))^3)$, we are done. $\square$

We are now ready to state the analogue of Lemma 4.5 for counting roots in ${(\mathbb {R}^*)}^n$:

Lemma 4.6

Given any $(n+2)$-nomial $n\times n$ system $F\!=\!(f_1,\ldots , f_n)\!\in \!\mathbb {Z}\!\left[ x^{\pm 1}_1,\ldots ,x^{\pm 1}_n\right] ^n$ supported on a circuit A with cardinality $n+2$, we can count exactly the number of roots of F in ${(\mathbb {R}^*)}^n$ in time $O\!\left( (31n^2\log (n\textrm{d}H))^{2n+2}(\log (nd)\log (n\log (\textrm{d}H)))^2\right)$, where d is the largest absolute value of an entry of A and $H\!:=\!\max _i|f_i|_\infty$.

Proof

The proof is almost identical to that of Lemma 4.5, save that we apply Corollary 2.22 instead of Proposition 2.19, Lemma 2.20 instead of Lemma 2.15, and that we use a modified version of Algorithm 4.3.

In particular, the modifications to Algorithm 4.3 are that (a) the output is now the number of roots in ${(\mathbb {R}^*)}^n$, (b) we re-index so that $b_{n+1}$ is odd and (c) we replace Step 4 by Step 4’ stated below: $\square$

Note in particular that b must have an odd coordinate since minimal circuit relations are assumed to have relatively prime coordinates. Also, the left or right-handed limits of L at a real (possibly infinite) pole are easy to compute via the sign of a suitable sum of $b_i$ (if the pole is finite) or the sign of $-b_{n+2}$ (if the pole is $\pm \infty$), as in the proof of Lemma 4.5. The correctness of our modified algorithm is then immediate.

The complexity analysis for our modified algorithm is almost identical to that of Algorithm 4.3, save that there is extra work taking time $O(n\cdot n^2)$ to compute the signs of $\Lambda (u_i)$ and the $\Gamma '_j(u_i)$. This is negligible compared to the other steps, so our final asymptotic complexity bound remains the same.

Remark 4.7

Reducing counting the roots of F in ${(\mathbb {R}^*)}^n$ to counting the roots of L in $\le \!n+2$ sub-intervals of $\mathbb {R}$ (as in our proof above) is much more efficient than naively applying Algorithm 4.3 to each of the $2^n$ orthants of ${(\mathbb {R}^*)}^n$. In particular, our proof helps enable the conditional speed-up to time $(n\log (\textrm{d}H))^{O(1)}$ from Theorem 1.6. $\diamond$

5 Affine Roots and Proving Theorem 1.1

Before finally proving our main theorem, we will need to establish some simple facts on roots of over-determined systems on coordinate subspaces. Our first observation is immediate from basic convexity (see, e.g., [54, Ch. 3–4]).

Proposition 5.1

If $A\!\subset \!\mathbb {Z}^n$ is a circuit (resp. the vertex set of a simplex), and X is any coordinate subspace of $\mathbb {R}^n$, then $A\cap X$ is either empty, the vertex set of a simplex, or a circuit (resp. either empty or the vertex set of a simplex). Furthermore, for any given circuit A, there is at most one coordinate subspace X with $A\cap X$ a non-degenerate circuit. $\square$

For any $I\!\subseteq \!\{1,\ldots ,n\}$ let $\mathbb {C}_I\!:=\!\{(x_1,\ldots , x_n)\!\in \!\mathbb {C}^n\; | \; i\!\in \!\{1,\ldots ,n\}\setminus I\Longrightarrow x_i\!=\!0\}$ and $\mathbb {C}^*_I\!:=\!\{(x_1,\ldots , x_n)\!\in \!\mathbb {C}^n\; | \; i\!\in \!\{1,\ldots ,n\}\setminus I\Longleftrightarrow x_i\!=\!0\}$. Note that $\mathbb {C}_\emptyset \!=\!\mathbb {C}^*_\emptyset \!=\!\{\textbf{O}\}$, $\mathbb {C}_I$ is a coordinate subspace of dimension $\#I$, and $\mathbb {C}^*_I$ is a dense open subset of $\mathbb {C}_I$ that we will call a sub-orbit. We also define $\mathbb {R}_I\!:=\!\mathbb {C}_I\cap \mathbb {R}^n$ and $\mathbb {R}^*_I\!:=\!\mathbb {C}^*_I\cap \mathbb {R}^n$. Note that if $I\!\subseteq \!J$, then $\mathbb {C}_I\!\subseteq \!\mathbb {C}_J$ and $\mathbb {C}_J$ is the disjoint union of $\mathbb {C}^*_I$ over all $I\!\subseteq \!J$. The corresponding containments hold for $\mathbb {R}_I$, $\mathbb {R}_J$, and $\mathbb {R}^*_I$ as well. In particular, $\mathbb {R}^*_{\{i\}}$ is the real $x_i$-axis sans the origin.

Lemma 5.2

Suppose $f\!\in \!\mathbb {C}\!\left[ x^{\pm 1}_1,\ldots ,x^{\pm 1}_n\right]$, $I\!\subseteq \!\{1,\ldots ,n\}$, and f is well-defined on $\mathbb {C}^*_I$. Then, f vanishes on all of $\mathbb {C}^*_I \Longleftrightarrow A\cap \mathbb {R}_I\!=\!\emptyset$.

Proof

By symmetry, we can simply permute coordinates so that $I\!=\!\{1,\ldots ,r\}$. By the Ideal-Variety Correspondence in the coordinate ring $R\!:=\!\mathbb {C}\! [x^{\pm 1}_1,\ldots ,x^{\pm 1}_r,x_{r+1},\ldots ,x_n]$ (see, e.g., [60, Thm. 1.23]), f vanishing on all of $\mathbb {C}^*_I$ is equivalent to f lying in the ideal of R generated by $x_{r+1},\ldots ,x_n$. Equivalently, for each monomial $x^s\!:=\!x^{s_1}_1\cdots x^{s_n}_n$ of f there must be an $i\!\in \!\{r+1,\ldots ,n\}$ with $x_i|x^s$. But then this is equivalent to each monomial $x^s$ of f having $s_i\!>\!0$ for some $i\!\in \!\{r+1,\ldots ,n\}$. In other words, $(s_1,\ldots ,s_n)$ can not lie in $\mathbb {R}_I$. $\square$

Lemma 5.3

[52, Ch. 8] Suppose $A\!=\!\{a_1,\ldots ,a_t\}\!\subset \!\mathbb {Z}^n$ has cardinality t and does not lie in any affine hyperplane, and $F\!=\!(f_1,\ldots ,f_{n+1})$ with $f_i(x)\!=\!\sum ^t_{j=1} c_{i,j} x^{a_j}$ for all i and the $c_{i,j}$ indeterminates. Then, there is an irreducible polynomial

$$\begin{aligned} R_A\!\in \!\mathbb {Z}\!\left[ c_{i,j}\; | \; (i,j)\!\in \!\{1,\ldots ,n\}\times \{1, \ldots ,t\}\right] \setminus \{0\}, \end{aligned}$$

such that $\left[ [c_{i,j}]\!\in \!\mathbb {C}^{n\times t}\right.$ and $\left. R_A(\ldots ,c_{i,j},\ldots )\!\ne \!0\right] \Longrightarrow F$ has no roots in ${(\mathbb {C}^*)}^n$. In particular, we can pick $R_A$ so that $\deg R_A\!\le \!(n+1)\cdot n!V$ (where V is the volume of the convex hull of A, normalized so that the unit n-cube has volume 1) and, if $t\!=\!n+1$, then we can use $R_A\!=\!\det [c_{i,j}]$. $\square$

Example 5.4

When $t\!=\!n+2$ the polynomial $R_A$ can already be far more unwieldy than an $(n+1)\times (n+1)$ determinant. For instance, with $n\!=\!1$, $A\!=\!\{0,1,d\}$, and $d\!\ge \!2$, the corresponding over-determined circuit system yields $R_A$ being a $2d\times 2d$ determinant (a special case of the Sylvester resultant) having degree 2d. One can also check via any reasonable computer algebra system that such an $R_A$ has exactly $3d+1$ monomial terms, at least for $d\!\in \!\{2,\ldots ,100\}$. $\diamond$

The polynomial $R_A$ above is an example of a sparse resultant, and is one of many ways to formulate the fact that $(n+1)$-tuples of n-variate polynomials generically have no roots in ${(\mathbb {C}^*)}^n$. The same of course holds for $(n+k)$-tuples of n-variate polynomials for $k\!\ge \!2$, but then the sufficient condition need not be determined by an irreducible polynomial that is unique up to sign.

Example 5.5

Consider $F\!=\!(c_1+c_2x_1,c_3+c_4x_1,c_5+c_6x_1)$. Then, the non-vanishing of either of $\det {\begin{bmatrix} c_1 &{} c_2\\ c_3 &{} c_4 \end{bmatrix}}$ or $\det {\begin{bmatrix} c_3 &{} c_4\\ c_5 &{} c_6 \end{bmatrix}}$ suffices to make F have no roots in $\mathbb {C}^*$. Put another way, the non-vanishing of the resultant of some sub-pair of the original triple of polynomials suffices to obstruct roots in $\mathbb {C}$ for the triple. $\diamond$

From Lemma 5.3 (and using resultants of suitable sub-$(d+1)$-tuples of F restricted to d-dimensional coordinate subspaces), it is easy to see that if $A\cap X$ is non-empty for every coordinate subspace $X\!\subset \!\mathbb {R}^n$, then a generic $n\times n$ system F supported on A can have no roots on the union of coordinate hyperplanes in $\mathbb {C}^n$. We will need a more explicit refinement of this fact.

Lemma 5.6

Suppose $A\!=\!\{a_1,\ldots ,a_t\}\!\subset \!\mathbb {Z}^n$ has cardinality $t\!\le \!n+2$ and does not lie in any affine hyperplane, $I\!:=\!\{i\!\in \!\{1,\ldots ,n\} \; | \; \min \limits _{(a_1,\ldots ,a_n)\in A} a_i\!<\!0\}$, and $F\!=\!(f_1,\ldots ,f_n)$ with $f_i(x)\!=\!\sum ^t_{j=1} c_{i,j} x^{a_j}\!\in \! \mathbb {R}\!\left[ x^{\pm 1}_1,\ldots ,x^{\pm 1}_n\right]$ for all $i\!\in \!\{1,\ldots ,n\}$. Suppose further that every square sub-matrix of $[c_{i,j}]$ is non-singular and, if $A\cap Y$ contains a non-degenerate sub-circuit for some proper coordinate subspace $Y\!\subsetneqq \!\mathbb {R}^n$, assume further that $R_{A\cap Y}(G)\!\ne \!0$ for some sub-tuple $G\!:=\! (f_\ell \; | \; \ell \!\in \!M)$ of F with $\#M\!=\!1+\dim Y$. Then, for all $J\!\supseteq \!I$ we have that F is well-defined on $\mathbb {C}^*_J$. Furthermore, for $I\!\subseteq \!J\!\ne \! \{1,\ldots ,n\}$, we have that F either vanishes on all of $\mathbb {R}^*_J$ or has no roots in $\mathbb {C}^*_J$, with the latter occuring if and only if $A\cap \mathbb {R}_J\!\ne \!\emptyset$.

Example 5.7

The additional condition involving $A\cap Y$ is necessary when $t\!=\!n+2$: For instance, taking $n\!=\!2$ and $I\!=\!\{1\}$, the system $F\!=\!(1+x_2+2x_1-3x^4_1,1+2x_2+3x_1-4x^4_1)$ has all square sub-matrices of its coefficient matrix non-singular, but F has a unique root in $\mathbb {C}^*_1$: (1, 0). The missing condition is in fact the non-vanishing of the resultant of $c_{1,1}+c_{1,3}x_1+c_{1,4}x^4_1$ and $c_{2,1}+c_{2,3}x_1+c_{2,4}x^4_1$. $\diamond$

Proof of Lemma 5.6:

The statement on F being well-defined on $\mathbb {C}^*_J$ is immediate since the only coordinate hyperplanes possibly containing poles for the $f_\ell$ are $\{x_i\!=\!0\}$ with $i\!\in \!I$.

Let us now assume that there is no subspace Y as stated. Then, the intersection of A with each coordinate subspace of $\mathbb {R}^n$ is the vertex set of a simplex, and Lemma 5.3 combined with our sub-matrix assumption implies that F has no roots in $\mathbb {C}^*_J$ if $A\cap \mathbb {R}_J\!\ne \!\emptyset$. If $A\cap \mathbb {R}_J\!=\!\emptyset$ then Lemma 5.2 implies that F vanishes on all of $\mathbb {C}^*_J$, and thus on all of $\mathbb {R}^*_J$.

Should there instead be a subspace Y as stated, then Lemma 5.3 combined with our augmented genericity assumption implies that F has no roots in $\mathbb {C}^*_J$ if $A\cap \mathbb {R}_J\!\ne \!\emptyset$. If $A\cap \mathbb {R}_J\!=\!\emptyset$, then Lemma 5.2 implies that F vanishes on all of $\mathbb {C}^*_J$, and thus on all of $\mathbb {R}^*_J$. $\square$

5.1 The Proof of Theorem 1.1

For convenience, let us first name the genericity assumptions we defined above:

$G^*_+$: Every $n\times n$ sub-matrix of $[c_{i,j}]$ is non-singular. $\diamond$

$G_{\textrm{aff}}$: Every square sub-matrix of $[c_{i,j}]$ is non-singular and, if $A\cap Y$ contains a non-degenerate sub-circuit for some proper coordinate subspace $Y\!\subsetneqq \!\mathbb {R}^n$, assume further that $R_{A\cap Y}(G)\!\ne \!0$ for some sub-tuple $G\!:=\! (f_\ell \; | \; \ell \!\in \!M)$ of F with $\#M\!=\!1+\dim Y$. $\diamond$

The cases of Theorem 1.1 for root counting in $\mathbb {R}^n_+$ and ${(\mathbb {R}^*)}^n$ then follow respectively from Lemmata 4.5 and 4.6 when $t\!=\!n+2$, under the genericity assumption $G^*_+$. For $t\!=\!n+1$, we simply use Lemma 2.9 and Corollary 2.11 instead. Note in particular that a consequence of Corollaries 2.11 and 2.22 is that F generically has only finitely many roots in ${(\mathbb {R}^*)}^n$.

Let $Z^*$ denote the zero set of F in ${(\mathbb {R}^*)}^n$. To count the roots of F in $\mathbb {R}^n$, let us switch our genericity assumption to $G_{\textrm{aff}}$, and count the roots of F in ${(\mathbb {R}^*)}^n$ as in the last paragraph, save for one small change: We assume our input is generic and skip Step 1 when applying Algorithm 4.3, i.e., we no longer check if our system is generic (since there are exponentially many determinants underlying $G_{\textrm{aff}}$). Observe now that Lemma 5.6 implies that the real zero set of F in $\mathbb {R}^n$ will either be (a) $Z^*\cup \{\textbf{O}\}$, (b) the union of $Z^*$ with a real positive-dimensional sub-orbit, or (c) $Z^*$. So now we merely need to distinguish these possibilities efficiently.

This will reduce to indexing, with complexity negligible compared to Algorithm 4.3 and its variants. First, observe that $\mu _j\!:=\!\min \limits _{(a_1,\ldots ,a_n)\in A} a_j\!>\!0$ for any j implies that $x_j|f_i$ for all i, which in turn implies F has infinitely many roots in $\mathbb {R}^n$. Computing all these minima takes time O(n). So we may assume $\mu _j\!\le \!0$ for all j, and let $I\!:=\!\{j\; | \; \mu _j\!<\!0\}$.

If $I\!=\!\emptyset$ then F is well-defined on all of $\mathbb {C}^n$, and thus F vanishes on all of $\mathbb {R}_J$—for some $J\!\subseteq \!\{1,\ldots ,n\}$ with $\#J\!\ge \!1$—if only if F vanishes on all of $\mathbb {R}^*_{\{j\}}$ for some $j\!\in \!\{1,\ldots ,n\}$. Lemma 5.6 then tells us this happens if and only if $A\cap \{j\}\!=\!\emptyset$. The last condition is decided easily by checking if, for each $\ell \!\in \!\{1,\ldots ,t\}$, $a_\ell$ has a positive $i^{{\underline{\textrm{th}}}}$ coordinate for some $i\!\in \!\{1,\ldots ,n\}\setminus \{j\}$. This can clearly be done in time $O(n^2)$, so let us now assume $I\!\ne \!\emptyset$.

Lemma 5.6 then implies that F has infinitely many roots in $\mathbb {R}^n$ if and only if there is a $J\!\supseteq \!I$ with $J\!\ne \!\{1,\ldots ,n\}$ and $A\cap \mathbb {R}_J\!=\!\emptyset$. The last condition holds if and only if $A\cap \mathbb {R}_I\!=\!\emptyset$ (since $I\!\subseteq \!J \Longrightarrow \mathbb {R}_I\!\subseteq \!\mathbb {R}_J$). Checking $A\cap \mathbb {R}_I\!{\mathop {=}\limits ^{?}}\!\emptyset$ can be done in time $O(n^3)$ simply by checking if, for each $\ell \!\in \!\{1,\ldots ,t\}$, $a_\ell$ has a positive $i^{{\underline{\textrm{th}}}}$ coordinate for some $i\!\in \!\{1,\ldots ,n\}\setminus I$. So we are done, and we see that the complexity of counting the roots of F on the union of real coordinate hyperplanes is well-dominated by the complexity of counting the roots of F in ${(\mathbb {R}^*)}^n$, thanks to our genericity assumptions. $\square$

Remark 5.8

Note that condition $G_\textrm{aff}$ involves the non-vanishing of each entry of $[c_{i,j}]$, as well as the determinants of each $k\times k$ sub-matrix of $[c_{i,j}]$ for $k\!\in \!\{2,\ldots ,n\}$. The product of all these determinants clearly has degree $D\!:=\!n(n+2)+2\left( {\begin{array}{c}n\\ 2\end{array}}\right) \left( {\begin{array}{c}n+2\\ 2\end{array}}\right) +\cdots +n\left( {\begin{array}{c}n\\ n\end{array}}\right) \left( {\begin{array}{c}n+2\\ n\end{array}}\right)$. Since $\sum ^n_{k=0}\left( {\begin{array}{c}n\\ k\end{array}}\right) ^2\!=\!\left( {\begin{array}{c}2n\\ n\end{array}}\right)$, it is then easy to see that $D\!<\!n\left( {\begin{array}{c}2n+4\\ n+2\end{array}}\right) \!=\!2^{O(n)}$. The resultant underlying condition $G_\textrm{aff}$ has degree $(nd)^{O(n)}$, thanks to Lemma 5.3 and Hadamard’s Inequality. So then, the DLSZ Lemma implies that $H\!\ge \!\frac{2^{\Omega (n)}+(nd)^{\Omega (n)}}{\varepsilon }$ is enough to guarantee that at worst an $\varepsilon$-fraction of the $[c_{i,j}]\!\in \! \{-H,\ldots ,H\}^{n\times (n+2)}$ fail condition $G_\textrm{aff}$. This implies our earlier statement on the number of bits needed for H to have $G_\textrm{aff}$ hold with probability $1-\varepsilon$. $\diamond$

Remark 5.9

Unlike our setting here—where we restrict the union of supports to be a circuit of cardinality $n+2$—we conjecture that counting real affine roots for arbitrary binomial systems is $\#\textbf{P}$-hard, parallelling the complex case studied in [34]. Indeed, $n\times n$ binomial systems can have union of supports with cardinality up to 2n, and this complicates counting real roots on coordinate sub-spaces. $\diamond$

6 Conditionally Speeding Up to Time $(n\log (\textrm{d}H))^{O(1)}$: Proving Theorem 1.6

The key to proving our conditional speed-up will be to modify (a) two key bounds from Lemma 3.4 and (b) the initial step of a key algorithm (Algorithm 4.1), by incorporating the Diophantine improvements granted by the RALC should it be true.

Lemma 6.1

Following the notation of Lemma 3.4, if the RALC is true, then we can respectively replace the bounds from Assertions (2) and (4) by:

$$\begin{aligned}{} & {} 2'.\ \ \ \log |\varepsilon |>-O\!\left( (m^2(\log (B)+m\log H))^C\right) .\\{} & {} 4'.\ \ \ \log \delta \ \; > -O\!\left( (m^2(\log (B)+m\log H))^C+m^2(\log (B)+m\log H)\right) . \end{aligned}$$

Proof

The critical juncture is Bound (9), from our proof of Assertion (2) of Lemma 3.4: Replacing the use of the Baker–Wustholtz theorem there with the bound from the RALC immediately yields Bound (2’).

Bound (4’) then follows easily from Bound (13) (near the end of the proof of Lemma 3.4), and the line following that bound, where see that $\log \delta \!\ge \!\log (2)+\log |\varepsilon |-\log |L'(\xi )|$ (in the notation of the proof of Lemma 3.4). So the last term (fully expanded in the proof of Lemma 3.4) accounts for the final term in Bound (4’). $\square$

Lemma 6.2

Suppose the RALC is true, $b_1,\ldots ,b_m\!\in \!\mathbb {Z}$, $\gamma _{1,1},\gamma _{1,0},\ldots ,\gamma _{m,1},\gamma _{m,0},u_0,u_\infty \!\in \mathbb {Q}$, with $m\!\ge \!2$, $\gamma _{i,1}u+\gamma _{i,0}\!>\!0$ for all $u\!\in \!(u_0,u_\infty )$ and $i\!\in \!\{1, \ldots ,m\}$, and $\displaystyle {L(u)\!=\!\sum \limits ^m_{i=1}b_i \log \left| \gamma _{i,1} u+\gamma _{i,0}\right| }$ is non-constant and differentiable on some non-empty open interval. Also let $B\!:=\!\max _i |b_i|$ and $\log H\!:=\!\max \left\{ 1,\max _{i,j} h\!\left( \gamma _{i,j}\right) \right\}$. Then, we can compute the signs of L at all its critical points in $(u_0,u_\infty )$ in time $O(m^{4+2\max \{1,C\}}(\log (B)+m\log H)^{2\max \{1,C\}} \log (m\log (BH)))$.

Proof

We simply use Algorithm 4.1with one crucial change: We replace the definition of $\mathcal {E}$ in Step 0 by $O\!\left( (m^2(\log (B)+m\log H))^C\right)$. We then proceed as in the proof of Lemma 4.2. In particular, Lemma 6.1 tells us that this modified version of Algorithm 4.1 is correct. As for complexity, instead of $\rho \!=\!O(\mathcal {E})$ with the old value of $\mathcal {E}$, the new value of $\mathcal {E}$ yields

$$\begin{aligned} \rho \!=\!O\!\left( m[\log (B)+m\log H]+(m^2(\log (B)+m\log H))^C\right) . \end{aligned}$$

Bound (17) from the proof of Lemma 4.2, combined with our new values of $\mathcal {E}$ and $\rho$, then easily yield complexity $O(m^4\rho ^2(\log (m)+\log \log (B)+ \log \log H))$. This reduces to our stated bound. $\square$

We can now give our final remaining proof.

Proof of Theorem 1.6:

To speed up root counting in $\mathbb {R}^n_+$, we use a modified version of Algorithm 4.3: We use Lemma 6.2 in place of Algorithm 4.1 in Step 4. We then proceed as in the proof of Lemma 4.5. In particular, correctness is immediate. As for complexity, Step 4 of our modified version of Algorithm 4.3 is the dominant part. Our final bound then amounts to substituting $(n+1,n\log (nd),n\log (nH))$ for $(m,\log B,\log H)$ into the bound from Lemma 6.2, easily yielding a complexity bound of

$$\begin{aligned} O\!\left( n^{4+4\max \{1,C\}}(\log (nd)+n\log (nH))^{2\max \{1,C\}} \log (n\log (n\textrm{d}H))\right) , \end{aligned}$$

which is clearly $(n\log (\textrm{d}H))^{O(1)}$.

To speed up root counting in $(\mathbb {R}^n)^*$, we further modify Algorithm 4.3: Lemma 4.6 gives a modification to Step 4 (called Step 4’) that enables counting in ${(\mathbb {R}^*)}^n$ instead of $\mathbb {R}^n_+$. We make one more modification: We replace the use of Algorithm 4.1 in Step 4’ with an application of Lemma 6.2. Continuing as in the proof of Lemma 4.6 then gives us correctness. The complexity analysis is almost identical, save for an extra step involving the quantities $\Lambda (u_i)$ and $\Gamma '_j(u_i)$ (with complexity still negligible compared to the dominant steps). So our bound remains of the same asymptotic order.

To speed up root counting in $\mathbb {R}^n$, the last three paragraphs of the proof of Theorem 1.1 from Sect. 5.1 tell us that we can count roots on the union of real coordinate hyperplanes in $\mathbb {R}^n$ in time $O(n^3)$ simply by checking the intersection of the support A against $\le \!n$ coordinate subspaces, thanks to Lemma 5.6 and our genericity condition $G_{\textrm{aff}}$. So counting roots in ${(\mathbb {R}^*)}^n$ dominates our complexity, and we are done. $\square$

7 Farewell to a Friend

Tien-Yien Li passed away a few months into the COVID-19 pandemic. TY (as he was known to his friends) was an immensely kind and generous man, and a dear friend, in addition to being a great mathematician. Through hours-long grilling sessions in October 1993, at the Centre de Recerca Matematica in Barcelona, he taught me lessons on perseverance, curiosity, scholarship, and generosity that I would always remember. It was there that I also got to know TY and his unique sense of humor. He always faced the greatest difficulties with a smile. I admired him both as a person and a mathematician. I truly miss him.