On the High Frequency Transfer of Mechanical Stimuli from the Surface of the Head to the Macular Neuroepithelium of the Mouse

Abstract

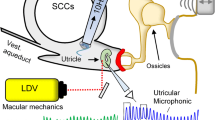
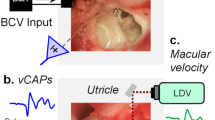
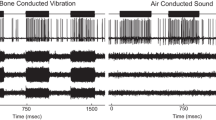
Vestibular macular sensors are activated by a shearing motion between the otoconial membrane and underlying receptor epithelium. Shearing motion and sensory activation in response to an externally induced head motion do not occur instantaneously. The mechanically reactive elastic and inertial properties of the intervening tissue introduce temporal constraints on the transfer of the stimulus to sensors. Treating the otoconial sensory apparatus as an overdamped second-order mechanical system, we measured the governing long time constant (Τ_L) for stimulus transfer from the head surface to epithelium. This provided the basis to estimate the corresponding upper cutoff for the frequency response curve for mouse otoconial organs. A velocity step excitation was used as the forcing function. Hypothetically, the onset of the mechanical response to a step excitation follows an exponential rise having the form Vel_shear = U(1-e^−t/TL), where U is the applied shearing velocity step amplitude. The response time of the otoconial apparatus was estimated based on the activation threshold of macular neural responses to step stimuli having durations between 0.1 and 2.0 ms. Twenty adult C57BL/6 J mice were evaluated. Animals were anesthetized. The head was secured to a shaker platform using a non-invasive head clip or implanted skull screws. The shaker was driven to produce a theoretical forcing step velocity excitation at the otoconial organ. Vestibular sensory evoked potentials (VsEPs) were recorded to measure the threshold for macular neural activation. The duration of the applied step motion was reduced systematically from 2 to 0.1 ms and response threshold determined for each duration (nine durations). Hypothetically, the threshold of activation will increase according to the decrease in velocity transfer occurring at shorter step durations. The relationship between neural threshold and stimulus step duration was characterized. Activation threshold increased exponentially as velocity step duration decreased below 1.0 ms. The time constants associated with the exponential curve were Τ_L = 0.50 ms for the head clip coupling and T_L = 0.79 ms for skull screw preparation. These corresponded to upper −3 dB frequency cutoff points of approximately 318 and 201 Hz, respectively. T_L ranged from 224 to 379 across individual animals using the head clip coupling. The findings were consistent with a second-order mass-spring mechanical system. Threshold data were also fitted to underdamped models post hoc. The underdamped fits suggested natural resonance frequencies on the order of 278 to 448 Hz as well as the idea that macular systems in mammals are less damped than generally acknowledged. Although estimated indirectly, it is argued that these time constants reflect largely if not entirely the mechanics of transfer to the sensory apparatus. The estimated governing time constant of 0.50 ms for composite data predicts high frequency cutoffs of at least 318 Hz for the intact otoconial apparatus of the mouse.

Appendix

Macular Otolith—Lumped Parameter Model

Equation of Motion

The governing equation of motion in terms of the relative displacement x (see Fig. 1) between the otoconial layer (OL) and the hair cell epithelium layer (HCE) of the sensory macula is

$$ m\ddot{x}+c\dot{x}+kx=-m\left(1-\frac{\rho_e}{\rho_{OL}}\right)\left({a}_{\mathrm{x}}-{g}_{\mathrm{x}}\right)=-mBA $$

(A-1)

where the over dot notation on x represents differentiation with respect to time t, x is the shear displacement, $\dot{x}$ is the shear velocity, $\ddot{x}$ is the shear acceleration, m is the mass of the OL and $m\ddot{x}$ is the inertial term, c is the damping coefficient associated with viscous drag and cẋ is the viscous damping term, k is the elastic coefficient, and kx is the elastic term, $B\equiv \left(1-\frac{\rho_{\mathrm{e}}}{\rho_{\mathrm{OL}}}\right)$ is the the buoyancy term of the OL, where ρ _e is the endolymph and tissue density and ρ _OL is the OL density, a _x is the head acceleration, and g _x is the acceleration of gravity, both in the x-direction of the plane of the OL, and combining the two accelerations into a single gravitoinertial acceleration term A ≡ (a _x  − g _x ). The negative sign on the acceleration term indicates that a positive x-displacement of the OL is produced by a negative a _x and positive g _x acceleration components. The x-direction is defined as the direction of the acceleration component in the plane of the macula (Fig. 1). A schematic representation of the lumped parameter mechanical model associated with Eq. A-1 is presented below in the “Lumped Parameter Mechanical Model” section as illustrated in Appendix-Figure 9.

Overdamped System Transfer Function

Dividing by mass m, taking the Laplace transform of Eq. A-1 with zero initial conditions [x(t = 0) = 0; ẋ(t = 0) = 0], where s is the Laplace transform variable, defining X(s) = L[x(t)] and A(s) = L[(A(t))], and solving for the transfer function results in

$$ \frac{X}{A}(s)=-B\frac{1}{\left({s}^2+\frac{c}{m}s+\frac{k}{m}\right)} $$

(A-2)

The ratio of the damping coefficient to mass (c/m) and elastic coefficient to mass (k/m) forms two undetermined coefficients that define the motion of the OL. For an overdamped solution, the denominator of the transfer function can be factored into two first-order terms to approximate the quadratic denominator

$$ \left({s}^2+\frac{c}{m}s+\frac{k}{m}\right)\cong \left(s+\frac{c}{m}\right)\left(s+\frac{k}{c}\right) $$

(A-3)

where the approximation

$$ \frac{c}{m}\gg \frac{k}{c\ }\kern0.5em \mathrm{and}/\mathrm{or}\ \left(\frac{km}{c^2}\right)\ll 1 $$

(A-4)

was used. The transfer function Eq. A-2 then becomes

$$ \frac{X}{A}(s)=-B\frac{1}{\left(s+\frac{c}{m}\right)\left(s+\frac{k}{c}\right)} $$

(A-5)

Overdamped Solution for a Step Change in Acceleration

Subjecting the system to a step in acceleration of magnitude A _x and initiating the step at time t = 0 using the unit step function u(t,) the acceleration becomes

$$ A(s)=\mathrm{\mathcal{L}}\left[{a}_{\mathrm{x}}(t)\right]=\mathrm{\mathcal{L}}\left[{A}_{\mathrm{x}}u(t)\right]={A}_{\mathrm{x}}\frac{1}{s} $$

(A-6)

and the transfer function Eq. A-5 becomes

$$ \frac{X}{A_{\mathrm{x}}}(s)=-B\frac{1}{s\left(s+\frac{c}{m}\right)\left(s+\frac{k}{c}\right)} $$

(A-7)

The inverse Eq. A-7, solving for the displacement as a function of time is

$$ x(t)=-{A}_{\mathrm{x}}B\left(\frac{m}{k}\right)\left[1+\left(\frac{mk}{c^2}\right){e}^{-\left(\frac{t}{\raisebox{1ex}{$m$}\!\left/ \!\raisebox{-1ex}{$c$}\right.}\right)}-{e}^{-\left(\frac{t}{\raisebox{1ex}{$c$}\!\left/ \!\raisebox{-1ex}{$k$}\right.}\right)}\right] $$

(A-8)

Two time constants arise from the overdamped solution; with T _S  = short time constant, and T _L  = long time constant, and they are defined as

$$ {T}_{\mathrm{S}}\equiv \frac{m}{c}\kern0.48em {T}_{\mathrm{L}}\equiv \frac{c}{k} $$

(A-9)

Using the relationship in Eq. A-4, $\left(\frac{mk}{c^2}\right)\ll 1$, it is seen that the second term in square brackets in Eq. A-8 is negligible compared to the other two terms. Eliminating the negligible middle term and using the time constant designation (T _L ), Eq. A-8 becomes

$$ x(t)=-{A}_{\mathrm{x}}B\left(\frac{m}{k}\right)\left[1-{e}^{-\left(\frac{t}{T_L}\right)}\right] $$

(A-10)

where it is seen that the short time constant T _S plays no role in the solution for an overdamped system response to a step in acceleration. This is an approximate solution. The only approximation utilized in this solution was that shown in Eq. A-4, and effects of the approximation are negligible in this solution. This is illustrated in the section below entitled “Overdamped Frequency Response” and in Appendix-Figure 8.

Note: Time constants used here are designated long and short (T _L and T _S ). In almost all earlier literature, these are defined as T ₁ and T ₂ , with T ₁ being the long or larger value time constant. This is true for both the otoliths and semicircular canals. This long-short designation is used here instead of the one-two version in order to avoid confusion.

Velocity of the OL in Response to a Step in Jerk

Jerk J(s) is defined as the time rate of change of acceleration and in terms of the Laplace transform variable it is defined as

$$ J(s)=sA(s) $$

(A-11)

The relative velocity V(s) of the OL in terms of its displacement X(s) in Laplace transform variables is the relative velocity between the OL and HCE, and is defined as

$$ V(s)=sX(s) $$

(A-12)

Combining the above two relationships (Eqs. A-11 and A-12), it is seen that the relationship $\frac{X}{A}(s)=\frac{V}{J}(s)$ and the two transfer factions are identical.

A unit step in J(s) of constant magnitude J _x results in a constant increase in acceleration, starting from zero. The unit step in jerk is defined as

$$ J(s)={J}_{\mathrm{s}}u(t)=\frac{1}{s}{J}_{\mathrm{s}}(s) $$

(A-13)

When the above are substituted into Eq. A-7, it becomes

$$ \frac{X}{A_{\mathrm{x}}}(s)=\frac{V}{J_{\mathrm{x}}}(s)=-B\frac{1}{s\left(s+\frac{c}{m}\right)\left(s+\frac{k}{c}\right)} $$

(A-14)

and it is seen that this expression (Eq. A-14) is identical to Eq. A-7, the right hand side of the transfer functions are identical. Likewise, the time solution for the velocity of the OL in response to a step in jerk of magnitude J_x will be identical to Eq. A-8 and is

$$ v(t)=-{J}_{\mathrm{x}}B\left(\frac{m}{k}\right)\left(1-{e}^{-\left(\frac{t}{T_L}\right)}\right) $$

(A-15)

This relationship was used in the measurements of this work.

Overdamped Frequncy Response

Factoring the two coefficient ratios $\left(\raisebox{1ex}{$c$}\!\left/ \!\raisebox{-1ex}{$m$}\right.\right)$ and $\left(\raisebox{1ex}{$k$}\!\left/ \!\raisebox{-1ex}{$c$}\right.\right)$ out of the denominator of Eq. A-5 results in

$$ \frac{X}{A}(s)=-B\frac{1}{\left(\frac{c}{m}\frac{k}{c}\right)}\frac{1}{\left(1+\frac{s}{\raisebox{1ex}{$k$}\!\left/ \!\raisebox{-1ex}{$c$}\right.}\right)\left(1+\frac{s}{\raisebox{1ex}{$c$}\!\left/ \!\raisebox{-1ex}{$m$}\right.}\right)} $$

(A-16)

and recognizing that the two factored terms are frequencies, that $\left(\frac{c}{m}\frac{k}{c}\right)=\frac{k}{m}={\omega}_n^2$, changing s = jω where $j=\sqrt{-1}$, and converting to magnitude notation in terms of the stimulus frequency ω, Eq. A-16 becomes

$$ \left|\frac{X}{A}\right|\left(\omega \right)=-B\frac{1}{\omega_n^2}\frac{1}{\left(\sqrt{1+{\left(\frac{\omega }{\raisebox{1ex}{$k$}\!\left/ \!\raisebox{-1ex}{$c$}\right.}\right)}^2}\right)\left(\sqrt{1+{\left(\frac{\omega }{\raisebox{1ex}{$c$}\!\left/ \!\raisebox{-1ex}{$m$}\right.}\right)}^2}\right)} $$

(A-17)

The magnitude term $\left|\frac{X}{A}\right|$ of Eq. A-17 has units of reciprocal seconds squared and this term can be converted to a non-dimensional form by dividing the equation by the reciprocal of ω ² _n . Also dividing by the buoyancy term B results in a non-dimensional magnitude form of Eq. A-17

$$ {M}_{\mathrm{ND}}=\left|\frac{X}{A}\right|\left(\frac{\omega_n^2}{B}\right)=-\frac{1}{\left(\sqrt{1+{\left(\frac{\omega }{\raisebox{1ex}{$k$}\!\left/ \!\raisebox{-1ex}{$c$}\right.}\right)}^2}\right)\left(\sqrt{1+{\left(\frac{\omega }{\raisebox{1ex}{$c$}\!\left/ \!\raisebox{-1ex}{$m$}\right.}\right)}^2}\right)} $$

(A-18)

where M_ND is defined as the non-dimensional magnitude.

Equation A-18 can be plotted with the horizontal axis as frequency f in Hz or as non-dimensional frequency defined as ω/ω _n and the vertical axis is in decibels. Using the frequency ratio of the two factors, R, which is defined as

$$ R=\frac{c/m}{k/c}=\frac{\omega_{\mathrm{S}}}{\omega_{\mathrm{L}}} $$

(A-19)

plots for several examples of R values are shown below in Appendix-Figure 8

Appendix-Figure

FIG. 8

Transfer magnitude as a function of R = ω_S/ω_L.

In Appendix-Figure 8 below, the non-dimensional magnitude, Mnd, is plotted in dB and frequency is represented in Hz, where f_L = ω_L/2π, and f_S = ω_S/2π. As can be seen, when R = 1, the two corner frequencies combine to produce a steep roll off slope of −40 dB per frequency decade. At f_L (dashed vertical line), the amplitude of the R = 1 curve is well below the other curves (−6 dB vs. −3 dB) indicating an important influence of f_S on the frequency corner when f_s approaches f_L. However, at higher values of R, f_S has little influence on the magnitude at f_L since curves R = 5, R = 10 and R = ∞ all superpose at f_L. f_S has negligible influence on the magnitudes at f_L in these cases. Dashed curve represents the resulting magnitudes when fs is infinite and this illustrates the slope of −20 dB/decade imposed by f_L alone. In the present study, frequencies well below 1000 Hz are of interest. As can be seen the influence of f_S is negligible below about 700 Hz even for R = 5. f_L = 318 Hz as determined in the present study. It is estimated that R ∼ 10 in the macular system.

Underdamped Transfer Function and Response

Recent work (Dunlap and Grant 2014) has shown that the utricle system dynamics is underdamped in the turtle. It is hypothesized that this may be the case for many animals, especially mammals that have dynamic body and head motion in excess of those of a turtle. Turtles have long flexible necks that are used for feeding strikes that necessitate high-frequency responses from their utricle. The mouse used in these experiments may have an underdamped utricle accelerometer system. Presented here is an underdamped transfer function and it is compared to the overdamped case for the stimulus used in the present study.

An underdamped transfer function is identical to Eq. A-2 and is repeated here with the velocity-jerk relationship included

$$ \frac{X}{A}(s)=\frac{V}{J}(s)=-B\frac{1}{\left({s}^2+\frac{c}{m}s+\frac{k}{m}\right)} $$

(A-20)

The transfer function for a step in acceleration or a step in jerk is

$$ \frac{X}{A_{\mathrm{x}}}(s)=\frac{V}{J_{\mathrm{x}}}(s)=-B\frac{1}{s\left({s}^2+\frac{c}{m}s+\frac{k}{m}\right)} $$

(A-21)

where the magnitudes of the steps have x-subscripts. The Laplace inversion of Eq. A-21 gives the time solution for the step excitation and that is

$$ \frac{x}{A_{\mathrm{x}}}(t)=\frac{v}{J_{\mathrm{x}}}(t)=-B\frac{1}{\omega_n^2}\left[1-\frac{1}{\sqrt{1-{\upzeta}^2}}{e}^{-\left(\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{$2{T}_s$}\right.\right)} \sin \left({\omega}_{\mathrm{d}}t+\varnothing \right)\right] $$

(A-22)

where:

$$ {\omega}_{\mathrm{n}}^2=\frac{k}{m}\kern0.6em 2\zeta {\omega}_{\mathrm{n}}=\frac{c}{m} $$

(A-23)

and ω _n is the natural resonant frequency and ζ is the damping ratio. The damping ratio is ζ < 1 in the case for an underdamped solution (ζ = 1 for critical damping);

$$ {\omega}_{\mathrm{d}}\equiv {\omega}_{\mathrm{n}}\sqrt{1-{\zeta}^2} $$

(A-24)

where ω _d is the damped natural frequency; and

$$ \varnothing ={ \tan}^{-1}\left(\frac{\sqrt{1-{\zeta}^2}}{\zeta}\right),\kern0.75em 0<\varnothing <\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right. $$

(A-25)

where ∅ is the phase angle. The additional terms introduced here are standards used for underdamped solutions. Unlike the overdamped solution, there are no approximations utilized in this solution.

Comparison of Underdamped and Overdamped Models

A comparison of the above underdamped solution (Eq. A-22) with the overdamped solution (Eqs. A-10 and A-15) is made here. The overall transfer function is rewritten in two terms: with amplitude term Amp and a time response term t _resp

$$ \frac{x}{A_{\mathrm{x}}}(t)=\frac{v}{J_{\mathrm{x}}}(t)=\left[ Amp\right]\left[{t}_{resp}\right] $$

(A-26)

where the amplitude $Amp=B\frac{1}{\omega_{\mathrm{n}}^2}$, and thus the amplitudes of the overdamped and underdamped responses are identical and this magnitude is set as one for this comparison. The two time response terms, t _RESP , are represented as

$$ {\left({t}_{resp}\right)}_{OvrDmp}=\left(1-{e}^{-\left(\frac{t}{T_L}\right)}\right) $$

(A-27)

$$ {\left({t}_{resp}\right)}_{UndrDmp}=\left(1-\frac{1}{\sqrt{1-{\upzeta}^2}}{e}^{-\left(\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{$2{T}_s$}\right.\right)} \sin \left({\omega}_dt+\varnothing \right)\right) $$

(A-28)

The underdamped solution (Eq. A-28) was fitted to the data reported in the present study to obtain values for the natural frequency (ω_n), damping ratio (ζ), and sum of the errors squared (Σe²) for the best fit.

Lumped Parameter Mechanical Model

Appendix Figure

FIG. 9

Schematic model representing the configuration of mechanical elements including mass (m), stiffness (k) and viscous drag/damping (C) that govern the response of the otoconial system. Components symbolize elements in the differential Eq. A-1 as follows: Stiffness is represented as a spring with stiffness k, where restoring forces develop with displacement (kx), inertial forces are associated with a lumped otoconial mass (m) and acceleration ($m\ddot{x}$) and the dashpot represents forces associated with viscous drag (C), which develop in association with kinematic velocity ($c\dot{x}$).