$\mathbf {2\times 2}$-Convexifications for convex quadratic optimization with indicator variables

Abstract

In this paper, we study the convex quadratic optimization problem with indicator variables. For the ${2\times 2}$ case, we describe the convex hull of the epigraph in the original space of variables, and also give a conic quadratic extended formulation. Then, using the convex hull description for the ${2\times 2}$ case as a building block, we derive an extended SDP relaxation for the general case. This new formulation is stronger than other SDP relaxations proposed in the literature for the problem, including the optimal perspective relaxation and the optimal rank-one relaxation. Computational experiments indicate that the proposed formulations are quite effective in reducing the integrality gap of the optimization problems.

1 Introduction

We consider the convex quadratic optimization with indicators:

$$\begin{aligned} \text {(QI)}\ \ \ \min \left\{ a'x+b'y+y'Qy: (x,y) \in {\mathcal {I}}_{n} \right\} , \end{aligned}$$

(1)

where the indicator set is defined as

$$\begin{aligned} {\mathcal {I}}_{n} = \left\{ (x,y)\in \{0,1\}^n\times {\mathbb {R}}_+^n: y_i(1-x_i)=0,\; \forall i\in [n] \right\} , \end{aligned}$$

where a and b are n-dimensional vectors, $Q\in {\mathbb {R}}^{n\times n}$ is a positive semidefinite (PSD) matrix and $[n]:= \{1,2, \ldots , n\}$. For each $i \in [n]$, the complementarity constraint $y_i (1-x_i) = 0$, along with the indicator variable $x_i \in \{0,1\}$, is used to state that $y_i=0$ whenever $x_i=0$. Numerous applications, including portfolio optimization [12], optimal control [26], image segmentation [34], signal denoising [9] are either formulated as $\text {(QI)}$ or can be relaxed to $\text {(QI)}$.

Building strong convex relaxations of $\text {(QI)}$ is instrumental in solving it effectively. A number of approaches for developing linear and nonlinear valid inequalities for $\text {(QI)}$ are considered in literature. Dong and Linderoth [22] describe lifted linear inequalities from its continuous quadratic optimization counterpart with bounded variables. Bienstock and Michalka [13] derive valid linear inequalities for optimization of a convex objective function over a non-convex set based on gradients of the objective function. Valid linear inequalities for $\text {(QI)}$ can also be obtained using the epigraph of bilinear terms in the objective [e.g. 14, 20, 30, 39]. In addition, several specialized results concerning optimization problems with indicator variables exist in the literature [6, 10, 11, 16, 19, 27, 28, 37, 40].

There is a substantial body of research on the perspective formulation of convex univariate functions with indicators [1, 21,22,23, 29, 33, 44]. When Q is diagonal, $y'Qy$ is separable and the perspective formulation provides the convex hull of the epigraph of $y'Qy$ with indicator variables by strengthening each term $Q_{ii}y_i^2$ with its perspective counterpart $Q_{ii}y_i^2/x_i$, individually. For the general case, however, convex relaxations based on the perspective reformulation may not be strong. The computational experiments in [25] demonstrate that as Q deviates from a diagonal matrix, the performance of the perspective formulation deteriorates.

Beyond the perspective reformulation, which is based on the convex hull of the epigraph of a univariate convex quadratic function with one indicator variable, the convexification for the ${2\times 2}$ case has received attention recently. Convex hulls of univariate and ${2\times 2}$ cases can be used as building blocks to strengthen $\text {(QI)}$ by decomposing $y'Qy$ into a sequence of low-dimensional terms. Castro et al. [17] study convexification of a special class of two-term quadratic function controlled by a single indicator variable. Jeon et al. [36] give conic quadratic valid inequalities for the ${2\times 2}$ case. Frangioni et al. [25] combine perspective reformulation and disjunctive programming and apply them to the ${2\times 2}$ case. Atamtürk et al. [8] study the convex hull of the mixed-integer set

$$\begin{aligned} \mathcal {Z}_-:=\left\{ (x,y,t) \in {\mathcal {I}}_{2} \times {\mathbb {R}}_+:t\ge d_1y_1^2-2y_1y_2+d_2y^2_2 \, \right\} , \end{aligned}$$

with coefficients $d \in \mathcal {D}:= \{d \in {\mathbb {R}}^2: d_1\ge 0, \, d_2\ge 0, \, d_1d_2\ge 1\}$, which subsumes the case where $d_1=d_2=1$ considered in [4]. The conditions on the coefficients $d_1, d_2$ imply convexity of the quadratic function. Atamtürk and Gómez [5] study the case where the continuous variables are free and the rank of the coefficient matrix is one in the context of sparse linear regression. Anstreicher and Burer [3] give an extended SDP formulation for the convex hull of the $2 \times 2$ bounded set $\left\{ (y,yy',xx'):0\le y\le x\in \{0,1 \}^2\right\}$. Their formulation does not assume convexity of the quadratic function and contain PSD matrix variables X and Y as proxies for $xx'$ and $yy'$ as additional variables. De Rosa and Khajavirad [18] give the explicit convex hull description of the set $\left\{ (y,yy',xx'):(x,y)\in \mathcal {I}_2\right\}$. Anstreicher and Burer [2] study computable representations of convex hulls of low dimensional quadratic forms without indicator variables. More general convexifications for low-rank quadratic functions [7, 31] or quadratic functions with tridiagonal matrices [38] have also been proposed.

To design convex relaxations for $\text {(QI)}$ based on convexifications for simpler substructures, a standard approach is to decompose the matrix Q as $Q=R+\sum _{j\in J}Q_j$, for some index set J, where $R,Q_j\succeq 0$, $j\in J$. After writing problem (1) as

$$\begin{aligned} \min \;&a'x+b'y+y'Ry+\sum _{j\in J}t_j \end{aligned}$$

(2a)

$$\begin{aligned} \text {s.t.}\,&t_j\ge y'Q_jy&\forall j\in J\end{aligned}$$

(2b)

$$\begin{aligned}&(x,y) \in {\mathcal {I}}_{n},\; t\in {\mathbb {R}}_+^{J}, \end{aligned}$$

(2c)

formulation (2) can then be strengthened based on convexifications of the simpler structures induced by constraints (2b) (e.g., matrices $Q_j$ are diagonal or $2\times 2$). There are two main approaches to implement convexifications based on (2). On the one hand, one may choose fixed R,  $Q_j, \, j \in J$, a priori and treat them as parameters, as done in [7, 24, 25, 38, 45], resulting in simpler formulations (e.g., conic quadratic representable) that may be amenable to use with off-the-shelf solvers for mixed-integer optimization. On the other hand, one may treat matrices $R,Q_j$, $j \in J$, as decision variables that are chosen with the goal of obtaining the optimal relaxation bound after strengthening, as done in [5, 8, 21]. The resulting formulations with the second approach are stronger but typically more complex to represent. In general, neither approach is preferable to the other.

1.1 Contributions

The contributions of this paper are two-fold.

1.1.1 1. ${2\times 2}$ case: we describe the convex hull of the epigraph of a convex bivariate quadratic with a positive cross product and indicators.

Consider

$$\begin{aligned} \mathcal {Z}_+:=\left\{ (x,y,t)\in {\mathcal {I}}_{2}\times {\mathbb {R}}_+:t\ge d_1y_1^2+2y_1y_2+d_2y^2_2 \, \right\} , \end{aligned}$$

where $d \in \mathcal {D}$. Observe that any bivariate convex quadratic with positive off-diagonals can be written as $d_1y_1^2+2y_1y_2+d_2y^2_2$, by scaling appropriately. Therefore, $\mathcal {Z}_+$ is the complementary set to $\mathcal {Z}_-$ and, together, $\mathcal {Z}_+$ and $\mathcal {Z}_-$ model epigraphs of all bivariate convex quadratics with indicators and nonnegative continuous variables.

In this paper, we propose conic quadratic extended formulations to describe ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_-)$ and ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_+)$. These extended formulations are more compact than alternatives previously proposed in the literature. More importantly, a distinguishing contribution of this paper is that we also give the explicit description of ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_+)$ in the original space of the variables. The corresponding convex envelope of the bivariate function is a four-piece function. While convexifications in the original space of variables are more difficult to implement using current off-the-shelf mixed-integer optimization solvers, they offer deeper insights on the structure of the convex hulls. Whereas the ideal formulations of $\mathcal {Z}_-$ can be conveniently described with two simple valid “extremal" inequalities [8], a similar result does not hold for $\mathcal {Z}_+$ (see Example 1 in Sect. 3). The derivation of ideal formulations for the more involved set $\mathcal {Z}_+$ differs significantly from the methods in [8]. The complementary results of this paper and [8] for $\mathcal {Z}_-$ complete the convex hull descriptions of bivariate convex functions with indicators and nonnegative continuous variables.

1.1.2 2. General case: we develop an optimal SDP relaxation based on $2\times 2$ convexifications for $\text {(QI)}$

In order to construct a strong convex formulation for $\text {(QI)}$, we extract a sequence of $2\times 2$ PSD matrices from Q such that the residual term is a PSD matrix as well, and convexify each bivariate quadratic term utilizing the descriptions of ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_+)$ and ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_-)$. This approach works very well when Q is $2\times 2$ PSD decomposable, i.e., when Q is scaled-diagonally dominant [15]. Otherwise, a natural question is how to optimally decompose $y'Qy$ into bivariable convex quadratics and a residual convex quadratic term so as to achieve the best strengthening.

We address this question by deriving an optimal convex formulation using SDP duality. The new SDP formulation dominates any formulation obtained through a $2\times 2$-decomposition scheme. This formulation is also stronger than other SDP formulations in the literature, including the optimal perspective formulation [21] and the optimal rank-one convexification [5]. In addition, the proposed formulation is solved many orders of magnitude faster than the $2\times 2$-decomposition approaches based on disjunctive programming [25], and delivers higher quality bounds than standard mixed-integer optimization approaches in difficult portfolio index tracking problems.

1.2 Outline

The rest of the paper is organized as follows. In Sect. 2 we review the convex hull results on $\mathcal {Z}_-$ and illustrate the structural difference between $\mathcal {Z}_+$ and $\mathcal {Z}_-$. In Sect. 3 we provide a conic quadratic formulation of ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_+)$ and ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_-)$ in an extended space and derive the explicit form of ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_+)$ in the original space. In Sect. 4, employing the results in Sect. 3, we give a strong convex relaxation for $\text {(QI)}$ using SDP techniques. In Sect. 5, we compare the strength of the proposed SDP relaxation with others in literature. In Sect. 6, we present computational results demonstrating the effectiveness of the proposed convex relaxations. Finally, in Sect. 7, we conclude with a few final remarks.

1.3 Notation

To simplify the notation throughout, we adopt the following convention for division by 0: given $x\ge 0$, $x^2/0=\infty$ if $x\ne 0$ and $x^2/0=0$ if $x=0$. Thus, $x^2/z$, the closure of the perspective of $x^2$, is a closed convex function (see [41], pages67-68). For a set $\mathcal {X}\subseteq {\mathbb {R}}^n$, ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {X})$ denotes the closure of the convex hull of $\mathcal {X}$. For a vector v, $\text {diag}(v)$ denotes the diagonal matrix V with $V_{ii} = v_i$ for each i. Finally, ${\mathbb {S}}_+^n$ refers to the cone of $n\times n$ real symmetric PSD matrices.

2 Preliminaries

In this section, we review the existing results on convex hulls of sets $\mathcal {Z}_-$, $\mathcal {Z}_+$, and their relaxation $\mathcal {Z}_f$ with free continuous variables:

$$\begin{aligned} \mathcal {Z}_f \! := \! \Big \{ (x,y,t) \! \in \! \{0,1\}^2 \! \times \! {\mathbb {R}}^3 \! :\;&t\ge d_1y_1^2\pm 2y_1y_2\!+\!d_2y^2_2, \, y_i(1\!-\!x_i)=0, i \in [2] \Big \} \cdot \end{aligned}$$

Note that when the continuous variables are free, the sign associated with the cross term $2y_1y_2$ is irrelevant, since one can state it equivalently with the opposite sign by substituting ${{\bar{y}}}_i=-y_i$. In contrast, if $y\ge 0$, such a substitution is not possible; hence, the need for separate analyses for sets $\mathcal {Z}_+$ and $\mathcal {Z}_-$.

We first point out that all three sets can be naturally seen as disjunctions of four convex sets corresponding to the four possible values for $x \in \{0,1\}^2$. Thus, a direct application of disjunctive programming yields similar (conic quadratic) representations of the three sets [25, 36] but such representations require several additional variables. While the disjunctive approach might suggest that $\mathcal {Z}_f$, $\mathcal {Z}_+$, $\mathcal {Z}_-$ may be similar, we now argue that the sign of the cross terms materially affect the complexity of the optimization problems as well as the structure of the convex hulls.

2.1 Optimization

The sign of the off-diagonals of matrix Q critically affect the complexity of the optimization problem $\text {(QI)}$. We first state a result concerning optimization with Stieltjes matrices Q, first proven in [4].

Proposition 1

(Atamtürk and Gómez [4]) Problem (1) can be solved in polynomial time if $Q\succ 0$ and $Q_{ij}\le 0$ for all $i\ne j$ and $b\le 0$.

In contrast, an analogous result does not hold if the off-diagonal terms of matrix Q are nonnegative.

Proposition 2

Problem (1) is ${{\mathcal {N}}}{{\mathcal {P}}}$-hard if $Q\succ 0$ and $Q_{ij}\ge 0$ for all $i\ne j$ and $b\le 0$.

Proof

We show that $\text {(QI)}$ includes the ${{\mathcal {N}}}{{\mathcal {P}}}-$hard subset sum problem as a special case under the assumptions of the proposition: given $w\in {\mathbb {Z}}^n_+, K\in {\mathbb {Z}}_+$, solve the equation

$$\begin{aligned} w'x=K,\;x\in \{0,1\}^n. \end{aligned}$$

(3)

Set $Q=(I+qq')/2\succ 0$ where $q\in {\mathbb {R}}_{++}^n$ is a parameter to be specified later. Let $p_i=q_i^2, \ i\in [n]$, $b=-q$ and $a=\gamma p$ for some $\gamma >0$ to be specified later as well. For a vector $z\in {\mathbb {R}}^n$ and matrix $M\in {\mathbb {S}}_+^n$, let $z_S$ and $M_S$ denote the subvector and principle submatrix defined by $S\subseteq [n]$, respectively. Then $\text {(QI)}$ reduces to

$$\begin{aligned}&\min _{(x,y)\in \mathcal {I}_n}\frac{1}{2}y'(I+qq')y-q'y+\gamma p' x\nonumber \\&\quad =\min _{S\subseteq [n], y_S\ge 0}\frac{1}{2}y_S'(I_{S}+q_Sq_S')y_S-{q_S'}{y_S}+\gamma \sum _{i\in S} p_i\qquad \qquad {(S:=\{i:x_i=1\})}\nonumber \\&\quad \min _{S\subseteq [n]}-\frac{1}{2}q_S'\left( I_{S}+q_Sq_S' \right) ^{-1}q_S+\gamma \sum _{i\in S} p_i \end{aligned}$$

(4a)

$$\begin{aligned}&\quad \min _{S\subseteq [n]}-\frac{1}{2}q_S'\left( I_S-\frac{q_Sq_S'}{1+\Vert q_S\Vert _{2}^2} \right) q_S+\gamma {\sum _{i\in S}} p_i\qquad \qquad \text {(Woodbury matrix identity)}\nonumber \\&\quad \min _{S\subseteq [n]}-\frac{1}{2}\frac{\Vert q_S\Vert _{2}^2}{1+\Vert q_S\Vert _{2}^2}+\gamma \Vert q_S\Vert _{2}^2\qquad \qquad {(p_i=q_i^2)}\nonumber \\&\quad \min _{S\subseteq [n]}\left[ \frac{1}{2(1+\Vert q_S\Vert _{2}^2)}+\gamma (1+\Vert q_S\Vert _{2}^2)\right] -\gamma -\frac{1}{2} \cdot \end{aligned}$$

(4b)

Note that the nonnegativity constraints are dropped in (4a) because they are trivially satisfied by the optimal solution as

$$\begin{aligned} y_S=\left( I_S-\frac{q_Sq_S'}{1+\Vert q_S\Vert _{2}^2} \right) q_S=\frac{1}{1+\Vert q_S\Vert _{2}^2}q_S\ge 0. \end{aligned}$$

Now, let $q_i= \sqrt{w_i}$, $i \in [n]$ and $\gamma =\frac{1}{2(1+K)^2}$. Then (4b) simplifies to (after dropping the constant term $-\gamma -1/2$ and multiplying by 2)

$$\begin{aligned} =&\min _S\;\frac{1}{1+w(S)}+\frac{1+w(S)}{(1+K)^2}\\ \ge&\frac{2}{1+K}, \end{aligned}$$

where the lower bound is attained if and only if $w(S)=K$. Hence, the subset sum problem (3) has a solution if and only if the optimal value of $\text {(QI)}$ as constructed above equals $2/(1+K).$ $\square$

Propositions 1 and 2 suggest that convex hulls of sets with negative cross terms are substantially simpler than those with positive terms.

2.2 Rank-one results

It is convenient to formulate convex hulls of sets via conic quadratic constraints as they are readily supported by modern mixed-integer optimization software. While such representations are easy to obtain via disjunctive programming, the resulting formulations generally have a prohibitive number of variables and constraints, which hamper the performance of solvers. Therefore, it is of interest to find the most compact conic quadratic formulations. In this regard, as well, $\mathcal {Z}_+$ is significantly more complex than $\mathcal {Z}_f$ and $\mathcal {Z}_-$. Consider the existing results for the simpler sets in the rank-one case, i.e., $d_1=d_2=1.$

Proposition 3

Atamtürk and Gómez [5] If $d_1=d_2=1$, then

$$\begin{aligned}{{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_f)\!=\!\Big \{(x,y,t)\in [0,1]^2\times {\mathbb {R}}^3: t\ge (y_1 \!\pm \! y_2)^2, \, t(z_1\!+\!z_2)\ge (y_1\pm y_2)^2\Big \} \cdot \end{aligned}$$

In particular, for the rank-one case with free continuous variables, the ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_f)$ is conic quadratic representable in the original space of variables, without the need for additional variables.

Proposition 4

Atamtürk and Gómez [4] If $d_1=d_2=1$, then

$$\begin{aligned} {{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_-)=\Big \{(x,y,t)\in [0,1]^2\times {\mathbb {R}}+^3:&\;t\ge \phi (x_1,x_2,y_1,y_2)\Big \}, \end{aligned}$$

where

$$\begin{aligned} \phi (x_1,x_2,y_1,y_2)={\left\{ \begin{array}{ll}(y_1-y_2)^2/x_1&{}\text {if }y_1\ge y_2\\ (y_1-y_2)^2/x_2&{}\text {if }y_1\le y_2.\end{array}\right. } \end{aligned}$$

In contrast to ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_f)$, since constraints $t\ge (y_1-y_2)^2/x_i$, $i \in [2]$, are not valid for $\mathcal {Z}_-$, it is unclear how to reformulate ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_-)$ using conic quadratic constraints in the original space of variables. A conic quadratic representation with two additional variables is given in [8].

In Sect. 3, Corollary 2, we describe ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_+)$ in the original space for the rank-one case. This description is more complex than $\mathcal {Z}_-$ as it requires four pieces instead of two and it is not conic-quadratic representable. We also provide a compact extended formulation with three additional variables.

2.3 Full-rank results

A description of ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_-)$ in the original space of variables is given in [8]. Interestingly, it can be expressed as two valid inequalities involving function $\phi$ introduced in Proposition 4.

Proposition 5

(Atamtürk et al. [8]) Set ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_-)$ is described by bound constraints $y\ge 0$, $0\le x\le 1$, and the two valid inequalities

$$\begin{aligned} t&\ge d_1\phi (x_1,x_2,y_1,y_2/d_1) +\frac{y_2^2}{x_2}\left( d_2-\frac{1}{d_1}\right) ,\\ t&\ge d_2\phi (x_1,x_2,y_1/d_2,y_2)+\frac{y_1^2}{x_1}\left( d_1-\frac{1}{d_2}\right) . \end{aligned}$$

Proposition 5 reveals that ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_-)$ requires only homogeneous functions that are sums of rank-one and perspective convexifications. In Sect. 3, Proposition 7, we give ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_+)$ in the original space of variables, and show that the resulting function does not have either of these properties. The discrepancy between the results highlights that ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_+)$ is fundamentally different from ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_-)$, and helps explain why optimization with positive matrices Q (Proposition 2) is substantially more difficult than optimization with Stieltjes matrices (Proposition 1).

3 Convex hull description of $\mathcal {Z}_+$

In this section, we give ideal convex formulations for

$$\begin{aligned} \mathcal {Z}_+=\left\{ (x,y,t)\in {{\mathcal {I}}_{2}}\times {\mathbb {R}}_+:t\ge d_1y_1^2+2y_1y_2+d_2y_2^2 \, \right\} . \end{aligned}$$

When $d_1=d_2=1$, $\mathcal {Z}_+$ reduces to the simpler rank-one set

$$\begin{aligned} \mathcal {X}_+=\left\{ (x,y,t)\in {{\mathcal {I}}_{2}}\times {\mathbb {R}}_+:t\ge (y_1+y_2)^2 \, \right\} . \end{aligned}$$

Set $\mathcal {X}_+$ is of special interest as it arises naturally in $\text {(QI)}$ when Q is a diagonally dominant matrix, see computations in Sect. 6.1 for details. As we shall see, the convex hulls of $\mathcal {Z}_+$ and $\mathcal {X}_+$ are significantly more complicated than their complementary sets $\mathcal {Z}_-$ and $\mathcal {X}_-$ studied earlier. In Sect. 3.1, we develop an SOCP-representable extended formulation of ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_+)$. Then, in Sect. 3.2, we derive the explicit form of ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_+)$ in the original space of variables.

3.1 Conic quadratic-representable extended formulation

We start by writing $\mathcal {Z}_+$ as the disjunction of four convex sets defined by all values of the indicator variables; that is,

$$\begin{aligned} \mathcal {Z}_+= \mathcal {Z}_+^1\cup \mathcal {Z}_+^2\cup \mathcal {Z}_+^3\cup \mathcal {Z}_+^4, \end{aligned}$$

where $\mathcal {Z}_+^i, i=1,2,3,4$ are convex sets defined as:

$$\begin{aligned}&\mathcal {Z}_+^1=\{ (1,0, u, 0,t_1):t_1\ge d_1 u^2, u\ge 0 \},\\&\mathcal {Z}_+^2=\{ (0,1, 0, v,t_2):t_2\ge d_2 v^2, v\ge 0 \},\\&\mathcal {Z}_+^3=\{ (1,1,w_1,w_2,t_3):t_3\ge d_1 w_1^2 + 2 w_1w_2+ d_2 w_2^2, w_1\ge 0, w_2\ge 0 \},\\&\mathcal {Z}_+^4 = \{ (0,0,0,0,t_4):t_4\ge 0 \}. \end{aligned}$$

By the definition, a point $(x_1,x_2,y_1,y_2,t)\in {{\,\textrm{conv}\,}}(\mathcal {Z}_+)$ if and only if it can be written as a convex combination of four points belonging in $\mathcal {Z}_+^i, i=1,2,3,4$. Using $\lambda =(\lambda _1,\lambda _2,\lambda _3,\lambda _4)$ as the corresponding weights, $(x_1,x_2,y_1,y_2,t)\in {{\,\textrm{conv}\,}}(\mathcal {Z}_+)$ if and only if the following inequality system has a feasible solution

$$\begin{aligned}&\lambda _1+\lambda _2+\lambda _3+\lambda _4=1 \end{aligned}$$

(5a)

$$\begin{aligned}&x_1=\lambda _1+\lambda _3, \; x_2=\lambda _2+\lambda _3 \end{aligned}$$

(5b)

$$\begin{aligned}&y_1=\lambda _1u+\lambda _3w_1,\; y_2=\lambda _2v+\lambda _3 w_2\end{aligned}$$

(5c)

$$\begin{aligned}&t=\lambda _1t_1+\lambda _2t_2+\lambda _3t_3+\lambda _4t_4\end{aligned}$$

(5d)

$$\begin{aligned}&t_1\ge d_1u^2,\; t_2\ge d_2v^2,\; t_3\ge d_1w_1^2+2w_1w_2+d_2w_2^2,\; t_4\ge 0\end{aligned}$$

(5e)

$$\begin{aligned}&u,v,w_1,w_2,\lambda _1,\lambda _2,\lambda _3,\lambda _4\ge 0. \end{aligned}$$

(5f)

We will now simplify (5). First, by Fourier–Motzkin elimination, one can substitute $t_1,t_2,t_3,t_4$ with their lower bounds in (5e) and reduce (5d) to $t\ge \lambda _1d_1u^2+\lambda _2d_2v^2+\lambda _3(d_1w_1^2+2w_1w_2+d_2w_2^2)$. Similarly, since $\lambda _4\ge 0$, one can eliminate $\lambda _4$ and reduce (5a) to $\sum _{i=1}^3 \lambda _i\le 1$. Next, using (5c), one can substitute $u=(y_1-\lambda _3w_1)/\lambda _1$ and $v=(y_2-\lambda _3w_2)/\lambda _2$. Finally, using (5b), one can substitute $\lambda _1=x_1-\lambda _3$ and $\lambda _2=x_2-\lambda _3$ to arrive at

$$\begin{aligned}&\max \{ 0,x_1+x_2-1 \}\le \lambda _3\le \min \{ x_1,x_2 \} \end{aligned}$$

(6a)

$$\begin{aligned}&\lambda _3 w_i\le y_i,\;\; i=1,2\end{aligned}$$

(6b)

$$\begin{aligned}&w_i\ge 0,\;\; i=1,2\end{aligned}$$

(6c)

$$\begin{aligned}&t\ge \frac{d_1 (y_1 \!- \!\lambda _3 w_1)^2}{x_1 \! - \!\lambda _3} \! + \! \frac{d_2(y_2 \! - \! \lambda _3 w_2)^2}{x_2 \! - \! \lambda _3} \! + \! \lambda _3(d_1w_1^2+2w_1w_2+d_2w_2^2), \end{aligned}$$

(6d)

where (6a) results from the nonnegativity of $\lambda _1,\lambda _2,\lambda _3,\lambda _4$, (6b) from the nonnegativity of u and v. Finally, observe that (6b) is redundant for (6): indeed, if there is a solution $(\lambda , w, t)$ satisfying (6a), (6c) and (6d) but violating (6b), one can decrease $w_1$ and $w_2$ such that (6b) is satisfied without violating (6d).

Redefining variables in (6), we arrive at the following conic quadratic-representable extended formulation for ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_+)$ and its rank-one special case ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {X}_+)$.

Proposition 6

The set ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_+)$ can be represented as

$$\begin{aligned} {{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_+)=\bigg \{&(x,y,t)\in [0,1]^2\times {\mathbb {R}}_+^3: \exists \lambda \in {\mathbb {R}}_+,z\in {\mathbb {R}}_+^2 \text { s.t.} \\&x_1+x_2-1 \le \lambda \le \min \{ x_1,x_2 \}, \\&\begin{matrix} t\ge \frac{d_1(y_1-z_1)^2}{x_1-\lambda }+\frac{d_2(y_2-z_2)^2}{x_2-\lambda } +\frac{d_1z_1^2+2z_1z_2+d_2z_2^2}{\lambda } \bigg \} \cdot \end{matrix} \end{aligned}$$

Corollary 1

The set ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {X}_+)$ can be represented as

$$\begin{aligned} {{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {X}_+)=\bigg \{&(x,y,t)\in [0,1]^2\times {\mathbb {R}}_+^3: \exists \lambda \in {\mathbb {R}}_+,z\in {\mathbb {R}}_+^2 \text { s.t. }\\ {}&x_1+x_2-1 \le \lambda \le \min \{ x_1,x_2 \}, \\&t\ge \frac{(y_1-z_1)^2}{x_1-\lambda }+\frac{(y_2-z_2)^2}{x_2-\lambda }+\frac{(z_1+z_2)^2}{\lambda } \bigg \} \cdot \end{aligned}$$

Remark 1

One can apply similar arguments to the complementary set $\mathcal {Z}_-$ to derive an SOCP representable formulation of its convex hull as

$$\begin{aligned} {{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_-)=\bigg \{&(x,y,t)\in [0,1]^2\times {\mathbb {R}}_+^3: \exists \lambda \in {\mathbb {R}}_+,z\in {\mathbb {R}}^2 \text { s.t. }\\&x_1+x_2-1 \le \lambda \le \min \{ x_1,x_2 \}, \\ {}&z_1\le y_1, \ z_2\le y_2, \\&\begin{matrix} t\ge \frac{d_1(y_1-z_1)^2}{x_1-\lambda }+\frac{d_2(y_2-z_2)^2}{x_2-\lambda }+\frac{d_1z_1^2-2z_1z_2+d_2z_2^2}{\lambda } \bigg \} \cdot \end{matrix} \end{aligned}$$

This extended formulation is smaller than the one given Atamtürk et al. [8] for ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_-)$.

3.2 Description in the original space of variables x, y, t

The purpose of this section is to express ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_+)$ and ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {X}_+)$ in the original space.

Let ${\Lambda _x}:=\left\{ \lambda \in {\mathbb {R}}:\max \{0,x_1+x_2-1\}\le \lambda \le \min \{x_1,x_2\}\right\}$, i.e., the set of feasible $\lambda$ implied by constraint (6a). Define

$$\begin{aligned} G(\lambda ,w):=\frac{d_1(y_1-\lambda w_1)^2}{x_1-\lambda }+\frac{d_2(y_2-\lambda w_2)^2}{x_2-\lambda }+\lambda (d_1w_1^2+2w_1w_2+d_2w_2^2) \end{aligned}$$

and $g(\lambda ):{\Lambda _x}\rightarrow {\mathbb {R}}$ as

$$\begin{aligned} g(\lambda ):=\min \limits _{w\in {\mathbb {R}}_+^2} G(\lambda ,w). \end{aligned}$$

Note that as G is SOCP-representable, it is convex. We first prove an auxiliary lemma that will be used in the derivation.

Lemma 1

Function $g(\lambda )$ is non-decreasing over ${\Lambda _x}$.

Proof

Note that for any fixed w and $\lambda <\min \{ x_1,x_2 \}$, we have

$$\begin{aligned} \frac{\partial G(\lambda ,w)}{\partial \lambda }=&\frac{d_1[2(\lambda w_1-y_1)w_1(x_1-\lambda )+(y_1-\lambda w_1)^2]}{(x_1-\lambda )^2}\\&+\frac{d_2[2(\lambda w_2-y_2)w_2(x_2-\lambda )+(y_2-\lambda w_2)^2]}{(x_2-\lambda )^2}\\&+(d_1w_1^2+2w_1w_2 +d_2w_2^2)\\ = \ {}&\frac{d_1[w_1^2(x_1-\lambda )^2+2(\lambda w_1-y_1)w_1(x_1-\lambda )+(y_1-\lambda w_1)^2]}{(x_1-\lambda )^2}\\&+\frac{d_2[w_2^2(x_2-\lambda _2)^2+2(\lambda w_2-y_2)w_2(x_2-\lambda )+(y_2-\lambda w_2)^2]}{(x_2-\lambda )^2}\\&+2w_1w_2\\ = \ {}&\frac{d_1(w_1x_1-y_1)^2}{(x_1-\lambda )^2}+\frac{d_2(w_2x_2-y_2)^2}{(x_2-\lambda )^2}+2w_1w_2\\ \ge \ {}&0. \end{aligned}$$

Therefore, for fixed w, $G(\cdot ,w)$ is nondecreasing. Now for ${\tilde{\lambda }}\le {\hat{\lambda }}$, let ${{\tilde{w}}}$ and ${{\hat{w}}}$ be optimal solutions defining $g({\tilde{\lambda }})$ and $g({\hat{\lambda }})$. Then,

$$\begin{aligned} g({{\tilde{\lambda }}})=G({{\tilde{\lambda }}},{{\tilde{w}}})\le G({{\tilde{\lambda }}},{{\hat{w}}})\le G({{\hat{\lambda }}},{{\hat{w}}})=g({{\hat{\lambda }}}), \end{aligned}$$

proving the claim. $\square$

We now state and prove the main result in this subsection.

Proposition 7

Define

$$\begin{aligned} f(x,y,\lambda ;d):= \frac{(d_1d_2-1)(d_1x_2y_1^2+d_2x_1y_2^2)+2\lambda d_1d_2y_1y_2+\lambda (d_1y_1^2+d_2y_2^2)}{(d_1d_2-1)x_1x_2-\lambda ^2+\lambda (x_1+x_2)}, \end{aligned}$$

and

$$\begin{aligned}f_+^*(x,y;d):={\left\{ \begin{array}{ll} \frac{d_1y_1^2}{x_1}+\frac{d_2y_2^2}{x_2}&{}\text {if }x_1+x_2\le 1\\ {\frac{d_1y_1^2}{1-x_2}+\frac{d_2y_2^2}{x_2}}&{}\text {if }0\le x_1+x_2-1\le (x_1y_2-d_1x_2y_1)/y_2\\ \frac{d_1y_1^2}{x_1}+\frac{d_2y_2^2}{1-x_1}&{}\text {if }0\le x_1+x_2-1\le (x_2y_1-d_2x_1y_2)/y_1\\ f(x,y,x_1+x_2-1)&{}\text {o.w.} \end{array}\right. } \end{aligned}$$

Then, the set ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_+)$ can be expressed as

$$\begin{aligned} {{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_+)=\{ (x,y,t)\in [0,1]^2\times {\mathbb {R}}^3_+:t\ge f_+^*(x_1,x_2,y_1,y_2;d_1,d_2) \}. \end{aligned}$$

Proof

First, observe that we may assume $x_1,x_2>0$, as otherwise $x_1 + x_2 \le 1$ and $f^*_+$ reduces to the perspective function for the univariate case. To find the representation in the original space of variables, we first project out variables z in Proposition 6. Specifically, notice that $g(\lambda )$ can be rewritten in the following form by letting $z_i=\lambda w_i,i=1,2$:

$$\begin{aligned} g(\lambda )=\min \;\;&\frac{d_1(y_1-z_1)^2}{x_1-\lambda }+\frac{d_2(y_2-z_2)^2}{x_2-\lambda }+ \frac{d_1z_1^2+2z_1z_2+d_2z_2^2}{\lambda }\nonumber \\ \text {s.t. }&z_i\ge 0,\;\; i=1,2. \ \ (s_i) \end{aligned}$$

(7)

By Proposition 6, a point $(x,y,t)\in [0,1]^2\times {\mathbb {R}}_+^3$ belongs to ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_+)$ if and only if $t\ge \min _{\lambda \in {\Lambda _x}}\;g(\lambda )$. We first assume $x_1+x_2-1>0$, which implies $\lambda >0,\forall \lambda \in \Lambda _x$. For given $\lambda \in {\Lambda _x}$, optimization problem (7) is convex with affine constraints, thus Slater condition holds. Hence, the following KKT conditions are necessary and sufficient for the minimizer:

$$\begin{aligned}&\frac{2d_1}{x_1-\lambda }(z_1-y_1)+\frac{2(d_1z_1+z_2)}{\lambda }-s_1=0 \end{aligned}$$

(8a)

$$\begin{aligned}&\frac{2d_2}{x_2-\lambda }(z_2-y_2)+\frac{2(d_2z_2+z_1)}{\lambda }-s_2=0\end{aligned}$$

(8b)

$$\begin{aligned}&z_1s_1=0\end{aligned}$$

(8c)

$$\begin{aligned}&z_2s_2=0\end{aligned}$$

(8d)

$$\begin{aligned}&s_i,z_i\ge 0,\;\; i=1,2. \end{aligned}$$

(8e)

Let us analyze the KKT system considering the positiveness of $s_1$ and $s_2$.

• Case $s_1>0$ . By (8c), $z_1=0$ and by (8a), $z_2>0$, which implies $s_2=0$ from (8d). Hence, (8a) and (8b) reduce to

  $$\begin{aligned}&\frac{2z_2}{\lambda }=\frac{2d_1}{x_1-\lambda }y_1+s_1\\&\frac{2d_2}{x_2-\lambda }(z_2-y_2)+\frac{2d_2z_2}{\lambda }=0. \end{aligned}$$

  Solving these two linear equations, we get $z_2=\frac{y_2}{x_2}\lambda$ and $s_1=2(\frac{y_2}{x_2}-\frac{d_1y_1}{x_1-\lambda })$. This also indicates $s_1\ge 0$ iff $\lambda \le (x_1y_2-d_1x_2y_1)/y_2$. By replacing the variables with their optimal values in the objective function (7), we find that

  $$\begin{aligned} g(\lambda )=&\frac{d_1y_1^2}{x_1-\lambda }+\frac{d_2}{x_2-\lambda }\bigg (y_2-\frac{y_2}{x_2}\lambda \bigg )^2+\frac{d_2}{\lambda } \bigg (\frac{y_2}{x_2}\lambda \bigg )^2 \end{aligned}$$

  (9a)
  $$\begin{aligned} =&\frac{d_1y_1^2}{x_1-\lambda }+\frac{d_2y_2^2}{x_2} \end{aligned}$$

  (9b)

  when $\lambda \in [0, (x_1y_2-d_1x_2y_1)/y_2]\cap {\Lambda _x}$.

• Case $s_2>0$ . Similarly, we find that

  $$\begin{aligned} g(\lambda )=\frac{d_1y_1^2}{x_1}+\frac{d_2y_2^2}{x_2-\lambda } \end{aligned}$$

  (10)

  when $\lambda \in [0, (x_2y_1-d_2x_1y_2)/y_1]\cap {\Lambda _x}$.

• Case $s_1=s_2=0$ . In this case, (8a) and (8b) reduce to

  $$\begin{aligned}\begin{pmatrix} d_1x_1&{}\,\,\, x_1-\lambda \\ x_2-\lambda &{}\,\,\, d_2x_2 \end{pmatrix}\begin{pmatrix} z_1\\ z_2 \end{pmatrix}=\lambda \begin{pmatrix} d_1y_1\\ d_2y_2 \end{pmatrix}. \end{aligned}$$

  If $\lambda >0$, the determinant of the matrix is $(d_1d_2-1)x_1x_2+\lambda (x_1+x_2-\lambda )>0$ and the system has a unique solution. It follows that

  $$\begin{aligned}\begin{pmatrix} z_1\\ z_2 \end{pmatrix}=\lambda \begin{pmatrix} d_1x_1&{}\,\,\, x_1-\lambda \\ x_2-\lambda &{}\,\,\, d_2x_2 \end{pmatrix}^{-1}\begin{pmatrix} d_1y_1\\ d_2y_2 \end{pmatrix}, \end{aligned}$$

  i.e.,

  $$\begin{aligned} z_1=\frac{\lambda (d_1d_2x_2y_1+(\lambda -x_1)d_2y_2)}{(d_1d_2-1)x_1x_2-\lambda ^2+\lambda (x_1+x_2)},\\ z_2=\frac{\lambda (d_1d_2x_1y_2+(\lambda -x_2)d_1y_1)}{(d_1d_2-1)x_1x_2-\lambda ^2+\lambda (x_1+x_2)}. \end{aligned}$$

  Therefore, the bounds $z_1, z_2\ge 0$ imply lower bounds

  $$\begin{aligned} \lambda \ge (x_1y_2-d_1x_2y_1)/y_2, \quad \lambda \ge (x_2y_1-d_2x_1y_2)/y_1 \end{aligned}$$

  on $\lambda$. Moreover, from (8a) and (8b), we have

  $$\begin{aligned} \frac{d_1(y_1-z_1)}{x_1-\lambda }=\frac{d_1z_1+z_2}{\lambda } \text { and } \frac{d_2(y_2-z_2)}{x_2-\lambda }=\frac{d_2z_2+z_1}{\lambda } \cdot \end{aligned}$$

  By substituting the two equalities in (7), we find that

  $$\begin{aligned} g(\lambda )&=\big (d_1y_1z_1+y_1z_2+d_2y_2z_2+y_2z_1 \big )/\lambda \\&= \frac{(d_1d_2-1)(d_1x_2y_1^2+d_2x_1y_2^2)+2\lambda d_1d_2y_1y_2+\lambda (d_1y_1^2+d_2y_2^2)}{(d_1d_2-1)x_1x_2-\lambda ^2+\lambda (x_1+x_2)}. \end{aligned}$$

  Therefore,

  $$\begin{aligned} g(\lambda )=f(x,y,\lambda ;d) \end{aligned}$$

  (11)

  when $\lambda \in {[ \max \{ (x_1y_2-d_1x_2y_1)/y_2,(x_2y_1-d_2x_1y_2)/y_1\},+\infty ) \cap {\Lambda _x} }.$

To see that the three pieces of $g(\lambda )$ considered above are, indeed, mutually exclusive, observe that when $\lambda \le (x_1y_2-d_1x_2y_1)/y_2$, this is, $\frac{y_2(x_1-\lambda )}{x_2y_1}\ge d_1$, we have $\frac{d_2y_2}{y_1}\frac{x_1-\lambda }{x_2}\ge d_1d_2\ge 1$. Since $\frac{x_1-\lambda }{x_2}\frac{x_2-\lambda }{x_1}\le \frac{x_1}{x_2}\frac{x_2}{x_1}=1$, it holds $\frac{d_2y_2}{y_1}\frac{x_1-\lambda }{x_2}\ge \frac{x_1-\lambda }{x_2}\frac{x_2-\lambda }{x_1},$ that is, $\lambda \ge (x_2y_1-d_2x_1y_2)/y_1$.

Finally, notice when $x_1+x_2-1\le 0$, $\lambda$ may take the value 0. In this case, (7) reduces to

$$\begin{aligned} g(0)=\frac{d_1y_1^2}{x_1}+\frac{d_2y_2^2}{x_2} \cdot \end{aligned}$$

By Lemma 1, $\min _{\lambda \in {\Lambda _x}}g(\lambda )=g(\max \{0,x_1+x_2-1 \})$. Combining this fact with the above discussion, Proposition 7 holds. $\square$

Remark 2

For further intuition, we now comment on the validity of each piece of $t\ge f^*_+(x,y;d)$ over $[0,1]^2\times {\mathbb {R}}^3_+$ for $\mathcal {Z}_+$. Because the first piece can be obtained by dropping the nonnegative cross product term $y_1y_2$ and then strengthening $t\ge y_1^2+y_2^2$ using perspective reformulation, it is valid everywhere. When $x_1+x_2<1$ and $y_1,y_2>0$, $t\ge y_i^2/x_i+y_j^2/(1-x_i)>f^*_+(x,y;1,1)$ for $i\ne j$. Therefore, the second and the third pieces are not valid on the domain $[0,1]^2\times {\mathbb {R}}^3_+$.

If $d_1d_2>1$, the last piece $t\ge f(x,y,x_1+x_2-1;d)$ is not valid for ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_+)$ everywhere, as seen by exhibiting a point $(x,y,t)\in {{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_+)$ violating $t\ge f(x,y,x_1+x_2-1;d)$. To do so, let

$$\begin{aligned} (x_1,x_2,y_1,y_2,t) = (0.5, \frac{1}{d_1d_2+1}+\epsilon , \frac{1}{\sqrt{d_1}},2\sqrt{d_1},f^*_+(x,y)), \end{aligned}$$

where $\epsilon >0$ is small enough so that $x_1+x_2<1$, i.e., $x_2<0.5$. With this choice, $f^*_+(x,y)=d_1y_1^2/x_1+d_2y_2^2/x_2.$ Let ${\tilde{\lambda }}=x_1+x_2-1$, then ${{\tilde{\lambda }}}(x_1+x_2)-{{\tilde{\lambda }}}^2={{\tilde{\lambda }}}$. Hence, for point (x, y, t), we have

$$\begin{aligned} f(x,y,{{\tilde{\lambda }}};d)=&\frac{(d_1d_2-1)(d_1x_2y_1^2+d_2x_1y_2^2)+2{{\tilde{\lambda }}} d_1d_2y_1y_2+{{\tilde{\lambda }}}(d_1y_1^2+d_2y_2^2)}{(d_1d_2-1)x_1x_2+{{\tilde{\lambda }}}}\\&= \frac{(d_1d_2-1)x_1x_2(d_1y_1^2/x_1+d_2y_2^2/x_2)+{{\tilde{\lambda }}} (d_1y_1^2+2d_1d_2y_1y_2+d_2y_2^2)}{(d_1d_2-1)x_1x_2+{{\tilde{\lambda }}}}\\&=(1-\alpha )f_+^*(x,y)+\alpha (d_1y_1^2+2d_1d_2y_1y_2+d_2y_2^2), \end{aligned}$$

where $\alpha = {{\tilde{\lambda }}}/((d_1d_2-1)x_1x_2+{{\tilde{\lambda }}})$. Since ${{\tilde{\lambda }}}<0$, $\alpha <0$ if and only if

$$\begin{aligned}&(d_1d_2-1)x_1x_2+x_1+x_2-1>0\\ \iff&d_1d_2>\frac{(1-x_1)(1-x_2)}{x_1x_2}=\frac{1}{x_2}-1\quad \text {(by}\ x_1=0.5)\\ \iff&x_2>\frac{1}{d_1d_2+1}, \end{aligned}$$

which is true by the choice of $x_2$. Moreover,

$$\begin{aligned}&f^*_+(x,y)=d_1y_1^2/x_1+d_2y_2^2/x_2=2+8d_1d_2\\ >\,&d_1y_1^2+2d_1d_2y_1y_2+d_2y_2^2=1+8d_1d_2. \end{aligned}$$

This indicates $f(x,y,{{\tilde{\lambda }}};d)> (1-\alpha )f_+^*(x,y)+\alpha f_+^*(x,y)=f_+^*(x,y)=t,$ that is, $t\ge f(x,y,x_1+x_2-1;d)$ is violated.

Observe that if $d_1 d_2 =1$, then $f(x,y,x_1+x_2-1;d)$ reduces to the original quadratic $d_1 y_1^2 + 2y_1 y_2 + d_2y_2$. Otherwise, although $t\ge f(x,y,x_1+x_2-1;d)$ appears complicated, the next proposition implies that it is convex over its restricted domain and can, in fact, be stated as an SDP constraint. This results strongly indicates that SOCP-representable relaxations of $\text {(QI)}$ may be inadequate to describe the convex hull of the relevant mixed-integer sets, unless a large number of additional variables are added. The proof of Proposition 8 can be found in the Appendix.

Proposition 8

If $d_1 d_2 > 1$ and $x_1+x_2-1>0$, then $t\ge f(x,y,x_1+x_2-1;d)$ can be rewritten as the SDP constraint

$$\begin{aligned} \begin{pmatrix} {t}/({d_1d_2-1}) &{}\,\,\, y_1 &{}\,\,\, y_2\\ y_1 &{}\,\,\, d_2x_1+x_2/d_1-1/d_1 &{}\,\,\, {-x_1-x_2+1}\\ y_2&{}\,\,\, {-x_1-x_2+1}&{}\,\,\, x_1/d_2+d_1x_2-1/d_2\\ \end{pmatrix}\succeq 0. \end{aligned}$$

From Proposition 7, we get the convex hull of rank-one case $\mathcal {X}_+$ by setting $d_1 = d_2 = 1$.

Corollary 2

$$\begin{aligned} {{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {X}_+)= \left\{ (x,y,t)\in [0,1 ]^2\times {\mathbb {R}}^3_+:t\ge f_{1+}(x,y)\right\} , \end{aligned}$$

where

$$\begin{aligned} f_{1+}(x,y)={\left\{ \begin{array}{ll} \frac{y_1^2}{x_1}+\frac{y_2^2}{x_2}&{}\text {if }\,\, x_1+x_2\le 1\\ \frac{y_2^2}{x_2}+\frac{y_1^2}{1-x_2}&{}\text {if }\,\, 0\le x_1+x_2-1\le (x_1y_2-x_2y_1)/y_2\\ \frac{y_1^2}{x_1}+\frac{y_2^2}{1-x_1}&{}\text {if }\,\, 0\le x_1+x_2-1\le (x_2y_1-x_1y_2)/y_1\\ (y_1+y_2)^2&{}\text {o.w.} \end{array}\right. } \end{aligned}$$

3.3 Rank-one approximations of $\mathcal {Z}_+$

We now consider valid inequalities analogous to the ones given in Proposition 5 for $\mathcal {Z}_-.$ Consider the two decompositions of the bivariate quadratic function given by

$$\begin{aligned} d_1y_1^2+2y_1y_2+d_2y_2^2&= \; d_1\left( y_1+\frac{y_2}{d_1}\right) ^2+\left( d_2-\frac{1}{d_1}\right) y_2^2\\&= \; d_2\left( \frac{y_1}{d_2}+y_2\right) ^2+\left( d_1-\frac{1}{d_2}\right) y_2^2. \end{aligned}$$

Applying perspective reformulation and Corollary 2 to the separable and pairwise quadratic terms, respectively, one can obtain two simple valid inequalities for $\mathcal {Z}_+$:

$$\begin{aligned} t&\ge d_1f_{1+}\left( x_1,x_2,y_1,\frac{y_2}{d_1}\right) +\left( d_2-\frac{1}{d_1}\right) \frac{y_2^2}{x_2} \end{aligned}$$

(12a)

$$\begin{aligned} t&\ge d_2f_{1+}\left( x_1,x_2,\frac{y_1}{d_2},y_2\right) +\left( d_1-\frac{1}{d_2}\right) \frac{y_1^2}{x_1}. \end{aligned}$$

(12b)

The following example shows that the inequalities above do not describe ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_+)$, highlighting the more complicated structure of ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_+)$ compared to its complementary set ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_-)$.

Example 1

Consider $\mathcal {Z}_+$ with $d_1=d_2=d=2$, and let $x_1=x_2=x=2/3$, $y_1=y_2=y>0$ and $t=f^*_+(x,y)$. Then $(x,y,t)\in {{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_+)$. On the one hand, $x_1+x_2>1$ implies

$$\begin{aligned} t=f^*_+(x,y)=f(2/3,2/3,y,y,1/3)=\frac{133}{11}y^2. \end{aligned}$$

On the other hand, $f_{1+}(x,x,y,y/d)=(y+y/d)^2=9/2y^2$ indicates that (12) reduces to

$$\begin{aligned} t\ge \frac{27}{4}y^2. \end{aligned}$$

Since $\frac{133}{11}y^2>\frac{27}{4}y^2$, (12) holds strictly at this point. $\square$

4 An SDP relaxation for $\text {(QI)}$

In this section, we will give an extended SDP relaxation for $\text {(QI)}$ utilizing the convex hull results obtained in the previous section. Introducing a symmetric matrix variable Y, let us write $\text {(QI)}$ as

$$\begin{aligned} \min \left\{ a'x+b'y+\langle Q,Y\rangle :Y\succeq yy', (x,y) \in {\mathcal {I}}_{n} \right\} . \end{aligned}$$

(13)

Suppose for a class of PSD matrices $\Pi \subseteq {\mathbb {S}}^n_+$ we have an underestimator $f_P(x,y)$ for $y'Py$ for any $P\in \Pi$. Then, since $\langle P,Y\rangle \ge y'Py$, we obtain a valid inequality

$$\begin{aligned} f_P(x,y)-\langle P,Y\rangle \le 0, \;P\in \Pi \end{aligned}$$

(14)

for (13). For example, if $\Pi$ is the set of diagonal PSD matrices and $f_P(x,y)=\sum _i P_{ii}y_i^2/x_i$, for $P\in \Pi$, then inequality (14) is the perspective inequality.

Furthermore, since (14) holds for any $P\in \Pi$, one can take the supremum over all $P\in \Pi$ to get an optimal valid inequality of the type (14)

$$\begin{aligned} \sup _{P\in \Pi }f_P(x,y)-\langle P,Y\rangle \le 0. \end{aligned}$$

(15)

In the example of perspective reformulation, inequality (15) becomes

$$\begin{aligned} \sup _{P\succeq 0\text { diagonal}} \left\{ \sum _i P_{ii} \bigg ( y_i^2/x_i-Y_{ii} \bigg ) \right\} \le 0, \end{aligned}$$

which can be further reduced to the closed form $y_i^2\le Y_{ii}x_i,\forall i\in [n]$. This leads to the the optimal perspective formulation [21]

$$\begin{aligned} \min \;&a'x+b'y+\langle Q,Y\rangle \end{aligned}$$

(16a)

$$\begin{aligned} (\textsf {OptPersp})\qquad \qquad \text {s.t.}\;&Y-yy'\succeq 0\end{aligned}$$

(16b)

$$\begin{aligned}&y_i^2\le Y_{ii}x_i&\forall i\in [n]\end{aligned}$$

(16c)

$$\begin{aligned}&0\le x \le 1,\;y\ge 0. \end{aligned}$$

(16d)

Han et al. [32] show that $\textsf {OptPersp}$ is equivalent to the Shor’s SDP relaxation [42] for problem (1).

Letting $\Pi$ be the class of $2\times 2$ PSD matrices and $f_P(\cdot )$ as the function describing the convex hull of the mixed-integer epigraph of $y'Py$, one can derive new valid inequalities for $\text {(QI)}$. Specifically, using the extended formulations for $f_+^*(x,y;d)$ and $f_-^*(x,y;d)$ describing ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_+)$ and ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_-)$, we have

$$\begin{aligned} f_+^*(x,y;d)=\min _{z,\lambda }&\frac{d_1(y_1-z_1)^2}{x_1-\lambda }+\frac{d_2(y_2-z_2)^2}{x_2-\lambda }+\frac{d_1z_1^2+2z_1z_2+d_2z_2^2}{\lambda }\end{aligned}$$

(17a)

$$\begin{aligned} \text {s.t.}&\ z_1\ge 0,z_2\ge 0\end{aligned}$$

(17b)

$$\begin{aligned}&\ \max \{ 0,x_1+x_2-1\} \le \lambda \le \min \{ x_1,x_2 \}, \end{aligned}$$

(17c)

and

$$\begin{aligned} f_-^*(x,y;d)=\min _{z,\lambda }&\frac{d_1(y_1-z_1)^2}{x_1-\lambda }+\frac{d_2(y_2-z_2)^2}{x_2-\lambda }+\frac{d_1z_1^2-2z_1z_2+d_2z_2^2}{\lambda }\end{aligned}$$

(18a)

$$\begin{aligned} \text {s.t.}&\ z_1\le y_1,z_2\le y_2\end{aligned}$$

(18b)

$$\begin{aligned}&\ \max \{ 0,x_1+x_2-1\} \le \lambda \le \min \{ x_1,x_2 \}. \end{aligned}$$

(18c)

Since any $2 \times 2$ symmetric PSD matrix P can be rewritten in the form of $P=p\left( \begin{matrix} d_1&{}1\\ 1&{}d_2 \end{matrix}\right)$ or $P=p\left( \begin{matrix} d_1&{}-1\\ -1&{}d_2 \end{matrix}\right) ,$ we can take $f_P(x,y)=pf_+^*(x,y;d)$ or $f_P(x,y)=pf_-^*(x,y;d)$, correspondingly. Since we have the explicit form of $f_+^*(\cdot )$ and $f_-^*(\cdot )$, for any fixed d, (14) gives a nonlinear valid inequality which can be added to (13). Alternatively, (17) and (18) can be used to reformulate these inequalities as conic quadratic inequalities in an extended space. Moreover, maximizing the inequalities gives the optimal valid inequalities among the class of of $2\times 2$ PSD matrices stated below. Recall that ${\mathcal {D}}:= \{d \in {\mathbb {R}}^2: d_1\ge 0, d_2\ge 0, d_1d_2\ge 1\}$.

Proposition 9

For any pair of indices $i<j$, the following inequalities are valid for $\text {(QI)}$:

$$\begin{aligned}&\max _{d \in {\mathcal {D}}}\left\{ f_+^*(x_i,x_j,y_i,y_j;d_1,d_2)\!-d_1Y_{ii}\!-d_2Y_{jj}\!-2Y_{ij} \right\} \le 0, \ \end{aligned}$$

(19a)

$$\begin{aligned}&\max _{d \in {\mathcal {D}}}\left\{ f_-^*(x_i,x_j,y_i,y_j;d_1,d_2)\!-d_1Y_{ii}\!-d_2Y_{jj}\!+2Y_{ij} \right\} \le 0. \ \end{aligned}$$

(19b)

Optimal inequalities (9) may be employed effectively if they can be expressed explicitly. We will now show how to write inequalities (9) explicitly using an auxiliary $3 \times 3$ matrix variable W.

Lemma 2

A point $(x_1,x_2,y_1,y_2,Y_{11},Y_{12},Y_{22})$ satisfies inequality (19a) if and only if there exists $W^+\in {\mathbb {S}}^3_+$ such that the inequality system

$$\begin{aligned}&W^+_{12}\le Y_{12} \end{aligned}$$

(20a)

$$\begin{aligned}&(Y_{11}-W^+_{11})(x_1-W^+_{33})\ge (y_1-W^+_{31})^2,W^+_{11}\le Y_{11},W^+_{33}\le x_1\end{aligned}$$

(20b)

$$\begin{aligned}&(Y_{22}-W^+_{22})(x_2-W^+_{33})\ge (y_2-W^+_{32})^2,W^+_{22}\le Y_{22},W^+_{33}\le x_2\end{aligned}$$

(20c)

$$\begin{aligned}&W^+_{31}\ge 0,W^+_{32}\ge 0\end{aligned}$$

(20d)

$$\begin{aligned}&W^+_{33}\ge x_1+x_2-1 \end{aligned}$$

(20e)

is feasible.

Lemma 3

A point $(x_1,x_2,y_1,y_2,Y_{11},Y_{12},Y_{22})$ satisfies inequality (19b) if and only if there exists $W^-\in {\mathbb {S}}^3_{+}$ such that the inequality system

$$\begin{aligned}&Y_{12}\le W^-_{12} \end{aligned}$$

(21a)

$$\begin{aligned}&(Y_{11}-W^-_{11})(x_1-W^-_{33})\ge (y_1-W^-_{31})^2,W^-_{11}\le Y_{11},W^-_{33}\le x_1\end{aligned}$$

(21b)

$$\begin{aligned}&(Y_{22}-W^-_{22})(x_2-W^-_{33})\ge (y_2-W^-_{32})^2,W^-_{22}\le Y_{22},W^-_{33}\le x_2\end{aligned}$$

(21c)

$$\begin{aligned}&W^-_{31}\le y_1,W^-_{32}\le y_2\end{aligned}$$

(21d)

$$\begin{aligned}&W^-_{33}\ge x_1+x_2-1 \end{aligned}$$

(21e)

is feasible.

Proof of Lemma 2

The Lemma is proved by means of conic duality. For brevity, dual variables associated with each constraint are introduced in the formulation below. Writing $f^*_+$ as a conic quadratic minimization problem as in (17), we first express inequality (19a) as

where $B_+^2=\left( \begin{matrix} d_1&{}1\\ 1&{}d_2 \end{matrix}\right) .$ Taking the dual of the inner minimization, the inequality can be written as

Note that one can obtain a strictly dual feasible solution by taking $s_i, i \in [3]$ sufficiently large. Due to Slater condition, we deduce that strong duality holds. We first assume $d_1d_2>1$. Then, the last equation implies $\gamma = B_+^{-1}(r/2-\eta )$. Substituting out $\gamma$ and $s_3$, and letting $u_i=\eta _i-r_i/2,i=1,2$, the maximization problem is further reduced to

$$\begin{aligned} 0\ge \max _{d \in {\mathcal {D}}}&\max _{\alpha ,\eta ,s, u} - \sum _{i=1,2} (x_i s_i + 2 y_i \eta _i)+(x_1+x_2-1)\alpha -d_1Y_{11}-d_2Y_{22}-2Y_{12}\\ \text {s.t. }&d_is_i\ge \eta _i^2, \;i=1,2\\&\eta _i\ge u_i,\;i=1,2\\&\alpha \ge 0\\&s_1+s_2-\alpha \ge u' \left[ \begin{matrix} d_1&{}1\\ 1&{}d_2 \end{matrix}\right] ^{-1} u. \end{aligned}$$

Applying Schur Complement Lemma to the last inequality, we reach

$$\begin{aligned} 2Y_{12}\ge \max _{\eta ,s,u,r,d}\;&- \sum _{i=1,2} (x_i s_i + 2 y_i \eta _i) +(x_1+x_2-1)\alpha -d_1Y_{11}-d_2Y_{22}\\ \text {s.t. }&d_is_i\ge \eta _i^2, \;i=1,2\qquad \qquad {{(p_i,q_i,w_i)}}\\&\eta _i\ge u_i,\;i=1,2\qquad \qquad {{(v_i)}}\\&\alpha \ge 0 \qquad \qquad {{(\beta )}}\\&\begin{pmatrix} s_1+s_2-\alpha &{}\,\,\, u_1&{}\,\,\, u_2\\ u_1&{}\,\,\, d_1&{}\,\,\, 1\\ u_2&{}\,\,\, 1&{}\,\,\, d_2 \end{pmatrix}\succeq 0.\qquad \qquad {{(W^+)}} \end{aligned}$$

Note the SDP constraint implies $d \in D$. If $d_1d_2=1$, then $B_+$ is singular. In this case, one can apply the same argument to the Moore-Penrose pseudo inverse of $B_+$ (see p108, Ch12 and Corollary 15.3.2 in [41]) and use the generalized Schur Complement Lemma (see 7.3.P8 in [35]) to deduce the last SDP constraint. Finally, taking the SDP dual of the maximization problem we arrive at

$$\begin{aligned}&2Y_{12}\ge \min _{p,q,w,v,W^+} \;2W^+_{12}\\&\text {s.t. } p_iq_i\ge w_i^2, \ p_i, q_i\ge 0, \ i=1,2\\&v_i \ge 0, \ i=1,2\\&q_i+W^+_{33}=x_i,\ i=1,2 \qquad \qquad {{(s_i)}}\\&p_i+W^+_{ii}=Y_{ii}, \ i=1,2 \qquad \qquad {{(d_i)}}\\&2w_i+v_i=2y_i, \ i=1,2\qquad \qquad {{(\eta _i)}}\\&2W^+_{3i}= v_i, \ i=1,2 \qquad \qquad \quad {{(u_i)}}\\&\beta -W^+_{33}=1-x_1-x_2\qquad \qquad {{(\alpha )}}\\&\beta \ge 0, \ W^+\succeq 0. \end{aligned}$$

One can obtain a strictly primal feasible solution by taking $d_i,s_i,i=1,2$ sufficiently large, which implies strong SDP duality holds due to Slater condtion. Substituting out $p,q,w,v,\beta$, we arrive at (20). $\square$

The proof of Lemma 3 is similar and is omitted for brevity. Since both (19a) and (19b) are valid, using (20) and (21) together, one can obtain an SDP relaxation of $\text {(QI)}$. While inequalities in (20) and (21) are quite similar, in general, $W^+$ and $W^-$ do not have to coincide. However, we show below that choosing $W^+ = W^-$, the resulting SDP formulation is still valid and it is at least as strong as the strengthening obtained by valid inequalities (9).

Let ${\mathcal {W}}$ be the set of points $(x_1,x_2,y_1,y_2,Y_{11},Y_{12},Y_{22})$ such that there exists a $3 \times 3$ matrix W satisfying

$$\begin{aligned}&W_{12}= Y_{12} \end{aligned}$$

(25a)

$$\begin{aligned}&(Y_{11}-W_{11})(x_1-W_{33})\ge (y_1-W_{31})^2,W_{11}\le Y_{11},W_{33}\le x_1 \end{aligned}$$

(25b)

$$\begin{aligned}&(Y_{22}-W_{22})(x_2-W_{33})\ge (y_2-W_{32})^2,W_{22}\le Y_{22},W_{33}\le x_2 \end{aligned}$$

(25c)

$$\begin{aligned}&0 \le W_{31}\le y_1, \, 0 \le W_{32}\le y_2 \end{aligned}$$

(25d)

$$\begin{aligned}&W_{33}\ge x_1+x_2-1 \end{aligned}$$

(25e)

$$\begin{aligned}&W\succeq 0 \end{aligned}$$

(25f)

Then, using ${\mathcal {W}}$ for every pair of indices, we can define the strengthened SDP formulation

$$\begin{aligned} \min \;&a'x+b'y+\langle Q,Y\rangle&\end{aligned}$$

(26a)

$$\begin{aligned} (\textsf {OptPairs}) \ \ \ \text {s.t. }&Y-yy'\succeq 0&\end{aligned}$$

(26b)

$$\begin{aligned}&(x_i, x_j, y_i, y_j, Y_{ii}, Y_{ij}, Y_{jj}) \in {\mathcal {W}}&\forall i< j \end{aligned}$$

(26c)

$$\begin{aligned}&0 \le x \le 1, \ y \ge 0. \end{aligned}$$

(26d)

Proposition 10

$\textsf {OptPairs}$ is a valid convex relaxation of $\text {(QI)}$ and every feasible solution to it satisfies all valid inequalities (9).

Proof

To see that $\textsf {OptPairs}$ is a valid relaxation, consider a feasible solution (x, y) of $\text {(QI)}$ and let $Y=yy'$. For $i<j$, if $x_i=x_j=1$, constraint (26c) is satisfied with $W=\left( \begin{matrix} Y_{ii}&{}Y_{ij}&{}{y_i}\\ Y_{ij}&{}Y_{jj}&{}y_j\\ y_i&{}y_j&{}1 \end{matrix}\right) .$ Otherwise, without loss of generality, one may assume $x_i=0$. It follows that $Y_{ii}=y_i^2=Y_{ij}=y_iy_j=0$. Then, constraint (26c) is satisfied with $W=0$. Moreover, if W satisfies (26c), then W satisfies (20) and (21) simultaneously. $\square$

5 Comparison of convex relaxations

In this section, we compare the strength of $\textsf {OptPairs}$ with other convex relaxations of $\text {(QI)}$. The perspective relaxation and the optimal perspective relaxation $\textsf {OptPersp}$ for $\text {(QI)}$ are well-known.

Proposition 11

$\textsf {OptPairs}$ is at least as strong as $\textsf {OptPersp}$.

Proof

Note that (26c) includes constraints

$$\begin{aligned} \begin{pmatrix} Y_{ii}&{}\,\,\, y_i\\ y_i&{}\,\,\, x_i \end{pmatrix}\succeq \begin{pmatrix} W_{11}&{}\,\,\, W_{31}\\ W_{31}&{}\,\,\, W_{33} \end{pmatrix}\succeq 0, \end{aligned}$$

corresponding to (25b)–(25c). Thus, the perspective constraints $Y_{ii} x_i \ge y_i^2$ are implied. $\square$

In the context of linear regression, Atamtürk and Gómez [5] study the convex hull of the epigraph of rank-one quadratic with indicators

$$\begin{aligned} \mathcal {X}_f=\left\{ (x,y,t)\in \{0,1\}^n \times {\mathbb {R}}^{n+1}:t\ge \bigg (\sum _{i=1}^n y_i \bigg )^2, \ y_i(1-x_i)=0, i \in [n] \right\} , \end{aligned}$$

where the continuous variables are unrestricted in sign. Their extended SDP formulation based on ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {X}_f)$, leads to the following relaxation for $\text {(QI)}$

$$\begin{aligned} \min \;&a'x+b'y+\langle Q,Y\rangle \end{aligned}$$

(27a)

$$\begin{aligned} \text {s.t.}\;&Y - yy' \succeq 0 \end{aligned}$$

(27b)

$$\begin{aligned}&y_i^2\le Y_{ii}x_i&\forall i\end{aligned}$$

(27c)

$$\begin{aligned} (\textsf {OptRankOne}) \ \ \&\begin{pmatrix}x_i+x_j&{}\,\,\, y_i &{}\,\,\, y_j\\ y_i &{}\,\,\, Y_{ii} &{}\,\,\, Y_{ij}\\ y_j &{}\,\,\, Y_{ij}&{}\,\,\, Y_{jj}\end{pmatrix}\succeq 0,&\forall i < j \end{aligned}$$

(27d)

$$\begin{aligned}&y \ge 0, \ 0\le x\le 1. \end{aligned}$$

(27e)

With the additional constraints (27d), it is immediate that $\textsf {OptRankOne}$ is stronger than $\textsf {OptPersp}$. The following proposition compares $\textsf {OptRankOne}$ and $\textsf {OptPairs}$.

Proposition 12

$\textsf {OptPairs}$ is at least as strong as $\textsf {OptRankOne}$.

Proof

It suffices to show that for each pair $i<j$, constraint (26c) of $\textsf {OptPairs}$ implies (27d) of $\textsf {OptRankOne}$. Rewriting (25b)–(25c), we get

$$\begin{aligned} W_{11}\le Y_{11}-\frac{(y_1-W_{31})^2}{x_1-W_{33}}, \; W_{22}\le Y_{22}-\frac{(y_2-W_{32})^2}{x_2-W_{33}} \cdot \end{aligned}$$

Combining the above and (25a) to substitute out $W_{11},W_{22}$ and $W_{12}$ in $W\succeq 0$, we arrive at

$$\begin{aligned} \begin{pmatrix} Y_{11}-\frac{(y_1-W_{31})^2}{x_1-W_{33}}&{}\,\,\,\, Y_{12}&{}\,\,\,\, W_{31}\\ Y_{12}&{}\,\,\,\, Y_{22}-\frac{(y_2-W_{32})^2}{x_2-W_{33}}&{}\,\,\,\, W_{32}\\ W_{31}&{}\,\,\,\, W_{32}&{}\,\,\,\, W_{33} \end{pmatrix} \succeq 0,\; W_{33}\le x_1,\; W_{33} \le x_2, \end{aligned}$$

which is equivalent to the following matrix inequality by Shur Complement Lemma

$$\begin{aligned} \begin{pmatrix} Y_{11}&{}\,\,\,\, Y_{12}&{}\,\,\,\, W_{31}&{}\,\,\,\, y_1-W_{31}&{}\,\,\,\, 0\\ Y_{12}&{}\,\,\,\, Y_{22}&{}\,\,\,\, W_{32}&{}\,\,\,\, 0&{}\,\,\,\, y_2-W_{32}\\ W_{31}&{}\,\,\,\, W_{32}&{}\,\,\,\, W_{33}&{}\,\,\,\, 0&{}\,\,\,\, 0\\ y_1-W_{31}&{}\,\,\,\, 0&{}\,\,\,\, 0&{}\,\,\,\, x_1-W_{33}&{}\,\,\,\, 0\\ 0&{}\,\,\,\, y_2-W_{32}&{}\,\,\,\, 0&{}\,\,\,\, 0&{}\,\,\,\, x_2-W_{33} \end{pmatrix} \succeq 0. \end{aligned}$$

By adding the third row/column to the forth row/column and then adding the forth row/column to the fifth row/column, the large matrix inequality can be rewritten as

$$\begin{aligned} \begin{pmatrix} Y_{11}&{}\,\,\, Y_{12}&{}\,\,\, W_{31}&{}\,\,\, y_1&{}\,\,\, y_1\\ Y_{12}&{}\,\,\, Y_{22}&{}\,\,\, W_{32}&{}\,\,\, W_{32}&{}\,\,\, y_2\\ W_{31}&{}\,\,\, W_{32}&{}\,\,\, W_{33}&{}\,\,\, W_{33}&{}\,\,\, W_{33}\\ y_1&{}\,\,\, W_{32}&{}\,\,\, W_{33}&{}\,\,\, x_1&{}\,\,\, x_1\\ y_1&{}\,\,\, y_2&{}\,\,\, W_{33}&{}\,\,\, x_1&{}\,\,\, x_1+x_2-W_{33} \end{pmatrix} \succeq 0. \end{aligned}$$

Because $W_{33}\ge 0$, it follows that

$$\begin{aligned} \begin{pmatrix} Y_{11}&{}\,\,\, Y_{12}&{}\,\,\, y_1\\ Y_{12}&{}\,\,\, Y_{22}&{}\,\,\, y_2\\ y_1&{}\,\,\, y_2&{}\,\,\, x_1+x_2 \end{pmatrix}\succeq \begin{pmatrix} Y_{11}&{}\,\,\, Y_{12}&{}\,\,\, y_1\\ Y_{12}&{}\,\,\, Y_{22}&{}\,\,\, y_2\\ y_1&{}\,\,\, y_2&{}\,\,\, x_1+x_2-W_{33} \end{pmatrix}\succeq 0. \end{aligned}$$

Therefore, constraints (27d) are implied by (26c), proving the claim. $\square$

The example below illustrates that $\textsf {OptPairs}$ is indeed strictly stronger than $\textsf {OptPersp}$ and $\textsf {OptRankOne}$.

Example 2

For $n=2$, $\textsf {OptPairs}$ is the ideal (convex) formulation of $\text {(QI)}$. For the instance of $\text {(QI)}$ with

$$\begin{aligned} a=\begin{pmatrix} 1\\ 5 \end{pmatrix}, b=\begin{pmatrix} -8\\ -5 \end{pmatrix}, Q=\begin{pmatrix} 5&{}2\\ 2&{}1\\ \end{pmatrix} \end{aligned}$$

each of the other convex relaxations has a fractional optimal solution as demonstrated in Table 1.

Notably, the fractional x values for $\textsf {OptPersp}$ and $\textsf {OptRankOne}$ are far from their optimal integer values. A common approach to quickly obtain feasible solutions to NP-hard problems is to round a solution obtained from a suitable convex relaxation. This example indicates that feasible solutions obtained in this way from formulation $\textsf {OptPairs}$ may be of higher quality than those obtained from weaker relaxations—our computations in Sect. 6.2 further corroborates this intuition. $\square$

Table 1 Comparison of convex relaxations of $\text {(QI)}$

An alternative way of constructing strong relaxations for $\text {(QI)}$ is to decompose the quadratic function $y'Qy$ into a sum of univariate and bivariate convex quadratic functions and utilize the convex hull results of $2\times 2$ quadratics

$$\begin{aligned} \alpha _{ij}q_{ij} (y_i, y_j) = \beta _{ij}{y_{i}^2} \pm 2 y_i y_j + \gamma _{ij} y_{j}^2, \end{aligned}$$

where $\alpha _{ij} > 0$, in Sect. 3 for each term, see [25] for such an approach. Specifically, let

$$\begin{aligned} y'Qy = y'Dy + \sum _{(i,j) \in {\mathcal {P}}} \alpha _{ij} q_{ij}(y_i, y_j) + \sum _{(i,j) \in {\mathcal {N}}} \alpha _{ij} q_{ij}(y_i, y_j) + y'Ry \end{aligned}$$

where D is a diagonal PSD matrix, ${\mathcal {P}}/{\mathcal {N}}$ is the set of quadratics $q_{ij}(\cdot )$ with positive/negative off-diagonals and R is PSD remainder matrix. Applying the convex hull description for each univariate and bivariate term we obtain the following convex relaxation for $\text {(QI)}$:

$$\begin{aligned} \begin{aligned} \min \;&a'x+b'y+\sum _{i=1}^n D_{ii} y_i^2/x_i +\sum _{(i,j)\in {\mathcal {P}}}\alpha _{ij}f^*_+(x_i,x_j,y_i,y_j;\beta _{ij},\gamma _{ij}) \\ (\textsf {Decomp}) \ \ \ {}&+\sum _{(i,j)\in {\mathcal {N}}}\alpha _{ij}f^*_-(x_i,x_j,y_i,y_j;\beta _{ij},\gamma _{ij}) +y'Ry\\ \text {s.t.}\;&\ 0\le x\le 1, \ y \ge 0. \end{aligned} \end{aligned}$$

The next proposition shows that $\textsf {OptPairs}$ dominates $\textsf {Decomp}$. Similar duality arguments were used in [21, 25, 45].

Proposition 13

$\textsf {OptPairs}$ is at least as strong as $\textsf {Decomp}$. Moreover, there exists a decomposition for which $\textsf {Decomp}$ is equivalent to $\textsf {OptPairs}$.

Proof

We prove the result via the minimax theory of concave-convex programs and show that $\textsf {Decomp}$ can be viewed as a dual formulation of $\textsf {OptPairs}$. To make the dual relationship more transparent, we define $z^{ij}_i=W^{ij}_{31}$, $z^{ij}_j=W^{ij}_{32}$, $\lambda _{ij}=W^{ij}_{33}$ and

$$\begin{aligned} \Lambda =\big \{(x,y,z,&\lambda )\in [0,1]^n\times {\mathbb {R}}_+^n\times {\mathbb {R}}^{n(n-1)}\times {\mathbb {R}}^{n(n-1)/2}:0\le z^{ij}_i\le y_i,\\&0\le z^{ij}_j\le y_j,\; \min \{0,x_i+x_j-1\}\le \lambda _{ij}\le \max \{x_i,x_j\},\; \forall i<j\big \}. \end{aligned}$$

Then, $\textsf {OptPairs}$ can be rewritten as

$$\begin{aligned} {\displaystyle \min _{x,y,z,\lambda }\min _{Y, W}}\;&a'x+b'y+\langle Q,Y\rangle \end{aligned}$$

(28a)

$$\begin{aligned} \text {s.t. }&Y\succeq yy'\qquad \qquad {(R)}\nonumber \\&Y_{ii}-\frac{\left( y_i-z^{ij}_i\right) ^2}{x_i-\lambda _{ij}}\ge W^{ij}_{11}\ge \frac{\left( z_i^{ij}\right) ^2}{\lambda _{ij}}\qquad \qquad \forall i<j \qquad \qquad {(\ell ^{ij}_i,u^{ij}_i)} \nonumber \\&Y_{jj}-\frac{\left( y_j-z^{ij}_j\right) ^2}{x_j-\lambda _{ij}}\ge W^{ij}_{22}\ge \frac{\left( z_j^{ij}\right) ^2}{\lambda _{ij}}\qquad \qquad \forall i<j \qquad \qquad {(\ell ^{ij}_j,u^{ij}_j)}\nonumber \\&\begin{pmatrix} W^{ij}_{11}&{}\,\,\, Y_{ij}\\ Y_{ij}&{}\,\,\, W^{ij}_{22} \end{pmatrix}\succeq \frac{1}{\lambda _{ij}}\begin{pmatrix} z^{ij}_i\\ z^{ij}_j \end{pmatrix}\begin{pmatrix} z^{ij}_i&z^{ij}_j \end{pmatrix}\qquad \qquad \quad \forall i<j \qquad \qquad {(Q^{ij})} \nonumber \\&(x,y,z,\lambda )\in \Lambda . \end{aligned}$$

(28b)

Taking the SDP dual with respect to the inner minimization problem, one arrives at

$$\begin{aligned} {\min _{x,y,z,\lambda }\max _{R,Q^{ij},\ell ,u}}&a'x+b'y+{\displaystyle \sum _{i<j}\left[ \ell ^{ij}_i\frac{\left( z^{ij}_i\right) ^2}{\lambda _{ij}} +\ell ^{ij}_j\frac{\left( z^{ij}_j\right) ^2}{\lambda _{ij}}+u^{ij}_i\frac{\left( y_i-z^{ij}_i\right) ^2}{x_i-\lambda _{ij}}+ \right. }\nonumber \\&{\displaystyle \left. u^{ij}_j\frac{\left( y_j-z^{ij}_j\right) ^2}{x_j-\lambda _{ij}}+ \frac{1}{\lambda _{ij}}\left( z^{ij}\right) 'Q^{ij}z^{ij}\right] +\langle R,yy'\rangle } \end{aligned}$$

(29a)

$$\begin{aligned} \text {s.t. }&Q_{ii}=R_{ii}+\sum _{i<j}u^{ij}_i+\sum _{i>j}u^{ji}_i\quad \qquad \qquad \forall i\qquad \qquad {(Y_{ii})}\nonumber \\&Q_{ij}=R_{ij}+Q^{ij}_{12}\qquad \qquad \forall i<j \qquad \qquad {(Y_{ij})}\nonumber \\&0=\ell ^{ij}_i-u^{ij}_i+Q^{ij}_{11}\qquad \qquad \forall i<j\qquad \qquad {(W^{ij}_{11})}\nonumber \\&0=\ell ^{ij}_j-u^{ij}_j+Q^{ij}_{22}\qquad \qquad \forall i<j\qquad \qquad {(W^{ij}_{22})}\nonumber \\&R\succeq 0, Q^{ij}\succeq 0, \ell ^{ij}\ge 0, u^{ij}\ge 0 \qquad \qquad \forall i<j \end{aligned}$$

(29b)

$$\begin{aligned}&(x,y,z,\lambda )\in \Lambda . \end{aligned}$$

(29c)

Since one can take the diagonal elements of Y and $W^{ij}$ large enough, there exists a strictly feasible solution to the inner minimization of (28), which implies strong duality holds and, thus, (28) is equivalent to (29). Next, substituting out $u^{ij}$ in (29a), one gets

$$\begin{aligned}&\ell ^{ij}_i\frac{\left( z^{ij}_i\right) ^2}{\lambda _{ij}} +\ell ^{ij}_j\frac{\left( z^{ij}_j\right) ^2}{\lambda _{ij}}+u^{ij}_i\frac{\left( y_i-z^{ij}_i\right) ^2}{x_i-\lambda _{ij}}+ u^{ij}_j\frac{\left( y_j-z^{ij}_j\right) ^2}{x_j-\lambda _{ij}}+ \frac{1}{\lambda _{ij}}\left( z^{ij}\right) 'Q^{ij}z^{ij}\\&\quad ={\tilde{Q}}^{ij}_{11}\frac{\left( y_i-z^{ij}_i\right) ^2}{x_i-\lambda _{ij}} +{\tilde{Q}}^{ij}_{22}\frac{\left( y_j-z^{ij}_j\right) ^2}{x_j-\lambda _{ij}} + \frac{\left( z^{ij}\right) '{\tilde{Q}}^{ij}z^{ij}}{\lambda _{ij}}, \end{aligned}$$

where ${\tilde{Q}}^{ij}=\begin{bmatrix} \ell ^{ij}_i+Q^{ij}_{11}&{}Q^{ij}_{12}\\ Q^{ij}_{12}&{}\ell ^{ij}_j+Q^{ij}_{22} \end{bmatrix}$. By changing variables $Q^{ij}\leftarrow {\tilde{Q}}^{ij}$, one arrives at

$$\begin{aligned} {\min _{(x,y,z,\lambda )\in \Lambda }\max _{R,Q^{ij}}}\;&{\displaystyle \sum _{i<j}\left[ Q^{ij}_{11}\frac{\left( y_i-z^{ij}_i\right) ^2}{x_i-\lambda _{ij}} +Q^{ij}_{22}\frac{\left( y_j-z^{ij}_j\right) ^2}{x_j-\lambda _{ij}} + \frac{\left( z^{ij}\right) 'Q^{ij}z^{ij}}{\lambda _{ij}}\right] }\nonumber \\&+\langle R,yy'\rangle +a'x+b'y \end{aligned}$$

(30a)

$$\begin{aligned} \text {s.t. }&Q_{ii}\ge R_{ii}+\sum _{i<j}Q^{ij}_{11}+\sum _{i>j}Q^{ji}_{22}\qquad \qquad \forall i\end{aligned}$$

(30b)

$$\begin{aligned}&Q_{ij}=R_{ij}+Q^{ij}_{12}\qquad \qquad \forall i<j\end{aligned}$$

(30c)

$$\begin{aligned}&R\succeq 0, Q^{ij}\succeq 0, \qquad \qquad \forall i<j \end{aligned}$$

(30d)

which is equivalent to (29). Notice that (30b) is, in fact, tight. Thus, (30b), (30c),and (30d) define a valid decomposition of Q. Moreover, $\Vert Q^{ij}\Vert _{2}, \Vert R\Vert _{2}\le \text {Trace}(Q)$ by (30b), which implies the feasible region of the inner maximization problem is compact. Therefore, according to Von Neumann’s Minimax Theorem [43], one can interchange $\max$ and $\min$ without loss of equivalence and arrive at

$$\begin{aligned} \max _{R,Q^{ij}:(30\text {b})\text {-}(30\text {d})}\min _{z^{ij},\lambda _{ij}}&\sum _{i<j}\left[ Q^{ij}_{11}\frac{\left( y_i-z^{ij}_i\right) ^2}{x_i-\lambda _{ij}} +Q^{ij}_{22}\frac{\left( y_j-z^{ij}_j\right) ^2}{x_j-\lambda _{ij}} + \frac{\left( z^{ij}\right) 'Q^{ij}z^{ij}}{\lambda _{ij}}\right] \\&+\langle R,yy'\rangle +a'x+b'y\\ \text {s.t. }&(x,y,z,\lambda )\in \Lambda \end{aligned}$$

where the inner minimization problem is in the form $\textsf {Decomp}$ from Proposition 6. $\square$

6 Computations

In this section, we report on computational experiments performed to test the effectiveness the formulations derived in the paper. Section 6.1 is devoted to synthetic portfolio optimization instances, where matrix Q is diagonally dominant and the conic quadratic-representable extended formulations developed in Sect. 3 can be readily used in a branch-and-bound algorithm without the need for an SDP constraint. The instances here are generated similarly to [4], and serve to check the incremental value of convexifications based on $\mathcal {Z}_+$ compared to those based on only $\mathcal {Z}_-$. In Sect. 6.2, we use real instances derived from stock market returns and test the SDP relaxation $\textsf {OptPairs}$ derived in Sect. 4, as well as mixed-integer optimization approaches based on decompositions of the quadratic matrices.

6.1 Synthetic instances—the diagonally dominant case

We consider a standard cardinality-constrained mean-variance portfolio optimization problem of the form

$$\begin{aligned} \min _{x,y}\; \left\{ y'Qy: \begin{array}{ll} &{}b'y\ge r, \ 1'x\le k \\ &{}0\le y\le x, \ x\in \{0,1\}^n \end{array} \right\} \end{aligned}$$

(31)

where Q is the covariance matrix of returns, $b\in {\mathbb {R}}^n$ is the vector of the expected returns, r is the target return and k is the maximum number of securities in the portfolio. All experiments are conducted using Mosek 9.1 solver on a laptop with a 2.30GHz Intel® $\text {Core}^{\text {\tiny TM}}$ i9-9880 H CPU and 64 GB main memory. The time limit is set to one hour and all other settings are default by Mosek.

6.1.1 Instance generation

We adopt the method used in [4] to generate the instances. The instances are designed to control the integrality gap of the instances and the effectiveness of the perspective formulation. Let $\rho \ge 0$ be a parameter controlling the ratio of the magnitude positive off-diagonal entries of Q to the magnitude of the negative off-diagonal entries of Q. Lower values of $\rho$ lead to higher integrality gaps. Let $\delta \ge 0$ be the parameter controlling the diagonal dominance of Q. The perspective formulation is more effective in closing the integrality gap for higher values of $\delta$. The following steps are followed to generate the instances:

• Construct an auxiliary matrix ${{\bar{Q}}}$ by drawing a factor covariance matrix $G_{20\times 20}$ uniformly from $[-1,1]$, and generating an exposure matrix $H_{n\times 20}$ such that $H_{ij}=0$ with probability 0.75, and $H_{ij}$ drawn uniformly from [0, 1], otherwise. Let ${\bar{Q}}=HGG'H'$.

• Construct off-diagonal entries of Q: For $i\ne j$, set $Q_{ij}={\bar{Q}}_{ij}$, if ${\bar{Q}}_{ij}<0$ and set $Q_{ij}=\rho {{\bar{Q}}}_{ij}$ otherwise. Positive off-diagonal elements of ${{\bar{Q}}}$ are scaled by a factor of $\rho$.

• Construct diagonal entries of Q: Pick $\mu _i$ uniformly from $[0,\delta {{\bar{\sigma }}}]$, where ${{\bar{\sigma }}}=\frac{1}{n}\sum _{i\ne j}|Q_{ij}|$. Let $Q_{ii}=\sum _{i\ne j}|Q_{ij}|+\mu _i$. Note that if $\delta =\mu _i=0$, then matrix Q is already diagonally dominant.

• Construct b, r, k: $b_i$ is drawn uniformly from $[0.5Q_{ii},1.5Q_{ii}]$, $r=0.25\sum _{i=1}^nb_i$, and $k=\lfloor n/5 \rfloor$.

Matrices Q generated in this way have only 20.1% of the off-diagonal entries negative on average.

6.1.2 Formulations

With above setting, the portfolio optimization problem can be rewritten as

$$\begin{aligned} \begin{aligned} \min&\sum _{i\in [n]}\mu _i z_i +\sum _{Q_{ij}<0}|Q_{ij}|t_{ij} +\sum _{Q_{ij}>0}|Q_{ij}|t_{ij}\\ \text {s.t.}\;\;&(x_i,y_i,z_i)\in \mathcal {X}_0,\;\forall i\in N,\\&(x_i,x_j,y_i,y_j,t_{ij})\in \mathcal {Z}_-,\;\forall {i>j}: Q_{ij}<0,\\&(x_i,x_j,y_i,y_j,t_{ij})\in \mathcal {Z}_+,\;\forall {i>j}: Q_{ij}>0,\\&b'y\ge r, \ 1'x\le k, \\ \end{aligned} \end{aligned}$$

(32)

where $\mathcal {Z}_+$ and $\mathcal {Z}_-$ are defined as before with $d_1=d_2=1$. Four strong formulations are tested by replacing the mixed-integer sets with their convex hulls: $\textsf {ConicQuadPersp}$ by replacing $\mathcal {X}_0$ with ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {X}_0)$ using the perspective reformulation (2) ConicQuadN by replacing $\mathcal {X}_0$ and $\mathcal {Z}_-$ with ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {X}_0)$ and ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_-)$ using the corresponding extended formulation, (3) ConicQuadP by replacing $\mathcal {X}_0$ and $\mathcal {Z}_+$ with ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {X}_0)$ and ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_+)$ respectively, and (4) ConicQuadP+N by replacing $\mathcal {X}_0$, $\mathcal {Z}_-$, and $\mathcal {Z}_+$ with ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {X}_0)$, ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_-)$ and ${{\,\textrm{cl}\,}}{{\,\textrm{conv}\,}}(\mathcal {Z}_+)$, correspondingly.

6.1.3 Results

Table 2 shows the results for matrices with varying diagonal dominance $\delta$ for $\rho =0.3$. Each row in the table represents the average for five instances generated with the same parameters. Table 2 displays the dimension of the problem n, the initial gap (igap), the root gap improvement (rimp), the number of branch and bound nodes (nodes), the elapsed time in secons (time), and the end gap provided by the solver at termination (egap). In addition, in brackets, we report the number of instances solved to optimality within the time limit. The initial gap is computed as $\texttt {igap}=\frac{\texttt {obj}_{\texttt {best}}-\texttt {obj}_{\texttt {cont}}}{|\texttt {obj}_{\texttt {best}}|}\times 100$, where $\texttt {obj}_{\texttt {best}}$ is the objective value of the best feasible solution found and $\texttt {obj}_{\texttt {cont}}$ is the objective value of the natural continuous relaxation of (31), i.e. obtained by dropping the integral constraints; rimp is computed as $\texttt {rimp}=\frac{\texttt {obj}_{\texttt {relax}}-\texttt {obj}_{\texttt {cont}}}{\texttt {obj}_{\texttt {best}}-\texttt {obj}_{\texttt {cont}}}\times 100$, where $\texttt {obj}_{\texttt {relax}}$ is the objective value of the continuous relaxation of the corresponding formulation.

Table 2 Experiments with varying diagonal dominance, $\rho =0.3$

Table 3 Experiments with varying positive off-diagonal entries, $\delta =0.1$

In Table 2, as expected, $\textsf {ConicQuadPersp}$ has the worst performance in terms of both root gap and end gap as well as the solution time. It can only solve instances with dimension $n=40$ and some instances with dimension $n=60$ to optimality. The rimp of $\textsf {ConicQuadPersp}$ is less than 10% when the diagonal dominance is small. This reflects the fact that $\textsf {ConicQuadPersp}$ provides strengthening only for diagonal terms. ConicQuadN performs better than $\textsf {ConicQuadPersp}$ with rimp about 10%–25%, and it can solve all low-dimensional instances and most instances of dimension $n=60$. However, ConicQuadN is still unable to solve high-dimensional instances effectively. ConicQuadP performs much better than ConicQuadN for the instances considered: The rimp results in significantly stronger root improvements (between 70–80% on average). Moreover, ConicQuadP can solve almost all instances to near-optimality for $n=80$. For the instances that ConicQuadP is unable to solve to optimality, the average end gap is less than 5%. By strengthening both the negative and positive off-diagonal terms, ConicQuadP+N provides the best performance with rimp above $90\%$. ConicQuadP+N can solve all instances and most of them are solved within 10 min. Finally, observe that as the diagonal dominance increases, the performance of all formulations improves. Specifically, larger diagonal dominance results in more instances solved to optimality, smaller egap and shorter solving time for all formulations. For these instances, on average, the gap improvement is raised from 50.69% to 92.90% by incorporating strengthening from off-diagonal coefficients.

Table 3 displays the computational results for different values of $\rho$ with fixed $\delta =0.1$. The relative comparison of formulations is similar as discussed before, with ConicQuadP+N resulting in the best performance. As $\rho$ increases, the performance of ConicQuadN deteriorates in terms of Rimp while the performance of ConicQuadP improves, as expected. The performance of ConicQuadP+N also improves for high values of $\rho$, and always results in significant improvement compared to other formulations for all instances. For these instances, on average, the gap improvement is raised from 9.77% to 85.38% by incorporating strengthening from off-diagonal coefficients.

In summary, we conclude that utilizing convexification for $\mathcal {Z}_+$ complement those previously obtained for $\mathcal {Z}_-$, and together result in significantly higher root gap improvement over the simpler perspective relaxation. For the experiments in this section, we use the results of Sect. 3 to convexify pairwise quadratic terms, but do not utilize the more sophisticated SDP formulations in Sect. 4. For the instances in this section, the optimal perspective formulation [21, 45] achieves close to 100% root improvement, and all the mixed-integer optimization problems are solved in a few seconds. Moreover, the new convex formulation $\textsf {OptPairs}$ produces integer (thus optimal) solutions in all instances. In the next section, we consider these stronger conic relaxations for the more realistic and challenging instances.

6.2 Real instances—the general case

Now using real stock market data, we consider portfolio index tracking problem of the form

$$\begin{aligned} \min \;&(y-y_B)'Q(y-y_B)\\ \text {(IT)} \ \ \ \ \text {s.t. }&1'y=1, \ 1'x\le k \\&0\le y\le x, \ x\in \{0,1\}^n, \end{aligned}$$

where $y_B\in {\mathbb {R}}^n$ is a benchmark index portfolio, Q is the covariance matrix of security returns and k is the maximum number of securities in the portfolio. The (continuous) conic formulations are solved using Mosek 9.1 and the mixed-integer formulations are solved using CPLEX 12.8. The experiments are conducted on a laptop with a 1.80 GHz Intel® $\text {Core}^{\text {\tiny TM}}$ i7 CPU and 16 GB main memory. The solver time limit is set to 1200 s and all other settings are kept at their default values.

6.2.1 Instance generation

We use the daily stock return data provided by Boris Marjanovic in Kaggle¹ to compute the covariance matrix Q. Specifically, given a desired start date (either 1/1/2010 or 1/1/2015 in our computations), we compute the sample covariance matrix based on the stocks with available data in at least 99% of the days since the start (returns for missing data are set to 0). The resulting covariance matrices are available at https://sites.google.com/usc.edu/gomez/data. We then generate instances as follows:

• we randomly sample an $n\times n$ covariance matrix Q corresponding to n stocks, and

• we draw each element of $y_B$ from uniform [0,1], and then scale $y_B$ so that $1'y_B=1$.

6.2.2 Convex relaxations

The natural convex relaxation of IT always yields a trivial lower bound of 0, as it is possible to set ${x}=y=y_B$. Thus, we do not report results concerning the natural relaxation. Instead, we consider the optimal perspective relaxation $\textsf {OptPersp}$ of [21]:

$$\begin{aligned} \min _{x,y,Y}\;&y_B'Qy_B-2y_B'Qy+\langle Q,Y\rangle \end{aligned}$$

(34a)

$$\begin{aligned} \text {s.t.}\;&Y-yy'\succeq 0\end{aligned}$$

(34b)

$$\begin{aligned} (\textsf {OptPersp})\qquad \qquad&y_i^2\le Y_{ii}x_i&\forall i\in [n]\end{aligned}$$

(34c)

$$\begin{aligned}&0\le x \le 1, \ y \ge 0 \end{aligned}$$

(34d)

$$\begin{aligned}&1'y=1, \ 1'x\le k \end{aligned}$$

(34e)

and the proposed $\textsf {OptPairs}$ exploiting off-diagonal elements of Q:

$$\begin{aligned} \min _{x,y,Y,W}\;&y_B'Qy_B-2y_B'Qy+\langle Q,Y\rangle \\ \text {s.t.}\;&Y-yy'\succeq 0\\&W^{ij}\succeq 0&\forall i<j\\&(Y_{ii}-W_{11}^{ij})(x_i-W_{33}^{ij})\ge (y_i-W_{31}^{ij})^2,\;W_{11}^{ij}\le Y_{ii}&\forall i<j\\ (\textsf {OptPairs})\qquad \qquad&(Y_{jj}-W_{22}^{ij})(x_j-W_{33}^{ij})\ge (y_j-W_{32}^{ij})^2,\;W_{22}^{ij}\le Y_{jj}&\forall i<j \\&W_{33}^{ij}\le x_i+x_j-1,\;W_{33}^{ij}\le x_i,\;W_{33}^{ij}\le x_j&\forall i<j\\&0\le W_{31}^{ij}\le y_i,\; 0\le W_{32}^{ij}\le y_j,\;W_{12}^{ij}=Y_{ij}&\forall i<j\\&0\le x \le 1, \ y \ge 0 \\&1'y=1, \ 1'x\le k, \end{aligned}$$

As pointed out in Example 2, formulation $\textsf {OptPairs}$ may yield high quality feasible solutions by rounding. Therefore, for each relaxation, we consider a simple rounding heuristic to obtain feasible solutions to (IT): given an optimal solution $({{\bar{x}}},{{\bar{y}}})$ to the continuous relaxation, we fix $x_i=1$ for the k-largest values of ${{\bar{x}}}$ and the remaining $x_i=0$, and resolve the continuous relaxation to compute y.

6.2.3 Exact mixed-integer optimization approaches

We also consider three mixed-integer optimization approaches, each associated with a different convex relaxation. The first one is the $\textsf {Natural}$ relaxation corresponding to the mixed-integer quadratic formulation (IT).

The second one is the corresponding $\textsf {OptPersp}$ formulation

$$\begin{aligned} \min \;&y_B'Qy_B-2y_B'Qy+y'Ry+\sum _{i=1}^n D_{ii} t_i \end{aligned}$$

(35a)

$$\begin{aligned} \text {s.t. }&t_ix_i\ge y_i^2, \ i \in [n] \end{aligned}$$

(35b)

$$\begin{aligned}&1'y=1, \ 1'x\le k \end{aligned}$$

(35c)

$$\begin{aligned}&0\le y\le x, \ x\in \{0,1\}^n, \end{aligned}$$

(35d)

where $D+R=Q$ and R are the dual variables associated with constraint (34b). The third one is the $\textsf {OptPairs}$ formulation based on the decomposition

$$\begin{aligned} \min \;&y_B'Qy_B-2y_B'Qy+y'Ry+\sum _{i<j} t_{ij}\end{aligned}$$

(36a)

$$\begin{aligned} \text {s.t. }&t_{ij}\ge Q_{ii}^{ij}y_i^2+Q_{jj}^{ij}y_j^2+2Q_{ij}^{ij}y_iy_j\qquad \forall i<j\end{aligned}$$

(36b)

$$\begin{aligned}&1'y=1, \ 1'x\le k \end{aligned}$$

(36c)

$$\begin{aligned}&0\le y\le x, \ x\in \{0,1\}^n, \end{aligned}$$

(36d)

where matrix R is the dual variable associated with constraint $Y-yy'\succeq 0$, and matrices $Q^{ij}$ are the dual variables associated with constraints $W^{ij}\succeq 0$. The formulation is then obtained from the SOCP-representable convexification of constraints (36b) using Proposition 6 (if $Q_{ij}^{ij}\ge 0$) or Remark 1 (if $Q_{ij}^{ij}< 0$). Specifically, the corresponding $\textsf {OptPairs}$ formulation is

$$\begin{aligned} \min _{t,x,y,z,\lambda }\;&y_B'Qy_B-2y_B'Qy+y'Ry+\sum _{i<j} t_{ij}\\ \text {s.t. }&t_{ij}\ge t^{ij}_i+t^{ij}_j+t^{ij}_{ij},\,\lambda _{ij}\ge 0,\,\lambda _{ij}\ge x_i+x_j-1&\forall i<j\\&t^{ij}_i(x_i-\lambda _{ij})\ge Q^{ij}_{ii}\left( y_i-z^{ij}_i\right) ^2,\, \lambda _{ij}\le x_i,\,0\le z_i^{ij}\le y_i&\forall i<j\\&t^{ij}_j(x_j-\lambda _{ij})\ge Q^{ij}_{jj}\left( y_j-z^{ij}_j\right) ^2,\, \lambda _{ij}\le x_j,\,0\le z_j^{ij}\le y_j&\forall i<j\\&t_{ij}^{ij}\lambda _{ij}\ge Q_{ii}^{ij}\left( z^{ij}_i \right) ^2+Q_{jj}^{ij}\left( z^{ij}_j \right) ^2+2Q_{ij}^{ij}z^{ij}_iz^{ij}_j&\forall i<j\\&1'y=1, \ 1'x\le k \\&0\le y\le x, \ x\in \{0,1\}^n. \end{aligned}$$

In practice, one may use solutions obtained from rounding the SDP relaxations as warm-starts for the mixed-integer optimization solvers for an improved performance. However, in the experiments, our goal is to compare the bounds obtained from the SDP rounding approach with the branch-and-bound approach. Therefore, we do not use solutions from one method in the other one in order to properly compare the two approaches.

Table 4 Results with stock return data since 2010

Table 5 Results with stock return data since 2015

6.2.4 Results

In these experiments, the solution time limit is set to 20 min, which includes the time required to solve the SDP relaxations to find suitable decompositions. Tables 4 and 5 present the results using historical data since 2010 and 2015, respectively. They show, for different values of n and k, and for each conic relaxation: the time required to solve the convex relaxations in seconds, the lower bound (LB) corresponding to the optimal objective value of the continuous relaxation, the upper bound (UB) corresponding to the objective value of the heuristic, the gap between these two values, computed as $\texttt {Gap}=\frac{\texttt {UB}-\texttt {LB}}{\texttt {UB}}$; they also show the best objective found at termination, and the associated gap, number of nodes explored, time spent in branch-and-bound in seconds, and number of instances that could be solved to optimality within the time limit (#). The lower bounds, upper bounds from the convex relaxations, and objective from branch-and-bound, are scaled so that the best upper bound found for a given instance is 100. Each row represents an average of five instances generated with the same parameters.

We first summarize our conclusions, then discuss in depth the relative performance of the mixed-integer optimization formulations, and finally discuss the performance of the conic formulations (which, we argue, perform best for this class of problems).

$\bullet$ Summary The perspective reformulation (35) remains the best approach to solve the problems to optimality with the current off-the-shelf MISOCP solvers, as MIP solvers struggle with more the sophisticated formulations. However, the stronger formulations are very effective in producing comparable or better solutions (especially in challenging instances with poor natural convex relaxations) via rounding the convex relaxation solutions in a fraction of the computational time.

$\bullet$ Comparison of mixed-integer optimization approaches For instances with $n=50$, we see that, among the mixed-integer optimization approaches, the one based on $\textsf {OptPersp}$ is arguably the best, solving to optimality 22/30 instances (compared with $\textsf {Natural}$: 15/22, and $\textsf {OptPairs}$: 8/22). The $\textsf {Natural}$ mixed-integer optimization formulation is able to explore more nodes, but the relaxations are weaker, ultimately leading to inferior performance. In contrast, the stronger mixed-integer formulation based on $\textsf {OptPairs}$ needs more time to process each node (by orders-of-magnitude) due to the increased complexity of the relaxations, resulting in poor performance overall. Nonetheless, for instances where it can prove optimality (e.g., $n=50$, $k=5$), it does so with substantially fewer nodes, illustrating the power of the stronger relaxations. Interestingly, in the more challenging instances with data from 2010, $n=50$ and $k=10$, $\textsf {OptPairs}$ is able to prove the best optimality gap of 9.6% (compared with $\textsf {OptPersp}$: 20.5%, and $\textsf {Natural}$: 4.8%).

For larger instances with $n=100$, all mixed-integer optimization formulations struggle. Formulations based on $\textsf {OptPairs}$ result in gaps well-above 100%, that is, the best lower bound achieved by branch-and-bound is negative; for instances with data since 2015 and $k=20$, the root node relaxations cannot be fully processed in 20 min, and the branch-and-bound solver terminates without an incumbent solution. Indeed, MISOCP solvers based on outer approximations struggle to solve highly nonlinear instances with a large number of variables and exhibit pathological behavior, e.g., see [4, 7, 31] for similar documented results. Formulations based on $\textsf {Natural}$ produce the best incumbent solutions, due to the large number of nodes explored, but terminate with optimality gaps close to 100% in all cases. Formulations based on $\textsf {OptPersp}$ achieve a middle ground of producing reasonably good solutions with moderate gaps, although the optimality gaps of 50% are still quite high.

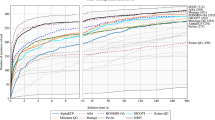
$\bullet$ Discussion of conic formulations First, note that the continuous conic formulation $\textsf {OptPairs}$ produces better lower bounds and upper bounds (via the rounding heuristic) than the continuous $\textsf {OptPersp}$: in particular, gaps are on average reduced by 66%, see Fig. 1 for a summary of the gaps across all instances. The better performance comes at the expense of increased computational times by a factor of three, which does not depend on the dimension of the problem. For the instances considered, the additional computation time is at most 30 s, which is negligible compared with the cost of solving the mixed-integer optimization problem.

Fig. 1

Distribution of gaps for $\textsf {OptPersp}$ and $\textsf {OptPairs}$

We now compare rounding $\textsf {OptPairs}$ solution with the mixed-integer optimization based on $\textsf {OptPersp}$, henceforth referred to as MIO, which produced the best results among branch-and-bound approaches. For instances MIO solves to optimality (typically requiring between one and ten minutes), $\textsf {OptPairs}$ produces optimality gaps under 2% in less than four seconds, indicating the effectiveness of rounding the strong $\textsf {OptPairs}$ solutions. More importantly, in all other instances, $\textsf {OptPairs}$ invariably produces much better gaps than MIO in a fraction of the time. For example, in Table 4 with $n=100$, $\textsf {OptPairs}$ provides optimality gaps under 2% in one minute, whereas MIO terminates with gaps above 40% after 20 min of branch-and-bound. While the improved gaps are mostly caused by considerably better lower bounds, in many cases the rounding heuristic based on $\textsf {OptPairs}$ delivers better primal bounds than MIO: for example, in Table 4, $n=100$ and $k=20$, $\textsf {OptPairs}$ produces feasible solutions with an average objective value of 100.4, whereas MIO results in incumbents with average value of 109.7.

7 Conclusions

In this paper, we describe the convex hull of the mixed-integer epigraph of the bivariate convex quadratic functions with nonnegative variables and off-diagonals with an SOCP-representable extended formulation as well as in the original space of variables. Furthermore, we develop a new technique for constructing an optimal convex relaxation from elementary valid inequalities. Using this technique, we develop a new strong SDP relaxation for $\text {(QI)}$, based on the convex hull descriptions of the bivariate cases as building blocks. Moreover, the computational results with synthetic and real portfolio optimization instances indicate that the proposed formulations provide substantial improvement over existing alternatives in the literature.

Appendices

Appendix

Proof of Proposition 8

Proof of Proposition 8

Notice that for $\lambda =x_1+x_2-1> 0$, $f(x,y,\lambda ;d)$ can be rewritten in the form

$$\begin{aligned} f(x,y,\lambda ;d)=\frac{1}{D}{\hat{y}}'A^*{\hat{y}}, \end{aligned}$$

where $D=(d_1d_2-1)x_1x_2+x_1+x_2-1>0, {\hat{y}}'=(\sqrt{d_1}y_1,\sqrt{d_2}y_2)$ and

$$\begin{aligned}A^*=\begin{pmatrix} (d_1d_2-1)x_2+\lambda &{}\,\,\,\, \sqrt{d_1d_2}\lambda \\ \sqrt{d_1d_2}\lambda &{}\,\,\,\, (d_1d_2-1)x_1+\lambda \end{pmatrix}. \end{aligned}$$

Observe $\det (A^*)=(d_1d_2-1)D$. Hence,

$$\begin{aligned} f(x,y,\lambda ;d)=\frac{(d_1d_2-1)}{\det (A^*)}{\hat{y}}^TA^*{\hat{y}}= (d_1d_2-1){\hat{y}}^TA^{-1}{\hat{y}}, \end{aligned}$$

where A is the adjugate of $A^*$, i.e.,

$$\begin{aligned} A=\begin{pmatrix} (d_1d_2-1)x_1+\lambda &{}\,\,\,\, -\sqrt{d_1d_2}\lambda \\ -\sqrt{d_1d_2}\lambda &{}\,\,\,\, (d_1d_2-1)x_2+\lambda \end{pmatrix} \cdot \end{aligned}$$

Note that $A\succ 0$. By Schur Complement Lemma, $t/(d_1d_2-1)\ge {\hat{y}}'A^{-1}{\hat{y}}$ if and only if

$$\begin{aligned} \begin{pmatrix} t/(d_1d_2-1) &{}\,\,\,\, {{\hat{y}}}^T\\ {{\hat{y}}} &{}\,\,\,\, A \end{pmatrix}\succeq 0, \end{aligned}$$

i.e.,

$$\begin{aligned} \begin{pmatrix} t/(d_1d_2-1) &{}\,\,\,\,\, \sqrt{d_1} y_1 &{}\,\,\,\,\, \sqrt{d_2}y_2\\ \sqrt{d_1} y_1 &{}\,\,\,\,\, (d_1d_2-1)x_1+\lambda &{}\,\,\,\,\, -\sqrt{d_1d_2}\lambda \\ \sqrt{d_2} y_2&{}\,\,\,\,\, -\sqrt{d_1d_2}\lambda &{}\,\,\,\,\, (d_1d_2-1)x_2+\lambda \\ \end{pmatrix}\succeq 0, \end{aligned}$$

which is further equivalent to

$$\begin{aligned} \begin{pmatrix} t/(d_1d_2-1) &{}\,\,\,\, y_1 &{}\,\,\,\, y_2\\ y_1 &{}\,\,\,\, (d_1d_2-1)x_1/d_1+\lambda /d_1 &{}\,\,\,\, -\lambda \\ y_2&{}\,\,\,\, -\lambda &{}\,\,\,\, (d_1d_2-1)x_2/d_2+\lambda /d_2\\ \end{pmatrix}\succeq 0. \end{aligned}$$

The conclusion follows by taking $\lambda = x_1+x_2-1$. $\square$