Abstract
We study a model for adversarial classification based on distributionally robust chance constraints. We show that under Wasserstein ambiguity, the model aims to minimize the conditional value-at-risk of the distance to misclassification, and we explore links to adversarial classification models proposed earlier and to maximum-margin classifiers. We also provide a reformulation of the distributionally robust model for linear classification, and show it is equivalent to minimizing a regularized ramp loss objective. Numerical experiments show that, despite the nonconvexity of this formulation, standard descent methods appear to converge to the global minimizer for this problem. Inspired by this observation, we show that, for a certain class of distributions, the only stationary point of the regularized ramp loss minimization problem is the global minimizer.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Optimization models have been used for prediction and pattern recognition in data analysis as early as the work of Mangasarian [34] in the 1960s. Recent developments have seen models grow in size and complexity, with success on a variety of tasks, which has spurred many practical and theoretical advances in data science. However, it has been observed that models that achieve remarkable prediction accuracy on unseen data can lack robustness to small perturbations of the data [26, 47]. For example, the correct classification of a data point for a trained model can often be switched to incorrect by adding a small perturbation, carefully chosen. This fact is particularly problematic for image classification tasks, where the perturbation that yields misclassification can be imperceptible to the human eyeFootnote 1.
This observation has led to the emergence of adversarial machine learning, a field that examines robustness properties of models to (potentially adversarial) data perturbations. Two streams of work in this area are particularly notable. The first is adversarial attack [12, 13, 36], where the aim is to “fool” a trained model by constructing adversarial perturbations. The second is adversarial defense, which focuses on model training methods that produce classifiers that are robust to perturbations [7, 15, 20, 33, 37, 48,49,50]. Most models for adversarial defense are based on robust optimization, where the training error is minimized subject to arbitrary perturbations of the data in a ball defined by some distance function (for example, a norm in feature space). As such, these algorithms are reminiscent of iterative algorithms from robust optimization [4, 27, 38]. Theoretical works on adversarial defense also focus on the robust optimization model, discussing several important topics such as hardness and fundamental limits [11, 22, 23, 25], learnability and risk bounds [56, 57], as well as margin guarantees and implicit bias for specific algorithms [14, 31].
In optimization under uncertainty and data-driven decision-making, the concept of distributional robustness offers an intriguing alternative to stochastic optimization and robust optimization [8, 17, 35, 52]. Instead of considering perturbations of the data (as in robust optimization), this approach considers perturbations in the space of distributions from which the data is drawn, according to some distance measure in distribution space (for example, \(\phi \)-divergence or Wasserstein distance). This technique enjoys strong statistical guarantees and its numerical performance often outperforms models based on stochastic or robust optimization. In particular, for perturbations based on Wasserstein distances, the new distributions need not have the same support as the original empirical distribution.
In this paper, we explore adversarial defense by using ideas from distributional robustness and Wasserstein ambiguity sets. We focus on the fundamental classification problem in machine learning, and its formulation as an optimization problem in which we seek to minimize the probability of misclassification. We study a distributionally robust version of this problem and explore connections between maximum-margin classifiers and conditional value-at-risk objectives. We then focus on the linear classification problem. While convex linear classification formulations are well-known [5], the model we study is based on a “zero-one” loss function \(r \mapsto \varvec{1} (r \le 0)\), which is discontinuous and thus nonconvex. However, we show that in the case of binary linear classification, the reformulation of the distributionally robust model gives rise to the “ramp loss” function \(L_R\) defined in (31), and we propose efficient first-order algorithms for minimization. While the ramp loss is nonconvex, the nonconvexity is apparently “benign”; the global minimizer appears to be found for sufficiently dense distributions. Indeed, we prove that for a certain class of distributions, the global minimizer is the only stationary point. Numerical experiments confirm this observation.
1.1 Problem description
Suppose that data \(\xi \) is drawn from some distribution P over a set S. In the learning task, we need to find a decision variable w, a classifier, from a space \(\mathcal {W}\). For each \((w,\xi ) \in \mathcal {W}\times S\), we evaluate the result of choosing classifier w for outcome \(\xi \) via a “safety function” \(z:\mathcal {W}\times S \rightarrow \mathbb {R}\cup \{+\infty \}\). We say that w “correctly classifies” the point \(\xi \) when \(z(w,\xi ) > 0\), and w “misclassifies” \(\xi \) when \(z(w,\xi ) \le 0\). Thus, we would like to choose w so as to minimize the probability of misclassification, that is,
This fundamental problem is a generalization of the binary classification problem, which is obtained when \(S = X \times \{\pm 1\}\), where \(\xi = (x,y)\) is a feature-label pair, \(\mathcal {W}\) describes the space of classifiers under consideration (e.g., linear classifiers or a reproducing kernel Hilbert space), and \(z(w,(x,y)) = y w(x)\); so w correctly classifies (x, y) if and only if \({{\,\mathrm{sign}\,}}(w(x)) = y\).
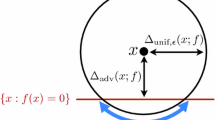
In the context of adversarial classification, we are interested in finding decisions \(w \in \mathcal {W}\) which are robust to (potentially adversarial) perturbations of the data \(\xi \). In other words, if our chosen w correctly classifies \(\xi \) (that is, \(z(w,\xi ) > 0\)), then any small perturbation \(\xi +\Delta \) should also be correctly classified, that is, \(z(w,\xi +\Delta )>0\) for “sufficiently small” \(\Delta \). To measure the size of perturbations, we use a distance function \(c:S \times S \rightarrow [0,+\infty ]\) that is nonnegative and lower semicontinuous with \(c(\xi ,\xi ') = 0\) if and only if \(\xi = \xi '\). (For binary classification \(\xi = (x,y)\) mentioned above, the distance function can be \(c((x,y),(x'y')) = \Vert x-x'\Vert +\mathbb {I}_{y=y'}(y,y')\) where \(\mathbb {I}_A\) is the convex indicator of the set A.) For a classifier \(w \in \mathcal{W}\), we define the margin, or distance to misclassification, of a point \(\xi \in S\) as
(Note that \(d(w,\xi )=0 \Leftrightarrow z(x,\xi ) \le 0\).)
Two optimization models commonly studied in previous works on adversarial classification are the following:
The first model (3a), which is the most popular such model, aims to minimize the probability that the distance of a data point \(\xi \) to a bad result will be smaller than a certain threshold \(\epsilon \ge 0\). This is more commonly stated as a robust optimization type problem:
Note that (1) is a special case of (3a) in which \(\epsilon = 0\). The second model (3b) maximizes the expected margin. This model removes the need to choose a parameter \(\epsilon \), but [23, Lemma 1] has shown that this measure is inversely related to the probability of misclassification \(\mathbb {P}_{\xi \sim P} [z(w,\xi ) \le 0]\), that is, a lower probability of misclassification (good) leads to a lower expected distance (bad), and vice versa. Thus, this model is not used often.
With distributional robustness, rather than guarding against perturbations in the data points \(\xi \), we aim to guard against perturbations of the distribution P of the data. In this paper, we study the following distributionally robust optimization (DRO) formulation (stated in two equivalent forms that will be used interchangeably throughout):
that is, we aim to minimize the worst-case misclassification probability over a ball of distributions \(\{Q : d_W(Q,P) \le \epsilon \}\). The ball is defined via the Wasserstein distance between two distributions, which is defined via the function c as follows:
We use the Wasserstein distance due to the fact that distributions in the Wasserstein ball can also capture perturbations in data points themselves, similar to (3a). Indeed, [41, Corollary 1] prove that (3a) is upper bounded by (4), thus the two are intimately related. One of our aims in this paper, however, is to understand the optimal solutions to (4) and how they differ to those of (3a).
In practice, the true distribution P is not known to us; we typically have only a finite sample \(\xi _i \sim P\), \(i \in [n]\) of training data, drawn from P, from which we can define the empirical distribution \(P_n := \frac{1}{n} \sum _{i \in [n]} \delta _{\xi _i}\). We use \(P_n\) as the center of the ball of distributions, that is, we solve the formulation (4) in which \(P_n\) replaces P.
1.2 Contributions and outline
In this paper, we first explore how using a Wasserstein ambiguity set in (4) can result in stronger guarantees for robustness to perturbations than (3a). Specifically, in Sect. 2.1, we show that for sufficiently small \(\epsilon \), (4) yields the maximum-margin classifier. In Sect. 2.2, we extend the link between the conditional value-at-risk of the distance function (2) and a chance-constrained version of (4) (observed by Xie [52]) to the probability minimization problem (4). This link yields an interpretation of optimal solutions of (4) for large \(\epsilon \), as optimizers of the conditional value-at-risk of the distance function (2). Thus, solving the DRO problem ensures that, for a certain fraction \(\rho \), the average of the \(\rho \)-proportion of smallest margins is as large as possible.
In Sect. 3, we give a reformulation of (4) for linear classifiers, obtaining a regularized risk minimization problem with a “ramp loss” objective. This formulation highlights the link between distributional robustness and robustness to outliers, a criterion which has motivated the use of ramp loss in the past. We suggest a class of smooth approximations for the ramp loss, allowing problems with this objective to be solved (approximately) with standard continuous optimization algorithms.
In Sect. 4, we perform some numerical tests of linear classification on three different data distributions. We observe that the regularized smoothed ramp loss minimization problem arising from (4), while nonconvex, is “benign” in the sense that the global minimum appears to be identified easily by smooth nonconvex optimization methods, for modest values of the training set size n. We also experiment with nonseparable data sets containing mislabelled points, showing that the problem arising from (4) is more robust to these “attacks” than the hinge-loss function often used to find the classifying hyperplane.
Motivated by the observations in Sect. 4, we prove in Sect. 5 that the ramp-loss problem indeed has only a single stationary point (which is therefore the global minimizer) for the class of spherically symmetric distributions.
1.3 Related work
There are a number of works that explore distributional robustness for machine learning model training. These papers consider a distributionally robust version of empirical risk minimization, which seeks to minimize the worst-case risk over some ambiguity set of distributions around the empirical distribution. Lee and Raginsky [30] consider a distributionally robust ERM problem, exploring such theoretical questions as learnability of the minimax risk and its relationship to well-known function-class complexity measures. Their work targets smooth loss functions, thus does not apply to (4). Works that consider a Wasserstein ambiguity, similar to (4), include Chen and Paschalidis [46], Shafieezadeh-Abadeh et al. [43, 44] Sinha et al. [16]; whereas Hu et al. [28] uses a distance measure based on \(\phi \)-divergences. For Wasserstein ambiguity, Sinha et al. [46] provide an approximation scheme for distributionally robust ERM by using the duality result of Lemma 2.3, showing convergence of this scheme when the loss is smooth and the distance c used to define the Wasserstein distance in (5) is strongly convex. When the loss function is of a “nice” form (e.g., logistic or hinge loss for classification, \(\ell _1\)-loss for regression),
Chen and Paschalidis [43], Kuhn et al. [16], Shafieezadeh-Abadeh et al. [29, 44] show that the incorporation of Wasserstein distributional robustness yields a regularized empirical risk minimization problem. This observation is quite similar to our results in Sect. 3, with a few key differences outlined in Remark 3.1. Also, discontinuous losses, including the “0-1” loss explored in our paper, are not considered by Chen and Paschalidis [46], Shafieezadeh-Abadeh et al. [43, 44], Sinha et al. [16]. Furthermore, none of these works provide an interpretation the optimal classifier like the one we provide in Sect. 2.
In this sense, the goals of Sect. 2 are similar to those of Hu et al. [28], who work with \(\phi \)-divergence ambiguity sets. Their paper shows that the formulation that incorporates \(\phi \)-divergence ambiguity does not result in classifiers different from those obtained by simply minimizing the empirical distribution. They suggest a modification of the ambiguity set and show experimental improvements over the basic \(\phi \)-divergence ambiguity set. The main difference between our work and theirs is that we consider a different (Wasserstein-based) ambiguity set, which results in an entirely different analysis and computations. Furthermore, using \(\phi \)-divergence ambiguity does not seem to have a strong theoretical connection with the traditional adversarial training model (3a), whereas we show that the Wasserstein ambiguity (4) has close links to (3a).
We mention some relevant works from the robust optimization-based models for adversarial training. Charles et al. [14] and Li et al. [31] both provide margin guarantees for gradient descent on an adversarial logistic regression model. We also give margin guarantees for the distributionally robust model (4) in Sect. 2, but ours are algorithm-independent, providing insight into use of the Wasserstein ambiguity set for adversarial defense. Bertsimas and Copenhaver [6] and Xu et al. [53, 54] have observed that for “nice” loss functions, (non-distributionally) robust models for ERM also reformulate to a regularized ERM problem.
Finally, we mention that our results concerning uniqueness of the stationary point in Sect. 5 are inspired by, and are similar in spirit to, local minima results for low-rank matrix factorization (see, for example, Chi et al. [18]).
2 Margin guarantees and conditional value-at-risk
In this section, we highlight the relationship between the main problem (4) and a generalization of maximum-margin classifiers, as well as the conditional value-at-risk of the margin function \(d(w,\xi )\).
2.1 Margin guarantees for finite support distributions
We start by exploring the relationship between solutions to (4) and maximum margin classifiers. We recall the definition (2) of margin \(d(w,\xi )\) for any \(w \in \mathcal {W}\) and data point \(\xi \in S\). We say that a classifier w has a margin of at least \(\gamma \) if \(d(w,\xi ) \ge \gamma \) for all \(\xi \in S\). When \(\gamma > 0\), this implies that a perturbation of size at most \(\gamma \) (as measured by the distance function c in (2)) for any data point \(\xi \) will still be correctly classified by w. In the context of guarding against adversarial perturbations of the data, it is clearly of interest to find a classifier w with maximum margin, that is, the one that has the largest possible \(\gamma \). On the other hand, some datasets S cannot be perfectly separated, that is, for any classifier \(w \in \mathcal{W}\), there will exist some \(\xi \in S\) such that \(d(w,\xi ) = 0\). To enable discussion of maximum margins in both separable and non-separable settings, we propose a generalized margin concept in Definition 2.1 as the value of a bilevel optimization problem. We then show that solving the DRO formulation (4) is exactly equivalent to finding a generalized maximum margin classifier for small enough ambiguity radius \(\epsilon \). This highlights the fact that the Wasserstein ambiguity set is quite natural for modeling adversarial classification. We work with the following assumption on P.
Assumption 2.1
The distribution P has finite support, that is, \(P = \sum _{i \in [n]} p_i \delta _{\xi _i}\), where each \(p_i > 0\) and \(\sum _{i \in [n]} p_i = 1\).
We make this assumption because for most continuous distributions, even our generalization of the margin will always be 0, so that a discussion of margin for such distributions is not meaningful. Since any training or test set we encounter in practice is finite, the finite-support case is worth our focus.
Under Assumption 2.1, we define the notion of generalized margin of P. For \(w \in \mathcal {W}\) and \(\rho \in [0,1]\), we define
The usual concept of margin is \(\gamma (0)\). Given these quantities, we define the generalized maximum margin of P with respect to the classifiers \(\mathcal{W}\) as the value of the following bilevel optimization problem.
Definition 2.1
Given P and \(\mathcal{W}\), the generalized maximum margin is defined to be
Note that Definition 2.1 implicitly assumes that the \(\arg \min \) over \(w' \in \mathcal {W}\) is achieved in (6). We show that under Assumption 2.1, this is indeed the case, and furthermore that \(\gamma ^* > 0\).
Proposition 2.1
Suppose Assumption 2.1 holds. Define
Then \(\rho ^* = \inf _{w' \in \mathcal {W}} \mathbb {P}_{\xi \sim P}[d(w',\xi )=0]\), there exists \(w \in \mathcal{W}\) such that
Proof
We first prove that under Assumption 2.1, the function \(\rho \mapsto \gamma (\rho )\) is a right-continuous non-decreasing step function. The fact that \(\gamma (\rho )\) is non-decreasing follows since \(\mathcal {I}(\rho ) \subseteq \mathcal {I}(\rho ')\) for \(\rho \le \rho '\). To show that it is a right-continuous step function, consider the finite set of all possible probability sums \(\mathcal {P}= \left\{ \sum _{i \in I} p_i : I \subseteq [n] \right\} \subset [0,1]\). Let us order \(\mathcal {P}\) as \(\mathcal {P}= \left\{ \rho ^1,\ldots ,\rho ^K \right\} \) where \(\rho ^1< \cdots < \rho ^K\). There is no configuration \(I \subseteq [n]\) such that \(\rho ^k< \sum _{i \in I} p_i < \rho ^{k+1}\). Thus, \(\mathcal {I}(\rho ) = \mathcal {I}(\rho ^k)\) and hence \(\gamma (\rho ) = \gamma (\rho ^k)\) for \(\rho \in [\rho _k, \rho _{k+1})\), proving the claim.
To prove the proposition, first note that there exists no classifier \(w \in \mathcal {W}\) such that \(\mathbb {P}_{\xi \sim P}[d(w,\xi )=0] = \underline{\rho } < \rho ^*\), otherwise, we have \(\gamma (\underline{\rho }) \ge \eta (w) > 0\), contradicting the definition of \(\rho ^*\). This shows that \(\rho ^* \le \inf _{w' \in \mathcal {W}} \mathbb {P}_{\xi \sim P}[d(w',\xi )=0]\). By the description of \(\rho ^*\) as the infimal \(\rho \) such that \(\gamma (\rho ) > 0\) and by the right-continuity of \(\gamma (\cdot )\) and the fact that \(\gamma (\cdot )\) is a step function, we must have \(\gamma (\rho ^*) > 0\). Since \(\gamma (\rho ^*) > 0\), there must exist some \(w \in \mathcal{W}\) such that \(I(w) \in \mathcal{I}(\rho ^*)\), that is, \(\sum _{i \in I(w)} p_i = \mathbb {P}_{\xi \sim P} [d(w,\xi )=0] \le \rho ^*\). Since we cannot have \(\mathbb {P}_{\xi \sim P} [d(w,\xi )=0] < \rho ^*\) we conclude that \(\mathbb {P}_{\xi \sim P} [d(w,\xi )=0] = \rho ^*\). Therefore \(\inf _{w \in \mathcal {W}} \mathbb {P}_{\xi \sim P} [d(w,\xi )=0] = \rho ^*\). Furthermore, by definition, we have \(\gamma ^* = \gamma (\rho ^*) > 0\). \(\square \)
The following result gives a precise characterization of the worst-case misclassification probability of a classifier w for a radius \(\epsilon \) that is smaller than the probability-weighted margin of w. It also gives a lower bound on worst-case error probability when \(\epsilon \) is larger than this quantity.
Proposition 2.2
Under Assumption 2.1, for \(w \in \mathcal {W}\) such that
we have
For \(w \in \mathcal {W}\) such that \(\epsilon > \min _{i \in [n] \setminus I(w)} d(w,\xi _i) p_i\), we have
To prove Proposition 2.2, we will use the following key key duality result for the worst-case error probability. Note that Lemma 2.3 does not need Assumption 2.1.
Lemma 2.3
([8, Theorem 1, Eq. 15]) For any \(w \in \mathcal {W}\), we have
Proof
First, by using (8a) in Lemma 2.3, using Assumption 2.1 and linear programming duality, we have
The right-hand side is an instance of a fractional knapsack problem, which is solved by the following greedy algorithm:
In increasing order of \(d(w,\xi _i)\), increase \(v_i\) up to \(p_i\) or until the budget constraint \(\sum _{i \in [n]} d(w,\xi _i) v_i \le \epsilon \) is tight, whichever occurs first.
Note that when \(i \in I(w)\) we have \(d(w,\xi _i) = 0\), so we can set \(v_i=p_i\) for such values without making a contribution to the knapsack constraint. Hence, the value of the dual program is at least \(\sum _{i \in I(w)} p_i\).
When \(w \in \mathcal {W}\) is such that \(\epsilon \le d(w,\xi _i) p_i\) for all \(i \in [n] \setminus I(w)\), we will not be able to increase any \(v_i\) up to \(p_i\) for those \(i \in [n] \setminus I(w)\) in the dual program. According to the greedy algorithm, we choose the smallest \(d(w,\xi _i)\) amongst \(i \in [n] \setminus I(w)\) — whose value corresponds to \(\eta (w)\) — and increase this \(v_i\) up to \(\epsilon /d(w,\xi _i) = \epsilon /\eta (w) \le p_i\). Therefore, we have
When \(w \in \mathcal {W}\) is such that \(\epsilon > d(w,\xi _i) p_i\) for some \(i \in [n] \setminus I(w)\), the greedy algorithm for the dual program allows us to increase \(v_i\) up to \(p_i\) for at least one \(i \in [n] \setminus I(w)\). Thus, by similar reasoning to the above, we have that a lower bound on the optimal objective is given by
verifying the second claim. \(\square \)
The main result in this section, which is a consequence of the first part of this proposition, is that as long as the radius \(\epsilon > 0\) is sufficiently small, solving the DRO formulation (4) is equivalent to solving the bilevel optimization problem (6) for the generalized margin, that is, finding the w that, among those that misclassifies the smallest fraction of points \(\mathbb {P}_{\xi \sim P}[d(w,\xi )=0] = \rho ^*\), achieves the largest margin \(\eta (w) = \gamma ^*\) on the correctly classified points. The required threshold for radius \(\epsilon \) is \(\epsilon = (\bar{\rho } - \rho ^*)\gamma ^*\), where \(\bar{\rho }\) is the smallest probability that is strictly larger than \(\rho ^*\), that is,
We show too that classifiers that satisfy \(\sum _{i \in I(w)} p_i = \rho ^*\) but whose margin may be slightly suboptimal (greater that \(\gamma ^* - \delta \) but possibly less than \(\gamma ^*\)) are also nearly optimal for (4).
Theorem 2.4
Let Assumption 2.1 be satisfied. Suppose that \(0< \epsilon < (\bar{\rho }-\rho ^*)\gamma ^*\). Then, referring to the DRO problem (4), we have
Furthermore, for any \(\delta \) with \(0< \delta < \gamma ^* - \epsilon /(\bar{\rho } - \rho ^*)\), we have
In particular, if there exists some \(w \in \mathcal {W}\) such that \(\mathbb {P}_{\xi \sim P}[d(w,\xi )=0] = \rho ^*\), \(\eta (w) = \gamma ^*\), then w solves (4), and vice versa.
Proof
Since \(\sup _{w \in \mathcal {W}: I(w) \in \mathcal {I}(\rho ^*)} \eta (w) = \gamma (\rho ^*) = \gamma ^* > \epsilon /(\bar{\rho } - \rho ^*)\), there exists some \(w \in \mathcal {W}\) such that \(\sum _{i \in I(w)} p_i = \rho ^*\) and \(\eta (w) > \epsilon /(\bar{\rho } - \rho ^*)\), that is, \(\epsilon < \eta (w)(\bar{\rho } - \rho ^*)\). Now, since \(\bar{\rho } - \rho ^* \le p_i\) for all \(i \in [n] \setminus I(w)\) (by definition of \(\mathcal {P}\) and \({\bar{\rho }}\) in (9)), and since \(\eta (w) \le d(w,\xi _i)\) for all \(i \in [n] \setminus I(w)\), we have that \(\epsilon < d(w,\xi _i) p_i\) for all \(i \in [n] \setminus I(w)\). Therefore, by Proposition 2.2, we have for this w that
This implies that any \(w \in \mathcal {W}\) such that \(\sum _{i \in I(w)} p_i \ge \bar{\rho }\) is suboptimal for (4). (This is because even when we set \(Q=P\) in (4), such a value of w has a worse objective than the w for which \(\sum _{i \in I(w)} p_i=\rho ^*\).) Furthermore, from Proposition 2.2 and the definition of \(\bar{\rho }\), any \(w \in \mathcal {W}\) such that \(\sum _{i \in I(w)} p_i = \rho ^*\) and \(\epsilon \ge \min _{i \in [n] \setminus I(w)} d(w,\xi _i) p_i\) has
hence is also suboptimal.
This means that all optimal and near-optimal solutions \(w \in \mathcal{W}\) to (4) with \(0< \epsilon < (\bar{\rho }-\rho ^*)\gamma ^*\) are in the set
and, by Proposition 2.2, the objective values corresponding to each such w are
By definition of \(\gamma (\rho ^*) = \gamma ^*\), the infimal value for this objective is \(\rho ^* + \epsilon /\gamma ^*\), and it is achieved as \(\eta (w) \rightarrow \gamma ^*\). The first claim is proved.
For the second claim, consider any \(\delta \in (0, \gamma ^* - \epsilon /(\bar{\rho } - \rho ^*))\). We have for any w with \(\sum _{i \in I(w)} p_i = \rho ^*\) that
Furthermore, for such w and \(\delta \), we have \(\epsilon < (\gamma ^* - \delta )(\bar{\rho } - \rho ^*) = (\gamma (\rho ^*) - \delta )(\bar{\rho } - \rho ^*) \le \eta (w)(\bar{\rho } - \rho ^*)\) so, by noting as in the first part of the proof that \(\bar{\rho }-\rho ^* \le p_i\) and \(\eta (w) \le d(w,\xi _i)\) for all \(i \in [n] \setminus I(w)\), we have \(\epsilon < d(w,\xi _i) p_i\) for all \(i \in [n] \setminus I(w)\). By applying Proposition 2.2 again, we obtain
as required.
The final claim follows because, using the second claim, we have
as desired. \(\square \)
Theorem 2.4 shows that, for small Wasserstein ball radius \(\epsilon \), the solution of (4) matches the maximum-margin solution of the classification problem, in a well defined sense. How does the solution of (4) compare with the minimizer of the more widely used model (3a)? It is not hard to see that when the parameter \(\epsilon \) in (3a) is chosen so that \(\epsilon < \gamma ^*\), the solution of (3a) will be a point w with margin \(\eta (w) \ge \epsilon \). (Such a point will achieve an objective of zero in (3a).) However, in contrast to Theorem 2.4, this point may not attain the maximum possible margin \(\gamma ^*\). The margin that we obtain very much depends on the algorithm used to solve (3a). For fully separable data, for which \(\rho ^*=0\) and \(\gamma ^* = \gamma (0) > 0\), Charles et al. [14] and Li et al. [31] show that gradient descent applied to a convex approximation of (3a) with parameter \(\epsilon \) achieves a separation of \(\epsilon \) in an iteration count polynomial in \((\gamma ^*-\epsilon )^{-1}\). Therefore, in order to strengthen the margin guarantee, \(\epsilon \) should be taken as close to \(\gamma ^*\) as possible, but this adversely affects the number of iterations taken to achieve this. By contrast, Theorem 2.4 shows that, in the more general setting of non-separable data, the maximum-margin solution is attained from (4) when the parameter \(\epsilon \) is taken to be any value below the threshold \(\gamma ^*(\bar{\rho } - \rho ^*)\). In particular, this guarantee is algorithm independent.
2.2 Conditional value-at-risk characterization
Section 2.1 gives insights into the types of solutions that the distributionally robust model (4) recovers when the Wasserstein radius \(\epsilon \) is below a certain threshold. When \(\epsilon \) is above this threshold however, (4) may no longer yield a maximum-margin solution. In this section, we show in Theorem 2.6 that, in general, (4) is intimately related to optimizing the conditional value-at-risk of the distance random variable \(d(w,\xi )\). Thus, when \(\epsilon \) is above the threshold of Theorem 2.4, (4) still has the effect of pushing data points \(\xi \) away from the error set \(\{\xi \in S : z(w,\xi ) \le 0\}\) as much as possible, thereby encouraging robustness to perturbations. We note that unlike Sect. 2.1, we make no finite support assumptions on the distribution P, that is, Assumption 2.1 need not hold for our results below.
In stochastic optimization, when outcomes of decisions are random, different risk measures may be used to aggregate these random outcomes into a single measure of desirability (see, for example, [3, 42]). The most familiar risk measure is expectation. However, this measure has the drawback of being indifferent between a profit of 1 and a loss of \(-1\) with equal probability, and a profit of 10 and a loss of \(-10\) with equal probability. In contrast, other risk measures can adjust to different degrees of risk aversion to random outcomes, that is, they can penalize bad outcomes more heavily than good ones. The conditional value-at-risk (CVaR) is a commonly used measure that captures risk aversion and has several appealing properties. Roughly speaking, it is the conditional expectation for the \(\rho \)-quantile of most risky values, for some user-specified \(\rho \in (0,1)\) which controls the degree of risk aversion. Formally, for a non-negative random variable \(\nu (\xi )\) where low values are considered risky (that is, “bad”), CVaR is defined as follows:
[52, Corollary 1] gives a characterization of the chance constraint
in terms of the CVaR of \(d(w,\xi )\) when \(P = P_n\), a discrete distribution. We provide a slight generalization to arbitrary P.
Lemma 2.5
Fix \(\rho \in (0,1)\) and \(\epsilon > 0\). Then, for all \(w \in \mathcal {W}\), we have
Proof
We prove first the reverse implication in (11). Suppose that (following (10)) we have
then for all \(0< \epsilon ' < \epsilon \), there exists some \(t > 0\) such that
Dividing by t, we obtain \(\rho + \mathbb {E}_{\xi \sim P}\left[ \min \left\{ 0, d(w,\xi )/t - 1\right\} \right] > \epsilon '/t\), so by rearranging and substituting \(t'=1/t\), we have
Note that the function
is concave and bounded, hence continuous. This fact together with the previous inequality implies that
which, when combined with (8a), proves that the reverse implication holds in (11).
We now prove the forward implication. Suppose that the left-hand condition in (11) is satisfied for some \(\rho \in (0,1)\), and for contradiction that there exists some \(\epsilon ' \in (0,\epsilon )\) such that
Then for all \(t > 0\), we have
Since \(\epsilon '<\epsilon \), and using the left-hand condition in (11) together with (8a), we have
Since \(\epsilon ' < \epsilon \), there cannot exist any \(t > 0\) such that
Let \(\rho _k\) and \(t_k\) be sequences such that \(1> \rho _k > \rho \), \(\rho _k \rightarrow \rho \), \(t_k>0\), and
Since \(\epsilon > 0\), there cannot be any subsequence of \(t_k\) that diverges to \(\infty \), since in that case \(\epsilon t_k + \mathbb {E}_{\xi \sim P}\left[ \max \left\{ 0, 1 - t_k d(w,\xi ) \right\} \right] \ge \epsilon t_k\) could not be bounded by \(\rho _k < 1\). Thus \(\{ t_k\}\) is bounded, and there exists a convergent subsequence, so we assume without loss of generality that \(t_k \rightarrow \tau \). By the dominated convergence theorem, \(\mathbb {E}_{\xi \sim P}\left[ \max \left\{ 0, 1 - t_k d(w,\xi ) \right\} \right] \rightarrow \mathbb {E}_{\xi \sim P}\left[ \max \left\{ 0, 1 - \tau d(w,\xi ) \right\} \right] \), and \(\epsilon t_k \rightarrow \epsilon \tau \). But then since
we have by the squeeze theorem that
But then, by the fact noted after (14), we must have \(\tau = 0\) so \(\rho = 1\) (from (14)), which contradicts our assumption that \(\rho \in (0,1)\). \(\square \)
In the case of classification, the minimizers of (4) correspond exactly to the maximizers of \({{\,\mathrm{CVaR}\,}}_\rho (d(w,\xi );P)\), where \(\rho \) is the optimal worst-case error probability, as we show now.
Theorem 2.6
Fix some \(\rho \in [0,1]\) and define \(\epsilon \) (using (10)) as follows:
If \(0< \epsilon < \infty \), then
Furthermore, the optimal values of w coincide, that is,
Proof
For any \(w \in \mathcal {W}\) and \(t > 0\), we have from (15) and (10) that
Dividing by t and rearranging, we obtain
Taking the infimum over \(t > 0\), using (8a) (noting that \(1/t > 0\)), then taking the infimum over \(w \in \mathcal {W}\), we obtain
In the remainder of the proof, we show that equality is obtained in this bound, when \(0<\epsilon <\infty \).
Trivially, the inequality in (16) can be replaced by an equality when \(\rho =1\). We thus consider the case of \(\rho <1\), and suppose for contradiction that there exists some \(\rho ' \in (\rho ,1]\) such that for all \(w \in \mathcal {W}\), we have
It follows from Lemma 2.5 that for all \(w \in \mathcal {W}\), we have
By taking the supremum over \(w \in \mathcal {W}\) in this bound, and using \(\rho '>\rho \) and the definition of \(\epsilon \) in (15), we have that
so that
From \(\rho <\rho '\), (17), and (18), we can define sequences \(\epsilon _k\), \(t_k > 0\), and \(w_k \in \mathcal {W}\) such that \(\epsilon _k \nearrow \epsilon \) and
By rearranging these inequalities, we obtain
Since \(\epsilon _k \rightarrow \epsilon \), we have either that \(t_k\) is bounded away from 0, in which case
or there exists a subsequence on which \(t_k \rightarrow 0\). In the former case, we have for k sufficiently large that
which contradicts (17). We consider now the other case, in which there is a subsequence for which \(t_k \rightarrow 0\), and assume without loss of generality that the full sequence has \(t_k \rightarrow 0\). Since \(\mathbb {E}_{\xi \sim P} [\min \{0, d(w_k,\xi ) - t_k\}] \le 0\) for any k, it follows that
so that \(\epsilon \le 0\). This contradicts the assumption that \(\epsilon > 0\), so we must have
This completes our proof of the first claim of the theorem.
Let \(w \in \mathcal {W}\) be a maximizer of the \({{\,\mathrm{CVaR}\,}}\), so that \(\epsilon = \rho {{\,\mathrm{CVaR}\,}}_\rho (d(w,\xi );P)\). Then by Lemma 2.5, we have
so the same value of w is also a minimizer of the worst-case error probability. A similar argument shows that minimizers of the worst-case error probability are also maximizers of the \({{\,\mathrm{CVaR}\,}}\). \(\square \)
3 Reformulation and algorithms for linear classifiers
In this section, we formulate (4) for a common choice of distance function c and safety function z, and discuss algorithms for solving this formulation. We make use of the following assumption.
Assumption 3.1
We have \(\mathcal {W}= \mathbb {R}^d \times \mathbb {R}\) and \(S = \mathbb {R}^d \times \{\pm 1\}\). Write \(\bar{w} = (w_0,b_0) \in \mathbb {R}^d \times \mathbb {R}\) and \(\xi = (x,y) \in \mathbb {R}^d \times \{\pm 1\}\). Define \(c(\xi ,\xi ') := \Vert x - x'\Vert + \mathbb {I}_{y=y'}(y,y')\) for some norm \(\Vert \cdot \Vert \) on \(\mathbb {R}^d\) and \(\mathbb {I}_A(\cdot )\) is the convex indicator function where \(\mathbb {I}_A(y,y')=0\) if \((y,y') \in A\) and \(\infty \) otherwise. Furthermore, \(z(\bar{w},\xi ) := y(w_0^\top \xi + b_0)\).
From Lemma 2.3, the DRO problem (4) is equivalent to
Letting \(\Vert \cdot \Vert _*\) denote the dual norm of \(\Vert \cdot \Vert \) from Assumption 3.1, the distance to misclassification \(d(\bar{w},\xi )\) is as follows
When \(w_0 \ne 0\), we can define the following nonlinear transformation:
noting that \(t = \Vert w\Vert _*\), and substitute (20) into (19) to obtain
In fact, the next result shows that this formulation is equivalent to (19) even when \(w_0=0\). (Here, we use the term “\(\delta \)-optimal solution” to refer to a point whose objective value is within \(\delta \) of the optimal objective value for that problem.)
Theorem 3.1
Under Assumption 3.1, (22) is equivalent to (19). Moreover, any \(\delta \)-optimal solution (w, b) for (22) can be converted into a \(\delta \)-optimal solution t and \(\bar{w}=(w_0,b_0)\) for (19) as follows:
Proof
The first part of the proof shows that the optimal value of (22) is less than or equal to that of (19), while the second part proves the converse.
To prove that the optimal value of (22) is less than or equal to that of (19), it suffices to show that given any \(\bar{w}=(w_0,b_0)\), we can construct a sequence \(\{(w^k,b^k)\}_{k \in \mathbb {N}}\) such that
Consider first the case of \(w_0 \ne 0\), and let \(t_k>0\) be a sequence such that
Following (21), we define \(w^k := t_k w_0/\Vert w_0\Vert _*\) and \(b^k := t_k b_0 / \Vert w_0 \Vert _*\). We then have from (20) that
Thus, the left-hand sides of (25) and (24) are equivalent, so (24) holds.
Next, we consider the case of \(\bar{w}=(w_0,b_0)\) with \(w_0 = 0\). Note that \(d(\bar{w},\xi ) = 0\) when \(y b_0 \le 0\) and \(d(\bar{w},\xi ) = \infty \) when \(y b_0 > 0\), we have \(\max \left\{ 0, 1 - t d(\bar{w},\xi ) \right\} = \varvec{1}(yb \le 0)\) for all \(t>0\), where \(\varvec{1}(\cdot )\) has the value 1 when its argument is true and 0 otherwise. Thus, we have
Now choose \(w^k=0\) and \(b^k = k b_0\) for \(k=1,2,\dotsc \). We then have
Now notice that for the first and last terms in this last expression, we have by taking limits as \(k \rightarrow \infty \) that
both pointwise, and everything is bounded by 1. Therefore, by the dominated convergence theorem, we have from (27) that
By comparing (26) with (28), we see that (24) holds for the case of \(w_0=0\) too. This completes our proof that the optimal value of (22) is less than or equal to that of (19).
We now prove the converse, that the optimal value of (19) is less than or equal to that of (22). Given w and b, we show that there exists \(\bar{w} = (w_0,b_0)\) such that
When \(w \ne 0\), we take \(t=\Vert w\Vert _*\), \(w_0 = w/\Vert w\Vert _* = w/t\), and \(b_0 = b/\Vert w\Vert _* = b/t\), and use (20) to obtain (29).
Specifically, we have
as claimed.
For the case of \(w = 0\), we set \(b_0=b\) and obtain
By comparing with (26), we see that (29) holds in this case too. Hence, the objective value of (19) is less than or equal to that of (22).
For the final claim, we note that the optimal values of the problems (19) and (22) are equal and, from the second part of the proof above, the transformation (23) gives a solution t and \(\bar{w}=(w_0,b_0)\) whose objective in (19) is at most that of (w, b) in (22). Thus, whenever (w, b) is \(\delta \)-optimal for (22), then the given values of t and \(\bar{w}\) are \(\delta \)-optimal for (19). \(\square \)
The formulation (22) can be written as the regularized risk minimization problem
where \(L_R\) is the ramp loss function defined by
Here, the risk of a solution (w, b) is defined to be the expected ramp loss \(\mathbb {E}_{\xi \sim P} \left[ L_R(y(w^\top x + b)) \right] \), and the regularization term \(\Vert w\Vert _*\) is defined via the norm that is dual to the one introduced in Assumption 3.1.
Remark 3.1
The formulation (22) is reminiscent of [29, Proposition 2] (see also references therein), where other distributionally robust risk minimization results were explored, except the risk was defined via the expectation of a continuous and convex loss function, and the reformulation was shown to be the regularized risk defined on the same loss function. In contrast, the risk in (4) is defined as the expectation of the discontinuous and non-convex 0-1 loss function \(\varvec{1}(y (w^\top x + b) \le 0)\), and the resulting reformulation uses the ramp loss \(L_R\), a continuous but still nonconvex approximation of the 0-1 loss. \(\square \)
Remark 3.2
The ramp loss \(L_R\) has been studied in the context of classification by Shen et al. [45], Wu and Liu [51], and Collobert et al. [21] to find classifiers that are robust to outliers. The reformulation (30) suggests that the ramp loss together with a regularization term may have the additional benefit of also encouraging robustness to adversarial perturbations in the data. In previous work, there has been several variants of ramp loss with different slopes and break points. The formulation (32) suggests a principled form for ramp loss in classification problems. \(\square \)
Remark 3.3
Instead of considering \((w,b) \in \mathbb {R}^d \times \mathbb {R}\), we may consider non-linear classifiers via kernels (and the associated reproducing kernel Hilbert space-based classifiers). [44, Section 3.3] examined kernelization of linear classifiers in the context of different Wasserstein DRO-based classification models. They provide approximation results relating the well-known kernel trick to these problems under some assumptions on the kernel k. Their results can easily be applied to the ramp loss reformulation (30) as well. \(\square \)
In practice, the distribution P in (30) is taken to be the empirical distribution \(P_n\) on given data points \(\{\xi _i\}_{i \in [n]}\), so (30) becomes
This problem can be formulated as a mixed-integer program (MIP) and solved to global optimality using off-the-shelf software; see [2, 10]. Despite significant advances in the computational state of the art, the scalability of MIP-based approaches with training set size m remains limited. Thus, we consider here an alternative approach based on smooth approximation of \(L_R\) and continuous optimization algorithms.
Henceforth, we consider \(\Vert \cdot \Vert = \Vert \cdot \Vert _* = \Vert \cdot \Vert _2\) to be the Euclidean norm. For a given \(\epsilon \) in (32), there exists \(\bar{\epsilon }\ge 0\) such that a strong local minimizer \((w(\epsilon ),b(\epsilon ))\) of (32) with \(w(\epsilon ) \ne 0\) is also a strong local minimizer of the following problem:
where we define \(\bar{\epsilon }= \epsilon /\Vert w(\epsilon ) \Vert \). In the following result, we use the notation
for the summation term in (32) and (33).
Theorem 3.2
Suppose that for some \(\epsilon >0\), there exists a local minimizer \((w(\epsilon ),b(\epsilon ))\) of (32) with \(w(\epsilon ) \ne 0\) and a constant \(\tau >0\) such that for all \((v,\beta ) \in {\mathbb {R}}^d \times {\mathbb {R}}\) sufficiently small, we have
Then for \(\bar{\epsilon }= \epsilon /\Vert w(\epsilon ) \Vert \), \(w(\epsilon )\) is also a strong local minimizer of (33), in the sense that
for all \((v,\beta )\) sufficiently small.
Proof
For simplicity of notation, we denote \((w,b) = (w(\epsilon ),b(\epsilon ))\) throughout the proof.
From a Taylor-series approximation of the term \(\Vert w+v \Vert \), we have
By rearranging this expression, and taking v small enough that the \(O(\Vert v\Vert ^3)\) term is dominated by \((\tau /2) \Vert v\Vert ^2\), we have
By substituting \(\bar{\epsilon }= \epsilon /\Vert w \Vert \), we obtain the result. \(\square \)
We note that the condition (34) is satisfied when the local minimizer satisfies a second-order sufficient condition.
To construct a smooth approximation for \(L_R(r) = \max \{0,1-r\} - \max \{0,-r\}\), we follow Beck and Teboulle [1] and approximate the two max-terms with the softmax operation: For small \(\sigma > 0\) and scalars \(\alpha \) and \(\beta \),
Thus, we can approximate \(L_R(r)\) by the smooth function \(\psi _{\sigma }(r)\), parametrized by \(\sigma >0\) and defined as follows:
For any \(r \in {\mathbb {R}}\), we have that \(\lim _{\sigma \downarrow 0} \psi _{\sigma }(r) = L_R(r)\), so the approximation (35) becomes increasingly accurate as \(\sigma \downarrow 0\).
By substituting the approximation \(\psi _{\sigma }\) in (35) into (33), we obtain
This is a smooth nonlinear optimization problem that is nonconvex because \(\psi _{\sigma }''(r) <0\) for \(r<1/2\) and \(\psi _{\sigma }''(r) >0\) for \(r>1/2\). It can be minimized by any standard method for smooth nonconvex optimization. Stochastic gradient approaches with minibatching are best suited to cases in which n is very large. For problems of modest size, methods based on full gradient evaluations are appropriate, such as nonlinear conjugate gradient methods (see [39, Chapter 5] or L-BFGS [32]. Subsampled Newton methods (see for example [9, 55]), in which the gradient is approximated by averaging over a subset of the n terms in the summation in (36) and the Hessian is approximated over a typically smaller subset, may also be appropriate. It is well known that these methods are highly unlikely to converge to saddle points, but they may well converge to local minima of the nonconvex function that are not global minima. We show in the next section that, empirically, the global minimum is often found, even for problems involving highly nonseparable data. In fact, as proved in Sect. 5, under certain (strong) assumptions on the data, spurious local solutions do not exist.
4 Numerical experiments
We report on computational tests on the linear classification problem described above, for separable and nonseparable data sets. We observe that on separable data, despite the nonconvexity of the problem, the the smoothed formulation (36) appears to have a unique local minimizer, found reliably by standard procedures for smooth nonlinear optimization, for sufficiently large training set size n. Moreover, the classifier obtained from the ramp loss formulation is remarkably robust to adversarial perturbations of the training data: A solution whose classification performance is similar to the original separating hyperplane is frequently identified even when a large fraction of the labels from the separable data set are flipped randomly to incorrect values and when the incorrectly labelled points are moved further away from the decision boundary.
Our results are intended to be “proof of concept" in that they both motivate and support our analysis in Sect. 5 that the minimizer of the regularized risk minimization problem (30) is the only point satisfying even first-order conditions, and that the ramp loss can identify classifiers that are robust to perturbations. Our analysis in Sect. 5 focuses on separable data sets and spherically symmetric distributions, but we test here for a non-spherically-symmetric distribution too, and also experiment with nonseparable data sets, which are discussed only briefly in Sect. 5.
4.1 Test problems, formulation details, and optimization algorithms
We generate three binary classification problems in which the training data \((x,y) \sim P\) is such that \(x \sim P_x\), where \(P_x\) one of three possible distributions over \(\mathbb {R}^d\): (1) N(0, 10I); (2) \(N(0, \Sigma )\) where \(\Sigma \) is a positive definite matrix with random orientation whose eigenvalues are log-uniformly distributed in [1, 10]; (3) a Laplace distribution with zero mean and covariance matrix 10I. For each x, we choose the label \(y = {{\,\mathrm{sign}\,}}\left( (w^*)^\top x \right) \) where the “canonical separating hyperplane” \(w^* = (1,0,0,\dotsc ,0)\), that is, y is determined by the sign of the first component of x.
We modify this separable data set to obtain nonseparable data sets as follows. First, we choose a random fraction \(\kappa \) of training points \((x_i,y_i)\) to modify. Within this fraction, we select the points for which the first component \((x_i)_1\) of \(x_i\) is positive, and “flip” the label \(y_i\) from \(+1\) to \(-1\). Second, we replace \((x_i)_1\) by \(2(x_i)_1+1\) for these points i, moving them further from the canonical separating hyperplane. In our experiments, we set \(\kappa \) to the values .1, .2 and .3. Since the points \((x_i,y_i)\) for which \((x_i)_1<0\) are not changed, and \((x_i)_1 < 0\) with probability 1/2 for \(P_x\) above, the total fractions of of training points that are altered by this process are (approximately) .05, .1 and .15, respectively.
We report on computations with the formulation (36) with \(\sigma =.05\) and \(\bar{\epsilon }=.1\), and various values of n. (The results are not particularly sensitive to the choice of \(\sigma \), except that smaller values yield functions that are less smooth and thus require more iterations to minimize. The value \(\bar{\epsilon }=.1\) tends to yield solutions (w, b) for which \(\Vert w\Vert = O(1)\).)
We tried various smooth unconstrained optimization solvers for the resulting smooth optimization problem — the PR\(+\) version of nonlinear conjugate gradient [39, Chapter 5], the L-BFGS method [32], and Newton’s method with diagonal damping — all in conjunction with a line-search procedure that ensures weak Wolfe conditions. These methods behaved in a roughly similar manner and all were effective in finding minimizers. Our tables report results obtained only with nonlinear conjugate gradient.
4.2 Unique local minimizer
We performed tests on the separable data sets generated from multiple instances of the three distributions described above, each from multiple starting points. Our goal was to determine which instances appear to have a unique local solution: If the optimization algorithm converges to the same point from a wide variety of starting points, we take this observation as empirical evidence that the instance has a single local minimizer, which is therefore the global minimizer. In particular, for each distribution and several values of dimension d, we seek the approximate smallest training set size n for which all instances of that distribution with that dimension appear to have a single local minimizer. In our experiment, we try \(d=5,10,20,40\), values of n of the form \(100 \times 2^i\) for \(i=0,1,2,\dotsc \), and 10 different instances generated randomly from each distribution. We solved (36) for each instance for the hyperplane (w, b), starting from 20 random points on the unit ball in \(\mathbb {R}^{d+1}\). If the same solution is obtained for all 20 starting points, and this event occurs on all 10 instances, we declare the corresponding value of n to be the value that yields a unique minimizer for this distribution and this value of d.
The values so obtained are reported in Table 1. We note that n grows only slowly with d, at an approximately linear rate. These results suggest not only that the underlying loss (33) has a single local minimizer, despite its nonconvexity, but also that this behavior can be observed for modest training set sizes n in the empirical problem (36).
4.3 Adversarial robustness
We now explore robustness of classifiers to adversarial perturbations via the nonseparable data. Note that the “flipping” of a point \((x_i,y_i)\) described in Sect. 4.1 can be interpreted as an adversarial perturbation. The motivation behind this is that for a positively labelled point \((x_i)_1 > 0\), we imagine that the “correct” side of the canonical hyperplane is the negative side \((w^*)^\top x_i \le 0\) (hence we set \(y=-1)\) but we perturb the \((x_i)_1\) to the “incorrect” positive side \((w^*)^\top x_i \ge 0\). For these experiments we fix the dimension to the value \(d=10\) and use \(n=10,000\) training points in (36). For comparison, we also solve a model identical to (36) except that the smoothed ramp-loss function \(\psi _{\sigma }\) is replaced by a smoothed version of the familiar hinge-loss function \(L_H(r) = \max \{0,1-r\}\), which is \(\sigma \mathop {\mathrm{log}}\left( 1 + \exp ((1-r)/\sigma )\right) \), where again \(\sigma =.05\). (Note that the latter formulation is convex, unlike (36).)
We measure the performance of the classifier (w, b) obtained from (36) for various values of the flip fraction \(\kappa \), and the performance of the classifier obtained from the corresponding empirical hinge-loss objective, in two different ways. For both methods, we generated 20 random instances of the problem from each of the three distributions, and measure the outcomes using Monte Carlo sampling from \(n_{\text {test}}=100,000\) test points drawn from the original separable distribution P. In the first method, we simply calculate the fraction of test points that are misclassified by (w, b), and calculate the mean and standard deviation of this quantity over the 20 instances, for each value of \(\kappa \). In the second method, following Sect. 2.2, we measure the adversarial robustness of a classifier (w, b) via the conditional value-at-risk \({{\,\mathrm{CVaR}\,}}_{\rho }(d((w,b),(x,y));P)\) of the distance function \(d((w,b),(x,y)) = \max \left\{ 0, \frac{y (w^\top x + b)}{\Vert w\Vert _2} \right\} \) according to (10). The empirical value of \({{\,\mathrm{CVaR}\,}}_{\rho }\) is calculated over the \(n_{\text {test}}=100,000\) test points. A higher value of \({{\,\mathrm{CVaR}\,}}_{\rho }\) value means more robustness to perturbations, as the distances to the classifying hyperplane are larger. Each \(\rho \in [0,1]\) gives a different risk measure, where smaller \(\rho \) means that we focus more on the lower tail of the distribution of d((w, b), (x, y)). We thus compute \({{\,\mathrm{CVaR}\,}}_{\rho }\) over a range of values of \(\rho \) and compare the CVaR curves obtained in this way.
Figures1 to 2 plot our results comparing ramp and hinge loss for the three distributions. As we increase the fraction of points flipped, Fig.1 shows that the test error of hinge loss degrades severely, while the test error of ramp loss is much more stable. Figure 2 shows that the ramp loss CVaR curve always lies on or above the hinge loss CVaR curve, with the gap increasing as the fraction of flips increases. These results provide convincing evidence that the ramp loss leads to more robust classifiers than the hinge loss.
5 Benign nonconvexity of ramp loss on linearly separable symmetric data
We consider (33), setting \(b = 0\) for simplicity to obtain
In this section, we explore the question: is the nonconvex problem (37) benign, in the sense that, for reasonable data sets, descent algorithms for smooth nonlinear optimization will find the global minimum? In the formulation (37), we make use of the true distribution P rather than its empirical approximation \(P_n\), because results obtained for P will carry through to \(P_n\) for large n, with high probability. Exploring this question for general data distributions is difficult, so we examine spherically symmetric distributions.
Definition 5.1
Let \(\Pi \) be a distribution on \(\mathbb {R}^d\). We say that \(\Pi \) is spherically symmetric about 0 if, for all measurable sets \(A \subset \mathbb {R}^d\) and all orthogonal matrices \(H \in \mathbb {R}^{d \times d}\), we have
Spherically symmetric distributions include normal distributions and Student’s t-distributions with covariances \(\sigma ^2 I\). One useful characterization is that \(x = r \cdot s\) where r is a random variable on \(\mathbb {R}_+\) and s is a uniform random variable on the unit sphere \(\{s \in \mathbb {R}^d : \Vert s\Vert _2 = 1\}\), with r and s independent.
We make the following assumption on the data-generating distribution
Assumption 5.1
The distribution P has the form \(y = {{\,\mathrm{sign}\,}}((w^*)^\top x)\) and \(x \sim P_x\) where \(P_x\) is some spherically symmetric distribution about 0 on \(\mathbb {R}^d\) which is absolutely continuous with respect to Lebesgue measure on \(\mathbb {R}^d\) (so the probability of lower-dimensional sets is 0) and \(w^*\) is some unit Euclidean norm vector in \(\mathbb {R}^d\).
Under this assumption, we will show that \(F_{\epsilon }\) defined in (37) has a single local minimizer \(w(\epsilon )\) in the direction of the canonical hyperplane \(w^*\): \(w(\epsilon ) = \alpha w^*\) for some \(\alpha >0\). Since the function is also bounded below (by zero) and coercive, this local minimizer is the global minimizer.
We now investigate differentiability properties of the objective \(F_\epsilon \).
Lemma 5.1
When \(w \ne 0\), the function \(F_\epsilon (w)\) is differentiable in w with gradient
At \(w=0\), the directional derivative of \(F_{\epsilon }\) in the direction \(w^*\) is \(F_\epsilon '(0;w^*) \le -\mathbb {E}_{x \sim P_x} [|(w^*)^\top x|] < 0\).
Proof
We appeal to [19, Theorem 2.7.2] which shows how to compute the generalized gradient of a function defined via expectations. We note that for every (x, y), \(w \mapsto L_R(y w^\top x)\) is a regular function since it is a difference of two convex functions, and is differentiable everywhere except when \(y w^\top x \in \{0,1\}\), with gradient \(-\varvec{1}(0< y w^\top x < 1) yx\). When \(w \ne 0\), the set of \((x,y) \sim P\) such that \(y w^\top x \in \{0,1\}\) is a measure-zero set under Assumption 5.1, so [19, Theorem 2.7.2] states that the generalized gradient of \(\mathbb {E}_{(x,y) \sim P}[L_R(y w^\top x)]\) is the singleton set \(\left\{ -\mathbb {E}_{(x,y) \sim P} \left[ \varvec{1}\left( 0< y w^\top x < 1 \right) y x \right] \right\} \). As it is a singleton, this coincides with the gradient at w. Furthermore, we can write \(\mathbb {E}_{(x,y) \sim P} \left[ \varvec{1}\left( 0< y w^\top x < 1 \right) y x \right] = \mathbb {E}_{(x,y) \sim P} \left[ \varvec{1}\left( 0 \le y w^\top x \le 1 \right) y x \right] \) since \(y w^\top x \in \{0,1\}\) is a set of measure 0 by Assumption 5.1. This proves the first claim.
For the final claim, note first that the gradient of the regularization term \(\tfrac{1}{2} \epsilon \Vert w\Vert _2^2\) is zero at \(w=0\). Thus we need consider only the \(L_R\) term in applying the definition of directional derivative to (37). For the direction \(w^*\), we have
Now observe that \(g_\alpha (x) := |(w^*)^\top x| \varvec{1}(0 \le \alpha |(w^*)^\top x| \le 1)\) monotonically increases pointwise to \(g(x) = |(w^*)^\top x|\) as \(\alpha \downarrow 0\), therefore by the monotone convergence theorem \(\lim _{\alpha \downarrow 0} \mathbb {E}_{x \sim P_x} [|(w^*)^\top x| \varvec{1}(0 \le \alpha |(w^*)^\top x| \le 1)] = \mathbb {E}_{x \sim P_x} [|(w^*)^\top x|]\). Furthermore, \(\lim _{\alpha \downarrow 0} \frac{1}{\alpha } \left( \mathbb {P}_{x \sim P_x}[0 \le \alpha |(w^*)^\top x| \le 1] - 1\right) \le 0\). Therefore
\(\square \)
Lemma 5.1 shows that \(w=0\) is not a local minimum of \(F_\epsilon \), hence any reasonable descent algorithm will not converge to it. We now investigate stationary points \(\nabla F_\epsilon (w) = 0\) for \(w \ne 0\) under Assumption 5.1. To this end, we will use the following properties of spherically symmetric distributions.
Lemma 5.2
([24, Corollary 4.3], [40, Theorem C.3]) Let \(x \sim P_x\) be a spherically symmetric distribution on \(\mathbb {R}^d\) about 0. Decompose \(x = (x^1,x^2)\) where \(x^1 \in \mathbb {R}^{p}\) and \(x^2 \in \mathbb {R}^{d-p}\), with \(1 \le p \le d-1\). The marginal distribution of \(x^1\) and the conditional distribution \(x^1 \mid x^2\) are spherically symmetric on \(\mathbb {R}^p\) about 0.
Lemma 5.3
Let P be a spherically symmetric distribution on \(\mathbb {R}^d\) absolutely continuous with respect to Lebesgue measure on \(\mathbb {R}^d\) (i.e., it is a nondegenerate distribution which has zero measure on any lower-dimensional set). Consider a closed full-dimensional unbounded polyhedron A that contains the origin. Then \(\mathbb {P}_{x \sim P_x}[x \in A] > 0\).
Proof
Consider the disjoint union
By our assumptions on A, each \(A_k\) is non-empty and full-dimensional. Note that \(\mathbb {P}_{x \sim P_x}[x \in A_k] \le \mathbb {P}_{x \sim P_x}[x \in A] \le \sum _{k' \in \mathbb {N}} \mathbb {P}_{x \sim P_x}[x \in A_{k'}]\) for every \(k \in \mathbb {N}\). Note that whenever \(\mathbb {P}_{x \sim P_x}[x \in A_k] = 0\), we must also have \(\mathbb {P}_{x \sim P_x}[k-1 \le \Vert x\Vert _2 < k] = 0\) also, since we can cover \(\{x : k-1 \le \Vert x\Vert _2 < k\}\) with finitely many rotated copies of \(A_k\), since it is full-dimensional, and each of these has identical measure by spherical symmetry of P. Now, if all \(\mathbb {P}_{x \sim P_x}[x \in A_k] = 0\), then \(\mathbb {P}_{x \sim P_x}[x \in \mathbb {R}^d] = \sum _{k \in \mathbb {N}} \mathbb {P}_{x \sim P_x}[k-1 \le \Vert x\Vert _2 < k] = 0\) which is a contradiction. This implies that there is at least one \(\mathbb {P}_{x \sim P_x}[x \in A_k] > 0\), hence \(\mathbb {P}_{x \sim P_x}[x \in A] > 0\). \(\square \)
We also use this general property of distributions, which we present without proof. Given a set \(A \subseteq \mathbb {R}^d\), let \({{\,\mathrm{Conv}\,}}(A)\) and \({{\,\mathrm{Cone}\,}}(A)\) be the convex and conic hull respectively.
Lemma 5.4
Let \(P_x\) be a distribution over \(\mathbb {R}^d\). For any measurable set \(A \subseteq \mathbb {R}^d\), \(\mathbb {E}_{x \sim P_x}[\varvec{1}(x \in A) x] = \mathbb {P}_{x \sim P_x}[x \in A] a \in {{\,\mathrm{Cone}\,}}(A)\) for some \(a \in {{\,\mathrm{Conv}\,}}(A)\).
We first prove that when \(d=2\), points which are not positive multiples of \(w^*\) cannot be stationary points. We will then show how the proof for general d essentially reduces to this setting. Since \(d=2\), we will write \(w = (w_1,w_2)\) and \(x = (x_1,x_2)\).
Theorem 5.5
Consider \(d=2\) and suppose Assumption 5.1 holds. For each vector \(w \ne (0,0)\) that is not a positive multiple of \(w^*\), we have \(\nabla F_{\epsilon }(w) \ne (0,0)\).
Proof
From the expression for \(\nabla F_\epsilon (w)\) in Lemma 5.1, the result will be proved if we can show that
is not a positive multiple of w whenever w is not a positive multiple of \(w^*\). Observe that the “good” region \(\{x : 0 \le {{\,\mathrm{sign}\,}}((w^*)^\top x) w^\top x \le 1\}\) is the union of two almost disjoint polyhedra \(\{x : (w^*)^\top x \ge 0, 0 \le w^\top x \le 1\} \cup \{x : (w^*)^\top x \le 0, -1 \le w^\top x \le 0\}\). Define
Since \(\{x : (w^*)^\top x \le 0, -1 \le w^\top x \le 0\} = \{-x : x \in \mathcal{R}\}\) can be obtained by an orthogonal transformation of \(\mathcal{R}\), we have by spherical symmetry of \(P_x\) that
Therefore we need to show that \(\mathbb {E}_{x \sim P_x} \left[ \varvec{1}(x \in \mathcal{R}) x \right] \) is not a positive multiple of w whenever w is not a positive multiple of \(w^*\). Since \(P_x\) is spherically symmetric, we can without loss of generality change the basis so that \(w^* = (1,0)\), so that \(y = {{\,\mathrm{sign}\,}}(x_1)\) and \(\mathcal{R}= \left\{ x : x_1 \ge 0, 0 \le w^\top x \le 1 \right\} \).
Notice that \({{\,\mathrm{sign}\,}}(x_1) x = (|x_1|,{{\,\mathrm{sign}\,}}(x_1) x_2)\), so that
has a non-negative first component. Therefore, whenever \(w_1 < 0\), (38) cannot be a positive multiple of w.
Consider now the case of \(w_1 = 0\). Since we have already dealt with the case \(w= (0,0)\) in Lemma 5.1, and are excluding it from consideration here, we must have \(w_2 \ne 0\). Then
For either sign of \(w_2\), since \(P_x\) is spherically symmetric and absolutely continous with respect to Lebesgue measure and \(\mathcal{R}\) is full-dimensional, unbounded, and contains the origin, by Lemma 5.3, \(\mathbb {P}_{x \sim P_x} \left[ x \in \mathcal{R}\right] > 0\). Additionally, by Assumption 5.1, \(\mathbb {P}_{x \sim P_x} \left[ x_1 = 0, x \in \mathcal{R}\right] = 0\), so that
Therefore \(\mathbb {E}_{x \sim P_x}[\varvec{1}(x \in \mathcal{R}) x_1] > 0\), hence \(\mathbb {E}_{x \sim P_x} \left[ \varvec{1}(x \in \mathcal{R}) x \right] \) is not a multiple of \(w=(0,w_2)\).
We now consider \(w_1 > 0\) and without loss of generality \(w_2 > 0\). (When \(w_2 < 0\), an analogous \(\mathcal{R}\) can be obtained via a reflection across the \(x_1\)-axis; See Fig.3 for an illustration.)
We define the lines \(R_1,R_2,R_3\) which bound \(\mathcal{R}\), and \(S = {{\,\mathrm{Span}\,}}(\{w\})\) which we will use in our analysis:
Note that S is orthogonal to \(R_2\) and \(R_3\). We consider the following decomposition of \(\mathcal{R}\):
This decomposition is illustrated in Fig. 4.
We will now show the following three facts.
-
1.
We show that \(\mathcal{T}' \subset \mathcal{R}\), so that in fact \(\mathcal{R}' \cup \mathcal{T}\cup \mathcal{T}' = \mathcal{R}\). To see that \(\mathcal{T}' \subset \mathcal{R}\), we will show that its three extreme points are in \(\mathcal{R}\). These correspond exactly to the three extreme points of \(\mathcal{T}\), namely \(p_1 = R_1 \cap S = (0,0)\), \(p_2 = R_1 \cap R_3\) and \(p_3 = S \cap R_3\). Clearly the reflection of \(p_1\) and \(p_3\) are themselves since they are already on S. For \(p_2 = R_1 \cap R_3\), we know its reflection \(p_2'\) is in \(R_3\) since \(R_3\) is orthogonal to S. We check that the first coordinate of \(p_2'\) is nonnegative in order to deduce that it is in \(\mathcal{R}\). In fact this claim follows from the fact that \(p_3 = t w\) for some \(t>0\), from \(w_1>0\), and from the explicit formula \(p_2' = p_3+ (p_3-p_2)\), which tells that the first component of \(p_2'\) is \(2tw_1\). Since this value is nonnegative, we are done.
-
2.
\(\mathbb {E}_{x \sim P_x} \left[ \varvec{1}(x \in \mathcal{T}\cup \mathcal{T}')x \right] \in S\). The distribution \(P_x\) is symmetric across S since a reflection across a line through the origin is an orthogonal transformation. By construction, \(\mathcal{T}\cup \mathcal{T}'\) is symmetric across S, hence \(\mathbb {E}_{x \sim P_x} \left[ \varvec{1}(x \in \mathcal{T}\cup \mathcal{T}') x \right] \in S\).
-
3.
We show now that \(\mathbb {E}_{x \sim P_x} \left[ \varvec{1}(x \in \mathcal{R}') x \right] \not \in S\). Since \(P_x\) is spherically symmetric and absolutely continous with respect to Lebesgue measure and \(\mathcal{R}'\) is full-dimensional, unbounded, and its closure \({{\,\mathrm{cl}\,}}(\mathcal{R}')\) contains the origin, by Lemma 5.3 we have \(0 < \mathbb {P}_{x \sim P_x}[x \in {{\,\mathrm{cl}\,}}(\mathcal{R}')] = \mathbb {P}_{x \sim P_x}[x \in \mathcal{R}']\), where the equality follows by absolute continuity of \(P_x\) (Assumption 5.1). Also, since \((0,0) \in \mathcal{T}\cup \mathcal{T}'\), it is not in \(\mathcal{R}'\) (but it is an extreme point). Therefore \((0,0) \not \in {{\,\mathrm{Conv}\,}}(\mathcal{R}')\). By Lemma 5.4, \(\mathbb {E}_{x \sim P_x} \left[ \varvec{1}(x \in \mathcal{R}') x \right] = \mathbb {P}_{x \sim P_x}[x \in \mathcal{R}'] a \ne (0,0)\) where \(a \in {{\,\mathrm{Conv}\,}}(\mathcal{R}')\). Finally, since \(\mathcal{T}\) was defined as a triangle with one side on S, we clearly have \(\mathcal{R}\cap S \subset \mathcal{T}\). Clearly, S cannot intersect any part of \(\mathcal{R}'\), hence \(S \cap {{\,\mathrm{Cone}\,}}(\mathcal{R}') = \{(0,0)\}\), so that \(\mathbb {E}_{x \sim P_x} \left[ \varvec{1}(x \in \mathcal{R}') x \right] \not \in S\).
Since we have
where the second fact shows that the first vector on the right-hand side is in S while the third fact shows that the second vector on the right-hand side is not in S, we conclude that \(\mathbb {E}_{x \sim P_x} \left[ \varvec{1}(x \in \mathcal{R}) x \right] \notin S\), as required. \(\square \)
We now prove the claim about uniqueness and form of the global minimizer for the case of general dimension d.
Theorem 5.6
For arbitrary dimension d, suppose Assumption 5.1 holds. Then for \(w \ne 0\), \(\nabla F_{\epsilon }(w) \ne 0\) whenever w is not a positive multiple of \(w^*\). Furthermore, a unique stationary point \(w(\epsilon ) = \alpha (\epsilon ) w^*\) exists for a unique \(\alpha (\epsilon ) > 0\).
Proof
Since \(P_x\) is spherically symmetric, without loss of generality, consider \(w^* = (1,0,\ldots ,0)\). Since \(y x_1 = {{\,\mathrm{sign}\,}}(x_1)x_1 = |x_1|\), we cannot have \(w = -\alpha w^*\) for \(\alpha > 0\) be a stationary point, because
Now consider \(w \ne 0\) that is not a multiple of \(w^*\). Consider the two-dimensional plane in \(\mathbb {R}^d\) spanned by w and \(w^*\). Change the basis if necessary so that \(w = (w_1,w_2,0,\ldots ,0)\) (this is without loss of generality as \(P_x\) is symmetric hence invariant to orthogonal transformations). With this change of basis, the first two entries of \(\mathbb {E}_{(x,y) \sim P} \left[ \varvec{1}(0 \le yw^\top x \le 1) yx \right] \) are determined fully by what happens on the \((x_1,x_2)\) coordinates. More formally, we can without loss of generality consider the marginal distribution \(P_x(x_1,x_2)\) on \(\mathbb {R}^2\) obtained by integrating out \(x_3,\ldots ,x_d\) (this is spherically symmetric by Lemma 5.2). Then Theorem 5.5 applies to prove our first claim.
Finally, consider \(w = \alpha w^* = (\alpha ,0,\ldots ,0)\) for \(\alpha > 0\). Then the components of
are, for \(j \in [d]\),
By Lemma 5.2 the conditional distribution \(P_x(x_j \mid x_1)\) is still spherically symmetric about 0 for \(j \ge 2\), therefore \(\mathbb {E}_{x \sim P_x} \left[ \varvec{1}(0 \le |x_1| \le 1/\alpha ) {{\,\mathrm{sign}\,}}(x_1) x_j \mid x_1 \right] = \varvec{1}(0 \le |x_1| \le 1/\alpha ) {{\,\mathrm{sign}\,}}(x_1) \mathbb {E}_{x \sim P_x} \left[ x_j \mid x_1 \right] = 0\) for any \(x_1\). Consequently, for \(j \ge 2\), we have
Now consider \(j=1\). Then first component of \(\mathbb {E}_{(x,y) \sim P} \left[ \varvec{1}(0 \le yw^\top x \le 1) yx \right] \) is
Consequently, by Lemma 5.1 the first component of the gradient is
Since \(P_x\) is absolutely continuous with respect to Lebesgue measure, g must be continuous. Also, we have \(\lim _{\alpha \rightarrow \infty } g(\alpha ) = 0\) and \(\lim _{\alpha \downarrow 0} g(\alpha ) = \mathbb {E}_{x \sim P_x}[|x_1|] > 0\). Furthermore, g is non-increasing by definition. We conclude that there must exist a unique \(\alpha (\epsilon ) > 0\) for which \(\epsilon \alpha (\epsilon ) = g(\alpha (\epsilon ))\), and \(w(\epsilon ) = \alpha (\epsilon ) w^*\) is the unique stationary point. \(\square \)
Label Flipping. Our experiments in Sect. 4 showed that solutions of the problems analyzed in this section showed remarkable resilience to “flipping” of the labels y on a number of samples. To give some insight into this phenomenon, suppose that \(y = \delta {{\,\mathrm{sign}\,}}((w^*)^\top x)\) where \(\delta \in \{\pm 1\}\) is a random variable independent of (x, y), and \(\delta = +1\) (resp. \(-1\)) with probability p (resp. \(1-p\)). Then some simple transformations give
where the last equality uses the fact that x and \(-x\) have the same distribution as \(P_x\) is spherically symmetric. We see that in the noisy label setting, the objective \(F_{\epsilon }\) is a combination of two noise-free objectives
one where labels are \(y = {{\,\mathrm{sign}\,}}((w^*)^\top x)\) with weight p, and the other where labels are \(y = {{\,\mathrm{sign}\,}}((-w^*)^\top x)\) generated by the opposite hyperplane. When \(p > 1-p\), more weight is dedicated to the \(w^*\)-generated points, hence the solution to (37) is \(w^*\), and vice versa. This informal analysis explains to a large extent the results reported in Sect. 4.3.
Notes
See, for example, https://adversarial-ml-tutorial.org/introduction/.
References
Beck, A., Teboulle, M.: Smoothing and first order methods: a unified framework. SIAM J. Optim. 22(2), 557–580 (2012)
Belotti, P., Bonami, P., Fischetti, M., Lodi, A., Monaci, M., Nogales-Gómez, A., Salvagnin, D.: On handling indicator constraints in mixed integer programming. Comput. Optim. Appl. 65(3), 545–566 (2016)
Ben-Tal, A., Teboulle, M.: An old-new concept of convex risk measures: the optimized certainty equivalent. Math. Finance 17(3), 449–476 (2007)
Ben-Tal, A., Hazan, E., Koren, T., Mannor, S.: Oracle-based robust optimization via online learning. Oper. Res. 63(3), 628–638 (2015)
Bennett, K.P., Mangasarian, O.L.: Robust linear programming discrimination of two linearly inseparable sets. Optim. Methods Softw. 1(1), 23–34 (1992)
Bertsimas, D., Copenhaver, M.S.: Characterization of the equivalence of robustification and regularization in linear and matrix regression. Eur. J. Oper. Res. 270(3), 931–942 (2018)
Bertsimas, D., Dunn, J., Pawlowski, C., Zhuo, Y.D.: Robust classification. INFORMS J. Optim. 1(1), 2–34 (2019)
Blanchet, J., Murthy, K.: Quantifying distributional model risk via optimal transport. Math. Oper. Res. 44(2), 565–600 (2019)
Bollapragada, R., Byrd, R.H., Nocedal, J.: Exact and inexact subsampled Newton methods for optimization. IMA J. Numer. Anal. 39(2), 545–578 (2019)
Brooks, J.P.: Support vector machines with the ramp loss and the hard margin loss. Oper. Res. 59(2), 467–479 (2011)
Bubeck, S., Lee, Y.T., Price, E., Razenshteyn, I.: Adversarial examples from computational constraints. In: Chaudhuri, K., Salakhutdinov, R. (eds.) Proceedings of the 36th International Conference on Machine Learning, pp. 831–840 (2019)
Carlini, N., Wagner, D.: Towards evaluating the robustness of neural networks. In: 2017 IEEE Symposium on Security and Privacy (SP), pp. 39–57 (2017a)
Carlini, N., Wagner, D.: Adversarial examples are not easily detected: bypassing ten detection methods. In: Proceedings of the 10th ACM Workshop on Artificial Intelligence and Security, p. 3–14 (2017b)
Charles, Z., Rajput, S., Wright, S., Papailiopoulos, D.: Convergence and margin of adversarial training on separable data. Technical report, May 2019. URL https://arxiv.org/abs/1905.09209
Chen, J., Wu, X., Rastogi, V., Liang, Y., Jha, S.: Robust attribution regularization. In: Wallach, H., Larochelle, H., Beygelzimer, A., d’ Alché-Buc, F., Fox, E., Garnett, R. (eds) Advances in Neural Information Processing Systems, pp. 14300–14310 (2019)
Chen, R., Paschalidis, I.C.: A robust learning approach for regression models based on distributionally robust optimization. J. Mach. Learn. Res. 19(13), 1–48 (2018)
Chen, Z., Kuhn, D., Wiesemann, W.: Data-driven chance constrained programs over Wasserstein balls. Technical report, Sep 2018. URL https://arxiv.org/abs/1809.00210
Chi, Y., Lu, Y.M., Chen, Y.: Nonconvex optimization meets low-rank matrix factorization: an overview. IEEE Trans. Signal Process. 67(20), 5239–5269 (2019)
Clarke, F.H.: Optimization and nonsmooth analysis. Society for Industrial and Applied Mathematics (1990)
Cohen, J., Rosenfeld, E., Kolter, Z.: Certified adversarial robustness via randomized smoothing. In: Chaudhuri, K., Salakhutdinov, R. (eds.) Proceedings of the 36th International Conference on Machine Learning, pp. 1310–1320 (2019)
Collobert, R., Sinz, F., Weston, J., Bottou, L.: Trading convexity for scalability. In: Proceedings of the 23rd International Conference on Machine Learning, pp. 201–208 (2006)
Fawzi, A., Fawzi, H., Fawzi, O.: Adversarial vulnerability for any classifier. In: Advances in Neural Information Processing Systems, pp. 1186–1195 (2018a)
Fawzi, A., Fawzi, O., Frossard, P.: Analysis of classifiers’ robustness to adversarial perturbations. Mach. Learn. 107(3), 481–508 (2018)
Fourdrinier, D., Strawderman, W.E., Wells, M.T.: Shrinkage estimation. Springer International Publishing (2018)
Gilmer, J., Ford, N., Carlini, N., Cubuk, E.: Adversarial examples are a natural consequence of test error in noise. In: Chaudhuri, K., Salakhutdinov, R. (eds) Proceedings of the 36th International Conference on Machine Learning, pp. 2280–2289 (2019)
Goodfellow, I.J., Shlens, J., Szegedy, C.: Explaining and harnessing adversarial examples. In: International Conference on Learning Representations. URL http://arxiv.org/abs/1412.6572 (2015)
Ho-Nguyen, N., Kılınç-Karzan, F.: Online first-order framework for robust convex optimization. Oper. Res. 66(6), 1670–1692 (2018)
Hu, W., Niu, G., Sato, I., Sugiyama, M.: Does distributionally robust supervised learning give robust classifiers? In: Dy, J., Krause, A. (eds) Proceedings of the 35th International Conference on Machine Learning, pp. 2029–2037 (2018)
Kuhn, D., Esfahani, P.M., Nguyen, V.A., Shafieezadeh-Abadeh, S.: Wasserstein distributionally robust optimization: theory and applications in machine learning, chapter 6, pp. 130–166. INFORMS TutORials in Operations Research (2019)
Lee, J., Raginsky, M.: Minimax statistical learning with Wasserstein distances. In: Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R. (eds) Advances in Neural Information Processing Systems, pp. 2687–2696 (2018)
Li, Y., Fang, E.X., Xu, H., Zhao, T.: Implicit bias of gradient descent based adversarial training on separable data. In: International Conference on Learning Representations. URL https://openreview.net/forum?id=HkgTTh4FDH (2020)
Liu, D.C., Nocedal, J.: On the limited memory BFGS method for large scale optimization. Math. Program. 45(1), 503–528 (1989)
Madry, A., Makelov, A., Schmidt, L., Tsipras, D., Vladu, A.: Towards deep learning models resistant to adversarial attacks. In: International Conference on Learning Representations. URL https://openreview.net/forum?id=rJzIBfZAb (2018)
Mangasarian, O.L.: Linear and nonlinear separation of patterns by linear programming. Oper. Res. 13(3), 444–452 (1965)
Mohajerin Esfahani, P., Kuhn, D.: Data-driven distributionally robust optimization using the Wasserstein metric: performance guarantees and tractable reformulations. Math. Program. 171(1), 115–166 (2018)
Moosavi-Dezfooli, S.M., Fawzi, A., Frossard, P.: Deepfool: a simple and accurate method to fool deep neural networks. In: 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 2574–2582 (2016)
Moosavi-Dezfooli, S.M., Fawzi, A., Frossard, P.: Robustness via curvature regularization, and vice versa. In: 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 9070–9078 (2019)
Mutapcic, A., Boyd, S.: Cutting-set methods for robust convex optimization with pessimizing oracles. Optim. Methods Softw. 24(3), 381–406 (2009)
Nocedal, J., Wright, S.J.: Numerical optimization, 2nd edn. Springer, New York (2006)
Paolella., M.S.: Linear models and time-aeries analysis. John Wiley & Sons, Ltd (2018)
Pydi, M.S., Jog, V.: Adversarial risk via optimal transport and optimal couplings. IEEE Trans. Inf. Theory 67(9), 6031–6052 (2021)
Rockafellar, R.T.: Coherent approaches to risk in optimization under uncertainty, chapter 3, pp. 38–61. INFORMS TutORials in Operations Research (2007)
Shafieezadeh-Abadeh, S., Mohajerin Esfahani, P., Kuhn, D.: Distributionally robust logistic regression. In: Proceedings of the 28th International Conference on Neural Information Processing Systems—Volume 1, pp. 1576–1584 (2015)
Shafieezadeh-Abadeh, S., Kuhn, D., Mohajerin Esfahani, P.: Regularization via mass transportation. J. Mach. Learn. Res. 20(103), 1–68 (2019)
Shen, X., Tseng, G.C., Zhang, X., Wong, W.H.: On \(\psi \)-learning. J. Am. Stat. Assoc. 98(463), 724–734 (2003)
Sinha, A., Namkoong, H., Duchi, J.C.: Certifying some distributional robustness with principled adversarial training. In: International Conference on Learning Representations. URL https://openreview.net/forum?id=Hk6kPgZA- (2018)
Szegedy, C., Zaremba, W., Sutskever, I., Bruna, J., Erhan, D., Goodfellow, I.,Fergus, R.: Intriguing properties of neural networks. In:International Conference on Learning Representations. URL https://openreview.net/forum?id=kklr_MTHMRQjG (2014)
Tramér, F., Kurakin, A., Papernot, N., Goodfellow, I., Boneh, D. Ensemble adversarial training: attacks and defenses. In International Conference on Learning Representations. URL https://openreview.net/forum?id=rkZvSe-RZ (2018)
Wang, Y., Ma, X., Bailey, J., Yi, J., Zhou, B., Gu, Q.: On the convergence and robustness of adversarial training. In: Chaudhuri, K., Salakhutdinov, R. (eds.) Proceedings of the 36th International Conference on Machine Learning, pp. 5586–6595 (2019)
Wong, E., Kolter, Z.: Provable defenses against adversarial examples via the convex outer adversarial polytope. In: Dy, J., Krause, A. (eds.) Proceedings of the 35th International Conference on Machine Learning, pp. 5286–5295 (2018)
Wu, Y., Liu, Y.: Robust truncated hinge loss support vector machines. J. Am. Stat. Assoc. 102(479), 974–983 (2007)
Xie, W.: On distributionally robust chance constrained programs with Wasserstein distance. Math. Program. 186(1), 115–155 (2021)
Xu, H., Caramanis, C., Mannor, S.: Robustness and regularization of support vector machines. J. Mach. Learn. Res. 10(51), 1485–1510 (2009)
HXu, H., Caramanis, C., Mannor, S:. Robust optimization in machine learning. In: Sra, S., Nowozin, S., Wright, S.J. (eds.) Optimization for Machine Learning. The MIT Press (2011)
Xu, P., Yang, J., Roosta, F., Ré, C., Mahoney, M.W.: Sub-sampled Newton methods with non-uniform sampling. In: Lee, D., Sugiyama, M., Luxburg, U., Guyon, I., Garnett, R. (eds.) Advances in Neural Information Processing Systems, pp. 3000–3008 (2016)
Yin, D., Kannan, R., Bartlett, P.: Rademacher complexity for adversarially robust generalization. In: Chaudhuri, K., Salakhutdinov, R. (eds.) Proceedings of the 36th International Conference on Machine Learning, pp. 7085–7094 (2019)
Zhang, H., Yu, Y., Jiao, J., Xing, E., El Ghaoui, E., Jordan, M.: Theoretically principled trade-off between robustness and accuracy. In: Chaudhuri, K., Salakhutdinov, R. (eds.) Proceedings of the 36th International Conference on Machine Learning, pp. 7472–7482 (2019)
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by NSF Awards 1628384, 1634597, 1740707, and 2023239; Subcontract 8F- 30039 from Argonne National Laboratory; and Award N660011824020 from the DARPA Lagrange Program. The research was conducted in part while the first author was a postdoctoral research associate at the University of Wisconsin–Madison.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ho-Nguyen, N., Wright, S.J. Adversarial classification via distributional robustness with Wasserstein ambiguity. Math. Program. 198, 1411–1447 (2023). https://doi.org/10.1007/s10107-022-01796-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-022-01796-6