Towards nonuniform distributions of unisolvent weights for high-order Whitney edge elements

Abstract

We propose to extend results on the interpolation theory for scalar functions to the case of differential k-forms. More precisely, we consider the interpolation of fields in ${\mathcal P}^-_r \varLambda ^k(T)$, the finite element spaces of trimmed polynomial k-forms of arbitrary degree $r \ge 1$, from their weights, namely their integrals on k-chains. These integrals have a clear physical interpretation, such as circulations along curves, fluxes across surfaces, densities in volumes, depending on the value of k. In this work, for $k=1$, we rely on the flexibility of the weights with respect to their geometrical support, to study different sets of 1-chains in T for a high order interpolation of differential 1-forms, constructed starting from “good” sets of nodes for a high order multi-variate polynomial representation of scalar fields, namely 0-forms. We analyse the growth of the generalized Lebesgue constant with the degree r and preliminary numerical results for edge elements support the nonuniform choice, in agreement with the well-known nodal case.

1 Introduction

New degrees of freedom, called weights to distinguish them from the classical moments introduced in [18], have been firstly proposed in [20] for the interpolation, on simplicial meshes, of physical fields, intended as differential k-forms, in Whitney finite element spaces of high polynomial degree $r\ge 1$ (see, [3, 6]). These weights are integrals of the field under consideration on a distribution of small k-simplices, that are particular subsimplices of dimension k in each element of the mesh. In [1] we have generalized this construction and now we develop that idea to establish how to select minimal and unisolvent sets of such small simplices as supports of the weights. This new methodology yields a flexibility, in the choice of the small simplices, that opens the way to nonuniform distributions, where the term nonuniform needs some care for $k\ne 0$ and $k \ne n$, being n the ambient dimension. The quality of the interpolation on uniform and nonuniform distributions of small k-simplices can be analysed in terms of the generalized Lebesgue constant [2].

Finite element spaces extending Whitney forms to higher degrees are widely used for discretizing physical balance laws in electromagnetism, fluid dynamics or elasticity. The degrees of freedom (dofs) associated with Whitney differential forms have a direct physical relevance. When considering polynomial interpolation of higher degree, dofs can be chosen in different ways. In [18] and its extension [15] (see also [16]), higher moments are used. They are also considered in the general framework of the finite element exterior calculus [3]. In [20], the localization issue has been addressed, namely, the relationship between dofs and measurable quantities (such as circulations, fluxes, densities) for the field they are related with. In the framework of high order Whitney finite element spaces, integrals on suitable subsimplices of the mesh are a valid alternative as dofs to the classical moments. Their definition is based on the introduction of the small simplices, that are subsimplices resulting from homothetic contractions of the elements of the mesh¹. New dofs are then the weights, integrals of a k-form on these small k-simplices. The weights make the connection between physics and geometry: the concept of small k-simplex was born from the necessity of extending to $r>1$ the geometrical construction proposed for $r=1$ by Weil-Whitney in a context other than finite elements but more related with algebraic cohomology and the proof of the de Rham’s theorem (see [23, 24]). Understanding and generalizing this construction has been fundamental to provide explicit bases for high order finite element spaces involved in the discretization of problems from electromagnetism and other areas of physics.

The concept of weight on a small k-simplex represents an important theoretical achievement to see that it is indeed possible to extend standard results of polynomial interpolation theory to k-forms with $k>0$. In the particular case of 0-forms the Whitney finite elements are in fact the Lagrange ones and the integrals on the small 0-simplices are the dofs used in the classical description of the Lagrange finite elements (see e.g. [8]), namely the values at the points of the principal lattices of the elements of the mesh. The weights of k-forms on small k-simplices for $k>0$, can be intended as a generalization of the values at nodes (small 0-simplices) of continuous scalar functions (differential 0-forms). It is well-known that the Lagrange interpolation at uniformly distributed points in the mesh elements can yield a poor approximation as soon as the polynomial degree increases, even when the interpolated function is rather smooth [4]. This is due to a rapid increase, with the approximation degree, of the Lebesgue constant that influences the sharpness of the bound on the interpolation error. In other words, the Lebesgue constant measures how the interpolating polynomial is close to or far from the best fit. For this reason there have been several attempts in the literature (see [11, 19, 21, 22] and the references therein) to produce nodal sets in a triangle or tetrahedron using direct (with explicit formula) and indirect (undergoing an optimization procedure) methods, satisfying criteria of low computational complexity and minimization of the Lebesgue constant. It naturally arises the following question: “Is it possible to do the same for $k>0$ ?”. In other words: “How small k-simplices, $0< k < n$, should be distributed in a triangle or a tetrahedron in order to interpolate differential k-forms by trimmed polynomial ones in a way that remains stable with the growth of the degree r ?”

In this work, we provide an answer to the question when $k=1$ by generalizing the construction of nonuniform distributions of nodes to that of small edges. We first detail how to construct unisolvent and minimal sets of small edges with ending points in distributions of nodes that are well-known in the literature². We then exploit this flexibility to analyse, for the weights on these new sets of small edges, the growth of the generalized Lebesgue constant introduced in [2] when increasing the polynomial degree. The behavior of the generalized Lebesgue constant will state the quality of the polynomial interpolation of 1-forms at the new nonuniform distributions of the small 1-simplices in the mesh. We will see that small changes on the data give rise to small changes on the interpolating form if the Lebesgue constant is small. This constant plays the role of the condition number for the interpolation problem.

The paper is organized as follows. In Sect. 2 we recall few notations and basic notions of polynomial differential forms and of the role of the Lebesgue constant in the classical interpolation theory. In Sect. 3, the notions of Vandermonde matrix and Lebesgue constant are presented for $k>0$. In Sect. 4 we describe how to generate sets of 1-simplices supporting weights for trimmed polynomial 1-forms that are unisolvent associated with classical choices of interpolation nodes, namely the uniform, the symmetrised Lobatto and warp & blend distributions. Section 5 starts with the adopted algorithm to compute the generalized Lebesgue constant and ends with a numerical comparison of the behavior, when increasing the polynomial degree, of such a constant associated with the considered families of dofs in two and three dimensions. In Sect. 6 we discuss the dependence on the shape of the element of the generalized Lebesgue constant for $k=1$. In Sect. 7 we analyse the stability of the interpolation for $k=1$ with respect to perturbations on the data, i.e., the weights. The paper ends with Sect. 8 containing some concluding remarks that point out the attained achievements.

2 Notation and preliminaries

In this section we explain the notation and some basic notions of polynomial differential forms. Given $n+1$ point in general position in ${\mathbb {R}}^n$, the n-simplex with these vertices is their closed convex hull. Any subset of $k+1$ vertices of a n-simplex defines a face of dimension k, with $0\le k \le n$. Faces are simplices themselves. Let $\varDelta _k(T)$ be the set of faces of dimension k (or k-subsimplices) of the n-simplex T. If we introduce an ordering³ of the vertices of T, $\{\mathbf{x}_0,\dots ,\mathbf{x}_n\}$, then we can identify univocally any k-face F of T with an increasing map $\sigma _F:\{0,\dots , k\} \rightarrow \{0,\dots , n\}$. The face F has vertices $\{ \mathbf{x}_{\sigma _F(0)},\dots ,\mathbf{x}_{\sigma _F(k)}\}$. With each point $\mathbf{x} \in T$ we may associate a $(n+1)$-uple $\left( \lambda _0(\mathbf{x}), \lambda _1(\mathbf{x}), \ldots , \lambda _n (\mathbf{x})\right)$ such that

$$\begin{aligned} \mathbf{x} = \sum _{i=0}^{n} \lambda _i (\mathbf{x})\, \mathbf{x}_i,\qquad \sum _{i=0}^n \lambda _i(\mathbf{x}) = 1, \qquad \lambda _i(\mathbf{x}) \ge 0. \end{aligned}$$

We call barycentric coordinates for $\mathbf{x}$ in T the values $\lambda _i(\mathbf{x})$ for $i=0,...,n$.

For the construction of small 1-simplices associated with particular sets of nodes in T, we need to introduce the concepts of simplicial complex and map (see, e.g., [17]). A simplicial complex K in ${\mathbb {R}}^n$ is a collection of simplices such that every face of a simplex of K is also in K and if $\sigma , \sigma '$ are two simplices of K then either $\sigma \cap \sigma ' = \sigma '' \in K$ or $\sigma \cap \sigma ' = \emptyset .$ The union of simplices of K is a subset of ${\mathbb {R}}^n$, denoted by |K| and called underlying space of K. Now, let K and $K'$ be simplicial complexes and let $\varDelta _0( K )$ and $\varDelta _0(K')$ denote the set of vertices of K and $K'$, respectively. Let us suppose to have a map $\varphi : \varDelta _0( K ) \rightarrow \varDelta _0(K')$ such that, whenever vertices $\mathbf{x}_0,..., \mathbf{x}_\ell$ of $\varDelta _0( K )$ span a simplex of K, the points $\varphi (\mathbf{x}_0),..., \varphi (\mathbf{x}_k)$ are vertices of a simplex of $K'$. Then $\varphi$ can be extended to a continuous map $g:|K|\rightarrow |K'|$ such that

$$\begin{aligned} \mathbf{x} = \sum _{i=0}^\ell \lambda _i(\mathbf{x})\, \mathbf{x}_i \qquad \Longrightarrow \qquad g(\mathbf{x}) = \sum _{i=0}^\ell \lambda _i(\mathbf{x})\, \varphi (\mathbf{x}_i)\, \end{aligned}$$

and g is called the simplicial map induced by the vertex map $\varphi$. Moreover, if the vertex map $\varphi$ is a bijection between $\varDelta _0( K)$ and $\varDelta _0( K')$ and $v_0, \ldots , v_\ell$ span a simplex of the complex K if and only if $\varphi (v_0), \ldots , \varphi (v_k)$ span a simplex of the complex $K'$, we say that the induced simplicial map g is a simplicial isomorphism of K with $K'$.

For the high-order case, multi-index notations are used. For each $m\in {\mathbb {N}}$, $m\ge 0$ and $s\in {\mathbb {N}}$ we denote by ${\mathcal {I}}(m+1,s)$ the set of $\left( {\begin{array}{c}m+s\\ s\end{array}}\right)$ multi-indices of length $m+1$ and weight s, namely

$$\begin{aligned} {\mathcal {I}}(m+1,s) = \{{\varvec{\eta }} \in {\mathbb {N}}^{m+1} \,: \, \sum _{i=0}^m \eta _i=s\}\,. \end{aligned}$$

Given ${\varvec{\alpha }} \in {\mathcal {I}} (n+1, s)$ we set $\lambda ^{\varvec{\alpha }} = \prod _{i=0}^n \lambda _i^{\alpha _i}$. We denote by $\varLambda ^k(T)$ the space of smooth differential k-forms in T. We associate with each $F\in \varDelta _k(T)$ the Whitney form $\omega _F \in \varLambda ^k(T)$ defined in the following way (see, e.g. [24]):

$$\begin{aligned} \omega _F=\sum _{i=0}^k (-1)^i \lambda _{\sigma _F(i)} \mathrm{d}\lambda _{\sigma _F(0)} \wedge \dots \wedge \widehat{ \mathrm{d}\lambda _{\sigma _F(i)} } \wedge \dots \wedge \mathrm{d}\lambda _{\sigma _F(k)}. \end{aligned}$$

If $k=0$ then F is a vertex $\mathbf{x}_i$ of T and $\omega _{\mathbf{x}_i} = \lambda _i$. If $k=n$ then $F=T$ and $\omega _T= \mathrm{d}\lambda _1 \wedge \dots \wedge \mathrm{d}\lambda _n$ is the volume form. We finally denote by

$$\begin{aligned} {\mathcal {P}}_{s+1}^- \varLambda ^k(T) := \mathrm{Span} \{ \lambda ^{{\varvec{\alpha }}} \omega _F \,: \, F\in \varDelta _k(T) \hbox { and } {\varvec{\alpha }} \in {\mathcal {I}} (n+1,s) \} \end{aligned}$$

the space of trimmed polynomial k-forms. Its elements are the Whitney polynomial k-forms of degree $s+1$. When $k=0$, we get $\ {\mathcal {P}}_{s+1}^- \varLambda ^0(T)= {\mathcal {P}}_{s+1} \varLambda ^0(T)$, the spaces of polynomial 0-forms of degree $s+1$. On the other hand for $k=n$ we have that $\ {\mathcal {P}}_{s+1}^- \varLambda ^n(T) := \mathrm{Span} \{ \lambda ^{\varvec{\alpha }} \mathrm{d}\lambda _1 \wedge \dots \wedge \mathrm{d}\lambda _n \,: \, \alpha \in \mathcal I (n+1,s) \} = {\mathcal {P}}_s \varLambda ^n(T)$, the space of polynomial n-forms of degree s.

We briefly recall classical notions for $k=0$ (see, e.g., [8, 9]) in order to compare them with the extensions that will be discussed later. A set $M =\{\mathbf{x}_j\}_{j=1}^m$ of points in $T\subset {{\mathbb {R}}}^n$, $n >0$, such that a polynomial $u \in \mathbb P_{r}(T)$ is univocally determined by its values $u(\mathbf{x}_j)$ at these points is said to be unisolvent for ${\mathbb {P}}_{r}(T)$. If $\mathrm{card}\, (M) = \mathrm{dim } \, {\mathbb {P}}_{r}(T)$ then M is said to be minimal. The Lebesgue constant is a well known indicator to estimate the quality of a set of nodes for the interpolation in ${\mathbb {P}}_{r}(T)$, with $T \subset {{\mathbb {R}}}^n$, $n >0$, of scalar functions. Given a set $M =\{\mathbf{x}_j\}_{j=1}^m$ unisolvent and minimal for the Lagrangian interpolation in ${\mathbb {P}}^r$, the Lebesgue constant associated to M is defined as $\mathtt{\varLambda }^0_M = \max _{\mathbf{x} \in T}\left( \sum _{j=1}^m | {\texttt {w}}_j(\mathbf{x})|\right)$ being $\{ \mathtt{w}_j\}_{j}$ the dual basis associated with the values at the set of nodes M, (i.e., ${\texttt {w}}_j \in , {\mathbb {P}}_{r}(T)$ such that ${\texttt {w}}_j (\mathbf{x}_i) = \delta _{ij}$, for all $\mathbf{x}_i \in M$). It plays the role of the condition number for the interpolation problem. In fact, let us suppose to have a vector $\tilde{\mathbf{u}}$ of values $(\tilde{\mathbf{u}}_j)_{j=1}^m$ that is a perturbation of $\mathbf{u}$, the array of data $(\mathbf{u}_j)_{j=1}^m$ at a unisolvent and minimal set M. The interpolating polynomials of degree r on the values $\mathbf{u}_j$ and $\tilde{\mathbf{u}}_j$ are, respectively, ${\varPi }^0_rf = \sum _{j=1}^m \mathbf{u}_j \, {\texttt {w}}_j$ and ${\varPi }_r^0 {{\tilde{f}}} = \sum _{j=1}^{m} \tilde{\mathbf{u}}_j\, {\texttt {w}}_j$. The following well-known result holds:

$$\begin{aligned} \Vert {\varPi }^0_rf - {\varPi }^0_r{{\tilde{f}}}\Vert _{\infty } \le \max _{\mathbf{x} \in T} \ \Big ( \, \sum _{j=1}^m | {\texttt {w}}_j(\mathbf{x})| \ \Big ) \, \max _{1\le j\le m} |\mathbf{u}_j - \tilde{\mathbf{u}}_j| = \mathtt{\varLambda }^0_M\, \Vert \mathbf{u} - \tilde{\mathbf{u}}\Vert _{\infty }. \end{aligned}$$

Here, by $\Vert \cdot \Vert _\infty$ we denote both the maximum norm of a function $f \in {{\mathcal {C}}}^0(T)$ ($\Vert f\Vert _{\infty } = \max _{\mathbf{x} \in T} |f(\mathbf{x})|$) and the infinity norm of a vector $\mathbf{v} \in {\mathbb {R}}^m$ ($\Vert \mathbf{v}\Vert _\infty = \max _{1 \le i \le m} |v_i|$).

Moreover, the Lebesgue constant appears when estimating the interpolation error. In deed, let $f^*_r$ be the best approximation polynomial of degree r of the scalar function f in T, for which $||f - f^*_r||_{\infty } \le ||f - z_r||_{\infty }$ for any other polynomial $z_r$ of degree r defined in T. The following well-known result holds:

$$\begin{aligned} || f - \varPi ^0_rf||_{\infty } \le (1 + \mathtt{\varLambda }^0_M)\, ||f-f^*_r||_{\infty }, \qquad \forall \, f \in {{\mathcal {C}}}^0(T). \end{aligned}$$

(1)

In (1), the growth of the Lebesgue constant $\varLambda ^0_M$ determines the convergence in the maximum norm. Moreover, the same inequality suggests that, when the Lebesgue constant does not grow too fast, we can have an approximation of f on T that is almost as good as the best approximation $f^*_r$ by taking ${\varPi }^0_rf$, that is easier to compute than $f^*_r$. There is a relevant literature for the case $k=0$ (see [11, 14, 19] and the references therein), widely dedicated to the problem of selecting a good and easy to be defined set of nodes M for the high order polynomial interpolation of continuous functions f on nontensorial domains as the simplex T.

3 Polynomial interpolation of forms and the Lebesgue constant

In order to introduce the definition of the generalized Lebesgue constant, we recall few essential concepts and refer to [2] for more details. The mass $|\sigma |_{_0}$ of a k-simplex $\sigma \subset {{\mathbb {R}}}^n$ is its k-dimensional Hausdorff’s measure. In particular, the mass of a point is 1. A simplicial k-chain c is a formal (finite) sum of k-simplices with real coefficients. The mass $|c|_{_0}$ of a simplicial chain $c = \sum _{i=1}^I a_i \, \sigma _i$ is defined as $|c|_{_0} = \sum _{i=1}^I |a_i|\, |\sigma _i|_{_0}$. We denote by ${{\mathcal {C}}}_k$ (resp. ${{\mathcal {C}}}_k(T)$) the space of simplicial k-chains in ${\mathbb {R}}^n$ (resp., supported in T). Spaces of differential k-forms $\omega$ in T are equipped with the norm

$$\begin{aligned} || \omega ||_{_0} = \sup _{c \,\in \,{{\mathcal {C}}}_k(T)} \frac{1}{|c|_{_0}} \,\Big | \int _c w \, \Big |. \end{aligned}$$

Note that if $\omega \in C^0 \varLambda ^k(T)$ then $||\omega ||_{_0} = ||\omega ||_{C^0}$, being the latter the maximum norm for $k=0$ (see, e.g., [12]).

We recall and extend some classical definitions to the context of polynomial interpolation of differential forms.

Definition 1

We say that the set $X^k_r= \{ \sigma _1,..., \sigma _{N_{k,r}}\}$ of k-simplices supported in T is unisolvent for the space ${\mathcal {P}}_r^- \varLambda ^k(T)$ if the weights $\int _{\sigma _j} \omega$ on the k-simplices $\sigma _j \in X^k_r$ are unisolvent degrees of freedom for $\omega \in {\mathcal {P}}_r^- \varLambda ^k(T)$, that is, if the unique differential k-form $\omega \in \mathcal P_r^- \varLambda ^k(T)$ verifying $\int _{\sigma _j} \omega =0$ for all $\sigma _j \in X^k_r$, is $\omega = 0$. We say that a unisolvent set $X^k_r$ of k-simplices supported in T is minimal if $\mathrm{card}\,(X^k_r) = \mathrm{dim}\, {\mathcal {P}}_r^- \varLambda ^k(T)$.

Definition 2

Given a basis ${\mathcal {B}} = \{ w_j \}_{j=1}^{N_{k,r}}$ for the space ${\mathcal {P}}_r^- \varLambda ^k(T)$ and a unisolvent set $X^k_r$ of k-simplices supported in T, the generalized Vandermonde matrix $V_{X^k_r,{\mathcal {B}}}$ is the matrix with entries

$$\begin{aligned} (V_{X^k_r,{\mathcal {B}}})_{i,j}= \int _{\sigma _i} w_j , \qquad \forall \, \sigma _i \in X^k_r, \qquad \forall \, w_j \in {\mathcal B}.\end{aligned}$$

Definition 3

Let $X^k_r$ be a unisolvent and minimal set for the space ${\mathcal {P}}_r^- \varLambda ^k(T)$. The collection $\{\mathtt{w}_j^{X^k_r}\}_{j=1}^{N_{k,r}}$ of differential k-forms of ${\mathcal {P}}_r^- \varLambda ^k({\mathbb {R}}^n)$ verifying $\int _{\sigma _i} {\texttt {w}}_j^{X^k_r} = \delta _{i,j}$ for $i,j =1,..., N_{k,r}$, is called the dual basis of ${\mathcal {P}}_r^- \varLambda ^k(T)$ associated with $X^k_r$.

Definition 4

Given a set $X^k_r= \{ \sigma _1,..., \sigma _{N_{k,r}}\}$ of $N_{k,r}$ distinct k-simplices in T, the interpolation problem associated with $X^k_r$ for a given differential k-form $\omega \in C^0 \varLambda ^k(T)$ consists in finding $\varPi ^k_r \omega \in {{\mathcal {P}}}_r^- \varLambda ^k(T)$, such that $\int _{\sigma _i} \varPi ^k_r \omega = \int _{\sigma _i} \omega$ for all $\sigma _i\in X^k_r$.

The interpolation problem associated with the set of k-simplices $X^k_r$ has a unique solution if and only if the generalized Vandermonde matrix $V_{X^k_r,{\mathcal {B}}}$ is invertible, for any basis ${{\mathcal {B}}}$ of the space ${{\mathcal {P}}}_r^- \varLambda ^k(T)$. In fact, since ${\mathcal {B}} = \{ w_j\}_{j=1}^{N^k_r}$ is a basis of ${\mathcal {P}}_r^- \varLambda ^k(T)$ and we look for $\varPi ^k_r \omega \in {\mathcal {P}}_r^- \varLambda ^k(T)$, the interpolation problem reduces to compute the vector $\mathbf{c} \in {{\mathbb {R}}}^{N^k_r}$ such that

$$\begin{aligned} \int _{\sigma _i} \left(\sum _{j=1}^{N^k_r} \mathbf{c}_j \, w_j\right) \, = \, \int _{\sigma _i} \omega , \qquad \forall \, \sigma _i \in X^k_r.\end{aligned}$$

Hence, the interpolation problem is equivalent to solve $V_{X^k_r,{\mathcal {B}}}\, \mathbf{c} = \mathbf{d}$, being $\mathbf{d}$ the vector of components $\mathbf{d}_i = \int _{\sigma _i} \omega \,$, with $\sigma _i \in X^k_r$ that has a unique solution if and only if the matrix $V_{X^k_r,{\mathcal {B}}}$ is invertible.

Definition 5

We say that we interpolate a differential k-form $\omega$ over the set $X^k_r$ of k-simplices in T when we construct $\varPi ^k_r \omega \in {{\mathcal {P}}}_r^- \varLambda ^k(T)$ as follows

$$\begin{aligned} \varPi ^k_r \,\omega = \sum _{\sigma _j \in X^k_r (T)} \Big (\int _{\sigma _j} \, \omega \, \Big )\, {\texttt {w}}_{j}^{X^k_r}, \end{aligned}$$

being $\{{\texttt {w}}_j^{X^k_r}\}_{j=1}^{N_{k,r}}$ the dual basis of ${\mathcal {P}}_r^- \varLambda ^k({\mathbb {R}}^n)$ associated with $X^k_r$.

The definition of the Lebesgue constant has been generalized in [2] to the case of interpolation of continuous differential k-forms $\omega \in C^0 \varLambda ^k(T)$ by polynomial k-forms $\omega \in {\mathcal {P}}_r^- \varLambda ^k(T)$, for $k\ge 0$ and a bound similar to (1) also holds for each $\omega \in C^0 \varLambda ^k(T)$ (see Prop. 2 in [2]).

Definition 6

(see [2]) Given a set $X^k_r= \{ \sigma _1,..., \sigma _{N_{k,r}}\}$ of $N_{k,r}$ k-simplices supported in T that is unisolvent and minimal for the space ${\mathcal {P}}_r^- \varLambda ^k(T)$, the Lebesgue function ${{\mathcal {L}}}_{X^k_r}:\mathcal C_k(T) \rightarrow {{\mathbb {R}}}^+$ is defined as

$$\begin{aligned} {{\mathcal {L}}}^k_{X^k_r}(c) = \sum _{j=1}^{N_{k,r}} \,|\sigma _j|_{_0} \left| \int _c {\texttt {w}}^{X^k_r}_j \right| \end{aligned}$$

with $\{{\texttt {w}}_j^{X^k_r}\}_{j=1}^{N_{k,r}}$ the dual basis of ${\mathcal {P}}_r^- \varLambda ^k(T)$ associated with $X^k_r$. The generalized Lebesgue constant is then defined as $\ \ \mathtt{\varLambda }^k_{X^k_r} =\sup _{c \in {{\mathcal {C}}}_k(T)} \frac{{\mathcal L}^k_{X^k_r}(c)}{|c|_{_0} }\,.$

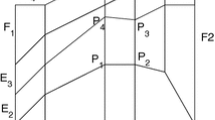
In Fig. 1 we illustrate the interaction among the principal ingredients at play in the polynomial interpolation. Given any basis $\{ w_j\}_j$ of the local polynomial space, and any set of unisolvent dofs, the values of these dofs for the elements of the given basis constitute the entries of the so-called Vandermonde matrix, simply denoted by V in the figure. This matrix has to be inverted once to construct the local dual basis $\{{\texttt {w}}_j\}_j$ associated with the selected set of dofs and its conditioning $\mathrm{cond}\, (V)$ depends on the local basis $\{w_j\}_j$. Hence it is convenient to look for an initial basis for which the condition number of the Vandermonde matrix is small enough to guarantee an accurate computation of the dual basis Note that the value of the Lebesgue constant is independent from the initial basis $\{w_j\}_j$ of the polynomial space, here ${\mathcal {P}}_r^- \varLambda ^k(T)$. The choice of this basis has influence on the values of the Vandermonde matrix conditioning when the approximation degree r increases. In this work we analyse different sets of weights, characterized by low values of the Lebesgue constant, in order to obtain a stable interpolation when the local discrete space is ${\mathcal {P}}_r^- \varLambda ^k(T)$ with $k=1$. This analysis is done locally, on one mesh element, before performing the approximation over the entire mesh. In the spirit of the geometrical construction proposed by Whitney, the question becomes how to construct different distributions of k-subsimplices, $k>0$, that are unisolvent and minimal for the interpolation in ${\mathcal {P}}_r^- \varLambda ^k(T)$ of differential k-forms and compare them in terms of the generalized Lebesgue constant.

Fig. 1

Simplified visualization of the interaction among decisive ingredients or steps for the success of the multivariate high-order polynomial approximation. The conditioning of the Vandermonde matrix V matters when computing the dual basis and the growth of the Lebesgue constant $\mathtt{\varLambda }$ with the approximation degree r has to be slow for a stable interpolation

4 Families of unisolvent and minimal 1-simplices

Starting from a distribution of nodes in T that are unisolvent and minimal for ${\mathcal {P}}_r^- \varLambda ^0(T)$, we wish to generate a set of small edges that are unisolvent and minimal for ${\mathcal {P}}_r^- \varLambda ^1(T)$. With the term uniform distribution, we indicate that the $N_{0,r} = \mathrm{dim} \,{\mathcal {P}}_r^- \varLambda ^0(T)$ nodes are those of the principal lattice of order r of T that is the set of points $\{\mathbf{x} \in T, \, \lambda _i(\mathbf{x}) \in \{\frac{j}{r}, j=0,...,r\}, \, \forall \, i = 0,...,n\}$. Any other distribution that does not fulfill this requirement will be referred to as nonuniform. In [20], a family of small k-simplices naturally associated with the uniform distribution of nodes in T has been defined. In [7] it has been proved that the set of the small k simplices is unisolvent, for any k. Following [1], a minimal and unisolvent subset $X^1_r$ of small 1-simplices can be identified.

$\diamondsuit .$ On the edges of a simplex T: In the interval $[-1,1]$ a classical nonuniform distribution of nodes is the one corresponding with the zeros of the Lobatto polynomials provided we add the interval extremities $\pm 1$. The Lobatto polynomial of degree s is defined as $Lb_s(t) = L_{s+1}'(t)$, where $L_{s+1}'(t)$ is the first derivative of the Legendre polynomial of degree $s+1$ in $t \in (-1,1)$. Therefore, Lobatto nodes $\{t_i\}_{i=0,r}$ associated with a degree r in $[-1,1]$ are the zeros of $(1-t^2)\, L_{r}'(t)= (1-t^2)\,{Lb_{r-1}(t)}$. It is well known that the Lobatto set of nodes is optimal for the scalar interpolation in $[-1,1]$, as proved in [10]. The nodal distribution of degree $r\ge 1$ on the edge $E= [\mathbf{x}_0,\mathbf{x}_1]$ is the set of nodes

$$\begin{aligned} X^0_r(E) = \{ \mathbf{x}_0 + (\mathbf{x}_1-\mathbf{x}_0)\,u_i\}_{i=0}^{r} , \quad u_i = \frac{i}{r} \quad (\mathrm{uniform})\,, \quad u_i = \frac{1+t_i}{2} \quad (\mathrm{Lobatto}). \end{aligned}$$

On the edge $E= [\mathbf{x}_0,\mathbf{x}_1]$, uniform and Lobatto nonuniform distributions $X^1_r(E)$ of small edges are obtained by chopping $[\mathbf{x}_0,\mathbf{x}_1]$ at, respectively, the uniform and Lobatto points (see an illustration drawn below for $r=4$)

It is well known that both the uniform and nonuniform distributions of small edges thus obtained in 1D are unisolvent and minimal for differential forms in ${\mathcal {P}}_r^- \varLambda ^1(T)$. Indeed, when $k=n=1$ we have ${\mathcal {P}}_r^- \varLambda ^1(T) \equiv {\mathbb {P}}_{r-1}(T)$. Numerical results on the conditioning of the Vandermonde matrix are given in Table 1. Assuming to move along E from $\mathbf{x}_0$ to $\mathbf{x}_1$, we label increasingly the small nodes of $X^0_r(E)$, from 0 (the small node that coincides with $\mathbf{x}_{0}$) to r (the small node that coincides with $\mathbf{x}_{1}$). By labeling the small edges $X^1_r(E)$ with the label of their first extremity, both sets $X^1_r(E)$ are characterized by the same small edge-to-small node connectivity table, whenever the spatial coordinates of the small nodes in $X^0_r(E)$ are. Therefore, we can construct the nonuniform set $X^1_r(E)$ by relying on the one defined for the uniform case, by just modifying the coordinates of the small edge extremities in order to have them coincident with those of the nodes belonging to the nonuniform Lobatto ones. This strategy will be extended to the faces F and to the interior of T, since all nonuniform distributions of small nodes we consider in T are obtained as suitable modifications of the uniform one.

Table 1 For $k=1$ in a segment E: Conditioning of the Vandermonde matrix $V_{X^{1}_{r},{\mathcal {B}}}$ with ${{\mathcal {B}}}$ the Bernstein basis of ${{\mathcal {P}}}^{-}_{r} \varLambda ^{1}(E)$ and $X^{1}_{r}$ the considered sets of 1-simplices

$\clubsuit .$ On the faces of a simplex T: To define $X^1_r(F)$ on a triangle F we wish to proceed with the same (chopping) strategy as the one adopted on the edges E of T. Before, we need to generate the set $X^0_r(F)$ of small nodes in F. As a first attempt, we use the Cartesian product of distributions of small nodes defined on two edges E of F as follows.

• 1. To construct the set $X^1_r(F)$ of the uniform distribution of 1-simplices in the triangle $F=[x_0,x_1,x_2]$, we start by considering the uniform distribution of nodes in F defined as

  $$\begin{aligned} X^0_r(F) = \{ \mathbf{x}_0 + (\mathbf{x}_{1}-\mathbf{x}_{0})\, u_i + (\mathbf{x}_2-\mathbf{x}_0)\,u_j, \quad i=0,...,r, \quad j = 0,...,r-i\,\} \end{aligned}$$

  with $u_i = i/r$ (see in Fig. 2 left, the green and red points obtained for $r=4$ in F). On each edge E, we define $X^1_r(E)$ as described in $\diamondsuit$. To generate the set $X^1_r({\mathring{F}})$ of small edges lying at the interior of F, we connect the points of $X^0_r(F)$ by segments parallel to the edges E of F that have one extremity in $\mathbf{x}_0$. Chop these segments at the intersection points in F (see in Fig. 2 center and right, respectively, the red nodes and the small edges obtained for $r=4$). The small nodes at the interior of F together with those on its boundary constitute a unisolvent and minimal set $X^0_r(F)$ of nodes for the interpolation of 0-forms, which is indeed the principal lattice of order r in $F=[x_0,x_1,x_2]$, defined as

  $$\begin{aligned} \begin{array}{r} X_r^0(F): = \Big \{ \mathbf{x} \in F \,: \,\lambda _i(\mathbf{x} ) \in \{ j/r \,: \, j \in \{0,1,\dots ,r\} \},\ \forall \, i\in \{0,1,2\} \Big \}\, \end{array} \end{aligned}$$

  in terms of the barycentric coordinates of F.

• 2. To construct the set $X^1_r(F)$ of the nonuniform distribution of 1-simplices associated with the Lobatto nodes on the edges E of F, we proceed similarly to the uniform case. We start by considering the Lobatto nonuniform distribution of nodes in F defined as

  $$\begin{aligned} X^0_r(F) = \{ \mathbf{x}_0 + (\mathbf{x}_1-\mathbf{x}_0)\, u_i + (\mathbf{x}_2-\mathbf{x}_0)\,u_j, \quad i=0,...,r, \quad j = 0,...,r-i\,\}\end{aligned}$$

  with $u_i = (1+t_i)/2$, being $t_i \in [-1,1]$ the roots of $(1-t^2) \,L'_{r}(t)$ (see in Fig. 3 left, the green points obtained for $r=4$ on the boundary of F). On each edge E, we define $X^1_r(E)$ as described in $\diamondsuit$. To generate the small edges $X^1_r({\mathring{F}})$ lying at the interior of F, as in the uniform case, we connect the small nodes of $X^0_r(F)$ by segments parallel to the edges E of F incident in $\mathbf{x}_0$ (see in Fig. 3 center and right, respectively, the red nodes and the small edges obtained for $r=4$). Note that the interior and the boundary points of $X^0_r(F)$ constitute a unisolvent and minimal set of nodes for the interpolation of 0-forms, which is the Lobatto distribution of degree r in F. In term of the barycentric coordinates of F the set of such points reads

  $$\begin{aligned} \begin{array}{r} X_r^0(F): = \Big \{ \mathbf{x} \in T \,: \,\lambda _i(\mathbf{x} ) \in \{ (1+t_j)/2 \,: \, j \in \{0,1,\dots ,r\}\},\qquad \\ \qquad \qquad \forall \, i\in \{1,2\}\,, \ \lambda _0(\mathbf{x}) = 1 - \sum _{i=1}^2 \lambda _i(\mathbf{x})\,\Big \}. \end{array} \end{aligned}$$

Fig. 2

Construction, in a triangle F, of a uniform and parallel distribution of small edges with ending points in the nodes of the principal lattice (here drawn for $r=4$). On the left, the points of the principal lattice $X^0_r(F)$; on the right, the set of edges $X^1_r(F)$

Fig. 3

Construction, in a triangle F, of a nonuniform distribution of small edges that are $\parallel$ to $E \in \varDelta _1(T)$, with ending points in the Lobatto nodes (here drawn for $r=4$). On the left, the set of points $X^0_r(F)$; on the right, the set of edges $X^1_r(F)$

The two sets $X^1_r(F)$ of small edges lying on a face F of T, associated with the uniform (in $\clubsuit .1$) and nonuniform Lobatto (in $\clubsuit .2$) distributions $X^0_r(F)$, are far from being “good” choices for the interpolation in ${\mathcal P}^-_r\varLambda ^1(F)$. This is also confirmed by the numerical results we present later. For the uniform set, this is an expected consequence of the well known fact that polynomial fitting on equally spaced nodes (and consequently on edges) can lead to poor interpolation properties for high degrees r. For the Lobatto points the reason can be related to the lack of rotational symmetry of the internal points (see Fig. 3). It is worth noting that Lobatto points can be straightforwardly extended to higher dimension, while keeping their property of being the zeros or the extrema of orthogonal polynomials, only on tensorial domains (Cartesian products of intervals).

In nontensorial domains, as triangles and tetrahedra here considered, there are three important requirements to fulfill with nodes:

• (i) interpolation nodes should be nonuniformly distributed and endowed of a rotational symmetry. In this way, wild oscillations are minimized and spectral convergence of the interpolation error is ensured for smooth functions;

• (ii) the generating algorithm should be simple, ideally with an explicit formula;

• (iii) the Lebesgue constant should not grow too fast with the degree r. So, to define reasonable sets $X^1_r$ in F or T, we need to start from distributions of nodes $X^0_r$ that are “good” for high order multivariate polynomial interpolation. The existing literature deals with the complex problem of generating interpolation points in a precise and efficient way by respecting the three requirements above, starting from the Lobatto distribution along the edges E of T (see [5, 13, 19, 21] and the references therein). Among all the possibilities, we consider the set of points introduced in [22]. The definition of such a set depends on a parameter $\alpha \in {{\mathbb {R}}}$. In the following, we refer to these points as the symmetrised Lobatto (sym. Lb) nodes when generated with $\alpha = 0$, and as the warp & blend (WB) nodes when $\alpha = \alpha _{opt}(r)$ (see Table 7 in [22]). They have been chosen because of their attractive features with respect to convergence and also because they are given through an explicit formula, which is of great practical interest, especially in three dimensions where the optimization procedures involved in the definitions of other nonuniform distributions of nodes become quite complicated. The generation of the symmetrised Lobatto and warp & blend distributions $X^{0}_{r}$ in a triangle or tetrahedron T is performed by running the Matlab software available in [22] for the triangle and in [14] for the tetrahedron. These nonuniform distributions of nodes in 2D and 3D are obtained by starting from the uniform one through a suitable vertex mapping, that induces a simplicial isomorphism between simplicial complexes, as we are going to explain.

• 3. To define $X^1_r(F)$ on a triangle $F= [x_0,x_1,x_2]$ by starting from the set $X^0_r(F)$ of symmetrised Lobatto or warp & blend nodes in F, we proceed as follows. Define in F the uniform distribution $X^0_{Un}(F) = X^0_r(F)$. Construct the set of small edges $X^1_{Un}(F) = X^1_r(F)$ corresponding with $X^0_{Un}(F)$ as described in $\clubsuit .1$ (see in Fig. 4 left, the red nodes and the small edges obtained for $r=4$). We thus have in F a simplicial complex $K = X^0_{Un}(F) \cup X^1_{Un}(F)$. We apply the vertex map $\varphi$ defined in [22] for the 2D case, that makes corresponding $X^0_{Un}(F)$ with the new (symmetrised Lobatto or warp & blend) point configuration, say $X^0_{new}(F)$, defined as $\varphi (X^0_{Un}(F) )$. Hence, the points on the edges E and at the interior of F are in the position corresponding with either the symmetrised Lobatto or the warp & blend ones (see in Fig. 4 center and right, respectively, the red nodes and the small edges obtained for $r=4$). We thus obtain the new simplicial complex $K' = X^0_{new}(F) \cup X^1_{new}(F)$ where $X^1_{new}(F)$ is the set of small segments on the edges and at the interior of F obtained from $X^1_{Un}(F)$ by following the node movement towards the new position. We then set $X^1_r(F) = X^1_{new}$. Note that the new small edges are thus stretched and, for those at the interior of F, their direction is no more parallel to the edges of F.

Fig. 4

Construction, in a triangle F, of a nonuniform distribution of small edges that are $\not \parallel$ to the edges E of F, with ending points in either the symmetrised Lobatto or warp & blend nodes (here drawn for the scalar interpolation of degree $r=4$). On the left, the uniform set of points and edges; at the center, points on edges and at the interior are moved in new positions thus defining the new set $X^{0}_{r}(F)$; on the right, the resulting set $X^1_r(F)$ of small edges in F

$\spadesuit .$ On a tetrahedron T: To define $X^1_r(T)$ on a tetrahedron T we wish to proceed with the same (chopping) strategy as the one adopted on the edges E and faces F of T. Before, we need to generate the set $X^0_r(T)$ of small nodes in T. To this purpose, we use either the uniform or the nonuniform symmetrised Lobatto and warp & blend distributions of small nodes in T and we proceed as follows.

• 1. To construct the set $X^1_r(T)$ of the uniform distribution of 1-simplices in the tetrahedron $T=[x_0,x_1,x_2,x_3]$, we start by considering the uniform distribution of nodes in T defined as

  $$\begin{aligned} \begin{array}{r} X^0_r(T) = \{ \mathbf{x}_0 + (\mathbf{x}_1-\mathbf{x}_0)\, u_i + (\mathbf{x}_2-\mathbf{x}_0)\,u_j+ (\mathbf{x}_3-\mathbf{x}_0)\,u_\ell ,\qquad \\ \quad i=0,...,r, \quad j = 0,...,r-i, \quad \ell = 0,..., r-i-j\}\end{array}\end{aligned}$$

  with $u_i = i/r$. On each edge E, we define $X^1_r(E)$ as described in $\diamondsuit$ and on each face F, we define $X^1_r(F)$ as explained before in $\clubsuit .1$ (see Fig. 2). Then, we repeat the uniform construction $\clubsuit .1$ for $X^1_r(L)$ over all $(r-1)$ triangular internal levels L which are parallel to the three faces F of T insisting in $\mathbf{x}_0$. These levels are located at the heights defined by the points on the edges of extremities $\mathbf{x}_0$ and $T\setminus F$, respectively. On each of these internal levels, we keep only the generated small edges that do not belong to one of the faces F of T. Note that, when moving from $\mathbf{x}_0$ towards $T\setminus F$, while remaining parallel to a face F, the degree for the node distribution on each new level has decreased of 1 with respect to the previous level. We thus obtain $X^1_r(T)$ collecting all the small edges defined on the edges, faces and internal levels of T.

• 2. To define $X^1_r(T)$ for the symmetrised Lobatto or warp & blend distribution $X^0_r(T)$ in T we consider the simplicial complex $K = X^0_{Un}(T) \cup X^1_{Un}(T)$, where $X^0_{Un}(T) = X^0_r(T)$ and $X^1_{Un}(T) = X^1_r(T)$ as defined for the uniform distribution in $\spadesuit .1$. We apply the vertex map $\Phi$ defined in [22] for the 3D case, that makes corresponding $X^0_{Un}(T)$ with the new (symmetrised Lobatto or warp & blend) point configuration, say $X^0_{new}(T)$ in T, defined as $\Phi (X^0_{Un}(T) )$. Hence, the points on the edges, faces and at the interior of T are in the new position corresponding with either the symmetrised Lobatto or the warp & blend ones. We thus obtain the new simplicial complex $K' = X^0_{new}(T) \cup X^1_{new}(T)$ where $X^1_{new}(T)$ is the set of small segments obtained from $X^1_{Un}(T)$ by following the node movement towards the new position. We then set $X^1_r(T) = X^1_{new}(T)$.

Even if these configurations are suitable perturbations of the uniform one, the proof of unisolvence and minimality for their associated set of weights becomes difficult. However, the Vandermonde matrix associated with any of the considered distributions is not singular. It can thus be inverted, and this yields the construction of the dual basis $\{\mathtt{w}^{X^1_r}_j\}_j$ associated with $X^1_r$, basis involved in Definition 6. The conditioning of $V_{X^1_r,{\mathcal {B}}}$ when ${{\mathcal {B}}}$ is the Bernstein basis of ${{\mathcal {P}}}^-_r \varLambda ^1(T)$ is presented in Table 2 (resp., Table 3) for the sets $X^1_r$ in a triangle (resp., in a tetrahedron) T.

Table 2 For $k=1$ in a triangle F: Conditioning of the Vandermonde matrix $V_{X^1_r,{\mathcal {B}}}$ with ${{\mathcal {B}}}$ the Bernstein basis of ${{\mathcal {P}}}^-_r \varLambda ^1(F)$ and $X^1_r$ the considered sets of 1-simplices in F

Table 3 For $k=1$ in a tetrahedron T: Conditioning of the Vandermonde matrix $V_{X^1_r,{\mathcal {B}}}$ with ${{\mathcal {B}}}$ the Bernstein basis of ${{\mathcal {P}}}^-_r \varLambda ^1(T)$ and $X^1_r$ the considered sets of 1-simplices in T

5 Estimation of the Lebesgue constant

In order to estimate $\mathtt{\varLambda }^k_{X^k_r}$, the supremum on the set of all k-chains in T is replaced by a maximum on the set $\varDelta _k({\tau })$ of k-simplices c of an additional mesh ${\tau }$ defined in T, finer enough to stabilize numerically the maximum. We thus have $\ \ \mathtt{\varLambda }^k_{X^k_r} \approx \max _{c \in \varDelta _k({\tau })} \frac{{{\mathcal {L}}}^k_{X^k_r}(c)}{|c|_0}.$ Hence, to estimate $\mathtt{\varLambda }^k_{X^k_r}$ we need to:

• 1. Choose a unisolvent and minimal set $X^k_r= \{ \sigma _1,..., \sigma _{N_{k,r}}\}$ of k-simplices in T.

• 2. Choose a basis ${\mathcal {B}} = \{ w_j \}_{j=1}^{N_{k,r}}$ for the space ${\mathcal {P}}_r^- \varLambda ^k(T)$.

• 3. Construct the generalized Vandermonde matrix $V_{X^k_r,{\mathcal {B}}}$ for all $i,j=1,...,N^k_r$, with $(V_{X^k_r,{\mathcal {B}}})_{i,j} = \int _{\sigma _i} w_j$ for all $i,j=1,...,N^k_r$,

• 4. Compute the inverse W of V by solving the linear system ${ W} = { V} \setminus { I}$ with I the identity matrix of size $N_{k,r}$.

• 5. Define a fine mesh $\tau$ in T and the set $Y_k = \{c_{\ell }\}_{\ell = 1,M_k}$ of the k-simplices of $\tau$.

Algorithm 1 has been used for a numerical estimation of the Lebesgue constant introduced in Definition 6, given $r \ge 1$ and $k >0$.

In this section we present some numerical results on the Lebesgue constant associated with these distributions of k-simplices in the standard simplex T, for $k=1$, in one, two and three dimensions. To construct the Vandermonde matrix, and thus the dual basis, we consider the basis $\{w_j\}_j$ of the space ${{\mathcal {P}}}^-_{r}\varLambda ^1(T)$ with elements $w_j$ that are products between Bernstein polynomials of degree $(r-1)$ and Whitney 1-forms of polynomial degree 1 (see for example [7]). With this choice of local basis, the conditioning of the Vandermonde matrix varies within an acceptable range of values when the approximation degree r increases (see Tables 2 and  3). Since the Lebesgue constant given in Definition 6 coincides, for $k=0$, with the classical one, we expect the results on this constant for $k=1$ to be similar, in a sense to be precised, to those for $k=0$ on the same (uniform or nonuniform) type of configurations of small supports for the degrees of freedom (the weights) of polynomial differential k-forms belonging to the discrete space.

5.1 In 1D

For the Lebesgue constant given in Definition 6, the computed values in the interval [0, 1] for $k=0$ and $k=1$ are given in Table 4. Numerical results on the Lebesgue constant confirm the interest of working with a nonuniform distribution of small edges supporting the degrees of freedom for the space ${\mathcal {P}}_r^- \varLambda ^1(T)$.

Table 4 For $k=0$ and $k=1$ in 1D: Lebesgue constants associated with the uniform and Lobatto distributions of nodes in a segment T for different numbers of subintervals $r \ge 2$. For $k=0$ (resp. $k=1$), r coincides with the degree (resp. the degree plus one) of the polynomial differential form

5.2 In 2D

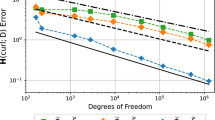
For the Lebesgue constant given in Definition 6, the computed values in the standard 2-simplex T in two dimensions for $k=1$ are given in Table 6 and are compared with those of Table 5 for $k=0$ taken from [5, 22]. The results for $k=1$ are obtained by considering the maximum on an independent test mesh $\tau$ in T, that is much finer than the one corresponding with degree 12 and not obtained as a refinement of those associated with the analysed degrees. In 2D, the mesh $\tau$ has been created by the software Triangle and it contains 513 edges with length between 0.011 and 0.120. It has to be said that by modifying the test mesh, the computed values can have slight changes in decimals but their magnitude order does not change. These values are visualized in Fig. 5  (for the same k) and in Fig. 6  (for the same type of distribution) in semi-log scale with respect to the polynomial degree r of the k-forms to be interpolated, with $k=0,1$, apart from those corresponding to the Lobatto distribution.

Table 5 For $k=0$ in 2D: Lebesgue constants associated with a uniform and nonuniform (symmetrised Lobatto and warp & blend) distributions of nodes in a triangle T for different polynomial degrees $r \ge 2$, as in [22]

Table 6 For $k=1$ in 2D: Lebesgue constants in a triangle T, associated with uniform and nonuniform distributions of small edges for different polynomial degrees $r\ge 2$. The ending points of the small edges are either in the uniform or in the nonuniform (symmetrised Lobatto, warp & blend or Lobatto) sets

Fig. 5

In 2D, the Lebesgue constant in semi-log scale as a function of the polynomial degree $r \ge 2$ of the k-form in a triangle T, with $k=0$ (left) and $k=1$ (right), respectively

Fig. 6

In 2D, the Lebesgue constant in semi-log scale as a function of the polynomial degree $r \ge 2$ of the k-form in a triangle T, uniform case (left) and nonuniform case (right), together with their fittings, respectively

By looking at Fig. 5, we remark that the difference of behavior in the Lebesgue constant for the uniform and nonuniform distribution, which is well-known for $k=0$, holds for $k=1$ too. For $k=0$, the warp & blend (WB) distribution is known to perform, in terms of the Lebesgue constant growth, as one of the best, among those that are nonuniform with rotational symmetry, thus better than the symmetrised Lobatto (Lb sym). In Table 6, we see that the behavior of the Lebesgue constant for the nonuniform distributions of small edges is analogous to that for the corresponding nonuniform distributions of nodes. The parallelism of the curves in Fig. 6 confirms the fact that the results on the Lebesgue constant for $k=1$ behave similarly to those for $k=0$ on the same (uniform or nonuniform) type of configuration of small supports for the degrees of freedom of the discrete space. An exponential behavior fits the curves in Fig. 6 for both $k=0,1$, with a smaller coefficient in front of r as soon as the distribution of the small simplices is nonuniform over T. Note that we have $\varLambda ^1_{X^1_r} > \varLambda ^0_{X^0_r}$ for all r and for sets of weights $X^0_r, X^1_r$ such that the ending points of the small edges supporting the weights of $X^1_r$ are the small nodes supporting the weights of $X_r^0$. Note that the considered distributions of small edges do not fulfill the rotational symmetry requirement over T. An improvement to get more symmetric layouts on a face of T or at the interior of T is possible but the strategy to perform it is not clear at the moment.

5.3 In 3D

Computed values for the Lebesgue constant in the standard 3-simplex T in three dimensions for $k=1$ are given in Table 8 and are compared with those of Table 7 for $k=0$ taken from [5, 22]. Again, the results for $k=1$ are obtained by estimating the supremum on an independent test mesh in T, much finer than the one corresponding with degree 9 and not obtained as a refinement of those associated with the analysed degrees. In 3D, the mesh $\tau$ has been created as uniform, with nodes in the principal lattice of degree 23 in T. It contains $13\,800$ edges with length varying between 0.0435 and 0.0615. The Lebesgue constant values, apart from those corresponding to the Lobatto distribution, are visualized in Fig. 7  (for the same k) and in Fig. 8  (for the same type of distribution) in semi-log scale with respect to the polynomial degree r of the k-forms to be interpolated, with $k=0,1$.

Table 7 For $k=0$ in 3D: Lebesgue constants associated with a uniform and nonuniform (symmetrised Lobatto and warp & blend) distributions of nodes in a tetrahedron T for different polynomial degrees $r\ge 2$, as in [22]

Table 8 For $k=1$ in 3D: Lebesgue constants in a tetrahedron T, associated with uniform and nonuniform distributions of small edges for different polynomial degrees $r \ge 2$. The ending points of the small edges are either in the uniform or in the nonuniform (Lobatto, symmetrised Lobatto or warp & blend) sets

Fig. 7

In 3D, the Lebesgue constant in semi-log scale as a function of the polynomial degree $r \ge 2$ of the k-form in a tetrahedron T with $k=0$ (left) and $k=1$ (right), respectively

Fig. 8

In 3D, the Lebesgue constant in semi-log scale as a function of the polynomial degree $r \ge 2$ of the k-form in a tetrahedron T, uniform case (left) and Lobatto nonuniform case (right), together with their fittings, respectively

By looking at Fig. 7, we remark that the behavior of the Lebesgue constant for the uniform and nonuniform distribution in two dimensions, also holds in three dimensions. Once again, the parallelism of the curves in Fig. 7, for $r>4$, confirms the fact that the results on the Lebesgue constant for $k=1$ behave similarly to those for $k=0$ on the same (uniform or nonuniform) type of configuration of small supports. An exponential behavior fits the curves in Fig. 7 for both $k=0,1$, with a smaller coefficient in front of r as soon as the distribution of the small simplices is nonuniform over T. Note that we have again $\varLambda ^1_{X^1_r} > \varLambda ^0_{X^0_r}$ for all r and for sets of weights $X^0_r, X^1_r$ such that the ending points of the small edges supporting the weights of $X^1_r$ are the small nodes supporting the weights of $X_r^0$.

By analyzing the values of the Lebesgue constant in Tables from 4 to 8, and their visualization, two interesting facts can be underlined. Firstly, the Lebesgue constant, for a given distribution of small k-simplices associated with a value of r, thus a given set $X^k_r$, grows with the spatial dimension n, namely

$$\begin{aligned} \varLambda _{\{X^k_r \text{ in } 3D\}}> \varLambda _{\{X^k_r \text{ in } 2D\}} >\varLambda _{\{X^k_r \text{ in } 1D\}} \end{aligned}$$

and this occurs for any r, k and distribution type of small k-simplices. Secondly, the fitting curve of the estimated Lebesgue constant curve changes of type with the dimension n. Precisely, for the uniform case, the behavior with r does not depend on n, namely, the curves that fit the results in Tables from 4 to 8, for the uniform configuration, are of exponential type for any n with the same coefficient 0.5 in front of r. This is not the case for the nonuniform cases: the small edges with ending points in either the symmetrised Lobatto or the warp & blend nodes yield to estimated Lebesgue constants with fitting curves going from polynomial ($n=1$) to exponential types for $n>1$, with coefficients 0.19 ($n=2$) and 0.30 ($n=3$) in front of r.

6 Dependence of the Lebesgue constant on the shape of the element

Unlike the case $k=0$, the generalized Lebesgue constant for $k=1$ does depend on the shape of the element T. Let ${{\hat{T}}}$ be a non degenerate n-simplex of ${\mathbb {R}}^n$, for instance, the standard one, and let us denote $F_{T}: {{\hat{T}}} \rightarrow T$ the affine invertible transformation between ${{\hat{T}}}$ and T. Such map is defined by $F_T(\hat{\mathbf{x}})= B_T \hat{\mathbf{x}} + \mathbf{b}_T$, with $B_T \in {\mathbb {R}}^{n \times n}$ and $\mathbf{b}_T \in {\mathbb {R}}^n$, and satisfies $T=F_T({{\hat{T}}})$. It is worth noting that if $X^k_{r,Un}({{\hat{T}}}) = \{ {{\hat{\sigma }}}_1, \dots , {{\hat{\sigma }}}_{N_{k,r}} \}$ then $\sigma _j = F_T({{\hat{\sigma }}}_j) \in X^k_{r,Un}({{\hat{T}}})$ for each $j=1,\dots , N_{k,r}$ and $F_T\left( X^k_{r,Un}({{\hat{T}}})\right) =X^k_{r,Un}(T)$. The vertex map that defines the symmetrised Lobatto nodes and the one that defines the warp & blend ones are given in terms of the barycentric coordinates of the vertices hence in both cases it holds that

$$\begin{aligned} F_T\left( X^k_{r,new}({{\hat{T}}})\right) =X^k_{r,new}(T)\,. \end{aligned}$$

Moreover if $X^k_{r,new}({{\hat{T}}})$ is a unisolvent and minimal set for the space ${\mathcal {P}}_r^- \varLambda ^k({{\hat{T}}})$ then so is $X^k_{r,new}(T)$ for ${\mathcal {P}}_r^- \varLambda ^k(T)$ since $F_T$ is invertible.

Lemma 1

Let $X_r^k({{\hat{T}}})=\{ {{\hat{\sigma }}}_1, \dots , {{\hat{\sigma }}}_{N_{k,r}} \}$ be a unisolvent and minimal set for the space ${\mathcal {P}}_r^- \varLambda ^k({{\hat{T}}})$ and put $X_r^k(T)=\{ \sigma _1, \dots , \sigma _{N_{k,r}} \}$ with $\sigma _j=F_T({{\hat{\sigma }}}_j)$ for $j=1,\dots , N_{k,r}$. For each $j=1,\dots , N_{k,r}$, let $\mathtt{w}_j^{X_r^k({{\hat{T}}})}$ (resp. ${\texttt {w}}_j^{X_r^k(T)}$) be the element of the dual basis of ${\mathcal {P}}_r^-\varLambda ^1({{\hat{T}}})$ (resp. ${\mathcal {P}}_r^-\varLambda ^1( T)$) associated with ${{\hat{\sigma }}}_j$ (resp. $\sigma _j$). Then

$$\begin{aligned} \mathtt{w}_j^{X_r^k({{\hat{T}}})} = F_T^* \, \mathtt{w}_j^{X_r^k(T)} \end{aligned}$$

where $F_T^*$ denotes the pullback induced by the affine map $F_T$.⁴

Proof

By definition of dual basis, $\mathtt{w}_j^{X_r^k({{\hat{T}}})}$ is the unique element of ${\mathcal {P}}_r^-\varLambda ^k({{\hat{T}}})$ such that

$$\begin{aligned} \int _{{{\hat{\sigma }}}_i} \mathtt{w}_j^{X_r^k({{\hat{T}}})} = \delta _{i,j}\,. \end{aligned}$$

Since $\mathtt{w}_j^{X_r^k(T)} \in {\mathcal {P}}_r^-\varLambda ^k( T)$ and $F_T$ is an affine map then $F_T^* \, \mathtt{w}_j^{X_r^k(T)} \in {\mathcal {P}}_r^-\varLambda ^k( {{\hat{T}}})$ (see, e.g. [3]). Moreover

$$\begin{aligned} \int _{{{\hat{\sigma }}}_i} F_T^* \, \mathtt{w}_j^{X_r^k(T)} = \int _{F_T(\hat{\sigma }_i)} \mathtt{w}_j^{X_r^k(T)} = \int _{\sigma _i} \mathtt{w}_j^{X_r^k(T)} = \delta _{i,j} \end{aligned}$$

where the last equality follows from the fact that $\mathtt{w}_j^{X_r^k(T)}$ is the element of the dual basis of $\mathcal P_r^-\varLambda ^k( T)$ associated with $\sigma _j$. Hence $\mathtt{w}_j^{X_r^k({{\hat{T}}})}=F_T^* \, \mathtt{w}_j^{X_r^k(T)}$. $\square$

Lemma 2

Let ${{\hat{T}}}$ and T be two non degenerate n-simplices of ${\mathbb {R}}^n$ and $F_{T}: {{\hat{T}}} \rightarrow T$ be the affine invertible transformation between ${{\hat{T}}}$ and T defined by $F_T(\hat{\mathbf{x}})= B_T \hat{\mathbf{x}} + \mathbf{b}_T$, with $B_T \in {\mathbb {R}}^{n \times n}$ and $\mathbf{b}_T \in {\mathbb {R}}^n$. For each 1-simplex ${{\hat{e}}}$ supported in ${{\hat{T}}}$

$$\begin{aligned} |F_T({{\hat{e}}})|_{_0} \le \Vert B_T\Vert _2 |{{\hat{e}}}|_{_0} \end{aligned}$$

(2)

and

$$\begin{aligned} |{{\hat{e}}}|_{_0} \le \Vert B_T^{-1}\Vert _2 |F_T({{\hat{e}}})|_{_0} \end{aligned}$$

(3)

where $\Vert \cdot \Vert _2$ denote the matrix norm induced by the Euclidean vector norm.

Proof

Let ${{\hat{e}}}=[\hat{\mathbf{p}}, \hat{\mathbf{q}}]$ be a 1-simplex supported in ${{\hat{T}}}$. Then the 1-simplex $F_T({{\hat{e}}})=[F_T(\hat{\mathbf{p}}), F_T(\hat{\mathbf{q}})]$ is supported in T and

$$\begin{aligned} |F_T({{\hat{e}}})|_{_0}= \Vert F_T(\hat{\mathbf{q}} )- F_T(\hat{\mathbf{p}})\Vert _2= \Vert B_T(\hat{\mathbf{q}} - \hat{\mathbf{p}})\Vert _2 \le \Vert B_T\Vert _2 \Vert \hat{\mathbf{q}} - \hat{\mathbf{p}}\Vert _2= \Vert B_T\Vert _2 |{{\hat{e}}}|_{_0} \,. \end{aligned}$$

The proof of (3) is analogous since $F_T^{-1}:T \rightarrow {{\hat{T}}}$ is the affine map defined by $F_T^{-1}(\mathbf{x})=B_T^{-1}(\mathbf{x}- \mathbf{b}_T)$. $\square$

Proposition 1

Let ${{\hat{T}}}$ and T be two non degenerate n-simplices of ${\mathbb {R}}^n$ and $F_{T}: {{\hat{T}}} \rightarrow T$ the affine invertible transformation between ${{\hat{T}}}$ and T defined by $F_T(\hat{\mathbf{x}})= B_T \hat{\mathbf{x}} + \mathbf{b}_T$, with $B_T \in {\mathbb {R}}^{n \times n}$ and $\mathbf{b}_T \in {\mathbb {R}}^n$. Let $X_r^1({{\hat{T}}})= \{ {{\hat{\sigma }}}_1, \dots , {{\hat{\sigma }}}_{N_{1,r}} \}$ be a unisolvent and minimal set for ${\mathcal {P}}_r^-\varLambda ^1({{\hat{T}}})$ and $X_r^1(T)=\{ \sigma _1, \dots , \sigma _{N_{1,r}} \}$ with $\sigma _j=F_T({{\hat{\sigma }}}_j)$ for $j=1,\dots , N_{1,r}$. Then

$$\begin{aligned} \varLambda ^1_{X_r^1(T)} \le \Vert B_T\Vert _2 \Vert B_T^{-1}\Vert _2 \, \varLambda ^1_{X_r^1({{\hat{T}}})}. \end{aligned}$$

(4)

Proof

By definition of the Lebesgue constant, the fact that $c\in \mathcal C_1(T)$ if and only if $c=F_T({{\hat{c}}})$ for some ${{\hat{c}}} \in \mathcal C_1({{\hat{T}}})$ and in particular $\sigma _j=F_T({{\hat{\sigma }}}_j)$, the definition of pullback, Lemma 1, (2) and (3) one has:

$$\begin{aligned} \begin{array}{rcl} \varLambda ^1_{X_r^1(T)}&{} = &{} \sup _{c \in {{\mathcal {C}}}_1(T)} \displaystyle \frac{1}{|c|_{_0}} \sum _{j=1}^{N^1_r}\, |\sigma _j|_{_0} \left| \int _{c} \mathtt{w}^{X^1_r(T)}_j \right| \\ &{} = &{} \sup _{{{\hat{c}}} \in {{\mathcal {C}}}_1({{\hat{T}}})} \displaystyle \frac{1}{|F_T({{\hat{c}}})|_{_0}} \sum _{j=1}^{N^1_r} \,| F_T({{\hat{\sigma }}}_j)|_{_0} \left| \int _{F_T({{\hat{c}}})} \mathtt{w}_j^{X^1_r({{\hat{T}}})} \right| \\ &{} = &{} \sup _{{{\hat{c}}} \in {{\mathcal {C}}}_1({{\hat{T}}})} \displaystyle \frac{1}{|F_T({{\hat{c}}})|_{_0}} \sum _{j=1}^{N^1_r} \,| F_T( {{\hat{\sigma }}}_j)|_{_0} \left| \int _{{{\hat{c}}}} F_T^*\mathtt{w}_j^{X^1_r(T)} \right| \\ &{} = &{} \sup _{{{\hat{c}}} \in {{\mathcal {C}}}_1({{\hat{T}}})} \displaystyle \frac{1}{|F_T({{\hat{c}}})|_{_0}} \sum _{j=1}^{N^1_r} \,| F_T( {{\hat{\sigma }}}_j)|_{_0} \left| \int _{{{\hat{c}}}} \mathtt{w}_j^{X^1_r({{\hat{T}}})} \right| \\ &{} \le &{} \sup _{{{\hat{c}}} \in {{\mathcal {C}}}_1({{\hat{T}}})} \displaystyle \frac{1}{|F_T({{\hat{c}}})|_{_0}} \sum _{j=1}^{N^1_r} \,\Vert B_T\Vert _2 | {{\hat{\sigma }}}_j|_{_0}\left| \int _{{{\hat{c}}}} \mathtt{w}_j^{X^1_r({{\hat{T}}})} \right| \\ &{} \le &{} \sup _{{{\hat{c}}} \in {{\mathcal {C}}}_1({{\hat{T}}})} \displaystyle \frac{\Vert B_T^{-1}\Vert _2}{|{{\hat{c}}}|_{_0}} \sum _{j=1}^{N^1_r} \,\Vert B_T\Vert _2 | {{\hat{\sigma }}}_j|_{_0} \left| \int _{{{\hat{c}}}} \mathtt{w}_j^{X^1_r({{\hat{T}}})} \right| \\ &{} = &{} \Vert B_T\Vert _2 \Vert B_T^{-1}\Vert _2 \, \sup _{{{\hat{c}}} \in {{\mathcal {C}}}_1({{\hat{T}}})} \displaystyle \frac{1}{|{{\hat{c}}}|_{_0}} \sum _{j=1}^{N^1_r} \, | {{\hat{\sigma }}}_j|_{_0} \left| \int _{{{\hat{c}}}} \mathtt{w}_j^{X^1_r({{\hat{T}}})} \right| \\ &{} = &{} \Vert B_T\Vert _2 \Vert B_T^{-1}\Vert _2 \, \varLambda ^1_{X_r^1({{\hat{T}}})}. \end{array} \end{aligned}$$

$\square$

Table 9 reports the quantity $\varLambda ^1_{X_r^1}(T) / \varLambda ^1_{X_r^1}({{\hat{T}}})$ when ${{\hat{T}}}$ is the standard 3-simplex and T is the equilateral tetrahedra with length of edges equal 2 centered in the origin. The vertices of T are $(-1, -1/\sqrt{3}, -1/\sqrt{6})$, $(1, -1/\sqrt{3}, -1/\sqrt{6})$, $(0, 2/\sqrt{3}, -1/\sqrt{6})$, and $(0, 0, 3/\sqrt{6})$. We consider the uniform, the symmetrised Lobatto and the warp & blend distributions of nodes, and different values of r. The quotient $\varLambda ^1_{X_r^1}(T) / \varLambda ^1_{X_r^1}({{\hat{T}}})$ is always lower than $\Vert B_T\Vert _2 \Vert B_T^{-1} \Vert _2$ that in this case is equal to 2.

Table 9 The ratio $\varLambda ^1_{X_r^1}(T) / \varLambda ^1_{X_r^1}({{\hat{T}}})$ when T is the equilateral tetrahedron with length of edges equal 2 centered in the origin for different values of r and different different distributions of nodes. In this case $\Vert B_T\Vert _2 \Vert B_T^{-1} \Vert _2 = 2$

We consider also the case in which ${{\hat{T}}}$ is the standard 3-simplex, and $T=T_\delta$ is the tetrahedron of vertices (0, 0, 0), $(1-2\delta , \delta ,\delta )$, $(\delta , 1-2\delta , \delta )$, $(\delta , \delta , 1-2\delta )$, with $\delta \in [0,1/3)$. (In particular ${{\hat{T}}} =T_0$). In this case $F_{T_\delta }(\hat{\mathbf{x}}) = B_\delta (\hat{\mathbf{x}})$ with $B_\delta = \left[ \begin{array}{ccc}1-2\delta &{} \delta &{} \delta \\ \delta &{} 1- 2\delta &{} \delta \\ \delta &{} \delta &{} 1- 2\delta \end{array} \right]$ and $\Vert B_\delta \Vert _2 \Vert B_\delta ^{-1} \Vert _2 = 1/(1-3 \delta )$. In this family of tetrahedra the height is constant area the area of the base decreases to zero when $\delta$ tends to 1/3. Clearly $\Vert B_\delta \Vert _2 \Vert B_\delta ^{-1} \Vert _2$ tends to infinity when $\delta$ tends to 1/3. Table 10 reports the quotient $\varLambda ^1_{X_r^1}(T_\delta ) / \varLambda ^1_{X_r^1}({{\hat{T}}})$ for different values of $\delta$, $r=7$, and the distributions of nodes uniform, symmetrised Lobatto and warp & blend. The quotient increases when the base shrinks, nevertheless it always remains below the theoretical bound.

Table 10 The quantity $\Vert B_\delta \Vert _2 \Vert B_\delta ^{-1} \Vert _2$ and the ratio $\varLambda ^1_{X_{7}^1}(T_\delta ) / \varLambda ^1_{X_{7}^1}({{\hat{T}}})$ when $T_\delta$ is the tetrahedron of vertices (0, 0, 0), $(1-2 \delta , \delta ,\delta )$, $(\delta ,1-2 \delta ,\delta )$, $(\delta ,\delta ,1-2 \delta )$, for different values of $\delta \in [0,1/3)$ and different distributions of nodes

Remark 1

Estimate (4) does not depend on the distribution of nodes. A sharper bound can be obtained introducing the following quantity depending on $X_r^1=\{ {{\hat{\sigma }}}_1,\dots , \hat{\sigma }_{N_{1,r}}\}$. If ${{\hat{\sigma }}}_j = [\hat{\mathbf{p}}_j, \hat{\mathbf{q}}_j]$ we denote

$$\begin{aligned} C_{T,X_r^1}{:}{=} \max _{j=1,\dots ,N_{1,r}} \left\| B_T \frac{\hat{\mathbf{q}}_j - \hat{\mathbf{p}}_j}{\Vert \hat{\mathbf{q}}_j - \hat{\mathbf{p}}_j\Vert _2} \right\| _2. \end{aligned}$$

Then for all $j =1,\dots ,N_r^1$

$$\begin{aligned} |F_T({{\hat{\sigma }}}_j)|_0 = \Vert B_T (\hat{\mathbf{q}}_j - \hat{\mathbf{p}}_j)\Vert _2 \le C_{T,X_r^1} |{{\hat{\sigma }}}_j|_0. \end{aligned}$$

Using in the proof of Proposition 1 this estimate instead of (4) it follows that

$$\begin{aligned} \varLambda ^1_{X_r^1(T)} \le C_{T,X_r^1} \Vert B_T^{-1}\Vert _2 \, \varLambda ^1_{X_r^1({{\hat{T}}})}. \end{aligned}$$

Table 11 reports the quantity $\varLambda ^1_{X_{7}^1}(T_\delta ) / \varLambda ^1_{X_{7}^1}({{\hat{T}}})$ and the ratio $\varLambda ^1_{X_{7}^1}(T_\delta ) / \varLambda ^1_{X_{7}^1}({{\hat{T}}})$ when $X_{7}^1$ corresponds to the uniform distribution of nodes. We consider also in this case the tetrahedron of vertices (0, 0, 0), $(1-2 \delta , \delta ,\delta )$, $(\delta ,1-2 \delta ,\delta )$, $(\delta ,\delta ,1-2 \delta )$ for different values of $\delta \in [0,1/3)$.

Table 11 The quantity $C_{T,X_7^1} \Vert B_T^{-1}\Vert _2$ and the ratio $\varLambda ^1_{X_{7}^1}(T_\delta ) / \varLambda ^1_{X_{7}^1}({{\hat{T}}})$ when $X_{7}^1$ corresponds to the uniform distribution of nodes and $T_\delta$ is the tetrahedron of vertices (0, 0, 0), $(1-2 \delta , \delta ,\delta )$, $(\delta ,1-2 \delta ,\delta )$, $(\delta ,\delta ,1-2 \delta )$ considering different values of $\delta \in [0,1/3)$

7 Stability of the interpolation

We now extend to the case $k>0$ a classical result for $k=0$, that relates the Lebesgue constant with the stability of Lagrangian interpolation. We are interested in studying the stability of the interpolation in ${\mathcal {P}}_r^- \varLambda ^1(T)$, namely, in stating how much perturbations of $\omega$ are transmitted to $\varPi ^1_r \omega$.

Proposition 2

Let $\omega$, ${\widetilde{\omega }}$ be smooth k-forms such that $|| \omega - {{\widetilde{\omega }}} ||_{_0} \le \varepsilon \,.$ Then

$$\begin{aligned} || \varPi ^k_r \omega - \varPi ^k_r {\widetilde{\omega }} ||_{_0} \le \varepsilon \, \mathtt{\varLambda }_{X_r^k}^k , \end{aligned}$$

(5)

where $\mathtt{\varLambda }_{X_r^k}^k$ is the generalized Lebesgue constant defined in (6).

Proof

of Proposition 2. Being $\varPi ^k_r \omega$ and $\varPi ^k_r {\widetilde{\omega }}$ two polynomial differential k-forms, we consider the quantity $||\varPi ^k_r \omega - \varPi ^k_r {\widetilde{\omega }} ||_{_0}$, namely

$$\begin{aligned}\begin{array}{ll} || \varPi ^k_r \, \omega - \varPi ^k_r \, {{\widetilde{\omega }}} ||_{_0} &{} = \displaystyle \sup _{c \,\in \,{\mathcal {C}}_k(T)} \frac{1}{|c|_{_0}} \Big | \int _c (\varPi ^k_r \omega - \varPi ^k_r {{\widetilde{\omega }}} ) \Big | = \displaystyle \sup _{c \,\in \,{\mathcal {C}}_k(T)} \frac{1}{|c|_{_0}} \Big | \int _c \varPi ^k_r (\omega - \widetilde{\omega }) \Big |\\ &{} =\displaystyle \sup _{c \,\in \,{\mathcal {C}}_k(T)} \frac{1}{|c|_{_0}} \Big | \int _c \Big [\sum _{\sigma \in X^k_r} \Big (\int _{\sigma } (\omega - {{\widetilde{\omega }}})\Big ) \varphi _{\sigma }\Big ] \Big |\,\\ &{} = \displaystyle \sup _{c \,\in \,{\mathcal {C}}_k(T)} \frac{1}{|c|_{_0}} \Big |\sum _{\sigma \in X^k_r} \int _{\sigma } \left( \omega - {{\widetilde{\omega }}}\right) \int _c \varphi _{\sigma } \Big |. \end{array} \end{aligned}$$

By using the triangular inequality and, then, the fact that $X_r^k (T) \subset {\mathcal {C}}_k(T)$, from $||\omega - {\tilde{\omega }}||_{_0} \le \epsilon$ we get

$$\begin{aligned} \begin{array}{ll} || \varPi ^k_r \omega - \varPi ^k_r {{\widetilde{\omega }}} ||_{_0} &{} \le \displaystyle \sup _{c \, \in \, {\mathcal {C}}_k(T)} \frac{1}{|c|_{_0}} \sum _{\sigma \in X^k_r} \Big | \int _{\sigma } \left( \omega - {{\widetilde{\omega }}}\right) \Big | \, \Big | \int _c \varphi _{\sigma } \Big | \\ &{} = \displaystyle \sup _{c \,\in \,{\mathcal {C}}_k(T)} \frac{1}{|c|_{_0}} \sum _{\sigma \in X^k_r} \frac{|\sigma |_{_0}}{|\sigma |_{_0}} \,\Big | \int _{\sigma } \left( \omega - {{\widetilde{\omega }}}\right) \Big | \, \Big | \int _c \varphi _{\sigma } \Big | \\ &{} \le \varepsilon \displaystyle \sup _{c \,\in \,{\mathcal {C}}_k(T)} \frac{1}{|c|_{_0}} \sum _{\sigma \in X^k_r} | \sigma |_{_0}\, \Big | \int _c \varphi _{\sigma } \Big |\,, \end{array}\end{aligned}$$

thus the result, by recalling the expression stated in (6). $\square$

Proposition 2 provides a way to estimate the Lebesgue constant $\mathtt{\varLambda }_{X_r^k}^k$. On the same reference mesh $\tau$, that has been used in (6) to compute the Lebesgue constants, we estimate $\frac{1}{\epsilon }\, ||\varPi ^1_r \omega - \varPi ^1_r {\widetilde{\omega }} ||_{_0}$. We thus consider two regular 1-forms such that $\frac{1}{| \sigma |_{_0}}|\int _{\sigma }( \omega - {\widetilde{\omega }}) | \le \varepsilon$ for all $\sigma \in X_r^1 (T)$. Indeed, what is important here is not the expression of $\omega$, ${\tilde{\omega }}$, but the weights of their difference. We thus set

$$\begin{aligned} \frac{1}{| \sigma |_{_0} }\int _{\sigma }( \omega - {\widetilde{\omega }}) = (2\mathtt {*rand(1)}-1) \mathtt {*} \varepsilon , \qquad \varepsilon = 10^{-m}, \qquad m = 1, 2, \ldots , 8 \end{aligned}$$

being $\mathtt{rand}(1)$ the $\mathtt{Matlab}$ command that gives random real positive values lower than 1. In Fig. 9 we report the quantities $\frac{1}{\varepsilon } ||\varPi ^1_r \omega - \varPi ^1_r {\widetilde{\omega }} ||_{_0}$ and compare them with their relative Lebesgue constants. For the sake of brevity, we have reported only the cases $\varepsilon = 10^{-2}$, $\varepsilon = 10^{-5}$ and $\varepsilon = 10^{-8}$. According to (5) results are independent from $\varepsilon$.

Distribution of edges constructed from nodes that are more suitable for high order Lagrange interpolation than the uniform ones, such as the symmetrised Lobatto and the warp & blend, improve the stability for $k=1$. The asymmetry of the distribution of nodes with respect to the vertices of T in the Lobatto grid results in a very fast increase of the amplification of the perturbation. Results confirm the behavior predicted by the Lebesgue constant. The amplification of the perturbation on the data with respect to the polynomial degree increases as the Lebesgue constant does. Indeed, a visual comparison in semilogarithmic scale as in Fig. 9 shows that $\frac{1}{\epsilon }\,||\varPi ^1_r \omega - \varPi ^1_r \tilde{\omega }||_{_0}$ grow simultaneously to the Lebesgue constant; we hence deduce that estimate (5) is sharp. In particular, Fig. 9 (left) depicts data relative to the uniform and warp & blend distributions. Data relative to symmetrised Lobatto are not shown as they offer a very similar behavior to that of warp & blend. The same computation for the tridimensional case, Fig. 9, right, shows a comparable behavior. The value of the Lebesgue constant estimated by (6) is thus an upper bound of $\frac{1}{\epsilon } \,||\varPi ^1_r \omega - \varPi ^1_r \tilde{\omega }||_{_0}$, for any $\epsilon$, the numerical one.

Fig. 9

Comparison between the estimated Lebesgue constants (straight lines) and the numerical ones, computed through the stability test (non-continuous lines) for small edges associated with uniform (red) and warp & blend (blue) node distributions, in 2D (left) and 3D (right)

8 Conclusions

We have proposed a flexible rule to select a minimal and unisolvent set of small edges to interpolate a differential 1-form $\omega$ using high order Whitney finite elements. The interpolating polynomial differential form has the same weights (integrals on the small edges) as $\omega$. Weights are alternative degrees of freedom to moments for high order trimmed polynomial spaces. We have tried different choices of supports for the weights and we have studied the growth of the generalized Lebesgue constant when increasing the polynomial degree r and the degree k of the polynomial differential forms. We have studied the dependence of the generalized Lebesgue constant on the shape of the simplex. Finding a minimal and unisolvent distribution of small edges that is optimized on the basis of a given property has not been considered in the present work.

Numerical results have evidenced the importance of the Lebesgue constant in qualifying a good distribution of small simplices supporting the weights. They are in agreement with the fact that to have a lower value of this constant, a nonuniform distribution of the geometrical supports for dofs is determinant both for $k=0,1$. They have also revealed that the behavior of the Lebesgue constant for $k=1$ is similar to that for $k=0$ (parallel curves), on each configuration we have considered. Moreover, for a given degree r, the value of this constant grows with k, once we fix the ambient dimension n, and with n, once we fix the degree k of the differential form. The stability analysis confirms that the amplification of the perturbations on the data behaves, with respect to the polynomial degree r, as the Lebesgue constant does. Interpolation results give further confidence on the quality of the warp & blend distribution. The very natural extension of this approach to differential k-forms for $0<k<n$ is also ongoing and first results for $k=2$ in 3D are in agreement with those provided in this work for $k=0,1$.