Skip to main content
SpringerLink
Log in

Spectral collocation method for nonlinear Riemann–Liouville fractional differential system

  • Published:
Calcolo Aims and scope Submit manuscript

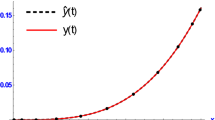
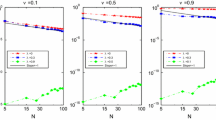
Abstract

The spectral collocation method is investigated for the system of nonlinear Riemann–Liouville fractional differential equations (FDEs). The main idea of the presented method is to solve the corresponding system of nonlinear weakly singular Volterra integral equations obtained from the system of FDEs. In order to carry out convergence analysis for the presented method, we investigate the regularity of the solution to the system of FDEs. The provided convergence analysis result shows that the presented method has spectral convergence. Theoretical results are confirmed by numerical experiments. The presented method is applied to solve multi-term nonlinear Riemann–Liouville fractional differential equations and multi-term nonlinear Riemann–Liouville fractional integro-differential equations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Brunner, H.: Collocation Methods for Volterra Integral and Related Functional Differential Equations, vol. 15. Cambridge University Press, Cambridge (2004)

    Book  Google Scholar 

  2. Bu, W., Xiao, A.: An h-p version of the continuous Petrov–Galerkin finite element method for Riemann–Liouville fractional differential equation with novel test basis functions. Numer. Algorithms 81, 529–545 (2019)

    Article  MathSciNet  Google Scholar 

  3. Canuto, C., Hussaini, M.Y., Quarteroni, A., Zang, T.A.: Spectral Methods (Fundamental in Single Domains). Springer, Berlin (2006)

    Book  Google Scholar 

  4. Caputo, M., Mainardi, F.: A new dissipation model based on memory mechanism. Pure Appl. Geophys. 91(1), 134–147 (1971)

    Article  Google Scholar 

  5. Denton, Z., Vatsala, A.S.: Monotone iterative technique for finite systems of nonlinear Riemann-Liouville fractional differential equations. Opusc. Math. 31(3), 327–339 (2011)

    Article  MathSciNet  Google Scholar 

  6. Diethelm, K.: The Analysis of Fractional Differential Equations. Springer, Berlin (2010)

    Book  Google Scholar 

  7. Faires, J.D., Burden, R.L.: Numerical Methods. Brooks/Cole Pub. Co., Grove (1998)

    MATH  Google Scholar 

  8. Finat, J., Cuesta-Montero, E.: Image processing by means of a linear integro-differential equation. In: Visualization, Imaging and Image processing, Vol. 1, IASTED (2003)

  9. Graef, J.R., Kong, L., Wang, M.: A Chebyshev spectral method for solving Riemann–Liouville fractional boundary value problems. Appl. Math. Comput. 241, 140–150 (2014)

    MathSciNet  MATH  Google Scholar 

  10. Gu, Z.: Spectral collocation method for system of weakly singular Volterra integral equations. Adv. Comput. Math. 45, 2677–2699 (2019)

    Article  MathSciNet  Google Scholar 

  11. Gu, Z.: Spectral collocation method for nonlinear Caputo fractional differential system. Adv. Comput. Math. 46, 1–21 (2020). https://doi.org/10.1007/s10444-020-09808-9

    Article  MathSciNet  MATH  Google Scholar 

  12. Gu, Z.: Spectral collocation method for nonlinear Riemann–Liouville fractional differential equations. Appl. Numer. Math. 157, 654–669 (2020)

    Article  MathSciNet  Google Scholar 

  13. Jin, B., Lazarov, R., Liu, Y., Zhou, Z.: The Galerkin finite element method for a multi-term time-fractional diffusion equation. J. Comput. Phys. 281(15), 825–843 (2016)

    MathSciNet  MATH  Google Scholar 

  14. Jin, B., Lazarov, R., Lu, X., Zhou, Z.: A simple finite element method for boundary value problems with a Riemann–Liouville derivative. J. Comput. Appl. Math. 293, 94–111 (2016)

    Article  MathSciNet  Google Scholar 

  15. Kopteva, N., Stynes, M.: Analysis and numerical solution of a Riemann–Liouville fractional derivative two-point boundary value problem. Adv. Comput. Math. 43, 77–99 (2017)

    Article  MathSciNet  Google Scholar 

  16. Lederman, C., Roquejoffre, J.M., Wolanski, N.: Mathematical justification of a nonlinear integro-differential equation for the propagation of spherical flames. Ann. Mat. Pura Ed Appl. 183(7), 173–239 (2004)

    Article  MathSciNet  Google Scholar 

  17. Liang, H., Stynes, M.: Collocation methods for general Riemann–Liouville two-point boundary value problems. Adv. Comput. Math. 45(2), 897–928 (2019)

    Article  MathSciNet  Google Scholar 

  18. Luchko, Y.: Initial-boundary-value problems for the generalized multi-term time-fractional diffusion equation. J. Math. Anal. Appl. 374(2), 538–548 (2011)

    Article  MathSciNet  Google Scholar 

  19. Lyu, P., Liang, Y., Wang, Z.: A fast linearized finite difference method for the nonlinear multi-term time-fractional wave equation. Appl. Numer. Math. 151, 448–471 (2020)

    Article  MathSciNet  Google Scholar 

  20. Magin, R.L.: Fractional calculus in bioengineering: A tool to model complex dynamics. In: Proceedings of the 13th International Carpathian Control Conference (ICCC), pp. 464–469 (2012)

  21. Marks, R., Hall, M.: Differintegral interpolation from a bandlimited signal’s samples. IEEE Trans. Acoust. Speech Signal Process. 29(4), 872–877 (1981)

    Article  Google Scholar 

  22. Nerantzaki, M.S., Babouskos, N.G.: Vibrations of inhomogeneous anisotropic viscoelastic bodies described with fractional derivative models. Eng. Anal. Bound. Elem. 36(12), 1894–1907 (2012)

    Article  MathSciNet  Google Scholar 

  23. Ogrekci, S.: Generalized taylor series method for solving nonlinear fractional differential equations with modified Riemann–Liouville derivative. Adv. Math. Phys. Article ID: 507970 (2015). https://doi.org/10.1155/2015/507970

  24. Ramirez, J.D., Denton, Z.: Generalized monotone method for multi-order 2-systems of Riemann–Liouville fractional differential equations. Nonlinear Dyn. Syst. Theory 16(3), 246–259 (2016)

    MathSciNet  MATH  Google Scholar 

  25. Song, L., Xu, S., Yang, J.: Dynamical models of happiness with fractional order. Commun. Nonlinear Sci. Numer. Simul. 15(3), 616–628 (2010)

    Article  MathSciNet  Google Scholar 

  26. Vong, S., Lyu, P., Chen, X., Lei, S.L.: High order finite difference method for time-space fractional differential equations with Caputo and Riemann–Liouville derivatives. Numer. Algorithms 72(1), 195–210 (2016)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Financial Mathematics and Statistic, Guangdong University of Finance, Guangzhou, 510521, China

    Zhendong Gu

  2. School of Accounting, Guangdong University of Finance and Economics, Guangzhou, 510320, China

    Yinying Kong

Authors
  1. Zhendong Gu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yinying Kong
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yinying Kong.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Z. Gu was supported by Guangdong Natural Science Foundation (2018A030313236), and National Natural Science Foundation of China (11971123); Y. Kong was supported by Guangdong Natural Science Foundation (2018A030313954), Guangdong University (New Generation Information Technology) Key Field Project (2020ZDZX3019), and Project of Guangdong Province Innovative Team (2020WCXTD011).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gu, Z., Kong, Y. Spectral collocation method for nonlinear Riemann–Liouville fractional differential system. Calcolo 58, 12 (2021). https://doi.org/10.1007/s10092-021-00403-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10092-021-00403-y

Keywords

Mathematics Subject Classification

Search

Navigation